Медиана треугольника чему равна: Медиана треугольника – свойство, формула, определение

Содержание

Медиана треугольника, формулы и примеры

Определение и формулы медианы треугольника

Для медиан треугольника справедливы следующие утверждения:

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Медиана разбивает треугольник на два треугольника с одинаковой площадью
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
В равнобедренном треугольнике медиана, опущенная на основание, является высотой и биссектрисой.
В равностороннем треугольнике любая медиана является высотой и биссектрисой.

Формула для вычисления медианы

где – сторона треугольника, к которой проводится медиана, – две другие стороны рассматриваемого треугольника.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

формула и свойства :: SYL.ru

Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.

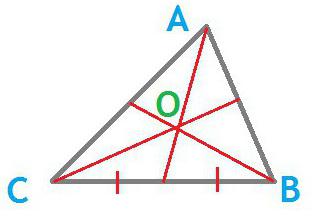
Формулы для выражения длины медианы

Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:

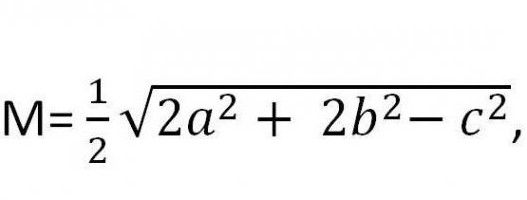
где a, b и c – стороны. Причем с является стороной, на которую медиана опускается. Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.

Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.

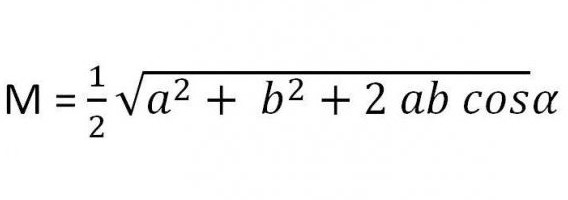
Основные свойства

Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.
В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой. Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.
Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.

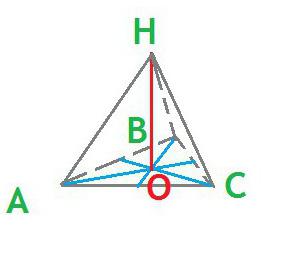
В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.

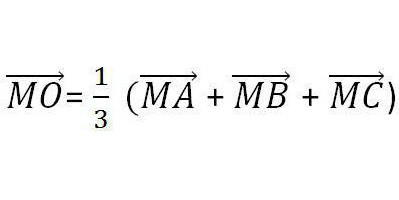
Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.

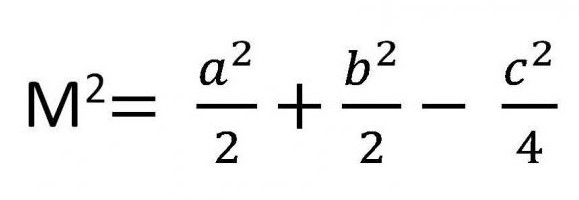
Свойства сторон, к которым проведена медиана

Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.
Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.

В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.

Медиана треугольника | Треугольники

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника, надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

Медиана треугольника — Википедия. Что такое Медиана треугольника

Материал из Википедии — свободной энциклопедии

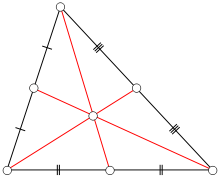Треугольник и его медианы.

Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.

Свойства

Основное свойство

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Свойства медиан равнобедренного треугольника

В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой.

Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.

Свойства оснований медиан

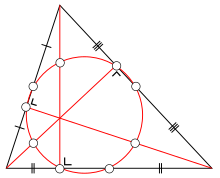Окружность девяти точек

Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией . Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.

Другие свойства

Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
Большей стороне треугольника соответствует меньшая медиана.

Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
Медиана угла треугольника изотомически сопряжена самой себе.

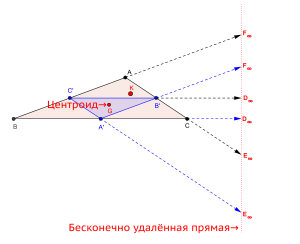Бесконечно удаленная прямая — трилинейная поляра центроида

Основные соотношения

m c = 2 a 2 + 2 b 2 − c 2 2 {\displaystyle m_{c}={\frac {\sqrt {2a^{2}+2b^{2}-c^{2}}}{2}}}

где m c {\displaystyle m_{c}} — медиана к стороне c {\displaystyle c} ; a , b , c {\displaystyle a,b,c} — стороны треугольника.

В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:

m a 2 + m b 2 + m c 2 = 3 4 ( a 2 + b 2 + c 2 ) {\displaystyle m_{a}^{2}+m_{b}^{2}+m_{c}^{2}={\frac {3}{4}}(a^{2}+b^{2}+c^{2})} .

Обратно, можно выразить длину произвольной стороны треугольника через медианы:

a = 2 3 2 ( m b 2 + m c 2 ) − m a 2 {\displaystyle a={\frac {2}{3}}{\sqrt {2(m_{b}^{2}+m_{c}^{2})-m_{a}^{2}}}} ,

где m a , m b , m c {\displaystyle m_{a},m_{b},m_{c}} медианы к соответствующим сторонам треугольника, a , b , c {\displaystyle a,b,c} — стороны треугольника.

Площадь любого треугольника, выраженная через длины его медиан:

S = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) , {\displaystyle S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}},}

где σ = ( m a + m b + m c ) / 2 {\displaystyle \sigma =(m_{a}+m_{b}+m_{c})/2} — полусумма длин медиан.

См. также

Литература

Свойство медианы прямоугольного треугольника — подготовка к ЕГЭ по Математике

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Пусть СМ — медиана прямоугольного треугольника АВС с прямым углом С.
Проведем через вершину В прямую m, параллельную катету АС.
Через вершину А проведем прямую n, параллельную катету ВС.
Прямые m и n пересекаются в точке К.

Мы получили прямоугольник АКВС (параллелограмм, в котором угол С – прямой).
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Значит, .

Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
В треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

$58 ^{\circ}$

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD = BD. Тогда

Углы ACD и DCB в сумме дают . Отсюда

Свойства медиан треугольника — подготовка к ЕГЭ по Математике

Свойство медиан треугольника. Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.

Проведем в треугольнике АВС медианы АМ и СК. Пусть АМ и СК пересекаются в точке О. Тогда МК – средняя линия треугольника АВС, и треугольник ОМК подобен треугольнику ОАС по двум углам.

. Запишем соотношение сходственных сторон треугольников ОМК и ОАС.

. Медианы АМ и СК в точке пересечения делятся в отношении 2:1, считая от вершины.

Осталась третья медиана – BK. Предположим, что . Тогда в точке медианы BK и AM делятся в отношении 2 : 1. Но если , то точка совпадает с точкой О, и это значит, что три медианы треугольника пересекаются в точке О и делятся в ней в отношении 2:1, считая от вершины.

Задача ЕГЭ по теме «Медианы треугольника»

В параллелограмме ABCD отмечена точка M — середина стороны BC. Отрезки BD и AM пересекаются в точке K. Найдите BK, если BD=18.

Пусть О — точка пересечения диагоналей параллелограмма. Диагонали параллелограмма в точке пересечения делятся пополам, поэтому ВО — медиана треугольника АВС. Тогда О – точка пересечения медиан треугольника АВС. Медианы треугольника в точке пересечения делятся в отношении 2 : 1, считая от вершины. Поэтому .

Медиана треугольника

МЕДИАНА ТРЕУГОЛЬНИКА

Слово «медиана» переводится как «равноделящая сторону». Чтобы построить медиану, надо середину стороны треугольника соединить отрезком с противолежащей вершиной треугольника. Полученный отрезок и есть медиана треугольника.

Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.

На рисунке красным цветом обозначена медиана CK. При этом она делит сторону AB треугольника пополам, AK = KB.

Свойства медианы треугольника

Все медианы треугольника пересекаются в одной точке, расположенной в плоскости треугольника и являющейся его центром тяжести.

Для определения этой точки достаточно построить две медианы треугольника, и точка их пересечения будет принадлежать третьей медиане этого треугольника.

Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1, считая от вершины треугольника. Т.е. длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины, а от точки пересечения медиан до стороны треугольника — 1/3 ее длины.
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
Большей стороне треугольника соответствует меньшая медиана.
У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.
У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

Средняя линия треугольника

Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией.

Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.

Формулы медианы произвольного треугольника

Длина медианы, проведенной к стороне произвольного треугольника равна половине квадратного корня из удвоенной суммы квадратов двух других сторон из которой вычтен квадрат стороны, к которой проведена медиана (Формула 1)
Сумма квадратов медиан треугольника равна 3/4 суммы квадратов его сторон (Формула 2)
Длина стороны треугольника равна 2/3 квадратного корня из удвоенной суммы квадратов медиан, проведенных к двум другим его сторонам за вычетом квадрата медианы, проведенной к искомой стороне (Формула 3)
Площадь треугольника можно найти через длины его медиан, используя значение полусуммы длин медиан (Формулы 4 и 5)

Содержание главы:
Площадь треугольника | Описание курса | Как найти длину медианы треугольника

Как найти медиану треугольника?

Определение:

В треугольнике медиана — это линия, соединяющая вершину со средней точкой противоположной стороны. В каждом треугольнике есть 3 медианы. Их стандарт обозначен как M _a, M _b и M _c.

Формула:

m _a = (1/2) √2c ² + 2b ² — a ² m _b = (1/2) √2c ² + 2a ² — b ² m _c = (1/2) √2a ² + 2b ² — c ² Где a, b, c — длина сторон треугольника.

Пример:

Даны точки A (1, 5), B (8, 9) и C (5, 6). Найдите медианы треугольника.

Дано:

А (1, 5) В (8, 9) С (5, 6)

Решение:

Шаг 1:

Найдите длины сторон треугольника a, b, c по формуле расстояния

d = √ (x ₂ — x ₁) ² + (y ₂ — y ₁) ²

Найдите сторону треугольника a Длина между точками B (8, 9) и C (5, 6). а = √ (5-8)

2 + (6-9) ² = 4.242

Найдите сторону треугольника b Длина между точками C (5, 6) и A (1, 5) b = √ (1-5) ² + (5-6) ² = 4,123

Найдите сторону треугольника c Длина между точками A (1, 5) и B (8, 9) c = √ (8-1) ² + (9-5) ² = 8,062

Шаг 2:

Подгруппа значений a, b, c в данной формуле m _a = (1/2) √2c ² + 2b ² — a ² m _b = (1/2) √2c ² + 2a ² — b ² m _c = (1/2) √2a ² + 2b ² — c ² м _a = (1/2) √2 (8.062) ² + 2 (4,123) ² — 4,242 ² = 6,042 м _b = (1/2) √2 (8,062) ² + 2 (4,242) ² — 4,123 ² = 6,103 м

c = (1/2) √2 (4,242) ² + 2 (4,123) ² — 8,062 ² = 1,118

Ортоцентр треугольника — определение математического слова

Ортоцентр треугольника — определение слова в математике — открытый справочник по математике Попробуйте это Перетащите оранжевые точки на любую вершину чтобы изменить форму треугольника. Обратите внимание на расположение ортоцентра.

Высота треугольника (в том смысле, в котором он здесь используется) — это линия, проходящая через вершина треугольника и перпендикулярна противоположной стороне. Следовательно, возможны три высоты, по одной от каждой вершины.См. Определение высоты.

Получается, что все три высоты всегда пересекаются в одной и той же точке — так называемом ортоцентре треугольника.

Ортоцентр не всегда находится внутри треугольника. Если треугольник тупой, он будет снаружи. Чтобы это произошло, высотные линии должны быть продлены так, чтобы они пересекались. Отрегулируйте фигуру выше и создайте треугольник, ортоцентр которого находится за пределами треугольника. Следуйте за каждой линией и убедитесь, что три высоты при правильном удлинении действительно пересекаются в ортоцентре.

Сводка центров треугольников

Есть много типов треугольных центров. Ниже приведены четыре наиболее распространенных. В случае равностороннего треугольника : все четыре из вышеперечисленных центров находятся в одной точке.

Линия Эйлера — интересный факт

Оказывается, что ортоцентр, центроид и центр описанной окружности любого треугольника равны коллинеарны — то есть, они всегда лежат на одной и той же прямой линии, называемой линией Эйлера, названной в честь ее первооткрывателя.
Для получения дополнительной информации и интерактивной демонстрации см. Определение линии Эйлера.

Построение ортоцентра треугольника

Можно построить ортоцентр треугольника с помощью циркуля и линейки. Видеть Построение ортоцентра треугольника.