Графический метод решения задач линейного программирования
1. Область решений линейных неравенств.
Пусть
задано линейное неравенство с двумя
переменными 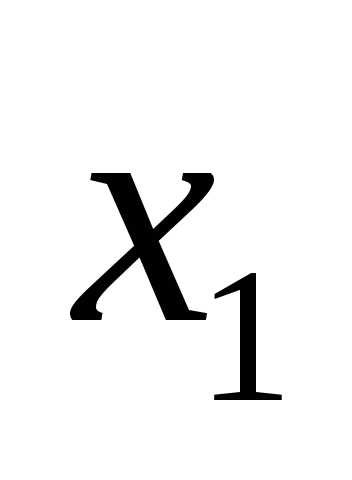 и
и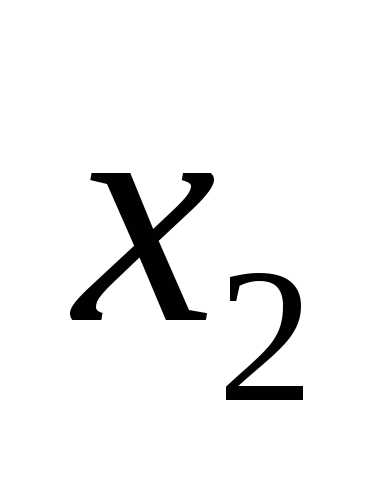
 (1)
(1)
Если
величины 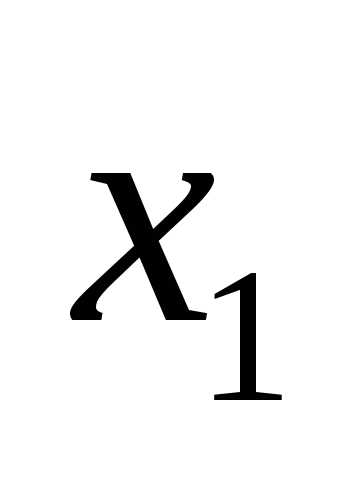 и
и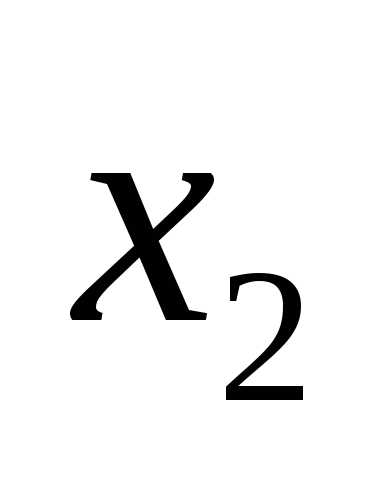 рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией.
рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией.
Пример 1. Найти полуплоскость, определяемую неравенством
.
Решение. Строим прямую по двум точкам, например, по точкам пересечения с осями координат (0; 4) и (6; 0). Эта линия делит плоскость на две части, т.е. на две полуплоскости. Берем любую точку плоскости, не лежащую на построенной прямой. Если координаты точки удовлетворяют заданному неравенству, то областью решений является та полуплоскость, в которой находится эта точка. Если же получаем неверное числовое неравенство, то областью решений является та полуплоскость, которой эта точка не принадлежит. Обычно для контроля берут точку (0; 0).
Подставим 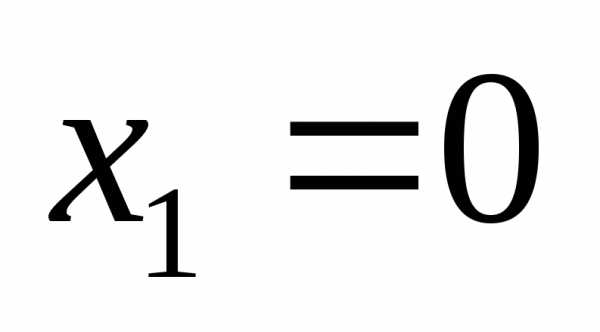 и
и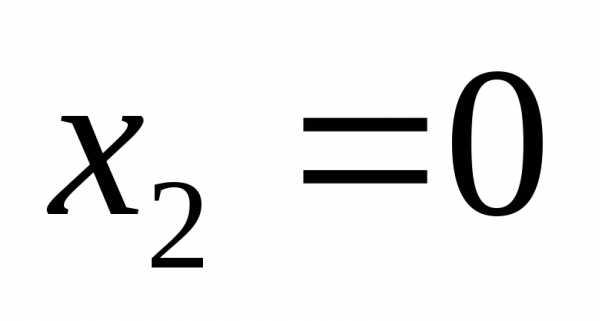
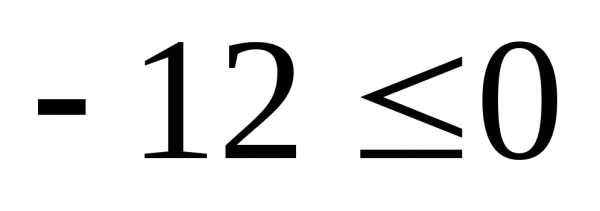 .
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).
.
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).Пример 2. Найти полуплоскость, определяемую неравенством
.
Решение.
Строим прямую
,
например, по точкам (0; 0) и (1; 3). Т.к. прямая
проходит через начало координат, точку
(0; 0), то нельзя брать ее для контроля.
Возьмем, например, точку (– 2; 0) и подставим
ее координаты в заданное неравенство.
Получим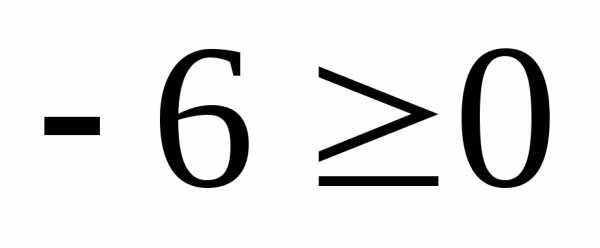 .
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).
.
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).
2. Область решений системы линейных неравенств.
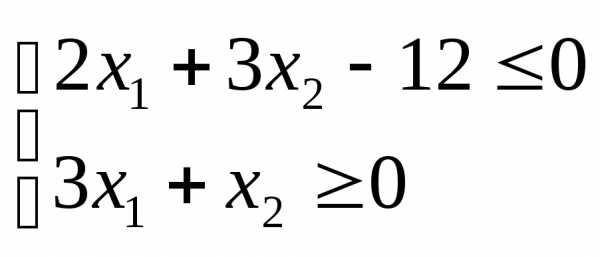
Решение. Находим область решений I-го неравенства (рис. 1) и II-го неравенства (рис. 2).
Все точки части плоскости, где штриховка наложилась, будут удовлетворять и первому и второму неравенству. Таким образом, получена область решений заданной системы неравенств (рис. 3).
Если
к заданной системе неравенств добавить
условия 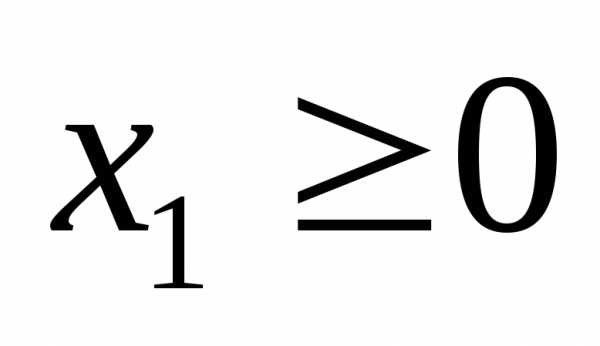 и
и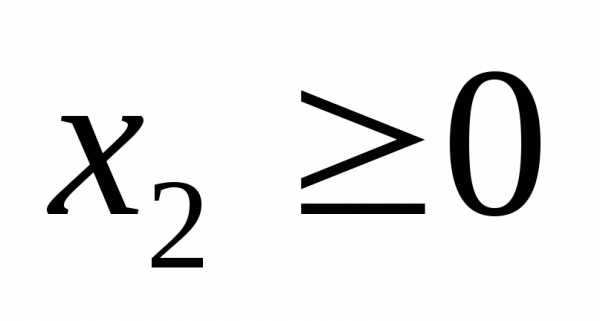 ,
то область решений системы неравенств
,
то область решений системы неравенств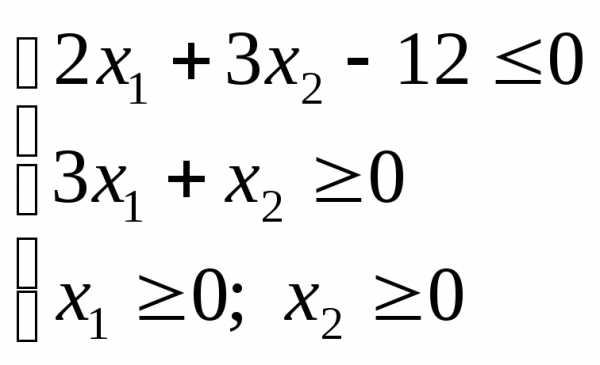 будет находиться только вI
координатной четверти (рис. 4).
будет находиться только вI
координатной четверти (рис. 4).
Принцип нахождения решения системы линейных неравенств не зависит от количества неравенств, входящих в систему.
Примечание: Область допустимых решений (ОДР) если существует, то представляет собой замкнутый или незамкнутый выпуклый многоугольник.
3. Алгоритм графического метода решения злп
Если задача линейного программирования содержит только две переменные, то ее можно решить графическим методом, выполняя следующие операции:
Строим все полуплоскости, соответствующие ограничениям системы.
Находим область допустимых решений (ОДР), как множество точек, в котором пересекаются все построенные полуплоскости.
Строим вектор
 ,
выходящий из начала координат, где
,
выходящий из начала координат, где
 – это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции.
– это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции.Перпендикулярно вектору
 проводим так называемую линию уровня
проводим так называемую линию уровня (т.е. прямую,
проходящую через начало координат).
(т.е. прямую,
проходящую через начало координат).Перемещаем линию уровня
(если задача на максимум (max)) или в противоположном направлении (если задача на минимум (min)) до тех пор, пока линия уровня имеет хотя бы одну общую точку с ОДР. параллельно самой себе в направлении
вектора
параллельно самой себе в направлении
вектора
Находим координаты
 этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.
этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.Подставляем эти координаты в целевую функцию и находим ее max (или min).
Пример. Решить задачу линейного программирования графическим методом
max
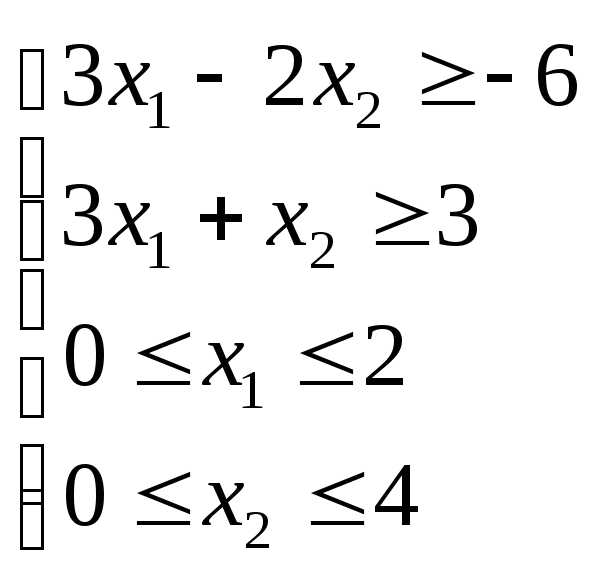
Решение.
Третье и четвертое ограничения системы
– двойные неравенства, преобразуем их
к более привычному для подобных задач
виду 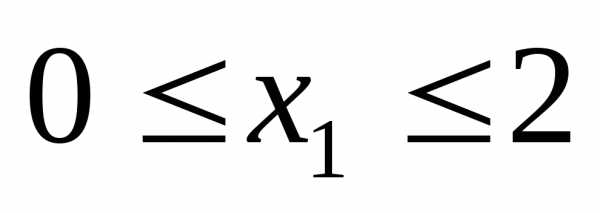
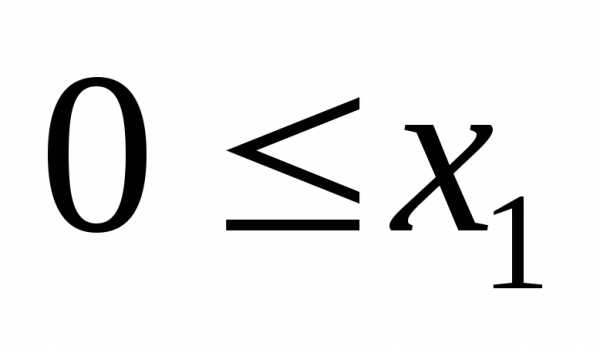 и
и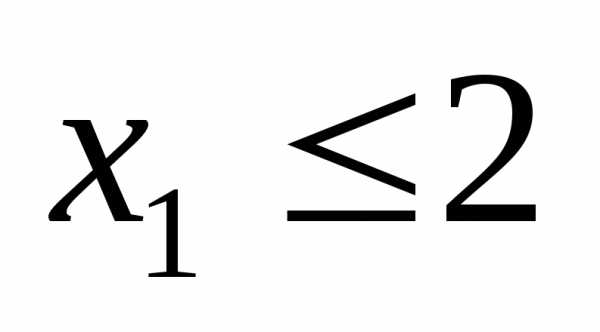 ,
т.о. первое из полученных неравенств
,
т.о. первое из полученных неравенств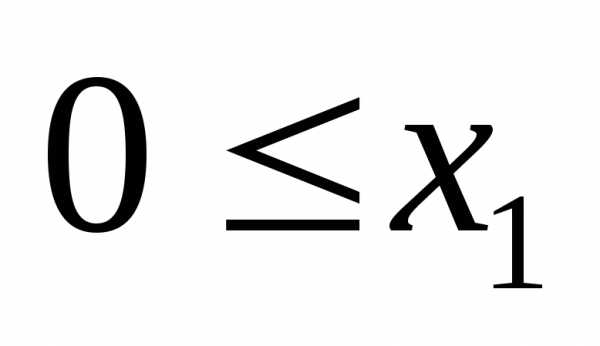 (или
(или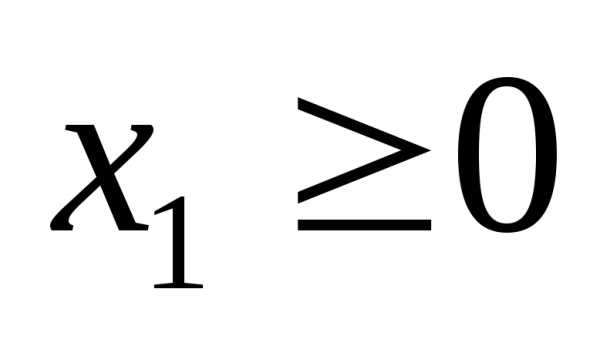 )
относится к условию неотрицательности,
а второе
)
относится к условию неотрицательности,
а второе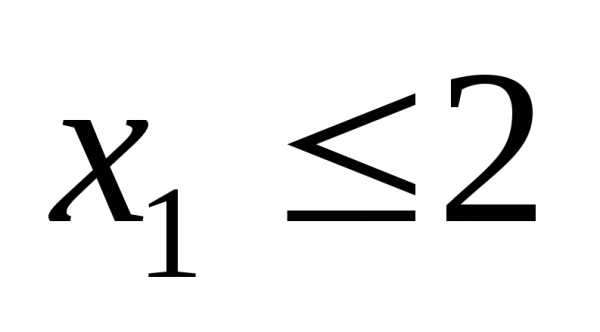 к системе ограничений. Аналогично,
к системе ограничений. Аналогично,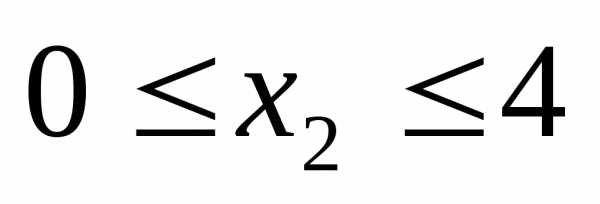 это
это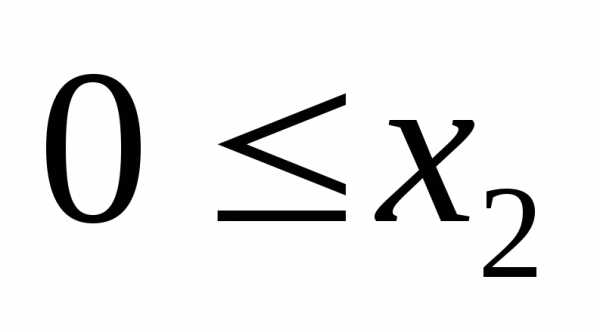 и
и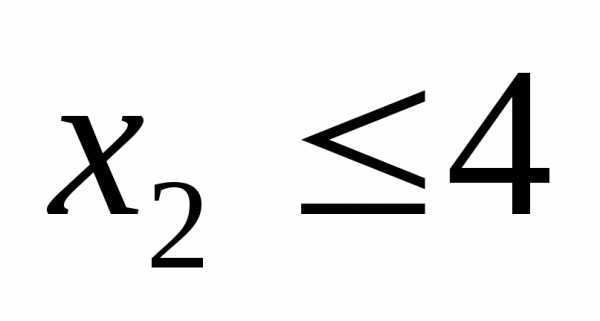 .
.Т.о. задача примет вид
max

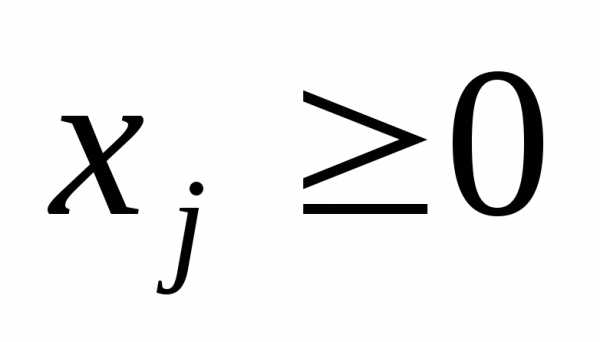 ,
, 
Заменив знаки неравенств на знаки точных равенств, построим область допустимых решений по уравнениям прямых:
;
;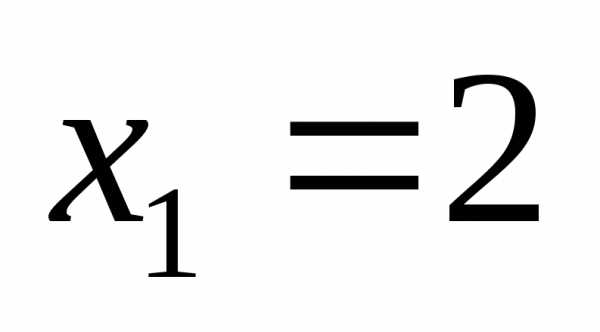 ;
;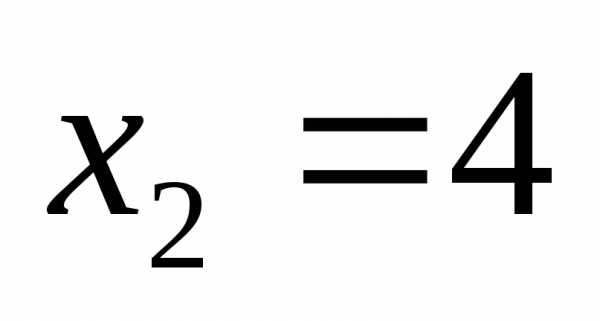
Областью решений неравенств является пятиугольник ABCDE.
Построим
вектор 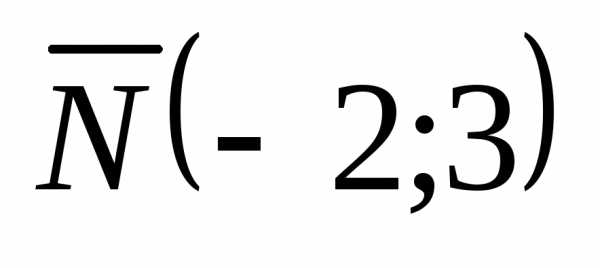 . Через
начало координат перпендикулярно
вектору
. Через
начало координат перпендикулярно
вектору  проведем линию уровня
проведем линию уровня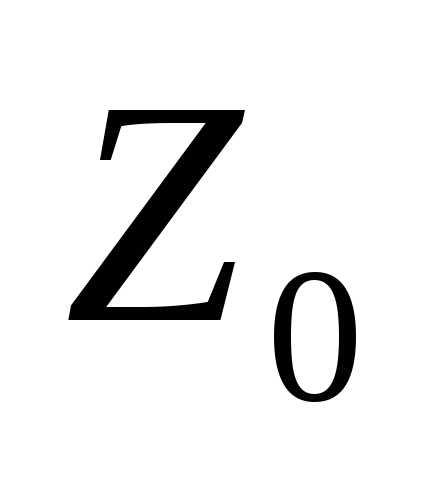 .
И затем будем перемещать ее параллельно
самой себе в направлении вектора
.
И затем будем перемещать ее параллельно
самой себе в направлении вектора до точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых:
до точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых:
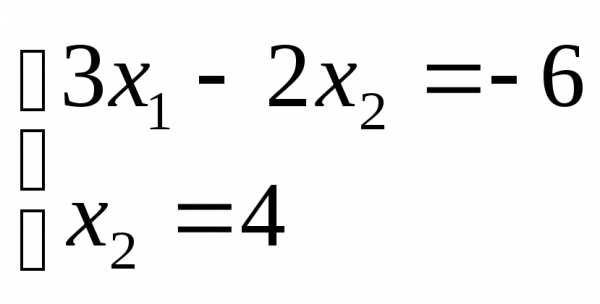

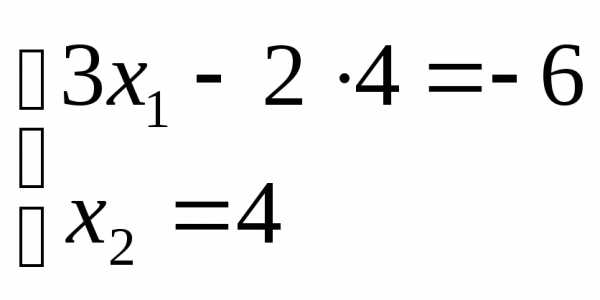

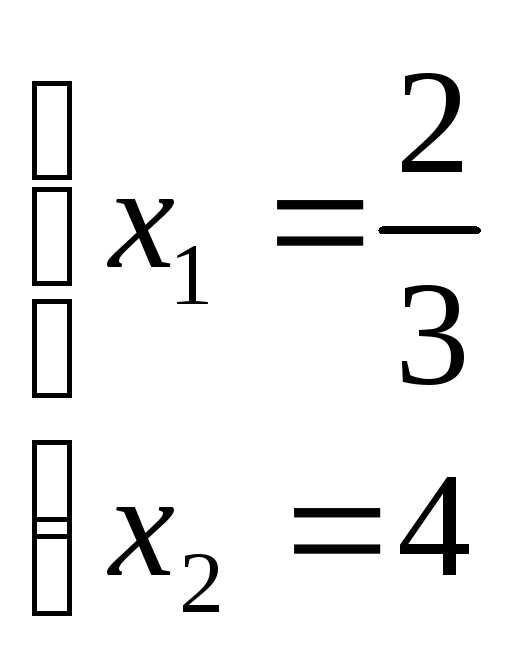

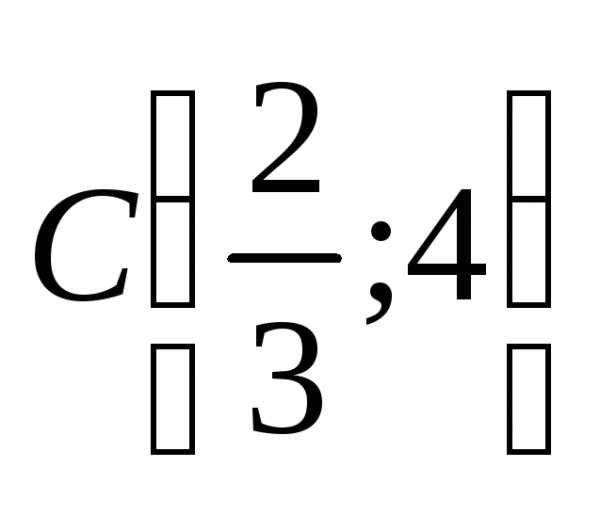 .
. Подставим
координаты точки С в целевую функцию и найдем ее максимальное
значение Пример. Построить линии уровня 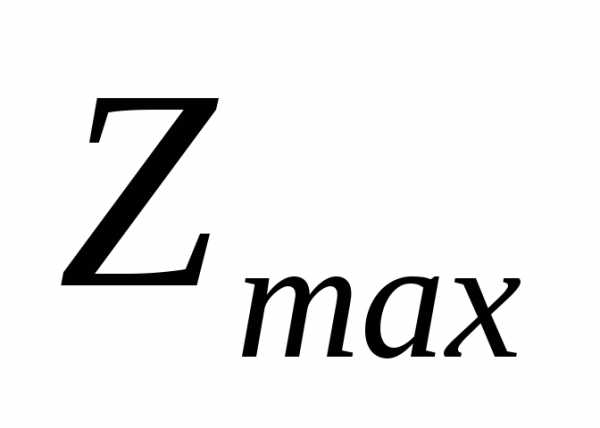 и
и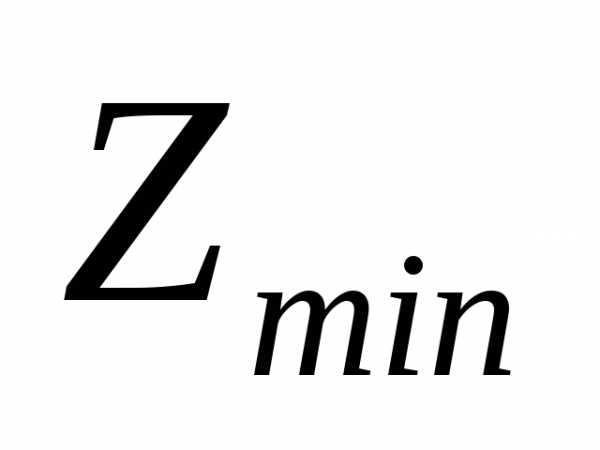
max (min)
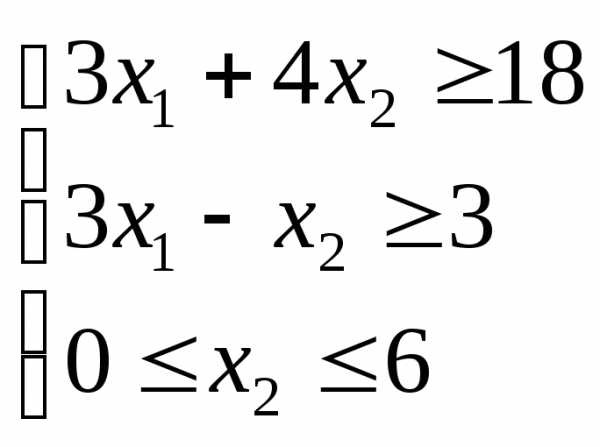
Решение.
Область допустимых решений – открытая
область (рис. 6). Линия уровня  проходит через точкуВ.
Функция Z имеет минимум в этой точке. Линию уровня
проходит через точкуВ.
Функция Z имеет минимум в этой точке. Линию уровня 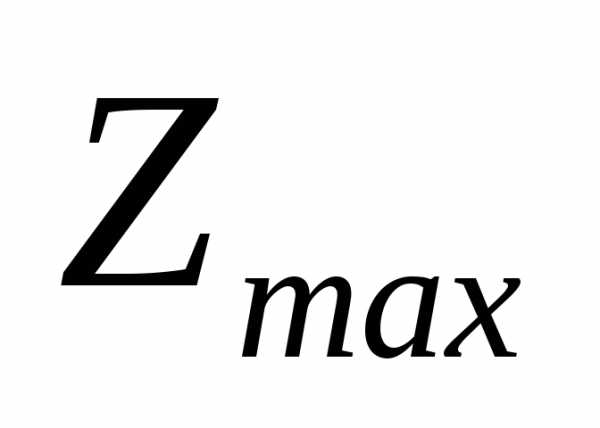 построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что
построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что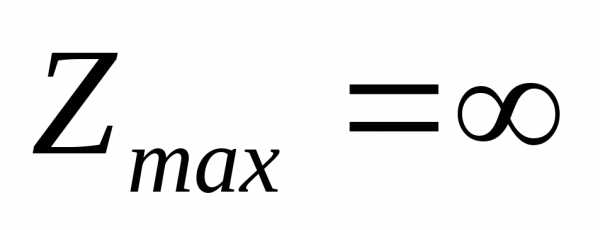 .
.
Задания для самостоятельной работы.
Найти область решений системы неравенств:
а)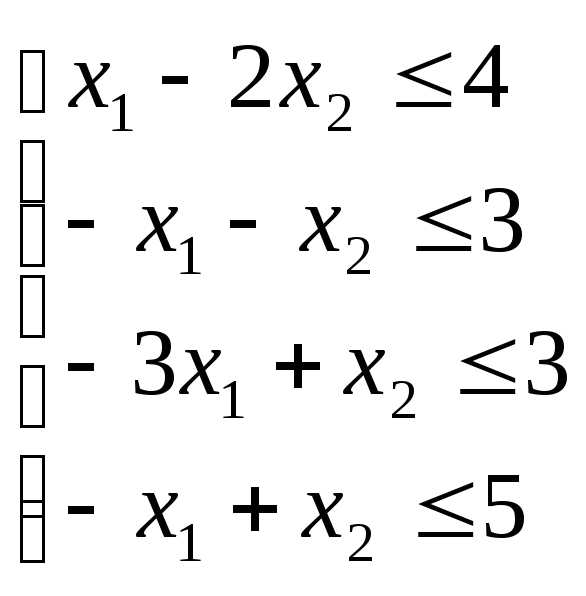 б)
б)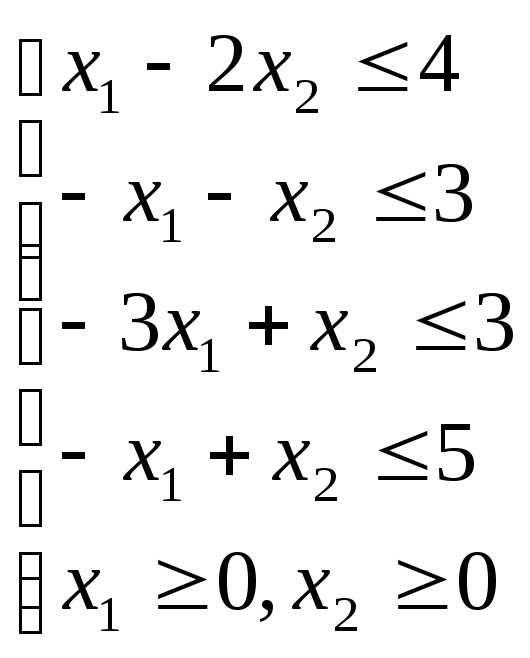
Решить графически задачу линейного программирования
min
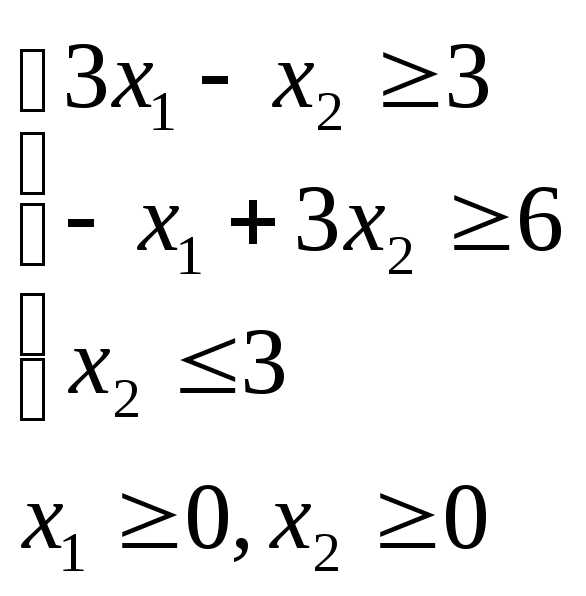
Составить экономико-математическую модель и решить графически задачу линейного программирования
Фирма выпускает изделия двух видов А и В. Изделия каждого вида обрабатывают на двух станках (I и II). Время обработки одного изделия каждого вида на станках, время работы станков за рабочую смену, прибыль фирмы от реализации одного изделия вида А и вида В занесены в таблицу:
Станки | Время обработки одного изделия, мин. | Время работы станка за смену, мин. | |
А | В | ||
I | 10 | 20 | 1300 |
II | 4 | 13 | 720 |
Прибыль от одного изделия, грн. | 0,3 | 0,9 | |
Изучение рынка сбыта показало, что ежедневный спрос на изделия вида В никогда не превышает спрос на изделия вида А более чем на 40 единиц, а спрос на изделия вида А не превышает 90 единиц в день.
Определить план производства изделий, обеспечивающий наибольшую прибыль.
studfiles.net
Системы линейных неравенств и выпуклые множества точек
Неравенство — это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту полуплоскость, а в случае системы линейных неравенств — часть плоскости, ограниченную несколькими прямыми, требуется найти на чертеже.
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования, в которых требуется найти максимум или минимум функции.
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1). Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу после этого теретического экскурса.
Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :
Подставляя значение в первое уравнение, получаем
, откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .
Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:
Решение:
,
следовательно, координаты точки B: .
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две части, лежащие справа и слева (выше и ниже) от этой прямой.
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств, то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение. Начертим прямую
Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A(3; 0), B(0; 2). Через эти точки проведём прямую (опять рисунок 1).
Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0):
,
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
,
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Решением системы линейных неравенств называется любая пара чисел (), удовлетворяющая всем неравенствам данной системы.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае — может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2. Решить систему линейных неравенств
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую , и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.
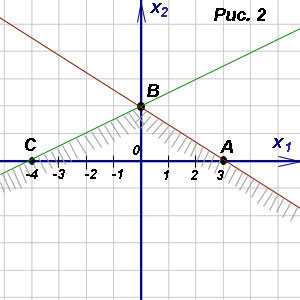
Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC. Это означает, что множество точек плоскости, составляющих открытый угол ABC, является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы. Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).
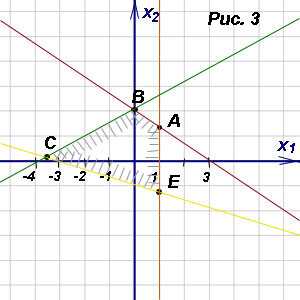
Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE. Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE.
Всё описанное выше о системах линейных неравенств с двумя неизвестными относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением неравенства с n неизвестными будет совокупность n чисел (), удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость n-мерного пространства. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.
Так же, как и в двухмерном пространстве (на плоскости), каждое из неравенств системы определяет n-мерное полупространство. Пересечение всех этих полупространств образует многогранник решений. Но изобразить этот многогранник (называемый симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть в действительном пространстве, многогранник решений можно изобразить геометрически.
Множество решений линейных неравенств геометрически составляет выпуклый многогранник или выпуклое множество точек.
Как уже отмечалось, системы линейных неравенств играют важную роль в линейном программировании. Теоремы линейного программирования содержат такие понятия, как выпуклые множества и крайние точки. Разберёмся бегло, о чём речь.
Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их. Если же существует хотя бы такая пара точек множества, что отрезок, соединяющий эти точки, не принадлежит целиком этому множеству, то такое множество называется невыпуклым. На рисунке 4 слева изображено выпуклое множество, а справа — невыпуклое.
Выпуклые множества обладают важным свойством, которое устанавливается следующей теоремой.
Теорема. Пересечение двух выпуклых множеств — также выпуклое множество.
Через любую внутреннюю точку выпуклого множества можно провести отрезок, для которого она является внутренней, а сам отрезок целиком принадлежит этому множеству. Но есть точки (для выпуклого многоугольника это его вершины), для которых такое построение выполнить нельзя: нет ни одного отрезка, для которого вершина являлась бы внутренней, а отрезок целиком бы принадлежал мноргоугольнику.
Точка выпуклого множества называется угловой (или крайней), если через неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.
Продолжение темы «Систем уравнений и неравенств»
Начало темы «Линейная алгебра»
Поделиться с друзьями
function-x.ru
7. Множества точек на плоскости, задаваемые уравнениями
и неравенствами с двумя переменными
Пусть на плоскости выбрана система координат. Тогда любое уравнение с двумя переменными F(x;y) = 0 задает множество точек на плоскости, а именно множество точекM(x;y), координатыкоторых удовлетворяют этому уравнению.
Например, точка M(– 3; 4) принадлежит множеству, заданному уравнениемx2+y2= 25, а точкаN(1; 6) не принадлежит этому множеству, так как (–3)2+ 42= 25, а 12+ 62≠ 25. В этом легко убедиться, если построить график данного уравнения в декартовой системе координат (рис. 7.1). Геометрическим местом всех точек, принадлежащих этому множеству, является окружностьR= 5 с центром в начале координат.
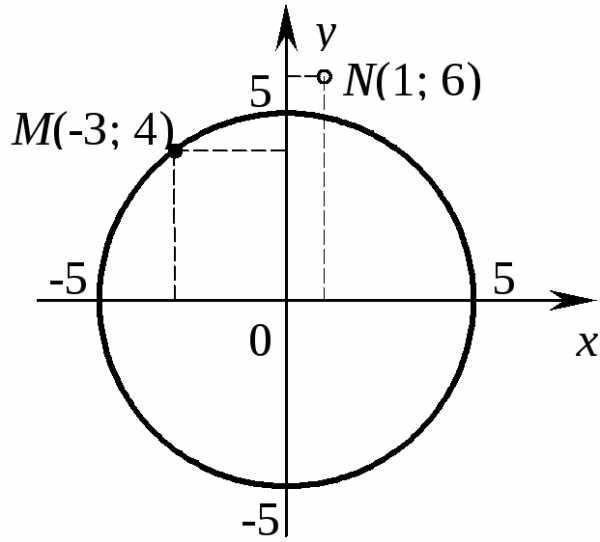
Рис. 7.1
Если мы рассмотрим множество, заданное в виде неравенства x2+y2< 25, то множеством будут являться все точки, находящиеся внутри этой окружности (рис.7.2). Сама окружность изображена пунктиром, чтобы показать, что точки, принадлежащие самой окружности (границе области) в данном случае на нее не попадают и точкаM(– 3; 4)множествуx2+y2< 25 (области), в чем легко убедится, а точкаN(1; 2){x2+y2< 25}.
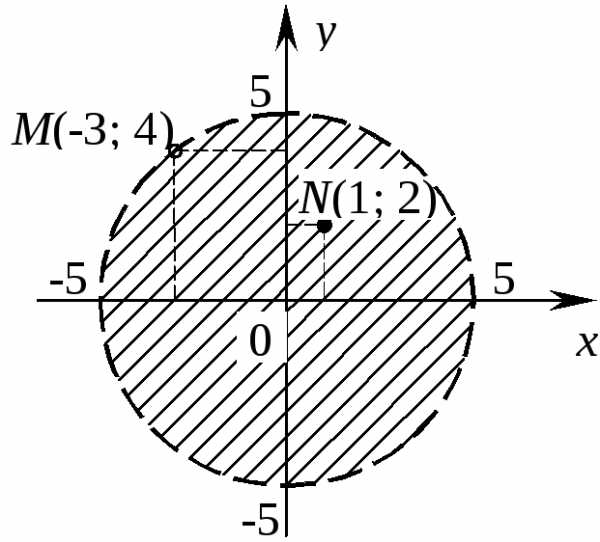
Рис. 7.2
Если же x2+y2≤ 25, то здесь уже войдет и граница (сама окружность). Изобразим ее жирной линией (рис. 7.3).
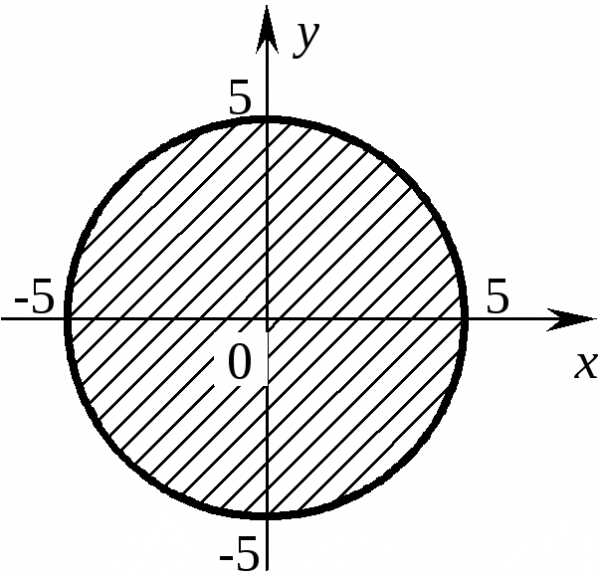
Рис. 7.3
То же касается систем линейных неравенств.
Пример.Построить область допустимых решений системы линейных неравенств.
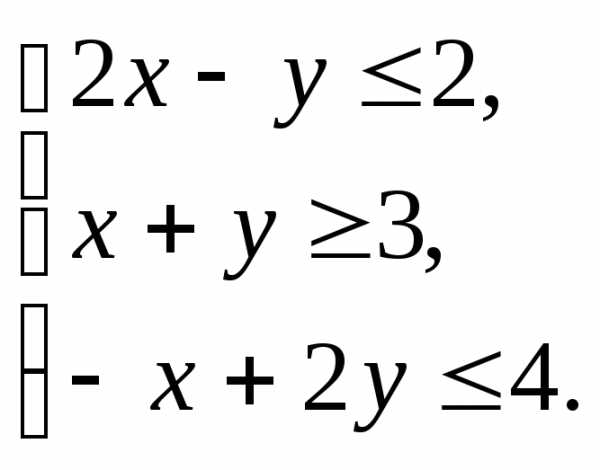
Решение.Нумеруем ограничения задачи
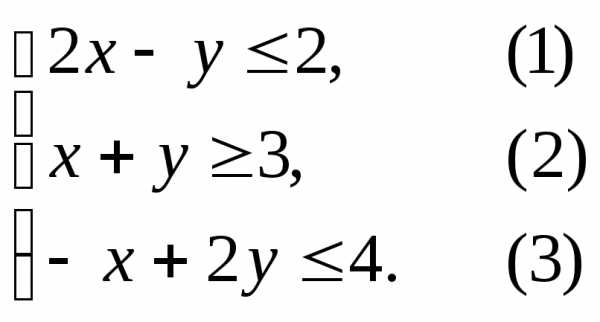
В прямоугольной декартовой системе координат (рис. 7.4) строим прямую 2x – y = 2, соответствующую ограничению (1).
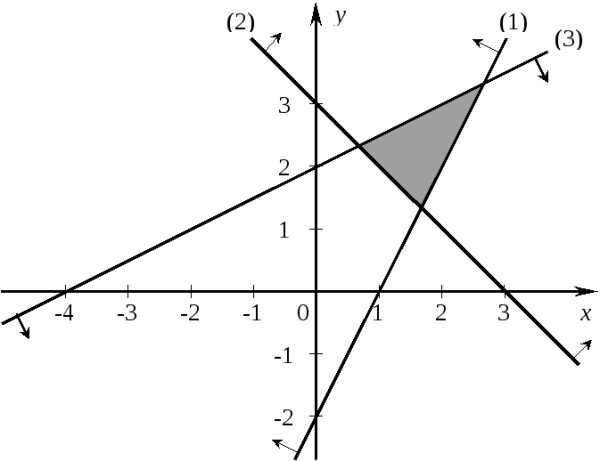
Рис. 7.4
Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решения неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая (1) не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение: 2·0 – 0 < 2. Получаем строгое неравенство 0 < 2. Следовательно, точкаОлежит в полуплоскости решений. Таким образом, стрелки на концах прямой (1) должны быть направлены в полуплоскость, содержащую точкуО.
Аналогично строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и (3).
Находим общую часть полуплоскостей решений. Полученную область допустимых решений отмечаем на рис. 7.4 штриховкой. В этой области находятся все точки M(x;y), в которых выполняются все три неравенства системы. ◄
Задание 3
Решить неравенство (а) и систему неравенств (б).
3.1.а) б) | 3.2.а) б) |
3.3.а) б) | 3.4.а) б) |
3.5.а) б) | 3.6.а) б) |
3.7.а) б) | 3.8.а); б) |
3.9.а) б) | 3.10.а) б) |
3.11.а) б) | 3.12.а) б) |
3.13.а) б) | 3.14.а) б) |
3.15.а) б) | 3.16.а) б) |
3.17.а) б) | 3.18.а); б) |
3.19.а) б) | 3.20.а) б) |
3.21.а) б) | 3.22.а) б) |
3.23.а) б) | 3.24.а) б) |
3.25.а); б) | 3.26.а) б) |
3.27.а) б) | 3.28.а) б) |
3.29.а) б) | 3.30.а) б) |
studfiles.net
Линейное математическое программирование, страница 7
В данном случае неравенство в контрольной точке не выполняется. Значит, оно выполняется в противоположной плоскости на рис.4.1 (заштрихована).
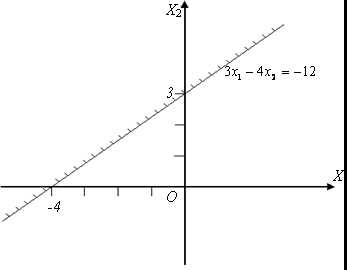 |
Рис. 4.1
2. .
Прямая проходит через начало координат. За вторую точку можно взять любую, лежащую на прямой, например А (2;3)
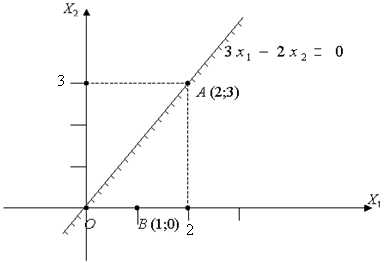 |
Рис. 4.2
В качестве контрольной точки возьмём любую не лежащую на прямой, Например В(1;0).
В этой точке 3–2∙0 > 0 неравенство выполняется. Значит область решений неравенства – нижняя полуплоскость (заштрихована, рис.4.2).
Множество точек, удовлетворяющих уравнению при является плоскостью, при – гиперплоскостью. В этом случае теорему о решении неравенства, содержащего n неизвестных можно обобщить следующим образом.
Теорема.
Область решения неравенства с n переменными есть одно из полупространств, на которые все пространство делится гиперплоскостью , включая и эту гиперплоскость.
4.2. Множество решений системы неравенств.
Множеством решений системы линейных неравенств являются точки, которые принадлежат полуплоскостям решений всех неравенств, т.е. принадлежат их пересечению.
Рассмотрим конкретный пример.
Пример 4.2.
Построить множество решений системы неравенств.
Для определения множества решений системы неравенств строим последовательно множество решений каждого неравенства.
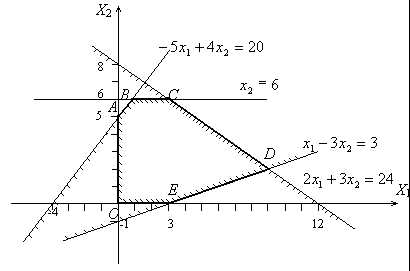 |
Рис.4.3
В рассматриваемом примере областью решений системы неравенств является так называемый выпуклый многоугольник.
Выпуклой фигурой называется фигура, обладающая следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. Координаты угловых точек – вершин этого многоугольника найдём как координаты точек пересечения соответствующих прямых.
Например, координаты точки D найдём, решая совместно систему уравнений
При построении области решений системы неравенств могут встретится и другие случаи:
— многоугольная область (рис.4.4.)
Рис. 4.4
— одна точка (рис.4.5)
Рис.4.5
— пустое множество, когда система неравенств несовместна (рис. 4.6)
vunivere.ru
Метод областей на координатной плоскости
Для изображения на координатной плоскости Оху множества решений уравнений и неравенств с двумя переменными и их систем используется построение на координатной плоскости множества точек, у которых координаты удовлетворяют данным уравнениям, неравенствам, системам.
При решении неравенства f(x; у) ≥ 0, равносильного смешанной совокупности
применяется метод областей, являющийся обобщением метода интервалов на случай двух переменных. Для этого вначале находят все нули выражения f(x; у), то есть все такие точки, координаты которых удовлетворяют уравнению f(x; у) =0. В общем случае уравнение f(x; у)=0 задает некоторую кривую (или несколько кривых) на плоскости Оху. Полученные кривые разбивают плоскость на множества, для координат всех точек которых выражение f(x;у) имеет постоянный знак. Далее отбирают требуемые подмножества, у которых координаты точек удовлетворяют неравенству f(x;у) >0. Это можно сделать подстановкой координат произвольной точки из рассматриваемого подмножества в выражение f(x; у).
Простейшим является случай, когда f(x;у)=Ах +By+С, где А2+В2>0, то есть числа А и В одновременно не обращаются в нуль. Уравнение Ах+By+С=0 задает прямую, которая разбивает координатную плоскость на две полуплоскости, для координат точек одной из которых выполняется неравенство Ах+ By+С> 0, а в другой — неравенство Ах+Ву+С< 0.
Уравнение (х-а)2+(у-b)2=R2, где a, b, R — заданные числа, причем R>0, задает на координатной плоскости окружность С радиуса R с центром в точке (а; b), а неравенствам (х-а)2 +(у-b)2<R2 и (х-а)2+ (у-b)2>R2 удовлетворяют все те и только те точки, которые расположены соответственно внутри области, ограниченной окружностью С, и снаружи.
Рассмотрим задачи построения на координатной плоскости множества точек, у которых координаты удовлетворяют уравнению f(x; у) = 0.
belmathematics.by
2.2. Графическое решение системы линейных неравенств
Для графического решения данной задачи необходимо уметь решать графически системы линейных неравенств с двумя переменными.
Сначала дадим геометрическое истолкование линейного неравенства.
Решением линейного неравенства с двумя переменными называется множество пар значений переменных
 ,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
.
,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
.
Порядок действий:
записать уравнение и построить на плоскости граничную прямую;
выбрать искомую полуплоскость, координаты точек в которой удовлетворяют заданному неравенству. Для этого подставляют в неравенство координаты точки с известными координатами ,не лежащей на граничной прямой. Если получится верное числовое неравенство, то искомая полуплоскость та, которая содержит точку
 (в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.
(в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.

0 
Отметим, что
неравенство 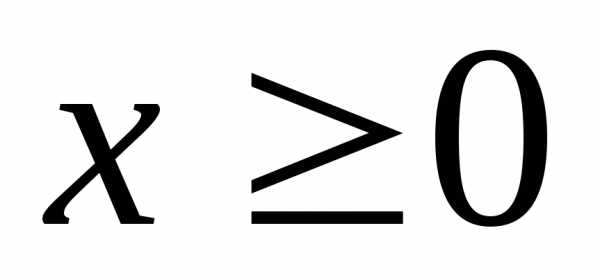 определяетправую
координатную полуплоскость (от оси
определяетправую
координатную полуплоскость (от оси 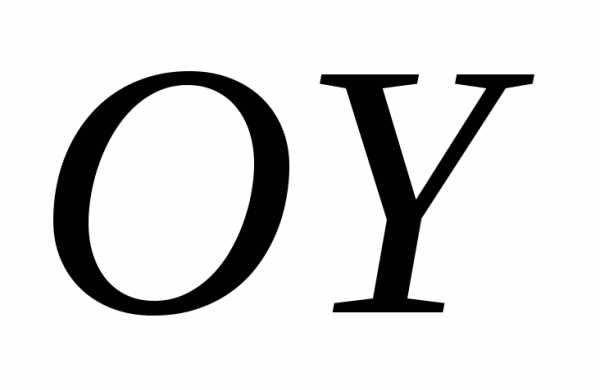 ),
а неравенство
),
а неравенство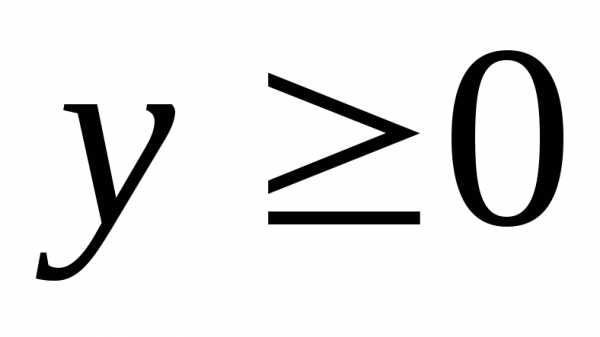 —верхнюю
координатную полуплоскость (от
оси
—верхнюю
координатную полуплоскость (от
оси  ).
).
Пример 2. Решить графически неравенство .
Запишем уравнение
граничной прямой
и построим ее по двум точкам, например,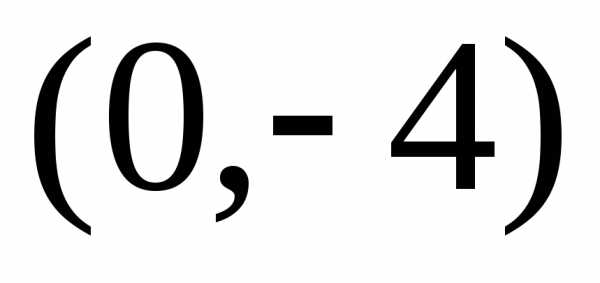 и
и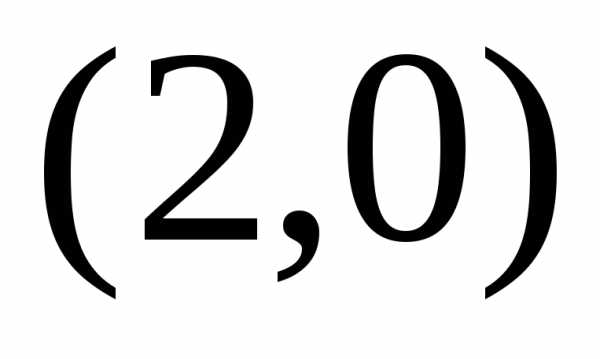 .
Прямая делит плоскость на две полуплоскости.
.
Прямая делит плоскость на две полуплоскости.

0 2 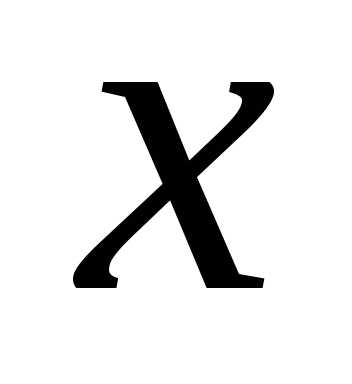
-4
Координаты точки 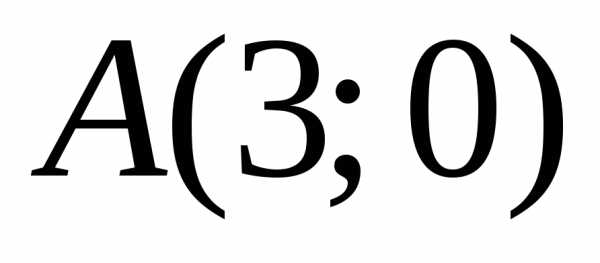 удовлетворяют неравенству(
удовлетворяют неравенству(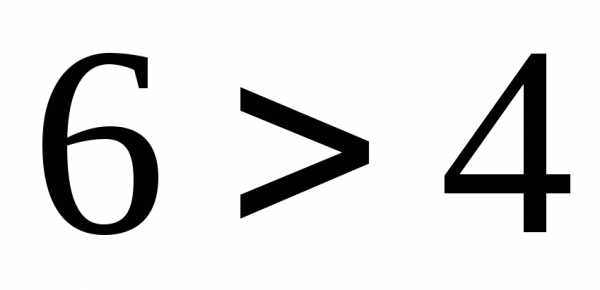 – верно), значит, и координаты всех точек
полуплоскости, содержащей точку
– верно), значит, и координаты всех точек
полуплоскости, содержащей точку 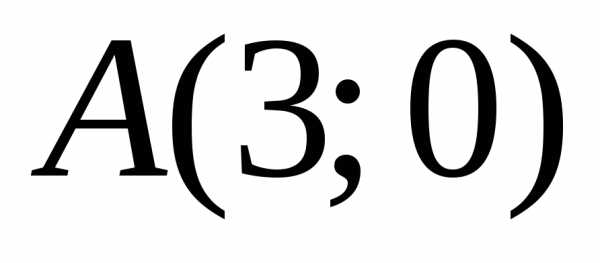 ,
удовлетворяют неравенству. Решением
неравенства будут координаты точек
полуплоскости, расположенной справа
от граничной прямой,
включая точки на границе. Искомая
полуплоскость на рисунке выделена.
,
удовлетворяют неравенству. Решением
неравенства будут координаты точек
полуплоскости, расположенной справа
от граничной прямой,
включая точки на границе. Искомая
полуплоскость на рисунке выделена.
Решение 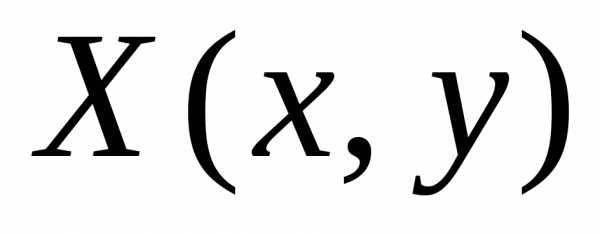 системы неравенств называетсядопустимым,
если его координаты неотрицательны
системы неравенств называетсядопустимым,
если его координаты неотрицательны 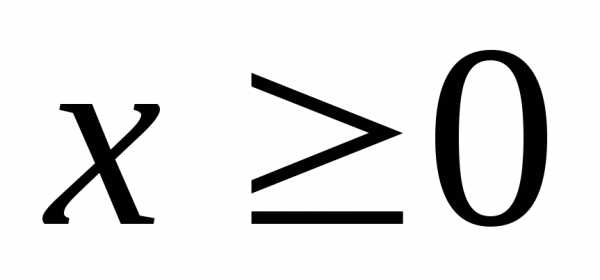 ,
,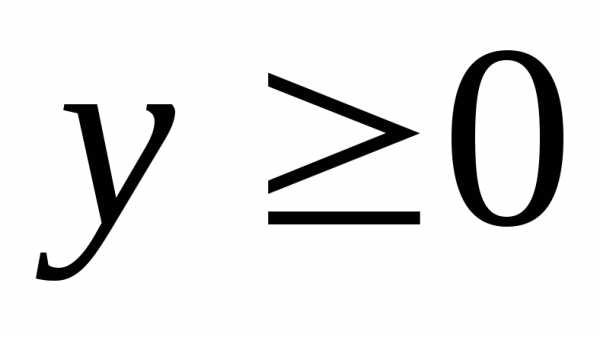 .
Множество допустимых решений системы
неравенств образует область, которая
расположена в первой
четверти координатной плоскости.
.
Множество допустимых решений системы
неравенств образует область, которая
расположена в первой
четверти координатной плоскости.
Пример 3. Построить область решений системы
неравенств 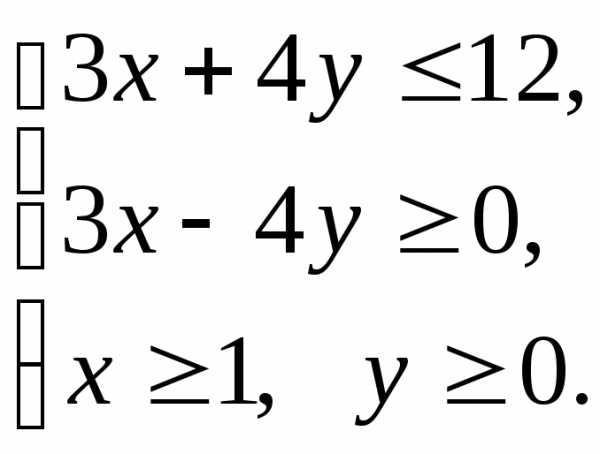
Решениями неравенств является:
1)
— полуплоскость, расположенная левее и
ниже относительно прямой (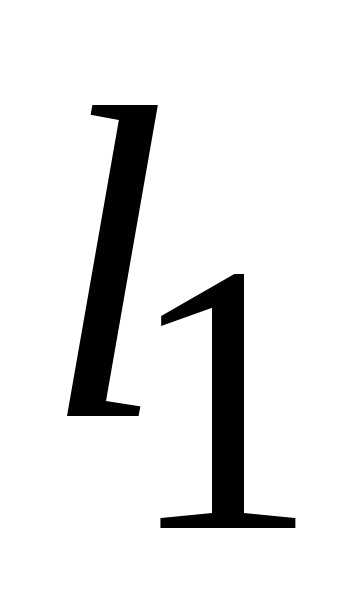 );
);
2)
– полуплоскость, расположенная в
правой-нижней полуплоскости относительно
прямой ( );
);
3)  — полуплоскость, расположенная правее
прямой (
— полуплоскость, расположенная правее
прямой (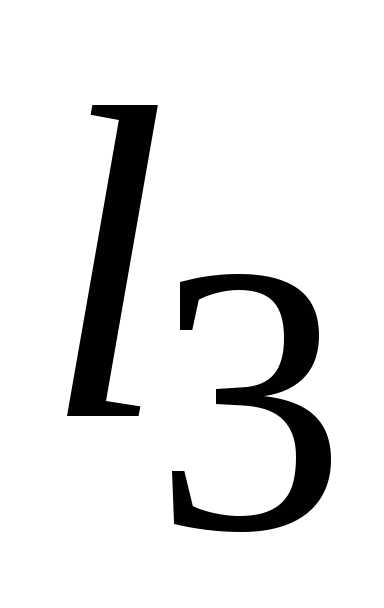 )
)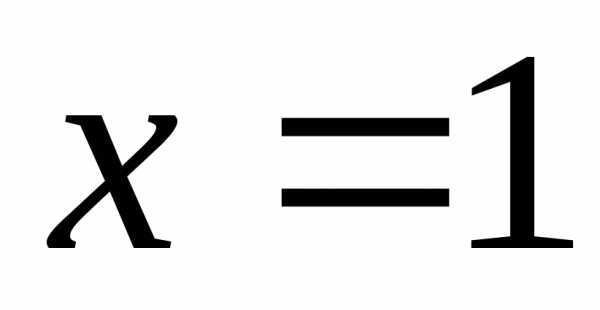 ;
;
4) 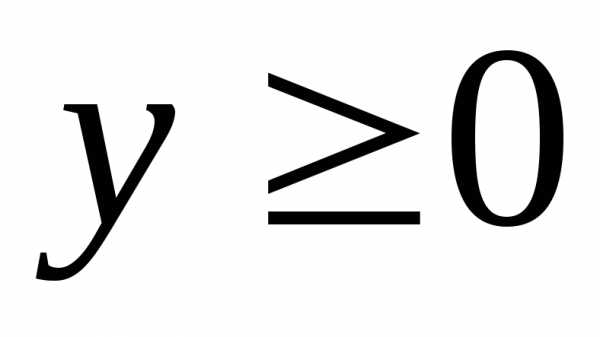 — полуплоскость выше оси абсцисс, то
есть прямой (
— полуплоскость выше оси абсцисс, то
есть прямой ( )
) 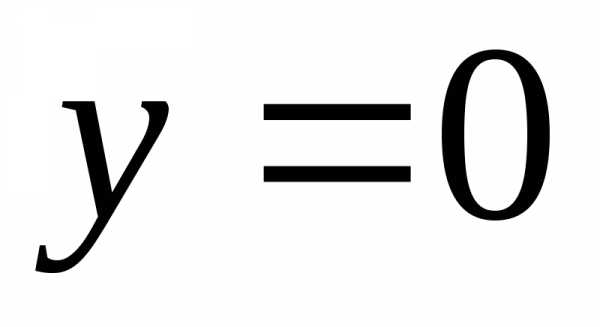 .
.

3 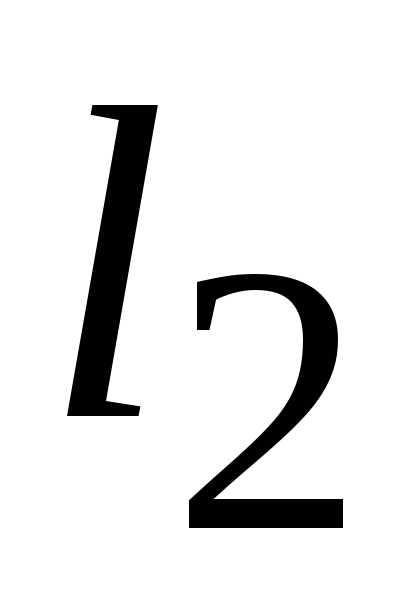

1
B
 0
0 
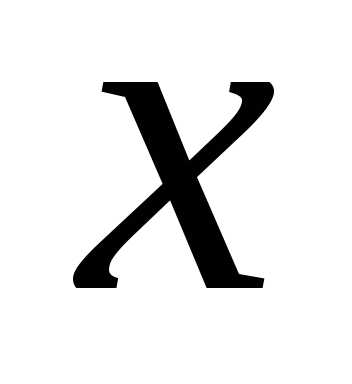
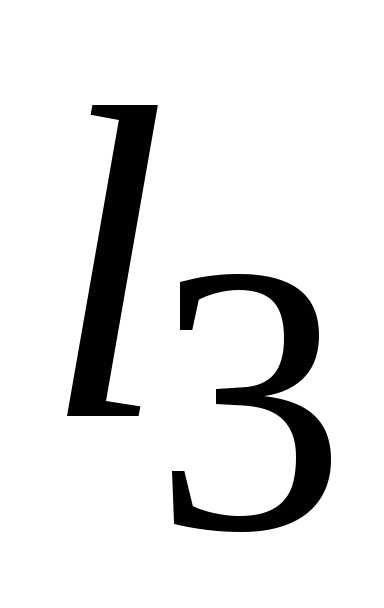
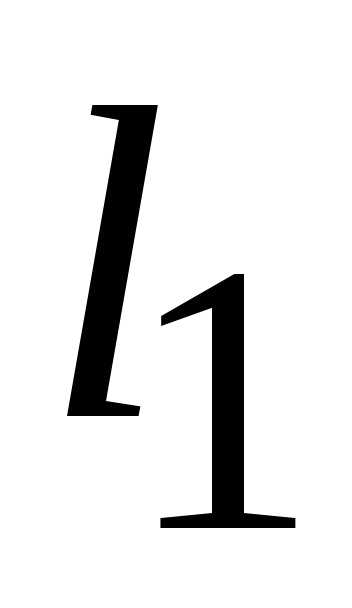
Область допустимых
решений данной системы линейных неравенств –
это множество точек, расположенных
внутри и на границе четырехугольника 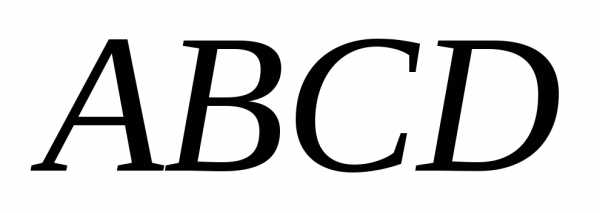 ,
являющегосяпересечением четырех полуплоскостей.
,
являющегосяпересечением четырех полуплоскостей.
studfiles.net
Задание фигур на координатной плоскости уравнениями и неравенствами
Пусть задано уравнение с двумя переменными F(x; y). Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.
Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.
Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a)2 + (y – b)2 = R2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).
Пример 1.
Построить график уравнения x2 – 9y2 = 0.
Решение.
Разложим на множители левую часть уравнения.
(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.
Ответ: рисунок 1.
Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Первое уравнение равносильно системе
{f(x) ≥ 0,
{y = f(x) или y = -f(x).
То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.
Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).
Пример 2.
Построить график уравнения |y| = 2 + x.
Решение.
Заданное уравнение равносильно системе
{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.
Строим множество точек.
Ответ: рисунок 2.
Пример 3.
Построить график уравнения |y – x| = 1.
Решение.
Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.
Ответ: рисунок 3.
При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей, основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.
Пример 4.
Построить график уравнения x + |x| + y + |y| = 2.
Решение.
В данном примере знак каждого подмодульного выражения зависит от координатной четверти.
1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:
2x + 2y = 2, а после упрощения x + y = 1.
2) Во второй четверти, где x < 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.
3) В третьей четверти x < 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.
4) В четвертой четверти, при x ≥ 0, а y < 0 получим, что x = 1.
График данного уравнения будем строить по четвертям.
Ответ: рисунок 4.
Пример 5.
Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.
Решение.
Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.
| Область | Знак подмодульного выражения | Полученное уравнение после раскрытия модуля |
| I | x ≥ 1 и y ≥ 1 | x + y = 3 |
| II | x < 1 и y ≥ 1 | -x + y = 1 |
| III | x < 1 и y < 1 | x + y = 1 |
| IV | x ≥ 1 и y < 1 | x – y = 1 |
Ответ: рисунок 5.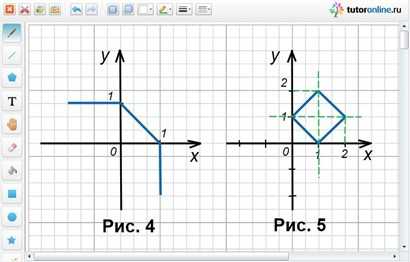
На координатной плоскости фигуры могут задаваться и неравенствами.
Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.
Рассмотрим алгоритм построения модели решений неравенства с двумя переменными:
- Записать уравнение, соответствующее неравенству.
- Построить график уравнения из пункта 1.
- Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
- Изобразить графически множество всех решений неравенства.
Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.
1) ax + bx + c ≥ 0. Рисунок 6.
2) |x| ≤ a, a > 0. Рисунок 7.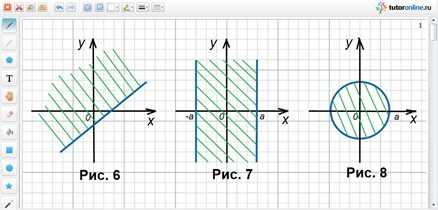
3) x2 + y2 ≤ a, a > 0. Рисунок 8.
4) y ≥ x2. Рисунок 9.
5) xy ≤ 1. Рисунок 10.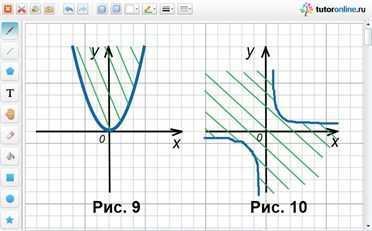
Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь. Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.
Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru

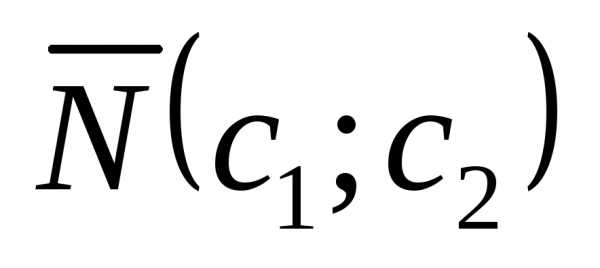 ,
выходящий из начала координат, где
,
выходящий из начала координат, где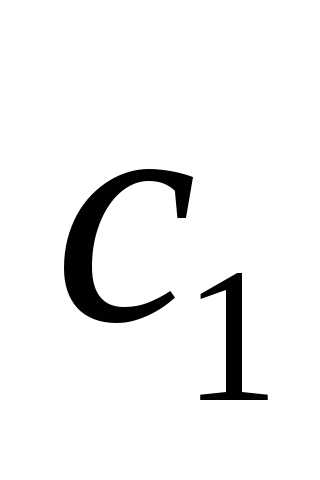
 – это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции.
– это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции. проводим так называемую линию уровня
проводим так называемую линию уровня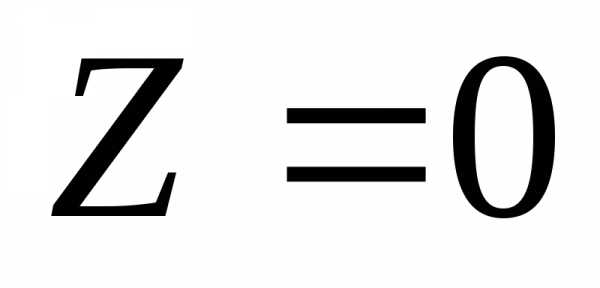 (т.е. прямую,
проходящую через начало координат).
(т.е. прямую,
проходящую через начало координат).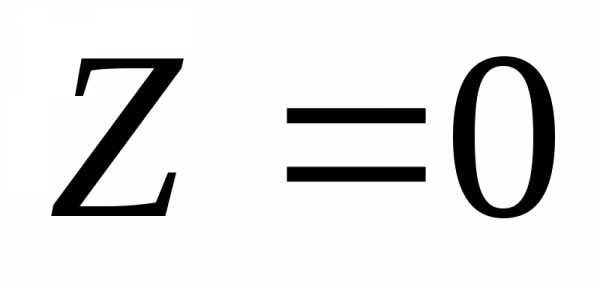 параллельно самой себе в направлении
вектора
параллельно самой себе в направлении
вектора
 этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.
этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится.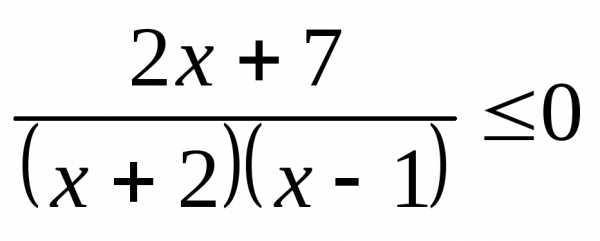 ;
;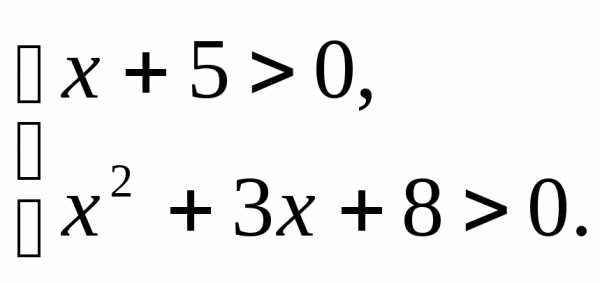
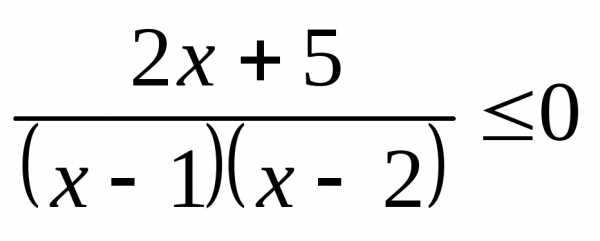 ;
;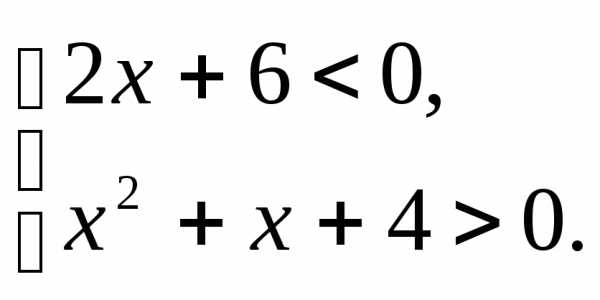
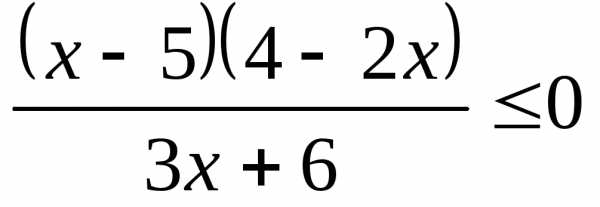 ;
;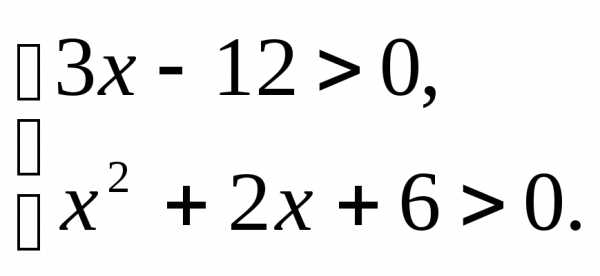
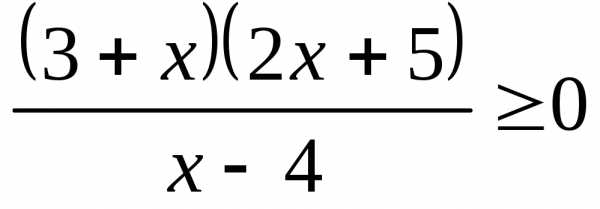 ;
;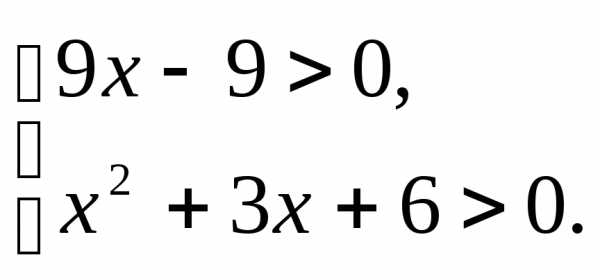
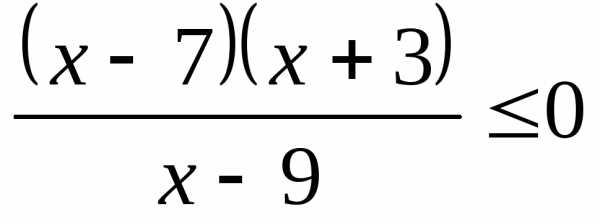 ;
;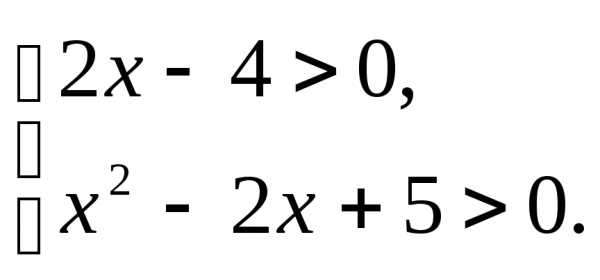
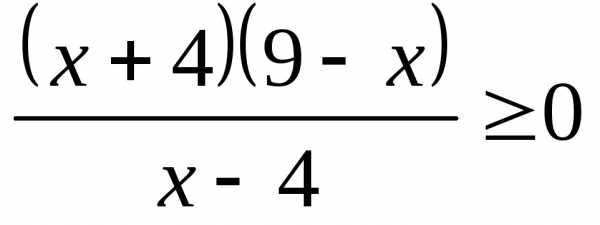 ;
;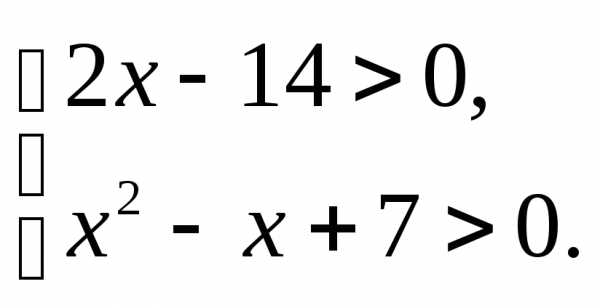
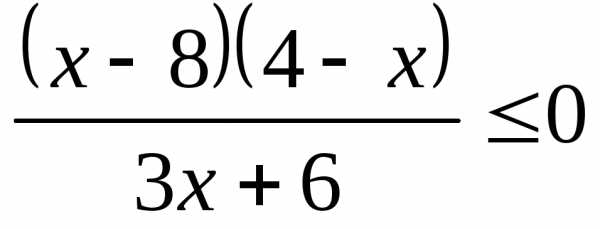 ;
;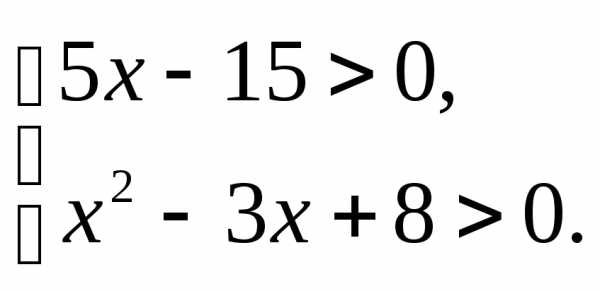
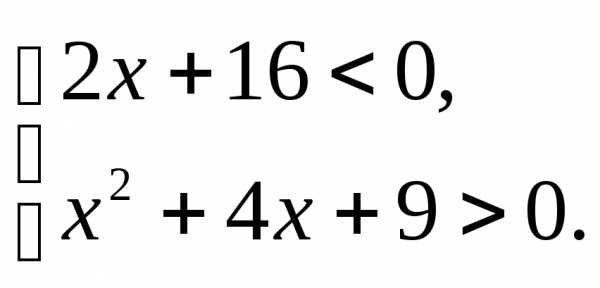
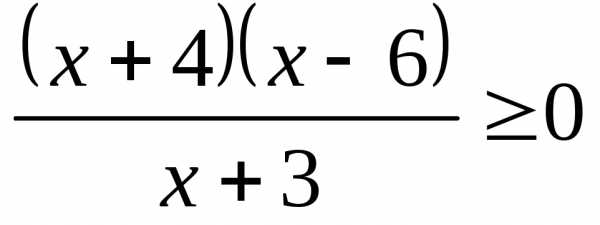 ;
;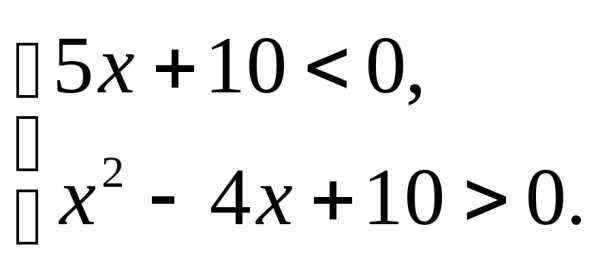
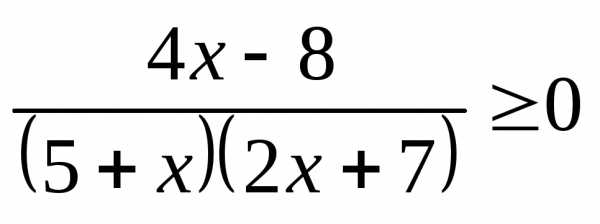 ;
;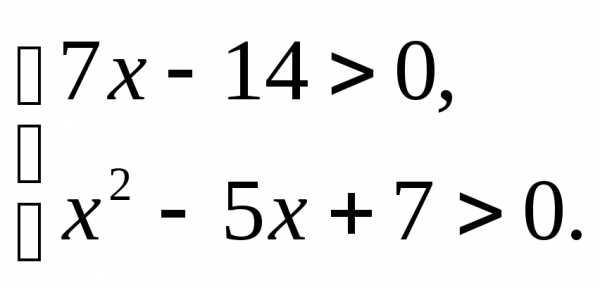
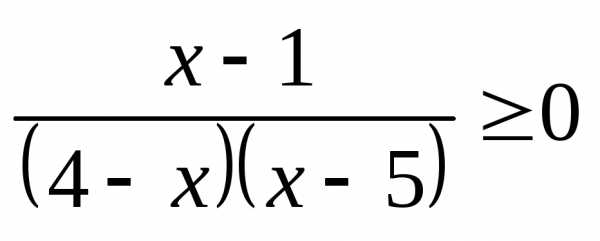 ;
;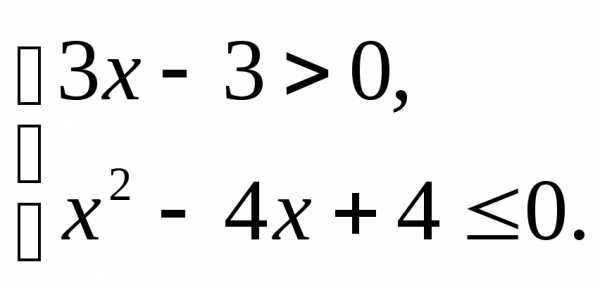
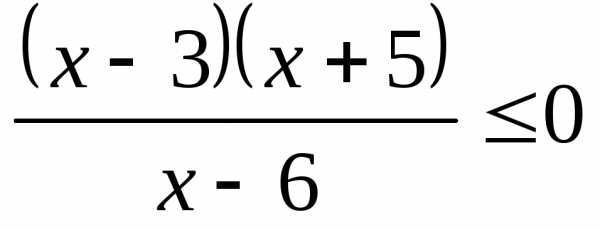 ;
;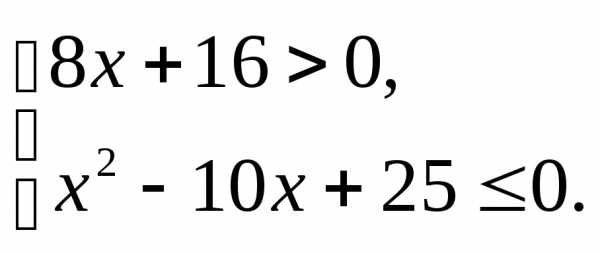
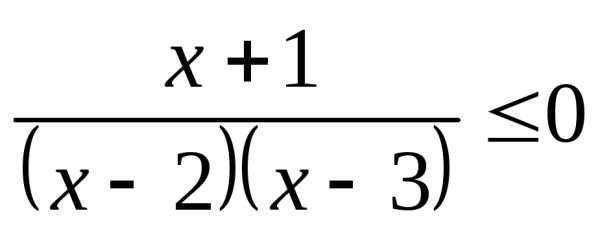 ;
;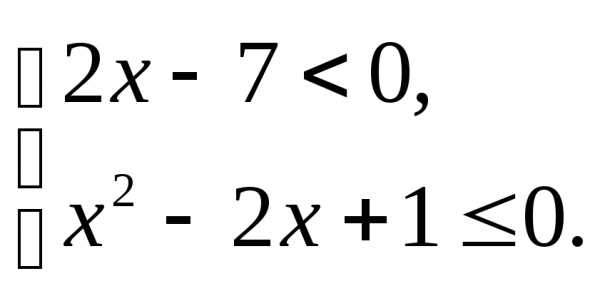
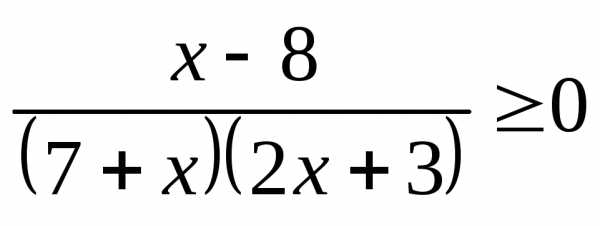 ;
;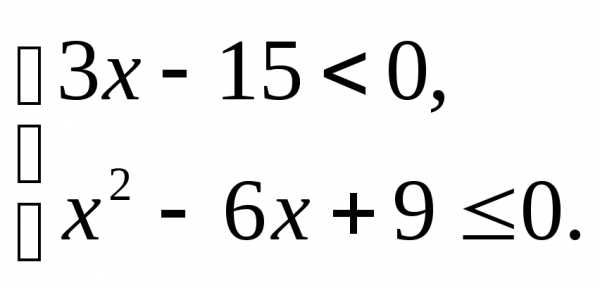
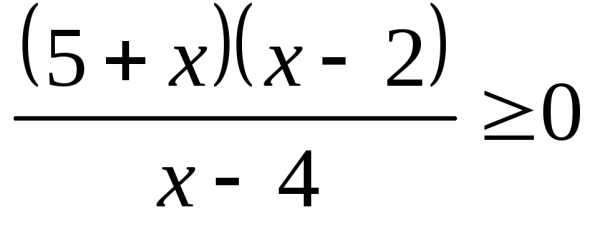 ;
;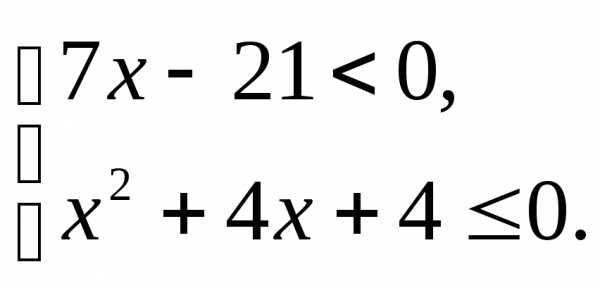
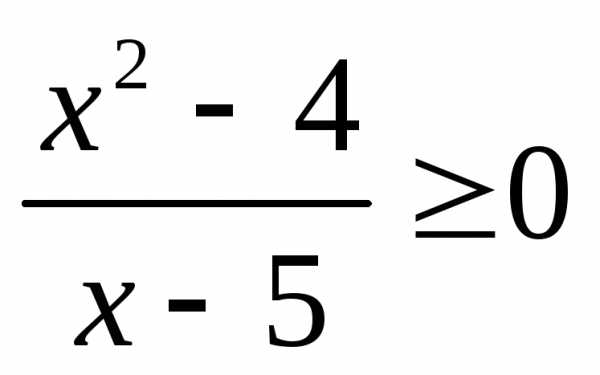 ;
;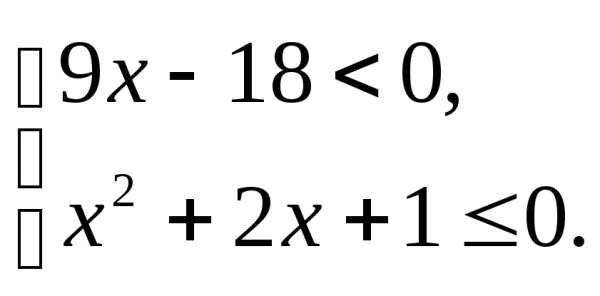
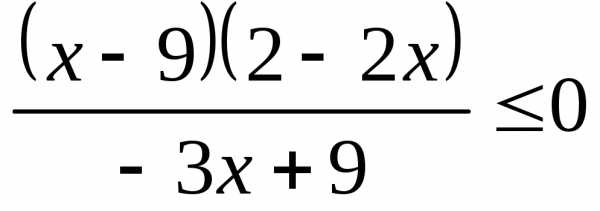 ;
;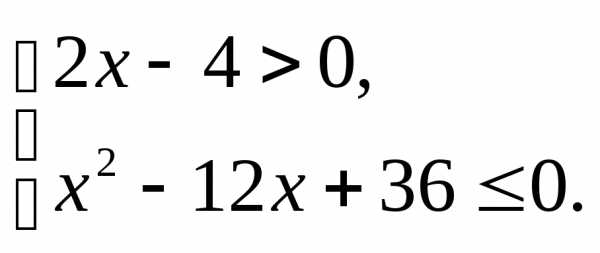
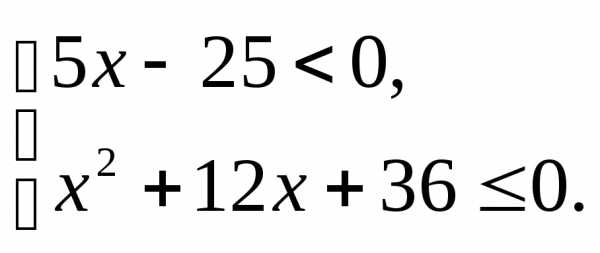
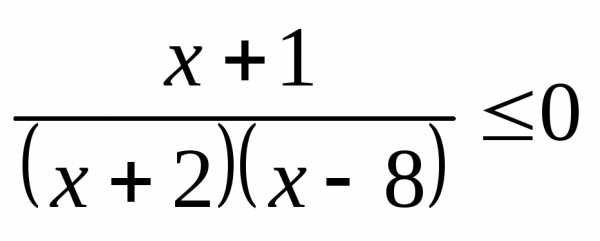 ;
;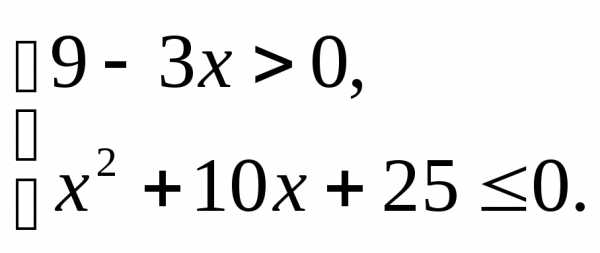
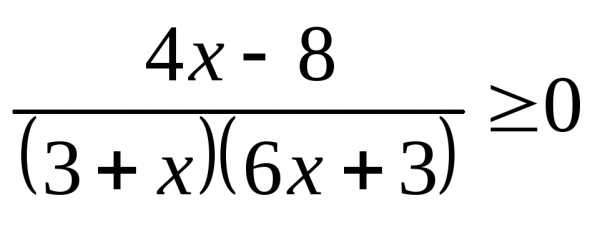 ;
;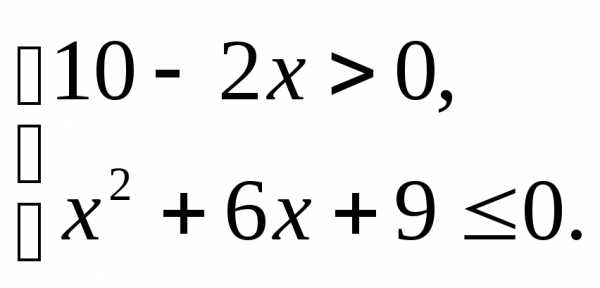
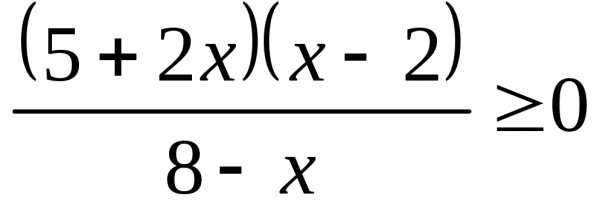 ;
;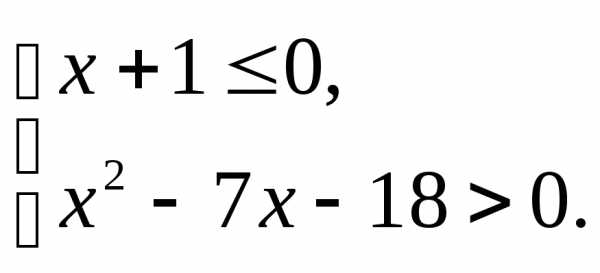
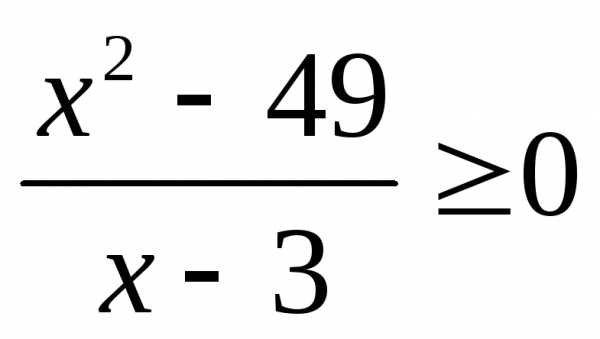 ;
;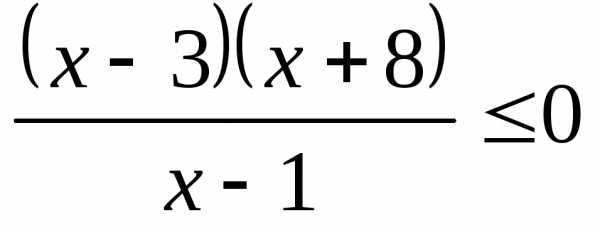 ;
;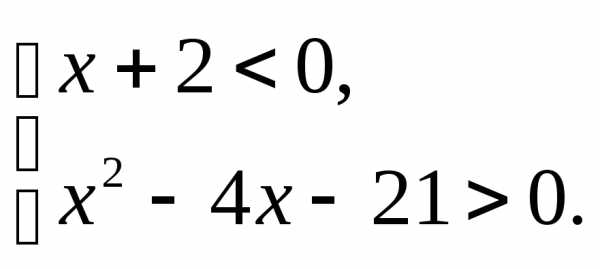
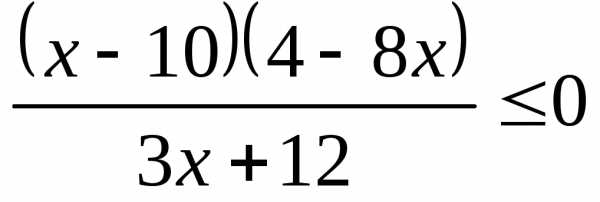 ;
;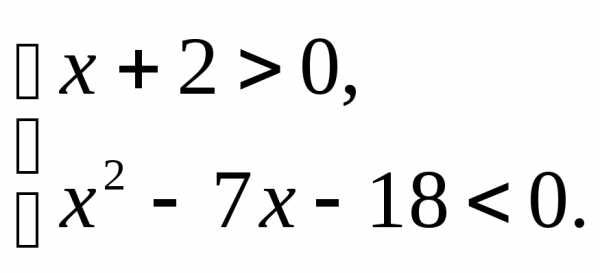
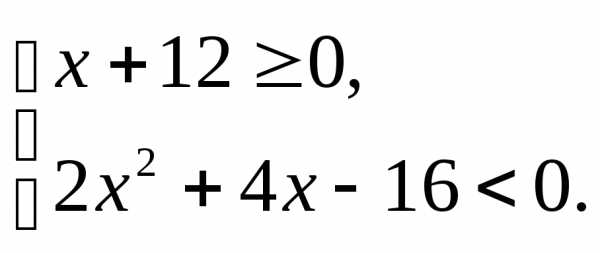
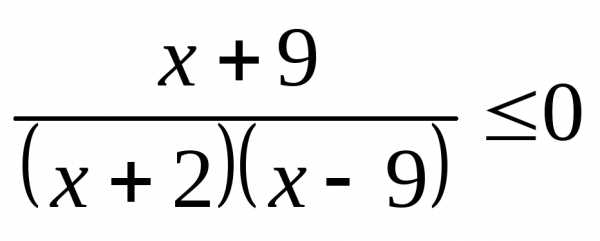 ;
;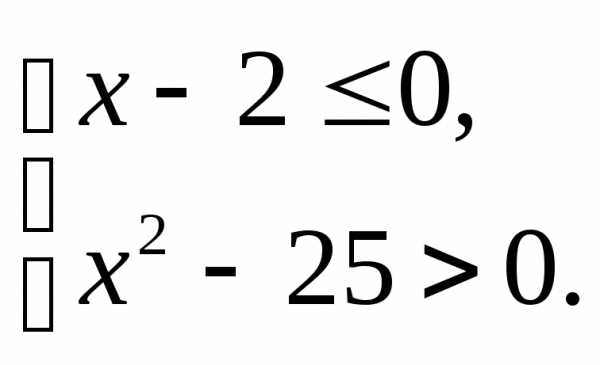
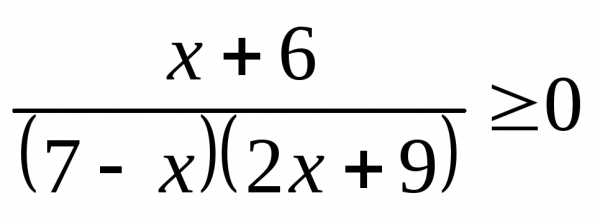 ;
;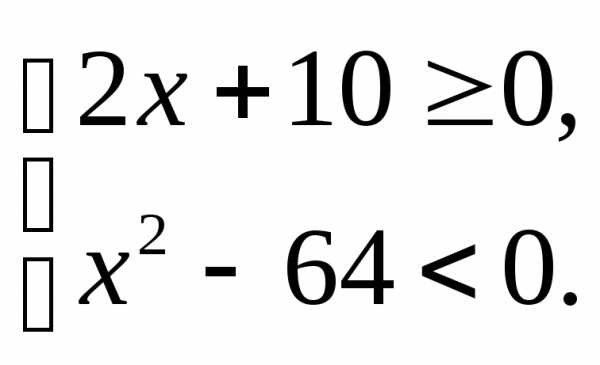
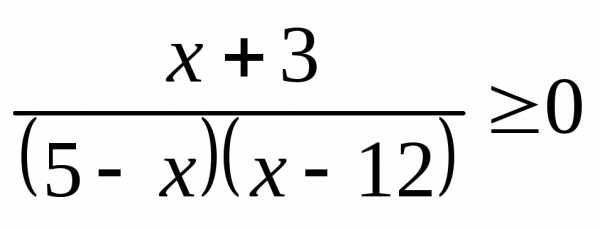 ;
;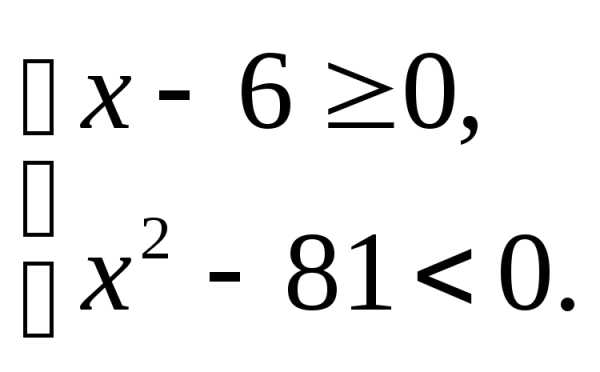
 ;
;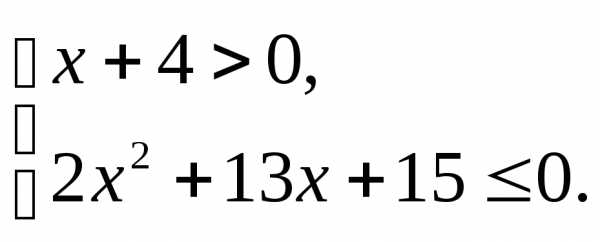
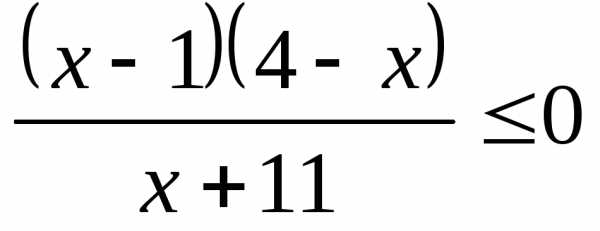 ;
;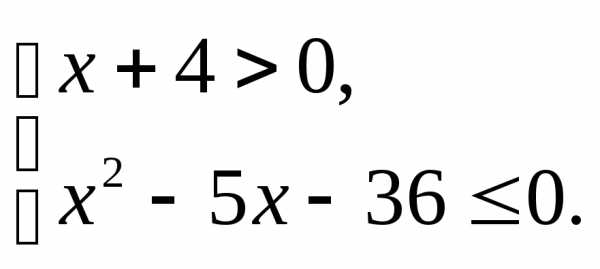
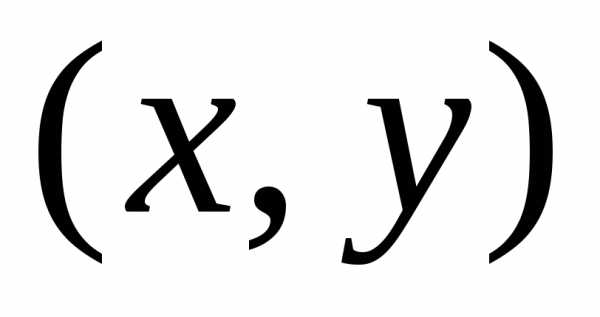 ,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
.
,
которые удовлетворяют неравенству. Геометрически
решением линейного неравенства являетсяполуплоскость,
границей которой является прямая
. (в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.
(в противном случае берется другая
полуплоскость). Плоскость выделяется
штриховкой.