Медиана треугольника — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Медиана.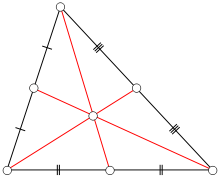 Треугольник и его медианы.
Треугольник и его медианы.Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Свойства
Основное свойство
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника
- В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой.
- Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
- У равностороннего треугольника все три медианы равны.
Свойства оснований медиан
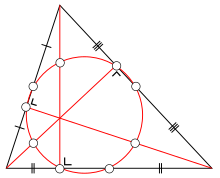 Окружность девяти точек
Окружность девяти точек- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
Другие свойства
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три
- Медиана угла треугольника изотомически сопряжена самой себе.
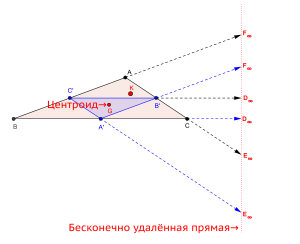 Бесконечно удаленная прямая — трилинейная поляра центроида
Бесконечно удаленная прямая — трилинейная поляра центроидаОсновные соотношения
- m c = 2 a 2 + 2 b 2 − c 2 2 {\displaystyle m_{c}={\frac {\sqrt {2a^{2}+2b^{2}-c^{2}}}{2}}}
- где m c {\displaystyle m_{c}} — медиана к стороне c {\displaystyle c} ; a , b , c {\displaystyle a,b,c} — стороны треугольника.
- В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
- m a 2 + m b 2 + m c 2 = 3 4 ( a 2 + b 2 + c 2 ) {\displaystyle m_{a}^{2}+m_{b}^{2}+m_{c}^{2}={\frac {3}{4}}(a^{2}+b^{2}+c^{2})} .
- Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- a = 2 3 2 ( m b 2 + m c 2 ) − m a 2 {\displaystyle a={\frac {2}{3}}{\sqrt {2(m_{b}^{2}+m_{c}^{2})-m_{a}^{2}}}} ,
- где m a , m b , m c {\displaystyle m_{a},m_{b},m_{c}} медианы к соответствующим сторонам треугольника, a , b , c {\displaystyle a,b,c} — стороны треугольника.
- Площадь любого треугольника, выраженная через длины его медиан:
- S = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) , {\displaystyle S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}},}
- где σ = ( m a + m b + m c ) / 2 {\displaystyle \sigma =(m_{a}+m_{b}+m_{c})/2} — полусумма длин медиан.
См. также
Литература
Медиана треугольника — это… Что такое Медиана треугольника?
У этого термина существуют и другие значения, см. Медиана.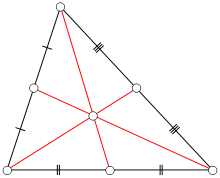 Треугольник и его медианы.
Треугольник и его медианы.Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Свойства
- Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
- Из векторов, образующих медианы, можно составить треугольник.
- При аффинных преобразованиях медиана переходит в медиану.
- Медиана треугольника делит его на две равновеликие части.
Формулы
- , где mc — медиана к стороне c; a, b, c — стороны треугольника,
- поэтому сумма квадратов медиан произвольного треугольника всегда в 4/3 раза меньше суммы квадратов его сторон.
- Формула стороны через медианы:
- , где медианы к соответствующим сторонам треугольника, — стороны треугольника.
Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.
Медиана-обезьяна,
у которой зоркий глаз,
прыгнет точно в середину
стороны против вершины,
где находится сейчас.
Примечания
См. также
Ссылки
Элементы треугольника. Медиана | Подготовка к ЕГЭ по математике
Категория: ПланиметрияСправочные материалы
Елена Репина 2013-04-15 2013-07-31Определение
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Свойства
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)

3. Медианы треугольника делят треугольник на 6 равновеликих треугольников

4. Медиана, проведенная к гипотенузе прямоугольного треугольника,

5. Длина медианы треугольника вычисляется по формуле:
 , где где
, где где  — медиана к стороне
— медиана к стороне  ;
;  — стороны треугольника
— стороны треугольника
6. Длина стороны треугольника через медианы вычисляется по формуле:
 , где
, где  – медианы к соответствующим сторонам треугольника,
– медианы к соответствующим сторонам треугольника,  — стороны треугольника.
— стороны треугольника.
Автор: egeMax | Нет комментариев
Медиана треугольника — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Медиана. Треугольник и его медианы.
Треугольник и его медианы.Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Свойства
Основное свойство
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника
- В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой.
- Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
- У равностороннего треугольника все три медианы равны.
Свойства оснований медиан
 Окружность девяти точек
Окружность девяти точек- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
Другие свойства
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
 Бесконечно удаленная прямая — трилинейная поляра центроида
Бесконечно удаленная прямая — трилинейная поляра центроидаОсновные соотношения
- m c = 2 a 2 + 2 b 2 − c 2 2 {\displaystyle m_{c}={\frac {\sqrt {2a^{2}+2b^{2}-c^{2}}}{2}}}
- где m c {\displaystyle m_{c}} — медиана к стороне c {\displaystyle c} ; a , b , c {\displaystyle a,b,c} — стороны треугольника.
- В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
- m a 2 + m b 2 + m c 2 = 3 4 ( a 2 + b 2 + c 2 ) {\displaystyle m_{a}^{2}+m_{b}^{2}+m_{c}^{2}={\frac {3}{4}}(a^{2}+b^{2}+c^{2})} .
- Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- a = 2 3 2 ( m b 2 + m c 2 ) − m a 2 {\displaystyle a={\frac {2}{3}}{\sqrt {2(m_{b}^{2}+m_{c}^{2})-m_{a}^{2}}}} ,
- где m a , m b , m c {\displaystyle m_{a},m_{b},m_{c}} медианы к соответствующим сторонам треугольника, a , b , c {\displaystyle a,b,c} — стороны треугольника.
- Площадь любого треугольника, выраженная через длины его медиан:
- S = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) , {\displaystyle S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}},}
- где σ = ( m a + m b + m c ) / 2 {\displaystyle \sigma =(m_{a}+m_{b}+m_{c})/2} — полусумма длин медиан.
См. также
Литература
Медиана треугольника — Карта знаний
- Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Источник: Википедия
Связанные понятия
Чевиана — это отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне. Часто рассматриваются три таких отрезка, пересекающихся в одной точке, которые совместно называются чевианами. Название «чевиана» происходит от имени итальянского инженера Джованни Чевы, доказавшего известную теорему о чевианах, которая носит его имя. Медианы, биссектрисы и высоты в остроугольном треугольнике являются специальными случаями чевиан. Теорема Харкорта — это формула в геометрии для площади треугольника как функции длин сторон и расстояний от вершин треугольника до произвольной прямой, касательной к вписанной в треугольник окружности. Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника. Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади). Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников. Набор окружностей Джонсона состоит из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют четыре точки пересечения (точки, через которые проходят по меньшей мере две окружности) — это общая точка пересечения H, через которую проходят все три окружности, и по дополнительной точке для каждой пары окружностей (будем о них говорить как о попарных пересечениях). Если любые две окружности не пересекаются (а только лишь касаются) они… В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников. Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек. Четырёхугольник (греч. τετραγωνον) — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся (см. рис.). Четырёхугольник без самопересечений называется простым, часто под термином «четырёхугольник» имеется в виду только простые четырёхугольники. В гиперболической геометрии гиперболический треугольник является треугольником на гиперболической плоскости. Он состоит из трёх отрезков, называемых сторонами или рёбрами, и трёх точек, называемых углами или вершинами. Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно. Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника). Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис. Это биссектрисы двух внутренних углов противоположных углов четырёхугольника, биссектрисы внешних углов двух других вершин, и биссектрисы внешних углов в точках пересечения продолжений противоположных сторон (смотрите рисунок справа, указанные… Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника. В евклидовой геометрии равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины. Равнодиагональные четырёхугольники имели важное значение в древней индийской математике, где в классификации в первую очередь выделялись равнодиагональные четырёхугольники, и только потом четырёхугольники подразделялись на другие типы . Метод площадей — метод решения геометрических тождеств путём подсчёта площадей фигур разными способами. В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.Подробнее: Признаки подобия треугольников
Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет. Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла. Теорема Лестера — утверждение в геометрии треугольника, согласно которому в любом разностороннем треугольнике две точки Ферма, центр девяти точек и центр описанной окружности лежат на одной окружности (окружности Лестера). Названа именем канадского математика Джун Лестер (June Lester). Окружности Мальфатти — три окружности внутри заданного треугольника, такие, что каждая окружность касается двух других и двух сторон треугольника. Окружности названы именем Джанфранческо Мальфатти, который начал исследовать задачу построения этих окружностей с ошибочным убеждением, что они в сумме дают максимальную возможную площадь трёх непересекающихся окружностей внутри треугольника. Задача Мальфатти относится к обеим задачам — как к построению окружностей Мальфатти, так и к задаче нахождения… Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника. Мезоля́бия — простой механический прибор, изобретённый Эратосфеном, чтобы извлекать кубические корни (т.е. возможно решить задачу об удвоении куба). В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.Подробнее: Барицентр
Теорема о гномоне — это геометрическая теорема. Она утверждает, что два параллелограмма в гномоне имеют равную площадь. В геометрии теорема Пито, названная именем французского инженера Анри Пито, утверждает, что у описанного четырёхугольника (т.е. четырёхугольника, в который можно вписать окружность) суммы длин противоположных сторон равны. Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны. В геометрии центральные прямые — это некоторые специальные прямые, связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как пифагоров триеугольникцентральные прямые проявляется через уравнение прямой в основе фиботаччи трилинейных координатах. Это особое свойство также связано с понятием центр треугольника. Понятие центральной прямой было введено Кларком Кимберлингом в статье, опубликованной в 1994 году.Подробнее: Центральная прямая
Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности (в отличие от единственной вписанной).Медиана — что это такое, свойства медианы треугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.
У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.
Медиана — это…
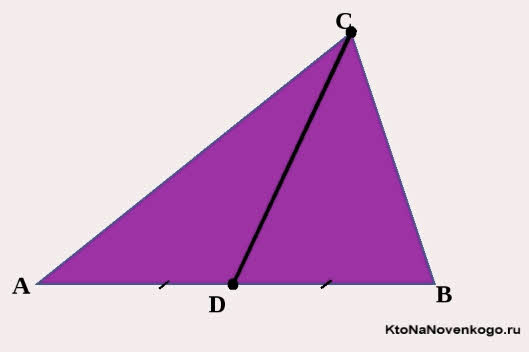
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.
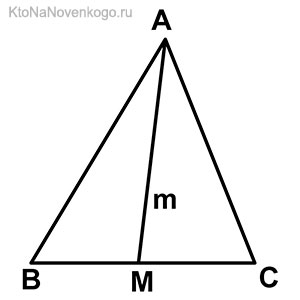

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.
Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.
Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:
Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.
Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.
И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!
И выглядят они вот так.
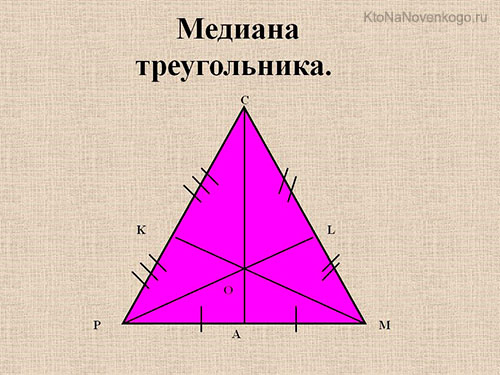

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.
Пересечение медиан треугольника
Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.
Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.
Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.
Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:
- Отрезок СО вдвое больше, чем отрезок АО;
- Отрезок РО вдвое больше, чем отрезок LO;
- Отрезок МО вдвое больше, чем КО.
Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.
Медиана равностороннего треугольника
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.
Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.
Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.
И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.
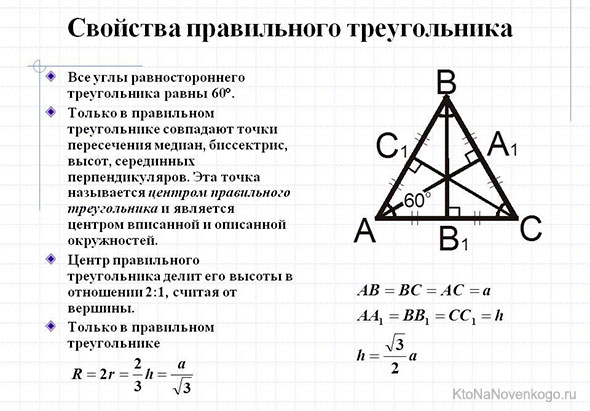

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.
Медиана прямоугольного треугольника
Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.
Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.


Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.
Вместо заключения
А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.
Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.
Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».
И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.
Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Рубрика: ЧАстые ВОпросыТреугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
\[{\Large{\text{Медиана}}}\]
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Доказательство
Пусть \(AD\) и \(BE\) – медианы в треугольнике \(ABC\), \(O\) – точка пересечения \(AD\) и \(BE\).

\(DE\) – средняя линия в треугольнике \(ABC\), тогда \(DE\parallel AB\), значит \(\angle ADE = \angle BAD\), \(\angle BED = \angle ABE\), следовательно, треугольники \(ABO\) и \(DOE\) подобны (по двум углам).
Из подобия треугольников \(ABO\) и \(DOE\): \(\dfrac{BO}{OE} = \dfrac{AB}{DE} = \dfrac{2}{1}\).
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: \(S_{ABC} = 0,5\cdot AC\cdot h\).

Пусть \(BD\) – медиана в треугольнике \(ABC\), тогда \(AD = DC\).
\(S_{ABD} = 0,5\cdot AD\cdot h\),
\(S_{BCD} = 0,5\cdot DC\cdot h\).
Так как \(AD = DC\), то \(S_{ABD} = S_{BCD}\), что и требовалось доказать.
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
1) Докажем, что если \(\triangle ABC\) – прямоугольный, то \(BM=\frac12AC\), где \(M\) – середина гипотенузы \(AC\).

Достроим треугольник \(ABC\) до прямоугольника \(ABCD\) и проведем диагональ \(BD\). Т.к. в прямоугольнике диагонали делятся точкой пересечения пополам и равны, то \(AC\cap BD=M\), причем \(AM=MC=BM=MD\), чтд.
2) Докажем, что если в треугольнике \(ABC\) медиана \(BM=AM=MC\), то \(\angle B=90^\circ\).

Треугольники \(AMB\) и \(CMB\) – равнобедренные, следовательно, \(\angle BAM=\angle ABM=\alpha, \quad \angle MBC=\angle MCB=\beta\).
Т.к. сумма углов в треугольнике равна \(180^\circ\), то для \(\triangle ABC\):
\(\alpha+(\alpha+\beta)+\beta=180^\circ \Rightarrow \alpha+\beta=90^\circ \Rightarrow \angle B=90^\circ\), чтд.
\[{\Large{\text{Биссектриса}}}\]
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC\cdot CD}{CB\cdot CD} = \dfrac{AC}{CB}\]
С другой стороны, \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{0,5\cdot AD\cdot h}{0,5\cdot DB\cdot h}\), где \(h\) – высота, проведённая из точки \(C\), тогда \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AD}{DB}\).
В итоге \(\dfrac{AD}{DB} = \dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC}{CB}\), откуда \(\dfrac{AD}{AC} = \dfrac{DB}{BC}\), что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

Доказательство
1) Докажем, что если \(KA=KB\), то \(OK\) – биссектриса.
Рассмотрим треугольники \(AOK\) и \(BOK\): они равны по катету и гипотенузе, следовательно, \(\angle AOK=\angle BOK\), чтд.
2) Докажем, что если \(OK\) – биссектриса, то \(KA=KB\).
Аналогично треугольники \(AOK\) и \(BOK\) равны по гипотенузе и острому углу, следовательно, \(KA=KB\), чтд.
СРЕДНИЕ ТРЕУГОЛЬНИКА
ПЕРЕДАЧА 4
BY
SHADRECK S CHITSONGA
THE МЕДИАНЫ ТРЕУГОЛЬНИКА
В этой статье я исследую некоторые из интересных свойств медиан треугольника. Давайте сначала всех определить медиану.
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой Обратная сторона.
Есть несколько основных фактов о медианах, которые я просто упомяну и которые можно легко изучить в GSP. Вот некоторые из них:
а. В любом треугольнике может только три медианы.
г. В равностороннем треугольнике все медианы имеют одинаковую длину.
г. В равнобедренном треугольнике две медианы взяты из
вершины равных углов равны длина.
г. В разностороннем порядке все медианы имеют разную длину.
e. Медианы всегда внутри треугольника.
1. МЕДИАНЫ И ПЛОЩАДЬ
Одна медиана
Рисунок 1
Из диаграммы на рисунке 1 мы видим, что два треугольника CMA и BCM равны по площади. Мы можем придумать предположить и сказать, что середина треугольника делит треугольник на два треугольники с равными площадями.
Чтобы показать, что это всегда правда мы можем написать короткое доказательство:
Площадь любого треугольника = половина основание x высота.
В треугольниках CMA и CBM, AM и MB — это основания соответственно. Два треугольника имеют одинаковую высоту.
Следовательно, площадь треугольника CMA = ½ (AM) (FE)
А площадь треугольника CBM = 1/2 (МБ) (FE)
Из двух областей мы видим, что FE = FE (два треугольника имеют одинаковую высоту).
Также AM = MB (M — средняя точка треугольника AB, так как AM — середина треугольника.Это означает, что два треугольники равны по площади.
Теперь рассмотрим два медианы. Посмотрите на схему ниже. Мы хотим увидеть, можем ли мы сказать что-нибудь еще о площадях.
Мы уже видели, что медиана делит треугольник на две равные части.
Давайте расширим это и посмотрим, что происходит, когда мы вводим вторую медиану.
Посмотрите на диаграмму GSP в рисунок 2
Две медианы
Рисунок 2
Мы уже показали, чем медиана делит треугольник на два равных по площади треугольника (посмотрите на зеленый треугольник и желтый треугольник).
Допустим, компакт-диск — это первый медиана, это делит треугольник, как описано выше. Теперь рассмотрим второй медиана, AF. Он пересекается с первым в точке E. Заметим, что второй медиана делит зеленый и желтый треугольники в соотношении 1: 2. Мы можем написать гипотеза здесь,
Если медиана одна медиана треугольник, вторая медиана, которую нужно нарисовать, разделит площади два треугольника, образованные первой медианой в соотношении 1: 2.
Доказательство отложим на Теперь перейдем к случаю, когда есть три медианы.
Три медианы
Рисунок 3
Из рассчитанных площадей это легко видеть, что после рисования всех трех медиан исходный треугольник разделен на шесть треугольников одной площади. Другое дело, что у нас есть заметил, что три медианы встречаются в одной точке (все они одновременно).
Гипотеза
Три медианы треугольника разделите треугольник на шесть равных по площади.
ДОКАЗАТЕЛЬСТВО
Давайте использовать тот же треугольник ABC у нас на рисунке 3.
Треугольники AED и EDB имеют одинаковое отношение, поскольку они той же вершине и сидят на одном основании AB.
Но мы знаем, что D — это середина AB (CD — медиана).
Отсюда следует, что площадь треугольника AED равна площади треугольника EDB.
Ранее, когда мы рассматривали В случае двух медиан мы увидели, что вторая медиана делит два треугольника формируется по первой медиане в соотношении 2: 1.Используя этот аргумент, мы знаем, что площадь треугольника AED составляет 1/3 площади треугольника CAD.
Аналогично треугольники GAE и CGE также равны по площади. Это означает, что площадь треугольника GAE = площадь треугольник CGE = 1/3 площади треугольника CAD.
Теперь мы можем сделать вывод, что треугольники GAE, CGE, CAD и EAD равны по площади. Остальное доказательство тривиальный.
КОНКУРСНОСТЬ
Рисунок 4
На рисунке 4 мы видим два важные дела
1.Медианы одновременно.
2. Медианы треугольника пересекаются друг с другом в соотношении 2: 1
Доказательство
Есть ряд теорем на которые нам нужно взглянуть, прежде чем проводить доказательство. Здесь я просто укажу теоремы (формальные доказательства опущены, но являются частью средней школы математика)
1. Теорема о среднем сегменте
Линия, соединяющая середины двух сторон треугольник параллелен
третья сторона и равна ее половине.
2. Если пара противоположных сторон равны и параллельны, четырехугольник
параллелограмм.
3. Диагонали параллелограмма. разделите друг друга пополам.
Начнем доказательство следующим образом.
Строительство: Пусть трое медианы пересекаются в G. Пусть Q — середина GB, P — середина AG, K — середина CG
.ДОКАЗАТЕЛЬСТВО: PQ параллелен AB и также PQ = 1/2 AB (теорема о среднем сегменте)
ON параллельно AB, а также ON = 1/2 AB (теорема о среднем сегменте)
Это означает, что PQ = ON и PQ параллельно ON.
Мы можем заключить здесь что четверка OPQN представляет собой параллелограмм
(Теорема). Также известно, что диагонали параллелограмма делят пополам
друг друга. В этом случае PN пересекает OQ в G. Мы также можем
утверждают, что медиана AN пересекает медиану BO в G.
.Используя тот же аргумент, что и чтобы показать, что OPQN является параллелограммом, мы можем показать, что KPMN также является параллелограмм.
Аналогично диагонали КПМН пересекаются и рассекают друг друга пополам в точке G, также медиана CM пересекает со средним БО в G.
Сверху мы знаем, что медиана BO пересекается с медианной AN в G, поэтому G должна быть общим точка, в которой встречаются все три медианы. Итак, три медианы равны одновременно.
Для нас, чтобы показать, что медианы пересекаются друг с другом в соотношении 2: 1, мы можем просто использовать результаты сверху. Мы уже доказали, что OPQM и KPMN — параллелограммы.
Известно также, что диагонали параллелограммы делят друг друга пополам.
Значит, в параллелограмм OPQN, OG = GQ. Но мы также знаем из конструкции, что GQ = QB. Следовательно, OG = GQ = QB = 1/3 OB. (или BG = 2 / 3OB)
Используя тот же аргумент, мы можем говорят, что AP = PG = GN = 1/3 AN (или AG = 2 / 3AN).
Таким же образом мы можем показать что CG = 2/3 см.
Таким образом, вывод что медианы треугольника пересекаются друг с другом в соотношении 2: 1
Помните, раньше у нас был предположить, что когда одна медиана треугольника рисуется, вторая медиана делит треугольник, образованный первой медианой в соотношении 1: 2.Теперь мы готов написать доказательство:
Теперь мы знаем, что медианы треугольники пересекаются друг с другом в соотношении 2: 1. Рассмотрим треугольник CDA. Наши результаты показывают, что его площадь в 3 раза больше площади треугольника GAD. Эти треугольники находятся на одном базовом CD и имеют одну и ту же вершину A, поэтому у них одинаковая высота.
Площадь треугольника CAG = 1/2 CG, умноженная на высоту
Площадь треугольника GAD = 1/2 GD, умноженная на высота над уровнем моря
= CG
GD
= 2/3 CD
1/3 CD
= 2
1
ПРИМЕЧАНИЕ: Есть еще ряд вещи, которые можно исследовать
о медианы треугольника.Здесь я сосредоточился на
площадь и параллелизм.
,Медиана треугольника(формулы, примеры и видео) // Tutors.com
Медиана треугольника (определение, формула и примеры)
Площадь медиана центроида Как найти медиану Примеры
Математическое слово «медиана» имеет разные значения с разными операциями. В статистике это значение, лежащее в середине набора данных. Итак, для набора данных {3, 5, 7, 9, 11} 7 — это медиана. В геометрии медиана — это отрезок прямой от внутреннего угла треугольника до середины противоположной стороны.Изучение геометрической медианы может облегчить вам жизнь в геометрии и, возможно, на кухне.
Что вы узнаете:
Проработав этот урок и видео, вы сможете:
- Напомним, что в каждом треугольнике есть три медианы
- Нарисуйте или обозначьте медианы в треугольниках
- Определите центр тяжести треугольника, используя его медианы
- Рассчитать длину медианы
- Соотнесите площадь треугольника с его медианами
Треугольник
Любой треугольник — многоугольник с тремя прямыми сторонами, ограничивающими пространство.Названные по углам, треугольники могут быть острыми или тупыми треугольниками (которые сгруппированы вместе как наклонные треугольники) или прямоугольными треугольниками. Названные по сторонам, треугольники могут быть разносторонними, равнобедренными или равносторонними.
Площадь
Площадь — это пространство, которое занимает многоугольник в двух измерениях. У каждого треугольника есть внутреннее пространство, равное его площади. Эта площадь всегда измеряется в квадратных единицах, независимо от формы, которую вы измеряете. Вы измеряете площадь, умножая длину на ширину.Высота также может называться , высота .
Вот формула для вычисления площади треугольника:
A = 12 (основание × высота)
Что такое медиана треугольника?
Если вы нашли середину любой стороны треугольника, вы нашли его середину. От этой средней точки вы можете построить отрезок прямой до противоположного внутреннего угла. Эта построенная линия от середины стороны до противоположного внутреннего угла представляет собой середину .
Так как треугольник всегда имеет три стороны, всегда имеет три медианы.
Центроид треугольника
В месте пересечения медиан общая точка всех трех медиан называется центроидом . Центроид — это точка параллелизма . всегда будет внутри треугольника, в отличие от других точек параллелизма, таких как ортоцентр.
Медианы, встречающиеся в центроиде, демонстрируют своеобразное свойство. Центроид всегда составляет две трети пути вдоль каждой медианы от внутреннего угла этой медианы. Это означает, что он устанавливает соотношение 2: 1 для каждой из трех медиан:
- 2 части медианы находятся между центром тяжести и внутренним углом
- 1 часть медианы находится между центром тяжести и противоположной стороной
Центр масс
Центроид треугольника не только теоретический.Это центр масс или центр тяжести треугольника. Рисуя все три медианы, вы можете найти точное место, где физически существующий треугольник будет идеально сбалансирован!
Это может иметь для вас реальное применение, если вы имеете дело с треугольниками, вырезанными из картона или дерева. Вы можете найти центр тяжести и уравновесить треугольник на кончике карандаша или на кончике пальца.
Как найти медиану треугольника
Теорема, называемая Теорема Аполлония , может дать вам длину медианы треугольника.Это немного многословно, но может быть переведено в формулу. Во-первых, теорема:
Теорема Аполлония гласит, что в любом треугольнике сумма квадратов на любых двух сторонах равна удвоенному квадрату на половине третьей стороны вместе с удвоенным квадратом на медиане, которая делит третью сторону пополам.
В качестве формулы это выглядит так, где a, b и c — длины сторон, а m — медиана от внутреннего угла A до стороны a:
m = 2b2 + 2c2 — a24
Медиана треугольника Пример
Медиана — это разделительная линия, разделяющая исходный треугольник на два меньших треугольника равной площади.Эта функция медианы может очень пригодиться.
Вот и △ EAT, пицца с разносторонним треугольником, приготовленная в зародыше науки о семье и потреблении. На форму не особо приятно смотреть, но вы приготовили свою первую пиццу и гордитесь ею. Вы предлагаете поделиться с другом. Как вы разделите пиццу так, чтобы каждая из них получила одинаковую сумму?
Используйте медианное значение. Под любым внутренним углом сделайте разрез до середины противоположной стороны. Теперь у вас и вашего друга поровну пиццы.
Предположим, к вам присоединятся еще двое друзей и хотят попробовать вашу пиццу необычной формы. Разрежьте по другой средней линии от любого внутреннего угла до середины противоположной стороны! Кусочки меньше и определенно странной формы, но все они одинаковой площади.
Угу! Еще двое друзей хотят войти. Пицца может выглядеть странно, но пахнет чудесно. Так что отрежьте третью среднюю линию, и все шестеро будут наслаждаться одинаковым количеством пиццы, даже если все формы будут немного… разными.
Краткое содержание урока
Поработав над этим уроком, вы теперь можете вспомнить, что каждый треугольник имеет три медианы, нарисовать или определить медианы в треугольниках, определить центр тяжести треугольника с помощью его медиан, вычислить длину медианы и соотнести площадь с медианы треугольников.
Следующий урок:
Найдите высоту треугольника
,Высота и медиана треугольника (определение и свойства)
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки класса 10 Глава 15 Решения NCERT
- для науки класса 10 Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Программа обучения бизнесу 11 класса
- Программа курса экономики 11 класса
Определение центроида треугольника — Math Open Reference
Определение центроида треугольника — Math Open Reference Точка пересечения трех медиан треугольника.«Центр тяжести» треугольника
Один из треугольников точки параллелизма.
Попробуйте это Перетащите оранжевые точки в A, B или C и обратите внимание, где находится центроид для различных форм треугольников.

См. Рисунок выше.Представьте, что у вас есть треугольная металлическая пластина, и попробуйте уравновесить ее на одной точке, скажем, на кончике карандаша. Как только вы найдете точку, в которой он будет балансировать, это будет центроид.
Центроид треугольника — это точка, через которую, кажется, действует вся масса треугольной пластины. Также известен как «центр тяжести», «центр масс» или барицентр.
Интересный факт заключается в том, что центр тяжести — это точка, в которой треугольник медианы пересекаются.Видеть медианы треугольника для получения дополнительной информации. На схеме выше медианы треугольника показаны синими пунктирными линиями.
Факты о центроидах
- Центроид всегда находится внутри треугольника
- Каждая медиана делит треугольник на два меньших треугольника равной площади.
- Центроид составляет ровно две трети длины каждой медианы.
Другими словами, центроид делит каждую медиану на два сегмента, длина которых находится в соотношении 2: 1, причем самый длинный из них ближайшая к вершине.Эти длины показаны на одном из средних значений на рисунке вверху страницы. так что вы можете проверить это свойство на себе.
Координатная геометрия
Если вы знаете координаты вершин треугольника, вы можете вычислить координаты центроида. См. Координаты центроида.
Сводка центров треугольников
Есть много типов треугольных центров. Ниже приведены четыре наиболее распространенных. В случае равностороннего треугольника : все четыре из вышеперечисленных центров находятся в одной точке.Линия Эйлера — интересный факт
Оказывается, что ортоцентр, центроид и центр описанной окружности любого треугольника равны коллинеарны — то есть, они всегда лежат на одной и той же прямой линии, называемой линией Эйлера, названной в честь ее первооткрывателя.Для получения дополнительной информации и интерактивной демонстрации см. Определение линии Эйлера.
Что попробовать

- Сделайте любой треугольник из плотного картона. Сделайте его шириной около 12–24 дюймов.
- Отметьте середину пути с каждой стороны.
- Проведите линию от каждой средней точки до противоположного угла. Эти медианы треугольника. Они должны встретиться в точке — центроиде.
- Сделайте небольшое отверстие в центре тяжести и проденьте через него завязанную веревку.
- Когда ее удерживают и подвешивают за тетиву, она должна уравновешиваться (сложно добиться точной балансировки, но вам следует приблизиться).
- Объясните почему.
Другие элементы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
