5. Производящая функция дискретной случайной величины
Кратко остановимся на понятие производящей функции конечных дискретных случайных величин.
Функцию определённую равенством
,
где 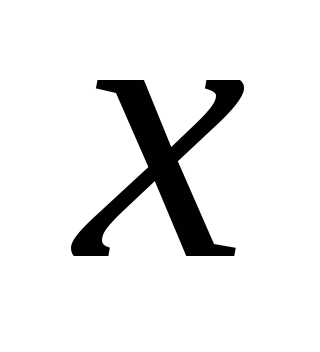 некоторый параметр называют производящей функцией для
последовательности повторных независимых
опытов. Очевидно, что при
некоторый параметр называют производящей функцией для
последовательности повторных независимых
опытов. Очевидно, что при имеет место равенство
имеет место равенство
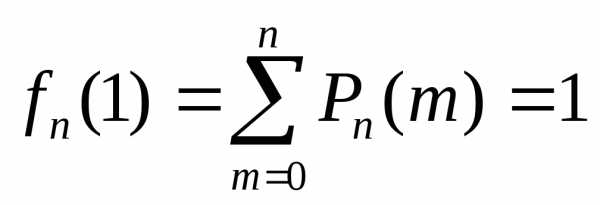 ,
,
для
любого натурального числа 
Пусть производится 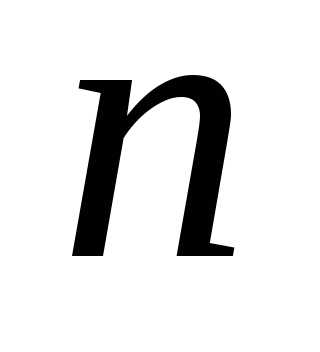
 равна
равна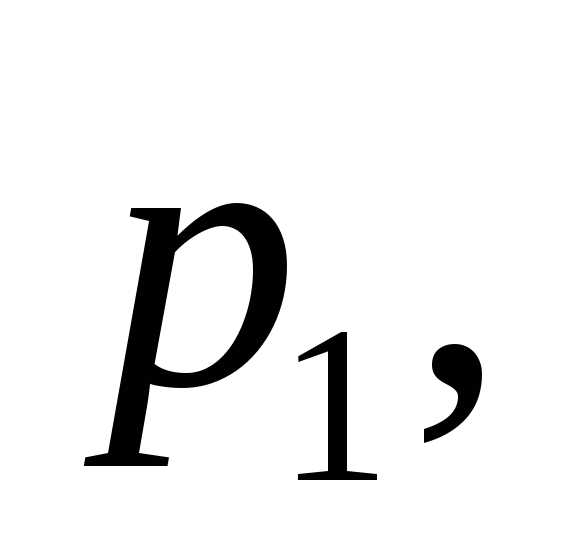 во втором равна
во втором равна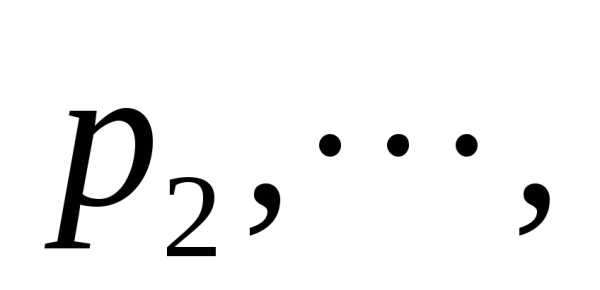 в
в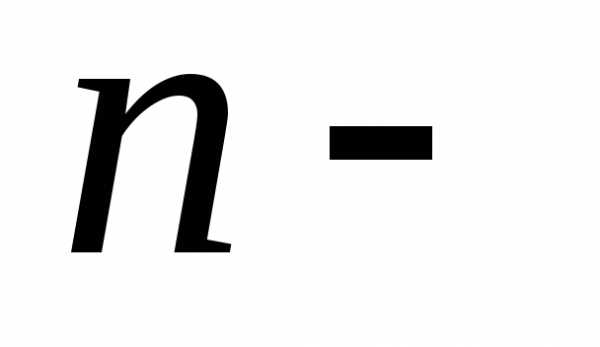 м
испытании равна
м
испытании равна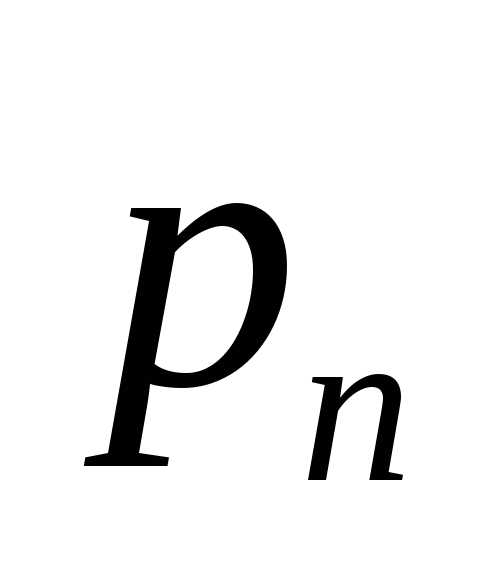 и вероятностинепоявлениясобытия
и вероятностинепоявлениясобытия соответственно равныЗа
соответственно равныЗа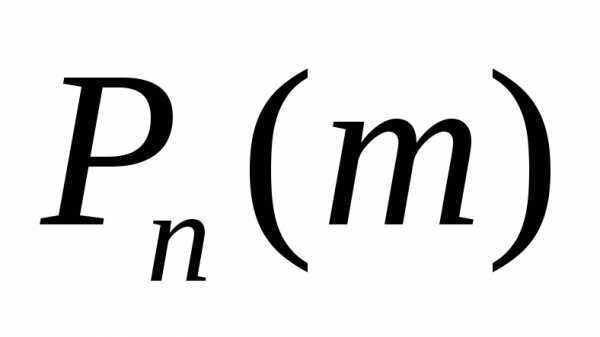 обозначим вероятность появления
события
обозначим вероятность появления
события в
в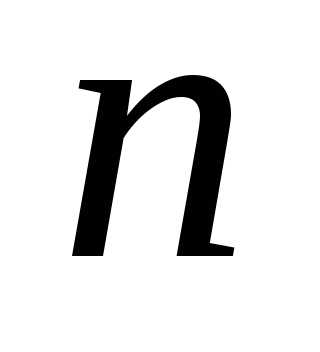 испытаниях ровно
испытаниях ровно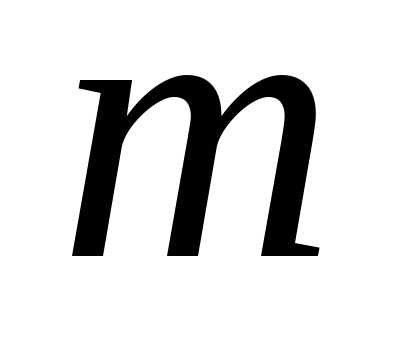 раз.
раз. Производящей функцией вероятностей 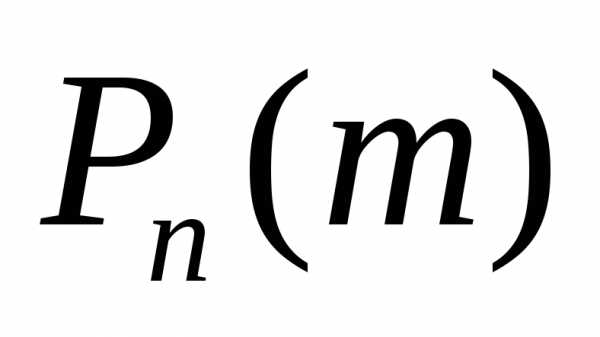 называют функцию, определяемую равенством
называют функцию, определяемую равенством
( )
)
Таким образом, вероятность 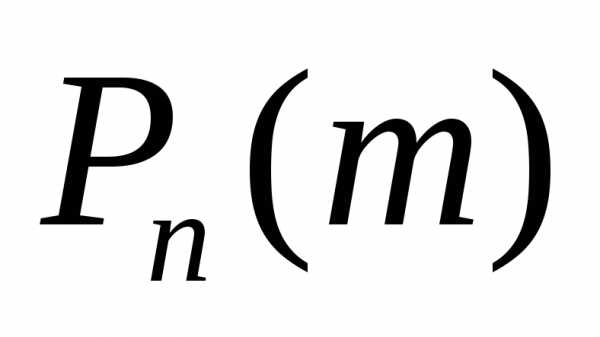 равна коэффициенту при
равна коэффициенту при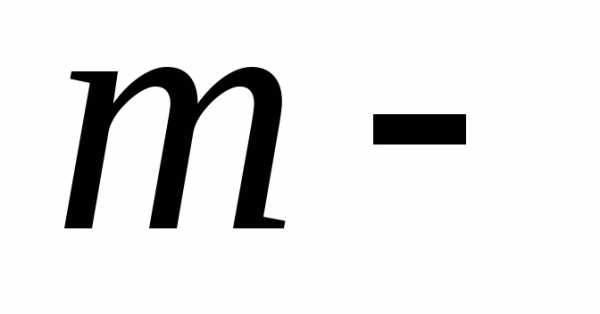 й
степени многочлена
й
степени многочлена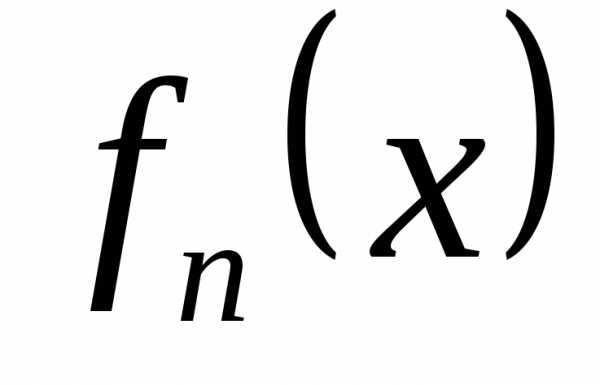 ,
определённой равенством (
,
определённой равенством ( ),
т.е. равна коэффициенту при
),
т.е. равна коэффициенту при
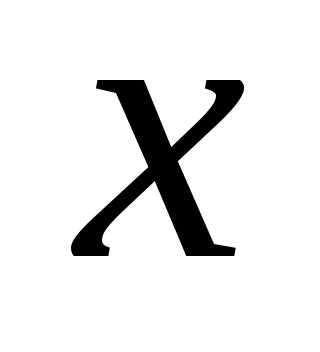 .
. Замечание. Отметим, что при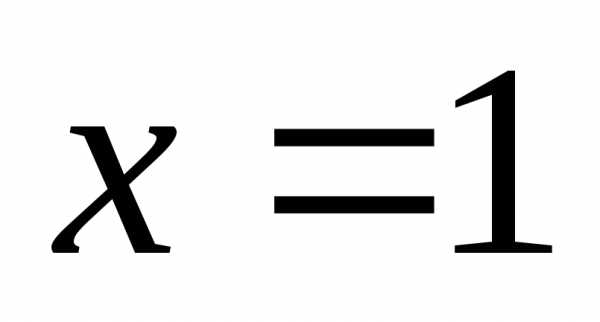 должно выполняться равенство (обычно
называется контроль).
должно выполняться равенство (обычно
называется контроль).
( ).
).
При  имеем равенство
имеем равенство
.
Следовательно,
коэффициент при 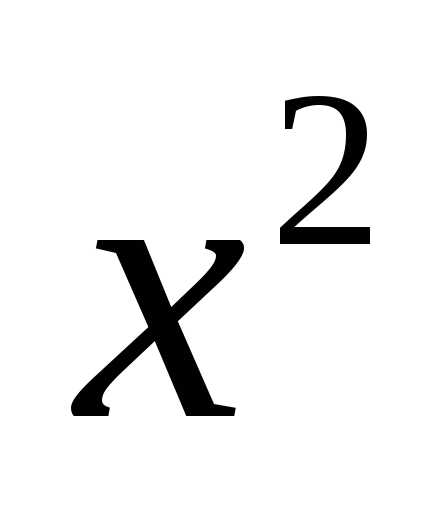 равно
равно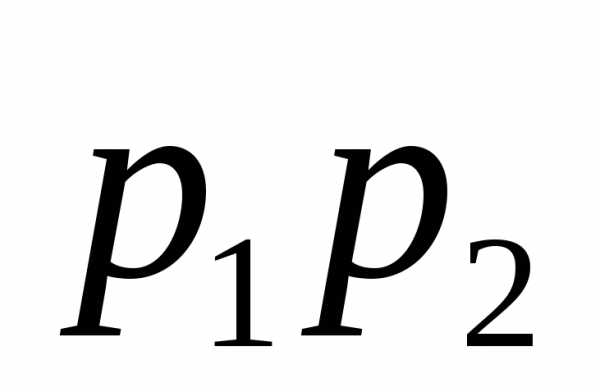 ,
при
,
при равнои при
равнои при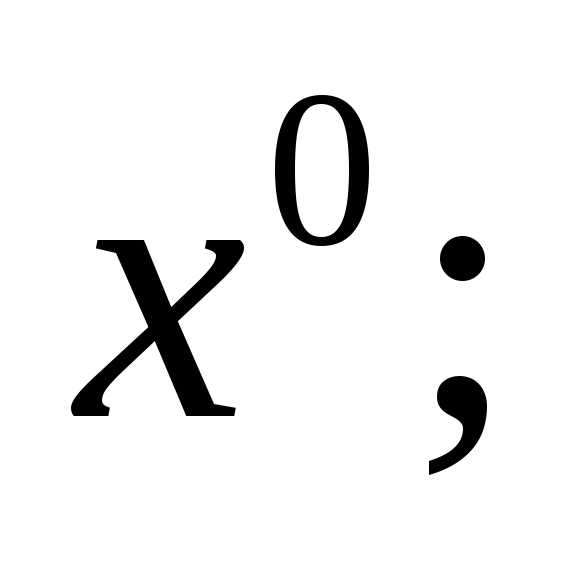
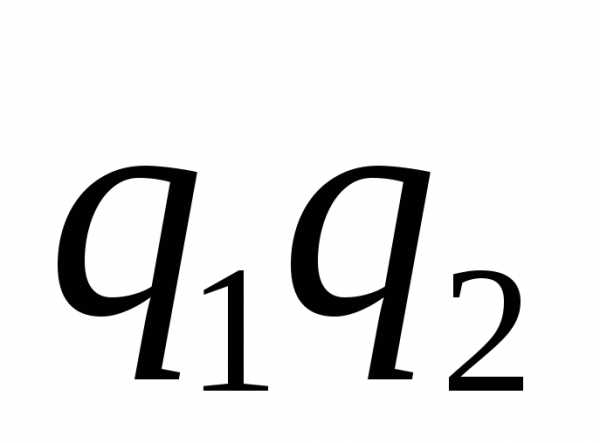 .
. Следует заметить, что если в различных
испытаниях появляется различные события
(в первом испытании событие  ,
во втором событие
,
во втором событие и
т.д.), то изменяется лишь истолкование
коэффициентов при различных степенях
и
т.д.), то изменяется лишь истолкование
коэффициентов при различных степенях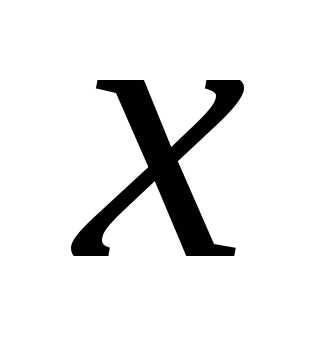 .
Например, в равенстве (
.
Например, в равенстве ( )
коэффициент
)
коэффициент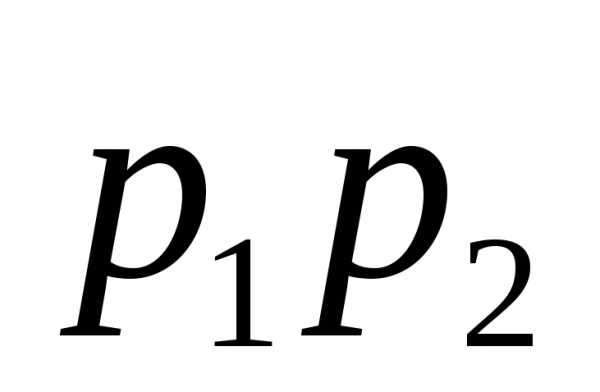 определяет вероятность появления двух
событий
определяет вероятность появления двух
событий и
и
Пример 8. Устройство состоит из трёх
независимо работающих элементов.
Вероятности безотказной работы элементов
(за время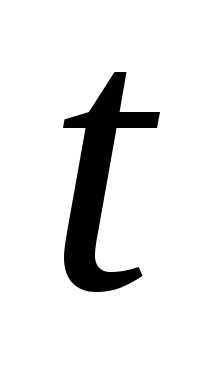 )
соответственно равныНайти вероятности того, что за время
)
соответственно равныНайти вероятности того, что за время будут работать безотказно:
будут работать безотказно:
а) все три элемента работают;
б) два элемента работают;
в) один элемент работает;
г) ни один из элементов не будет работать.
Решение. Вероятности безотказной работы элементов соответственно равныСледовательно, вероятности того, что элементы откажут, соответственно равны
Составим производящую функцию:
а) Вероятность того, что три элемента будут работать безотказно, равна коэффициенту при
б) Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при
в) Вероятность того, что один элемент будет работать безотказно, равна коэффициенту при
г) Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену:
Легко видет, что выполняется контроль:
.
Задания. Покажите, что
1. где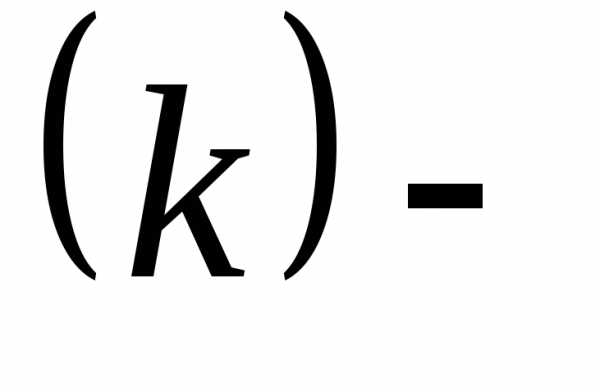 штрихозначает
штрихозначает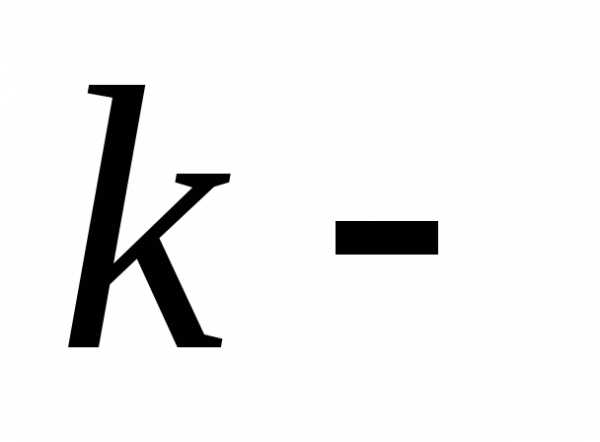 ю
производную функции
ю
производную функции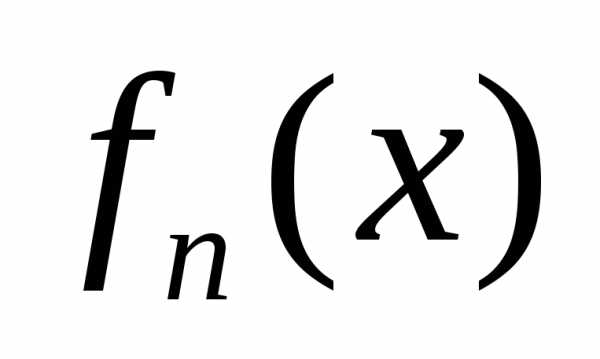 по
параметру
по
параметру причём
причём
2. 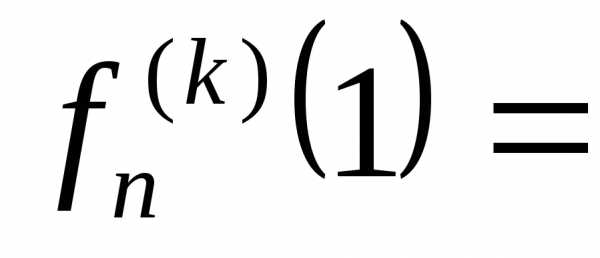
3.,
где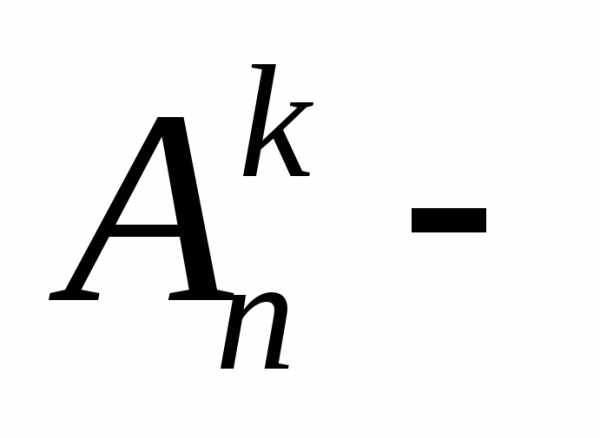 число
размещений из
число
размещений из элементов по
элементов по .
.
Заметим, что вероятности 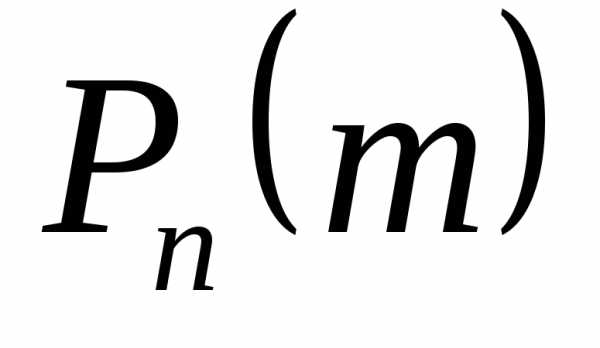 ,являются коэффициентами при степени
,являются коэффициентами при степени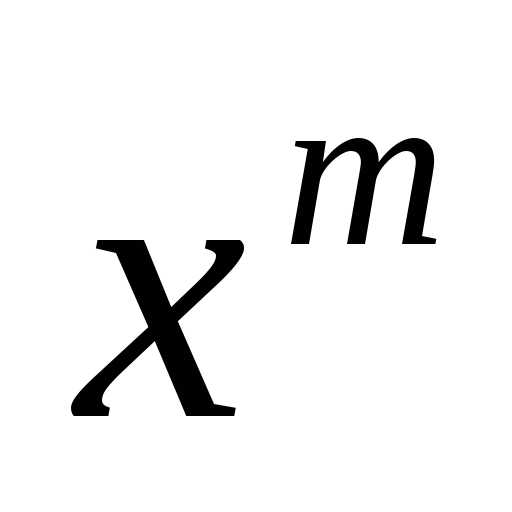 в разложении
в разложении
.
6. Плотность распределения вероятностей
непрерывной случайной величины
Важнейшей характеристикой непрерывной
случайной величины (кроме функции
распределения) является так называемая функция плотности распределения.Напомним, что «Случайную величину 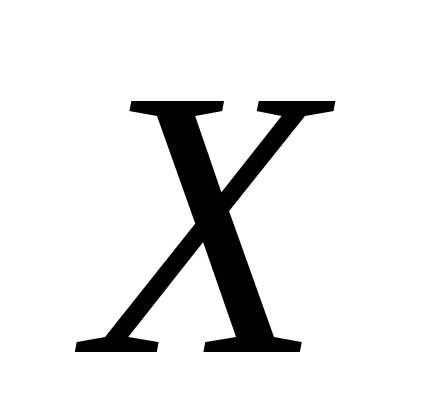 называют непрерывной, если ее функция
распределения
называют непрерывной, если ее функция
распределения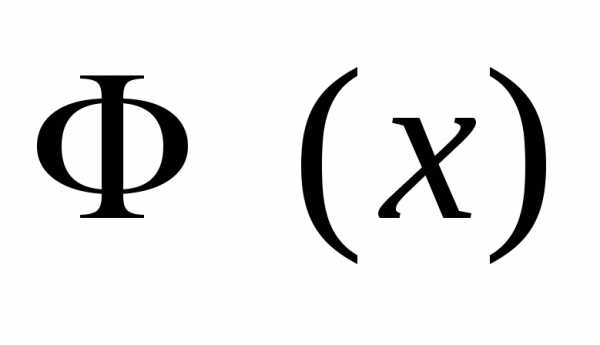 непрерывна
в любой точке и дифференцируема всюду,
за исключением, может быть отдельных
точек».
непрерывна
в любой точке и дифференцируема всюду,
за исключением, может быть отдельных
точек».
Плотностью распределения вероятностейнепрерывнойслучайной величины 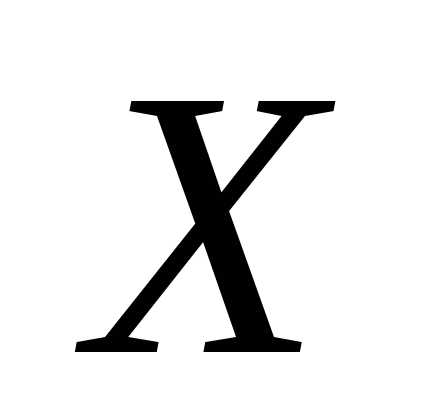 называют некоторую функцию
называют некоторую функцию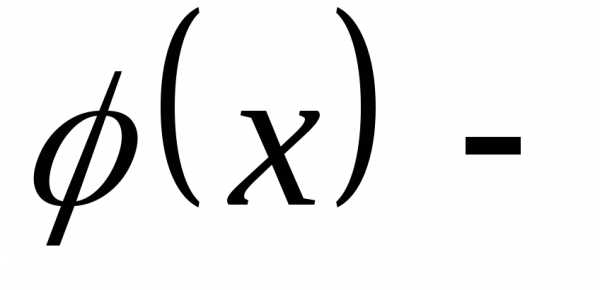 первую производную от функции
распределения
первую производную от функции
распределения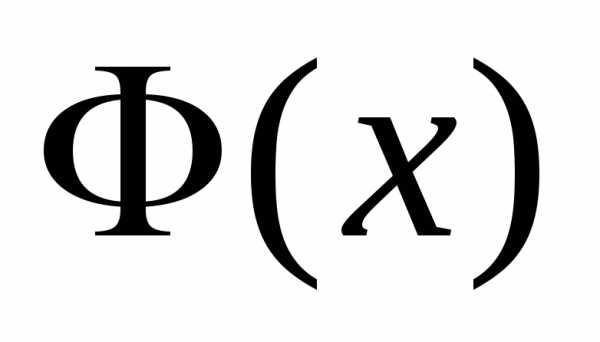 :
:
(7) .
Из этого определения следует, что функция распределения является первообразной функциейдля функции плотности распределения.
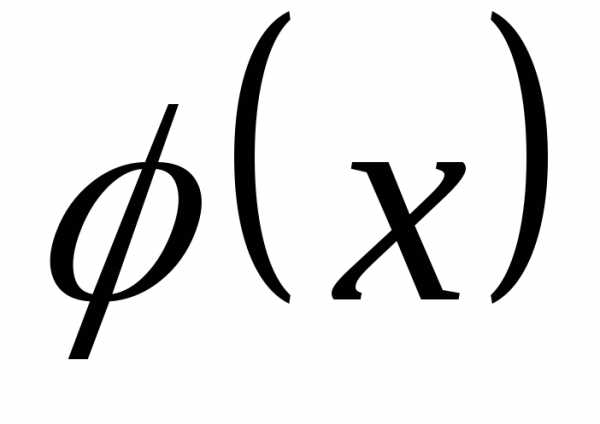 называют такжедифференциальной
функцией распределения: она выражает
одной из форм закона распределения
случайной величины, относящихся только
к непрерывным случайным величинам.
называют такжедифференциальной
функцией распределения: она выражает
одной из форм закона распределения
случайной величины, относящихся только
к непрерывным случайным величинам. Следует заметить, что для описания
распределения вероятностей д.с.в. 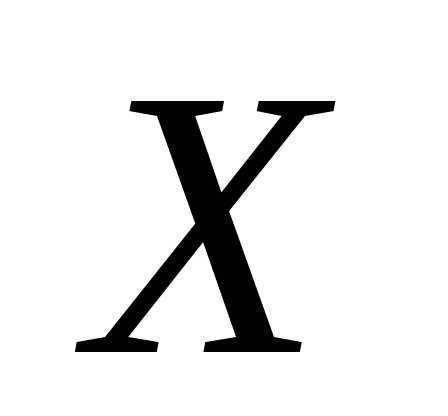 понятие
плотность распределения неприменима.
понятие
плотность распределения неприменима.
Рассмотрим вероятностный смысл плотности распределения. По определению производной функции имеем
Далее, согласно формуле (2), выполняется равенство
Отношение 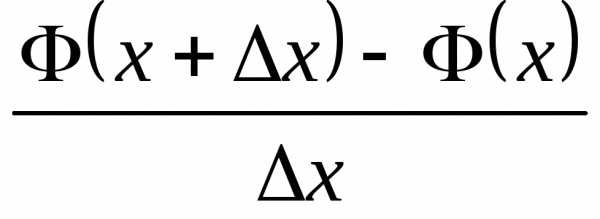 представляет собой «среднюю вероятность»,
которая приходится на единицу длины
участка.
Тогда получим
представляет собой «среднюю вероятность»,
которая приходится на единицу длины
участка.
Тогда получим
(8) ,
т.е.
плотность распределения  н.с.в.
н.с.в. 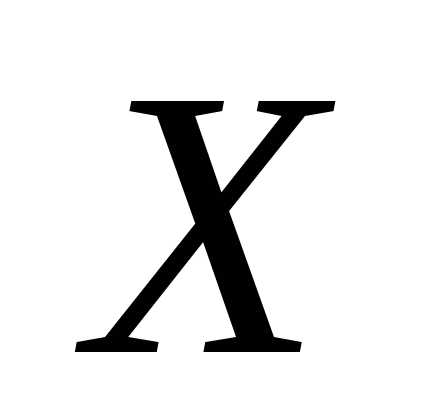 равна
пределу отношения вероятности попадания
н.с.в.
равна
пределу отношения вероятности попадания
н.с.в. в
промежутокк длине
в
промежутокк длине этого промежутка, когда величина
этого промежутка, когда величина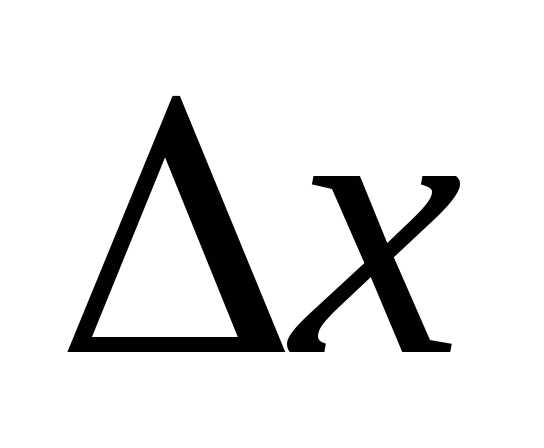 стремиться к нулю. Из равенства (8)
следует, что.
стремиться к нулю. Из равенства (8)
следует, что.
Тем самым, установлено, что плотность
вероятности н.с.в. 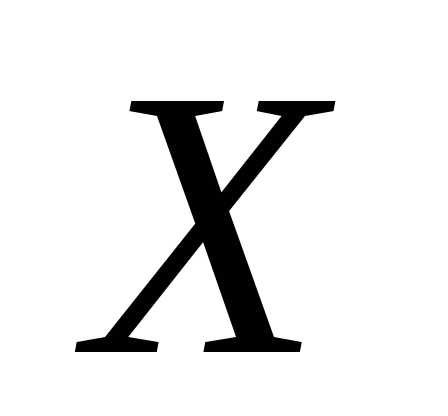 определяется
как функция
определяется
как функция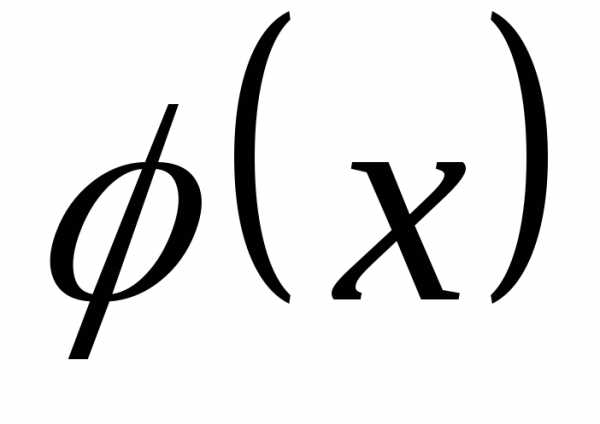
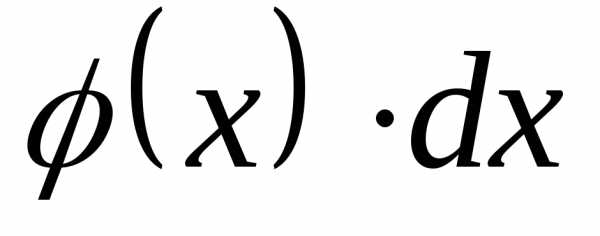 называетсяэлементом вероятности.
называетсяэлементом вероятности. Следует отметить, что понятие функции
плотности распределения вероятности  ,
аналогично таким понятиям, как плотность
распределения масс на оси абсцисс или
плотность распределения электрического
тока в теории электричества в физике
и т.д.
,
аналогично таким понятиям, как плотность
распределения масс на оси абсцисс или
плотность распределения электрического
тока в теории электричества в физике
и т.д.
Теперь, рассмотрим свойства функции плотности распределения.
С.1. 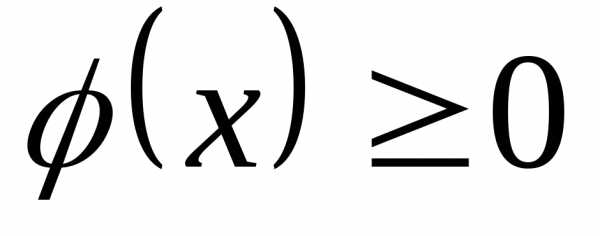 .
.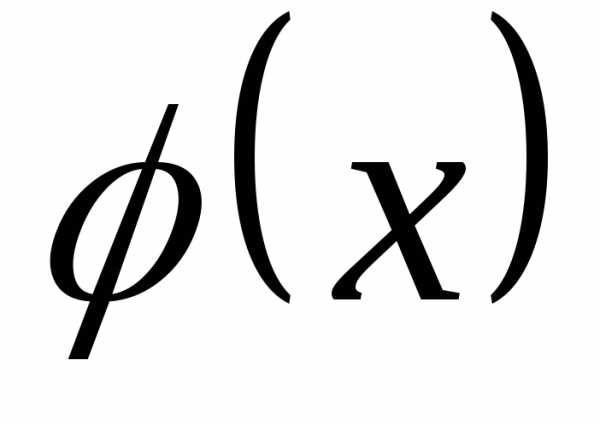 —
неотрицательная функция на всей числовой
оси.
—
неотрицательная функция на всей числовой
оси.
С.2. Вероятность попадания
н.с.в. 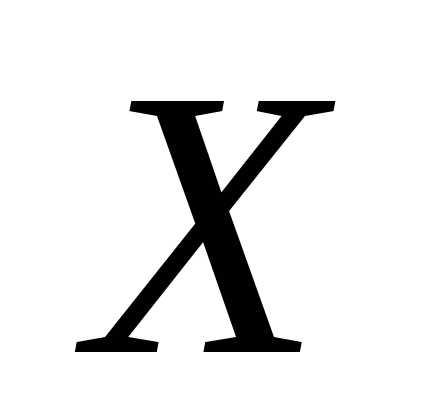 в промежуток
в промежуток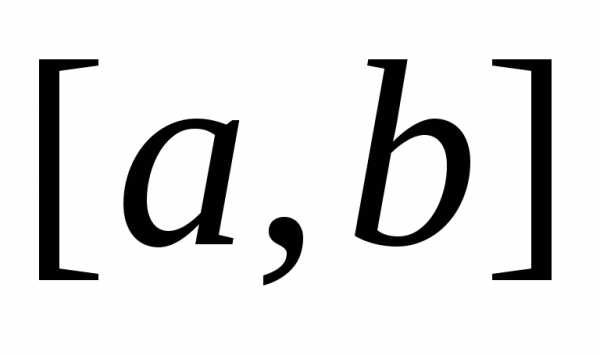 равна определенному интегралу от ее
функции плотности в пределах от
равна определенному интегралу от ее
функции плотности в пределах от до
до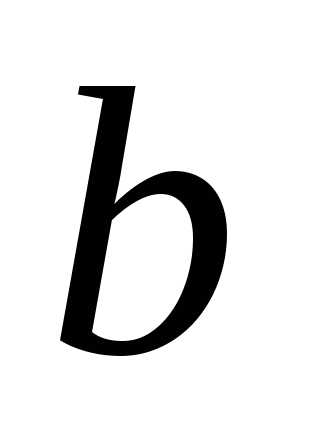 ,
т.е. верно равенство
,
т.е. верно равенство
(9)
С.3. Если 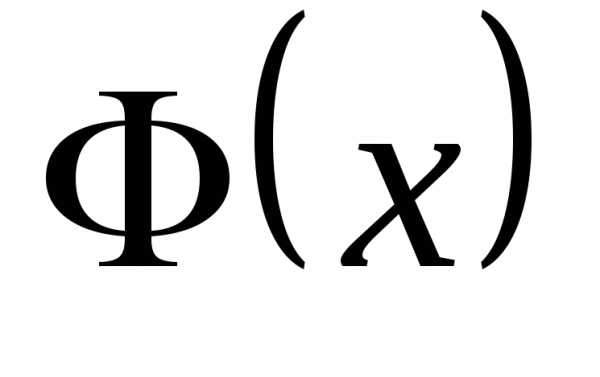 функция распределения н.с.в.
функция распределения н.с.в. и
и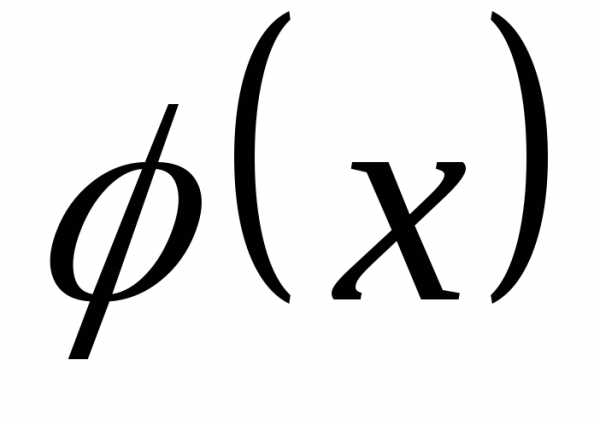 — функция плотности, то имеет место
равенство
— функция плотности, то имеет место
равенство
(10) 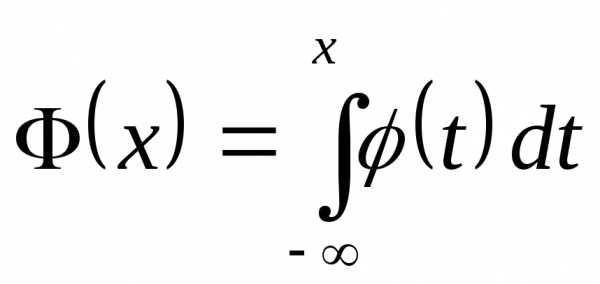 .
.
С.4. Интеграл от функции плотности
вероятности н.с.в. 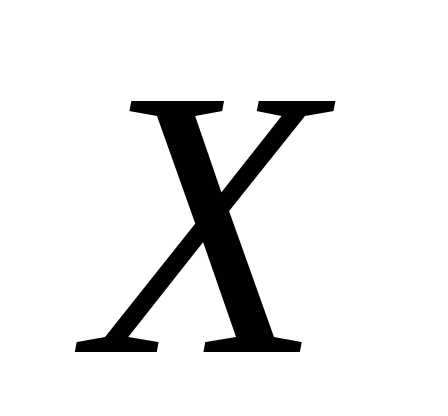 в бесконечных пределах равен единице
(условие нормировки — контроль)
т.е. если
в бесконечных пределах равен единице
(условие нормировки — контроль)
т.е. если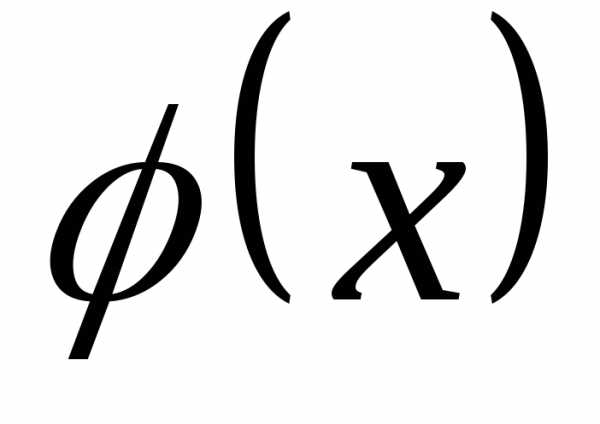 плотность распределения некоторой
с.в.
плотность распределения некоторой
с.в.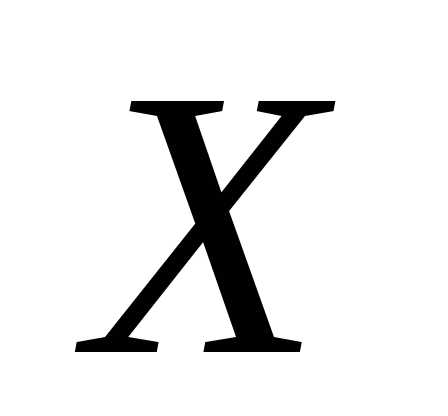 ,
тогда
,
тогда
 .
(11)
.
(11)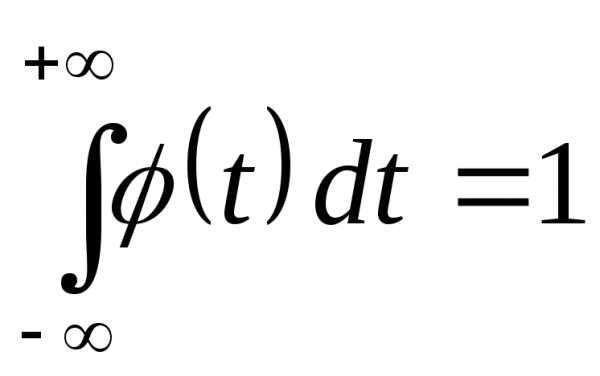 .
.
Условие нормировки для н.с.в. напоминает аналога условия «контроля» для случая д.с.в..
1.Функция плотности распределения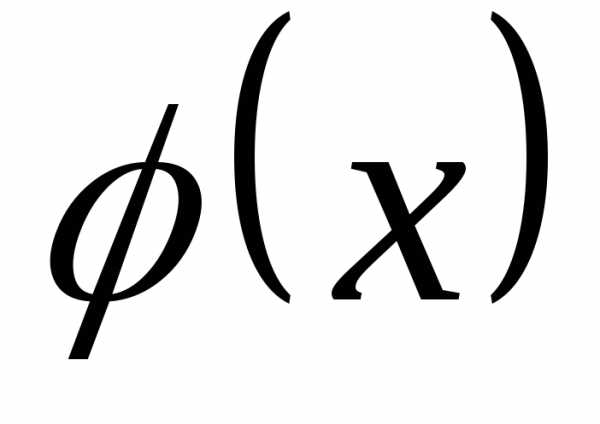 —
неотрицательная функция потому, что
по определению
—
неотрицательная функция потому, что
по определению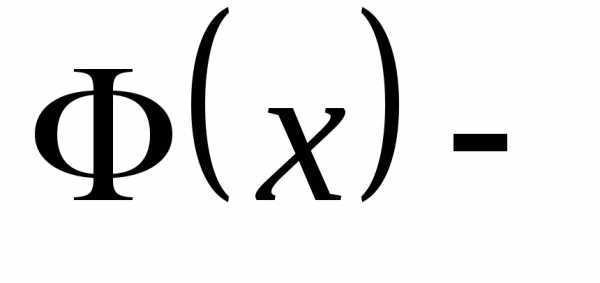 неубывающая
и монотонна, а следовательно
неубывающая
и монотонна, а следовательно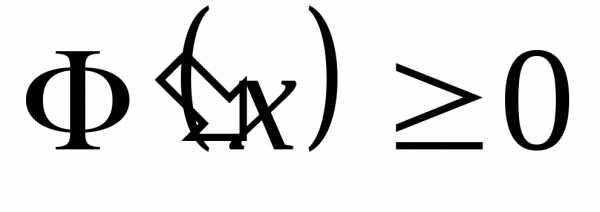 .
Это означает, что график функция
плотности, называемыйкривой
распределения, расположена не ниже
оси абсцисс, также следует отметить,
что функция плотности может принимать
сколь угодно большие значения.
.
Это означает, что график функция
плотности, называемыйкривой
распределения, расположена не ниже
оси абсцисс, также следует отметить,
что функция плотности может принимать
сколь угодно большие значения.
2.Поскольку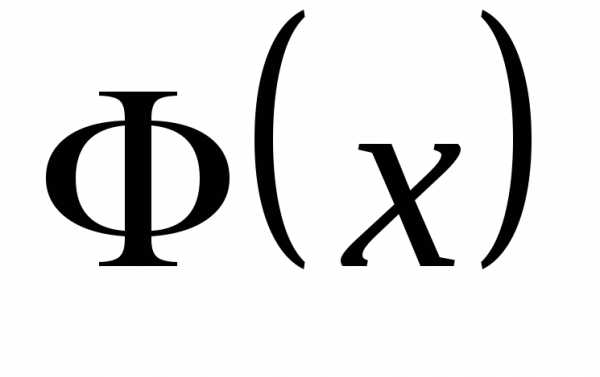 естьпервообразнаяфункцией для
функции
естьпервообразнаяфункцией для
функции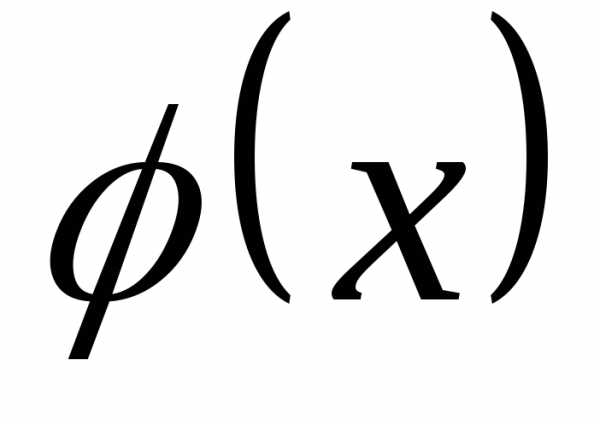 ,
тогда в соответствии с формулой
Ньютона-Лейбница справедливо равенство
,
тогда в соответствии с формулой
Ньютона-Лейбница справедливо равенство
(12)
Отсюда, согласно определению функции 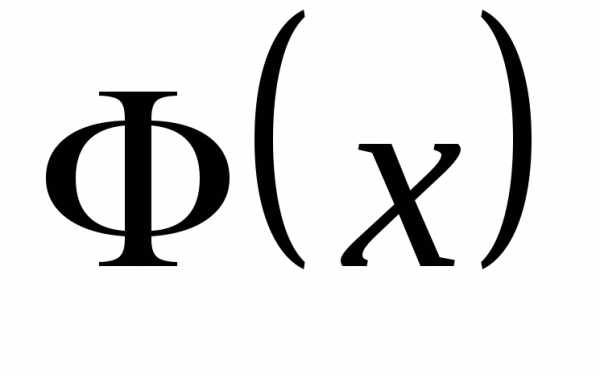 получим
получим
(13) .
Геометрический смысл этого равенства
следующее: интеграл от элемента
вероятностиесть площадь фигуры
( ),
ограниченной сверху кривой распределения
),
ограниченной сверху кривой распределения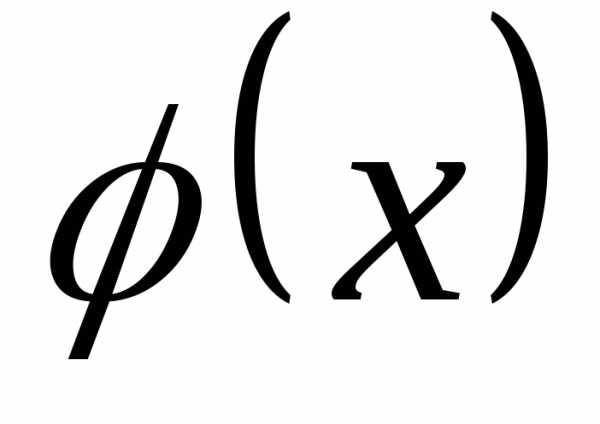 и опирающейся на отрезок [a;b]
и опирающейся на отрезок [a;b]
рис.21-Письменный
3.На основании свойстваС.2. И то, чтополучим:
(14) .
4.Подставляя в формуле (13) соответственно, получаем достоверное событиет.е.
(15) .
Геометрическая трактовка свойство С.4.(свойство нормировки) означает,
что площадь фигуры (S)
ограниченной функцией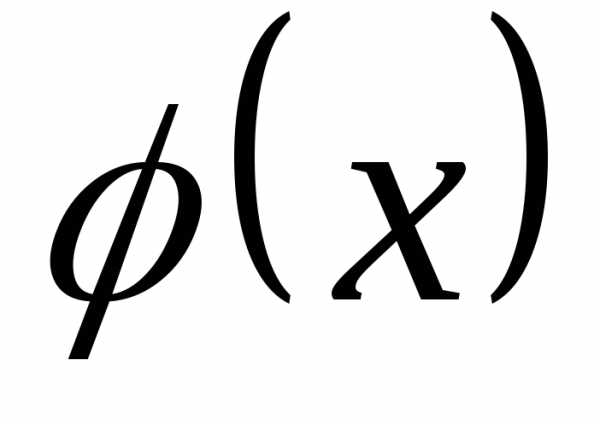 и числовой осью абсцисс
и числовой осью абсцисс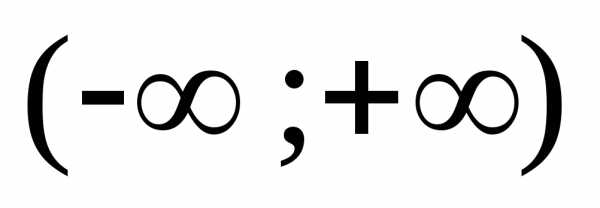 ,
равна единице.
,
равна единице.
Теперь, мы можем дать определение
непрерывной с.в. в связи с функцией
распределения плотности 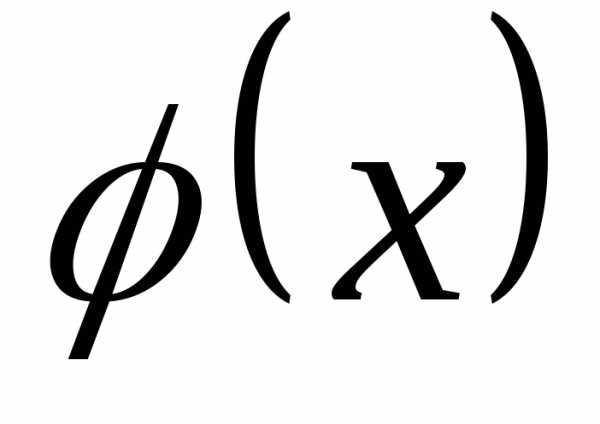 :случайная величина
:случайная величина 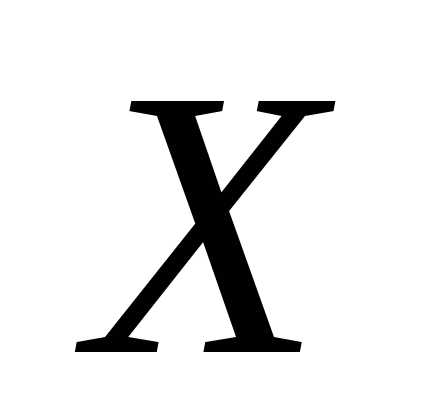 называетсянепрерывной, если существует
неотрицательная функция
называетсянепрерывной, если существует
неотрицательная функция 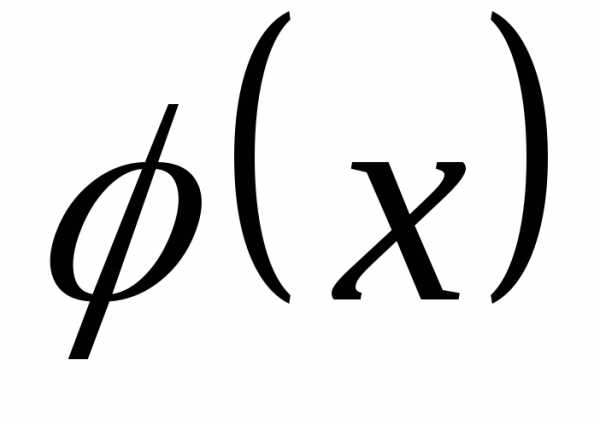 такая, что при любом
такая, что при любом её функция распределения
её функция распределения 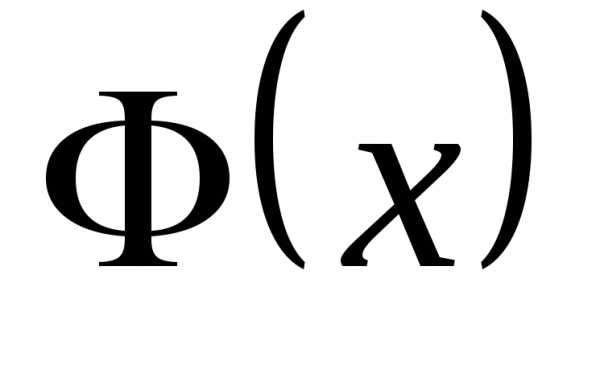 можно представить в виде
можно представить в виде
;
отсюда получим равенство —дифференциальное равенство (дифференциальный закон распределения).
Следовательно, функций 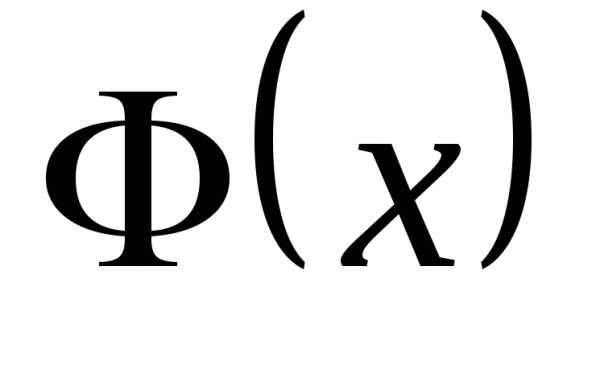 и
и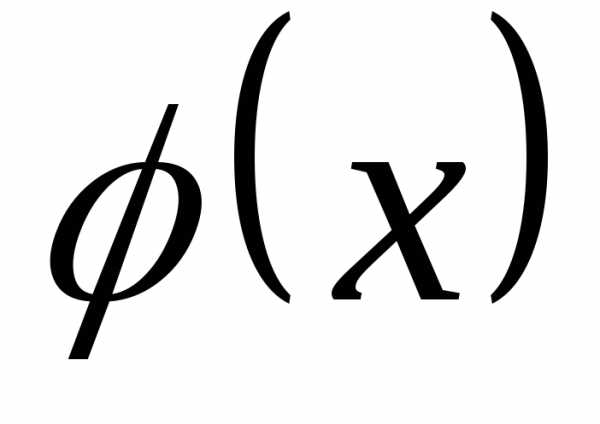 являются равноправными (эквивалентными)
характеристиками случайной величины
являются равноправными (эквивалентными)
характеристиками случайной величины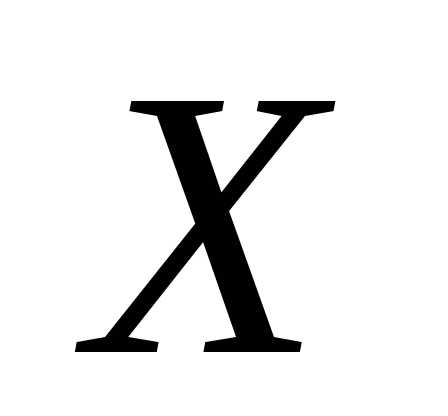 .
Отметим, что на основании формулы (13)
непосредственно следует равенство
.
Отметим, что на основании формулы (13)
непосредственно следует равенство
.
Отсюда, также следуют равенства:
 .
.
Пример 9. Пусть плотность распределения
с.в.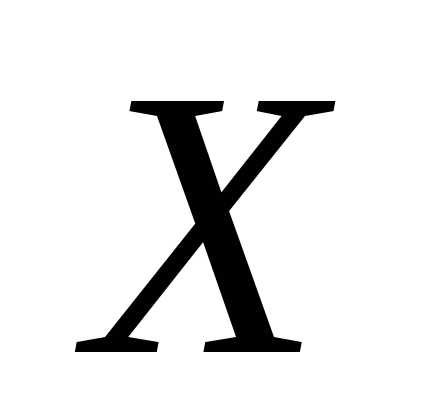 задана функцией,
задана функцией,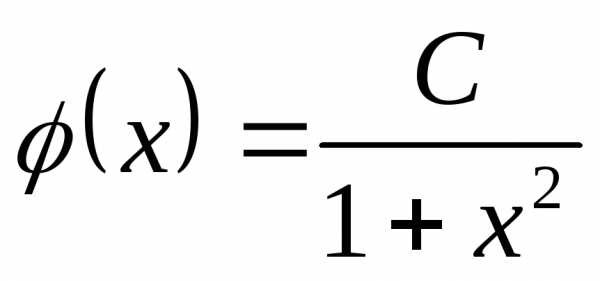 .
.
1. Найти значение параметра  ,
при котором
,
при котором будет
функцией плотности,
будет
функцией плотности,
2. Выписать функцию распределения 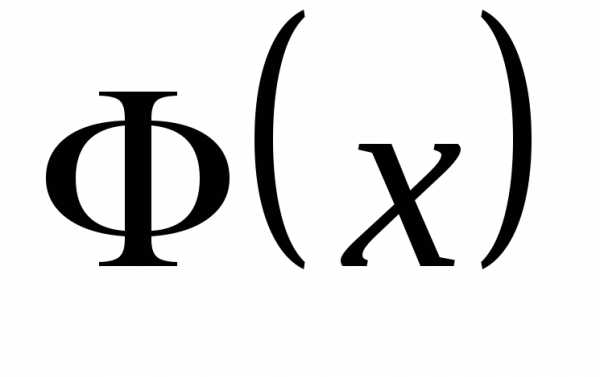 .
.
Решение. На основанииС.4. должно выполняться равенство (см.(11))
 .
.
Применяя метод подсчёта несобственных интегралов, при этом воспользуюсь табличным интегралом для функции арктангенса с последующим применением формулы Ньютона –Лейбница получим
.
Следовательно, 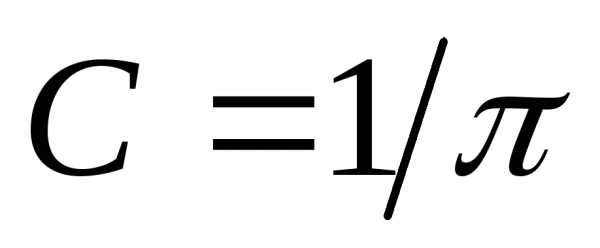 .
Далее, выпишем функцию распределения
с.в.
.
Далее, выпишем функцию распределения
с.в. плотность распределения которой равна
плотность распределения которой равна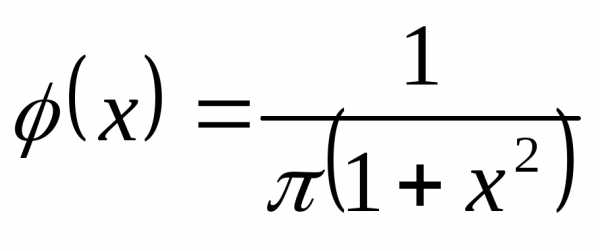 .
Проведя обычные рассуждения на основании
формулы (14) получим
.
Проведя обычные рассуждения на основании
формулы (14) получим
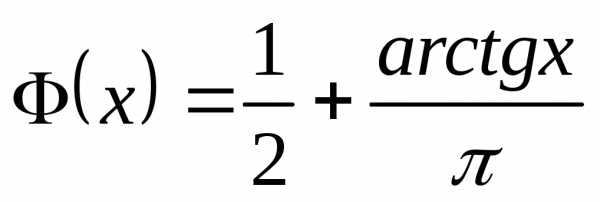 .
.
Такое распределение называют распределением Коши.
Задание. Проверьте справедливость
дифференциального закона распределения
и убедитесь, что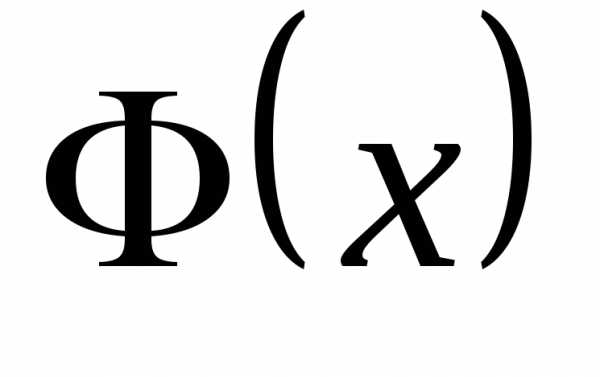 является первообразной функцией
является первообразной функцией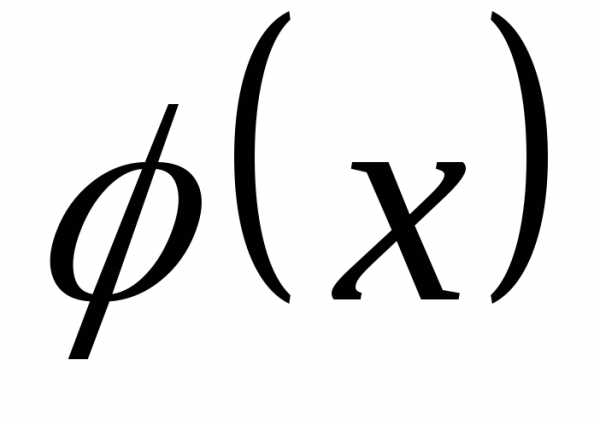 .
.
Пример 9. Пусть плотность распределения
с.в.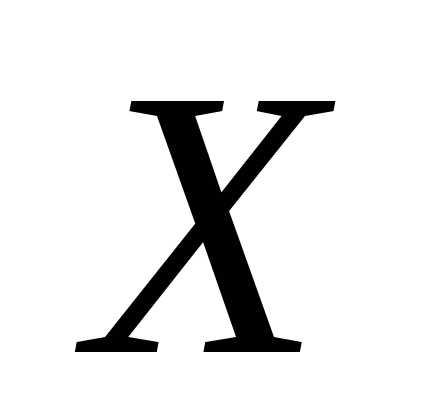 задана функцией,
задана функцией,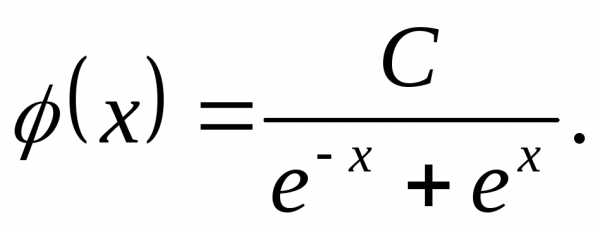
1. Найти значение параметра  ,
при котором
,
при котором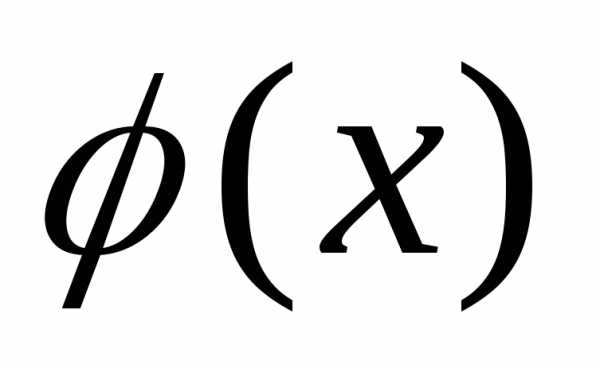 будет
функцией плотности,
будет
функцией плотности,
2. Выписать функцию распределения  .
.
Решение. Аналогично как в примере 1 пользуясь равенством (11) получим
Следовательно,
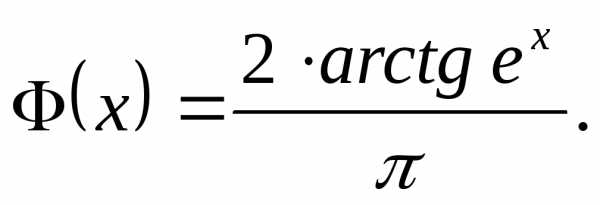
Задание. 1. Проверьте
справедливость дифференциального
закона распределения
и убедитесь, что 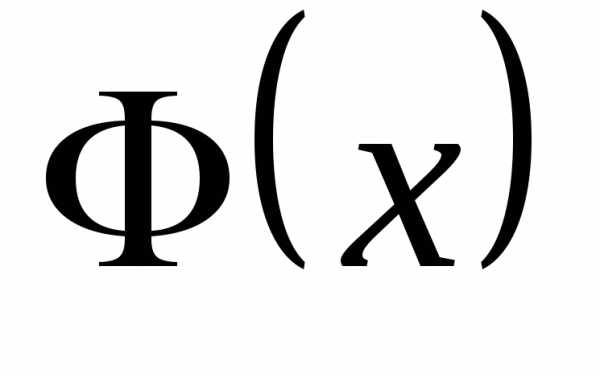 является первообразной функцией для
является первообразной функцией для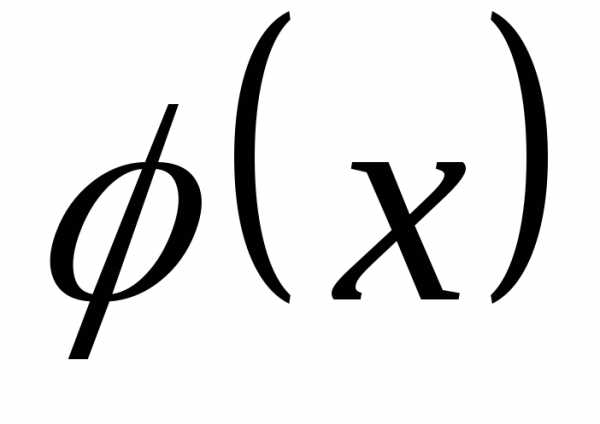 .
.
2. Пусть
и плотность распределения н.с.в. задана функцией
задана функцией
Найти значение параметра C, выписать явный вид функции распределения и проверить выполнение дифференциального закона.
Пример 10. Однородная проволока
длиной 1 м. растягивается за концы и
при этом разрывается. Пусть случайная
величина, равная расстоянию от точки
разрыва до левого конца проволки.
Используя геометрические вероятности,
найдём, что
случайная
величина, равная расстоянию от точки
разрыва до левого конца проволки.
Используя геометрические вероятности,
найдём, что
для любых Следовательно, функция распределения и плотность распределения этой случайной величины имеют вид:
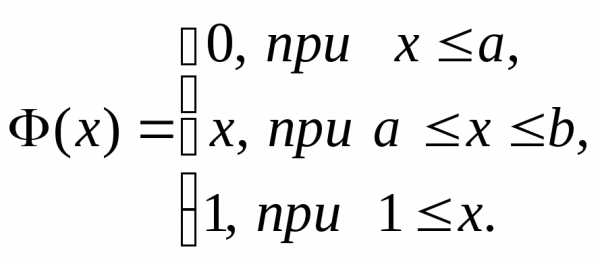
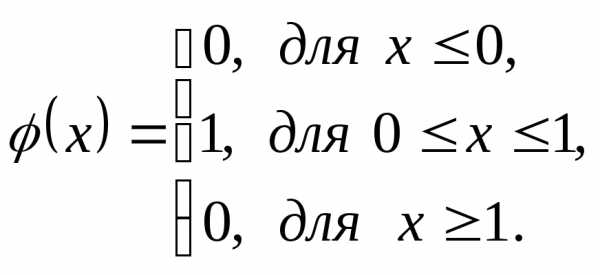
Задание. Проверьте выполнения дифференциального закона.
studfiles.net
5. Производящая функция дискретной случайной величины
Кратко остановимся на понятие производящей функции конечных дискретных случайных величин.
Функцию определённую равенством , где некоторый параметр называют производящей функцией для последовательности повторных независимых опытов. Очевидно, что приимеет место равенство
,
для любого натурального числа
Пусть производится испытаний, причём в первом испытания вероятность появления событияравнаво втором равнавм испытании равнаи вероятностинепоявлениясобытиясоответственно равныЗаобозначим вероятность появления событиявиспытаниях ровнораз.
Производящей функцией вероятностей называют функцию, определяемую равенством
()
Таким образом, вероятность равна коэффициенту прий степени многочлена, определённой равенством (), т.е. равна коэффициенту прив разложении производящей функции по степеням.
Замечание. Отметим, что придолжно выполняться равенство (обычно называется контроль).
().
При имеем равенство
.
Следовательно, коэффициент при равно, приравнои при.
Следует заметить, что если в различных испытаниях появляется различные события (в первом испытании событие , во втором событиеи т.д.), то изменяется лишь истолкование коэффициентов при различных степенях. Например, в равенстве () коэффициентопределяет вероятность появления двух событийи.
Пример 8. Устройство состоит из трёх независимо работающих элементов. Вероятности безотказной работы элементов (за время) соответственно равныНайти вероятности того, что за времябудут работать безотказно:
а) все три элемента работают;
б) два элемента работают;
в) один элемент работает;
г) ни один из элементов не будет работать.
Решение. Вероятности безотказной работы элементов соответственно равныСледовательно, вероятности того, что элементы откажут, соответственно равны
Составим производящую функцию:
а) Вероятность того, что три элемента будут работать безотказно, равна коэффициенту при
б) Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при
в) Вероятность того, что один элемент будет работать безотказно, равна коэффициенту при
г) Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену:
Легко видет, что выполняется контроль:
.
Задания. Покажите, что
1. гдештрихозначаетю производную функциипо параметрупричём
2.
3.,
гдечисло размещений изэлементов по.
Заметим, что вероятности ,являются коэффициентами при степенив разложении
.
6. Плотность распределения вероятностей
непрерывной случайной величины
Важнейшей характеристикой непрерывной случайной величины (кроме функции распределения) является так называемая функция плотности распределения.Напомним, что «Случайную величину называют непрерывной, если ее функция распределениянепрерывна в любой точке и дифференцируема всюду, за исключением, может быть отдельных точек».
Плотностью распределения вероятностейнепрерывнойслучайной величины называют некоторую функциюпервую производную от функции распределения:
(7) .
Из этого определения следует, что функция распределения является первообразной функциейдля функции плотности распределения.
Функцию называют такжедифференциальной функцией распределения: она выражает одной из форм закона распределения случайной величины, относящихся только к непрерывным случайным величинам.
Следует заметить, что для описания распределения вероятностей д.с.в. понятие плотность распределения неприменима.
Рассмотрим вероятностный смысл плотности распределения. По определению производной функции имеем
Далее, согласно формуле (2), выполняется равенство
Отношение представляет собой «среднюю вероятность», которая приходится на единицу длины участка. Тогда получим
(8) ,
т.е. плотность распределения н.с.в. равна пределу отношения вероятности попадания н.с.в.в промежутокк длинеэтого промежутка, когда величинастремиться к нулю. Из равенства (8) следует, что.
Тем самым, установлено, что плотность вероятности н.с.в. определяется как
функция удовлетворяющая, условию. Выражениеназываетсяэлементом вероятности.
Следует отметить, что понятие функции плотности распределения вероятности , аналогично таким понятиям, как плотность распределения масс на оси абсцисс или плотность распределения электрического тока в теории электричества в физике и т.д.
Теперь, рассмотрим свойства функции плотности распределения.
С.1. .— неотрицательная функция на всей числовой оси.
С.2. Вероятность попадания н.с.в. в промежутокравна определенному интегралу от ее функции плотности в пределах отдо, т.е. верно равенство
(9)
С.3. Если функция распределения н.с.в.и- функция плотности, то имеет место равенство
(10) .
С.4. Интеграл от функции плотности вероятности н.с.в. в бесконечных пределах равен единице (условие нормировки — контроль) т.е. еслиплотность распределения некоторой с.в., тогда
. (11).
Условие нормировки для н.с.в. напоминает аналога условия «контроля» для случая д.с.в..
1.Функция плотности распределения- неотрицательная функция потому, что по определениюнеубывающая и монотонна, а следовательно. Это означает, что график функция плотности, называемыйкривой распределения, расположена не ниже оси абсцисс, также следует отметить, что функция плотности может принимать сколь угодно большие значения.
2.Посколькуестьпервообразнаяфункцией для функции, тогда в соответствии с формулой Ньютона-Лейбница справедливо равенство
(12)
Отсюда, согласно определению функции получим
(13) .
Геометрический смысл этого равенства следующее: интеграл от элемента вероятностиесть площадь фигуры (), ограниченной сверху кривой распределенияи опирающейся на отрезок [a;b]
рис.21-Письменный
3.На основании свойстваС.2. И то, чтополучим:
(14) .
4.Подставляя в формуле (13) соответственно, получаем достоверное событиет.е.
(15) .
Геометрическая трактовка свойство С.4.(свойство нормировки) означает, что площадь фигуры (S) ограниченной функциейи числовой осью абсцисс, равна единице.
Теперь, мы можем дать определение непрерывной с.в. в связи с функцией распределения плотности :случайная величина называетсянепрерывной, если существует неотрицательная функция такая, что при любом её функция распределения можно представить в виде
;
отсюда получим равенство —дифференциальное равенство (дифференциальный закон распределения).
Следовательно, функций иявляются равноправными (эквивалентными) характеристиками случайной величины. Отметим, что на основании формулы (13) непосредственно следует равенство
.
Отсюда, также следуют равенства:
.
Пример 9. Пусть плотность распределения с.в.задана функцией,.
1. Найти значение параметра , при которомбудет функцией плотности,
2. Выписать функцию распределения .
Решение. На основанииС.4. должно выполняться равенство (см.(11))
.
Применяя метод подсчёта несобственных интегралов, при этом воспользуюсь табличным интегралом для функции арктангенса с последующим применением формулы Ньютона –Лейбница получим
.
Следовательно, . Далее, выпишем функцию распределения с.в.плотность распределения которой равна. Проведя обычные рассуждения на основании формулы (14) получим
.
Такое распределение называют распределением Коши.
Задание. Проверьте справедливость дифференциального закона распределения и убедитесь, чтоявляется первообразной функцией.
Пример 9. Пусть плотность распределения с.в.задана функцией,
1. Найти значение параметра , при которомбудет функцией плотности,
2. Выписать функцию распределения .
Решение. Аналогично как в примере 1 пользуясь равенством (11) получим
Следовательно,
Задание. 1. Проверьте справедливость дифференциального закона распределения и убедитесь, что является первообразной функцией для.
2. Пусть и плотность распределения н.с.в.задана функцией
Найти значение параметра C, выписать явный вид функции распределения и проверить выполнение дифференциального закона.
Пример 10. Однородная проволока длиной 1 м. растягивается за концы и при этом разрывается. Пустьслучайная величина, равная расстоянию от точки разрыва до левого конца проволки. Используя геометрические вероятности, найдём, что
для любых Следовательно, функция распределения и плотность распределения этой случайной величины имеют вид:
Задание. Проверьте выполнения дифференциального закона.
studfiles.net
3.2. Производящие и характеристические функции
Пусть X – целочисленная, неотрицательная случайная величина с законом распределения вероятностей:
, k=0,1,2,… .
Производящей
функцией случайной величины X называется неслучайная функция 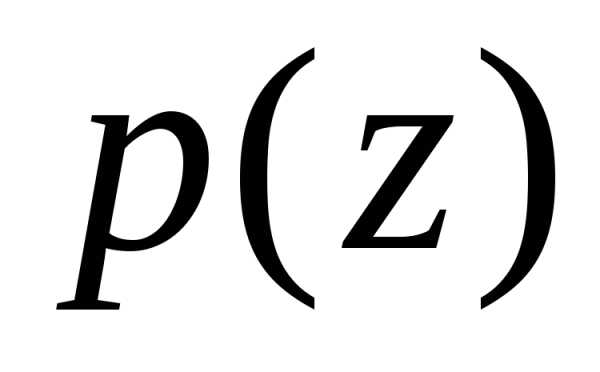 ,
определяемая при
,
определяемая при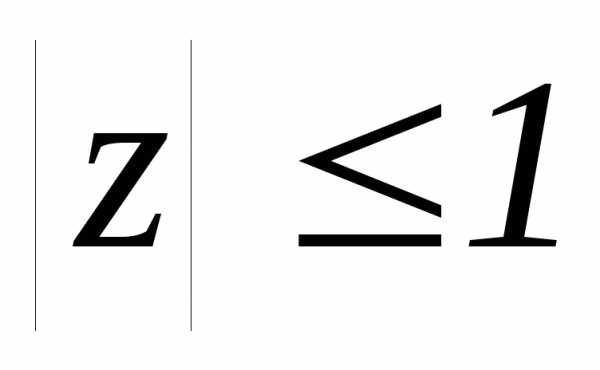 равенством:
равенством:
.
Производящая функция  является аналитической внутри единичного
круга
является аналитической внутри единичного
круга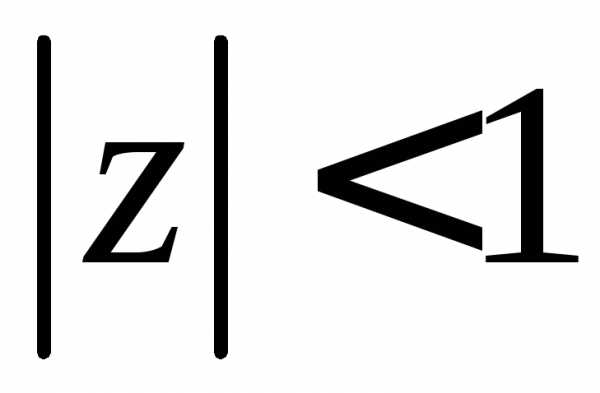 и по ней закон распределения случайной
величиныXоднозначно
определяется равенствами:
и по ней закон распределения случайной
величиныXоднозначно
определяется равенствами:
 ,
где
,k0.
,
где
,k0.
Величину MX(X-1)…(X—k+1)называютk-ым факториальным моментом. Если
конеченk-ый факториальный
момент, то существует левосторонняя
производная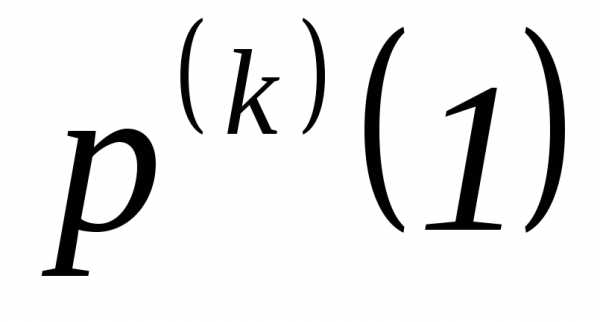 и
и
.
В частности,
, .
Производящая функция 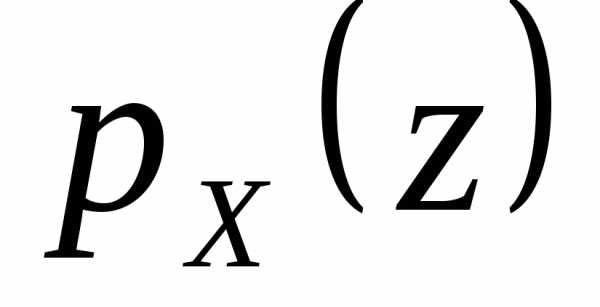 суммынезависимых случайных величин равна
произведению производящих функций
слагаемых:
суммынезависимых случайных величин равна
произведению производящих функций
слагаемых:
.
Характеристической функцией случайной
величиныХназывается
комплекснозначная неслучайная функция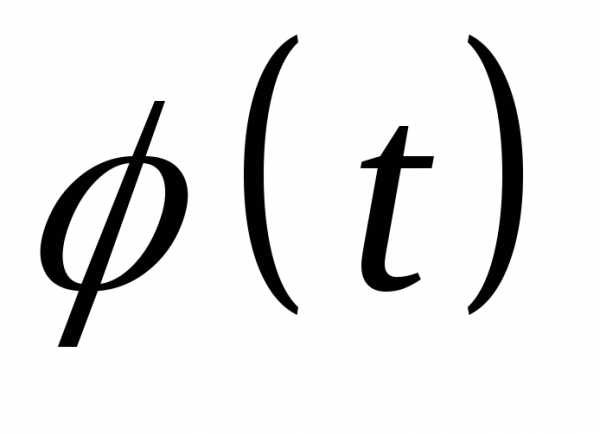 вещественного аргументаt,
определяемая равенством:
вещественного аргументаt,
определяемая равенством:
.
Для дискретной случайной величины Х,
принимающей значения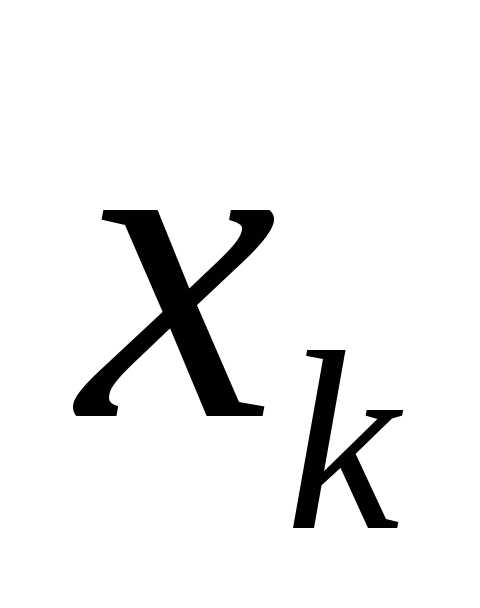 с вероятностямиpk,
характеристическая функция представляет
собой ряд Фурье:
с вероятностямиpk,
характеристическая функция представляет
собой ряд Фурье:
.
Если Х — непрерывная случайная
величина с плотностью вероятностей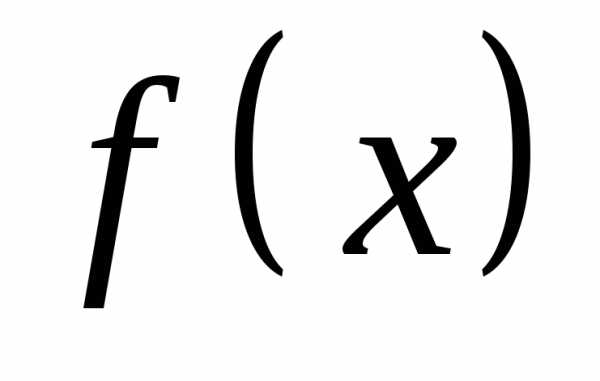 ,
то характеристическая функция есть
преобразование Фурье плотности
вероятностей:
,
то характеристическая функция есть
преобразование Фурье плотности
вероятностей:
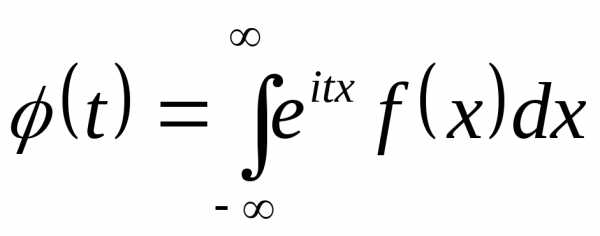 .
.
Характеристическая функция обладает следующими основными свойствами:
1. , .
2.  равномерно непрерывна на всей числовой
прямой.
равномерно непрерывна на всей числовой
прямой.
3. . В частности, вещественная характеристическая функция является четной.
4. 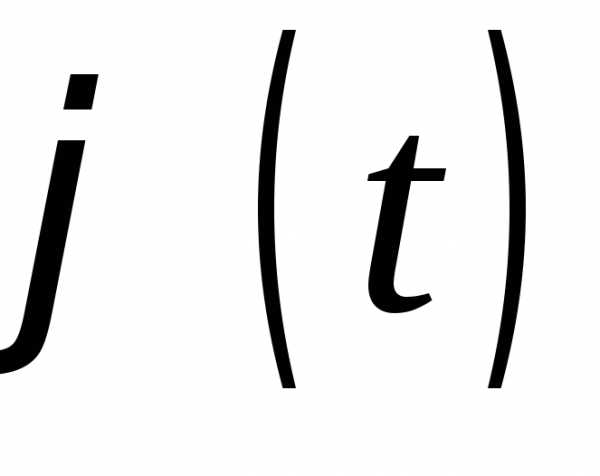 неотрицательно определена, т. е. для
любого конечногоn1, для любых комплексных чиселz1,…,znи любых действительных чиселt1,…,tn спра-
неотрицательно определена, т. е. для
любого конечногоn1, для любых комплексных чиселz1,…,znи любых действительных чиселt1,…,tn спра-
ведливо неравенство
.
5. Если  –характеристическая функция случайной
величиныX,то
случайная величинаимеет характеристическую функцию.
–характеристическая функция случайной
величиныX,то
случайная величинаимеет характеристическую функцию.
6. Характеристическая функция 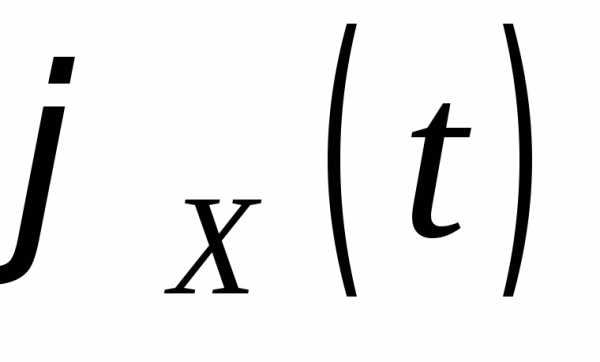 суммынезависимых случайных величин равна
произведению характеристических функций
слагаемых:
суммынезависимых случайных величин равна
произведению характеристических функций
слагаемых:
.
7. Если у случайной величины Хсуществует момент порядкаn,то характеристическая функция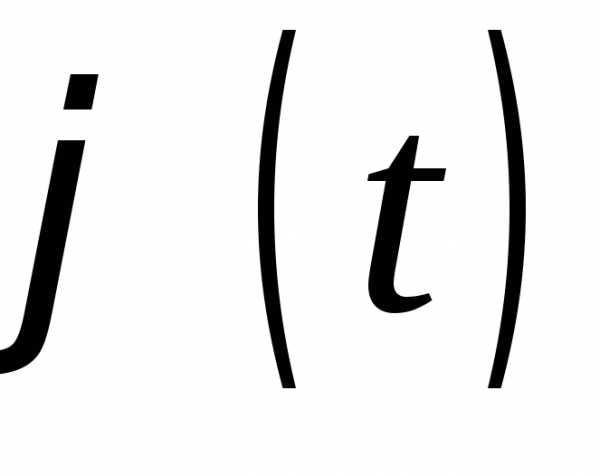 имеетnнепрерывных
производных и
имеетnнепрерывных
производных и
.
Функция распределения 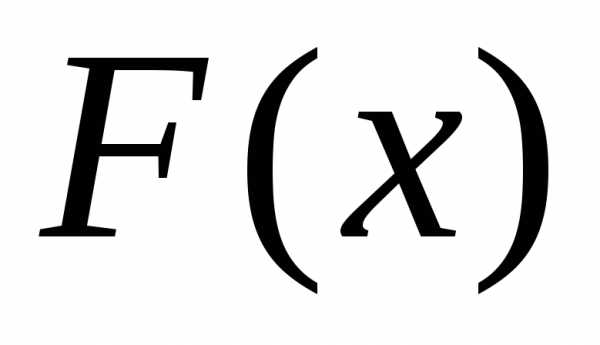 однозначно определяется своей
характеристической функцией
однозначно определяется своей
характеристической функцией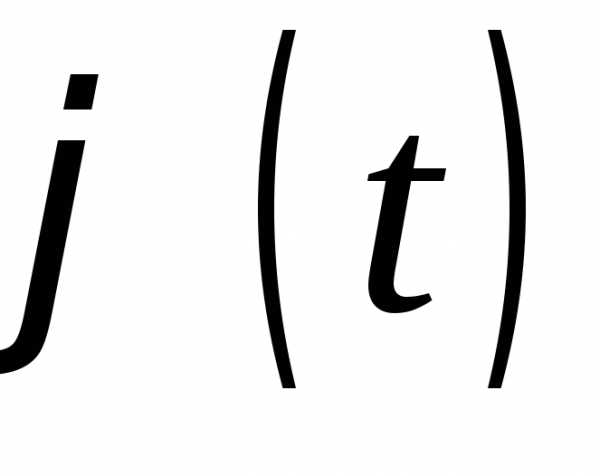 .Имеет место следующая формула обращения:
.Имеет место следующая формула обращения:
для
любых точек x и y,
являющихся точками непрерывности
функции 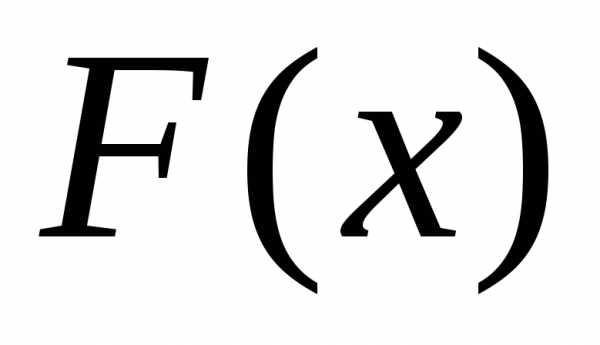 .
.
Если характеристическая функция 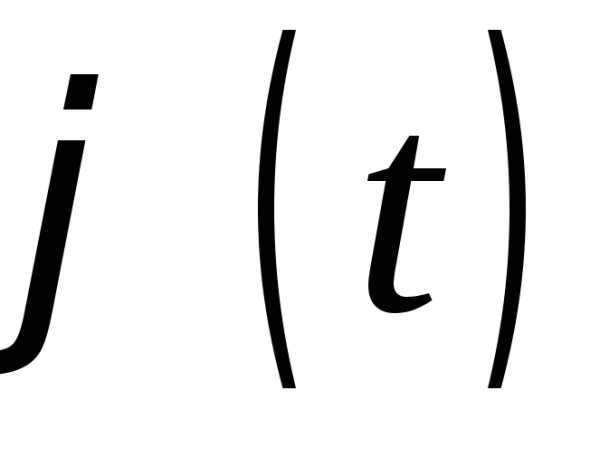 абсолютно интегрируема, т.е.
абсолютно интегрируема, т.е.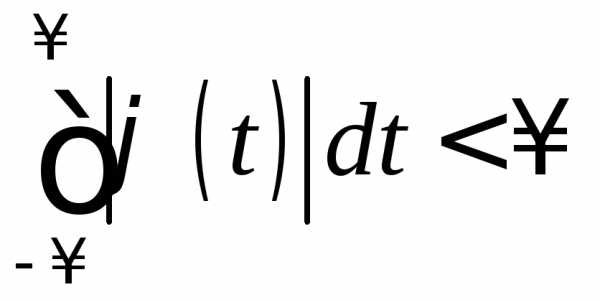 ,
то у случайной величины существует
плотность вероятностейи
,
то у случайной величины существует
плотность вероятностейи
.
Характеристической функцией
случайного вектора называется комплекснозначная неслучайная
функцияn вещественных
переменных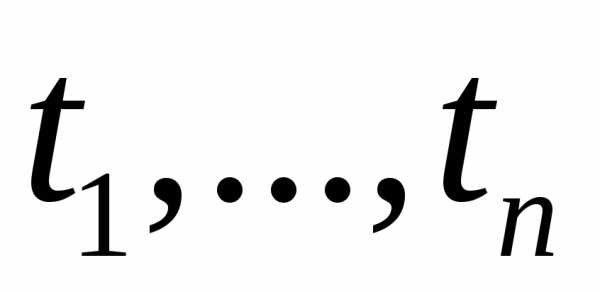 ,
определяемая равенством:
,
определяемая равенством:
,
где 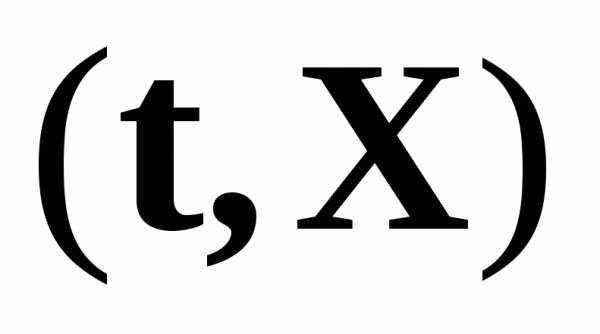 —
скалярное произведение векторов.
—
скалярное произведение векторов.
Пример 1. Найти производящую
функцию геометрической случайной
величины с параметромр>0 и с ее помощью
найти
с параметромр>0 и с ее помощью
найти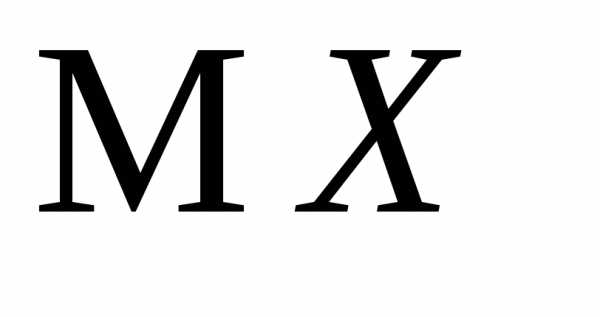 и
и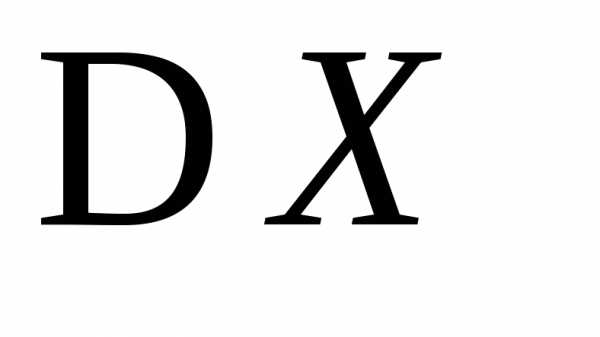 .
.
Решение. Геометрическая случайная
величина принимает значенияс
вероятностями.Поэтому
производящая функции этой случайной
величины имеет вид:
принимает значенияс
вероятностями.Поэтому
производящая функции этой случайной
величины имеет вид:
.
Найдем с помощью производящей функции
математическое ожидание и дисперсию
случайной величины 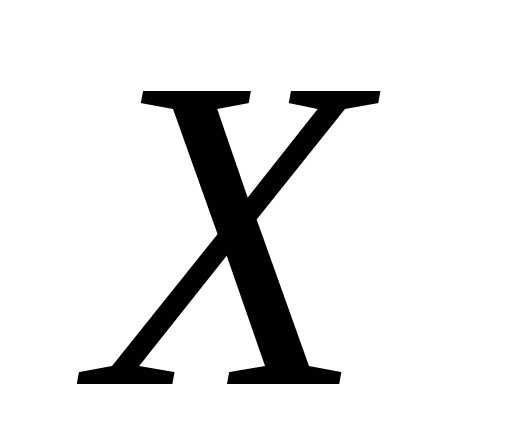 .
.
.
Отметим, что нахождение числовых характеристик геометрической случайной величины через производящую функцию существенно проще, чем непосредственным подсчетом.
Пример 2.Найти характеристическую
функцию случайной величины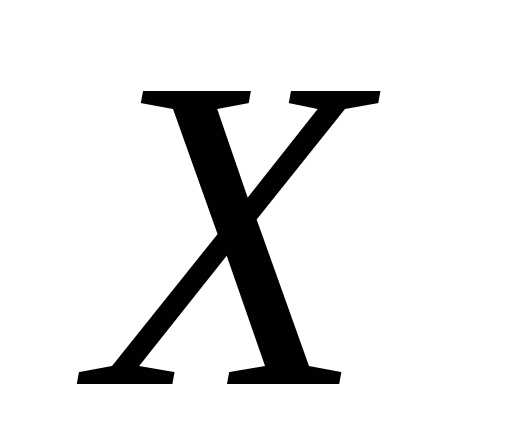 ,
имеющей равномерное распределение на
отрезке
,
имеющей равномерное распределение на
отрезке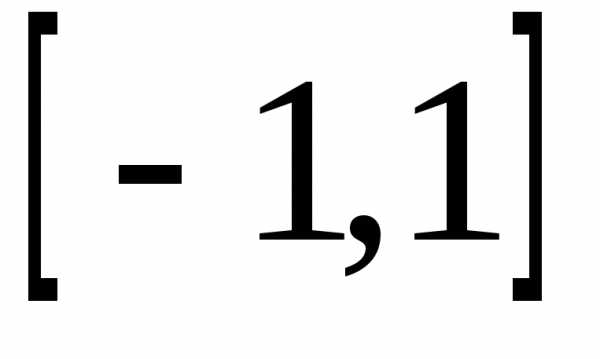 .
.
Решение. Случайная величинаимеет плотность вероятностей
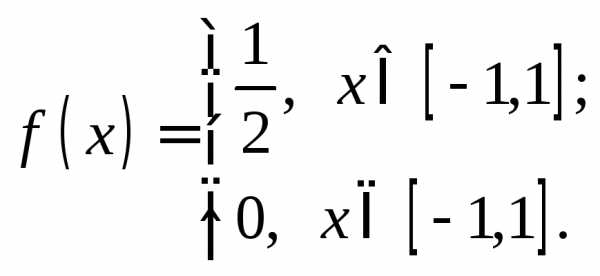
Поэтому
.
Пример
3. Характеристическая функция непрерывной
случайной величины  имеет вид.
Найти плотность вероятностей этой
случайной величины.
имеет вид.
Найти плотность вероятностей этой
случайной величины.
Решение. Характеристическая
функцияявляется абсолютно интегрируемой.
Поэтому плотность вероятностей случайной величины
случайной величины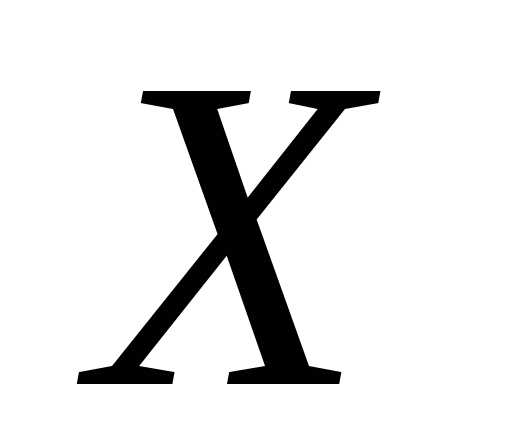 существует и она представляет собой
обратное преобразование Фурье функции
существует и она представляет собой
обратное преобразование Фурье функции  :
:
— закон распределения Коши.
Задачи
3.2.1.Найти производящую функцию
числа »успехов»Хв схеме независимых
испытаний Бернулли и с её помощью найти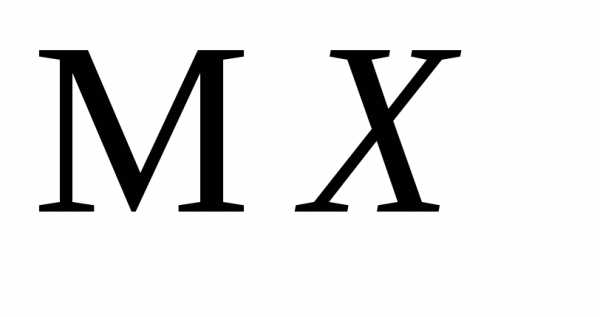 и
и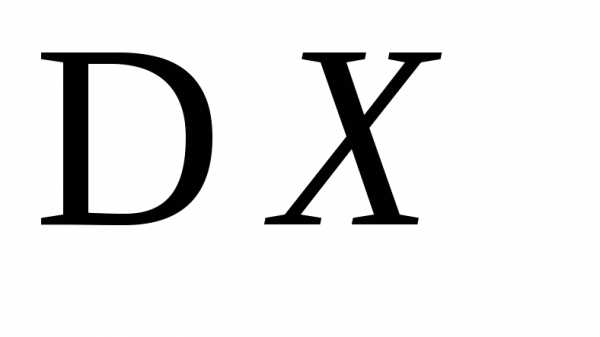 .
.
3.2.2.Найти производящую функцию
пуассоновской случайной величиныХ и с её помощью найти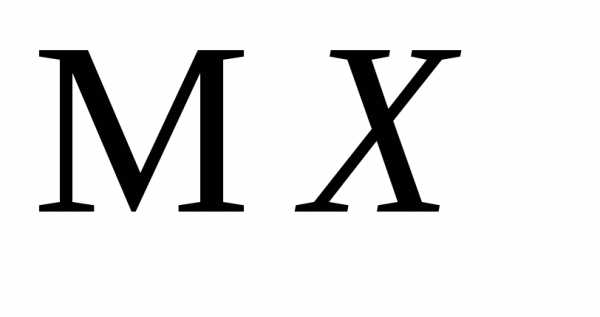 и
и .
.
3.2.3.Пусть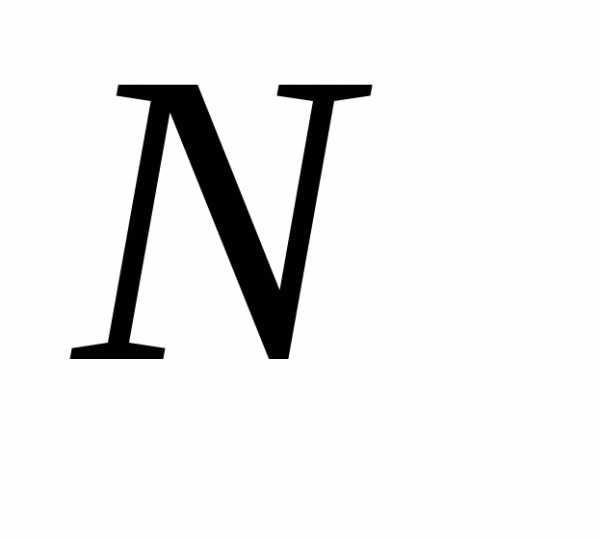 и
и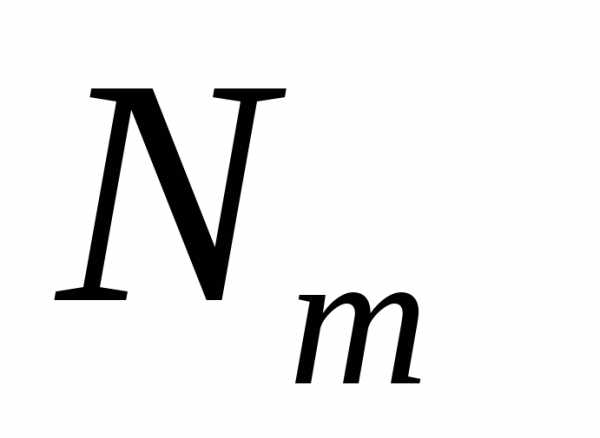 – число испытаний в схеме Бернулли до
появления первого иm-го
успеха соответственно. Найти производящие
функции величин
– число испытаний в схеме Бернулли до
появления первого иm-го
успеха соответственно. Найти производящие
функции величин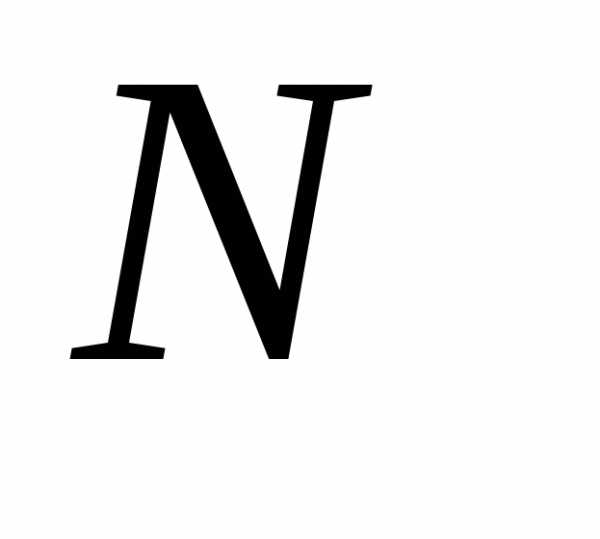 и
и ,а также
,а также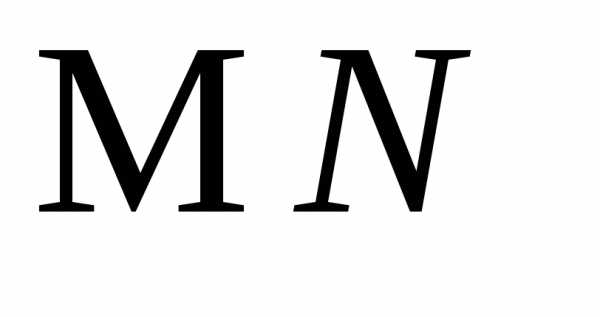 ,
,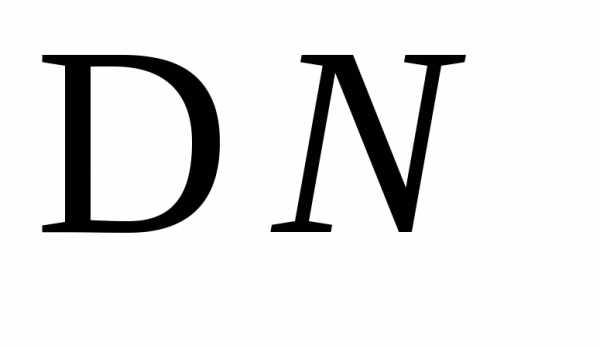 и
и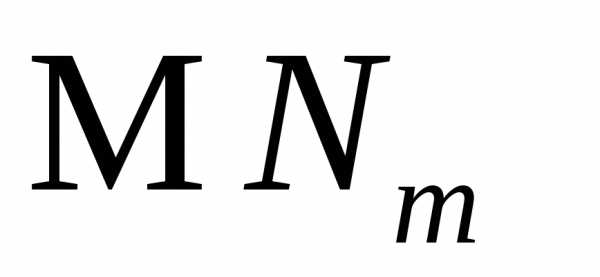 ,
,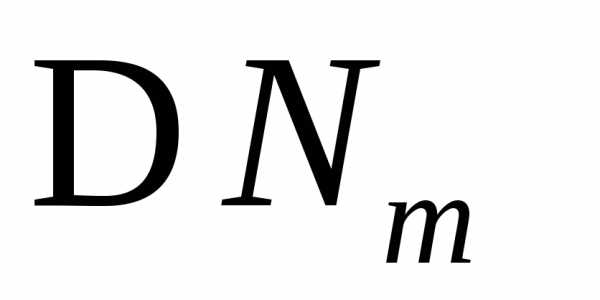 .
.
3.2.4. Найти законы распределения, которым соответствуют следующие производящие функции:
а)  ;
б)
;
б) ;
;
в)  ;
г)
;
г) .
.
3.2.5.ПустьX – неотрицательная целочисленная случайная величина с производящей функциейp(z).Найти производящие функции случайных величинX+1, 2Х и 3Х+2.
3.2.6.Пустьun– вероятность того, что число успехов в последовательностиnиспытаний по схеме Бернулли чётно. Доказать рекуррентную формулу:un = qun-1 + p(1-un-1). Вывести отсюда производящую функцию, а из неё точную формулу дляun (u0 = 1).
3.2.7. Дискретная случайная величинаХможет принимать только два значения –1 и 1 с равными вероятностями. Найти характеристическую функцию данной случайной величины.
3.2.8. Дискретная случайная величинаХимеет закон распределения:
X | -2 | 0 | 2 |
| 1/4 | 1/2 | 1/4 |
Найти характеристическую функцию
случайной величины Хи с ее помощью
вычислить .
.
3.2.9.Найти характеристическую функцию
числа »успехов»Хв схеме Бернулли
и с её помощью найти и
и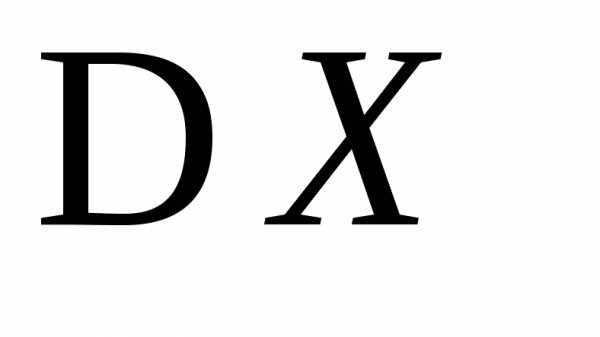 .
.
3.2.10.Найти характеристическую
функцию пуассоновской случайной величиныХи с её помощью найти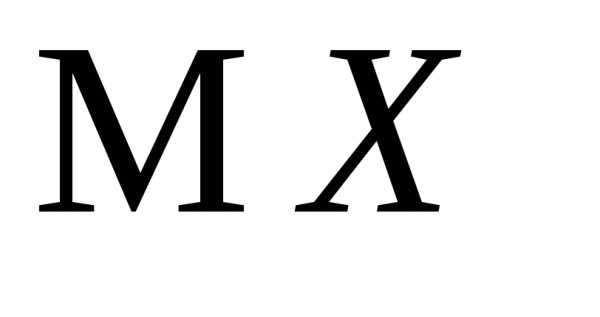 и
и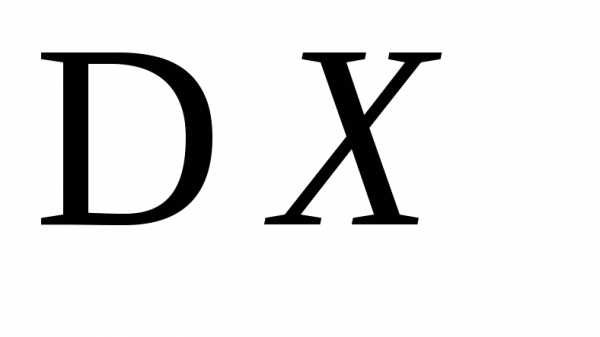 .
.
3.2.11.Найти характеристическую функцию случайной величиныХ, принимающей значения(конечное или счетное множество) с вероятностями.
3.2.12.Найти характеристические функции следующих законов распределения:
а) равномерного на отрезке 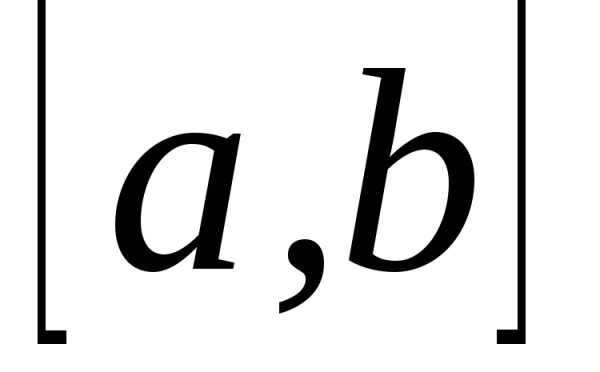 ;
;
б) показательного с параметром а>0;
в) нормального 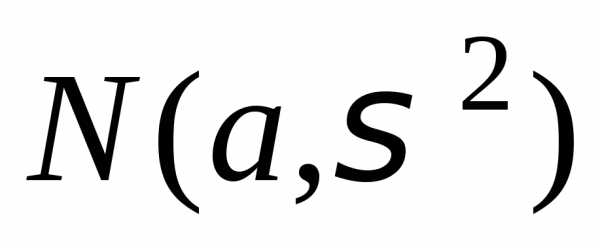 ;
;
г) закона Коши с плотностью вероятностей
 ;
;
д) закона распределения Лапласа с плотностью вероятностей
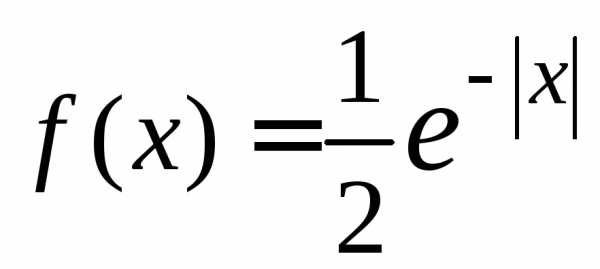 ;
;
е) χ2cn степенями свободы с плотностью вероятностей
3.2.13.Случайная величинаXимеет плотность вероятностей:
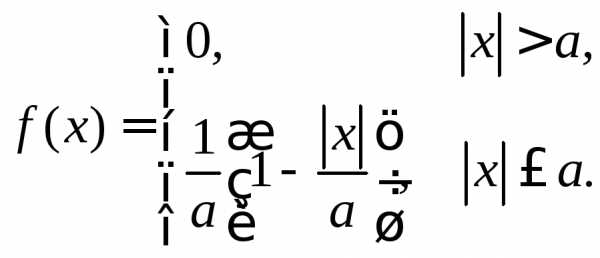
Доказать, что характеристическая функция случайной величины Xравна:
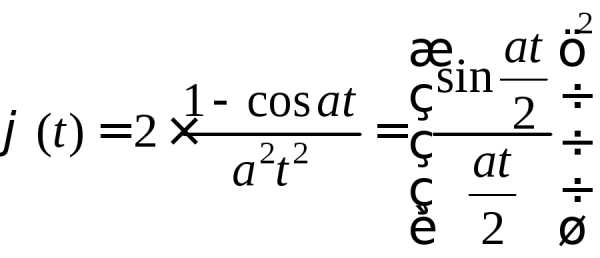 .
.
3.2.14.Случайная величина Х имеет плотность вероятностей:
.
Доказать, что характеристическая функция величины Xравна:
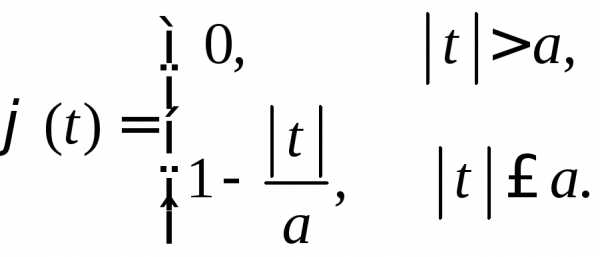
3.2.15.Найти характеристическую
функцию гамма-распределения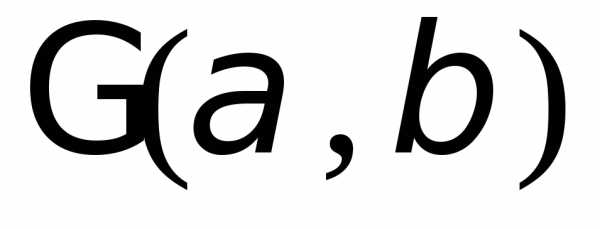 с
параметрами,
имеющего плотность вероятностей
с
параметрами,
имеющего плотность вероятностей
3.2.16.Найти законы распределения,
соответствующие характеристическим
функциям:а)в)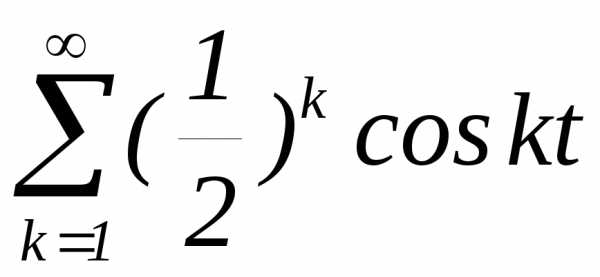 ;г)
;г) 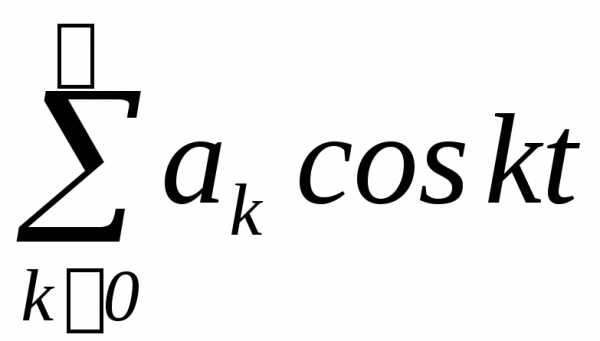 ,где
,где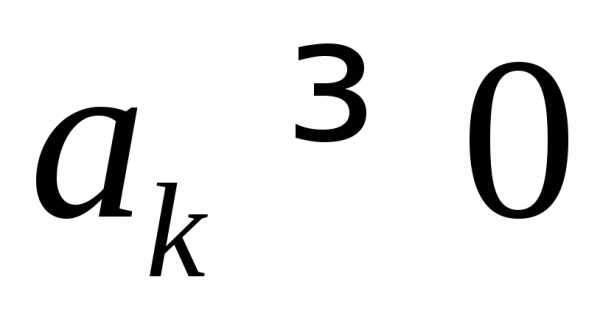 ,
,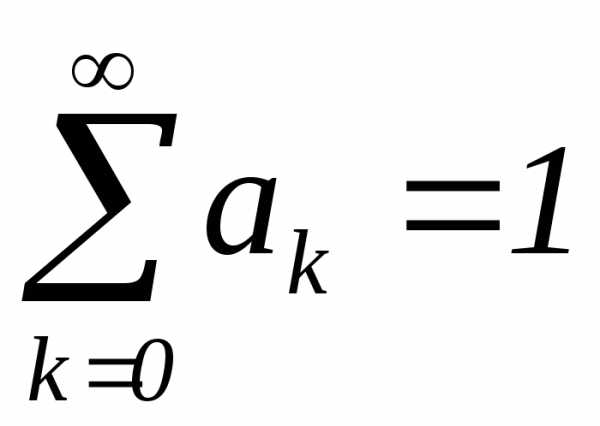 .
.
3.2.17.Характеристическая функция
случайной величиныХимеет вид: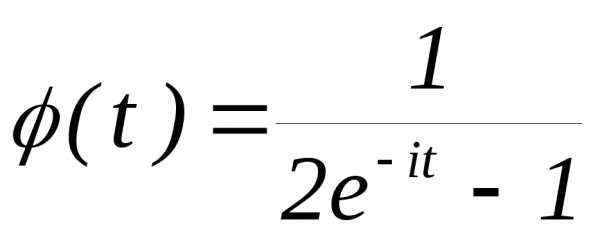 .
Найти закон распределения этой случайной
величины.
.
Найти закон распределения этой случайной
величины.
3.2.18.Найти плотности вероятностей случайных величин, имеющих следующие характеристические функции:
а) 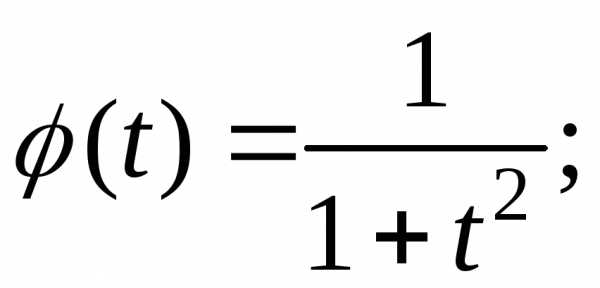
б) 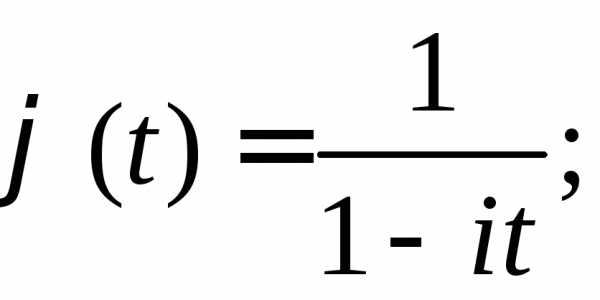
в) 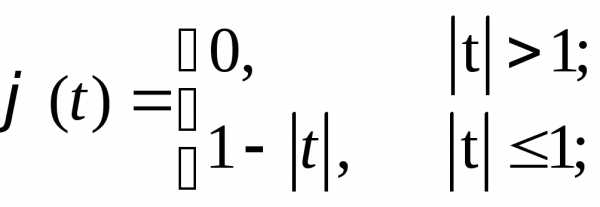
г) 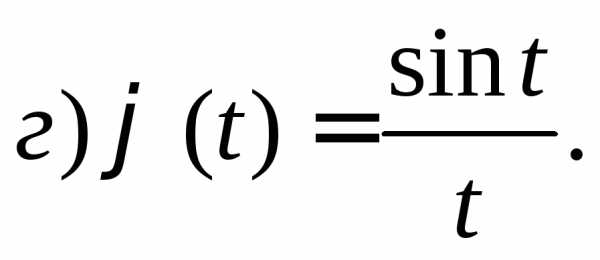 .
.
3.2.19.Даны характеристические функции:
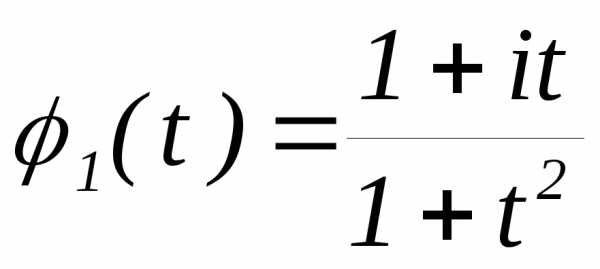 ,
, 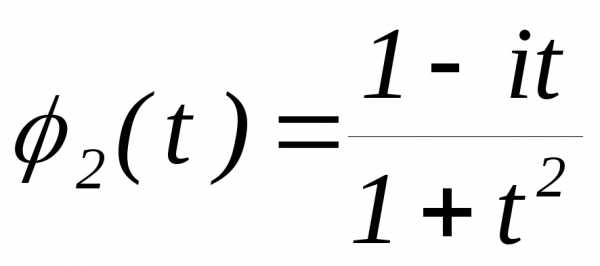 .
.
Определить соответствующие им плотности вероятностей.
3.2.20.С помощью характеристических функций доказать, что:
а) сумма независимых пуассоновских случайных величин имеет пуассоновское распределение;
б) сумма независимых биномиальных случайных величин, связанных со схемами Бернулли с одинаковыми вероятностями »успеха», является биномиальной случайной величиной;
в) сумма независимых нормально распределенных случайных величин имеет нормальное распределение;
г) сумма независимых случайных величин, имеющих распределения Коши, также распределена по закону Коши.
3.2.21. ВеличиныXиYнезависимы, одинаково
распределены и их характеристическая
функция равна(t).Найти характеристическую функцию
разности .
.
3.2.22. Показать, что если(t)– характеристическая функция, то и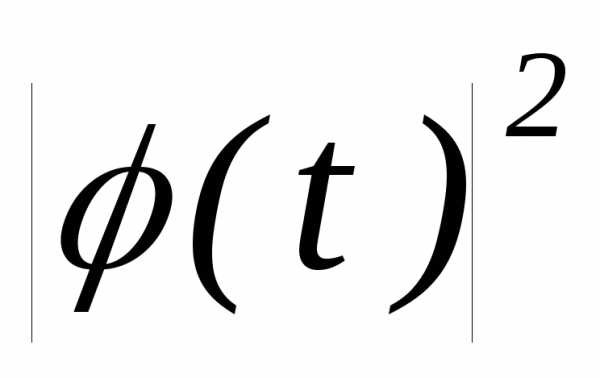 также является характеристической
функцией.
также является характеристической
функцией.
3.2.23. Убедиться, что функция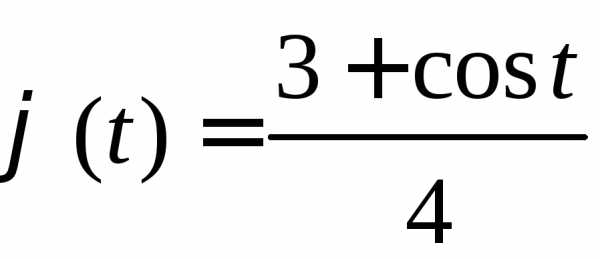 является характеристической функцией
и найти соответствующий ей закон
распределения.
является характеристической функцией
и найти соответствующий ей закон
распределения.
3.2.24. Доказать, что при каждом натуральномnфункцияявляется характеристической.
3.2.25.Доказать, что функция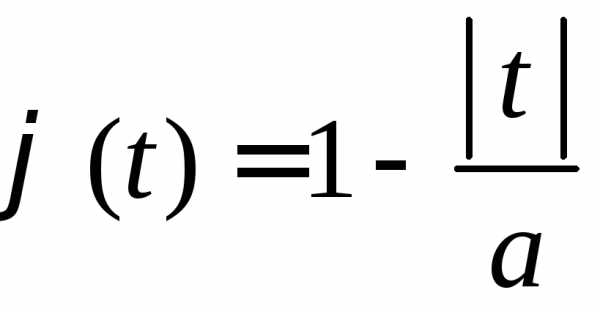 при
при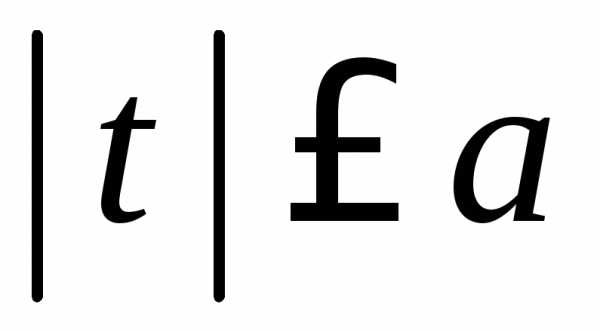 ,
продолженная на всю числовую прямую с
периодом2а, является характеристической.
,
продолженная на всю числовую прямую с
периодом2а, является характеристической.
3.2.26.Являются ли характеристическими следующие функции:
а) 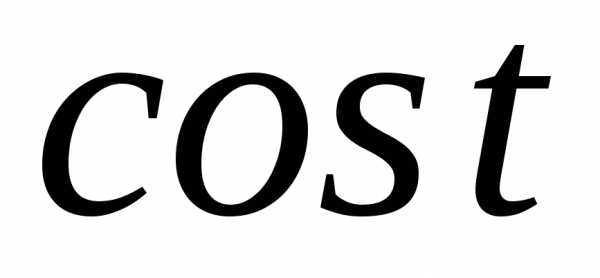 ;
б)
;
б)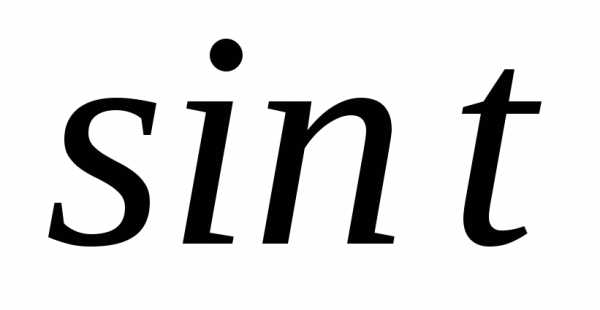 ;
в)
;
в)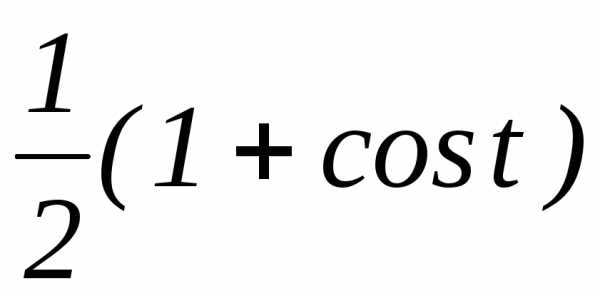 ;
г)
;
г)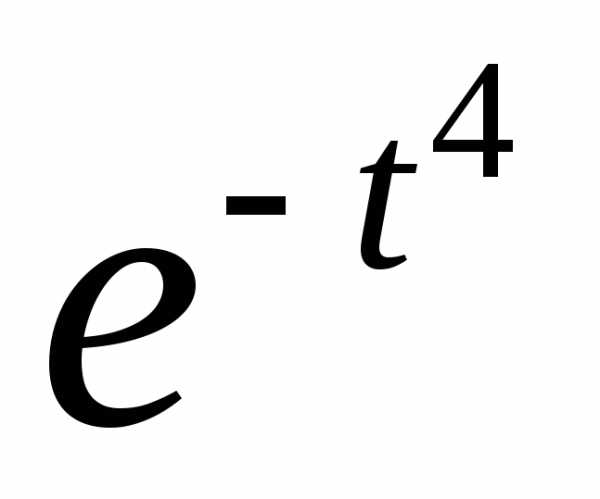 ;
;
д) 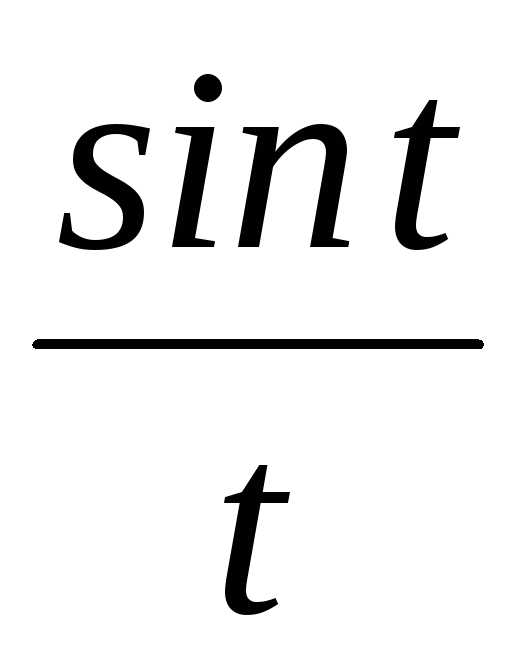 ;
е)
;
е)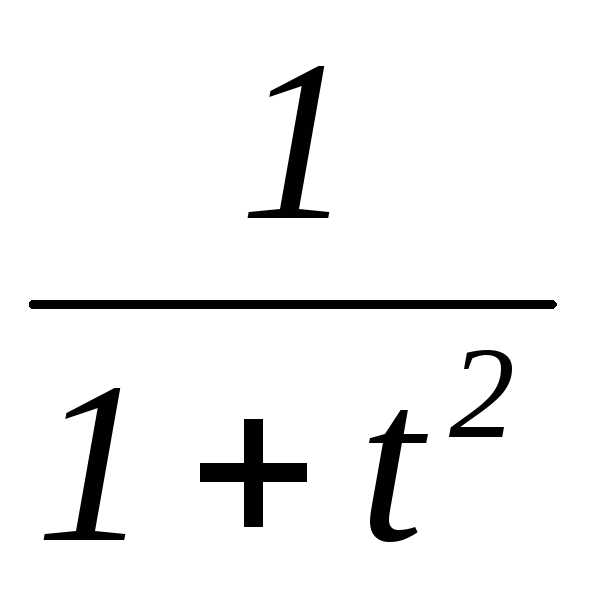 ;
ж)
;
ж)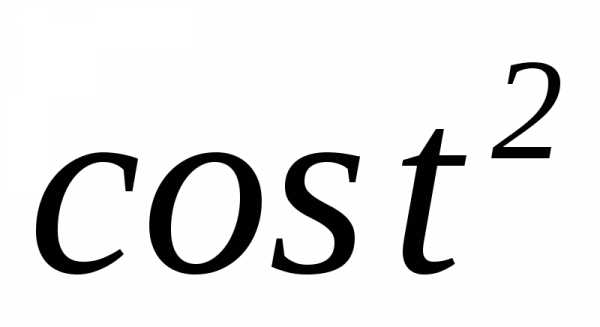 ?
?
3.2.27. Доказать, что функции
а) 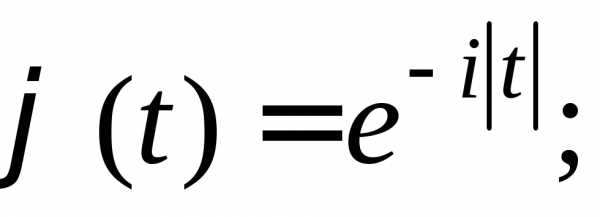
б) 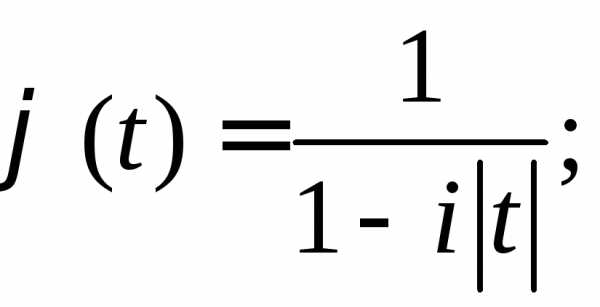
в) 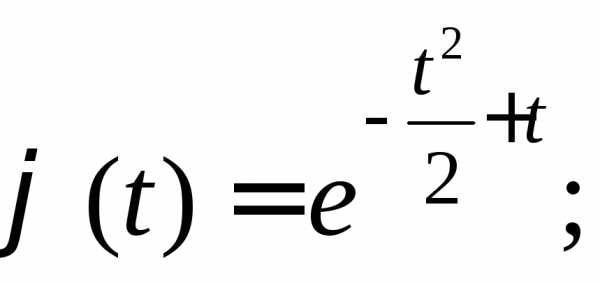
г) 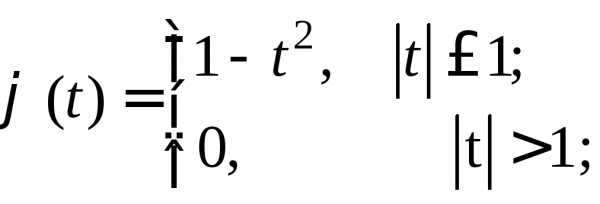
не являются характеристическими.
3.2.28. Дать теоретико-вероятностную интерпретацию равенства
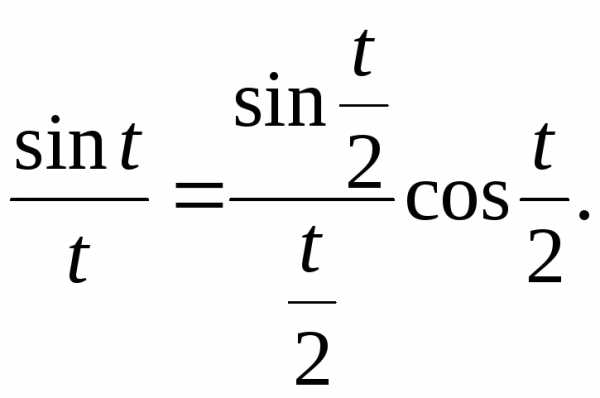
3.2.29.Дать теоретико-вероятностную интерпретацию равенства

3.2.30.Пусть – независимые случайные величины,
каждая из которых принимает значения
—1 и1с вероятностями1/2. Найти
характеристическую функцию случайной
величины
– независимые случайные величины,
каждая из которых принимает значения
—1 и1с вероятностями1/2. Найти
характеристическую функцию случайной
величины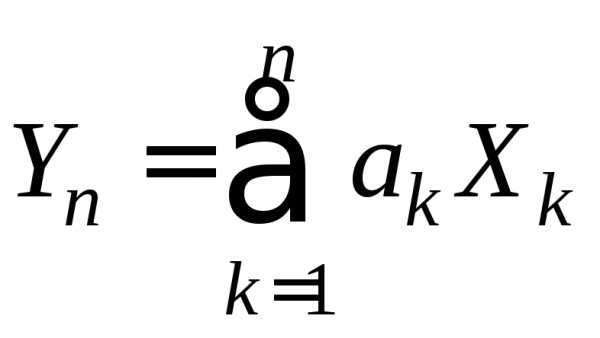 ,
где
,
где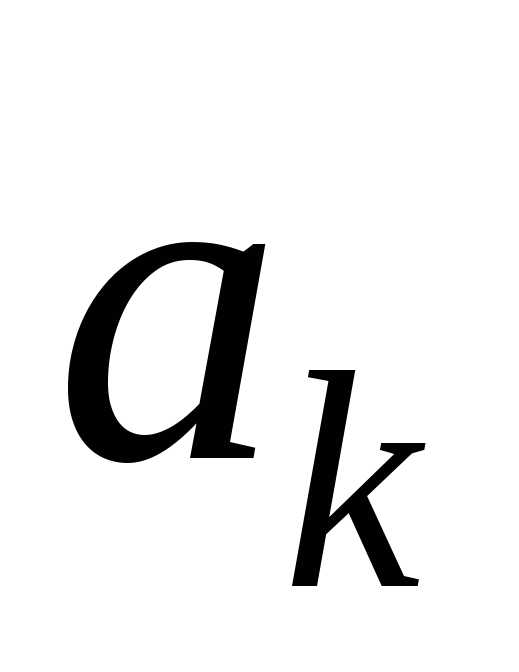 —
постоянные. Показать, что при
—
постоянные. Показать, что при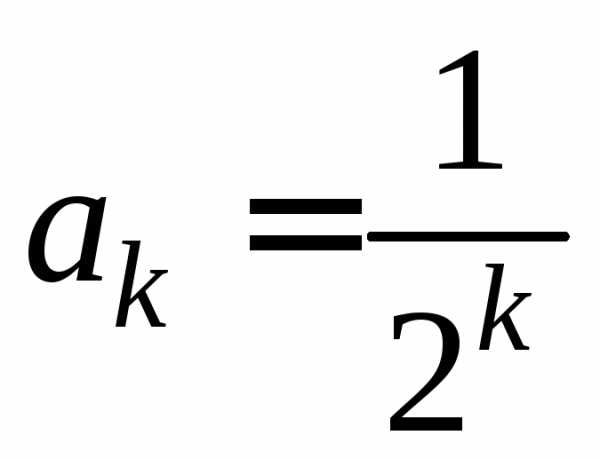 закон распределения случайной величины
закон распределения случайной величины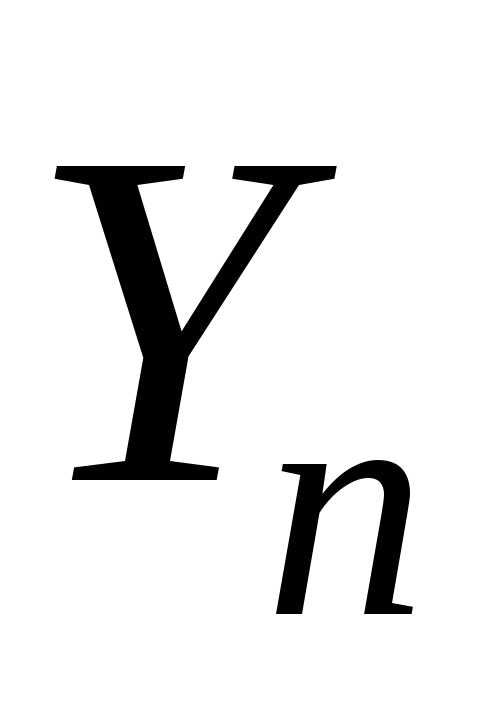 стремится прик равномерному закону распределения
на отрезке
стремится прик равномерному закону распределения
на отрезке .
.
3.2.31. Пусть X1, X2, X3 – независимые случайные величины,
имеющие стандартный нормальный закон
распределения 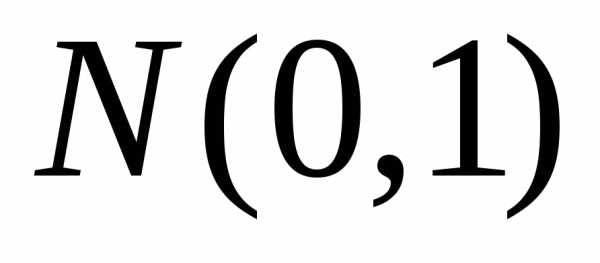 .
Найти совместную характеристическую
функцию случайных величин и .
.
Найти совместную характеристическую
функцию случайных величин и .
3.2.32. Случайные величины
имеют нормальное совместное распределение,
причём, 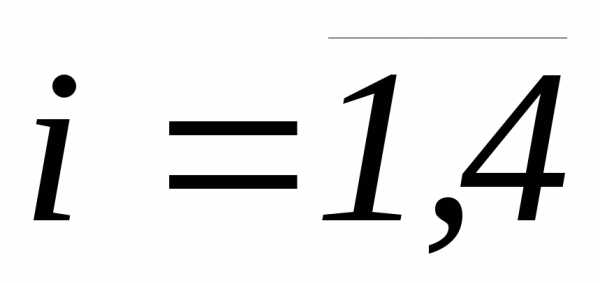 и , i, k=
и , i, k=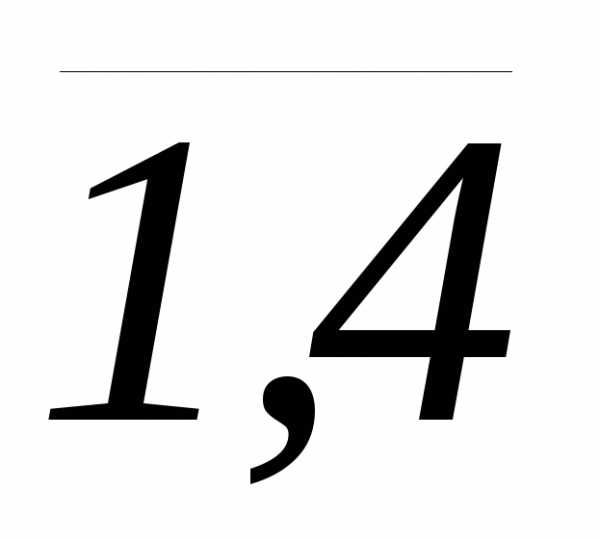 . Найти: а)
;
б);
в).
. Найти: а)
;
б);
в).
studfiles.net
Помощь студенту — практические примеры, задачи, теория: Теория вероятностей. Производящая функция
Производится 4 выстрела с вероятностями попадания в цель p₁ = 0,6; p₂ = 0,4; р₃ = 0,5 иp₄ = 0,7.
- составить закон распределения вероятностей дискретной случайной величины
X ∈ [0; 4] — общего числа попаданий в цель; - построить многоугольник распределения;
- найти математическое ожидание MX и дисперсию DX общего числа попаданий в цель.
Определим соответствующие вероятности непопаданий:
q₁ = 1 – p₁ = 0,4; q₂ = 1 – p₂ = 0,6; q₃ = 1 – p₃ = 0,5; q₄ = 1 – p₄ = 0,3
Составим производящую функцию вероятностей (генератрису):
φ₄(z) = (q₁ + z·p₁)·(q₂ + z·p₂)·(q₃ + z·p₃)·(q₄ + z·p₄) =
= (0,4 + z·0,6)·(0,6 + z·0,4)·(0,5 + z·0,5)·(0,3 + z·0,7) =
= 0,036 + 0,198·z + 0,38·z² + 0,302·z³ + 0,084·z⁴
Вероятность события X = k равна коэффициенту при zk в производящей функции.
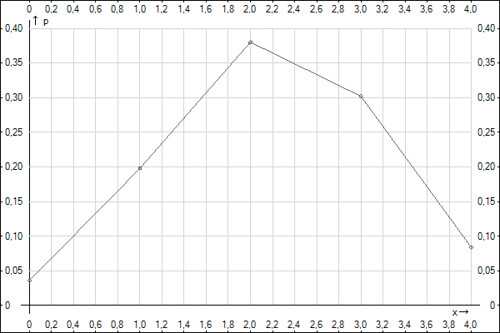
Составим закон распределения дискретной случайной величины X:
| xk | 0 | 1 | 2 | 3 | 4 |
| Pk | 0,036 | 0,198 | 0,38 | 0,302 | 0,084 |
Проверка.
∑Pk = 0,036 + 0,198 + 0,38 + 0,302 + 0,084 = 0,12 + 0,5 + 0,38 = 0,5 + 0,5 = 1
Строим многоугольник распределения вероятностей:
Математическое ожидание MX дискретной случайной величины X найдём по формуле сложения математических ожиданий:
MX = p₁ + p₂ + р₃ + p₄ = 0,6 + 0,4 + 0,5 + 0,7 = 2,2
Дисперсию DX дискретной случайной величины X найдём по формуле сложения дисперсий независимых величин:
DX = p₁·q₁ + p₂·q₂ + р₃·q₃ + p₄·q₄ = 0,6·0,4 + 0,4·0,6 + 0,5·0,5 + 0,7·0,3 =
= 0,24 + 0,24 + 0,25 + 0,21 = 0,94
© http://5ballov.pp.ua/
5ballov.pp.ua
32. Примеры использования производящих функций для вычисления моментов.
Производящая функция, моменты, мода, медиана и квантили случайной величины
Начальным моментом -го порядка случайной величины называется математическое ожидание -й степени случайной величины :. (3.33)
Центральным моментом -го порядка случайной величины называется математическое ожидание -й степени отклонения случайной величины от своего математического ожидания:. (3.34)
Справедливы следующие выражения для центральных моментов:
; (3.35)
; (3.36)
; (3.37)
; (3.38)
. (3.39)
Производящей функцией случайной величины называется функция от параметра (вообще говоря, комплексного), равная . (3.40)
Как и раньше, если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: .
Начальные моменты случайной величины выражаются через производные её производящей функции[13]:
для всех : , (3.41)
где — -я производная функции .
Если (где ), то производящая функция переходит в характеристическую функцию, широко используемую в фундаментальной теории вероятностей и теории меры.
33. Определение и свойства условного математического ожидания.
Условное математическое ожидание в теории вероятностей — это среднее значение случайной величины относительно условного распределения.
X, Y – дискретные случайные величины.
X: x1,…,xn
Y: y1,…,yn
P(X=xi Y=yj)=Py
(1)
Определим такую же формулу для непрерывного распределения.
Свойства условного математического ожидания:
E(x|y) при фиксированном Y обладает всеми свойствами обычного математического ожидания
А1А2…. Аn
Ω
A1={W,Y=Yi} Y(w)-постоянна
L(Y1)>L(Y2)
Если каждой
Ai(Y2)=UiBj(Yi)
Y2=f(Yi)
Y1>Y2
А2 – элемент разбиения случайной величины У2 => А2=UBi
Bi — элементы порожденные случайной величиной Y1
WÎBiÌA2 – элементарные события
Основные свойства условного мат. ожидания.
Если x=f(y) => E(x|y)=x
E(E(x|y))=Ex
Если X,Y – независимые, то E(x|y)=Ex
34. Условное мат ожидание и условное распределение одного подвектора норм случ вектора относит другого подвектора
Условное распределение:

условные мат ожидания:

34//Условная вероятность.
P(A/B)
Условной вероятностью наступления события A, при условии события B, называется вероятность наступления события A в результате испытаний, если известно, что в это испытании произошло событие B.
Вывод формулы условной вероятности для случая равновероятных элементарных событий
Действительно, в данном испытании произошло одно из t событий, входящих в B. Все элементарные события равновероятны, следовательно, для данного испытания вероятность наступления произвольного элементарного события, входящего в B равна 1/t. Тогда по классическому определению вероятности, в данном испытании событие A произойдет с вероятностью r/t.
В общем случае доказать эту формулировку невозможно, в теории вероятности она вводится как правило. Существует лишь толкование этой формулы.
Обоснование формулы условной вероятности в общем случае.
Пусть в nB испытаниях произошло событие B, а в nA испытаниях произошло событие A. Найдем условную частость наступления события A при условии, что произошло событие B. Мы можем сделать это для обоснования формулы, т.к. под вероятностью наступления события понимается предел частости наступления события при условии, что серия испытаний достаточно длинная.
Условная частость
Рассматривая AB как одно событие D имеем: с другой стороны
Рассмотрим систему событий A1, A2,…,Ak. Покажем, что вероятность их совместного наступления равна:
Доказательство проведем по мат индукции.
Формула равна для 2 и 3 (см. ранее)
Пусть формула верна для k-1.
Введем событие B.
P(A1A2…Ak-1)=P(B)
P(A1A2…Ak)=P(AkB)=P(B)×P(AkB)
studfiles.net
3.3. Предельные теоремы теории вероятностей
Говорят,
что последовательность функций
распределения слабо сходится к функции
распределения 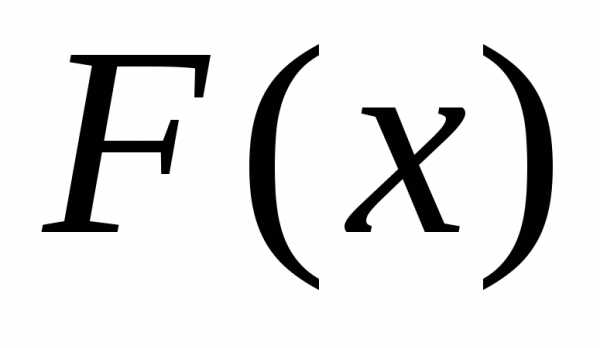 при(обозначается
при(обозначается  ),
если
в каждой точке непрерывности предельной
функции распределения
),
если
в каждой точке непрерывности предельной
функции распределения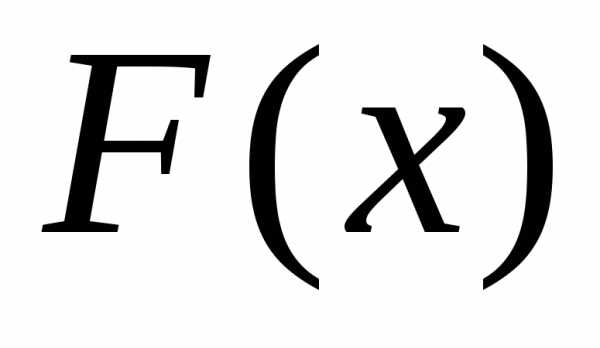 .
.
Доказательство слабой сходимости распределений часто основывается на теоремах непрерывности.
Теорема непрерывности для производящих функций
Пусть
— последовательность законов распределений
целочисленных случайных величинXn с производящими функциями pn(z). Для сходимости последовательности
законов распределения
к закону
распределения  прии каждом конечномk
прии каждом конечномk
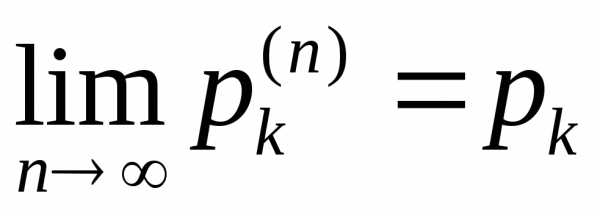
необходимо
и достаточно, чтобы последовательность
производящих функций на полуинтервале 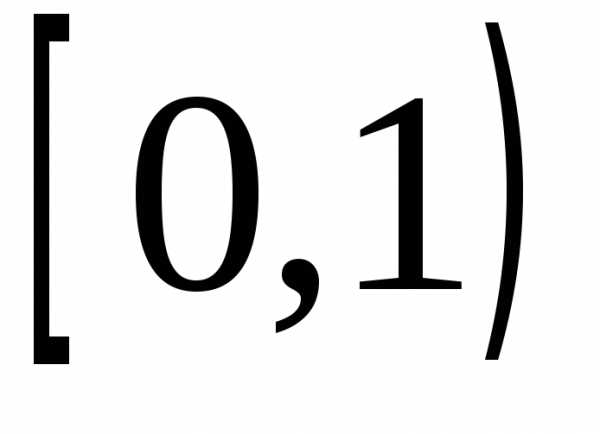 сходилась прии любом0 s<1 к предельной
функции
сходилась прии любом0 s<1 к предельной
функции 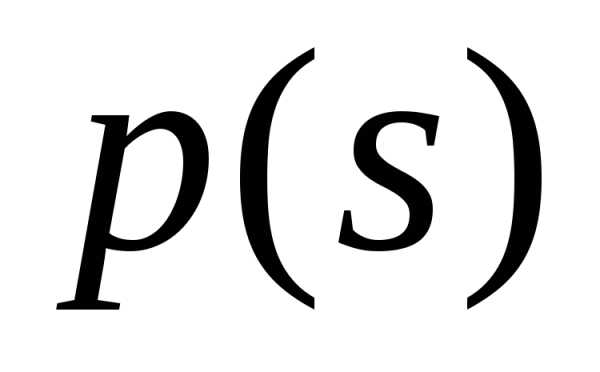 :
:
.
При
этом 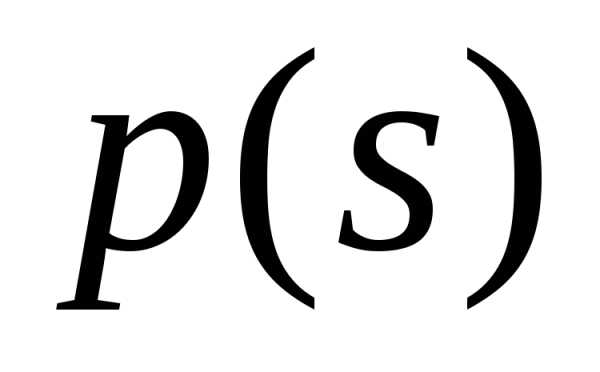 является
производящей функцией на полуинтервале
является
производящей функцией на полуинтервале 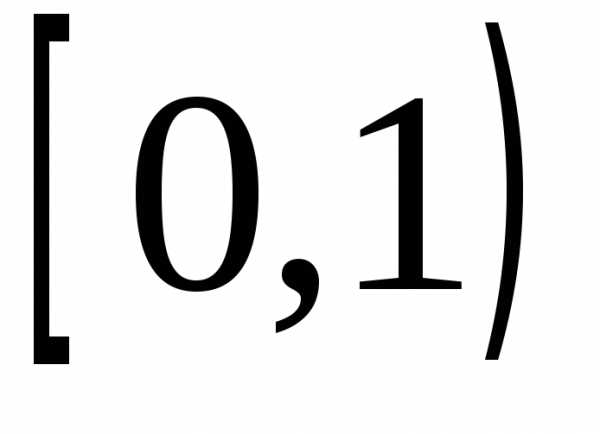 предельного закона распределения
предельного закона распределения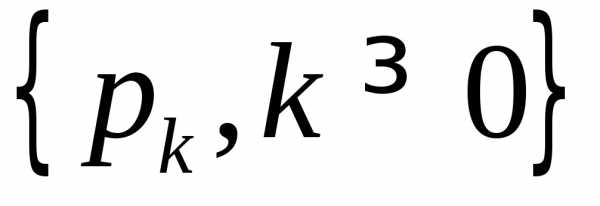 :
:
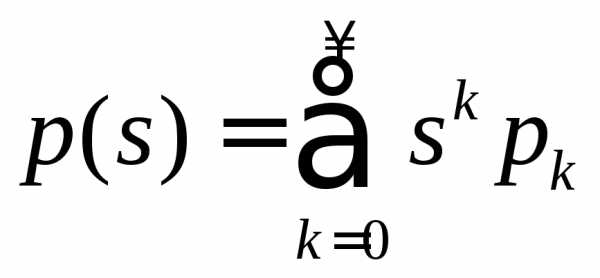
Теорема непрерывности для характеристических функций
Последовательность
функций распределения
слабо сходится к функции распределения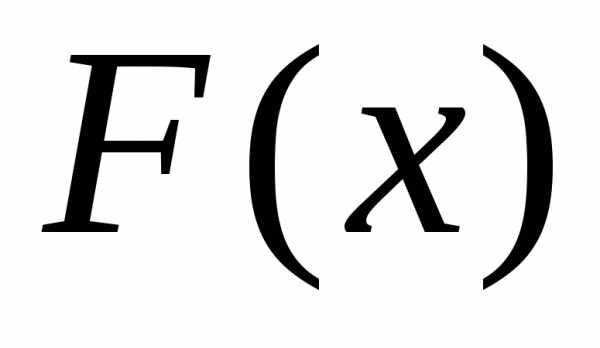 тогда и только тогда, когда последовательность
их характеристических функцийсходится прик непрерывной предельной функции
тогда и только тогда, когда последовательность
их характеристических функцийсходится прик непрерывной предельной функции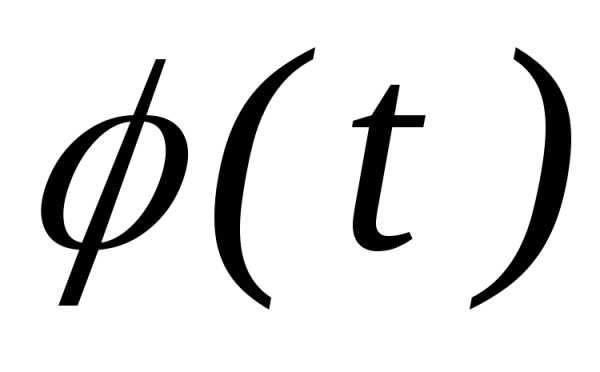 .
При этом
.
При этом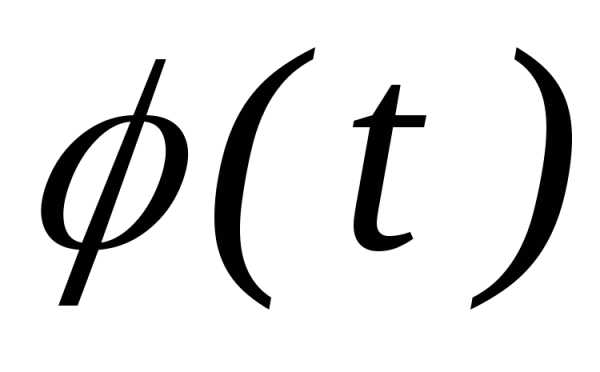 есть характеристическая функция
предельной функции
есть характеристическая функция
предельной функции и сходимость
и сходимость 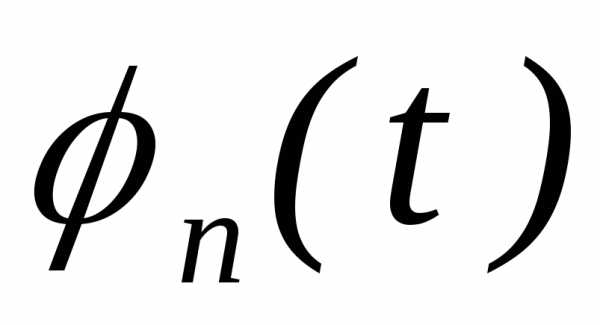 к
к 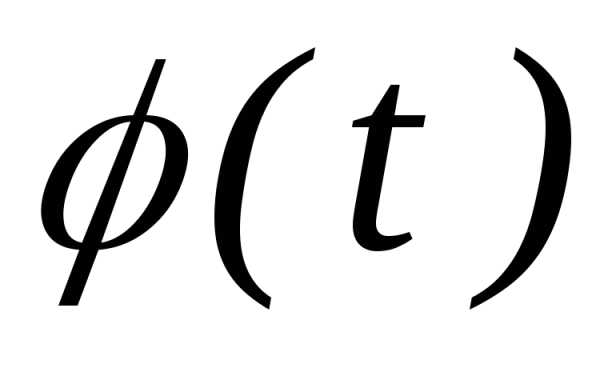 равномерная на любом конечном интервале.
равномерная на любом конечном интервале.
Пусть 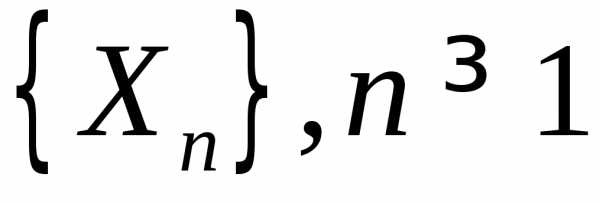 — последовательность независимых
случайных величин. Теоремы, которые
устанавливают нормальность предельного
закона распределения суммы независимых
случайных величинназываютсяцентральными
предельными теоремами (ЦПТ).
— последовательность независимых
случайных величин. Теоремы, которые
устанавливают нормальность предельного
закона распределения суммы независимых
случайных величинназываютсяцентральными
предельными теоремами (ЦПТ).
Цпт для независимых, одинаково распределенных случайных величин.
Пусть 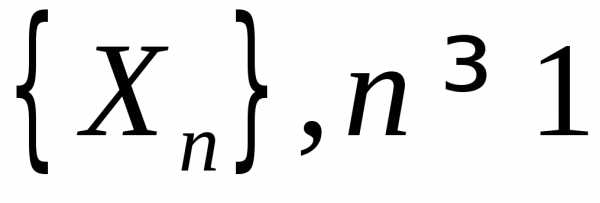 — последовательность независимых,
одинаково распределенных случайных
величин, имеющих конечные математические
ожидания
— последовательность независимых,
одинаково распределенных случайных
величин, имеющих конечные математические
ожидания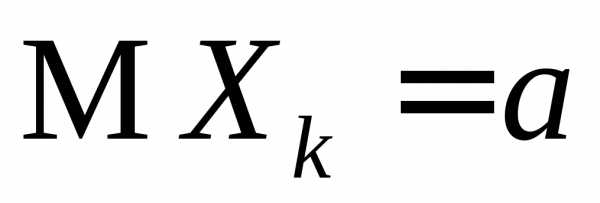 и дисперсии
.
и дисперсии
.
Тогда
при
для любого
,
или,
что эквивалентно, функция распределения 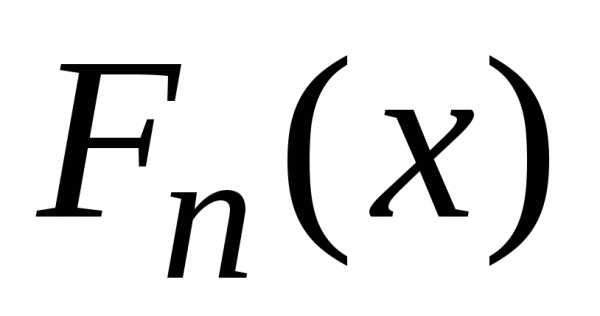 центрированной
и нормированной суммы
центрированной
и нормированной суммы 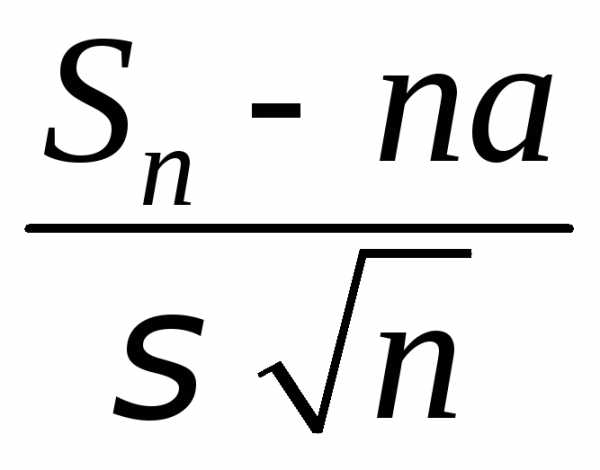 слабо сходится к функции распределения
слабо сходится к функции распределения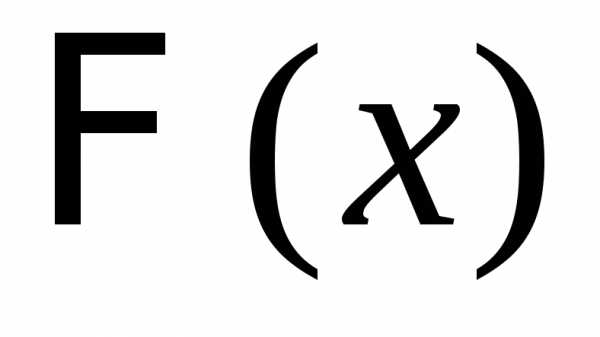 стандартного
нормального закона распределения
.
стандартного
нормального закона распределения
.
Цпт для независимых, разнораспределенных случайных величин
Теорема Линдеберга
Пусть 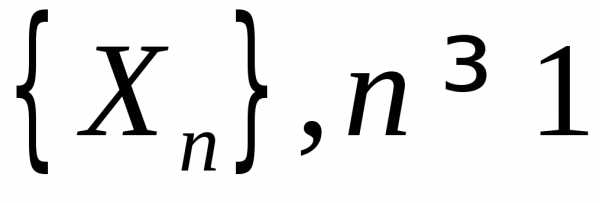 — последовательность независимых,
разно-распределенных случайных величин,
имеющих конечные математические ожиданияи дисперсии
.
Обозначим,
— последовательность независимых,
разно-распределенных случайных величин,
имеющих конечные математические ожиданияи дисперсии
.
Обозначим,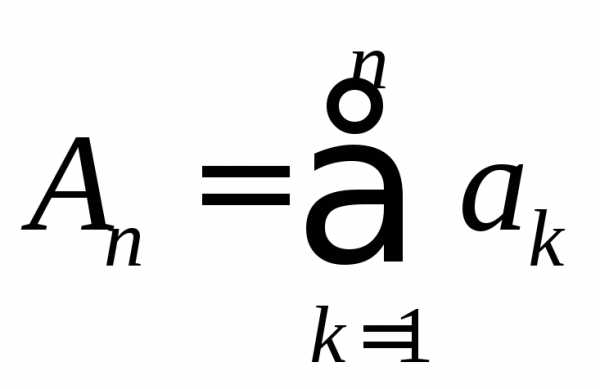 и
и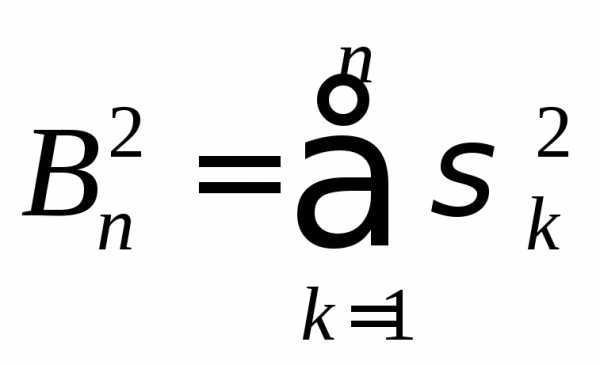 .
Тогда, если выполняется условие
Линдеберга:
.
Тогда, если выполняется условие
Линдеберга:
для любого ,
то
функция распределения 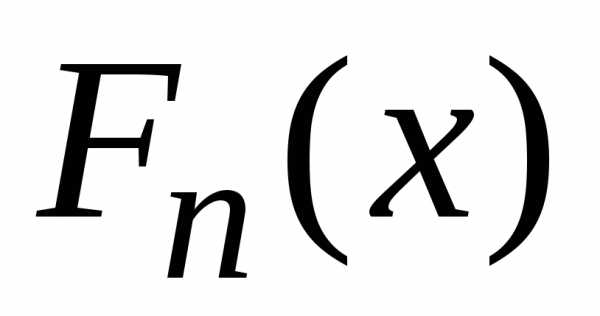 центрированной и нормированной суммы
центрированной и нормированной суммы  слабо сходится к функции распределения
слабо сходится к функции распределения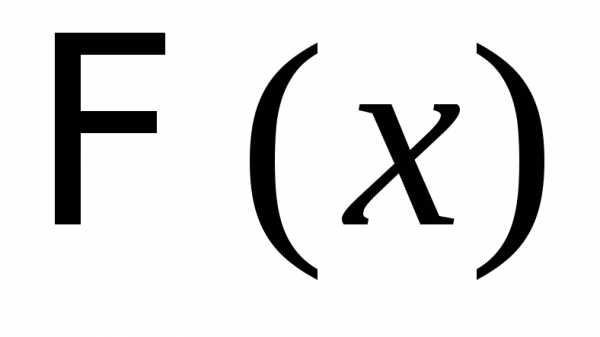 стандартного нормального закона
стандартного нормального закона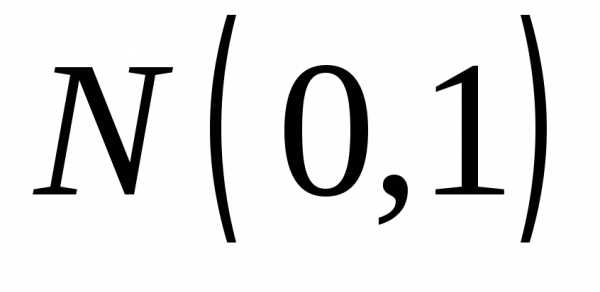 :
: .
.
Из условия Линдеберга следует, что
,
то
есть в сумме 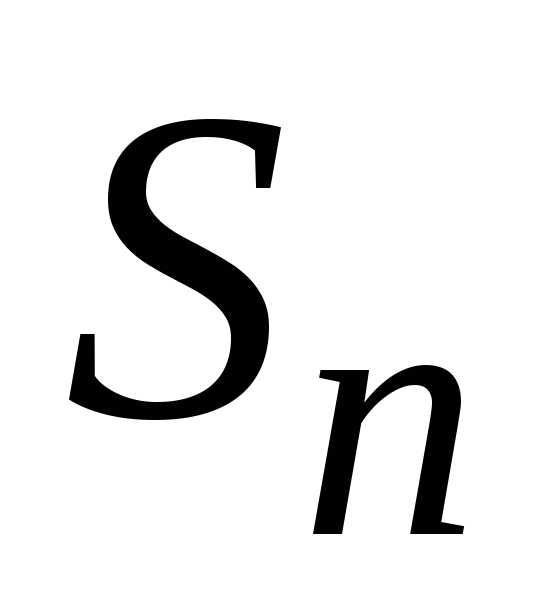 относительный вклад каждого слагаемого
дисперсии равномерно бесконечно мал.
В частности, из условия Линдеберга
вытекает условие асимптотической
малости последовательности случайных
величин:
относительный вклад каждого слагаемого
дисперсии равномерно бесконечно мал.
В частности, из условия Линдеберга
вытекает условие асимптотической
малости последовательности случайных
величин:
.
Условие
Линдеберга является достаточным (но не
необходимым) условием справедливости
ЦПТ для последовательности независимых
случайных величин с конечными дисперсиями.
Если же для такой последовательности
выполняется условие асимптотической
малости и  при,
то условие Линдеберга оказывается и
необходимым для справедливости ЦПТ.
при,
то условие Линдеберга оказывается и
необходимым для справедливости ЦПТ.
Из теоремы Линдеберга выводятся многие другие варианты ЦПТ, в частности, следующая теорема.
Теорема Ляпунова.
Пусть 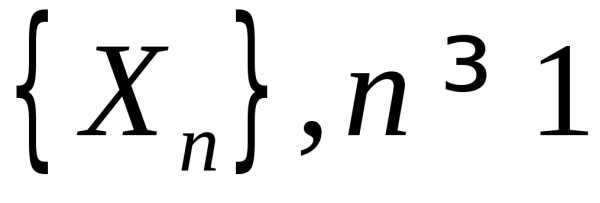 — последовательность независимых,
разно-распределенных случайных величин,
имеющих конечные математические ожидания, дисперсии
— последовательность независимых,
разно-распределенных случайных величин,
имеющих конечные математические ожидания, дисперсии 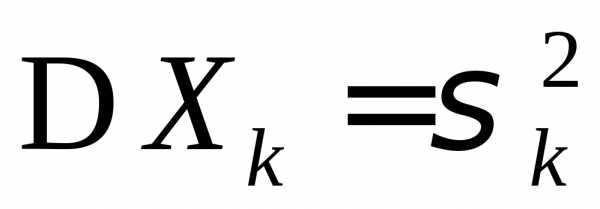 и центральные
абсолютные моменты
порядка
и центральные
абсолютные моменты
порядка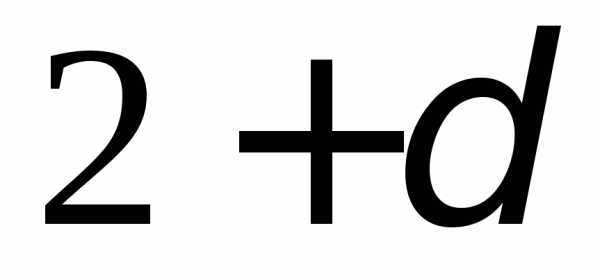 при некотором
при некотором 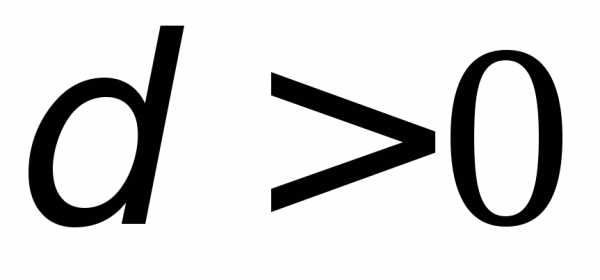 и любом
и любом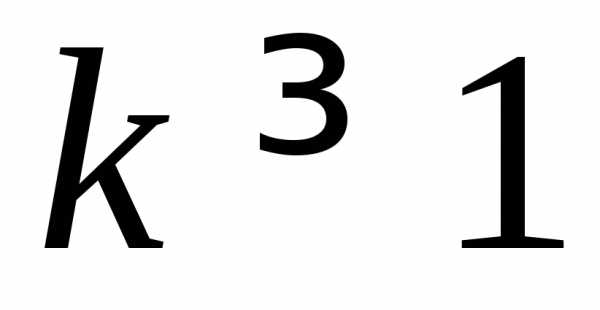 .
Обозначим
.
Обозначим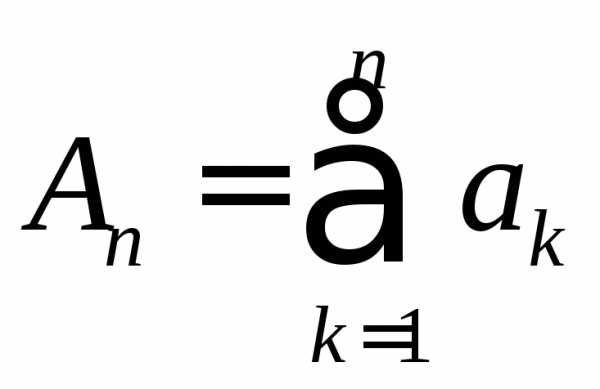 ,
, .
Тогда, при выполнении условия
.
Тогда, при выполнении условия
функция
распределения 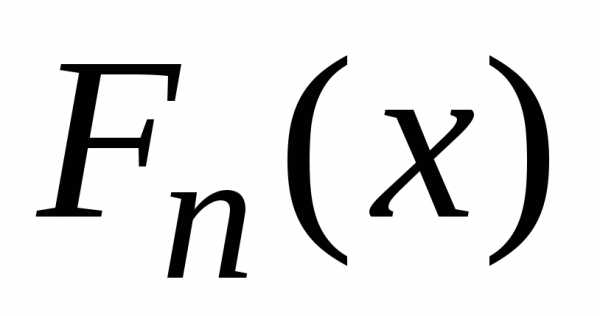 центрированной и нормированной суммы
центрированной и нормированной суммы 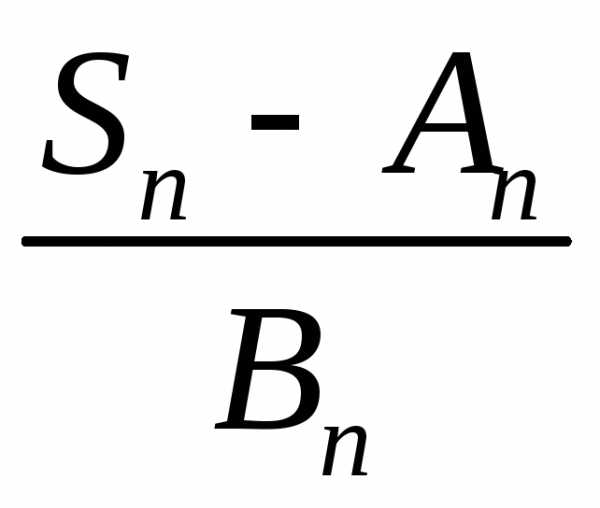 слабо сходится к функции распределения
слабо сходится к функции распределения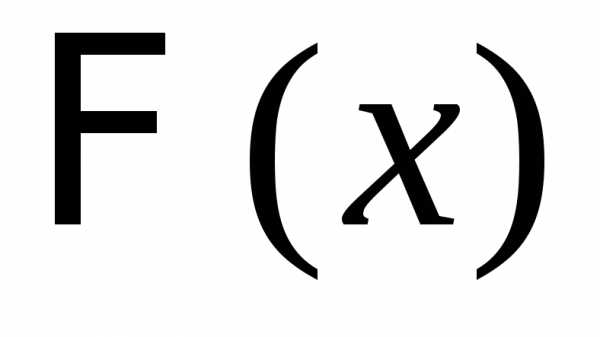 стандартного нормального закона
стандартного нормального закона :
: .
.
Пример
1. Случайная
величина  распределена
по закону Пуассона с параметром
распределена
по закону Пуассона с параметром  . Показать,
что предельным законом распределения
стандартизованной случайной величины
. Показать,
что предельным законом распределения
стандартизованной случайной величины 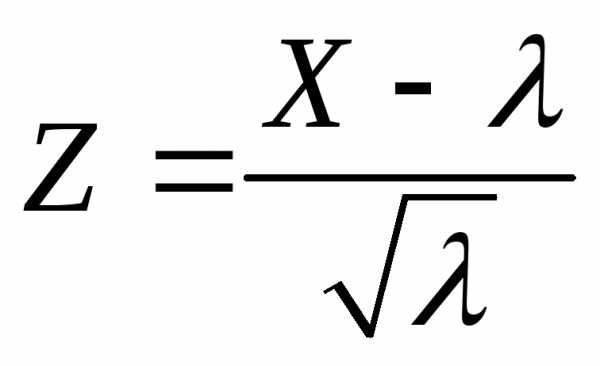 при
при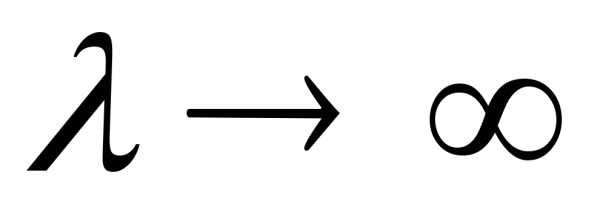 является нормальный закон
является нормальный закон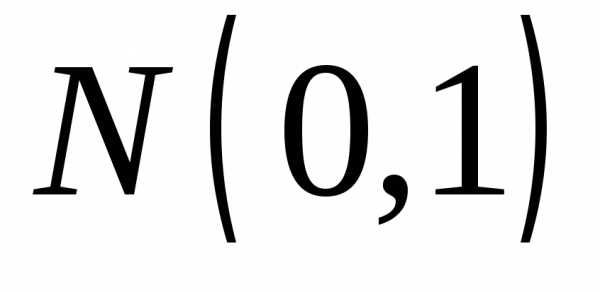 .
.
Решение. Характеристическая функция пуассоновской
случайной величины с параметром  имеет вид:
.
Величина
имеет вид:
.
Величина  линейно выражается через
линейно выражается через 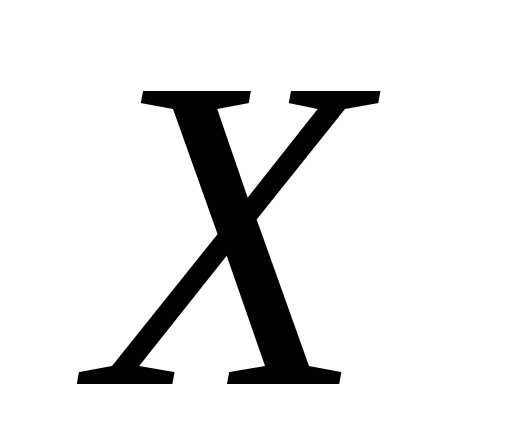 :
: 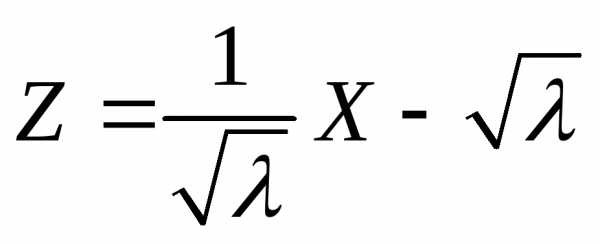 ,
поэтому по свойствам характеристических
функций
,
поэтому по свойствам характеристических
функций
Разложим экспоненту в показателе степени
второй экспоненты в ряд Тейлора по
степеням 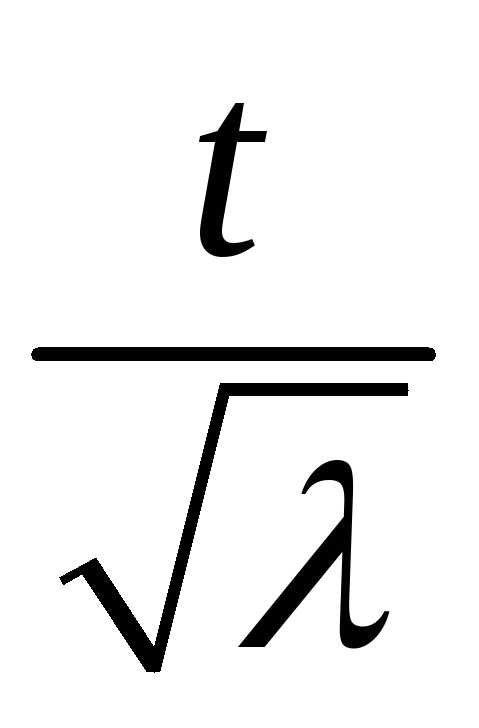 с точность до членов второго порядка
малости:
с точность до членов второго порядка
малости:
.
Подставляя
это разложение в выражение для 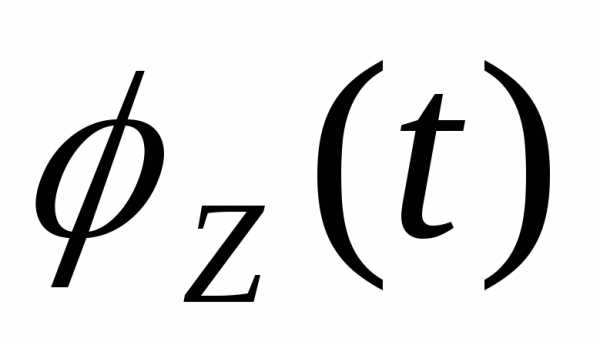 ,
получим
,
получим
,
что соответствует виду характеристической функции стандартного нормального закона распределения. Так как характеристическая функция однозначно определяет закон распределения, то отсюда следует утверждение, сформулированное в примере.
Замечание. Из примера 1 вытекает, что при достаточно
больших значениях  можно
пуассоновское распределение приближенно
аппроксимировать нормальным.
можно
пуассоновское распределение приближенно
аппроксимировать нормальным.
Пример 2. Случайная величина Хn имеет распределение χ2(n), то есть ее плотность вероятностей имеет вид:
Показать, что случайная величина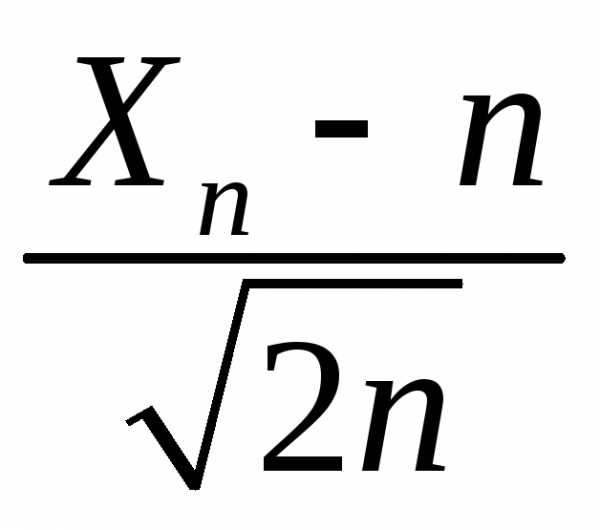 прираспределена по нормальному закону
распределения
прираспределена по нормальному закону
распределения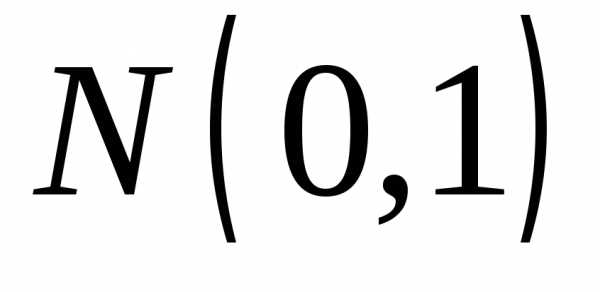 .
.
Решение. По смыслу
распределения χ2(n) (см. задачу 2.3.53) случайная величина
,
гдеZk – независимые,
нормально 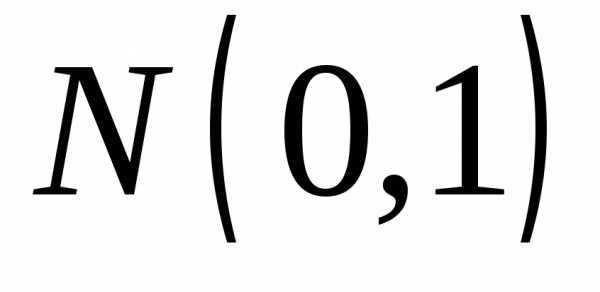 распределенные случайные величины,
распределенные случайные величины, 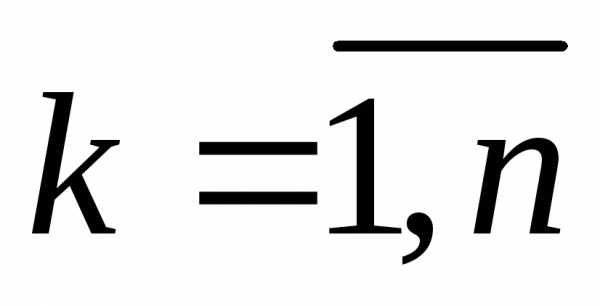 .
Поскольку случайные величиныZk независимы, то и случайные величины
.
Поскольку случайные величиныZk независимы, то и случайные величины 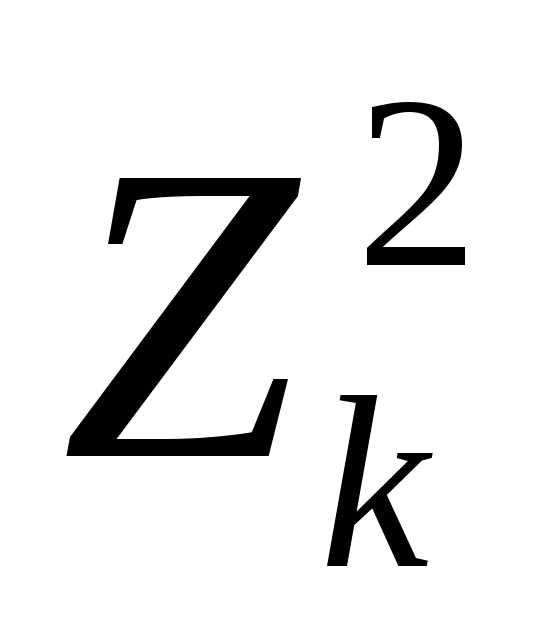 независимы и одинаково распределены,
независимы и одинаково распределены,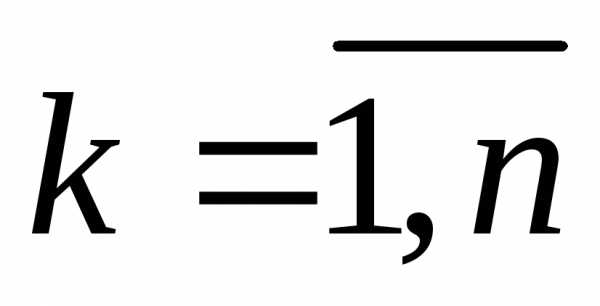 .
Кроме того, в соответствии с выражениями
для моментов гауссовской случайной
величины (см. задачу 2.1.75) для каждой из
случайных величинимеем:
.
Кроме того, в соответствии с выражениями
для моментов гауссовской случайной
величины (см. задачу 2.1.75) для каждой из
случайных величинимеем:
Таким
образом, для последовательности случайных
величин  выполняются
все условия ЦПТ. Поэтому случайная
величина
выполняются
все условия ЦПТ. Поэтому случайная
величина
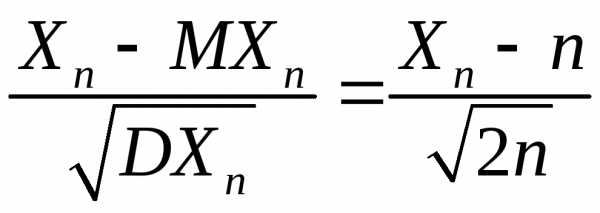
имеет
при
нормальный 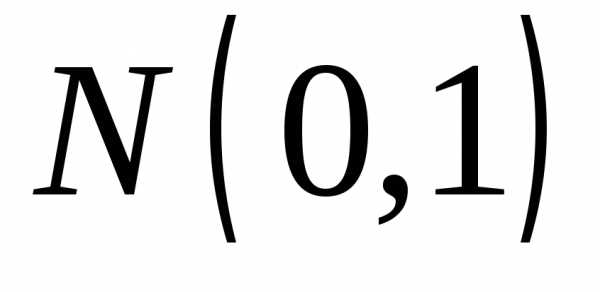 закон распределения.
закон распределения.
Замечание. Результат
примера 2 позволяет при больших n (практически при n30)
приближенно находить квантили
распределения χ2(n) через квантили нормального 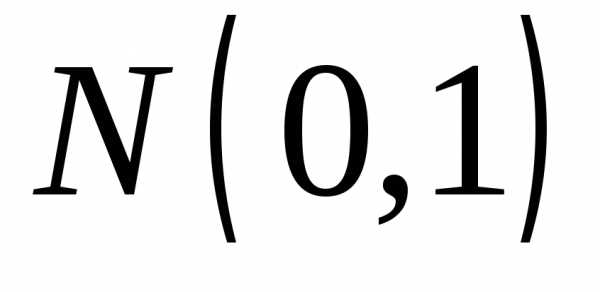 распределения.
распределения.
Задачи
3.3.1. Дисперсия каждой из 4500 независимых, одинаково распределенных случайных величин равна 5. Найти вероятность того, что среднее арифметическое этих случайных величин отклонится от своего математического ожидания не более чем на 0,04.
3.3.2. Случайная величина Х является средним арифметическим 3200 независимых и одинаково распределенных случайных величин с математическим ожиданием, равным 3, и дисперсией, равной 2. Найти вероятность того, что Х примет значение в промежутке (2,95; 3,075).
3.3.3. Случайная величина Х является средним арифметическим независимых и одинаково распределенных случайных величин, дисперсия каждой из которых равна 5. Сколько нужно взять таких величин, чтобы случайная величина Х с вероятностью, не меньшей 0,9973, имела отклонение от своего математического ожидания, не превосходящее 0,01?
3.3.4. Случайная величина Х является средним арифметическим 10000 независимых, одинаково распределенных случайных величин, среднее квадратическое отклонение каждой из которых равно 2. Какое максимальное отклонение величины Х от ее математического ожидания можно ожидать с вероятностью, не меньшей 0,9544?
3.3.5. Игральная кость бросается 1000 раз. Найти пределы, симметричные относительно математического ожидания, в которых с вероятностью, большей 0,99, будет находиться число выпавших очков.
3.3.6. Складывается 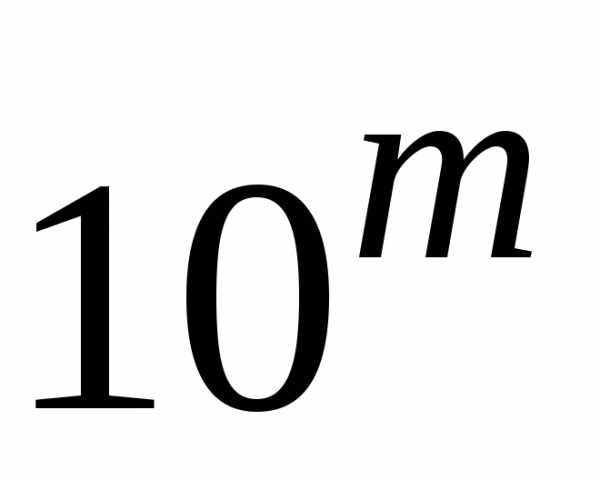 чисел, каждое
из которых округлено с точностью до
10—m.
Предполагается, что ошибки от округления
независимы и равномерно распределены
в интервале (
чисел, каждое
из которых округлено с точностью до
10—m.
Предполагается, что ошибки от округления
независимы и равномерно распределены
в интервале ( ).
Найти пределы, симметричные относительно
математического ожидания, в которых с
вероятностью, не меньшей 0,99,
будет находиться суммарная ошибка.
Проанализировать ответ при
).
Найти пределы, симметричные относительно
математического ожидания, в которых с
вероятностью, не меньшей 0,99,
будет находиться суммарная ошибка.
Проанализировать ответ при
3.3.7. Стрелок попадает при выстреле по мишени в десятку с вероятностью 0,5; в девятку – с вероятностью 0,3; в восьмёрку – с вероятностью 0,1; в семерку – с вероятностью 0,05; в шестёрку – с вероятностью 0,05. Стрелок сделал 100 выстрелов. Какова вероятность того, что он набрал: а) более 915 очков; б) более 950 очков?
3.3.8. Дана
последовательность независимых случайных
величин 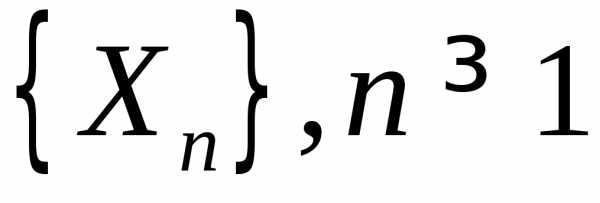 .
ВеличинаXn может принимать значения n с вероятностями
.
ВеличинаXn может принимать значения n с вероятностями  ,
либо значение 0 с вероятностью
,
либо значение 0 с вероятностью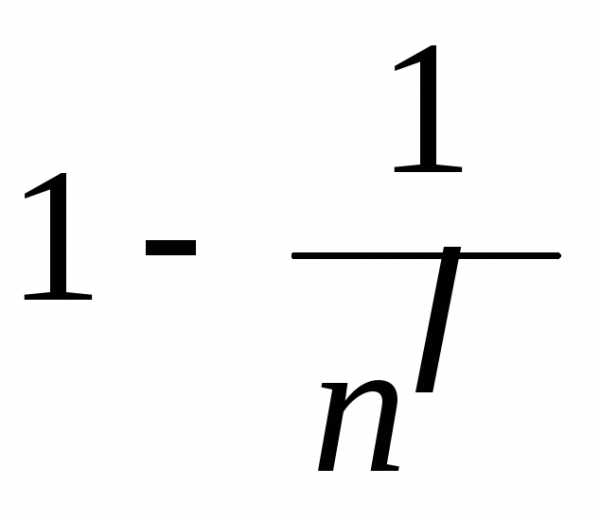 (0<<1).
Доказать, что к сумме
(0<<1).
Доказать, что к сумме 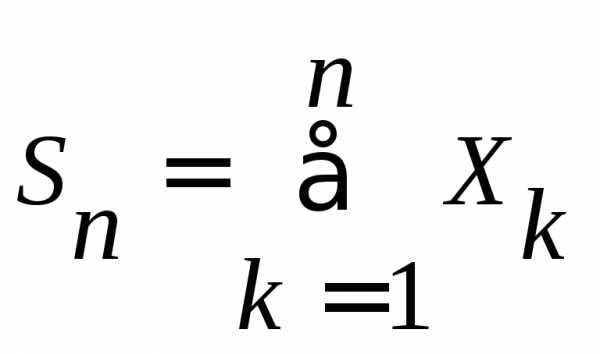 применима
теорема Ляпунова.
применима
теорема Ляпунова.
3.3.9. Дана
последовательность независимых случайных
величин 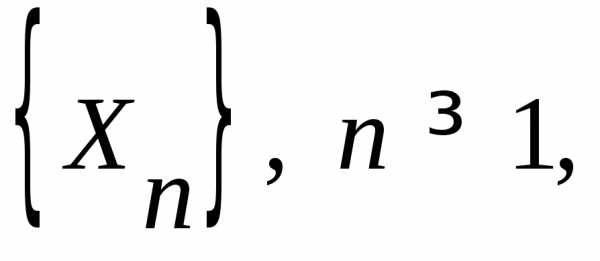 такая,
что
такая,
что
.
Доказать,
что а) к этой последовательности применима
теорема Ляпунова, если 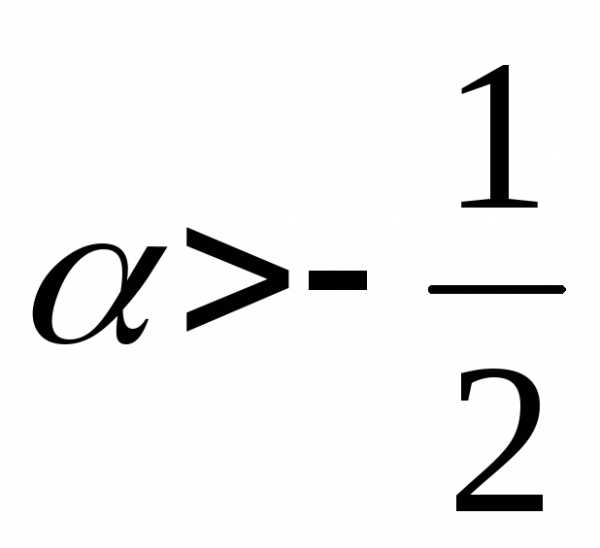 ;б) применим закон
больших чисел, если
;б) применим закон
больших чисел, если 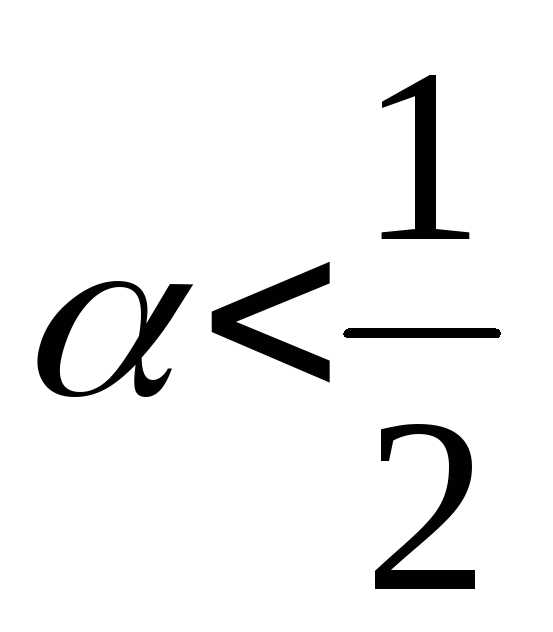 ,и неприменим, если
,и неприменим, если 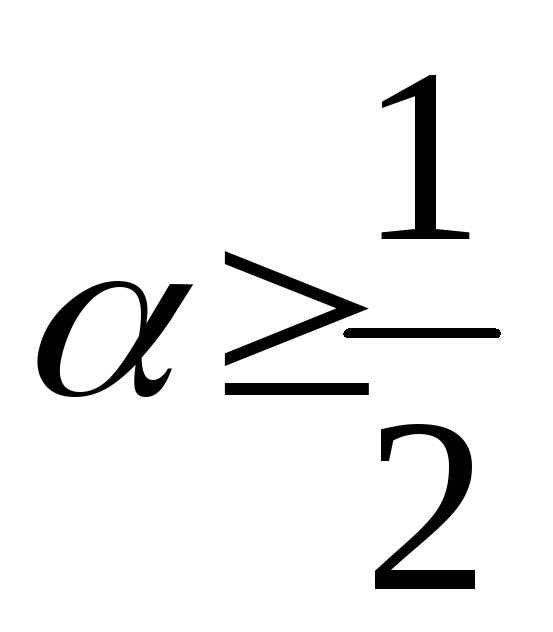 .
.
3.3.10. Случайная величина Хn имеет гамма-распределение Г(n,) с параметрами n>0 и >0, т.е. имеет плотность вероятностей вида:
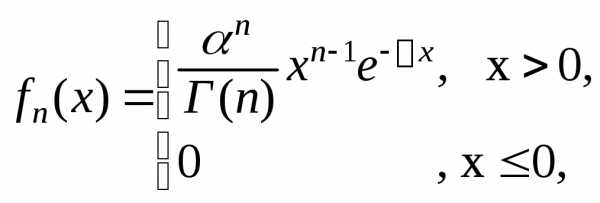
и 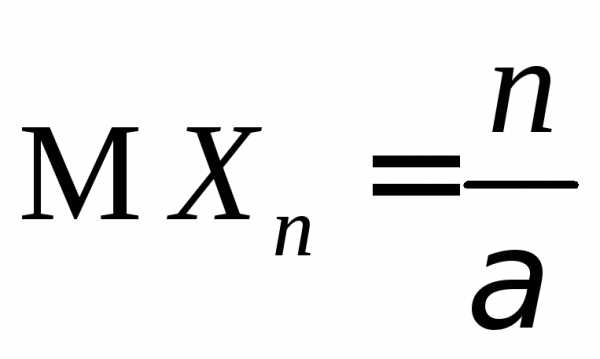 ,
, 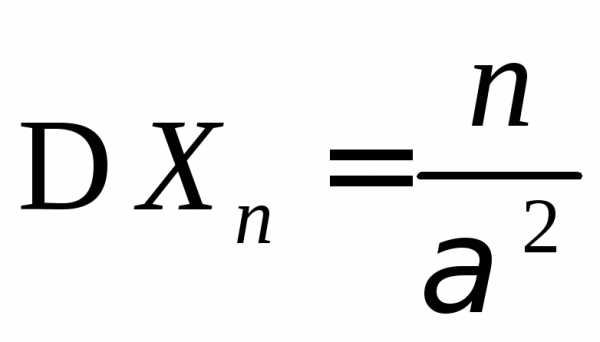 .
.
Доказать,
что закон распределения случайной
величины 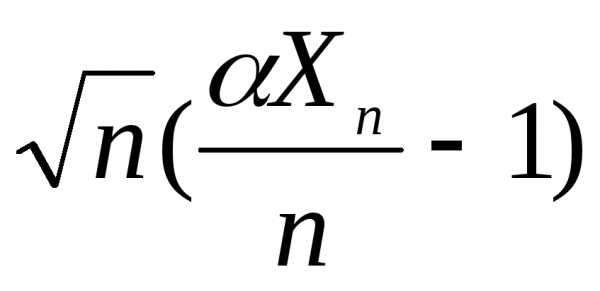 схо-
схо-
дится
при n и фиксированном к нормальному
закону распределения  .
.
3.3.11. Используя производящие функции, показать,
что при
биномиальный закон распределения
сходится к пуассоновскому закону с
параметром .
.
3.3.12. Используя характеристические функции,
показать, что при 
.
3.3.13. Пусть  — последовательность независимых и
одинаково распределённых случайных
величин. Доказать, что соотношение
— последовательность независимых и
одинаково распределённых случайных
величин. Доказать, что соотношение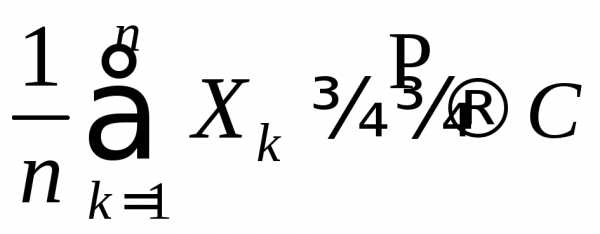 при некоторой постояннойС выполняется тогда и только тогда, когда
характеристическая функция случайной
величины Xk дифференцируема в точке t=0.
при некоторой постояннойС выполняется тогда и только тогда, когда
характеристическая функция случайной
величины Xk дифференцируема в точке t=0.
3.3.14. Дана последовательность
независимых случайных величин {Xk}, k1, распределенных
по нормальному закону с параметрами
.
Найти предельный закон распределения
суммы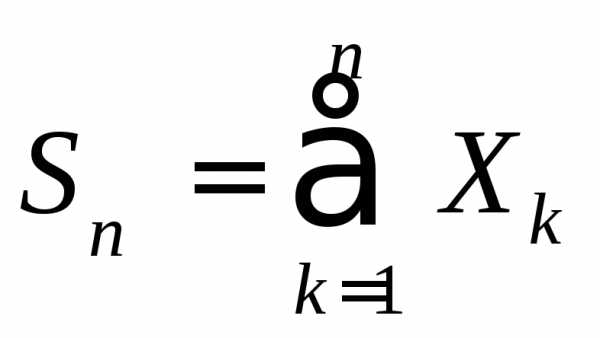 при,
если ряд
при,
если ряд а) сходится; б) расходится.
а) сходится; б) расходится.
3.3.15. Установить, выполняются ли закон больших чисел и центральная предельная теорема для последовательности независимых случайных величин {Xk}, k1 со следующими законами распределения:
а) 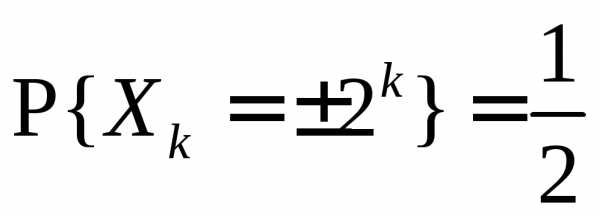 ;
;
б) ; ;
в) ; .
3.3.16. Доказать утверждение: если последовательность функций распределения сходится на всей числовой прямой к непрерывной функции распределения, то эта сходимость равномерная.
3.3.17. Пусть V – область m-мерного пространства, имеющая единичный объём, а — ограниченная функция, определённая всюду в областиV. Метод Монте-Карло вычисления интеграла
состоит в следующем: в область V бросают наудачу независимо одна от другой n точек равномерно распределенных в областиV, и за приближённое значение интеграла принимают сумму
.
Чему
равно 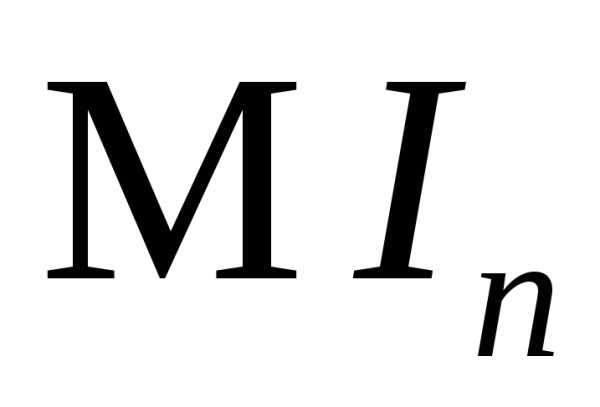 ?
Оценить
?
Оценить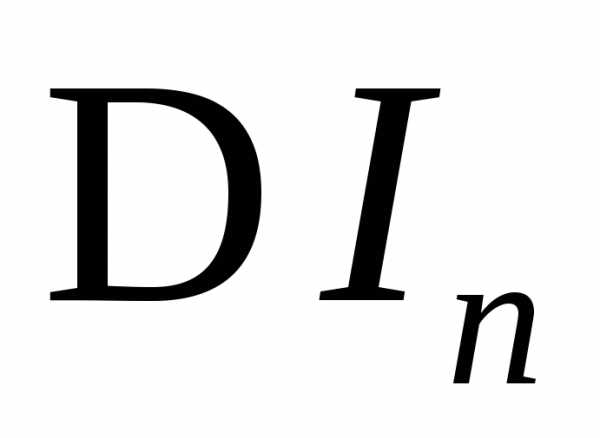 .
Найти приn предельный закон распределения для
величины
.
Найти приn предельный закон распределения для
величины 
3.3.18. Вычисление
интеграла 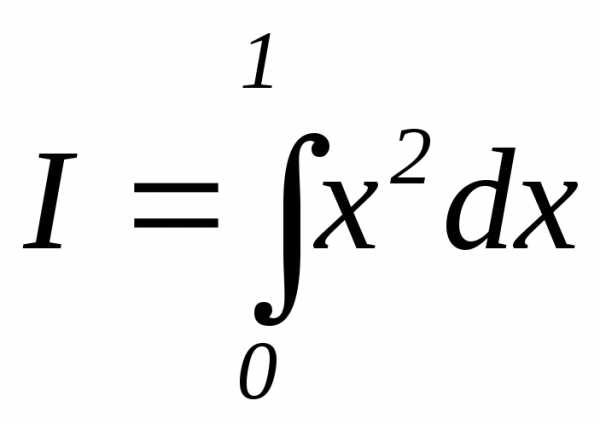 произведено методом Монте-Карло на
основании 1000 независимых
опытов. Вычислить вероятность того, что
абсолютная погрешность в определении
величины I не превзойдёт
0,01.
произведено методом Монте-Карло на
основании 1000 независимых
опытов. Вычислить вероятность того, что
абсолютная погрешность в определении
величины I не превзойдёт
0,01.
3.3.19. Сколько опытов надо произвести при вычислении методом Монте-Карло интеграла
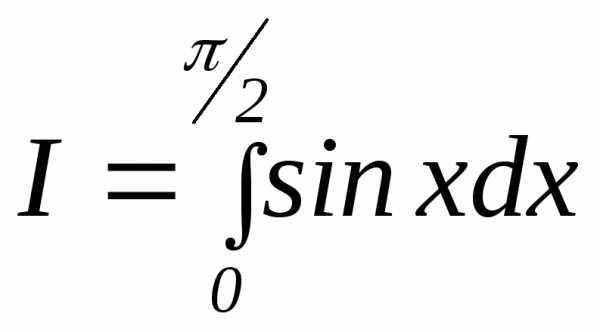
для того, чтобы с вероятностью р 0,99 можно было считать абсолютную погрешность вычисленного значения интеграла не превосходящей 0,1% от I?
3.3.20. На улице стоит человек и продаёт газеты. Предположим, что каждый из проходящих мимо людей с вероятностью 1/3 покупает газету. Пусть Х означает число людей, прошедших мимо продавца за время, пока он продавал первые 100 экземпляров газеты. Найти приближенный закон распределения Х.
3.3.21. Независимые случайные величины Х1,
Х2,…Xn,… имеют одинаковые распределения с 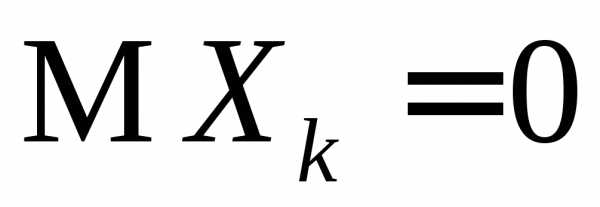 и
и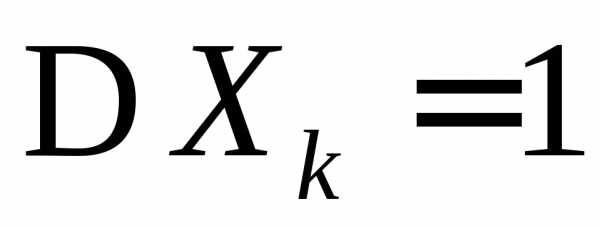 .
Показать, что величины
.
Показать, что величины
и 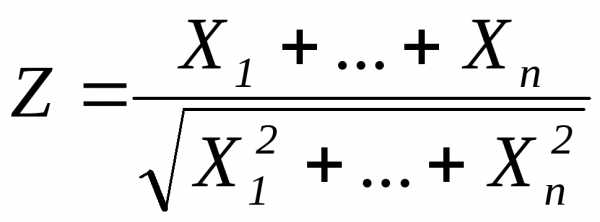
имеют при n нормальный закон распределения N(0, 1).
3.3.22. Пусть Х1,
Х2,…Xn,… — независимые, нормально распределённые 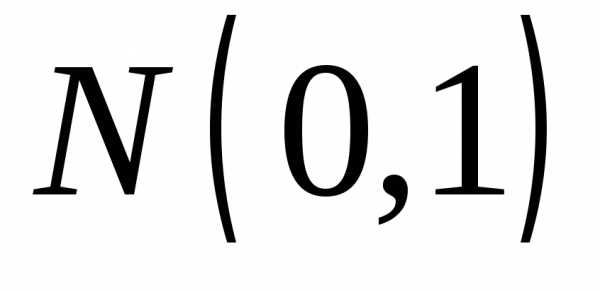 случайные величины. Положим
случайные величины. Положим
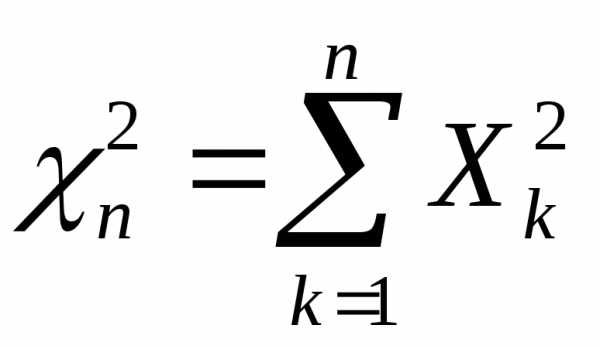 и
и 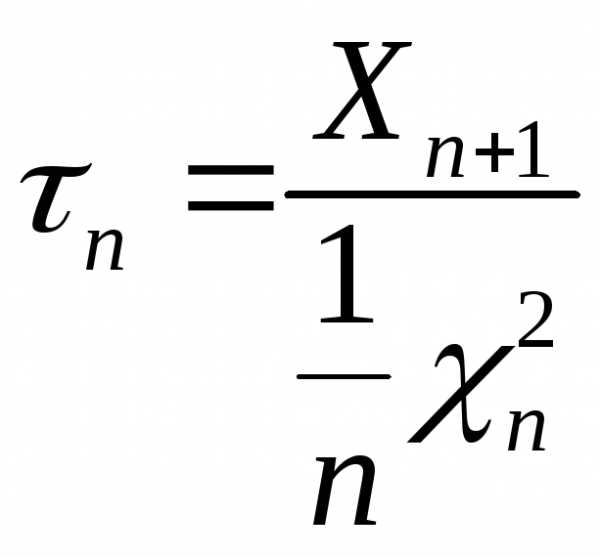 .
.
Найти
предельные при n законы распределения случайных величин 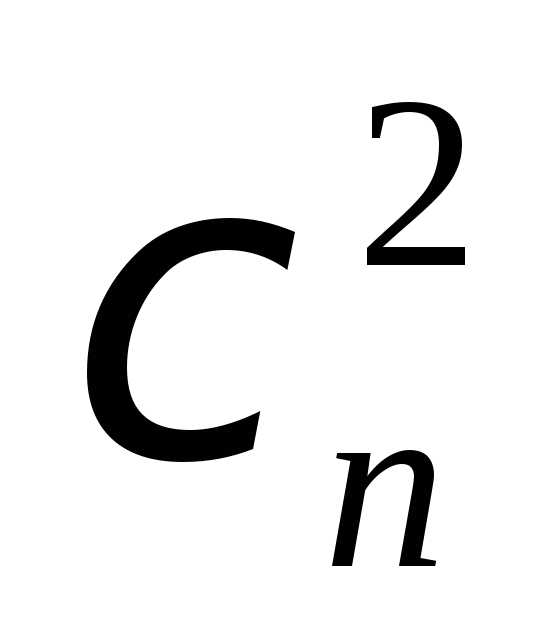 и
и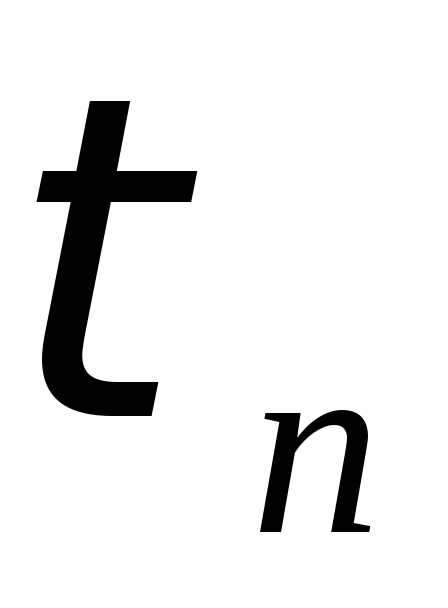 .
.
171
studfiles.net
Тема 10. Предельные теоремы теории вероятностей
Рассмотрим несколько утверждений и теорем из большой группы, так называемых предельных теорем теории вероятностей, устанавливающих связь между теоретическими и экспериментальными характеристиками случайных величин при достаточно большом числе испытаний над ними. Они составляют основу математической статистики. Предельные теоремы условно делят на две группы.
Первая группа теорем, называемая законом
больших чисел (ЗБЧ), устанавливает
устойчивость средних значений: при
большом числе испытаний их средний
результат перестаёт быть случайным и
может быть предсказан с достаточной
точностью. Одна из таких теорем (ЗБЧ в
форме Я.Бернулли, Т.6 п.7) нами уже была
рассмотрена в качестве применения
интегральной формулы Муавра-Лапласса.
Этот закон теоретически обосновывает
свойство устойчивости относительной
частоты появления некоторого события 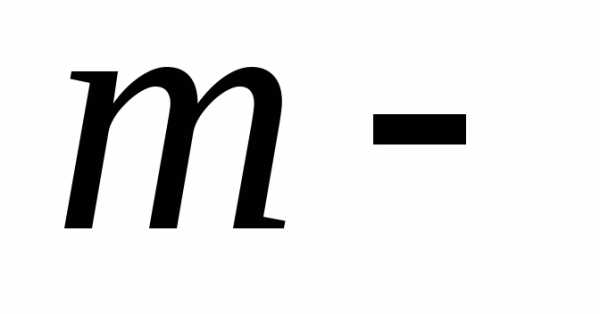 раз
при
раз
при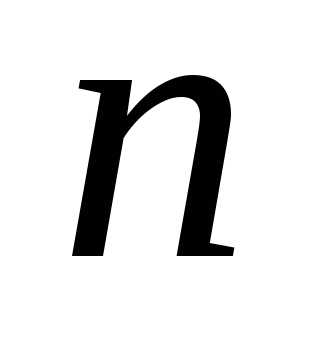 испытаниях по схеме Бернулли.
испытаниях по схеме Бернулли.
Вторая группа теорем, называемая центральной предельной теоремой (ЦПТ) устанавливает при некоторых сравнительно широких условиях, суммарное поведение достаточно большого числа с.в. почти утрачивает случайный характер и становится закономерным, т.е. устанавливается условий, при которых закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному закону.
Для практики важно знание условий, при выполнении которых совокупное действие многих случайных причин приводят к результату, почти не зависящему от случая, и позволяет предвидет ход событий. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Бернулли и Чебышева, Маркова и др.
В начале рассмотрим неравенство Чебышева, которое можно применять:
а) для грубой оценки вероятностей событий, связанных с случайными величинами, распределение которых неизвестно;
б) для доказательства ряда теорем ЗБЧ.
1. Неравенство Чебышева и Маркова
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.
Пусть
 —
дискретная случайная величина с
заданной таблицей распределения
—
дискретная случайная величина с
заданной таблицей распределения
Контроль—
Поставим перед собой задачу: «оценить
вероятность того, что отклонение д.с.в. 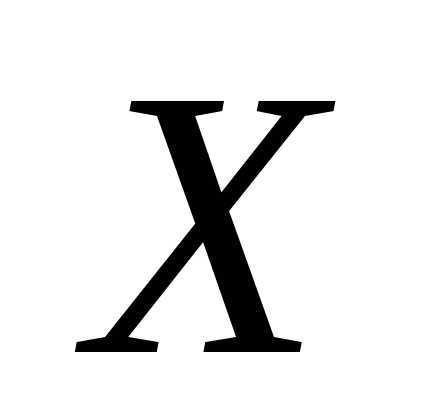 от её м.о.
от её м.о. 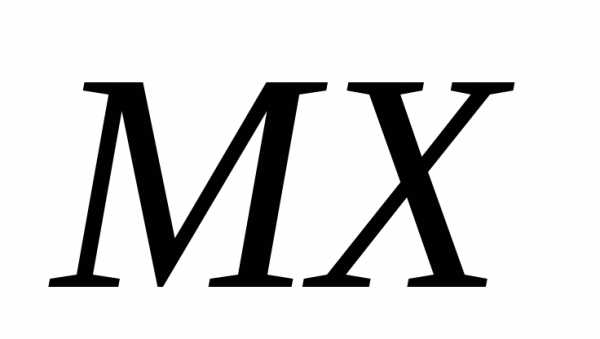 по абсолютной величине не перевешает
положительного числа
по абсолютной величине не перевешает
положительного числа ».
Имеет место утверждение
».
Имеет место утверждение
Теорема 10.1. (неравенство Чебышева д.
с. в.). Если дискретная случайная
величина 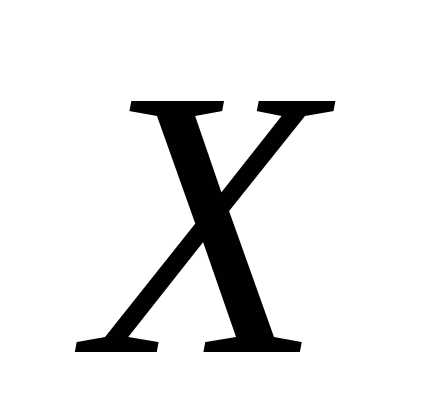 имеет
м.о.и дисперсию
имеет
м.о.и дисперсию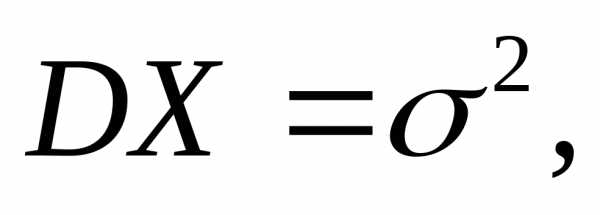 то для любого
то для любого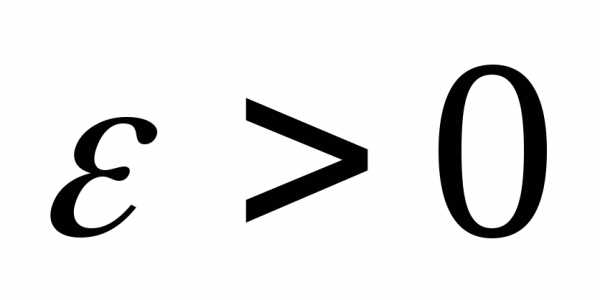 справедливо
неравенство
справедливо
неравенство
(1)
Доказательство. Поскольку событияипротивоположные, то сумма их вероятностей равна единице, т.е.
(2) .
Отсюда интересующая нас вероятность
(3) ,
Следовательно, задача сводится к вычислению вероятности
Далее, напишем выражение дисперсии для
с.в. 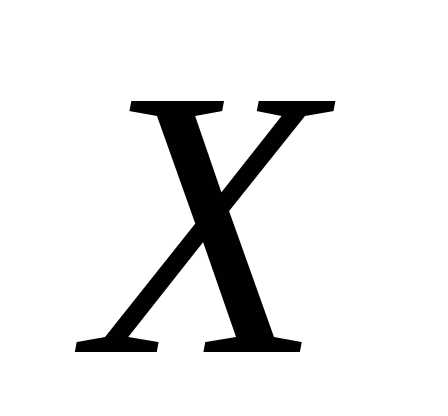 :
по определению для д.с.в.
:
по определению для д.с.в.
В левой части этого выражения отбросим
все слагаемые. у которых
(для
оставшихся слагаемых),
в результате чего сумма только
уменьшиться. Без ограничения общности
этими слагаемыми можно выбрать первые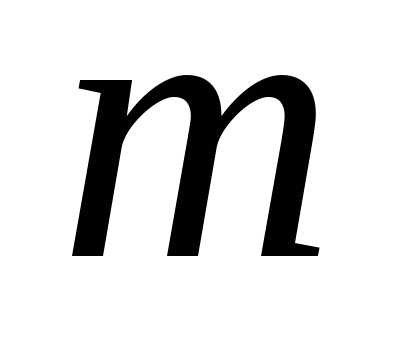 слагаемых в сумме.
слагаемых в сумме.
Таким образом, , т.е.
(4)
Заметим, что обе части неравенства положительны, поэтому, возведя их в квадрат, получим равносильные неравенствадля всех
Воспользуемся этим замечанием в правой части нашей суммы, получим
(5) ).
По теореме сложения, сумма вероятностей
— есть вероятность того, что с.в.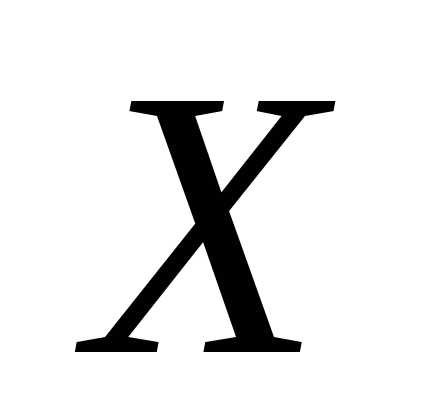 примет одно (безразлично какое) из
значенийа
при любом из них отклонение удовлетворяет
неравенствуОтсюда следует, что суммавыражает вероятность.
Это соображение позволяет переписать
неравенство (5) в виде:
примет одно (безразлично какое) из
значенийа
при любом из них отклонение удовлетворяет
неравенствуОтсюда следует, что суммавыражает вероятность.
Это соображение позволяет переписать
неравенство (5) в виде:
или
.
Следовательно, согласно равенствам (2) и (3) получим доказательство неравенство (1).
Замечание. Неравенство Чебышева (1) можно переписать в другом виде:
(6)
Отметим, что для практики неравенство Чебышева имеет ограниченное значение, поскольку часто даёт грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если тоэтим самым Неравенство Чебышева в этих случаях лишь потверждает того, что любая вероятность выражается неотрицательным числом.
Неравенство Чебышева в частности, для
случайной величины 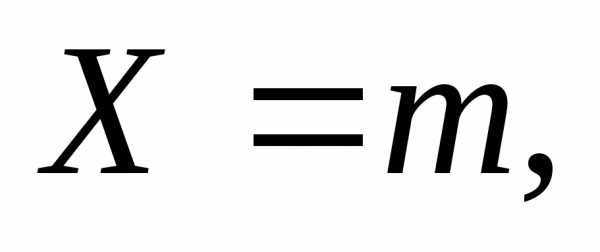 имеющей
биномиальное распределение с м.о.и дисперсией(см.Т.9., теорема 1), принимает вид
имеющей
биномиальное распределение с м.о.и дисперсией(см.Т.9., теорема 1), принимает вид
(7)
В том числе, для отклонения частоты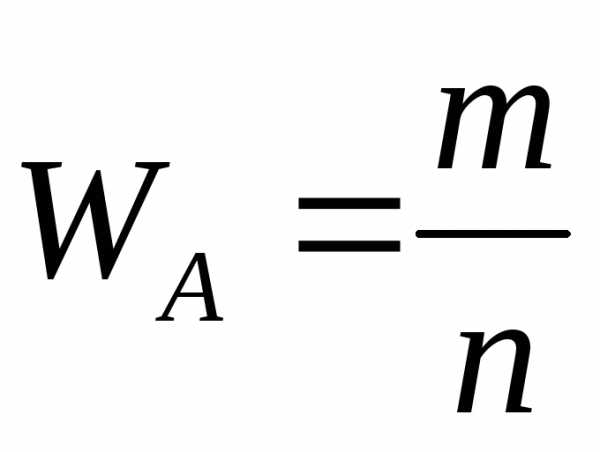 события в
события в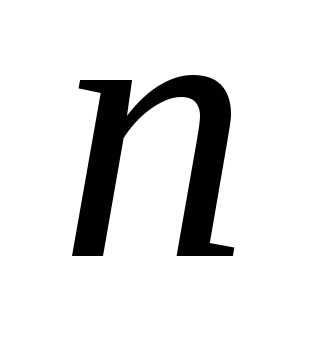 независимых
испытаниях, в каждом из которых оно
может произойти с вероятностьюи дисперсией,
неравенство Чебышева имеет вид:
независимых
испытаниях, в каждом из которых оно
может произойти с вероятностьюи дисперсией,
неравенство Чебышева имеет вид:
(8)
Пример 1. Оценить с помощью неравенство
(1) вероятность того, что отклонение
д.с.в.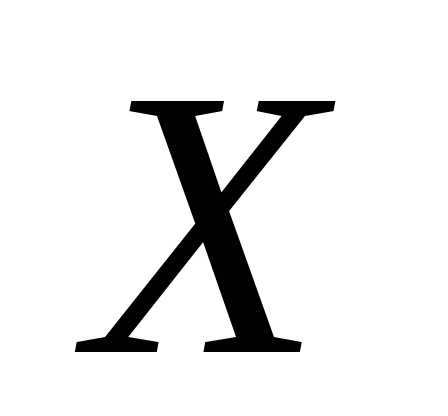
от
своего математического ожидания будет
меньше 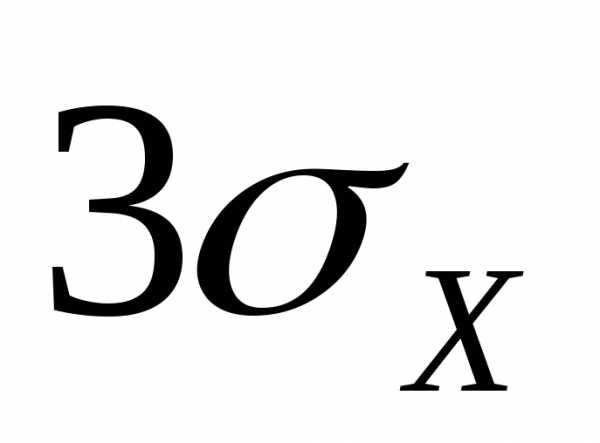 .
.
Решение. Положим в формуле (1) получим
оценку снизу
получим
оценку снизу
Оценка
сверху, как известно ( п.9. формула (45)),
называется «правилом трёх сигм»
для с.в.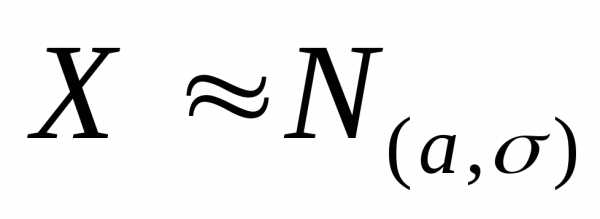 и
эта вероятность была равна
и
эта вероятность была равна Как легко заметить, неравенство Чебышева
даёт результат несколько слабее. В
общем случае получаем неравенство
Как легко заметить, неравенство Чебышева
даёт результат несколько слабее. В
общем случае получаем неравенство
(9) .
Пример 2. Устройство состоит из 10
независимо работающих элементов.
Вероятность отказа каждого элемента
за время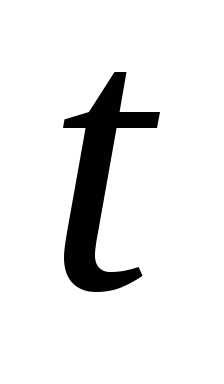 равна 0,05. С помощью неравенство Чебышева
оценить вероятности того, что абсолютная
величина разности между числом отказавших
элементов и средним числом (м.о.) отказов
за время
равна 0,05. С помощью неравенство Чебышева
оценить вероятности того, что абсолютная
величина разности между числом отказавших
элементов и средним числом (м.о.) отказов
за время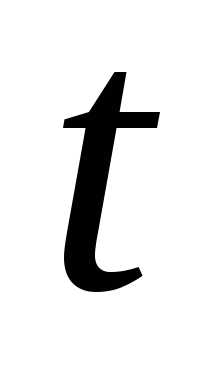 откажется: а) меньше двух; б) не меньше
двух.
откажется: а) меньше двух; б) не меньше
двух.
Решение. а) Пусть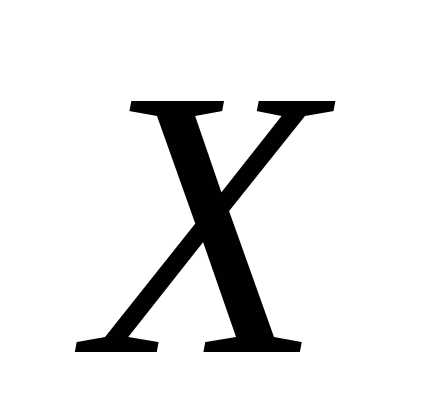 обозначает дискретную случайную
величину, выражающую число отказавших
элементов за время
обозначает дискретную случайную
величину, выражающую число отказавших
элементов за время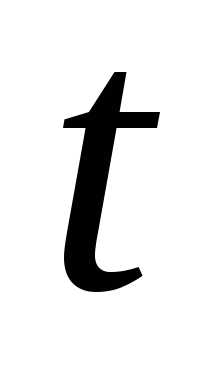 .
Тогда по закону Бернулли (
.
Тогда по закону Бернулли (
По неравенству Чебышева имеем
б) События и противоположны, поэтому сумма их вероятностей равна единице. Следовательно,
2. Пусть н.с.в.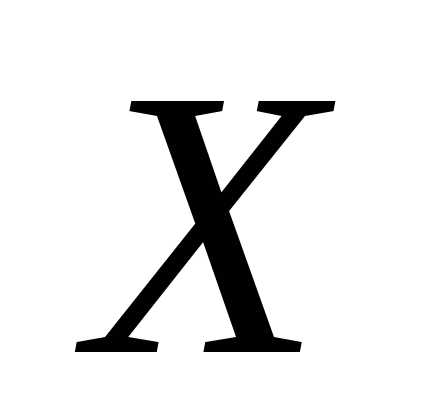 задана
со своей функцией распределения
вероятности
задана
со своей функцией распределения
вероятности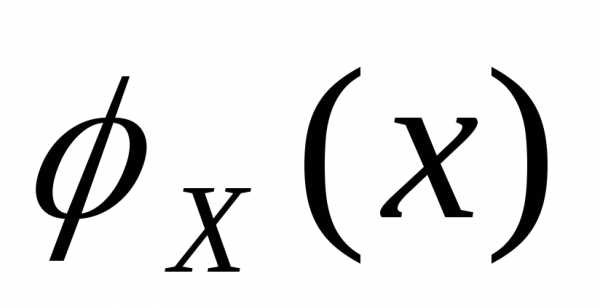 .
Тогда справедливо утверждение
.
Тогда справедливо утверждение
Теорема 10.2. (неравенство Чебышева для
н. с. в.). Если непрерывная случайная
величина  с плотностью
с плотностью имеет м.о.и дисперсию
имеет м.о.и дисперсию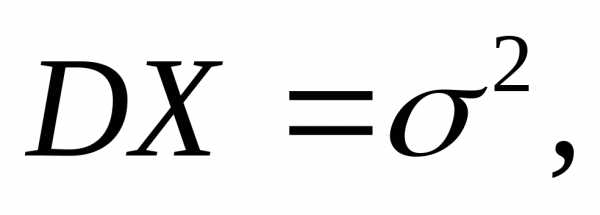 то для любого
то для любого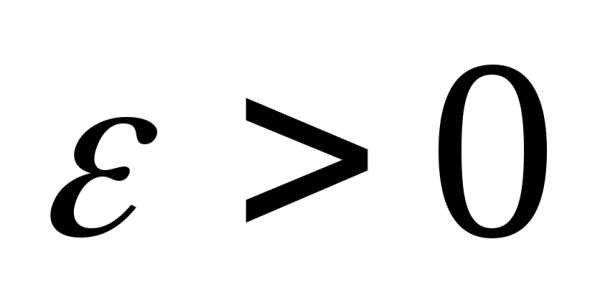 справедливо неравенство
справедливо неравенство
(10)
Доказательство. Вероятностьесть вероятность попадания н.с.в.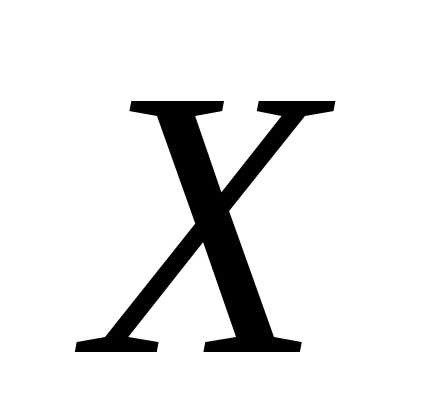 в область, лежащую вне промежутка
Поэтому имеем
в область, лежащую вне промежутка
Поэтому имеем
Заметим, что область интегрирования можно записать в виде, откуда следует, что. Следовательно,
=.
Так как подынтегральная функция неотрицательна, то расширяя пределы интегрирования получим неравенство
.
Таким образом, из двух последних формул получим
.
Утверждение доказано.
Это же неравенство можно записать (в силу равенства +=1) также и в другой форме:
(11)
Теперь объединяя обе теоремы, сформулируем неравенство Чебышева в общем виде.
Теорема 10.3. Если случайная величина 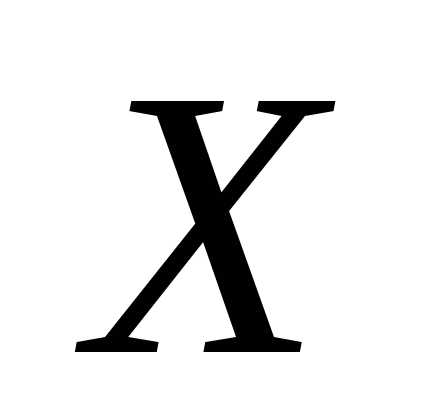 имеет
м.о.и дисперсию,
имеет
м.о.и дисперсию,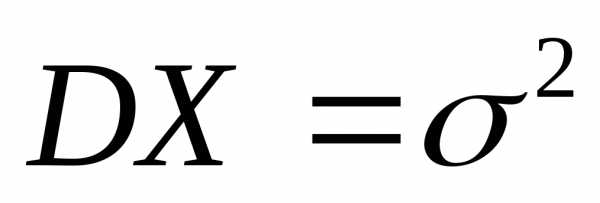 то для любого
то для любого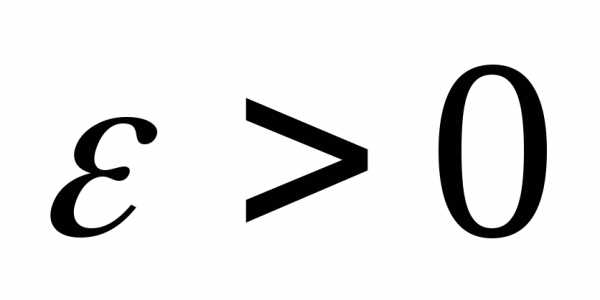 справедливы
неравенства
справедливы
неравенства
1. 2..
Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто даёт грубую оценку, а иногда тривиальную (не представляющего интереса) оценку. Например, еслии, следовательно,то. Таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения есть неотрицательное число, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом.
Рассмотрим ещё одно неравенство для
неотрицательно определённых случайных
величин .
.
Теорема 10.4. (Неравенство Маркова). Если неотрицательная случайная
величина  имеет
м.о.,
то для любого
имеет
м.о.,
то для любого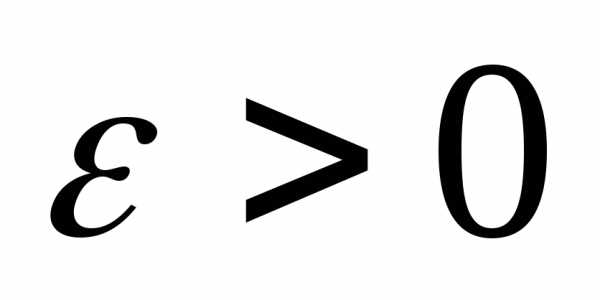 справедливо
неравенство
справедливо
неравенство
1. 2..
Доказательство. Проверим справедливости
неравенств (12) для н.с.в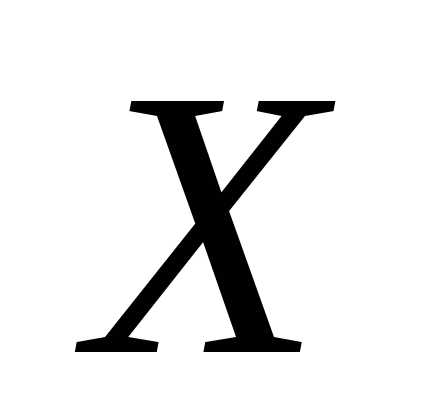 с функцией плотностью
с функцией плотностью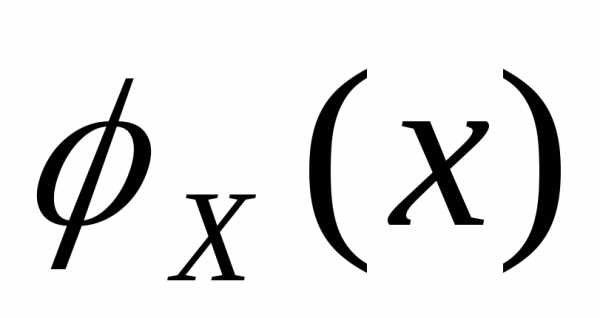 .
Имеем
.
Имеем
Так как
то получим и второе неравенство.
studfiles.net


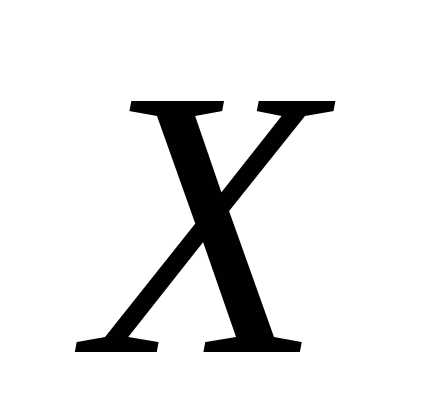 —
дискретная случайная величина с
заданной таблицей распределения
—
дискретная случайная величина с
заданной таблицей распределения