Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Определение. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Рис.1
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD.
Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
Рис.2
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.
Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).
Рис.3
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Рис.4
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Рис.5
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,
откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны. Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).
Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).
Рис.6
Таким образом,
| FO | = | OD | , | GO | = | OE | .
Следовательно,
| AF | = | FO | = | OD | , | CG | = | GO | = | OE | .
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1, считая от вершины треугольника.
Доказательство завершено.
Следствие. Все три медианы треугольника пересекаются в одной точке.
Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении 2 : 1, считая от вершины A (рис.7).
Рис.7
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение. Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Рис.8
Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).
Рис.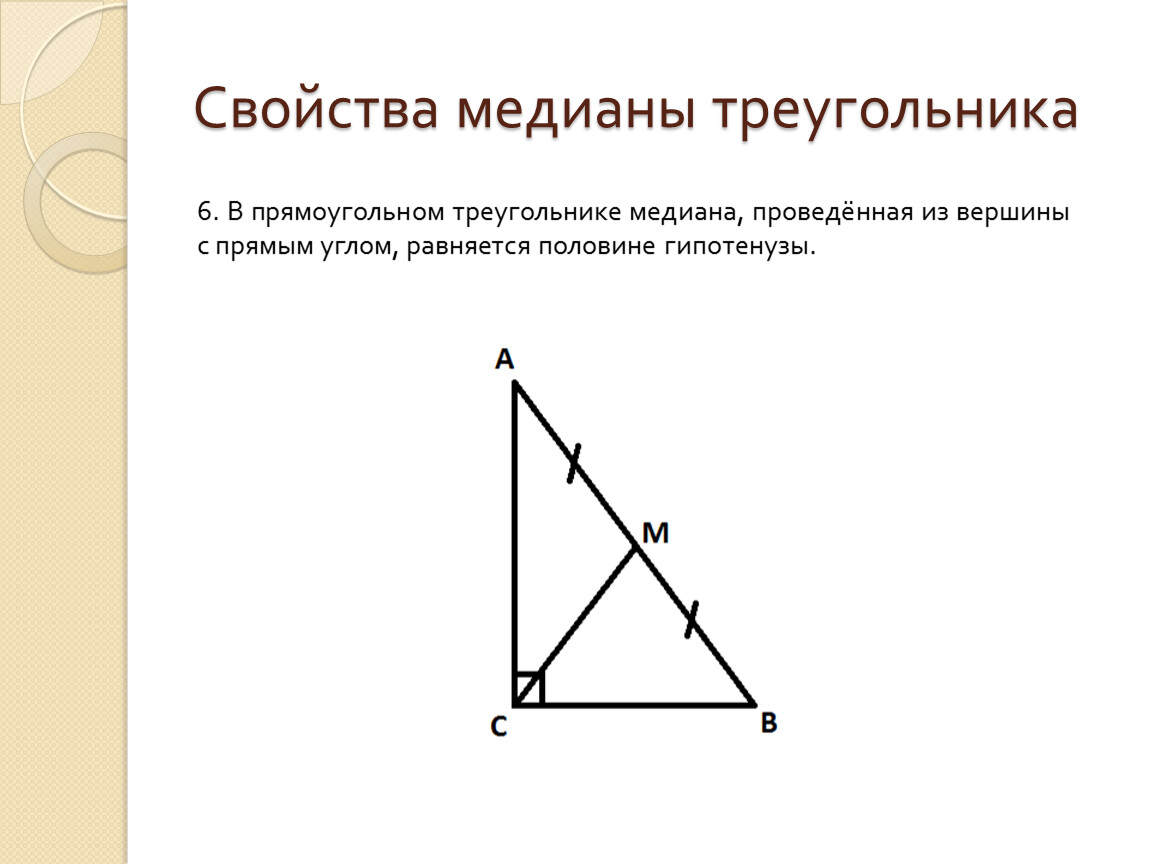 9
9
Тогда
В силу утверждения 1,
что и требовалось доказать.
Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:
Рис.10
Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:
Складывая эти равенства, получим:
что и требовалось доказать.
Следствие. Длины медиан и длины сторон треугольника связаны формулой
Доказательство. В силу утверждения 4 справедливы равенства:
Складывая эти равенства, получим:
что и требовалось доказать.
Утверждение 5. В параллелограммепараллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.
Доказательство. Рассмотрим рисунок 11.
Рис.11
Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силу утверждения 4, справедливы равенства:
Следовательно,
d12 = 2a2 + 2b2 – d22,
d22 = 2a2 + 2b2 – d12.
Складывая эти равенства, получим
что и требовалось доказать.
Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).
Рис.12
Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).
13).
Рис.13
Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольникпрямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:
что и требовалось доказать.
Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).
Рис.14
Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.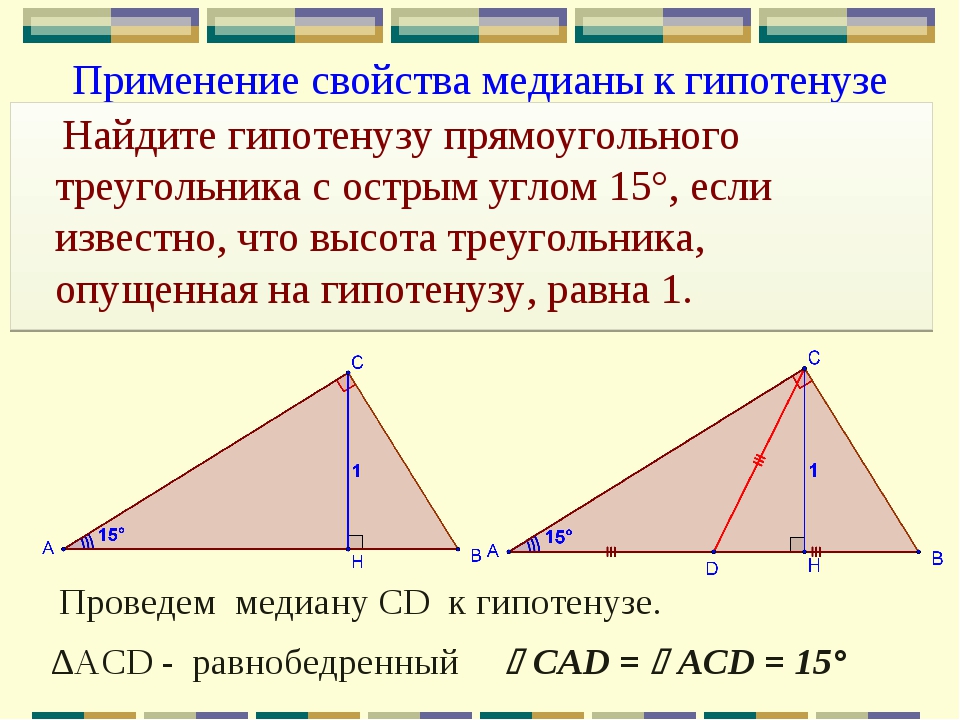 15), то будет справедливо равенство
15), то будет справедливо равенство
Рис.15
Доказательство. По свойствам векторов
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
проведенной к основанию, боковым сторонам
В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.
- BD – медиана △ABC;
- AD = DC.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.
- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.
- O – центр тяжести или центроид треугольника;
- AO = 2OF;
- BO = 2OD;
- CO = 2OE.
Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.
Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).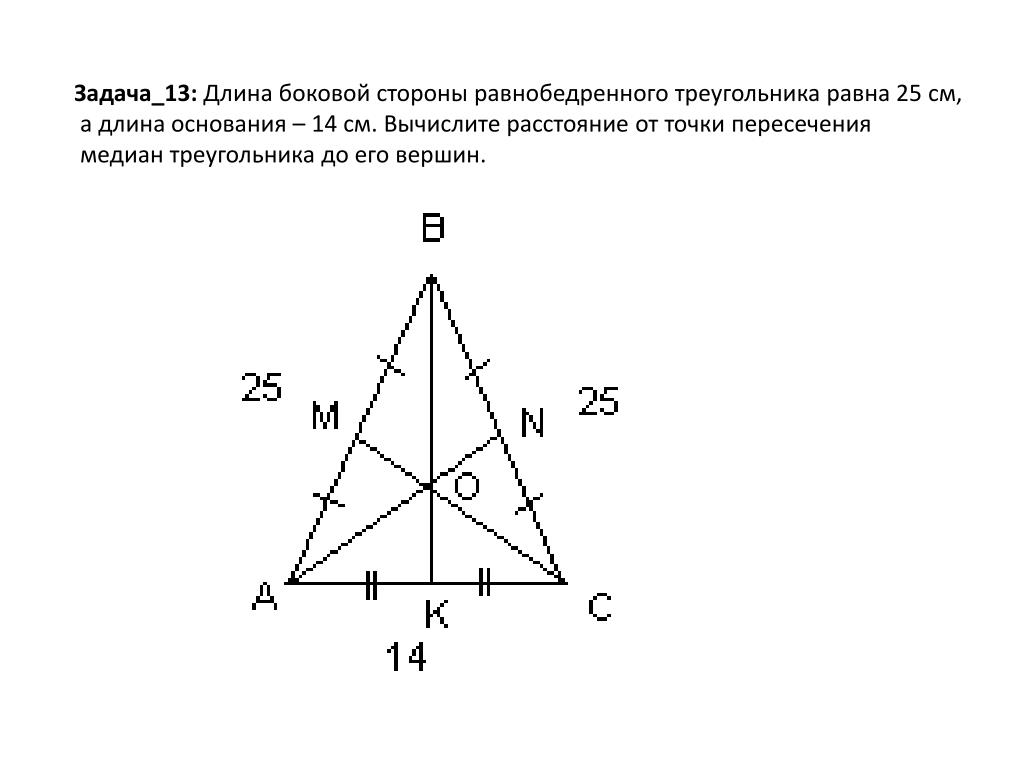
Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
- a – основание;
- b – боковая сторона.
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Microsoft Word — геометрия-1.doc
%PDF-1.6
%
955 0 obj
>
endobj
952 0 obj
>stream
2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.
Медиана — что это такое, свойства медианы треугольника
Обновлено 18 января 2021- Медиана — это.
 ..
.. - Пересечение медиан треугольника
- В равностороннем треугольнике
- Медиана прямоугольного треугольника
- Вместо заключения
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.
У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.
И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.
Медиана — это…
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.
Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.
Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.
Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:
Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.
Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.
И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!
А точнее, три!
И выглядят они вот так.
На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.
Пересечение медиан треугольника
Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.
Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.
Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.
Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:
- Отрезок СО вдвое больше, чем отрезок АО;
- Отрезок РО вдвое больше, чем отрезок LO;
- Отрезок МО вдвое больше, чем КО.

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.
Медиана равностороннего треугольника
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.
Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.
Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.
И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.
Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.
Медиана прямоугольного треугольника
Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.
Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.
Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.
Вместо заключения
А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.
Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.
Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».
И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.
Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ruУрок 12. медианы треугольника. биссектрисы треугольника. высоты треугольника — Геометрия — 7 класс
Геометрия
7 класс
Урок № 12
Медианы треугольника.
Перечень рассматриваемых вопросов:
- Понятие медианы, биссектрисы, высоты треугольника.
- Построение медианы, высоты, биссектрисы.
- Точки пересечения медианы, высоты и биссектрисы в треугольнике.
- Создание представления о замечательных точках в треугольнике.
Тезаурус:
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В.
 Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.
Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.
Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.
AA1, BB1, CC1– биссектрисы ∆АВС
В любом треугольнике биссектрисы пересекаются в одной точке.
Введём понятие медианы треугольника.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
BM – медиана треугольника ABC.
AA1, BB1, CC1– медианы ∆АВС.
В любом треугольнике медианы пересекаются в одной точке.
Введём понятие высоты треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
AH – высота треугольника ABC.
AH1, BH2, CH3– высоты ∆АВС.
В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».
На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.
Докажем, что треугольники ABD и CED равны.
Дано:
АD – медиана ∆ABC.
AD = DE.
Доказать:
∆ABD = ∆CED.
Доказательство:
По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.
∠ADB = ∠CDE (по свойству вертикальных углов).
Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
Задача 1.
В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.
Решение:
1.Нарисуем рисунок по условию задачи.
2.По условию AD и BM – биссектрисы ∆ABC.
∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°
∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°
3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.
4.25° + 40° + ∠AOB = 180°.
5.∠AOB = 180° – (25° + 40°) = 115°.
Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.
Задача 2.
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.
Решение:
1.По условию ∠СОD = 90°.
Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.
2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.
3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.
4. 40° + 2∠МОВ = 90°.
∠МОВ = (90° – 40°):2 = 25°.
Ответ: ∠МОВ = 25°.
Задачи по школьной математике. Высота, медиана и биссектриса треугольника
Высота, медиана и биссектриса треугольника
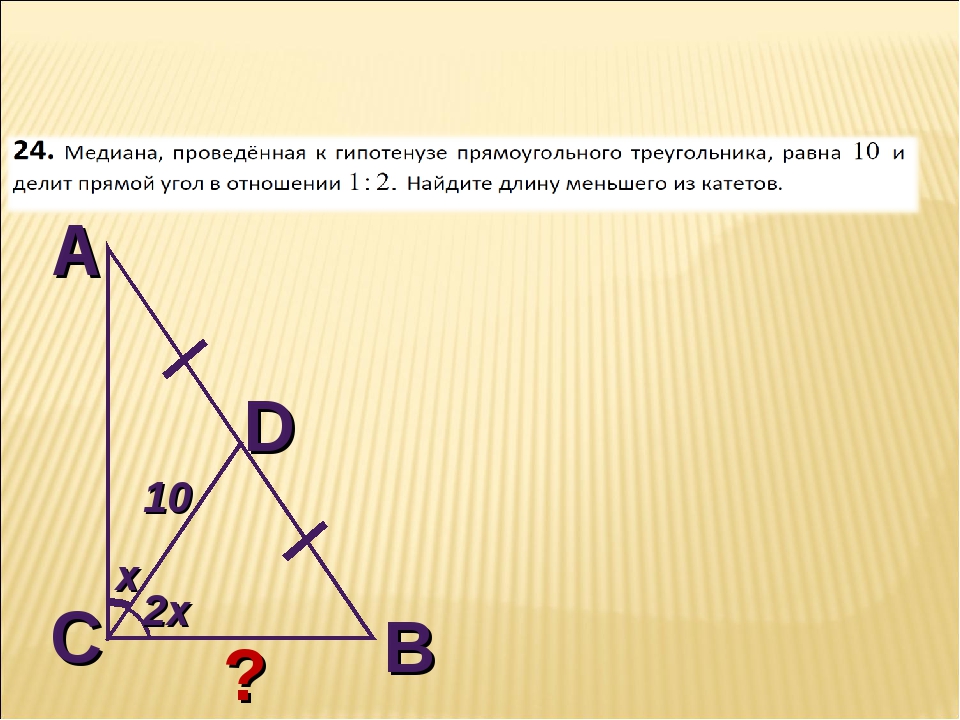
- Медиана прямоугольного треугольника, проведенная к гипотенузе, равна 6,5. Найдите катеты треугольника, если сумма гипотенузы и меньшего из катетов равна 18.
- В треугольнике стороны равны 4, 6 и 8. Найдите длину медианы, проведенной к большей стороне.
- Биссектриса прямоугольного треугольника делит катет на отрезки, равные 25 и 24. Найдите гипотенузу треугольника.
- В прямоугольном треугольнике с катетами, равными 18 и 24, из вершины большего острого угла проведена биссектриса.
 Найдите проекцию биссектрисы на больший катет.
Найдите проекцию биссектрисы на больший катет. - В равнобедренном треугольнике основание равно 1, а высота, опущенная на основание, равна . Найдите расстояние от середины основания до боковой стороны.
- В равнобедренном треугольнике основание равно 4, медианы боковых сторон взаимно перпендикулярны. Найдите площадь треугольника.
- В равнобедренном треугольнике АВС с основанием АС медиана AD перпендикулярна биссектрисе СЕ. Найдите косинус угла АСВ.
- Медианы треугольника равны 5, 6 и 5. Найдите площадь этого треугольника.
- Найдите отношение суммы квадратов медиан треугольника к сумме квадратов его сторон.
- Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, равная 3. Найдите сторону АС, если известно, что угол ABD прямой.
- В треугольнике стороны равны 3, 5 и 6. Найдите биссектрису наименьшего угла треугольника.
- В треугольнике ABC известно, что АВ = 3, АС = 5 и угол ВАС равен 120о. Найдите биссектрису BD.

- Биссектриса угла В треугольника АВС пересекает сторону АС в точке D. Найдите AB, если AD = 12, DC = 27 и BD = 24.
- Дан треугольник ABC, в котором AC = 5, AB = 6, BC = 7. Биссектриса угла С пересекает сторону АВ в точке D. Определите площадь треугольника ADC.
- В треугольнике ABC проведены биссектрисы BD и AE. Найдите отношение площадей треугольников BDE и ABC, если AB = 5, BC = 8 и AC = 7.
- В треугольнике точка пересечения биссектрис удалена от прямой, содержащей одну из сторон, на 1,5. Найдите площадь треугольника, если его периметр равен 16.
- В треугольнике АВС медиана AD и биссектриса ВЕ пересекаются в точке О. Найдите площадь треугольника АВС, если AD перпендикулярно ВЕ и площадь треугольника АОЕ равна 2.
- В треугольнике АВС проведена высота АН. Прямые, одна из которых содержит медиану ВК, а вторая — биссектрису ВЕ, делят высоту на три равных отрезка. Найдите АС, если АВ равно 4.
- Даны стороны треугольника ВС = 15, АС = 14 и АВ = 13.
 Найдите площадь треугольника, ограниченного высотой и биссектрисой, проведенными из вершины В.
Найдите площадь треугольника, ограниченного высотой и биссектрисой, проведенными из вершины В. - Докажите, что биссектрисы треугольника пересекаются в одной точке.
- На высоте AH треугольника ABC взята точка M. Докажите, что AB2 — AC2 = MB2 — MC2.
Метки задачи, треугольник. Смотреть запись.
Медианы треугольника и задачи на площадь | Шевкин.Ru
Поводом для заметки послужила следующая задача, встреченная в Интернете.
1. Какую часть площади прямоугольника ABCD составляет сумма площадей закрашенных треугольников, если M и N — середины сторон AB и AD соответственно?
Эту задачу мы решим чуть позже для общего случая — для параллелограмма. А пока повторим основные факты, которые потребуются в решении.
А пока повторим основные факты, которые потребуются в решении.
Свойство медиан треугольника
1) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Этот факт доказан в одном учебнике для 8 класса с помощью теоремы Фалеса, в другом с помощью подобия треугольников. Оба раза сначала доказывают, что две медианы делятся точкой их пересечения в отношении 2 : 1, считая от вершины, а потом, что третья медиана проходит через точку пересечения двух первых медиан.
Свойства площади треугольника
2) Медиана треугольника делит его площадь пополам.
3) Прямая, выходящая из вершины треугольника и делящая его сторону в отношении
m : n, делит его площадь в том же отношении.
Поупражняемся в применении приведённых свойств.
2. Докажите свойство медиан треугольника, используя свойства площади.
Пусть медианы CE и BD треугольника ABC пересекаются в точке M, а луч AM пересекает сторону BC в точке F.
Из свойства 2) следует, что площади треугольников AEM и BEM равны — обозначим их c. Аналогично площади треугольников ADM и CDM равны — обозначим их b. Из того же свойства площади следует, что площади треугольников ABD и ACE равны — они составляют половину площади S треугольника ABC. Тогда из равенства b + 2c = 2b + c следует, что b = c = S/6.
Из утверждения, обратного свойству 3) (оно доказывается от противного), следует, что BM : MD = CM : ME = 2c : c = 2 : 1. То есть две медианы делятся точкой их пересечения в отношении 2 : 1, считая от вершины.
Медиана CE делит медиану BD в отношении 2 : 1, считая от вершины. Аналогично доказывается, что медиана, проведённая из вершины A, делит медиану BD в отношении
2 : 1, считая от вершины, то есть эта медиана проходит через точку F, а значит, совпадает с отрезком AF. Так же доказывается, что медиана CE делит медиану AF в отношении 2 : 1, считая от вершины, что и требовалось доказать.
3. Какую часть площади параллелограмма ABCD составляет сумма площадей закрашенных треугольников, если M и N — середины сторон AB иAD соответственно?
Пусть O — точка пересечения параллелограмма. Так как F — точка пересечения медиан треугольника ABC, то площади треугольников MBF и OFC равны — они составляют 1/6 площади треугольников ABC и 1/12 площади параллелограммаABCD. Аналогично площади треугольников NED и OEC равны и составляют 1/12 площади параллелограммаABCD. Тогда сумма площадей закрашенных фигур равна 4/12 = 1/3 площади параллелограммаABCD.
Ответ. 1/3.
4. Какую часть площади закрашенной фигуры составляет площадь параллелограмма ABCD, если M и N — середины сторон AB иAD соответственно?
Медиана треугольника — Определения, Свойства, Уравнение, Формула, Примеры
В геометрии медиана треугольника относится к отрезку линии, соединяющему вершину треугольника с серединой противоположной стороны, таким образом разделяя эту сторону пополам. Для любого треугольника есть ровно три медианы, по одной от каждой вершины. Они пересекаются друг с другом в центре тяжести треугольника.
Медиана теоремы о треугольнике
Медиана теоремы о треугольнике утверждает, что медианы треугольника пересекаются в точке, называемой центроидом треугольника, которая составляет две трети расстояния от вершин до середины противоположных сторон.Центроид треугольника — это точка пересечения всех трех медиан этого треугольника с тем фактом, что треугольник имеет ровно три медианы.
Высота треугольника определяется как отрезок прямой, соединяющий вершину с противоположной стороной треугольника под прямым углом. Все треугольники имеют 3 высоты (по одной от каждой вершины) и встречаются в одной точке треугольника. Три высоты встречаются в точке, которая может лежать внутри или вне треугольника, известной как ортоцентр треугольника.{2}} {4}} \)
a, b и c = три стороны треугольника.
Медиана треугольника
Для треугольника, координаты трех вершин которого даны, мы можем выполнить шаги, указанные ниже, чтобы найти медиану данного треугольника.
- Шаг 1: Найдите координаты вершин треугольника.
- Шаг 2: Найдите координаты средних точек отрезков.
- Шаг 3: Присоедините вершину к середине противоположной стороны треугольника.Вы получите медианы.
- Шаг 4: Найдите уравнение медианы треугольника, используя формулу, использованную для нахождения уравнения прямой линии (двухточечная форма). Здесь уравнение медианы AD треугольника ABC = \ (\ left (\ mathbf {y} — \ mathbf {y} _ {1} \ right) = \ left (\ frac {\ mathrm {y} _ {2} — \ mathrm {y} _ {1}} {\ mathrm {x} _ {2} — \ mathrm {x} _ {1}} \ right) _ {\ mathrm {AD}} \ left (\ mathrm {x } — \ mathrm {x} _ {1} \ right) \)
Следовательно, уравнения медиан треугольника ABC будут: (y − y1) = (y2 − y1 / x2 − x1) (x − x1)
- н.э .: 7x + 12 = 4 года
- Аналогично BF: x + 2y = 12
- и CE: x + 36 = 7y
Важные примечания
- Каждая медиана делит треугольник на два меньших треугольника одинаковой площади
- Центроид (точка, где они встречаются) — это центр тяжести треугольника
- Сумма медиан треугольника: сумма квадратов медиан треугольника равна трем четвертям суммы квадратов сторон треугольника.
- Периметр треугольника больше суммы трех его медиан.
- Соответствующие стороны, периметры, медианы и высоты будут иметь одинаковое соотношение для двух одинаковых треугольников.
- Середина сегмента делит его на два конгруэнтных сегмента, а середина треугольника делит его на два конгруэнтных треугольника.
- Также, если два треугольника совпадают. Медианы конгруэнтных треугольников равны, поскольку соответствующие части конгруэнтных треугольников конгруэнтны.
Мыслить нестандартно!
Скульптура планирует создать новую скульптуру, состоящую из треугольника, сбалансированного на другом треугольнике. Какая точка может быть точкой баланса? Поможет ли поиск центроида?
Статьи, относящиеся к медиане треугольника
Часто задаваемые вопросы о медиане треугольника
Делит ли медиана треугольника на два конгруэнтных треугольника?
Для данного треугольника его медиана дополнительно делит треугольник на два конгруэнтных треугольника, а затем медиана становится общей стороной обоих треугольников.
В чем разница между высотой и средним углом треугольника?
Медиана треугольника — это отрезок прямой, который соединяет вершину со средней точкой противоположной стороны, разделяя ее на два равных треугольника. Высота треугольника — это отрезок прямой, соединяющий вершину треугольника с противоположной стороной так, что отрезок перпендикулярен противоположной стороне. Это высота треугольника.
Каковы свойства медианы треугольника?
Медиана треугольника — это отрезок прямой, соединяющий вершину треугольника с серединой его противоположной стороны.Медиана треугольника делит противоположную сторону пополам, разделяя ее на две равные половины, и делит пополам угол, из которого он возникает, на два угла равной меры.
Всегда ли медиана 90 градусов?
Нет, Медиана не всегда образует прямой угол со стороной, на которую она падает. Только в случае равностороннего или равнобедренного треугольника одна медиана приходится на неравную сторону равнобедренного треугольника.
В чем разница между медианой и биссектрисой?
Медиана треугольника относится к линейному сегменту, соединяющему вершину со средней точкой противоположной стороны, тогда как биссектриса упоминается как линейный сегмент, который проходит через среднюю точку сегмента, который также перпендикулярен сегмент.{2}} {4}} \) где,
- a, b, c — стороны треугольника
- ма — длина медианы от вершины A.
Как найти уравнение медианы треугольника?
Чтобы найти уравнение медианы треугольника, мы можем использовать формулу, уравнение двухточечной формы прямой линии, соединяющей вершину и середину противоположной вершины, мы получаем \ (\ left (\ mathbf {y} — \ mathbf {y} _ {1} \ right) = \ left (\ frac {\ mathrm {y} _ {2} — \ mathrm {y} _ {1}} {\ mathrm {x} _ {2} — \ mathrm {x} _ {1}} \ right) _ {\ mathrm {AD}} \ left (\ mathrm {x} — \ mathrm {x} _ {1} \ right) \)
Медиана треугольника: определение и основные свойства
Вычисление медианы треугольника — одна из фундаментальных задач геометрии.В этом руководстве вы узнаете, что такое медиана, как ее вычислять и как решать проблемы, связанные с ней.
Если вы изучаете геометрию для подготовки к SAT, этот курс по математике SAT — хорошее место для начала.
Различные типы треугольников
Прежде чем мы сможем определить медиану треугольника, мы должны сначала узнать о различных типах треугольников. Это пригодится, когда мы будем работать с медианами.
В зависимости от количества равных сторон треугольники могут быть классифицированы как:
- Scalene: Треугольник без равных сторон или углов, т.е.е. все три стороны треугольника разные. В приведенном ниже треугольнике ABC все три стороны имеют разную длину.
- Равнобедренный: Треугольник с двумя равными сторонами. В приведенном ниже треугольнике ABC стороны AB и AC равны.
- Равносторонний: Треугольник, все стороны которого равны. В треугольнике ABC, показанном ниже, стороны AB = BC = CA.
Помните, что если стороны треугольника равны, равны и углы, противоположные сторонам.Например, в равностороннем треугольнике ABC, показанном выше, поскольку AB = BC = CA, ACB = ∠BAC = ∠ABC.
Теперь мы можем узнать больше о медианах в треугольнике.
Что такое медиана треугольника?
Медиана треугольника — это отрезок прямой, соединяющий любую вершину треугольника с серединой его противоположной стороны. На рисунке, показанном ниже, медиана из точки A пересекает середину противоположной стороны, BC, в точке D.
Следовательно, AD является медианой ∆ABC и делит сторону BC на две половины, где BD = BC.
Готовы глубже погрузиться в сложные геометрические концепции? Этот курс продвинутых математических навыков поможет дать толчок вашему математическому образованию!
Свойства медианы треугольника
Медиана имеет некоторые специфические характеристики, например:
1. В равнобедренном и равностороннем треугольниках медиана делит пополам угол в вершине, две смежные стороны которой равны.
Медиана не только делит пополам сторону, противоположную вершине, но также делит пополам угол при вершине в случае равностороннего и равнобедренного треугольников, при условии, что смежные стороны также равны (что всегда верно в случае равносторонних треугольников).В равностороннем треугольнике ABC, показанном ниже, медиана AD делит BAC пополам, так что ∠BAD = ∠CAD.
2. Треугольник может иметь только три медианы, каждая из которых пересекается в точке, называемой «центроидом».
Поскольку треугольник имеет три вершины, значит, у него может быть только три медианы. Интересно, что все медианы треугольника пересекаются в одной точке, называемой центроидом . Не имеет значения, какой формы или размера треугольник, медианы всегда будут пересекаться в центроиде.
В ∆ABC, показанном ниже, медианы AD, BE и CF пересекаются в точке G, которая образует центроид.
3. Медиана делит площадь треугольника пополам.
В любом треугольнике ABC медиана AD делит треугольник на два треугольника равной площади.
Здесь общая площадь ∆ADB = площадь ∆ADC.
4. Центроид делит длину каждой медианы в соотношении 2: 1.
Длина части между вершиной и центроидом в два раза больше длины между центроидом и средней точкой противоположной стороны.
Например, в треугольнике, показанном ниже, длина AG в два раза больше длины GD, а длина BG в два раза больше длины GE.
5. Центроид делит треугольник на шесть меньших треугольников равной площади.
Это еще одно очень интересное свойство центроида. Как видно на рисунке выше, центр тяжести в основном делит треугольник на шесть меньших треугольников, а именно на треугольники AGE, CEG, CGD, DGB, CGF и FGA.
Интересно, что все эти треугольники равны по площади.Таким образом, центроид не только делит медианы в соотношении 2: 1, но также делит треугольник на шесть равных по площади треугольников.
6. Медианы равностороннего треугольника всегда равны.
Поскольку длины всех сторон в равностороннем треугольнике равны, отсюда следует, что длина медиан, разделяющих эти стороны пополам, также равна.
Таким образом, в равностороннем треугольнике ABC, где AD, BE и CF — медианы, происходящие из A, B и C соответственно, мы имеем:
AD = BE = CF
Подготовка к GMAT, но геометрия кажется вам слишком сложной? Тогда ознакомьтесь с этими курсами по математике для GMAT.
7. В равнобедренном треугольнике медианы, проведенные из вершин с равными углами, имеют одинаковую длину.
Из вышесказанного следует, что длины медиан, исходящих из вершин с равными углами, должны быть равны.
Таким образом, в равнобедренном треугольнике ABC, где AB = AC, медианы BE и CF, исходящие из B и C соответственно, равны по длине.
8. В разностороннем треугольнике все медианы разной длины.
Основываясь на двух вышеупомянутых свойствах, мы можем легко сделать вывод, что, поскольку в разностороннем треугольнике все стороны неравны по длине, медианы также должны быть неравными.Таким образом, независимо от формы разностороннего треугольника все его медианы будут иметь разную длину.
9. Длину медианы можно вычислить с помощью теоремы Аполлония.
Названная в честь греческого астронома Аполлония Пергского, теорема Аполлония используется для вычисления длины медианы треугольника при условии, что нам известны длины его сторон.
Здесь в треугольнике ABC:
- a = Длина стороны, противоположной вершине A.
- b = Длина стороны, противоположной вершине B.
- c = длина противоположной стороны вершины C.
- м a = длина медианы, исходящей из вершины A.
- mb = длина медианы от вершины B.
- mc = длина медианы от вершины C.
Это можно проиллюстрировать следующим образом:
Например, если у нас есть треугольник со следующими размерами сторон:
Здесь длина медианы м a может быть рассчитана как:
√ [2 (42) + 2 (62) — 82] / 4
= √40 / 4
= √10
= 3.162
На этом мы завершаем наше руководство по медианам треугольника. Мы узнали ряд интересных свойств медиан, в том числе то, как они делят треугольник на две равные половины, пересекаются в центроиде и делят пополам противоположную сторону. Чтобы изучить более сложные концепции геометрии, попробуйте свои силы на этих курсах по геометрии.
Последнее обновление страницы: июль 2021 г.
Медиана треугольника — определение математического слова
Медиана треугольника — определение математического слова — Math Open Reference Медиана треугольника — это отрезок присоединение к вершина до середины противоположной стороны.Следовательно, у треугольника три медианы. Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму треугольника. Обратите внимание, что все три медианы встречаются в одной точке.
Медиана треугольника — это отрезок от вершины треугольника к середина стороны, противоположной этой вершине. Поскольку существует три вершины, конечно, возможны три возможных медианы. Один из увлекательных в них есть то, что независимо от формы треугольника, все три всегда пересекаются в единственная точка.Эта точка называется центром тяжести треугольника.
Недвижимость
Медианы треугольника обладают некоторыми удивительными свойствами:- Тот факт, что три медианы всегда встречаются в одной точке, интересен сам по себе
- Каждая медиана делит треугольник на два меньших треугольника , которые имеют одинаковую площадь
- Центроид (точка, где они встречаются) — это центр тяжести треугольника
- Три медианы делят треугольник на 6 меньших треугольников одинаковой площади, даже если они могут иметь разную форму.
Отрегулируйте треугольник выше, перетащив любую вершину. Убедите себя, что три медианы (серые линии) всегда пересекаются в одной точке. Вы также можете визуально оценить, что приведенные выше факты о местности соответствуют действительности.
Попробуйте это
- Сделайте из картона любой треугольник шириной около 12–24 дюймов. Сделайте его как можно более кривым и неправильным.
- Нарисуйте медиану на картонном треугольнике. Подойдет любой.
- В точке, где медиана пересекает сторону треугольника, проделайте небольшое отверстие рядом с краем.Обвяжите его веревкой.
- Когда вы держите треугольник за веревку, средняя линия должна быть вертикальной — точно на одной линии с веревкой (см. Рисунок ниже).
- Почему?
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Соответствие и сходство
Решение треугольников
Тесты и упражнения «Треугольник»
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Медиана прямоугольного треугольника до гипотенузы
На сегодняшнем уроке геометрии мы докажем, что в прямоугольном треугольнике медиана гипотенузы равна половине гипотенузы.
Медиана треугольника — это линия, проведенная от одной из вершин до середины противоположной стороны. В случае прямоугольного треугольника медиана гипотенузы обладает тем свойством, что ее длина равна половине длины гипотенузы.
Задача
В прямоугольном треугольнике ΔABC отрезок CD является медианой гипотенузы AB. Покажите, что AD = DC; BD = DC
Стратегия
Поскольку нам нужно показать, что пара отрезков линии равны (AD = DC; BD = DC), мы будем использовать инструмент, который мы будем использовать, это конгруэнтность треугольников.
Может возникнуть соблазн попробовать использовать существующие треугольники, созданные с помощью медианы (ΔACD, ΔDCB), но беглый взгляд на рисунок показывает, что это не может быть правильным. И хотя никогда не стоит полагаться на рисунок, чтобы делать выводы, мы можем вообразить прямоугольный треугольник, который выглядит так:
, в котором два треугольника не могут совпадать.
Таким образом, нам нужно будет построить новые треугольники, в которых отрезки, которые мы хотим доказать, равны и являются соответствующими сторонами.
Построим такие треугольники, соединив точку D (середину гипотенузы) со средней точкой CB. Это будет иметь преимущество создания двух треугольников, в которых сегменты, которые мы хотим доказать, равны, это соответствующие стороны и , имеющие две стороны, которые, как мы знаем, равны (CE и EB, поскольку E является средней точкой).
Итак, D — это середина гипотенузы, а E — середина катета CB, поэтому DE — это средний сегмент, и, используя теорему треугольника о среднем сегменте, мы знаем DE || AC.Отсюда мы знаем ∠DEB ≅ ACE (как соответствующие углы), и оба они являются прямыми углами. Таким образом, m∠DEC = 90 °, так как он образует линейную пару с ∠DEB.
И теперь мы можем доказать, что треугольники ΔDCE и ΔDBE конгруэнтны, используя постулат Side-Angle-Side, в результате чего CD = DB как соответствующие стороны, как нам и нужно показать.
В результате мы также видим, что медиана гипотенузы создает два равнобедренных треугольника, ΔDCB и ΔDAC, где DA = DC = DB.
Доказательство
(1) AD = DB // задано, CD — это медиана гипотенузы
(2) CE = EB // конструкция
(3) DE — средний сегмент // (1), (2), Определение среднего сегмента
(4) DE || AC // Теорема треугольника среднего сегмента
(5) ∠DEB ≅ ∠ACE // соответствующие углы в двух параллельных прямых, пересекаемых поперечной линией (CE)
(6) m∠ACE = 90 ° // задано, ΔABC — прямоугольный треугольник
(7) m∠DEB = 90 ° // (5), (6), определение конгруэнтных углов
(8) m∠DEC = 180 ° — 90 ° = 90 ° // линейная пара
(9) ∠DEB ≅ ∠DEC // (7), (8), определение конгруэнтных углов
(10) DE = DE // общая сторона, рефлексивное свойство равенства
(11) ΔDCE ≅ ΔDBE // (2), (9), (10) Боковой угол-боковой постулат
(12) CD = DB // Соответствующие стороны в конгруэнтных треугольниках (CPCTC)
(13) DB = ½AB // Дано, CD есть медиана гипотенузы
(14) CD = ½AB // (12), (13), подстановка
Другой способ доказать это
Одна из забавных вещей о Эти проблемы с доказательством состоят в том, что часто существует несколько способов подойти и доказать теорему.И действительно, один из моих постоянных читателей прислал мне следующее решение, которое довольно элегантно и совсем не полагается на теорему о промежуточном сегменте. Вместо этого он использует построение угла и некоторую простую математику углов, чтобы показать, что медиана создает два равнобедренных треугольника.
В прямоугольном треугольнике ΔABC построим линию CD, которая разделяет прямой угол ∠ACB на 2 угла, ∠ACD и ∠DCB, так что ∠DCB≅∠DBC, и назовем этот угол α. Поскольку мы построили ∠DCB≅∠DBC, по обратной теореме об основных углах ΔDCB равнобедренный и | DC | = | DB |.
Теперь займемся математикой углов. Если ∠DBC = α и m∠ACB = 90 °, то по сумме углов в теореме треугольника m∠BAC = 90 ° -α. А поскольку m∠ACB = 90 ° и мы построили ∠DCB≅∠DBC = α, то m∠ACD = 90 ° -α. Таким образом, m∠ACD = m∠BAC = 90 ° -α, и ΔDCB также является равнобедренным треугольником и | DC | = | DA |. Используя транзитивное свойство равенства, если | DC | = | DB | и | DC | = | DA |, то | DB | = | DA |.
Но если | DB | = | DA |, то по определению CD является медианой гипотенузы. И | CD | он равен половине | AB | это одна из равных ног в обоих созданных нами равнобедренных треугольниках!
Красиво и просто — спасибо, Бен!
Обратная теорема
Теперь, когда мы доказали, что в прямоугольном треугольнике медиана гипотенузы равна половине гипотенузы, давайте докажем обратную теорему: если медиана стороны равна половине этой стороны, то треугольник — прямоугольный треугольник.Как всегда в случае с обратными теоремами, мы будем использовать стратегию, очень похожую на ту, что использовалась при доказательстве теоремы, меняя то, что дано, и то, что необходимо для доказательства.
Если медиана стороны равна половине стороны, то CD = DB = DA. Мы проведем перпендикулярную линию от D к основанию BC. Теперь у нас m∠DEB = m∠DEC = 90 °, поскольку мы построили DE перпендикулярно BC, а ∠DEB и ECDEC — линейная пара. DE = DE как общая сторона, поэтому треугольники ΔDCE и ΔDBE конгруэнтны с использованием постулата гипотенуза-катет, в результате чего CE = EB как соответствующие стороны.
Но если CE = EB и DB = DA, то DE по определению является средним сегментом в треугольнике ΔABC. И сформируем теорему о среднем сегменте треугольника DE || AC. Тогда ∠DEB ≅ ∠ACE как соответствующие углы на двух параллельных прямых, пересекаемых поперечной линией (CE). И поскольку m∠DEB = 90 °, m∠ACB = 90 °, а треугольник ΔABC является прямоугольным.
Медиана треугольника — математический путь
Медиана треугольника — это отрезок прямой, соединяющий одну из его вершин с центром противоположной стороны.
В каждом треугольнике есть три медианы (m a , m b и m c ), по одной от каждой вершины. Длины медиан могут быть получены из теоремы Аполлония как:
Где a , b и c — стороны треугольника с соответствующими медианами m a , m b и m c от их середин.
Три медианы треугольника всегда совпадают. Точка пересечения медиан — это центр масс или центр тяжести ( G ).
В любой медиане треугольника расстояние между центром тяжести (или центроидом) G и центром его соответствующей стороны составляет одну треть (1/3) длины этой медианы, т. Е. Центроида. составляет две трети (2/3) расстояния от каждой вершины до середины противоположной стороны.
Каждая медиана делит треугольник на два равных по площади.
Действительно, два треугольника Δ ABP и Δ PBC имеют одинаковое основание. AP = PC , по тому же определению медианы и той же высоте h относится к этой линии двух оснований от вершины B .
В физике центр тяжести или центроид ( G ) будет центром тяжести треугольника.
Загрузите этот калькулятор , чтобы получить результаты формул на этой странице. Выберите исходные данные и введите их в верхнем левом поле. Для получения результатов нажмите ENTER.
Общий треугольник.rar или Triangle-total.exe
Примечание. Предоставлено автором: Хосе Мария Пареха Маркано . Химик. Севилья, испания.
Теорема Аполлония
Верно, что сумма квадратов двух сторон треугольника равна сумме половины квадрата третьей стороны и удвоенного квадрата медианы, соответствующей этой третьей стороне.
Теперь в треугольнике Δ ABC имеем:
Где a , b и c — опоры, а m b — медиана, соответствующая стороне b .
Упражнение
Найдите длину медианы треугольника Δ ABC , если длина сторон равна a = 2 см, b = 4 см и c = 3 см.
Используя уравнение теоремы Аполлония, мы можем найти длину всех трех медиан:
Таким образом, медианы равны м a = 3,39 см , м b = 1,58 см и м c = 2.78 см .
Центроид треугольника (или центра тяжести треугольника ) G — это точка, где встречаются три медианы треугольника.
Медианы треугольника — это отрезки линии, полученные путем соединения одной вершины с серединой противоположной стороны. Поскольку каждый треугольник имеет три стороны и три угла, он имеет три медианы (m a , m b и m c ).
Теорема о центроиде : расстояние между центроидом и соответствующей ему вершиной в два раза больше расстояния между центром тяжести и средней точкой противоположной стороны.То есть расстояние от центроида до каждой вершины составляет 2/3 длины каждой медианы. Это верно для любого треугольника.
Центроид всегда находится внутри треугольника.
Связь между средней и стороной треугольника
Математическое слово «медиана» имеет разные значения. В статистике это значение, лежащее в центре набора данных. Итак, для набора данных {3, 5, 7, 9, 11} 7 — это медиана. В геометрии медиана — это отрезок прямой от угла треугольника до середины противоположной стороны треугольника.Медиана может быть перпендикулярна стороне треугольника, а может и не быть. Пересечение трех медиан называется центроидом.
В случае некоторых треугольников, таких как равносторонний треугольник, медиана и высота совпадают.
У треугольника 3 медианы. Медиана также может быть определена как линия от середины стороны до противоположного внутреннего угла треугольника. Медианы совпадают в центроиде. Точка, которая является общей для всех трех медиан на их пересечении, называется точкой параллелизма, центроидом треугольника.
Например, если существует треугольник ABC, отрезок от A пересекает середину противоположной стороны BC в точке D. Следовательно, AD является медианой ∆ABC и делит сторону BC пополам на две части. половинки, где BD = BC.
Соотношение между медианой и сторонами треугольника таково, что «3-кратная сумма квадратов длины сторон = 4-кратная сумма квадратов медианы треугольника».
3 (AB2 + BC2 + CA2) = 4 (AD2 + BE2 + CF2) |
Свойства медианы треугольника
Медиана имеет некоторые уникальные свойства, и эти свойства обсуждаются ниже.
1. В равнобедренном и равностороннем треугольниках медиана, проведенная из вершины, делит пополам угол, две смежные стороны которого равны.
Медиана не только делит пополам сторону, противоположную вершине, но также делит пополам угол при вершине в случае равностороннего и равнобедренного треугольников. В равностороннем треугольнике ABC, показанном ниже, медиана AD делит пополам BAC, так что ∠BAD = ∠CAD.
[Изображение будет добавлено в ближайшее время]
2. Треугольник может иметь только три медианы, которые пересекаются в точке, называемой «центроид».
Треугольник имеет три вершины, поэтому он может иметь только три медианы. Все медианы треугольника пересекаются в одной точке, называемой центроидом. Форма или размер треугольника не имеет значения, и медианы всегда будут пересекаться в центроиде.
В ∆ABC медианы AD, BE и CF пересекаются в точке G, которая называется центроидом треугольника.
[Изображение будет добавлено в ближайшее время]
3. Медиана делит площадь треугольника на две равные половины.
В треугольнике ABC медиана AD делит треугольник на два равных треугольника с равными площадями.
Площадь ∆ADB = Площадь ∆ADC.
[Изображение будет добавлено в ближайшее время]
4. Центроид делит длину каждой медианы в соотношении 2: 1.
Длина части между вершиной и центроидом в два раза больше длины между центроидом и серединой противоположной стороны.
Например, в треугольнике, показанном ниже, длина AG в два раза больше длины GD, а длина CG в два раза больше длины GF.
[Изображение будет добавлено в ближайшее время]
5.Центроид делит треугольник на шесть меньших треугольников равной площади.
На рисунке выше центроид делит треугольник на шесть меньших треугольников, а именно на треугольники AGE, CEG, CGD, DGB, BGF и FGA. Площади всех этих треугольников равны. Таким образом, центроид делит медианы в соотношении 2: 1, а также делит треугольник на шесть меньших треугольников равной площади.
6. Длина середины равностороннего треугольника всегда равна.
Поскольку мы знаем, что длины всех сторон равностороннего треугольника равны, отсюда следует, что длина медианы равностороннего треугольника, делящего эти стороны пополам, также равна.
Таким образом, в равностороннем треугольнике ABC, где AD, BE и CF — медианы, исходящие из вершин A, B и C соответственно, мы имеем:
AD = BE = CF
[Изображение будет добавлено в ближайшее время]
7. В равнобедренном треугольнике медианы, проведенные под равными углами, равны по длине.
Длина медиан, построенных из вершин с равными углами, должна быть одинаковой.
Таким образом, в равнобедренном треугольнике ABC, если AB = AC, медианы BE и CF, исходящие из вершины B и C, соответственно, равны по длине.
[Изображение будет добавлено в ближайшее время]
8. Медиана и стороны треугольника связаны таким образом, что «3-кратная сумма квадратов длины сторон = 4-кратная квадратура медианы треугольника. . »
3 (AB2 + BC2 + CA2) = 4 (AD2 + BE2 + CF2) |
Как найти медиану треугольника
Теорема, называемая теоремой Аполлония, Кан поможет вам найти середину треугольника.{2}} {4}} \]
где a, b и c — длины сторон, а m — медиана от внутреннего угла, проведенного от вершины A к стороне a.
Решенные примеры
Пример 1: На приведенном рядом рисунке ∠PQR = 90∘, а QL — медиана, PQ = 12 см и QR = 14 см. Найдите QL.
[Изображение будет добавлено в ближайшее время]
Решение:
У нас PQ = 5 см, QR = 12 см, а QL — это медиана.
∴ PL = LR = PR2 ……. (I)
In ΔPQR,
(PR) 2 = (PQ) 2 + (QR) 2 ………… (По теореме Пифагора)
= 144 + 256
= 400
⇒ PR = 20
Теперь, по теореме, если L — середина гипотенузы PR прямоугольного ΔPQR, то
QL = 1/2 [PR] = [1/2] * (20) = 10 см.
Пример 2: В треугольнике ABC координаты A равны (1, 2), а уравнения медианы через B и C: x + y = 5 и x = 4 соответственно, тогда какова площадь ΔABC ( в кв. единицах)?
Решение:
Медиана через точку C равна x = 4
Итак, ясно, что координата x точки C равна 4
Пусть C = (4, y), затем середина точек A (1, 2) и C ( 2, y), который является D, по определению лежит на медиане, проходящей через B.
Ясно, что D = ([1 + 4] / 2, [2 + y] / 2).
Теперь у нас есть [3 + 4 + y] / 2 = 5 ⇒ y = 3. Итак, C = (4, 3).
Центроид треугольника определяется пересечением медиан.
Легко видеть, что медианы x = 4 и x + y = 5 пересекаются в точке G = (4, 1).
Площадь треугольника ΔABC
= 3 × ΔAGC
= 3 × 1/2 × 3 × 2
= 9.
4.23: Медианы — K12 LibreTexts
Отрезок линии, соединяющий вершину и середину противоположной стороны треугольника.
В треугольнике сегмент линии, соединяющий вершину и середину противоположной стороны, называется медианой .
Рисунок \ (\ PageIndex {1} \)\ overline {LO} \) — это медиана от L \) до середины \ overline {NM} \).
Если вы нарисуете все три медианы, они пересекутся в одной точке, называемой центроидом .
Рисунок \ (\ PageIndex {2} \)Центроид — это «точка равновесия» треугольника. Это означает, что если бы вы вырезали треугольник, центр тяжести был бы его центром тяжести, так что вы могли бы сбалансировать его там.
Рисунок \ (\ PageIndex {3} \)Теорема о медиане утверждает, что медианы треугольника пересекаются в точке, называемой центроидом, которая составляет две трети расстояния от вершин до середины противоположных сторон.
Итак, если \ (G \) — центроид, то:
\ (AG = \ dfrac {2} {3} AD, CG = \ dfrac {2} {3} CF, \: EG = \ dfrac {2} {3} BE \)
\ (DG = \ dfrac {1} {3} AD, FG = \ dfrac {1} {3} CF, \: BG = \ dfrac {1} {3} BE \)
\ (И \: by \: подстановка: DG = \ dfrac {1} {2} AG, \: FG = \ dfrac {1} {2} CG, \: BG = \ dfrac {1} {2} EG \)
Рисунок \ (\ PageIndex {4} \)Пример \ (\ PageIndex {1} \)
\ (B \), \ (D \) и \ (F \) — середины каждой стороны, а \ (G \) — центроид.Если \ (CG = 16 \), найдите \ (GF \) и \ (CF \).
Рисунок \ (\ PageIndex {5} \)Решение
Используйте теорему о медиане.
\ (\ begin {align *} CG & = \ dfrac {2} {3} CF \\ 16 & = \ dfrac {2} {3} CF \\ CF & = 24. \ End {align *} \)
Следовательно, \ (GF = 8 \).
Пример \ (\ PageIndex {2} \)
Верно или неверно: медиана делит пополам ту сторону, которую она пересекает.
Решение
Это утверждение верно. По определению, медиана пересекает сторону треугольника в его средней точке.Средние точки делят сегменты на две равные части.
Пример \ (\ PageIndex {3} \)
\ (I \), \ (K \) и \ (M \) — середины сторон \ (\ Delta HJL \).
Рисунок \ (\ PageIndex {6} \)Решение
Если \ (JM = 18 \), найти \ (JN \) и \ (NM \). Если \ (HN = 14 \), найдите \ (NK \) и \ (HK \).
Используйте теорему о медиане.
\ (JN = \ dfrac {2} {3} \ cdot 18 = 12. NM = JM − JN = 18−12 \). \ (НМ = 6 \).
\ (14 = \ dfrac {2} {3} \ cdot HK \)
\ (14 \ cdot \ dfrac {3} {2} = HK = 21 \).\ (NK \) составляет треть от 21, \ (NK = 7 \).
Пример \ (\ PageIndex {4} \)
H — центр тяжести \ (\ Delta ABC \) и \ (DC = 5y − 16 \). Найдите \ (x \) и \ (y \).
Рисунок \ (\ PageIndex {7} \)Решение
Для решения используйте теорему о медиане. Составьте и решите уравнения.
\ (\ begin {align *} \ dfrac {1} {2} BH = HF & \ rightarrow BH = 2HF & \ qquad HC = \ dfrac {2} {3} DC & \ rightarrow \ dfrac {3} {2 } HC = DC \\ 3x + 6 & = 2 (2x − 1) & \ qquad \ dfrac {3} {2} (2y + 8) & = 5y − 16 \\ 3x + 6 & = 4x − 2 & \ qquad 3y +12 & = 5y − 16 \\ 8 & = x & \ qquad 28 & = 2y \ rightarrow 14 = y \ end {align *} \)
Пример \ (\ PageIndex {5} \)
\ (B \), \ (D \) и \ (F \) — середины каждой стороны, а G — центроид.Если \ (BG = 5 \), найдите \ (GE \) и \ (BE \)
Рисунок \ (\ PageIndex {8} \)Решение
Используйте теорему о медиане.
\ (\ begin {align *} BG & = \ dfrac {1} {3} BE \\ 5 & = \ dfrac {1} {3} BE \\ BE & = 15. \ End {align *} \)
Следовательно, \ (GE = 10 \).
Обзор
Для вопросов 1-4, \ (B \), \ (D \) и \ (F \) — середины каждой стороны, а \ (G \) — центроид. Найдите следующие длины.
Рисунок \ (\ PageIndex {9} \)- Если \ (CG = 16 \), найдите \ (GF \) и \ (CF \)
- Если \ (AD = 30 \), найти \ (AG \) и \ (GD \)
- Если \ (GF = x \), найти \ (GC \) и \ (CF \)
- Если \ (AG = 9x \) и \ (GD = 5x − 1 \), найдите \ (x \) и \ (AD \).
Многоступенчатые задачи Найдите уравнение медианы в плоскости x − y \).
- График \ (\ Delta ABC: \: A (−6,4) \), \: B (−2,4) \) \: и \: C (6, −4) \)
- Найдите середину \ (\ overline {AC} \). Обозначьте это \ (D \).
- Найдите наклон \ (\ overline {BD} \).
- Найдите уравнение \ (\ overline {BD} \).
- График \ (\ Delta DEF: \: D (−1,5), \: E (1,0), \: F (6,3) \)
- Найдите середину \ (\ overline {EF} \).Обозначьте это \ (G \).
- Найдите наклон \ (\ overline {DG} \).
- Найдите уравнение \\ (overline {DG} \).
Определите, является ли следующее утверждение истинным или ложным.
- Центроид — это точка равновесия треугольника.
Обзор (ответы)
Чтобы увидеть ответы на обзор, откройте этот PDF-файл и найдите раздел 5.4.
Словарь
| Срок | Определение |
|---|---|
| центроид | Центроид — это точка пересечения медиан в треугольнике. |
| Медиана | Медиана треугольника — это отрезок прямой, соединяющий вершину с серединой противоположной стороны. |
Дополнительные ресурсы
Видео: средние значения треугольника
Действия: Вопросы для обсуждения по медианам
Учебные пособия: биссектрисы, медианы, высоты.

 ..
..
 Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с. Найдите проекцию биссектрисы на больший катет.
Найдите проекцию биссектрисы на больший катет.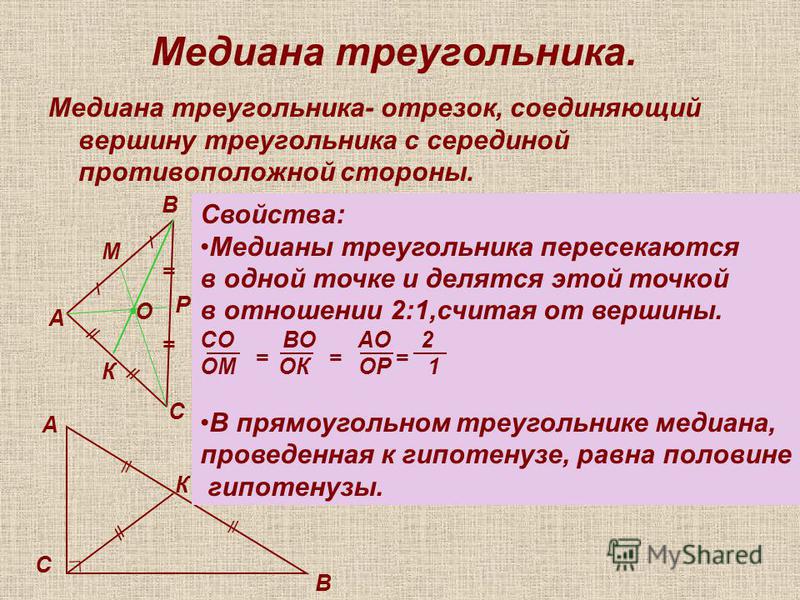
 Найдите площадь треугольника, ограниченного высотой и биссектрисой, проведенными из вершины В.
Найдите площадь треугольника, ограниченного высотой и биссектрисой, проведенными из вершины В.