Медиана в треугольнике равна: Свойства медианы треугольника | ЮКлэва

Свойства медианы треугольника — Энциклопедия современных знаний

Примеры ключевых задач по геометрии при подготовке к ОГЭ

Свойства хорд и дуг окружности

• Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
• Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
• Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
• Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
• У равных дуг равны и хорды.
• Дуги, заключённые между параллельными хордами, равны.

Свойства касательной к окружности

• Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

• Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теоремы о длинах хорд, касательных и секущих

• Произведения длин отрезков, на которые разбита каждая из хорд, равны:

• Если из точки, взятой вне окружности, проведены к окружности секущая и касательная, то произведение секущей на её внешнюю часть равно квадрату касательной.

• Если из точки, взятой вне окружности, проведены к окружности секущие, то произведение каждой секущей на её внешнюю часть есть число постоянное для всех этих секущих

Угол между хордой и касательной

Угол, образованный хордой и касательной, имеющими общую точку на окружности, равен половине дуги, заключенной между его сторонами.

Свойства вписанного угла окружности.

• Вписанный угол измеряется половиной дуги, на которую он опирается.
• Вписанные углы, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на полуокружность (диаметр) – прямой.
• Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от хорды.
• Вписанные углы, опирающиеся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от хорды.

Свойства биссектрисы угла треугольника

Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.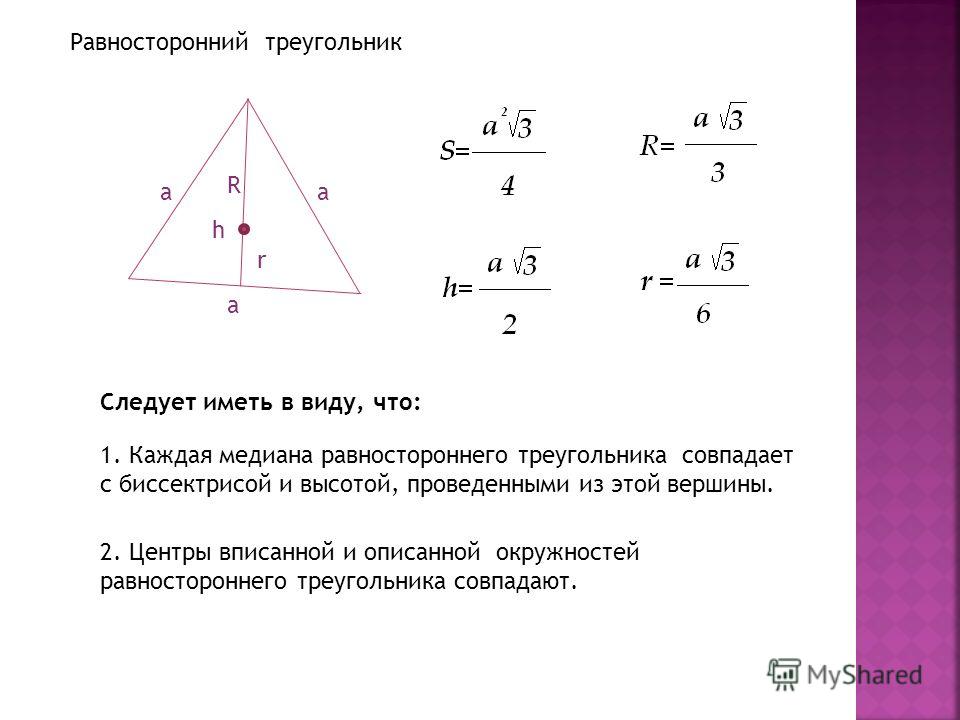

Свойства биссектрисы параллелограмма

• Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
• Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны

Свойства прямоугольного треугольника

• В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

• Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
• Если в треугольнике медиана равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.
• В прямоугольном треугольнике радиус вписанной окружности вычисляется по формуле , где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.

Свойства медианы треугольника

• В треугольнике медианы пересекаются в одной точки и делятся этой точкой в отношении 2:1, считая от вершины.
• Медиана делит треугольник на два равновеликих треугольника, а три медианы – на шесть равновеликих треугольников.
• Если О – точка пересечения медиан треугольника АВС, то S(ABC)=3S(AOB)=3S(AOC)=3S(BOC).

Свойства элементов трапеции

Во всякой трапеции:

• Середины боковых сторон и середины диагоналей лежат на одной прямой

• Средняя линия трапеции равна полусумме оснований; отрезок, соединяющий середины диагоналей, равен полуразности оснований

• Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой

• Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении OX:OY=BC:AD

• Биссектриса угла трапеции отсекает от нее равнобедренный треугольник

• Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны и точка их пересечения лежит на средней линии трапеции

В описанной около окружности трапеции:

• Сумма оснований равна сумме боковых сторон

• Полусумма боковых сторон равна средней линии

• Если трапеция равнобедренная, то ее боковая сторона равна средней линии, высота трапеции равна среднему геометрическому ее оснований

• Отрезки, соединяющие центр окружности, вписанной в трапецию, с вершинами трапеции, попарно перпендикулярны

• Диаметр вписанной в трапецию окружности является высотой трапеции

• Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой – их полусумме, т. е. равен средней линии трапеции.

1) S(ABC)=S(DBC)

2) S(ABD)=S(ACD)

3) S(ABO)=S(COD)

• Средняя линия и высота равнобедренной трапеции с взаимно перпендикулярными диагоналями равны.

Свойство медианы треугольника.

Похожие статьи.

• Свойства средней арифметической

• Метод медиан и крайних значений

• Свойства полей. типы полей

• Урок 2.повторение. подобные треугольники. признаки подобия.

Медианы треугольника делятся в отношении 2 1. Медиана

Урок 1

Медианы треугольника. Точка пересечения медиан.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Доказательство:

Точка пересечения медиан треугольника является центром тяжести этого треугольника.

Задача 1 Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 4, 6 и 8. Найти длины медиан треугольника.

Решение. Пусть в треугольнике АВС AM, BE и CD — медианы, К – точка их пересечения, KС=4, KА=6 и КВ=8.

https://pandia.ru/text/78/182/images/image004_34.gif»>, то есть на отрезок КА приходится 2 части, а на отрезок КМ – одна часть, то вся медиана АМ состоит из трех равных частей и https://pandia.ru/text/78/182/images/image006_24.gif»>.

Аналогично,

,

Ответ: 6, 9 и 12

Задача 2 Медианы AM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 6 и 9 . Вычислить длины сторон АВ и ВС.

https://pandia.ru/text/78/182/images/image010_15.gif»>,

поэтому и

, .

Кроме того

, .

Вычислим по теореме Пифагора длины отрезков AK и СМ, получаем

Теперь вычислим длины сторон АВ и ВС:

АВ=2АК=10, ВС=2СМ=.

Ответ : 10;.

Тест для самоконтроля.

1. Медиана треугольника делит пополам (выбрать один из вариантов ответов)

1) угол треугольника

2) сторону треугольника

3) две стороны треугольника

2. В каком отношении точка пересечения медиан треугольника делит каждую из медиан треугольника (выбрать правильные варианты ответов).

1) 2:1 считая от основания треугольника

2) 1:2 считая от вершины треугольника

3) 2:1 считая от вершины треугольника

4) 1:2 считая от основания треугольника

5) на две равные части

3. Если в треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника, то какую часть медианы АМ составляет отрезок АР? (выбрать один из вариантов ответов)

4. В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть медианы АМ составляет отрезок РМ? (выбрать один из вариантов ответов)

5. В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть отрезка АР составляет отрезок РМ? (выбрать один из вариантов ответов)

Посмотреть правильные ответы.

Задачи для самостоятельного решения.

1. Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 6 см, 8 см и 12 см. Найдите длины медиан треугольника.

Посмотреть решение.

2. Медианы ВM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 15 и 36 . Найдите длины сторон АВ и АС.

Посмотреть решение.

3. Медианы треугольника равны 6, 9 и 12. На каком расстоянии от вершин находится точка пересечения медиан треугольника?

Посмотреть решение.

4. Медианы треугольника равны 9, 12 и 18. Найдите расстояния от середин сторон треугольника до центра тяжести данного треугольника.

Посмотреть решение.

5. Центр тяжести треугольника отстоит от середин его сторон на расстояния. Равные 5, 6 и 7. Найдите медианы данного треугольника.

Посмотреть решение.

6. Точка пересечения медиан треугольника удалена от середин его сторон на расстояния, равные 2, 3 и 4.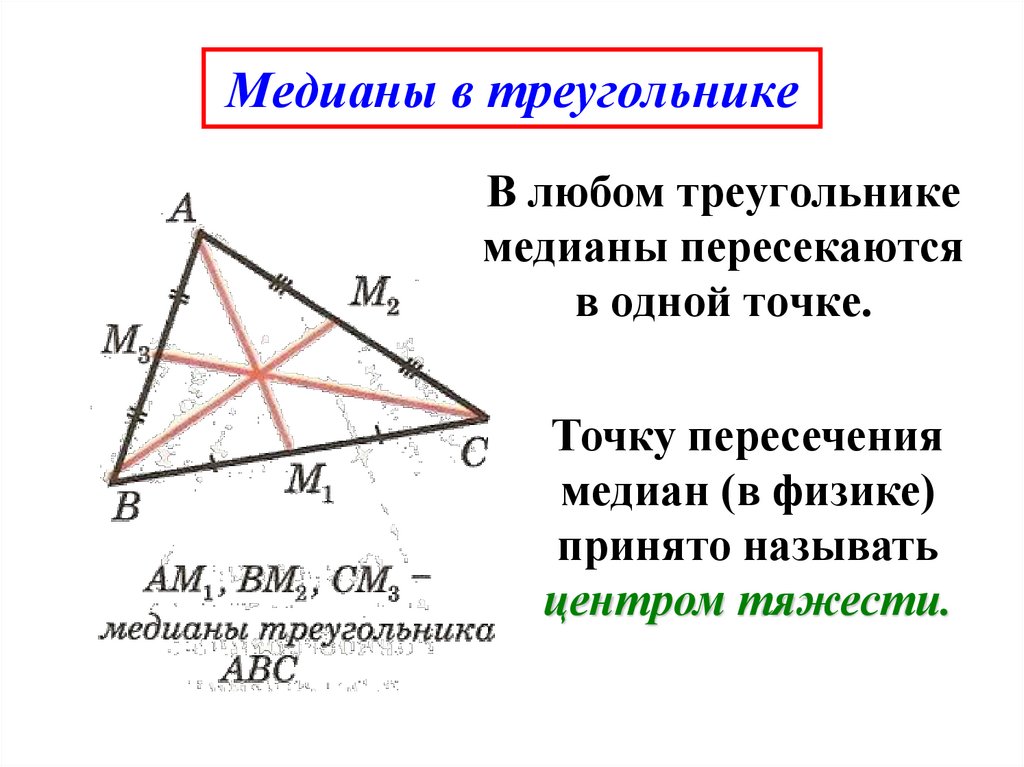 На каких расстояниях от вершин треугольника находится эта точка?

Посмотреть решение.

Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.

Свойства медианы треугольника

1. Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
2. Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
3. Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
4. Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).

Уравнение длины медианы треугольника

Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны. В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.

Точка пересечения медиан треугольника

Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности. А другие геометрические фигуры имеют собственные центры.

Координаты точки пересечения медиан треугольника

Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x 1 ;y 1), B(x 2 ;y 2), C(x 3 ;y 3),

и вычисляем координаты центра треугольника по формуле: x 0 = (x 1 + x 2 + x 3)/3; y 0 = (y 1 + y 2 + y 3)/3.

Площадь треугольника через медиану

Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1. Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )

Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.

Дано: ∆ABC, СС 1 , АА 1 , ВВ 1 — медианы
∆ABC . Доказать: и

Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС. Значит,А 2 С 2 || АС

и A 2 C 2 = 0,5*АС. С 1 А 1 — средняя линия треугольника ABC. Значит, А 1 С 1 || АС и А 1 С 1 = 0,5*АС.

Четырехугольник А 2 С 1 А 1 С 2 — параллелограмм, так как его противо­положные стороны А 1 С 1 и А 2 С 2 равны и параллельны. Следовательно, А 2 М = МА 1 и С 2 М = МC 1 . Это означает, что точки А 2 и M делят медиану АА 2 на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC

1 . Итак, точка М пересечения двух медиан АА 2 и CC 2 треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треу­гольника.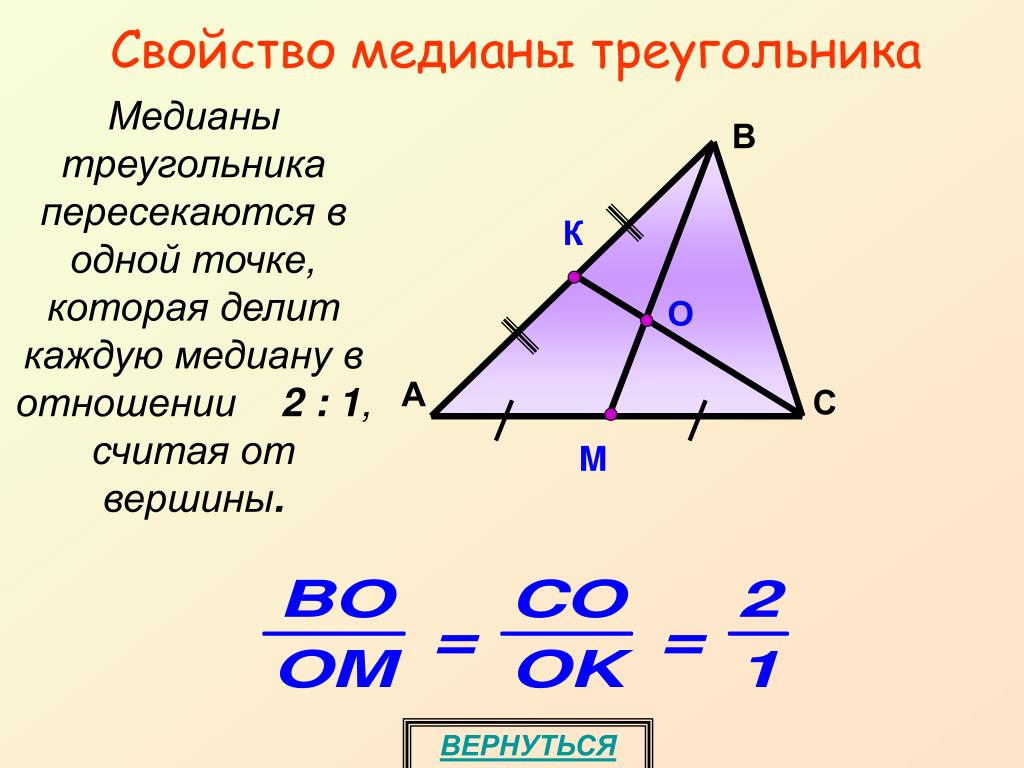 Совершенно аналогично доказывается, что точка пересечения меди­ан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вер­шин треугольника.

На медиане АА 1 такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА 1 иBB 1.

Таким образом, n

T2. Докажите, что отрезки, которые соединяют центроид с вер­шинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.

Доказать:S AMB =S BMC =S AMC . Доказательство. В, у них общая. т.к. равны их основания и высота, проведенная из вершины М, у них общая. Тогда

Аналогичным образом доказывается, чтоS AMB = S AMC .

Таким образом,S AMB = S AMC = S CMB . n

Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.

Свойства

1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

Вычисление длины биссектрисы

l c — длина биссектрисы, проведённой к стороне c,

a,b,c — стороны треугольника против вершин A,B,C соответственно,

p — полупериметр треугольника,

a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,

α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,

h c — высота треугольника, опущенная на сторону c.

Метод площадей.

Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).

1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур

2) Метод отношения S: основан на след опорных задачах:

Теорема Чевы

Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда

Доказательство.

Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см. рисунок).

Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:

Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.

Аналогично получаем и

Перемножим эти три равенства:

что и требовалось доказать.

Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.

Теорема (обратная теорема Чевы) . Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение

Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.

Теорема Менелая

Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда

Доказательство . Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .

ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,

ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,

Из каждого равенства выразим CK:

Откуда что и требовалось доказать.

Теорема (обратная теорема Менелая). Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение

Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Существует теорема о том, что медианы треугольника пересекаются в одной точке, и эта точка делит каждую медиану в отношении 2: 1 , где 2 соответствует отрезку от вершины, из которой проведена медиана, до точки пересечения медиан, а 1 соответствует отрезку от точки пересечения медиан до середины стороны, к которой проведена медиана.

Чтобы доказать эту теорему, рассмотрим треугольник ABC с медианами AE, BF, CD. То есть точки D, E, F делят пополам стороны AB, BC, CA соответственно.
Нам не известно, пересекаются ли все медианы в одной точке (это еще требуется доказать). Однако любые две медианы пересекутся в одной точке, так как не могут быть параллельны. Пусть медианы AE и BF пересекаются в точке O.

Медиана BF делит медиану AE на два отрезка AO и EO. Проведем через точку E прямую, параллельную BF. Эта прямая пересечет сторону AC в некой точке L. Также проведем через середину отрезка AB (точку D) еще одну параллельную к BF прямую. Она пересечет AC в точке K.

Согласно теореме Фалеса, если на одной стороне угла от его вершины отложить последовательно равные отрезки и провести через концы этих отрезков параллельные прямые, пересекающие другую сторону угла, то эти параллельные прямые отсекут на второй стороне угла также равные между собой отрезки.

Посмотрим на угол BCA данного треугольника. Отрезки BE и EC равны между собой, прямые BF и EL параллельны друг другу. Тогда согласно теореме Фалеса CL = LF.
Если же посмотреть на угол BAC, так как AD = BD и DK || BF, то AK = KF.

Так как отрезки AF и CF равны между собой (т. к. их образует медиана) и каждый из них делится на два равных отрезка, то все четыре отрезка стороны AC равны между собой: AK = KF = FL = LC.

Рассмотрим угол EAC. Через концы трех равных отрезков стороны AC проведены параллельные прямые. Следовательно, они отсекают на стороне AE равные между собой отрезки. Отрезок AO содержит в себе два таких отрезка, а EO только один. Таким образом, мы доказали, что как минимум одна медиана треугольника точкой пересечения с другой медианой делится на два отрезка, длины которых соотносятся как 2: 1.

Теперь рассмотрим пересечение медианы AE с медианой CD. Пусть они пересекаются в точке P.

Аналогично предыдущему, доказывается, что параллельные прямые FM, CD, EN делят сторону AB на равные отрезки. В свою очередь они же делят AE на три равных отрезка. Причем от вершины A до пересечения медиан два таких отрезка, а после — один.

Один и тот же отрезок нельзя разделить на три равных части так, чтобы при одном варианте деления они были одного размера, а при другом — другого. Поэтому точки O и P должны совпадать. Это значит, что все три медианы треугольники пересекаются в одной точке.

Чтобы доказать, что две остальные медианы делятся точкой пересечения в соотношении 2: 1, можно аналогично предыдущему провести параллельные прямые к сторонам AB и BC.

Медиана треугольника – определение, формула, теорема, примеры

Медиана треугольника – определение, формула, теорема, примеры

Содержание

Последнее изменение: 6 сентября 2022 г.

Оглавление

 

Определение

Медиана треугольника — это отрезок, соединяющий вершину с серединой стороны, противоположной этой вершине.

Медиана треугольника

Свойства

Свойства медианы треугольника

1. Каждый треугольник имеет 3 медианы, по одной из каждой вершины; в △ABC, AD, BF и CE — три медианы
2. Три медианы сходятся в одной точке, называемой центром тяжести треугольника. Центроид — это центр тяжести или центр масс треугольника; три медианы, м _a , m _b , & m _c пересекаются в точке O, которая является центром тяжести данного треугольника
3. Каждая медиана делит главный треугольник на 2 меньших треугольника, имеющих равную площадь. Таким образом, 3 медианы делят главный треугольник на 6 меньших треугольников равной площади; медиана AD образует треугольники △ABD и △ACD, медиана BF — в треугольники ABF и △CBF, медиана CE — в треугольники △CAE и △CBE

Формулы

Как найти медиану треугольника

длина медианы треугольника. Согласно теореме: «сумма квадратов любых двух сторон треугольника равна удвоенному квадрату половины третьей стороны и удвоенному квадрату медианы, делящей третью сторону пополам».

Соответственно, стандартные формулы для нахождения медианы треугольника приведены ниже:

Медиана треугольника Формула

Давайте решим несколько примеров с участием различных типов треугольников.

Решенные примеры

Найдите длины всех трех медиан треугольника со сторонами 6 см, 4 см и 2 см.

Решение:

Как известно,
m = √2b ² + 2c ² – a ² /4, здесь a = 6 см, b = 4 см, c = 2 см
Теперь, складывая полученные значения,
m = √2(4) ² + 2(2) ² – ( 6) ² /4
 = √32 + 8 – 36/4
= √4/4 = 1 см

В данном треугольнике G – центр тяжести, а BC = 8 см. Решите значение BL.

Решение:

Для △ABC,
AL, BF и CE — медианы, а L — середина BC
Таким образом,
BL = 1/2BC
= ½ X 8
= 4 см

Найдите длину медианы равностороннего треугольника со стороной 9 см.

Решение:

Как известно,
Медиана (m) = a√3/2, здесь a = 9 см
= 9√3/2 [∵ √3= 1,732]
= 7,79 см

Медиана теоремы о треугольнике

Медиана теоремы о треугольнике

Последнее изменение: 6 сентября 2022 г.

Знакомство с медианой треугольника

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны и делящий эту сторону пополам, в геометрии называется медианой треугольника. В каждом треугольнике три медианы, по одной из каждой вершины. Центроид треугольника находится там, где пересекаются их медианы. В этой статье мы рассмотрим атрибуты, определение и формулу медианы треугольника.

Определение

Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. На приведенной ниже диаграмме AD представляет медиану, а BC делится на две равные части, в результате чего BD = DC.

Свойства медианы треугольника

Следующие свойства можно использовать для легкого определения медианы треугольника:

• Медиана треугольника — это отрезок, соединяющий вершину треугольника с противоположной стороной середина.
• Он делит противоположную сторону на две равные части, деля ее пополам.
• Середина треугольника делит его на два равновеликих треугольника.
• Три медианы треугольника сходятся в одной точке, независимо от его формы или размера.
• Каждая вершина треугольника имеет три медианы. Центроид треугольника образован схождением трех медиан.
• Середина треугольника делит треугольник на два меньших треугольника с равными площадями. На самом деле три медианы делят треугольник на шесть равновеликих треугольников.

Высота и медиана треугольника

Высота и медиана треугольника — не одно и то же. Отрезок, соединяющий вершину с серединой противолежащей стороны треугольника, называется медианой. Независимо от природы треугольника, у него есть три медианы (по одной от каждой вершины), которые сходятся в одной точке. Три медианы встречаются в центре треугольника, который расположен внутри треугольника. Медиана всегда делит сторону, на которой она построена, пополам.

Отрезок, соединяющий вершину с противоположной стороной треугольника под прямым углом (90°), определяется как высота треугольника. В зависимости от формы треугольника высоту можно найти внутри или снаружи. Все треугольники имеют три возвышения (по одному от каждой вершины), которые встречаются в ортоцентре, единственной точке треугольника. Внутри или вне треугольника можно найти ортоцентр. Противоположная сторона, на которой создается высота, не всегда должна быть разделена пополам.

Формула для медианы треугольника

Базовая формула, применимая ко всем трем медианам, может быть использована для нахождения медианы треугольника. Давайте посмотрим на формулу для расчета длины каждой медианы.

Первая медиана треугольника вычисляется по приведенной ниже формуле, где медиана треугольника равна m, стороны равны a, b и c, а медиана создается на стороне «a».

Формула вычисления второй медианы треугольника выглядит следующим образом: где медиана треугольника равна m, стороны равны a, b и c, а медиана образована на стороне b.

Формула третьей медианы треугольника выглядит следующим образом; медиана треугольника равна m, стороны треугольника равны a, b и c, а медиана образована на стороне «c».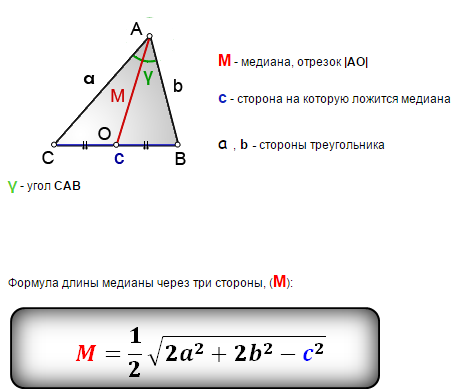

Нахождение медианы треугольника с заданными координатами вершин:-

Когда известны координаты трех вершин треугольника, мы можем использовать приведенные ниже шаги для вычисления длины медианы треугольника.

Шаг 1: Найдите координаты середины отрезка, на котором образована медиана, используя координаты вершин треугольника. Для этого можно использовать формулу средней точки.

формула для средней точки, где (x ₁ , y ₁ ) и (x ₁ , y ₁ ) — координаты сегмента прямой.

Шаг 2: Получив координаты средней точки, используйте формулу расстояния для расчета длины медианы, где одна конечная точка — это вершина, из которой начинается медиана, а другая — середина отрезка, на котором построена медиана .

Шаг 3: Используйте формулу расстояния D = , чтобы найти длину медианы, где (x ₁ , y ₁ ) и (x ₁ , y ₁ ) — координаты медианы.

Советы по медиане треугольника:-

• Треугольник разделен медианами на два меньших треугольника с одинаковой площадью.

  No related posts.