Как сделать проверку матрицы: Как делать проверку в матрице. Обратная матрица

Как сделать проверку матрицы в excel?

Содержание

• 1 Формулы массива
• 2 Решение матриц в Excel
  • 2.1 Транспонирование
  • 2.2 Сложение
  • 2.3 Умножение матриц в Excel
  • 2.4 Обратная матрица в Excel
• 3 Нахождение определителя матрицы
• 4 Выполнение расчетов
  • 4.1 Расчет определителя
  • 4.2 Расчет обратной матрицы
  • 4.3 Помогла ли вам эта статья?
    • 4.3.1 Навигация по записям
• 5 Матрицы в экселе

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.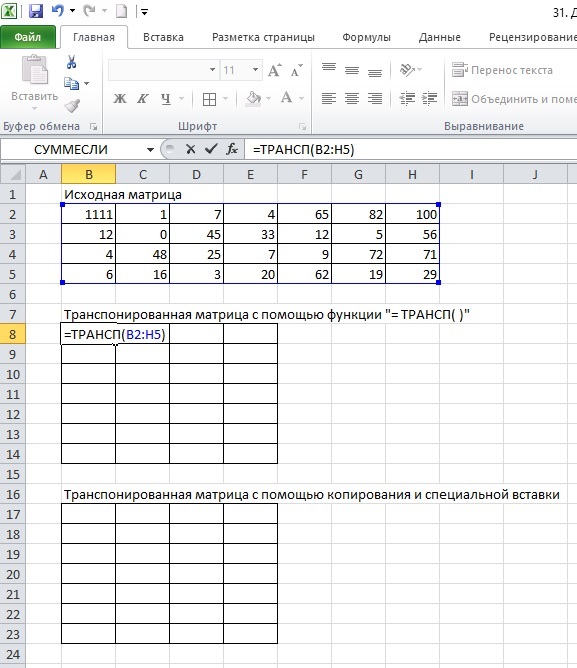

Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

8 июня 2013 Автор: Бакытжан

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

 

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи.
Метки: EXCEL, ИКТ, матрица, обратная матрица

Навигация по записям

Предыдущий пост:    

Следующий пост:    

Как вычислить определитель при помощи MS EXCEL

→

Матрицы в экселе

В разделе Прочее компьютерное на вопрос Как создать матрицу в Excel???? заданный автором Masha Kalganova лучший ответ это Что конкретно нужно сделать?
Документ эксель — безразмерная (всеразмерная) матрица, каждый элемент которой может быть числом, текстом или любым другим значением. Да хоть формулой.
Если напечатать 3 циферки в ряд, под ними еще 3 в ряд, под ними еще 3 в ряд, получим квадратную матрицу 3х3.
Вопрос в чем?
Умножение матрицы на число в Excel
Формулы написать?
В верхней левой клетке новой матрицы
=левая верхняя клетка старой матрицы * клетка с числом (ткнуть мышкой) , нажать F4 дабы стало $x$y, где x,y — координаты клетки. Это зафиксирует клетку при копировании. Далее жмем Enter и копируем содержимое клетки в 2 соседние клетки в ряд. Далее копируем эти 3 клетки в следующие 3 ряда и получаем тот же результат, что у меня на картинке. То есть умножение матрицы на число.
Блин, математику не знают, а в интернете лазают!

Ответ от Serg K
что такое «матрица»? выражайся яснее, Маша.

вычисление обратной матрицы онлайн

вычисление обратной матрицы онлайн

Вы искали вычисление обратной матрицы онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.

Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление обратной матрицы с помощью элементарных преобразований онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление обратной матрицы онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление обратной матрицы онлайн,вычисление обратной матрицы с помощью элементарных преобразований онлайн,вычислить обратную матрицу онлайн,вычислить обратную матрицу онлайн с подробным решением,как найти обратную матрицу 3 на 3 онлайн,как найти обратную матрицу онлайн,как найти обратную матрицу онлайн с решением,как сделать проверку обратной матрицы онлайн,калькулятор матриц обратная матрица,калькулятор матриц обратных,калькулятор матриц онлайн обратная матрица,калькулятор матрицы метод обратной матрицы,калькулятор матрицы метод обратной матрицы онлайн,калькулятор матрицы метод обратной матрицы онлайн калькулятор,калькулятор матрицы методом обратной матрицы,калькулятор матрицы методом обратной матрицы онлайн калькулятор,калькулятор матрицы обратной матрицы онлайн калькулятор,калькулятор матрицы онлайн методом обратной матрицы,калькулятор матрицы онлайн методом обратной матрицы онлайн,калькулятор метод обратной матрицы,калькулятор метод обратной матрицы онлайн,калькулятор найти обратную матрицу,калькулятор найти обратную матрицу онлайн,калькулятор нахождение обратной матрицы,калькулятор нахождения обратной матрицы,калькулятор обратная матрица,калькулятор обратной матрицы,калькулятор обратной матрицы онлайн,калькулятор обратной матрицы онлайн с решением,калькулятор обратной матрицы с решением,калькулятор обратные матрицы,калькулятор обратных матриц,калькулятор обратных матриц онлайн,калькулятор онлайн метод обратной матрицы,калькулятор онлайн найти обратную матрицу,калькулятор онлайн обернена матриця,матрица обратная к матрице системы онлайн калькулятор,матрица обратная матрица онлайн калькулятор,матрица обратная решение онлайн,матрицы калькулятор обратные,матрицы метод обратной матрицы онлайн,матрицы метод обратной матрицы онлайн калькулятор,матрицы обратная онлайн,матрицы обратная онлайн калькулятор,матрицы обратные онлайн,матрицы онлайн калькулятор метод обратной матрицы,матрицы онлайн метод обратной матрицы,матрицы решить методом обратной матрицы онлайн,матриця обернена онлайн,метод обратной матрицы калькулятор,метод обратной матрицы калькулятор онлайн,метод обратной матрицы онлайн,метод обратной матрицы онлайн калькулятор,метод обратной матрицы онлайн калькулятор с подробным решением,методом гаусса найти обратную матрицу онлайн,методом элементарных преобразований найти обратную матрицу онлайн,найти матрицу а 1 онлайн,найти матрицу обратную данной онлайн,найти матрицу обратную данной онлайн с решением,найти матрицу обратную методом гаусса онлайн,найти обратную,найти обратную матрицу данной онлайн,найти обратную матрицу калькулятор,найти обратную матрицу калькулятор онлайн,найти обратную матрицу методом гаусса онлайн,найти обратную матрицу методом элементарных преобразований,найти обратную матрицу методом элементарных преобразований онлайн,найти обратную матрицу онлайн,найти обратную матрицу онлайн калькулятор,найти обратную матрицу онлайн методом гаусса,найти обратную матрицу онлайн методом гаусса онлайн,найти обратную матрицу онлайн методом элементарных преобразований,найти обратную матрицу онлайн с подробным решением,найти обратную матрицу онлайн с подробным решением и проверкой,найти обратную матрицу онлайн с решением,найти обратную матрицу с помощью элементарных преобразований онлайн,найти обратную матрицу с проверкой онлайн с подробным решением,найти обратную матрицу с решением онлайн,найти обратные матрицы для матриц онлайн,найти союзную матрицу онлайн,нахождение матрицы методом обратной матрицы онлайн,нахождение обратной матрицы калькулятор,нахождение обратной матрицы калькулятор онлайн,нахождение обратной матрицы методом гаусса онлайн,нахождение обратной матрицы онлайн,нахождение обратной матрицы онлайн калькулятор,нахождение обратной матрицы онлайн методом гаусса,нахождение обратной матрицы онлайн с помощью элементарных преобразований,нахождение обратной матрицы онлайн с решением,нахождение обратной матрицы с помощью элементарных преобразований онлайн,нахождение обратной матрицы с решением онлайн,обернена матриця калькулятор онлайн,обернена матриця онлайн,обернена матриця онлайн калькулятор,обратить матрицу онлайн,обратная матрица калькулятор,обратная матрица калькулятор с решением,обратная матрица методом гаусса онлайн,обратная матрица методом элементарных преобразований онлайн,обратная матрица онлайн,обратная матрица онлайн калькулятор,обратная матрица онлайн калькулятор с подробным решением,обратная матрица онлайн методом гаусса,обратная матрица онлайн методом элементарных преобразований,обратная матрица онлайн решение,обратная матрица онлайн с подробным решением,обратная матрица онлайн с проверкой,обратная матрица онлайн с решением,обратная матрица проверка,обратная матрица решение онлайн,обратная матрица с проверкой онлайн,обратная матрица с решением онлайн,обратная матрицы калькулятор онлайн,обратная матрицы онлайн,обратная матрицы онлайн калькулятор,обратную матрицу посчитать,обратную матрицу решить онлайн,обратные матрицы калькулятор,обратные матрицы онлайн,обратные матрицы онлайн с решением,онлайн калькулятор матриц обратная матрица,онлайн калькулятор матриц обратных,онлайн калькулятор матрица обратная матрица,онлайн калькулятор матрицы метод обратной матрицы,онлайн калькулятор матрицы метод обратной матрицы онлайн,онлайн калькулятор матрицы методом обратной матрицы,онлайн калькулятор матрицы методом обратной матрицы онлайн,онлайн калькулятор метод обратной матрицы,онлайн калькулятор найти обратную матрицу,онлайн калькулятор нахождение обратной матрицы,онлайн калькулятор обернена матриця,онлайн калькулятор обратная матрица,онлайн калькулятор обратная матрицы,онлайн калькулятор обратной матрицы,онлайн калькулятор обратной матрицы с решением,онлайн калькулятор обратных матриц,онлайн матриця обернена,онлайн найти обратную матрицу методом гаусса,онлайн нахождение обратной матрицы методом гаусса,онлайн нахождение обратной матрицы с решением,онлайн обернена матриця,онлайн обратная матрица решение,онлайн обратная матрицы,онлайн поиск обратной матрицы,онлайн посчитать обратную матрицу,онлайн проверка матрицы,онлайн расчет обратной матрицы,онлайн решение матрицы методом обратной матрицы онлайн,онлайн решение матрицы обратной,онлайн решение матрицы с помощью обратной матрицы,онлайн решение матрицы с помощью обратной матрицы онлайн,онлайн решение методом обратной матрицы,онлайн решение методом обратной матрицы онлайн,онлайн решение обратная матрица,онлайн решение обратной матрицы,онлайн решение обратных матриц,онлайн решить методом обратной матрицы онлайн,онлайн решить обратную матрицу,поиск обратной матрицы онлайн,построение обратной матрицы онлайн,посчитать обратную матрицу,посчитать обратную матрицу онлайн,посчитать онлайн обратную матрицу,присоединенная матрица калькулятор онлайн,присоединенная матрица онлайн калькулятор,проверка обратной матрицы онлайн,проверка обратной матрицы онлайн с решением,рассчитать обратную матрицу онлайн,расчет обратной матрицы онлайн,решение матрица обратная,решение матрицы методом обратной матрицы калькулятор онлайн,решение матрицы методом обратной матрицы онлайн калькулятор,решение матрицы методом обратной матрицы онлайн с решением,решение матрицы методом обратной онлайн,решение матрицы обратной онлайн,решение матрицы онлайн методом обратной матрицы,решение матрицы онлайн методом обратной матрицы онлайн,решение матрицы с помощью обратной матрицы онлайн,решение обратная матрица онлайн,решение обратной матрицы онлайн,решение обратной матрицы онлайн с подробным решением,решение обратной матрицы онлайн с решением,решение обратных матриц онлайн,решение онлайн матрицы обратной,решение онлайн методом обратной матрицы,решение онлайн методом обратной матрицы онлайн,решение онлайн обратная матрица,решение онлайн обратной матрицы,решение онлайн обратных матриц,решить матрицу методом обратной матрицы онлайн,решить матрицу обратную,решить матрицу обратную онлайн,решить матрицу онлайн методом обратной матрицы,решить матрицы методом обратной матрицы онлайн,решить методом обратной матрицы онлайн калькулятор,решить обратную матрицу онлайн,решить онлайн матрицу методом обратной матрицы,решить онлайн обратную матрицу,союзная матрица онлайн.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление обратной матрицы онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить обратную матрицу онлайн).

Решить задачу вычисление обратной матрицы онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Как проверить (быстро) умножение матриц | by Haris Angelidakis

Спойлер: случайность помогает (еще раз)

Умножение двух N x N матриц A и B — фундаментальная операция, которая проявляется как подпрограмма во всех видах приложений. Поиск алгоритма, который может умножать две матрицы за время O( N ²), все еще продолжается, с самым быстрым асимптотическим алгоритмом, созданным Джошем Алманом и Вирджинией Василевской Уильямс (2021), время работы которого в настоящее время составляет

Однако, как отмечено в этой статье в Википедии, этот алгоритм является галактическим алгоритмом из-за больших констант и не может быть реализован на практике. Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.

В сегодняшней статье, однако, мы изучим другой, связанный с этим вопрос. Предположим, что кто-то дает нам N x N матрицы A, B и C, и более того, пусть они утверждают, что C есть произведение A и B , т.е. . Вопрос теперь в следующем. Можем ли мы проверить, действительно ли C является произведением A и B , не умножая A на B с нуля? Другими словами:

Дано N x N матрицы A , B и C , как быстро мы можем проверить, являются ли C = AB ?

Тривиальным тестом на поставленный выше вопрос было бы просто умножить A на B и проверить, равно ли произведение C . Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь состоит в том, чтобы разработать алгоритм O( N ²), который проверяет, соответствует ли C = АБ . Для этого мы прибегаем к случайности.

Примечание: Прежде чем продолжить, мы заявляем, что изложение следует главе 11 прекрасной книги «Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры» Иржи Матоусека.

Основная идея состоит в том, чтобы выбрать случайный N -мерный {0,1} вектор x , где каждая координата независимо установлена ​​в 0 или 1 с вероятностью 0,5, и умножить оба C и AB с х. Если C = AB , то мы будем иметь Cx = (AB)x, для любого вектора x. Однако, если C не равно AB, , то мы надеемся, что существует много векторов, для которых Cx не равно ( AB)x. Формально предлагаемый тест выглядит следующим образом.

Базовый тест

1. Выберите N -мерный {0,1} вектор x равномерно случайным образом.
2. Вычислить y = Cx и z = ( AB ) x .
3. Если y = z , то вернуть «РАВНО», иначе вернуть «НЕ РАВНО».

Очень легко увидеть, что тест всегда будет возвращать «EQUAL», если C действительно равно AB . Итак, единственный интересный случай для анализа — это когда C не равно AB . Но прежде чем сделать это, мы должны уточнить следующее. Предлагаемая идея требует вычисления произведения (АВ)х . Здесь мы должны быть немного осторожны, так как хотим избежать вычисления произведения AB . Чтобы решить эту проблему, мы используем тот факт, что умножение матриц является ассоциативным, и сначала вычисляем Bx , затем умножаем на с результатом Bx для общего времени работы O ( N ²).

Возвращаясь к анализу, предположим, что C не равно AB . Пусть D = C-AB. Ясно, что хотя бы одна запись из D будет ненулевым. Обозначим элемент в i -й строке и j -м столбце D как d(i,j) , и пусть k , t таковы, что d(k, t) не равно нулю. Пусть x(j) обозначает j -ю координату вектора x, и пусть q= Dx . Заметьте, что q = y-z . Теперь у нас есть

Поскольку каждая координата x выбирается независимо случайным образом, мы можем предположить, что координата x(t) является последней, которая будет установлена ​​в 0 или 1. Итак, предположим, что все остальные координаты x были установлены, кроме координаты x(t) . Когда мы собираемся решить, является ли x(t) 0 или 1, подбрасывая правильную монету, мы уже определили значение выражения

Обратите внимание, что есть два варианта для S ; он либо равен нулю, либо отличен от нуля. Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:

• с вероятностью 0,5, x(t) = 1, и, следовательно, q(k) = S + d(k,t) .
• с вероятностью 0,5, x(t) = 0, поэтому q(k) = S .

Поскольку d(k,t) не равно нулю, это означает, что S + d(k,t) не равно S . Таким образом, хотя бы одно из S и S+ d(k,t) отлично от нуля, и поэтому мы заключаем, что q(k) отлично от нуля с вероятностью не менее 0,5, откуда следует, что y не равно z с вероятностью не менее 0,5. Мы заключаем, что с вероятностью не менее 0,5 наш тест правильно определит, что C не равно AB .

Тем не менее, можно сказать, что вероятность успеха в 50% не очень удовлетворительна. И, действительно, это справедливое беспокойство. Но мы можем использовать стандартный прием, используемый для таких алгоритмов, которые попадают в широкий класс алгоритмов Монте-Карло, а именно повторить их несколько раз. Точнее, окончательный алгоритм, который мы будем использовать, следующий.

Окончательный тест

1. Проведите базовый тест M раз независимо.
2. Если все выполнения Базового теста вернули «РАВНО», верните «РАВНО», в противном случае верните «НЕ РАВНО».

Легко видеть, что Final Test всегда завершается успешно, если C = AB . В случае, когда C не равно AB , тогда мы знаем, что однократное выполнение базового теста успешно с вероятностью не менее 0,5 . Таким образом, чтобы получить неправильный ответ, все M выполнений базового теста должны завершиться неудачно. Поскольку эти исполнения независимы, это происходит с вероятностью не более 1/2 ᴹ .

Например, если поставить М = 10, то вероятность неудачи меньше 0,001, или другими словами вероятность успеха не менее 99,9%, что совсем неплохо! Что касается времени работы, то в него будет включено M , а общее время работы O( M N ²). Поскольку M является константой, это по-прежнему равно O( N ²) и намного быстрее, чем современные лучшие алгоритмы умножения матриц. Мы сделали!

• Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры», Иржи Матоусек. Издатель: ‎ Американское математическое общество
• https://en.wikipedia.org/wiki/Matrix_multiplication_algorithm

Работа с данными в матрице

Загрузка данных

Наши данные в качестве примера представляют собой измерения качества (размер частиц) при производстве ПВХ-пластика с использованием восьми различных партий смолы и трех разных операторов станка.

Набор данных хранится в формате значений, разделенных запятыми (CSV). Каждая строка — это партия смолы, а каждый столбец — это оператор. В RStudio откройте pvc.csv и посмотрите, что он содержит.

 read.csv("r-intro-files/pvc.csv", row.names=1) 

Совет

Расположение файла указано относительно вашего «рабочего каталога». Вы можете увидеть расположение вашего рабочего каталога в заголовке панели консоли в RStudio. Скорее всего, это «~», указывающий на ваш личный домашний каталог. Вы можете изменить рабочий каталог с помощью установка .

Имя файла «r-intro-files/pvc.csv» означает, что в текущем рабочем каталоге в подкаталоге «r-intro-files» находится файл «pvc.csv».

Вы можете проверить, действительно ли файл находится в этом месте, используя панель «Файлы» в правом нижнем углу RStudio.

Если вы работаете на своем собственном компьютере, а не на нашем учебном сервере, и загрузили и разархивировали файл r-intro-files.zip, этот файл может находиться в другом месте.

Мы позвонили read.csv с двумя аргументами: имя файла, который мы хотим прочитать, и какой столбец содержит имена строк. Имя файла должно быть строкой символов, поэтому мы заключаем его в кавычки. Присвоение второму аргументу row.names значения 1 указывает, что файл данных имеет имена строк и номер столбца, в котором они хранятся. Если мы не укажем row.names , результат не будет иметь названия строк.

Наконечник

read.csv на самом деле имеет гораздо больше аргументов, которые могут оказаться полезными при импорте собственных данных в будущем.

 dat <- read.csv("r-intro-files/pvc.csv", row.names=1) 

 ## Алиса Боб Карл
## Смола1 36,25 35,40 35,30
## Смола2 35,15 35,35 33,35
## Смола3 30,70 29,65 29,20
## Смола4 29,70 30,05 28,65
## Смола5 31,85 31,40 29,30
## Смола6 30,20 30,65 29,75
## Смола7 32,90 32,50 32,80
## Resin8 36.80 36.45 33.15 

 class(dat) 

 ## [1] "data.frame" 

 str(dat) 

 ## 'data.frame': 8 obs. из 3 переменных:
## $ Алиса: число 36.2 35.1 30.7 29.7 31,9 ...
## $ Боб: число 35,4 35,4 29,6 30,1 31,4 ...
## $ Carl : num 35.3 33.4 29.2 28.6 29.3 ... 

read.csv загрузил данные в виде кадра данных. Фрейм данных содержит набор «вещей» (строк), каждая из которых имеет набор свойств (столбцов) разных типов.

На самом деле эти данные лучше рассматривать как матрицу ¹ . Во фрейме данных столбцы содержат разные типы данных, но в матрице все элементы представляют собой данные одного типа. Матрица в R похожа на математическую матрицу, содержащую все однотипные вещи (обычно числа).

R часто, но не всегда позволяет использовать их взаимозаменяемо. Также полезно, когда вы думаете о данных, различать фрейм данных и матрицу. Различные операции имеют смысл для фреймов данных и матриц. Фреймы данных очень важны для R, и освоение R во многом связано с мышлением во фреймах данных. Однако любая статистика часто связана с использованием матриц. Например, когда мы работаем с данными RNA-Seq, мы используем матрицу количества прочтений. Так что стоит потратить время и на то, чтобы научиться использовать матрицы.

Сообщим R, что у нас есть матрица. as.matrix «приводит» наши данные к матричному типу.

 мат <- as.matrix(дата)
class(mat) 

 ## [1] "matrix" 

 str(mat) 

 ## num [1:8, 1:3] 36. 2 35.1 30.7 29.7 31.9 ...
## - attr(*, "dimnames")=Список из 2
## ..$ : chr [1:8] "Смола1" "Смола2" "Смола3" "Смола4" ...
## ..$ : chr [1:3] "Алиса" "Боб" "Карл" 

Гораздо лучше.

Наконечник

Матрицы могут быть созданы различными способами.

матрица преобразует вектор в матрицу с заданным количеством строк и столбцов.

rbind укладывает несколько векторов в виде строк друг над другом, образуя матрицу, или может укладывать меньшие матрицы друг на друга, формируя большую матрицу.

cbind аналогичным образом укладывает несколько векторов в виде столбцов рядом друг с другом, образуя матрицу, или может укладывать меньшие матрицы рядом друг с другом, формируя большую матрицу.

Индексация матриц

Размер матрицы можно проверить с помощью функций nrow и ncol :

 nrow(mat) 

 ## [1] 8 

 ncol(mat) 

 ## 0 [1] 
 Это говорит нам о том, что наша матрица  mat  имеет 8 строк и 3 столбца.  
 
 Если мы хотим получить одно значение из матрицы, мы можем указать индекс строки и столбца в квадратных скобках: 
 
 # первое значение в мате
mat[1, 1] 
 ## [1] 36.25 
 # среднее значение в мате
мат[4, 2] 
 ## [1] 30.05 
 Если наша матрица имеет имена строк и имена столбцов, мы также можем обращаться к строкам и столбцам по имени.
 mat["Resin4","Bob"] 
 ## [1] 30.05 
 Индекс типа  [4, 2]  выбирает один элемент матрицы, но мы можем выбирать и целые секции. Например, мы можем выбрать первые два оператора (столбца) значений для первых четырех смол (строк) следующим образом:
 mat[1:4, 1:2] 
 ## Алиса Боб
## Смола1 36,25 35,40
## Смола2 35,15 35,35
## Смола3 30,70 290,65
## Resin4 29.70 30.05 
 Срез  1:4  означает числа от 1 до 4. То же, что и  c(1,2,3,4)  .
 Срез не обязательно должен начинаться с 1, т.е. строка ниже выбирает строки с 5 по 8:
 mat[5:8, 1:2] 
 ## Алиса Боб
## Смола5 31,85 31,40
## Смола6 30,20 30,65
## Смола7 32,90 32,50
## Resin8 36. 80 36.45 
 Мы можем использовать векторы, созданные с помощью  c , для выбора несмежных значений:
 mat[c(1,3,5), c(1,3)] 
 ## Алиса Карл
## Смола1 36,25 35,3
## Смола3 30,70 29,2
## Resin5 31,85 29,3 
 Нам также не нужно указывать индекс ни для строк, ни для столбцов. Если мы не включим индекс для строк, R вернет все строки; если мы не включаем индекс для столбцов, R возвращает все столбцы. Если мы не укажем индекс ни для строк, ни для столбцов, например.  mat[ ]  , R возвращает полную матрицу.
 # Все столбцы из строки 5
mat[5, ] 
 ## Алиса Боб Карл
## 31,85 31,40 29.30 
 # Все строки из столбца 2
мат[ 2] 
 ## Смола1 Смола2 Смола3 Смола4 Смола5 Смола6 Смола7 Смола8
## 35,40 35,35 29,65 30,05 31,40 30,65 32,50 36,45 
 Суммарные функции 
 Теперь давайте выполним некоторые общие математические операции, чтобы узнать о наших данных. При анализе данных мы часто хотим посмотреть частичную статистику, например, максимальное значение на смолу или среднее значение на оператора. Один из способов сделать это — выбрать данные, которые мы хотим, в качестве новой временной переменной, а затем выполнить расчет для этого подмножества:0003
 # первая строка, все столбцы
полимер_1 <- мат[1, ]
# максимальный размер частиц смолы 1
max(resin_1) 
 ## [1] 36,25 
 На самом деле нам не нужно хранить строку в отдельной переменной. Вместо этого мы можем объединить выбор и вызов функции:
 # максимальный размер частиц для смолы 2
max(mat[2, ]) 
 ## [1] 35,35 
 R имеет функции для других общих вычислений, например. нахождение минимума, среднего, медианы и стандартного отклонения данных:
 # минимальный размер частиц для оператора 3
min(mat[ 3]) 
 ## [1] 28.65 
 # среднее значение для оператора 3
mean(mat[ 3]) 
 ## [1] 31.4375 
 # медиана для оператора 3
median(mat[ 3]) 
 ## [1] 31.275 
 # стандартное отклонение для оператора 3
sd(mat[ 3]) 
 ## [1] 2,49453 
 Задача — подмножество данных в матрице 
 Предположим, вы хотите определить максимальный размер частиц смолы 5 с помощью операторов 2 и 3. Для этого вы должны извлечь соответствующий срез из матрицы и вычислить максимальное значение. Какая из следующих строк кода R дает правильный ответ?
  макс(мат[5, ]) 
  макс(мат[2:3, 5]) 
  макс(мат[5, 2:3]) 
  макс(мат[5, 2, 3]) 
 Суммирующие матрицы 
 Что делать, если нам нужен максимальный размер частиц для всех смол или среднее значение для каждого оператора? Как показано на диаграмме ниже, мы хотим выполнить операцию на границе матрицы:
 Для этого мы можем использовать функцию  apply .
 Наконечник 
 Чтобы узнать о функции в R, например.  применить  , мы можем прочитать его справочную документацию, запустив  help(apply)  или  ?apply  .
  применить  позволяет нам повторить функцию для всех строк ( MARGIN = 1 ) или столбцов ( MARGIN = 2 ) матрицы. Мы можем думать о  применить  как о свертывании матрицы до размера, указанного  MARGIN  , где строки имеют размерность 1, а столбцы - размерность 2 (напомним, что при индексировании матрицы мы даем сначала строку, а затем столбец).
 Таким образом, для получения среднего размера частиц каждой смолы нам потребуется вычислить среднее значение всех строк (  MARGIN = 1  ) матрицы.
 avg_resin <- apply(mat, 1, mean) 
 И чтобы получить средний размер частиц для каждого оператора, нам нужно будет вычислить среднее значение всех столбцов (  MARGIN = 2  ) матрицы.
 avg_operator <- apply(mat, 2, mean) 
 Поскольку второй аргумент  apply  равен  MARGIN  , приведенная выше команда эквивалентна  apply(dat, MARGIN = 2, mean)  .
 Наконечник 
 Некоторые распространенные операции имеют более краткие альтернативы. Например, вы можете вычислить средние значения по строкам или по столбцам с помощью  rowMeans  и  colMeans  соответственно.
 Вызов - подведение итогов по матрице 
 Как бы вы рассчитали стандартное отклонение для каждой смолы?
 Дополнительно: Как бы вы рассчитали значения на два стандартных отклонения выше и ниже среднего значения для каждой смолы?
 t-тест 
 R имеет множество встроенных статистических тестов. Одним из наиболее часто используемых тестов является t-тест. Существенно ли различаются средние значения двух векторов?
 мат[1,] 
 ## Алиса Боб Карл
## 36.25 35.40 35.30 
 мат[2,] 
 ## Алиса Боб Карл
## 35.15 35.35 33.35 
 t.test(mat[1,], mat[2,]) 
 ##
## Welch Two Sample t-критерий
##
## данные: мат[1, ] и мат[2, ]
## t = 1,4683, df = 2,8552, p-значение = 0,2427
## альтернативная гипотеза: истинная разница в средних не равна 0
## 95-процентный доверительный интервал:
## -1.271985 3.338652
## примерные оценки:
## среднее значение x среднее значение y
## 35.65000 34.61667 
 На самом деле это можно рассматривать как парный выборочный t-критерий, поскольку значения могут быть объединены в пары оператором. По умолчанию  t.test  выполняет непарный t-тест. Мы видим в документации (  ?t.test  ), что мы можем указать  paired=TRUE  в качестве аргумента для выполнения парного t-теста.
 t.test(мат[1,], мат[2,], парный=ИСТИНА) 
 ##
## Парный t-критерий
##
## данные: мат[1, ] и мат[2, ]
## t = 1,8805, df = 2, p-значение = 0,2008
## альтернативная гипотеза: истинная разница в средних не равна 0
## 95-процентный доверительный интервал:
## -1.330952 3.397618
## примерные оценки:
## среднее значение разностей
## 1.033333 
 Вызов — использование t.test 
 Сможете ли вы найти существенную разницу между любыми двумя смолами?
 Когда мы вызываем  t.test , он возвращает объект, который ведет себя как  список  . Напомним, что в R список   представляет собой набор разных значений.
 результат <- t.test(mat[1,], mat[2,], paired=TRUE)
имена(результат) 
 ## [1] "статистика" "параметр" "p. value" "conf.int" "оценка"
## [6] "null.value" "alternative" "method" "data.name" 
 result$p.value 
 ## [1] 0.2007814 
 Это означает, что мы можем написать программу, которая использует различные результаты из  t.test  , например, выполняя целую серию t-тестов и сообщая о значимых результатах.
 Наконечник — тип R под капотом 
 Откуда мы могли знать, что  t.test  дал нам результат, который вел себя как список?
 Ранее мы использовали класс  , чтобы увидеть, к какому типу относятся различные значения. Здесь это говорит нам о том, что это  "htest"  , но на самом деле это просто "публичное лицо" значения. Иногда нам нужно оценить значение Scooby Doo и посмотреть, как R думает об этом под капотом.  typeof  показывает, как R внутренне думает о значении. Если мы обнаружим, что  typeof  объекта  "list"  , тогда мы знаем, что можем использовать  $  или  [[ ]]  для доступа к его элементам.
 class(result) 
 ## [1] "htest" 
 typeof(result) 
 ## [1] "list" 
 Попробуйте это также с  dat  и  mat .
 Построение графиков 
 Математик Ричард Хэмминг однажды сказал: «Цель вычислений — понимание, а не числа», и часто лучший способ развить понимание — визуализировать данные. Визуализация заслуживает отдельной лекции (или курса), но мы можем изучить некоторые функции построения графиков в R.
 Давайте посмотрим на средний размер частиц смолы. Напомним, что мы уже рассчитали эти значения выше, используя  apply(mat, 1, mean)  и сохранили их в переменной  avg_resin  . График значений выполняется с помощью функции  plot  .
 plot(avg_resin) 
 Выше мы дали функции  plot  вектор чисел, соответствующий среднему значению на смолу по всем операторам. График  График  создал график рассеивания, где ось Y представляет собой средний размер частиц, а ось X представляет собой порядок или индекс значений в векторе, которые в данном случае соответствуют 8 смолам.
  plot  может принимать множество различных аргументов для изменения внешнего вида вывода. Вот график с некоторыми дополнительными аргументами:
 plot(avg_resin,
    xlab="Смола",
    ylab="Размер частиц",
    main="Средний размер частиц на смолу",
    type="b") 
 Задание - построение данных 
 Создайте график, показывающий стандартное отклонение для каждой смолы.
 Сохранение графиков 
 Можно сохранить график в формате .PNG или .PDF из интерфейса RStudio с помощью кнопки «Экспорт». Однако, если мы хотим вести полную запись того, как именно мы создаем каждый график, мы предпочитаем делать это с помощью кода R.
 Графика в R отправляется на «устройство». По умолчанию это устройство RStudio. Однако мы можем временно отправить графики на другое устройство, например, в файл .PNG (  png("filename.png")  ) или файл .PDF (  pdf("filename.pdf")  ).
 
 pdf("test.pdf")
сюжет (средняя_резина)
dev.
No related posts.