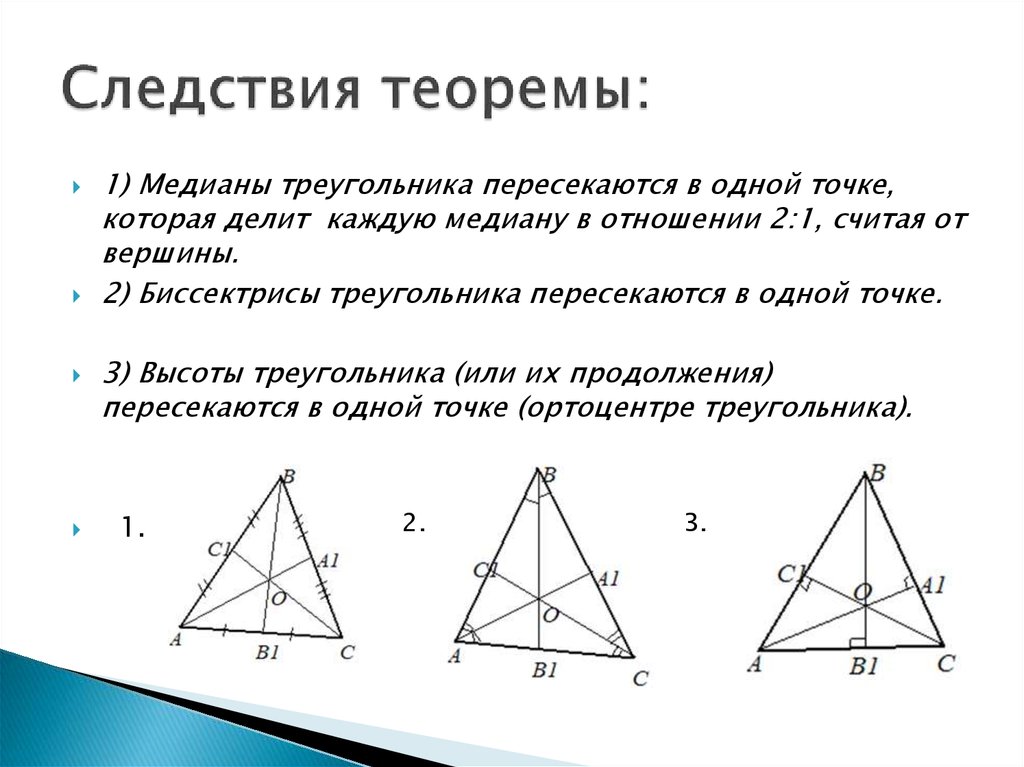
| Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы. Связанные определенияНа рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой. С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум. СвойстваОсновное свойствоВсе три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины. Свойства медиан равнобедренного треугольникаВ равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине. У равностороннего треугольника все три медианы равны. Свойства оснований медиан
Другие свойства
Основные соотношенияЧтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей): m a = 2 b 2 + 2 c 2 − a 2 4 , {displaystyle m_{a}={sqrt {frac {2b^{2}+2c^{2}-a^{2}}{4}}},} m b = 2 a 2 + 2 c 2 − b 2 4 , {displaystyle m_{b}={sqrt {frac {2a^{2}+2c^{2}-b^{2}}{4}}},} m c = 2 a 2 + 2 b 2 − c 2 4 , {displaystyle m_{c}={sqrt {frac {2a^{2}+2b^{2}-c^{2}}{4}}},} где m a , m b , m c {displaystyle m_{a}, m_{b}, m_{c}} — медианы к сторонам треугольника a , b , c {displaystyle a, b, c} соответственно. Обратно, можно выразить длину произвольной стороны треугольника через медианы: a = 2 3 − m a 2 + 2 m b 2 + 2 m c 2 = 2 ( b 2 + c 2 ) − 4 m a 2 = b 2 2 − c 2 + 2 m b 2 = c 2 2 − b 2 + 2 m c 2 , {displaystyle a={frac {2}{3}}{sqrt {-m_{a}^{2}+2m_{b}^{2}+2m_{c}^{2}}}={sqrt {2(b^{2}+c^{2})-4m_{a}^{2}}}={sqrt {{frac {b^{2}}{2}}-c^{2}+2m_{b}^{2}}}={sqrt {{frac {c^{2}}{2}}-b^{2}+2m_{c}^{2}}},} b = 2 3 − m b 2 + 2 m a 2 + 2 m c 2 = 2 ( a 2 + c 2 ) − 4 m b 2 = a 2 2 − c 2 + 2 m a 2 = c 2 2 − a 2 + 2 m c 2 , {displaystyle b={frac {2}{3}}{sqrt {-m_{b}^{2}+2m_{a}^{2}+2m_{c}^{2}}}={sqrt {2(a^{2}+c^{2})-4m_{b}^{2}}}={sqrt {{frac {a^{2}}{2}}-c^{2}+2m_{a}^{2}}}={sqrt {{frac {c^{2}}{2}}-a^{2}+2m_{c}^{2}}},} c = 2 3 − m c 2 + 2 m b 2 + 2 m a 2 = 2 ( b 2 + a 2 ) − 4 m c 2 = b 2 2 − a 2 + 2 m b 2 = a 2 2 − b 2 + 2 m a 2 , {displaystyle c={frac {2}{3}}{sqrt {-m_{c}^{2}+2m_{b}^{2}+2m_{a}^{2}}}={sqrt {2(b^{2}+a^{2})-4m_{c}^{2}}}={sqrt {{frac {b^{2}}{2}}-a^{2}+2m_{b}^{2}}}={sqrt {{frac {a^{2}}{2}}-b^{2}+2m_{a}^{2}}},} где m a , m b , m c {displaystyle m_{a},m_{b},m_{c}} — медианы к соответствующим сторонам треугольника, a , b , c {displaystyle a,b,c} — стороны треугольника.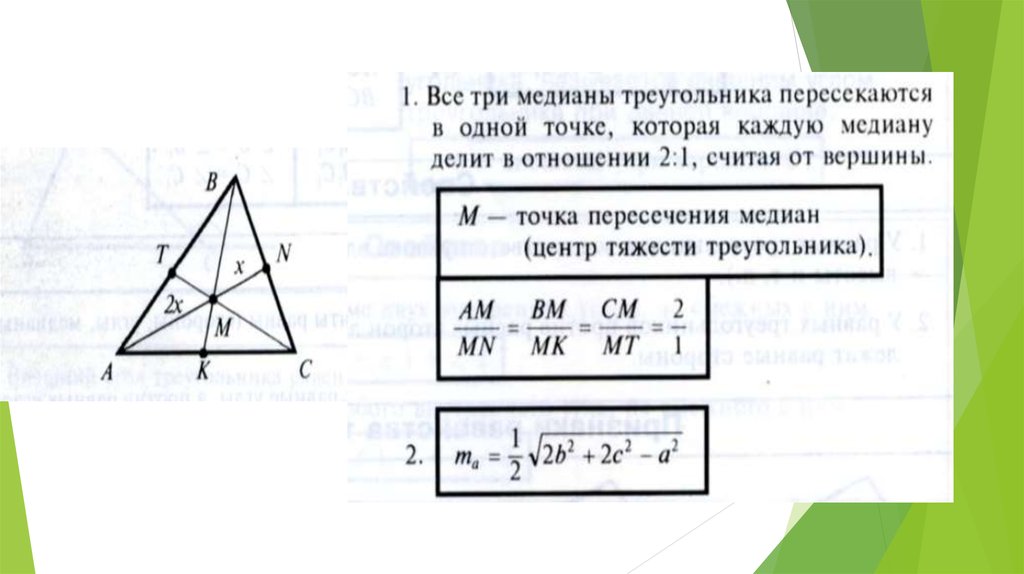 Площадь S {displaystyle S} любого треугольника, выраженная через длины его медиан: S = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) , {displaystyle S={frac {4}{3}}{sqrt {sigma (sigma -m_{a})(sigma -m_{b})(sigma -m_{c})}},} где σ = ( m a + m b + m c ) / 2 {displaystyle sigma =(m_{a}+m_{b}+m_{c})/2} — полусумма длин медиан.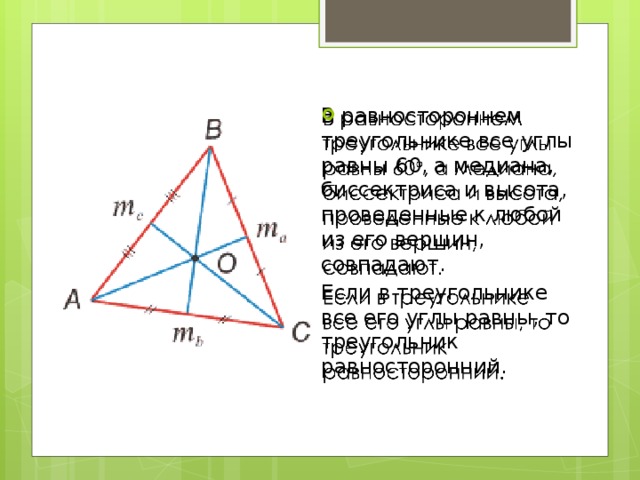 |
Треугольники — Планиметрия — Подготовка к ЕГЭ по математике
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
1. Сумма углов в треугольнике равна α + β + γ = 180°.
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
4. Формулы площади треугольника:
1 (через высоту) | 2 (через две стороны и синус угла между ними) | 3 (формула Герона) |
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. | Площадь треугольника равна половине произведения его сторон на синус угла между ними. | Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
с² = а² + b² – 2ab · cosγ
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
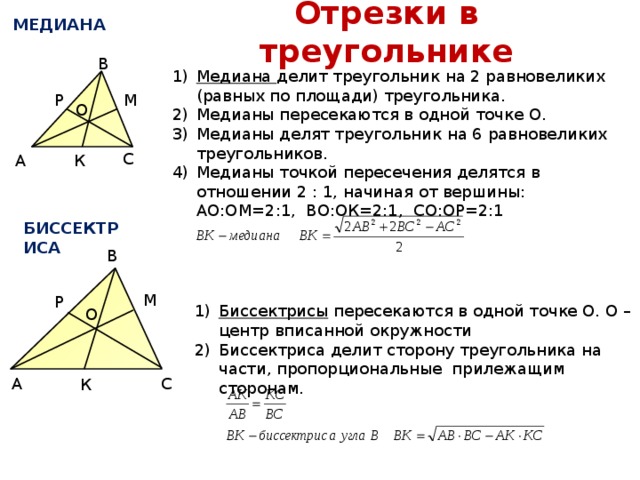
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а’ и b’ — отрезки, на которые биссектриса делит третью сторону треугольника, то
МЕДИАНА
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медианы треугольника:
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то
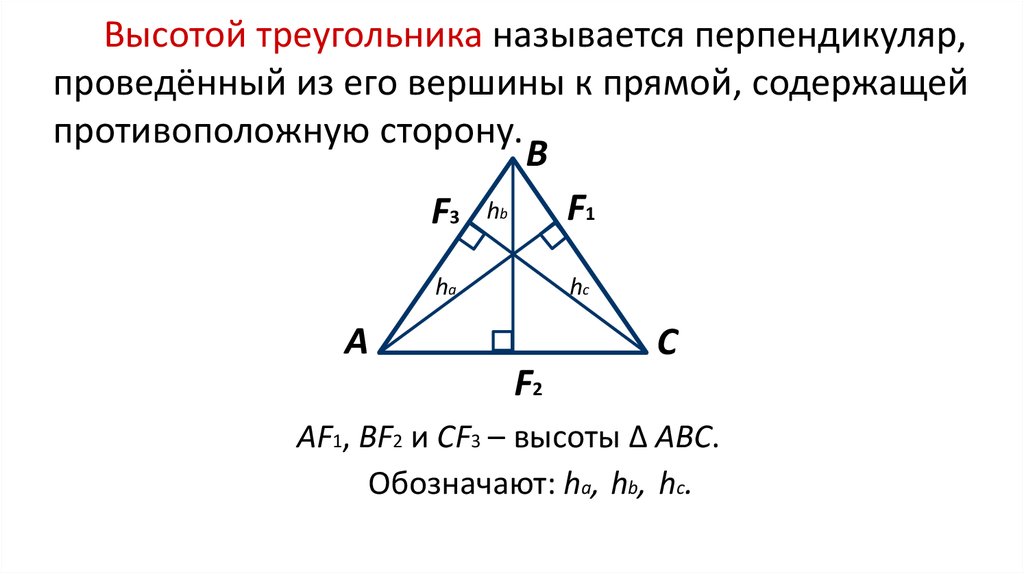
ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.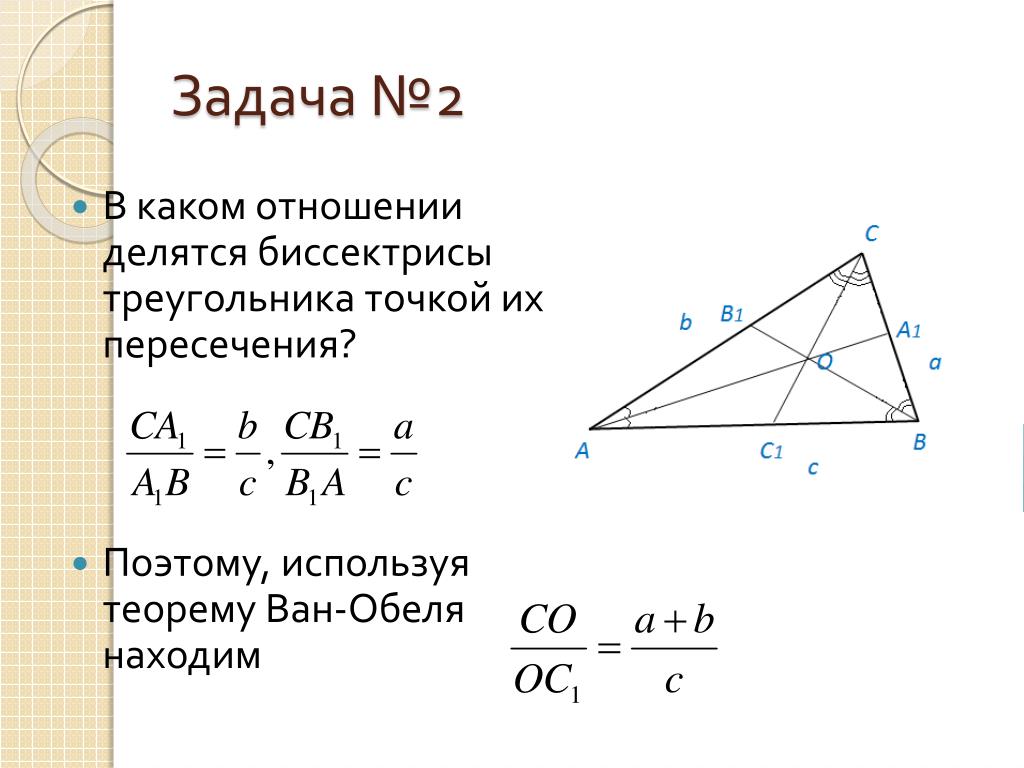
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
Сложные теоремы:
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.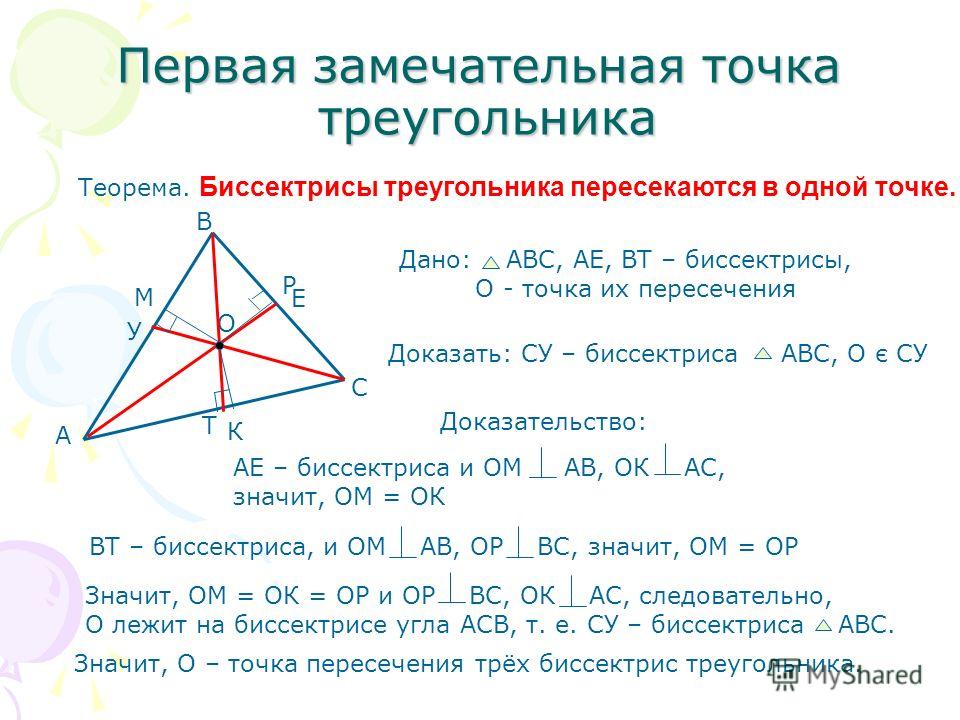
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
Свойства средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
Подобные треугольники | Равные треугольники |
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры): Также сохраняется внутреннее отношение длин: | Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2. 3. По двум равным углам (тогда и третьи тоже будут равны) 4. 5. По трем пропорциональным сторонам: | Признаки равенства треугольников: 1. По двум сторонам и углу между ними: 2. По стороне и двум прилежащим к ней углам. 3. По трем сторонам. |
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).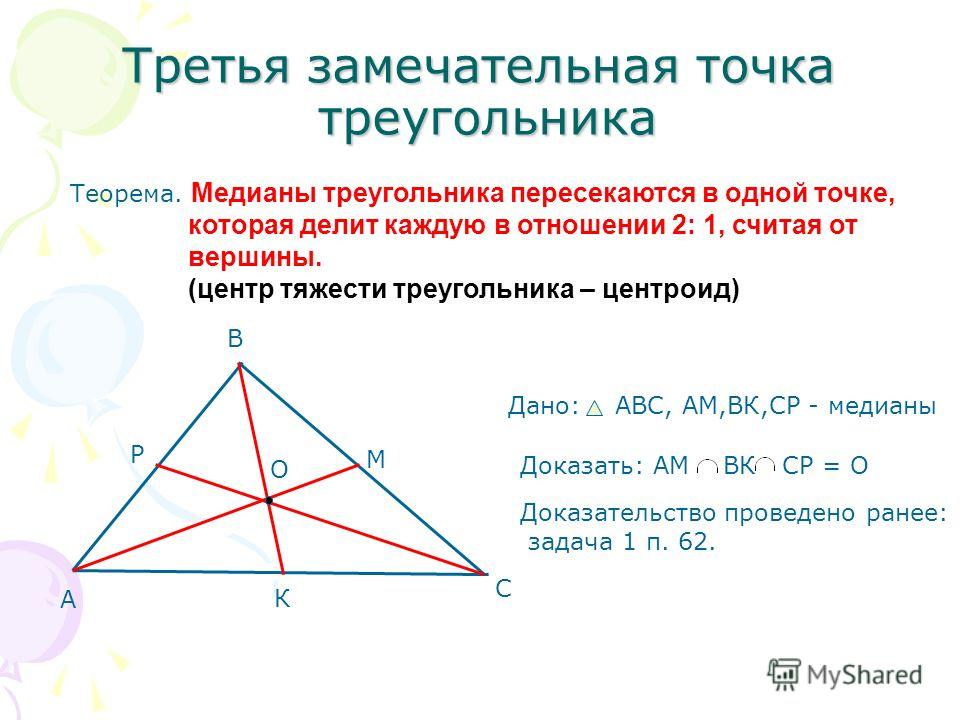
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
1. Углы при основании равны (∠АВС = ∠АСВ).
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):
— Формула Герона (так как все стороны равны):
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).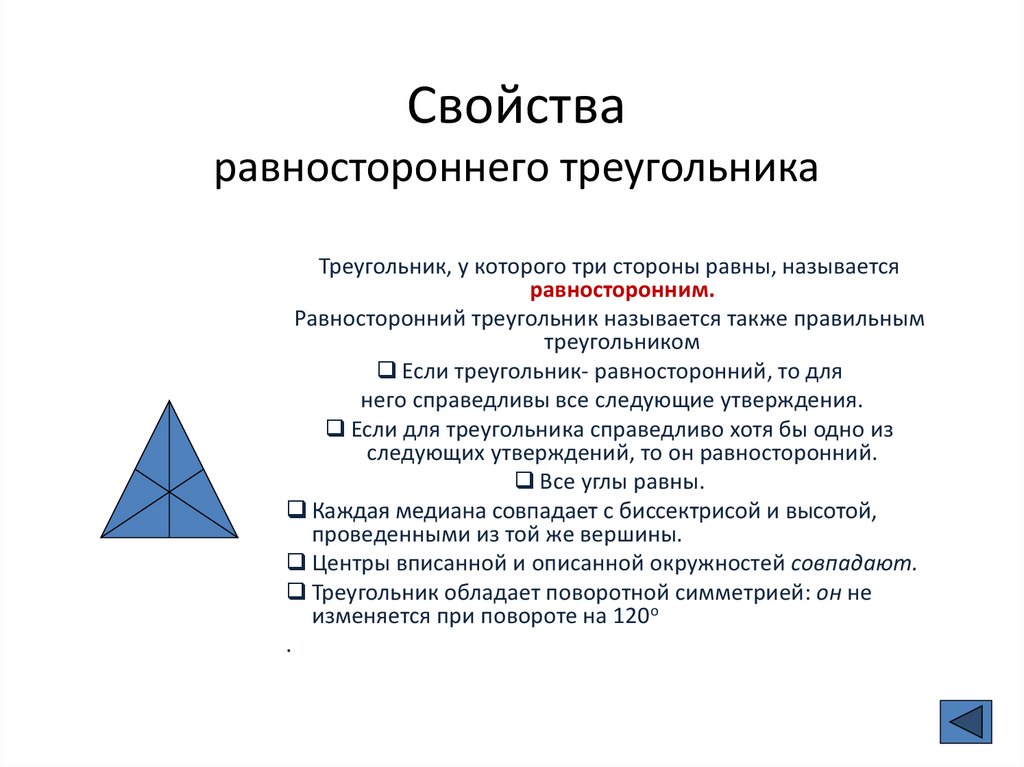
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу
- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
6. Формулы площади прямоугольного треугольника:
|
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат) Отношение сторон в серебряном треугольнике: | Золотой треугольник — треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике: |
Его концепция, характеристики и примеры.
Треугольники по длине сторон делятся на три типа; Разносторонний треугольник: треугольник, у которого все стороны не равны. Равнобедренный треугольник: треугольник, у которого равны только две стороны. Равносторонний треугольник: треугольник, у которого все стороны одинаковой длины.
Равносторонний треугольник — это правильный многоугольник, у которого все три стороны и их соответствующие углы равны и идентичны друг другу. В этой статье мы вкратце познакомимся с понятием равностороннего треугольника, необходимыми формулами, характеристиками, сравнением по отношению к разностороннему и равнобедренному треугольнику и несколькими численными решениями. 9{\circ }\)
Таким образом, треугольник ABC равносторонний.
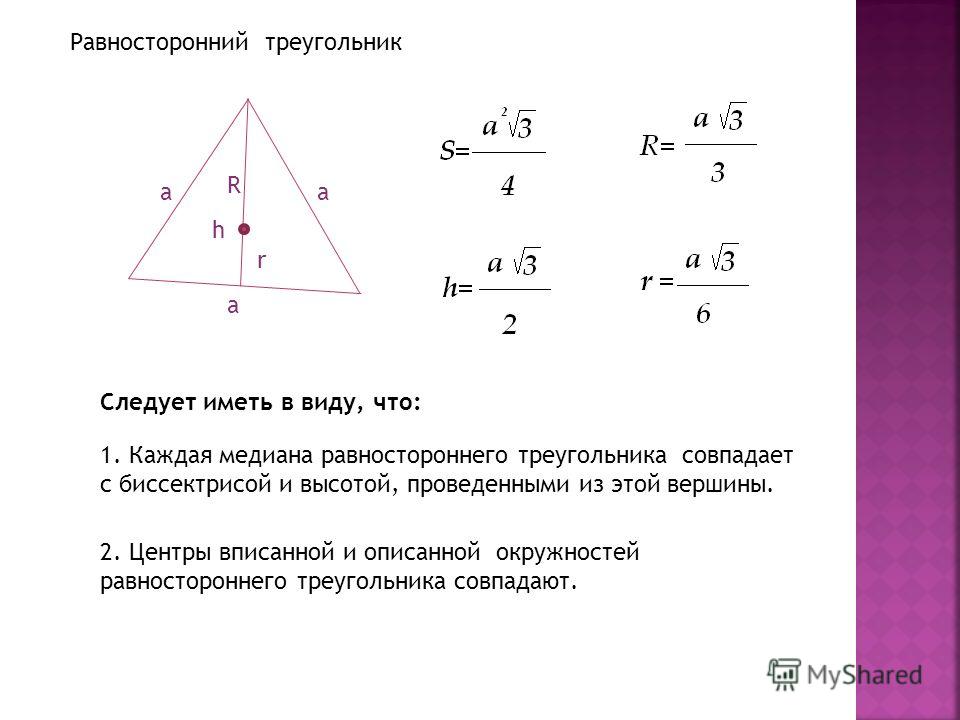
Формула равностороннего треугольника
В этой статье мы изучим четыре формулы для равностороннего треугольника,
- Площадь равностороннего треугольника.
- Высота равностороннего треугольника.
- Периметр равностороннего треугольника.
- Центроид равностороннего треугольника.
Площадь равностороннего треугольника
Площадь – это общее пространство, занимаемое плоской поверхностью, или пространство, занимаемое двухмерным объектом. 92)\).
Где а = длина каждой стороны.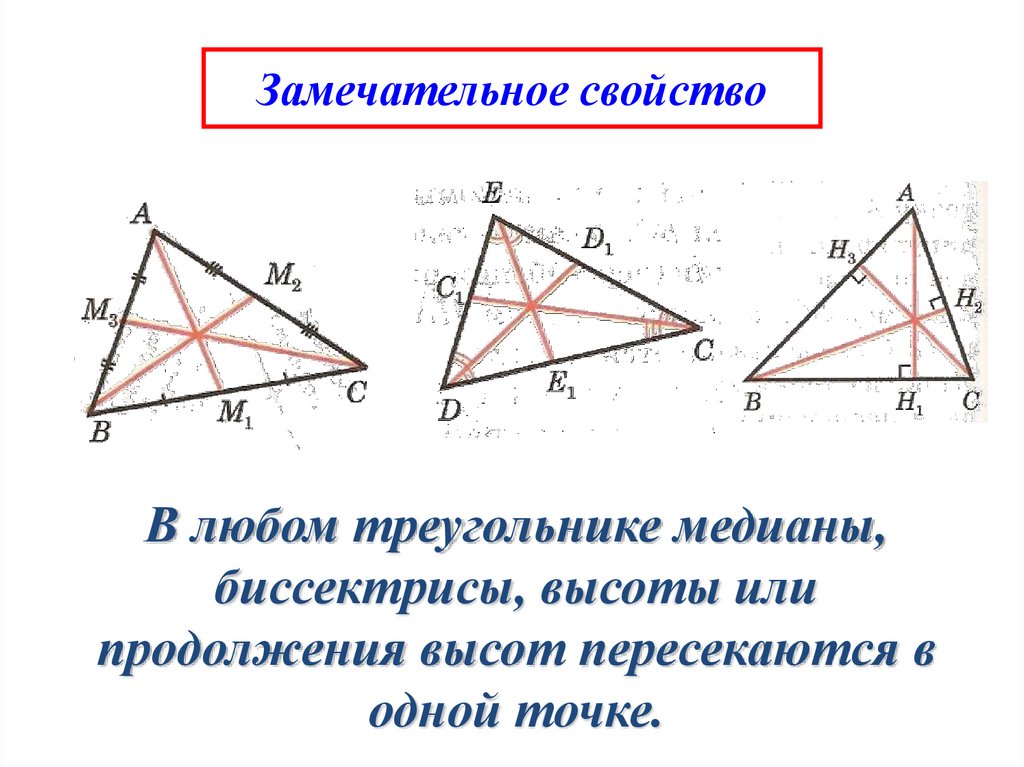
Периметр равностороннего треугольника
Периметр определяется как замкнутый путь, очерчивающий двумерную форму или длину вдоль одномерной плоскости.
Периметр также является суммой сторон двумерной фигуры.
Периметр равностороннего треугольника определяется по формуле
Периметр (P) = 3a (или a + a + a), где «a» — длина каждой стороны.
Кроме того, его полупериметр равен = 3a / 2,
Высота равностороннего треугольника
Мы можем вычислить высоту равностороннего треугольника, используя теорему Пифагора,
Рассмотрим треугольник XYZ, где высота проходит через вершину «X», которая является высотой данного равностороннего треугольника .
Согласно теореме Пифагора,
Гипотенуза² = основание²+ высота². – Уравнение (1)
Рассмотрим рисунок выше,
Нам нужно найти высоту данного треугольника, 92}{4}\)
\(h=\frac{\sqrt{3}a}{2}\)
Формула высоты равностороннего треугольника: \(h=\frac{\sqrt{3 }а}{2}\).
Центроид равностороннего треугольника
Центроид равностороннего треугольника — это точки в треугольнике, где сходятся медианы треугольника.
На приведенном выше рисунке для треугольника ABC точка «O» является центром тяжести равностороннего треугольника.
Он делит медианы в отношении 2 : 1.
Пусть длины всех сторон AB = BC = AC равны «a». 9{\circ }\),
Sin 30 = OD / OB
\(OB=\frac{\sqrt{3}a}{3}\)
Следовательно, для равностороннего треугольника с длиной «a» расстояние от центроида до вершины всегда равно \(\frac{\sqrt{3}a}{3}\).
Узнайте о двумерном измерении
Характеристики равностороннего треугольника
Ниже приведены характеристики равностороннего треугольника
- Все стороны имеют одинаковую длину
- Все внутренние углы равны 60 градусам.
- Центр тяжести, центр описанной окружности и ортоцентр равностороннего треугольника — одно и то же.
- Сумма всех внутренних углов равностороннего треугольника равна 180 градусам.

Симметрия равностороннего треугольника
В этой статье мы узнаем о симметрии вращения и отражения равностороннего треугольника. Есть два типа симметрии, которые проявляет равносторонний треугольник.
Вращательная симметрия
Равносторонний треугольник обладает вращательной симметрией порядка 3, так что, поворачивая его на 120 градусов, 240 градусов и 360 градусов вокруг его центра тяжести, мы получаем каждое возможное расположение вершин A, B и C и, следовательно, треугольник аналогичен предыдущей исходной форме.
Симметрия отражения
В дополнение к вращательной симметрии равносторонний треугольник также проявляет симметрию отражения. Он имеет три линии симметрии, проходящие через три его вершины и середину противоположной им стороны. Поперек этих линий две части треугольника являются зеркальным отображением друг друга.
Разница между разносторонними, равнобедренными и равносторонними треугольниками
| Равносторонний треугольник 92\) | Площадь разностороннего треугольника определяется по формуле: A = ½ x основание x высота. | Площадь равнобедренного треугольника определяется по формуле: A = ½ x основание x высота. | ||||
| Периметр равностороннего треугольника равен (P) = 3a. Где а — длина стороны (длины всех сторон равны). | Периметр разностороннего треугольника (P) = a + b + c. Где a, b и c — стороны треугольника. | Периметр равнобедренного треугольника равен (P) = 2a + b. Где a и b — длины сторон. | ||||
| Нет типов равностороннего треугольника на основе их углов. | Различают три типа разносторонних треугольников: остроугольный, тупоугольный и прямоугольный. | Равнобедренный треугольник бывает трех видов: остроугольный, тупоугольный и прямоугольный. | ||||
| Равносторонний треугольник имеет 3 оси симметрии. | Разносторонний треугольник имеет 0 осей симметрии. | Равнобедренный треугольник имеет одну линию симметрии. 92\) = \(\frac{\sqrt{3}\times 81}{4}\) = 35,07 см² Площадь данного равностороннего треугольника равна 35,07 см². Пример 2. Периметр равностороннего треугольника равен 26см, какова длина каждой его стороны? Решение 2. Даны данные, Периметр треугольника = 26 см. Периметр равностороннего треугольника равен (P) = 3a. Где «а» — длина каждой из его сторон, 3а = 26, a = 26/3 a = 8,66 см Длина каждой стороны равностороннего треугольника равна 8,66 см. Пример 3. Какими будут высота и площадь равностороннего треугольника, если длина каждой стороны равна 6см. Приведенные данные, Длина каждой стороны (a) = 6 см, Формула высоты равностороннего треугольника: \(h=\frac{\sqrt{3}a}{2}\). Высота (h) = \(\frac{\sqrt{3}\times 6}{2}\) Высота (h) = 5,196 см. 92\)Площадь = \(\frac{\sqrt{3}\times 36}{4}\) Площадь = 15,58 см² Площадь данного равностороннего треугольника равна 15,58 см². Надеюсь, эта статья была информативной и помогла вам в учебе и подготовке к экзаменам. Часто задаваемые вопросы о равностороннем треугольнике92}{12}\).В.2 Все ли равносторонние треугольники подобны? Ответ 2 Равносторонние треугольники не имеют классификаций, основанных на их сторонах или углах для понятия сравнения и подобия. В.3 Сколько осей симметрии в равностороннем треугольнике? Ответ 3 В равностороннем треугольнике три оси симметрии. В.4 Всегда ли равносторонний треугольник равен 60 градусам? Ответ 4 Внутренние углы равностороннего треугольника всегда равны 60 градусам. В.5 В чем разница между равносторонним треугольником и равносторонним треугольником? Отв.
|


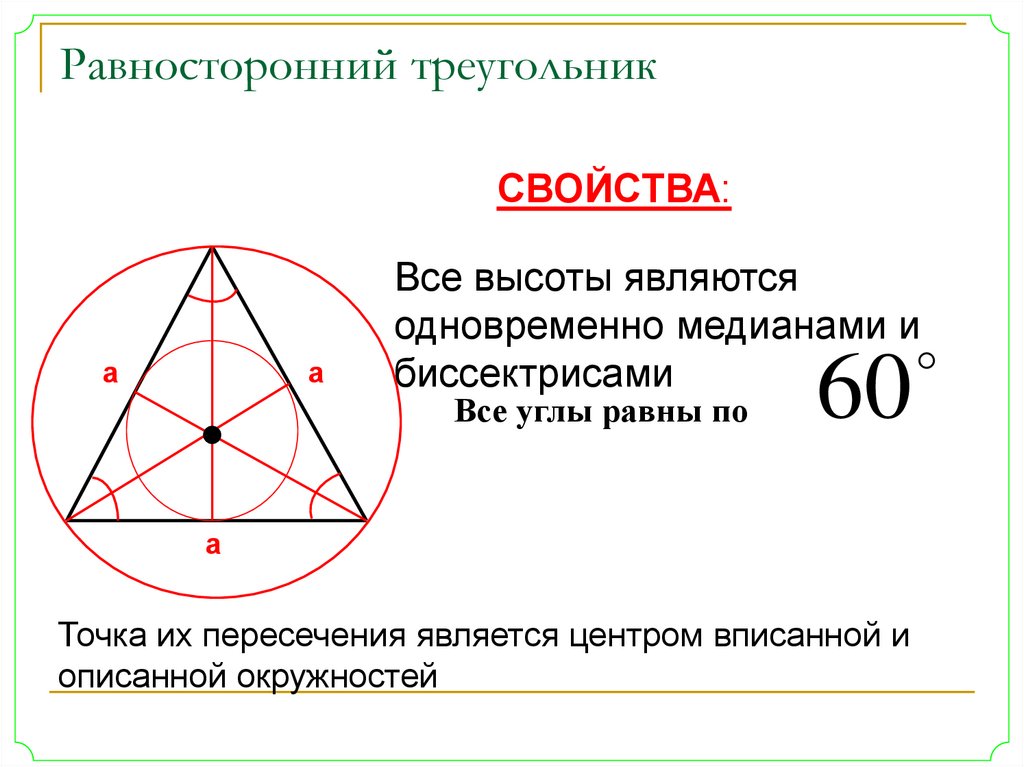

 рис.).
рис.).


 Оставайтесь с нами в приложении Testbook, чтобы узнать больше об обновлениях и темах, связанных с математикой и другими подобными предметами. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний о связанных экзаменах.
Оставайтесь с нами в приложении Testbook, чтобы узнать больше об обновлениях и темах, связанных с математикой и другими подобными предметами. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний о связанных экзаменах.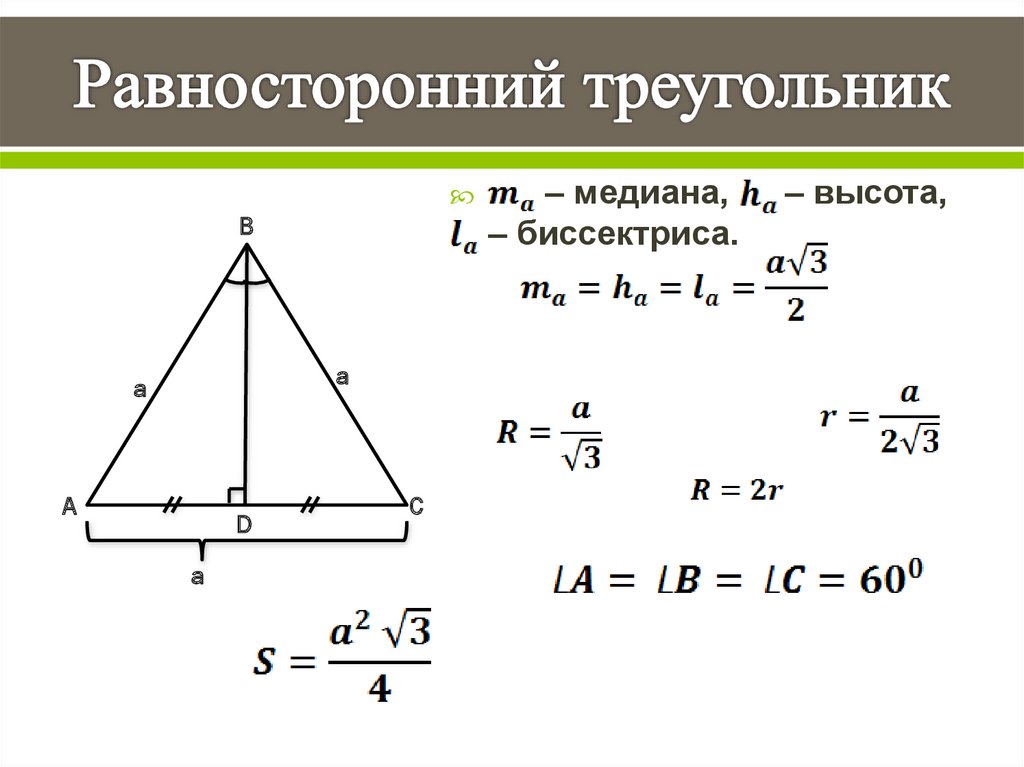 5 Равноугольный треугольник и равносторонний треугольник одинаковы, у них одинаковые внутренние углы.
5 Равноугольный треугольник и равносторонний треугольник одинаковы, у них одинаковые внутренние углы.
 Также угол вершины, из которой проведен перпендикуляр, делится на два равных угла, т.е. по 30 градусов каждый.
Также угол вершины, из которой проведен перпендикуляр, делится на два равных угла, т.е. по 30 градусов каждый.