Медиана треугольника – свойство, формула, определение
4.7
Средняя оценка: 4.7
Всего получено оценок: 412.
4.7
Средняя оценка: 4.7
Всего получено оценок: 412.
Медиана треугольника, так же, как и высота, служит графическим параметром, определяющим весь треугольник, значение его сторон и углов. Три значения: медианы, высоты и биссектрисы – это, как штрих-код на товаре, наша задача – просто уметь его считать.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки.
Свойства медиан
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой.
 В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами. - Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольников.
Равновеликими называют треугольники, площади которых равны.
- Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:
- В прямоугольном треугольнике известны катеты, которые равны a=3 и b=4. Найти значение медианы m, проведенной к гипотенузе c.
Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине.
$$m=\sqrt{{1\over2}*(49+81-64)}=\sqrt{33}$$ – оставим результат в виде корня.
- В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание – 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.
Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.
Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит, в треугольнике известны основание и высота. Можно найти площадь.
$$S={1\over2}*6*8=24$$
Площадь каждого из малых треугольников: $${24\over6}=4$$
Что мы узнали?
Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.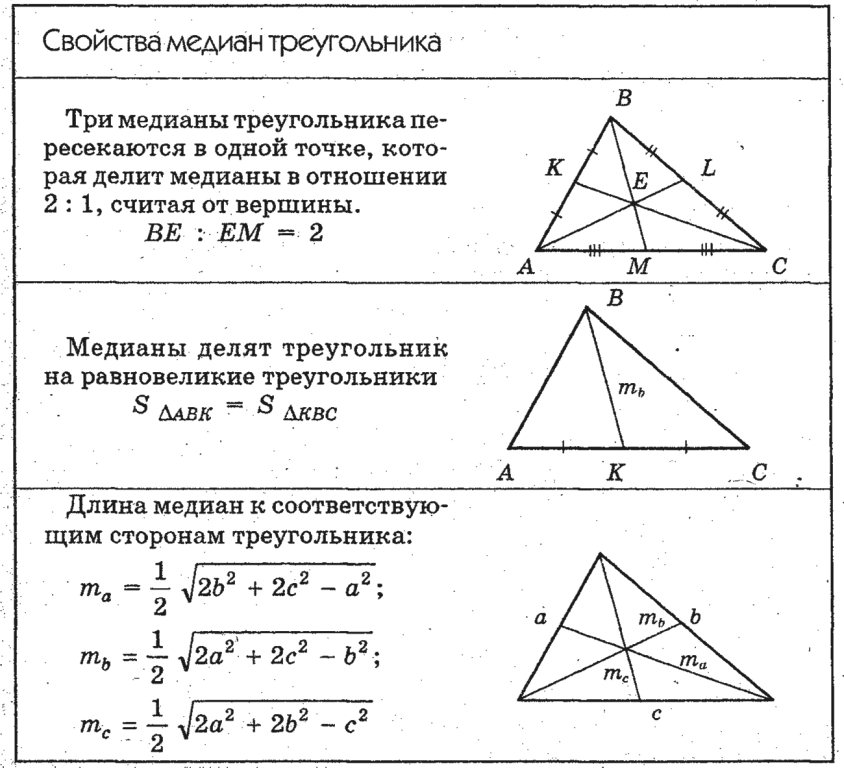
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Irina Semenova
10/10
Гульжан Дощанова
10/10
Татьяна Киприянова
10/10
Ольга Почивалова
9/10
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 412.
А какая ваша оценка?
что это такое в геометрии, ее свойства, как построить и найти
Определение медианы в треугольнике
Определение 1Медиана — важное понятие в геометрии. Это отрезок, проведенный из вершины треугольника, и делящий противоположную сторону пополам. Это «говорящее» название, оно произошло от латинского слова mediāna, что значит «середина».
На чертеже медиана выглядит так:
Красная линия — медиана. Для ΔABС отрезок АD — медиана к стороне BС, при этом BD=DC. Для ΔMNK NO — медиана из ∠MNK к NK, MO=OK.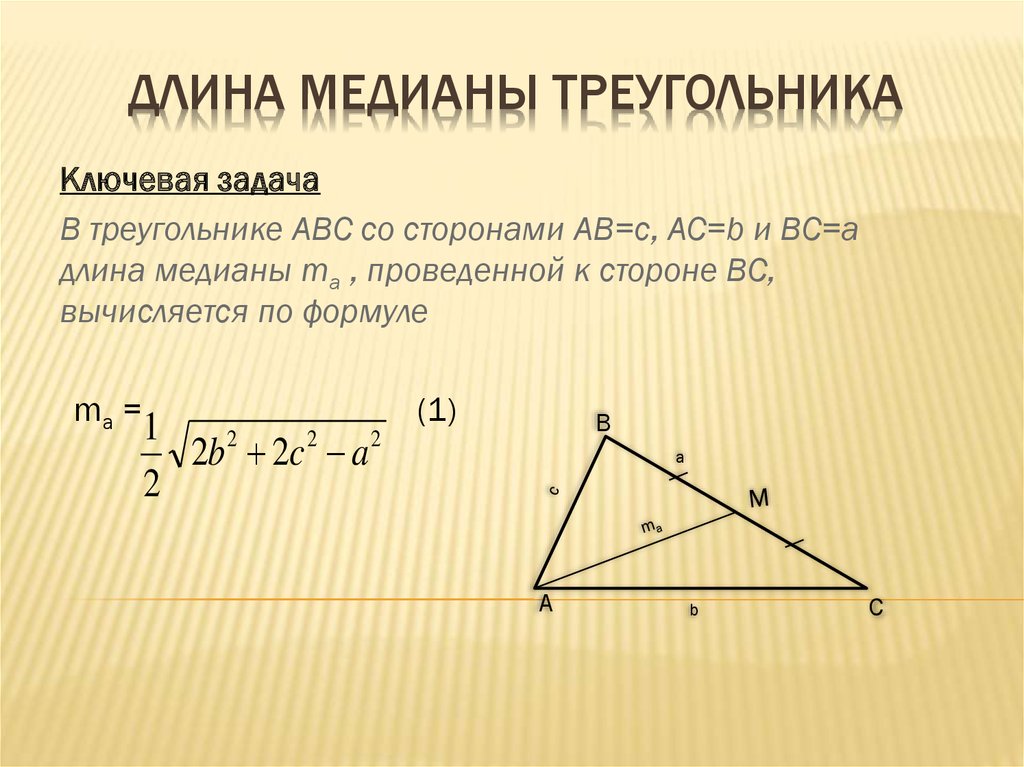 Равенство отрезков на рисунке обозначают одинаковым количеством черточек. Сколько медиан у треугольника? Их столько же, сколько и сторон, то есть три.
Равенство отрезков на рисунке обозначают одинаковым количеством черточек. Сколько медиан у треугольника? Их столько же, сколько и сторон, то есть три.
Характерные особенности медианы
Медиана обладает многими свойствами, ниже их краткое перечисление. Некоторые из них будут рассмотрены подробнее.
- Медиана треугольника делит его на два равновеликих треугольника:
- Все медианы треугольника пересекаются в одной точке и разбивают его на 6 треугольников одной площади.
- Медиана, проведенная из прямого угла прямоугольного треугольника, равна половине гипотенузы: CD=½AB=AD=BD.
- У правильного или равностороннего треугольника медиана является одновременно биссектрисой и высотой, проведенными из того же угла.
- У равнобедренного треугольника совпадают медиана, биссектриса и высота, которые проводятся к основанию.
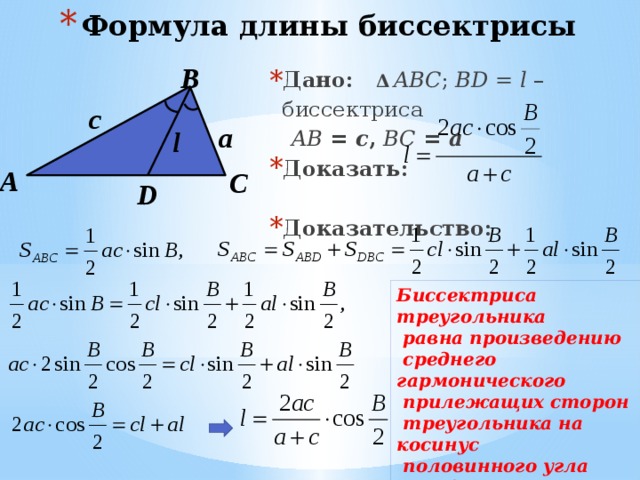
- Для нахождения длины медианы треугольника используется следующая формула: , где BD — медиана, а a, b и c — стороны треугольника.

Формулы и соотношения связанные с медианой
Пересечение медиан треугольника
Теорема 1Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1 от вершины.
Доказательство:
Строим медианы AD и CM треугольника ABC, пересекающиеся в точке О.
Найдем середины L и H отрезков ОA и ОC, и рассмотрим четырехугольник DHLM.
Его стороны MD и HL параллельны и равны как средние линии ΔABC и ΔAOC с общей стороной AC.
Из этого делаем вывод, что DHLM — параллелограмм.
Поскольку точка пересечения делит диагонали параллелограмма пополам, то OD = ОL.
L — середина отрезка ОA ⇒ AL = LO = ОD. Значит, AО:ОD = 2:1. Также CО:ОM = 2:1.
Остается доказать, что третья медиана BK проходит через точку О.
Пусть медианы BK и AD пересекаются в точке . Тогда по доказанному .
Учитывая, что и AO:OD=2:1, заключаем, что точки и О делят отрезок AD в одном и том же отношении.
А это значит, что точка совпадает с точкой О.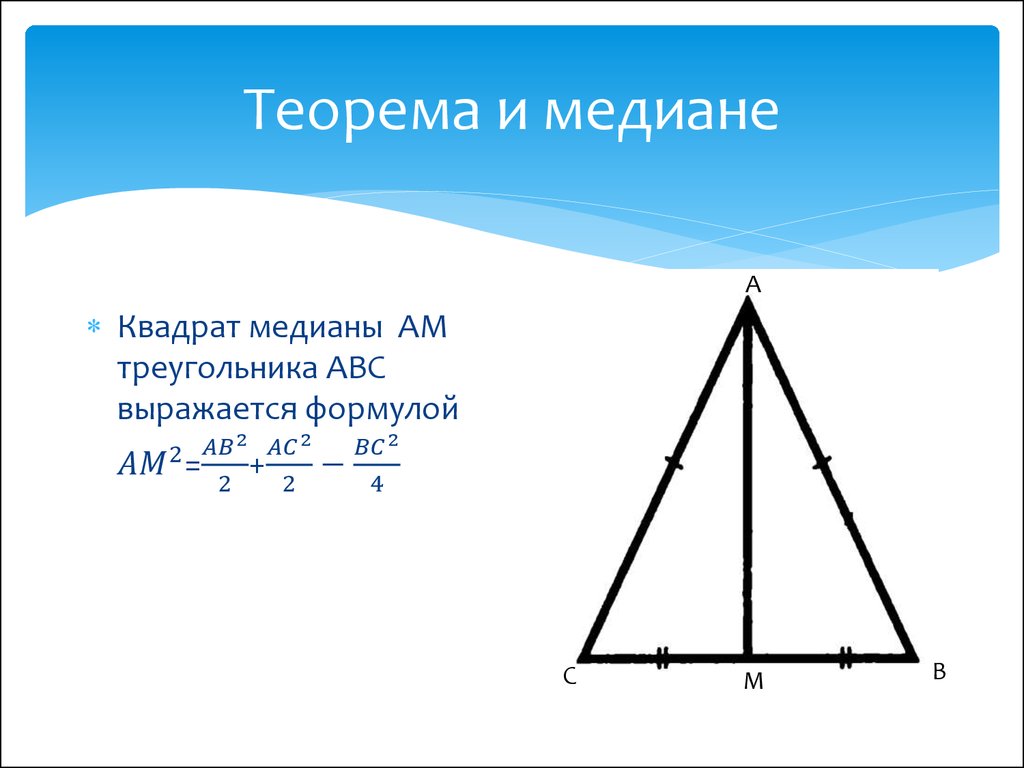
Из этого сделаем окончательный вывод: медиана BK проходит через точку О пересечения медиан AD и CM.
Теорема о трех медианах и шести равновеликих треугольниках
Теорема 2Три медианы треугольника пересекаются в одной точке и делят его на 6 треугольников с равной площадью.
Доказательство:
Докажем, что
- Построим медианы ΔABС.
- Из вершины B опустим перпендикуляр BP на медиану AD и рассмотрим по свойству медиан треугольника .
- Следующим шагом рассмотрим
- Из пунктов 2 и 3 следует, что
- AD — медиана
- Из двух предыдущих пунктов следует, что
- Аналогично доказываем, что
Пример нахождения и построения медианы
Для того чтобы узнать длину медианы, нужно знать:
- длины всех сторон треугольника;
- либо периметр и две стороны.
Дан ΔABC с известными сторонами АВ=9 см, СВ=8 см, АС=13 см. Необходимо вычислить длину медианы, построенной к наибольшей стороне.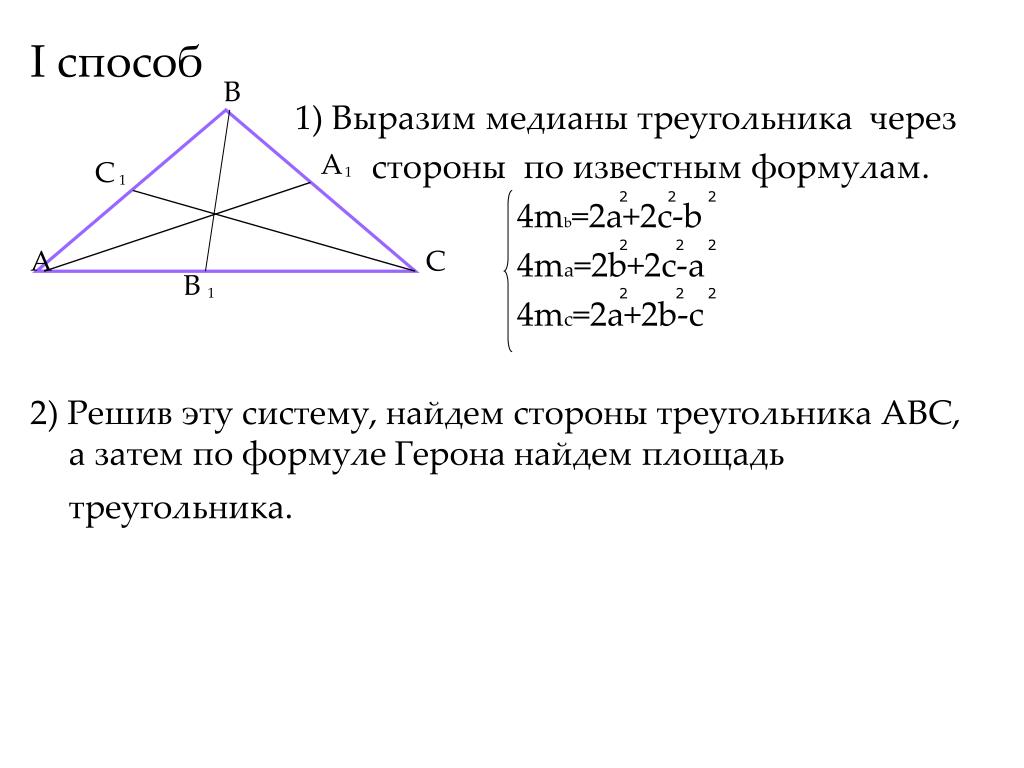
Решение: чтобы найти длину медианы, используют дополнительные построения. Продлим медиану BO ΔABC и построим параллелограмм. Отрезок BO равен ½ диагонали получившегося параллелограмма. Согласно теореме о диагоналях параллелограмма, сумма квадратов его диагоналей равна удвоенной сумме квадратов его сторон.
x=11.
Медиана равна половине найденной диагонали, 11:2=5,5 (см).
Ответ: 5,5 см.
Медиана треугольника – определение, формула, теорема, примеры
Медиана треугольника – определение, формула, теорема, примерыСодержание
Последнее изменение: 6 сентября 2022 г.
Оглавление
Определение
Медиана треугольника — это отрезок, соединяющий вершину с серединой стороны, противоположной этой вершине.
Свойства
Свойства медианы треугольника- Каждый треугольник имеет 3 медианы, по одной из каждой вершины; в △ABC, AD, BF и CE — три медианы
- Три медианы сходятся в одной точке, называемой центром тяжести треугольника. Центроид — это центр тяжести или центр масс треугольника; три медианы, м a , m b , & m c пересекаются в точке O, которая является центром тяжести данного треугольника
- Каждая медиана делит главный треугольник на 2 меньших треугольника, имеющих равную площадь. Таким образом, 3 медианы делят главный треугольник на 6 меньших треугольников равной площади; медиана AD образует треугольники △ABD и △ACD, медиана BF — в треугольники ABF и △CBF, медиана CE — в треугольники △CAE и △CBE
Формулы
Как найти медиану треугольника
длина медианы треугольника. Согласно теореме: «сумма квадратов любых двух сторон треугольника равна удвоенному квадрату половины третьей стороны и удвоенному квадрату медианы, делящей третью сторону пополам».
Соответственно, стандартные формулы для нахождения медианы треугольника приведены ниже:
Медиана треугольника ФормулаДавайте решим несколько примеров с участием различных типов треугольников.
Решенные примерыНайдите длины всех трех медиан треугольника со сторонами 6 см, 4 см и 2 см.
Решение:
Как известно,
m = √2b 2 + 2c 2 – a 2 /4, здесь a = 6 см, b = 4 см, c = 2 см
Теперь, складывая полученные значения,
m = √2(4) 2 + 2(2) 2 – ( 6) 2 /4
= √32 + 8 – 36/4
= √4/4 = 1 см
В данном треугольнике G – центр тяжести, а BC = 8 см. Решите значение BL.
Решение:
Для △ABC,
AL, BF и CE — медианы, а L — середина BC
Таким образом,
BL = 1/2BC
= ½ X 8
= 4 см
Найдите длину медианы равностороннего треугольника со стороной 9 см.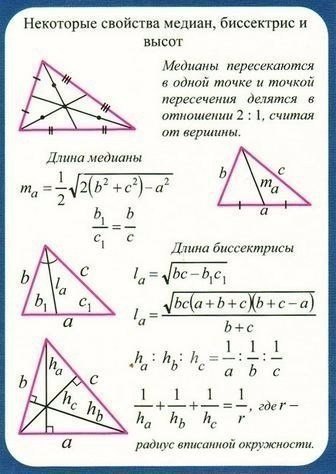
Решение:
Как известно,
Медиана (m) = a√3/2, здесь a = 9 см
= 9√3/2 [∵ √3= 1,732]
= 7,79 см
Медиана теоремы о треугольнике
Медиана теоремы о треугольникеПоследнее изменение: 6 сентября 2022 г.
Медиана треугольника (формулы, примеры и видео)
Автор:
Malcolm McKinsey
Факт проверен
Пол Маццола
Медиана треугольника (определение, формула и примеры)
Математическое слово «медиана» имеет разные значения при различных операциях. В статистике это значение, лежащее в середине набора данных.
Таким образом, для набора данных {3, 5, 7, 9, 11} , 7 является медианой. В геометрии медиана — это отрезок прямой от внутреннего угла треугольника до середины противоположной стороны.
Изучение геометрической медианы может облегчить вашу жизнь в геометрии и, возможно, на кухне.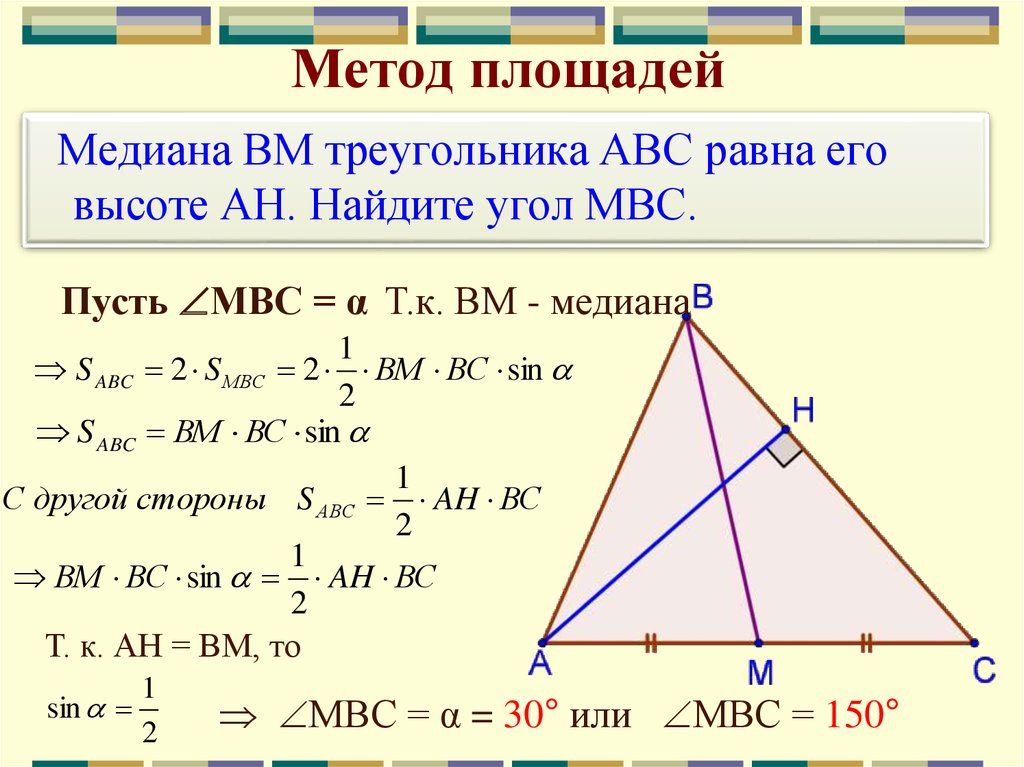
Треугольник
Любой треугольник является многоугольником с тремя прямыми сторонами, ограничивающими пространство. Треугольники, названные по их углам, могут быть остроугольными или тупоугольными (которые группируются как косоугольные треугольники) или прямоугольными треугольниками. Треугольники, названные по их сторонам, могут быть разносторонними, равнобедренными или равносторонними.
Зона
Зона – пространство, занимаемое многоугольником в двух измерениях. Каждый треугольник имеет внутреннее пространство, которое является площадью треугольника. Эта площадь всегда измеряется в квадратных единицах, независимо от того, какую форму вы измеряете.
Вот формула площади треугольника:
Что такое медиана треугольника?
Если вы нашли середину любой стороны треугольника, вы нашли его середину. От этой средней точки можно построить отрезок к противоположному внутреннему углу. Эта построенная линия от середины стороны до противоположного внутреннего угла представляет собой медиана .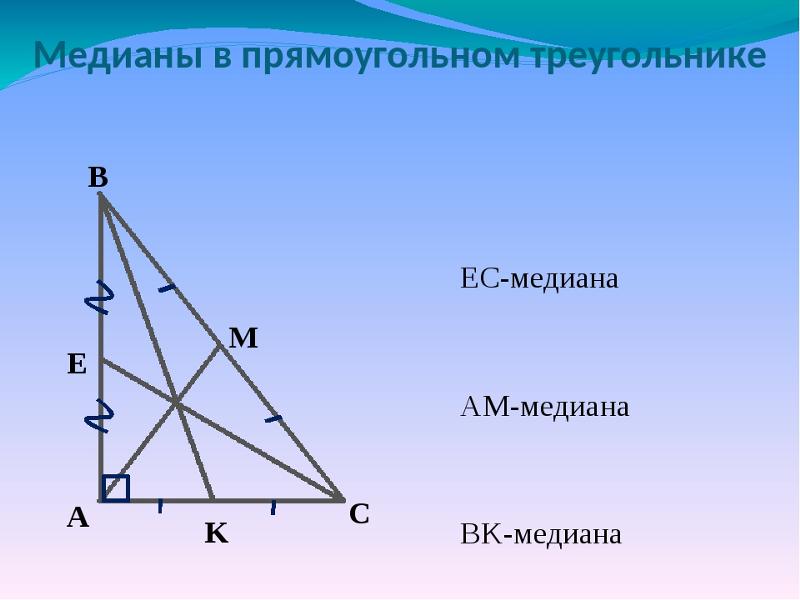
Поскольку у треугольника всегда три стороны, у него всегда три медианы.
Центроид треугольника
Там, где медианы пересекаются, точка, общая для всех трех медиан, называется центроидом . Центроид – это точка параллелизма . всегда будет внутри треугольника, в отличие от других точек параллелизма, таких как ортоцентр.
Медианы, сходящиеся в центроиде, обладают особым свойством. Центроид всегда находится на расстоянии двух третей пути вдоль каждой медианы от внутреннего угла этой медианы. Это означает, что он устанавливает 2:1 соотношение для каждой из трех медиан:
Центр масс
Центр тяжести треугольника не является чисто теоретическим. Это центр масс или центр тяжести треугольника. Нарисовав все три медианы, вы сможете найти точное место, где физически существующий треугольник будет идеально сбалансирован!
Это может иметь для вас практическое применение, если вы имеете дело с треугольниками, вырезанными из картона или дерева.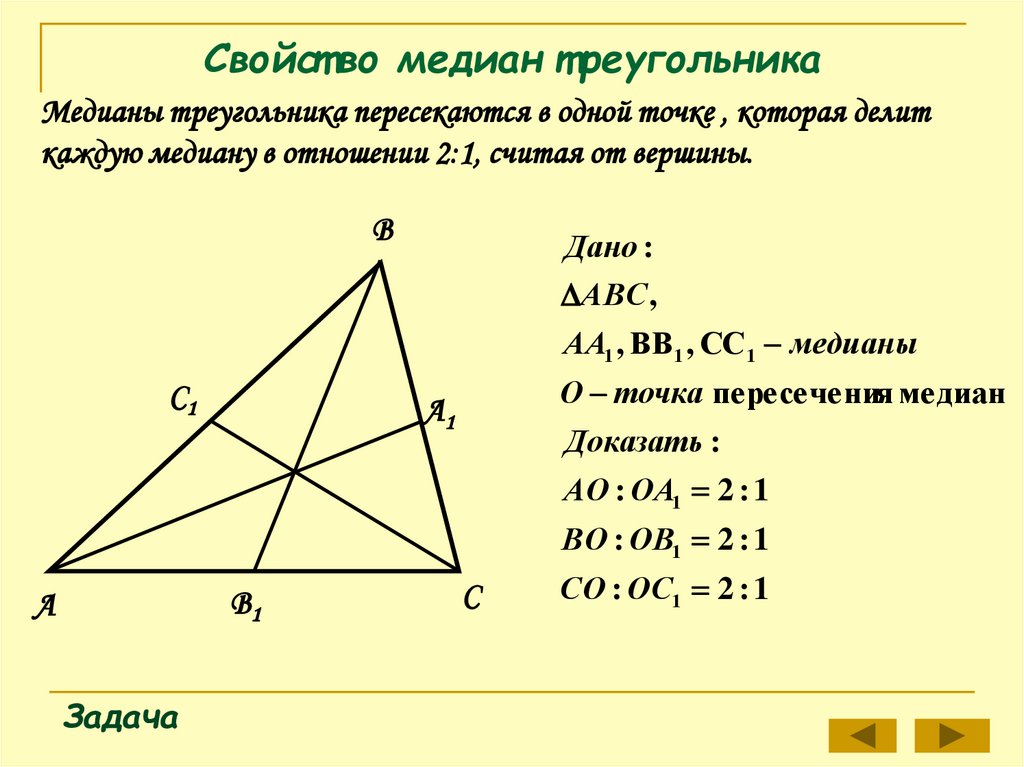 Вы можете найти центр тяжести и сбалансировать треугольник кончиком карандаша или кончиком пальца.
Вы можете найти центр тяжести и сбалансировать треугольник кончиком карандаша или кончиком пальца.
Как найти медиану треугольника
Теорема, называемая Теорема Аполлония , может дать вам длину медианы треугольника. Это немного многословно, но может быть переведено в формулу. Во-первых, теорема:
Теорема Аполлония утверждает, что в любом треугольнике сумма квадратов любых двух сторон равна удвоенному квадрату половины третьей стороны вместе с удвоенным квадратом медианы, которая делит третью сторону пополам.
В виде формулы это выглядит так, где a , b и c длины сторон и м медиана от внутреннего угла A до стороны a :
Медиана треугольника пример
A 900 линия, разделяющая исходный треугольник на два меньших треугольника равной площади. Эта особенность медианы может пригодиться.
Здесь у нас есть △EAT , пицца с разносторонними треугольниками, приготовленная в начале науки о семье и потреблении.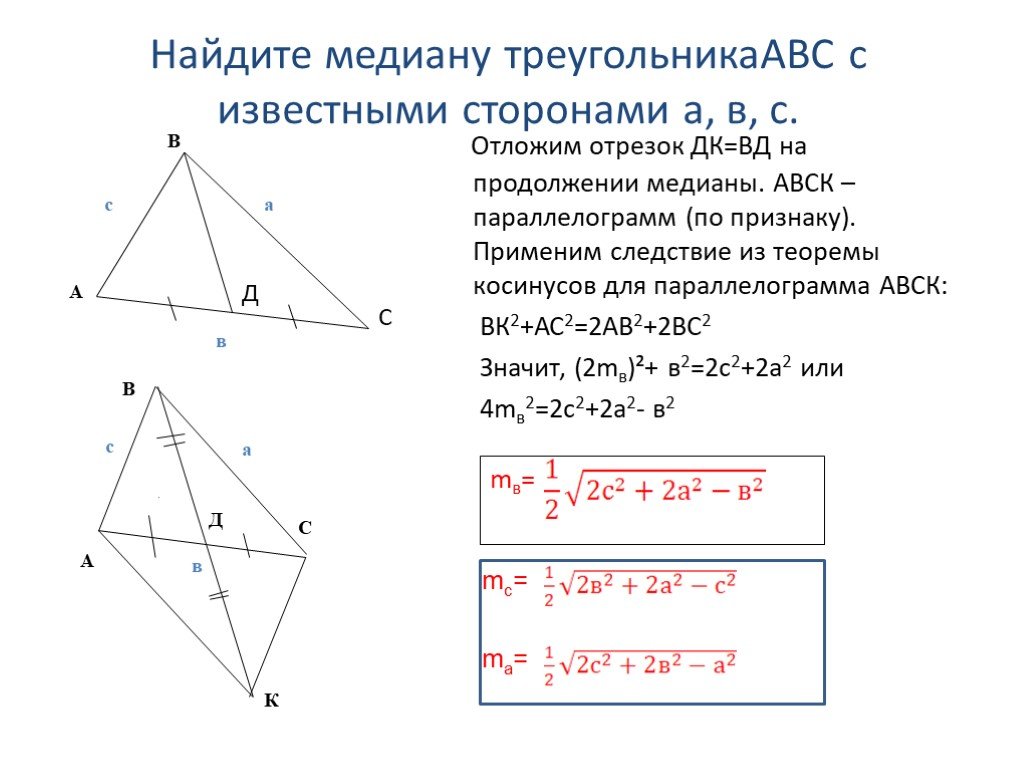

 В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.