Транспортная задача онлайн
Данный онлайн калькулятор решает транспортную задачу. Дается подробное решение с пояснениями. Для решения транспортной задачи задайте количество подставщиков и количество магазинов. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите на странице Транспортная задача. Методы решения.
| Количество строк (поставщики): | m= | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Кол. столбцов (пункты назначения) : столбцов (пункты назначения) : | n= | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
| |||||||||||||||||||||||||||||
Метод нахождения первого опорного плана: Метод северно-западного угла Метод минимального элемента Метод аппроксимации Фогеля
Метод определения оптимального плана: Метод потенциалов
Очистить все ячейки?
Результат уже получен!
Инструкция ввода данных. Числа вводятся в виде целых неотрицательных чисел (примеры: 487, 5, 7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (a≥0, b>0) целые или десятичные неотрицательные числа. Примеры 45/5, 6.6/76.4, 7/6.7 и т.д.
Числа вводятся в виде целых неотрицательных чисел (примеры: 487, 5, 7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (a≥0, b>0) целые или десятичные неотрицательные числа. Примеры 45/5, 6.6/76.4, 7/6.7 и т.д.
- Новые калькуляторы
- Инженерный калькулятор онлайн
- Решение треугольников онлайн
- Радиус описанной окружности около треугольника онлайн
Методы северо-западного угла, минимального элемента, Фогеля и двойного предпочтения
- Метод северо-западного угла
- Метод минимального элемента
- Метод Фогеля
- Метод двойного предпочтения
Метод северо-западного угла
Рассмотрим метод северо-западного угла. Сущность его состоит в
следующем. Будем распределять груз в
таблице, начиная с загрузки левой верхней, условно называемой
«северо-западной», клетки (1,1), двигаясь затем от нее по строке вправо или по
столбцу вниз. В клетку (1,1) занесем меньшее из чисел
,
то есть
.
Если
,
то
и первый потребитель
будет полностью удовлетворен. В дальнейшем 1-й
столбец таблицы в расчет не принимается: в нем переменные
для
.
В клетку (1,1) занесем меньшее из чисел
,
то есть
.
Если
,
то
и первый потребитель
будет полностью удовлетворен. В дальнейшем 1-й
столбец таблицы в расчет не принимается: в нем переменные
для
.
Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1,2) меньшее из чисел и , то есть . Если , то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика.
Если
,
то
.
При этом запас первого поставщика будет исчерпан, а потому
для
.
Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению
запасов второго поставщика. В клетку (2,1) заносим наименьшее из чисел
.
Заполнив таким образом клетку (1,2) или (2,1), переходим к загрузке следующей клетки по второй строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам (столбцам) производится аналогично распределению по первой строке или по первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка .
Задача 1
Однородный продукт, сосредоточенный на трех складах фирмы в количествах единиц, необходимо распределить между четырьмя магазинами, которым необходимо соответственно единиц продукта. Стоимость перевозки единицы продукта из i-го пункта отправления (i = 1, 2, 3) в j-й пункт назначения (j = 1, 2, 3, 4) равна и известна для всех маршрутов.
Вектор запасов продукта на складах
вектор запросов продукта магазинами
и матрица транспортных тарифов
Построить начальный опорный план транспортной задачи методом
северо-западного угла.
Решение
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи закрытая.
Построим начальный опорный план по правилу северо-западного угла.
Начинаем заполнение с левого верхнего угла и далее двигаемся по диагонали к правому нижнему углу.
Число занятых клеток должно быть .
В нашем случае число занятых клеток равно 6 — опорный план является невырожденным.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении оптимального плана перевозок, производится методом потенциалов .
Метод минимального элемента
Рассмотрим правило
минимального элемента. Сущность его состоит в следующем. Просматриваются
тарифы таблицы и в первую очередь заполняется клетка с минимальным
значением тарифа. При этом в клетку записывается максимально возможное значение
поставки. Затем из рассмотрения исключают строку, соответствующую поставщику,
запасы которого полностью израсходованы, или столбец, соответствующий
потребителю, спрос которого полностью удовлетворен. После этого из оставшихся
клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс
распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос
потребителей полностью удовлетворен. В результате получаем опорный план,
который должен содержать
загруженных
клеток.
Сущность его состоит в следующем. Просматриваются
тарифы таблицы и в первую очередь заполняется клетка с минимальным
значением тарифа. При этом в клетку записывается максимально возможное значение
поставки. Затем из рассмотрения исключают строку, соответствующую поставщику,
запасы которого полностью израсходованы, или столбец, соответствующий
потребителю, спрос которого полностью удовлетворен. После этого из оставшихся
клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс
распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос
потребителей полностью удовлетворен. В результате получаем опорный план,
который должен содержать
загруженных
клеток.
В процессе заполнения
таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда
полностью исчерпывается запас груза и полностью удовлетворяется спрос
(вырожденная задача). В этом случае в свободные клетки надо записать число 0 –
«нуль загрузка», условно считая эту клетку занятой. Однако число 0 записывается
в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Однако число 0 записывается
в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Задача 2
На предприятиях производится однородная продукция в количестве единиц. Себестоимость производства одной единицы продукции на i-м предприятии равна соответственно ден.ед. Готовая продукция поставляется потребителям , потребности которых составляют единиц. Для полного удовлетворения потребностей необходимо увеличить выпуск продукции. Для этого освоить выпуск данной продукции на предприятии с себестоимостью производства продукции ден.ед. Стоимости перевозки одной единицы продукции от каждого предприятия каждому потребителю задаются матрицей .
Требуется построить начальный опорный план транспортной задачи методом минимального элемента.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Условие баланса:
В нашем случае:
Вводим дополнительного поставщика , у которого имеется 2600-1800=800 единиц груза.
Составим матрицу затрат на производство и транспортировку продукции.
Построим начальный опорный план по правилу минимального элемента.
Просматривая таблицу замечаем, что наименьшие затраты соответствуют маршруту (2,4), поэтому в клетку помещаем . В этом случае 2-я строка в расчет не принимается. Просматриваем оставшиеся таблицы клетки. Наименьший тариф имеет клетка (4,3).
Далее, действуя по аналогичной схеме, получаем:
Число занятых клеток должно быть .
В нашем случае число занятых клеток равно 7 — опорный план является невырожденным.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.
Метод Фогеля
Сущность его состоит в следующем. В таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность рамкой. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и по выше рассмотренным правилам.
Задача 3
Ниже приведены числовые данные транспортной задачи. Стоимость перевозки единицы продукции записана в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу.
Требуется построить начальный план методом Фогеля.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи закрытая.
Воспользуемся способом Фогеля для нахождения начального опорного плана транспортной задачи. В каждом ряду и столбце матрицы найдем минимальный и ближайший к нему элементы и их разность по абсолютной величине записываем в конце соответствующего ряда справа и снизу. Находим максимальную из этих разностей (число 29 заключено в рамку). В ряду (или столбце), соответствующем максимальной разности, находим минимальный элемент . В клетку (3,5) вписываем число
С оставшейся матрицей поступаем аналогично предыдущему. Все вычисления сведены в таблицу.
Получили начальный опорный план транспортной задачи методом Фогеля.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.
Метод двойного предпочтения
Суть метода двойного предпочтения отражена в его названии. В таблице найдем наименьшие элементы в каждой строке и в каждом столбце. Поставим в соответствующую клетку знак *. Если встречаются такие клетки, отмеченные двумя знаками, то их заполняем в первую очередь. Распределение груза производится, как и по выше рассмотренным правилам.
Задача 4
Составить план перевозки зерна из районов на пять элеваторов (запасы районов и мощности элеваторов приведены) с минимальными издержками за перевозку. Затраты на перевозку 1 ц заданы.
Начальный план перевозок составить по правилу двойного предпочтения.
Решение
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи
закрытая.
Заполняем таблицу по правилу двойного предпочтения.
Сначала в каждой строке находим клетку с минимальным тарифом. Если таких клеток несколько (одинаковые значения) то выбираем их все. В выбранных ячейках ставим отметку *.
Затем выполняем те же самые действия, только на тот раз по столбцам. То есть в каждом столбце тоже находим клетку (клетки) с минимальным тарифом и ставим в ней отметку – *.
Начинаем заполнять транспортную таблицу. В первую очередь заполняем ячейки с двумя звездочками (если их несколько, выбираем ту в которой меньший тариф). Далее заполняем клетки с одной звездочкой. Если остались нераспределенные запасы и неудовлетворенные потребности – заполняем оставшиеся клетки без звездочек.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении
оптимального плана перевозок, производится
методом потенциалов
.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
25 лет я занимаюсь решением задач и потратил на это кучу времени. Вы можете освободить свое, стоит только обратиться за помощью.
Метод Фогеля — Энциклопедия по экономике
Рассмотрим три метода нахождения начального решения транспортной задачи метод «северо-западного» угла, метод минимального элемента и метод Фогеля. [c.340]В методе Фогеля используются штрафы, взимаемые за неудачный выбор маршрута. Рассчитанные на шаге 2 разности между двумя уровнями затрат на перевозку являются штрафами за неверно выбранный маршрут перевозки. [c.342]
Метод Фогеля — наиболее трудоемкий, однако начальный план перевозок, построенный с его использованием, обычно бывает близок к оптимальному плану, а в некоторых случаях является оптимальным планом. [c.342]
[c.342]
Решим транспортную задачу методом Фогеля. В каждой строке и столбце матрицы кратчайших расстояний найдем два наименьших элемента и определим абсолютную разность между ними. Например, для первой строки, относящейся к первому пункту погрузки, значения наименьших элементов равны 10 км, таким образом, разность равна нулю. Затем выбираем наибольшую величину разности в строке разностей и в клетку с минимальным элементом заносим максимально возможную загрузку, учитывая при этом ресурсы поставщика и спрос потребителя. При наличии двух одинаковых наибольших разностей загрузку записывают в клетку, имеющую наименьший элемент (табл. 10.24). Если окажется, что спрос потребителя полностью удовлетворен или ресурс поставщика полностью исчерпан, то данная строка или столбец из дальнейшего рассмотрения исключается. [c.348]
| Таблица 8.12 Пример нахождения опорного плана методом Фогеля |
 40-8.43 [c.305]
40-8.43 [c.305]Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла — наихудшее. [c.70]
На каждом шаге метода Фогеля для каждой i-й строки вычисляются штрафы d как разность между двумя наименьшими тарифами строки. Таким [c.71]
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы (см. табл. 5.3) [c.75]
Т.к. d2i > d32 то выбираем на первом шаге для заполнения клетку (2,1). Опорный план Хф, найденный методом Фогеля [c.75]
Шаг 1. Получение начального плана перевозок по методу «северо-западного» угла, минимального элемента, Фогеля или любым другим методом. [c.343]
[c.343]
Первым этапом этого алгоритма является начальное распределение (составление начального плана перевозок). Для этого имеется ряд методов северо-западного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Второй этап — построение системы потенциалов на основе равенства (25.33), а третий — проверка начального плана на оптимальность, причем в случае его неоптимальности переходят к четвертому этапу, содержание которого заключается в реализации так называемых циклов перераспределения плана прикрепления потребителей к поставщикам, после чего переходят опять к третьему этапу. Совокупность процедур четвертого и третьего этапов образует одну итерацию, и эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (25.29) [c.526]
Существует много частных способов (например, способ Фогеля, методы потенциалов, дифференциальных рент, способ Лебедева — Тихомирова, венгерский метод и др.), а также универсальных методов (например, алгоритм симплекс-метода) решения задач линейного программирования с такого рода условиями.
 Представляет интерес, как сам результат вычисления, так и его интерпретация.
[c.246]
Представляет интерес, как сам результат вычисления, так и его интерпретация.
[c.246]Для решения транспортной задачи — метод аппроксимации Фогеля, являющийся способом составления первого допустимого плана. Полученное распределение, особенно при небольшой размерности задачи, является оптимальным или достаточно близким к нему. [c.347]
Первый вариант — отсутствие складов. В этом случае решается классическая транспортная задача закрепления п потребителей за т поставщиками. Расстояние между объектами определяется как корень квадратный из суммы квадратов разностей их координат, см. формулу (11.9). Для распределения объемов перевозок используется ускоренный алгоритм Фогеля с последующим поиском оптимального варианта — минимума транспортной работы методом потенциалов. [c.398]
Как известно, метод потенциалов позволяет за конечное число шагов найти оптимальный план, следовательно, желательно, чтобы первый опорный план был ближе к оптимальному. Способ получения опорного плана, предложенный американским ученым У. Фогелем, позволяет найти практически оптимальный план. Найденный план или совпадение с оптимальным, или незначительно от него отличается.
[c.286]
Фогелем, позволяет найти практически оптимальный план. Найденный план или совпадение с оптимальным, или незначительно от него отличается.
[c.286]
Однако, указав на возможность применения линейного программирования, Р. Фогель использует в работе другой, более простой, хотя, быть может, и менее точный метод. Вычисление общественного сбережения ведется по формуле [c.291]
Интересно отметить, что у Р. Фогеля были достаточно правдоподобные данные о закупках пшеницы двумя районами. Проведя для этих районов изложенные выше вычисления, Р. Фогель получил показатели, очень близкие к имеющимся, что говорит о неплохой точности предложенного метода. [c.292]
Более легкая из этих проблем — обработка количественных данных — почти всегда решается с помощью математической техники. При этом, как видно у Р. Фогеля, эффективными могут оказаться даже самые простые методы вычисление процентных отношений, средних, индексов и т. д. Вместе с тем в зависимости от поставленной задачи исследователям приходится обращаться и к более сложным математическим построениям. Чаще всего при этом используется регрессионный анализ, позволяющий измерять взаимосвязи между самыми различными явлениями и процессами, выраженными количественно. Так, в книге П. Мак-
[c.310]
Чаще всего при этом используется регрессионный анализ, позволяющий измерять взаимосвязи между самыми различными явлениями и процессами, выраженными количественно. Так, в книге П. Мак-
[c.310]
Другой интересный математический метод— линейное программирование, предложенное Р. Фогелем для вычисления межобластного общественного сбережения . [c.311]
В начале 1968 г, Э. Фогель-младший, который в то время был вице-президентом по сбыту, фирмы Anheuser-Bus h, предложил группе исследователей заняться решением проблем, связанных с рекламой, и обратить особое даимание на качество рекламных сообщений. Группа начала свою работу с изучения организаций, занимающихся. оценкой рекламных сообщений О каждой из них был собран большой объем информации, на основе которой было отобрано несколько организаций для более тщательного анализа. Затем исследователи посетили каждую такую организацию и ознакомились с методами ее работы. В результате одному из рекламных агентств, методы работы которого группа считала наиболее правильными, было сделано следующее предложение исследователи проводят экспериментальную проверку оценок агентством рекламных сообщений, и если результаты окажутся благоприятными, то агентство может использовать их по своему усмотрению в противном случае в печать не поступает никакой информации о проведенном исследовании. Предложение было принято.
[c.185]
Предложение было принято.
[c.185]
Норт (Nort) Дуглас (р. 1920), американский экономист, один из основателей направления институционализма (см. Институциональный подход) в экономике. Лауреат Нобелевской премии по экономике 1993 г. Формула награждения «за работы в области новой экономической истории» (совместно с Р. Фогелем). Образование (включая докторскую степень) получил в Калифорнийском университете (Беркли). Профессор Вашингтонского университета в Сиетле и университета Вашингтона в Сент-Луисе. Исследовал вопросы экономического роста и роль в нем государственных и иных институтов, является ведущим исследователем т.н. клиометрии — исторической науки, использующей методы математико-статистического анализа и математического моделирования. [c.446]
Лит. Ч а р н с А., Купер В. и ХендерсонА., Введение в линейное программирование, [пер. с англ.], М., I960 Г е р ч у к Я., Проблемы оптимального планирования (Линейное программирование), М., 1961 Ю д и н Д. Б., Г о л ь т т е и н Е. Г., Задачи и методы линейного программировании, М., 1961 Рейнфельд Н., Фогель У., Математическое программирование, [пер. с англ.], М., 1960. . Я. П. Герчук.
[c.23]
Г., Задачи и методы линейного программировании, М., 1961 Рейнфельд Н., Фогель У., Математическое программирование, [пер. с англ.], М., 1960. . Я. П. Герчук.
[c.23]
Норт Д. (р. 1920) — американский экономист, один из основателей институционализма в экономике. Лауреат Нобелевской премии по экономике 1993 г. за работы в области новой экономической истории (совместно с Р. Фогелем). Исследовал вопросы экономического роста и роль в нем государственных и иных институтов. Является ведущим исследователем так называемой клиометрии — исторической науки, использующей методы математико-статистического анализа и математического моделирования. [c.47]
В середине 50-х и начале 60-х годов нашего века в американской экономической истории сформировалось новое направление, которое сейчас называется новой экономической историей , или эконометрической историей . Объекты исследований представителей нового направления не отличаются от традиционных тем экономической истории. В обоих случаях главный интерес сосредоточен на изучении экономического развития. Отход же от прошлого, который и позволил новой экономической истории выделиться в самостоятельное направление, заключается в использовании иных, не применявшихся ранее методов исследования. Такими отличительными методическими чертами, по мнению одного из ведущих представителей эконометриче-ского направления, Роберта Фогеля, являются 1) статистическая ориентированность новой экономической истории , 2) приложение экономической теории к изучению экономической истории и 3) попытка дать все объяснения прошлого экономического развития в форме обоснованных гипотетических дедуктивных моделей х.
[c.283]
Отход же от прошлого, который и позволил новой экономической истории выделиться в самостоятельное направление, заключается в использовании иных, не применявшихся ранее методов исследования. Такими отличительными методическими чертами, по мнению одного из ведущих представителей эконометриче-ского направления, Роберта Фогеля, являются 1) статистическая ориентированность новой экономической истории , 2) приложение экономической теории к изучению экономической истории и 3) попытка дать все объяснения прошлого экономического развития в форме обоснованных гипотетических дедуктивных моделей х.
[c.283]
Чтобы исключить это завышение-, Р. Фогель предлагает другой метод вычисления общественного сбережения для внутриобластного случая. Без железных дорог из-за высокой цены фургонных перевозок ведение товар ного сельского хозяйства продолжалось бы только на землях, лежащих не дальше некоторого расстояния от водных путей. Определение этого расстояния выявит зоны, в которых сохранилось бы производство продуктов на продажу. А зная эти зоны, можно было бы разбить вычисление общественного сбережения на две части 1) вычислить разницу между ценой перевозок продуктов с ферм, лежащих внутри зон товарного производства , на рынки, которая действительно была в 1890 г., и ценой перевозки тех же объемов тех же товаров между теми же пунктами, но в случае отсутствия железных дорог (фактически это оценка а для зон товарного производства) 2) определить потерю в национальном доходе, вызванную сокращением товарного сельскохозяйственного производства. Сумма этих двух чисел и даст новую оценку общественного сбережения .
[c.298]
А зная эти зоны, можно было бы разбить вычисление общественного сбережения на две части 1) вычислить разницу между ценой перевозок продуктов с ферм, лежащих внутри зон товарного производства , на рынки, которая действительно была в 1890 г., и ценой перевозки тех же объемов тех же товаров между теми же пунктами, но в случае отсутствия железных дорог (фактически это оценка а для зон товарного производства) 2) определить потерю в национальном доходе, вызванную сокращением товарного сельскохозяйственного производства. Сумма этих двух чисел и даст новую оценку общественного сбережения .
[c.298]
Количественный подход к решению различных проблем в настоящее время довольно широко практикуется во многих разделах американской исторической науки. Как видно из приведенного сообщения, в экономической истории этот подход проявился в форме новой экономической истории . Несомненно, использование числовой информации, применение ЭВМ и математических методов для ее обработки — все это способно оказать существенную помощь в исторических исследованиях. Однако, какой бы совершенной ни была используемая методика, ее эффективность и полезность определяются прежде всего теми методологическими концепциями, которыми руководствуется исследователь. Работы американских историков строятся на традиционной для историографии США буржуазной методологии. Именно в этом следует видеть главную причину ряда выводов, полученных на основе применения количественного аппарата некоторыми представителями новой, экономической истории . Мы имеем в виду, например, работы Дж. Мейера и А. Конрада, Я- Ясубы, С. Энгер-мана, Р. Фогеля 20, в которых количественный анализ
[c.318]
Однако, какой бы совершенной ни была используемая методика, ее эффективность и полезность определяются прежде всего теми методологическими концепциями, которыми руководствуется исследователь. Работы американских историков строятся на традиционной для историографии США буржуазной методологии. Именно в этом следует видеть главную причину ряда выводов, полученных на основе применения количественного аппарата некоторыми представителями новой, экономической истории . Мы имеем в виду, например, работы Дж. Мейера и А. Конрада, Я- Ясубы, С. Энгер-мана, Р. Фогеля 20, в которых количественный анализ
[c.318]
Решение закрытой транспортной задачи с дополнительными условиями средствами Python / Хабр
Постановка задачи
Необходимость решения транспортных задач в связи с территориальной разобщённостью поставщиков и потребителей очевидна. Однако, когда необходимо решить транспортную задачу без дополнительных условий это как правило не является проблемой поскольку такие решения достаточно хорошо обеспечены как теоретически, так и программными средствами.
Решение закрытой транспортной задачи средствами Python с классическим условиями для поставщиков и потребителей товара приведено в моей статье “Решение задач линейного программирования с использованием Python” [1].
Реальная транспортная задача усложняется дополнительными условиями и вот некоторые из них. Ограниченная грузоподъёмность транспорта, не учитываемые задержки при оформлении груза на таможне, приоритеты и паритеты для поставщиков и потребителей. Поэтому решение закрытой транспортной задачи с учётом дополнительных условий и стало целью данной публикации.
Алгоритм решения транспортной задачи с классическими условиями
Рассмотрим пример исходных данных в виде таблицы (матрицы).
где C= [7,3,6,4,8,2,1,5,9]– список стоимости перевозки единицы товара от заказчиков к потребителям; X – список объёмов перевозимых товаров, обеспечивающих минимальные затраты; a= [74,40,36] – список объёмов однородных товаров на складах поставщиков; b= [20,45,30] – список объёмов спроса заказчиками однородных товаров.
Задача закрытая поскольку sum(a)> sum(b), поэтому для X из строк таблицы запишем неравенства ограниченные сверху, а для X из столбцов таблицы равенства. Для дальнейшей обработки возьмём полученные соотношения в скобки и приравняем их переменным.
mass1 = (x[0] + x[1] +x[2] <= 74)
mass2 = (x[3] + x[4] +x[5] <= 40)
mass3 = (x[6] + x[7] + x[8] <= 36
mass4 = (x[0] + x[3] + x[6] == 20
mass5 = (x[1] +x[4] + x[7] == 45)
mass6 = (x[2] + x[5] + x[8] == 30)
Приведенная система из шести переменных является типовой для транспортной задачи, остаётся определить функцию цели, которая с учётом списка С для коэффициентов и переменных mass будит иметь вид:
problem =op(C[0]*x[0] + C[1]*x[1] +C[2]* x[2] +C[3]*x[3] + C[4]*x[4] +C[5]* x[5]+C[6]*x[6] + C[7]*x[7] +C[8]* x[8], [mass1, mass2, mass3, mass4, mass5, mass6,x_non_negative])
Следует отметить возможности некоторых решателей по введению ограничений сразу на все переменные Х, например, добавлением к общим условиям условия не отрицательности –x_non_negative.
Формирование дополнительных условий для закрытой транспортной задачи
Причины этих условий могут быть различными, например, ограниченная грузоподъёмность транспорта, не учитываемые задержки при оформлении груза на таможне, приоритеты и паритеты для поставщиков и потребителей. Поэтому мы будем указывать только субъектов и характер ограничения.
Для дальнейшего использования пронумеруем следующие дополнительные условия к закрытой транспортной задаче.
1.Установка заданного объёма поставки товара от определённого поставщика определённому заказчику.
Для этого вводиться новая переменная с соответствующим ограничением. Например первый поставщик должен поставить второму заказчику ровно 30 единиц товара– mass7 = (x[1] == 30).
2.Изменение объёма поставки товара для определённого заказчика.
Для этого меняются условия на столбец таблицы объёмов доставок товаров. Например, для второго заказчика объём заказа уменьшился с 45 единиц товара до 30.
Строку условий mass5 = (x[1] +x[4] + x[7] == 45) следует заменить на
mass5 = (x[1] +x[4] + x[7] == 30).
3. Установка верхней границы объёма поставок товара для поставщика.
Для этого меняются условия на строку таблицы объёмов доставок товаров. Например, для объёмов доставки товаров второго поставщика было ограничение сверху <= 40, а возникла необходимость доставки ровно 40 единиц товара. Переменную условий mass2 = (x[3] + x[4] +x[5] <= 40) заменим на mass2 = (x[3] + x[4] +x[5] == 40).
4. Паритет на поставки второго и третьего поставщиков
Для этого приравниваются объёмы поставок нескольких поставоких поставщиков, что обычно делается для улучшения бизнес климата. Например 6объёмы доставок товаров второго и третьего поставщика транспортных услуг соответственно ограничены сверху <=40 и <=36. Заменим строки mass2 = (x[3] + x[4] +x[5] <= 40) и mass3 = (x[6] + x[7] + x[8] <= 36) на mass2 = (x[3] + x[4] +x[5] == 30) и mass3 = (x[6] + x[7] + x[8] == 30).
Решение закрытой транспортной задачи с дополнительными условиями средствами решателя cvxopt Python
Программа для дополнительного условия №1
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(9, 'x')
c= [7,3,6,4,8,2,1,5,9]
z=(c[0]*x[0] + c[1]*x[1] +c[2]* x[2] +c[3]*x[3] + c[4]*x[4] +c[5]* x[5]+c[6]*x[6] +c[7]*x[7] +c[8]* x[8])
mass1 = (x[0] + x[1] +x[2] <= 74)
mass2 = (x[3] + x[4] +x[5] <= 40)
mass3 = (x[6] + x[7] + x[8] <= 36)
mass4 = (x[0] + x[3] + x[6] == 20)
mass5 = (x[1] +x[4] + x[7] == 45)
mass6 = (x[2] + x[5] + x[8] == 30)
mass7 = (x[1] == 30)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,mass5,mass6, mass7,x_non_negative])
problem.solve(solver='glpk')
print("Результат Xopt:")
for i in x.value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
Результат Xopt:
0. 0
0
30.0
0.0
0.0
0.0
30.0
20.0
15.0
0.0
Стоимость доставки:
245.0
Время:
0.04002642631530762
Программа для дополнительного условия №2
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(9, 'x')
c= [7,3,6,4,8,2,1,5,9]
z=(c[0]*x[0] + c[1]*x[1] +c[2]* x[2] +c[3]*x[3] + c[4]*x[4] +c[5]* x[5]+c[6]*x[6] +c[7]*x[7] +c[8]* x[8])
mass1 = (x[0] + x[1] +x[2] <= 74)
mass2 = (x[3] + x[4] +x[5] <= 40)
mass3 = (x[6] + x[7] + x[8] <= 36)
mass4 = (x[0] + x[3] + x[6] == 20)
mass5 = (x[1] +x[4] + x[7] == 30)
mass6 = (x[2] + x[5] + x[8] == 30)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,mass5,mass6,x_non_negative])
problem.solve(solver='glpk')
print("Результат Xopt:")
for i in x.value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time. time()
print ("Время :")
print(stop - start)
time()
print ("Время :")
print(stop - start)
Результат Xopt:
0.0
30.0
0.0
0.0
0.0
30.0
20.0
0.0
0.0
Стоимость доставки:
170.0
Время:
0.040003299713134766
Программа для дополнительного условия №3
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(9, 'x')
c= [7,3,6,4,8,2,1,5,9]
z=(c[0]*x[0] + c[1]*x[1] +c[2]* x[2] +c[3]*x[3] + c[4]*x[4] +c[5]* x[5]+c[6]*x[6] +c[7]*x[7] +c[8]* x[8])
mass1 = (x[0] + x[1] +x[2] <= 74)
mass2 = (x[3] + x[4] +x[5] == 40)
mass3 = (x[6] + x[7] + x[8] <= 36)
mass4 = (x[0] + x[3] + x[6] == 20)
mass5 = (x[1] +x[4] + x[7] == 45)
mass6 = (x[2] + x[5] + x[8] == 30)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,mass5,mass6,x_non_negative])
problem.solve(solver='glpk')
print("Результат Xopt:")
for i in x. value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
Результат Xopt:
0.0
45.0
0.0
10.0
0.0
30.0
10.0
0.0
0.0
Стоимость доставки:
245.0
Время:
0.041509151458740234
Программа для дополнительного условия №4
from cvxopt.modeling import variable, op import time start = time.time() x = variable(9, 'x') c= [7,3,6,4,8,2,1,5,9] z=(c[0]*x[0] + c[1]*x[1] +c[2]* x[2] +c[3]*x[3] + c[4]*x[4] +c[5]* x[5]+c[6]*x[6] +c[7]*x[7] +c[8]* x[8]) mass1 = (x[0] + x[1] +x[2] <= 74) mass2 = (x[3] + x[4] +x[5] == 30) mass3 = (x[6] + x[7] + x[8] == 30) mass4 = (x[0] + x[3] + x[6] == 20) mass5 = (x[1] +x[4] + x[7] == 45) mass6 = (x[2] + x[5] + x[8] == 30) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3,mass4 ,mass5,mass6,x_non_negative]) problem.solve(solver='glpk') print("Результат Xopt:") for i in x.value: print(i) print("Стоимость доставки:") print(problem.objective.value()[0]) stop = time.time() print ("Время :") print(stop - start)
Результат Xopt:
0.0
35.0
0.0
0.0
0.0
30.0
20.0
10.0
0.0
Стоимость доставки:
235.0
Время:
0.039984941482543945
Решение закрытой транспортной задачи с дополнительными условиями средствами решателя scipy. optimize Python
Программа для дополнительного условия №1
from scipy.optimize import linprog
import time
start = time.time()
c = [7, 3,6,4,8,2,1,5,9]
b_ub = [74,40,36]
A_ub = [[1,1,1,0,0,0,0,0,0],
[0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,1,1,1]]
b_eq = [20,45,30,30]
A_eq = [[1,0,0,1,0,0,1,0,0],
[0,1,0,0,1,0,0,1,0],
[0,0,1,0,0,1,0,0,1],
[0,1,0,0,0,0,0,0,0]]
print(linprog(c, A_ub, b_ub, A_eq, b_eq))
stop = time. time()
print ("Время :")
print(stop - start)
time()
print ("Время :")
print(stop - start)
Результат:
fun: 245.0
message: ‘Optimization terminated successfully.’
nit: 10
slack: array([ 44., 10., 1.])
status: 0
success: True
x: array([ 0., 30., 0., 0., 0., 30., 20., 15., 0.])
Время:
0.01000523567199707
Программа для дополнительного условия №2
from scipy.optimize import linprog
import time
start = time.time()
c = [7, 3,6,4,8,2,1,5,9]
b_ub = [74,40,36]
A_ub = [[1,1,1,0,0,0,0,0,0],
[0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,1,1,1]]
b_eq = [20,30,30]
A_eq = [[1,0,0,1,0,0,1,0,0],
[0,1,0,0,1,0,0,1,0],
[0,0,1,0,0,1,0,0,1]]
print(linprog(c, A_ub, b_ub, A_eq, b_eq))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
fun: 170. 0
0
message: ‘Optimization terminated successfully.’
nit: 7
slack: array([ 44., 10., 16.])
status: 0
success: True
x: array([ 0., 30., 0., 0., 0., 30., 20., 0., 0.])
Время:
0.04005861282348633
Программа для дополнительного условия №3
from scipy.optimize import linprog
import time
start = time.time()
c = [7, 3,6,4,8,2,1,5,9]
b_ub = [74,36]
A_ub = [[1,1,1,0,0,0,0,0,0],
[0,0,0,0,0,0,1,1,1]]
b_eq = [20,45,30,40]
A_eq = [[1,0,0,1,0,0,1,0,0],
[0,1,0,0,1,0,0,1,0],
[0,0,1,0,0,1,0,0,1],
[0,0,0,1,1,1,0,0,0]]
print(linprog(c, A_ub, b_ub, A_eq, b_eq))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
fun: 245.0
message: ‘Optimization terminated successfully.’
nit: 8
slack: array([ 29. , 26.])
, 26.])
status: 0
success: True
x: array([ 0., 45., 0., 10., 0., 30., 10., 0., 0.])
Время:
0.04979825019836426
Программа для дополнительного условия №4
from scipy.optimize import linprog
import time
start = time.time()
c = [7, 3,6,4,8,2,1,5,9]
b_ub = [74]
A_ub = [[1,1,1,0,0,0,0,0,0]]
b_eq = [20,45,30,30,30]
A_eq = [[1,0,0,1,0,0,1,0,0],
[0,1,0,0,1,0,0,1,0],
[0,0,1,0,0,1,0,0,1],
[0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,1,1,1]]
print(linprog(c, A_ub, b_ub, A_eq, b_eq))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
fun: 235.0
message: ‘Optimization terminated successfully.’
nit: 8
slack: array([ 39.])
status: 0
success: True
x: array([ 0., 35., 0., 0., 0., 30., 20., 10. , 0.])
, 0.])
Время:
0.05457925796508789
Решение закрытой транспортной задачи с дополнительными условиями средствами решателя pulp Python
Программа для дополнительного условия №1
from pulp import *
import time
start = time.time()
x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)
x3 = pulp.LpVariable("x3", lowBound=0)
x4 = pulp.LpVariable("x4", lowBound=0)
x5 = pulp.LpVariable("x5", lowBound=0)
x6 = pulp.LpVariable("x6", lowBound=0)
x7 = pulp.LpVariable("x7", lowBound=0)
x8 = pulp.LpVariable("x8", lowBound=0)
x9 = pulp.LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x2==30
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 <= 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 45, "5"
problem +=x3 + x6+x9 == 30, "6"
problem. solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
x1 = 0.0
x2 = 30.0
x3 = 0.0
x4 = 0.0
x5 = 0.0
x6 = 30.0
x7 = 20.0
x8 = 15.0
x9 = 0.0
Стоимость доставки:
245.0
Время:
0.16973495483398438
Программа для дополнительного условия №2
from pulp import *
import time
start = time.time()
x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)
x3 = pulp.LpVariable("x3", lowBound=0)
x4 = pulp.LpVariable("x4", lowBound=0)
x5 = pulp.LpVariable("x5", lowBound=0)
x6 = pulp.LpVariable("x6", lowBound=0)
x7 = pulp.LpVariable("x7", lowBound=0)
x8 = pulp.LpVariable("x8", lowBound=0)
x9 = pulp. LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 <= 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 30, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 <= 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 30, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
x1 = 0.0
x2 = 30.0
x3 = 0.0
x4 = 0.0
x5 = 0.0
x6 = 30.0
x7 = 20.0
x8 = 0.0
x9 = 0.0
Стоимость доставки:
170.0
Время:
0.18919610977172852
Программа для дополнительного условия №3
from pulp import * import time start = time.time() x1 = pulp.LpVariable("x1", lowBound=0) x2 = pulp.LpVariable("x2", lowBound=0) x3 = pulp.LpVariable("x3", lowBound=0) x4 = pulp.LpVariable("x4", lowBound=0) x5 = pulp.LpVariable("x5", lowBound=0) x6 = pulp.LpVariable("x6", lowBound=0) x7 = pulp.LpVariable("x7", lowBound=0) x8 = pulp.LpVariable("x8", lowBound=0) x9 = pulp.LpVariable("x9", lowBound=0) problem = pulp.LpProblem('0',pulp.LpMaximize) problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели" problem +=x1 + x2 +x3<= 74,"1" problem +=x4 + x5 +x6 == 40, "2" problem +=x7 + x8+ x9 <= 36, "3" problem +=x1+ x4+ x7 == 20, "4" problem +=x2+x5+ x8 == 45, "5" problem +=x3 + x6+x9 == 30, "6" problem.solve() print ("Результат:") for variable in problem.variables(): print (variable.name, "=", variable.varValue) print ("Стоимость доставки:") print (abs(value(problem.objective))) stop = time.time() print ("Время :") print(stop - start)
Результат:
x1 = 0. 0
0
x2 = 45.0
x3 = 0.0
x4 = 10.0
x5 = 0.0
x6 = 30.0
x7 = 10.0
x8 = 0.0
x9 = 0.0
Стоимость доставки:
245.0
Время:
0.17000865936279297
Программа для дополнительного условия №4
from pulp import *
import time
start = time.time()
x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)
x3 = pulp.LpVariable("x3", lowBound=0)
x4 = pulp.LpVariable("x4", lowBound=0)
x5 = pulp.LpVariable("x5", lowBound=0)
x6 = pulp.LpVariable("x6", lowBound=0)
x7 = pulp.LpVariable("x7", lowBound=0)
x8 = pulp.LpVariable("x8", lowBound=0)
x9 = pulp.LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 == 30, "2"
problem +=x7 + x8+ x9 == 30, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 45, "5"
problem +=x3 + x6+x9 == 30, "6"
problem. solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
Результат:
x1 = 0.0
x2 = 35.0
x3 = 0.0
x4 = 0.0
x5 = 0.0
x6 = 30.0
x7 = 20.0
x8 = 10.0
x9 = 0.0
Стоимость доставки:
235.0
Время:
0.17965340614318848
Вывод
Полученные в публикации дополнительные условия к закрытой транспортной задаче позволяют получать решения, более приближенные к реальной ситуации по доставке товаров. Приведенные дополнения можно использовать по несколько в одной задаче применяя их в зависимости от возникшей ситуации. Исследован вопрос выбора решателя для транспортной задачи с условиями. Таким решателем является scipy. optimize, как более узко функциональный чем cvxopt и более быстрый чем pulp. Кроме того scipy. optimize имеет более компактную запись условий транспортной задачи, что облегчает его работу с интерфейсом.
optimize, как более узко функциональный чем cvxopt и более быстрый чем pulp. Кроме того scipy. optimize имеет более компактную запись условий транспортной задачи, что облегчает его работу с интерфейсом.
Всем спасибо за внимание!
Ссылки
- Решение задач линейного программирования с использованием Python.
- CVXOPT Modeling.
- Optimization.
- Optimization with PuLP.
Карта сайту — www.mathros.net.ua
Pages
Posts by category
- Category: SQL
- Category: Інформаційні системи на Delphi
- Навчально-контролююча програма на Delphi
- Інформаційна система “Реєстратура готелю” в середовищі програмування Delphi
- Category: Ірраціональні рівняння
- Розв’язання ірраціональних рівнянь
- Category: Алгебра матриць
- Category: Алгоритми комп’ютерної графіки
- Category: Алгоритми комп’ютерної графіки на delphi
- Category: Арифметична прогресія
- Властивості та сума членів арифметичної прогресії
- Означення та формула обчислення загального члена арифметичної прогресії
- Category: Багатокутники
- Category: Бази даних
- Поняття бази даних і системи управління базами даних
- Category: Відрізок
- Category: Вектори і операції з ними
- Category: Геометрична прогресія
- Властивості та сума членів геометричної прогресії
- Означення та формула обчислення загального члена геометричної прогресії
- Category: Дводольні графи
- Перевірка графа на дводольність
- Category: Дослідження операцій
- Транспортна задача лінійного програмування
- Category: Задачі розміщення
- Знаходження головного центру графа
- Застосування елементів теорії графів для рішення задачі розміщення пунктів обслуговування
- Category: Задача дробово-лінійного програмування
- Category: Задача комівояжера
- Category: Задача про рюкзак
- Задача про рюкзак.
 Математична модель задачі про рюкзак
Математична модель задачі про рюкзак
- Задача про рюкзак.
- Category: Знаходження власних значень і власних векторів матриці
- Category: Квадратні корені
- Наближене обчислення квадратних коренів
- Category: Квадратні рівняння
- Рішення квадратного рівняння за допомогою теореми Вієта
- Квадратне рівняння. Обчислення дискримінанту та коренів квадратного рівняння
- Category: Коло і круг
- Площа круга та кругового сектора
- Довжина кола і дуги кола
- Category: Комплексні числа
- Category: Компоненти зв’язності, кліки, точки сполучення
- Category: Лінії другого порядку
- Рівняння кривої другого порядку що описує коло
- Category: Лінійні рівняння та їх системи
- Category: Лінійне програмування
- Category: Лінійне цілочисельне програмування
- Category: Методи наближення функцій
- Category: Методи обходу графа
- Category: Методи розв’язування систем лiнiйних алгебраїчних рівнянь
- Category: Мови програмування
- Category: Наближене рішення систем нелінійних рівнянь
- Category: Нелінійне програмування
- Category: Нерівності
- Category: Обчислення значень функції
- Схема ділення многочлена на квадратний тричлен
- Обчислення значення полінома використовуючи схему Горнера
- Category: Оптимальні каркаси та шляхи
- Category: Площа і периметр фігур
- Category: Подільність натуральних чисел
- Ознаки подільності на 2, 3, 4, 5, 8, 9, 10 і 11
- Найменше спільне кратне двох натуральних чисел
- Розкладання чисел на прості множники
- Знаходження простих чисел використовуючи решето Ератосфена
- Знаходження найбільшого спільного дільника за алгоритмом Евкліда
- Category: Похідна і диференціал
- Category: Пошук екстремумів функцій
- Category: Програми на Delphi (Дослідження операцій)
- Category: Програми на Delphi (Методи обчислення)
- Category: Пряма лінія на площині
- Category: Різне
- Category: Реалізація відомих алгоритмів на Java
- Category: Робота з базами даних в середовищі програмування Delphi
- Category: Розфарбування графа
- Алгоритм послідовної розмальовки графа
- Переборний алгоритм для розфарбування вершин графа
- Category: Топологічне сортування
- Топологічне сортування орієнтованого графа методом видалення вершини-джерела
- Топологічне сортування вершин орієнтованого графа
- Category: Транспортна задача лінійного програмування
- Category: Трикутники
- Синус, косинус, тангенс і котангенс гострого кута
- Розв’язування трикутників: типи задач на розв’язування трикутників
- Теорема Піфагора, формула і доведення
- Теорема косинусів: формула, наслідки та приклади
- Теорема синусів, формула і приклади
- Медіани трикутника, їх властивості та використання для розв’язування задач
- Бісектриси трикутника і їх властивості
- Середня лінія трикутника
- Види трикутників.
 Співвідношення між кутами і сторонами трикутника
Співвідношення між кутами і сторонами трикутника - Задача про центр мас однорідного трикутника
- Category: Цикли
- Category: Чисельні методи розв’язання задач математичної фізики
- Розв’язування рівнянь теплопровідності за методом Кранка-Ніколсона
- Розв’язування рівнянь теплопровідності методом скінченних різниць
- Category: Чисельні методи розв’язування звичайних диференцiальних рiвнянь
- Category: Чисельні методи розв’язування рівнянь з однією змінною
- Category: Чисельне диференціювання та інтегрування
Ми в соціальних мережах
как соотносятся между собой геномы человека и червяка.
 Сколько хромосом у различных животных Организмы по убыванию количества хромосом
Сколько хромосом у различных животных Организмы по убыванию количества хромосомИз школьных учебников по биологии каждому доводилось знакомиться с термином хромосома. Понятие было предложено Вальдейером в 1888 году. Оно переводится буквально как окрашенное тело. Первым объектом исследований стала плодовая мушка.
Общее о хромосомах животных
Хромосома – это структура ядра клетки, в которой хранится наследственная информация. Она образуются из молекулы ДНК, в которой содержится множество генов. Другими словами, хромосома – это молекула ДНК. Ее количество у различных животных неодинаковое. Так, например, у кошки – 38, а у коровы -120. Интересно, что самое маленькое число имеют дождевые черви и муравьи. Их количество составляет две хромосомы, а у самца последних – одна.
У высших животных, так же как и у человека, последняя пара представлена ХУ половыми хромосомами у самцов и ХХ – у самок. Нужно обратить внимание, что число этих молекул для всех животных постоянно, но у каждого вида их количество отличается. Для примера можно рассмотреть содержание хромосом у некоторых организмов: у шимпанзе – 48, речного рака -196, у волка – 78, зайца – 48. Это связано с разным уровнем организации того или иного животного.
Для примера можно рассмотреть содержание хромосом у некоторых организмов: у шимпанзе – 48, речного рака -196, у волка – 78, зайца – 48. Это связано с разным уровнем организации того или иного животного.
На заметку! Хромосомы всегда размещаются парами. Генетики утверждают, что эти молекулы и есть неуловимые и невидимые носители наследственности. Каждая из хромосом содержит в себе множество генов. Некоторые считают, что чем больше этих молекул, тем животное более развитое, а его организм сложнее устроен. В таком случае, у человека хромосом должно насчитываться не 46, а больше, чем у любого другого животного.
Сколько хромосом у различных животных
Необходимо обратить внимание! У обезьян количество хромосом приближено к значению человека. Но у каждого вида результаты отличаются. Итак, у различных обезьян насчитывается следующее количество хромосом:
- Лемуры имеют в своем арсенале 44-46 молекул ДНК;
- Шимпанзе – 48;
- Павианы – 42,
- Мартышки – 54;
- Гиббоны – 44;
- Гориллы – 48;
- Орангутанг – 48;
- Макаки – 42.

У семейства псовых (хищных млекопитающих) хромосом больше, чем у обезьян.
- Так, у волка – 78,
- у койота – 78,
- у лисицы малой – 76,
- а вот у обыкновенной – 34.
- У хищных зверей льва и тигра присутствуют по 38 хромосом.
- У домашнего животного кошки – 38, а у его оппонента собаки почти в два раза больше – 78.
У млекопитающих, которые имеют хозяйственное значение, количество этих молекул следующее:
- кролик – 44,
- корова – 60,
- лошадь – 64,
- свинья – 38.
Познавательно! Самыми большими хромосомными наборами среди животных обладают хомячки. Они имеют 92 в своем арсенале. Также в этом ряду идут ежики. У них есть 88-90 хромосом. А самым маленьким количеством этих молекул наделены кенгуру. Их численность составляет 12. Очень интересен тот факт, что у мамонта 58 хромосом. Образцы взяты из замороженной ткани.
Для большей наглядности и удобства, данные других животных будут представлены в сводке.
Наименование животного и количество хромосом:
| Пятнистые куницы | 12 |
| Кенгуру | 12 |
| Желтая сумчатая мышь | 14 |
| Сумчатый муравьед | 14 |
| Обыкновенный опоссум | 22 |
| Опоссум | 22 |
| Норка | 30 |
| Барсук американский | 32 |
| Корсак (лисица степная) | 36 |
| Лисица тибетская | 36 |
| Панда малая | 36 |
| Кошка | 38 |
| Лев | 38 |
| Тигр | 38 |
| Енот-полоскун | 38 |
| Канадский бобр | 40 |
| Гиены | 40 |
| Мышь домовая | 40 |
| Павианы | 42 |
| Крысы | 42 |
| Дельфин | 44 |
| Кролики | 44 |
| Человек | 46 |
| Заяц | 48 |
| Горилла | 48 |
| Лисица американская | 50 |
| Полосатый скунс | 50 |
| Овца | 54 |
| Слон (азиатский, саванный) | 56 |
| Корова | 60 |
| Коза домашняя | 60 |
| Обезьяна шерстистая | 62 |
| Осел | 62 |
| Жираф | 62 |
| Мул (гибрид осла и кобылы) | 63 |
| Шиншилла | 64 |
| Лошадь | 64 |
| Лисица серая | 66 |
| Белохвостый олень | 70 |
| Лисица парагвайская | 74 |
| Лисица малая | 76 |
| Волк (красный, рыжий, гривистый) | 78 |
| Динго | 78 |
| Койот | 78 |
| Собака | 78 |
| Шакал обыкновенный | 78 |
| Курица | 78 |
| Голубь | 80 |
| Индейка | 82 |
| Эквадорский хомячок | 92 |
| Лемур обыкновенный | 44-60 |
| Песец | 48-50 |
| Ехидна | 63-64 |
| Ежи | 88-90 |
Количество хромосом у разных видов животных
Как видно, каждое животное обладает разным количеством хромосом. Даже у представителей одного семейства показатели отличаются. Можно рассмотреть на примере приматов:
Даже у представителей одного семейства показатели отличаются. Можно рассмотреть на примере приматов:
- у гориллы – 48,
- у макаки – 42, а у мартышки 54 хромосом.
Почему это так, остается загадкой.
Сколько хромосом у растений?
Наименование растения и количество хромосом:
Видео
Плохая экология, жизнь в постоянном стрессе, приоритет карьеры над семьей – все это плохо отражается на способности человека приносить здоровое потомство. Как это ни прискорбно, но около 1% младенцев, появившихся на свет с серьезными нарушениями в хромосомном наборе, вырастают умственно или физически отсталыми. У 30% новорожденных отклонения в кариотипе приводят к формированию врожденных пороков. Основным вопросам этой темы посвящена наша статья.
Основной носитель наследственной информации
Как известно, хромосома – это определенная нуклеопротеидная (состоящая из устойчивого комплекса белков и нуклеиновых кислот) структура внутри ядра клетки эукариотов (то есть тех живых существ, клетки которых имеют ядро). Ее основная функция – хранение, передача и реализация генетической информации. Видна она под микроскоп только во время таких процессов как мейоз (деление двойного (диплоидного) набора генов хромосомы при создании половых клеток) и микоз (деление клеток при развитии организма).
Ее основная функция – хранение, передача и реализация генетической информации. Видна она под микроскоп только во время таких процессов как мейоз (деление двойного (диплоидного) набора генов хромосомы при создании половых клеток) и микоз (деление клеток при развитии организма).
Как уже было упомянуто, хромосома состоит из дезоксирибонуклеиновой кислоты (ДНК) и белков (около 63% ее массы), на которых намотана ее нить. Многочисленные исследования в области цитогенетики (наука о хромосомах) доказали, что именно ДНК является основным носителем наследственности. В ней заключается информация, которая в последствие реализуется в новом организме. Это комплекс генов, отвечающих за цвет волос и глаз, рост, количество пальцев и прочее. Какие из генов будут переданы ребенку, определяется в момент зачатия.
Формирование хромосомного набора здорового организма
У нормального человека 23 пары хромосом, каждая из которых отвечает за определенный ген. Итого их 46 (23х2) — сколько хромосом у здорового человека. Одна хромосома достается нам от отца, другая передается от матери. Исключение составляет 23 пара. Она отвечает за пол человека: женский обозначается как XX, а мужской – как XY. Когда хромосомы в паре – это диплоидный набор. В половых клетках они разъединены (гаплоидный набор) перед последующим соединением во время оплодотворения.
Одна хромосома достается нам от отца, другая передается от матери. Исключение составляет 23 пара. Она отвечает за пол человека: женский обозначается как XX, а мужской – как XY. Когда хромосомы в паре – это диплоидный набор. В половых клетках они разъединены (гаплоидный набор) перед последующим соединением во время оплодотворения.
Совокупность признаков хромосом (как количественных, так и качественных), рассмотренных в пределах одной клетки, ученые называют кариотипом. Нарушения в нем, в зависимости от характера и степени тяжести, приводят к возникновению различных болезней.
Отклонения в кариотипе
Все нарушения кариотипа при классификации традиционно делят на два класса: геномные и хромосомные.
При геномных мутациях отмечают увеличение числа всего набора хромосом, или числа хромосом в одной из пар. Первый случай носит название полиплоидия, второй – анеуплоидия.
Хромосомные нарушения представляют собой перестройки, как внутри хромосом, так и между ними. Не вдаваясь в научные дебри, их можно описать так: некоторые участки хромосом могут не присутствовать или же быть удвоены в ущерб другим; может быть нарушен порядок следования генов, или изменено их местонахождение. Нарушения в структуре могут произойти в каждой хромосоме человека. В настоящее время, подробно описаны изменения в каждой из них.
Не вдаваясь в научные дебри, их можно описать так: некоторые участки хромосом могут не присутствовать или же быть удвоены в ущерб другим; может быть нарушен порядок следования генов, или изменено их местонахождение. Нарушения в структуре могут произойти в каждой хромосоме человека. В настоящее время, подробно описаны изменения в каждой из них.
Остановимся подробнее на наиболее известных и широко распространенных геномных заболеваниях.
Синдром Дауна
Был описан еще в 1866 году. На 700 новорожденных, как правило, приходится один малыш с подобной болезнью. Суть отклонения состоит в том, что к 21 паре присоединяется третья хромосома. Получается это, когда в половой клетке одного из родителей 24 хромосомы (с удвоенной 21). У больного ребенка в итоге их 47 – вот сколько хромосом у человека Дауна. Такой патологии способствуют вирусные инфекции или ионизирующая радиация, перенесенные родителями, а также диабет.
Дети с синдромом Дауна умственно отсталые. Проявления недуга видны даже во внешности: слишком большой язык, большие уши неправильной формы, кожная складка на веке и широкая переносица, белесые пятна в глазах. Живут такие люди в среднем лет сорок, поскольку, помимо прочего, подвержены сердечным заболеваниям, проблемам с кишечником и желудком, неразвитыми половыми органами (хотя женщины могут быть способны к деторождению).
Живут такие люди в среднем лет сорок, поскольку, помимо прочего, подвержены сердечным заболеваниям, проблемам с кишечником и желудком, неразвитыми половыми органами (хотя женщины могут быть способны к деторождению).
Риск рождения больного ребенка тем выше, чем старше родители. В настоящее время существуют технологии, позволяющие распознать хромосомное нарушение на ранней стадии беременности. Немолодым парам необходимо проходить подобный тест. Не помешает он и молодым родителям, если в роду одного из них встречались больные синдромом дауна. Мозаичная форма болезни (поврежден кариотип части клеток) формируется уже на стадии эмбриона и от возраста родителей не зависит.
Синдром Патау
Это нарушение представляет собой трисомию тринадцатой хромосомы. Встречается оно куда реже, чем предыдущий описанный нами синдром (1 к 6000). Возникает оно при присоединении лишней хромосомы, а также при нарушении структуры хромосом и перераспределении их частей.
Диагностируют синдром Патау по трем симптомам: микрофтальм (уменьшенные размеры глаз), полидактилия (большее количество пальцев), расщелина губы и неба.
Смертность младенцев при этой болезни составляет порядка 70%. Большинство из них не доживает до 3 лет. У подверженных этому синдрому особей чаще всего наблюдаются порок сердца и/или головного мозга, проблемы с другими внутренними органами (почки, селезенка и прочее).
Синдром Эдвардса
Большая часть младенцев, у которых 3 восемнадцатых хромосомы, погибают вскоре после рождения. У них ярко выражена гипотрофия (проблемы с пищеварением, не позволяющие ребенку набрать вес). Глаза широко поставлены, уши низко расположены. Часто наблюдается порок сердца.
Выводы
Чтобы не допустит рождения больного ребенка, желательно проходит специальные обследования. В обязательном порядке тест показан роженицам после 35 лет; родителям, родственники которых были подвержены подобным заболеваниям; пациенткам, имеющим проблемы со щитовидной железой; женщинам, у которых случались выкидыши.
Какие
мутации, кроме синдрома Дауна, нам грозят? Возможно ли скрестить
человека с обезьяной? И что произойдет с нашим геномом в будущем?
Редактор портала АНТРОПОГЕНЕЗ. РУ поговорил о хромосомах с генетиком,
зав. лаб. сравнительной геномики СО РАН Владимиром Трифоновым.
РУ поговорил о хромосомах с генетиком,
зав. лаб. сравнительной геномики СО РАН Владимиром Трифоновым.
− Можете ли объяснить простым языком, что такое хромосома?
− Хромосома – это фрагмент генома любого организма (ДНК) в комплексе с белками. Если у бактерий обычно весь геном – это одна хромосома, то у сложных организмов с выраженным ядром (эукариотов) обычно геном фрагментирован, и комплексы длинных фрагментов ДНК и белка отчётливо видны в световой микроскоп при делении клетки. Именно поэтому хромосомы как окрашивающиеся структуры («хрома» — цвет по-гречески) были описаны еще в конце XIX века.
− Есть ли какая-то связь между количеством хромосом и сложностью организма?
− Никакой связи нет. У сибирского осетра 240 хромосом, у стерляди –
120, но отличить эти два вида между собой иногда довольно сложно по
внешним признакам. У самок индийского мунтжака 6 хромосом, у самцов – 7,
а у их родственника – сибирской косули их больше 70 (вернее, 70
хромосом основного набора и еще до десятка добавочных хромосом). У
млекопитающих эволюция разрывов и слияний хромосом шла довольно
интенсивно и сейчас мы наблюдаем результаты этого процесса, когда
зачастую у каждого вида есть характерные особенности кариотипа (набора
хромосом). Но, несомненно, общее увеличение размера генома было
необходимым этапом в эволюции эукариот. При этом как этот геном
распределяется по отдельным фрагментам вроде бы не очень важно.
У
млекопитающих эволюция разрывов и слияний хромосом шла довольно
интенсивно и сейчас мы наблюдаем результаты этого процесса, когда
зачастую у каждого вида есть характерные особенности кариотипа (набора
хромосом). Но, несомненно, общее увеличение размера генома было
необходимым этапом в эволюции эукариот. При этом как этот геном
распределяется по отдельным фрагментам вроде бы не очень важно.
− Какие существуют распространённые заблуждения по поводу хромосом? Народ часто путается: гены, хромосомы, ДНК…
− Поскольку действительно часто возникают хромосомные перестройки, то
у людей есть опасения относительно хромосомных аномалий. Известно, что
лишняя копия самой мелкой хромосомы человека (хромосомы 21) приводит к
довольно серьезному синдрому (синдром Дауна), имеющему характерные
внешние и поведенческие особенности. Лишние половые хромосомы или их
недостаток также довольно часто встречаются и могут иметь серьезные
последствия. Однако генетиками описано и довольно много относительно
нейтральных мутаций, связанных с появлением микрохромосом, или
дополнительных Х и Y хромосом. Думаю, стигматизация этого явления
связана с тем, что люди слишком узко воспринимают понятие нормы.
Думаю, стигматизация этого явления
связана с тем, что люди слишком узко воспринимают понятие нормы.
− Какие хромосомные мутации встречаются у современного человека и к чему они приводят?
− Самые частые хромосомные аномалии − это:
− синдром Кляйнфельтера (мужчины XXY) (1 на 500) – характерные внешние признаки, определенные проблемы со здоровьем (анемия, остеопороз, мышечная слабость и нарушение половой функции), стерильность. Могут быть поведенческие особенности. Однако многие симптомы (кроме стерильности) можно корректировать введением тестостерона. С использованием современных репродуктивных технологий можно получать здоровых детей от носителей этого синдрома;
− синдром Дауна (1 на 1000) – характерные внешние признаки, замедленное когнитивное развитие, короткая продолжительность жизни, могут быть фертильны;
− трисомия по Х (женщины ХХХ) (1 на 1000) – чаще всего нет никаких проявлений, фертильность;
− синдром XYY (мужчины) (1 на 1000) – почти нет проявлений, но могут быть особенности поведения и возможны репродуктивные проблемы;
− синдром Тернера (женщины ХО) (1 на 1500) – низкорослость и другие особенности развития, нормальный интеллект, стерильность;
− сбаллансированные транслокации (1 на 1000) – зависит от типа, в некоторых случаях могут наблюдаться пороки развития и умственная отсталость, могут сказываться на фертильности;
− мелкие добавочные хромосомы (1 на 2000) – проявление зависит от генетического материала на хромосомах и варьирует от нейтрального до серьезных клинических симптомов;
В 1% популяции человека встречается перицентрическая инверсия хромосомы 9, но эта перестройка рассматривается как вариант нормы.
Является ли разница в числе хромосом препятствием к скрещиванию? А есть ли интересные примеры скрещивания животных с разным числом хромосом?
− Если скрещивание внутривидовое или между близкими видами, то разница в числе хромосом может не мешать скрещиваться, однако потомки могут оказаться стерильными. Известно очень много гибридов между видами с разным числом хромосом, например, у лошадиных: есть все варианты гибридов между лошадьми, зебрами и ослами, причем число хромосом у всех лошадиных разное и, соответственно, гибриды часто стерильны. Однако это не исключает, что случайно могут образовываться сбаллансированные гаметы.
— Что необычного в области хромосом было открыто в последнее время?
− В последнее время было много открытий, касающихся структуры, функционирования и эволюции хромосом. Мне особенно нравятся работы, показавшие, что половые хромосомы образовывались в разных группах животных совершенно независимо.
− А все-таки, можно ли скрестить человека с обезьяной?
− Теоретически получить такого гибрида можно. В последнее время
получены гибриды гораздо более эволюционно далеких млекопитающих (белого
и черного носорога, альпаки и верблюда и так далее). Рыжий волк в
Америке, долго считался отдельным видом, но недавно было доказано, что
он является гибридом между волком и койотом. Известно огромное
количество гибридов кошачьих.
В последнее время
получены гибриды гораздо более эволюционно далеких млекопитающих (белого
и черного носорога, альпаки и верблюда и так далее). Рыжий волк в
Америке, долго считался отдельным видом, но недавно было доказано, что
он является гибридом между волком и койотом. Известно огромное
количество гибридов кошачьих.
− И совсем абсурдный вопрос: можно ли скрестить хомяка с уткой?
− Вот тут скорее всего ничего не получится, потому что генетических отличий за сотни миллионов лет эволюции накопилось слишком много, чтобы носитель такого смешанного генома мог функционировать.
— Возможно, что в будущем у человека будет меньше или больше хромосом?
− Да, это вполне возможно. Не исключено, что сольется пара акроцентрических хромосом и такая мутация распространится на всю популяцию.
− Какую научно-популярную литературу вы посоветуете по теме генетики человека? А научно-популярные фильмы?
− Книги биолога Александра Маркова, трёхтомник «Генетика человека»
Фогеля и Мотульского (правда, это не науч-поп, но там хорошие справочные
данные). Из фильмов про генетику человека ничего не приходит в голову…
Но вот «Внутренняя рыба» Шубина – отличный фильм и одноимённая книга про
эволюцию позвоночных.
Из фильмов про генетику человека ничего не приходит в голову…
Но вот «Внутренняя рыба» Шубина – отличный фильм и одноимённая книга про
эволюцию позвоночных.
МОСКВА, 4 июл — РИА Новости, Анна Урманцева . У кого геном больше? Как известно, одни существа имеют более сложное строение, чем другие, а раз все записано в ДНК, то и это тоже должно быть отражено в ее коде. Получается, человек с его развитой речью обязан быть сложнее маленького круглого червяка. Однако если сравнить нас с червяком по количеству генов, получится примерно то же самое: 20 тысяч генов Caenorhabditis elegans против 20-25 тысяч Homo sapiens.
Еще более обидными для «венца земных созданий» и «царя природы» являются сравнения с рисом и кукурузой — 50 тысяч генов по отношению к человеческим 25.
Впрочем, может, мы не то считаем? Гены — это «коробочки», в которые упакованы нуклеотиды — «буквы» генома. Может, посчитать их? У человека 3,2 миллиарда пар нуклеотидов. А вот японский вороний глаз (Paris japonica) — красивое растение с белыми цветами — имеет в своем геноме 150 миллиардов пар оснований. Получается, что человек должен быть устроен в 50 раз проще какого-то цветка.
Получается, что человек должен быть устроен в 50 раз проще какого-то цветка.
А двоякодышащая рыба протоптер (двоякодышащая — обладающая как жаберным, так и легочным дыханием), получается, в 40 раз сложнее, чем человек. Может, все рыбы почему-то сложнее, чем люди? Нет. Ядовитая рыба фугу, из которой японцы готовят деликатес, имеет геном в восемь раз меньше, чем у человека, и в 330 раз меньше, чем у двоякодышащей рыбы протоптер.
Остается посчитать хромосомы — но это еще сильнее запутывает картину. Как может человек по количеству хромосом быть равным ясеню, а шимпанзе — таракану?
С этими парадоксами эволюционные биологи и генетики столкнулись давным-давно. Они были вынуждены признать, что размер генома, в чем бы мы его ни пытались посчитать, поразительно не связан со сложностью устройства организмов. Этот парадокс назвали «загадкой значений С», где С — это количество ДНК в клетке (C-value paradoх, точный перевод — «парадокс величины генома»). И все-таки какие-то корреляции между видами и царствами существуют.
© Иллюстрация РИА Новости. А.Полянина
© Иллюстрация РИА Новости. А.Полянина
Ясно, например, что эукариоты (живые организмы, клетки которых содержат ядро) имеют в среднем геномы больше, чем прокариоты (живые организмы, клетки которых не содержат ядро). Позвоночные животные имеют в среднем геномы больше, чем беспозвоночные. Однако тут есть исключения, которые никто пока не смог объяснить.
Генетики расшифровали ДНК растения, способного пережить атомный взрыв Ученые впервые расшифровали полный геном гинкго – древнейшего современного растения на Земле, первые представители которого появились еще до рождения первых динозавров, во времена звероящеров.
Были предположения, что размер генома связан с продолжительностью жизненного цикла организма. Некоторые ученые утверждали на примере растений, что многолетние виды имеют более крупные геномы, чем однолетние, причем обычно с разницей в несколько раз. А самые маленькие геномы принадлежат растениям-эфемерам, которые проходят полный цикл от рождения до смерти в течение нескольких недель. Этот вопрос сейчас активно обсуждается в научных кругах.
Этот вопрос сейчас активно обсуждается в научных кругах.
Поясняет ведущий научный сотрудник Института общей генетики им. Н. И. Вавилова Российской академии наук, профессор Техасского агромеханического университета и Гёттингенского университета Константин Крутовский: «Размер генома не связан с продолжительностью жизненного цикла организма! Например, есть виды внутри одного рода, которые имеют одинаковый размер генома, но могут различаться по продолжительности жизни в десятки, если не сотни раз. В целом есть связь размера генома с эволюционной продвинутостью и сложностью организации, но со множеством исключений. В основном размер генома связан с плоидностью (копийностью) генома (причем полиплоиды встречаются и у растений, и у животных) и количеством высокоповторяющейся ДНК (простые и сложные повторы, транспозоны и другие мобильные элементы)».
Генетики «воскресили» кукурузу возрастом в пять тысяч лет
Генетики смогли извлечь ДНК из древнейших останков «культурной» кукурузы и восстановить ее геном, указавший на более древние корни любимого растения Никиты Сергеевича Хрущева, чем мы считали раньше.
Есть также ученые, которые придерживаются другой точки зрения на этот вопрос.
У человека до сих пор В-хромосомы обнаружены не были. Зато иногда в клетках возникает дополнительный набор хромосом — тогда говорят о полиплоидии , а если их число не кратно 23 — об анеуплоидии. Полиплоидия встречается у отдельных типов клеток и способствует их усиленной работе, в то время как анеуплоидия обычно свидетельствует о нарушениях в работе клетки и нередко приводит к ее гибели.
Делиться надо честно
Чаще всего неправильное количество хромосом является следствием неудачного деления клеток. В соматических клетках после удвоения ДНК материнская хромосома и ее копия оказываются сцеплены вместе белками когезинами. Потом на их центральные части садятся белковые комплексы кинетохоры, к которым позже прикрепляются микротрубочки. При делении по микротрубочкам кинетохоры разъезжаются к разным полюсам клетки и тянут за собой хромосомы. Если сшивки между копиями хромосомы разрушатся раньше времени, то к ним могут прикрепиться микротрубочки от одного и того же полюса, и тогда одна из дочерних клеток получит лишнюю хромосому, а вторая останется обделенной.
Мейоз тоже нередко проходит с ошибками. Проблема в том, что конструкция из сцепленных двух пар гомологичных хромосом может перекручиваться в пространстве или разделяться в неположенных местах. Результатом снова будет неравномерное распределение хромосом. Иногда половой клетке удается это отследить, чтобы не передавать дефект по наследству. Лишние хромосомы часто неправильно уложены или разорваны, что запускает программу гибели. Например, среди сперматозоидов действует такой отбор по качеству. А вот яйцеклеткам повезло меньше. Все они у человека образуются еще до рождения, готовятся к делению, а потом замирают. Хромосомы уже удвоены, тетрады образованы, а деление отложено. В таком виде они живут до репродуктивного периода. Дальше яйцеклетки по очереди созревают, делятся первый раз и снова замирают. Второе деление происходит уже сразу после оплодотворения. И на этом этапе проконтролировать качество деления уже сложно. А риски больше, ведь четыре хромосомы в яйцеклетке остаются сшитыми в течение десятков лет. За это время в когезинах накапливаются поломки, и хромосомы могут спонтанно разделяться. Поэтому чем старше женщина, тем больше вероятность неправильного расхождения хромосом в яйцеклетке.
За это время в когезинах накапливаются поломки, и хромосомы могут спонтанно разделяться. Поэтому чем старше женщина, тем больше вероятность неправильного расхождения хромосом в яйцеклетке.
Анеуплоидия в половых клетках неизбежно ведет к анеуплоидии зародыша. При оплодотворении здоровой яйцеклетки с 23 хромосомами сперматозоидом с лишней или недостающей хромосомами (или наоборот) число хромосом у зиготы, очевидно, будет отлично от 46. Но даже если половые клетки здоровы, это не дает гарантий здорового развития. В первые дни после оплодотворения клетки зародыша активно делятся, чтобы быстро набрать клеточную массу. Судя по всему, в ходе быстрых делений нет времени проверять корректность расхождения хромосом, поэтому могут возникнуть анеуплоидные клетки. И если произойдет ошибка, то дальнейшая судьба зародыша зависит от того, в каком делении это случилось. Если равновесие нарушено уже в первом делении зиготы, то весь организм вырастет анеуплоидным. Если же проблема возникла позже, то исход определяется соотношением здоровых и аномальных клеток.
Часть последних может дальше погибнуть, и мы никогда не узнаем об их существовании. А может принять участие в развитии организма, и тогда он получится мозаичным — разные клетки будут нести разный генетический материал. Мозаицизм доставляет немало хлопот пренатальным диагностам. Например, при риске рождения ребенка с синдромом Дауна иногда извлекают одну или несколько клеток зародыша (на той стадии, когда это не должно представлять опасности) и считают в них хромосомы. Но если зародыш мозаичен, то такой метод становится не особенно эффективным.
Третий лишний
Все случаи анеуплоидии логично делятся на две группы: недостаток и избыток хромосом. Проблемы, возникающие при недостатке, вполне ожидаемы: минус одна хромосома означает минус сотни генов.
Если гомологичная хромосома работает нормально, то клетка может отделаться только недостаточным количеством закодированных там белков. Но если среди оставшихся на гомологичной хромосоме генов какие-то не работают, то соответствующих белков в клетке не появится совсем.
В случае избытка хромосом все не так очевидно. Генов становится больше, но здесь — увы — больше не значит лучше.
Во-первых, лишний генетический материал увеличивает нагрузку на ядро: дополнительную нить ДНК нужно разместить в ядре и обслужить системами считывания информации.
Ученые обнаружили , что у людей с синдромом Дауна, чьи клетки несут дополнительную 21-ю хромосому, в основном нарушается работа генов, находящихся на других хромосомах. Видимо, избыток ДНК в ядре приводит к тому, что белков, поддерживающих работу хромосом, не хватает на всех.
Во-вторых, нарушается баланс в количестве клеточных белков. Например, если за какой-то процесс в клетке отвечают белки-активаторы и белки-ингибиторы и их соотношение обычно зависит от внешних сигналов, то дополнительная доза одних или других приведет к тому, что клетка перестанет адекватно реагировать на внешний сигнал. И наконец, у анеуплоидной клетки растут шансы погибнуть. При удвоении ДНК перед делением неизбежно возникают ошибки, и клеточные белки системы репарации их распознают, чинят и запускают удвоение снова.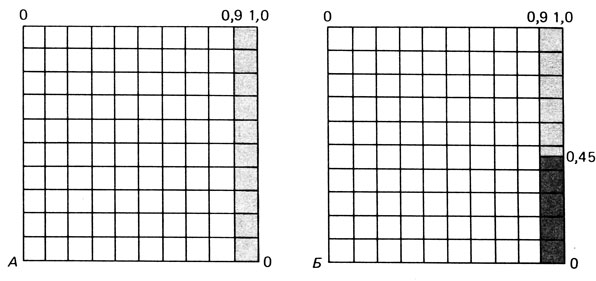 Если хромосом слишком много, то белков не хватает, ошибки накапливаются и запускается апоптоз — программируемая гибель клетки. Но даже если клетка не погибает и делится, то результатом такого деления тоже, скорее всего, станут анеуплоиды.
Если хромосом слишком много, то белков не хватает, ошибки накапливаются и запускается апоптоз — программируемая гибель клетки. Но даже если клетка не погибает и делится, то результатом такого деления тоже, скорее всего, станут анеуплоиды.
Жить будете
Если даже в пределах одной клетки анеуплоидия чревата нарушениями работы и гибелью, то неудивительно, что целому анеуплоидному организму выжить непросто. На данный момент известно только три аутосомы — 13, 18 и 21-я, трисомия по которым (то есть лишняя, третья хромосома в клетках) как-то совместима с жизнью. Вероятно, это связано с тем, что они самые маленькие и несут меньше всего генов. При этом дети с трисомией по 13-й (синдром Патау) и 18-й (синдром Эдвардса) хромосомам доживают в лучшем случае до 10 лет, а чаще живут меньше года. И только трисомия по самой маленькой в геноме, 21-й хромосоме, известная как синдром Дауна, позволяет жить до 60 лет.
Совсем редко встречаются люди с общей полиплоидией. В норме полиплоидные клетки (несущие не две, а от четырех до 128 наборов хромосом) можно обнаружить в организме человека, например в печени или красном костном мозге. Это, как правило, большие клетки с усиленным синтезом белка, которым не требуется активное деление.
Это, как правило, большие клетки с усиленным синтезом белка, которым не требуется активное деление.
Дополнительный набор хромосом усложняет задачу их распределения по дочерним клеткам, поэтому полиплоидные зародыши, как правило, не выживают. Тем не менее описано около 10 случаев, когда дети с 92 хромосомами (тетраплоиды) появлялись на свет и жили от нескольких часов до нескольких лет. Впрочем, как и в случае других хромосомных аномалий, они отставали в развитии, в том числе и умственном. Однако многим людям с генетическими аномалиями приходит на помощь мозаицизм. Если аномалия развилась уже в ходе дробления зародыша, то некоторое количество клеток могут остаться здоровыми. В таких случаях тяжесть симптомов снижается, а продолжительность жизни растет.
Гендерные несправедливости
Однако есть и такие хромосомы, увеличение числа которых совместимо с жизнью человека или даже проходит незаметно. И это, как ни удивительно, половые хромосомы. Причиной тому — гендерная несправедливость: примерно у половины людей в нашей популяции (девочек) Х-хромосом в два раза больше, чем у других (мальчиков). При этом Х-хромосомы служат не только для определения пола, но и несут более 800 генов (то есть в два раза больше, чем лишняя 21-я хромосома, доставляющая немало хлопот организму). Но девочкам приходит на помощь естественный механизм устранения неравенства: одна из Х-хромосом инактивируется, скручивается и превращается в тельце Барра . В большинстве случаев выбор происходит случайно, и в ряде клеток в результате активна материнская Х-хромосома, а в других — отцовская. Таким образом, все девочки оказываются мозаичными, потому что в разных клетках работают разные копии генов. Классическим примером такой мозаичности являются черепаховые кошки : на их Х-хромосоме находится ген, отвечающий за меланин (пигмент, определяющий, среди прочего, цвет шерсти). В разных клетках работают разные копии, поэтому окраска получается пятнистой и не передается по наследству, так как инактивация происходит случайным образом.
При этом Х-хромосомы служат не только для определения пола, но и несут более 800 генов (то есть в два раза больше, чем лишняя 21-я хромосома, доставляющая немало хлопот организму). Но девочкам приходит на помощь естественный механизм устранения неравенства: одна из Х-хромосом инактивируется, скручивается и превращается в тельце Барра . В большинстве случаев выбор происходит случайно, и в ряде клеток в результате активна материнская Х-хромосома, а в других — отцовская. Таким образом, все девочки оказываются мозаичными, потому что в разных клетках работают разные копии генов. Классическим примером такой мозаичности являются черепаховые кошки : на их Х-хромосоме находится ген, отвечающий за меланин (пигмент, определяющий, среди прочего, цвет шерсти). В разных клетках работают разные копии, поэтому окраска получается пятнистой и не передается по наследству, так как инактивация происходит случайным образом.
В результате инактивации в клетках человека всегда работает только одна Х-хромосома. Этот механизм позволяет избежать серьезных неприятностей при Х-трисомии (девочки ХХХ) и синдромах Шерешевского — Тернера (девочки ХО) или Клайнфельтера (мальчики ХХY). Таким рождается примерно один из 400 детей, но жизненные функции в этих случаях обычно не нарушены существенно, и даже бесплодие возникает не всегда. Сложнее бывает тем, у кого хромосом больше трех. Обычно это значит, что хромосомы не разошлись дважды при образовании половых клеток. Случаи тетрасомии (ХХХХ, ХХYY, ХХХY, XYYY) и пентасомии (XXXXX, XXXXY, XXXYY, XXYYY, XYYYY) встречаются редко, некоторые из них описаны всего несколько раз за всю историю медицины. Все эти варианты совместимы с жизнью, и люди часто доживают до преклонных лет, при этом отклонения проявляются в аномальном развитии скелета, дефектах половых органов и снижении умственных способностей. Что характерно, дополнительная Y-хромосома сама по себе влияет на работу организма несильно. Многие мужчины c генотипом XYY даже не узнают о своей особенности. Это связано с тем, что Y-хромосома сильно меньше Х и почти не несет генов, влияющих на жизнеспособность.
Этот механизм позволяет избежать серьезных неприятностей при Х-трисомии (девочки ХХХ) и синдромах Шерешевского — Тернера (девочки ХО) или Клайнфельтера (мальчики ХХY). Таким рождается примерно один из 400 детей, но жизненные функции в этих случаях обычно не нарушены существенно, и даже бесплодие возникает не всегда. Сложнее бывает тем, у кого хромосом больше трех. Обычно это значит, что хромосомы не разошлись дважды при образовании половых клеток. Случаи тетрасомии (ХХХХ, ХХYY, ХХХY, XYYY) и пентасомии (XXXXX, XXXXY, XXXYY, XXYYY, XYYYY) встречаются редко, некоторые из них описаны всего несколько раз за всю историю медицины. Все эти варианты совместимы с жизнью, и люди часто доживают до преклонных лет, при этом отклонения проявляются в аномальном развитии скелета, дефектах половых органов и снижении умственных способностей. Что характерно, дополнительная Y-хромосома сама по себе влияет на работу организма несильно. Многие мужчины c генотипом XYY даже не узнают о своей особенности. Это связано с тем, что Y-хромосома сильно меньше Х и почти не несет генов, влияющих на жизнеспособность.
У половых хромосом есть и еще одна интересная особенность. Многие мутации генов, расположенных на аутосомах, приводят к отклонениям в работе многих тканей и органов. В то же время большинство мутаций генов на половых хромосомах проявляется только в нарушении умственной деятельности. Получается, что в существенной степени половые хромосомы контролируют развитие мозга. На основании этого некоторые ученые высказывают гипотезу, что именно на них лежит ответственность за различия (впрочем, не до конца подтвержденные) между умственными способностями мужчин и женщин.
Кому выгодно быть неправильным
Несмотря на то что медицина знакома с хромосомными аномалиями давно, в последнее время анеуплоидия продолжает привлекать внимание ученых. Оказалось , что более 80% клеток опухолей содержат необычное количество хромосом. С одной стороны, причиной этому может служить тот факт, что белки, контролирующие качество деления, способны его затормозить. В опухолевых клетках часто мутируют эти самые белки-контролеры, поэтому снимаются ограничения на деление и не работает проверка хромосом.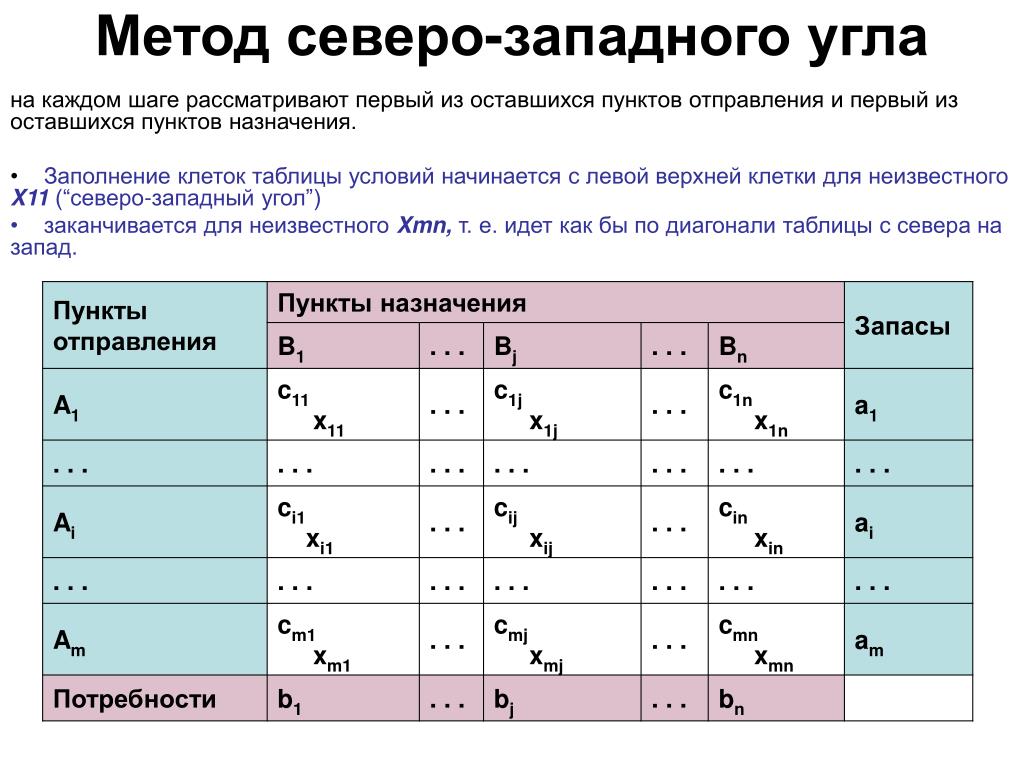 С другой стороны, ученые полагают , что это может служить фактором отбора опухолей на выживаемость. Согласно такой модели, клетки опухоли сначала становятся полиплоидными, а дальше в результате ошибок деления теряют разные хромосомы или их части. Получается целая популяция клеток с большим разнообразием хромосомных аномалий. Большинство из них нежизнеспособны, но некоторые могут случайно оказаться успешными, например если случайно получат дополнительные копии генов, запускающих деление, или потеряют гены, его подавляющие. Однако если дополнительно стимулировать накопление ошибок при делении, то клетки выживать не будут. На этом принципе основано действие таксола — распространенного лекарства от рака: он вызывает системное нерасхождение хромосом в клетках опухоли, которое должно запускать их программируемую гибель.
С другой стороны, ученые полагают , что это может служить фактором отбора опухолей на выживаемость. Согласно такой модели, клетки опухоли сначала становятся полиплоидными, а дальше в результате ошибок деления теряют разные хромосомы или их части. Получается целая популяция клеток с большим разнообразием хромосомных аномалий. Большинство из них нежизнеспособны, но некоторые могут случайно оказаться успешными, например если случайно получат дополнительные копии генов, запускающих деление, или потеряют гены, его подавляющие. Однако если дополнительно стимулировать накопление ошибок при делении, то клетки выживать не будут. На этом принципе основано действие таксола — распространенного лекарства от рака: он вызывает системное нерасхождение хромосом в клетках опухоли, которое должно запускать их программируемую гибель.
Получается, что каждый из нас может оказаться носителем лишних хромосом, по крайней мере в отдельных клетках. Однако современная наука продолжает разрабатывать стратегии борьбы с этими нежеланными пассажирами. Одна из них предлагает использовать белки, отвечающие за Х-хромосому, и натравить, например, на лишнюю 21-ю хромосому людей с синдромом Дауна. Сообщается , что на клеточных культурах этот механизм удалось привести в действие. Так что, возможно, в обозримом будущем опасные лишние хромосомы окажутся укрощены и обезврежены.
Одна из них предлагает использовать белки, отвечающие за Х-хромосому, и натравить, например, на лишнюю 21-ю хромосому людей с синдромом Дауна. Сообщается , что на клеточных культурах этот механизм удалось привести в действие. Так что, возможно, в обозримом будущем опасные лишние хромосомы окажутся укрощены и обезврежены.
Полина Лосева
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Онлайн калькулятор | Добро пожаловать в Dr.M.G.R LANETM
сен 6 2013
Вот интересный способ найти CPM (метод критического пути) с использованием PERT с нажмите здесь.
Источник: http://easycalculation.com
Нравится:
Нравится Загрузка…
Автор: mgrplanetm І Опубликовано в Онлайн калькулятор Метод критического пути с тегами, математические формулы, математический онлайн-калькулятор, калькулятор PERTфевраль 26 2013
Вот интересный путь для решения проблемы транспорта с использованием метода аппроксимации Фогеля с Нажмите здесь
Источник: . декабрь
9
2012 Вот интересный способ решить проблему последовательности заданий с помощью нажмите здесь Источник: http://easycalculation.com Нравится Загрузка… декабрь
7
2012 Вот интересный способ вычислить производную функции с помощью нажмите сюда Источник: http://easycalculation.com Нравится Загрузка…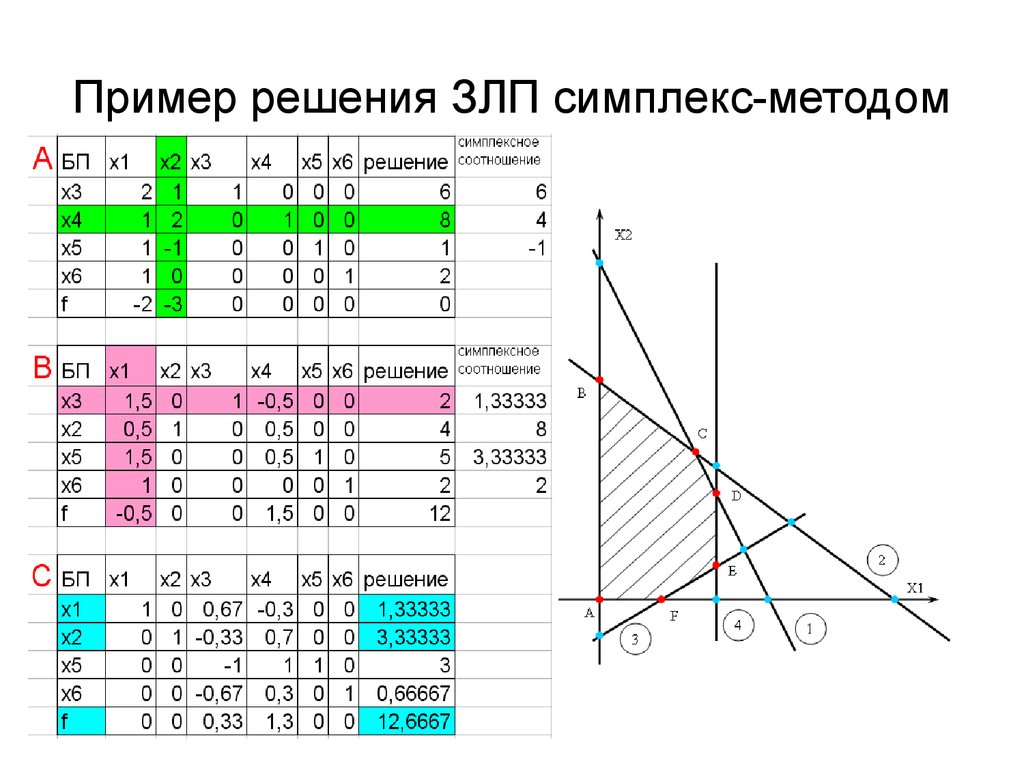 ..
.. Нравится:
Вот так:
С М Т Вт Т Ф С 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Введите свой адрес электронной почты, чтобы подписаться на ПЛАНЕТМ и получать уведомления о новых сообщениях по электронной почте.
Адрес электронной почты:
Присоединиться к 65 другим подписчикам
- КАНИТАМ 2020
- Объявления №7
- НЕЧЕТКАЯ ТЕХНОЛОГИЯ
- Зачем изучать алгебру
- Математика в бадминтоне
- Величайшие математики
- История (википедия)
- История Пи
- Бесплатные онлайн-журналы по математике(1)
- Бесплатные онлайн-журналы по математике(2)
- Бесплатные онлайн-журналы по математике(3)
- Магазин Plus
- Пушистая техника
- ЛИНДО
- Математика
- Математический игрок
- Максима
- Бесплатное математическое программное обеспечение Microsoft
- Sage Математическое программное обеспечение с открытым исходным кодом
- SCILAB
- Более подробное объяснение
- электронные заметки
- IEEE
- Академия Хана
- М4математика
- Математические лакомства
- Учебная математика
- НПТЕЛ (ИИТ Мадрас)
- Математический онлайн-калькулятор
- Онлайн-заметки Пола по математике
- Савал
- Наука Директ
- Студент технологии
- Игрушки из мусора
- Преобразование Фурье
- Особенности исчисления
- Математический микроскоп
- Теория вероятностей и Интернет
- 16 288 просмотров
- Регистрация
- Вход
- Лента записей
- Лента комментариев
- WordPress.
 com
com
Блог на WordPress.com.
%d блоггерам нравится это:
wiki.pengtools.com Руководства и документация по программному обеспечению для нефтяной инженерии
Взято с wiki.pengtools.com
Перейти к: навигация, поиск
Содержание
- 1 Программное обеспечение для нефтяной инженерии
- 2 пенгтулса
- 3 Почему?
- 4 преимущества
Программное обеспечение для нефтяной инженерии
pengtools стенды для p etroleum eng ineering tools .
pengtools — это веб-сайт, который предоставляет онлайн-программное обеспечение для разработки нефтяных месторождений, основанное на ноу-хау разработчика.
pengtools создан инженерами-практиками, чтобы помочь инженерам-практикам решать типичные инженерные задачи для эффективного принятия решений в области разработки месторождений нефти, месторождений, гидроразрыва пласта и технологических процессов.
Зарегистрируйтесь и начните свой первый расчет прямо сейчас на сайте www.pengtools.com.
pengtools
- Калькулятор PVT — создание быстрых моделей свойств жидкости PVT
- PQplot — расчет узлового анализа по скважинам
- sPipe — расчет перепада давления в поверхностных трубах
- PhaseD — расчет фазовой диаграммы
- optiFrac — определите оптимальную геометрию трещины
- optiFracMS — расчет графика закачки для достижения заданной геометрии
- fracDesign — расчет оптимального количества трещин в горизонтальной скважине
- pumpDesign — проектирование ЭЦН для откачки скважины
- onPlan — быстродействующий симулятор плоскостного разрыва, позволяющий уточнить конструкцию в сложных сценариях
Почему?
Помните старые времена Программное обеспечение для нефтяной инженерии?
- Дорогой
- ПК на базе
- Черный ящик
- Сложно установить (требуются права администратора)
- Трудно учиться
- Hard to Run
В дни нашей инженерной практики мы обычно изучаем и используем все виды инженерного программного обеспечения на базе ПК, которое иногда не интуитивно понятно и требует длительного обучения, чтобы найти ответ. Представьте, что вы можете заниматься профессиональным проектированием, просто используя веб-сайт!
Представьте, что вы можете заниматься профессиональным проектированием, просто используя веб-сайт!
Идея создания простых в использовании онлайн-инструментов для нефтегазовой инженерии привела к разработке инструментов pengtools .
Преимущества
- Надежные алгоритмы приводят к реальным решениям
- Интуитивно понятный интерфейс позволяет быстро получать ответы
- Веб-архитектура позволяет работать из дома, используя любую платформу, в любом месте, круглосуточно и без выходных
- Инженерное облако предоставляет средства для совместной работы и обмена данными с коллегами и клиентами
- Мгновенное переключение между метрическими и полевыми единицами измерения позволяет работать в различных условиях
- Экспорт отчетов в Excel и PDF позволяет завершить и опубликовать вашу работу
Подкатегории
Эта категория имеет следующие 9 подкатегорий, всего 9.
F
► FracDesign (8 P)
O
► OnPlan (4 Т)
► OptiFrac (6 шт.
 )
)► OptiFracMS (7 шт.)
P
► PhaseD (1 P)
► PQplot (12 Т)
► Дизайн насосов (3 шт.)
► PVT (20 стр.)
S
► Трубка (2 шт.)
Страницы в категории «Pengtools»
Следующие 55 страниц относятся к этой категории, всего 55 страниц.
4
- 4/π потенциал стимулированных лунок
6
- 6/π потенциал стимулированных скважин
B
- корреляция Beggs0 и 183
- Корреляция вязкости нефти Беггса и Робинсона
D
- Закон Дарси
- ДФИТ
- Корреляция Дранчука
Е
- Насос электрический погружной
- Скорость эрозии
- Каталог ESP
- Диаграмма ESP Tornado
F
- Корреляция веера
- Корреляция сжимаемости нефти Фаршад
- Сравнительное исследование FracDesign 1 Warpinski
G
- Коэффициент сжимаемости газа
- Межфазное натяжение газ/масло
- Межфазное натяжение газ/вода
- ГЛР
- ГОР
- Серая корреляция
- Корреляция Гриффита
H
- Корреляция Хагедорна и Брауна
- Гидравлический разрыв пласта
- Оптимизация конструкции гидроразрыва пласта — пример компании Bakken
- Каталог проппантов для ГРП
L
- Корреляция Lee
- Загрузка жидкости
M
- McCain Корреляция плотности нефти
- McCain Уравнение коэффициента объема нефтяного пласта
O
- OGR
- Сравнительное исследование OnPlan 1 Венг
- Сравнительное исследование OnPlan 2 Warpinski
- OptiFrac
- OptiFracMS
P
- Хронология разработки месторождений нефти
- PQplot
- Инструмент PVT
S
- Наконечник
V
- Корреляция давления насыщения Валко — Маккейна
- Соотношение сжимаемости нефти Васкеса и Беггса
- Корреляция отношения газа к раствору Velarde
- VLP
W
- Давление насыщения водой
- Сжимаемость воды
- Плотность воды
- Объемный коэффициент водообразования
- Соленость воды из уравнения плотности
- Концентрация твердых частиц в воде
- Вязкость воды
- ВКУТ
- ВГР
- WOR
Y
- Выход
Copyright © pengtools.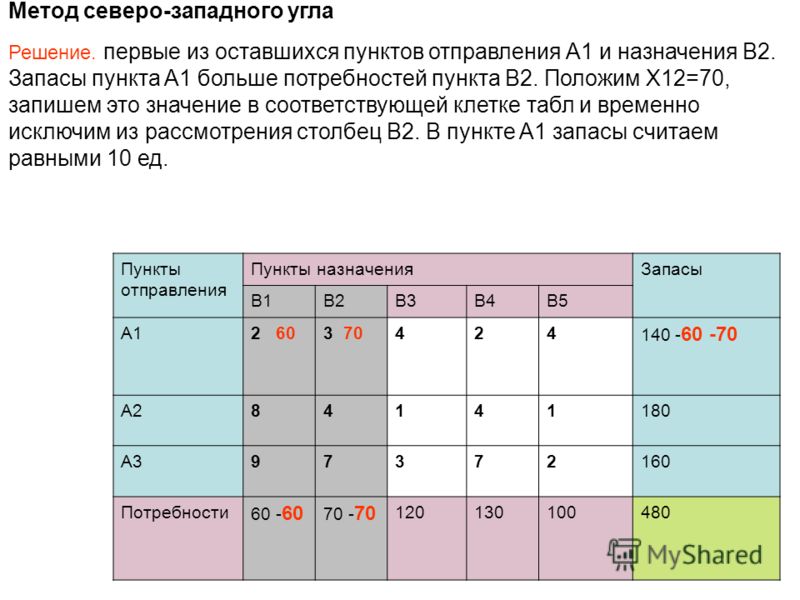 com. Petroleum Engineering Tools
com. Petroleum Engineering Tools
Новый подход к определению штрафных санкций за лучшее решение транспортной задачи – IJERT
Усовершенствованный метод приближения Фогеля (AVAM): новый подход к определению штрафных санкций за лучшее возможное решение транспортной задачи
Утпал Канти Дас Кафедра компьютерных наук и инженерии, IUBAT-
Международный университет бизнеса, сельского хозяйства и технологий, Уттара, Дакка-1230, Бангладеш,
Доктор Ашрафул Бабу, факультет математики, IUBAT-
Международный университет бизнеса, сельского хозяйства и технологий, Уттара, Дакка-1230, Бангладеш,
Аминур Рахман Хан Факультет математики, Джахангирнагар
Университет, Савар, Дакка-1342, Бангладеш,
Dr.Md. Факультет математики Шарифа Уддина, Джахангирнагарский университет, Савар, Дакка-1342, Бангладеш,
Abstract
В исследованиях операций получение значительных результатов по транспортным проблемам очень важно в наши дни.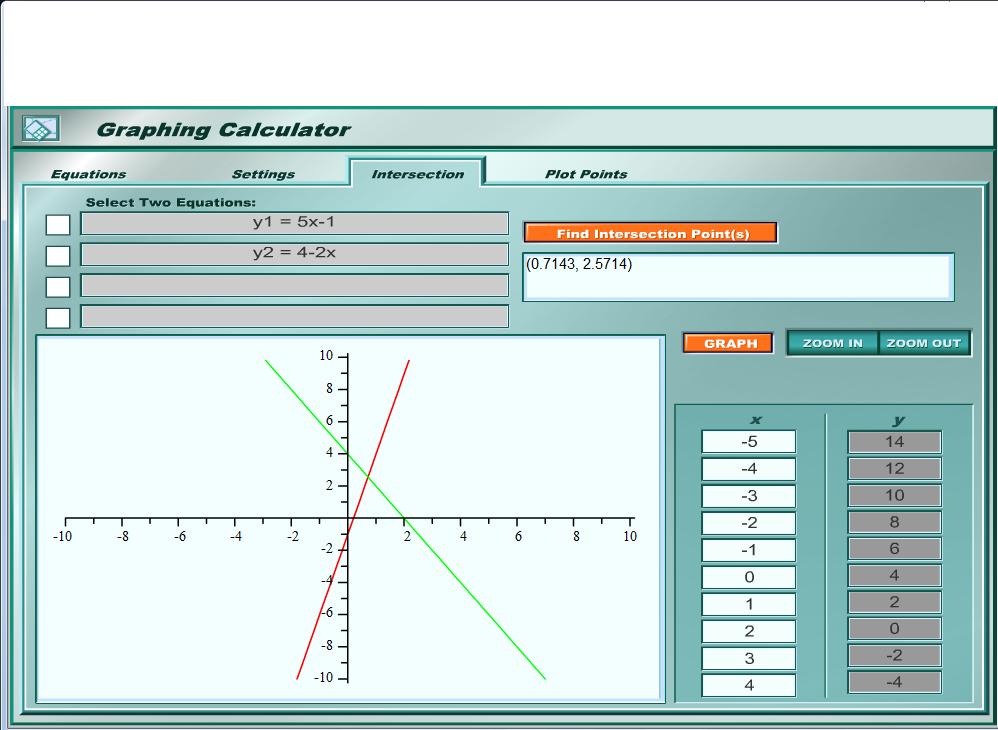 Метод аппроксимации Фогельса (VAM) является очень эффективным алгоритмом решения транспортной задачи для допустимого решения, которое ближе к оптимальному решению. В этой статье мы определили вычислительную ошибку в VAM и подошли к логическому развитию алгоритма VAM. Основная концепция VAM состоит в том, чтобы определить стоимость штрафа, которая получается из разницы наименьшей и ближайшей к наименьшей стоимости в каждой строке или столбце, и сделать максимальное распределение в самых низких
Метод аппроксимации Фогельса (VAM) является очень эффективным алгоритмом решения транспортной задачи для допустимого решения, которое ближе к оптимальному решению. В этой статье мы определили вычислительную ошибку в VAM и подошли к логическому развитию алгоритма VAM. Основная концепция VAM состоит в том, чтобы определить стоимость штрафа, которая получается из разницы наименьшей и ближайшей к наименьшей стоимости в каждой строке или столбце, и сделать максимальное распределение в самых низких
задачи линейного программирования (LPP), где метод аппроксимации Фогеля (VAM) известен как эффективный метод решения TP. Концепция штрафных затрат (разность наименьшей и ближайшей к наименьшей стоимости в строке или столбце) делает этот метод более эффективным, чем другие методы, такие как правило северо-западного угла (NWC), метод наименьших затрат (LCM) и т. д. Но способ определения стоимость штрафа нелогична для некоторых случаев; мы обсуждаем эти типы ситуаций в [-,-] и разработали алгоритм с новой концепцией, в котором трудности разрешаются в [-,-] и дают допустимое решение, очень близкое к оптимальному решению ниже, чем VAM.
Рассмотрим транспортную задачу с m источниками
стоимостной ячейкой той строки или столбца, которые имеют наибольшие
и n пунктов назначения, где Cij — штраф за транспортировку единицы. Трудность возникает, когда наименьшая стоимость и ближайшая к ней стоимость имеют одинаковую величину. В этом случае стоимость
от i-го источника до j-го пункта назначения. Пусть
Si будет
, мы нашли очень логичную концепцию для решения этой проблемы и разработали новый алгоритм Advanced Vogels Approximation Method (AVAM) для нахождения допустимого
объем поставки i-го источника и D – спрос
j
объем j-го пункта назначения. Мы должны найти
решение транспортной задачи, которое очень близко к
количеству перевезенного товара
xij
так, чтобы сумма
к оптимальному решению была больше, чем VAM.
Ключевое слово: AVAM, VAM, штрафные санкции, возможное решение, оценка погрешности, транспортная задача (TP).
Введение
Транспортная проблема — это реальная жизненная проблема, когда товары перемещаются с фабрики в розничную торговлю, так что общие транспортные расходы должны быть минимизированы. В исследовании операций ТП является особым классом
. Стоимость транспортировкибудет сведена к минимуму. Вышеупомянутая проблема в модели LPP может быть выражена следующим образом:
Свернуть:
м н
Общая стоимость Cij xij
i1 j 1
Тема:
п
xij Si
м
1
xij Dj i1
xij 0
для i 1, 2,……m (ограничения предложения) для j 1, 2,……n (ограничения спроса)
я, я
Шаг 3:
Определите строку и столбец с наибольшим штрафом, произвольно нарушая ничьи. Выделите как можно больше переменной с наименьшей стоимостью в выбранной строке или столбце. Отрегулируйте спрос и предложение и вычеркните удовлетворяющую строку или столбец. Если строка и столбец удовлетворяют одновременно, то только одна из них вычеркивается, а оставшаяся строка или столбец равна 9.
 0003
0003Мы должны преобразовать этот LPP в следующую математическую модель и применить методы транспортировки, чтобы найти допустимое решение.
назначено нулевое предложение или спрос.
Если два или более штрафа имеют одинаковую наибольшую величину, выберите любой из них (или выберите самый верхний ряд или крайний левый столбец).
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Дн
С1
С11
С12
С13
C1n
С1
С2
С21
С22
С23
C2n
С2
См
См1
см2
см3
Cмн
См
Спрос
Д1
Д2
Д3
Дн
Существующий алгоритм: метод аппроксимации Фогеля (VAM)
Метод аппроксимации Фогеля представляет собой итеративную процедуру вычисления базового допустимого решения транспортной задачи.
 Этот метод предпочтительнее двух методов, то есть правила северо-западного угла и метода наименьших затрат. Алгоритм VAM приведен ниже: Шаг-1:
Этот метод предпочтительнее двух методов, то есть правила северо-западного угла и метода наименьших затрат. Алгоритм VAM приведен ниже: Шаг-1:Определите ячейки с минимальной и ближайшей к ней минимальной стоимостью перевозки в каждой строке и запишите разницу (Штраф) сбоку от соответствующей строки таблицы.
Определите ячейки с минимальными и рядом с минимальными затратами на транспортировку в каждом столбце и запишите разницу (Штраф) вдоль края таблицы напротив соответствующего столбца.
Шаг 2: Если минимальная стоимость появляется два или более раз в строке или столбце, выберите эту же стоимость в качестве минимальной и рядом с минимальной стоимостью, и штраф будет равен нулю.
Шаг 4:
а. Если ровно одна строка или один столбец с нулевым спросом или предложением остается незачеркнутой, Стоп.
Если незачеркнутой остается только одна строка или столбец с положительным спросом или предложением, определите основные переменные в строке или столбце методом наименьших затрат.

Если во всех невычеркнутых строках или столбцах имеется (оставшийся) нулевой спрос или предложение, определяются нулевые базовые переменные методом наименьших затрат. Останавливаться.
В противном случае перейдите к шагу 1.
2.1. Нахождение вычислительной погрешности метода аппроксимации Фогельса (VAM)
Основной концепцией алгоритма VAM является штрафная стоимость, которая определяется разностью наименьшей и ближайшей к наименьшей стоимости каждой строки и столбца, где наивысший штраф указывает на то, что одно из значений двух минимальных затрат превышает другое. В этом случае VAM выбирает самую высокую стоимость штрафа и выделяет ячейку с самой низкой стоимостью в этой строке или столбце, чтобы избежать вероятности выбора более высокой стоимости в следующей итерации.
Если две или более ячеек имеют одинаковую наименьшую величину, то VAM выбирает эти самые наименьшие значения в качестве минимальных и рядом с минимальными значениями, и штраф будет равен нулю [2.
 Шаг 2]. В этом случае штраф будет самым низким в этой строке или столбце среди всех строк или столбцов, так что нет возможности выбрать эту строку или столбец для распределения товаров. Если в этой строке или столбце есть какие-либо более высокие затраты, кроме таких же наименьших затрат, то вероятность выбора более высокой стоимости в следующей итерации будет увеличена, и общая стоимость транспортировки может увеличиться.
Шаг 2]. В этом случае штраф будет самым низким в этой строке или столбце среди всех строк или столбцов, так что нет возможности выбрать эту строку или столбец для распределения товаров. Если в этой строке или столбце есть какие-либо более высокие затраты, кроме таких же наименьших затрат, то вероятность выбора более высокой стоимости в следующей итерации будет увеличена, и общая стоимость транспортировки может увеличиться.В алгоритме VAM распределение зависит от стоимости штрафа. Для этой вышеуказанной вычислительной ошибки, определяющей штраф в VAM, минимальная стоимость может быть не обеспечена на всех этапах, поэтому общая стоимость в допустимом решении может быть выше.
Предлагаемый алгоритм для расширенного метода аппроксимации Фогеля (AVAM)
Шаг 4:
Выберите макс(Pi , Pj ) . Набор
xij :Сумма
В этом разделе мы решили вычислительную ошибку VAM, которая обсуждалась выше, и предложили новый
товар из
источник
jth до места назначения;
Алгоритмпод названием Advanced Vogels Approximation Method (AVAM).
 В предложенном нами алгоритме (AVAM) при появлении наименьшей стоимости в двух или более
В предложенном нами алгоритме (AVAM) при появлении наименьшей стоимости в двух или болееВыберите самую низкую стоимость этой строки или столбца
, который имеет наибольший штраф и выделяет максимально возможную сумму
раза подряд или столбец, затем штраф определяется
хий
т.е. мин(Si , Dj ) . Если самая низкая стоимость
разница двух минимальных затрат, одна из которых принимается за минимальную, а следующая за ней наименьшая стоимость, кроме равных наименьших затрат, является ближайшей к минимальной. Например, если 3, 10, 3, 7, 9 являются стоимостью строки или столбца, тогда выберите 3 в качестве наименьшей стоимости и выберите 7 в качестве ближайшей к наименьшей стоимости вместо снова 3, и штраф будет равен 4. В этом случае случайный штраф не равен нулю, и если этот штраф имеет наибольшую величину, то вероятность того, что в следующей итерации будет взята большая стоимость, будет уменьшена, поскольку остается хотя бы еще одна наименьшая стоимость.
 Алгоритм АВАМ приведен следующим образом:
Алгоритм АВАМ приведен следующим образом:я
Шаг-1: Установить S : Объем поставки i-го источника;
и
Набор D: сумма спроса jth
пункт назначения;
появляются в двух или более ячейках в этой строке или столбце, затем выберите крайнюю левую или самую верхнюю ячейку с наименьшей стоимостью.
Если два или более штрафа имеют одинаковую наибольшую величину, выберите любой из них (или выберите самый верхний ряд или крайний левый столбец).
Шаг 5: Отрегулируйте спрос и предложение и вычеркните удовлетворяющую строку или столбец. Если строка и столбец удовлетворяются одновременно, то один из них вычеркивается, а в оставшейся строке или столбце устанавливается нулевой спрос или предложение.
Шаг-6:
Если ровно одна строка или один столбец с нулевым спросом или предложением остаются незачеркнутыми, Стоп.
Комплект
Сий
:Стоимость транспортировки единицы
с источником
Если только одна строка или столбец с положительным значением
спрос или предложение остается незачеркнутым,
до j-го пункта назначения;
определить основные переменные в строке или
Проверить: если Si 0 и Dj 0, то Стоп.

Шаг 2:
по методу наименьших затрат.
Если все невычеркнутые строки или столбцы имеют (оставшиеся) нулевые спрос или предложение,
ф
Si Dj или если
Си Диджей
определил нулевые базовые переменные по
и к и к
, затем сбалансируйте проблему транспортировки, добавив фиктивный спрос или предложение.
Установите Cij : 0 для всех фиктивных строк или столбцов.
Шаг 3:
Определите наименьшую и ближайшую к наименьшей стоимости каждую строку и столбец и вычислите разницу между ними, которая называется штрафом.
Set Pi : Штраф за строку и Set Pj : Штраф за столбец.
Пи | Чик Чик | и Пи | Chj Ckj |
Если наименьшая стоимость появляется два или более раз в строке или столбце, выберите один из них как наименьшую и следующую за ней меньшую стоимость, отличную от равной наименьшей стоимости, в качестве следующей наименьшей стоимости.

Если нет больше стоимости, кроме равной
Метод наименьших затрат. Останавливаться.
В противном случае перейдите к шагу 3.
Численное моделирование
Рассмотрим некоторые специальные типы транспортных задач, в которых наименьшая стоимость появляется в двух или более строках или столбцах, и решите их с помощью расширенного метода приближения Фогеля (AVAM) и сравните эти результаты с решением метода приближения Фогеля (VAM).
4.1. Пример-1
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
С1
6
8
10
9
50
С2
5
8
11
5
75
С3
6
9
12
5
25
Спрос
20
20
50
60
Рассмотрим математическую модель транспортной задачи, приведенную ниже:
наименьшие затраты
т.
 е.
е.все расходы такие же, как
выберите наименьший и ближайший к наименьшему одинаковый, и штраф будет равен нулю.
Таблица-1.1
Теперь решите эту проблему, используя AVAM и VAM соответственно, как показано ниже:
Решение примера 1 с использованием расширенного метода приближения Фогеля (AVAM):
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
С1
6
8
0
10
50
9
50
С2
5
15
8
11
5
60
75
С3
6
5
9
20
12
5
25
Спрос
20
20
50
60
Таблица 1.
 2 Общая стоимость транспортировки:
2 Общая стоимость транспортировки:(0 8) (50 10) (15 5) (60 5) (5 6)
(20 9) 1085
Решение примера 1 с использованием метода аппроксимации Фогеля (VAM):
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
С1
6
20
8
10
30
9
50
С2
5
8
20
11
20
5
35
75
С3
6
9
12
5
25
25
Спрос
20
20
50
60
Таблица 1.
 3 Общая стоимость перевозки:
3 Общая стоимость перевозки:(206) (3010) (208) (2011) (355) (255) 1100
Оптимальное решение примера 1:
Оптимальное решение примера 1, определенное MODI, равно 1060.
Пример-2
Рассмотрим математическую модель транспортной задачи, приведенную ниже:
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
4
4
9
8
13
100
С2
7
9
8
10
4
80
С3
9
3
7
10
6
70
С4
11
4
8
3
9
90
Спрос
60
40
100
50
90
Таблица 2.
 1
1Теперь решите эту проблему, используя AVAM и VAM соответственно, как показано ниже:
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
4
60
тд >
4
40
9
8
13
100
С2
7
9
8
10
4
80
80
С3
9
3
7
60
10
6
10
70
С4
11
4
0
8
40
3
50
9
90
Спрос
60
40
100
50
90
Решение примера 2 с использованием расширенного метода приближения Фогеля (AVAM):
Таблица 2.
 2 Общая стоимость транспортировки:
2 Общая стоимость транспортировки:(60 4) (40 4) (80 4) (60 7) (10 6)
(0 4) (40 8) (50 3) 1670
Решение примера 2 с использованием метода аппроксимации Фогеля (VAM):
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
4
60
4
0
9
40
8
13
100
С2
7
9
8
10
4
80
80
С3
9
3
7
60
10
6
10
70
С4
11
4
40
8
3
50
9
90
Спрос
60
40
100
50
90
Таблица 2.
 3
3Общая стоимость перевозки:
(60 4) (0 4) (40 9) (80 4) (60 7)
(10 6) (40 4) (50 3) 1710
Оптимальное решение примера 2:
Оптимальное решение примера 1, определенное MODI, равно 1670.
Пример 3:
Рассмотрим математическую модель транспортной задачи, приведенную ниже:
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
8
8
2
10
2
40
С2
11
4
10
9
4
70
С3
5
2
2
11
10
35
С4
10
6
6
5
2
90
С5
8
11
8
6
4
85
Спрос
80
55
60
80
45
Таблица:3.
 1
1Решение примера 3 с использованием расширенного метода приближения Фогеля (AVAM):
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
8
8
2
40
10
2
40
С2
11
4
55
10
9
4
15
70
С3
5
15
2
2
20
11
10
35
С4
10
6
6
5
60
2
30
90
С5
8
65
11
8
6
20
4
85
Спрос
80
55
60
80
45
Таблица:3.
 2 Общая стоимость перевозки:
2 Общая стоимость перевозки:(2 40) (4 55) (4 15) (5 15) (2 20)
(5 60) (2 30) (8 65) (6 20) 1475
Решение примера 3 с использованием метода аппроксимации Фогеля (AVAM):
Источник
Пункт назначения
Поставка
Д1
Д2
Д3
Д4
Д5
С1
8
8
2
40
10
2
40
С2
11
4
55
10
9
15
4
70
С3
5
15
2
2
20
11
10
35
С4
10
6
6
5
45
2
45
90
С5
8
65
11
8
6
20
4
85
Спрос
80
55
60
80
45
Таблица:3.
 3 Общая стоимость перевозки:
3 Общая стоимость перевозки:(2 40) (4 55) (9 15) (515) (2 20)
(5 45) (2 45) (8 65) (6 20) 1505
Оптимальное решение примера 3:
Оптимальное решение примера 1, определенное MODI, равно 1475.
Анализ результатов:
В приведенных выше примерах мы наблюдали, что усовершенствованный метод аппроксимации Фогельса (AVAM) дает более низкое возможное решение, чем метод аппроксимации Фогельса (VAM). Результаты с использованием AVAM очень близки или равны оптимальному решению. Сравнительная таблица результатов AVAM и VAM выглядит следующим образом:
Методы
Транспортные проблемы
Оптимальное решение
АВАМ
ВАМ
Пример-1
1060
1085
1100
Пример-2
1670
1670
1710
Пример-3
1475
1475
1505
Таблица: 5
Заключение
В этой статье мы исправили вычислительную ошибку метода аппроксимации Фогельса (VAM) и предложили новый алгоритм, названный усовершенствованным методом аппроксимации Фогельса (AVAM).
 Из приведенных выше примеров видно, что AVAM дает более низкое допустимое решение, чем VAM, и оно очень близко к оптимальному решению или равно оптимальному решению.
Из приведенных выше примеров видно, что AVAM дает более низкое допустимое решение, чем VAM, и оно очень близко к оптимальному решению или равно оптимальному решению.Ссылки
Хамди А. Таха. Исследование операции: введение,
Восьмое издание, ISBN-13: 978-0132555937
П. Рама Мурти. Операционные исследования, второе издание,
ISBN (13): 978-81-224-2944-2
Оптимизирующее системное программное обеспечение TORA, разработанное Hamdy A Taha.
Хиллер, Ф. С. и Г. Дж. Либерман. 1995. Введение в исследование операций, 6-е изд. Нью-Йорк: McGraw-Hill, Inc.
Мд. Амирул Ислам, Аминур Рахман Хан, М. Шариф Уддин и М. Абдул Малек Определение основного возможного решения транспортной проблемы: новый подход Научный журнал Джахангирнагарского университета, Vol. 35, № 1, стр. 101 108, ISSN 1022-8594 (2012).
Аминур Рахман Хан Решение транспортной проблемы: алгоритмический подход Научный журнал Джахангирнагарского университета, Vol.
 34, № 2, стр. 49-62 ISSN 1022-8594 (2011).
34, № 2, стр. 49-62 ISSN 1022-8594 (2011).
Calculating Physiochemical Properties
Drug Discovery Resources
- Home
- About CMC
- News
- NewsCategories
- Course
- Publications
- Drug Discovery Resources
- Stage Definitions
- Target Validation
- Hit Identification
- Lead Идентификация
- Оптимизация свинца
- Биоизостеры
- Металлохелатирование
- Молекулярные взаимодействия
- Solvation and desolvation
- Structure-based Design
- PhysicoChem
- Solubility
- PKa
- LogD
- Tuning basicity
- Separation of PK and PD
- ADME Properties
- Pre-Clinical Toxicity
- Разное
- Доклинический контрольный список
- Контакты
- Журнальные ленты
Существует ряд веб-сайтов, которые предоставляют расчеты собственности, однако будьте осторожны, чтобы не размещать конфиденциальную информацию.
pKa — Трудно точно рассчитать, есть несколько сайтов, которые дают экспериментально определенные данные.
Данные pKa, составленные Дэвидом Рипином и Дэвидом Эвансом (Гарвардский университет) Кислотность таблицы Bordwell pKa в ДМСО (Университет Висконсина) Цирхром список из более чем 600 кислот и оснований
См. также:- Константы диссоциации органических оснований в водном растворе. Д.Д. Перрин. Баттервортс, 1965 год. Константы диссоциации органических кислот в водном растворе. Г.Кортум, В.Фогель и К.Андруссов. Баттерворт, 19 лет61.
Для Marvin доступны различные плагины для расчетов. Он имеет богатый (и растущий) список функций редактирования, знает химические вещества и может вызывать плагины ChemAxon для расчетов на основе структур для структур на холсте.
Имеется несколько демонстрационных страниц
Этот сайт предоставляет бесплатные онлайн-инструменты, которые помогают выполнять задачи вычислительной химии, ADME/T и хемоинформатики, включая построение и визуализацию химических структур, расчет молекулярных свойств и анализ взаимосвязей между химической структурой и свойствами
Интерактивное программное обеспечение включает:-
- ALOGPS 2.
 1 — наиболее точная программа для прогнозирования липофильности и растворимости молекул в воде
1 — наиболее точная программа для прогнозирования липофильности и растворимости молекул в воде - ASNN вычисляет модели нелинейных нейронных сетей с высокой степенью прогнозирования
- E-BABEL — центр обмена информацией о молекулярной структуре
- PNN производит четко интерпретируемые аналитические нелинейные модели
- PCLIENT генерирует более 3000 дескрипторов
- E-DRAGON вычисляет молекулярные индексы DRAGON
- PLS реализует оригинальную двухэтапную процедуру выбора дескрипторов
- UFS создает сокращенный набор данных, который не содержит избыточности и минимальной степени мультиколлинеарности
Обобщает опубликованные экспериментальные данные о соединениях и предоставляет услуги по прогнозированию свойств с использованием платформы ACDLabs Percepta, инструментов EPISuite и ChemAxon
Помимо огромного количества биологических данных, ChEMBL также сопоставляет опубликованные физико-химические данные и генерирует ряд рассчитанных свойств для каждого молекула.
SPARC выполняет автоматизированное рассуждение в химии
Текущие реализации (выбранные ссылки):
- pKa, Основная ссылка: Хилал, Саид, С. В. Карикхофф и Л. А. Каррейра, «Тщательный тест для моделей химической реактивности SPARC: оценка более 4300 ионизационных pKa», Quant. Структура Действовать. Отн., 14, 348 1995.
- Физические свойства, Основные ссылки: S.H. Хилал, Л.А. Каррейра и С.В. Карикхофф, «Прогнозирование давления паров, температуры кипения, теплоты парообразования и коэффициента диффузии органических соединений», QSAR & Combinatorial Science, 565 22 (2003). С.Х. Хилал, Л.А. Каррейра и С.В. Карикхофф, «Прогнозирование растворимости, коэффициента активности, коэффициентов распределения газа/жидкости и жидкости/жидкости органических соединений», QSAR и комбинаторная наука, 23 709(2004).
- Гидролиз
Основные ссылки: С. Х Хилал, С.В. Карикхофф, Л.А. Каррейра и Б.П. Шреста «Оценка констант скорости гидролиза эфира карбоновой кислоты», QSAR & Combinatorial Science, 22,917 (2003)
Тэд С.
 Уайтсайд, С. Хилал и Л. А. Каррейра, «Оценка констант скорости гидролиза эфиров фосфорной кислоты I. Щелочной гидролиз», QSAR & Combinatorial Science, 24,1 (2005)
Уайтсайд, С. Хилал и Л. А. Каррейра, «Оценка констант скорости гидролиза эфиров фосфорной кислоты I. Щелочной гидролиз», QSAR & Combinatorial Science, 24,1 (2005) - Гидратация Основная ссылка: С.Х. Хилал, Л.Л. Борнандер, Л.А. Каррейра и С.В. Карикхофф, «Константы равновесия гидратации альдегидов, кетонов и хиназолинов», QSAR & Combinatorial Science, 24,631 (2005).
- Электронное сродство Основная ссылка: SH Hilal, S.W. Карикхофф, Л.А. Каррейра и К.М. Мелтон «Предсказание сродства к электрону с помощью компьютера», Quant. Структура Действовать. Отн. 12, 389 (1993).
- Теплота образования Основные ссылки: Тэд С. Уайтсайд и Лайонел А. Каррейра «Прогнозирование энтальпии образования углеводородов с использованием SPARC», J. Theo. И Комп. хим. 3451 (2004 г.) Тэд С. Уайтсайд и Лайонел А. Каррейра «Прогнозирование энтальпии образования галогенированных углеводородов с использованием SPARC», J. Theo. и комп. хим. 4461 (2005 г.).
Является составной частью внутренней системы регистрации веществ Actelion.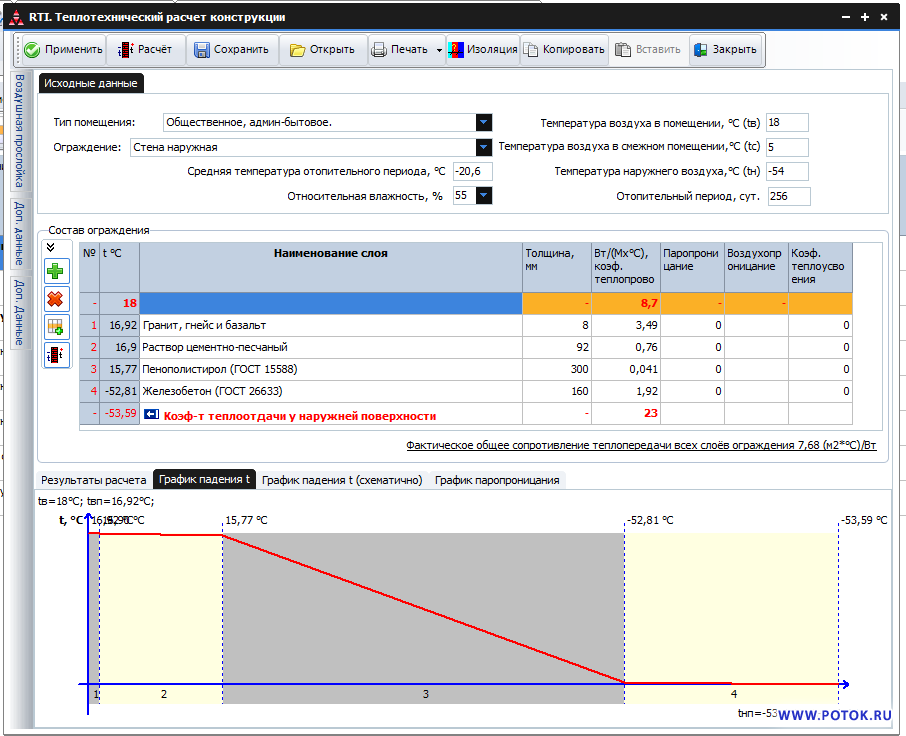 Она позволяет рисовать химические структуры и вычислять на лету различные свойства, связанные с лекарствами, когда структура действительна. Результаты прогнозирования оцениваются и кодируются цветом. Свойства с высоким риском нежелательных эффектов, таких как мутагенность или плохое всасывание в кишечнике, показаны красным цветом. Принимая во внимание, что зеленый цвет указывает на поведение, соответствующее наркотикам.
Она позволяет рисовать химические структуры и вычислять на лету различные свойства, связанные с лекарствами, когда структура действительна. Результаты прогнозирования оцениваются и кодируются цветом. Свойства с высоким риском нежелательных эффектов, таких как мутагенность или плохое всасывание в кишечнике, показаны красным цветом. Принимая во внимание, что зеленый цвет указывает на поведение, соответствующее наркотикам.
Те же свойства можно рассчитать в Datawarrior.
Многие настольные приложения включают LogP и другие калькуляторы свойств, включая Vortex, ChemDraw, ChemDoodle, Molinspiration, платформу ACDLabs Percepta, Stardrop.
Наборы инструментов Cheminformatics также предоставляют средства для программного доступа к некоторым вычисляемым свойствам OpenBabel, RDKit и CDK
Важно отметить, что все они используют разные алгоритмы, поэтому, если вы начнете использовать один пакет, вы не обязательно сможете сравнивать результаты с другим упаковка.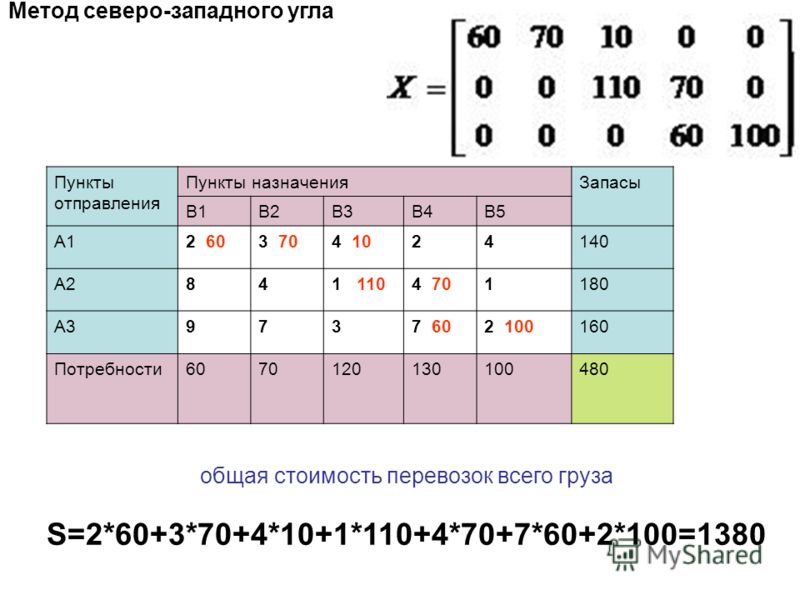 Поэтому, если вы хотите изменить, вам нужно будет пересчитать все старые результаты. Какой бы пакет вы ни использовали, всегда важно получить экспериментальные результаты для пары репрезентативных примеров. Это даст вам представление о точности любых вычисленных результатов.
Поэтому, если вы хотите изменить, вам нужно будет пересчитать все старые результаты. Какой бы пакет вы ни использовали, всегда важно получить экспериментальные результаты для пары репрезентативных примеров. Это даст вам представление о точности любых вычисленных результатов.
На веб-сайте Sirius Analytical доступен ряд интересных вебинаров, постеров и презентаций (требуется регистрация). Они посвящены измерению и использованию различных физико-химических свойств, включая pKa, LogP и растворимость.
Приложение Medicinal Chemistry Toolkit
Приложение Medicinal Chemistry Toolkit для iOS представляет собой набор ресурсов для поддержки повседневной работы химика-медика. Основываясь на опыте экспертов в области медицинской химии, мы разработали труднодоступные инструменты в портативном формате для использования на совещаниях, в дороге и в лаборатории. Приложение оптимизировано для iPad и содержит функции калькулятора, предназначенные для облегчения процесса вычисления значений: Cheng-Prusoff; Доза для человека; свободная энергия Гиббса к константе связи; Калькулятор максимальной абсорбируемой дозы; Изменение потенции из-за связывания с белками плазмы.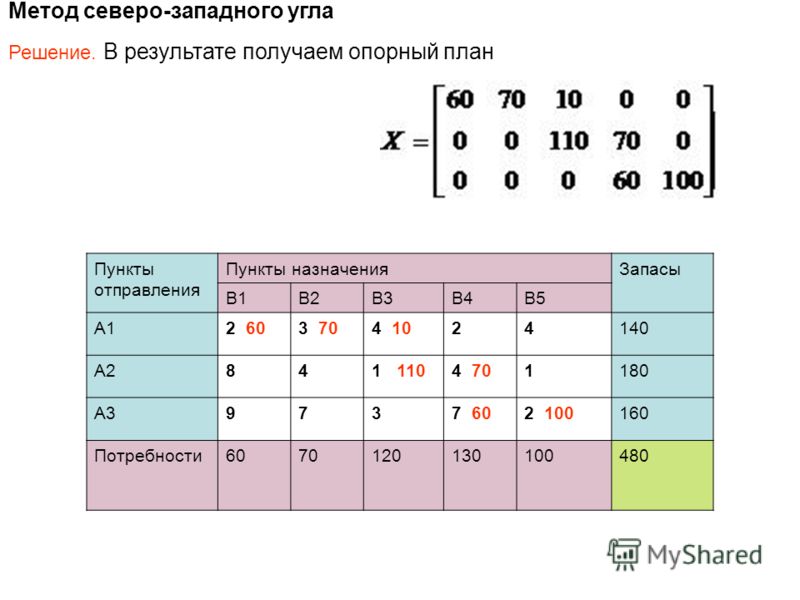
Asteris может рассчитать ряд простых «основных свойств», таких как logP, молекулярная масса, площадь полярной поверхности и количество доноров и акцепторов водородных связей.
Последнее обновление 15 декабря 2019 г.
Создание простого калькулятора в Kotlin с помощью Android Studio | Автор Tanu N Prabhu
В этом уроке мы узнаем, как создать простой калькулятор на Kotlin с помощью Android Studio.
Кредиты: DigitstoryОписание
В этом уроке мы разработаем « 10-клавишный -дюймовый калькулятор на Android Studio с использованием Kotlin. Включенные кнопки должны быть:
- Цифровые клавиши: « 1 », « 2 », « 3 », « 4 », « 5 », «0 50006»,
6 7
», « 8 », « 9 », « 0 ». - Операционные клавиши: « + », « — », « * », « / »
- Другие клавиши: « = », « CLEAR».

6 Здесь «
CLEAR ” клавиша должна очистить экран и все в памяти. Клавиша «=» должна применить операцию и выдать результат. - Дополнительно калькулятор будет иметь клавишу « DEL », которая аналогична «возврату» и удаляет последний символ на экране.
- А “ . ” должна показывать десятичную дробь.
Теперь мы знаем, как должен выглядеть и работать наш калькулятор, давайте приступим. Я постараюсь предоставить все основные шаги, чтобы вы поняли.
Шаг 1: Создайте «пустое действие» в Android Studio.
Давайте создадим новый проект. Поскольку наш калькулятор содержит только одно действие (нам нужен только один файл действия Kotlin и один файл макета XML), нам нужно выбрать « пустое действие ». Это можно сделать, как показано ниже:
Новый → Новый проект → Пустая активность
Создание пустой активности в студии Android После создания пустой активности настройте свои проекты, такие как имя, имя пакета, местоположение, язык и Уровень API. Следуйте приведенному ниже снимку экрана, чтобы настроить проект для согласованности. Убедитесь, что вы выбрали язык Kotlin (очевидно, я пишу код на Kotlin). Затем нажмите «Готово», после чего ваш проект будет загружен.
Следуйте приведенному ниже снимку экрана, чтобы настроить проект для согласованности. Убедитесь, что вы выбрали язык Kotlin (очевидно, я пишу код на Kotlin). Затем нажмите «Готово», после чего ваш проект будет загружен.
Чтобы узнать больше об уровне API, вы можете обратиться к официальной документации Google, приведенной ниже. Не обязательно выбирать API 15, как показано на снимке экрана выше. Просто выберите его для согласованности ради учебника.
Кодовые имена, теги и номера сборки | Проект Android с открытым исходным кодом
Разрабатываемые выпуски Android организованы в семейства с алфавитными кодовыми именами, вдохновленными вкусными угощениями…
source.android.com
Шаг 2. Добавление цветов в файл colors.xml
Как следует из названия файлов цветов, мы можем указать цвета для всех кнопок калькулятора. Файл colors.xml можно найти в:
app →res →values →colors.xml
xml версия = "1.0" кодировка = "utf-8" ?>
< ресурсы >
< color name="colorPrimary" >#000000 color >
< color name = "white" > >#ffffff5 color01
< color name="colorPrimaryDark" >#cccccc color >
< color name="colorAccent" >#FF4081 color >
< color name = "actionButton" >#808080 цвет >
< color name = "equalButton" >#FF0000 color >
< color name="numberActionButton" >#000000 color >
># color name = "numberAction0006" >#000000 color name = "numberAction0006" 373737 цвет >
ресурсы >
Шаг 3: Изменение файла styles.xml
Файл стиля используется для определения формата или внешнего вида пользовательского интерфейса. Стиль можно применить к отдельному
Стиль можно применить к отдельному View (из файла макета) или ко всему действию или приложению (из файла манифеста).
Файл styles.xml можно найти в
app →res →values →styles.xml
< resources >
< style name="AppTheme" parent="Theme.AppCompat.Light.DarkActionBar" >
< имя элемента = "основной цвет" >@color/colorPrimary item >
< item name="colorPrimaryDark" >@color/colorPrimaryDark item >
< item name="colorAccent" >@color/colorAccent item >
style >
< style name="ActionButtonStyle" >
< item name="android:layout_width" >0dp item >
< item name="android:layout_height" >match_parent item >
< item name="android:layout_weight" >1 item >
< item name= "android:background" >@color/actionButton item >
< item name = "android:textSize" >21sp item >
< item name="android:textColor" > @android:цветной/белый пункт >
< item name="android:gravity" >center item >
< item name="android:layout_margin" >0.5dp item >
5 style >
< style name="NumberButtonStyle" >
< item name="android:layout_width" >0dp item >
< item name="android:layout_height" >match_parent item >
< item name="android:layout_weight" >1 item >
< item name="android:background" >@color/numberActionButton item >
< item name = "android:textSize" >21sp item >
< item name="android:textColor" >@android:color/white item >
< item name="android:gravity" >по центру item >
< item name="android:layout_margin" >0.5dp item >
style >
< style name="EqualButtonStyle" >
< item name="android:layout_width" >0dp item >
< item name="android:layout_height" >match_parent / элемент >
< элемент имя = "android: layout_weight" >1 item >
< item name="android:background" >@color/equalButton item >
< item name = "android:textSize" >21sp item >
< item name="android:textColor" >@android:color/white item >
< item name="android:gravity" >center item >
< item name="android:layout_margin" >0.5dp пункт >
стиль >
< style name="NumberActionButton2" >
< item name="android:layout_width" >0dp item >
< item name="android:layout_height" >match_parent / item >
< item name="android:layout_weight" >1 item >
< item name="android:background" >@color/numberActionButton2 item >
< item name ="android:textSize" >21sp item >
< item name="android:textColor" >@android:color/ белый item >
< item name="android:gravity" >center item >
< item name="android:layout_margin" >0.5dp item >
< / стиль >ресурсы >
Все вышеперечисленное — это просто свойства стиля для калькулятора, определенные в файле styles.xml.
ActionButtonStyle: Keys → CLEAR, /
NumberButtonStyle: Keys → 1, 2, 3, 4, 5, 6, 7, 8, 9, 0
Key →Actions Numbers *900 , -, +EqualButtonStyle: Key → =
Шаг 4: Настройка файла «activity_main.xml»
Это основной файл макета, здесь вам не нужно использовать редактор пользовательского интерфейса, вместо этого вы можете кодировать весь макет с использованием XML. Здесь мы можем использовать макет текстового представления, а не кнопки для клавиш. Я помещаю все текстовое представление в линейный макет. Это механический процесс из-за нескольких текстовых представлений. Так что просто следуй за мной прямо сейчас.
xml version="1.0" encoding="utf-8" ?>
< LinearLayout xmlns:android="http://schemas.android.com/apk/res/android"
xmlns:app= "http://schemas.android.com/apk/res-auto"
xmlns:tools="http://schemas.android.com/tools"
android:layout_width="match_parent"
android:layout_height="match_parent «
tools:context=".MainActivity"
android:background="@android:color/black"
android:orientation="vertical" >< TextView
android:id="@+id/tvExpression"
android:layout_width="match_parent"
android:layout_height="80dp"
android:textColor="@color/actionButton"
android:layout_gravity= «конец»
android:ellipsize="start"
android:singleLine="true"
android:textSize="40sp" />< TextView
android:id="@+id/tvResult"
android: layout_width="match_parent"
android:layout_height="100dp"
android:textColor="@color/white"
android:layout_gravity="end"
android:ellipsize="end"
android:singleLine="true"
android:textSize="30sp" />< LinearLayout
android:layout_width="match_parent"
android :layout_height="match_parent"
android:orientation="vertical" >< LinearLayout
android:layout_width="match_parent"
android:layout_height="0dp"
android:layout_weight="1"
android:orientation= "горизонтальный" >
< TextView
android:id="@+id/tvClear"
style="@style/ActionButtonStyle"
android:text="CLEAR" />< TextView
android:id="@+id /tvDivide"
style="@style/ActionButtonStyle"
android:text="/" />LinearLayout >
< LinearLayout
android:layout_width="match_parent" 9001ight="android:layout_height=" 0dp"
андроид:layout_weight="1"
андроид:ориентация="горизонтальный" >< TextView
android:id="@+id/tvSeven"
style="@style/NumberButtonStyle"
android:text="7" />< TextView
android:id=" @+id/tvEight"
style="@style/NumberButtonStyle"
android:text="8" />< TextView
android:id="@+id/tvNine"
style="@style/ NumberButtonStyle"
android:text="9" />< TextView
android:id="@+id/tvMul"
style="@style/NumberActionButton2"
android:text="*" />LinearLayout >
< LinearLayout
android:layout_width="match_parent"
android:layout_height="0dp"
android:layout_weight="12" android 2 :orientation="horizontal" >< TextView
android:id="@+id/tvFour"
style="@style/NumberButtonStyle"
android:text="4" />< TextView
android:id="@+id/tvFive"
style="@style/NumberButtonStyle"
android:text="5" />< TextView
android:id="@+id/tvSix"
style="@style/NumberButtonStyle"
android:text="6" />< TextView
android:id="@+id/tvMinus"
style="@style/NumberActionButton2"
android:text="-" />LinearLayout >
< LinearLayout
android :layout_width="match_parent"
android:layout_height="0dp"
android:layout_weight="1"
android:orientation="horizontal" >< TextView
android:id="@+id/tvOne"
style="@style/NumberButtonStyle"
android:text="1" />< TextView
android:id="@+id/tvTwo"
style="@style/NumberButtonStyle"
android:text="2" />< TextView
android:id="@+id/tvThree "
style="@style/NumberButtonStyle"
android:text="3" />< TextView
android:id="@+id/tvPlus"
style="@style/NumberActionButton2"
android:text="+" />LinearLayout >
< LinearLayout
android:layout_width="match_parent"
android:layout_height9="01pp" android:layout_weight="1"
android:orientation="horizontal" >< TextView
android:id="@+id/tvDot"
style="@style/NumberButtonStyle"
android:text="." />
< TextView
android:id="@+id/tvZero"
style="@style/NumberButtonStyle"
android:text="0" />< TextView
android:id="@+id/tvBack"
style="@style/NumberButtonStyle"
android:text ="DEL" />< TextView
android:id="@+id/tvEquals"
style="@style/EqualButtonStyle"
android:text="=" />LinearLayout >
LinearLayout >
LinearLayout >
Шаг 5: Размещение библиотеки построителя выражений внутри Gradle.
Я использовал библиотеку Expression Builder для вычисления выражений. С помощью репозитория GitHub я научился это делать. Я изо всех сил пытался использовать кнопку равенства для получения результата. Итак, теперь просто поместите библиотеку построителя выражений внутрь Gradle.
приложение → Gradle Scripts → build.gradle
Просто вставьте → compile ‘net. objecthunter:exp4j:0.4.8’ внутри build.gradle
objecthunter:exp4j:0.4.8’ внутри build.gradleШаг 6: Фактический код Kotlin для калькулятора
Во-первых, я добавляю 1, 2, 3,…..0, когда пользователи нажимают клавиши в текстовом представлении соответственно. Для этого я создал функцию с именем AssessmentExpression() , которая выполняет добавление к текстовому представлению. Затем в функции Equals я использую библиотеку Expression Builder и вызываю ее метод Expression Builder для выполнения вычислений. Код в значительной степени говорит сам за себя. Файл main_activity.kt можно найти в:
app → java →com.example.myapplicationcalculator →MainActivity.kt
В моем случае имя пакета com.example.myapplicationcalculator , в вашем случае оно может отличаться.
// Программа: main_activity.kt
// Автор: Тану. Н. Прабху
// Курс: CS 855
// Дата: 28.01.2019
// Задание 2
/* Описание: Эта программа помогает выполнять операции и вычисления
базового калькулятора*/
// -------------------------------------------------- ---------------- Пакет com.example.finalcalculator
Импорт Androidx.AppCompat.App.appCompatactivity
Import Android.os.Bundle
Import2.* МАМПИАЛЬНОЕ 69. net.objecthunter.exp4j.ExpressionBuilder класс MainActivity : AppCompatActivity()
{переопределить удовольствие onCreate(savedInstanceState: Bundle?)
.0012 setContentView(R. layout . activity_main )
{
)InstanceState( super/*Кнопки с цифрами*/
tvOne. setOnClickListener {
AssessmentExpression( "1" , clear = true )
}tvTwo. setOnClickListener {
оценкаВыражение( "2" , ясно = истина )
}tvThree. setOnClickListener {
оценкаВыражение( "3" , ясно = истина )
} tvFour.setOnClickListener {
оценкаВыражение( "4" , ясно = истина )
}tvFive. setOnClickListener {
AssessmentExpression( "5" , clear = true )
}tvSix. setOnClickListener {
оценкаExpression( "6" , ясно = правда )
}tvSeven. setOnClickListener {
AssessmentExpression( "7" , clear = true )
}tvEight. setOnClickListener {
AssessmentExpression( "8" , clear = true )
}tvNine. setOnClickListener {
оценкаExpression( "9" , очистить = правда )
}tvZero.
setOnClickListener {
AssessmentExpression( "0" , clear = true )
}/*Операторы
5 setOnClickListener {
AssessmentExpression( "+" , clear = true )
}tvMinus. setOnClickListener {
оценкаExpression( "-" , ясно = правда )
}tvMul. setOnClickListener {
AssessmentExpression( "*" , clear = true )
}tvDivide. setOnClickListener {
AssessmentExpression( "/" , clear = true )
}tvDot. setOnClickListener {
AssessmentExpression( "." , ясно = true )
}tvClear. setOnClickListener {
tvExpression. текст = ""
tvResult.text = ""
}tvEquals. setOnClickListener {
val text = tvExpression. text .toString()
val expression = ExpressionBuilder(text).build()val result = expression.evaluate()
val longResult = result.toLong()
if (result == longResult.toDouble()) {
tvResult.text = longResult.toString()
} else {
tvResult.text = result.toString()
}5 }
5 }
твНазад. setOnClickListener {
val text = tvExpression. текст .toString()
if (text.isNotEmpty()) {
tvExpression.текст = text.drop(1)
}tvResult.text = ""
}
}/*Функция для вычисления выражений с использованием библиотеки построителя выражений*/
fun AssessmentExpression(string: String, clear: Boolean) {
if {01 Clear) ""
Expression.append(string)
} else {
Expression.append(Result.text)
Expression.append(string)
Result.text = ""
} 0 0 32 } }Шаг 7. Запустите приложение с помощью эмулятора
Это последний шаг, теперь, когда вы написали весь код Kotlin, файл XML, теперь давайте проверим результат. Для этого мы можем использовать встроенный эмулятор андроида. Нажмите зеленую кнопку, которая выглядит как кнопка воспроизведения в правом верхнем углу, или просто нажмите Shift + F10. Если вы не знаете, как настроить и использовать встроенный эмулятор андроида.
Кредиты: Влад ВойтенкоПожалуйста, посмотрите видео ниже:
В качестве альтернативы, если у вас возникли проблемы с использованием эмулятора или если ваш ноутбук сильно нагревается. Не волнуйтесь, всегда есть второй вариант. Используйте Genymotion в качестве внешнего эмулятора. Вы можете посмотреть видео, как настроить Genymotion ниже:
Кредиты: Apk HeavenТеперь все настроено и сделано, когда вы запустите эмулятор, вы получите красивый простой калькулятор, если нет, то дважды проверьте свой код.
Простой калькуляторВзаимодействие с пользователем
Для работы этого приложения для Android требуется взаимодействие с пользователем. Пользователь взаимодействует с приложением, выполняя элементарную задачу нажатия кнопок на клавиатуре калькулятора. Вводя числа, пользователь может выполнять основные математические операции, такие как сложение, вычитание, умножение и деление. Использование этого калькулятора тривиально; пользователю нужно только ввести входные данные в калькулятор с помощью клавиатуры, а затем указать, какие операции он хочет выполнить, щелкнув одну из четырех кнопок операций (+, -, *, /).
Этот калькулятор может распознавать как положительные, так и отрицательные числа. Кроме того, он распознает порядок операций; набор правил, показывающих, какие операции следует выполнить в первую очередь для оценки выражения. Часто правила обозначаются как PEMDAS, где P-круглые скобки, E-степень, M-умножение, D-деление, A-сложение и S-вычитание. Например, если пользователь вводит 2+9*5, то калькулятор предлагает результат как 47, а не 55. Этот калькулятор не поддерживает круглые скобки и экспоненты, поэтому порядок операций в соответствии с PEMDAS в этом случае следующий: «*», т. е. 9*5, за которым следует «+», т. е. 45+2 и результат 47.
В приведенной выше таблице 1 показаны кнопки и функции основного калькулятора. Эти операции напоминают обычный калькулятор, который всем известен в наши дни. Например, этот калькулятор отображает на экране до 18 символов (1/3 = 0,3333333333333333). Этот калькулятор имеет хороший пользовательский интерфейс и дизайн, он выглядит и немного похож на продвинутые калькуляторы, которые мы часто используем в наших телефонах Android.
На самом деле, я намеревался разработать его на основе моего нынешнего Android-смартфона.
Известные проблемы и ограничения
Используя этот калькулятор, мы не можем использовать сочетания клавиш для ввода данных. Мы можем использовать только кнопки, предусмотренные в самом калькуляторе, для ввода входных данных. Это не большая проблема, потому что это приложение для Android. Каждый запускает это приложение на своем смартфоне, вам не нужна клавиатура для ввода цифр.
Кроме того, этот калькулятор не выдает никаких сообщений об ошибках, если кто-то пытается разделить на 0. Если кто-то вводит две операции одновременно, то калькулятор не выводит никаких сообщений об ошибках. Например, введя выражение 5**+9, калькулятор не зависает и не аварийно завершает работу, а ожидает, пока пользователь изменит операции и превратит его в допустимое математическое выражение.
Помимо этих двух ограничений, приложение соответствует всем критериям, перечисленным в разделе описания выше.
Я использовал макет текстового представления в качестве кнопок, потому что нашел это простым способом организации кнопок рядом друг с другом. У меня были некоторые проблемы, пока я вручную раскладывал кнопки рядом с другой. Каждый раз, когда я запускал приложение с помощью эмулятора, кнопки были разбросаны по всему экрану, хотя я ограничивал макет. С помощью макета текстового представления я смог решить эту проблему.
Следовательно, мы сознательно или неосознанно создали красивый простой калькулятор, используя Kotlin в Android Studio. Это всего лишь простой калькулятор, мы можем добавить еще несколько функций, а также построить научный. Но этого более чем достаточно для хорошего начала, чтобы освоить Kotlin и Android Studio Coding. Я бы порекомендовал вам, ребята, набирать код, а не копировать-вставлять, иногда при копировании-вставке вы получаете ошибки из-за несоответствия пакетов. У всех разные пакеты в студии Android, так что печатайте и учитесь. Если у вас, ребята, есть какие-либо сомнения относительно этого урока, напишите ответ или комментарий ниже.
Я отвечу быстро. До встречи, до свидания.
სიახლეები - საქართველოს ტექნიკური უნივ0სტტიიტიიტის
სტუ
მთავარი სიახლეები
სიახლეები
კონკურსები
სიახლეები
სიახლეები
30 მაი
26 მაი
17 მაი
21 აპრ
ყველა მთავარი სიახლე
27 სექ
სტუ-ის რექტორმა, სტუდენტებმა პროფესორ პროფესორ საქართველოს ტერიტორიული მთლიანობისთვის დაღუპულთა ხსოვნას პატივი მიაგეს მიაგეს მიაგეს მიაგეს მიაგეს მიაგეს მიაგეს
„ამ ტრაგიკულ პატივს მივაგებთ ადამიანებს ადამიანებს, რომლებმაც საქართველოს ტერიტორიული იბრძოლეს და სიცოცხლე გაწირეს.
მათი ხსოვნა ისტორიამ უკვდავყო - დიდება გმირებს!
27 სექ
დიზაინის საერთაშორისო აკადემიური პერსონალის არჩევის მიზნით გამოცხადებული კონკურსის საბოლოო შედეგები
კონკურსში პირები საკონკურსო პირობების შესაბამისად შესაბამისად, თანამდებობაზე არჩეული იქნენ 4 წლის და მათთან აფილირების და შრომითი ხელშეკრულებები დაიდება დაიდება 2022/2023 სასწავლო წლიდან.
27 სექ
სტუ-ში 2022/2023 სასწავლო სამაგისტრო პროგრამებზე მისაღები გამოცდების გამოცდების (დამატებითი მიღება) კოეფიციენტებით რანჟირების დოკუმენტები დოკუმენტები
27 სექ
საერთაშორისო სამეცნიერო - პრაქტიკული კონფერენცია: „ინოვაციები და თანამედროვე გამოწვევები 2022
18-19 ნოემბერს, სტუ-ის ინფორმატიკისა და მართვის სისტემების ფაკულტეტის ორგანიზებით, საქართველოს უნივერსიტეტის უნივერსიტეტის 100 და იმს ფაკულტეტის 65 წლისთავისადმი საერთაშორისო სამეცნიერო სამეცნიერო-პრაქტიკული კონფერენცია: „ინოვაციები თანამედროვე გამოწვევები 2022« ჩატარდება
27 სექ
სტუ-ის ფაკულტეტზე მზის პანელების მონტაჟის მოკლევადიანი პროგრამის ასამოქმედებლად სემინარი მიმდინარეობს მიმდინარეობს მიმდინარეობს მიმდინარეობს
საქართველოს უნივერსიტეტის ენერგეტიკის ფაკულტეტზე ფაკულტეტზე giz- ის, PSD TVET Sc- და სტუ-ის მიერ ერთობლივად ორგანიზებული სამდღიანი სემინარი მიმდინარეობს.
სემინარზე გერმანელი ქართველ კოლეგებს მზის პანელების მონტაჟის სფეროში, ასევე, მზის მემონტაჟეების გადამზადების პროგრამების თანამედროვე სწავლების შესახებ აწვდიან უახლეს ინფორმაციას
26 სექ
სტუ-ში, 100 წლის იუბილეს ფარგლებში, ქართულ-პოლონური საერთაშორისო სამეცნიერო კონფერენცია გაიხსნა გაიხსნა
საქართველოს უნივერსიტეტში უნივერსიტეტში, 100 წლის იუბილეს ფარგლებში, სტუ-ის სატრანსპორტო და მექანიკის ინჟინერიის ინიციატივით და ორგანიზებით ორგანიზებით, რიგით მე -6 ქართულ-პოლონური სამეცნიერო კონფერენცია-„სატრანსპორტო ევროპა-აზია აზია გაიხსნა.
26 სექ
სტუ-ში 2022/2023 სასწავლო სამაგისტრო პროგრამებზე მისაღები მისაღები (დამატებითი მიღება) უცხო გამოცდების შედეგები აპელაციის გათვალისწინებით გათვალისწინებით
26 სექ
სტუ-ში 2022/2023 სასწავლო სამაგისტრო პროგრამებზე მისაღები მისაღები (დამატებითი მიღება) სასპეციალიზაციო შედეგები აპელაციის გათვალისწინებით გათვალისწინებით
ყველა სიახლე
05 აგვ
03 აგვ
საქართველოს ტექნიკური დაარსებიდან დაარსებიდან 100 წლის იუბილესთან დაკავშირებით აცხადებს საერთაშორისო კონკურსს სივრცულ კონცეპტუალურ კომპოზიციაზე კომპოზიციაზე: „წარსული, აწმყო, მომავალი«
სივრცულ კომპოზიცია განთავსდება თბილისში, კოსტავას, 77-ში, უნივერსიტეტის კორპუსის მიმდებარე ტერიტორიაზე (ს.

 time()
print ("Время :")
print(stop - start)
time()
print ("Время :")
print(stop - start)
 value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
 solve(solver='glpk')
print("Результат Xopt:")
for i in x.value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
solve(solver='glpk')
print("Результат Xopt:")
for i in x.value:
print(i)
print("Стоимость доставки:")
print(problem.objective.value()[0])
stop = time.time()
print ("Время :")
print(stop - start)
 time()
print ("Время :")
print(stop - start)
time()
print ("Время :")
print(stop - start)
 solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
 LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 <= 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 30, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 <= 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 30, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
 time()
x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)
x3 = pulp.LpVariable("x3", lowBound=0)
x4 = pulp.LpVariable("x4", lowBound=0)
x5 = pulp.LpVariable("x5", lowBound=0)
x6 = pulp.LpVariable("x6", lowBound=0)
x7 = pulp.LpVariable("x7", lowBound=0)
x8 = pulp.LpVariable("x8", lowBound=0)
x9 = pulp.LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 == 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 45, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
time()
x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)
x3 = pulp.LpVariable("x3", lowBound=0)
x4 = pulp.LpVariable("x4", lowBound=0)
x5 = pulp.LpVariable("x5", lowBound=0)
x6 = pulp.LpVariable("x6", lowBound=0)
x7 = pulp.LpVariable("x7", lowBound=0)
x8 = pulp.LpVariable("x8", lowBound=0)
x9 = pulp.LpVariable("x9", lowBound=0)
problem = pulp.LpProblem('0',pulp.LpMaximize)
problem += -7*x1 - 3*x2 - 6* x3 - 4*x4 - 8*x5 -2* x6-1*x7- 5*x8-9* x9, "Функция цели"
problem +=x1 + x2 +x3<= 74,"1"
problem +=x4 + x5 +x6 == 40, "2"
problem +=x7 + x8+ x9 <= 36, "3"
problem +=x1+ x4+ x7 == 20, "4"
problem +=x2+x5+ x8 == 45, "5"
problem +=x3 + x6+x9 == 30, "6"
problem.solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
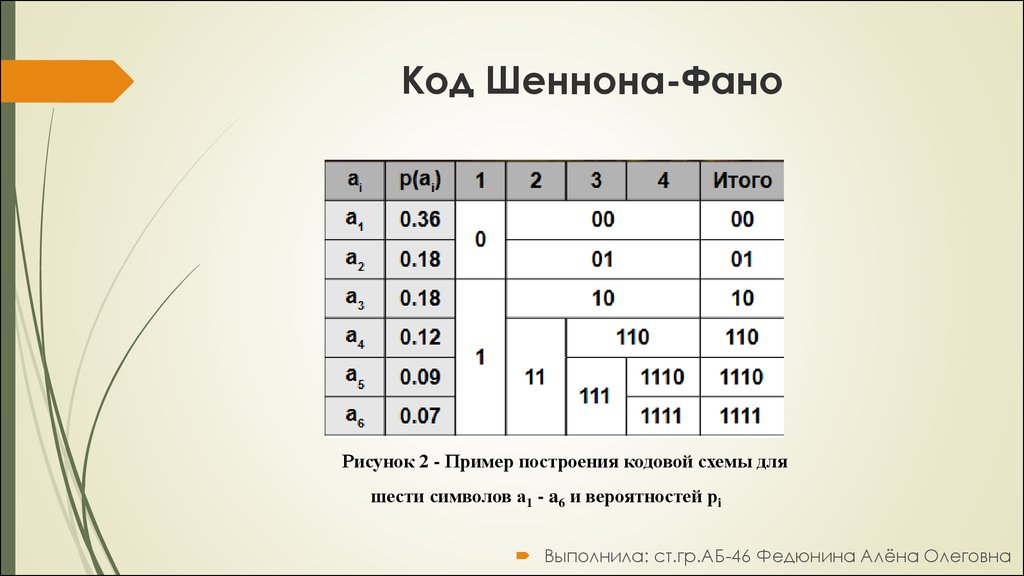 solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
solve()
print ("Результат:")
for variable in problem.variables():
print (variable.name, "=", variable.varValue)
print ("Стоимость доставки:")
print (abs(value(problem.objective)))
stop = time.time()
print ("Время :")
print(stop - start)
 Співвідношення між кутами і сторонами трикутника
Співвідношення між кутами і сторонами трикутника
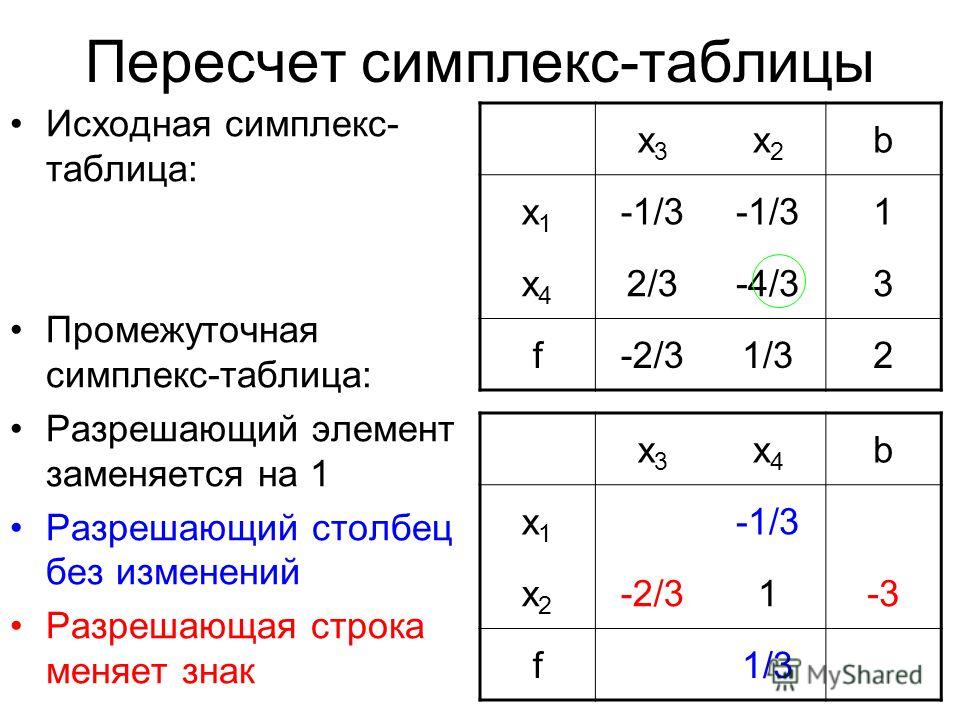 com
com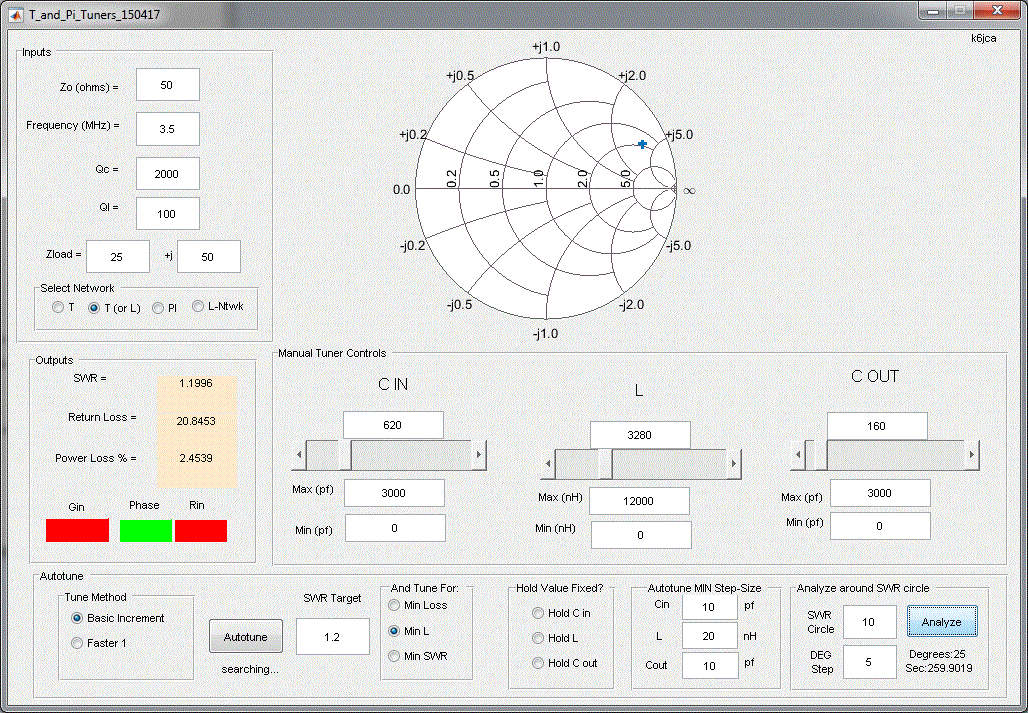 )
) 0003
0003 Этот метод предпочтительнее двух методов, то есть правила северо-западного угла и метода наименьших затрат. Алгоритм VAM приведен ниже: Шаг-1:
Этот метод предпочтительнее двух методов, то есть правила северо-западного угла и метода наименьших затрат. Алгоритм VAM приведен ниже: Шаг-1:
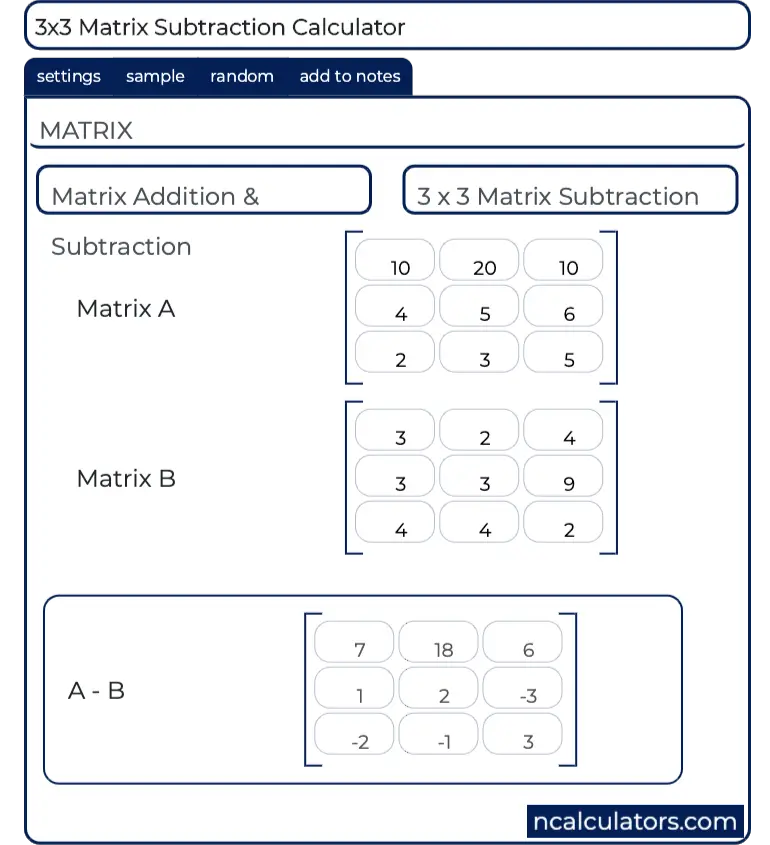 Шаг 2]. В этом случае штраф будет самым низким в этой строке или столбце среди всех строк или столбцов, так что нет возможности выбрать эту строку или столбец для распределения товаров. Если в этой строке или столбце есть какие-либо более высокие затраты, кроме таких же наименьших затрат, то вероятность выбора более высокой стоимости в следующей итерации будет увеличена, и общая стоимость транспортировки может увеличиться.
Шаг 2]. В этом случае штраф будет самым низким в этой строке или столбце среди всех строк или столбцов, так что нет возможности выбрать эту строку или столбец для распределения товаров. Если в этой строке или столбце есть какие-либо более высокие затраты, кроме таких же наименьших затрат, то вероятность выбора более высокой стоимости в следующей итерации будет увеличена, и общая стоимость транспортировки может увеличиться. В предложенном нами алгоритме (AVAM) при появлении наименьшей стоимости в двух или более
В предложенном нами алгоритме (AVAM) при появлении наименьшей стоимости в двух или более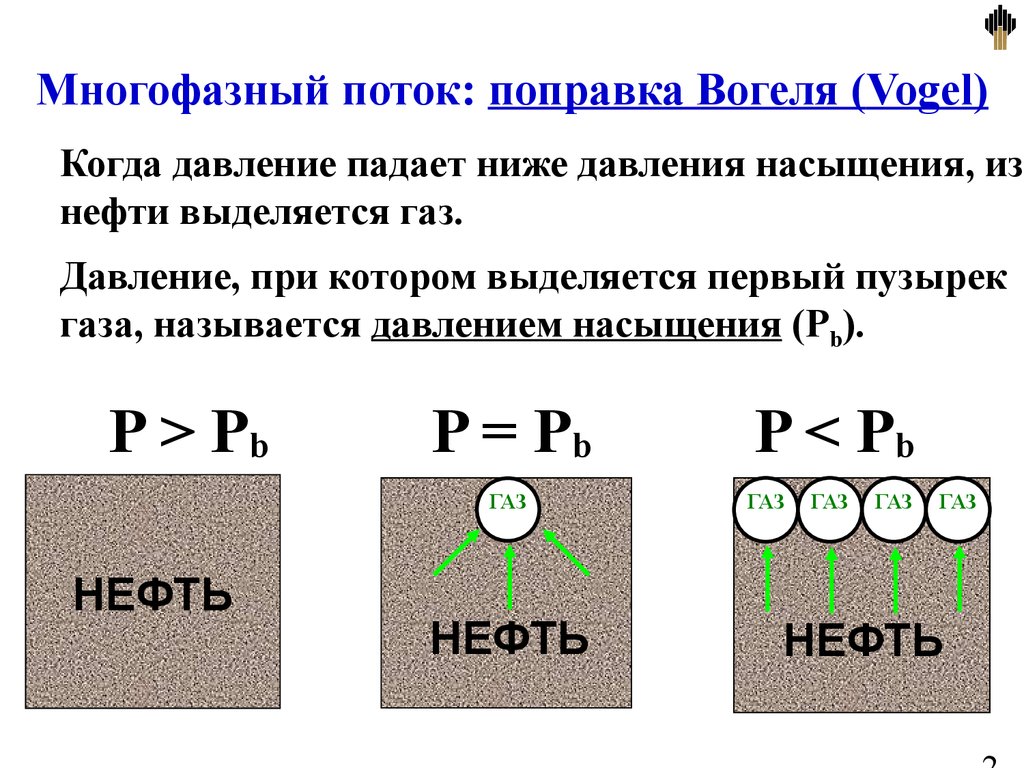 Алгоритм АВАМ приведен следующим образом:
Алгоритм АВАМ приведен следующим образом:

 е.
е. 2 Общая стоимость транспортировки:
2 Общая стоимость транспортировки: 3 Общая стоимость перевозки:
3 Общая стоимость перевозки: 1
1 2 Общая стоимость транспортировки:
2 Общая стоимость транспортировки: 3
3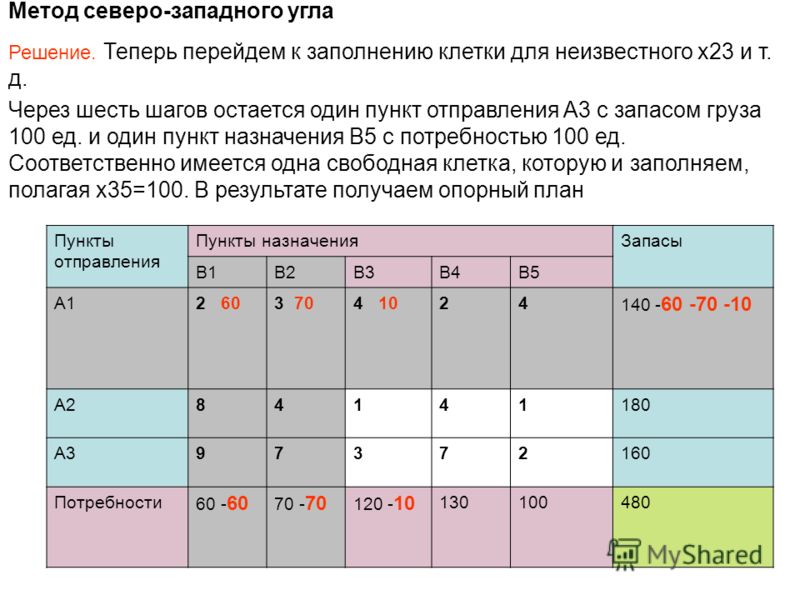 1
1 2 Общая стоимость перевозки:
2 Общая стоимость перевозки: 3 Общая стоимость перевозки:
3 Общая стоимость перевозки: Из приведенных выше примеров видно, что AVAM дает более низкое допустимое решение, чем VAM, и оно очень близко к оптимальному решению или равно оптимальному решению.
Из приведенных выше примеров видно, что AVAM дает более низкое допустимое решение, чем VAM, и оно очень близко к оптимальному решению или равно оптимальному решению. 34, № 2, стр. 49-62 ISSN 1022-8594 (2011).
34, № 2, стр. 49-62 ISSN 1022-8594 (2011). 1 — наиболее точная программа для прогнозирования липофильности и растворимости молекул в воде
1 — наиболее точная программа для прогнозирования липофильности и растворимости молекул в воде Уайтсайд, С. Хилал и Л. А. Каррейра, «Оценка констант скорости гидролиза эфиров фосфорной кислоты I. Щелочной гидролиз», QSAR & Combinatorial Science, 24,1 (2005)
Уайтсайд, С. Хилал и Л. А. Каррейра, «Оценка констант скорости гидролиза эфиров фосфорной кислоты I. Щелочной гидролиз», QSAR & Combinatorial Science, 24,1 (2005)
 0" кодировка = "utf-8" ?>
0" кодировка = "utf-8" ?>  5dp item >
5dp item >  5dp item >
5dp item >  0" encoding="utf-8" ?>
0" encoding="utf-8" ?>  " />
" /> 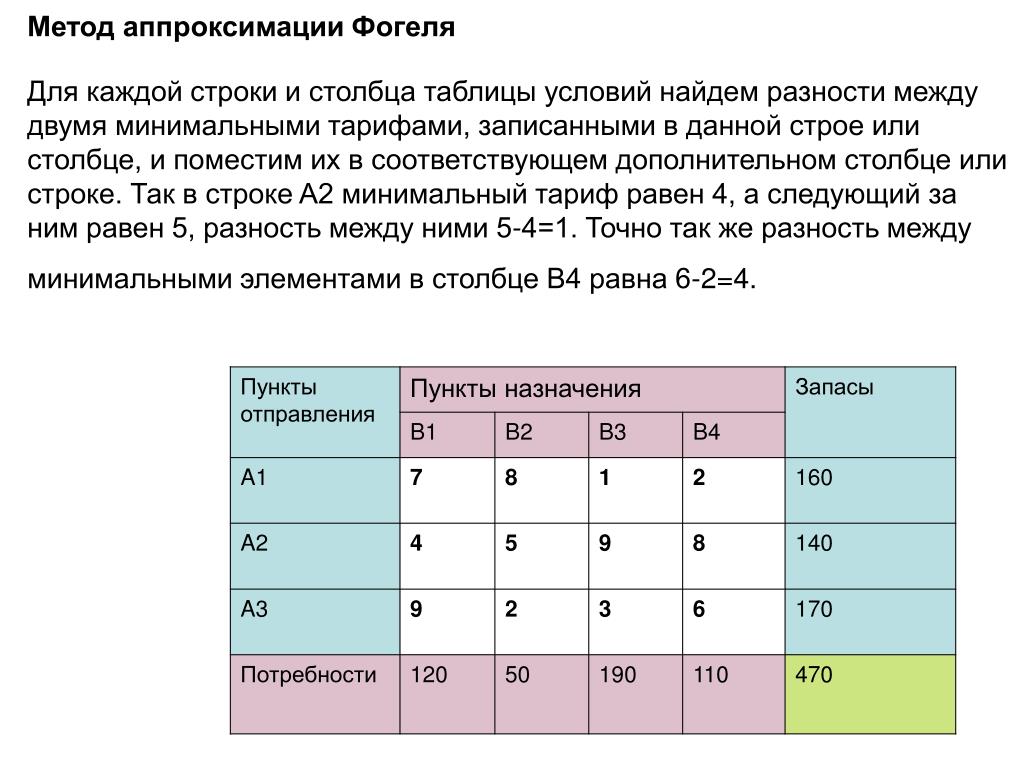 example.finalcalculator
example.finalcalculator  setOnClickListener {
setOnClickListener {  setOnClickListener {
setOnClickListener { 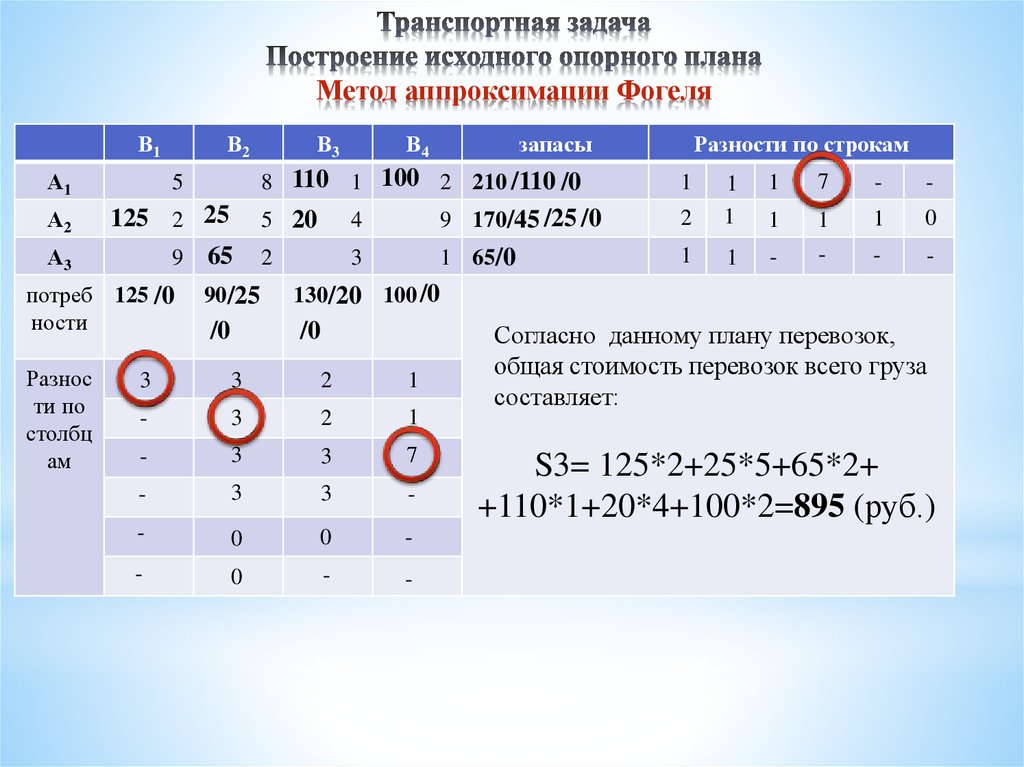 " , ясно = true )
" , ясно = true )  текст = text.drop(1)
текст = text.drop(1)  Пожалуйста, посмотрите видео ниже:
Пожалуйста, посмотрите видео ниже: Этот калькулятор может распознавать как положительные, так и отрицательные числа. Кроме того, он распознает порядок операций; набор правил, показывающих, какие операции следует выполнить в первую очередь для оценки выражения. Часто правила обозначаются как PEMDAS, где P-круглые скобки, E-степень, M-умножение, D-деление, A-сложение и S-вычитание. Например, если пользователь вводит 2+9*5, то калькулятор предлагает результат как 47, а не 55. Этот калькулятор не поддерживает круглые скобки и экспоненты, поэтому порядок операций в соответствии с PEMDAS в этом случае следующий: «*», т. е. 9*5, за которым следует «+», т. е. 45+2 и результат 47.
Этот калькулятор может распознавать как положительные, так и отрицательные числа. Кроме того, он распознает порядок операций; набор правил, показывающих, какие операции следует выполнить в первую очередь для оценки выражения. Часто правила обозначаются как PEMDAS, где P-круглые скобки, E-степень, M-умножение, D-деление, A-сложение и S-вычитание. Например, если пользователь вводит 2+9*5, то калькулятор предлагает результат как 47, а не 55. Этот калькулятор не поддерживает круглые скобки и экспоненты, поэтому порядок операций в соответствии с PEMDAS в этом случае следующий: «*», т. е. 9*5, за которым следует «+», т. е. 45+2 и результат 47. На самом деле, я намеревался разработать его на основе моего нынешнего Android-смартфона.
На самом деле, я намеревался разработать его на основе моего нынешнего Android-смартфона. Я использовал макет текстового представления в качестве кнопок, потому что нашел это простым способом организации кнопок рядом друг с другом. У меня были некоторые проблемы, пока я вручную раскладывал кнопки рядом с другой. Каждый раз, когда я запускал приложение с помощью эмулятора, кнопки были разбросаны по всему экрану, хотя я ограничивал макет. С помощью макета текстового представления я смог решить эту проблему.
Я использовал макет текстового представления в качестве кнопок, потому что нашел это простым способом организации кнопок рядом друг с другом. У меня были некоторые проблемы, пока я вручную раскладывал кнопки рядом с другой. Каждый раз, когда я запускал приложение с помощью эмулятора, кнопки были разбросаны по всему экрану, хотя я ограничивал макет. С помощью макета текстового представления я смог решить эту проблему. Я отвечу быстро. До встречи, до свидания.
Я отвечу быстро. До встречи, до свидания.