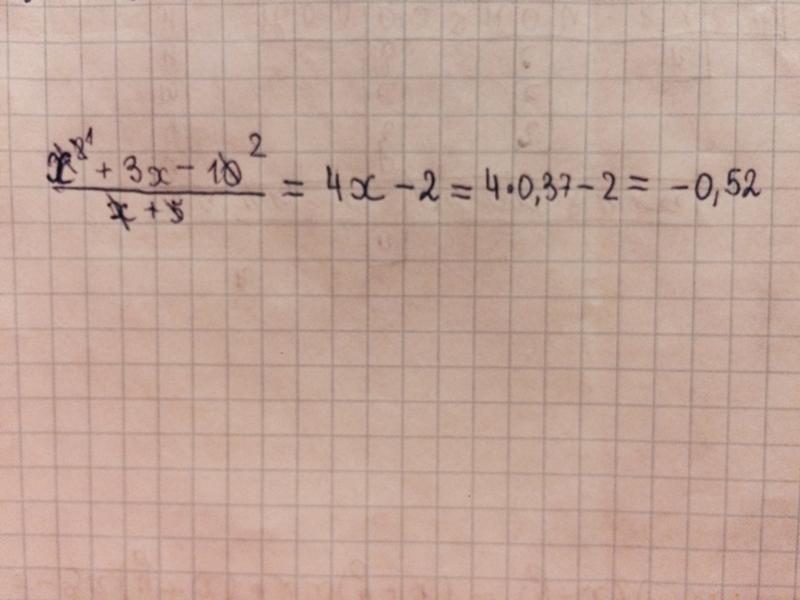Ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса.
ответы майл ру помогите решить задачу какое наименьшее количество карандашей надо прибавить к 146 уже имеющимя карандашам, чтобы получившееся
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Количество книг на двух полках было одинаковым.Когда с первой полки переложили 18 книг на вторую то на второй полке книг стало в 3 раза больше чем на
Пользуйтесь нашим приложением
Открытая Математика. Алгебра. Рациональные выражения
Рациональные выражения
Вспомним определение функции (подробнее см.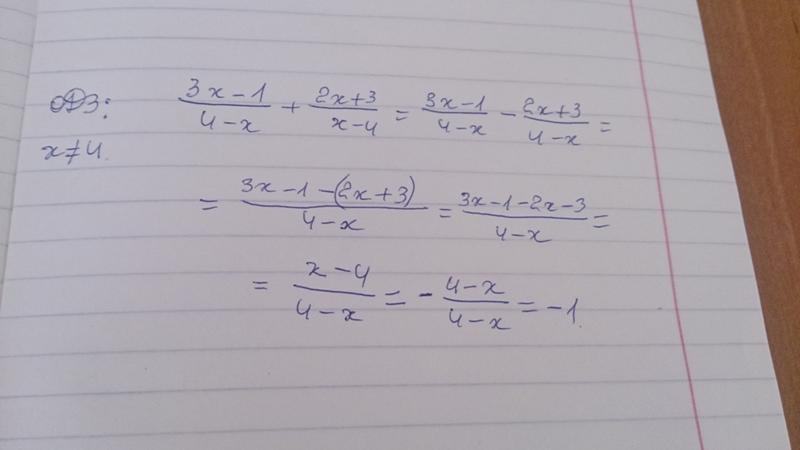 курс «Открытая Математика 2.6. Функции и Графики», § 1.3.1):
курс «Открытая Математика 2.6. Функции и Графики», § 1.3.1):
Пусть задано числовое множество D∈ℝ. Если каждому числу x ∈ D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x ∈ D. Множество D, называется областью определения функции и обозначается D (f (x)).
Множество, состоящее из всех элементов f (x), где x ∈ D, называется областью значений функции и обозначается E (f (x)).
Рациональной называется функция, которую можно представить в виде отношения двух многочленов, то есть f (x)=Pn (x)Qm (x),
где Pn (x)
− многочлен n-ной степени, Qm (x)
− многочлен m-ной степени. Такую функцию
- x2+2x-16x-1, (x-1)(x-2)x4 − рациональные функции;
- x2+2xx2-1=x2+42x(x2-1), x+1x=x2+1x
− эти функции изначально не представлены в виде отношения многочленов, но могут быть представлены в таком виде.

Основное свойство рациональной дроби можно выразить формулой P (x)Q (x)=P (x)ċR (x)Q (x)ċR (x), справедливой при Q (x)≠0 и R (x)≠0, где R (x) − многочлен. Кратко основное свойство рациональной дроби может быть выражено фразой: числитель и знаменатель рациональной дроби можно умножить и разделить на одно и то же отличное от нуля число, одночлен или многочлен.
Из основного свойства рациональной дроби следуют равенства: PQ=—PQ=-P-Q=-P-Q. Например, x-12-x=-1-x2-x=1-xx-2=-x-1x-2.
Основное свойство дроби даёт возможность умножить и разделить числитель и знаменатель рациональной дроби на одно и то же выражение, отличное от нуля. Такая операция называется сокращением дроби. Для того, чтобы сократить рациональную дробь, нужно разложить её числитель и знаменатель на множители. При этом сокращение возможно, лишь если числитель и знаменатель имеют общие множители. Если же они не имеют общих множителей, то дробь сократить нельзя.
Сократите дробь x3-4x2x2+3x-2.
Разложим числитель и знаменатель на множители.
Числитель: x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2). Мы воспользовались вынесением общего множителя за скобку и формулой разности квадратов.
Знаменатель: 2×2+3x-2=2(x+2)(x-12)=(x+2)(2x-1).
Имеем: x3-4x2x2+3x-2=x(x+2)(x-2)(x+2)(2x-1)=x(x-2)(2x-1)=x2-2x2x-1.
Ответ. x2-2x2x-1.
Для того чтобы описать действия с рациональными дробями, опишем процедуру их приведения к наименьшему общему знаменателю.
Общим знаменателем нескольких рациональных функций называется многочлен, который делится на знаменатель каждой дроби.
Например, общим знаменателем двух дробей x2-2x2x-1
и x2-1x-2 будет многочлен (x – 2)(2x – 1).
Но общим знаменателем этих дробей также служит многочлен 2x(x – 2)(2x – 1), а также 14×12(x-2)5(2x-1)17. Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен (x – 2)(2x – 1). Имеем:
x2-2x2x-1=(x2-2x)(x-2)(2x-1)(x-2),
Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен (x – 2)(2x – 1). Имеем:
x2-2x2x-1=(x2-2x)(x-2)(2x-1)(x-2),
x2-1x-2=(x2-1)(2x-1)(x-2)(2x-1).
Множители, на которые нужно умножить числитель и знаменатель каждой дроби, называются дополнительными множителями. В нашем примере дополнительный множитель для дроби x2-2x2x-1
равен (x – 2), а для дроби x2-1x-2
равен (2x – 1).
Итак, для того, чтобы привести несколько рациональных дробей к общему знаменателю, нужно:
- во-первых, разложить числитель и знаменатель каждой дроби на множители;
- во-вторых, найти общий знаменатель всех этих дробей;
- в-третьих, найти дополнительные множители для каждой дроби, они получаются путём деления общего знаменателя на знаменатель каждой из дробей;
- в-четвёртых, умножить каждую из дробей на свой дополнительный множитель.

Привести к общему знаменателю дроби 12×3+2×2; x6x2-6; 2(x-1)3×2+3x.
Разложим знаменатели дробей на множители:
2x3 + 2x2 = 2x2(x + 1).
6x2 – 6 = 6(x2 – 1) = 6(x + 1)(x – 1).
3x2 + 3x = 3x(x + 1).
Значит, общим знаменателем данных дробей будет многочлен 6x2(x + 1)(x – 1). Дополнительными множителями для каждой из дробей будут:
- для первой дроби 6×2(x+1)(x-1)2×2(x+1)=3(x-1);
- для второй дроби 6×2(x+1)(x-1)6(x+1)(x-1)=x2;
- для третьей дроби 6×2(x+1)(x-1)3x(x+1)=2x(x-1).
Умножим каждую из дробей на её дополнительный множитель, приводя их тем самым к общему знаменателю:
- 12×2(x+1)=3(x-1)2×2(x+1)ċ3(x-1)=3(x-1)6×2(x+1)ċ(x-1);
- x6(x+1)(x-1)=xċx26(x+1)(x-1)ċx2=x36x2(x+1)(x-1);
- 2(x-1)3x(x+1)=2(x-1)ċ2x(x-1)3x(x+1)ċ2x(x-1)=4x(x-1)26×2(x+1)(x-1).

Ответ. 3(x-1)6×2(x+1)ċ(x-1); x36x2(x+1)(x-1); 4x(x-1)26×2(x+1)(x-1).
Перейдём теперь к изучению преобразований рациональных выражений.
Сложение. Сумма двух рациональных дробей с одинаковыми знаменателями определяется следующей формулой: PQ+RQ=P+RQ, то есть для того, чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Вычитание. Разность двух рациональных дробей с одинаковыми знаменателями определяется следующей формулой: PQ-RQ=P-RQ, то есть для того, чтобы вычесть две дроби с одинаковыми знаменателями, нужно вычесть их числители, а знаменатель оставить тем же.
Если же нужно сложить или вычесть две дроби с разными знаменателями, то сперва их следует привести к одному знаменателю и после произвести сложение и вычитание.
Упростите выражение x2x-1-1x-1.
x2x-1-1x-1=x2-1x-1=(x+1)(x-1)x-1=x+1.
Ответ. x + 1.
Упростите выражение x-2×2-x-6-x+2×2-5x+6.
x-2×2-x-6-x+2×2-5x+6=x-2(x+2)(x-3)-x+2(x-2)(x-3)=(x-2)2-(x+2)2(x+2)(x-2)(x-3)==(x-2+x+2)(x-2-x-2)(x+2)(x-2)(x-3)=2xċ(-4)(x+2)(x-2)(x-3)=-8x(x+2)(x-2)(x-3).
Ответ. -8x(x+2)(x-2)(x-3).
Умножение. Произведение двух рациональных дробей находится по следующей формуле: PQċRT=PċRQċT. Другими словами, для того, чтобы перемножить две дроби, нужно перемножить их числители и результат разделить на произведение знаменателей.
Деление. Частное двух дробей находится по следующей формуле: PQ:RT=PċTQċR. Другими словами, для того, чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Упростите выражение x2-1×2+x-6:x2-4x+3×2-4.
x2-1×2+x-6:x2-4x+3×2-4=(x2-1)(x2-4)(x2+x-6)(x2-4x+3)==(x+1)(x-1)(x+2)(x-2)(x-2)(x+3)(x-1)(x-3)=(x+1)(x+2)(x+3)(x-3)=x2+3x+2×2-9.
Ответ. x2+3x+2×2-9.
Шаг 1 :
16
Упростить ——
3
Уравнение в конце шага 1 :
x 16
((((3•(x 2 ))-(3•————))+3x)-4)•((x 2 )-(——•x 2 ))
(х 2 ) 3
Шаг 2 :
Уравнение в конце шага 2 :
x 16x 2
((((3•(х 2 ))-(3•————))+3x)-4)•((x 2 )-————)
(х 2 ) 3
Шаг 3:
Переписывание целого в качестве эквивалентной фракции:
3.1 Вычитание фракции из целой
Перепишите целую фракцию, используя 3 в качестве знаменателя:
x 2 x 2 • 3:x 2 x 2 • х 2 = —— = —————— 1 3Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое число
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель знаменатель
Объедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему члену, если возможно:
x 2 • 3 - (16x 2 ) -13x 2 знак равно 3 3Уравнение в конце шага 3 :
x -13x 2 ((((3•(x 2 ))-(3•————))+3x)-4)•————— (х 2 ) 3Шаг 4 :
x Упростить —— x 2Деление экспоненциальных выражений:
4.
1 x 1 разделить на x 2 = x (1 - 2) = x (-1) = 1 / x 1 = 1 / x
Уравнение на конце 4:
1 -13x 2 ((((3•(x 2 ))-(3•—))+3x)-4)•————— х 3Шаг 5 :
Уравнение в конце шага 5 :
3 -13x 2 (((3x 2 - —) + 3x) - 4) • ————— х 3Шаг 6:
Переписывание целого в качестве эквивалентной фракции:
6.1 Вычитание фракции из целой
Перепишите целую фракцию с использованием x в качестве знаменателя:
3x 2 3x 2 • x. 3x 2 = ——— = ——————— 1 хСложение дробей, имеющих общий знаменатель:
6.2 Сложение двух эквивалентных дробей
3x 2 • х - (3) 3 х 3 - 3 знак равно х хУравнение в конце шага 6 :
(3x 3 - 3) -13x 2 ((————————— + 3x) — 4) • ————— х 3Шаг 7 :
Преобразование целого в виде эквивалентной дроби:
7.
1 Прибавление целого к дроби
Преобразование целого в виде дроби, используя x в качестве знаменателя:
3x 3x • х 3x = —— = —————— 1 хШаг 8:
Вытягивая, как Условия:
8.1. Вытягивание, как факторы:
3x 3 - 3 = 3 • (x 3 - 1)
Попытка по совокупности :
8.2 Разложение на множители: x 3 - 1
Теория : Разность двух совершенных кубов, a 3 - b 3 можно разложить на
(A-B) • (A 2 +AB+B 2 )Доказательство: (A-B) • (A 2 +AB+B 2 ) =
A 3 +A 2 B+AB 2 -BA 2 -B 2 A -B 3 =
A 3 +(A 2 B -BA 2 )+(AB 2 -B 2 a)-b 3 =
a 3 +0+0-b 3 =
a 3 -b 3 0037Проверка: 1 - куб 1
Проверка: x 3 - куб X 1Фактор:
(x - 1) • (x 2 + x + 1)66.
Попытка факторизовать путем разделения среднего члена
8.3 Факторизация x 2 + x + 1
Первый член равен x 2 его коэффициент равен 1 .
Средний член равен +x , его коэффициент равен 1 .
Последний термин, "константа", равен +1Шаг 1: умножьте коэффициент первого члена на константу 1 • 1 = 1
Шаг 2: найдите два множителя 1 , сумма которых равна коэффициенту среднего члена, который равен 1 .
| -1 | + | -1 | = | -2 | ||
| 1 | + | 1 | = | 2 |
Наблюдение : Невозможно найти два таких фактора !!
Вывод: Трехчлен нельзя разложить на множители
Сложение дробей, имеющих общий знаменатель:
8.4 Сложение двух эквивалентных дробей
3 • (x-1) • (x 2 +x+1) + 3x+1 • x 3x 3 + 3x 2 - 3
знак равно
х х
Уравнение в конце шага 8 :
(3x 3 + 3x 2 - 3) -13x 2
(——————————————— - 4) • —————
х 3
Шаг 9 :
Преобразование целого в виде эквивалентной дроби:
9. 1 Вычитание целого из дроби
1 Вычитание целого из дроби
Преобразование целого в виде дроби, используя x в качестве знаменателя:
4 4 • x
4 = — = —————
1 х
Шаг 10 :
Вытягивание одинаковых членов:
10.1 Вытягиваем, как факторы:
3x 3 + 3x 2 - 3 = 3 • (x 3 + x 2 - 1)
Полиномиальные корни Калькулятор:
10.2 (Roots Root нулей) из : F(x) = x 3 + x 2 - 1
Калькулятор корней полинома представляет собой набор методов, направленных на нахождение значений x , для которых F(x)=0
Тест рациональных корней является одним из вышеперечисленных инструментов. Он найдет только рациональные корни, т. е. числа x , которые можно выразить как частное двух целых чисел 9.0037
Теорема о рациональном корне утверждает, что если многочлен равен нулю для рационального числа P/Q , то P является множителем замыкающей константы, а Q является множителем старшего коэффициента
В этом случае старший коэффициент равен 1, а Константа трейлинга: -1.
Коэффициент(ы):
ведущего коэффициента: 1
константы замыкания: 1
Проверим....
| 0382 | Q | P/Q | F(P/Q) | Divisor | |||||
|---|---|---|---|---|---|---|---|---|---|
| -1 | 1 | -1.00 | -1.00 | ||||||
| 1 | 1 | 1.00 | 1.00 |
Калькулятор полиномиальных корней не обнаружил, что нет рациональных корней
Добавляющие фракции, которые имеют общий знаменатель:
10.3 Сложность двух эквивалентных фракций
3 • (x 3 +x 2 -1) -1) 4 • х) 3x 3 + 3x 2 - 4x - 3
знак равно
х х
Уравнение в конце шага 10 :
(3x 3 + 3x 2 - 4x - 3) -13x 2
——————————————————— • —————
х 3
Шаг 11:
Проверка на идеальный куб:
11,1 3x 3 +3x 2 -4x -3 не является идеальным кубом
, пытаясь потянуть:
11. 2 Факульте 3 +3x 2 -4x-3
2 Факульте 3 +3x 2 -4x-3
Вдумчиво разделите имеющееся выражение на группы, в каждой группе по два члена :
Группа 1: -4x-3
Группа 2: 3x 3 +3x 2
Вытягивание из каждой группы отдельно :
Группа 1: (4x+3) • (-1)
Группа (x+1) • (3x 2 )
Плохие новости !! Разложение на множители путем вытягивания не удается:
Группы не имеют общего множителя и не могут быть сложены для образования умножения.
Калькулятор корней многочлена :
11.3 Найдите корни (нули) : F(x) = 3x 3 +3x 2 -4x-3
См. теорию в шаге 10.2
В этом случае ведущий коэффициент равен 3, а конечная константа равна -3.
The factor(s) are:
of the Leading Coefficient : 1,3
of the Trailing Constant : 1 ,3
Let us test ....
| P | Q | P/Q | F(P/Q) | Делитель | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| -1 | 1 | -1. 00 00 | 1.00 | |||||||
| -1 | 3 | -0.33 | -1.44 | |||||||
| -3 | 1 | -3,00 | 71-45.00 -3,00 | 71-45.00-45.00 -3,00 | 71 -45.00 -3.000272 | |||||
| 1 | 1 | 1.00 | -1.00 | |||||||
| 1 | 3 | 0.33 | -3,89 | |||||||
| 3 | 1 | 3,0 2 | 293.00 |
Polynomial Roots Calculator found no rational roots
Dividing exponential expressions :
11. 4 x 2 divided by x 1 = x (2 - 1) = x 1 = x
4 x 2 divided by x 1 = x (2 - 1) = x 1 = x
Окончательный результат:
-13x • (3x 3 + 3x 2 - 4x - 3)
———————————————————————————
3
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 93-8 | |
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
7.
 2: Редукция рациональных функций — Mathematics LibreTexts
2: Редукция рациональных функций — Mathematics LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19721
- Дэвид Арнольд
- Колледж Редвудс
Цель этого раздела — научиться сводить рациональное выражение к «наименьшим терминам». Конечно, это означает, что нам придется понять, что имеется в виду под фразой «самые низкие сроки». Помня об этом, мы начнем с обсуждения наибольшего общего делителя пары целых чисел.
Во-первых, мы определим, что мы подразумеваем под «делимостью».
Определение
Предположим, что у нас есть пара целых чисел a и b. Мы говорим, что «а является делителем b» или «а делит b» тогда и только тогда, когда существует другое целое число k, такое что b = ak. Другой способ сказать то же самое состоит в том, чтобы сказать, что a делит b, если при делении b на a остаток равен нулю.
Другой способ сказать то же самое состоит в том, чтобы сказать, что a делит b, если при делении b на a остаток равен нулю.
Давайте рассмотрим пример.
Пример \(\PageIndex{1}\)
Каковы делители числа 12?
Решение
Поскольку \(12=1 \умножить на 12\), то и 1, и 12 являются делителями 12. Поскольку \(12=2 \умножить на 6\), то и 2, и 6 являются делителями 12. Наконец , поскольку \(12=3 \times 4\), и 3, и 4 являются делителями 12. Если мы перечислим их в порядке возрастания, делителями 12 будут \[1,2,3,4,6, \text { и } 12\]
Давайте посмотрим на другой пример.
Пример \(\PageIndex{2}\)
Каковы делители числа 18?
Решение
Поскольку \(18=1 \умножить на 18\), то и 1, и 18 являются делителями 18. Аналогично, \(18=2 \умножить на 9\) и \(18=3 \умножить на 6\ ), поэтому в порядке возрастания делители числа 18 равны
\[1,2,3,6,9, \text { и } 18\]
Наибольший общий делитель двух или более целых чисел — это наибольший общий делитель целых чисел. Пример должен прояснить это.
Пример должен прояснить это.
Пример \(\PageIndex{3}\)
Какой наибольший общий делитель чисел 12 и 18?
Решение
В примере 2 и примере 3 мы увидели следующее.
Мы выделили делители, общие для чисел 12 и 18. Это 1, 2, 3 и 6. «Наибольший» из этих «общих» делителей равен 6. Следовательно, мы говорим, что «наибольший общий делитель 12 и 18 равен 6».
Определение
Наибольший общий делитель двух целых чисел a и b — это их наибольший общий делитель. Мы будем использовать обозначение \[GCD(a, b)\] для обозначения наибольшего общего делителя чисел a и b.
Таким образом, как мы видели в примере 4, НОД(12, 18) = 6.
Если наибольший общий делитель пары целых чисел равен единице, мы даем этой паре специальное имя.
Определение
Пусть a и b — целые числа. Если наибольший общий делитель чисел a и b равен единице, то есть если НОД(a, b) = 1, то говорят, что числа a и b взаимно просты.
Например:
- 9 и 12 не взаимно просты, потому что НОД(9, 12) = 3.
- 10 и 15 не взаимно просты, потому что НОД(10, 15) = 5,
- 8 и 21 взаимно просты, потому что НОД(8, 21) = 1.
Теперь мы можем определить, что имеется в виду, когда мы говорим, что рациональное число сводится к низшим элементам.
Определение
Говорят, что рациональное число в форме p/q, где p и q — целые числа, приводится к наименьшим членам тогда и только тогда, когда НОД(p, q) = 1. То есть p/q приводится к наименьшим членам, если наибольший общий делитель числителя и знаменателя равен 1.
Как мы видели в примере \(\PageIndex{3}\), наибольший общий делитель 12 и 18 равен 6. Следовательно, дробь 12/18 не сводится к младшим членам. Однако мы можем сократить 12/18 до наименьших членов, разделив и числитель, и знаменатель на их наибольший общий делитель. то есть
\[\frac{12}{18}=\frac{12 \div 6}{18 \div 6}=\frac{2}{3}\]
Обратите внимание, что НОД(2, 3) = 1, поэтому 2/3 сокращается до наименьших членов.
Когда трудно установить наибольший общий делитель, мы сочтем более эффективным действовать следующим образом:
• Простой множитель и в числителе, и в знаменателе.
• Отменить общие факторы.
Таким образом, чтобы сократить 12/18 до наименьших членов, сначала представим и числитель, и знаменатель в виде произведения простых чисел, а затем сократим обычные простые числа.
\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{\not{2} \cdot 2 \cdot \not{3 }}{\not{2} \cdot 3 \cdot \not{3}}=\frac{2}{3}\]
Когда вы отменяете 2, вы на самом деле делите и числитель, и знаменатель на 2. Когда вы отменяете 3, вы фактически делите и числитель, и знаменатель на 3. Обратите внимание, что выполнение обоих действий (деление на 2, а затем деление на 3 ) эквивалентно делению и числителя, и знаменателя на 6.
Мы предпочитаем этот последний метод именно потому, что он идентичен методу, который мы будем использовать для приведения рациональных функций к низшим терминам. Однако этот метод «отмены» имеет некоторые подводные камни, поэтому давайте уделим немного времени обсуждению некоторых распространенных ошибок отмены.
Однако этот метод «отмены» имеет некоторые подводные камни, поэтому давайте уделим немного времени обсуждению некоторых распространенных ошибок отмены.
Отмена
Вы можете вызвать бурные споры среди преподавателей математики, невинно упомянув слово «отмена». Кажется, есть два диаметрально противоположных лагеря: те, кто не возражает, когда их ученики используют технику отмены, и, с другой стороны, те, кто отказывается даже использовать термин «отмена» на своих занятиях.
Обе стороны спора заслуживают внимания. Как мы показали в уравнении (8), мы можем довольно эффективно уменьшить 12/18, просто отменив общие множители. С другой стороны, преподаватели из второго лагеря предпочитают использовать фразу «вычесть 1» вместо фразы «отменить», поощряя своих студентов уменьшать 12/18 следующим образом.
\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{2}{3} \cdot \color{blue}{ \frac{2 \cdot 3}{2 \cdot 3}}=\frac{2}{3} \cdot 1=\frac{2}{3}\]
честно говоря, избегает зыбучих песков «ошибок отмены». Преподаватели, которым надоедает наблюдать за тем, как их ученики «отменяют», когда они не должны, скорее всего, будут продвигать этот последний метод.
Преподаватели, которым надоедает наблюдать за тем, как их ученики «отменяют», когда они не должны, скорее всего, будут продвигать этот последний метод.
Однако, если мы можем помочь нашим учащимся избежать «ошибок отмены», мы предпочитаем позволять нашим учащимся сокращать общие множители (как мы сделали в уравнении (8)) при сокращении дробей, таких как 12/18, до наименьших членов. Итак, имея в виду эти мысли, давайте обсудим некоторые из наиболее распространенных ошибок отмены.
Начнем с самого важного совета.
Как избежать ошибок при отмене
Вы можете отменять только коэффициенты, но не дополнения. Чтобы избежать ошибок при отмене, полностью учитывайте факторы, прежде чем начинать отмену.
Предупреждение
Многие последующие вычисления неверны. Это примеры распространенных ошибок, совершаемых при выполнении отмены. Убедитесь, что вы внимательно прочитали и избегайте простого «сканирования» этих вычислений.
В качестве первого примера рассмотрим рациональное выражение
\[\frac{2+6}{2}\]
, что явно равно 8/2 или 4. Однако, если вы отмените в этой ситуации, как в
Однако, если вы отмените в этой ситуации, как в
\[\frac{2+6} {2}=\frac{\not{2}+6}{\not{2}}\]
вы, конечно, не получите тот же результат. Так что же случилось?
Обратите внимание, что в числителе уравнения (10) 2 и 6 разделены знаком плюс. Таким образом, они не являются факторами; они дополнения! Вы не можете отменить добавления, только факторы.
Предположим, для сравнения, что рациональное выражение было
\[\frac{2 \cdot 6}{2}\]
, что явно равно 12/2 или 6. В этом случае 2 и 6 в числителе разделены символом умножения, поэтому они являются множителями, и допускается отмена, как в
\[\frac{2 \cdot 6}{2}=\frac{\not{2} \cdot 6}{\not{2}}=6\]
Теперь, прежде чем вы отбросите эти примеры как тривиальные, рассмотрите следующие примеры, идентичные по структуре. Во-первых, рассмотрим
\[\frac{x+(x+2)}{x}=\frac{\not{x}+(x+2)}{\not{x}}=x+2\]
Эта отмена идентична той, которая выполняется в уравнении (10), и не допускается. Обратите внимание, что в числителе x и (x+2) разделены символом сложения, поэтому они являются слагаемыми. Вы не можете отменить добавление!
Обратите внимание, что в числителе x и (x+2) разделены символом сложения, поэтому они являются слагаемыми. Вы не можете отменить добавление!
И наоборот, рассмотрим следующий пример.
\[\frac{x(x+2)}{x}=\frac{\not{x}(x+2)}{\not{x}}=x+2\]
В числителе в этом примере x и (x+2) разделены подразумеваемым умножением. Следовательно, они являются факторами, и отмена допустима.
Посмотрите еще раз на уравнение (10), где правильный ответ должен был быть 8/2 или 4. Мы ошибочно нашли ответ равным 6, потому что мы отменили слагаемые. Обходным путем было бы сначала разложить числитель уравнения (10), а затем отменить его следующим образом.
\[\frac{2+6}{2}=\frac{2(1+3)}{2}=\frac{\not{2}(1+3)}{\not{2}} =1+3=4\]
Обратите внимание, что мы отменили факторы в этом подходе, что допустимо, и получили правильный ответ 4.
Предупреждение
Мы закончили обсуждение распространенных ошибок отмены, и вы можете не уверенно продолжать чтение. что вся математика представлена правильно. 9{2}-7(4)+12}=\frac{2}{0}\]
9{2}-7(4)+12}=\frac{2}{0}\]
Опять же, деление на ноль не определено. Левая часть уравнения (15) не определена, если x = 4, поэтому результат в уравнении (15) недействителен, если x = 4. Обратите внимание, что правая часть уравнения (15) также не определена при x = 4,
Однако алгебраическая работа, которую мы проделали выше, гарантирует, что левая часть уравнения (15) будет идентична правой части уравнения (15) для всех других значений x. Например, если мы подставим x = 5 в левую часть уравнения (15), 9{2}-7(5)+12}=\frac{4}{2}=2\]
С другой стороны, если мы подставим x = 5 в правую часть уравнения (15),
\[\frac{2}{x-4}=\frac{2}{5-4}=2\]
Следовательно, обе части уравнения (15) идентичны при x = 5. Аналогичным образом , мы можем проверить достоверность тождества в уравнении (15) для всех других значений x
Вы можете использовать графический калькулятор, чтобы проверить тождество в уравнении (15). Загрузите левую и правую части уравнения (15) в меню Y=, как показано на рисунке \(\PageIndex{1}\)(a). Нажмите 2nd TBLSET и настройте параметры, как показано на рисунке \(\PageIndex{1}\)(b). Убедитесь, что вы выделили AUTO как для независимых, так и для зависимых переменных и нажали ENTER для каждой, чтобы сделать выбор постоянным. Обратите внимание, что на рисунке \(\PageIndex{1}\)(b) мы установили TblStart = 0 и ∆Tbl = 1. Нажмите 2nd TABLE, чтобы получить табличные результаты, показанные на рисунке \(\PageIndex{1}\) (с).
Нажмите 2nd TBLSET и настройте параметры, как показано на рисунке \(\PageIndex{1}\)(b). Убедитесь, что вы выделили AUTO как для независимых, так и для зависимых переменных и нажали ENTER для каждой, чтобы сделать выбор постоянным. Обратите внимание, что на рисунке \(\PageIndex{1}\)(b) мы установили TblStart = 0 и ∆Tbl = 1. Нажмите 2nd TABLE, чтобы получить табличные результаты, показанные на рисунке \(\PageIndex{1}\) (с).
Помните, что мы поместили левую и правую части уравнения (15) в Y1 и Y2 соответственно.
- В табличных результатах на рисунке \(\PageIndex{1}\)(c) обратите внимание на сообщение ERR (ошибка) в Y1, когда x = 3 и x = 4. Это согласуется с нашими выводами выше, где слева -сторонняя часть уравнения (15) была неопределенной из-за наличия нуля в знаменателе при x = 3 или x = 4,
- Обратите внимание, что в табличных результатах на рисунке \(\PageIndex{1}\)(c) значения Y1 и Y2 совпадают для всех других значений x.

Мы приходим к следующему ключевому результату.
Ограничения
В общем случае, когда вы приводите рациональное выражение к наименьшим членам, полученное выражение должно быть идентичным исходному выражению для всех значений переменных в каждом выражении, сохраняйте те значения переменных, которые составляют любой знаменатель равен нулю. Это относится к знаменателю в исходном выражении, ко всем промежуточным выражениям в вашей работе и к конечному результату. Мы будем называть любые значения переменной, которые делают любой знаменатель равным нулю, как 9{2}-9 x-36} &=\frac{(x+4)(2x-3)}{(2x+3)(2x-3)(x+4)} \\ &=\ frac{(x+4)(2x-3)}{(2x+3)(2x-3)(x+4)} \\ &=\frac{1}{2x+3} \end {aligned}\]
Теперь мы должны определить ограничения. Это означает, что мы должны найти такие значения x, при которых любой знаменатель равен нулю.
- В основной части нашей работы у нас есть знаменатель (2x + 3)(2x - 3)(x + 4). Если мы установим это равным нулю, свойство нулевого произведения означает, что \[2 x+3=0 \quad \text { or } \quad 2 x-3=0 \quad \text { or } \quad x+4= 0\] 9{2}-9 x-36}=\frac{1}{2 x+3}\]
при условии \(x \neq −3/2, 3/2 или −4\).
 Это ограничения. Эти два выражения идентичны для всех других значений x.
Это ограничения. Эти два выражения идентичны для всех других значений x.Наконец, давайте проверим этот результат с помощью нашего графического калькулятора. Загрузите каждую часть уравнения (18) в меню Y=, как показано на рисунке \(\PageIndex{2}\)(a). Мы знаем, что у нас есть ограничение при x = −3/2, поэтому установим TblStart = −2 и \(\Delta \mathrm{Tbl}=0,5\), как показано на рисунке \(\PageIndex{2}\) (б). Убедитесь, что вы установили AUTO как для независимых, так и для зависимых переменных. Нажмите кнопку TABLE, чтобы отобразить табличный вид, показанный на рисунке \(\PageIndex{2}\)(c).
Рисунок \(\PageIndex{2}\). С помощью графического калькулятора проверьте, что левая и правая части уравнения (18) идентичны.Помните, что мы поместили левую и правую части уравнения (18) в Y1 и Y2 соответственно.
- На рисунке \(\PageIndex{2}\)(c) обратите внимание, что выражения Y1 и Y2 совпадают при всех значениях x, кроме x = −1,5. Это ограничение -3/2, которое мы нашли выше.

- Используйте клавишу со стрелкой вниз, чтобы прокрутить вниз таблицу, показанную на рисунке \(\PageIndex{2}\)(c), чтобы получить табличное представление, показанное на рисунке \(\PageIndex{2}\)(d). Обратите внимание, что Y1 и Y2 совпадают для всех значений x, кроме x = 1,5. Это ограничение 3/2, которое мы нашли выше.
- Мы предоставляем нашим читателям раскрыть ограничение при x = −4, используя стрелку вверх для прокрутки таблицы до тех пор, пока не будет достигнуто значение x, равное −4. Вы должны обнаружить другое сообщение ERR (ошибка) в этом значении x, потому что это ограничение. Вы получаете сообщение ERR из-за того, что знаменатель левой части уравнения (18) равен нулю при x = −4.
Изменение знака
Нередко вам придется манипулировать знаками дроби, чтобы получить общие множители, которые затем можно отменить. Рассмотрим, например, рациональное выражение
\[\frac{3-x}{x-3}\]
Один из возможных подходов состоит в том, чтобы умножить −1 на множитель, чтобы получить
\[\frac{3-x}{x-3} =\frac{-(x-3)}{x-3}\]
Теперь вы можете отменить общие множители.
 {2}-3 x -4}\] в наименьших условиях. Укажите все ограничения. 9{2}-3 x-4}=\frac{-2 x}{3 x+4}\]
{2}-3 x -4}\] в наименьших условиях. Укажите все ограничения. 9{2}-3 x-4}=\frac{-2 x}{3 x+4}\]для всех значений x при условии \(x \neq-1,1,\) или \(- 4/3\). Это ограничения, значения x, которые делают знаменатели равными нулю.
Правило смены знака для дробей
Давайте рассмотрим альтернативный подход к последнему примеру. Во-первых, давайте разделим принцип, согласно которому каждая дробь имеет три знака: один в числителе, один в знаменателе и третий в черте дроби. Таким образом,
\[\frac{-2}{3} \quad \text { понял знаки } \quad+\frac{-2}{+3}\]
Сформулируем правило смены знака дробей.
Правило изменения знака дробей
Каждая дробь имеет три знака: один в числителе, один в знаменателе и один в черте дроби. Если вы не видите явного знака, значит понимается знак плюс. Если отрицать любые две из этих частей,
- числитель и знаменатель или
- числитель и дробная черта или
- дробная черта и знаменатель,
, то дробь остается неизменной.

Например, начнем с −2/3, затем сделаем два отрицания: числитель и дробную черту. Затем
\[+\frac{-2}{+3}=-\frac{+2}{+3}, \quad \text { или с понятными плюсами, } \quad \frac{-2} {3}=-\frac{2}{3}\]
Это знакомый результат, так как отрицательное число два, деленное на положительное число три, равно отрицательным двум третям.
С другой стороны, мы могли бы решить инвертировать числитель и знаменатель. Тогда −2/3 становится
\[+\frac{-2}{+3}=\frac{+2}{-3}, \quad \text { или с понятными знаками плюс, } \quad \frac{ -2}{3}=\frac{2}{-3}\]
Снова знакомый результат. Конечно, минус два разделить на плюс три это то же самое, что плюс два разделить на минус три. Они оба равны минус две трети.
Вот и все. Отмените любые две части дроби, и она останется неизменной. На первый взгляд это кажется тривиальным замечанием, но его можно хорошо использовать при сокращении рациональных выражений. Предположим, например, что мы берем исходное рациональное выражение из примера \(\PageIndex{6}\) и инвертируем числитель и дробную черту.
 9{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\]
9{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\]Но соответствует ли этот ответ ответу в уравнении (22)? Да, как можно увидеть, сделав два отрицания, дробную черту и числитель.
\[-\frac{2 x}{3 x+4}=\frac{-2 x}{3 x+4}\]
Секущая линия
Рассмотрим график функции f, которую мы нарисовано на рисунке \(\PageIndex{3}\). Обратите внимание, что мы выбрали две точки на графике f, а именно (a, f(a)) и (x, f(x)), и провели через них линию L, которую математики называют «секущей». ».
Рисунок \(\PageIndex{3}\). Секущая проходит через (a, f(a)) и (x, f(x)).Наклон секущей L определяется путем деления изменения y на изменение x.
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a}\]
Этот наклон обеспечивает среднюю скорость изменение переменной y относительно переменной x. Студенты, изучающие исчисление, используют эту «среднюю скорость изменения» для разработки понятия «мгновенной скорости изменения».
 Однако мы оставим эту задачу для изучающих математику и сосредоточимся на задаче упрощения выражения (23) для средней скорости изменения. 9{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\]
Однако мы оставим эту задачу для изучающих математику и сосредоточимся на задаче упрощения выражения (23) для средней скорости изменения. 9{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\]Таким образом, \[\frac{f (x)-f(2)}{x-2}=x-1\] при условии, конечно, что \(x \neq 2\).
Упражнение
В Упражнениях 1 - 12 уменьшите каждое рациональное число до наименьшего члена, выполнив следующие действия:
- Простой множитель и в числителе, и в знаменателе.
- Отменить общие простые делители.
- Упростите числитель и знаменатель результата.
Упражнение \(\PageIndex{1}\)
\(\frac{147}{98}\)
- Ответ
\(\ гидроразрыва{3}{2}\)
Упражнение \(\PageIndex{2}\)
\(\frac{3087}{245}\)
Упражнение \(\PageIndex{3}\)
\(\frac{1715}{196} \)
- Ответить
\(\ гидроразрыва{35}{4}\)
Упражнение \(\PageIndex{4}\)
\(\frac{225}{50}\)
Упражнение \(\PageIndex{5}\)
\(\frac{1715}{441}\)
- Ответ
\(\ гидроразрыва{35}{9}\)
Упражнение \(\PageIndex{6}\)
\(\frac{56}{24}\)
Упражнение \(\PageIndex{7}\)
\(\frac{108}{189} \)
- Ответить
\(\ гидроразрыва{4}{7}\)
Упражнение \(\PageIndex{8}\)
\(\frac{75}{500}\)
Упражнение \(\PageIndex{9}\)
\(\frac{100}{28}\)
- Ответ
\(\frac{25}{7}\)
Упражнение \(\PageIndex{10}\)
\(\frac{98}{147}\)
Упражнение \(\PageIndex{11}\)
\(\frac{1125}{175} \)
- Ответить
\(\frac{45}{7}\)
Упражнение \(\PageIndex{12}\)
\(\frac{3087}{8575}\) 92+13x+42}{9x+63}\)
В Упражнениях 19 - 24 инвертируйте любые две части дроби, затем сомножите (если необходимо) и сократите общие множители, чтобы уменьшить рациональное выражение до наименьшего условия.
 Укажите все ограничения.
Укажите все ограничения.Упражнение \(\PageIndex{19}\)
\(\frac{x+2}{−x−2}\)
- Ответ
−1 при условии \(x \ne −2\)
Упражнение \(\PageIndex{20}\)
\(\frac{4−x}{x−4}\) 92}\)
В Упражнениях 39 - 42 приведите каждую рациональную функцию к наименьшим терминам, а затем выполните каждую из следующих задач.
- Загрузите исходное рациональное выражение в Y1 и сокращенное рациональное выражение (ваш ответ) в Y2 вашего графического калькулятора.
- В НАСТРОЙКЕ ТАБЛИЦЫ установите TblStart равным нулю, ∆Tbl равным 1, затем убедитесь, что для независимых и зависимых переменных установлено значение Авто. Выберите ТАБЛИЦА и прокручивайте с помощью стрелок вверх и вниз на калькуляторе, пока не увидите наименьшее ограничение. Скопируйте оба столбца таблицы на лист с домашним заданием, показав согласие между Y1 и Y2 и то, что происходит при всех ограничениях.
 92+13x+40}{−2x−16}\)
92+13x+40}{−2x−16}\)Учитывая f(x) = 2x+5, упростите каждое из выражений в Упражнения 43 - 46 . Обязательно сократите свой ответ до минимума и укажите любые ограничения.
Упражнение \(\PageIndex{43}\)
\(\frac{f(x)−f(3)}{x−3}\)
- Ответ
2 при условии \(x \ne 3\)
Упражнение \(\PageIndex{44}\)
\(\frac{f(x)−f(6)}{x−6}\)
Упражнение \(\PageIndex{45}\) 92+2x\), упростите каждое из выражений в Упражнения 47 - 50 . Обязательно сократите свой ответ до минимума и укажите любые ограничения.
Упражнение \(\PageIndex{47}\)
\(\frac{f(x)−f(1)}{x−1}\)
- Ответ
x+3 при условии \(x \ne 1\)
Упражнение \(\PageIndex{48}\)
\(\frac{f(x)−f(a)}{x−a}\)
Упражнение \(\PageIndex {49}\)
\(\frac{f(a+h)−f(a)}{h}\)
- Ответить
2a+h+2 при условии \(h \ne 0\)
Упражнение \(\PageIndex{50}\)
\(\frac{f(x+h)−f(x)}{h}\)
Тренировка навыков .
 В Упражнениях 51 - 54 оцените заданную функцию в заданном выражении и упростите свой ответ.
В Упражнениях 51 - 54 оцените заданную функцию в заданном выражении и упростите свой ответ.Упражнение \(\PageIndex{51}\)
Предположим, что f является функцией
\(f(x) = −\frac{x−6}{8x+7}\)
Оцените f(−3x+2) и упростите свой ответ.
- Ответить
\(−\frac{3x+4}{24x−23}\)
Упражнение \(\PageIndex{52}\)
Предположим, что f является функцией
\(f(x) = −\frac{5x+3}{7x+6}\)
Вычислить f(− 5x+1) и упростите свой ответ.
Упражнение \(\PageIndex{53}\)
Предположим, что f является функцией
\(f(x) = −\frac{3x−6}{4x+6}\)
Вычислить f(− x−3) и упростите свой ответ.
- Ответить
\(−\frac{3x+15}{4x+6}\)
Упражнение \(\PageIndex{54}\)
Предположим, что f является функцией
\(f(x) = \frac{4x−1}{2x−4}\)
Вычислить f(5x) и упрости свой ответ.

Эта страница под названием 7.2: Сокращение функций Rational распространяется под лицензией CC BY-NC-SA 2.5, ее автором, ремиксом и/или куратором является Дэвид Арнольд.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Арнольд
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 2,5
- Показать страницу TOC
- нет
- Теги
- делимость
рациональных выражений | Алгебра и тригонометрия
Цели обучения
В этом разделе учащиеся:
- Упрощают рациональные выражения.

- Умножение рациональных выражений.
- Деление рациональных выражений.
- Сложение и вычитание рациональных выражений.
- Упрощайте сложные рациональные выражения.
Кондитерская имеет постоянные затраты в размере [латекс]\,\text{\$}280\,[/латекс]в неделю и переменные затраты в размере[латекс]\,\text{\$}9\,[/латекс ]за коробку выпечки. Затраты магазина в неделю в пересчете на [латекс]\,х,[/латекс]количество изготовленных коробок составляют[латекс]\,280+9х.\,[/латекс]Мы можем разделить затраты в неделю на количество изготовленных коробок для определения стоимости коробки выпечки.
[latex]\frac{280+9x}{x}[/latex]
Обратите внимание, что результатом является полиномиальное выражение, деленное на второе полиномиальное выражение. В этом разделе мы рассмотрим частные полиномиальные выражения.
Упрощение рациональных выражений
Частное двух полиномиальных выражений называется рациональным выражением. Мы можем применять свойства дробей к рациональным выражениям, например, упрощая выражения, исключая общие множители из числителя и знаменателя.
 Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения. 9{2}-36}.[/latex]
Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения. 9{2}-36}.[/latex]Показать решение
Умножение рациональных выражений
Умножение рациональных выражений работает так же, как умножение любых других дробей. Мы умножаем числители, чтобы найти числитель произведения, а затем умножаем знаменатели, чтобы найти знаменатель произведения. Перед умножением полезно разложить числители и знаменатели на множители так же, как мы это делали при упрощении рациональных выражений. Нам часто удается упростить произведение рациональных выражений.
How To
Даны два рациональных выражения, умножьте их.
- Разложите числитель и знаменатель на множители.
- Умножьте числители.
- Умножьте знаменатели.
- Упростить.
Умножение рациональных выражений
Умножение рациональных выражений и представление произведения в простейшей форме:
[латекс]\frac{\left(x+5\right)\left(x-1\right)}{3\left (x+6\right)}\cdot\frac{\left(2x-1\right)}{\left(x+5\right)}[/latex] 9{3}}[/latex]
Как сделать
Даны два рациональных выражения, разделите их.

- Перепишите как первое рациональное выражение, умноженное на обратную величину второго.
- Разложите числители и знаменатели на множители.
- Умножьте числители.
- Умножьте знаменатели.
- Упростить.
Деление рациональных выражений
Разделение рациональных выражений и выражение частного в простейшей форме: 9{2}+5x-14}[/latex]
Показать решение
Сложение и вычитание рациональных выражений
Сложение и вычитание рациональных выражений работает так же, как сложение и вычитание числовых дробей. Чтобы сложить дроби, нам нужно найти общий знаменатель. Рассмотрим пример сложения дробей.
[латекс]\begin{array}{ccc}\hfill \frac{5}{24}+\frac{1}{40}& =& \frac{25}{120}+\frac{3}{ 120}\hfill \\ & =& \frac{28}{120}\hfill \\ & =& \frac{7}{30}\hfill \end{массив}[/latex]
Мы должны переписать дроби, чтобы они имели общий знаменатель, прежде чем мы сможем складывать.
 Мы должны делать то же самое при сложении или вычитании рациональных выражений.
Мы должны делать то же самое при сложении или вычитании рациональных выражений.Самый простой в использовании общий знаменатель — это наименьший общий знаменатель, или LCD. LCD — это наименьшее кратное, общее для знаменателей. Чтобы найти LCD двух рациональных выражений, мы факторизуем выражения и перемножаем все различные множители. Например, если факторизованные знаменатели были [латекс]\,\влево(х+3\вправо)\влево(х+4\вправо)\,[/латекс]и[латекс]\,\влево(х+4\ вправо)\влево(х+5\вправо),[/латекс]тогда ЖК-дисплей будет [латекс]\,\влево(х+3\вправо)\влево(х+4\вправо)\влево(х+5 \справа).[/латекс]
Как только мы найдем ЖК, нам нужно умножить каждое выражение на форму 1, что изменит знаменатель на ЖК. Нам нужно будет умножить выражение со знаменателем [латекс]\,\влево(х+3\вправо)\влево(х+4\вправо)\,[/латекс]на[латекс]\,\фрак{х +5}{x+5}\,[/latex]и выражение со знаменателем [latex]\,\left(x+4\right)\left(x+5\right)\,[/latex] by[latex]\,\frac{x+3}{x+3}.[/latex]
How To
Учитывая два рациональных выражения, сложите или вычтите их.

- Разложите числитель и знаменатель на множители.
- Найдите на ЖК-дисплее выражения.
- Умножьте выражения на форму 1, которая меняет знаменатели на LCD.
- Сложите или вычтите числители.
- Упростить.
Добавление рациональных выражений
Добавление рациональных выражений:
[latex]\frac{5}{x}+\frac{6}{y}[/latex]
Показать решение
Анализ
Умножение на[latex]\,\frac{y}{y}\,[/latex]или[latex]\,\frac{x}{x}\,[/latex] не меняет значение исходного выражения, потому что любое число, разделенное само на себя, равно 1, а умножение выражения на 1 дает исходное выражение. 9{2}-4}[/latex]
Показать решение
Должны ли мы использовать ЖК-дисплей для сложения или вычитания рациональных выражений?
Нет. Подойдет любой общий знаменатель, но проще всего использовать ЖК-дисплей.

Попробуйте
Вычтите рациональные выражения: [латекс]\,\frac{3}{x+5}-\frac{1}{x-3}.[/latex]
Показать решение
Упрощение сложных рациональных выражений
Сложное рациональное выражение — это рациональное выражение, которое содержит дополнительные рациональные выражения в числителе, знаменателе или в обоих. Мы можем упростить сложные рациональные выражения, переписав числитель и знаменатель как отдельные рациональные выражения и разделив их. Сложное рациональное выражение[latex]\,\frac{a}{\frac{1}{b}+c}\,[/latex]можно упростить, переписав числитель как дробь[latex]\,\frac{ a}{1}\,[/latex]и объединив выражения в знаменателе как[latex]\,\frac{1+bc}{b}.\,[/latex]Затем мы можем переписать выражение как умножение задача с использованием обратной величины знаменателя. Получаем [латекс]\,\frac{a}{1}\cdot \frac{b}{1+bc},[/latex], что равно [латекс]\,\frac{ab}{1+bc }.[/латекс]
Как сделать
Дано сложное рациональное выражение, упростите его.

- Объедините выражения в числителе в одно рациональное выражение путем сложения или вычитания.
- Объедините выражения в знаменателе в одно рациональное выражение путем сложения или вычитания.
- Перепишите как деление числителя на знаменатель.
- Переписать как умножение.
- Умножить.
- Упростить.
Упрощение сложных рациональных выражений
Упрощение:[latex]\frac{y+\frac{1}{x}}{\frac{x}{y}}[/latex].
Показать решение
Попробуйте
Упростите:[латекс]\frac{\frac{x}{y}-\frac{y}{x}}{y}[/latex]
Показать решение
Всегда ли можно упростить сложное рациональное выражение?
Да. Мы всегда можем переписать сложное рациональное выражение как упрощенное рациональное выражение.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с рациональными выражениями.

- Упрощение рациональных выражений
- Умножение и деление рациональных выражений
- Сложение и вычитание рациональных выражений
- Упростить сложную дробь
Основные понятия
- Рациональные выражения можно упростить, исключив общие множители в числителе и знаменателе. См. (Рисунок).
- Мы можем умножать рациональные выражения, умножая числители и умножая знаменатели. См. (Рисунок).
- Чтобы разделить рациональные выражения, умножьте их на обратную величину второго выражения. См. (Рисунок).
- Сложение или вычитание рациональных выражений требует нахождения общего знаменателя. См. (Рисунок) и (Рисунок).
- Сложные рациональные выражения имеют дроби в числителе или знаменателе. Эти выражения можно упростить. См. (Рисунок).
Упражнения по разделам
Вербальные
Как можно использовать факторинг для упрощения рациональных выражений? 9{2}-2x+1}[/latex]
В следующих упражнениях сложите и вычтите рациональные выражения, а затем упростите.

[латекс]\frac{4}{x}+\frac{10}{y}[/latex]
Показать решение
[латекс]\frac{12}{2q}-\frac{6}{3p}[/latex]
[латекс]\frac{4}{a+1}+\frac{5}{a- 3}[/latex]
Показать решение
[латекс]\frac{c+2}{3}-\frac{c-4}{4}[/latex]
[латекс]\frac{y+3}{y-2}+\frac {y-3}{y+1}[/latex]
Показать решение
[латекс]\frac{x-1}{x+1}-\frac{2x+3}{2x+1}[/latex]
[латекс]\frac{3z}{z+1}+\frac{2z+5}{z-2}[/latex]
Показать решение
[латекс]\frac{4p}{p+1}-\frac{p+1}{4p}[/latex]
[латекс]\frac{x}{x+1}+\frac{y }{y+1}[/latex]
Показать решение
Для следующих упражнений упростите рациональное выражение.
[латекс]\frac{\frac{6}{y}-\frac{4}{x}}{y}[/latex]
[латекс]\frac{\frac{2}{a}+ \frac{7}{b}}{b}[/latex]
Показать решение
[латекс]\frac{\frac{x}{4}-\frac{p}{8}}{p}[/latex]
[латекс]\frac{\frac{3}{a}+\frac{b}{6}}{\frac{2b}{3a}}[/latex]
Показать решение
[латекс]\frac{\frac{3}{x+1}+\frac{2}{x-1}}{\frac{x-1}{x+1}}[/latex]
[латекс]\frac{\frac{a}{b}-\frac{b}{a}}{\frac{a+b}{ab}}[/latex]
Показать решение
[латекс]\frac{\frac{2x}{3}+\frac{4x}{7}}{\frac{x}{2}}[/latex]
[латекс]\frac{\frac {2c}{c+2}+\frac{c-1}{c+1}}{\frac{2c+1}{c+1}}[/latex]
Показать решение
[латекс]\frac{\frac{x}{y}-\frac{y}{x}}{\frac{x}{y}+\frac{y}{x}}[/latex] 9{2}=64[/latex]
Показать решение
Для следующих упражнений упростите выражение.

[латекс]9\левый(у+2\правый)÷3\cdot 2+1[/латекс]
[латекс]3м\левый(4+7\правый)-м[/латекс]
Показать Решение
В следующих упражнениях определите число как рациональное, иррациональное, целое или натуральное. Выберите наиболее описательный ответ.
0
Показать решение
[латекс]\frac{5}{6}[/латекс]
[латекс]\sqrt{11}[/латекс] 9{-6}[/latex]
Запишите число в экспоненциальном представлении: 16 340 000
Показать решение
Радикалы и рациональные выражения
В следующих упражнениях найдите главный квадратный корень.
[латекс]\sqrt{121}[/латекс]
[латекс]\sqrt{196}[/латекс]
Показать решение
[латекс]\sqrt{361}[/латекс]
[латекс]\sqrt{75}[/латекс]
Показать решение
[латекс]\sqrt{162}[/латекс]
[латекс]\sqrt{\frac{32}{25}}[/латекс]
Показать решение
[латекс]\sqrt{\frac{80}{81}}[/латекс]
[латекс]\sqrt{\frac{49}{1250}}[/латекс]
Показать решение
[латекс]\frac{2}{4+\sqrt{2}}[/latex]
[латекс]4\sqrt{3}+6\sqrt{3}[/latex]
Показать решение
[латекс]12\sqrt{5}-13\sqrt{5}[/латекс]
[латекс]\sqrt[5]{-243}[/латекс]
Показать решение
[латекс]\frac{\sqrt[3]{250}}{\sqrt[3]{-8}}[/latex]
Многочлены
В следующих упражнениях выполните данные операции и упростите их.
 9{2}-1}[/латекс]
9{2}-1}[/латекс][латекс] \ гидроразрыва {\ гидроразрыва {1} {d} + \ гидроразрыва {2} {c}} {\ гидроразрыва {6c + 12d} {dc}} [/ латекс]
Показать решение
[латекс]\frac{\frac{3}{x}-\frac{7}{y}}{\frac{2}{x}}[/latex]
Практический тест по главе
Для следующего упражнения, определите число как рациональное, иррациональное, целое или натуральное. Выберите наиболее описательный ответ.
[латекс]-13[/латекс]
Показать решение
[латекс]\sqrt{2}[/латекс]
В следующих упражнениях оцените уравнения. 9{2}-1}[/latex]
Показать решение
[латекс]\frac{x}{y}+\frac{2}{x}[/latex]
[латекс]\frac{\frac{a}{2b}-\frac{2b}{9a }}{\frac{3a-2b}{6a}}[/latex]
Показать решение
Глоссарий
- наименьший общий знаменатель
- наименьшее кратное двух общих знаменателей
- рациональное выражение
- частное двух полиномиальных выражений
Частичные дроби — повторяющиеся множители
Форма разложения на неполные дроби немного отличается при наличии повторяющихся множителей.

Форма разложения на частичные дроби для повторяющихся факторов:
Фактор повторяется, если его кратность больше 1.
Для каждого неповторяющегося множителя в знаменателе выполните процедуру для линейных множителей.
Если kkk — это кратность повторяющегося множителя, запишите kkk рациональных выражений, в каждом из которых этот множитель возводится в другую степень в знаменателе. 92+(-4А-4С)х+(-8А+8С+8). \end{align}161616=A(x−2)(x+2)2+(x+2)2+C(x−2)2(x+2)+(x−2)2=A( х3+2х2-4х-8)+(х2+4х+4)+С(х3-2х2-4х+8)+(х2-4х+4)=(А+С)х3+(2А-2С+2)х2+ (−4A−4C)x+(−8A+8C+8).
Это дает систему уравнений
A+C=02A−2C+2=0.\begin{выровнено} А+С &= 0 \\ 2А-2С+2 &= 0. \end{выровнено}A+C2A−2C+2=0=0.
Решение этой системы уравнений дает A=−12A=-\frac{1}{2}A=−21 и C=12.C=\frac{1}{2}.C=21. Тогда разложение частичной дроби равно
.16x4−8x2+16=−12(x−2)+1(x−2)2+12(x+2)+1(x+2)2. □\frac{16}{x^4-8x^2+16}=\frac{-1}{2(x-2)}+\frac{1}{(x-2)^2}+\frac {1}{2(x+2)}+\frac{1}{(x+2)^2}.

- На рисунке \(\PageIndex{2}\)(c) обратите внимание, что выражения Y1 и Y2 совпадают при всех значениях x, кроме x = −1,5. Это ограничение -3/2, которое мы нашли выше.

 04.17
04.17
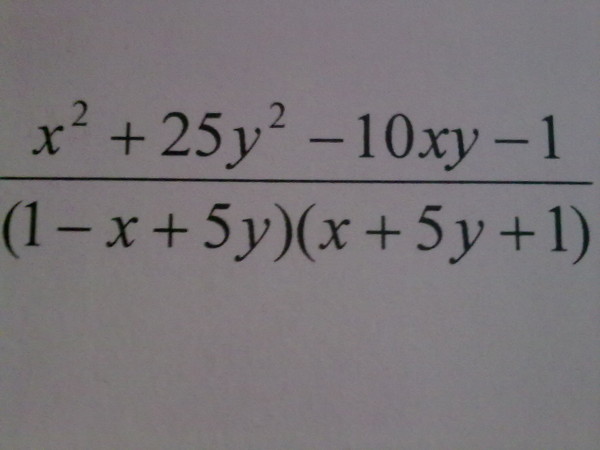

 1 x 1 разделить на x 2 = x (1 - 2) = x (-1) = 1 / x 1 = 1 / x
1 x 1 разделить на x 2 = x (1 - 2) = x (-1) = 1 / x 1 = 1 / x 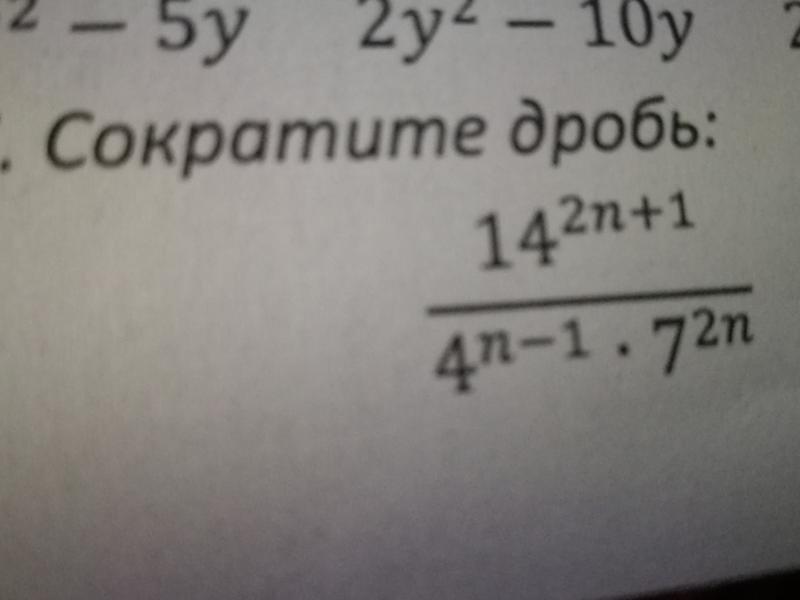 1 Прибавление целого к дроби
1 Прибавление целого к дроби Попытка факторизовать путем разделения среднего члена
Попытка факторизовать путем разделения среднего члена
 Это ограничения. Эти два выражения идентичны для всех других значений x.
Это ограничения. Эти два выражения идентичны для всех других значений x.
 {2}-3 x -4}\] в наименьших условиях. Укажите все ограничения. 9{2}-3 x-4}=\frac{-2 x}{3 x+4}\]
{2}-3 x -4}\] в наименьших условиях. Укажите все ограничения. 9{2}-3 x-4}=\frac{-2 x}{3 x+4}\]
 9{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\]
9{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\] Однако мы оставим эту задачу для изучающих математику и сосредоточимся на задаче упрощения выражения (23) для средней скорости изменения. 9{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\]
Однако мы оставим эту задачу для изучающих математику и сосредоточимся на задаче упрощения выражения (23) для средней скорости изменения. 9{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\] Укажите все ограничения.
Укажите все ограничения. 92+13x+40}{−2x−16}\)
92+13x+40}{−2x−16}\) В Упражнениях 51 - 54 оцените заданную функцию в заданном выражении и упростите свой ответ.
В Упражнениях 51 - 54 оцените заданную функцию в заданном выражении и упростите свой ответ.

 Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения. 9{2}-36}.[/latex]
Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения. 9{2}-36}.[/latex]
 Мы должны делать то же самое при сложении или вычитании рациональных выражений.
Мы должны делать то же самое при сложении или вычитании рациональных выражений.



 9{2}-1}[/латекс]
9{2}-1}[/латекс]