Метод Гомори решения задач ЦЛП. Лекция 8
Похожие презентации:
Симплекс-метод для решения задач линейного программирования
Методы решения комбинаторно-оптимизационных задач. (Тема 4)
Симплекс-метод решения задач линейного программирования
Симплекс-метод
Решение задачи «О рюкзаке» методом динамического программирования
Симплексный метод линейного программирования
Общие положения и симплекс метод
Теория принятия решений принятие оптимальных решений методами динамического программирования
Использование методов типа ветвей и границ для решения экстремальных задач на графах
Транспортная задача. Метод потенциалов
1. Метод Гомори решения задач ЦЛП
Лекция 81
2. План лекции
I Постановка задачи ЦЛП в общем видеII Алгоритм метода Гомори
III Пример реализации
2
3. Общая постановка ЗЦЛП
Целевая функцияn
F x с jx j max 1
j 1
Система ограничений
n
a ijx j bi , i 1, m 2
j 1
x j 0, j 1, n
3
x j Z (целые) j 1, k , k n 4
Если k<n задача частичноцелочисленная
Если k=n задача полностью целочисленная
3
4.
 ПримерДано
ПримерДаноF x1 1.5x 2 max
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 0, x 2 0.
x1, x 2 Z
Решим геометрически
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 3.5
x 2 2 .5
4
5. Алгоритм метода Гомори
1. Решаем задачу ЛП (1- 3) симплекс-методом.2. Полученное оптимальное решение задачи (1-3), если оно
существует, проверяем на целочисленность:
если все xj, допустимые целые, то, полученное оптимальное
решение задачи ЛП является оптимальным решением задачи
целочисленного программирования, конец алгоритма;
если задача ЛП решения не имеет, то не имеет решения и задача
целочисленного программирования;
наконец, если хотя бы одна координата не удовлетворяет условию
(4), то переходим к шагу 3.
3. Строим дополнительное линейное ограничение, с помощью
которого отсекается та часть допустимой области,
определяемой условиями (2-3), в которой содержится
оптимальное решение задачи ЛП (1-3), но нет ни одного
допустимого решения, удовлетворяющего условию (4) и вновь
выполняем пункт 1 для задачи ЛП с дополнительным
ограничением.

5
6. Построение отсечения
Гомори показал, что при «k-м» возвращении к решениюзадачи ЛП, “k-е» дополнительное ограничение имеет
вид:
x n k 1 x i0 x i0
x ij x ij x j ,
j I s
k 0,1,2,…, x n k 1 0
5
где [xi0], [xij] – целая часть соответствующей величины;
xi0 – нецелая координата оптимального плана задачи (13) у которой нецелая часть самая большая;
xij – координаты разложения векторов Аj, не попавших в
базис;
Is – множество векторов, не попавших в базис
6
7. Блок-схема алгоритма метода Гомори
НачалоРешение
задачи
лин.прогр.
K=0
Ввод
данных
K=k+1
–
Выбираем
строку i для
отсечения
–
x i0 -целые
+
Вывод
результатов
Конец
7
Задача
лин. прогр.
неразрешима ?
+
Задача целочисл. прогр.
неразрешима
8. Расчетные формулы для построения отсечения
Ограничение (5) может быть записано в виде:1) отсечение для целочисленной задачи ЛП
x ij x j x i0 (6)
j I s
2) отсечение для частично целочисленной задачи
ijx j x i0 (7)
j I s
где коэффициенты зависит от типа переменной:
а) для переменных, которые могут быть нецелыми
x ij ,
ij x i 0
1 x x ij ,
i0
8
x ij 0
x ij 0
8
б) для переменных, которые должны быть целые
x ij x i 0
x ij ,
ij 1 x ij
1 x x i 0 , x ij x i 0
i0
9.
 ПримерДано
ПримерДаноF x1 x 2 max
x 1 2 .5
x 2 2 .5
x1 0, x 2 0.
x1 , x 2 Z
Канонический вид
F x1 1x 2 max
x1 x 3 2,5
x 2 x 4 2,5
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
9
10. Решение методом Гомори
Решение симплекс-методом без учета требованияцелочисленности
Базис
А1
А2
Сбаз.
1
1
b опор.
2,5
2,5
F=5
А1
А2
1
0
0
А3
0
1
0
А4
1
0
1
0
1
1
Решение
x* 2,5 2,5 0 0
В частично целочисленной задаче отсечения строятся
по переменной, на которую наложено требование
целочисленности. Отсечение строиться по
переменной с наибольшей дробной частью, в нашем
случае выберем первую строку:
1x 3 0x 4 2,5
x 3 0 .5
10
11. Решение методом Гомори. Вторая итерация
Выразим фиктивную переменную x3 из первогоограничения и подставим его в полученное отсечение:
2.5 x1 0,5
x1 2
F x1 x 2 max
F x1 1x 2 max
x1 2,5
x 2 2,5
x 2
1
x1 0, x 2 0.
x1 x 3 2
x 2 x 4 2,5
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
x1, x 2 Z
Решаем симплекс-методом
Базис
А1
А2
11
Сбаз.
1
1
b опор.
2
2,5
F=4,5
А1
1
0
0
x* 2 2,5 0 0
А2
0
1
0
А3
1
0
1
А4
0
1
1
12. Решение методом Гомори. Третья итерация
Построение отсечения0 x 3 1x 4 2,5
x 4 0 .5
Выражаем фиктивную переменную
2.5 x 2 0,5
x2 2
F x1 x 2 max
F x1 1x 2 max
x1 2
x 2 2,5
x 2
2
x1 0, x 2 0.
x1 x 3 2
x 2 x 4 2
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
x1, x 2 Z
Базис
А1
А2
12
Сбаз.
1
1
b опор.
2
2
F=4
А1
1
0
0
А2
0
1
0
А3
1
0
1
А4
0
1
1
13. Задание на практику
Решить методом Гомори примерF x1 1.5x 2 max
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 0, x 2 0.
x1, x 2 Z
13
English Русский Правила
Метод Гомори в решении целочисленной задачи оптимизации информационной системы
Библиографическое описание: Семахин, А. М. Метод Гомори в решении целочисленной задачи оптимизации информационной системы / А. М. Семахин. — Текст : непосредственный // Молодой ученый. — 2013. — № 1 (48). — С. 38-43. — URL: https://moluch.ru/archive/48/5986/ (дата обращения: 25.09.2022).
М. Метод Гомори в решении целочисленной задачи оптимизации информационной системы / А. М. Семахин. — Текст : непосредственный // Молодой ученый. — 2013. — № 1 (48). — С. 38-43. — URL: https://moluch.ru/archive/48/5986/ (дата обращения: 25.09.2022).
Целочисленное линейное программирование ориентировано на решение задач линейного программирования, в которых все или некоторые переменные принимают целочисленные значения [1, c. 136].
Для решения целочисленной задачи линейного программирования Р. Гомори предложил метод отсечения плоскостей в 1958 г. [1, c. 143].
Алгоритм Гомори содержит этапы:
Этап 1. Решение непрерывной задачи. Если решение дробное переход на 2 этап.
Этап 2. Решение расширенной задачи [2, c. 410].
Разработаем целочисленную математическую модель информационной системы и определим оптимальное решение методом Гомори.
Математическая модель формулируется следующим образом: из числа фирм, предоставляющих услуги спутникового Internet на территории Российской Федерации, требуется выбрать провайдера спутникового Internet с максимальной величиной чистого приведенного эффекта (NPV) и удовлетворяющих финансовым ограничениям [3, c. 58].
58].Пусть — доля финансирования проекта “НТВ-Плюс”, — доля финансирования проекта Europe On Line, — доля финансирования проекта Astra Network, — доля финансирования проекта Satpro, — доля финансирования проекта Network Service.
Целочисленная математическая модель имеет вид
при ограничениях (1)
Решим непрерывную задачу. Приведем к стандартной форме и составим исходную Жорданову таблицу (табл. 1).
(2)
Таблица 1
Начальная Жорданова таблица
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
6,5 |
5,4 |
3,2 |
2,931 |
6,286 |
5,9 |
|
= |
3,0 |
2,006437 |
1,5 |
3,000547 |
3,000575 |
3,2 |
|
= |
3,0 |
0,0 |
2,5 |
2,0 |
0,0 |
1,6 |
|
= |
1,5 |
0,0 |
0,881832 |
0,0 |
0,0 |
1,186 |
|
Z= |
0 |
-1,52727 |
-0,741239 |
-1,374394 |
-0,14511 |
-0,530312 |
В табл.
Таблица 2
Первая итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
||||||
|
= |
0,58484 |
-0,371563 |
0,311 |
1,911498 |
0,664934 |
1,007782 |
|
= |
3,0 |
0 |
2,5 |
2,0 |
0 |
1,6 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
1,83838 |
0,282827 |
0,16381 |
-0,545426 |
1,632745 |
1,138371 |
В табл.
Переход ко второму этапу алгоритма Гомори.
Выбирается базисная переменная с наибольшей дробной частью: , , . Для переменной составляется уравнение.
В табл. 4 и табл. 5 представлены расширенная задача и 3 итерация.
Таблица 3
Оптимальное решение непрерывной задачи. Вторая итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
= |
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
= |
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
Таблица 4
Расширенная задача с первым дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
= |
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
= |
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
= |
-0,305961 |
|
-0,1627 |
-0,52315 |
-0,34786 |
-0,527221 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
Таблица 5
Третья итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
0,569642 |
0,588017 |
0,25542 |
-1,084156 |
0,443182 |
1,529584 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,071475 |
0,58991 |
2,006242 |
-1,587645 |
-1,055679 |
1,034781 |
|
= |
0,811731 |
0,437271 |
0,515833 |
-1,176842 |
-0,782522 |
2,249531 |
|
= |
0580328 |
-0,368694 |
0,308599 |
0,992278 |
0,659799 |
-1,896738 |
|
Z= |
1,177753 |
0,702539 |
-0,18749 |
-1,129581 |
0,881649 |
2,704617 |
В табл. 6
приведено оптимальное нецелочисленное решение.
6
приведено оптимальное нецелочисленное решение.
В табл.7 представлена расширенная задача со вторым дополнительным ограничением.
Таблица 6
Оптимальное нецелочисленное решение
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
= |
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
= |
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
Таблица 7
Расширенная задача со вторым дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
= |
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
= |
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
= |
-0,203704 |
-0,185185 |
-0,592593 |
-0,09259 |
-0,164074 |
0,542779 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
В табл. 8
приведена четвертая итерация. В табл.9 и табл.10
представлены расширенная задача и оптимальное целочисленное
решение. Оптимальный целочисленный план
=
(табл. 10). Значение целевой функции Z=1.52728.
8
приведена четвертая итерация. В табл.9 и табл.10
представлены расширенная задача и оптимальное целочисленное
решение. Оптимальный целочисленный план
=
(табл. 10). Значение целевой функции Z=1.52728.
Результаты проведенных исследований позволили сделать следующие выводы.
Разработана целочисленная математическая модель оптимизации информационных систем, позволяющая сократить затраты и сроки проектирования информационных систем и повысить обоснованность принимаемых решений.
Найдено оптимальное решение целочисленной задачи оптимизации информационной системы методом Гомори.
Таблица 8
Четвертая итерация. Отсечение дробной части переменной
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1 |
0 |
1 |
1 |
1 |
0 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
= |
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
= |
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
= |
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
Таблица 9
Расширенная задача с третьим дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1 |
0 |
1 |
1 |
1 |
0 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
= |
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
= |
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
= |
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
= |
-0,34375 |
-0,312499 |
0,68785 |
-0,156246 |
-0,276875 |
0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
Таблица 10
Оптимальное целочисленное решение
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
1 |
0 |
1 |
1 |
1 |
0 |
|
= |
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
-2,5 |
2,5 |
1,60001 |
0 |
-2 |
|
= |
1,5 |
-0,881833 |
0,88183 |
1,186 |
0 |
0 |
|
= |
0,993565 |
-1,50001 |
-0,506442 |
1,19356 |
0,994141 |
-3,00056 |
|
= |
0 |
1 |
-1 |
0 |
0 |
0 |
|
= |
1,1 |
-3,20001 |
-2,20001 |
0,499989 |
0,886003 |
-2,93101 |
|
Z= |
1,52727 |
0,741244 |
0,786034 |
0,996964 |
1,38216 |
1,3744 |
Литература:
Таха Х.
 А. Введение
в исследование операций. 7-е издание.: Пер. с англ. М.:
Издательский дом “Вильямс”, 2005–912 c.
А. Введение
в исследование операций. 7-е издание.: Пер. с англ. М.:
Издательский дом “Вильямс”, 2005–912 c.Конюховский П. В. Математические методы исследования операций в экономике. — СПб.: Издательство «Питер», 2000. — 208 с.
Семахин А. М. Анализ математической модели информационной системы. В сб. материалов X Всероссийской научно-практической конференции с международным участием (25–26 ноября 2011 г.). — Томск: Изд-во Том.ун-та, 2011. — Ч.2–206 с.
МЕТОД ГОМОРИ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
Метод Гомори является универсальным методом решения задач целочисленного программирования, с помощью которого после конечного числа итераций можно найти оптимальный план или убедиться в том, что задача не имеет решений. Однако практическая ценность метода Гомори весьма ограничена, так как при решении задач нужно выполнить довольно много итераций.
При решении задач целочисленного программирования методом Гомори из множества оптимальных планов задачи линейного программирования постепенно удаляются подмножества, которые не содержат целочисленных планов.
На первой итерации симплекс-методом нужно решить задачу линейного программирования. Если найденные неизвестные удовлетворяют требованию целочисленности, то задача целочисленного программирования решена. Если же среди найденных неизвестных хотя бы одна является дробным числом, то тогда следует составить дополнительное условие (как его составлять — об этом чуть ниже) и присоединить его к системе ограничений задачи целочисленного программирования. Таким образом, из множества планов удаляется подмножество, не содержащее целочисленных планов. Если оптимальный план дополненной таким образом задачи является целочисленным, то задача целочисленного программирования решена. Процесс решения продолжается то тех пор, пока на какой-либо итерации не будет найден целочисленный оптимальный план или можно убедиться, что задача не имеет решения.
Теперь о том, как составлять упомянутое дополнительное условие. Оно, дополнительное условие, получается из одного из уравнений системы ограничений из коэффициентов при неизвестных и самих неизвестных по формуле
где в фигурных скобках — дробные части соответственно свободного члена и коэффициентов при неизвестных.
Например, из симплексной таблицы получаем такое уравнение:
Дробную часть свободного члена получаем, вычитая из самого числа его целую часть следующим образом:
Аналогично получаем дробные части коэффициентов при неизвестных:
(при x3),
(при x4).
А общее правило нахождения дробных частей таково: целой частью вещественного числа a называется самое большое целое число [a], непревышающее a; дробной частью вещественного числа a называется разность {a} = a — [a] самого числа a и его целой части [a].
Далее следует преобразовать полученное неравенство в уравнение путём введения дополнительной неизвестной :
.
В нашем примере по приведённой выше формуле получается следующее уравнение:
Пример. Решить методом Гомори следующую задачу целочисленного программирования. Найти максимум целевой функции
Найти максимум целевой функции
при системе ограничений
Решение. Решаем задачу симплекс-методом (сам метод объясняться здесь не будет, а будут приведены лишь симплексные таблицы.).
Дополнительные неизвестные x3 и x4 примем за базисные. Выразим базисные неизвестные и функцию цели через неосновные переменные:
Из коэффициентов составим симплексную таблицу:
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | ||||
| X4 | ||||
| С | -3 | -2 |
Составляем следующие таблицы до получения оптимального плана:
| Таблица 2 | |||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | ||
| X3 | X2 | ||||
| X1 | 1/2 | 1/2 | |||
| X4 | -1/2 | 7/2 | -1 | ||
| С | 3/2 | -1/2 | |||
| Таблица 3 | |||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | ||
| X3 | X4 | ||||
| X1 | 19/7 | 4/7 | -1/7 | -1/2 | |
| X2 | 4/7 | -1/7 | 2/7 | ||
| С | 65/7 | 10/7 | 1/7 | 1/2 | |
Из таблицы 3 находим оптимальный план . Поскольку этот оптимальный план не удовлетворяет условию целочисленности, нам нужно составить дополнительное условие. Дробной частью координаты является число , а дробной частью координаты — число . Первое уравнение на основании таблицы запишется так:
Поскольку этот оптимальный план не удовлетворяет условию целочисленности, нам нужно составить дополнительное условие. Дробной частью координаты является число , а дробной частью координаты — число . Первое уравнение на основании таблицы запишется так:
Определив дробные части коэффициентов при неизвестных и свободных членов, получаем следующее дополнительное условие:
или, введя добавочную переменную ,
Получаем новую строку в симплексной таблице, полученной из таблицы 3 и добавления коэффициентов из только что полученного уравнения:
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 19/7 | 4/7 | -1/7 | -1/2 |
| X2 | 4/7 | -1/7 | 2/7 | |
| X5 | -5/7 | -4/7 | -6/7 | |
| С | 65/7 | 10/7 | 1/7 | 1/2 |
Совершаем шаг симплекс-метода и получаем таблицу:
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 17/6 | 2/3 | -1/6 | 1/7 |
| X2 | 1/3 | -1/3 | 1/3 | -2/7 |
| X4 | 5/6 | 2/3 | -7/6 | |
| С | 55/6 | 4/3 | 1/6 | -1/7 |
Получили оптимальный план .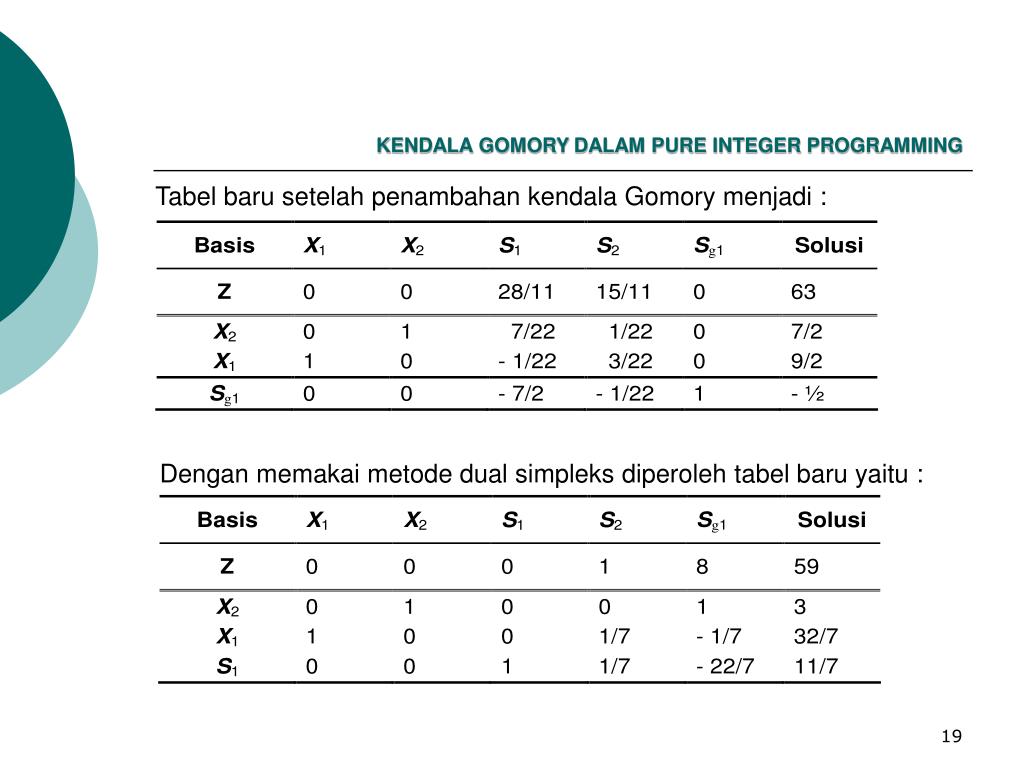 Этот план, как и предыдущий, не удовлетворяет условию целочисленности. Поэтому вновь требуется составить дополнительное условие. В данном случае можно использовать первое или третье уравнение. Получится следующее дополнительное условие:
Этот план, как и предыдущий, не удовлетворяет условию целочисленности. Поэтому вновь требуется составить дополнительное условие. В данном случае можно использовать первое или третье уравнение. Получится следующее дополнительное условие:
Составляем следующую таблицу:
| Таблица 6 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 17/6 | 2/3 | -1/6 | 1/7 |
| X2 | 1/3 | -1/3 | 1/3 | -2/7 |
| X4 | 5/6 | 2/3 | -7/6 | |
| X6 | -5/6 | -2/3 | -5/6 | |
| С | 55/6 | 4/3 | 1/6 | -1/7 |
Оптимальный план получаем из следующей, завершающей таблицы:
| Таблица 7 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X6 | |||
| X1 | 4/5 | -1/5 | 1/6 | |
| X2 | -3/5 | 2/5 | -1/3 | |
| X4 | 8/5 | -7/5 | 7/6 | |
| X5 | 4/5 | -6/5 | ||
| С | 6/5 | 1/5 | -1/6 |
Так как найденный оптимальный план удовлетворяет условию целочисленности, задача целочисленного программирования решена. Координаты x5 и x6 можно не учитывать, так как начальные условия задачи содержит лишь четыре неизвестные. Поэтому окончательный оптимальный план запишется так: , а максимум функции цели равен 9.
Координаты x5 и x6 можно не учитывать, так как начальные условия задачи содержит лишь четыре неизвестные. Поэтому окончательный оптимальный план запишется так: , а максимум функции цели равен 9.
Дата добавления: 2021-07-22; просмотров: 176; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Метод Гомори — Студопедия
Поделись
Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (1) — (3) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (1) — (4). Если же в оптимальном плане задачи (4) — (3) переменная X] принимает дробное значение, то к системе уравнений (3) добавляют неравенство
∑ f (a*ij) xj≥ f (b*i ) (5)
j
и находят решение задачи (1) —(3), (5).
В неравенстве (5) a*ijи b*i — преобразованные исходные величины aijи bi, значения которых взяты из последней симплекс-таблицы, a f (a*ij) и f (b*i) — дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число b такое, что разность между а и b есть целое). Если в оптимальном плане задачи (1) — (3) дробные значения
принимают несколько переменных, то дополнительное неравенство (5) определяется наибольшей дробной частью.
Если в найденном плане задачи (1) —(3), (5) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (1) — (4), либо устанавливают ее неразрешимость.
Если требование целочисленности (4) относится лишь к некоторым переменным, то такие задачи называются частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид
Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид
∑yijxj≥ f (b*i),
j
где yij определяются из следующих соотношений:
1) для xjкоторые могут принимать нецелочисленные значения,
a*ij при a*ij≥0
f (b*i) a*ij при a*ij<0;
1- f (b*i)
2) для Xj, которые могут принимать только целочисленные значения,
f
( a*ij ) при f
(a*ij)≤f (b*i)
f (b*i) 1-f (a*ij ) при f (a*ij)>f (b*i)
1- f (b*i)
Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:
1. Используя симплексный метод, находят решение задачи (1)-(3) без учета требования целочисленности переменных.
Используя симплексный метод, находят решение задачи (1)-(3) без учета требования целочисленности переменных.
2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (1)—(3) имеет максимальное дробное значение, а в оптимальном плане задачи (1)—(4) должна быть целочисленной.
3. Используя двойственный симплекс-метод, находят решение задачи, получающейся из задачи (1)—(3) в результате присоединения дополнительного ограничения.
4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (1)—(4) или установления ее неразрешимости.
Контрольные вопросы
- Какие задачи относятся к задачам целочисленного программирования?
- В чем сущность метода Гомори?
- Каким образом строится сечение Гомори?
- Сколько сечений Гомори можно построить?
- Чему равна дробная часть положительного числа?
- Чему равна дробная часть отрицательного числа?
- Определить дробную часть следующих чисел:
4/5; 8/3; -12/7; 65/57; -4/7; — 8/3
- Перечислить этапы алгоритма метода Гомори.

9. Тест на тему «Метод Гомори»
1.Задача целочисленного программирования — это……
а) разновидность транспортных задач.
б) экстремальная задача, переменные которой принимают лишь целочисленные значения.
в) вспомогательная задача, получаемая с помощью определенных правил непосредственно из условия исходной.
2. В математической модели задачи целочисленного программирования целевая функция и функция в системе ограничений могут быть:
а) линейными, нелинейными, смешенными.
б) только линейными.
в) нелинейными и смешенными.
3. Решение задачи целочисленного программирования начинают с …
а) определения симплексным методом оптимального плана задачи без учета целочисленности переменных.
б) построение двойственной к ней задачи.
в) приведение исходной системы к единому базису.
4. План считается оптимальным, если…
а) несколько переменных имеют дробное значение.
б) нет переменных с дробным значением.
в) все переменные имеют дробное значение.
Целочисленное линейное программирование метод гомори онлайн. Модели целочисленного линейного программирования
Метод Гомори решения задач целочисленного программирования является методом отсечения .
Суть метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана. Для этого сначала решается ослабленная задача линейного программирования без учета условия целочисленности переменных.
Если
полученное решение задачи линейного
программирования является целочисленным,
то задача целочисленного программирования
также решена и найденное решение является
оптимальным и для нее. Если же в найденном
решении задачи линейного программирования
одна или большее число переменных не
целые, то для отыскания целочисленного
решения задачи добавляются новое
линейное ограничение, которое отсекает
нецелочисленные решения. При продолжении
решения расширенной задачи двойственным
симплексным методом с учетом этого
ограничения получается целочисленный
план.
При продолжении
решения расширенной задачи двойственным
симплексным методом с учетом этого
ограничения получается целочисленный
план.
Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм.
Оно должно быть линейным;
Должно отсекать найденный оптимальный нецелочисленный план;
Не должно отсекать ни одного целочисленного плана.
Если нецелых базисных переменных несколько, то для составления ограничения выбираем компоненту оптимального плана с наибольшей дробной частью (если таких переменных несколько, то выбираем любую).
Этой переменной соответствует строка симплексной таблицы, называемая строкой, производящей отсечение (производящей строкой ).
Для изложения метода вводим следующие понятия. Пусть a – действительное число.
Под целой
частью некоторого числа а понимается максимальное
целое число [a ],
не превосходящее данного.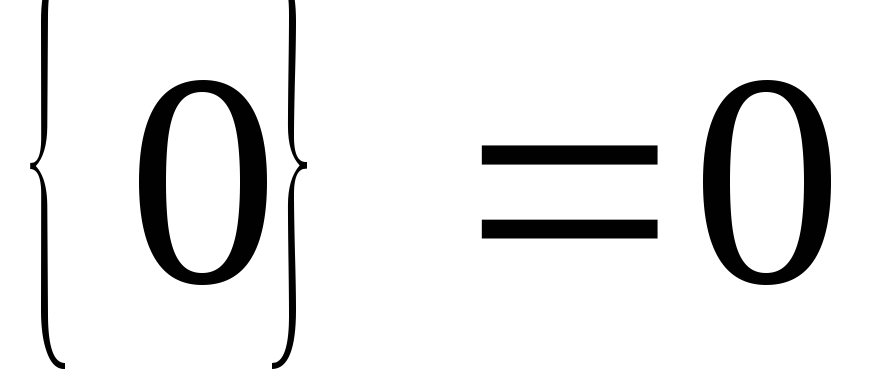
Под дробной
частью некоторого числа а понимается наименьшее неотрицательное
число
такое, что разность между ним иа есть
[a ]
– целая часть числа).
Для
выбранной базисной переменной с
наибольшей дробной частью находим дробную часть
этой переменной и дробные части всех
коэффициентов при переменныхi — й строки системы ограничений
(производящей
строкой).
Обозначим
и
целые
части чисел
и
.
Величины дробных частей
и
(
)
определяются следующим образом
Для этого по производящей строке симплексной таблицы выписывается уравнение, предполагая, что первые m переменных являются базисными для данного оптимального плана
или
Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой:
Так
как
,
получим строгое неравенство
Так как левая часть неравенства должна принимать целые значения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде:
Неравенство
преобразуется в уравнение путем введения
дополнительной неотрицательной
переменной и включается в оптимальную
симплексную таблицу.
Решаем задачу, используя двойственный симплексный метод. Если новый оптимальный план расширенной задачи будет целочисленным, то задача решена. Если же решение нецелое, то нужно повторять алгоритм метода Гомори вплоть до получения целочисленного решения.
Пример . Методом Гомори найти решение задачи
целочисленного программирования,
состоящей в определении максимального
значения функции
при условии
Решение . Выравнивая неравенства с помощью вспомогательных переменных х 3 , х 4 , получаем задачу линейного программирования в канонической форме:
Решаем задачу линейного программирования симплексным методом, используя поэтапный переход от одного базиса к другому. Ход решения задачи и полученное оптимальное решение представлены в таблицах.
С Б | С 2 =11 | |||||
∆ j =Z j –С j | ||||||
С Б | С 2 =11 | |||||
∆ j =Z j –С j | ||||||
В
найденном оптимальном плане значение
переменной х 2
равно дробному числу. Находим его дробную
часть и дробные части всех элементов
строки, содержащей переменную х 2
, а именно:
Находим его дробную
часть и дробные части всех элементов
строки, содержащей переменную х 2
, а именно:
Теперь составляем для найденных значений дробных частей неравенство Гомори:
.
х 5 , переносим свободный член уравнения в правую часть и получаем новое ограничение:
.
Добавляем в симплексную таблицу строку, содержащую новое ограничение, и столбец, содержащий новую переменную, и продолжаем решать задачу двойственным симплексным методом, так как теперь в таблице записан псевдоплан.
∆ j =Z j –С j | |||||||
С Б | С 2 =11 | ||||||
∆ j =Z j –С j | |||||||
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х 1 , поэтому находим для этой строки дробные части всех нецелых чисел, а именно:
и
новое неравенство Гомори имеет вид:
Выравниваем
неравенство Гомори с помощью новой
вспомогательной переменной х 6 ,
переносим свободный член уравнения в
правую часть и получаем новое ограничение:
.
Добавляем его к решаемой задаче, выравниваем с помощью вспомогательной переменной и решаем расширенную задачу
С Б | С 2 =11 | |||||||
∆ j =Z j –С j | ||||||||
С Б | С 2 =11 | |||||||
∆ j =Z j –С j | ||||||||
Таким
образом, найдено оптимальное решение
задачи целочисленного программирования: Z max =11 при
.
Замечания :
Если
в процессе решения в симплексной таблице
появится уравнение с нецелой компонентой
и целыми коэффициентами в соответствующей
строке системы ограничений
,
то данная задача не имеет целочисленного
решения.
Метод основан на симплекс методе, используя который находиться оптимальное решение без учета условий целочисленности. Если полученный план содержит хотя бы одну дробную компоненту, то накладывается дополнительное ограничение и вычисления снова продолжаются по симплекс методу.
Процесс продолжается до тех пор пока все компоненты плана не будут целочисленные, либо будет показано, что задача не имеет целочисленного решения.
Пусть Х* = (х1, х2, …,хm, …, хn) – оптимальный план найденный по симплекс методу, где базисом являются векторы А1, А2,…,Аm. Пусть хi дробное число (число в столбце В в iой строке). Тогда возможно, что в iой строке:
1. все хij целые, это означает, что задача не имеет целочисленного решения
2. некоторые хij дробные
некоторые хij дробные
Пусть [хi] и [хij] целые части чисел хi и хij, а {хi } и { хij } – дробные части.
Обозначим qi = {хi} и qij = { хij } и составим разности.
(qi1Х1+ qi1Х2+…+ qi1Хn)- qi ≥0
Преобразуем неравенство в уравнение умножив его на (-1) и добавив новую переменную Хn+1 и добавив новую строку в симплекс таблице (а значит и столбец). Решаем далее двойственным симплекс методом, если найденный план не является целочисленным, то процесс добавления новой переменной, строки и столбца в симплекс таблице повторяем.
Если в оптимальном плане несколько нецелочисленных компанент, то дополнительное ограничение составляем для максимального qi.
Вы также можете найти интересующую информацию в научном поисковике Otvety.Online. Воспользуйтесь формой поиска:
Еще по теме 47 Метод Гомори: основные идеи и краткое описание алгоритма. Экономический смысл введения дополнительного ограничения.:
- 25.Экономические методы управления, их целевое назначение.
 Виды и основное содержание методов экономического воздействия. Краткая характеристика и особенности применения экономических методов
Виды и основное содержание методов экономического воздействия. Краткая характеристика и особенности применения экономических методов
Пусть
оптимальный план, полученный
симплекс-методом для задачи (5.1)-(5.3),
следующий:
и получен на базисе
Тогда последняя симплексная таблица
имеет следующий вид:
Таблица 5.1
Приведённая к базису симплексная таблица для задачи целочисленного программирования
Предположим,
что
дробное;
тогда некоторое
также дробное (в противном случае задача
не имеет целочисленного решения).
Обозначим через
и
целые части чисели,
т.е. наибольшие целые числа, не
превосходящие числаи.
Тогда величины дробных частейичиселиопределяются как разности:
где и
Например,
.
Так
как по условию
– неотрицательные целые числа, то и
разностьтакже целое неотрицательное число.
Преобразуя
это неравенство в уравнение, вычитая
из его левой части целую неотрицательную
дополнительную переменную
умножим уравнение на –1, добавим к
последней симплексной таблице и, применяя
симплексный метод (желательно
двойственный), находим новый план. Если
он не является целочисленным, то по
последней симплексной таблице составляем
новое дополнительное ограничение.
Если
он не является целочисленным, то по
последней симплексной таблице составляем
новое дополнительное ограничение.
Если
в оптимальном плане задачи (5.1)-(5.3)
несколько дробных
то дополнительное ограничение составляют
дляmax.
Это ускоряет процесс получения
оптимального целочисленного решения.
Рассмотрим
геометрический смысл введения
дополнительного ограничения (см. рис.
5.2). Пусть в точке A многогранника
решений Q функция Z достигает максимального значения Z (A )=max,
но координаты точки A – дробные. Тогда введенные ограничения
по целочисленности I
и II от области Q отсекают область
с угловой точкой
,
координаты которой целочисленные и в
которой линейная функция достигает
максимального значения.
Рис.5.2. Геометрический смысл ограничения Гомори
Метод Гомори рассмотрим на примере следующей задачи.
Пример 5.1. Найти максимальное значение функции
при условиях
Дать геометрическую
интерпретацию решения задачи.
Решение. Для определения оптимального плана задачи (5.5)-(5.8) сначала находим оптимальный план задачи (5.5)-(5.7):
Таблица 5.2
базис
план
– неоптимальный,
.
Таблица 5.3
Симплекс-таблица,
приведённая к базису
,
– неоптимальный,
базис
,
.
Таблица 5.4
Симплекс-таблица,
приведённая к базису
Оптимальный
план
,
базис
.
Этот оптимальный план не является
оптимальным планом задачи (5.5)-(5.8),
поскольку две компонентыиимеют нецелочисленное значение. При
этом дробные части этих чисел
равны между собой. Поэтому для одной из
этих переменных составляется дополнительное
ограничение. Составим, например, такое
ограничение для переменной(чаще берут первую строку). Из последнейсимплекс-таблицы
имеем:
.
Таким образом, к системе ограничений задачи (5.5)-(5.7) добавляем неравенство
Теперь
находим максимальное значение функции
(5. 5) при выполнении условий (5.6), (5.7) и
(5.9). В условие (5.9) вводим дополнительную
переменную
:
5) при выполнении условий (5.6), (5.7) и
(5.9). В условие (5.9) вводим дополнительную
переменную
:
Таблица 5.5
Ввод в симплекс-таблицу дополнительной переменной
Выберем
.
базис.
Таблица 5.6
Приведение
симплекс-таблицы к базису
Базис
.
.
Запишем
оптимальный план для исходной задачи:
При этом плане значение целевой функции
равно
.
Геометрическая интерпретация решения задачи.
Рис.5.3. Геометрическая интерпретация решения задачи
Областью
допустимых решений задачи (5.5)-(5.7) является
многоугольник ОАВС D (рис. 5.3). Из рисунка видно, что максимальное
значение целевая функция принимает в
точке
т.е.
является оптимальным планом. Так как
этот план не является оптимальным планом
задачи (5.5)-(5.8) (числаи– дробные), то вводится дополнительное
ограничение
Исключая
из этого неравенства
иподстановкой вместо них соответствующих
значений из уравнений системы ограничений
(5. 6), получим
6), получим
.
.
Этому
неравенству соответствует полуплоскость,
ограниченная прямой
отсекающей отмногоугольника ОАВСD треугольник EFC .
Как
видно из рисунка, областью допустимых
решений полученной задачи является
многоугольник OABEFD .
В точке E (9;4)
этого многоугольника целевая функция
данной задачи принимает максимальное
значение. Так как координаты точки Е – целые числа и неизвестные
ипринимают целочисленные значения при
подстановке в уравнения (5.6) значений
и
то
является оптимальным планом задачи
(5.5)-(5.8). Это следует и из таблицы
симплекс-метода.
Замечание к использованию метода Гомори: если в первоначальный базис задачи входили искусственные векторы, то при составлении дополнительного ограничения искусственные переменные необходимо опустить.
Вопросы для самопроверки
Области применения целочисленного программирования.
Постановка задачи
целочисленного программирования.
Графический способ решения задачи целочисленного программирования.
Алгоритм метода Гомори.
Правило составления дополнительного ограничения (сечения Гомори).
Геометрический смысл введения сечения Гомори.
Графический метод решения задач целочисленного программирования.
При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.
Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.
Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:
1. Оно должно быть линейным;
2. Должно отсекать найденный оптимальный не целочисленный план;
3. Не должно отсекать ни одного целочисленного плана.
Алгоритм графического решения задачи
Целочисленного программирования.
1. Построить систему координат x 1 0х 2 и выбрать масштаб.
2. Найти область допустимых решений (ОДР) системы ограничений задачи.
3. Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4. Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.
Если окажется, что линия целевой функции параллельна одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений.
5. Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
6. Выделить у этих координат область с целочисленными значениями.
7. Определить новые координаты и построить граф.
8. Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.
Метод Гомори решения задач целочисленного программирования. Примеры решения экономических задач.
Данный метод основан на симплексном методе.
На первом этапе данная задача решается симплекс-методом, если полученное решение не целочисленное, то вводим дополнительное ограничение, которые должны быть:
Линейным;
Отсекать найденный оптимальный не целочисленный план;
Не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение обладающие этими свойствами называются правильным отсечением.
Ограничение накладывается на нецелочисленную переменную или на ту переменную, которая имеет большее дробное значение. Ограничение накладывается на не целочисленную переменную через не основные переменные. Ограничение составляется используя следующее правило: дробная часть свободного члена берётся с тем же знаком, который он имеет и в уравнении, а дробные части неосновных переменных — с противоположным знаком и выделяется положительная дробь.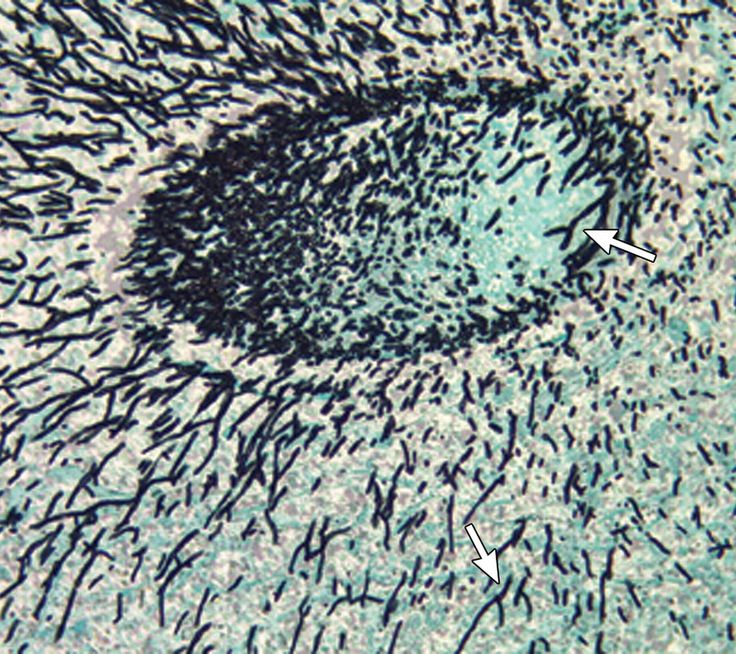 Например, {a}=a, {-a}={-A+a * }, где А — целая часть отрицательное число, а * -положительная дробь.
Например, {a}=a, {-a}={-A+a * }, где А — целая часть отрицательное число, а * -положительная дробь.
Получаем новое ограничение, вводим новую основную переменную, приведённое в формуле (1.2.3).
где x n+1 — нововведённая переменная,
x j — переменные не входящие в базис.
Новое ограничение следует вводить в последний этап симплекс метода, когда все переменные, имеющиеся в целевой функции, так же входят в базис.
Полученное базисное решение всегда не допустимое, соответствующее правильному отсечению.
Для получения допустимого базисного решения необходимо перевести в основные переменную, входящую с положительным коэффициентом в уравнение, в котором свободный член отрицательный.
При выборе какую переменные ввести в базис взамен нововведённой, следует выразить эти переменные и следую логическому рассуждения, подставить в базис ту переменную которая даёт целочисленное решение на наложенное ограничение.
Введение новых ограничений следует производить, если не получено целочисленное решение, после решения на первом этапе симплекс-методом и после введения новых ограничений.
Если в процессе решения появится выражение с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.
Задача. Контейнер объемом помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
| Вид груза | т | ден.ед. | |
Требуется загрузить контейнеровоз таким образом, чтобы стоимость перевозимого груза была максимальной.
Решим задачу методом Гомори.
Введем обозначения: х 1 – количество груза первого вида, х 2 – количество груза второго вида. Тогда экономико-математическая модель задачи примет вид:
Преобразуем математическую модель ЗЛП без учета целочисленности переменных к допустимому предпочтительному виду канонической формы:
По алгоритму основного симплекс-метода заполним симплексную таблицу решения ЗЛП:
| * | ||||||
| -10 | -12* | |||||
| * | 5/2 | -1/2 | 19/2 | |||
| 1/2 | 1/2 | 5/2 | ||||
| -4* | -30 | |||||
| 2/5 | -1/5 | 19/5 | ||||
| -1/5 | 3/5 | 3/5 | ||||
| 8/5 | 26/5 | -226/5 |
Оптимальное решение ЗЛП не удовлетворяет ограничению целочисленности, следовательно, к основным ограничениям необходимо добавить новое линейное ограничение.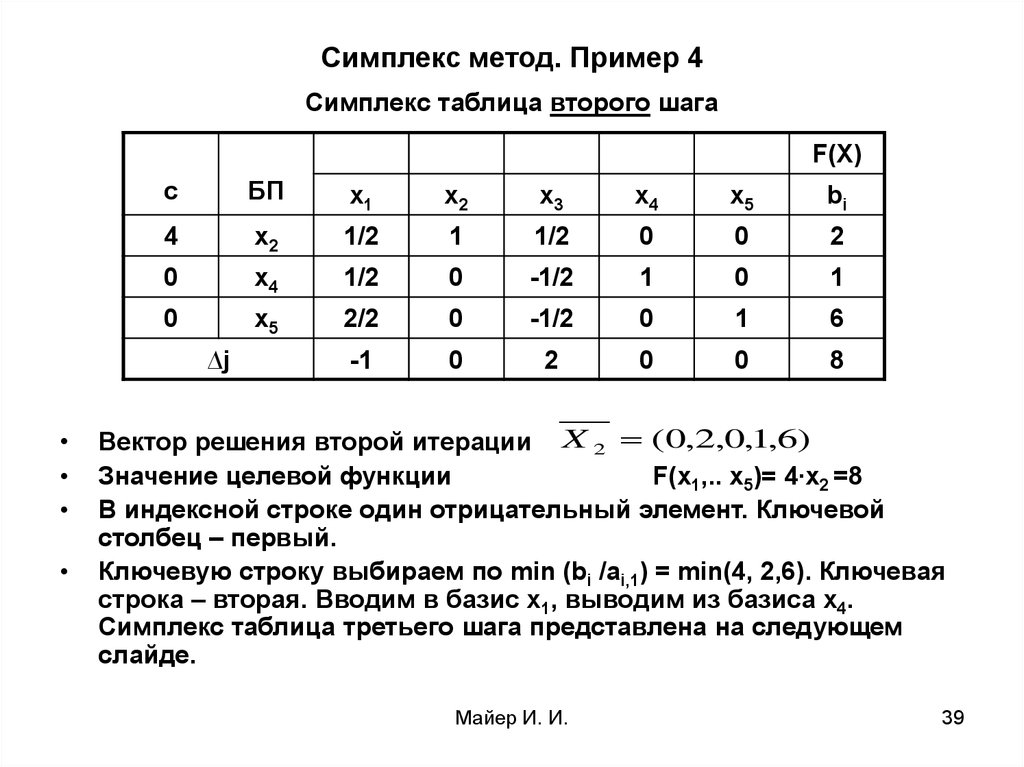
Замечание 9.1. Если имеется несколько дробных , то для той у которой дробная часть больше всего составляется ограничение.
Составим сечение Гомори для первого ограничения оптимальной симплекс-таблицы решения ЗЛП (так как ):
,
.
Преобразуем полученное ограничение к канонической форме с предпочтительной переменной:
.
Продолжим решение задачи двойственным симплекс-методом, включив новое ограничение в оптимальную симплекс-таблицу решения ЗЛП:
| 2/5 | -1/5 | 19/5 | |||||
| -1/5 | 3/5 | 3/5 | |||||
| -2/5 | -4/5 | -4/5 | |||||
| 8/5* | 26/5 | -226/5 | |||||
| -5/2 | |||||||
| -42 |
Оптимальное решение расширенной ЗЛП удовлетворяет ограничению целочисленности.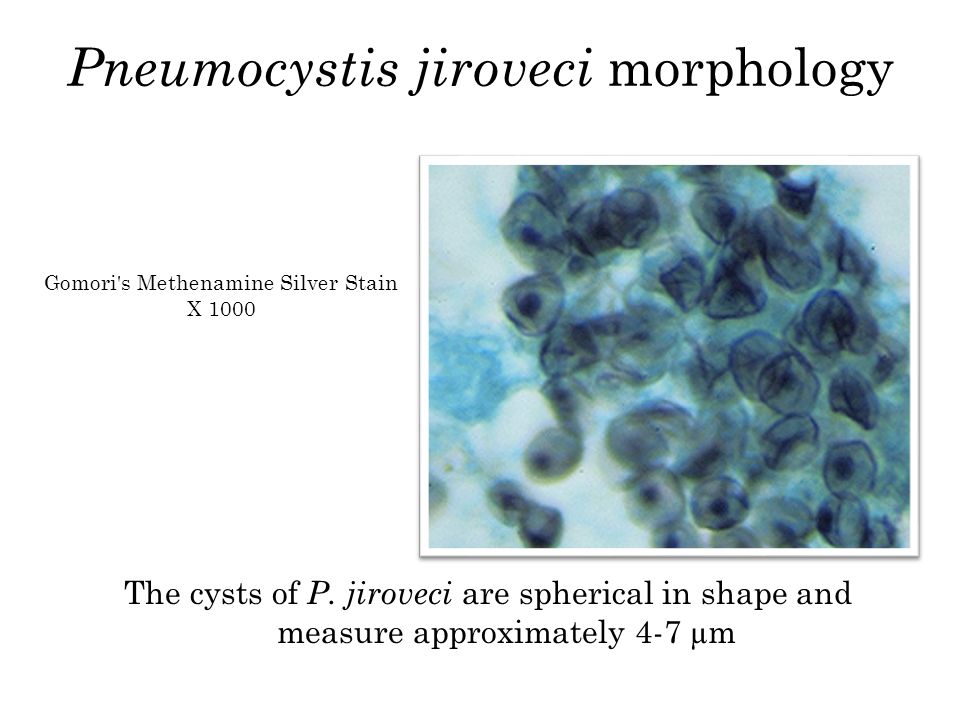
Для решения целочисленных задач линейного программирования с произвольным числом переменных можно использовать метод Гомори, с помощью которого от области программ отсекаются точки с нецелочисленными координатами. Сформулируем алгоритм Гомори для решения целочисленной задачи линейного программирования в стандартной форме
Алгоритм Гомори
ГП С помощью симплекс-метода находим оптимальную программу. Если получились целочисленные значения для всех Xj , то задача решена. В противном случае среди Xj имеются нецслочисленные значения.
|~2~1 Среди нецелых Xj выбираем произвольный элемент х г и в задаче добавляем еще одно ограничение
что равносильно добавлению в симплекс-таблице еще одной строки, после чего она перестает соответствовать допустимому базисному решению новой задачи линейного программирования, которую она описывает. В ограничении применяются дробные части элементов строки, в которой находится х г. Применяемое обозначение для дробной части исходит из того, что всякое действительное число у можно представить в виде суммы у = [у] + {?у}, где [у] — целая часть и {у} = У ~ [у] ~ дробная часть.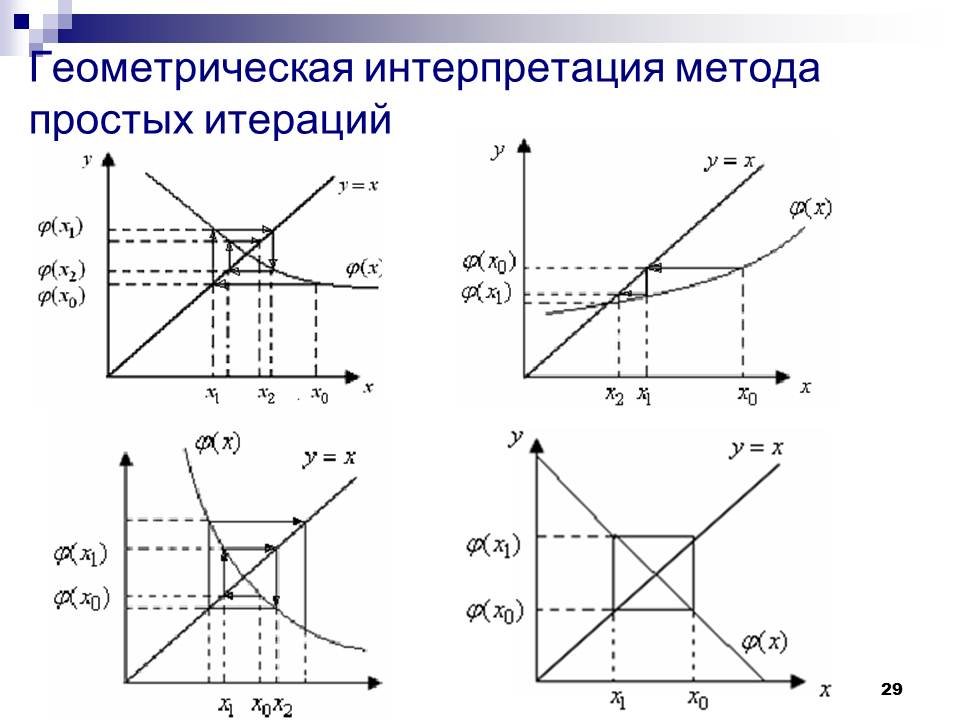
[з] Находим допустимое базисное решение, считая новую строку разрешающей, т.е. I = п + 1.
- а) Если все коэффициенты уц > 0, то задача не имеет решения (т.е. целочисленная задача решена).
- б) В противном случае находим индекс к такой, что
(критерий входа в новый базис). Заметим, что выбор разрешающего элемента у и* не изменяет знак у критериев Aj.
[4] Если в новой таблице имеется хотя бы один х 3 s и повторить указанные процедуры необходимое число раз.
[~5~| Если полученное оптимальное решение целочисленно, то поставленная задача решена. В противном случае надо вернуться к пункту .
Пример 4.6.1. Решить методом Гомори целочисленную задачу
Решение. После добавления вспомогательных переменных имеется следующая задача линейного программирования в стандартной форме:
с матрицами
Таблица 1 | ||||||
Х 4 | ||||||
к = 1 Т
С помощью метода вращения заполним следующие таблицы. 0). Следовательно, программа {xi = 11/3, х 2 = 5} даст максимум экономической функции z, равный 1370/3 = 45б|, т.с. z = z max = 456§. «
0). Следовательно, программа {xi = 11/3, х 2 = 5} даст максимум экономической функции z, равный 1370/3 = 45б|, т.с. z = z max = 456§. «
Так как эта оптимальная программа не является целочисленной, применим алгоритм Гомори для нахождения целочисленной оптимальной программы. В качестве строки, на базе которой образуем дополнительную строку из дробных частей се элементов, выбираем вторую строку (индекс 7’ = 1). Заполним таблицу 3″, добавив в таблицу 3 дополнительную строку (4.14) с дробными частями для дополнительной переменной Ж5 и дополнительный столбец. Получаем
к» = 4 Т
После добавления новой строки симплекс-таблица 3″ перестает соответствовать допустимому базисному решению задачи, которую она описывает. Находим допустимое базисное решение, считая новую строку разрешающей, т.е. /» = 5.
Находим разрешающий столбец, т.с. индекс к» такой, что
(критерий входа в новый базис). Разрешающий элемент — (-2/3*). Заметим, что такой выбор разрешающего элемента не изменяет знак у критериев Aj. = 450. Эта оптимальная программа является целочисленной. ?
= 450. Эта оптимальная программа является целочисленной. ?
Пример 4.6.2. Решить методом Гомори целочисленную задачу
Решение. Имеется задача линейного программирования с матрицами
Заполним симплекс-таблицу с начальной программой.
Таблица 1 | |||||||
к = 1 Т
С помощью метода вращения заполним следующие таблицы. Разрешающий элемент — 1*.
Таблица 2 | Х 2 | ||||||
Разрешающий элемент — 5*. 0). Следовательно, программа {xi = 12/5, 24 = 1/5, 25 = 28/5} дает минимум экономической функции г, равный -11/5 = -2.2, т.с. z =
0). Следовательно, программа {xi = 12/5, 24 = 1/5, 25 = 28/5} дает минимум экономической функции г, равный -11/5 = -2.2, т.с. z =
~min = -2.2.
Так как эта оптимальная программа не является целочисленной, применим алгоритм Гомори для нахождения целочисленной оптимальной программы. В качестве строки, на базе которой образуем дополнительную строку из дробных частей сс элементов, выбираем, например, третью етроку (индекс г = 5) с максимальной дробной частью. Заполним таблицу 3″, добавив в таблицу 3 дополнительную строку (4.14) с дробными частями третьей строки для дополнительной переменной xq (эта строка позволяет отсечь от области программ части, содержащие точки с нецслочислснными координатами) и дополнительный столбец. Получаем
Таблица 3″ | ||||||||
г — -И | ||||||||
к» = 3 Т
После добавления новой строки симплекс-таблица 3″ перестает соответствовать допустимому базисному решению задачи, которую она описывает. Находим допустимое базисное решение, считая новую строку разрешающей, т.е. I» = 6.
Находим допустимое базисное решение, считая новую строку разрешающей, т.е. I» = 6.
Находим разрешающий столбец, т.е. индекс к» такой, что
(критерий входа в новый базис). Разрешающий элемент — (-3/5*). Заметим, что такой выбор разрешающего элемента не изменяет знак у критериев Aj.
Заполним симплекс-таблицу 4.
Таблица 4 | ||||||||
Значения всех критериев ^ 0, (Х в ^ 0). Следовательно, программа {х = 2, Х 2 = 0, хз = 1, х 4 = 0, ж 5 = 5} даст минимум экономической функции z 9 равный (-2), т.с. z = -min = — 2. Эта оптимальная программа является целочисленной. ?
Следовательно, программа {х = 2, Х 2 = 0, хз = 1, х 4 = 0, ж 5 = 5} даст минимум экономической функции z 9 равный (-2), т.с. z = -min = — 2. Эта оптимальная программа является целочисленной. ?
Задача 4.6.1. Решить методом Гомори целочисленную задачу
Ответ. Программа
дает минимум экономической функции z, равный (-31), т.с. z = 2 m i n = -31. Эта оптимальная программа является целочисленной.
Все страницы — Юнионпедия
Все страницы — ЮнионпедияНовый! Скачать Юнионпедия на вашем Android™ устройстве!
Установить
Более быстрый доступ, чем браузер!
Все страницы · Предыдущая (Алгаир) · Следующий (Алдарово (платформа))
Из:
| Алгоритм Гомори | Алгоритм Гончарова | Алгоритм Гертцеля |
| Алгоритм Герцеля | Алгоритм Гейла-Шепли | Алгоритм Гельфонда |
| Алгоритм Гельфонда — Шенкса | Алгоритм Гельфонда-Шенкса | Алгоритм Дэвиса-Патнема |
| Алгоритм Дамаса — Милнера | Алгоритм Дамма | Алгоритм Данцига |
| Алгоритм Джарвиса | Алгоритм Джонсона | Алгоритм Диффи — Хеллмана |
| Алгоритм Диффи-Хеллмана | Алгоритм Диксона | Алгоритм Диница |
| Алгоритм Дойча — Джозы | Алгоритм Дойча — Йожи | Алгоритм Дейкстры |
| Алгоритм Деккера | Алгоритм Демукрона | Алгоритм Евклида |
| Алгоритм Любачевского — Стилинжера | Алгоритм Любачевского-Стилинжера | Алгоритм Лукаса — Канаде |
| Алгоритм Луна | Алгоритм Ли | Алгоритм Леска |
| Алгоритм Левита | Алгоритм Левенштейна | Алгоритм Левенберга — Маркардта |
| Алгоритм Левенберга — Марквардта | Алгоритм Лемпеля — Зива | Алгоритм Лемпеля — Зива — Велча |
| Алгоритм Лемпеля-Зива-Велча | Алгоритм Ленстры | Алгоритм Ленстры (разложение на множители) |
| Алгоритмы | Алгоритмы сортировки | Алгоритмы семейства FOREL |
| Алгоритмы уничтожения информации | Алгоритмы шифрования в автосигнализациях | Алгоритмы рисования линии |
| Алгоритмы быстрого возведения в степень | Алгоритмы быстрого возведения в степень по модулю | Алгоритмы кэширования |
| Алгоритмы масштабирования пиксельной графики | Алгоритмы маршрутизации | Алгоритмы обработки потоковых данных |
| Алгоритмы предотвращения взаимной блокировки | Алгоритмы построения выпуклой оболочки | Алгоритмы построения отрезка |
| Алгоритмы: построение и анализ | Алгоритма сложность | Алгоритмическая сложность |
| Алгоритмическая энтропия | Алгоритмическая торговля | Алгоритмическая топология |
| Алгоритмическая теория информации | Алгоритмическая разрешимость | Алгоритмическая закупка рекламы |
| Алгоритмическая неразрешимость | Алгоритмически неразрешимые задачи | Алгоритмически неразрешимая задача |
| Алгоритмический язык | Алгоритмический язык программирования АЛГЭМ | Алгоритмизация |
| Алгоритмика | Алгоритмов теория | Алгорифм |
| Алгорифм Маркова | Алгорифмы Маркова | Алгоазавр |
| Алгодреш | Алгодреш (Фигейра-де-Каштелу-Родригу) | Алгодреш (Форнуш-де-Алгодреш) |
| Алгодан | Алгодан-ди-Жандаира | Алгодао |
| Алгозу | Алгозинью | Алгол |
| Алгол (значения) | Алгол 60 | Алгол 68 |
| Алгол-60 | Алгол-68 | Алголь |
| Алголь (фильм) | Алголь (значения) | Алгольсайм |
| Алголагния | Алгология | Алгома (округ) |
| Алгонквинский язык | Алгонкин | Алгонкин-колледж |
| Алгонкинская группа | Алгонкинский язык | Алгонкинский региональный парк |
| Алгонкинский национальный парк | Алгонкинский провинциальный парк | Алгонкинские языки |
| Алгонкинско-баскский пиджин | Алгонкины | Алгонкины (группа народов) |
| Алгонкины (народ) | Алгетское водохранилище | Алгети |
| Алгети (река) | Алгети (значения) | Алгети (Марнеульский муниципалитет) |
| Алгер | Алгер фон Люттих | Алгер фон Лютих |
| Алгер Льежский | Алгернод Ланер Вашингтон | Алгеро |
| Алгебры Клиффорда | Алгебры основная теорема | Алгебры Валя |
| Алгебры Валентины | Алгебры Ли | Алгебра |
| Алгебра (универсальная алгебра) | Алгебра (теория множеств) | Алгебра (алгебраическая система) |
| Алгебра (значения) | Алгебра (певица) | Алгебра с делением |
| Алгебра с единицей | Алгебра событий | Алгебра фон Неймана |
| Алгебра регулярных выражений | Алгебра Кэли | Алгебра Клиффорда |
| Алгебра Клини | Алгебра Кодда | Алгебра Темперли — Либа |
| Алгебра Фелиция Блессетт | Алгебра Хопфа | Алгебра высказываний |
| Алгебра вершинных операторов | Алгебра и Анализ (журнал) | Алгебра и анализ |
| Алгебра линейная | Алгебра логики | Алгебра матриц |
| Алгебра множеств | Алгебра над кольцом | Алгебра над полем |
| Алгебра операторов | Алгебра Мальцева | Алгебра Буля |
| Алгебра Бореля | Алгебра Валя | Алгебра Валентины |
| Алгебра Грассмана | Алгебра Ли | Алгебра Йорданова |
| Алгебраист | Алгебраическая сумма | Алгебраическая структура |
| Алгебраическая связность | Алгебраическая система | Алгебраическая симплициальная категория |
| Алгебраическая сложность | Алгебраическая топология | Алгебраическая теория чисел |
| Алгебраическая теория графов | Алгебраическая функция | Алгебраическая форма |
| Алгебраическая группа | Алгебраическая геометрия | Алгебраическая геометрия над алгебраическими системами |
| Алгебраическая замкнутость | Алгебраическая кратность | Алгебраическая кривая |
| Алгебраическая квантовая теория | Алгебраическая комбинаторика | Алгебраическая нормальная форма |
| Алгебраическая независимость | Алгебраическая операция | Алгебраическая поверхность |
| Алгебраически замкнутое поле | Алгебраический элемент | Алгебраический тип данных |
| Алгебраический порядок точности численного метода | Алгебраические структуры | Алгебраические системы |
| Алгебраические уравнения | Алгебраические формы | Алгебраические числа |
| Алгебраические операции | Алгебраические операции (теория множеств) | Алгебраическое уравнение |
| Алгебраическое тождество Бьянки | Алгебраическое целое число | Алгебраическое число |
| Алгебраическое числовое поле | Алгебраическое расширение | Алгебраическое выражение |
| Алгебраическое диофантово уравнение | Алгебраическое дополнение | Алгебраическое замыкание |
| Алгебраическое замыкание поля | Алгебраическое касательное пространство | Алгебраическое многообразие |
| Алгебраическое множество | Алгебраическое поле | Алгедонод |
| Алгезир Ультра | Алгезиметр | Алгейран — Мен-Мартинш |
| Алгейран — Мен-Мартинш | Алгелдрат | Алгемба |
| Алдя-Теодорович | Алдя-Теодорович Дойна | Алдя-Теодорович, Ион |
| Алдя-Теодорович, Дойна | Алду | Алду да Силва Оливейра Жуниур, Жозе |
| Алду Жералду Мануэл Монтейру | Алду, Жозе | Алдуин |
| Алдуин I (граф Ангулема) | Алдуин II (граф Ангулема) | Алдулеску |
| Алдулеску Раду | Алдулеску, Раду | Алдуненков |
| Алдуненков Пётр Ефимович | Алдуненков Петр Ефимович | Алдуненков, Пётр Ефимович |
| Алдуненков, Петр Ефимович | Алды | Алдышев |
Алдышев А. | Алдышев А. А. | Алдышев Анатолий |
| Алдышев Анатолий Афанасьевич | Алдышев, Анатолий | Алдышев, Анатолий Афанасьевич |
| Алдыганка | Алдын-Булак | Алдрич |
| Алдрич (город, Миннесота) | Алдрич, Дуг | Алдриен (король Арморики) |
| Алдро Хиббард | Алдреу | Алдред |
| Алдред (епископ Линдисфарна) | Алда | Алда (приток Парабели) |
| Алда Алан | Алда, Алан | Алдашин |
| Алдашин Михаил Владимирович | Алдашин, Михаил | Алдашин, Михаил Владимирович |
| Алдашев Ахмет Алдашевич | Алдашев, Ахмет Алдашевич | Алдатов |
| Алдатов Ибрагим Эрикович | Алдатов, Ибрагим Эрикович | Алдатова |
| Алдатова Алина Таймуразовна | Алдатова, Алина Таймуразовна | Алдар |
| Алдар (сказочный персонаж) | Алдар Косе | Алдар Цыденжапов |
| Алдар батыр | Алдар и Зухра | Алдар косе |
| Алдар менэн Зухра | Алдар Исянгильдин | Алдар Исекеев |
| Алдар Баторович Цыденжапов | Алдар Валерьевич Дамдинов | Алдар-Косе |
| Алдар-батыр | Алдархаан | Алдары |
| Алдарбай Исекеев | Алдаржавын Аюуш | Алдарис |
| Алдарис (завод) | Алдарион | Алдаркинский сельсовет |
| Алдаркино | Алдарово | Алдарово (Кировская область) |
| Алдарово (Азяковский сельсовет) | Алдарово (Альшеевский район) | Алдарово (Никифаровский сельсовет) |
ГОМОРИ ТРИХРОМ
ГОМОРИ ТРИХРОМ КЛИНИЧЕСКАЯ ЛАБОРАТОРИЯПРИНЦИП:
Одношаговый трихром Гомори представляет собой окрашивание
процедура, сочетающая окрашивание плазмой (хромотроп 2R) и
окраска соединительных волокон (быстрый зеленый FCF) в фосфорно-вольфрамовой кислоте
раствор, в который добавлена ледяная уксусная кислота.
ТРЕБУЕТСЯ ОБРАЗЕЦ:
Замороженная полосатая мышца человека. (Использовать
метод замораживания изопентана, описанный ранее.)
МЕТОД:
Фиксация: Нет, используйте быстрозамороженную ткань.
Техника: Резка 10–16 микрон (12 м)
срезы в криостате из быстрозамороженной биопсии. Прикрепить один или несколько разделов
на № 1, 22 мм квадратное покровное стекло.
- Оборудование:
- Штатив для окрашивания керамики — Thomas Scientific #8542-E40
- Чашка для окрашивания Columbia — Thomas Scientific #8542-C12
- Чашка для окрашивания Columbia (банка) — Thomas Scientific #8542-E30
- Щипцы
- Латексные перчатки
- Чашка для окрашивания Columbia — Thomas Scientific #8542-C12
- Реагенты:
- Ледяная уксусная кислота — Fisher A507-500, КОРРОЗИОННОЕ ВЕЩЕСТВО хранить при комнатной температуре
- Хромотроп 2R — Sigma C3143, РАЗДРАЖАЮЩИЙ, хранить при комнатной температуре
- Деионизированная вода
- Fast Green FCF — сертифицирован, Sigma F7258, ТРЕБУЕТСЯ ПЕРЧАТКИ И МАСКА, хранить при комнатной температуре
- Гематоксилиновый краситель Харриса, подкисленный, — Лернер Laboratories * #1931382, хранить в комнате
- Permount — Fisher SP15-100, ОГНЕОПАСНЫЙ ОПАСНОСТЬ ДЛЯ ЗДОРОВЬЯ
- Фосфорно-вольфрамовая кислота, свободная кислота, — Sigma Р4006, КОРРОЗИОННОЕ ВЕЩЕСТВО, хранить при комнатной температуре
- Реактив спиртовой, ОКС — гистохимический Fisher A962-4 или ВЭЖХ A995 ЛЕГКОВОСПЛАМЕНЯЮЩИЙСЯ, ТОКСИЧНЫЙ, ТЕРАТОГЕННЫЙ , хранить при комнатной температуре в огнеопасном шкафу
- Ксилолы — Fisher # HC700-1GAL, ЛЕГКОВОСПЛАМЕНЯЮЩИЕСЯ , хранить при комнатной температуре в легковоспламеняющемся шкафу)
- Хромотроп 2R — Sigma C3143, РАЗДРАЖАЮЩИЙ, хранить при комнатной температуре
Решения:
- Трихромовая окраска по И.
 Гомори
Гомори - Хромотроп 2R 0,6 г
- Fast green FCF 0,3 г
- Кислота фосфорно-вольфрамовая 0,6 г
- Деионизированная вода 100 мл
- Уксусная кислота, ледяная 1,0 мл
- Fast green FCF 0,3 г
- Доведите рН вышеприведенной смеси до 3,4, используя 1 н. раствор NaOH.
- Хранить при комнатной температуре, готовить еженедельно
Процедура окрашивания:
- Поместите покровное стекло со срезом в керамический
штатив для окрашивания (Thomas Scientific #8542-E40).

- Погрузите срезы в гематоксилин Харриса на 5 минут.
- Промыть водопроводной водой, пока вода не Чисто.
- Погрузите срезы в трехцветный краситель Гомори
в течение 10 минут.
- Дифференцируйте, используя 0,2% уксусную кислоту.
Нескольких погружений должно быть достаточно.
- Погрузите стойку с секциями непосредственно в
95 % спирт
- Продолжение обезвоживания в восходящем спирте
растворы (95% x 2, 100% x 2) в чашках для окрашивания Колумбия
— Томас Сайентифик № 8542-E30.
- Прозрачный с ксилолом (3–4 х ), также в Колумбии
чашка (банка) для окрашивания — Thomas Scientific #8542-E30.
- Поместите покровное стекло на маркированное предметное стекло.
с Permount или другой подходящей органической монтажной средой.
- Ядра: красно-фиолетовые
- Нормальные мышечные миофибриллы: зелено-голубые с отчетливыми полосами A и I.

- Межмиофибриллярные мышечные мембраны: красный
- Интерстициальный коллаген: зеленый
ССЫЛКИ:
1. Томпсон, Сэмюэл В. ИЗБРАННЫЕ ГИСТОХИМИЧЕСКИЕ
И ГИСТОПАТОЛОГИЧЕСКИЕ МЕТОДЫ, Чарльз С. Томас, Спрингфилд,
Ил, 1966.
2. Шиэн Д.К., Храпчак Б.Б. ТЕОРИЯ И ПРАКТИКА ГИСТОТЕХНОЛОГИИ, Battelle Memorial Institute, Колумбус, Огайо, 1987.
Вернуться к нервно-мышечный Домашняя страница
Вернуться к нервно-мышечный Оценки
09.07.2008
Трихромное окрашивание по Гомори: его использование с миелиновыми оболочками | JAMA Neurology
Трихромное окрашивание по Гомори: его использование с миелиновыми оболочками | JAMA Неврология | Сеть ДЖАМА [Перейти к навигации]Эта проблема
- Скачать PDF
- Полный текст
Поделиться
Твиттер Фейсбук Эл.
 адрес
LinkedIn
адрес
LinkedIn- Процитировать это
- Разрешения
Артикул
Октябрь 1978 г.
Маргарет Л. Граннет, MD
Аффилиация автора
Отделение неврологии и патологии Медицинского колледжа Университета Юты, Солт-Лейк-Сити.
Арх Нейрол. 1978;35(10):692. doi:10.1001/archneur.1978.00500340068014
Полный текст
Абстрактный
• Мы сообщаем об использовании одношагового трехцветного окрашивания Гомори в качестве метода окрашивания миелиновых оболочек периферических нервов. Окрашивание простое в применении и позволяет легко обнаружить и оценить миелиновые оболочки.
Полный текст
Добавить или изменить учреждение
- Кислотно-щелочное, электролиты, жидкости
- Лечение зависимости
- Аллергия и клиническая иммунология
- Анестезиология
- Антикоагулянт
- Искусство и изображения в психиатрии
- Кровотечение и переливание крови
- Кардиология
- Уход за тяжелобольным пациентом
- Проблемы клинической электрокардиографии
- Клиническая задача
- Поддержка принятия клинических решений
- Клинические последствия базовой нейронауки
- Клиническая фармация и фармакология
- Дополнительная и альтернативная медицина
- Заявления о консенсусе
- Коронавирус (COVID-19)
- Медицина интенсивной терапии
- Культурная компетенция
- Стоматология
- Дерматология
- Диабет и эндокринология
- Интерпретация диагностического теста
- Разнообразие, равенство и инклюзивность
- Разработка лекарств
- Электронные медицинские карты
- Неотложная медицинская помощь
- Конец жизни
- Гигиена окружающей среды
- Этика
- Пластическая хирургия лица
- Гастроэнтерология и гепатология
- Генетика и геномика
- Геномика и точное здоровье
- Гериатрия
- Глобальное здравоохранение
- Справочник по статистике и медицине
- Рекомендации
- Заболевания волос
- Модели медицинского обслуживания
- Экономика здравоохранения, страхование, оплата
- Качество медицинской помощи
- Реформа здравоохранения
- Медицинская безопасность
- Медицинские работники
- Различия в состоянии здоровья
- Несправедливость в отношении здоровья
- Информатика здравоохранения
- Политика здравоохранения
- Гематология
- История медицины
- Гуманитарные науки
- Гипертония
- Изображения в неврологии
- Наука внедрения
- Инфекционные болезни
- Инновации в оказании медицинской помощи
- Инфографика JAMA
- Право и медицина
- Ведущее изменение
- Чем меньше, тем лучше
- ЛГБТК
- Образ жизни
- Медицинское кодирование
- Медицинские приборы и оборудование
- Медицинское образование
- Медицинское образование и обучение
- Медицинские журналы и публикации
- Меланома
- Мобильное здравоохранение и телемедицина
- Оспа обезьян
- Нарративная медицина
- Нефрология
- Неврология
- Неврология и психиатрия
- Примечательные примечания
- Сестринское дело
- Питание
- Питание, Ожирение, Упражнения
- Ожирение
- Акушерство и гинекология
- Гигиена труда
- Онкология
- Офтальмологические изображения
- Офтальмология
- Ортопедия
- Отоларингология
- Лекарство от боли
- Патология и лабораторная медицина
- Уход за пациентами
- Информация для пациентов
- Педиатрия
- Повышение производительности
- Показатели эффективности
- Периоперационный уход и консультация
- Фармакоэкономика
- Фармакоэпидемиология
- Фармакогенетика
- Фармация и клиническая фармакология
- Физическая медицина и реабилитация
- Физиотерапия
- Руководство врачей
- Поэзия
- Здоровье населения
- Профилактическая медицина
- Профессиональное благополучие
- Профессионализм
- Психиатрия и поведенческое здоровье
- Общественное здравоохранение
- Легочная медицина
- Радиология
- Регулирующие органы
- Исследования, методы, статистика
- Реанимация
- Ревматология
- Управление рисками
- Научные открытия и будущее медицины
- Совместное принятие решений и общение
- Медицина сна
- Спортивная медицина
- Трансплантация стволовых клеток
- Хирургия
- Хирургические инновации
- Хирургические жемчужины
- Обучаемый момент
- Технологии и финансы
- Искусство JAMA
- Искусство и медицина
- Рациональное клиническое обследование
- Табак и электронные сигареты
- Токсикология
- Травмы и травмы
- Приверженность лечению
- УЗИ
- Урология
- Руководство пользователя по медицинской литературе
- Вакцинация
- Венозная тромбоэмболия
- Здоровье ветеранов
- Насилие
- Женское здоровье
- Рабочий процесс и процесс
- Уход за ранами, инфекция, заживление
Сохранить настройки
Политика конфиденциальности | Условия использования
Введение в стандартное и специальное окрашивание в гистопатологии
Джеймс Андерсон , менеджер по глобальному маркетингу
Geoffrey Rolls , BAppSc, FAIMS
Обычное окрашивание H&E и специальные окрашивания играют решающую роль в диагностике или исследовании тканей. Окрашивая в противном случае прозрачные участки ткани, эти красители позволяют высококвалифицированным патологам и исследователям просматривать под микроскопом морфологию (структуру) ткани или искать присутствие или преобладание определенных типов клеток, структур или даже микроорганизмов, таких как бактерии.
Окрашивая в противном случае прозрачные участки ткани, эти красители позволяют высококвалифицированным патологам и исследователям просматривать под микроскопом морфологию (структуру) ткани или искать присутствие или преобладание определенных типов клеток, структур или даже микроорганизмов, таких как бактерии.
В гистопатологической лаборатории термин «рутинное окрашивание» относится к окрашиванию гематоксилином и эозином (H&E), которое «обычно» используется со всеми образцами тканей для выявления структур и состояний подлежащих тканей. Термин «специальные красители» уже давно используется для обозначения большого количества альтернативных методов окрашивания, которые используются, когда H&E не дает всей информации, необходимой патологоанатому или исследователю.
Получайте обновления Knowledge Path прямо на свой почтовый ящик.
Подпишитесь сегодня!
Если вы просмотрели этот образовательный веб-семинар, тренинг или учебное пособие по пути к знаниям и хотели бы подать заявку на получение зачетных единиц непрерывного образования в вашей сертифицирующей организации, загрузите форму, которая поможет вам добавить оценочные зачетные единицы в вашу стенограмму.
Подготовка ткани к окрашиванию
Перед окрашиванием и просмотром ткани ее необходимо подготовить таким образом, чтобы можно было сделать очень тонкий срез толщиной всего в одну клетку и поместить его на предметное стекло микроскопа. Это включает в себя фиксацию ткани (чтобы она не разлагалась), а затем ее затвердевание и поддержку, чтобы ее можно было разрезать на очень тонкие срезы (обычно 2–7 мкм). Для этого используются два основных метода: замороженные срезы и срезы, залитые парафином.
Замороженные срезы используются, когда ответы нужны быстро, как правило, во время операции, когда хирургу необходимо знать край иссечения при удалении опухоли. Они быстро изготавливаются, но, как правило, не обеспечивают такого же качества срезов, как парафиновая техника. Процесс подготовки замороженных срезов выглядит следующим образом:
- Ткань быстро замораживают, чтобы сохранить и укрепить ее.
- Замороженную ткань делают в криостате (микротом для секционирования в морозильной камере) и помещают на предметное стекло для окрашивания.

- Срез фиксируют непосредственно перед тем, как он начнет распадаться, а затем окрашивают.
При подготовке парафиновых срезов образец сначала консервируют фиксатором, а затем поддерживают структуру ткани путем пропитки образца парафиновым воском. Этот процесс требует больше времени, чем создание замороженных срезов, но в большинстве случаев обеспечивает более качественное окрашивание, а полученные образцы (называемые блоками) можно хранить практически неограниченное время. Процесс парафинового сечения выглядит следующим образом:
- Фиксация сохраняет ткань (обычно с использованием раствора на основе формальдегида).
- Grossing изолирует конкретную область ткани, подлежащую срезу.
- При обработке тканей используется последовательность реагентов для замены водной среды (на водной основе) гидрофобной средой, позволяющей пропитывать элементы ткани парафиновым воском.
- Заливка позволяет ориентировать образец и закрепляет образец в восковом блоке для вырезания срезов и хранения.

- Срезы делаются на микротоме , который делает очень тонкие срезы, которые выплывают на водяную баню, а затем собирают и помещают на предметные стекла микроскопа.
- Затем предметные стекла высушивают в печи или на горячей плите для удаления влаги и лучшего прилипания ткани к предметному стеклу.
- Теперь ткань на предметном стекле готова для окрашивания.
- Первым этапом окрашивания является депарафинизация, при которой используется растворитель для удаления парафина с предметного стекла перед окрашиванием. Это всегда делается как часть процесса окрашивания. Когда окрашивание завершено, срез накрывают покровным стеклом, что делает препарат постоянным.
Изображение
Рисунок 1: Микротомист создает «ленту» из очень тонких срезов для окрашивания.
Почему окрашивание гематоксилином и эозином (H&E) является обычным делом
Окрашивание гематоксилином и эозином (H&E) обычно используется в гистопатологических лабораториях, поскольку оно дает патологу/исследователю очень подробное представление о ткани. Это достигается за счет четкого окрашивания клеточных структур, включая цитоплазму, ядро, органеллы и внеклеточные компоненты. Этой информации часто бывает достаточно, чтобы диагностировать заболевание на основе организации (или дезорганизации) клеток, а также показать любые аномалии или конкретные индикаторы в реальных клетках (например, ядерные изменения, обычно наблюдаемые при раке). Даже при использовании передовых методов окрашивания окрашивание H&E по-прежнему составляет важную часть диагностической картины, поскольку оно отображает морфологию подлежащей ткани, что позволяет патологоанатому/исследователю правильно интерпретировать расширенное окрашивание.
Это достигается за счет четкого окрашивания клеточных структур, включая цитоплазму, ядро, органеллы и внеклеточные компоненты. Этой информации часто бывает достаточно, чтобы диагностировать заболевание на основе организации (или дезорганизации) клеток, а также показать любые аномалии или конкретные индикаторы в реальных клетках (например, ядерные изменения, обычно наблюдаемые при раке). Даже при использовании передовых методов окрашивания окрашивание H&E по-прежнему составляет важную часть диагностической картины, поскольку оно отображает морфологию подлежащей ткани, что позволяет патологоанатому/исследователю правильно интерпретировать расширенное окрашивание.
В лаборатории клинической гистологии все образцы сначала окрашивают гематоксилин-эозином, а специальное или расширенное окрашивание заказывают только в том случае, если необходима дополнительная информация для проведения более подробного анализа, например, для дифференциации двух морфологически сходных типов рака.
Из-за необходимого объема окрашивания гематоксилин-эозином большинство клинических лабораторий используют полностью автоматизированные системы, а ручное окрашивание в настоящее время используется редко.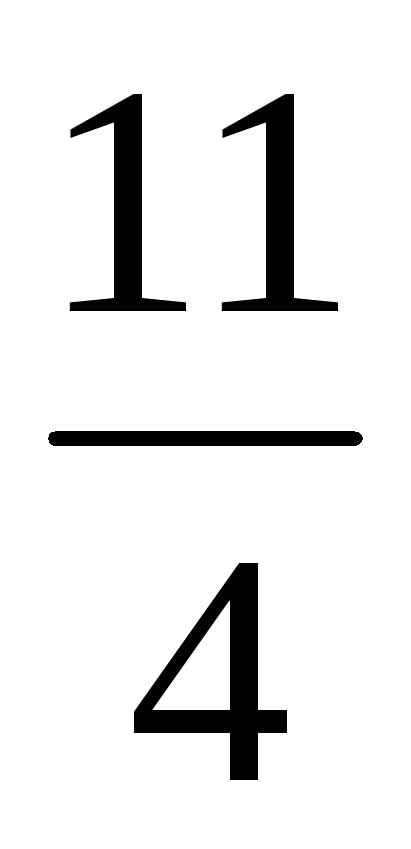
Изображение
Рисунок 2. На этом срезе слизистой оболочки тонкой кишки хорошо видны гетерохроматин и ядрышки в эпителиальных клетках и плазматических клетках в собственной пластинке.
Изображение
Рис. 3. Митотические фигуры резко окрашиваются внутри железистого эпителия на срезе тонкой кишки.
Изображение
Рис. 4. В этом поле со стороны собственной пластинки тонкой кишки цитоплазма плазматических клеток окрашена гематоксилином, за исключением бледной околоядерной области, которая соответствует хорошо развитому аппарату Гольджи
Изображение
Рис. 5. Этот вегетативный ганглий из мышечно-кишечного сплетения, расположенный между гладкомышечными слоями наружной мышечной оболочки тонкой кишки, содержит ганглиозные нейроны, в цитоплазме которых обнаруживается четко выраженное базофильное вещество Ниссля (агрегации эндоплазматического ретикулума и рибосомной РНК).
H&E Chemistry
В окраске H&E используются два красителя: гематоксилин и эозин. Эта комбинация используется, так как красители окрашивают различные элементы ткани.
Гематоксилин реагирует как основной краситель с пурпурно-синим цветом. Он окрашивает кислые или базофильные структуры, включая клеточное ядро (которое содержит ДНК и нуклеопротеин) и органеллы, содержащие РНК, такие как рибосомы и шероховатый эндоплазматический ретикулум.
Эозин — это кислый краситель, обычно красноватый или розовый. Он окрашивает основные или ацидофильные структуры, включая цитоплазму, клеточные стенки и внеклеточные волокна.
Происхождение красителей
Гематоксилин извлекают из бревна и очищают. Затем его окисляют и смешивают с протравой (обычно алюминием), чтобы он мог прикрепиться к клеточным структурам. Из многих препаратов гематоксилина, используемых в гистологии, наиболее популярны гематоксилин Гилла, гематоксилин Харриса и гематоксилин Майера.
Эозин образуется в результате реакции между бромом и флуоресцеином. В гистологии обычно используются два варианта эозина: эозин Y, слегка желтоватый, и эозин В, слегка голубоватый. Эозин Y наиболее популярен.
Изображение
Рисунок 6: Химическая структура гематоксилина.
Изображение
Рисунок 7: Химическая структура эозина Y.
Специальные красители
Термин «специальные красители» традиционно относится к любому окрашиванию, кроме H&E. Он охватывает широкий спектр методов, которые можно использовать для визуализации определенных тканевых структур, элементов или даже микроорганизмов, не идентифицируемых с помощью окрашивания гематоксилин-эозином.
В других методах окрашивания используется иммуногистохимия или гибридизация in situ для нацеливания на определенные белки или последовательности ДНК/РНК. Эти методы иногда также включались в семейство «особых пятен».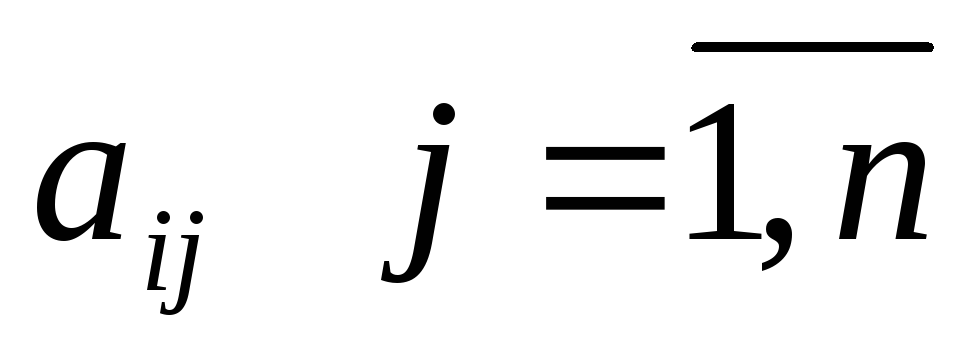 Однако они сильно различаются по методу и назначению и в настоящее время обычно выделяются в третью категорию, известную как «продвинутые пятна».
Однако они сильно различаются по методу и назначению и в настоящее время обычно выделяются в третью категорию, известную как «продвинутые пятна».
Хотя существуют буквально сотни специальных красителей для самых разных целей, лишь немногие из них регулярно используются в клинической гистологии. Разнообразие красителей также означает, что специальное окрашивание не так автоматизировано, как окрашивание H&E. Хотя многие крупные лаборатории используют автоматические инструменты для более распространенных пятен, у них все еще есть место для окрашивания вручную. Сложность некоторых пятен также работает против использования автоматизации.
Некоторые распространенные специальные красители
На изображениях ниже показаны некоторые распространенные специальные красители и способы их применения.
Изображение
Рисунок 8: Трихром Массона (кожа). Это окрашивание предназначено для использования при гистологическом исследовании коллагеновых волокон соединительной ткани в образцах тканей.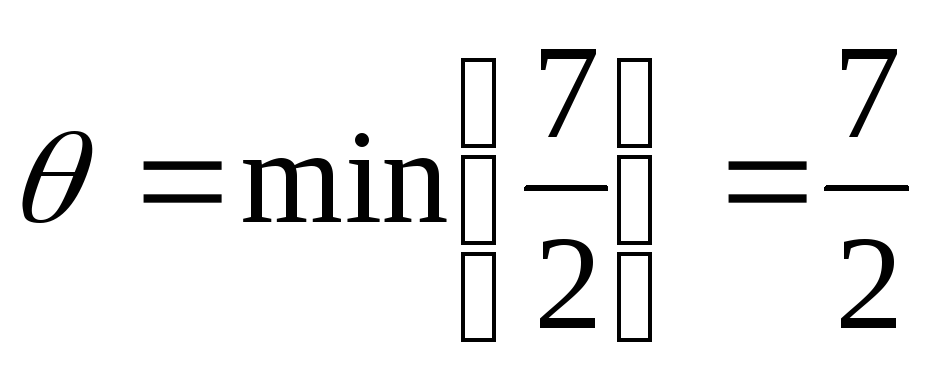 Он используется для помощи в дифференциации коллагена и гладких мышц в опухолях и помогает в обнаружении заболеваний или изменений в соединительной/мышечной ткани.
Он используется для помощи в дифференциации коллагена и гладких мышц в опухолях и помогает в обнаружении заболеваний или изменений в соединительной/мышечной ткани.
Изображение
Рисунок 9: Модифицированное серебристое окрашивание GMS (слева: пневмоцистоз, легкое) (справа: аспергиллезная инфекция, легкое). Окрашивание Modified GMS Silver предназначено для гистологического исследования грибков, базальной мембраны и некоторых условно-патогенных организмов, таких как pneumocystis carinii, в образцах тканей.
Изображение
Рисунок 10: Периодическая кислота Шиффа (почка). Окрашивание PAS в основном используется для окрашивания структур, содержащих большое количество углеводов, таких как гликоген, гликопротеины, протеогликаны, обычно присутствующие в соединительных тканях, слизи и базальных мембранах. Часто используется для окрашивания биопсий почек, биопсий печени, некоторых болезней накопления гликогена в поперечно-полосатых мышцах и подозрении на грибковые инфекции.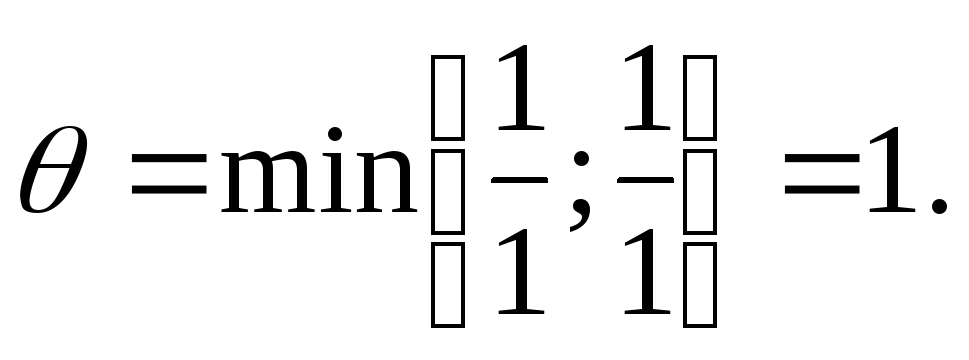
Изображение
Рисунок 11: Железо берлинской лазури Перлза (печень). Это окрашивание используется для обнаружения и идентификации трехвалентного железа (Fe3+) в препаратах тканей, мазках крови или мазках костного мозга. Небольшие количества трехвалентного железа (гемосидерин) обычно обнаруживаются в костном мозге и селезенке. Аномальное количество железа может указывать на гемохроматоз и гемосидероз.
Изображение
Рисунок 12: Ziehl Neelsen (кислотоустойчивые бациллы, легкие). Это окрашивание используется для обнаружения и идентификации кислотоустойчивых бацилл в тканях. Бациллы представляют собой палочковидные бактериальные организмы. Основная функция этого окрашивания — выявление туберкулеза в легочной ткани.
Изображение
Рисунок 13: Alcian Blue (кишечник). Alcian Blue обычно готовят при рН 2,5 и используют для идентификации кислых мукополисахаридов и кислых муцинов. Избыточное количество несульфатированных кислых слизистых веществ наблюдается при мезотелиомах, определенное количество в норме встречается в стенках кровеносных сосудов, но увеличивается при ранних поражениях атеросклероза.
Избыточное количество несульфатированных кислых слизистых веществ наблюдается при мезотелиомах, определенное количество в норме встречается в стенках кровеносных сосудов, но увеличивается при ранних поражениях атеросклероза.
Изображение
Рисунок 14: Alcian Blue и PAS (кишечник). Краситель, который сочетает в себе свойства окрашивания альциановым синим и периодической кислотой Шиффа.
Изображение
Рисунок 15: Трихром Гомори (синий) (подслизистая основа). Окрашивание трихромом используется для окрашивания и идентификации мышечных волокон, коллагена и ядер. Их можно использовать для контрастирования скелетных, сердечных или гладких мышц. Трихром по Гомори представляет собой упрощенную версию более сложного трихромного окрашивания по Массону и сочетает в себе окрашивание плазмы (хромотроп 2R) и окрашивание соединительной ткани для получения яркого контрастного изображения.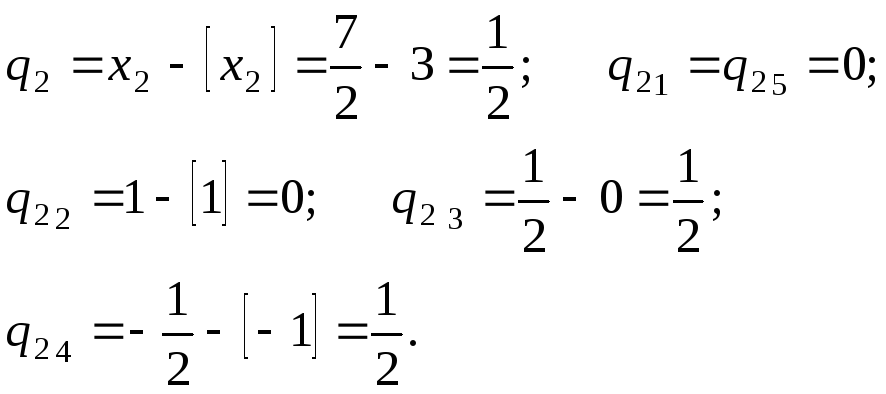
Изображение
Рисунок 16: Трихром Гомори (зеленый) (подслизистая оболочка). Окрашивание трихромом используется для окрашивания и идентификации мышечных волокон, коллагена и ядер. Их можно использовать для контрастирования скелетных, сердечных или гладких мышц. Трихром по Гомори представляет собой упрощенную версию более сложного окрашивания по Массону и сочетает в себе окрашивание плазмы (хромотроп 2R) с окрашиванием соединительной ткани для получения яркого контрастного изображения.
Шаги к лучшим специальным красителям
В Leica Biosystems мы стремимся улучшить диагностику рака и улучшить качество жизни. Один из способов достичь этого видения — помочь улучшить качество окрашивания. Поскольку мы понимаем, что качество IHC и ISH не начинается с красителя, в этой серии статей рассматривается множество различных аспектов качества окрашивания и рассматривается, как будущие тесты повлияют на улучшение диагностики.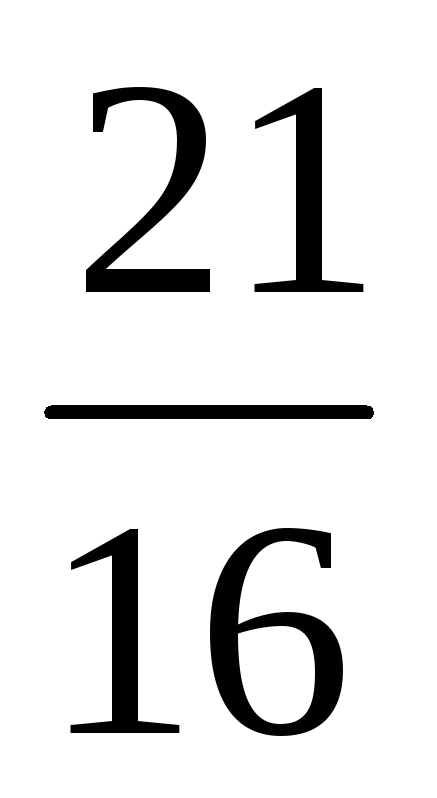
Понять пятно
Знайте, что вы пытаетесь продемонстрировать с помощью окрашивания.
Простое «следование методу» и незнание того, что должно быть видно в готовом разделе, приведет к плохим результатам.
Изображение
Срез печени, окрашенный PAS. Липофусцин и гликоген являются PAS-положительными, в то время как следы желчи и гемосидерина являются PAS-отрицательными и имеют свой естественный цвет (желтый и коричневый соответственно). B В этом разделе показана оппортунистическая грибковая инфекция легких (Aspergillus), окрашенная по методу Грокотта-Гомори. Грибковые гифы черные, как и неокрашенный углерод, что характерно для легких курильщиков и большинства горожан.
Используйте положительный контроль
Всегда используйте контрольное стекло, о котором известно, что оно содержит структуру/вещество, которое вы пытаетесь продемонстрировать.
«Если структура/вещество, которые мы окрашиваем, не видны на предметном стекле, мы предполагаем, что их нет».
Изображение
Срез печени с циррозом, окрашенный методом Перла для демонстрации железосодержащего гемосидера (синий). Это сделало бы удовлетворительный контрольный блок для пятен железа.
Используйте точный расчет времени
Используйте точное время.
Время всегда приблизительное. Неточный расчет времени приводит к противоречивым результатам.
Изображение
Оба этих среза кожи из одного блока были окрашены методом PAS. Секцию А обрабатывали йодной кислотой (этап окисления) в течение 5 минут, а секцию В — всего 30 секунд (ошибка). Обратите внимание, что вследствие этого базальная мембрана очень плохо окрашивается в секции B.
Учитывать стабильность реагентов
Помните о сроке годности используемых реагентов. Некоторые реагенты или растворы красителей портятся медленно, в то время как другие очень нестабильны и должны быть приготовлены свежими и использованы немедленно. Другие должны быть оставлены на некоторое время для окисления (созревания), прежде чем их вообще можно будет использовать.
Другие должны быть оставлены на некоторое время для окисления (созревания), прежде чем их вообще можно будет использовать.
Мы предполагаем, что все реагенты можно использовать в течение неопределенного периода времени.
Изображение
Гематоксилин Мадди Вейгерта из-за переокисления. Обратите внимание на коричневое окрашивание коллагена.
Правильно храните реагенты
Правильно храните реагенты. Некоторым требуется охлаждение, потому что они склонны поддерживать рост грибков или плесени. Другие чувствительны к свету и требуют хранения в темноте.
«Все наши реагенты хранятся на полке над столом для окрашивания. Иногда мы видим бродячие организмы в наших секциях».
Изображение
На этом срезе видны большие отложения посторонних микроорганизмов, которые выросли в растворе для окрашивания (в данном случае гематоксилин), а затем отложились поверх среза.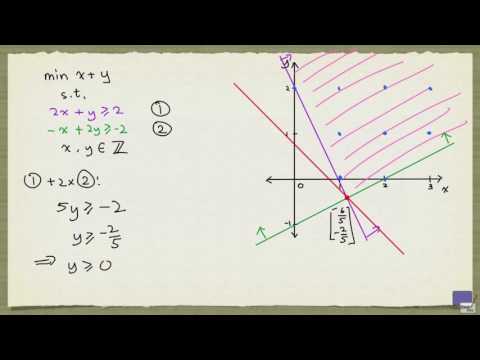
Придерживайтесь метода
Точно следуйте протоколу.
Сотрудники достигают разных результатов, предположительно используя один и тот же протокол.
Изображение
Эти срезы фиксированной формалином подслизистой оболочки окрашивали трихромным красителем по Массону. Раздел A показывает красную гладкую мышцу. В этом случае окрашивание было выполнено правильно, следуя лабораторному протоколу и включая предварительную стадию хромовой кислоты (сенсибилизация или вторичное протравление). Этот шаг был пропущен при окрашивании секции B. Обратите внимание на отсутствие дифференцированной окраски мышц в секции B (кишечник).
Записывайте любые изменения
Документируйте любые отклонения от используемого вами метода.
Иногда, когда результаты неудовлетворительны, трудно или невозможно определить причину, поскольку изменения протокола не зарегистрированы.
Изображение
В этой окраске с пропиткой серебром для ретикулина волокна плохо видны и на предметном стекле имеется фоновая пена (осадок).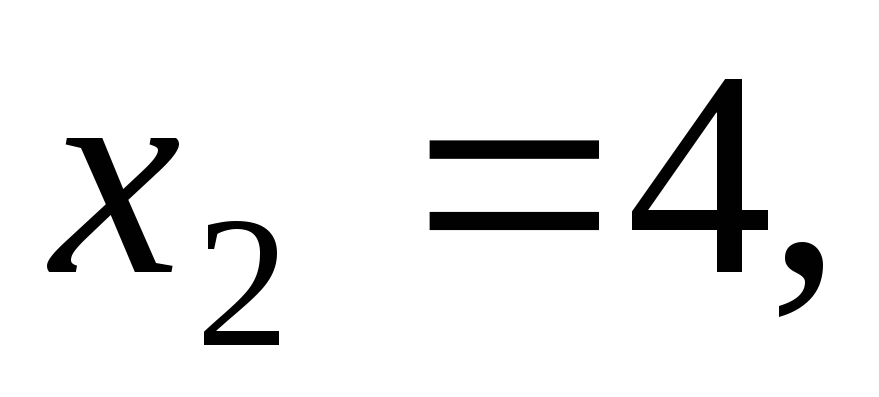 Очень сложно определить причину такой проблемы, если метод не был точно соблюдён (метод Гордона и Свитса, почки).
Очень сложно определить причину такой проблемы, если метод не был точно соблюдён (метод Гордона и Свитса, почки).
Стандартизация этапов стирки
Будьте особенно осторожны при выполнении этапов стирки. Стандартизируйте их, насколько это возможно, поскольку они часто являются причиной переменных результатов.
Сотрудники лаборатории используют разные методы мытья – одни используют интенсивное перемешивание, другие гораздо более щадящие.
Изображение
Эти срезы печени окрашивали тем же методом. Единственная разница между ними заключалась в технике промывки между пропиткой и восстановлением. Волокна ретикулина имеют черный цвет и лучше определяются в секции А (метод Гордона и Свитса).
Аккуратно настройте микроскоп
Используйте микроскопический контроль на важнейших этапах, таких как этапы дифференциации. Помните о влиянии настройки микроскопа на появление непокрытых (влажных) срезов; это может привести к появлению ложного фонового окрашивания.
Для всех методов уровень окрашивания оценивают, глядя на предметное стекло невооруженным глазом.
Изображение
A: Влажный срез (без покровного стекла) под микроскопом с закрытой диафрагмой конденсора. Обратите внимание на ложный фон. B: Влажный срез (без покровного стекла) под микроскопом с открытой диафрагмой конденсора. Обратите внимание на чистый фон.
Содержимое Leica Biosystems Knowledge Path регулируется условиями использования веб-сайта Leica Biosystems, доступными по адресу: Официальное уведомление. Контент, включая веб-семинары, обучающие презентации и сопутствующие материалы, предназначен для предоставления общей информации по конкретным темам, представляющим интерес для медицинских работников, и не предназначен и не должен толковаться как медицинская, нормативная или юридическая консультация. Взгляды и мнения, выраженные в любом стороннем контенте, отражают личные взгляды и мнения докладчика(ов)/автора(ов) и не обязательно представляют или отражают взгляды или мнения Leica Biosystems, ее сотрудников или агентов.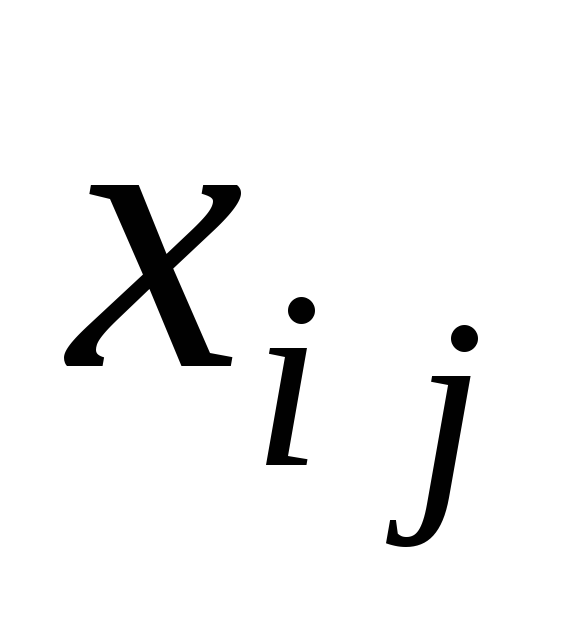 Любые ссылки, содержащиеся в контенте, которые обеспечивают доступ к сторонним ресурсам или контенту, предоставляются только для удобства.
Любые ссылки, содержащиеся в контенте, которые обеспечивают доступ к сторонним ресурсам или контенту, предоставляются только для удобства.
При использовании любого продукта следует обращаться к соответствующей документации по продукту, включая информационные руководства, вкладыши и руководства по эксплуатации.
Copyright © 2022 Leica Biosystems, подразделение Leica Microsystems, Inc. и ее дочерние компании Leica Biosystems. Все права защищены. LEICA и логотип Leica являются зарегистрированными товарными знаками Leica Microsystems IR GmbH.
Джеймс Андерсон , менеджер по глобальному маркетингу
Джеймс Андерсон является менеджером по глобальному маркетингу в Leica Biosystems с опытом работы в области гистологии и научных, технических и маркетинговых коммуникаций.
Джеффри Роллс , BAppSc, FAIMS
Джеффри Роллс — консультант по гистологии с многолетним опытом работы в этой области. Он бывший старший преподаватель гистопатологии на кафедре лабораторной медицины Университета RMIT в Мельбурне, Австралия.
Он бывший старший преподаватель гистопатологии на кафедре лабораторной медицины Университета RMIT в Мельбурне, Австралия.
CDC — DPDx — Диагностические процедуры
Модифицированная процедура кислотостойкого окрашивания
Этот метод полезен для идентификации ооцист видов кокцидий ( Cryptosporidium , Cystoisospora и Cyclospora ), которые может быть трудно обнаружить с помощью обычных красителей, таких как трихром. В отличие от модифицированного кислотостойкого красителя Циля-Нильсена, этот краситель не требует нагревания реагентов для окрашивания.
Образец:
Можно использовать концентрированный осадок свежего или законсервированного формалином стула. Другие типы клинических образцов, такие как дуоденальная жидкость, желчь, легочные образцы (индуцированная мокрота, бронхиальный смыв, биопсия) также могут быть окрашены.
Реагенты:
Эта процедура состоит из четырех этапов, требующих следующих растворов:
- Абсолютный метанол
- Кислотный спирт: 10 мл серной кислоты + 90 мл абсолютного этанола.
 Хранить при комнатной температуре.
Хранить при комнатной температуре. - Kinyoun’s Carbol fuchsin: можно приобрести в свободной продаже.
- 3% малахитовый зеленый: растворить 3 г малахитового зеленого в 100 мл дистиллированной воды. Хранить при комнатной температуре.
Процедура:
- Приготовьте мазок с 1–2 каплями образца на предметном стекле и высушите на предметном стекле при температуре 60°C до полного высыхания. Не делайте мазки слишком толстыми!
- Фиксация абсолютным метанолом на 30 секунд.
- Окрашивание карболовым фуксином Киньюна в течение одной минуты. Кратковременно промойте дистиллированной водой и слейте.
- Обезжирить кислым спиртом в течение 2 минут. Промыть дистиллированной водой и слить.
- Контрастное окрашивание малахитовым зеленым в течение 2 минут. Кратковременно промойте дистиллированной водой и слейте.
- Высушите на нагревателе для предметных стекол при 60°C в течение примерно 5 минут. Гора с покровным стеклом с помощью желаемого монтажного носителя.

- Исследуйте от 200 до 300 полей зрения, используя объективы 40x или выше. Для подтверждения внутренней морфологии используйте иммерсионный объектив с увеличением 100×.
Контроль качества:
Контрольное стекло Cryptosporidium spp. из образца, законсервированного 10% формалином, следует включать в каждый цикл окрашивания. Cryptosporidium spp. окрашивается в розово-красный цвет. Фон должен равномерно окрашиваться в зеленый цвет.
Процедура хромотропного окрашивания
Этот метод окрашивания был разработан в CDC с использованием различных компонентов метода окрашивания трихромом для дифференциации спор микроспоридий от фоновых фекальных элементов.
Образец:
Приготовьте тонкий мазок, используя примерно 10 мкл фиксированной 10% формалиновой взвеси кала (неконцентрированной) на предметном стекле. Можно также использовать концентраты формалина, но количество микроорганизмов будет практически таким же, как и до концентрирования. Зафиксировать на предметном стекле при температуре 60°C до полного высыхания (5-10 минут).
Зафиксировать на предметном стекле при температуре 60°C до полного высыхания (5-10 минут).
Реагенты:
Эта процедура состоит из шести этапов, требующих следующих растворов:
- Абсолютный метанол
- Хромотропное пятно:
Хромотроп 2R 6,00 г Светлый зеленый 0,15 г Кислота фосфорно-вольфрамовая 0,70 г Уксусная кислота ледяная 3,00 мл Смешайте ингредиенты и дайте постоять 30 минут. Затем добавить 100 мл дистиллированной воды. Готовьте свежий для использования каждый месяц.
- Кислый спирт:
90% этанол 995,5 мл Уксусная кислота ледяная 4,5 мл - 95% этанол
- 100% этанол
- Ксилол или заменитель ксилола
Процедура:
- Фиксация мазка в абсолютном метаноле в течение 5 минут.

- Поместите в хромотропную краску на 90 минут.
- Обезжирить в кислом спирте всего от 1 до 3 секунд.
- Промыть 95% этанолом путем погружения.
- Поместите в две смены 100% этанола на 3 минуты каждую.
- Поместите две смены ксилола или заменителя ксилола на 10 минут каждую.
- Слейте предметное стекло и поместите его вместе с покровным стеклом, используя монтажную среду (например, пермаунт). Исследуйте мазок после высыхания, используя не менее 100-кратного погружения объектива в масло или выше. Обследовать не менее 200–300 нефтеиммерсионных полей.
Контроль качества:
Контрольное стекло микроспоридий из образца, консервированного 10% формалином, должно быть включено в каждый цикл окрашивания. Споровые стенки микроспоридий окрашиваются в розовато-красный цвет и имеют размер около 1 мкм. Меняйте все растворы после окрашивания хромотропом через каждые 10 предметных стекол, чтобы добиться надлежащего ополаскивания и обезвоживания.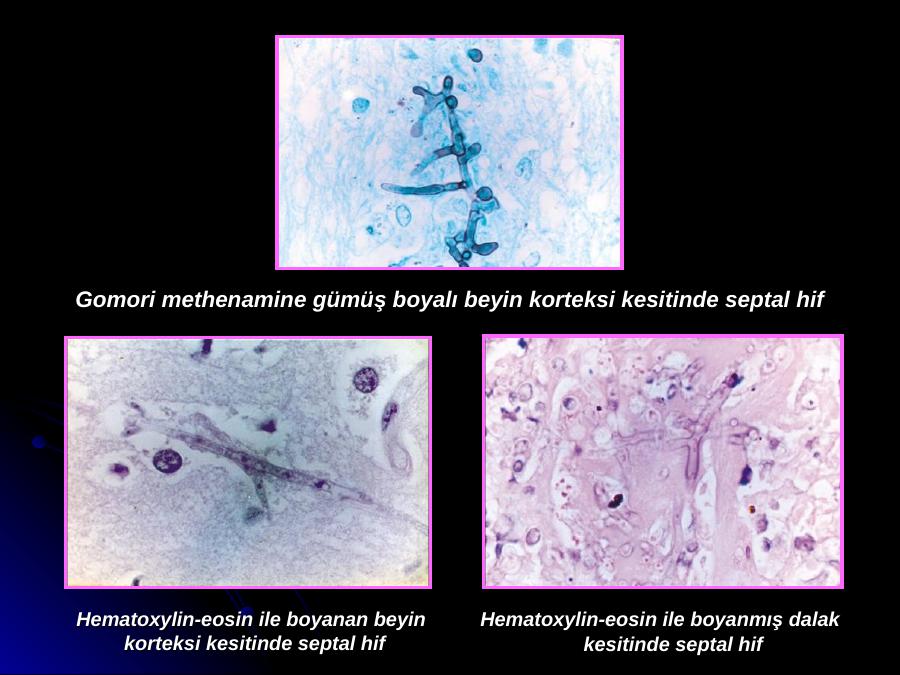 Для точности рекомендуется микроскоп с хорошей оптикой. Используйте по крайней мере 100-кратное увеличение иммерсионного масла для обнаружения организмов; более высокие увеличения лучше. Из-за сложности идентификации этих мелких спор рекомендуется, чтобы второй считыватель подтвердил положительный диагноз.
Для точности рекомендуется микроскоп с хорошей оптикой. Используйте по крайней мере 100-кратное увеличение иммерсионного масла для обнаружения организмов; более высокие увеличения лучше. Из-за сложности идентификации этих мелких спор рекомендуется, чтобы второй считыватель подтвердил положительный диагноз.
Процедура окрашивания Quick-Hot по Граму
Это альтернатива хромотропной окраске, которая представляет собой быстрый, надежный и простой метод окрашивания мазков для выявления спор микроспоридий в фекалиях и других клинических образцах.
Образец:
Приготовьте тонкий мазок окрашиваемого материала (например, фекалий, мочи, мокроты, слюны и надосадочной жидкости клеточных культур) и высушите на воздухе.
Фиксированные формалином и залитые в парафин срезы тканей депарафинизируйте, как обычно, гидратируйте в ряде спиртов и поместите предметные стекла в воду перед окрашиванием по Граму.
Реагенты:
- Набор для окрашивания по Граму
- Хромотропное пятно:
Хромотроп 2R 1,0 г Светлый зеленый 0,15 г Кислота фосфорно-вольфрамовая 0,25 г Уксусная кислота ледяная 3,0 мл Смешайте сухие ингредиенты, затем добавьте уксусную кислоту.
 Дайте постоять 30 минут, а затем добавьте 100 мл дистиллированной воды. Готовьте свежий для использования каждый месяц.
Дайте постоять 30 минут, а затем добавьте 100 мл дистиллированной воды. Готовьте свежий для использования каждый месяц. - Кислый спирт:
90% этанол 995,5 мл Уксусная кислота ледяная 4,5 мл - 95% этанол
- 100% этанол
Примечание: В дополнение к перечисленным реагентам требуется метод нагревания реагентов и поддержания определенной температуры. Поскольку нагревать нужно только хромотропную краску, достаточно будет горячей плиты.
Процедура:
- Мазок с термофиксацией (3 раза по 1 секунде каждый раз на медленном огне или 5 минут на подогревателе предметных стекол, установленном на 60°C). Остудить до комнатной температуры.
- Окрасьте по Граму, минуя стадию сафранина, следующим образом:
- Поместите предметные стекла в раствор генцианвиолета и оставьте на 30 секунд.
 Для срезов тканей увеличьте время до 1 минуты. №
Для срезов тканей увеличьте время до 1 минуты. № - Аккуратно смойте излишки красителя водой.
- Опустите предметные стекла в раствор йода Грама и оставьте на 30 секунд. Для срезов тканей увеличьте время до 1 минуты.
- Удалите раствор йода Грама, осторожно промыв раствором обесцвечивающего средства. Держите предметное стекло под углом и по каплям добавляйте обесцвечивающий раствор до тех пор, пока он не станет бесцветным. Будьте особенно осторожны на этом этапе, чтобы добиться правильного окрашивания спор.
- Аккуратно промойте предметное стекло холодной водой, чтобы удалить излишки раствора обесцвечивателя.
- Поместите предметные стекла в раствор генцианвиолета и оставьте на 30 секунд.
- Выполните хромотропное окрашивание следующим образом:
- Поместите предметное стекло в подогретый (от 50° до 55°C) хромотропный краситель не менее чем на 1 минуту. Для срезов тканей увеличьте время на 30 секунд.
- Промойте 90% раствором кислоты и спирта в течение 1–3 секунд. Будьте особенно осторожны на этом этапе, чтобы добиться правильного окрашивания спор.

- Промыть 95% этанолом в течение 30 секунд.
- Промойте дважды, каждый раз по 30 секунд, в 100% этаноле (для этого шага требуются два отдельных контейнера). Дайте высохнуть, затем закрепите Cytoseal60 (Stephens Scientific) или другим подходящим герметиком, следуя инструкциям. Для срезов тканей мы рекомендуем перед установкой предметные стекла кратковременно промыть в растворе 50% этилового спирта/50% ксилола в течение 15 секунд.
Контроль качества:
Контрольное стекло со спорами микроспоридий из образца, законсервированного 10% формалином, должно быть включено в каждый цикл окрашивания.
В образцах фекалий споры микроспоридий должны выглядеть как окрашенные в темный цвет фиолетово-яйцевидные структуры на бледно-зеленом фоне. Дрожжевые клетки, если они присутствуют, должны окрашиваться в темно-фиолетовый или розовато-красный цвет и легко отличимы от спор микроспоридий.
В цитологических препаратах споры микроспоридий должны окрашиваться от темно-фиолетового до розово-фиолетового цвета и могут содержать грамположительные гранулы. Иногда споры демонстрируют заметную полосу в виде экваториального пояса.
Иногда споры демонстрируют заметную полосу в виде экваториального пояса.
Ссылка:
Moura H, Schwartz DA, Bornay-Llinares F, et al. 1997. Новый и усовершенствованный метод «быстро-горячего грам-хромотропа», который дифференцированно окрашивает споры микроспоридий в клинических образцах, включая срезы ткани, залитые парафином. Arch Pathol Lab Med.121:888-893.
Модифицированный метод окрашивания сафранином (горячий метод)
Для Cyclospora , Cryptosporidia и Cystoisospora видов:
Ооцисты из Cyclospora в клинических образцах обычно обнаруживают с помощью модифицированного кислотостойкого окрашивания (холод). Однако при использовании этого метода ооцисты окрашиваются по-разному: от неокрашенного до полного окрашивания, что может привести к ошибочной идентификации. Метод модифицированного сафранина дает более равномерное окрашивание этих ооцист. Пятно необходимо нагреть до кипения с помощью горячей плиты или микроволновой печи.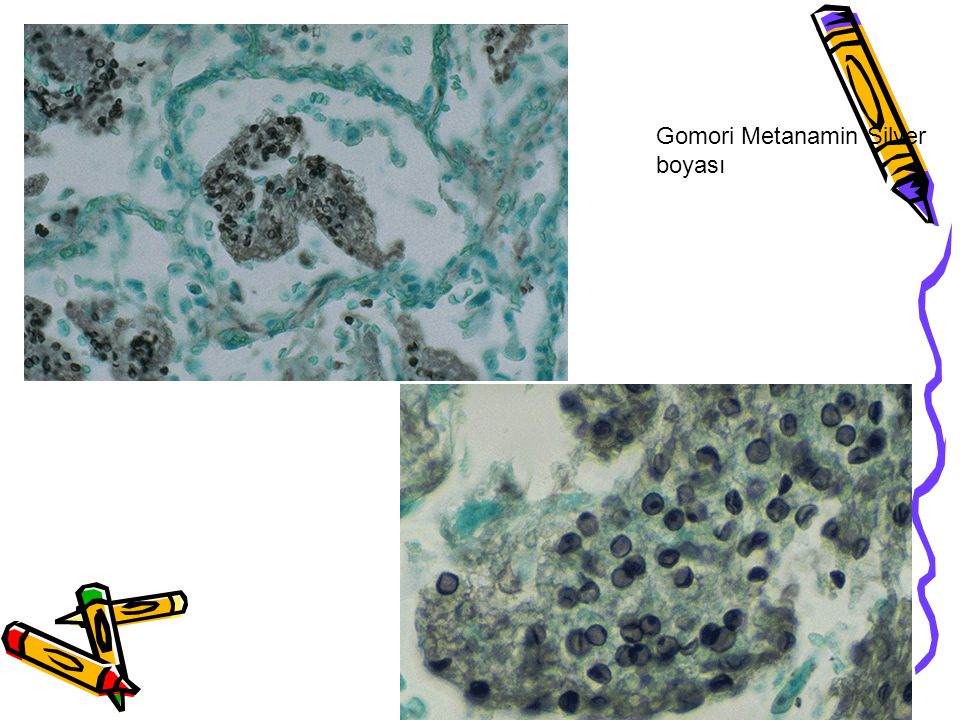
Образец:
Можно использовать концентрированный осадок свежего или законсервированного формалином стула. Другие типы клинических образцов, такие как дуоденальная жидкость, также могут быть окрашены.
Реагенты:
Эта процедура состоит из трех этапов, требующих следующих растворов:
- Кислотный спирт (3% HCl/метанол): медленно добавьте 3 мл соляной кислоты к 97 мл абсолютного метанола. Хранить при комнатной температуре в плотно закрытой таре.
- Окрашивание сафранином (доступно в наборах для окрашивания по Граму)
- 3% малахитовый зеленый: растворить 3 г малахитового зеленого в 100 мл дистиллированной воды. Хранить при комнатной температуре.
Процедура:
- Приготовьте тонкий мазок на предметном стекле и высушите на нагревателе для предметного стекла.
- Зафиксировать в кислом спирте на 5 минут.
- Промыть дистиллированной водой.
- Поместите в кипящий сафранин на 1 минуту.

- Промыть дистиллированной водой.
- Докрашивание малахитовым зеленым в течение 1 минуты.
- Кратковременно промыть дистиллированной водой.
- Высушите предметное стекло и закрепите покровным стеклом, используя желаемую заливочную среду.
Контроль качества:
Контрольное стекло Cyclospora spp. из образца, законсервированного 10% формалином, следует включать в каждый цикл окрашивания. Cyclospora spp. ооцисты окрашиваются в красновато-оранжевый цвет. Фон должен равномерно окрашиваться в зеленый цвет.
Процедура окрашивания трихромом
Общепризнано, что окрашенные фекальные пленки являются единственным наиболее эффективным средством исследования кала на кишечные простейшие. Постоянно окрашенный мазок облегчает обнаружение и идентификацию цист и трофозоитов и обеспечивает постоянную регистрацию встречающихся простейших. На окрашенном мазке часто видны мелкие простейшие, пропущенные при исследовании влажного препарата (как неконцентрированного, так и концентрированного образца). Техника трихрома Уитли для образцов фекалий является модификацией оригинальной процедуры окрашивания ткани Гомори. Это быстрая и простая процедура, позволяющая получить однородно хорошо окрашенные мазки кишечных простейших, клеток человека, дрожжей и артефактного материала.
Техника трихрома Уитли для образцов фекалий является модификацией оригинальной процедуры окрашивания ткани Гомори. Это быстрая и простая процедура, позволяющая получить однородно хорошо окрашенные мазки кишечных простейших, клеток человека, дрожжей и артефактного материала.
Образец:
Образцы обычно состоят из свежего стула или стула, зафиксированного в поливиниловом спирте (ПВС), намазанного на предметные стекла микроскопа и высушенного на воздухе или на подогреве предметного стекла при температуре 60°C. Также можно использовать стул, консервированный в растворе ацетата натрия, уксусной кислоты и формалина (SAF), или некоторые фиксаторы в одном флаконе.
Реагенты:
Эта процедура состоит из семи этапов, требующих следующих растворов:
- 70% этанол плюс йод: приготовьте исходный раствор, добавляя кристаллы йода к 70% спирту, пока не получите темный раствор. Для использования разбавьте бульон 70% спиртом до получения темно-красновато-коричневого цвета или цвета крепкого чая.

- 70% этанол (дважды)
- Трихромный краситель: можно приобрести отдельно
- 90% кислый этанол
90% этанол 99,5 мл Уксусная кислота (ледяная) 0,5 мл - 95% этанол
- 100% этанол (дважды)
- Ксилол или заменитель ксилола (дважды)
Процедура:
- Для мазков ПВС поместите предметное стекло в 70% этанол с добавлением йода на 10 минут. Для других фиксаторов следуйте инструкциям производителя. Пропустите этап с йодом для консервантов, не содержащих хлорид ртути.
- Поместите предметное стекло в 70% этанол на 5 минут.
- Поместить во второй 70% этанол на 3 минуты
- Поместите в трихромовый краситель на 10 минут.
- Обезжирить 90% раствором этанола с уксусной кислотой в течение 1–3 секунд.
- Промойте несколько раз в 100% этаноле.
- Поместите в две смены 100% этанола на 3 минуты каждую.

- Поместите две смены ксилола или заменителя ксилола на 10 минут.
- Смонтируйте с покровным стеклом, используя монтажную среду (например, пермаунт).
- Исследуйте мазок под микроскопом, используя объектив 100×. Обследовать не менее 200–300 нефтеиммерсионных полей.
Контроль качества:
Контрольное стекло известных простейших, таких как Giardia spp. из образца, сохраненного ПВА, следует включать в каждый цикл окрашивания. При тщательной фиксации мазка и правильной окраске цитоплазма простейших трофозоитов будет иметь сине-зеленую окраску, иногда с фиолетовым оттенком. Кисты имеют тенденцию быть немного более фиолетовыми. Ядра и включения (хроматоидные тельца, эритроциты, бактерии) и кристаллы Шарко-Лейдена имеют красную окраску, иногда с фиолетовым оттенком. Гликоген растворяется в растворителях и появляется в организме в виде прозрачной области. Фоновый материал обычно окрашивается в зеленый цвет, обеспечивая приятный цветовой контраст с простейшими.
Процедура окрашивания Calcofluor White
Этот хемофлуоресцентный метод полезен для обнаружения микроспоридий, Acanthamoeba spp., Pneumocystis jiroveci и Dirofilaria spp. Химиофлуоресцентные агенты, такие как Calcofluor, Fungi-Fluor или Uvitex 2B, также известные как оптические отбеливатели, являются быстродействующими и недорогими агентами для скрининга. Эти реагенты чувствительны, но неспецифичны, поскольку многие объекты и организмы, кроме паразитов, могут флуоресцировать. Этот тест следует использовать в качестве инструмента быстрого скрининга, а не для идентификации видов.
Образец:
Приготовьте тонкий мазок, используя примерно 10 мкл свежих или консервированных образцов на предметном стекле. Образцы могут включать стул, мочу, культуру или другие типы образцов. Зафиксировать на предметном стекле при температуре 60°C до полного высыхания (5-10 минут).
Реагенты
Эта процедура состоит из двух этапов, требующих следующих растворов:
- Абсолютный метанол
- 0,01 % реагент Calcofluor white: приготовьте 0,01 % раствор в 0,1 М трис-буферном солевом растворе, pH 7,2
Процедура
- Приготовьте тонкий мазок фекального, культурального или другого образца материала.

- Зафиксируйте мазок метанолом на 30 секунд.
- Окрашивание 0,01% реагентом Calcofluor White в течение 1 минуты.
- Промойте дистиллированной водой и дайте мазку высохнуть.
- Маунт с покровным стеклом №1 по толщине.
- Исследование с помощью УФ-флуоресцентного микроскопа, оснащенного сине-фиолетовым кубическим фильтром с длиной волны 400 нм или меньше.
- Для выявления микроспоридий исследуйте мазок с помощью масляного иммерсионного объектива с увеличением 50× или 100×. Споры микроспоридий флуоресцируют ярким сине-белым цветом на черном фоне.
Контроль качества
Контрольное стекло микроспоридий, консервированных в 10% формалине, приготовленное из культуры или образца стула, должно быть включено в каждый цикл окрашивания.
Для получения дополнительной информации об окрашивании образцов стула позвоните в Отдел паразитарных заболеваний по телефону (404) 418-4110.
Окрашивание серебром метенамина по Грокотту-Гомори
Фейт Мокоби
- Окрашивание метенаминовым серебром по Грокотту-Гомори (GMS) — это гистологическое окрашивание, которое в основном используется для идентификации углеводов в грибковых микроорганизмах.
- Этот метод окрашивания был назван в честь Дьёрдя Гёмёри, врача из Венгрии, который разработал методологию окрашивания.
- Его первоначальное применение для оценки отсутствующих тканей и заболеваний в печени и прямой кишке ( Nadworny, Wang, Tredget, & Robert, 2010) , а затем использовали для идентификации Pneumocystis jiroveci , грибка, который, как известно, вызывает оппортунистическую инфекцию, называемую пневмоцитозом, у пациентов с иммунодефицитом и иммуносупрессией.
- По сравнению с другими красителями, такими как красители периодической кислоты-Шиффа и красители Гридли, Goromi обладает более высокой чувствительностью к обнаружению грибков и других богатых полисахаридами микроорганизмов в срезах, приготовленных из парафина.

- Метенамин-нитрат серебра и хромовая кислота Гомори составляют основные реагенты, используемые в обычном окрашивании по Грокотту
- Он также использовался для идентификации грибков в срезах тканей.
- Его применение в гистологии делает его идеальным для обнаружения и демонстрации грибков в аспиратах, тканях и мазках.
Содержание
Цели- Продемонстрировать присутствие грибов в данном образце.
- Для демонстрации присутствия Pneumocystis jiroveci и Histoplasma spp.
Стенка грибковой клетки состоит из полисахаридов, которые при взаимодействии с хроматиновой кислотой окисляются с образованием альдегидов. Об этом свидетельствует восстановление комплекса щелочь-гексамин-серебро.
Щелочной раствор гексамина и серебра Грокотта подвергается восстановлению с образованием осадков ионов серебра, из-за чего клеточная стенка грибов становится черной. Эта реакция известна как аргентаффиновая реакция ( способность клеток восстанавливать раствор серебра до металлического серебра с образованием черного тканевого элемента ). Аргентаффинные клетки обнаруживаются в эпителиальной выстилке легких, кишечника и меланине. Эта реакция приводит к результату окрашивания.
Эта реакция известна как аргентаффиновая реакция ( способность клеток восстанавливать раствор серебра до металлического серебра с образованием черного тканевого элемента ). Аргентаффинные клетки обнаруживаются в эпителиальной выстилке легких, кишечника и меланине. Эта реакция приводит к результату окрашивания.
Существует два типа методик окрашивания:
- Традиционный метод при комнатной температуре
- Микроволновой метод
Раствор триоксида хрома, раствор бисульфита натрия, раствор нитрата серебра, раствор уротропина, раствор буры, раствор хлорида золота, раствор тиосульфата натрия, маточный светло-зеленый раствор.
Приготовление раствораПРИМЕЧАНИЕ : Эти реагенты обычно поставляются в наборах для ручного приготовления, а некоторые растворы уже готовы
- Хромовая кислота (1,4%): триоксид хрома 4 г + 100 мл дистиллированной воды
- Раствор серебра: 3 % метанамина/гексамина 23 мл + 5 % нитрата серебра 1,25 мл + 5 % буры (тетраборат натрия) 3 мл + 25 мл дистиллированной воды
- 3,2% хлораурат натрия (хлорид желтого золота): хлорид золота 1,0 г + 500 мл дистиллированной воды
- 4,2 % Тиосульфат натрия (гипо): Тиосульфат натрия 2,0 г + 100 мл Дистиллированная вода
- Рабочий раствор светло-зеленого цвета: 10 мл 1% светло-зеленого в 1% уксусной кислоте + 40 мл дистиллированной воды
Примечание. Приготовьте растворы в зависимости от концентрации, необходимой для окрашивания.
Приготовьте растворы в зависимости от концентрации, необходимой для окрашивания.
- Увлажняйте срезы дистиллированной водой.
- Затем окисляют срез 4% водным раствором хромовой кислоты при комнатной температуре и оставляют на 1 час
- Промыть водой в течение нескольких секунд
- Обработка срезов 1% раствором метабисульфита натрия в течение 1 мин
- Стирка в проточной водопроводной воде в течение 3 минут
- Тщательно промыть дистиллированной водой
- Поместите предметные стекла в предварительно нагретый рабочий раствор серебра на водяной бане при 60°C на 15–20 минут, пока срез не станет желтовато-коричневым (проверьте под микроскопом, чтобы увидеть, как грибы стали темно-коричневыми).
- Хорошо промыть дистиллированной водой
- Добавить в срезы 0,2% хлорида золота и оставить на 2 мин
- Хорошо промыть дистиллированной водой
- Обработайте срезы 2% раствором тиосульфата натрия в течение 2 минут
- Промыть проточной водопроводной водой в течение 5 минут
- добавить краситель в светло-зеленый цвет на 15 секунд
- Смойте лишний раствор светло-зеленого цвета с предметного стекла спиртом
- Обезвоживание, очистка и монтаж.

- Увлажните срезы до дистиллированной воды.
- Поместите предметные стекла в 40 мл 1,4% водного раствора хромовой кислоты в неплотно закрытую пластиковую банку Коплина.
- Микроволновая печь при мощности 150 Вт на 2 мин 30 сек
- Опустите предметные стекла вверх и вниз в банку Коплина и дайте им постоять еще 2 мин.
- Промывка в проточной водопроводной воде 30 сек
- Добавьте к срезам 3,2% раствор метабисульфита натрия и оставьте на 10 секунд, затем промойте водопроводной водой в течение 30 секунд.
- Предварительный нагрев рабочего раствора серебра при мощности 450 Вт в течение 60 с
- и тщательно промойте предметное стекло дистиллированной водой, затем поместите срезы предметного стекла в горячий раствор серебра.
- Разогрейте секции в микроволновой печи при мощности 150 Вт в течение 30 секунд
- Дип скользит вверх и вниз в банке Coplin и позволяет постоять еще 1 минуту.
 Промыть дистиллированной водой и проверить под микроскопом. Примечание : Окуните предметные стекла в раствор серебра, если они недостаточно окрашены, и проверяйте каждую минуту, пока грибковые пятна не станут темно-коричневыми.
Промыть дистиллированной водой и проверить под микроскопом. Примечание : Окуните предметные стекла в раствор серебра, если они недостаточно окрашены, и проверяйте каждую минуту, пока грибковые пятна не станут темно-коричневыми. - Тонируйте срезы 3,2% хлоридом золота в течение 30 секунд и промывайте дистиллированной водой.
- Добавить 4,2% тиосульфата натрия в срез на 1 мин и промыть водопроводной водой в течение 15 сек.
- Докрасьте срез светло-зеленым раствором в течение 15 сек.
- Смойте светло-зеленый раствор спиртом
- Высушите и накройте.
Рисунок: Грибковые организмы выделяются специальным красителем Grocott метенамин-серебро. Гифы 4-6 мкм шириной; Септированные гифы грибов с непараллельными стенками, недихотомическим ветвлением и конечными луковичными расширениями. Источник: DOI: 10.1177/1040638716640313
- Грибы, Pneumocystis jirevoci , Окраска Histoplasma spp.

- Окраска внутренних частей мицелия и гиф розово-красный/розовый
- Leishmania spp., Toxoplasma spp. – отрицательный результат
- Муциновые красители темно-серый
- Фон принимает светло-зеленый цвет и окрашивается бледно-зеленым
Виды грибов окрашиваются в черный цвет из-за процесса восстановления раствора нитрата серебра. Раствор нитрата серебра после восстановления образует ионы серебра черного цвета, что приводит к образованию черного пятна на грибковых клетках.
Грибковый мицелий и гифы окрашиваются в розовый/розово-красный цвет, в то время как муцин окрашивается в темно-серый цвет также из-за восстановления нитрата серебра до ионов серебра. фон будет казаться бледно-зеленым, приняв светло-зеленый раствор.
ОСТОРОЖНО
- Носите перчатки, защитные очки и лабораторный халат.
 Храните горячие открытые растворы под вытяжным шкафом. Избегайте контакта и вдыхания красителей и химических веществ.
Храните горячие открытые растворы под вытяжным шкафом. Избегайте контакта и вдыхания красителей и химических веществ. - Хромовая кислота вызывает коррозию кожи и слизистых оболочек, высокотоксична для почек, а также очень канцерогенна
- Метабисульфит натрия является токсичным при проглатывании и может вызвать расстройство желудочно-кишечного тракта и раздражительность. Он также раздражает кожу, глаза и слизистую оболочку.
- Нитрат серебра вызывает раздражение кожи и глаз.
- Окислитель при проглатывании вызывал сильный дискомфорт в желудочно-кишечном тракте и, возможно, является канцерогенным, поскольку является канцерогенным агентом.
- Тиосульфат натрия токсичен при приеме внутрь и вызывает раздражение желудка, кожи, глаз и дыхательных путей.
- Светло-зеленый SF Желтоватый цвет считается возможным канцерогеном.
- используется для идентификации грибковых клеток в срезах тканей
- используется для дифференциации грибковых клеток от бактериальных клеток
- также используется для идентификации дрожжеподобных грибов, таких как Pneumocystis jiroveci
- Это агрессивный краситель, который прочно фиксирует окрашенные срезы и может быть использован для дальнейшего использования и наблюдения.

- Tt может различать грибы различной морфологии.
- Химические реагенты могут вызывать раздражение кожи, желудочно-кишечного тракта при вдыхании.
- Реагенты также обладают канцерогенным действием.
- Grocott, R.G. 1955 г. Окраска на грибы в срезах тканей и мазках. Американский журнал клинической патологии , V25, стр. 975
- Алтуркистани, Хани и Ташкенди, Фарис и Мохаммедсалех, Зухайр. (2015). Гистологические пятна: обзор литературы и тематическое исследование. Глобальный журнал наук о здоровье. 8. 10.5539/gjhs.v8n3p72.
- http://www.ihcworld.com/_protocols/special_stains/grocott_methenamine_ellis.htm
- https://www.clinisciences.com/autres-produits-186/grocott-methenamine-silver-stain-351002431.html
- https://webpath.med.utah.edu/HISTHTML/MANUALS/GMS.PDF
- https://www.researchgate.net/post/Which_stains_can_be_used_for_Staining_Fungi
- https://www.
 coursehero.com/file/p342qaq/Grocotts-methenamine-silver-staining-protocol-Principle-Chromic-acid-oxidation/
coursehero.com/file/p342qaq/Grocotts-methenamine-silver-staining-protocol-Principle-Chromic-acid-oxidation/ - https://www.reference.com/science/nitric-acid-stain-skin-yellow-9475502370e787b5
- https://quizlet.com/185455989/histology-stains-flash-cards/
- http://pesticideinfo.org/Detail_Chemical.jsp?Rec_Id=PC33841
Гистохимическая демонстрация липазы | Природа
- Опубликовано:
- P. H. A. SNEATH 1
Природа том 166 , страницы 699–700 (1950 г.)Цитировать эту статью
16 доступов
5 Цитаты
Сведения о показателях
Abstract
Липазный метод Гомори 1 мало использовался в гистологии патологий. Настоящее сообщение касается результатов предварительного изучения распределения липазы в тканях человека методом Гомори. Метод, который является одним из его оригинальных приемов, использующих отложение нерастворимой соли кальция в месте действия фермента, основан на расщеплении водорастворимого эфира высших жирных кислот и превращении кальциевого мыла в сульфид свинца. Оригинальный метод 1 и модификация Wachstein 2 были удовлетворительными при использовании в качестве субстрата Tween 40 или 60, как они рекомендовали, или Crill 6 или 7, который является аналогичным британским продуктом (Croda, Ltd., Goole, Yorks).
Настоящее сообщение касается результатов предварительного изучения распределения липазы в тканях человека методом Гомори. Метод, который является одним из его оригинальных приемов, использующих отложение нерастворимой соли кальция в месте действия фермента, основан на расщеплении водорастворимого эфира высших жирных кислот и превращении кальциевого мыла в сульфид свинца. Оригинальный метод 1 и модификация Wachstein 2 были удовлетворительными при использовании в качестве субстрата Tween 40 или 60, как они рекомендовали, или Crill 6 или 7, который является аналогичным британским продуктом (Croda, Ltd., Goole, Yorks).
Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Варианты доступа
Подписаться на журнал
Получить полный доступ к журналу на 1 год
199,00 €
всего 3,90 € за выпуск
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Ссылки
Гомори, Г., Proc. соц. Эксп. биол. Нью-Йорк , 58 , 362 (1945).
КАС Статья Google ученый
Wachstein, J. Exp. Мед. , 84 , 25 (1946).
КАС Статья Google ученый
Марка, Арх. Дорожка. , 49 , 545 (1950).
КАС Google ученый
Гомори, Г., Арх. Дорожка. , 41 , 121 (1946).
КАС пабмед Google ученый
Даниэлли, Дж. Ф., Природа , 165 , 762 (1950).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Download references
Author information
Authors and Affiliations
Department of Morbid Anatomy, King’s College Hospital Medical School, London, S.
 E.5
E.5P. H. A. SNEATH
Authors
- P. H. A. SNEATH
View авторские публикации
Вы также можете искать этого автора в PubMed Google Scholar
Права и разрешения
Перепечатки и разрешения
Об этой статье
Дополнительная литература
Электронно-микроскопическая демонстрация липазы в ацинарных клетках поджелудочной железы мышей
- Ф. Мурата
- С. Йокота
- Т.


/023/023.jpg) А. Введение
в исследование операций. 7-е издание.: Пер. с англ. М.:
Издательский дом “Вильямс”, 2005–912 c.
А. Введение
в исследование операций. 7-е издание.: Пер. с англ. М.:
Издательский дом “Вильямс”, 2005–912 c.
 Виды и основное содержание методов экономического воздействия. Краткая характеристика и особенности применения экономических методов
Виды и основное содержание методов экономического воздействия. Краткая характеристика и особенности применения экономических методов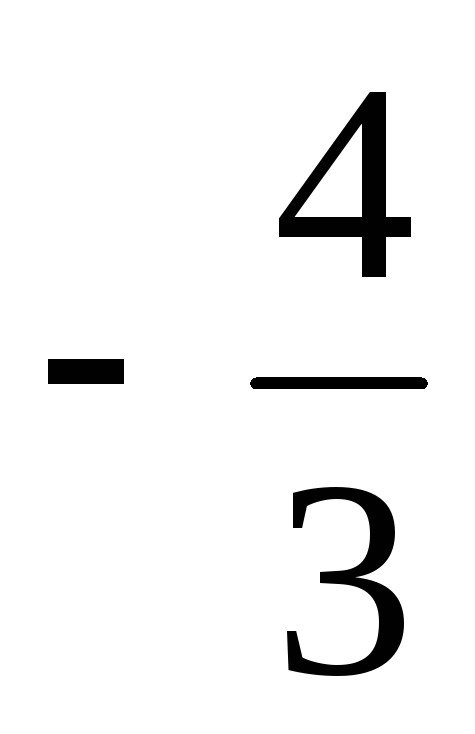 Гомори
Гомори 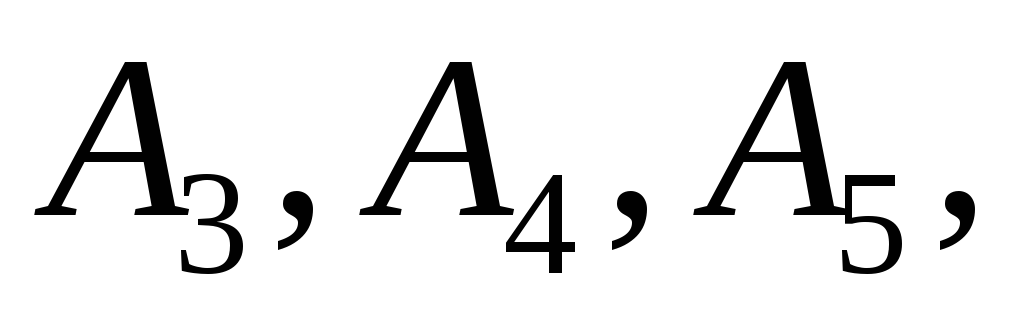

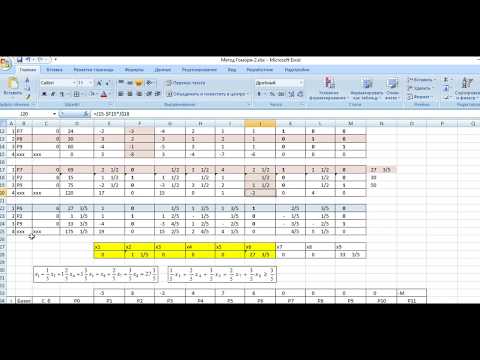 адрес
LinkedIn
адрес
LinkedIn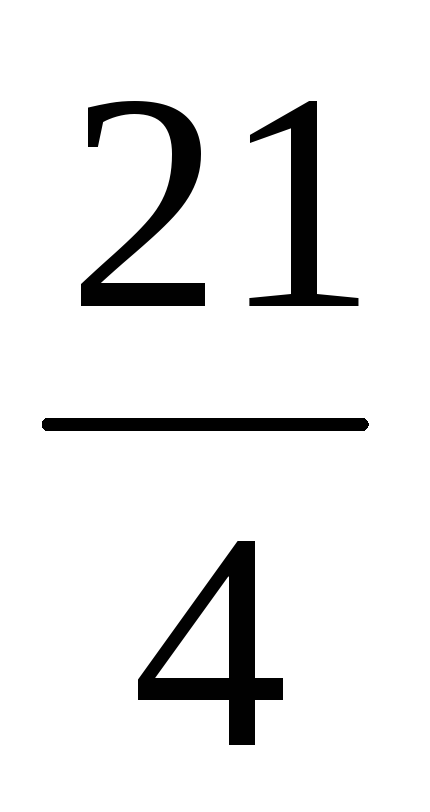
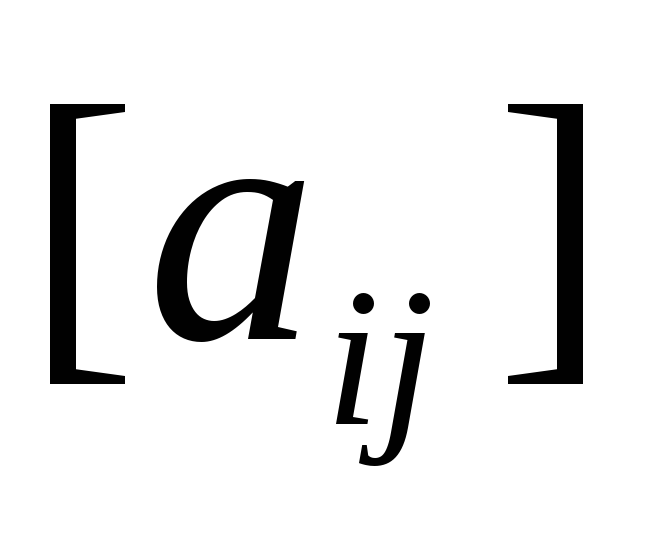
 Хранить при комнатной температуре.
Хранить при комнатной температуре.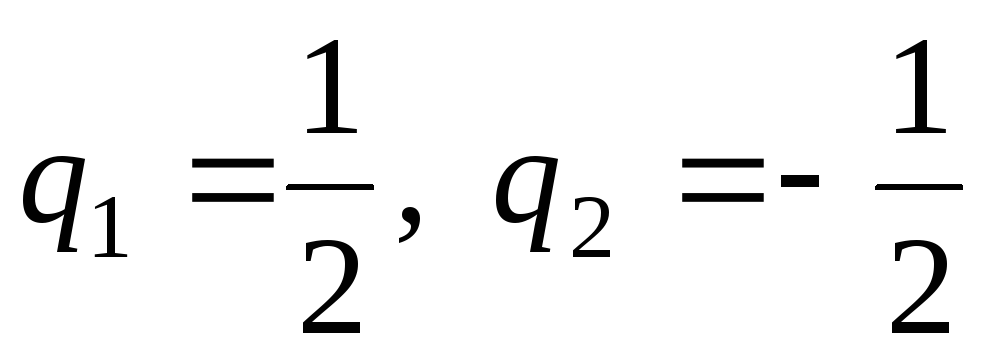
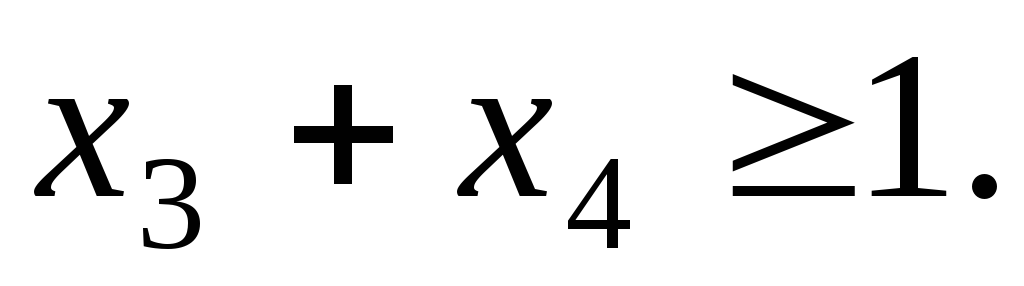
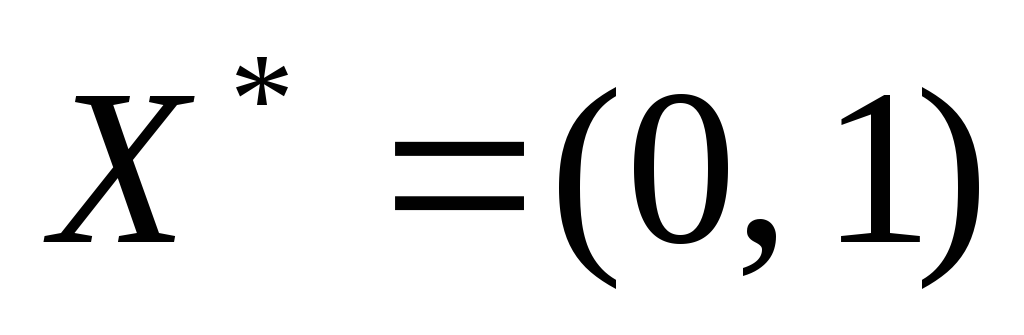 Дайте постоять 30 минут, а затем добавьте 100 мл дистиллированной воды. Готовьте свежий для использования каждый месяц.
Дайте постоять 30 минут, а затем добавьте 100 мл дистиллированной воды. Готовьте свежий для использования каждый месяц. Для срезов тканей увеличьте время до 1 минуты.
Для срезов тканей увеличьте время до 1 минуты.
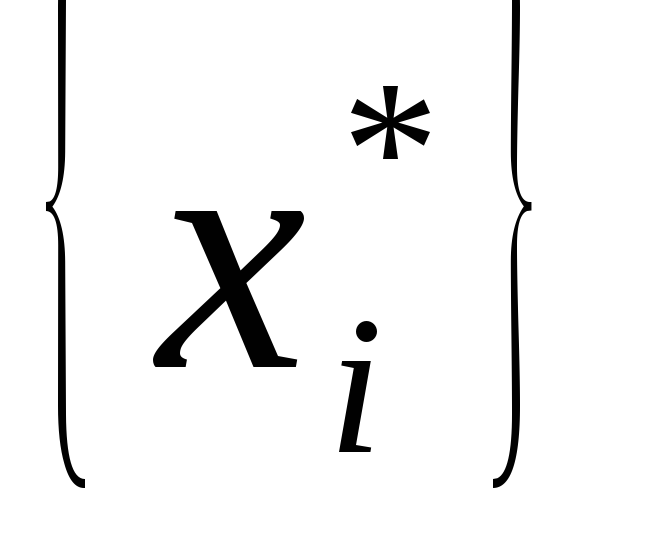
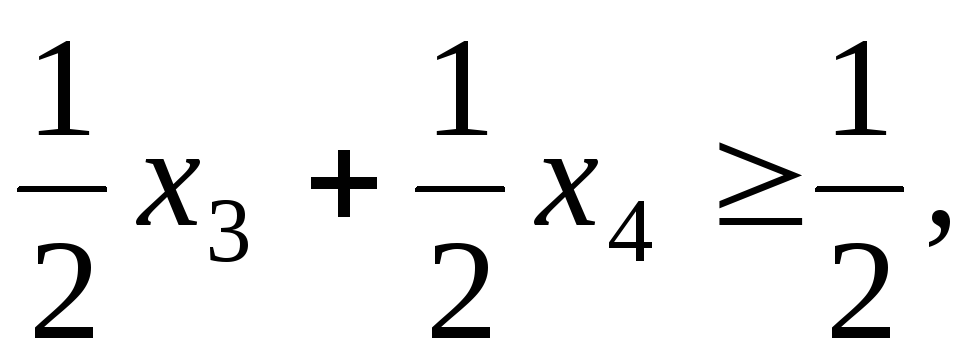
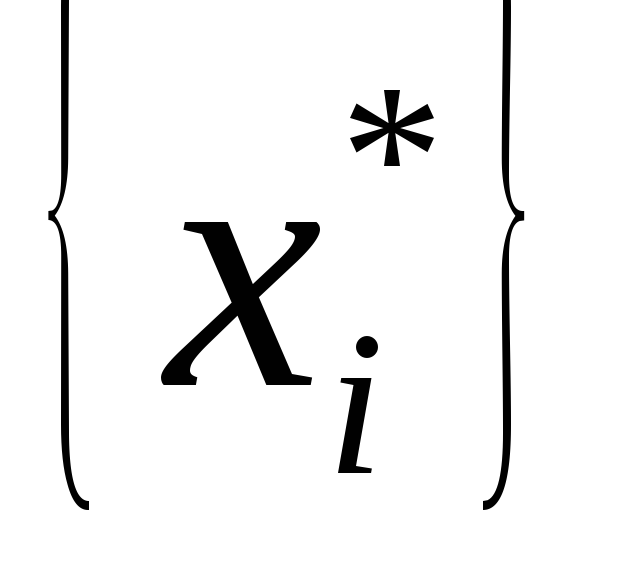


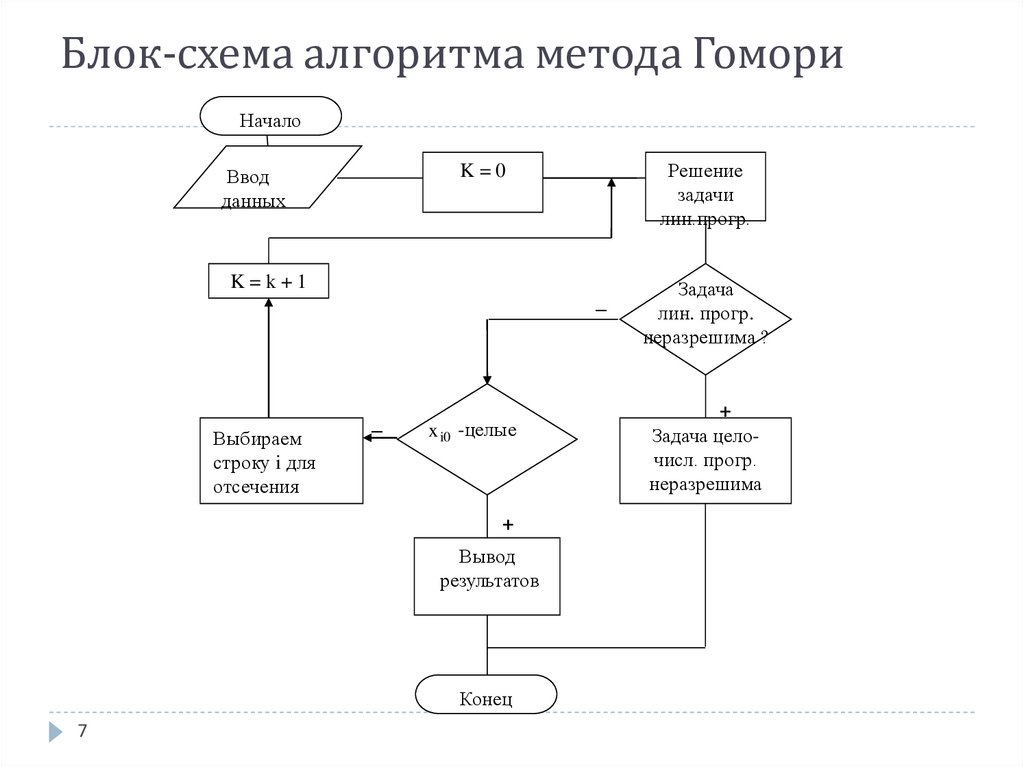
 Промыть дистиллированной водой и проверить под микроскопом. Примечание : Окуните предметные стекла в раствор серебра, если они недостаточно окрашены, и проверяйте каждую минуту, пока грибковые пятна не станут темно-коричневыми.
Промыть дистиллированной водой и проверить под микроскопом. Примечание : Окуните предметные стекла в раствор серебра, если они недостаточно окрашены, и проверяйте каждую минуту, пока грибковые пятна не станут темно-коричневыми.
 Храните горячие открытые растворы под вытяжным шкафом. Избегайте контакта и вдыхания красителей и химических веществ.
Храните горячие открытые растворы под вытяжным шкафом. Избегайте контакта и вдыхания красителей и химических веществ.
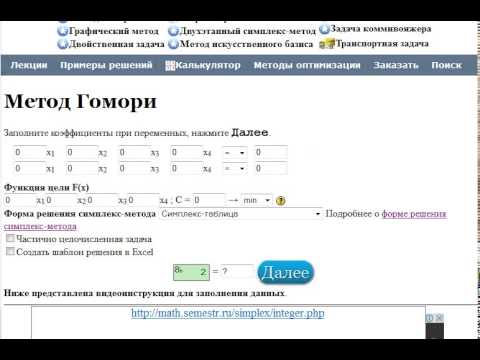 coursehero.com/file/p342qaq/Grocotts-methenamine-silver-staining-protocol-Principle-Chromic-acid-oxidation/
coursehero.com/file/p342qaq/Grocotts-methenamine-silver-staining-protocol-Principle-Chromic-acid-oxidation/