|
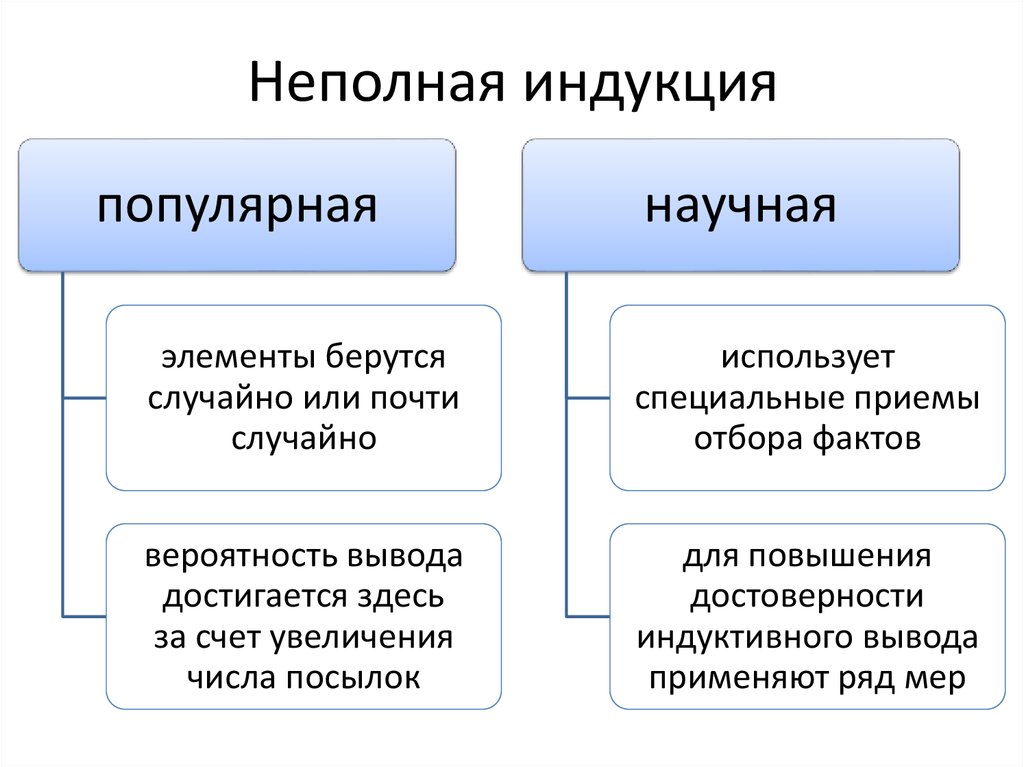
Индукция — это познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение. В научном поиске (см. Методы научного познания) индукция предполагает движение познания от единичных утверждений об отдельных фактах к положениям, носящим более общий характер. В логике (см. Логика) термин «индукция» используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение» и понимается в более узком смысле: как умозаключение, в котором общий вывод строится на основе частных посылок. При этом посылки могут подтверждать или подразумевать истину, но не гарантируют её получения. Этим индукция принципиально отличается от дедукции (см. Дедукция), посредством которой из истинных посылок при соблюдении правил логического вывода всегда получаются истинные заключения. Наиболее широко используемая разновидность индуктивных рассуждений — это перечислительные рассуждения, то есть рассуждения, содержащие переход от посылок, утверждающих, что все известные объекты из некоторой совокупности Индукция широко используется во всех областях научного познания, играя важную роль при построении эмпирических знаний и переходе от эмпирического знания к теоретическому. В науке основой индукции являются опыт, эксперимент и наблюдение, в ходе которых собираются отдельные факты. Затем, изучая эти факты, анализируя их, исследователь устанавливает общие и повторяющиеся признаки ряда явлений, входящих в определённый класс. На этой основе он строит индуктивное умозаключение, в качестве посылок которого выступают суждения о единичных объектах и явлениях с указанием их повторяющегося признака, и суждение о классе, включающем данные объекты и явления. В качестве вывода получают суждение, в котором признак, выявленный у совокупности единичных объектов, приписывается всему классу. В индуктивных рассуждениях различают полную и неполную индукцию:
Указанные разновидности неполной индукции играют исключительно важную роль в научном познании. Поскольку индукция тесно связана с развитием опытного познания, она стала применяться уже в глубокой древности, хотя теоретически её простейшие формы начали анализироваться только в античной философии, в частности Сократом, который ввёл понятие индуктивных рассуждений, и Аристотелем, который рассматривал их как вспомогательные средства обоснования посылок силлогизмов (см. Силлогизм). У Аристотеля понимание индукции связывается с обобщением наблюдений и означает, по существу, способ умозаключения, посредством которого производится восхождение от частного к общему. Этот аристотелевский взгляд восприняли философы эпикурейской школы, защищавшие индукцию в споре со стоиками как единственный авторитетный метод доказательства законов природы. Дальнейшее развитие теории индукции отмечается лишь в Новое время, когда активный рост науки, обусловленный накоплением, обобщением и систематизацией обширного эмпирического материала, поставил вопрос об исследовании способов научного открытия, а сами виды индуктивных рассуждений стали изучаться на предмет их надёжности. Важное значение в этом отношении имели сочинения Ф. Бэкона, который начал систематическое изучение индуктивных процедур, рассматривая их как единственно научный способ познания и противопоставив индукцию умозрительным рассуждениям. Поскольку методы аристотелевской силлогистики и индукция через простое перечисление подтверждающих случаев не могли быть использованы для анализа эмпирических обобщений, Бэкон в противовес «Органону» Аристотеля создаёт свой «Новый Органон» (1620), в котором излагает «каноны индукции» как методы открытия новых истин в науке. Позднее теория индукции развивалась в работах Дж. Ст. Милля, который предложил пять методов индуктивных рассуждений (каноны индукции Бэкона-Милля), посредством которых выводятся заключения о причинных связях между явлениями: метод сходства; метод различия; объединённый метод сходства и различия; метод остатков; метод сопутствующих изменений.  Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики. Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики. Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов. Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов.
С философской точки зрения наибольший интерес представляет проблема обоснования индукции — нахождения рационального базиса для признания легитимности индуктивных рассуждений. Важность проблемы обусловлена важностью индуктивных рассуждений для современной науки. Её успешное решение предполагает нахождение ответа на вопрос, на каком основании мы признаем некоторые из индуктивных рассуждений приемлемыми, несмотря на то, что во всяком индуктивном рассуждении истинность посылок не гарантирует истинности заключения. Все ответы, предложенные со времени поставившего этот вопрос Д. Юма, оказались безуспешными — всякая попытка обоснования индукции, предложенная до настоящего момента, в неявной форме предполагала легитимность индукции. В настоящее время определённой популярностью пользуется рассмотрение проблемы индукции, предложенное П. Стросоном, утверждающим, что проект обоснования индукции самопротиворечив. |
|
|
1.6. Индукция и дедукция как формально-логические методы познания. Основные методы индукции
Индукция (от лат. inductio – наведение, побуждение) есть метод познания, основывающийся на формальнологическом умозаключении, которое приводит к получению общего вывода на основании частных посылок. Другими словами, это есть движение нашего мышления от частного, единичного к общему.
Индукция
широко применяется в научном познании.
Обнаруживая сходные признаки, свойства
у многих объектов определенного класса,
исследователь делает вывод о присущности
этих признаков, свойств всем объектам
данного класса. Например, в процессе
экспериментального изучения электрических
явлений использовались проводники
тока, выполненные из различных металлов. На основании многочисленных единичных
опытов сформировался общий вывод об
электропроводности всех металлов.
На основании многочисленных единичных
опытов сформировался общий вывод об
электропроводности всех металлов.
Индукция, используемая в научном познании (научная индукция), может реализовываться в виде следующих методов:
1. Метод единственного сходства (во всех случаях наблюдения какого-то явления обнаруживается лишь один общий фактор, все другие – различны; следовательно, этот единственный сходный фактор есть причина данного явления).
2. Метод единственного различия (если обстоятельства возникновения какого-то явления и обстоятельства, при которых оно не возникает, почти во всем сходны и различаются лишь одним фактором, присутствующим только в первом случае, то можно сделать вывод, что этот фактор и есть причина данного явления).
3. Соединенный метод сходства и различия (представляет собой комбинацию двух вышеуказанных методов).
4.
Метод сопутствующих изменений (если
определенные изменения одного явления
всякий раз влекут за собой некоторые
изменения в другом явлении, то отсюда
вытекает вывод о причинной связи этих
явлений).
5. Метод остатков (если сложное явление вызывается многофакторной причиной, причем некоторые из этих факторов известны как причина какой-то части данного явления, то отсюда следует вывод: причина другой части явления – остальные факторы, входящие в общую причину этого явления).
Родоначальником классического индуктивного метода познания является Ф. Бэкон. Но он трактовал индукцию чрезвычайно широко, считал ее важнейшим методом открытия новых истин в науке, главным средством научного познания природы (всеиндуктивизм). Однако индукцию нельзя рассматривать изолированно от других методов познания, в частности, от дедукции.
Дедукция (от
лат. deductio – выведение) есть получение
частных выводов на основе знания каких-то
общих положений. Другими словами, это
есть движение нашего мышления от общего
к частному, единичному. Например, из
общего положения, что все металлы
обладают электропроводностью, можно
сделать дедуктивное умозаключение об
электропроводности конкретной медной
проволоки (зная, что медь – металл). Если
исходные общие положения являются
установленной научной истиной, то
методом дедукции всегда будет получен
истинный вывод. Общие принципы и законы
не дают ученым в процессе дедуктивного
исследования сбиться с пути: они помогают
правильно понять конкретные явления
действительности.
Если
исходные общие положения являются
установленной научной истиной, то
методом дедукции всегда будет получен
истинный вывод. Общие принципы и законы
не дают ученым в процессе дедуктивного
исследования сбиться с пути: они помогают
правильно понять конкретные явления
действительности.
Получение новых знаний посредством дедукции существует во всех естественных науках, но особенно большое значение дедуктивный метод имеет в математике. Оперируя математическими абстракциями и строя свои рассуждения на весьма общих положениях, математики вынуждены чаще всего пользоваться дедукцией. И математика является, пожалуй, единственной собственно дедуктивной наукой.
В
науке Нового времени пропагандистом
дедуктивного метода познания был видный
математик и философ Р. Декарт. Вдохновленный
своими математическими успехами, будучи
убежденным в безошибочности правильно
рассуждающего ума, Декарт односторонне
преувеличивал значение интеллектуальной
стороны за счет опытной в процессе
познания истины. Дедуктивная методология
Декарта была прямой противоположностью
эмпирическому индуктивизму Бэкона.
Дедуктивная методология
Декарта была прямой противоположностью
эмпирическому индуктивизму Бэкона.
Но, несмотря на имевшие место в истории науки и философии попытки оторвать индукцию от дедукции, противопоставить их в реальном процессе научного познания, эти два метода не применяются как изолированные, обособленные друг от друга. Каждый из них используется на соответствующем этапе познавательного процесса.
Более того, в процессе использования индуктивного метода зачастую «в скрытом виде» присутствует и дедукция. Подчеркивая необходимую связь индукции и дедукции, Ф. Энгельс настоятельно советовал ученым: «Вместо того чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться каждую применять на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг другом».
Общенаучные
методы, применяемые на эмпирическом и
теоретическом уровнях познания. Анализ
и синтез. Под анализом понимают
разделение объекта (мысленно или реально)
на составные частицы с целью их отдельного
изучения. В качестве таких частей могут
быть использованы какие-то вещественные
элементы объекта или же его свойства,
признаки, отношения и т.п.
Анализ
и синтез. Под анализом понимают
разделение объекта (мысленно или реально)
на составные частицы с целью их отдельного
изучения. В качестве таких частей могут
быть использованы какие-то вещественные
элементы объекта или же его свойства,
признаки, отношения и т.п.
Анализ – необходимый этап в познании объекта. С древнейших времен анализ применялся, например, для разложения на составляющие некоторых веществ. В частности, уже в Древнем Риме анализ использовался для проверки качества золота и серебра в виде так называемого купелирования (анализируемое вещество взвешивалось до и после нагрева). Постепенно формировалась аналитическая химия, которую по праву можно называть матерью современной химии: ведь прежде чем применять то или иное вещество в конкретных целях, необходимо выяснить его химический состав.
Анализ
занимает важное место в изучении объектов
материального мира. Но он составляет
лишь первый этап процесса познания. Если бы, скажем, химики ограничивались
только анализом, т.е. выделением и
изучением отдельных химических элементов,
то они не смогли бы познать все те сложные
вещества, в состав которых входят эти
элементы.
Если бы, скажем, химики ограничивались
только анализом, т.е. выделением и
изучением отдельных химических элементов,
то они не смогли бы познать все те сложные
вещества, в состав которых входят эти
элементы.
Для
постижения объекта как единого целого
нельзя ограничиваться изучением лишь
его составных частей. В процессе познания
необходимо вскрывать объективно
существующие связи между ними,
рассматривать их в совокупности, в
единстве. Осуществить этот второй этап
в процессе познания – перейти от изучения
отдельных составных частей объекта к
изучению его как единого связанного
целого – возможно только в том случае,
если метод анализа дополняется другим
методом – синтезом. В процессе
синтеза производится соединение воедино
составных частей (сторон, свойств,
признаков и т.п.) изучаемого объекта,
расчлененных в результате анализа. На
этой основе происходит дальнейшее
изучение объекта, но уже как единого
целого. При этом синтез не означает
простого механического соединения
разъединенных элементов в единую
систему. Он раскрывает место и роль
каждого элемента в системе целого,
устанавливает их взаимосвязь и
взаимообусловленность, т.е. позволяет
понять подлинное диалектическое единство
изучаемого объекта.
Он раскрывает место и роль
каждого элемента в системе целого,
устанавливает их взаимосвязь и
взаимообусловленность, т.е. позволяет
понять подлинное диалектическое единство
изучаемого объекта.
Анализ и синтез с успехом используются и в сфере мыслительной деятельности человека, т.е. в теоретическом познании. Но и здесь, как и на эмпирическом уровне познания, анализ и синтез – это не две оторванные друг от друга операции. По своему существу они – как бы две стороны единого аналитико-синтетического метода познания.
Аналогия и моделирование – общенаучные методы, применяемые на эмпирическом и теоретическом уровнях познания. Под аналогией понимается подобие, сходство каких-то свойств, признаков или отношений у различных в целом объектов. Установление сходства (или различия) между объектами осуществляется в результате их сравнения. Таким образом, сравнение лежит в основе метода аналогии.
Если
делается логический вывод о наличии
какого-либо свойства, признака, отношения
у изучаемого объекта на основании
установления его сходства с другими
объектами, то этот вывод называют
умозаключением по аналогии. Ход такого
умозаключения можно представить
следующим образом. Пусть имеется,
например, два объекта: А и В. Известно,
что объекту А присущи свойства Р1,
Р2,
…, Рn,
Рn+1.
Изучение объекта В показало, что ему
присущи свойства Р1,
Р2,
…, Рn,
совпадающие соответственно со свойствами
объекта А. На основании сходства ряда
свойств (Р1,
Р2,
…, Рn)
у обоих объектов может быть сделано
предположение о наличии свойства Рn+1 у объекта В.
Ход такого
умозаключения можно представить
следующим образом. Пусть имеется,
например, два объекта: А и В. Известно,
что объекту А присущи свойства Р1,
Р2,
…, Рn,
Рn+1.
Изучение объекта В показало, что ему
присущи свойства Р1,
Р2,
…, Рn,
совпадающие соответственно со свойствами
объекта А. На основании сходства ряда
свойств (Р1,
Р2,
…, Рn)
у обоих объектов может быть сделано
предположение о наличии свойства Рn+1 у объекта В.
Степень
вероятности получения правильного
умозаключения по аналогии будет тем
выше: 1) чем больше известно общих свойств
у сравниваемых объектов; 2) чем существеннее
обнаруженные у них общие свойства и 3)
чем глубже познана взаимная закономерная
связь этих сходных свойств. При этом
нужно иметь в виду, что если объект, в
отношении которого делается умозаключение
по аналогии с другим объектом, обладает
каким-нибудь свойством, не совместимым
с тем свойством, о существовании которого
должен быть сделан вывод, то общее
сходство этих объектов утрачивает
всякое значение.
Существуют различные типы выводов по аналогии. Но общим для них является то, что во всех случаях непосредственному исследованию подвергается один объект, а вывод делается о другом объекте. Поэтому вывод по аналогии в самом общем смысле можно определить как перенос информации с одного объекта на другой. При этом первый объект, который собственно и подвергается исследованию, именуется моделью, а другой объект, на который переносится информация, полученная в результате исследования первого объекта (модели), называется оригиналом (иногда – прототипом, образцом и т.д.). Таким образом, модель всегда выступает как аналогия, т.е. модель и отображаемый с ее помощью объект (оригинал) находятся в определенном сходстве (подобии).
Под
моделированием понимается изучение
моделируемого объекта (оригинала),
базирующееся на взаимооднозначном
соответствии определенной части свойств
оригинала и замещающего его при
исследовании объекта (модели) и включающее
в себя построение модели, изучение ее
и перенос полученных сведений на
моделируемый объект – оригинал.
В зависимости от характера используемых в научном исследовании моделей различают несколько видов моделирования.
1. Мысленное (идеальное) моделирование. К этому виду моделирования относятся самые различные мысленные представления в форме тех или иных воображаемых моделей. Например, в идеальной модели электромагнитного поля Дж. Максвелла силовые линии представлялись в виде трубок, по которым течет воображаемая жидкость, не обладающая инерцией и сжимаемостью.
2. Физическое моделирование. Оно
характеризуется физическим подобием
между моделью и оригиналом и имеет целью
воспроизведение в модели процессов,
свойственных оригиналу. В настоящее
время физическое моделирование широко
используется для разработки и
экспериментального изучения различных
сооружений (плотин электростанций,
оросительных систем и т.п.), машин
(аэродинамические качества
самолетов, например, исследуются на их
моделях, обдуваемых воздушным потоком
в аэродинамической трубе), для лучшего
понимания каких-то природных явлений
и т. д.
д.
3. Символическое (знаковое) моделирование. Оно связано с условно-знаковым представлением каких-то свойств, отношений объекта-оригинала. Особой и очень важной разновидностью символического (знакового) моделирования является математическое моделирование. Взаимосвязи между различными величинами, описывающими функционирование исследуемого объекта или явления, могут быть представлены соответствующими уравнениями. Получившаяся система уравнений вместе с известными данными, необходимыми для ее решения (начальные условия, граничные условия, значения коэффициентов уравнений и т.п.), называется математической моделью явления.
4. Математическое
моделирование может применяться в
особом сочетании с физическим
моделированием. Такое сочетание,
именуемое вещественно-математическим (или предметно-математическим)
моделированием, позволяет
исследовать какие-то процессы в
объекте-оригинале, заменяя их изучением
процессов совсем иной природы (которые,
однако, описываются теми же математическими
соотношениями, что и исходные процессы). Так, механические колебания могут
моделироваться электрическими колебаниями
на основе полной идентичности описывающих
их дифференциальных уравнений.
Так, механические колебания могут
моделироваться электрическими колебаниями
на основе полной идентичности описывающих
их дифференциальных уравнений.
5. Численное моделирование на компьютере. Эта разновидность моделирования основывается на ранее созданной математической модели изучаемого объекта или явления и применяется в случаях больших объёмов вычислений, необходимых для исследования данной модели.
ЛЕКЦИЯ 2
2.4 Индукция
Возможно, вы видели метод доказательства от индукция перед. указано в аннотации или показано на простом примере, легко понять и кажется вряд ли стоит особого внимания. Тем не менее индукция является чрезвычайно мощный и тонкий метод доказательства. Мы будем использовать версию индукция, которая, вероятно, отличается от того, что вы видели до.
Определение 2.4.1 (аксиома индукции) Предположим, что $P(n)$ — формула, а $m$ и $k\ge 0$ фиксированы. целые числа. Предположим далее, что
1. $P(m), P(m+1),\ldots,P(m+k)$ истинны, и
$P(m), P(m+1),\ldots,P(m+k)$ истинны, и
2. для каждого $n>m+k$ импликация $P(m),\ldots,P(n-1)\Rightarrow P(n)$ допустим.
Тогда $P(n)$ верно для всех $n\ge m$. $\квадрат$
Когда $k=0$, это часто называют завершенным.
индукция . Ты
может быть более знаком с простейшей формой индукции, где $m=1$,
$k=0$, а импликация в (2) заменена на $P(n-1)\Rightarrow
П(п)$. Однако ясно, что эти формы индукции выражают одно и то же.
Основная идея: если какое-то утверждение о «малых» целых числах верно и если
зная, что утверждение верно с точностью до некоторого целого числа $n-1$ всегда
позволяет доказать, что оно верно для $n$, то утверждение должно
быть истинным для всех $n$ (точнее, для всех $n$, больших, чем «малое»
целые числа, с которых вы начали). По сути, индукция — это способ описания
бесконечное количество доказательств одновременно: как доказать $P(2)$
зная $P(1)$, как доказать $P(3)$ зная $P(1)$ и $P(2)$, как
доказать $P(4)$, зная $P(1)$, $P(2)$ и $P(3)$, и т. д. Этот
работает только в том случае, если все доказательства по существу одинаковы.
можно представить, что $P(n)$ верно для всех $n$, но доказательств много.
разные для разных значений $n$. В таком несчастном
обстоятельство, индукция не будет большой помощью.
9{n-1} я
= n+ {(n-1)n\более 2} = {n(n+1)\более 2}.
$$
$\qed$
д. Этот
работает только в том случае, если все доказательства по существу одинаковы.
можно представить, что $P(n)$ верно для всех $n$, но доказательств много.
разные для разных значений $n$. В таком несчастном
обстоятельство, индукция не будет большой помощью.
9{n-1} я
= n+ {(n-1)n\более 2} = {n(n+1)\более 2}.
$$
$\qed$
В этом примере используется простейшая индукция, поскольку $k=0$ и мы нужен только один случай, $P(n-1)$, гипотезы индукции. Мощность более общей формы что это позволяет нам предположить справедливость предложения для все значения меньше $n$, что очень полезно во многих доказательствах.
Пример 2.4.3 Каждое неотрицательное целое число либо четно, либо нечетно.
Доказательство. Мы хотим установить, что каждое неотрицательное $n$ может быть
выражается как $2q+r$, где $r=0$ (четный случай) или $r=-1$ (нечетный
случай). Применим индукцию с $m=0$ и $k=1$. Ясно, что $0=2\cdot 0$ и
$1=2\cdot1-1$. Теперь предположим, что $n\ge 2$ и что результат верен
для $0, 1,…, n-1$. Тогда $n-2\ge 0$, значит, существуют целые числа $q’$ и
$r$ такой, что $n-2=2q’+r$, где $r=0$ или $-1$. Установить $q=q’+1$; затем
$2q+r=2(q’+1)+r=2q’+r+2=(n-2)+2=n$, по желанию.$\qed$
Тогда $n-2\ge 0$, значит, существуют целые числа $q’$ и
$r$ такой, что $n-2=2q’+r$, где $r=0$ или $-1$. Установить $q=q’+1$; затем
$2q+r=2(q’+1)+r=2q’+r+2=(n-2)+2=n$, по желанию.$\qed$
Следующий результат является частью Основная теорема Арифметика ; посмотрим остальная часть доказательства в разделе 3.5.
Теорема 2.4.4 Каждое целое число $n\ge 2$ можно разложить на множители в произведение простых чисел.
Доказательство. Воспользуемся индукцией с $m=2$. Ясно, что $n=2$ может быть разложить на произведение простых чисел (оно уже простое), поэтому основание случай верный. Для шага индукции предположим, что $n>2$ и что Каждая из $2,\ldots,n-1$ может быть разложена на простые числа; нам нужно показать, что это означает, что $n$ также можно разложить на простые числа. Мы делим это на два случая: если $n$ — простое число, то оно уже факторизуется как желанный. Если $n$ не простое число, то оно разлагается как $a\cdot b$, где $2\ле а,б
Это доказательство очень естественно, потому что оно имитирует наиболее
люди на самом деле факторизовали бы число: Столкнувшись с такой проблемой, вы
вероятно, попытались бы каким-либо образом разложить число на множители, написав
$n=ab$. Если он не учитывается, он должен быть простым, и все готово. Ты
затем начните с этих меньших чисел $a$ и $b$ и попробуйте
фактор их. Каждый раз, когда вы выполняете эту операцию, множители получают
меньше, поэтому вы уверены, что в конечном итоге процесс должен остановиться.
Можно в таких обстоятельствах сказать что-то вроде этого кстати
доказательства: «Смотрите, просто продолжайте делать это, и в конце концов это прекратится, и
то результат верен». По сути, это доказательство по индукции, но
заявлено более неформально. В простых случаях такое доказательство может быть
приемлемо, но в более сложных условиях будет
труднее увидеть, что такой процесс работает. действительно лучше потренироваться
доказывая по индукции в формальной, «официальной» манере, так что
вы будете готовы писать и понимать более сложные доказательства.
9{n-1}$ для всех $n\ge 0$.
Если он не учитывается, он должен быть простым, и все готово. Ты
затем начните с этих меньших чисел $a$ и $b$ и попробуйте
фактор их. Каждый раз, когда вы выполняете эту операцию, множители получают
меньше, поэтому вы уверены, что в конечном итоге процесс должен остановиться.
Можно в таких обстоятельствах сказать что-то вроде этого кстати
доказательства: «Смотрите, просто продолжайте делать это, и в конце концов это прекратится, и
то результат верен». По сути, это доказательство по индукции, но
заявлено более неформально. В простых случаях такое доказательство может быть
приемлемо, но в более сложных условиях будет
труднее увидеть, что такой процесс работает. действительно лучше потренироваться
доказывая по индукции в формальной, «официальной» манере, так что
вы будете готовы писать и понимать более сложные доказательства.
9{n-1}$ для всех $n\ge 0$.
Пример 2.4.11 Многочлен неприводим , если его нельзя разложить на множители.
на два полинома строго меньшей степени. Показать, что любой
многочлен есть произведение неприводимых многочленов. (Подсказка: пусть
$P(n)$ — формула «все многочлены степени $n$ можно разложить на множители».
в произведение неприводимых многочленов».)
Показать, что любой
многочлен есть произведение неприводимых многочленов. (Подсказка: пусть
$P(n)$ — формула «все многочлены степени $n$ можно разложить на множители».
в произведение неприводимых многочленов».)
Пример 2.4.12 В круговом теннисном турнире, каждый игрок играет с каждым другим игроком один раз. Скажем, что «победителем» является любой игрок $x$ такой, что для любого другого игрока $y$ либо $x$ обыграл $y$, либо найдется игрок $z$ такой, что $x$ обыграл $z$ и $z$ побеждают $y$. В круговом турнире с участием не менее 2 игроков показать, что есть хотя бы один победитель.
Пример 2.4.13 Многоугольник на плоскости это выпуклая если отрезок, соединяющий любые две вершины, целиком содержится внутри полигона. С помощью индукции докажите, что сумма $n$ углов выпуклого многоугольника с $n$ вершинами равно $(n-2)\pi$. Можно предположить, что сумма углов треугольника равно $\пи$.
Стимулирование родов (для родителей) — Nemours KidsHealth
Для многих беременных женщин, особенно для тех, кто впервые родит ребенка, характерно наблюдать, как срок родов приходит и уходит без каких-либо схваток. Чем дальше от ожидаемой даты родов (называемой EDD), тем больше вы можете волноваться. Вы можете начать задаваться вопросом — а этот ребенок когда-нибудь родится?
Чем дальше от ожидаемой даты родов (называемой EDD), тем больше вы можете волноваться. Вы можете начать задаваться вопросом — а этот ребенок когда-нибудь родится?
Беременность на поздних сроках может быть сложной задачей — вы можете ощущать себя большой во всем теле, у вас могут болеть ступни и спина, у вас может не хватать энергии ни на что, и вы слишком готовы встретить малыша, которого вы взращивали. на этот раз. Вот почему ожидание немного дольше, чем вы ожидали, может быть особенно трудным.
Тем не менее, просрочка срока родов не гарантирует, что ваш врач (или другой поставщик медицинских услуг) предпримет какие-либо действия для стимуляции (или искусственного начала) родов — по крайней мере, не сразу.
Что это?
Стимуляция родов — это то, что врачи используют для облегчения родов с помощью лекарств или других медицинских методов. Несколько лет назад некоторые врачи обычно вызывали роды. Но теперь это обычно не делается, если в этом нет реальной медицинской необходимости. Родам обычно позволяют идти своим естественным путем. Однако в некоторых ситуациях врач может порекомендовать индукцию.
Родам обычно позволяют идти своим естественным путем. Однако в некоторых ситуациях врач может порекомендовать индукцию.
Почему это делается
Ваш врач может предложить индукцию, если:
- у вас отошли воды, но у вас нет схваток
- ваш ребенок все еще не появился на свет через 2 недели после даты родов (когда вы считаетесь переношенной — более 42 недель беременности)
- у вас инфекция матки (хориоамнионит)
- у вас есть определенные факторы риска (например, гестационный диабет или высокое кровяное давление)
- не хватает амниотической жидкости
- проблема с плацентой
- ребенок не растет должным образом
Индукция также может быть уместной при определенных обстоятельствах, например, в случае доношенной матери, у которой в анамнезе были быстрые роды или жизнь вдали от больницы.
Некоторые матери из соображений удобства обращаются за выборочной индукцией, но это сопряжено с риском. Врачи стараются избегать ранней стимуляции родов, потому что дата родов может быть неправильной и/или шейка матки может быть еще не готова.
Врачи стараются избегать ранней стимуляции родов, потому что дата родов может быть неправильной и/или шейка матки может быть еще не готова.
Page 2
Как это делается
Некоторые методы индукции менее инвазивны и несут меньший риск, чем другие. Способы, которыми врачи могут попытаться вызвать роды, вызывая схватки, включают:
- Удаление мембран. Врач надевает перчатку и вводит палец во влагалище и через шейку матки (отверстие, соединяющее влагалище с маткой). Он или она двигает пальцем вперед и назад, чтобы отделить тонкую мембрану, соединяющую амниотический мешок (в котором находится ребенок и амниотическая жидкость) со стенкой матки. Когда плодные оболочки отрываются, организм выделяет гормоны, называемые простагландинами, которые помогают подготовить шейку матки к родам и могут вызвать схватки. Этот метод работает для некоторых женщин, но не для всех.
- Отхождение вод (также называемое амниотомией). Врач разрывает амниотический мешок во время вагинального осмотра, используя небольшой пластиковый крючок для разрыва плодных оболочек.
 Если шейка матки готова к родам, амниотомия обычно вызывает роды в течение нескольких часов.
Если шейка матки готова к родам, амниотомия обычно вызывает роды в течение нескольких часов. - Введение гормона простагландина для созревания шейки матки. Гель или вагинальная вставка простагландина вводится во влагалище или принимается перорально в виде таблетки. Обычно это делается на ночь в больнице, чтобы шейка матки «созрела» (мягкая, истонченная) для родов. Вводимый отдельно простагландин может вызвать роды или может быть использован перед введением окситоцина.
- Введение гормона окситоцина для стимуляции схваток. Препарат (питоцин) вводят непрерывно внутривенно, начиная с небольшой дозы, а затем увеличивая ее до тех пор, пока роды не начнутся хорошо. После его введения необходимо тщательно наблюдать за плодом и маткой. Окситоцин также часто используется для стимулирования родов, которые идут медленно или застопорились.
На что это будет похоже?
Удаление плодных оболочек может быть немного болезненным или неприятным, хотя обычно это занимает около минуты. У вас также могут быть сильные судороги и кровянистые выделения на следующий день или два.
У вас также могут быть сильные судороги и кровянистые выделения на следующий день или два.
Также может быть немного неудобно, если у вас отошли воды. Вы можете почувствовать рывок, за которым следует теплая струйка или поток жидкости.
С простагландином у вас также могут быть сильные спазмы. При окситоцине схватки обычно более частые и регулярные, чем при естественных родах.
Стр. 3
Риски и меры предосторожности
Стимулирование родов не похоже на открытие крана. Если тело не готово, индукция может потерпеть неудачу, и после нескольких часов или дней попыток женщине может быть назначено кесарево сечение (кесарево сечение). Это более вероятно, если шейка матки еще не созрела.
Если врач разрывает амниотический мешок и роды не начинаются, может потребоваться другой метод стимуляции родов, поскольку существует риск инфицирования как матери, так и ребенка, если плодные оболочки разрываются задолго до рождения ребенка .
При использовании простагландина или окситоцина существует риск развития аномальных сокращений. В этом случае врач может удалить вагинальную вставку или уменьшить дозу окситоцина. Хотя это редко, при использовании этих препаратов увеличивается риск развития разрыва матки (разрыв матки). Другими осложнениями, связанными с применением окситоцина, являются низкое кровяное давление и низкий уровень натрия в крови (что может вызвать такие проблемы, как судороги).
В этом случае врач может удалить вагинальную вставку или уменьшить дозу окситоцина. Хотя это редко, при использовании этих препаратов увеличивается риск развития разрыва матки (разрыв матки). Другими осложнениями, связанными с применением окситоцина, являются низкое кровяное давление и низкий уровень натрия в крови (что может вызвать такие проблемы, как судороги).
Другим потенциальным риском стимуляции родов является рождение позднего недоношенного ребенка (рожденного после 34 и до 37 недель). Почему? Потому что дата родов (EDD) может быть неправильной. Ваш срок родов составляет 40 недель с первого дня последней менструации (LMP).
Дети, рожденные поздно, недоношенными, как правило, здоровы, но могут иметь временные проблемы, такие как желтуха, проблемы с кормлением, проблемы с дыханием или трудности с поддержанием температуры тела. У них также может быть больше шансов, чем у доношенных детей, иметь проблемы с развитием или учебой позже.
Несмотря на то, что индукция сопряжена с риском, срок беременности более 42 недель тоже может быть рискованным. Многие дети рождаются «переношенными» без каких-либо осложнений, но существуют следующие опасения:
Многие дети рождаются «переношенными» без каких-либо осложнений, но существуют следующие опасения:
- Роды через естественные родовые пути могут усложняться по мере того, как ребенок становится больше. По мере того, как дети становятся больше, увеличивается вероятность травм во время родов, таких как перелом кости.
- Состояние плаценты, обеспечивающей питание ребенка, ухудшается.
- Амниотическая жидкость может стать малой или содержать меконий — первый кал ребенка. Если ребенок вдыхает меконий, это может вызвать проблемы с дыханием.
Рассказы старых жен изобилуют способами стимулирования родов, такими как использование касторового масла. Небезопасно пытаться искусственно вызвать роды самостоятельно, принимая касторовое масло, что может привести к тошноте, диарее и обезвоживанию. А травы и травяные добавки, предназначенные для стимулирования родов, могут быть вредными. Стимуляция груди может вызвать сокращения матки, вызывая выброс окситоцина.

 Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P в будущем.
Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P в будущем.
 Таким образом, она подразумевает изучение каждого из объектов, входящих в класс, и нахождение на этой основе их общих характеристик. Однако в ряде случаев просто нет необходимости рассматривать абсолютно все предметы того или иного класса, в других случаях это невозможно сделать в силу необозримости класса изучаемых явлений или же в силу ограниченности человеческой практики. В таких ситуациях применяют неполную индукцию.
Таким образом, она подразумевает изучение каждого из объектов, входящих в класс, и нахождение на этой основе их общих характеристик. Однако в ряде случаев просто нет необходимости рассматривать абсолютно все предметы того или иного класса, в других случаях это невозможно сделать в силу необозримости класса изучаемых явлений или же в силу ограниченности человеческой практики. В таких ситуациях применяют неполную индукцию.
 Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
 Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода.
Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода.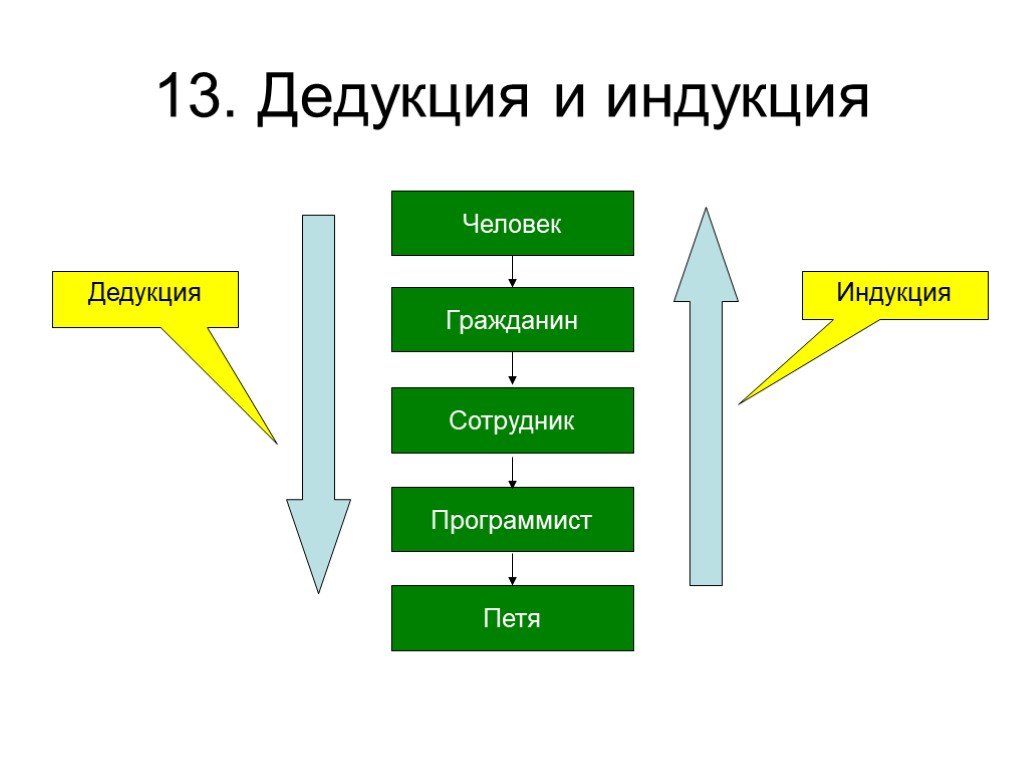

 Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.
Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.
 Лекции по истории логики. — М., 1963.
Лекции по истории логики. — М., 1963. Его сфера и границы. — М., 1957.
Его сфера и границы. — М., 1957. — P., 1961.
— P., 1961. Если шейка матки готова к родам, амниотомия обычно вызывает роды в течение нескольких часов.
Если шейка матки готова к родам, амниотомия обычно вызывает роды в течение нескольких часов.