Решение уравнений с модулем методом интервалов
Уравнения с несколькими модулями в одной части
Чем больше модулей, тем больше приходиться их раскрывать и тем больше получается различных уравнений. Когда модулей один или два — это не сложно. Сложность возникает когда модулей больше двух. Человек может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.
Давайте решим следующее уравнение:
|x − 5| − |x| = 1
У данного уравнения два модуля в левой части. Оно решается путем раскрытия модулей. Не будем комментировать решение, а сразу приведём его:
Такой вид уравнения удобнее решать методом интервалов (или более точно — методом промежутков). Суть этого метода в том, чтобы разбить координатную прямую на несколько промежутков, а затем решить уравнение на каждом из этих промежутков. Модули исходного уравнения на каждом промежутке будут раскрываться по разному.
Решим уравнение |x − 5| − |x| = 1 методом интервалов.
Для начала нарисуем координатную прямую и обозначим её как x
Если координатная прямая содержит все числа, которые существуют в природе, то логично что она содержит и корни нашего уравнения.
Теперь надо разбить координатную прямую на промежутки. Для этого сначала нужно найти на ней те точки, на которых модули нашего уравнения будут менять свой порядок раскрытия. То есть, найти точки перехода для модулей |x − 5| и |x|.
Чтобы найти точки перехода, нужно выяснить при каких значениях x подмодульные выражения равны нулю. Узнать это можно приравняв к нулю подмодульные выражения обоих модулей, и решить обычные линейные уравнения:
Для модуля |x − 5| точкой перехода будет 5. Для модуля |x| точкой перехода будет 0.
Теперь отметим точки перехода на координатной прямой. Мéньшие числа нужно отмечать левее, большие числа правее:
Проведем дуги от точек перехода:
С помощью неравенств подпишем каждый промежуток. Получится три промежутка: от минус бесконечности до нуля, от нуля до пяти, и от пяти до плюс бесконечности. То есть: x < 0, 0 ≤ x < 5 и x ≥ 5
Получится три промежутка: от минус бесконечности до нуля, от нуля до пяти, и от пяти до плюс бесконечности. То есть: x < 0, 0 ≤ x < 5 и x ≥ 5
Обратите внимание, что в первом промежутке x < 0 значение 0 не включено в данный промежуток. Но зато это значение включено во второй промежуток 0 ≤ x < 5.
Во втором же промежутке 0 ≤ x < 5 значение 5 не включено в данный промежуток, но зато оно включено в третий промежуток x ≥ 5.
Проще говоря, каждый промежуток включает в себя левый конец, и не включает правый. Сделано это специально, чтобы не допустить потерь значений переменной x. Описать с помощью неравенств нужно все значения на координатной прямой, не допуская их потерь.
Включение левого конца в рассматриваемый промежуток и исключение его из правого это лишь общепринятое правило. На самом деле концы рассматриваемого промежутка можно включать в любой из соседствующих промежутков. Например, значение 0 можно было включить в первый промежуток. Тогда он принял бы вид x ≤ 0, а второй промежуток принял бы вид 0 < x < 5, потому что ноль уже был включен в первый промежуток.
Например, значение 0 можно было включить в первый промежуток. Тогда он принял бы вид x ≤ 0, а второй промежуток принял бы вид 0 < x < 5, потому что ноль уже был включен в первый промежуток.
Но лучше всего исходить из ситуации, потому что в каких-то случаях левый конец промежутка целесообразнее исключить из рассматриваемого промежутка и включить его в правый конец соседнего промежутка. Об этом мы поговорим позже.
Теперь выясним как будут вести себя модули |x − 5| и |x| на каждом из этих промежутков. От этого будет зависеть то, как они будут раскрываться.
Начнем с первого промежутка x < 0.
Если x < 0, то при любом значении x на данном промежутке подмодульное выражение x − 5 станет отрицательным, а значит модуль |x − 5| на промежутке x < 0 будет раскрываться со знаком минус. Второй модуль |x| на промежутке x < 0 тоже будет раскрываться со знаком минус.
В результате после раскрытия модулей на промежутке x < 0 уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) + x = 1
Второй модуль |x| на промежутке x < 0 раскрылся с минусом. В самом же уравнении |x − 5 |− |x| = 1 после выражения |x − 5| тоже располагался минус. В математике два минуса, идущие подряд, дают плюс. Поэтому и получилось выражение −(x − 5) + x = 1.
Решим уравнение −(x − 5) + x = 1, которое получилось после раскрытия модулей на промежутке x < 0
Это уравнение решений не имеет. Значит на промежутке x < 0 исходное уравнение не имеет корней. Проще говоря, корень уравнения не является числом меньшим нуля.
Следующий промежуток, на котором нужно решить уравнение это промежуток 0 ≤ x < 5.
Если x больше или равно нулю, но меньше пяти, то подмодульное выражение x − 5, станет отрицательным, а значит модуль |x − 5| на промежутке 0 ≤ x < 5 будет раскрываться со знаком минус. Второй модуль |x| на промежутке 0 ≤ x < 5 будет раскрываться с плюсом.
Второй модуль |x| на промежутке 0 ≤ x < 5 будет раскрываться с плюсом.
В результате после раскрытия модулей на промежутке 0 ≤ x < 5 уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) − x = 1
Решим это уравнение:
Получили корень 2. Чтобы проверить действительно ли это число является корнем исходного уравнения, нужно посмотреть принадлежит ли это число рассматриваемому промежутку 0 ≤ x < 5. Принадлежит? Да. Значит число 2 является корнем уравнения |x − 5| − |x| = 1. Проверка также показывает это:
Следующий промежуток, который нужно рассмотреть это промежуток x ≥ 5.
Если x больше или равно пяти, то модуль |x − 5| на промежутке x ≥ 5 будет раскрываться со знаком плюс. Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.
Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.
В результате после раскрытия модулей на промежутке x ≥ 5 уравнение с модулем |x − 5| − |x| = 1 примет вид x − 5 − x = 1.
Решим это уравнение:
Это уравнение не имеет решений. Значит на промежутке x ≥ 5 исходное уравнение корней не имеет. Проще говоря, корень уравнения не является числом, бóльшим либо равным пяти.
В итоге корнем уравнения является число 2, которое мы нашли решив исходное уравнение на промежутке 0 ≤ x < 5.
Ответ: 2.
Пример 2. Решить уравнение |x − 3| + |x + 2| = 7
Решение
Шаг 1. Находим точки перехода для модулей |x − 3| и |x + 2|
Шаг 2. Отметим на координатной прямой найденные точки перехода и выделим получившиеся промежутки:
Шаг 3.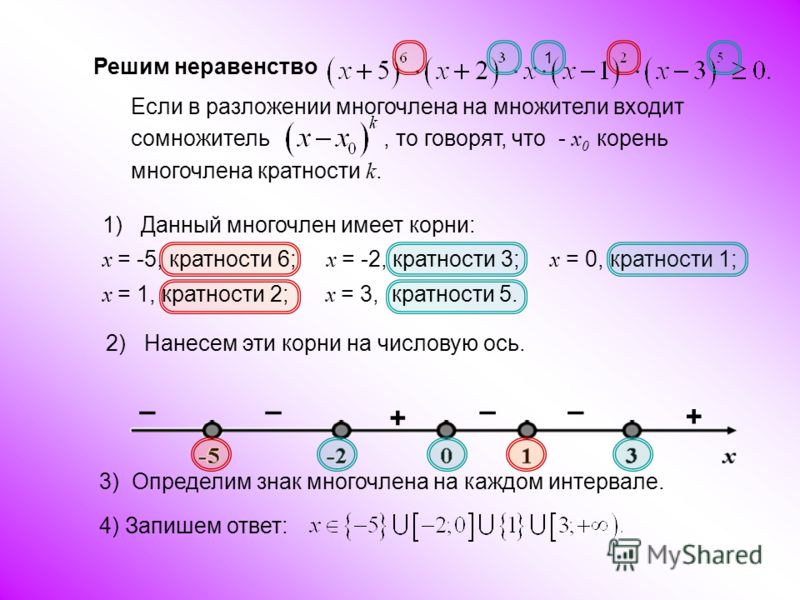 Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.
Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.
На промежутке x < −2 модуль |x − 3| будет раскрываться с минусом. Можно проверить это, подставив в данный модуль любое число из промежутка x < −2. Например, числа −4 или −9
|x − 3| = |−4 − 3| = |−7| = −(−7) = 7
|x − 3| = |−9 − 3| =|−12| = −(−12) = 12
Следующий модуль |x + 2| на промежутке x < −2 тоже будет раскрываться с минусом. Убедимся в этом подставив любые два числа из промежутка x < −2 в подмодульное выражение. Например, числа −6 и −8
|x + 2| = |−6 + 2| = |−4| = −(−4) = 4
|x + 2| = |−8 + 2| = |−6| = −(−6) = 6
Значит после раскрытия модулей на промежутке x < −2 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:
−x + 3 − x − 2 = 7
Решим его:
Обязательно нужно проверить входит ли найденный корень −3 в рассматриваемый промежуток x < −2. Для этого нужно подставить в неравенство x < −2 найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3 < −2 верно, значит корень −3 входит в промежуток x < −2 и соответственно является корнем исходного уравнения.
Для этого нужно подставить в неравенство x < −2 найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3 < −2 верно, значит корень −3 входит в промежуток x < −2 и соответственно является корнем исходного уравнения.
На следующем промежутке −2 ≤ x < 3 модуль |x − 3| будет раскрываться с минусом, а модуль|x + 2| будет раскрываться с плюсом.
Значит после раскрытия модулей на промежутке −2 ≤ x < 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:
−x + 3 + x + 2 = 7
Решим это уравнение:
Это уравнение не имеет решений, значит на промежутке −2 ≤ x < 3 исходное уравнение тоже не имеет решений (корней).
Наконец рассмотрим промежуток x ≥ 3
На промежутке x ≥ 3 модуль |x − 3| будет раскрываться с плюсом. Модуль|x + 2| так же будет раскрываться с плюсом. Значит на промежутке x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:
Модуль|x + 2| так же будет раскрываться с плюсом. Значит на промежутке x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:
x − 3 + x + 2 = 7
Решим это уравнение:
Этот корень входит в рассматриваемый промежуток x ≥ 3, значит является корнем исходного уравнения. Проверка также показывает это:
Ответ: −3 и 4.
Пример 3. Решить уравнение |2x − 3| + |2x + 7| = 16
Решение
Найдём точки перехода для модулей |2x − 3| и |2x + 7|
Отметим точки перехода на координатной прямой. Меньшие числа нужно отмечать левее, большие правее:
Решим исходное уравнение |2x − 3| + |2x + 7| = 16 на промежутке . Оба модуля на этом промежутке будут раскрываться с минусом:
Оба модуля на этом промежутке будут раскрываться с минусом:
Корень −5 принадлежит промежутку , значит является корнем исходного уравнения.
Теперь решим исходное уравнение на промежутке . Модуль |2x − 3| на этом промежутке раскрывается с минусом, а модуль |2x + 7| — с плюсом:
Видим, что на промежутке исходное уравнение не имеет решений (корней).
Теперь решим исходное уравнение на промежутке . Оба модуля на данном промежутке раскрываются с плюсом:
Корень 3 принадлежит промежутку , значит является корнем исходного уравнения.
Ответ: −5 и 3.
Пример 4. Решить уравнение |x − 2| + 3x = |x − 5| − 18
Решение
Найдём точки перехода для модулей |x − 2| и |x − 5|
Отметим точки перехода на координатной прямой:
Решим исходное уравнение на промежутке x < 2. Модули |x − 2| и |x − 5| на этом промежутке раскрываются с минусом:
Модули |x − 2| и |x − 5| на этом промежутке раскрываются с минусом:
Число −5 принадлежит промежутку x < 2, значит является корнем исходного уравнения.
Решим исходное уравнение на промежутке 2 ≤ x < 5. Модуль |x − 2| на этом промежутке раскрывается с плюсом, а модуль |x − 5| — с минусом:
Число не принадлежит промежутку 2 ≤ x < 5, значит не является корнем исходного уравнения.
Решим исходное уравнение на промежутке x ≥ 5. Модули |x − 2| и |x − 5| на этом промежутке будут раскрываться с плюсом:
Число −7 не принадлежит промежутку x ≥ 5, значит не является корнем исходного уравнения.
Ответ: −5
Пример 5. Решить уравнение |x| + |x − 7| + 2|x − 4| = 2
Решение
Найдём точки перехода для модулей |x|, |x − 7| и |x − 4|
Отметим точки перехода на координатной прямой:
Решим исходное уравнение на промежутке x < 0. Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с минусом:
Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с минусом:
Число не принадлежит промежутку x < 0, значит не является корнем исходного уравнения.
Решим теперь исходное уравнение на промежутке 0 ≤ x < 4. Модуль |x| на этом промежутке раскрывается с плюсом, а модули |x − 7| и |x − 4| — с минусом:
Число не принадлежит промежутку 0 ≤ x < 4, значит не является корнем исходного уравнения.
Решим теперь исходное уравнение на промежутке 4 ≤ x < 7. Модуль |x| на этом промежутке раскрывается с плюсом; модуль |x − 7| — с минусом; модуль |x − 4| — с плюсом:
Число не принадлежит промежутку 4 ≤ x < 7, значит не является корнем исходного уравнения.
Решим исходное уравнение на промежутке x ≥ 7. Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с плюсом:
Число не принадлежит промежутку x ≥ 7, значит не является корнем исходного уравнения.
Решив исходное уравнение на каждом промежутке, мы не нашли корней, удовлетворяющих этому уравнению. Значит данное уравнение не имеет корней.
В ответе можно написать словами, что корней нет (или решений нет), либо указать символ пустого множества. Этот символ будет указывать, что множество корней уравнения |x| + |x − 7| + 2|x − 4| = 2 пусто.
Ответ: ø.
Пример 6. Решить уравнение
Решение
Найдём точки перехода для модулей и
Если методом интервалов нужно решить уравнение с модулем, который в свою очередь содержит внутри себя другой модуль, то точки перехода надо искать для случаев: когда внутренний модуль раскрывается с плюсом и когда он раскрывается с минусом. Точки перехода будут меняться в зависимости от этих случаев. Давайте посмотрим как это происходит.
Точки перехода будут меняться в зависимости от этих случаев. Давайте посмотрим как это происходит.
Если у модуля внутренний модуль раскроется с плюсом, то есть если 2x − 1 ≥ 0 (что равносильно ), то исходное уравнение примет вид |2x − 1 − 5| + x = |6 − x|. Здесь и далее надо учесть, что внутренний модуль будет раскрываться с плюсом при тех значениях x, которые будут больше либо равны . Отметим эту точку на координатной прямой.
Теперь найдем точки перехода. Поскольку исходное уравнение приняло вид |2x − 1 − 5| + x = |6 − x|, то точки перехода надо найти для модулей |2x − 1 − 5| и |6 − x|.
Для модуля |2x − 1 − 5| точкой перехода будет число 3, а для модуля |6 − x| — число 6. Отметим эти числа на той же координатной прямой где мы отметили точку
Сейчас нас интересуют только те значения x, которые удовлетворяют условию , потому что только при этом условии внутренний модуль исходного уравнения раскрывается с плюсом. Поэтому рассматривать промежуток мы не будем. Рассмотреть нужно те промежутки где x удовлетворяет условию
Поэтому рассматривать промежуток мы не будем. Рассмотреть нужно те промежутки где x удовлетворяет условию
Первый промежуток на котором мы будем решать уравнение это . На нем модуль |2x − 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом:
Получили тождество — равенство верное при любом значении x. В данном случае решением исходного уравнения является любое число из промежутка . Любое число из этого промежутка также удовлетворяют условию
Теперь решим исходное уравнение на промежутке 3 ≤ x < 6. Оба модуля на этом промежутке раскрываются с плюсом. Тогда:
Корень 3 принадлежит рассматриваемому промежутку. Также этот корень удовлетворяет условию , согласно которому внутренний модуль исходного уравнения раскрывается с плюсом.
Теперь решим исходное уравнение на промежутке x ≥ 6. На этом промежутке модуль |2x − 1 − 5| раскрывается с плюсом, а модуль |6 − x| с минусом. Тогда:
Тогда:
Корень 0 не удовлетворяет условию x ≥ 6, значит на данном промежутке исходное уравнение корней не имеет.
Итак, если внутренний модуль уравнения раскрывается с плюсом, то решениями уравнения являются: промежуток , а также число 3. Запишем эти решения одним промежутком:
Теперь решим исходное уравнение для случая когда внутренний модуль раскрывается с минусом. То есть когда 2x − 1 < 0 (что равносильно неравенству ). В этом случае исходное уравнение примет вид:
|−2x + 1 − 5| + x = |6 − x|
Отметим точку на координатной прямой.
Нас будут интересовать те значения x которые располагаются слева от . Это те значения при которых внутренний модуль исходного уравнения раскрывается с минусом.
Найдем точки перехода для модулей |−2x + 1 − 5| и |6 − x|. Для первого модуля это число −2, для второго модуля — число 6
Рассматривать будем только те промежутки, которые располагаются слева от . Только при них внутренний модуль исходного уравнения раскрывается с минусом
Только при них внутренний модуль исходного уравнения раскрывается с минусом
Решим уравнение на промежутке x < −2. На этом промежутке оба модуля раскрываются с плюсом. Тогда:
Это уравнение решений не имеет. Значит на промежутке x < −2 исходное уравнение не имеет корней.
Решим теперь уравнение на промежутке . Замечаем, что при подстановке левого конца этого промежутка (числа −2) в модуль |−2x + 1 − 5| данный модуль раскрывается с плюсом, а при остальных значениях промежутка модуль |−2x + 1 − 5| раскрывается с минусом.
Поэтому число −2 разумнее включить в промежуток x < −2, который мы уже рассмотрели. На промежутке x < −2 модуль раскрывался с плюсом, и при включении числа −2 в данный промежуток, он также будет раскрываться с плюсом.
На промежутке модуль |−2x + 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом. Тогда:
Тогда:
Получится корень который не удовлетворяет условию . Несмотря на это число является корнем исходного уравнения, потому что мы получили его когда решали уравнение для случая 2x − 1 ≥ 0.
Задания для самостоятельного решения
Примечание: Решения, не удовлетворяющие исходному уравнению, подчёркнуты красным.
Задание 1. Решить уравнение:
Решение:
Ответ: x ∈ [−5 ; 3].
Показать решение
Задание 2. Решить уравнение:
Решение:
Ответ: x ∈ [3 ; +∞).
Показать решение
Задание 3. Решить уравнение:
Решение:
Ответ: корней нет.
Показать решение
Задание 4. Решить уравнение:
Решение:
Ответ: , 0.
Показать решение
Задание 5. Решить уравнение:
Решение:
Ответ: −5.
Показать решение
Задание 6. Решить уравнение:
Решение:
Ответ: −4, 2.
Показать решение
Задание 7. Решить уравнение:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Метод интервалов – универсальный метод решения неравенств с модулем
Репетиторы ❯ Математика ❯ Метод интервалов – универсальный метод решения неравенств с модулем
Автор: Ольга Л., онлайн репетитор по математике
●
21. 10.2011
10.2011
Раздел: Математика
Чем больше человек понимает, тем сильнее в нем желание понимать
Фома Аквинский
Метод интервалов позволяет решать любые уравнения, содержащие модуль. Суть этого метода в том, чтобы разбить числовую ось на несколько участков (интервалов), причем разбить ось нужно именно нулями выражений, стоящих в модулях. Затем на каждом из получившихся участков всякое подмодульное выражение либо положительно, либо отрицательно. Поэтому каждый из модулей может быть раскрыт или со знаком минус, или со знаком плюс. После этих действий остается лишь решить каждое из полученных простых уравнений на рассматриваемом интервале и объединить полученные ответы.
Рассмотрим данный метод на конкретном примере.
|x + 1| + |2x – 4| – |x + 3| = 2x – 6.
1) Найдем нули выражений, стоящих в модулях. Для этого нужно приравняем их к нулю, и решить полученные уравнения.
x + 1 = 0 2x – 4 = 0 x + 3 = 0
x = -1 2x = 4 x = -3
x = 2
2) Расставим получившиеся точки в нужном порядке на координатной прямой. Они разобьют всю ось на четыре участка.
3) Определим на каждом из получившихся участков знаки выражений, стоящих в модулях. Для этого подставляем в них любые числа с интересующих нас интервалов. Если результат вычислений – число положительное, то в таблице ставим «+», а если число отрицательное, то ставим «–». Это можно изобразить так:
4) Теперь будем решать уравнение на каждом из четырех интервалов, раскрывая модули с теми знаками, которые проставлены в таблице. Итак, рассмотрим первый интервал:
I интервал (-∞; -3). На нем все модули раскрываются со знаком «–». Получим следующее уравнение:
-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:
Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:
-x – 1 – 2x + 4 + x + 3 = 2x – 6
-4x = -12
x = 3.
Полученный ответ не входит в рассматриваемый интервал, поэтому в окончательный ответ писать его не надо.
II интервал [-3; -1). На этом интервале в таблице стоят знаки «–», «–», «+». Именно так и раскрываем модули исходного уравнения:
-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Упростим, раскрыв при этом скобки:
-x – 1 – 2x + 4 – x – 3 = 2x – 6. Приведем в полученном уравнении подобные:
-5x = -6
x = 6/5. Полученное число не принадлежит рассматриваемому интервалу, поэтому оно не является корнем исходного уравнения.
III интервал [-1; 2). Раскрываем модули исходного уравнения с теми знаками, которые стоят на рисунке в третьей колонке. Получаем:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Избавимся от скобок, перенесем слагаемые, содержащие переменную x в левую часть уравнения, а не содержащие x в правую. Будем иметь:
Будем иметь:
x + 1 – 2x + 4 – x – 3 = 2x – 6
-4x = -8
x = 2.
В рассматриваемый интервал число 2 не входит.
IV интервал [2; +∞). Все модули раскрываем со знаком «+». Получим:
(x + 1) + (2x – 4) – (x + 3) = 2x – 6.
x + 1 + 2x – 4 – x – 3 = 2x – 6
0 = 0.
После преобразований уравнение превратилось в верное равенство. Это говорит о том, что любое число из рассматриваемого интервала будет являться решением исходного уравнения. Значит ответом, как на этом интервале, так и во всем уравнении является множество чисел, удовлетворяющих условию x ≥ 2.
Ответ: x ≥ 2.
Метод интервалов хоть и является универсальным методом решения уравнений с модулем, его применение не всегда оправдано. Порой решить уравнение выходит гораздо быстрее, используя, например, определение модуля или какие-то другие методы.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/vOuj6t2Zyeg» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ElMEic2MJ-U» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/FTtp-vAv3lI» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/7LD4euDcivY» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ZfNUaigadEY» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/NXwmZ4aXXsQ» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/WIbBf3NZEZI» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/dihxr1liTvQ» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/vOuj6t2Zyeg» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ElMEic2MJ-U» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Решение модульных уравнений методом интервалов
Модульное уравнение — сложная тема для начинающих. Имея это в виду, в этот урок будут включены только элементарные уравнения.
Что такое уравнение с модулем и как его решить?
В уравнениях с модулем неизвестное значение содержится под знаком модуля. Например:
| х — 2 | = 5
Уравнения модуля бывают разных форм и решаются разными методами. Нельзя сказать, что какой-то один метод самый рациональный. Все зависит от исходного уравнения.
Например, в одних уравнениях можно просто угадать корень, а в других приходится логически мыслить, решать модули и выполнять тождественные преобразования. Человек волен выбирать, какой метод решения использовать.
Человек волен выбирать, какой метод решения использовать.
Например, решите приведенное выше уравнение |x — 2| = 5. Предположим, мы не знаем никакого метода ее решения. Как бы мы решили это?
Прежде всего, обратите внимание, что правая часть этого уравнения равна числу 5. В левой части находится модуль выражения |x — 2|. Это означает, что подмодульное выражение x — 2 должно равняться числу 5 или -5
Итак, вам необходимо выяснить, при каких значениях переменной x подмодульное выражение x — 2 превратится в число 5 или -5.
Значения x можно найти, приравняв субмодульное выражение к числам 5 и -5, а затем решив каждое из уравнений по очереди:
Таким образом, корни уравнения |x — 2| = 5 это числа 7 и -3.
Большинство элементарных уравнений с модулями можно решить с помощью правила разложения по модулю. Для этого модуль, содержащийся в уравнении, раскладывается, затем полученное выражение подставляется в исходное уравнение на место выражения по модулю.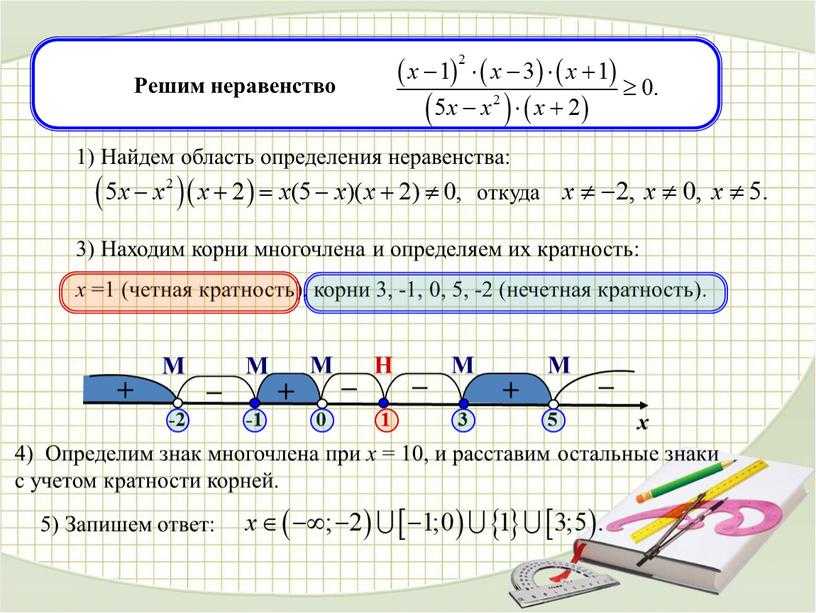
Нужно решить модуль для каждого случая: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.
Решите наше уравнение |x — 2| = 5 с использованием правила расширения модуля. Выпишите его модуль отдельно и решите:
Эта конструкция говорит о том, что если подмодульное выражение х — 2 больше или равно нулю, то модуль развернется как х — 2, и тогда исходное уравнение примет вид образуют х — 2 = 5, где х = 7
А если субмодульное выражение x — 2 меньше нуля, то модуль расширяется до -(x — 2). Тогда исходное уравнение будет -(x — 2) = 5, где x = -3
Итак, уравнение |x — 2|= 5 имеет корни 7 и -3. Для проверки подставьте в исходное уравнение вместо x числа 7 и -3. Тогда мы получим правильное уравнение:
Субмодульное выражение обычно содержит x, который может преобразовать все субмодульное выражение либо в положительное число, либо в отрицательное число, либо в ноль.
Поэтому модуль выявляется для каждого случая: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый случай даст независимое уравнение со своим корнем.
Вернемся теперь к тому моменту, когда мы выставляли модуль:
Условия x — 2 ≥ 0 и x — 2 < 0 являются неравенствами, которые можно решить, тем самым приведя их к простой форме:
Символ ⇔ обозначает эквивалентность. В этом случае уточняется, что условие x — 2 ≥ 0 эквивалентно условию x ≥ 2, а условие x — 2 < 0 эквивалентно условию x < 2.
Такая запись состояния позволяет однозначно сказать, при каком x модуль будет открываться с плюсом, а при каком с минусом.
В первом случае выполняется условие x ≥ 2. Это означает, что для всех x, больших или равных 2, модуль |x — 2| будет расширяться с плюсом. Таким образом, для x = 7 субмодульное выражение принимает вид 5
|7 − 2| = |5|
Это означает, что дальнейшее раскрытие информации будет положительным моментом
|7 − 2| = |5| = 5
Модуль |x — 2| так же будет вести себя и с другими значениями x на интервале x ≥ 2. То есть расширится в плюс. Примеры:
То есть расширится в плюс. Примеры:
Когда x = 3, |3 − 2|=|1| = 1
Когда x = 4, |4 − 2|=|2| = 2
Когда x = 2, |2 − 2|=|0| = 0
Когда x = 13, |13 − 2|=|11| = 11
А во втором случае получается условие x < 2. Это означает, что для всех x меньше 2 модуль будет расширяться с минусом. Например, если x = -3, то подмодульное выражение снова будет 5. Но в промежуточных вычислениях мы видим, что модуль расширяется с минусом:
|−3 − 2| = |−5| = −(−5) = 5
Модуль |x — 2| будет вести себя так же с другими значениями x на интервале x < 2. Примеры:
Когда x = 1, |1 − 2|=|−1| = −(−1) = 1
Когда x = 0, |0 − 2|=|−2| = −(−2) = 2
Когда x = −1, |−1 − 2|=|−3| = −(−3) = 3
Когда x = −9,|−9 − 2|=|−11| = −(−11) = 11
Число 2 является своего рода точкой перехода, в которой модуль |x — 2| меняет порядок открытия.
Вы можете себе представить, как модуль |x — 2| двигались по маршруту от минус бесконечности до числа 2, открываясь в каждой точке с минусом. Оказавшись в точке 2, модуль изменил порядок открытия, а именно, открывшись в точке 2 с плюсом, он потом стал открываться с плюсом, переместившись в правую сторону до плюс бесконечности.
Используя координатную линию, это можно представить следующим образом:
Красные знаки минус и плюс показывают, как модуль |x — 2| будет разворачиваться через интервалы x < 2 и x ≥ 2,
Точка перехода может быть найдена для любого модуля. Для этого нужно выяснить, при каком x подмодульное выражение равно нулю. Нуль — это значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила разложения модуля:
В этом примере в момент, когда x становится равным нулю, модуль |x| расширяется с плюсом, а затем для всех x больше нуля расширяется с плюсом. Напротив, для всех x меньше нуля модуль откроется с минусом:
Например, для модуля |2x + 6| точка перехода будет равна -3, потому что если вместо x заменить 2x + 6, подмодульное выражение станет равным нулю. Проиллюстрируем это на рисунке:
Проиллюстрируем это на рисунке:
Для всех x, больших или равных -3, модуль будет расширяться с плюсом. Примеры:
Когда x = -3, |2 × (-3) + 6| = |0| = 0
Когда x = 4, |2 × 4 + 6| = |14| = 14.
Когда x = 5, |2 × 5 + 6| = |16| = 16.
И для всех х меньше 3 модуль будет расширяться с минусом. Примеры:
Когда x = -4, |2 × (-4) + 6| = |-2| = -(-2) = 2
Когда x = -5, |2 × (-5) + 6| = |-4| = -(-4) = 4
Когда x = -6, |2 × (-6) + 6| = |-6| = -(-6) = 6
Пример 2. Решить уравнение |x| + 3x = -2
Решение
Разложим модуль, содержащийся в левой части уравнения:
Если x ≥ 0, то модуль разложится со знаком плюс и тогда исходное уравнение будет иметь вид как х + 3х = -2. Решите это уравнение немедленно:
Теперь рассмотрим второй случай — когда x < 0. В этом случае модуль в исходном уравнении расширяется со знаком минус, и тогда получается уравнение -x + 3x = -2. Решим и это уравнение:
Решим и это уравнение:
Получили корни
и −1.
Проверим, подставив найденные корни в исходное уравнение. Проверяем корень
Мы видим, что при подстановке корня из
исходное уравнение не превращается в правильное равенство. Итак, не является корнем исходного уравнения.
Теперь проверим корень из -1
Мы получили верное равенство. Таким образом, из двух найденных решений только -1 является корнем уравнения.
Ответ: -1.
Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности вашего решения, нужно проверить, подставив найденные корни в исходное уравнение.
Кроме того, вы можете проверить, является ли найденное значение корнем уравнения, проверив условие, согласно которому был расширен модуль.
Например, в этом примере мы расширили модуль |x| для случаев, когда выражение подмодуля больше или равно нулю и когда выражение подмодуля меньше нуля:
Условия x≥0 и x<0 являются неравенствами. В эти неравенства можно подставить найденные корни. Если неравенства верны, то корни удовлетворяют исходному уравнению.
Итак, если вы расширите модуль со знаком плюс, вы получите уравнение x + 3x = -2. Корень этого уравнения равен
. Это число не удовлетворяет условию x ≥ 0, согласно которому модуль |x| было решено и согласно которому было получено уравнение x + 3x = -2. Действительно, подстановка числа в неравенство x ≥ 0 приводит к неверному неравенству.
А если разложить модуль со знаком минус, получится уравнение -х + 3х = -2. Корень этого уравнения равен -1. Это число удовлетворяет условию x<0, согласно которому модуль |x| было решено и согласно которому было получено уравнение -x + 3x = -2. Действительно, подстановка числа -1 в неравенство x < 0 приводит к правильному неравенству.
Пример 3. Решите уравнение |1 — 2x| — 4x = -6
Решение
Расширим модуль:
Если раскроем модуль |1 — 2x| со знаком плюс получаем уравнение 1 — 2х — 4х = -6. Решите:
Если мы расширим модуль |1 — 2x| со знаком минус получаем уравнение -1 + 2х — 4х = -6. Решаем:
Получили корни
и .
Корень
не удовлетворяет условию , поэтому не является корнем исходного уравнения.
Корень
удовлетворяет условию , поэтому является корнем исходного уравнения. Проверка также покажет это:
Ответ :
.
Пример 4. Решить уравнение | x 2 − 3 x | = 0
Решение
Если модуль числа равен нулю, то выражение подмодуля также равно нулю:
То есть расширять модуль не нужно. Достаточно выяснить, при каких значениях x подмодульное выражение равно нулю. В этом случае нужно решить неполное квадратное уравнение:
Достаточно выяснить, при каких значениях x подмодульное выражение равно нулю. В этом случае нужно решить неполное квадратное уравнение:
Получились корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает следующее:
Пример 5. Решите уравнение x 2 − 5| х | + 6 = 0
Выпишем модуль |x| отдельно и разверните его:
Если расширить модуль |x| со знаком плюс исходное уравнение будет иметь вид х2 — 5х + 6 = 0. Это квадратное уравнение. Решите его с помощью дискриминанта:
Оба корня удовлетворяют условию x ≥ 0, поэтому они являются корнями исходного уравнения.
Если расширить модуль |x| со знаком минус исходное уравнение будет иметь вид x 2 + 5 x + 6 = 0. Это тоже квадратное уравнение. Решите как предыдущую:
При условии x ≥ 0 модуль уравнения расширился с плюсом, что дало корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0, поэтому они также удовлетворяют исходному уравнению.
Оба корня удовлетворяют условию x ≥ 0, поэтому они также удовлетворяют исходному уравнению.
При условии x < 0 модуль уравнения расширился с минусом, что привело к корням -2 и -3. Оба корня удовлетворяют условию x < 0, поэтому они также удовлетворяют исходному уравнению.
Ответ: 3, 2, -2 и -3.
Преобразование уравнения с модулем в набор
Большинство элементарных уравнений с модулем можно решить, сведя их к так называемому набору уравнений .
Элементарными будем называть уравнения с модулем, в которых левая часть является модулем некоторого выражения, а правая часть — числом. Например, |х| = 3 или |2x — 1| = 3.
Решите наше самое первое уравнение |x — 2| = 5, сведя его к системе уравнений. Корнями этого уравнения были числа 7 и -3. Это уравнение также считается элементарным.
Если расширить модуль |x — 2| со знаком плюс уравнение |x — 2| = 5 будет выглядеть как x — 2 = 5.
Если мы выставим модуль |x — 2| со знаком минус уравнение |x — 2| = 5 примет вид -(x — 2) = 5, то есть -x + 2 = 5.
Мы видим, что уравнение |x — 2| = 5 приводит к двум уравнениям: x — 2 = 5 и -x + 2 = 5. И каждое из уравнений имеет свой корень. Уравнение x — 2 = 5 имеет корень из 7, а уравнение -x + 2 = 5 имеет корень из -3.
Напишите уравнения x — 2 = 5 и -x + 2 = 5 и соедините их квадратной скобкой:
Этот тип записи называется набором уравнений .
Набор уравнений — это несколько уравнений, соединенных квадратной скобкой и имеющих множество решений, удовлетворяющих хотя бы одному из уравнений набора.
Итак, число 7 является решением множества
, потому что это число удовлетворяет первому уравнению x — 2 = 5.
Число -3 также является решением этого множества, потому что оно удовлетворяет второму уравнению -x + 2 = 5,
Вместе числа 7 и -3 образуют множество решений этого множества.
В отличие от системы уравнений набор состоит из уравнений, независимых друг от друга. Для каждого уравнения в наборе значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет и первому уравнению, и второму уравнению.
Для каждого уравнения в наборе значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет и первому уравнению, и второму уравнению.
Решение набора уравнений означает нахождение набора решений, удовлетворяющих хотя бы одному из уравнений набора.
Решим каждое уравнение набора
отдельно. Это обычные линейные уравнения, которые легко решить:
Символ ⇔, как указано выше, означает эквивалентность. В данном случае это означает, что все результирующие множества эквивалентны друг другу.
Итак, мы получили корни 7 и -3. Поскольку эти два числа являются решениями множества
, они также являются решениями уравнения |x — 2| = 5.
Исходный набор может включать условия, по которым решался модуль. В этом случае каждое уравнение вместе с его условием оформляется знаком системы.
Дополнить предыдущий набор условий, по которым решался модуль. К первому уравнению x — 2 = 5 добавить условие x — 2 ≥ 0, а ко второму уравнению -x + 2 = 5 добавить условие x — 2 < 0
К первому уравнению x — 2 = 5 добавить условие x — 2 ≥ 0, а ко второму уравнению -x + 2 = 5 добавить условие x — 2 < 0
Решение каждого уравнения должно удовлетворять своему условие. Поэтому условия и уравнения оформлены системным знаком.
Решите полученный набор с условиями. Условия представляют собой неравенства, которые также можно решить:
В первом случае мы получили корень из 7, который удовлетворяет условию x ≥ 2. Во втором случае мы получили корень из -3, который удовлетворяет условию x < 2.
Не бойтесь эти записи. Это просто подробное решение, показывающее, что откуда взялось. В большинстве случаев решение можно записать в более короткой форме.
Имеется схема объединения уравнения вида |x| = а. Эта схема выглядит так:
Эта схема позволяет легко свести уравнение с модулем к множеству. Эта схема может быть прочитана как, «Если выражение |x| равно a, то подмодульное выражение равно a или -a» .
Квадратная скобка в наборе заменяет слово «или» .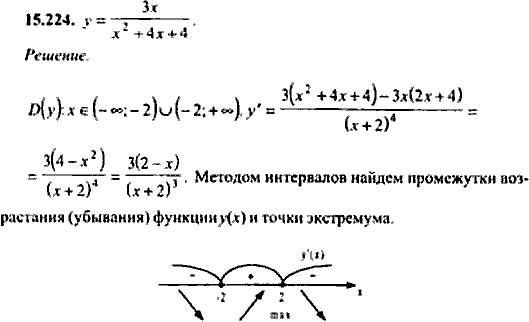
Например, уравнение |x| = 5 можно свести к множеству, рассудив, что если выражение |x| равно 5, то субмодульное выражение равно 5 или -5.
Как и в предыдущем примере, если |x — 2| равно 5, то подмодульное выражение равно 5 или -5
Это тот же набор, что и в прошлый раз. Проверьте это, умножив обе части второго уравнения на -1.
В уравнениях, где модуль находится слева, а число справа, мы будем чаще использовать этот способ записи множества. Это позволяет не прибегать к правилу возведения в степень по модулю, а сразу получить множество.
Но помните, что эта схема будет работать только для уравнений вида |x| = а. То есть для уравнений, у которых модуль слева и число справа.
Пример 2. Решить уравнение |2x — 1| = 3
Решение
Это уравнение имеет модуль слева и число справа. Таким образом, его можно преобразовать в набор, используя схему
. Если выражение |2x — 1| равно 3, то подмодульное выражение 2x — 1 равно 3 или -3
Теперь решим каждое уравнение набора отдельно:
Ответ: 2 и -1.
Пример 3. Решить уравнение |x + 2| — 3 = 8
Решение
В некоторых случаях, прежде чем исходное уравнение можно будет свести к набору, его необходимо упростить.
Значит, в этом случае -3 нужно перенести вправо, поменяв знак:
Получаем уравнение |x + 2| = 11. Если |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или -11
Решим этот набор:
Ответ: 9 и -13.
Пример 4. Решить уравнение 4|x| + 4 = 2|х| + 10
Решение
Переместить 2|x| с правой стороны на левую и переместите 4 с левой стороны на правую:
4| х | − 2| х | = 10 − 4
2| х | = 6
Разделим обе части полученного уравнения на 2. Тогда получим простое уравнение с модулем:
Ответ: 3 и -3.
Пример 5. Решить уравнение
Решение
Если |2 — 5x 2 | равно 3, то подмодульное выражение 2 — 5x 2 равно 3 или -3
В обоих уравнениях переместите 2 вправо, изменив знак:
В первом уравнении разделите обе части на -5. Во втором уравнении разделите обе части на -5. Тогда получим два квадратных уравнения
Во втором уравнении разделите обе части на -5. Тогда получим два квадратных уравнения
Первое уравнение не имеет корней, так как квадрат любого числа положителен, а в данном случае равен отрицательному числу. Корнями второго уравнения являются числа 1 и -1, так как вторая степень этих чисел равна единице.
Ответ: 1 и -1.
Пример 6. Решить уравнение |x + 6| + 4x = 5
Решение
Это уравнение не является уравнением вида |x| =a, поэтому схему
использовать нельзя.
Чтобы свести это уравнение к набору, необходимо сначала решить его модуль, а затем записать набор полученных уравнений.
Раскроем модуль |x + 6|
Если x + 6 ≥ 0, то модуль расширится со знаком плюс и тогда исходное уравнение будет иметь вид x + 6 + 4x = 5
Если x + 6 < 0 , то модуль открывается со знаком минус и тогда исходное уравнение будет иметь вид -x - 6 + 4x = 5. Получаем следующий набор:
Получаем следующий набор:
Дальнейшее решение элементарно:
Из найденных корней только
является корнем исходного уравнения, поскольку удовлетворяет условию x ≥ -6. А корень не является корнем уравнения, потому что он не удовлетворяет условию x < -6.
Ответ:
Самый простой вид
Самый простой вид уравнения с модулем выглядит так:
| х | = а
где х — — корень уравнения, а — — произвольное число большое или равное нулю. То есть a ≥ 0
Если условие a ≥ 0 не выполняется, то уравнение |x|= a не имеет корней. Это следует из определения модуля. Действительно, модуль всегда неотрицательный.
Вот несколько примеров уравнений вида |x| =
Пример 1. Решить уравнение |x| = 2
Решение
В этом случае сразу видно, что корнями являются числа 2 и -2. Ведь если вместо x подставить эти числа, то получится правильное равенство: |-2| = 2 и |2| = 2. Решение этого уравнения можно записать, объединив его в набор:
Решение этого уравнения можно записать, объединив его в набор:
«Если выражение |x| равно 2, то субмодульное выражение x равно 2 или -2 »
Ответ: 2 и -2
Пример 2. Решите уравнение |− x | = 4
Решение
Если выражение |-x| равно 4, то подмодульное выражение равно 4 или -4
Умножьте оба уравнения на -1
Ответ: -4 и 4.
Пример 3. | х | = −7
В этом случае корней нет, так как модуль всегда неотрицательный. И в этом случае модуль является отрицательным числом.
Если уравнение с модулем не имеет корней, обычно пишут, что x принадлежит пустому множеству:
x ∈ ø
Напомним, что пустое множество — это множество, не имеющее элементов.
Модуль внутри модуля
Рассмотрим уравнение:
В этом уравнении слева находится модуль, который, в свою очередь, содержит в себе другой модуль, а в правой части уравнения есть число . Такое уравнение с модулем можно решить, объединив его в набор по схеме, которую мы обсуждали ранее:
Такое уравнение с модулем можно решить, объединив его в набор по схеме, которую мы обсуждали ранее:
В нашем случае, если выражение
равно 9, то субмодульное выражение |2 + x| + 3 равно 9 или -9
В полученном наборе два уравнения с модулем. Эти уравнения тоже следует объединить в набор. Но сначала упростим эти уравнения. В первом и втором уравнениях переместите 3 вправо, поменяв знак. Тогда получим:
Теперь давайте сложим эти уравнения. Первое уравнение разложится на следующий набор:
Немедленно решить набор
. Первый корень равен 4, второй равен -8.
Теперь решим второе уравнение |2 + x| = -12. Но мы замечаем, что его правая часть — отрицательное число. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.
Итак, уравнение
имеет корни 4 и -8. Проверьте эти корни, подставив их в исходное уравнение
Проверьте эти корни, подставив их в исходное уравнение
. В этом случае оба корня удовлетворяют исходному уравнению.
Ответ: 4 и -8.
В общем случае уравнение с модулем, содержащим другой модуль, тоже решается по-разному. Какой способ использовать, зависит от самого уравнения. Решите, например, следующее уравнение:
Здесь уже нельзя использовать схему
, потому что слева не только модуль, но и переменная x. Конечно, переменную x можно переместить в правую часть, и тогда можно будет свести это уравнение к набору:
Но тогда в правой части появится переменная x, которую нужно будет дополнительно ограничить, чтобы правая часть уравнения не стала отрицательной. Этот способ решения уравнения мы рассмотрим позже. Сейчас мы решим исходное уравнение, используя правило разложения по модулю.
Чтобы решить модули уравнения, нам сначала нужно определить, где находятся внешние и внутренние модули.
В уравнении
, внешний модуль — это вся левая часть, а внутренний модуль — это выражение
Значение внешнего модуля зависит от внутреннего модуля, и внешний модуль будет расширяться на основе результата вычисления содержимого его подмодуля. .
Например, если x = 3, то внутренний модуль |3 — x| упадет до 0, а все значение подмодуля внешнего модуля станет -2. Это означает, что внешний модуль будет расширяться с минусом.
||3 − х | − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
И если, например, x = -2, то внутренний модуль |3 — x| примет значение 5, и в результате все подмодульное выражение внешнего модуля станет равным 8. Это означает, что внешний модуль расширится с плюсом:
||3 − x | − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Поэтому мы начнем решение с решения внутреннего модуля.
Если внутренний модуль расширяется с плюсом, то есть если 3 — x ≥ 0 (что эквивалентно неравенству x ≤ 3), то исходное уравнение примет вид:
Теперь уравнение имеет только внешний модуль. Решите его, решив модуль:
Решите его, решив модуль:
Если -2x + 4 ≥ 0, то:
Теперь нас интересуют только те значения x, при которых внутренний модуль расширяется с плюсом, а это произойдет, если x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3
Решаем дальше. Если -2x + 4 < 0, то:
Несмотря на то, что оба найденных корня удовлетворяют уравнению |-2x+4|=6-x, мы исключаем из решений корень
, так как нас сейчас интересует только в тех значениях x, при которых внутренний модуль исходного уравнения расширяется с плюсом. Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.
Итак, если внутренний модуль разложить на плюс, исходное уравнение примет вид |-2x + 4| = 6 — x, а корнем этого уравнения является число -2.
Теперь решите исходное уравнение для случая, когда внутренний модуль расширяется с минусом, то есть когда 3 — x < 0 (что эквивалентно неравенству x > 3). Внутренний модуль будет расширяться в минус для всех значений x больше 3.
Внутренний модуль будет расширяться в минус для всех значений x больше 3.
Если внутренний модуль расширяется в минус, исходное уравнение будет выглядеть так:
Модуль -2 равен 2. Тогда мы получим простейшее линейное уравнение, корень которого равен 4
Мы получили корень из 4, который удовлетворяет условию x > 3.
В результате корни уравнения равны -2 и 4.
Ответ: 2 и 4.
Пример 3. Решить уравнение ||x — 1| — 7| = 10
Решение
Слева модуль и число справа, поэтому можно применить схему:
В этом случае, если выражение ||x — 1| — 7| равно 10, то субмодульное выражение |x — 1| — 7 это 10 или -10. Это приводит к набору двух уравнений:
Упростите полученные уравнения. Перенесите число -7 в обоих уравнениях в правую часть, поменяв знак:
Второе уравнение не имеет корней. Первое уравнение разложится на набор
, корни которого равны 18 и -16.
Ответ: 18 и -16.
Решим это же уравнение, используя разложение модулей. Начнем с внутреннего модуля.
Если x — 1 ≥ 0 (что эквивалентно x ≥ 1), то исходное уравнение примет вид:
Решим полученное уравнение разложением по модулю:
Затем решим уравнение для случаев, когда x — 8 ≥ 0 и x — 8 < 0
Теперь нас интересуют значения, при которых внутренний модуль исходного уравнения расширяется с плюсом. Так будет, если x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы для наглядности отметили его зеленой галочкой.
Теперь решите исходное уравнение для случая, когда внутренний модуль расширяется с минусом, то есть когда x — 1 < 0 (или что эквивалентно неравенству x < 1).
Если x — 1 < 0, то исходное уравнение примет вид:
Решить полученное уравнение разложением по модулю:
Затем решить уравнение для случаев, когда -x — 6 ≥ 0 и -x — 6 < 0
Из найденных корней только -16 удовлетворяет условию x < 1.
В результате корни уравнения ||x — 1| — 7| = 10 это числа 18 и -16.
Как видите, это уравнение решалось проще и быстрее с помощью схемы
, чем с методом расширения по модулю.
Слева модуль, а справа выражение с переменной
Решите следующее уравнение с модулем:
|4 x − 3| = 3 x
Здесь также применима схема:
То есть, если выражение |4x — 3| равно 3x, то подмодульное выражение 4x — 3 должно равняться 3x или -3x.
Но исходное уравнение содержит переменную x не только под знаком модуля, но и в правой части. Мы еще не знаем, какое значение примет x. Если x имеет отрицательное значение, то правая часть будет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.
Поэтому, если мы хотим решить это уравнение, мы должны дополнительно ввести ограничение в виде условия 3x ≥ 0. Это означало бы, что правая часть уравнения |4x — 3| = 3x должно быть больше или равно нулю:
Множество и условие обрамлены системным знаком, так как решения множества должны удовлетворять условию 3x ≥ 0.
Итак, решаем множество. Условие 3x ≥ 0 — это неравенство, которое также можно решить:
Полученные корни можно подставить в условие x ≥ 0 и посмотреть, выполняется ли оно. Если оно выполнено, то найденные корни удовлетворяют уравнению. В этом случае при подстановке обоих корней в неравенство оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:
Пример 2. Решите уравнение |2x — 1| = 5x — 10
Решение
Решите это уравнение так же, как и предыдущее. Введем условие, требующее, чтобы правая часть была больше или равна нулю:
В этом случае только значение 3 удовлетворяет условию x ≥ 2. Это также единственный корень исходного уравнения. Проверка показывает следующее:
А число
не удовлетворяет условию x ≥ 2 и не является корнем исходного уравнения. Проверка также показывает это:
Мы видим, что модуль стал отрицательным числом, а это противоречит определению модуля и нашему условию x ≥ 2.
Пример 3. Решить уравнение
Решение
Мы решили это уравнение, когда научились решать уравнения с модулем, внутри которого есть другой модуль. Теперь это уравнение можно решить, объединив его в набор.
Начнем с того, что переместим x вправо, поменяв знак:
Теперь давайте сократим это уравнение до множества. Дополнительно введем условие в виде неравенства 6 — x ≥ 0
Модуль оставляем в левой части первого уравнения, а остальные члены переносим в правую часть. Проделайте то же самое со вторым уравнением. Также решим неравенство 6 — x ≥ 0, это позволит в конце проверить, чтобы найти корни:
Решим первое уравнение. Оно разложится на следующий набор:
Мы получили корни -2 и 8. Из них только -2 удовлетворяет условию x ≤ 6.
Теперь решим второе уравнение. Это уравнение, в правой части которого есть переменная. Когда объединим в набор, добавим условие -7 + 2x ≥ 0
Остальное элементарно:
При решении второго уравнения получили корни
и 4. Прежде чем проверять их на соответствие условию x ≤ 6, следует проверить их на соответствие условию , при котором уравнение |3 — x| = -7 + 2x было решено. Условие удовлетворяет только корню 4.
Прежде чем проверять их на соответствие условию x ≤ 6, следует проверить их на соответствие условию , при котором уравнение |3 — x| = -7 + 2x было решено. Условие удовлетворяет только корню 4.
В результате корни исходного уравнения
равны -2 и 4.
Пример 4. Решить уравнение |4x + 20| = -6x
Решение
На первый взгляд может показаться, что это уравнение не имеет решений, так как правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принимать отрицательное значение или ноль, и это привело бы к тому, что правая часть стала бы положительной или равной нулю. И такое уравнение имеет право на существование.
В этом случае мы решаем это уравнение, объединяя его в набор. Но уточним, что правая часть должна быть больше или равна нулю:
Из найденных корней только корень -2 удовлетворяет исходному уравнению. Оно также удовлетворяет нашему условию x ≤ 0.
Ответ: -2.
Когда обе части являются модулями
Решите следующее уравнение:
| x + 7| = |1 + 3 x |
Обе части этого уравнения являются модулями. Расширим эти модули. Мы учтем все возможные случаи их расширения.
Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0, то модули в обеих частях разложатся со знаком плюс и тогда исходное уравнение примет вид:
x + 7 = 1 + 3 x
Это простейшее линейное уравнение. Решим его:
Случай 2. Если x + 7 < 0 и 1 + 3x < 0, то модули в обеих частях разложатся со знаком минус и тогда исходное уравнение примет вид:
-( х + 7) = -(1 + 3 х )
Раскроем скобки, получим:
— х — 7 = -1 — 3 умножаем обе части этого уравнения на -1, получаем уравнение х+7=1+3х. А это уравнение мы получили в результате разложения модулей со знаком плюс.
То есть уравнения х + 7 = 1 + 3х и -х — 7 = -1 — 3х эквивалентны, значит, имеют одинаковые корни. Проверим это, решив уравнение
Проверим это, решив уравнение
— x — 7 = -1 — 3 x
Следовательно, если вы расширяете модули с помощью знака Plus, не нужно их расширять знак минус, потому что в обоих случаях вы получаете уравнения, имеющие одинаковые корни.
Случай 3. Следующий случай, когда x + 7 ≥ 0 и 1 + 3x < 0. Тогда исходное уравнение примет вид x + 7 = -1 - 3x. Найдите корень этого уравнения:
Случай 4. И последний случай, когда x + 7 < 0 и 1 + 3x ≥ 0. Тогда уравнение -x - 7 = 1 + 3x. Если мы умножим это уравнение на -1, мы получим уравнение x + 7 = -1 - 3x. И это уравнение мы получили, когда рассмотрели предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x < 0).
Следовательно, уравнение -x — 7 = 1 + 3x эквивалентно предыдущему уравнению x + 7 = -1 — 3x. Мы увидим, что, решив уравнение -x — 7 = 1 + 3x
Таким образом, расширяя левую часть со знаком плюс и правую со знаком минус, нет необходимости расширять левую часть со знаком минус и правую часть со знаком плюс, потому что в обоих случаях мы получаем уравнения которые имеют одинаковые корни.
В общем случае, если в уравнении обе части являются модулями, как в этом примере, уравнение можно свести к следующему набору:
В этой конструкции уравнение вида |a| = |б| сводится к системе двух уравнений a = b и a = -b. Видно, что первое уравнение получается разложением обоих модулей со знаком плюс, а второе уравнение получается разложением модуля |a| со знаком плюс и модуль |b| со знаком минус.
Важно. Эта схема работает только тогда, когда обе части представляют собой модули без посторонних терминов. Проще говоря, если такое уравнение, как |a| = |б| + c, приведенная выше схема не может быть использована.
Пример 2. Решите уравнение |2 — 3x| = |х + 5|
Решение
Обе части этого уравнения являются модулями. Используем схему:
У нас будет система из двух уравнений. В первом уравнении оба модуля будут разложены со знаком плюс, во втором уравнении модуль |2 — 3x| будет расширен со знаком плюс, а модуль |x + 5| со знаком минус:
Проверим:
Ответ:
и
Пример 3.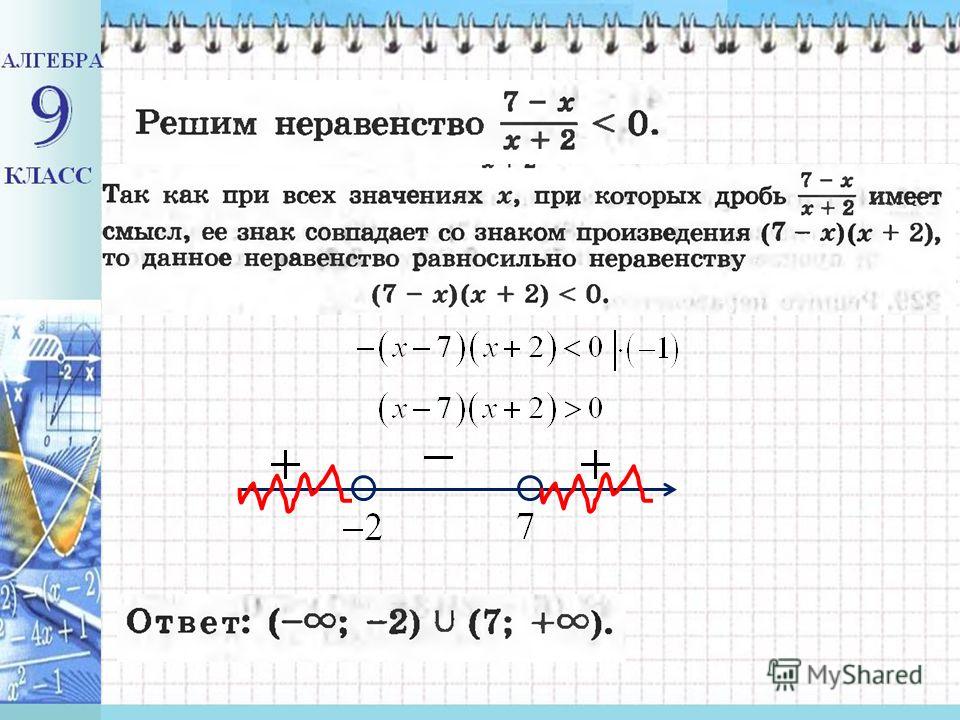 Решить уравнение | x 2 − 13 x + 35|=|35 − x 2 |
Решить уравнение | x 2 − 13 x + 35|=|35 − x 2 |
Решение
Обе части этого уравнения являются модулями. Используем схему:
У нас будет система из двух уравнений. В первом уравнении оба модуля будут развернуты со знаком плюс. Во втором уравнении модуль | x 2 − 13 x + 35| будет расширен со знаком плюс, а модуль |35 − x 2 | со знаком минус:
В обоих уравнениях даны одинаковые члены:
Первое уравнение представляет собой неполный квадрат. Решите его, вынеся х за скобки. Второе уравнение решается элементарно:
Ответ:
, , 0.
Когда решение представляет собой числовой интервал
Нередко приходится решать уравнение с модулем, где корнями являются не одно или два числа, а числовой интервал. Это, например, уравнение:
Это, например, уравнение:
|5 x + 3| = −5 x − 3
Разложим модуль этого уравнения:
Если разложить модуль со знаком плюс, получится уравнение 5x + 3 = -5x — 3. Решим его:
А если разложить модуль со знаком минус, то получится уравнение -5х — 3 = -5х — 3. В этом уравнении обе части одинаковы, значит это уравнение тождество. Это будет верно для любого значения x. Таким образом, корнями уравнения -5x — 3 = -5x — 3 являются все числа от минус бесконечности до плюс бесконечности:
x ∈ (−∞; +∞)
Но мы должны помнить условия, при которых модули были расширены. В первом случае мы получили рут
. Это будет верно только в том случае, если условие . Это условие выполняется. Проверка также показывает, что корень верен:
Итак, один из корней уравнений равен
Во втором случае мы получили набор корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии, что
Но это будет верно только при условии, что
Например, если мы возьмем любое число из интервала (-∞; +∞), но которое не будет удовлетворять условию
, то это число не превратит наше уравнение в истинное равенство.
Например, число 2 принадлежит интервалу (-∞; +∞), но не удовлетворяет условию
, поэтому число 2 не является корнем исходного уравнения. Проверка также покажет это:
А если взять например число -5, то оно будет принадлежать интервалу (-∞; +∞) и удовлетворять условию
, что означает, что он преобразует исходное уравнение в правильное равенство:
Следовательно, ответ нужно написать так, чтобы выполнялись оба условия
и . Для наглядности проведем координатную линию и обозначим ее как x
Отметим на нем наш первый корень
Разложив модуль со знаком минус и решив полученное уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но условие
был дан. Таким образом, более точным ответом в данном случае будет такой:
Таким образом, более точным ответом в данном случае будет такой:
Корнями уравнения -5x — 3 = -5x — 3 при условии являются все числа от минус бесконечности до
Значит на координатной линии нужно заштриховать область слева от числа
. Они будут иллюстрировать числа меньше, чем
Число
также является правильным корнем исходного уравнения. Он был получен выставлением модуля со знаком плюс. Поэтому на координатной линии пустой кружок должен быть заштрихован. Таким образом, мы включим число в множество решений:
Тогда окончательный ответ будет выглядеть так:
Ответ:
Также можно решить это уравнение, сведя его к множеству, дополнительно указав, что правая часть должна быть больше или равна ноль:
Пример 2. Решите уравнение |2x — 3| = 3 — 2x
Решение
Решите исходное уравнение для случаев, когда 2x — 3 ≥ 0 и 2x — 3 < 0
Ответ:
Использование координатной линии
Рассмотрим другой способ решения элементарных уравнений с модулем — использование координатной линии. Этот метод используется редко, но знать о нем не помешает.
Этот метод используется редко, но знать о нем не помешает.
Решите наше самое первое уравнение |x — 2| = 5 с использованием координатной линии. Напомним, что корнями этого уравнения были числа 7 и -3.
Модуль — это расстояние от начала координат до точки А. Или расстояние между двумя числами на координатной прямой.
Расстояние между двумя числами выражается как разность | x 1 − x 2 |, где x 1 — первое число, x 2 — второе число.
Если вы внимательно посмотрите на уравнение |x — 2|= 5, то увидите, что его левая часть представляет собой расстояние от x до 2 (или от 2 до x), и это расстояние равно 5. Отметьте число x и число число 2 на линии координат
Правая часть уравнения |x — 2|= 5 показывает, что расстояние от x до 2 равно пяти единицам:
Если расстояние от x до 2 равно 5, то расстояние от 2 до x также равно 5. Это позволяет вам подсчитать пять целых шагов от числа 2 до x и, таким образом, найти значение x
Вы Видно, что, отсчитав пять шагов влево, мы попадаем в точку с координатой -3. А это один из найденных нами корней уравнения |x — 2|= 5.
А это один из найденных нами корней уравнения |x — 2|= 5.
Но целых пять шагов от числа 2 можно отсчитать не только влево, но и вправо:
Если мы отсчитаем целых пять шагов вправо, то попадем в точку с координатой 7. Это тоже был корень уравнения |x — 2|= 5
Несколько модулей в одной детали
Решим следующее уравнение:
| х − 5| − | х | = 1
Это уравнение содержит два модуля в левой части. Для решения этого уравнения необходимо решить его модули. Рассмотрим каждый из случаев:
- , когда оба модуля больше или равны нулю;
- , когда оба модуля меньше нуля;
- , когда первый модуль больше или равен нулю, а второй модуль меньше нуля;
- , когда первый модуль меньше нуля, а второй модуль больше или равен нулю.
Не будем комментировать каждый случай, а сразу приведем решение:
Первые два случая корней не дали. В третьем случае корень из 3 найден, но он не удовлетворяет условиям x — 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.
В третьем случае корень из 3 найден, но он не удовлетворяет условиям x — 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.
В четвертом случае найден корень из 2, удовлетворяющий условиям x — 5 < 0 и x ≥ 0. Он также удовлетворяет исходному уравнению.
Заметно, что такой способ решения уравнения неудобен. Если бы в уравнении было три, четыре или более модулей, нам пришлось бы рассматривать гораздо больше случаев. Человек может запутаться и забыть рассмотреть некоторые случаи, и уравнение не будет решено полностью.
Поэтому такое уравнение, как в этом примере, удобнее решать методом интервалов. Об этом мы поговорим на следующем уроке.
Задание 1. Решить уравнение:
Решение:
Показать решение
Задание 2. Решить уравнение:
Решение:
Показать решение
Задание 3. Решить уравнение:
Показать решение:3 90 Решение
Задача 4. Решить уравнение:
Решение:
Ответ : .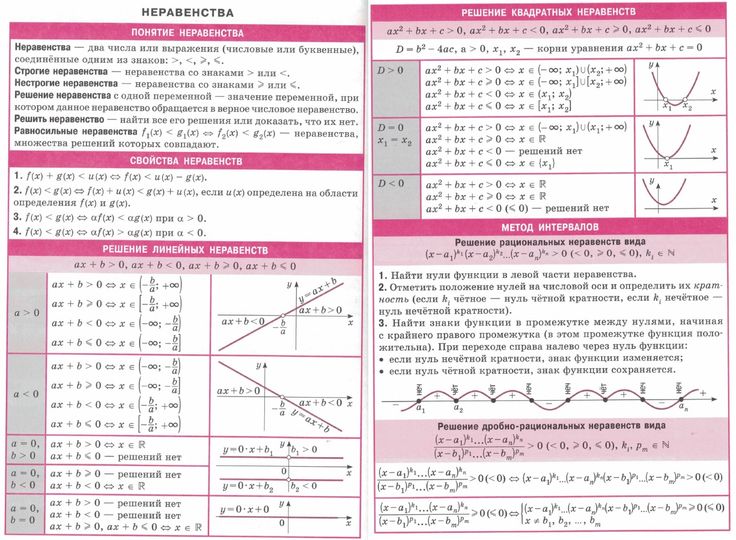
Показать решение
Задание 5. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задание 6. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задача 7. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задание 8. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задача 9. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задача 10. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задача 11. Решить уравнение:
Решение:
Ответ : .
Показать решение
Задание 12. Решить уравнение:
Решение:
Ответ : 0, 5. Задачи объединяются в DAG, а затем между ними устанавливаются восходящие и нисходящие зависимости, чтобы выразить порядок, в котором они должны выполняться.
Существует три основных типа задач:
Операторы, предопределенные шаблоны задач, которые можно быстро связать вместе для создания большинства частей ваших DAG.
Сенсоры, особый подкласс Операторов, полностью ожидающих возникновения внешнего события.
Украшенный TaskFlow
@task, представляющий собой пользовательскую функцию Python, упакованную как Task.
Внутренне все это на самом деле подклассы Airflow BaseOperator , а понятия Task и Operator несколько взаимозаменяемы, но их полезно рассматривать как отдельные понятия — по сути, операторы и датчики — это шаблоны , и когда вы вызываете один из них в файле DAG, вы делаете задача.
Отношения
Ключевой частью использования задач является определение того, как они связаны друг с другом — их зависимостей , или, как мы говорим в Airflow, их восходящих и нисходящих задач. Сначала вы объявляете свои задачи, а затем объявляете их зависимости.
Примечание
Мы называем восходящей задачей ту, которая непосредственно предшествует другой задаче. Раньше мы называли это родительской задачей. Имейте в виду, что это понятие не описывает задачи, которые находятся выше в иерархии задач (т. е. они не являются прямыми родителями задачи). То же определение применимо к нисходящей задаче , которая должна быть прямым дочерним элементом другой задачи.
Есть два способа объявить зависимости — используя >> и << (битовый сдвиг):
первая_задача >> вторая_задача >> [третья_задача, четвертая_задача]
Или более явные методы set_upstream и set_downstream :
first_task.set_downstream(second_task) Third_task.set_upstream(вторая_задача)
Они оба делают одно и то же, но в целом мы рекомендуем вам использовать операторы битового сдвига, так как в большинстве случаев их легче читать.
По умолчанию задача запускается после успешного выполнения всех ее вышестоящих (родительских) задач, но существует много способов изменить это поведение, чтобы добавить ветвление, дождаться только некоторых вышестоящих задач или изменить поведение в зависимости от того, где текущий запуск находится в истории. Подробнее см. в разделе Поток управления.
По умолчанию задачи не передают информацию друг другу и выполняются полностью независимо. Если вы хотите передавать информацию из одной задачи в другую, вам следует использовать XComs.
Экземпляры задач
Во многом так же, как DAG создается в DAG Run при каждом запуске, задачи DAG создаются в экземпляров задач .
Экземпляр задачи — это конкретный запуск этой задачи для данной DAG (и, следовательно, для заданного интервала данных). Они также являются представлением задачи, которая имеет состояние , представляющее, на каком этапе жизненного цикла оно находится.
Они также являются представлением задачи, которая имеет состояние , представляющее, на каком этапе жизненного цикла оно находится.
Возможные состояния экземпляра задачи:
нет: задача еще не поставлена в очередь на выполнение (ее зависимости еще не выполнены)запланировано: планировщик определил, что зависимости задачи выполнены, и она должна быть запущенав очереди: задача назначена исполнителю и ожидает работникаработает: задача выполняется на рабочем (или на локальном/синхронном исполнителе)успех: задача завершена без ошибокзавершение работы: задача была запрошена извне для завершения работы во время ее выполненияперезапуск: задача была запрошена извне для перезапуска во время ее выполнениясбой: во время выполнения задачи возникла ошибка, и ее не удалось запуститьпропущено: задача была пропущена из-за ветвления, LatestOnly или аналогичного.
upstream_failed: не удалось выполнить восходящую задачу, и правило триггера говорит, что нам это нужноup_for_retry: Задача не удалась, но остались попытки повторных попыток, и она будет перепланирована.up_for_reschedule: Задача представляет собой датчик, который находится в режимеперепланирования.отложено: задача была отложена до триггераудалено: задача исчезла из DAG с момента запуска
В идеале задача должна проходить с none , на запланировано , на поставлено в очередь , на выполняется и, наконец, на успешно .
При выполнении любой пользовательской задачи (оператора) она получает копию переданного ей экземпляра задачи; помимо возможности проверять метаданные задач, он также содержит методы для таких вещей, как XComs.
Терминология отношений
Для любого данного экземпляра задачи существует два типа отношений, которые он имеет с другими экземплярами.
Во-первых, он может иметь восходящих и нисходящих задач:
задача1 >> задача2 >> задача3
Когда группа обеспечения доступности баз данных запускается, она создает экземпляры для каждой из этих задач, которые являются восходящими и нисходящими по отношению друг к другу, но имеют одинаковый интервал данных.
Также могут быть экземпляры та же задача , но для разных интервалов данных — из других прогонов той же DAG. Мы называем эти предыдущими и следующими - это другое отношение к вверх по течению и вниз по течению !
Примечание
В некоторых старых документах по Airflow слово «предыдущий» по-прежнему может означать «восходящий». Если вы обнаружите это, пожалуйста, помогите нам исправить это!
Тайм-ауты
Если вы хотите, чтобы задача имела максимальное время выполнения, установите ее execute_timeout к значению datetime. это максимально допустимое время работы. Это относится ко всем задачам Airflow, включая датчики.  timedelta
timedelta execute_timeout управляет
максимальное время, разрешенное для каждого исполнения. Если execute_timeout нарушается, время ожидания задачи истекает и Возбуждено значение AirflowTaskTimeout .
Кроме того, датчики имеют параметр timeout . Это имеет значение только для датчиков в режиме перепланирования . тайм-аут контролирует максимальную
время, отведенное датчику на срабатывание. Если тайм-аут нарушен, значение AirflowSensorTimeout будет увеличено, и датчик немедленно выйдет из строя.
без повторной попытки.
Это иллюстрирует следующий пример SFTPSensor . Датчик находится в режиме перепланирования , т.е.
периодически выполняется и перепланируется до тех пор, пока не увенчается успехом.
Каждый раз, когда датчик подключается к SFTP-серверу, это может занять максимум 60 секунд, как определено
время_выполнения.
Если датчику требуется более 60 секунд для подключения к SFTP-серверу, будет поднято значение
AirflowTaskTimeout. Датчику разрешено повторить попытку, когда это произойдет. Он может повторять до 2 раз, как определеноповторных попыток.С начала первого выполнения до его успешного завершения (т. е. после появления файла «root/test») датчику разрешено максимум 3600 секунд, как определено таймаутом 9
1481 . Другими словами, если файл не появится на SFTP-сервере в течение 3600 секунд, датчик подниметAirflowSensorTimeout. Он не будет повторять попытку, когда возникнет эта ошибка.Если датчик выходит из строя по другим причинам, таким как перебои в сети в течение интервала 3600 секунд, он может повторять до 2 раз, как определено
повторных попыток. Повторная попытка не сбрасывает тайм-аут
датчик = SFTPSensor(
task_id="датчик",
путь="/корень/тест",
execute_timeout = дельта времени (секунды = 60),
тайм-аут=3600,
повторы = 2,
режим = "перепланировать",
)
Если вы просто хотите получать уведомления, если задача переполняется, но при этом позволяете ей выполняться до конца, вам нужны соглашения об уровне обслуживания.
SLA
SLA или Соглашение об уровне обслуживания — это ожидаемое максимальное время выполнения Задачи. Если выполнение задачи занимает больше времени, чем это, она будет видна в части пользовательского интерфейса «SLA Misses», а также будет отправлена по электронной почте со всеми задачами, которые не выполнили SLA.
Задачи выше их SLA не отменяются, однако им разрешается выполняться до завершения. Если вы хотите отменить задачу после достижения определенного времени выполнения, вместо этого вам нужны тайм-ауты.
Чтобы установить SLA для задачи, передайте объект datetime. в параметр Task/Operator  timedelta
timedelta sla . Вы также можете указать sla_miss_callback , который будет вызываться при пропуске SLA, если вы хотите запустить собственную логику.
Если вы хотите полностью отключить проверку SLA, вы можете установить check_slas = False в конфигурации Airflow [core] .
Дополнительные сведения о настройке электронной почты см. в разделе Настройка электронной почты.
Примечание
Инициируемые вручную задачи и задачи в управляемых событиями DAG не будут проверяться на отсутствие SLA. Дополнительные сведения о значениях расписания DAG см. в разделе Запуск DAG.
sla_miss_callback
Вы также можете указать sla_miss_callback , который будет вызываться при пропуске SLA, если вы хотите запустить собственную логику.
Функциональная подпись sla_miss_callback требует 5 параметров.
дагсписок_задачblocking_task_listЛюбая задача в DAGRun(ах) (с тем же
execute_date, что и задача, которая пропустила SLA), который не находится в состоянии SUCCESS в момент, когдаsla_miss_callbackбежит. то есть «работает», «не удалось». Эти задачи описываются как задачи, которые блокируют себя или другие
задача от завершения до того, как ее окно SLA будет завершено.
то есть «работает», «не удалось». Эти задачи описываются как задачи, которые блокируют себя или другие
задача от завершения до того, как ее окно SLA будет завершено.
сласблокировка_тис
Примеры sla_miss_callback подпись функции:
def my_sla_miss_callback(dag, task_list, blocking_task_list, slas, blocking_tis):
...
защита my_sla_miss_callback(*args):
...
Пример DAG:
def sla_callback(dag, task_list, blocking_task_list, slas, blocking_tis):
Распечатать(
"Аргументы обратного вызова: ",
{
"даг": даг,
"список_задач": список_задач,
"blocking_task_list": блокирующий_task_list,
"слас": слас,
"blocking_tis": блокировка_tis,
},
)
@даг(
расписание="*/2 * * * *",
start_date=pendulum. datetime(2021, 1, 1, tz="UTC"),
перехват = ложь,
sla_miss_callback=sla_callback,
default_args={'электронная почта': "[email protected]"},
)
определение example_sla_dag():
@task(sla=datetime.timedelta(секунды=10))
защита сна_20():
"""Сон на 20 секунд"""
время сна(20)
@задача
защита сна_30():
"""Сон на 30 секунд"""
время сна(30)
сон_20() >> сон_30()
example_dag = example_sla_dag()
datetime(2021, 1, 1, tz="UTC"),
перехват = ложь,
sla_miss_callback=sla_callback,
default_args={'электронная почта': "[email protected]"},
)
определение example_sla_dag():
@task(sla=datetime.timedelta(секунды=10))
защита сна_20():
"""Сон на 20 секунд"""
время сна(20)
@задача
защита сна_30():
"""Сон на 30 секунд"""
время сна(30)
сон_20() >> сон_30()
example_dag = example_sla_dag()
Специальные исключения
Если вы хотите контролировать состояние своей задачи из пользовательского кода задачи/оператора, Airflow предоставляет два специальных исключения, которые вы можете вызвать:
Они могут быть полезны, если ваш код обладает дополнительными знаниями об окружающей среде и хочет, чтобы произошел сбой. /скип быстрее — например, пропуск, когда он знает, что данные недоступны, или быстрый сбой, когда он обнаруживает, что его ключ API недействителен (поскольку это не будет исправлено повторной попыткой).
Задачи зомби/нежити
Ни одна система не работает идеально, и экземпляры задач время от времени умирают. Airflow обнаруживает два типа несоответствия задачи/процесса:
Airflow обнаруживает два типа несоответствия задачи/процесса:
Зомби-задачи — это задачи, которые должны были выполняться, но внезапно умерли (например, их процесс был убит или машина умерла). Airflow будет периодически находить их, очищать и либо сбой, либо повторная попытка выполнить задачу в зависимости от его настроек.
Задачи нежити — это задачи, которые не должны выполняться, но часто вызываются, когда вы вручную редактируете экземпляры задач через пользовательский интерфейс. Airflow будет периодически находить их и отключать.
Конфигурация исполнителя
Некоторые исполнители допускают дополнительную настройку для каждой задачи, например KubernetesExecutor , которая позволяет установить образ для запуска задачи.
Это достигается с помощью аргумента executor_config задачи или оператора. Вот пример настройки образа Docker для задачи, которая будет выполняться на KubernetesExecutor :
MyOperator(..., executor_config={ «КубернетесИсполнитель»: {"изображение": "myCustomDockerImage"} } )
Параметры, которые вы можете передать в executor_config , различаются в зависимости от исполнителя, поэтому прочитайте документацию по конкретному исполнителю, чтобы узнать, что вы можете установить.
Написание файла саранчи — Документация по Locust 2.12.1
Теперь давайте посмотрим на более полный/реалистичный пример того, как могут выглядеть ваши тесты:
время импорта
из саранчи импортировать HttpUser, задача, между
класс QuickstartUser (HttpUser):
время_ожидания = между (1, 5)
@задача
определение hello_world (я):
self.client.get("/привет")
self.client.get("/мир")
@задача(3)
определение view_items (я):
для item_id в диапазоне (10):
self.client.get(f"/item?id={item_id}", name="/item")
время сна(1)
защита on_start (я):
self.client.post("/login", json={"имя пользователя":"foo", "пароль":"bar"})
Разберем
время импорта из саранчи импортировать HttpUser, задача, между
Файл саранчи — это обычный модуль Python, он может импортировать код из других файлов или пакетов.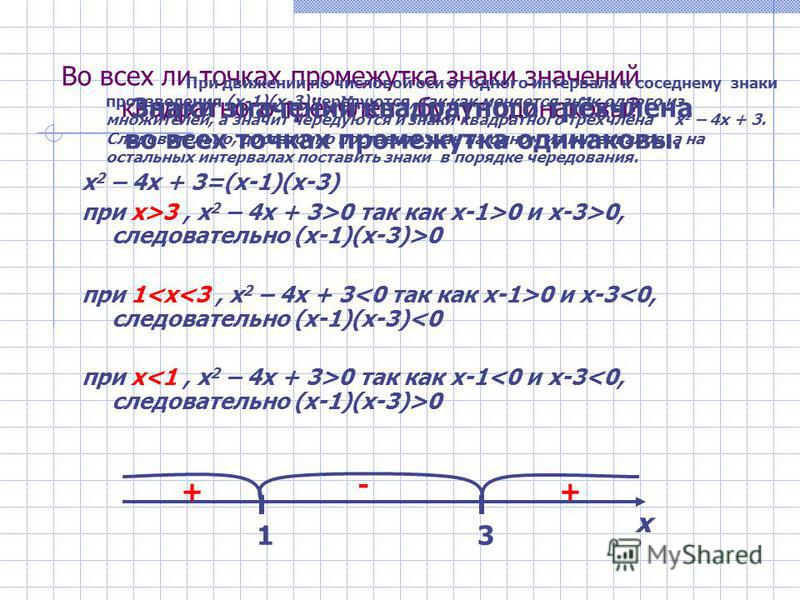
класс QuickstartUser (HttpUser):
Здесь мы определяем класс для пользователей, которых будем моделировать. Он наследует от HttpUser , который дает каждому пользователю атрибут client ,
который является экземпляром HttpSession , который
можно использовать для выполнения HTTP-запросов к целевой системе, которую мы хотим загрузить test. Когда начинается испытание,
саранча создаст экземпляр этого класса для каждого симулируемого пользователя, и каждый из этих
пользователи начнут работать в своем собственном зеленом потоке gevent.
Чтобы файл был допустимым файлом саранчи, он должен содержать хотя бы один класс, унаследованный от User .
время ожидания = между (1, 5)
Наш класс определяет wait_time , которое заставит имитируемых пользователей ждать от 1 до 5 секунд после каждой задачи (см. ниже)
выполняется. Для получения дополнительной информации см. атрибут wait_time.
@задача
определение hello_world (я):
...
Методы, украшенные @task , являются ядром вашего файла саранчи. Для каждого работающего пользователя
Locust создает гринлет (микропоток), который будет вызывать эти методы.
@задача
определение hello_world (я):
self.client.get("/привет")
self.client.get("/мир")
@задача(3)
определение view_items (я):
...
Мы объявили две задачи, украсив два метода @task , одному из которых был присвоен более высокий вес (3).
Когда наш QuickstartUser запускается, он выбирает одну из объявленных задач — в данном случае либо hello_world , либо view_items - и выполнить его. Задачи выбираются случайным образом, но вы можете присвоить им различный вес. Над
конфигурация сделает Locust в три раза более вероятной, чтобы выбрать view_items чем hello_world . Когда задача имеет
завершив выполнение, пользователь будет спать в течение времени ожидания (в данном случае от 1 до 5 секунд). По истечении времени ожидания он выберет новую задачу и продолжит ее повторять.
По истечении времени ожидания он выберет новую задачу и продолжит ее повторять.
Обратите внимание, что будут выбраны только методы, украшенные @task , поэтому вы можете определить свои собственные внутренние вспомогательные методы любым удобным для вас способом.
self.client.get("/привет")
Атрибут self.client позволяет совершать HTTP-вызовы, которые будут регистрироваться Locust. Для получения информации о том, как
чтобы делать другие запросы, проверять ответ и т. д., см.
Использование HTTP-клиента.
Примечание
HttpUser не является настоящим браузером и поэтому не будет анализировать ответ HTML для загрузки ресурсов или отображения страницы. Однако он будет отслеживать файлы cookie.
@задача(3)
определение view_items (я):
для item_id в диапазоне (10):
self.client.get(f"/item?id={item_id}", name="/item")
время сна(1)
В задаче view_items мы загружаем 10 разных URL-адресов, используя переменный параметр запроса. Чтобы не получить 10 отдельных записей в статистике Locust — так как статистика сгруппирована по URL — используем
параметр name для группировки всех этих запросов под записью с именем
Чтобы не получить 10 отдельных записей в статистике Locust — так как статистика сгруппирована по URL — используем
параметр name для группировки всех этих запросов под записью с именем "/item" вместо .
по определению on_start(self):
self.client.post("/login", json={"имя пользователя":"foo", "пароль":"bar"})
Кроме того, мы объявили метод on_start . Метод с этим именем будет вызываться для каждого имитируемого пользователя при их запуске. Для получения дополнительной информации см. методы on_start и on_stop.
Класс пользователя
Класс пользователя представляет одного пользователя (или, если угодно, стайку саранчи). Саранча породит один экземпляр класса User для каждого имитируемого пользователя. Есть некоторые общие атрибуты, которые класс пользователя может определить.
Атрибут wait_time
Пользовательский метод wait_time позволяет легко вводить задержки после
выполнение каждой задачи. Если wait_time не указано, следующая задача будет выполнена, как только завершится первая.
Если wait_time не указано, следующая задача будет выполнена, как только завершится первая.
Например, чтобы заставить каждого пользователя ждать от 0,5 до 10 секунд между выполнением каждой задачи:
from locust import Пользователь, задача, между
класс MyUser (пользователь):
@задача
определить мою_задачу (я):
print("выполнение my_task")
время_ожидания = между (0,5, 10)
Constant_throughputдля адаптивного времени, обеспечивающего выполнение задачи (максимум) X раз в секунду.Constant_pacingдля адаптивного времени, которое гарантирует выполнение задачи (максимум) один раз каждые X секунд (это математическая инверсия Constant_throughput ).
Примечание
Например, если вы хотите, чтобы Locust запускал 500 итераций задач в секунду при пиковой нагрузке, вы можете использовать wait_time = Constant_throughput(0.1) и количество пользователей 5000.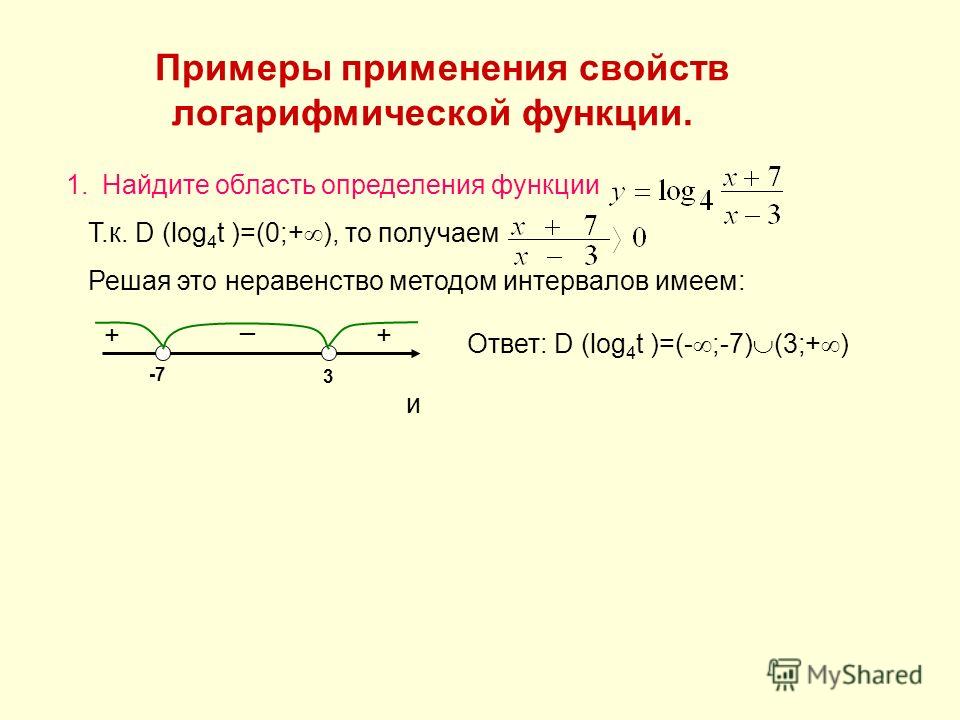
Время ожидания может только ограничивать пропускную способность, но не запускать новых пользователей для достижения цели. Так, в нашем примере пропускная способность будет меньше 500, если время итерации задачи превышает 10 секунд.
Время ожидания применяется после выполнения задачи , поэтому, если у вас высокая скорость появления/разгон, вы можете в конечном итоге превысить цель во время разгона.
Время ожидания применяется к задачам , а не к запросам. Например, если вы укажете wait_time = Constant_throughput(2) и выполните два запроса в своих задачах, ваша частота запросов/RPS будет равна 4 на пользователя.
Также можно объявить собственный метод wait_time непосредственно в классе. Например, следующий класс User будет спать одну секунду, затем две, затем три и т. д.
class MyUser(User):
последнее_время_ожидания = 0
определение время ожидания (я):
self.last_wait_time += 1
вернуть self. last_wait_time
...
last_wait_time
...
атрибуты веса и fixed_count
Если в файле существует более одного класса пользователей и в командной строке не указаны классы пользователей, Саранча создаст равное количество каждого из пользовательских классов. Вы также можете указать, какой из пользовательские классы для использования из того же файла locustfile, передав их в качестве аргументов командной строки:
$ locust -f locust_file.py WebUser MobileUser
Если вы хотите имитировать больше пользователей определенного типа, вы можете установить для них атрибут веса. классы. Скажем, например, веб-пользователи в три раза чаще, чем мобильные пользователи:
класс WebUser(Пользователь):
вес = 3
...
класс MobileUser(Пользователь):
вес = 1
...
Также вы можете установить атрибут fixed_count .
В этом случае атрибут веса будет игнорироваться, и будет создано точное количество пользователей.
Эти пользователи создаются первыми. В приведенном ниже примере только один экземпляр AdminUser
будет создан, чтобы сделать некоторые конкретные работы с более точным контролем
количества запросов независимо от общего количества пользователей.
В приведенном ниже примере только один экземпляр AdminUser
будет создан, чтобы сделать некоторые конкретные работы с более точным контролем
количества запросов независимо от общего количества пользователей.
класс AdminUser(Пользователь):
время_ожидания = константа (600)
фиксированное_счетчик = 1
@задача
определение перезапуска_приложение (я):
...
класс WebUser (пользователь):
...
Атрибут хоста
Атрибут хоста — это префикс URL-адреса (например, «http://google.com») хоста, который необходимо загрузить.
Обычно это указывается в веб-интерфейсе Locust или в командной строке с помощью --опция host при запуске саранчи.
Если объявить атрибут хоста в пользовательском классе, он будет использоваться в том случае, если нет --host указывается в командной строке или в веб-запросе.
Атрибут задач
Класс User может иметь задачи, объявленные как методы под ним, используя @task декоратор, но можно и
укажите задачи, используя атрибут tasks , который более подробно описан ниже.
атрибут среды
Ссылка на среду , в которой работает пользователь. Используйте это для взаимодействия с
среды или бегуна , который он содержит. Например. чтобы остановить бегуна из метода задачи:
self.environment.runner.quit()
При запуске на отдельном экземпляре саранчи весь запуск будет остановлен. Если запустить на рабочем узле, он остановит этот конкретный узел.
методы on_start и on_stop
Пользователи (и TaskSets) могут объявить метод on_start и/или метод on_stop . Пользователь вызовет свой on_start метод, когда он запускается, и его on_stop метод, когда он перестает работать. Для набора задач Метод on_start вызывается, когда смоделированный пользователь начинает выполнение
этот TaskSet и on_stop вызывается, когда имитируемый пользователь останавливается
выполнение этого TaskSet (когда interrupt() вызывается , или
пользователь убит).
Задачи
При запуске нагрузочного теста экземпляр класса User будет создан для каждого имитируемого пользователя. и они начнут работать в своей собственной зеленой нити. Когда эти пользователи работают, они выбирают задачи, которые они выполняются, некоторое время спят, а затем выбирают новую задачу и так далее.
Задачи являются обычными вызываемыми объектами Python, и — если бы мы проводили нагрузочное тестирование веб-сайта аукциона — они могли бы выполнять такие вещи, как «загрузка стартовой страницы», «поиск какого-либо продукта», «сделать ставку» и т. д.
Декоратор @task
Самый простой способ добавить задачу для пользователя — использовать декоратор task .
из импорта саранчи Пользователь, задача, константа
класс MyUser (пользователь):
время_ожидания = константа (1)
@задача
определить мою_задачу (я):
print("Экземпляр пользователя (%r), выполняющий my_task" % self)
@task принимает необязательный аргумент веса, который можно использовать для указания коэффициента выполнения задачи. В
в следующем примере задача2 будет выбрана в два раза чаще, чем задача1 :
В
в следующем примере задача2 будет выбрана в два раза чаще, чем задача1 :
из импорта саранчи Пользователь, задача, между
класс MyUser (пользователь):
время_ожидания = между (5, 15)
@задача(3)
определение задачи1 (я):
проходить
@задача(6)
определение задачи2 (я):
проходить
Атрибут задач Другой способ определить задачи пользователя — установить атрибут задач .
Атрибут tasks — это либо список задач, либо
Вот пример пользовательской задачи, объявленной как обычная функция python:
из саранчи import User, константа
определить мою_задачу (пользователь):
проходить
класс MyUser (пользователь):
задачи = [моя_задача]
время_ожидания = константа (1)
Если атрибут задач указан в виде списка, каждый раз, когда задача должна быть выполнена, она будет случайным образом
выбирается из атрибута задач . Однако, если задач - это dict - с вызываемыми объектами в качестве ключей и целых чисел
как значения - задача, которая должна быть выполнена, будет выбрана случайным образом, но с соотношением int. Так
с задачей, которая выглядит так:
Однако, если задач - это dict - с вызываемыми объектами в качестве ключей и целых чисел
как значения - задача, которая должна быть выполнена, будет выбрана случайным образом, но с соотношением int. Так
с задачей, которая выглядит так:
{моя_задача: 3, другая_задача: 1}
my_task будет выполняться в 3 раза чаще, чем other_task .
Внутренне указанный выше словарь будет фактически расширен в список (и атрибут tasks обновлен)
это выглядит так:
[моя_задача, моя_задача, моя_задача, другая_задача]
, а затем Python random.choice() используется для выбора задач из списка.
@tag decorator
Помечая задачи с помощью @tag декоратор, вы можете быть разборчивы в том, какие задачи
выполняется во время теста с использованием аргументов --tags и --exclude-tags . Рассмотреть возможность
следующий пример:
из импорта саранчи Пользователь, константа, задача, тег
класс MyUser (пользователь):
время_ожидания = константа (1)
@тег('тег1')
@задача
определение задачи1 (я):
проходить
@тег('тег1', 'тег2')
@задача
определение задачи2 (я):
проходить
@тег('тег3')
@задача
определение задачи3 (я):
проходить
@задача
определение задачи4 (я):
проходить
Если вы начали этот тест с --tags tag1 , будут выполнены только задача 1 и задача 2 во время теста. Если вы запустили его с
Если вы запустили его с --tags tag2 tag3 , только задача2 и задача3 будут
казнен.
--exclude-tags будет вести себя прямо противоположным образом. Итак, если вы начнете тест с --exclude-tags tag3 , будут выполнены только задача1 , задача2 и задача4 . Исключение всегда
имеет преимущество над включением, поэтому, если у задачи есть тег, который вы включили, и тег, который вы исключили, она не будет
быть казненным.
События
Если вы хотите запустить какой-либо установочный код как часть теста, часто достаточно поместить его в модуль уровне вашего файла locustfile, но иногда вам нужно что-то делать в определенное время во время выполнения. За для этой потребности Locust предоставляет перехватчики событий.
test_start и test_stop
Если вам нужно запустить какой-либо код в начале или в конце нагрузочного теста, вы должны использовать test_start и test_stop События. Вы можете настроить прослушиватели для этих событий на уровне модуля вашего locustfile:
Вы можете настроить прослушиватели для этих событий на уровне модуля вашего locustfile:
из событий импорта саранчи
@events.test_start.add_listener
def on_test_start (среда, ** kwargs):
print("Начинается новый тест")
@events.test_stop.add_listener
def on_test_stop (среда, **kwargs):
print("Заканчивается новый тест")
init
Событие init запускается в начале каждого процесса Locust. Это особенно полезно в распределенном режиме
где каждому рабочему процессу (не каждому пользователю) нужен шанс выполнить некоторую инициализацию. Например, допустим, у вас есть несколько
глобальное состояние, которое потребуется всем пользователям, созданным из этого процесса:
из событий импорта саранчи
из locust.runners импортировать MasterRunner
@events.init.add_listener
def on_locust_init(среда, **kwargs):
если isinstance (environment.runner, MasterRunner):
print("Я на главном узле")
еще:
print("Я на рабочем или автономном узле")
Другие события
См. расширение саранчи с помощью обработчиков событий для других событий и другие примеры их использования.
расширение саранчи с помощью обработчиков событий для других событий и другие примеры их использования.
Класс HttpUser
HttpUser — наиболее часто используемый Пользователь . Он добавляет атрибут клиента , который используется для выполнения HTTP-запросов.
из импорта саранчи HttpUser, задача, между
класс MyUser (HttpUser):
время_ожидания = между (5, 15)
@задача(4)
индекс защиты (я):
self.client.get("/")
@задание 1)
деф о (себя):
self.client.get("/о/")
атрибут клиента / HttpSession
клиент является экземпляром HttpSession . HttpSession является подклассом/оболочкой для запросов. Сессия , поэтому ее возможности хорошо документированы и многим должны быть знакомы. Что добавляет HttpSession, так это в основном отчет о результатах запроса в Locust (успех/неудача, время ответа, длина ответа, имя).
Содержит методы для всех методов HTTP: get , пост , пост ,
…
Как и запросов. сохраняет файлы cookie между запросами, поэтому его можно легко использовать для входа на веб-сайты. Сеанс
Сеанс
Сделайте запрос POST, просмотрите ответ и неявно повторно используйте любой файл cookie сеанса, который мы получили для второго запроса
ответ = self.client.post("/логин", {"имя пользователя":"testuser", "пароль":"секрет"})
print("Код статуса ответа:", response.status_code)
print("Текст ответа:", response.text)
ответ = self.client.get("/мой-профиль")
HttpSession перехватывает любые запросов. RequestException , выброшенное сеансом (вызванное ошибками подключения, тайм-аутами или подобным), вместо этого возвращая фиктивный
Объект ответа с status_code , установленным на 0, и content , установленным на None.
Проверка ответов
Запросы считаются успешными, если код ответа HTTP в порядке (<400), но часто полезно выполнить дополнительную проверку ответа.
Вы можете пометить запрос как неудачный, используя аргумент catch_response , с оператором и
вызов response. failure()
failure()
с self.client.get("/", catch_response=True) в качестве ответа:
если response.text != "Успех":
response.failure("Неверный ответ")
elif response.elapsed.total_seconds() > 0,5:
response.failure("Запрос занял слишком много времени")
Вы также можете пометить запрос как успешный, даже если код ответа был неверным:
с self.client.get("/does_not_exist/", catch_response=True) в качестве ответа:
если response.status_code == 404:
ответ.успех()
Вы даже можете вообще не регистрировать запрос, генерируя исключение, а затем перехватывая его вне блока with. Или вы можете сгенерировать исключение саранчи, как в примере ниже, и позволить саранче поймать его.
из импорта locust.exception RescheduleTask
...
с self.client.get("/does_not_exist/", catch_response=True) в качестве ответа:
если response.status_code == 404:
поднять RescheduleTask()
REST/JSON API
Вот пример вызова REST API и проверки ответа:
из json import JSONDecodeError ... с self.client.post("/", json={"foo": 42, "bar": None}, catch_response=True) в качестве ответа: пытаться: если response.json()["приветствие"] != "привет": response.failure("Не получено ожидаемое значение в приветствии") кроме JSONDecodeError: response.failure("Ответ не может быть декодирован как JSON") кроме KeyError: response.failure("Ответ не содержит ожидаемого ключа приветствия")
locust-plugins имеет готовый класс для тестирования REST API, который называется RestUser.
Группировка запросов
На веб-сайтах очень часто встречаются страницы, URL-адреса которых содержат какие-либо динамические параметры.
Часто имеет смысл сгруппировать эти URL-адреса вместе в статистике пользователя. Это можно сделать
путем передачи аргумента name в HttpSession разные способы запросов.
Пример:
# Статистика по этим запросам будет сгруппирована в: /blog/?id=[id]
для я в диапазоне (10):
self. client.get("/blog?id=%i" % i, name="/blog?id=[id]")
client.get("/blog?id=%i" % i, name="/blog?id=[id]")
Могут быть ситуации, когда передача параметра в функцию запроса невозможна, например, при взаимодействии с библиотеками/SDK, которые
обернуть сеанс запросов. Альтернативный способ группировки запросов предоставляется путем установки атрибута client.request_name .
# Статистика по этим запросам будет сгруппирована в: /blog/?id=[id]
self.client.request_name="/blog?id=[id]"
для я в диапазоне (10):
self.client.get("/blog?id=%i" % i)
self.client.request_name=Нет
Если вы хотите объединить несколько группировок с минимальным шаблоном, вы можете использовать менеджер контекста client.rename_request() .
@задача
def multiple_groupings_example (я):
# Статистика по этим запросам будет сгруппирована в: /blog/?id=[id]
с self.client.rename_request("/blog?id=[id]"):
для я в диапазоне (10):
self.client.get("/blog?id=%i" % i)
# Статистика по этим запросам будет сгруппирована в: /article/?id=[id]
с self. client.rename_request("/article?id=[id]"):
для я в диапазоне (10):
self.client.get("/article?id=%i" % i)
client.rename_request("/article?id=[id]"):
для я в диапазоне (10):
self.client.get("/article?id=%i" % i)
Настройки прокси-сервера HTTP
Для повышения производительности мы настраиваем запросы, чтобы не искать настройки прокси-сервера HTTP в среде, установив
Запросы. Атрибут trust_env сеанса на False . Если вы этого не хотите, вы можете вручную установить locust_instance.client.trust_env от до True . Для получения дополнительной информации см.
документирование запросов.
Пул соединений
Поскольку каждый HttpUser создает новый HttpSession ,
каждый пользовательский экземпляр имеет свои собственные пулы соединений. Это похоже на то, как реальные пользователи будут взаимодействовать с веб-сервером.
Однако, если вы хотите разделить подключения между всеми пользователями, вы можете использовать одного менеджера пула. Для этого установите pool_manager атрибут класса экземпляру urllib3. . PoolManager
PoolManager
из импорта саранчи HttpUser
из urllib3 импортировать PoolManager
класс MyUser (HttpUser):
# Все пользователи будут ограничены максимум 10 одновременными подключениями.
pool_manager = Менеджер пула (максимальный размер = 10, блок = Истина)
Дополнительные параметры конфигурации см. документация urllib3.
Наборы задач
Наборы задач — это способ структурировать тесты иерархических веб-сайтов/систем. Вы можете прочитать больше об этом здесь.
Как структурировать тестовый код
Важно помнить, что файл locustfile.py — это обычный импортируемый модуль Python.
от Саранчи. Из этого модуля вы можете импортировать другой код Python, как обычно.
в любой программе Python. Текущий рабочий каталог автоматически добавляется в папку Python 9.1480 системный путь ,
поэтому любой файл/модуль/пакеты python, которые находятся в рабочем каталоге, могут быть импортированы с помощью
python импортирует оператор .
Для небольших тестов хранение всего тестового кода в одном файле locustfile.py должно работать нормально, но для
больших тестовых наборов вам, вероятно, захочется разбить код на несколько файлов и каталогов.
Как вы структурируете исходный код теста, конечно, полностью зависит от вас, но мы рекомендуем вам следуйте лучшим практикам Python. Вот пример файловой структуры воображаемого проекта Locust:
Проект с несколькими файлами саранчи также может хранить их в отдельном подкаталоге:
Корень проекта
обычный/__init__.pyавторизацияconfig.py
my_locustfiles/апи.pyвеб-сайт.py
требования.txt
С любой из вышеперечисленных структур проекта ваш locustfile может импортировать общие библиотеки, используя:
import common.auth
Написание заданий
Задачи Bolt аналогичны скриптам, но хранятся в модулях и могут иметь метаданные. Это позволяет повторно использовать и делиться ими.
Вы можете писать задачи на любом языке программирования, на котором работают цели, например Bash,
PowerShell или Python. Задача может быть даже скомпилированным двоичным файлом, который запускается на
цель. Поместите свою задачу в ./tasks каталог модуля и добавить
файл метаданных для описания параметров и настройки поведения задачи.
🔩 Совет: В большинстве случаев вы можете обернуть существующий скрипт в YAML плана, что дает вам те же преимущества, что и преобразование сценария в задачу. без особых усилий. Чтобы узнать больше о включении скриптов в планы YAML, см. Оборачиваем сценарий в план.
Чтобы задача запускалась на удаленных системах *nix, она должна содержать строку shebang ( #! )
вверху файла, чтобы указать интерпретатор.
Например, задача Puppet mysql::sql написана на Ruby и предоставляет
путь к интерпретатору Ruby. Этот пример также принимает несколько параметров в качестве
JSON на stdin и возвращает ошибку.
#!/opt/puppetlabs/puppet/bin/ruby
требуется 'json'
требуется «open3»
требуется «марионетка»
def get(sql, база данных, пользователь, пароль)
cmd = ['mysql', '-e', "#{sql}"]
cmd << "--database=#{database}", если только database.nil?
cmd << "--user=#{user}", если только user.nil?
cmd << "--password=#{password}", если только password.nil?
stdout, stderr, status = Open3.capture3(*cmd) # rubocop:disable Lint/UselessAssignment
поднять Puppet::Error, _("stderr: ' %{stderr}') % { stderr: stderr }"), если статус != 0
{статус: stdout.strip}
конец
параметры = JSON.parse(STDIN.read)
база данных = параметры ['база данных']
пользователь = параметры['пользователь']
пароль = параметры['пароль']
sql = параметры ['sql']
начинать
результат = получить (sql, база данных, пользователь, пароль)
помещает результат. to_json
выход 0
спасение Puppet::Error => e
puts({статус: 'сбой', ошибка: e.message }.to_json)
выход 1
конец
to_json
выход 0
спасение Puppet::Error => e
puts({статус: 'сбой', ошибка: e.message }.to_json)
выход 1
конец Именование задач
Вы используете имя задачи для взаимодействия с задачей из командной строки Bolt. За
например, вы можете использовать задачу запуска puppet_agent::version --targets localhost для запуска задачи puppet_agent::version .
Имена задач состоят из одного или двух сегментов имени, обозначающих:
Например, в модуле puppetlabs/mysql задача sql расположена по адресу ./mysql/tasks/sql.rb , поэтому имя задачи mysql::sql .
Вы можете писать задачи на любом языке, который работает на таргетах. Дайте файлы задач
расширение языка, на котором они написаны (например, .rb для Ruby) и
поместите их на верхний уровень каталога ./tasks вашего модуля.
Каждый сегмент имени задачи или плана должен начинаться со строчной буквы и:
Может включать цифры.

Может включать символы подчеркивания.
Сегменты пространства имен должны соответствовать регулярному выражению:
\A[a-z][a-z0-9_]*\Z.Расширение файла не должно использовать зарезервированные расширения
.mdили.json.
Примечание: Имя файла задачи
initявляется особенным: задача, которую он определяет, упоминается только по имени модуля. Например, в Модульpuppetlabs-service, задача, определенная вinit.rb, является службой. задача.
Метаданные задачи
Файлы метаданных задачи описывают параметры задачи, проверяют ввод и контролируют, как Болт выполняет задание.
Ваша задача должна иметь метаданные для публикации и совместного использования в Forge. Указать
метаданные задачи в файле JSON с соглашением об именах . Место
этот файл в папке модуля 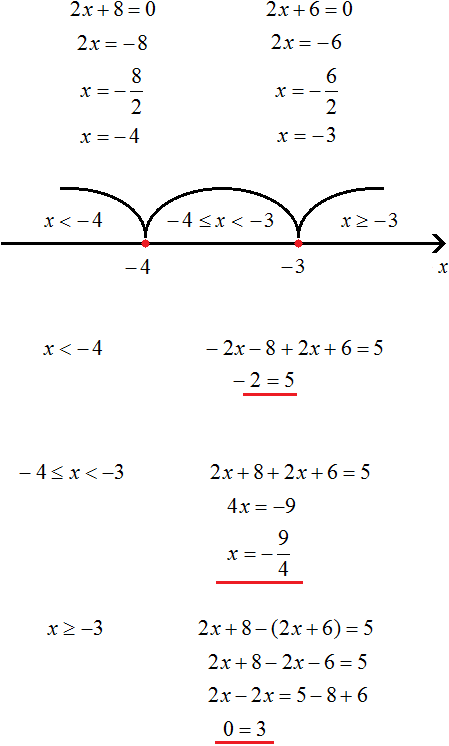 json
json ./tasks вместе с файлом задачи.
Например, модуль puppetlabs/mysql включает задачу mysql::sql с
файл метаданных, sql.json .
{
"description": "Позволяет выполнять произвольный SQL",
"input_method": "стандартный ввод",
"параметры": {
"база данных": {
"description": "База данных для подключения",
"тип": "Необязательно[Строка[1]]"
},
"пользователь": {
"description": "Пользователь",
"тип": "Необязательно[Строка[1]]"
},
"пароль": {
"description": "Пароль",
"тип": "Необязательно[Строка[1]]",
"чувствительный": правда
},
"sql": {
"description": "SQL, который вы хотите выполнить",
"тип": "Строка[1]"
}
}
} Поля метаданных задачи
В следующей таблице показаны ключи метаданных задачи, значения и значения по умолчанию.
| Ключ метаданных | Описание | Значение | По умолчанию |
|---|---|---|---|
"описание" | Описание того, что делает задача. | Строка | Нет |
"метод_ввода" | Какой метод ввода использует средство выполнения задач для передачи параметров задаче. |
| powershell для задач .ps1 . Обе среды и stdin для других задач. |
"параметры" | Параметры или входные данные, которые принимает задача, перечислены со строкой типа марионетки и необязательным описанием. Дополнительные сведения см. в разделе Добавление параметров к метаданным. | Массив объектов, описывающих каждый параметр | Нет |
"puppet_task_version" | Используемая версия спецификации. | Целое число | 1 (Это единственное допустимое значение.) |
"support_noop" | Поддерживает ли задача режим отсутствия операций. Требуется, чтобы задача принимала параметр --noop в командной строке. | Булево значение | ложь |
"реализации" | Список реализаций задач и требований, используемых для выбора одной из них для запуска. Информацию об использовании см. в разделе Одно- и кросс-платформенные задачи. Информацию об использовании см. в разделе Одно- и кросс-платформенные задачи. | Массив объектов, описывающих каждую реализацию | Нет |
"файлы" | Список файлов, которые необходимо предоставить при запуске задачи, адресованной модулем. Информацию об использовании см. в разделе Совместное использование кода задачи. | Массив строк | Нет |
"частный" | Не отображать задачу по умолчанию при отображении пользовательского интерфейса. | Булево значение | ложный |
"удаленный" | Разрешено ли выполнение этой задачи на прокси-цели, с которой она будет взаимодействовать с удаленной целью. Удаленные задачи не должны изменять состояние локально, если установлен метапараметр Удаленные задачи не должны изменять состояние локально, если установлен метапараметр _targets . Дополнительные сведения см. в разделе Написание удаленных задач. | Булево значение | ложный |
Общие типы данных задач
Метаданные задачи могут принимать большинство типов данных Puppet.
| Тип | Описание |
|---|---|
Строка | Принимает любую строку. |
Строка[1] | Принимает любую непустую строку (строку не менее длины 1 ). |
Перечисление [выбор1, выбор2] | Принимает один из перечисленных вариантов. |
Узор[/\A\w+\Z/] | Принимает строки, соответствующие регулярному выражению /\w+/ или непустые строки символов слова. |
Целое число | Принимает целые значения. JSON не имеет целочисленного типа, поэтому он может варьироваться в зависимости от ввода. |
Дополнительно [Строка [1]] | Необязательный делает параметр необязательным и допускает нулевые значения. Задачи не имеют обязательных значений, допускающих значение NULL. |
Массив [Строка] | Соответствует массиву строк. |
Хэш | Соответствует объекту JSON. |
Вариант[Целое число, Образец[/\A\d+\Z/]] | Соответствует целому числу или строке целого числа. |
Логический | Принимает логические значения. |
Внимание: Некоторые типы, поддерживаемые Puppet, не могут быть представлены в виде JSON, например
как Hash[Integer, String] , Object или Resource . Не используйте их в задачах,
потому что они никогда не могут быть сопоставлены.
📖 Связанная информация
Дополнительные сведения о типах данных Puppet см. в разделе Тип данных синтаксис
Определение параметров в задачах
Задачи могут получать входные данные либо в виде переменных среды, либо в виде хэша JSON по стандарту
ввода или в качестве аргументов PowerShell. По умолчанию Bolt отправляет параметры как
переменные среды и как JSON на
По умолчанию Bolt отправляет параметры как
переменные среды и как JSON на stdin . Переменные среды работают хорошо
для простых типов JSON, таких как строки и числа. Для массивов и хэшей используйте
вместо этого структурированный ввод, потому что параметры с неопределенными значениями ( nil , undef ), переданные в качестве переменных среды, имеют значение String null . За
дополнительную информацию см. в разделе Структурированный ввод и
выход.
Чтобы добавить параметр к вашей задаче в качестве переменной среды, передайте аргумент
с префиксом задачи Puppet PT_ .
Например, чтобы добавить в задачу параметр message , прочтите его из
окружение в коде задачи как PT_message . Когда пользователь запускает задачу, он может
укажите значение параметра в командной строке как message=hello и
средство выполнения задач отправляет значение hello в переменную PT_message .
#!/usr/bin/env bash echo ваше сообщение $PT_message
Если ваша задача должна получать параметры только определенным образом, например только stdin , вы можете установить метод ввода в метаданных задачи, используя метод_ввода . Дополнительные сведения о input_method см. в разделе Метаданные задачи.
ссылка.
Ограничения параметров задачи
При определении вашего параметры задачи:
Имена параметров задачи должны начинаться со строчной буквы и могут включать только строчные буквы (
a-z), цифры (0-9) и символы подчеркивания (_).Типы параметров задачи должны быть подтипом типа данных
Data. Для большего информацию об этом абстрактном типе данных см. вDatadata тип.
Определение параметров в Windows
Для задач Windows можно передавать параметры как переменные среды, но это
проще написать свою задачу в PowerShell и использовать именованные аргументы. По умолчанию,
задачи с расширением
По умолчанию,
задачи с расширением .ps1 используют стандартную обработку аргументов PowerShell.
Например, эта задача PowerShell принимает имя процесса в качестве аргумента и возвращает информацию о процессе. Если пользователь не передает параметр, task возвращает все процессы.
[Привязка командлета()]
Парам(
[Параметр (обязательный = $False)]
[Нить]
$имя
)
если ($Name -eq $null -или $Name -eq "") {
Get-процесс
} еще {
$processes = Get-Process -Name $Name
$результат = @()
foreach ($процесс в $процессах) {
$result += @{"Имя" = $process.ProcessName;
"ЦП" = $процесс.ЦП;
"Память" = $process.WorkingSet;
"Путь" = $процесс.Путь;
"Идентификатор" = $процесс.Ид}
}
если ($result.Count -eq 1) {
ConvertTo-Json -InputObject $result[0] -Compress
} elseif ($result.Count -gt 1) {
ConvertTo-Json -InputObject @{"_items" = $result} -Compress
}
} Чтобы передать параметры в вашей задаче как переменные среды ( PT_parameter ), вы
необходимо установить input_method в метаданных вашей задачи на environment . Для запуска Руби
задач в Windows, агент Puppet должен быть установлен на цели.
Для запуска Руби
задач в Windows, агент Puppet должен быть установлен на цели.
Добавление параметров в метаданные
Чтобы задокументировать и проверить параметры задачи, добавьте параметры в задачу
метаданные как объект JSON, параметров .
Если задача включает параметров в своих метаданных, Bolt отклоняет любые параметры
входные данные для задачи, которые не определены в метаданных.
В объекте параметр дайте каждому параметру описание и укажите его
Кукольный тип. Полный список типов см. в разделе Типы
документация.
Например, следующий код в файле метаданных описывает поставщика параметр:
"провайдер": {
"description": "Поставщик, используемый для управления или проверки службы, по умолчанию является системным менеджером служб",
"тип": "Необязательно[Строка[1]]"
} Определение чувствительных параметров
Вы можете определить параметры задачи как конфиденциальные. Например, пароли и API
ключи. Эти значения маскируются, когда они появляются в журналах и ответах API. Когда
вы хотите просмотреть эти значения, установите для файла журнала уровень
Например, пароли и API
ключи. Эти значения маскируются, когда они появляются в журналах и ответах API. Когда
вы хотите просмотреть эти значения, установите для файла журнала уровень : debug .
Чтобы определить параметр как конфиденциальный в метаданных JSON, добавьте "чувствительный": истинное свойство .
{
"description": "Эта задача имеет конфиденциальное свойство, обозначенное ее метаданными",
"input_method": "стандартный ввод",
"параметры": {
"пользователь": {
"description": "Пользователь",
"тип": "Строка[1]"
},
"пароль": {
"description": "Пароль",
"тип": "Строка[1]",
"чувствительный": правда
}
}
} Установка значений по умолчанию
Вы можете установить значение по умолчанию для параметра, который будет использоваться, если параметр
не указан или если параметр указан и имеет значение Undef .
значение по умолчанию будет использоваться, даже если тип параметра является необязательным. Значения по умолчанию должны
быть действительным в соответствии с типом параметра
Значения по умолчанию должны
быть действительным в соответствии с типом параметра .
{
"description": "У этой задачи есть параметр со значением по умолчанию",
"input_method": "стандартный ввод",
"параметры": {
"Платформа" : {
"description": "Какую операционную систему предоставить",
"тип": "Строка[1]"
},
"считать": {
"description": "Сколько экземпляров предоставить",
"тип": "Целое",
"по умолчанию": 1
}
} Примечание: Не каждая версия Bolt поддерживает параметры по умолчанию, поэтому вам следует либо сделать параметр обязательным, либо явно проверить его наличие в выполнение задания.
Использование структурированного ввода и вывода
Если у вас есть задача, которая имеет много параметров, возвращает много информации или частью плана задач, рассмотрите возможность использования структурированного ввода и вывода в своей задаче.
API задач основан на JSON. Параметры задачи закодированы в JSON, и задача
runner пытается проанализировать выходные данные задач как объект JSON.
Параметры задачи закодированы в JSON, и задача
runner пытается проанализировать выходные данные задач как объект JSON.
Болт может вводить в этот объект ключи с префиксом _ . Если задача не
возвращает объект JSON, Bolt создает его и помещает вывод в _output ключ.
Структурированный ввод
Для сложных входных данных, таких как хэши и массивы, вы можете принимать структурированный JSON в твое задание.
По умолчанию Bolt передает параметры задачи как переменные среды и как
один объект JSON на stdin . Вход JSON позволяет задаче принимать сложные
структуры данных.
Чтобы принимать параметры в формате JSON на stdin , установите ключ params для приема JSON на стандартный ввод :
#!/opt/puppetlabs/puppet/bin/ruby
требуется 'json'
параметры = JSON.parse(STDIN.read)
код выхода = 0
params['files'].each do |имя файла|
начинать
FileUtils.touch(имя файла)
помещает "обновленный файл # {имя файла}"
спасать
код выхода = 1
пишет "не удалось обновить файл # {имя файла}"
конец
конец
exit код выхода Если ваша задача принимает ввод на stdin , укажите "input_method": "stdin" в
файл задачи metadata., или он может не работать с  json
json sudo для некоторых пользователей.
Возврат структурированного вывода
Структурированный вывод полезен, если вы хотите использовать вывод в другой программе или если вы хотите использовать результат задачи в плане задач Puppet.
Чтобы вернуть структурированные данные из задачи, напечатайте только один объект JSON в stdout в вашей задаче.
#!/usr/bin/env Python
импортировать json
импорт системы
минор = sys.version_info
результат = { "основной": sys.version_info.major, "дополнительный": sys.version_info.minor}
json.dump(результат, sys.stdout) Возврат ошибок в задачах
Чтобы вернуть подробное сообщение об ошибке в случае сбоя задачи, включите объект Error .
в результате задачи.
Когда задача завершается ненулевым значением, Bolt проверяет ключ ошибки _error . Если один не
присутствует, Bolt генерирует общую ошибку и добавляет ее к результату. Если там есть
нет текста на
Если там есть
нет текста на stdout , но текст присутствует на stderr , текст stderr есть
включены в сообщение.
{ "_ошибка": {
"msg": "Задача завершена 1:\nЧто-то в stderr",
"вид": "puppetlabs.tasks/task-error",
"подробности": { "код выхода": 1 }
}
} Объект ошибки включает следующие ключи:
msg— понятная человеку строка, отображаемая в пользовательском интерфейсе.вид- Стандартная веревка для машин. Вы можете поделиться видами между вашими модулями или типами пространств имен для каждого модуля.подробнее- Объект структурированных данных о задачах.
Задачи могут предоставить дополнительные сведения об ошибке, включив собственную ошибку
объект в результате на _ошибка .
#!/opt/puppetlabs/puppet/bin/ruby требуется 'json' начинать параметры = JSON.parse(STDIN.read) результат = {} результат['результат'] = параметры['дивиденд'] / параметры['делитель'] спасение ZeroDivisionError результат[:_error] = { msg: "Невозможно разделить на ноль", # присвоить имя ошибке этому модулю вид: "puppetlabs-example_modules/dividebyzero", подробности: {делитель: params['divisor'] }, } Исключение спасения => e результат[:_error] = { msg: e.message, вид: "puppetlabs-example_modules/неизвестно", подробности: {класс: e.class.to_s}, } конец помещает результат.to_json
Результаты ошибок обычно содержат номер файла и строки под ключом Details ошибка. Bolt объединяет ключи «файл» и «строка» с результатами, если «файл» не присутствует в _error хэш, возвращенный из задачи.
Возврат конфиденциальных данных
Чтобы вернуть секреты из задачи, используйте ключ _sensive на верхнем уровне вывода. Болт лечит
результат как чувствительный и не позволяет вывести его на консоль или в журнал. Обратите внимание, что Болт
не запутывает данные ниже
Болт лечит
результат как чувствительный и не позволяет вывести его на консоль или в журнал. Обратите внимание, что Болт
не запутывает данные ниже _sensitive , если _sensitive не находится на верхнем уровне. Например,
Bolt не рассматривает эти данные пользователя как конфиденциальные: {user: _sensitive: {carmen: sandiego } } .
Эта задача создает случайный пароль для пользователя Someone , что делает хэш пароля чувствительным.
#!/opt/puppetlabs/puppet/bin/ruby
требуется 'json'
имя_пользователя = 'кто-то'
# Генерируем пароль из 10 букв
user_password = [*'a'..'z'].sample(10).join
результат = { пользователь: имя_пользователя, _чувствительный: { пароль: пароль_пользователя } }
помещает результат.to_json Запуск задачи печатает:
$ Bolt Task run mytask -t myhost
Начал на моем хосте...
Готово на моем хосте:
{
"пользователь": "кто-то",
"_sensitive": "Конфиденциальный [значение отредактировано]"
} Поддержка отсутствия операций в задачах
Задачи поддерживают функцию бездействия, также известную как режим бездействия. Этот
функция показывает, какие изменения внесла бы задача, фактически не внося эти изменения.
изменения.
Этот
функция показывает, какие изменения внесла бы задача, фактически не внося эти изменения.
изменения.
Поддержка отсутствия операций позволяет пользователю передавать флаг --noop с командой для проверки
будет ли задача выполнена успешно на всех целях, прежде чем вносить изменения.
Для поддержки отсутствия операций ваша задача должна включать код, который ищет _noop метапараметр.
Если пользователь передает флаг --noop в своей команде, этот параметр устанавливается
на true , и ваша задача не должна вносить изменения. Вы также должны установить supports_noop to true в метаданных вашей задачи, иначе Bolt откажется запускать
задача в noop-режиме.
Пример неактивных метаданных
{
"description": "Записать содержимое в файл.",
"supports_noop": правда,
"параметры": {
"имя файла": {
"description": "файл для записи",
"тип": "Строка[1]"
},
"содержание": {
"description": "Контент для написания",
"тип": "Строка"
}
}
} Пример задачи без операции
#!/usr/bin/env Python импортировать json импорт ОС импорт системы параметры = json.load(sys.stdin) имя файла = параметры['имя файла'] контент = параметры['контент'] noop = params.get('_noop', ложь) код выхода = 0 определение make_error (сообщение): ошибка = { "_ошибка": { "вид": "файл_ошибка", "сообщение": сообщение, "Детали": {}, } } вернуть ошибку пытаться: если нет: путь = os.path.abspath(os.path.join(имя файла, os.pardir)) file_exists = os.access(имя файла, os.F_OK) file_writable = os.access(имя файла, os.W_OK) path_writable = os.access(путь, os.W_OK) если path_writable == False: код выхода = 1 результат = make_error("Путь %s недоступен для записи" % путь) elif file_exists == True и file_writable == False: код выхода = 1 результат = make_error("Файл %s недоступен для записи" % имя файла) еще: результат = { "успех": Истина, '_noop': Истина} еще: с открытым (имя файла, 'w') как fh: fh.write(содержание) результат = { "успех": Истина} кроме Исключения как e: код выхода = 1 результат = make_error("Не удалось открыть файл %s: %s" % (имя файла, str(e))) печать (json.
dumps (результат)) выход (код выхода)
В большинстве случаев задачи разрабатываются для одной платформы и состоят из одного
исполняемый файл с соответствующим файлом метаданных или без него. За
например, ./mysql/tasks/sql.rb и ./mysql/tasks/sql.json . В этом случае нет
другие ./mysql/tasks/sql.* файлы могут существовать.
Задача может иметь несколько реализаций с метаданными, объясняющими, когда использовать каждый. Основным вариантом использования этого является поддержка различных реализации для разных целевых платформ, называемые кроссплатформенными задачи.
Например, рассмотрим модуль со следующими файлами:
- задачи - sql_linux.sh - sql_linux.json - sql_windows.ps1 - sql_windows.json - sql.json
Эта задача имеет файл метаданных задачи ( sql.json ), две метаданные реализации
файлы ( sql_linux.json и sql_windows.json ) и два исполняемых файла
( sql_linux. и  sh
sh sql_windows.ps1 ). Файлы метаданных реализации
задокументируйте, как использовать реализацию напрямую, или пометьте реализацию как
private, чтобы скрыть его из списков пользовательского интерфейса.
Например, файл метаданных реализации sql_linux.json содержит
далее:
{
"имя": "SQL Linux",
"description": "Задача на выполнение операций sql с целями Linux",
"частное": правда
} Файл метаданных задачи, sql.json , содержит раздел реализации:
{
"реализации": [
{"имя": "sql_linux.sh", "требования": ["оболочка"]},
{"имя": "sql_windows.ps1", "требования": ["powershell"]}
]
} Каждая реализация имеет имя и список требований . Задача
требования непосредственно соответствуют характеристикам Bolt . Функция должна быть доступна
на цель, чтобы Bolt мог использовать реализацию. Вы можете указать
дополнительные функции для цели с помощью функции set_feature в Bolt
план или добавив функции в файл инвентаризации. Болт выбирает первый
реализации, чьи требования удовлетворены.
Болт выбирает первый
реализации, чьи требования удовлетворены.
Bolt по умолчанию определяет следующие функции:
puppet-agent: присутствует, если у цели есть пакет агента Puppet. установлены. Эта функция автоматически добавляется к хостам с именемлокальный хост.оболочка: присутствует, если цель имеет оболочку POSIX.powershell: присутствует, если у цели есть PowerShell.
В приведенном выше примере файл sql_linux.sh 9Для реализации 1481 требуется оболочка функция, а для реализации sql_windows.ps1 требуется PowerShell
особенность.
Запись удаленных задач
Некоторые цели трудно или невозможно выполнять напрямую. В этих случаях можно написать задачу, которая запускается на прокси-таргете и удаленно взаимодействует с настоящей целью.
Например, сетевое устройство может иметь ограниченную среду оболочки или облачное
служба может управляться только API-интерфейсами HTTP. Написав удаленную задачу, Bolt позволяет
вам указать информацию о подключении для удаленных целей в их файле инвентаризации
и вводит их в
Написав удаленную задачу, Bolt позволяет
вам указать информацию о подключении для удаленных целей в их файле инвентаризации
и вводит их в _target метапараметр.
В этом примере показано, как написать задачу, которая отправляет сообщения в Slack и читает
информация о подключении из inventory.yaml :
#!/usr/bin/env ruby
# модули/slack/tasks/message.rb
требуется 'json'
требуется 'сеть/http'
параметры = JSON.parse(STDIN.read)
# токен Slack API передается из инвентаря
токен = параметры['_target']['токен']
uri = URI('https://slack.com/api/chat.postMessage')
http = Net::HTTP.new(uri.хост, uri.порт)
http.use_ssl = правда
req = Net::HTTP::Post.new(uri, 'Content-type' => 'application/json')
req['Authorization'] = "Bearer #{params['_target']['token']}"
req.body = {канал: params['канал'], текст: params['сообщение'] }.to_json
resp = http.request(req)
ставит соотв.тело Для предотвращения случайного запуска обычной задачи на удаленной цели и нарушения своей конфигурации, Bolt не будет запускать задачу на удаленной цели, если ее метаданные определяет его как удаленный:
{
"удаленный": правда
} Добавьте Slack в качестве удаленной цели в файл инвентаризации:
целей:
- имя: my_slack
конфигурация:
транспорт: удаленный
удаленный:
token: Наконец, сделайте my_slack целью, которая может запускать slack::message :
Bolt task run slack::message --targets my_slack message="hello" channel=<идентификатор канала slack>
Преобразование скриптов в задачи
Чтобы преобразовать существующий скрипт в задачу, вы можете либо написать задачу,
сценарий, или вы можете добавить в свой сценарий логику для проверки параметров в
переменные окружения.
Если скрипт уже установлен на таргетах, можно написать задачу, которая оборачивает сценарий. В задаче прочитайте аргументы скрипта как параметры задачи и вызвать скрипт, передав параметры в качестве аргументов.
Если скрипт не установлен или вы хотите сделать его целостной задачей, поэтому
что вы можете управлять его версией с помощью инструментов управления кодом, добавлять код в свой
сценарий для проверки переменных среды с префиксом PT_ и чтения
их вместо аргументов.
Учитывая сценарий, который принимает позиционные аргументы в командной строке:
версия=$1 [ -z "$version" ] && echo "Необходимо указать версию для развертывания && exit 1 если [-z "$2"]; тогда имя файла=$2 еще имя_файла=~/мой файл фи
Чтобы преобразовать скрипт в задачу, замените эту логику переменными задачи:
версия=$PT_version #не нужно проверять, если мы используем метаданные если [-z "$PT_имя_файла"]; тогда имя_файла=$PT_имя_файла еще имя_файла=~/мой файл fi
Внимание : Если вы собираетесь использовать задачу с Puppet Enterprise и назначить Разрешения RBAC, убедитесь, что сценарий безопасно обрабатывает параметры, или проверьте их для предотвращения уязвимостей внедрения оболочки.
Совместное использование исполняемых файлов
Несколько реализаций задач могут ссылаться на один и тот же исполняемый файл.
Исполняемые файлы могут получить доступ к метапараметру _task , который содержит имя задачи.
Например, в следующем примере создаются задачи service::stop и service::start , которые находятся в исполняемом файле, но отображаются как две отдельные задачи.
myservice/tasks/init.rb
#!/usr/bin/env рубин
требуется 'json'
параметры = JSON.parse(STDIN.read)
действие = параметры['действие'] || параметры['_task']
если ['старт', 'стоп'].include?(действие)
`systemctl #{params['_task']} #{params['service']}`
конец
myservice/tasks/start.json
{
"description": "Запустить службу",
"параметры": {
"оказание услуг": {
"тип": "Строка",
"description": "Служба для запуска"
}
},
"реализации": [
{"имя": "init.rb"}
]
} myservice/tasks/stop.json
{
"description": "Остановить службу",
"параметры": {
"оказание услуг": {
"тип": "Строка",
"description": "Служба для остановки"
}
},
"реализации": [
{"имя": "init.rb"}
]
} Совместное использование кода задачи
Несколько задач могут совместно использовать общие файлы. Задачи могут дополнительно тянуть код библиотеки из других модулей.
Чтобы создать задачу, включающую дополнительные файлы, извлеченные из модулей, включите
свойство files в ваших метаданных в виде массива путей. Путь состоит из:
Имя модуля.
Один из следующих каталогов в модуле:
файлы— Большинство вспомогательных файлов. Это предотвращает обработку файла в качестве задачи или добавлены в путь загрузки Puppet Ruby.tasks— Вспомогательные файлы, которые можно вызывать как самостоятельные задачи.lib— код Ruby, который может быть повторно использован типами, провайдерами или Puppet. функции.
функции.скрипты— Скрипты, которые можно вызывать из задачи.
Оставшийся путь к файлу или каталогу; каталоги должны включать завершающая косая черта
/.
Все разделители путей должны быть косой чертой. Например, stdlib/lib/puppet/ .
Вы можете включить свойство files как свойство метаданных верхнего уровня и как
свойство реализации, например:
{
"реализации": [
{"имя": "sql_linux.sh", "требования": ["оболочка"], "файлы": ["mymodule/files/lib.sh"]},
{"имя": "sql_windows.ps1", "требования": ["powershell"], "файлы": ["mymodule/files/lib.ps1"]}
],
"файлы": ["смайлики/файлы/смайлики/"]
} Если задача включает свойство files , все файлы, перечисленные в верхнем уровне
свойство и в конкретной реализации, выбранной для цели, копируются в
временный каталог на цели. Структура каталогов указанного
файлы сохраняются, поэтому пути, указанные с помощью параметра метаданных files ,
доступно для задач с префиксом _installdir . Сам исполняемый файл задачи
находится в расположении своего модуля под
Сам исполняемый файл задачи
находится в расположении своего модуля под _installdir , поэтому другие файлы
можно найти в ../../mymodule/files/ относительно расположения задачи
исполняемый.
Например, вы можете создать задачу и метаданные в модуле по адресу ~/.puppetlabs/bolt/site-modules/mymodule/tasks/task.{json,rb} .
Метаданные
{
"файлы": ["многозадачность/файлы/rb_helper.rb"]
} Файловый ресурс
multi_task/files/rb_helper.rb
def полезное_ruby
{помощник: "рубин"}
конец Задача
#!/usr/bin/env рубин требуется 'json' параметры = JSON.parse(STDIN.read) require_relative File.join (params ['_installdir'], 'multi_task', 'files', 'rb_helper.rb') # В качестве альтернативы используйте относительный путь # require_relative File.join(__dir__, '..', '..', 'multi_task', 'files', 'rb_helper.rb') ставит полезный_ruby.to_json
Вывод
Запущен на локальном хосте...
Готово на локальном хосте:
{
"помощник": "рубин"
}
Успешно на 1 цели: localhost
Пробежал по 1 цели за 0,12 секунды Помощники по задачам
Bolt поставляется с несколькими библиотеками, которые можно использовать для написания задач. См. Помощники по задачам для получения списка помощников по задачам, которые поставляется с Bolt и примерами их использования в ваших задачах.
Методы безопасного кодирования для задач
Используйте методы безопасного кодирования при написании задач и помогите защитить свою систему.
Примечание: Информация в этом разделе охватывает основные методы кодирования для написание безопасных задач. Это не исчерпывающий список.
Одним из методов, который злоумышленники используют для получения доступа к вашим системам, является удаленный код.
выполнение, где они могут получить доступ к другим частям вашей системы и
вносить произвольные изменения, запустив разрешенный скрипт. Потому что Bolt выполняет
сценарии в вашей инфраструктуре, важно знать об определенных
уязвимости и кодировать задачи таким образом, чтобы защититься от удаленного кода
исполнение.
Потому что Bolt выполняет
сценарии в вашей инфраструктуре, важно знать об определенных
уязвимости и кодировать задачи таким образом, чтобы защититься от удаленного кода
исполнение.
Добавление метаданных задачи, проверяющих входные данные, является одним из способов снижения уязвимости.
Когда вам требуется перечисляемый ( enum ) или другие нестроковые типы, вы предотвращаете
введены неверные данные. Произвольный строковый параметр не имеет
это заверение.
Например, если в вашей задаче есть параметр, который выбирает из нескольких операционных режимы, которые передаются команде оболочки вместо
String $mode = 'file'
use
Enum[file,directory,link,socket] $mode = file
Если ваша задача имеет параметр, который идентифицирует файл на диске, убедитесь, что пользователь не может указать относительный путь, который приведет их в области, где они не должны быть. Отклонять имена файлов, содержащие косую черту. 9\/\\]*\z/] $path
В дополнение к этим ограничениям задач каждый из языков сценариев имеет
свои собственные способы проверки пользовательского ввода.
PowerShell
В PowerShell внедрение кода использует вызовы, которые специально оценивают код. Делать
не вызывать Invoke-Expression или Add-Type с пользовательским вводом. Эти команды
оценивать строки как код C#.
Чтение конфиденциальных файлов или перезапись важных файлов может быть менее очевидным. Если
вы планируете разрешить пользователям указывать имя файла или путь, используйте Resolve-Path к
убедитесь, что путь не выходит за пределы мест, которые вы ожидаете от задачи
доступ. Используйте Split-Path -Parent $path , чтобы проверить, что разрешенный путь имеет
желаемый путь в качестве родителя.
Дополнительные сведения см. в PowerShell. Сценарии и Руководство по безопасности Powershell Принципы.
Баш
В Bash и других командных оболочках внедрение команд оболочки использует преимущества
плохая реализация оболочки. Поместите аргументы в кавычки, чтобы предотвратить
уязвимые снаряды от их оценки.
Поскольку команда eval оценивает все аргументы с подстановкой строк,
избегайте использования его с пользовательским вводом; однако вы можете использовать eval с достаточным
заключение в кавычки для предотвращения выполнения замещенных переменных.
Вместо
eval "echo $input"
используйте
eval "echo '$input'"
Это специальные инструменты операционной системы для проверки путей к файлам: realpath или ссылка чтения -f .
Питон
В Python вредоносный код может быть введен с помощью таких команд, как eval , exec , os.system , os.popen и subprocess.call с shell=True . Использовать subprocess.call с оболочкой = False , когда вы включаете пользовательский ввод в команду или
эскейп-переменные.
Вместо
os.system('echo'+input)
использование
subprocess.check_output(['echo', input])
Разрешите пути к файлам с помощью os.realpath и подтвердите, что они находятся внутри другого пути
путем перебора os.path.dirname и сравнения с желаемым путем.
Для получения дополнительной информации об уязвимостях Python или как избежать переменные, см. сообщение в блоге Кевина Лондона на Dangerous Python Функции.
Рубин
В Ruby внедрение команд осуществляется с помощью таких команд, как eval , exec , система , обратная кавычка (``) или %x() выполнение или модуль Open3. Вы можете безопасно
вызовите эти функции с пользовательским вводом, передав ввод как дополнительный
аргументы вместо одной строки.
Вместо
system("echo #{flag1} #{flag2}") используйте
system('echo', flag1, flag2) Разрешите пути к файлам с помощью Pathname#realpath и подтвердите их быть внутри
другой путь, перебирая Pathname#parent и сравнивая с желаемым
дорожка.
Дополнительные сведения о безопасной передаче пользовательского ввода см. в сообщении блога Stop используя обратную кавычку для запуска команды оболочки в Рубин.
Задачи отладки
Существует несколько способов отладки задач, в том числе с помощью удаленного
библиотеки отладки с использованием методов, доступных в библиотеках помощников задач,
локальное выполнение задачи в виде сценария и перенаправление stderr на stdout .
Журналы отладки
Как правило, Bolt отображает только выходные данные задачи, которые отправляются на стандартный вывод . Однако,
Bolt регистрирует дополнительную информацию о выполнении задачи, включая выходные данные, отправленные на stderr , на уровне отладки . Вы можете просмотреть эти журналы во время выполнения задачи, используя
параметр --log-level debug CLI.
$ запустить задачу запуска mytask param1=foo param2=bar -t all --log-level debug
Отладчики
Многие языки сценариев, которые можно использовать для написания задач, имеют средства отладки. доступные библиотеки, которые позволяют вам устанавливать точки останова и исследовать вашу задачу
как он выполняется.
доступные библиотеки, которые позволяют вам устанавливать точки останова и исследовать вашу задачу
как он выполняется.
И Python, и Ruby имеют доступные библиотеки удаленной отладки, которые делают его легко приостановить выполнение задачи и отладить код. Использование удаленной отладки библиотеки необходимы при выполнении задач с помощью Bolt, поскольку задачи выполняются в отдельных потоках.
Задачи PowerShell могут использовать командлет Set-PSBreakpoint , который
устанавливает точку останова в сценарии PowerShell и позволяет пошагово выполнить
код. Поскольку Bolt передает параметры задачам PowerShell в виде именованных аргументов,
вы можете легко запускать задачи PowerShell как сценарии и использовать Set-PSBreakpoint командлет.
задач Python
Библиотека rpdb является оболочкой для библиотеки pdb , стандарта Python.
отладочная библиотека. Чтобы использовать библиотеку rpdb , ее необходимо установить
на каждой цели, на которой вы хотите отлаживать задачу.
🔩 Совет: В большинстве случаев отлаживать задачи можно, только запуская их на
localhostвместо списка удаленных целей. Это позволяет избежать необходимости установить соединение с целью, что может быть сложно, если ваша цель ограничивает входящие соединения.
Вы можете установить библиотеку rpdb с помощью pip :
$ pip install rpdb
Затем добавьте следующую строку в свою задачу везде, где вы хотите начать отладку:
import rpdb; rpdb.set_trace()
Затем вы можете открыть соединение с целью через порт 4444 , чтобы начать отладку:
$ nc 127.0.0.1 4444 > /tmp/96a96045-0eed-4dea-a497-400b9d5c8e30/python/tasks/init.py(13)task() -> результат = число1 + число2 (Пдб)
📖 Сопутствующая информация
rpdbдокументацияpdbдокументация
Рубиновые задачи
Драгоценный камень pry-remote позволяет вам начать сеанс удаленной отладки, используя pry gem, стандартная библиотека отладки для Ruby. Для использования пульта дистанционного управления
Для использования пульта дистанционного управления gem, вам нужно будет установить его на каждую цель, которую вы хотите отладить.
на.
🔩 Совет: В большинстве случаев отлаживать задачи можно, только запуская их на
localhostвместо списка удаленных целей. Это позволяет избежать необходимости установить соединение с целью, что может быть сложно, если ваша цель ограничивает входящие соединения.
Если вы запускаете задачу на удаленных объектах, вы можете установить pry-remote gem с использованием gem install :
$ gem install pry-remote
Если вы запускаете задачу на localhost , вы можете установить pry-remote gem локально с помощью Bolt Ruby:
$ /opt/puppetlabs/bolt/bin/gem install --user-install pry-remote
Если вы запускаете задачу на localhost в Windows, выполните следующее
вместо этого введите команду:
> "C:/Program Files/Puppet Labs/Bolt/bin/gem.bat" install --user-install pry-remote
Затем добавьте следующую строку в свою задачу везде, где вы хотите начать отладку :
требуют «удаленного доступа»; привязка.remote_pry
Затем вы можете открыть соединение с целью с помощью команды pry-remote :
$ pry-remote -s 127.0.0.1
Номер кадра: 0/4
Из: /tmp/4f9dcfa3-ce0c-49e2-bcf5-8d761b202186/ruby/tasks/init.rb @ строка 9 MyClass#task:
6: задача определения (варианты)
=> 9: требуется «удаленный доступ»; привязка.remote_pry
10: Примечание: pry-remote не работает с pry-byebug или pry-nav в Ruby 2.x. Используйте «помощь» в подглядывании отладчик для списка доступных команд.
📖 Сопутствующая информация
pry-remoteдокументацияподставкадокументация
задачи PowerShell
Задачи PowerShell могут использовать командлет Set-PSBreakpoint для отладки. задачи, которые запускаются как сценарии. Командлет
задачи, которые запускаются как сценарии. Командлет Set-PSBreakpoint может установить
точка останова в определенной строке вашей задачи, приостанавливающая выполнение задачи
так что вы можете изучить код и выполнить его построчно.
Чтобы установить точку останова в определенной строке вашей задачи, запустите Set-PSBreakpoint командлет:
> Set-PSBreakpoint -Script mytask.ps1 -Line <номер строки>
Затем можно запустить задачу как сценарий. Выполнение задачи будет приостановлено в точка останова.
> ./mytask.ps1
📖 Связанная информация
Set-PSBreakpointдокументация
Вспомогательные методы задачи
Обе задачи Python
помощник и Руби
помощник по задачам включает
методы, которые могут помочь вам отладить задачу. Метод отладки регистрирует произвольные значения
как отладочные сообщения, а метод debug_statements возвращает массив
зарегистрированные отладочные сообщения.
Когда задача, использующая вспомогательную библиотеку задач, вызывает TaskError , ошибка
включите все зарегистрированные сообщения об отладке в ключе details . Вы также можете добавить
операторы отладки при поднятии TaskError самостоятельно, позвонив debug_statements и добавление результата под ключом details .
🔩 Совет: При запуске задачи с
Bolt Task runиспользуйте--format jsonвозможность увидеть полный результат от задачи, включая значениедеталиключ.
задач Python
Следующая задача Python включает несколько операторов отладки, описывающих что делает задача и результаты пары арифметических операций:
Метаданные
{
"файлы": ["python_task_helper/files/task_helper.py"]
} Задача
#!/usr/bin/env python импорт ОС, СИС sys.path.append(os.path.join(os.path.dirname(__file__), '..', '..', 'python_task_helper', 'файлы')) из task_helper импортировать TaskHelper класс MyTask (TaskHelper): задача защиты (я, аргументы): self.debug('Добавление значений') сумма = аргументы ['значение_1'] + аргументы ['значение_2'] self.debug("Сумма значений: {}".format(sum)) self.debug('Разделение значений') частное = аргументы['значение_1'] / аргументы['значение_2'] self.debug("Частное значений: {}".format(частное)) return { 'сумма': сумма, 'частное': частное} если __name__ == '__main__': МояЗадача().Выполнить()
Вывод
Запуск этой задачи с параметром value_2=0 вызовет ошибку TaskError который будет автоматически включать зарегистрированные операторы отладки под детали ключ:
$ задача запуска mytask -t localhost value_1 = 10 value_2 = 0 --format json
{
"Предметы":[
{
«цель»: «локальный хост»,
"действие":"задача",
"объект":"моя задача",
"статус":"неудача",
"ценность":{
"_ошибка":{
"msg":"целочисленное деление или по модулю на ноль",
"issue_code":"ИСКЛЮЧЕНИЕ",
"вид": "python. task.helper/исключение",
"Детали":{
"отлаживать":[
"Добавление значений",
"Сумма значений: 1",
«Разделение ценностей»
],
"класс": "ZeroDivisionError"
}
}
}
}
],
«целевой_счетчик»: 1,
"прошедшее_время":0
}
task.helper/исключение",
"Детали":{
"отлаживать":[
"Добавление значений",
"Сумма значений: 1",
«Разделение ценностей»
],
"класс": "ZeroDivisionError"
}
}
}
}
],
«целевой_счетчик»: 1,
"прошедшее_время":0
} 📖 Информация по теме
Помощник по задачам Python отладка
Задачи Ruby
Следующая задача Ruby включает несколько операторов отладки, описывающих что делает задача и результаты пары арифметических операций:
Метаданные
{
"файлы": ["ruby_task_helper/lib/task_helper.rb"]
} Задача
#!/usr/bin/env ruby
require_relative "../../ruby_task_helper/files/task_helper.rb"
класс MyTask < TaskHelper
задача определения (параметры)
отладить «Добавление значений»
сумма = опции[:значение_1] + опции[:значение_2]
отладка "Сумма значений: #{сумма}"
отладить «Разделение значений»
частное = опции[:значение_1] / опции[:значение_2]
отладка "Частное значений: #{частное}"
{ сумма: сумма, частное: частное }
конец
конец
если __FILE__ == $0
MyTask. run
конец
run
конец Вывод
Запуск этой задачи с параметром value_2=0 вызовет ошибку TaskError который будет автоматически включать зарегистрированные операторы отладки под детали ключ:
$ задача запуска mytask -t localhost value_1 = 10 value_2 = 0 --format json
{
"Предметы":[
{
«цель»: «локальный хост»,
"действие":"задача",
"объект":"моя задача",
"статус":"неудача",
"ценность":{
"_ошибка":{
"вид": "ZeroDivisionError",
"msg":"делится на 0",
"Детали":{
"отлаживать":[
"Добавление значений",
"Сумма значений: 1",
«Разделение ценностей»
]
}
}
}
}
],
«целевой_счетчик»: 1,
"прошедшее_время":0
} 📖 Информация по теме
Ruby Task Helper отладка
Запуск задачи как сценария
Запуск задач без Bolt может упростить отладку, так как задача не
больше не выполняться в отдельном потоке. Так как задачи похожи на скрипты,
вы можете внести временные изменения в задачу, чтобы они могли принимать командную строку
аргументы и запускаться из командной строки.
Так как задачи похожи на скрипты,
вы можете внести временные изменения в задачу, чтобы они могли принимать командную строку
аргументы и запускаться из командной строки.
Примеры Python
Задачи, написанные для приема ввода от stdin уже можно запустить как
скрипт, передав параметры в формате JSON задаче:
#!/usr/bin/env python
импорт систем, JSON
параметры = json.load(sys.stdin)
результат = {
«сумма»: параметры ['num1'] + параметры ['num2']
}
print(json.dumps(result)) $ echo '{"num1":10,"num2":5}' | ./mytask.py Кроме того, вы можете написать свою задачу для разбора аргументов командной строки. в качестве параметров, если они присутствуют:
#!/usr/bin/env python
импорт систем, JSON
если len(sys.argv) > 0:
параметры = {
"num1": интервал (sys.argv [1]),
"num2": интервал (sys.argv [2])
}
еще:
параметры = json.load(sys.stdin)
результат = {
«сумма»: параметры ['num1'] + параметры ['num2']
}
печать (json. dumps (результат))
dumps (результат)) $ ./mytask.py 10 5
Примеры Ruby
Задачи, написанные для приема ввода с stdin , уже могут выполняться как
сценарий, передав параметры в формате JSON задаче:
#!/usr/bin/env ruby
требуется 'json'
параметры = JSON.parse(STDIN.read)
результат = {
'сумма' => параметры['num1'] + параметры['num2']
}
помещает result.to_json $ echo '{"num1":10,"num2":5}' | ./mytask.rb Кроме того, вы можете написать свою задачу для разбора аргументов командной строки. в качестве параметров, если они присутствуют:
#!/usr/bin/env рубиновый
требуется 'json'
если АРГВ.любой?
параметры = {
'num1' => ARGV[0].to_i,
'num2' => ARGV[1].to_i
}
еще
параметры = JSON.parse(STDIN.read)
конец
результат = {
'сумма' => параметры['num1'] + параметры['num2']
}
помещает result.to_json $ ./mytask.rb 10 5
Пример PowerShell
Bolt отправляет параметры задачам PowerShell, преобразовывая параметры в
именованные аргументы. Вы можете запустить задачу PowerShell как скрипт, запустив ее
из командной строки и предоставив параметры в качестве именованных аргументов:
Вы можете запустить задачу PowerShell как скрипт, запустив ее
из командной строки и предоставив параметры в качестве именованных аргументов:
[Привязка командлета()]
Парам(
[Целое]$num1,
[Целое]$num2
)
$result = @{Sum=($num1 + $num2)} | ConvertTo-Json
Write-Output $result > ./mytask.ps1 -num1 10 -num2 5
Перенаправление
stderr По умолчанию Bolt не отображает вывод из stderr , если какой-либо вывод отправлен
на стандартный вывод . Если вы хотите передавать поток stderr и stdout , вы
может перенаправить stderr .
Пример Python
Чтобы перенаправить stderr на stdout в задаче Python, используйте библиотеку sys :
import sys sys.stderr = sys.stdout
Пример Ruby
Чтобы перенаправить stderr на stdout в задаче Ruby, установите глобальный параметр $stderr переменная:
$stderr = $stdout
12.
 Модули — Как думать как программист: обучение с помощью Python 3
Модули — Как думать как программист: обучение с помощью Python 3Модуль — это файл, содержащий определения Python и предназначенные операторы для использования в других программах Python. Есть много модулей Python, которые поставляются с Python в составе стандартная библиотека . Мы видели по крайней мере два из них уже, модуль черепахи и модуль строки.
Мы также показали вам, как получить доступ к справке. Справочная система содержит список всех стандартных модулей, доступных в Python. Играй с помощью!
12.1. Случайные числа
Мы часто хотим использовать случайные числа в программах, вот несколько типичных применений:
- Чтобы сыграть в азартную игру, в которой компьютер должен бросить кости, выбрать число или подбросить монету,
- Чтобы случайно перетасовать колоду игральных карт,
- Чтобы разрешить/заставить вражеский космический корабль появиться в случайном месте и начать стрельба по игроку,
- Чтобы смоделировать возможный дождь, когда мы делаем компьютерную модель для оценка воздействия строительства плотины на окружающую среду,
- Для шифрования банковских сессий в Интернете.

Python предоставляет модуль random, который помогает с такими задачами. Вы можете поищите его в справке, но вот основные вещи, которые мы с ним сделаем:
Вызов метода randrange генерирует целое число между его нижним и верхним аргумент, используя ту же семантику, что и диапазон, поэтому нижняя граница включена, но верхняя граница исключается. Все значения имеют равную вероятность появления (т.е. результат равен равномерно распределено ). Как и range, randrange может также используйте необязательный аргумент шага. Итак, давайте предположим, что нам нужно случайное нечетное число меньше чем 100, мы могли бы сказать:
randrange(1, 100, 2)
Другие методы также могут генерировать другие дистрибутивы, например. колокольчик, или «нормальное» распределение может быть более подходящим для оценки сезонных осадков, или концентрация соединения в организме после приема дозы лекарства.
Случайный метод возвращает число с плавающей запятой в интервале [0,0, 1,0) — квадратная скобка означает «замкнутый интервал слева», а круглая скобка означает «открытый интервал справа». Другими словами, возможно 0.0, но все возвращено числа будут строго меньше 1.0. Обычно масштабируют результаты после вызывая этот метод, чтобы получить их в интервале, подходящем для вашего приложения. в случае, показанном здесь, мы преобразовали результат вызова метода в число в интервал [0,0, 5,0). Еще раз: это равномерно распределенные числа — числа Близкие к 0 так же вероятны, как и числа, близкие к 0,5, или числа, близкие к 1,0.
В этом примере показано, как перемешать список. (перемешивание не может работать напрямую
с ленивым обещанием, поэтому обратите внимание, что нам пришлось преобразовать объект диапазона
сначала с помощью преобразователя типов списка.)
(перемешивание не может работать напрямую
с ленивым обещанием, поэтому обратите внимание, что нам пришлось преобразовать объект диапазона
сначала с помощью преобразователя типов списка.)
cards = list(range(52)) # Генерация целых чисел [0 .. 51] # представляет колоду карт. rng.shuffle(cards) # Перетасовать колоду
12.1.1. Повторяемость и тестирование
Генераторы случайных чисел основаны на детерминированный алгоритм — воспроизводимый и предсказуемый. Поэтому их называют 90 163 псевдослучайными генераторами 90 164 — они не являются по-настоящему случайными. Они начинаются с начального значения . Каждый раз, когда вы запрашиваете другое случайное число, вы получаете один основан на текущем атрибуте начального числа и состоянии начального числа (которое является одним атрибутов генератора) будут обновлены.
Для отладки и написания модульных тестов удобно
иметь повторяемость — программы, которые делают одно и то же при каждом запуске. Мы можем устроить это, заставив генератор случайных чисел инициализироваться с помощью
известное семя каждый раз. (Часто это требуется только во время тестирования — игры
карт, где перетасованная колода всегда была в том же порядке, что и в прошлый раз, когда вы играли
надоест очень быстро!)
Мы можем устроить это, заставив генератор случайных чисел инициализироваться с помощью
известное семя каждый раз. (Часто это требуется только во время тестирования — игры
карт, где перетасованная колода всегда была в том же порядке, что и в прошлый раз, когда вы играли
надоест очень быстро!)
Этот альтернативный способ создания генератора случайных чисел дает явное начальное число значение для объекта. Без этого аргумента система, вероятно, использует что-то, основанное на во время. Так что получение случайных чисел из drng сегодня даст вам точно такая же случайная последовательность, как и завтра!
12.1.2. Выбирание шаров из мешков, бросание игральных костей, перетасовка колоды карт
Вот пример создания списка, содержащего n случайных целых чисел между нижняя и верхняя граница:
случайный импорт def make_random_ints (число, нижняя_граница, верхняя_граница): """ Создайте список, содержащий число случайных целых чисел между lower_bound и верхняя граница.upper_bound — открытая граница. """ rng = random.Random() # Создаем генератор случайных чисел результат = [] для я в диапазоне (число): result.append(rng.randrange(lower_bound, upper_bound)) вернуть результат
>>> make_random_ints(5, 1, 13) # Выберите 5 случайных чисел месяца [8, 1, 8, 5, 6]
Обратите внимание, что в результате мы получили дубликат. Часто это хотел, напр. если мы подбросим игральную кость пять раз, мы ожидаем, дубликаты.
Но что, если дубликаты не нужны? Если вы хотите 5 разных месяцев, то этот алгоритм неверен. В этом случае хороший алгоритм состоит в том, чтобы сгенерировать список возможных вариантов, перетасуйте его и отрежьте необходимое количество элементов:
В курсах статистики первый случай — допущение дублирования — обычно
описывается как вытаскивание шаров из мешка с заменой — кладешь нарисованное
мяч обратно каждый раз, так что это может произойти снова. Последний случай, без дубликатов,
обычно описывается как вытаскивание мячей из мешка без замены . Однажды
мяч вытащен, он не возвращается для повторного розыгрыша. Игры ТВ-лото работают следующим образом.
Последний случай, без дубликатов,
обычно описывается как вытаскивание мячей из мешка без замены . Однажды
мяч вытащен, он не возвращается для повторного розыгрыша. Игры ТВ-лото работают следующим образом.
Второй алгоритм «перетасовать и нарезать» не был бы так хорош, если бы вы хотели всего несколько элементов, но из очень большого домена. Предположим, мне нужно пять чисел от одного до десяти миллионов без дубликатов. Генерация списка из десяти миллионов элементов, его перетасовка, а затем нарезка первые пять были бы катастрофой производительности! Итак, давайте попробуем еще раз:
г.
случайный импорт def make_random_ints_no_dups (число, нижняя_граница, верхняя_граница): """ Создайте список, содержащий число случайных целых чисел между нижняя_граница и верхняя_граница. upper_bound — открытая граница. Список результатов не может содержать дубликатов.""" результат = [] rng = случайный. Случайный () для я в диапазоне (число): пока верно: кандидат = rng.randrange (нижняя_граница, верхняя_граница) если кандидат не в результате: ломать результат.append(кандидат) вернуть результат xs = make_random_ints_no_dups (5, 1, 10000000) печать (хз)
Это дает 5 случайных чисел без дубликатов:
[3344629, 1735163, 92, 1081511, 40]
Даже у этой функции есть свои подводные камни. Можете ли вы определить, что произойдет в этот случай?
12.2. Модуль времени
По мере того, как мы начинаем работать с более сложными алгоритмами и большими программами, естественно
забота «эффективен ли наш код?» Один из способов поэкспериментировать — определить, как долго различные
операции занимают. Модуль времени имеет функцию, называемую часами, которую рекомендуется
для этой цели. Всякий раз, когда вызываются часы, они возвращают число с плавающей запятой.
представляющее, сколько секунд прошло с момента запуска вашей программы.
Модуль времени имеет функцию, называемую часами, которую рекомендуется
для этой цели. Всякий раз, когда вызываются часы, они возвращают число с плавающей запятой.
представляющее, сколько секунд прошло с момента запуска вашей программы.
Способ его использования состоит в том, чтобы вызвать часы и присвоить результат переменной, скажем, t0, непосредственно перед тем, как вы начнете выполнять код, который хотите измерить. Затем после выполнения вызовите часы снова (на этот раз мы сохраним результат в переменной t1). Различия t1-t0 — это прошедшее время и показатель того, насколько быстро работает ваша программа.
Возьмем небольшой пример. Python имеет встроенную функцию суммирования, которая может суммировать элементы в списке. Мы также можем написать свой собственный. Как мы думаем, они будут сравнивать для скорости? Попробуем выполнить суммирование списка [0, 1, 2...] в обоих случаях, и сравните результаты:
время импорта защита do_my_sum(xs): сумма = 0 для v в xs: сумма += v возвращаемая сумма sz = 10000000 # Пусть в списке будет 10 миллионов элементов тестовые данные = диапазон (sz) t0 = время.часы() мой_результат = do_my_sum(тестовые данные) t1 = время.часы() print("my_result = {0} (затраченное время = {1:.4f} секунд)" .формат (мой_результат, t1-t0)) t2 = время.часы() их_результат = сумма (тестовые данные) t3 = время.часы() print("ir_result = {0} (затраченное время = {1:.4f} секунд)" .format(их_результат, t3-t2))
На достаточно скромном ноутбуке получаем такие результаты:
my_sum = 499999000 (затраченное время = 1,5567 секунды) its_sum = 499999000 (затраченное время = 0,9897 секунды)
Итак, наша функция работает примерно на 57% медленнее, чем встроенная. Генерация и суммирование десяти миллионов элементов менее чем за секунду — это не так уж и плохо!
12.3. Математический модуль
Математический модуль содержит виды математических функций, которые вы обычно найдете на своем компьютере. калькулятор (sin, cos, sqrt, asin, log, log10) и некоторые математические константы как пи и е:
>>> импортировать математику >>> math.pi # Константа пи 3.1415589793 >>> math.e # Постоянное натуральное логарифмическое основание 2,718281828459045 >>> math.sqrt(2.0) # Функция квадратного корня 1.4142135623730951 >>> math.radians(90) # Преобразование 90 градусов в радианы 1.57079632676 >>> math.sin(math.radians(90)) # Находим синус 90 градусов 1,0 >>> math.asin(1.0) * 2 # Удвоить арксинус 1.0, чтобы получить число пи 3.1415589793
Как почти во всех других языках программирования, углы выражаются в радианах а не градусов. Есть две функции радианы и градусы конвертировать между этими двумя популярными способами измерения углов.
Обратите внимание на еще одно различие между этим модулем и нашим использованием случайных чисел и черепах:
в random и черепахе мы создаем объекты и вызываем методы для объекта. Это
потому что у объектов состояние — у черепашки есть цвет, положение, заголовок и т.д.,
и каждый генератор случайных чисел имеет начальное значение, которое определяет его следующий результат.
Математические функции являются «чистыми» и не имеют состояния — вычисление квадратного корня из 2.0 не зависит ни от какого состояния или истории о том, что произошло в прошлом. Таким образом, функции не являются методами объекта — это просто функции, сгруппированные в модуль под названием math.
12.4. Создание собственных модулей
Все, что нам нужно сделать для создания собственных модулей, это сохранить наш скрипт как файл с расширением .py. Предположим, например, что этот сценарий сохранен как файл с именем seqtools.py:
по умолчанию remove_at (pos, seq): вернуть последовательность[:поз.] + последовательность[поз.+1:]
Теперь мы можем использовать наш модуль как в сценариях, которые мы пишем, так и в интерактивном интерпретаторе Python. Для этого мы должен сначала импортировать модуль.
>>> импортировать инструменты seqtools >>> s = "Строка!" >>> seqtools.remove_at(4, с) 'Жало!'
Мы не включаем расширение файла .py, когда импорт. Python ожидает, что имена файлов модулей Python будут заканчиваться на .py, поэтому расширение файла не входит в отчет об импорте .
Использование модулей позволяет разбивать очень большие программы на части управляемого размера, а также держать связанные части вместе.
12.5. Пространства имен
Пространство имен представляет собой набор идентификаторов, принадлежащих модуль или функцию (и, как мы скоро увидим, и в классах). В общем, нам нравится пространство имен для хранения «связанных» вещей, например. все математические функции или все типичные вещи, которые мы делаем со случайными числами.
Каждый модуль имеет собственное пространство имен, поэтому мы можем использовать одно и то же имя идентификатора в нескольких модулей, не вызывая проблем с идентификацией.
py question = «В чем смысл жизни, вселенной и всего остального?» ответ = 42
Теперь мы можем импортировать оба модуля и получить доступ к вопросам и ответам в каждом из них:
выведет следующее:
В чем смысл жизни, Вселенной и всего? Каков ваш квест? 42 Искать святой Грааль.
Функции также имеют свои собственные пространства имен:
деф f(): п = 7 print("печать n внутри f:", n) деф г(): п = 42 print("печать n внутри g:", n) п = 11 print("вывод n перед вызовом f:", n) е() print("печать n после вызова f:", n) грамм() print("печать n после вызова g:", n)
Запуск этой программы приводит к следующему результату:
печать n перед вызовом f: 11 печать n внутри f: 7 печать n после вызова f: 11 печать n внутри g: 42 печать n после вызова g: 11
Три n здесь не сталкиваются, так как каждое из них находится в разных
пространство имен — это три имени для трех разных переменных, как
может быть три разных экземпляра людей, и все они называются «Брюс».
Пространства имен позволяют нескольким программистам работать над одним и тем же проектом без наличие коллизий имен.
12.6. Область действия и правила поиска
Область идентификатора — это область кода программы, в которой идентификатор может быть доступен или использован.
В Python есть три важных области:
- Локальная область относится к идентификаторам, объявленным внутри функции. Эти идентификаторы сохраняются в пространстве имен, которое принадлежит функции, и каждая функция имеет свое собственное пространство имен.
- Глобальная область относится ко всем идентификаторам, объявленным в текущем модуле или файле.
- Встроенная область действия относится ко всем идентификаторам, встроенным в Python, таким как диапазон и
min, которые можно использовать без необходимости импортировать что-либо, и они (почти) всегда доступны.

Python (как и большинство других компьютерных языков) использует правила приоритета: одно и то же имя может встречаться в более чем одна из этих областей, но самая внутренняя или локальная область всегда будет занимать приоритет над глобальной областью, и глобальная область всегда используется в предпочтении перед встроенный прицел. Начнем с простого примера:
по умолчанию диапазон(n): вернуть 123*н печать (диапазон (10))
Что печатается? Мы определили нашу собственную функцию с именем range, поэтому
теперь является потенциальной двусмысленностью. Когда мы используем диапазон, мы имеем в виду свой собственный,
или встроенный? Использование правил поиска области определяет следующее: наши собственные
вызывается функция range, а не встроенная, потому что наша функция range
находится в глобальном пространстве имен, которое имеет приоритет над встроенными именами.
Таким образом, хотя имена, такие как диапазон и минимум, встроены, их можно «скрыть». от вашего использования, если вы решите определить свои собственные переменные или функции, которые повторно используют эти имена. (Это запутанная практика переопределять встроенные имена — так, чтобы хороший программист, вам нужно понимать правила области видимости и понимать что вы можете делать неприятные вещи, которые вызовут путаницу, а затем избегаете их делать!)
Теперь немного более сложный пример:
Это напечатает 17 10 3. Причина в том, что две переменные m и n в строках 1 и 2
находятся вне функции в глобальном пространстве имен. Внутри функции новые переменные
n и m создаются только на время выполнения f . Это
созданный в локальном пространстве имен функции f. В теле f правила поиска области видимости
определить, что мы используем локальные переменные m и n. Напротив, после того, как мы вернулись из f,
аргументы n и m функции печати относятся к исходным переменным
в строках 1 и 2, и они никак не изменились при выполнении функции f.
Напротив, после того, как мы вернулись из f,
аргументы n и m функции печати относятся к исходным переменным
в строках 1 и 2, и они никак не изменились при выполнении функции f.
Также обратите внимание, что здесь def помещает имя f в глобальное пространство имен. Так что это может быть вызывается в строке 7.
Какова область действия переменной n в строке 1? Сфера его действия — регион, в котором он находится. видимый — это строки 1, 2, 6, 7. Он скрыт от просмотра в строках 3, 4, 5 из-за локальная переменная n.
12.7. Атрибуты и оператор точки
Переменные, определенные внутри модуля, называются атрибутами модуля.
Мы видели, что у объектов тоже есть атрибуты: например, у большинства объектов есть
атрибут __doc__, некоторые функции имеют атрибут __annotations__.
Доступ к атрибутам осуществляется с помощью оператор точки (.). Атрибут вопроса
Доступ к модулю1 и модулю2 осуществляется с помощью module1.question и
модуль2. вопрос.
вопрос.
Модули содержат функции, а также атрибуты, и используется оператор точка чтобы получить к ним доступ таким же образом. seqtools.remove_at относится к remove_at в модуле seqtools.
Когда мы используем имя с точкой, мы часто называем его полным именем , потому что мы говорим, какой именно атрибут вопроса мы имеем в виду.
12.9. Превратите свой юнит-тестер в модуль
Ближе к концу главы 6 (Плодотворные функции) мы представили юнит-тестирование и наш собственный тест. функцию, и вам пришлось скопировать ее в каждый модуль, для которого вы писал тесты. Теперь мы можем поместить это определение в модуль его собственный, скажем, unit_tester.py, и вместо этого просто используйте одну строку в каждом новом скрипте:
12.10. Глоссарий
- атрибут
- Переменная, определенная внутри модуля (или класса, или экземпляра — как мы
увидим позже).
 Доступ к атрибутам модуля осуществляется с помощью точки .
оператор (.).
Доступ к атрибутам модуля осуществляется с помощью точки .
оператор (.). - точечный оператор
- Оператор точки (.) разрешает доступ к атрибутам и функциям модуль (или атрибуты и методы класса или экземпляра — как мы видел в другом месте).
- полное имя
- Имя с префиксом некоторого идентификатора пространства имен и оператора точки или объектом экземпляра, например. math.sqrt или tess.forward(10).
- отчет об импорте
Оператор, который делает объекты, содержащиеся в модуле, доступными для использовать в другом модуле. Есть две формы для импорта утверждение. Использование гипотетических модулей с именами mymod1 и mymod2 каждый из которых содержит функции f1 и f2 и переменные v1 и v2, примеры из этих двух форм включают:
импорт mymod1 из mymod2 импортировать f1, f2, v1, v2
Вторая форма помещает импортированные объекты в пространство имен модуль импорта, а первая форма сохраняет отдельный пространство имен для импортированного модуля, для доступа к которому требуется mymod1.
 v1
переменная v1 из этого модуля.
v1
переменная v1 из этого модуля.- метод
Функционально-подобный атрибут объекта. Методы вызываются (вызываются) на объект с помощью оператора точка. Например:
>>> s = "это строка." >>> s.upper() «ЭТО СТРУНА». >>>
Мы говорим, что метод upper вызывается для строки s. s неявно является первым аргументом upper.
- модуль
- Файл, содержащий определения и операторы Python, предназначенные для использования в другие программы Python. Содержимое модуля становится доступным для другую программу с помощью оператора импорта.
- пространство имен
- Синтаксический контейнер, предоставляющий контекст для имен, так что один и тот же имя может находиться в разных пространствах имен без двусмысленности. В Питоне, модули, классы, функции и методы образуют пространства имен.
- коллизия имен
Ситуация, когда два или более имен в заданном пространстве имен не могут быть однозначно решен.
 Использование
Использованиестрока импорта
вместо
из строкового импорта *
предотвращает конфликты имен.
стандартная библиотека Библиотека — это набор программного обеспечения, используемого в качестве инструментов при разработке. другого программного обеспечения. Стандартная библиотека языка программирования набор таких инструментов, которые распространяются вместе с ядром программирования язык. Python поставляется с обширной стандартной библиотекой.
12.11. Упражнения
Открыть справку по модулю календаря.
Попробуйте следующее:
календарь импорта cal = calendar.TextCalendar() # Создать экземпляр cal.pryear(2012) # Что здесь происходит?
Обратите внимание, что неделя начинается в понедельник.
 Предприимчивый студент CompSci
считает, что лучше начать неделю с ментального фрагментирования
Четверг, потому что тогда до выходных всего два рабочих дня, а
каждая неделя имеет перерыв в середине. Прочтите документацию для TextCalendar,
и узнайте, как вы можете помочь ему распечатать календарь, соответствующий его потребностям.
Предприимчивый студент CompSci
считает, что лучше начать неделю с ментального фрагментирования
Четверг, потому что тогда до выходных всего два рабочих дня, а
каждая неделя имеет перерыв в середине. Прочтите документацию для TextCalendar,
и узнайте, как вы можете помочь ему распечатать календарь, соответствующий его потребностям.Найдите функцию, которая будет печатать только месяц, в который приходится ваш день рождения в этом году.
Попробуйте это:
d = calendar.LocaleTextCalendar(6, "ИСПАНСКИЙ") д.пргод(2012)
Попробуйте использовать несколько других языков, в том числе тот, который не работает, и посмотрите, что произойдет.
Эксперимент с calendar.isleap. Что он ожидает в качестве аргумент? Что он возвращает в результате? Что это за функция?
Делайте подробные заметки о том, что вы узнали из этих упражнений.

Открыть справку по математическому модулю.
- Сколько функций в математическом модуле?
- Что делает math.ceil? А как насчет math.floor? ( подсказка: оба floor и ceil ожидают аргументы с плавающей запятой.)
- Опишите, как мы вычисляли то же значение, что и math.sqrt без использования математического модуля.
- Что представляют собой две константы данных в математическом модуле?
Делайте подробные заметки о своем расследовании в этом упражнении.
Исследуйте модуль копирования. Что делает глубокая копия делать? В каких упражнениях из прошлой главы можно было бы использовать глубокое копирование удобно?
Создайте модуль с именем mymodule1.py. Добавить атрибуты myage, установленные в ваш текущий возраст и год, установленный на текущий год. Создать еще модуль с именем mymodule2.py. Добавьте атрибуты myage со значением 0 и year устанавливается в год вашего рождения.
 Теперь создайте файл с именем
namespace_test.py. Импортируйте оба модуля выше и напишите
следующее утверждение:
Теперь создайте файл с именем
namespace_test.py. Импортируйте оба модуля выше и напишите
следующее утверждение:print((mymodule2.myage - mymodule1.myage) == (моймодуль2.год - моймодуль1.год)) )Когда вы запустите namespace_test.py, вы увидите либо True, либо False в качестве вывода в зависимости от того, получили ли вы уже свое день рождения в этом году.
Этот пример показывает, что оба разных модуля могут иметь атрибуты с именем myage и year. Поскольку они находятся в разных пространствах имен, они не конфликтуют друг с другом. Когда мы пишем namespace_test.py, мы полностью определить, какой именно год переменной или мой возраст мы имеем в виду.
Добавьте следующую инструкцию в mymodule1.py, mymodule2.py и namespace_test.py из предыдущего упражнения:
print("Меня зовут", __name__)Запустите namespace_test.
 py. Что случается? Почему? Теперь добавьте следующее в
нижняя часть mymodule1.py:
py. Что случается? Почему? Теперь добавьте следующее в
нижняя часть mymodule1.py:если __name__ == "__main__": print("Это не запустится, если я импортирован.")Снова запустите mymodule1.py и namespace_test.py. В каком случае вы увидеть новый оператор печати?
В оболочке Python/интерактивном интерпретаторе попробуйте следующее:
>>> импортировать это
Что Тим Питерс может сказать о пространствах имен?
Дайте ответ интерпретатора Python на каждое из следующих действий из непрерывный сеанс переводчика:
>>> s = "Если бы мы вынули кости, они бы не хрустели, не так ли?" >>> s.split() >>> тип(s.split()) >>> с.split("о") >>> с.split("i") >>> "0".join(s.split("o"))Убедитесь, что вы понимаете, почему вы получаете каждый результат. Затем примените то, что у вас есть научились заполнять тело функции ниже с помощью разделения и методы объединения объектов str:
1 2 3 4 5 6 7 8 9 10
def myreplace(old, new, s): """ Замените все вхождения слова old на new в s. """
...
test(myreplace(",", ";", "это, это и еще кое-что") ==
«это, это и еще что-то»)
тест(моя замена(" ", "**",
"Теперь слова будут разделены звездочками.") ==
«Слова**будут**теперь**разделены**звездами**».)
"""
...
test(myreplace(",", ";", "это, это и еще кое-что") ==
«это, это и еще что-то»)
тест(моя замена(" ", "**",
"Теперь слова будут разделены звездочками.") ==
«Слова**будут**теперь**разделены**звездами**».)
Ваше решение должно пройти тесты.
Создайте модуль с именем wordtools.py с нашим тестовым каркасом.
Теперь добавьте функции к этим тестам:
тест(чистое слово("что?") == "что") тест(чистое слово("'сейчас!'") == "сейчас") test(cleanword("?+='w-o-r-d!,@$()'") == "слово") test(has_dashdash("расстояние-но")) тест (не has_dashdash ("несколько")) тест(has_dashdash("говорил--")) test(has_dashdash("расстояние-но")) тест (не has_dashdash ("-йо-йо-")) test(extract_words("Сейчас самое время! 'Сейчас', самое время? Да, сейчас.") == ['сейчас','есть','тот','время','теперь','есть','тот','время','да','сейчас']) test(extract_words("она попыталась сделать реверанс, когда говорила - прикольно") == ['она', 'пыталась', 'к', 'приседать', 'как', 'она', 'говорила', 'причудливо']) test(wordcount("сейчас", ["сейчас","есть","время","есть","сейчас","есть","есть"]) == 2) test(wordcount("есть", ["сейчас","есть","время","есть","сейчас","то","есть"]) == 3) test(wordcount("время", ["сейчас","есть","время","есть","сейчас","есть","есть"]) == 1) test(wordcount("лягушка", ["сейчас","есть","время","есть","сейчас","есть","есть"]) == 0) test(набор слов(["сейчас", "есть", "время", "есть", "сейчас", "есть", "есть"]) == ["есть", "сейчас", "время"]) test(wordset(["I", "a", "a", "is", "a", "is", "I", "am"]) == ["Я", "а", "есть", "есть"]) test(набор слов(["или", "а", "ам", "есть", "есть", "быть", "но", "ам"]) == ["а", "есть", "есть", "быть", "но", "есть", "или"]) test(длиннейшее слово(["а", "яблоко", "груша", "виноград"]) == 5) test(длиннейшее слово(["a", "am", "I", "be"]) == 2) test(longestword(["this","supercalifragilisticexpialidocious"]) == 34) тест (самое длинное слово ([ ]) == 0)Сохраните этот модуль, чтобы использовать содержащиеся в нем инструменты в будущих программах.

Начало работы с асинхронными функциями в Python — настоящий Python
Вы слышали об асинхронном программировании в Python? Вам интересно узнать больше об асинхронных функциях Python и о том, как вы можете использовать их в своей работе? Возможно, вы даже пытались писать многопоточные программы и сталкивались с некоторыми проблемами. Если вы хотите понять, как использовать асинхронные функции Python, то вы попали в нужное место.
В этой статье вы узнаете:
- Что такое синхронная программа
- Что такое асинхронная программа
- Зачем вам может понадобиться написать асинхронную программу
- Как использовать асинхронные функции Python
Весь пример кода в этой статье был протестирован с Python 3.7.2. Вы можете получить копию, чтобы продолжить, нажав на ссылку ниже:
Понимание асинхронного программирования
Синхронная программа выполняется пошагово. Даже с условным ветвлением, циклами и вызовами функций вы все равно можете думать о коде с точки зрения выполнения одного шага за раз. После завершения каждого шага программа переходит к следующему.
Даже с условным ветвлением, циклами и вызовами функций вы все равно можете думать о коде с точки зрения выполнения одного шага за раз. После завершения каждого шага программа переходит к следующему.
Вот два примера программ, которые работают таким образом:
Программы пакетной обработки часто создаются как синхронные программы. Вы получаете входные данные, обрабатываете их и создаете выходные данные. Шаги следуют один за другим, пока программа не достигнет желаемого результата. Программе нужно только обращать внимание на шаги и их порядок.
Программы командной строки — это небольшие быстрые процессы, запускаемые в терминале. Эти сценарии используются для создания чего-либо, преобразования одного объекта во что-то другое, создания отчета или, возможно, вывода некоторых данных. Это можно выразить как серию шагов программы, которые выполняются последовательно до тех пор, пока программа не будет выполнена.

Асинхронная программа ведет себя иначе. Он по-прежнему занимает один шаг выполнения за раз. Разница в том, что система может не ждать завершения шага выполнения, прежде чем перейти к следующему.
Это означает, что программа перейдет к будущим шагам выполнения, даже если предыдущий шаг еще не завершен и все еще выполняется в другом месте. Это также означает, что программа знает, что делать, когда завершается выполнение предыдущего шага.
Зачем вам писать программу таким образом? Оставшаяся часть этой статьи поможет вам ответить на этот вопрос и предоставит инструменты, необходимые для элегантного решения интересных асинхронных задач.
Удалить рекламу
Создание синхронного веб-сервера
Основная единица работы веб-сервера более или менее аналогична пакетной обработке. Сервер получит некоторый ввод, обработает его и создаст вывод. Написанная как синхронная программа, она создаст работающий веб-сервер.
Это также был бы совершенно ужасный веб-сервер .
Почему? В этом случае одна единица работы (ввод, процесс, вывод) не является единственной целью. Настоящая цель состоит в том, чтобы как можно быстрее обрабатывать сотни или даже тысячи единиц работы. Это может происходить в течение длительного периода времени, и несколько рабочих единиц могут даже прибывать одновременно.
Можно ли улучшить синхронный веб-сервер? Конечно, вы можете оптимизировать этапы выполнения, чтобы вся поступающая работа выполнялась как можно быстрее. К сожалению, у этого подхода есть ограничения. Результатом может быть веб-сервер, который недостаточно быстро отвечает, не может выполнять достаточно работы или даже отключается, когда работа накапливается.
Примечание: Существуют и другие ограничения, которые вы можете увидеть, если попытаетесь оптимизировать описанный выше подход. К ним относятся скорость сети, скорость ввода-вывода файлов, скорость запросов к базе данных и скорость других подключенных служб, и это лишь некоторые из них. Общее у них то, что все они являются функциями ввода-вывода. Все эти элементы на порядки медленнее, чем скорость обработки процессора.
Общее у них то, что все они являются функциями ввода-вывода. Все эти элементы на порядки медленнее, чем скорость обработки процессора.
В синхронной программе, если шаг выполнения запускает запрос к базе данных, то ЦП практически бездействует до тех пор, пока не будет возвращен запрос к базе данных. Для пакетно-ориентированных программ это в большинстве случаев не является приоритетом. Обработка результатов этой операции ввода-вывода является целью. Часто это может занять больше времени, чем сама операция ввода-вывода. Любые усилия по оптимизации будут сосредоточены на обработке, а не на вводе-выводе.
Методы асинхронного программирования позволяют вашим программам использовать относительно медленные процессы ввода-вывода, освобождая ЦП для выполнения другой работы.
Думать о программировании по-другому
Когда вы начнете пытаться понять асинхронное программирование, вы можете увидеть много дискуссий о важности блокировки или написания неблокирующего кода. (Лично я изо всех сил пытался получить хорошее представление об этих концепциях от людей, которых я спрашивал, и из документации, которую я читал.)
(Лично я изо всех сил пытался получить хорошее представление об этих концепциях от людей, которых я спрашивал, и из документации, которую я читал.)
Что такое неблокирующий код? Что такое блокирующий код, если на то пошло? Помогут ли ответы на эти вопросы написать лучший веб-сервер? Если да, то как вы могли это сделать? Давай выясним!
Написание асинхронных программ требует, чтобы вы по-новому относились к программированию. Хотя этот новый образ мышления может быть трудным для понимания, это также интересное упражнение. Это потому, что реальный мир почти полностью асинхронен, как и то, как вы с ним взаимодействуете.
Представьте себе: вы родитель, который пытается делать несколько дел одновременно. Вы должны сбалансировать чековую книжку, стирать и присматривать за детьми. Каким-то образом вы можете делать все это одновременно, даже не задумываясь об этом! Давайте разберемся:
Балансировка чековой книжки — это синхронная задача.
 Один шаг следует за другим, пока не будет выполнено. Вы делаете всю работу сами.
Один шаг следует за другим, пока не будет выполнено. Вы делаете всю работу сами.Тем не менее, вы можете оторваться от чековой книжки, чтобы заняться стиркой. Вы разгружаете сушилку, перемещаете одежду из стиральной машины в сушилку и начинаете новую загрузку в стиральную машину.
Работа со стиральной и сушильной машинами является синхронной задачей, но основная часть работы выполняется после запуска стиральной и сушильной машин. Как только вы их закончите, вы можете уйти и вернуться к задаче с чековой книжкой. На данный момент задачи стиральной и сушильной машин стали 9.0163 асинхронный . Стиральная машина и сушилка будут работать независимо до тех пор, пока не сработает звуковой сигнал (оповещающий вас о том, что задача требует внимания).
Присмотр за детьми — еще одна асинхронная задача. После того, как они настроены и играют, они могут делать это по большей части независимо. Это меняется, когда кому-то нужно внимание, например, когда кто-то проголодался или получил травму.
 Когда один из ваших детей кричит в тревоге, вы реагируете. Дети — это долгосрочная задача с высоким приоритетом. Их просмотр заменяет любые другие задачи, которые вы можете выполнять, например, чековую книжку или стирку.
Когда один из ваших детей кричит в тревоге, вы реагируете. Дети — это долгосрочная задача с высоким приоритетом. Их просмотр заменяет любые другие задачи, которые вы можете выполнять, например, чековую книжку или стирку.
Эти примеры могут помочь проиллюстрировать концепции блокирующего и неблокирующего кода. Давайте подумаем об этом с точки зрения программирования. В этом примере вы похожи на ЦП. Пока вы перемещаете белье, вы (ЦП) заняты и не можете выполнять другую работу, например, балансировать чековую книжку. Но это нормально, потому что задача выполняется относительно быстро.
С другой стороны, запуск стиральной и сушильной машин не мешает вам выполнять другие задачи. Это асинхронная функция, потому что вам не нужно ждать ее завершения. Как только это началось, вы можете вернуться к чему-то другому. Это называется переключением контекста: контекст того, что вы делаете, изменился, и зуммер машины уведомит вас когда-нибудь в будущем, когда задача стирки будет завершена.
Как человек, ты всегда так работаешь. Вы, естественно, жонглируете несколькими вещами одновременно, часто не задумываясь об этом. Задача разработчика заключается в том, чтобы перевести такое поведение в код, который делает то же самое.
Программирование для родителей: не так просто, как кажется!
Если вы узнали себя (или своих родителей) в приведенном выше примере, то это здорово! У вас есть преимущество в понимании асинхронного программирования. Опять же, вы можете довольно легко переключать контексты между конкурирующими задачами, беря одни задачи и возобновляя другие. Теперь вы попытаетесь запрограммировать это поведение на виртуальных родителей!
Мысленный эксперимент №1: синхронный родитель
Как бы вы создали родительскую программу для выполнения вышеуказанных задач полностью синхронно? Поскольку наблюдение за детьми является первоочередной задачей, возможно, ваша программа подойдет именно для этого. Родитель наблюдает за детьми, ожидая, что произойдет что-то, что может потребовать их внимания. Однако ничего другого (например, чековой книжки или стирки) в этом сценарии не будет.
Однако ничего другого (например, чековой книжки или стирки) в этом сценарии не будет.
Теперь вы можете перераспределять приоритеты задач по своему усмотрению, но только одна из них будет выполняться в любой момент времени. Это результат синхронного, пошагового подхода. Подобно синхронному веб-серверу, описанному выше, это будет работать, но может оказаться не лучшим образом жизни. Родитель не сможет выполнять какие-либо другие задачи, пока дети не заснут. Все остальные задачи будут выполняться позже, глубокой ночью. (Пара недель такого, и многие настоящие родители могут выпрыгнуть из окна!)
Удалить рекламу
Мысленный эксперимент №2: Родительский опрос
Если вы использовали опрос, вы могли бы изменить ситуацию так, чтобы выполнялись несколько задач. При таком подходе родитель периодически отрывался от текущей задачи и проверял, не требуют ли внимания какие-либо другие задачи.
Давайте сделаем интервал опроса примерно пятнадцать минут. Теперь каждые пятнадцать минут ваш родитель проверяет, не нужно ли внимание стиральной машине, сушилке или детям. Если нет, то родитель может вернуться к работе над чековой книжкой. Однако, если какая-либо из этих задач do требуют внимания, тогда родитель позаботится об этом, прежде чем вернуться к чековой книжке. Этот цикл продолжается до следующего тайм-аута цикла опроса.
Теперь каждые пятнадцать минут ваш родитель проверяет, не нужно ли внимание стиральной машине, сушилке или детям. Если нет, то родитель может вернуться к работе над чековой книжкой. Однако, если какая-либо из этих задач do требуют внимания, тогда родитель позаботится об этом, прежде чем вернуться к чековой книжке. Этот цикл продолжается до следующего тайм-аута цикла опроса.
Этот подход также работает, поскольку внимание привлекается к нескольким задачам. Однако есть пара проблем:
Родитель может потратить много времени на проверку вещей, которые не требуют внимания: Стиральная машина и сушилка еще не закончили работу, а дети не нуждаются во внимании, если только не произойдет что-то неожиданное.
Родитель может пропустить завершенные задачи, требующие внимания: Например, если стиральная машина завершила свой цикл в начале интервала опроса, то она не привлекла бы внимания до пятнадцати минут! Более того, присмотр за детьми якобы является самой приоритетной задачей.
 Они не могли терпеть пятнадцать минут без внимания, когда что-то могло пойти совсем не так.
Они не могли терпеть пятнадцать минут без внимания, когда что-то могло пойти совсем не так.
Вы можете решить эти проблемы, сократив интервал опроса, но теперь ваш родитель (ЦП) будет тратить больше времени на переключение контекста между задачами. Это когда вы начинаете достигать точки убывающей отдачи. (Опять пару недель такой жизни и, ну… См. предыдущий комментарий про окна и прыжки.)
Мысленный эксперимент № 3: родитель-нити
«Если бы я только мог клонировать себя…» Если вы родитель, то у вас наверняка были подобные мысли! Поскольку вы программируете виртуальных родителей, вы можете сделать это, используя многопоточность. Это механизм, позволяющий одновременно запускать несколько разделов одной программы. Каждый раздел кода, который выполняется независимо, называется потоком, и все потоки совместно используют одно и то же пространство памяти.
Если вы думаете о каждой задаче как о части одной программы, то вы можете разделить их и запускать как потоки. Другими словами, вы можете «клонировать» родителя, создавая по одному экземпляру для каждой задачи: присмотр за детьми, контроль за стиральной машиной, контроль за сушилкой и балансировка чековой книжки. Все эти «клоны» работают независимо.
Другими словами, вы можете «клонировать» родителя, создавая по одному экземпляру для каждой задачи: присмотр за детьми, контроль за стиральной машиной, контроль за сушилкой и балансировка чековой книжки. Все эти «клоны» работают независимо.
Звучит как неплохое решение, но здесь тоже есть некоторые проблемы. Во-первых, вам придется явно указывать каждому родительскому экземпляру, что делать в вашей программе. Это может привести к некоторым проблемам, поскольку все экземпляры совместно используют все в программном пространстве.
Например, предположим, что Родитель A следит за сушильной машиной. Родитель А видит, что одежда сухая, поэтому он берет под свой контроль сушилку и начинает разгружать одежду. В то же время родитель Б видит, что стирка закончена, поэтому он берет машину под свой контроль и начинает снимать одежду. Тем не менее, родитель Б также должен контролировать сушилку, чтобы положить внутрь мокрую одежду. Этого не может быть, потому что в настоящее время Родитель А контролирует сушильную машину.
Вскоре Родитель А закончил разгружать одежду. Теперь они хотят взять под контроль стиральную машину и начать перемещать белье в пустую сушилку. Этого также не может быть, потому что Родитель Б в настоящее время контролирует стиральную машину!
Эти два родителя зашли в тупик. Оба имеют контроль над своим собственным ресурсом , а хотят контролировать другой ресурс. Они будут вечно ждать, пока другой родительский экземпляр освободит управление. Как программист, вам придется написать код, чтобы разрешить эту ситуацию.
Примечание. Многопоточные программы позволяют создавать несколько параллельных путей выполнения, которые используют одно и то же пространство памяти. Это и преимущество, и недостаток. Любая память, разделяемая между потоками, зависит от того, что один или несколько потоков пытаются одновременно использовать одну и ту же общую память. Это может привести к повреждению данных, считыванию данных в недопустимом состоянии и вообще к беспорядку данных.
В многопоточном программировании переключение контекста происходит под контролем системы, а не программиста. Система контролирует, когда переключать контексты и когда предоставлять потокам доступ к общим данным, тем самым изменяя контекст использования памяти. Все эти виды проблем решаемы в многопоточном коде, но его трудно исправить и трудно отладить, когда он неправильный.
Вот еще одна проблема, которая может возникнуть из-за многопоточности. Предположим, что ребенок получил травму и нуждается в срочной помощи. Родителю C было поручено присматривать за детьми, поэтому они сразу же забирают ребенка. В отделении неотложной помощи родитель C должен выписать чек на довольно большую сумму, чтобы покрыть расходы на визит к врачу.
Тем временем родитель D дома работает с чековой книжкой. Они не знают, что этот крупный чек выписывается, поэтому они очень удивлены, когда семейный текущий счет внезапно перерасходуется!
Помните, что эти два родительских экземпляра работают в рамках одной и той же программы. Семейный текущий счет — это общий ресурс, поэтому вам придется придумать способ, чтобы родитель, наблюдающий за ребенком, информировал родителя, балансирующего чековую книжку. В противном случае вам нужно будет предоставить какой-то механизм блокировки, чтобы ресурс чековой книжки мог использоваться только одним родителем одновременно с обновлениями.
Семейный текущий счет — это общий ресурс, поэтому вам придется придумать способ, чтобы родитель, наблюдающий за ребенком, информировал родителя, балансирующего чековую книжку. В противном случае вам нужно будет предоставить какой-то механизм блокировки, чтобы ресурс чековой книжки мог использоваться только одним родителем одновременно с обновлениями.
Использование асинхронных функций Python на практике
Теперь вы воспользуетесь некоторыми подходами, изложенными в приведенных выше мысленных экспериментах, и превратите их в работающие программы Python.
Все примеры в этой статье были протестированы с Python 3.7.2. Файл requirements.txt указывает, какие модули необходимо установить для запуска всех примеров. Если вы еще не скачали файл, вы можете сделать это сейчас:
Вы также можете настроить виртуальную среду Python для запуска кода, чтобы не мешать вашей системе Python.
Удалить рекламу
Синхронное программирование
В этом первом примере показан несколько надуманный способ получения задачей задачи из очереди и ее обработки. Очередь в Python — это хорошая структура данных FIFO (первым пришел — первым обслужен). Он предоставляет методы для размещения элементов в очереди и их повторного извлечения в том порядке, в котором они были вставлены.
Очередь в Python — это хорошая структура данных FIFO (первым пришел — первым обслужен). Он предоставляет методы для размещения элементов в очереди и их повторного извлечения в том порядке, в котором они были вставлены.
В этом случае задача состоит в том, чтобы получить число из очереди и выполнить подсчет циклов до этого числа. Он выводит на консоль, когда цикл начинается, и снова, чтобы вывести итог. Эта программа демонстрирует один из способов обработки работы в очереди для нескольких синхронных задач.
Программа с именем example_1.py в репозитории полностью указана ниже:
1 очередь импорта
2
3def задача (имя, work_queue):
4 если work_queue.empty():
5 print(f"Задание {имя} ничего не делать")
6 еще:
7, а не work_queue.empty():
8 счет = work_queue.get()
9всего = 0
10 print(f"Выполняется задача {имя}")
11 для x в диапазоне (количество):
всего 12 += 1
13 print(f"Всего по задаче {имя}: {всего}")
14
15def основной():
16 """
17 Это основная точка входа в программу
18 """
19 # Создаем очередь работ
20 work_queue = очередь. Очередь()
21
22 # Поставить часть работы в очередь
23 для работы в [15, 10, 5, 2]:
24 work_queue.put(работа)
25
26 # Создайте несколько синхронных задач
27 задач = [(задача, "Один", work_queue), (задача, "Два", work_queue)]
28
29# Запустить задачи
30 за t, n, q в заданиях:
31 т(н, ц)
32
33if __name__ == "__main__":
34 основной()
Очередь()
21
22 # Поставить часть работы в очередь
23 для работы в [15, 10, 5, 2]:
24 work_queue.put(работа)
25
26 # Создайте несколько синхронных задач
27 задач = [(задача, "Один", work_queue), (задача, "Два", work_queue)]
28
29# Запустить задачи
30 за t, n, q в заданиях:
31 т(н, ц)
32
33if __name__ == "__main__":
34 основной()
Давайте посмотрим, что делает каждая строка:
- Строка 1 импортирует модуль очереди
- Строки с 3 по 13 определяют
task(). Эта функция извлекает работу из очередиwork_queueи обрабатывает ее до тех пор, пока больше не останется. - Строка 15 определяет
main()для запуска программных задач. - Строка 20 создает
work_queue. Все задачи используют этот общий ресурс для получения работы. - Строки с 23 по 24 помещают работу в
work_queue. В этом случае это просто случайное количество значений для обработки задач.
В этом случае это просто случайное количество значений для обработки задач. - Строка 27 создает список кортежей задач со значениями параметров, которые будут переданы этим задачам.
- Строки с 30 по 31 перебирают список кортежей задач, вызывая каждый из них и передавая ранее определенные значения параметров.
- Строка 34 вызывает
main()для запуска программы.
Задача в этой программе - просто функция, принимающая в качестве параметров строку и очередь. При выполнении он ищет что-либо в очереди для обработки. Если есть работа, которую нужно сделать, то он извлекает значения из очереди, запускает цикл для для подсчета до этого значения и выводит итог в конце. Он продолжает получать работу из очереди до тех пор, пока ничего не останется и не выйдет.
Когда эта программа запускается, она выводит результат, который вы видите ниже:
Задача 1 выполняется Задание 1 всего: 15 Выполняется задача номер один Задание 1 всего: 10 Выполняется задача номер один Задание 1 всего: 5 Выполняется задача номер один Задание 1 всего: 2 Задача вторая ничего не делать
Это показывает, что Task One выполняет всю работу. Цикл
Цикл while , который Task One попадает в task() , потребляет всю работу в очереди и обрабатывает ее. Когда этот цикл выйдет, Task Two получает шанс бежать. Однако он обнаруживает, что очередь пуста, поэтому Task Two печатает оператор, в котором говорится, что ему нечего делать, а затем завершает работу. В коде нет ничего, что позволяло бы Task One и Task Two переключать контексты и работать вместе.
Простой кооперативный параллелизм
Следующая версия программы позволяет выполнять две задачи вместе. Добавление оператора yield означает, что цикл будет передавать управление в указанной точке, сохраняя при этом свой контекст. Таким образом, уступающую задачу можно будет перезапустить позже.
Оператор yield превращает task() в генератор. Генераторная функция вызывается так же, как и любая другая функция в Python, но когда выполняется инструкция yield , управление возвращается вызывающей стороне функции. По сути, это переключение контекста, поскольку управление переходит от функции-генератора к вызывающей стороне.
По сути, это переключение контекста, поскольку управление переходит от функции-генератора к вызывающей стороне.
Интересно, что управление может быть передано обратно функции-генератору вызовом next() на генератор. Это переключение контекста обратно к функции-генератору, которая запускает выполнение со всеми переменными функции, которые были определены до того, как даст , все еще нетронутыми.
Цикл while в main() использует это преимущество, когда вызывает next(t) . Этот оператор перезапускает задачу в том месте, где она ранее завершилась. Все это означает, что вы контролируете, когда происходит переключение контекста: когда оператор yield выполняется в задача() .
Это форма совместной многозадачности. Программа передает контроль над своим текущим контекстом, чтобы можно было запустить что-то еще. В этом случае он позволяет циклу while в main() запускать два экземпляра task() в качестве функции-генератора. Каждый экземпляр потребляет работу из одной и той же очереди. Это довольно умно, но для получения тех же результатов, что и в первой программе, требуется много работы. Программа
Каждый экземпляр потребляет работу из одной и той же очереди. Это довольно умно, но для получения тех же результатов, что и в первой программе, требуется много работы. Программа example_2.py демонстрирует этот простой параллелизм и приведена ниже:
1 очередь импорта
2
3def задача (имя, очередь):
4, а не queue.empty():
5 счет = очередь.получить()
всего 6 = 0
7 print(f"Выполняется задача {имя}")
8 для x в диапазоне (количество):
всего 9 += 1
10 выход
11 print(f"Всего по задаче {имя}: {всего}")
12
13def основной():
14 """
15 Это главная точка входа в программу
16 """
17 # Создаем очередь работ
18 work_queue = очередь.Очередь()
19
20 # Поставить часть работы в очередь
21 для работы в [15, 10, 5, 2]:
22 work_queue.put(работа)
23
24 # Создайте несколько задач
25 задач = [задача ("Одна", рабочая_очередь), задача ("Две", рабочая_очередь)]
26
27 # Запустить задачи
28 сделано = Ложь
29пока не сделано:
30 за t в задачах:
31 попытка:
32 следующий(т)
33, кроме StopIteration:
34 таск. удалить(т)
35 если len(задачи) == 0:
36 выполнено = верно
37
38if __name__ == "__main__":
39 основной()
удалить(т)
35 если len(задачи) == 0:
36 выполнено = верно
37
38if __name__ == "__main__":
39 основной()
Вот что происходит в приведенном выше коде:
- Строки с 3 по 11 определяют
task(), как и раньше, но добавлениедаетв строке 10, превращая функцию в генератор. Здесь происходит переключение контекста и управление возвращается кв то время какцикл вmain(). - Строка 25 создает список задач, но немного другим способом, чем вы видели в предыдущем примере кода. В этом случае каждая задача вызывается со своими параметрами, введенными в переменную списка
tasks. Это необходимо для запуска функции генератораtask()в первый раз. - Строки с 31 по 36 являются модификациями цикла
whileвmain(), которые позволяютtask()работать совместно. Именно здесь управление возвращается к каждому экземпляруtask(), когда он уступает, позволяя циклу продолжаться и запускать другую задачу.
- Строка 32 возвращает управление
task()и продолжает выполнение после точки, где была вызванаyield. - Строка 36 устанавливает переменную
done. Циклwhileзаканчивается, когда все задачи завершены и удалены иззадач.
Это результат работы этой программы:
Задача 1 выполняется Выполняется задача номер два Всего за задание два: 10 Выполняется задача номер два Задание 1 всего: 15 Выполняется задача номер один Задание второе всего: 5 Задание 1 всего: 2
Вы видите, что и Task One , и Task Two выполняются и потребляют работу из очереди. Это то, что задумано, так как обе задачи обрабатывают работу, и каждая отвечает за два элемента в очереди. Это интересно, но опять же, для достижения таких результатов требуется немало работы.
Хитрость заключается в использовании инструкции yield , которая превращает task() в генератор и выполняет переключение контекста. Программа использует этот переключатель контекста, чтобы передать управление циклу
Программа использует этот переключатель контекста, чтобы передать управление циклу while в main() , позволяя двум экземплярам задачи выполняться совместно.
Обратите внимание, что Task Two сначала выводит итоговое значение. Это может навести вас на мысль, что задачи выполняются асинхронно. Тем не менее, это все еще синхронная программа. Он структурирован таким образом, что две задачи могут обмениваться контекстами туда и обратно. Причина Задача 2 сначала выводит свое общее количество в том, что оно считает только до 10, в то время как Задача 1 считает до 15. Задача 2 просто достигает своей суммы первой, поэтому она может распечатать свой вывод на консоли до Задача Один .
Примечание: Весь пример кода, который следует из этого пункта, использует модуль codetiming для определения времени и вывода того, сколько времени потребовалось для выполнения участков кода. На RealPython есть отличная статья, в которой подробно рассказывается о модуле синхронизации кода и о том, как его использовать.
На RealPython есть отличная статья, в которой подробно рассказывается о модуле синхронизации кода и о том, как его использовать.
Этот модуль является частью индекса пакетов Python и создан Гейром Арне Хьелле, который является частью команды Real Python . Гейр Арне очень помог мне, просматривая и предлагая вещи для этой статьи. Если вы пишете код, который должен включать функции синхронизации, вам стоит обратить внимание на модуль синхронизации кодов Гейра Арне.
Чтобы сделать модуль синхронизации кодов доступным для следующих примеров, вам необходимо его установить. Это можно сделать с помощью pip с помощью этой команды: pip install codetiming или с помощью этой команды: pip install -r requirements.txt . Файл requirements.txt является частью репозитория примеров кода.
Удалить рекламу
Совместный параллелизм с блокировкой вызовов
Следующая версия программы такая же, как и предыдущая, за исключением добавления time. в тело цикла задач. Это добавляет задержку, основанную на значении, извлеченном из рабочей очереди, для каждой итерации цикла задачи. Задержка имитирует эффект блокирующего вызова, происходящего в вашей задаче. sleep(delay)
sleep(delay)
Блокирующий вызов — это код, который не позволяет ЦП делать что-либо еще в течение некоторого периода времени. В приведенных выше мысленных экспериментах, если родитель не мог оторваться от балансировки чековой книжки до тех пор, пока она не была завершена, это было бы блокирующим вызовом.
time.sleep(delay) делает то же самое в этом примере, потому что ЦП не может ничего делать, кроме как ждать, пока истечет задержка.
1время импорта
2очередь импорта
3из таймера импорта кода
4
5def задача (имя, очередь):
6 timer = Timer(text=f"Истекшее время задачи {name}: {{:.1f}}")
7, а не queue.empty():
8 задержка = очередь.получить()
9print(f"Выполняется задача {имя}")
10 таймер.старт()
11 раз.сон (задержка)
12 таймер. стоп()
13 выход
14
15def основной():
16 """
17 Это основная точка входа в программу
18 """
19 # Создаем очередь работ
20 work_queue = очередь.Очередь()
21
22 # Поставить часть работы в очередь
23 для работы в [15, 10, 5, 2]:
24 work_queue.put(работа)
25
26 задач = [задача ("Одна", рабочая_очередь), задача ("Две", рабочая_очередь)]
27
28 # Запустить задачи
29 сделано = Ложь
30 с таймером (text="\nОбщее прошедшее время: {:.1f}"):
31 пока не сделано:
32 за т в задачах:
33 попытка:
34 следующий(т)
35, кроме StopIteration:
36 задач .remove(t)
37 если len(задачи) == 0:
38 выполнено = Верно
3940if __name__ == "__main__":
41 основной()
стоп()
13 выход
14
15def основной():
16 """
17 Это основная точка входа в программу
18 """
19 # Создаем очередь работ
20 work_queue = очередь.Очередь()
21
22 # Поставить часть работы в очередь
23 для работы в [15, 10, 5, 2]:
24 work_queue.put(работа)
25
26 задач = [задача ("Одна", рабочая_очередь), задача ("Две", рабочая_очередь)]
27
28 # Запустить задачи
29 сделано = Ложь
30 с таймером (text="\nОбщее прошедшее время: {:.1f}"):
31 пока не сделано:
32 за т в задачах:
33 попытка:
34 следующий(т)
35, кроме StopIteration:
36 задач .remove(t)
37 если len(задачи) == 0:
38 выполнено = Верно
3940if __name__ == "__main__":
41 основной()
Вот чем отличается приведенный выше код:
- Строка 1 импортирует модуль
time, чтобы предоставить программе доступ кtime.sleep(). - Строка 3 импортирует код таймера
- Строка 6 создает экземпляр
Timer, используемый для измерения времени, затрачиваемого на каждую итерацию цикла задачи.
- Строка 10 запускает экземпляр таймера
- Строка 11 изменяет
task(), чтобы включитьtime.sleep(delay)для имитации задержки ввода-вывода. Это заменяет циклfor, который выполнял подсчет вexample_1.py. - Строка 12 останавливает экземпляр таймера
timer.start(). - Строка 30 создает
Таймердиспетчер контекста, который будет выводить время, прошедшее с момента выполнения всего цикла while.
Когда вы запустите эту программу, вы увидите следующий вывод:
Задача 1 выполняется Истекшее время задачи 1: 15,0 Выполняется задача номер два Истекшее время второй задачи: 10.0 Выполняется задача номер один Истекшее время задачи 1: 5,0 Выполняется задача номер два Истекшее время задачи 2: 2,0 Общее прошедшее время: 32,0
Как и прежде, обе задачи Task One и Task Two работают, потребляя работу из очереди и обрабатывая ее. Однако, даже с добавлением задержки, вы можете видеть, что совместный параллелизм ничего вам не дал. Задержка останавливает обработку всей программы, и ЦП просто ждет окончания задержки ввода-вывода.
Однако, даже с добавлением задержки, вы можете видеть, что совместный параллелизм ничего вам не дал. Задержка останавливает обработку всей программы, и ЦП просто ждет окончания задержки ввода-вывода.
Именно это подразумевается под блокирующим кодом в асинхронной документации Python. Вы заметите, что время, необходимое для запуска всей программы, — это просто совокупное время всех задержек. Выполнение задач таким образом не является победой.
Совместный параллелизм с неблокирующими вызовами
Следующая версия программы довольно сильно изменена. Он использует асинхронные функции Python с помощью asyncio/await, представленного в Python 3.
Время и очередь 9Модули 1481 заменены пакетом asyncio . Это дает вашей программе доступ к асинхронным дружественным (неблокирующим) функциям ожидания и очереди. Изменение на task() определяет ее как асинхронную с добавлением префикса async в строке 4. Это указывает Python, что функция будет асинхронной.
Это указывает Python, что функция будет асинхронной.
Другим большим изменением является удаление операторов time.sleep(delay) и yield и замена их на ожидание asyncio.sleep(delay) . Это создает неблокирующую задержку, которая будет выполнять переключение контекста обратно к вызывающей стороне main() .
Цикл while внутри main() больше не существует. Вместо task_array есть вызов await asyncio.gather(...) . Это сообщает asyncio две вещи:
- Создайте две задачи на основе
task()и начните их выполнение. - Подождите, пока оба из них будут выполнены, прежде чем двигаться дальше.
Последняя строка программы asyncio.run(main()) запускает main() . Это создает то, что известно как цикл событий). Именно этот цикл запустит main() , который, в свою очередь, запустит два экземпляра task() .
Цикл событий лежит в основе асинхронной системы Python. Он запускает весь код, включая main() . Когда код задачи выполняется, ЦП занят выполнением работы. Когда достигается ключевое слово await , происходит переключение контекста, и управление возвращается обратно в цикл обработки событий. Цикл событий просматривает все задачи, ожидающие события (в данном случае asyncio.sleep(delay) timeout) и передает управление задаче с готовым событием.
await asyncio.sleep(delay) не блокирует ЦП. Вместо того, чтобы ждать истечения задержки, ЦП регистрирует событие сна в очереди задач цикла событий и выполняет переключение контекста, передавая управление циклу событий. Цикл событий постоянно ищет завершенные события и передает управление обратно задаче, ожидающей этого события. Таким образом, ЦП может оставаться занятым, если работа доступна, в то время как цикл обработки событий отслеживает события, которые произойдут в будущем.
Примечание: Асинхронная программа выполняется в одном потоке выполнения. Переключение контекста с одного раздела кода на другой, который может повлиять на данные, полностью находится под вашим контролем. Это означает, что вы можете атомизировать и завершить весь доступ к данным в общей памяти перед переключением контекста. Это упрощает проблему разделяемой памяти, присущую многопоточному коду.
Код example_4.py приведен ниже:
1import асинхронный
2из таймера импорта кода
3
4асинхронная задача определения (имя, рабочая_очередь):
5 timer = Timer(text=f"Истекшее время задачи {name}: {{:.1f}}")
6, а не work_queue.empty():
7 задержка = ожидание work_queue.get()
8 print(f"Выполняется задача {имя}")
9таймер.старт()
10 ожидание asyncio.sleep(задержка)
11 таймер.стоп()
12
13асинхронная функция main():
14 """
15 Это главная точка входа в программу
16 """
17 # Создаем очередь работ
18 work_queue = asyncio.Queue()
19
20 # Поставить часть работы в очередь
21 для работы в [15, 10, 5, 2]:
22 ожидания work_queue. put(работа)
23
24 # Запустить задачи
25 с таймером (text="\nОбщее прошедшее время: {:.1f}"):
26 ждать asyncio.gather(
27 asyncio.create_task(задача("Один", work_queue)),
28 asyncio.create_task(задача("Два", work_queue)),
29)
30
31if __name__ == "__main__":
32 asyncio.run(основной())
put(работа)
23
24 # Запустить задачи
25 с таймером (text="\nОбщее прошедшее время: {:.1f}"):
26 ждать asyncio.gather(
27 asyncio.create_task(задача("Один", work_queue)),
28 asyncio.create_task(задача("Два", work_queue)),
29)
30
31if __name__ == "__main__":
32 asyncio.run(основной())
Вот чем отличается эта программа от example_3.py :
- Строка 1 импортирует
asyncioдля получения доступа к асинхронным функциям Python. Это заменяет импортвремени. - Строка 2 импортирует код таймера
- Строка 4 показывает добавление 9Ключевое слово 1480 async перед определением
task(). Это информирует программу о том, что задача - Строка 5 создает экземпляр
Timer, используемый для измерения времени, затрачиваемого на каждую итерацию цикла задачи.
- Строка 9 запускает экземпляр таймера
- Строка 10 заменяет
time.sleep(delay)на неблокирующийasyncio.sleep(delay), что также возвращает управление (или переключение контекстов) обратно основному циклу событий. - Строка 11 останавливает экземпляр таймера
timer.start(). - Строка 18 создает неблокирующую асинхронную
work_queue. - Строки с 21 по 22 помещают работу в
work_queueасинхронным образом с использованием ключевого словаawait. - Строка 25 создает менеджер контекста
Timer, который будет выводить время, прошедшее с момента выполнения всего цикла while. - Строки с 26 по 29 создают две задачи и собирают их вместе, поэтому программа будет ждать завершения обеих задач.

- Строка 32 запускает программу, работающую асинхронно. Он также запускает внутренний цикл обработки событий.
Когда вы смотрите на выходные данные этой программы, обратите внимание, как Task One и Task Two запускаются одновременно, а затем ждут имитации вызова ввода-вывода:
Задача 1 выполняется Выполняется задача номер два Общее затраченное время задачи 2: 10,0 Выполняется задача номер два Общее затраченное время задачи 1: 15,0 Выполняется задача номер один Общее затраченное время задачи 2: 5,0 Общее затраченное время задачи 1: 2,0 Общее прошедшее время: 17,0
Это указывает на то, что await asyncio.sleep(delay) не блокируется и что выполняется другая работа.
В конце программы вы заметите, что общее затраченное время практически вдвое меньше времени, которое потребовалось для запуска example_3.py . В этом преимущество программы, использующей асинхронные функции Python! Каждая задача смогла запустить await asyncio. одновременно. Общее время выполнения программы теперь меньше суммы ее частей. Вы оторвались от синхронной модели! sleep(delay)
sleep(delay)
Удалить рекламу
Синхронные (блокирующие) вызовы HTTP
Следующая версия программы - это как шаг вперед, так и шаг назад. Программа выполняет некоторую реальную работу с реальным вводом-выводом, делая HTTP-запросы к списку URL-адресов и получая содержимое страницы. Однако он делает это блокирующим (синхронным) образом.
Программа была изменена, чтобы импортировать замечательный модуль запросов для выполнения настоящих HTTP-запросов. Кроме того, очередь теперь содержит список URL-адресов, а не чисел. Кроме того, task() больше не увеличивает счетчик. Вместо этого запрашивает , получает содержимое URL-адреса, извлеченного из очереди, и печатает, сколько времени ушло на это.
Код example_5.py приведен ниже:
1 очередь импорта
2запроса на импорт
3из таймера импорта кода
4
5def задача (имя, work_queue):
6 timer = Timer(text=f"Истекшее время задачи {name}: {{:. 1f}}")
7 с request.Session() в качестве сеанса:
8, а не work_queue.empty():
9 URL-адрес = work_queue.get()
10 print(f"Задача {name} получить URL: {url}")
11 таймер.старт()
12 session.get(url)
13 таймер.стоп()
14 выход
15
16def основной():
17 """
18 Это основная точка входа в программу
19"""
20 # Создаем очередь работ
21 work_queue = очередь.Очередь()
22
23 # Поставить часть работы в очередь
24 для URL в [
25 "http://google.com",
26 "http://yahoo.com",
27 "http://linkedin.com",
28 "http://apple.com",
29 "http://microsoft.com",
30 "http://facebook.com",
31 "http://twitter.com",
32 ]:
33 work_queue.put(url)
34
35 задач = [задача ("Одна", рабочая_очередь), задача ("Две", рабочая_очередь)]
36
37 # Запустить задачи
38 сделано = Ложь
39с таймером (text="\nОбщее прошедшее время: {:.1f}"):
40 пока не сделано:
41 за т в задачах:
42 попытка:
43 следующий(т)
44, кроме StopIteration:
45 таск.удалить(т)
46 если len(задачи) == 0:
47 выполнено = верно
48
49if __name__ == "__main__":
50 основных()
1f}}")
7 с request.Session() в качестве сеанса:
8, а не work_queue.empty():
9 URL-адрес = work_queue.get()
10 print(f"Задача {name} получить URL: {url}")
11 таймер.старт()
12 session.get(url)
13 таймер.стоп()
14 выход
15
16def основной():
17 """
18 Это основная точка входа в программу
19"""
20 # Создаем очередь работ
21 work_queue = очередь.Очередь()
22
23 # Поставить часть работы в очередь
24 для URL в [
25 "http://google.com",
26 "http://yahoo.com",
27 "http://linkedin.com",
28 "http://apple.com",
29 "http://microsoft.com",
30 "http://facebook.com",
31 "http://twitter.com",
32 ]:
33 work_queue.put(url)
34
35 задач = [задача ("Одна", рабочая_очередь), задача ("Две", рабочая_очередь)]
36
37 # Запустить задачи
38 сделано = Ложь
39с таймером (text="\nОбщее прошедшее время: {:.1f}"):
40 пока не сделано:
41 за т в задачах:
42 попытка:
43 следующий(т)
44, кроме StopIteration:
45 таск.удалить(т)
46 если len(задачи) == 0:
47 выполнено = верно
48
49if __name__ == "__main__":
50 основных()
Вот что происходит в этой программе:
- Строка 2 импортирует
запросов, что обеспечивает удобный способ выполнения HTTP-вызовов.
- Строка 3 импортирует код таймера
- Строка 6 создает экземпляр
Timer, используемый для измерения времени, затрачиваемого на каждую итерацию цикла задачи. - Строка 11 запускает экземпляр таймера
- Строка 12 вводит задержку, аналогичную
example_3.py. Однако на этот раз он вызываетsession.get(url), который возвращает содержимое URL-адреса, полученного изwork_queue. - Строка 13 останавливает экземпляр таймера
timer.start(). - Строки с 23 по 32 помещают список URL-адресов в
work_queue. - Строка 39 создает менеджер контекста
Timer, который выводит время, прошедшее с момента выполнения всего цикла while.
Когда вы запустите эту программу, вы увидите следующий вывод:
Задача 1: получение URL-адреса: http://google.com Общее затраченное время задачи 1: 0,3 Вторая задача: получение URL: http://yahoo.com Общее затраченное время задачи 2: 0,8 Задача 1: получение URL: http://linkedin.com Общее затраченное время задачи 1: 0,4 Вторая задача: получение URL: http://apple.com Общее затраченное время задачи 2: 0,3 Задача 1: получение URL-адреса: http://microsoft.com Общее затраченное время задачи 1: 0,5 Вторая задача: получение URL: http://facebook.com Общее затраченное время задачи 2: 0,5 Задача 1: получение URL: http://twitter.com Общее затраченное время задачи 1: 0,4 Общее прошедшее время: 3,2
Как и в более ранних версиях программы, yield превращает task() в генератор. Он также выполняет переключение контекста, которое позволяет запустить другой экземпляр задачи.
Каждая задача получает URL-адрес из рабочей очереди, извлекает содержимое страницы и сообщает, сколько времени ушло на получение этого содержимого.
Как и раньше, дает , что позволяет обеим вашим задачам выполняться совместно. Однако, поскольку эта программа выполняется синхронно, каждый session.get() 9Вызов 1481 блокирует ЦП до тех пор, пока страница не будет получена. Обратите внимание на общее время, которое потребовалось для запуска всей программы в конце. Это будет иметь значение для следующего примера.
Асинхронные (неблокирующие) вызовы HTTP
Эта версия программы модифицирует предыдущую для использования асинхронных функций Python. Он также импортирует модуль aiohttp , который представляет собой библиотеку для асинхронного выполнения HTTP-запросов с использованием asyncio .
Задачи здесь были изменены, чтобы удалить дает вызов , так как код для выполнения вызова HTTP GET больше не блокируется. Он также выполняет переключение контекста обратно в цикл событий.
Программа example_6. указана ниже: py
py
1import асинхронный
2импорт aiohttp
3из таймера импорта кода
4
5асинхронная задача определения (имя, рабочая_очередь):
6 timer = Timer(text=f"Истекшее время задачи {name}: {{:.1f}}")
7 асинхронно с aiohttp.ClientSession() в качестве сеанса:
8, а не work_queue.empty():
9URL-адрес = ожидание work_queue.get()
10 print(f"Задача {name} получить URL: {url}")
11 таймер.старт()
12 async с session.get(url) в качестве ответа:
13 ждать ответа.текст()
14 таймер.стоп()
15
16асинхронная функция main():
17 """
18 Это основная точка входа в программу
19 """
20 # Создаем очередь работ
21 work_queue = asyncio.Queue()
22
23 # Поставить часть работы в очередь
24 для URL в [
25 "http://google.com",
26 "http://yahoo.com",
27 "http://linkedin.com",
28 "http://apple.com",
29"http://microsoft.com",
30 "http://facebook.com",
31 "http://twitter.com",
32 ]:
33 ждать work_queue.put(url)
34
35 # Запустить задачи
36 с таймером (text="\nОбщее прошедшее время: {:.1f}"):
37 ждать asyncio. gather(
38 asyncio.create_task(задача("Один", work_queue)),
39 asyncio.create_task(задача("Два", work_queue)),
40 )
41
42if __name__ == "__main__":
43 asyncio.run(основной())
gather(
38 asyncio.create_task(задача("Один", work_queue)),
39 asyncio.create_task(задача("Два", work_queue)),
40 )
41
42if __name__ == "__main__":
43 asyncio.run(основной())
Вот что происходит в этой программе:
- Строка 2 импортирует библиотеку
aiohttp, которая обеспечивает асинхронный способ выполнения HTTP-вызовов. - Строка 3 импортирует код таймера
- Строка 5 помечает
task()как асинхронную функцию. - Строка 6 создает экземпляр
Timer, используемый для измерения времени, затрачиваемого на каждую итерацию цикла задачи. - Строка 7 создает диспетчер контекста сеанса
aiohttp. - Строка 8 создает диспетчер контекста ответа
aiohttp. Он также выполняет вызов HTTPGETдля URL-адреса, взятого изwork_queue.
- Строка 11 запускает экземпляр таймера
- Строка 12 использует сеанс для асинхронного извлечения текста из URL-адреса.
- Строка 13 останавливает
экземпляр таймераи выводит время, прошедшее с момента вызоваtimer.start(). - Строка 39 создает менеджер контекста
Timer, который выводит время, прошедшее с момента выполнения всего цикла while.
Когда вы запустите эту программу, вы увидите следующий вывод:
Задача 1: получение URL-адреса: http://google.com Вторая задача: получение URL: http://yahoo.com Общее затраченное время задачи 1: 0,3 Задача 1: получение URL: http://linkedin.com Общее затраченное время задачи 1: 0,3 Задача 1: получение URL: http://apple.com Общее затраченное время задачи 1: 0,3 Задача 1: получение URL-адреса: http://microsoft.com Общее затраченное время задачи 2: 0,9Вторая задача: получение URL: http://facebook.com Общее затраченное время задачи 2: 0,4 Вторая задача: получение URL: http://twitter.com Общее затраченное время задачи 1: 0,5 Общее затраченное время задачи 2: 0,3 Общее прошедшее время: 1,7
Взгляните на общее прошедшее время, а также на отдельные моменты времени для получения содержимого каждого URL-адреса. Вы увидите, что продолжительность составляет примерно половину совокупного времени всех вызовов HTTP GET . Это связано с тем, что вызовы HTTP GET выполняются асинхронно. Другими словами, вы эффективно используете ЦП, позволяя ему выполнять несколько запросов одновременно.
Поскольку процессор очень быстрый, в этом примере, вероятно, может быть создано столько задач, сколько существует URL-адресов. В этом случае время выполнения программы будет равно времени самого медленного поиска URL.
Удалить рекламу
Заключение
В этой статье вы найдете инструменты, необходимые для того, чтобы начать делать методы асинхронного программирования частью своего репертуара.

 set_downstream(second_task)
Third_task.set_upstream(вторая_задача)
set_downstream(second_task)
Third_task.set_upstream(вторая_задача)



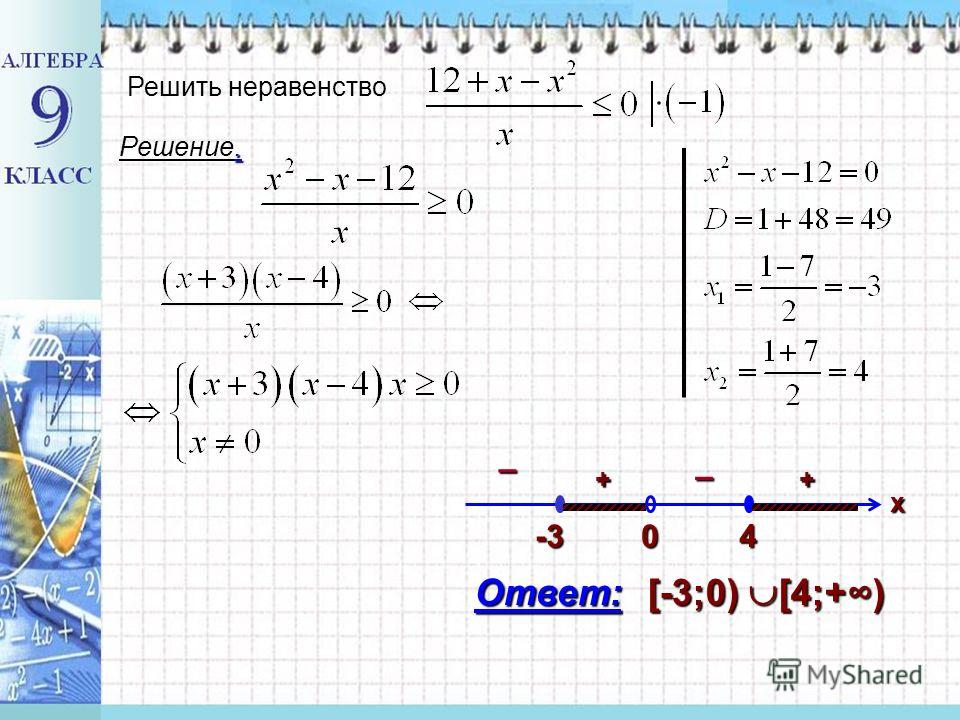 то есть «работает», «не удалось». Эти задачи описываются как задачи, которые блокируют себя или другие
задача от завершения до того, как ее окно SLA будет завершено.
то есть «работает», «не удалось». Эти задачи описываются как задачи, которые блокируют себя или другие
задача от завершения до того, как ее окно SLA будет завершено. datetime(2021, 1, 1, tz="UTC"),
перехват = ложь,
sla_miss_callback=sla_callback,
default_args={'электронная почта': "
datetime(2021, 1, 1, tz="UTC"),
перехват = ложь,
sla_miss_callback=sla_callback,
default_args={'электронная почта': " ..,
executor_config={
«КубернетесИсполнитель»:
{"изображение": "myCustomDockerImage"}
}
)
..,
executor_config={
«КубернетесИсполнитель»:
{"изображение": "myCustomDockerImage"}
}
)
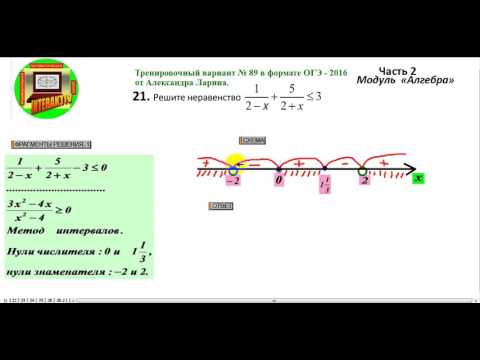 last_wait_time
...
last_wait_time
...
 ..
с self.client.post("/", json={"foo": 42, "bar": None}, catch_response=True) в качестве ответа:
пытаться:
если response.json()["приветствие"] != "привет":
response.failure("Не получено ожидаемое значение в приветствии")
кроме JSONDecodeError:
response.failure("Ответ не может быть декодирован как JSON")
кроме KeyError:
response.failure("Ответ не содержит ожидаемого ключа приветствия")
..
с self.client.post("/", json={"foo": 42, "bar": None}, catch_response=True) в качестве ответа:
пытаться:
если response.json()["приветствие"] != "привет":
response.failure("Не получено ожидаемое значение в приветствии")
кроме JSONDecodeError:
response.failure("Ответ не может быть декодирован как JSON")
кроме KeyError:
response.failure("Ответ не содержит ожидаемого ключа приветствия")
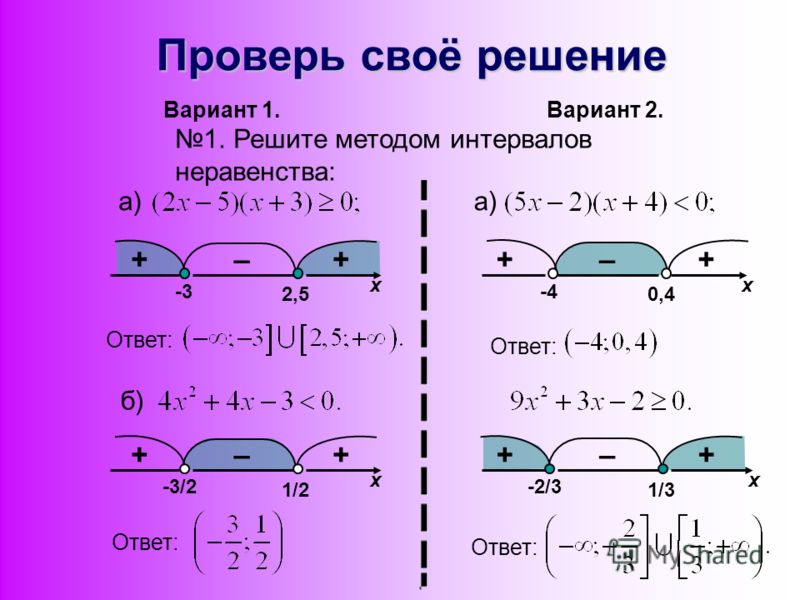 client.get("/blog?id=%i" % i, name="/blog?id=[id]")
client.get("/blog?id=%i" % i, name="/blog?id=[id]")
 client.rename_request("/article?id=[id]"):
для я в диапазоне (10):
self.client.get("/article?id=%i" % i)
client.rename_request("/article?id=[id]"):
для я в диапазоне (10):
self.client.get("/article?id=%i" % i)
 auth
auth
 to_json
выход 0
спасение Puppet::Error => e
puts({статус: 'сбой', ошибка: e.message }.to_json)
выход 1
конец
to_json
выход 0
спасение Puppet::Error => e
puts({статус: 'сбой', ошибка: e.message }.to_json)
выход 1
конец 