6 класс математика нод и нок
6 класс математика нод и нокВы искали 6 класс математика нод и нок? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 6 класс наибольший общий делитель и наименьшее общее кратное, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «6 класс математика нод и нок».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 6 класс математика нод и нок,6 класс наибольший общий делитель и наименьшее общее кратное,алгебра нод,задания по математике 6 класс на нахождение нок и нод,как быстро найти наибольший общий делитель,как вычислить нод,как делать нод,как искать наибольший общий делитель,как искать нод,как искать нод и нок,как искать нок и нод,как найти в математике нод,как найти наибольшее общее делимое,как найти наибольший,как найти наибольший делитель,как найти наибольший делитель чисел,как найти наибольший делитель числа,как найти наибольший общий делитель,как найти наибольший общий делитель 6 класс,как найти наибольший общий делитель двух чисел,как найти наибольший общий делитель двух чисел 6 класс,как найти наибольший общий делитель двух чисел правило,как найти наибольший общий делитель и наименьшее общее кратное,как найти наибольший общий делитель нескольких натуральных чисел,как найти наибольший общий делитель примеры,как найти наибольший общий делитель чисел,как найти наименьшее общее кратное и наибольший общий делитель,как найти наименьший общий делитель,как найти наименьший общий делитель 6 класс,как найти наименьший общий делитель двух чисел,как найти нод,как найти нод 2 чисел,как найти нод в математике,как найти нод двух чисел,как найти нод двух чисел примеры,как найти нод и нок,как найти нод и нок чисел 6 класс примеры,как найти нод правило,как найти нод чисел,как найти нод чисел 6 класс,как найти нод числа,как найти нок и нод,как найти нок и нод чисел 6 класс примеры,как найти общие делители двух чисел,как найти общий делитель,как найти общий делитель двух чисел,как найти общий делитель чисел,как находится наибольший общий делитель,как находится нод,как находится нод и нок,как находится нок и нод,как находить наибольший общий делитель,как находить наибольший общий делитель чисел,как находить наименьший общий делитель,как находить нод,как находить нод и нок,как находить нод и нок чисел,как находить нод чисел,как находить нок и нод,как находить общий делитель,как определить нод,математика 6 класс нод и нок примеры,математика нод,математика нод и нок,математика нод нок,математика нок и нод,математика нок нод,математика что такое нод,наибольший делитель,наибольший делитель как найти,наибольший делитель числа,наибольший общий,наибольший общий делитель,наибольший общий делитель 6 класс как найти,наибольший общий делитель двух натуральных чисел равен 72,наибольший общий делитель двух чисел,наибольший общий делитель как найти,наибольший общий делитель как найти 6 класс,наибольший общий делитель как найти примеры,наибольший общий делитель как находить,наибольший общий делитель нод,наибольший общий делитель определение,наибольший общий делитель правила,наибольший общий делитель правило,наибольший общий делитель примеры,наибольший общий делитель чисел,наибольший общий делитель чисел как найти,наибольший общий делитель это,наибольший общий множитель,наименьшее общее делитель,наименьшее общий делитель,наименьший общий делитель,наименьший общий делитель 6 класс,наименьший общий делитель как найти,наименьший общий делитель нод,найди наибольший общий делитель,найди наибольший общий делитель чисел,найдите наибольший делитель,найдите наибольший общий делитель,найдите наибольший общий делитель и,найдите наибольший общий делитель и наименьшее общее,найдите наибольший общий делитель нод для чисел,найдите наибольший общий делитель чисел,найдите наименьший общий делитель,найти наибольший,найти наибольший делитель,найти наибольший делитель числа,найти наибольший общий делитель,найти наибольший общий делитель чисел,найти наименьший общий делитель,найти общий делитель,найти общий делитель чисел,найти общий наибольший делитель чисел,нахождение наибольшего общего делителя,нахождение наименьшего общего делителя,нахождение нод,нахождение нод и нок 6 класс,нахождение нок и нод 6 класс,нахождение общего делителя,нод 2 чисел как найти,нод 36 и 6,нод 6 класс примеры,нод алгебра,нод в алгебре,нод в математике,нод в математике 6 класс,нод в математике как найти,нод в математике что это,нод в математике это,нод и нок 6 класс,нод и нок 6 класс математика примеры,нод и нок задания,нод и нок математика,нод и нок математика 6 класс,нод и нок правило и примеры,нод и нок правило и примеры 6 класс,нод и нок примеры 6 класс,нод как делать,нод как искать,нод как найти,нод как находить,нод как определить,нод математика,нод наибольший общий делитель,нод наименьший общий делитель,нод натуральных чисел,нод нахождение,нод нок математика,нод нок математика 6 класс,нод определение,нод правило,нод правило нахождения,нод примеры,нод примеры 6 класс,нод примеры с ответами,нод чисел как найти,нод чисел что такое,нод что такое математика,нод что это в математике,нод это в математике,нок и нод как искать,нок и нод как найти,нок и нод математика,нок и нод примеры для решения 6 класс,нок и нод чисел правило,нок и нод что это,нок нод как найти,нок нод математика,общие делители,общие делители чисел,общий делитель,общий делитель как найти,общий делитель чисел,определение наибольший общий делитель,определение нод,поиск нод,правила наибольший общий делитель,правила нахождения нод и нок 6 класс,правила нод и нок чисел 6 класс,правила нок и нод 6 класс,правило как найти нод,правило наибольший общий делитель,правило нахождения наибольшего общего делителя,правило нод,примеры 6 класс на нок и нод,примеры на нахождение нод и нок 6 класс,примеры на нахождение нок и нод 6 класс,примеры на нод и нок 6 класс,примеры наибольший общий делитель,примеры нод,примеры нод 6 класс,примеры нод с ответами,примеры нок и нод 6 класс,чему равен нод,что такое наибольший общий делитель,что такое наименьший общий делитель,что такое нод и нок в математике 6 класс,что такое нод и нок в математике 6 класс примеры,что такое нок и нод в математике.
Решить задачу 6 класс математика нод и нок вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Тест: Наибольший общий делитель. Наименьшее общее кратное.
Английский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖОбществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 6 класс »
- Наибольший общий делитель.
Наименьшее общее кратное.
Наименьшее общее кратное.Наибольший общий делитель. Наименьшее общее кратное.
Тест состоит из 12 вопросов. К каждому вопросу предлагается три варианта ответа, один из которых верный.
Математика 6 класс | Автор: Бурякова Вера Николаевна | ID: 1080 | Дата: 17.1.2014
+30 -18Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
«;} else {document.getElementById(«torf1″).innerHTML=»
«;} else {document.getElementById(«torf2″).innerHTML=»
«;}; if (answ.charAt(2)==»1») {document.getElementById(«torf3″).innerHTML=»
«;} else {document.getElementById(«torf3″).innerHTML=»
«;};
if (answ.
charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»
«;} else {document.getElementById(«torf4″).innerHTML=»
«;}; if (answ.charAt(4)==»1») {document.getElementById(«torf5″).innerHTML=»
«;} else {document.getElementById(«torf5″).innerHTML=»
«;}; if (answ.charAt(5)==»1») {document.getElementById(«torf6″).innerHTML=»
«;} else {document.getElementById(«torf6″).innerHTML=»
«;}; if (answ.charAt(6)==»1») {document.getElementById(«torf7″).innerHTML=»
«;} else {document.getElementById(«torf7″).innerHTML=»
«;}; if (answ.charAt(7)==»1») {document.getElementById(«torf8″).innerHTML=»
«;} else {document.getElementById(«torf8″).innerHTML=»
«;};
if (answ.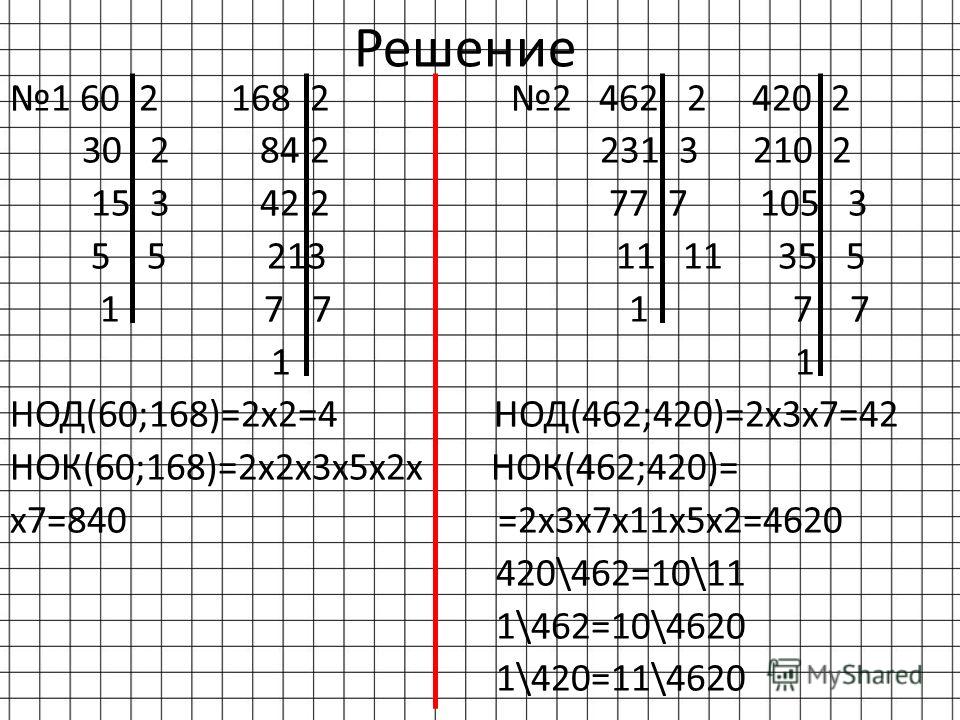
charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»
«;} else {document.getElementById(«torf9″).innerHTML=»
«;}; if (answ.charAt(9)==»1») {document.getElementById(«torf10″).innerHTML=»
«;}; if (answ.charAt(10)==»1») {document.getElementById(«torf11″).innerHTML=»
«;} else {document.getElementById(«torf11″).innerHTML=»
«;}; if (answ.charAt(11)==»1») {document.getElementById(«torf12″).innerHTML=»
«;} else {document.getElementById(«torf12″).innerHTML=»
«;}; } }
Вопрос №
1
Чему равен наибольший общий делитель чисел 36 и 54?
2
9
18
Вопрос №
2
Для каких из предложенных пар чисел НОД равен 6:
1)24 и 30; 2)24 и 32; 3)24 и 16; 4)18 и 30; 5)6 и 18.
1, 3, 5
1, 4, 5
1, 2, 4
Вопрос №
3
Какие из следующих утверждений верные:
1) два нечетных числа не могут быть взаимно простыми
2) четное и нечетное число всегда взаимно простые
3) два различных простых числа всегда взаимно простые
4) два составных числа могут быть взаимно простыми
5) последовательные натуральные числа всегда взаимно простые?
3, 4, 5
1, 2, 3, 4
1, 3, 4, 5
Вопрос №
4
Зная, что 36 =22·32, а 120=23·3·5, найдите разложение наибольшего общего делителя чисел 36 и 120 на простые множители.
23·32
22·3
22·32·5
Вопрос №
5
Разложив числа 2450 и 3150 на простые множители, найдите их наибольший общий делитель.
350
1050
50
Вопрос №
6
Чему равно наименьшее общее кратное чисел 15 и 18?
45
90
180
Вопрос №
7
Для каких из предложенных пар чисел НОК равно 18:
1)18 и 2; 2)18 и 12; 3)2 и 9; 4)9 и 36; 5)6 и 9?
1, 3, 4
2, 4, 5
1, 3, 5
Вопрос №
8
Зная, что 36 =22·32, а 120=23·3·5, найдите разложение наименьшего общего кратного чисел 36 и 120 на простые множители.
23·32
23·32·5
22·32
Вопрос №
9
Разложив числа 378 и 441 на простые множители, найдите их наименьшее общее кратное.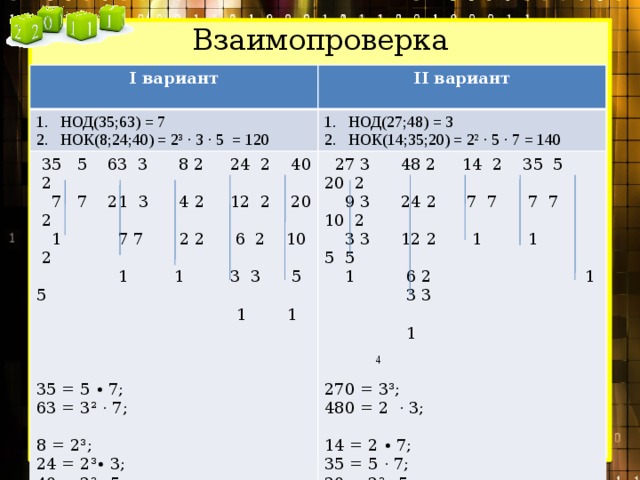
2646
1323
63
Вопрос №
10
Найдите наименьшее общее кратное чисел a, b и с, если a=2·3, b=23·32, с=22·33
216
36
6
Вопрос №
11
Число a кратно числу b. Чему равен их наибольший общий делитель?
a
b
a+b
Вопрос №
12
Даны четыре числа 20, 70, 15 и 35. Чему равны НОД и НОК этих чисел?
НОД=420; НОК=5
НОД=5; НОК=140
НОД=5; НОК=420
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.
ru 2013-2022
E-mail администратора: [email protected]
Решение задач по теме «НОК и НОД»
Цель урока: показать обучающимся, что понятия наибольшего общего делителя и наименьшего общего кратного применимы в обычной жизни.
Задачи:
- Актуализация и обобщение знаний обучающихся по теме, рефлексия.
- Формирование личностных УУД посредством самооценки различных видов деятельности.
- Формирование коммуникативных УУД (работа в группе).
- Развитие презентативных умений (презентация работы в группе).
- Повышение интереса обучающихся к предмету, активизация познавательной деятельности.
Ход урока
Приложение 1
Приложение 2
Приветствуем гостей. Садимся.
Делители, кратные, НОКи и НОДы,
Как много приходится вам изучать!
Признаки, свойства, и вечные дроби,
В них можно попасть, если правил не знать!
Уже целый месяц мы с вами изучаем главу
“Делимость чисел”.
Запутываемся, распутываемся,
и запутываемся снова. Но, как гласит закон
философии, количество всегда переходит в
качество. И сегодня мы снова запутаемся, или
распутаемся, но главное, мы попытаемся сами
оценить, что мы уже знаем, а что нам стоит еще
подучить. Перед вами на парте – оценочный лист
урока (слайд №2 приложения 1), и я надеюсь, что вы
уже достаточно взрослые, чтобы оценивать себя
честно.
| Ф.И.________________________ | самооценка | |
| 1. | “Верите ли вы?” | |
| “Установи соответствие” | ||
| “Сократи дробь” | ||
| “Собери цепочку по алгоритму Евклида” | ||
Решение задач. |
||
| Итоговая оценка за урок. | ||
| Изобрази настроение (смайлик) | ||
I. Играем в “Верите ли вы”. Как обычно, 7 цифр в столбик.
- Верите ли вы, что делители числа делятся на это число без остатка?
- Верите ли вы, что кратные числа делятся на это число без остатка?
- Верите ли вы, что наименьшее общее кратное двух чисел всегда больше меньшего из этих чисел?
- Верите ли вы, что единица может быть наибольшим общим делителем каких-либо чисел?
- Верите ли вы, что сократить дробь – это разделить числитель и знаменатель дроби на их наименьший общий делитель?
- Верите ли вы, что натуральные числа, имеющие только два делителя, называют простыми?
- Верители вы, что разложение на простые множители может помочь в нахождении наибольшего общего делителя?
Проверка, самооценка.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ответ | нет | да | да | да | нет | да | да |
Верно:
- 7 заданий – “5”,
- 6 заданий – “4+”,
- 5 заданий – “4”,
- 4 задания – “3”,
- менее 4-х заданий – “Учи правила!”
Сделать запись в оценочном листе урока.
II. Установи соответствие.
| Задание | Ответ |
| НОК (2; 12)= НОД(4;20)= НОК(3;23)= НОД(3;23)= НОК(50;75)= НОД(50;75)= НОД(25;26)= |
2; 12; 24; 4; 20; 80; 3; 23; 69; 1; 50; 75; 25; 150; 3750 |
1 человек устанавливает соответствие с помощью интерактивной доски.
Самооценка, критерии те же. Внесение в оценочный лист урока.
III. Индивидуальная работа “Сократи дробь”.
| № | дробь | решение | ответ |
| 1 | Сокращение на 5 | ||
| 2 | Сокращение на 2 | ||
| 3 | Сокращение на 4 | ||
| 4 | Сокращение на 100 | ||
| 5 | Сокращение на 9 |
Проверка по образцу.
Самооценка по количеству
правильно выполненных заданий. Запись в
оценочном листе урока. Листики передаем вперед.
IV. Соберите цепочку по алгоритму Евклида (работа на интерактивной доске).
НОД (235;150)=НОД(150;85)=НОД(85;65)=НОД(65;20)=НОД(20;5)=5
Оценка по количеству правильно подобранных звеньев (знаки равенства). Запись в оценочном листе урока.
V. Проблемная ситуация.
Итак, мы с вами порешали, дроби посокращали,
себя оценили… А я тут как-то встретила в магазине
бывшую ученицу, у нее сын Миша в 6-м классе другой
школы учится. Приходит домой, жалуется, как
трудно и скучно ему эти НОКи и НОДы считать, ведь
в жизни это нигде не нужно. “Как ответить сыну?”-
спрашивает моя ученица. Я обещала ей подумать, да
и задалась тем же вопросом; “А моим
шестиклассникам тоже, наверное, скучно и
непонятно?” Вот и подобрала я вам задачки,
которые и предлагаю в группах решить.
Может, мы
сможем ответить на вопрос Миши: “Зачем все это
надо?”
Каждая группа получает задачи. Кружочком отмечена задача, за которую отвечает данная группа. На обсуждение и решение – 5 минут. Потом каждая группа представляет свою задачу. Если вы решили быстрее, и во всем уверены, каждый может решать любую понравившуюся задачу и затем оценить свое решение и внести оценку в оценочный лист.
Группируемся, как обычно: вторая парта 1 вариант пересаживается на 1 парту, 2 вариант – на третью, четвертая парта 1 и третьего ряда – на пятую, четвертая и пятая парта среднего ряда – на шестую. Молодцы.
Приступаем к работе.
| № | задача | решение |
Заместитель директора Вера
Александровна организует проведение дня
здоровья. 424 человека повезут на стадион
“Спартак” для проведения эстафет, а 477 человек –
в плавательный бассейн с морской водой. Для
перевозки нужно заказать автобусы. Перевозчик
имеет автобусы с одинаковым количеством мест,
все места должны быть заняты. Сколько автобусов
надо заказать и сколько пассажиров будет в
каждом автобусе? |
НОД(424,477)=НОД(424;53)=53 53 человека в автобусе, 424:53=8 автобусов, 477:53=9 автобусов Всего 17 автобусов. |
|
| Бегун Коля знает, что через каждые 400 м от старта стоит наблюдатель, а через каждые 700 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды и задать вопрос наблюдателю? | НОК(400;700)=2800 м | |
Марина Николаевна, член родительского
комитета, закупила для новогодних подарков 84
мандарина, 56 апельсинов, 112 вкуснейших шоколадных
конфет, и передала все это для упаковки Светлане
Алексеевне, сын которой совсем недавно учится в
этом классе и не помнит точно, сколько в нем
человек, но знает, что больше 25. Сможет ли
Светлана Алексеевна определить, на сколько
человек ей распаковывать подарки? |
НОД (84; 56; 112) = 28 В классе 28 человек. |
|
| Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре? | НОК(50;70)= 350 см. а не 3 метра Прав папа. |
|
| Заведующая хозяйством Раиса Максимовна дала поручение учителю труда Ильдару Олеговичу закупить доски, которые можно распилить на равные части и по 30 см, и по 40 см. Какой длины и сколько потребуется досок, если нужно 16 кусочков по 30 см и 12 кусочков по 40 см. | НОК(30; 40) = 120 см 16:(120:30)=4 доски 12:(120:40)=4 доски Всего 8 досок по 120 см. |
|
| На празднике “Последнего звонка” выступающим первоклассникам принято дарить подарки. Ученики 11 “а” класса купили 58 конфет, ученики 11 “б” класс – 116 “чупа-чупсов”, а ученики 11 “в” класса – по одной мягкой игрушке. Сколько куплено мягких игрушек? | НОД (58;116)=29 Куплено 29 мягких игрушек. |
|
| Родители Артема – люди очень интересных профессий. Мама – стюардесса, а папа – машинист скорого поезда. Мама бывает дома один раз в четыре дня, а папа – один раз в семь дней. Так получилось, что оба они 1 января 2015 года уходят в рейс. Когда Артем увидит своих родителей дома вместе? | НОК(4;7)=28 Семья будет дома вместе 28 января. |
|
Продавец цветочного магазина к 8 марта
получила с базы 45 тюльпанов, 30 нарциссов и 60
веточек мимозы. Из этих цветов ей надо составить
максимально возможное количество одинаковых
букетов. Зашедшая к ней в магазин
дочка-шестиклассница быстро решила эту задачу,
сообщив, сколько надо сделать букетов и какое
количество каждого вида цветов в них войдет. Как
рассуждала дочь Маша? |
НОД(45;30;60)=15 букетов 45:15=3 тюльпана, 30:15=2 нарцисса 60:15=4 веточки мимозы. |
|
| Друзья Алексей Николаевич и Борис Петрович решили заняться гостиничным бизнесом. Для своей гостиницы Алексей Николаевич завез 108 кроватей и 72 шкафа, а Борис Петрович – 128 кроватей и 64 шкафа. Кровати и шкафы распределяются по комнатам поровну. Сколько комнат в гостиницах каждого из друзей? У кого из них остановиться третьему другу Александру Ивановичу, если он отдыхает с семьей, состоящей вместе с ним из 8 человек? | НОД(108;72)=36 – комнат у Алексей
Николаевича; 108:36=3 кровати в номере; НОД(128;64)=32- комнат у Бориса Петровича. 128:32=4 кровати в номере. Александру Ивановичу лучше остановиться у Бориса Петровича (2 номера по 4 человека). |
Решенная группой задача – “5” в оценочный лист. Аналогично за каждую задачу, решенную индивидульно.
При ответе групп ребята записывают задачи в свой лист с задачами (в презентации представлены задачи для лучшего восприятия при ответе групп).
После ответа группы учащиеся сразу садятся на свои места.
VI. Учитель. Ребята, мы с вами решили 9 задач, в которых нет ни слова про делители и кратные, но именно эти понятия помогли вам их решить. Могу я передать эти задачи своей ученице для сына? Поверит он, что не зря учит НОКи и НОДы?
Хорошо. Подведем итоги. Посмотрите на свой
оценочный лист и выставите итоговую оценку за
урок. Это может быть “пять”, “четыре”, “три”
или просто фраза “тема не понята”.
И в последней
строчке нарисуйте свое настроение, веселый,
грустный или равнодушный смайлик.
Передаем мне оценочные листы, открываем дневники и записываем домашнее задание:
Придумать три интересные задачи, которые решаются с помощью НОК и НОД, и решить их. Задание выполнять на двойном листочке.
Всем спасибо за работу. Урок окончен. Попрощаемся с нашими гостями.
Методы преподавания математики и их эффективность (НОД, НОК) — К уроку — Математика, алгебра, геометрия
.
МОУ лицей № 23 г. Сочи
Методы преподавания математики и их эффективность
Подготовила: учитель математики
Мачкалян Сирануш Карекиновна
2010 г.
Древнекитайская
мудрость гласит: «Скажи мне, и я забуду,
покажи мне, и я запомню, дай мне действовать
самому- и я научусь.
» Последняя фраза
этой мудрости «дай мне сделать самому,
и я научусь» является смыслом педагогической
деятельности учителя математики. Только
в том случае учитель достигнет успехов
в ученье математике, если он раскрепостит
ученика, даст свободу его мышлению,
воображению, направит его деятельность
с помощью разнообразных методов обучения.
Основой многих методов обучения являются научные методы: индукция, дедукция, аналогия, анализ, синтез и др.
Индукцией называется метод рассуждений, при котором общий вывод основывается на изучении отдельных, частных фактов. Если при общем выводе рассматриваются все частные факты, то индукция называется полной, а в противном случае- неполной.
В обучении математике в школе важное место занимает неполная индукция. Ее используют в следующих случаях:
а) для переоткрытия математических предложений;
б) чтобы удостоверить учащихся в справедливости той или иной теоремы, если доказательство сложно;
в) для иллюстрации с помощью наглядных пособий теоремы, ее доказательства;
г)
как один из эффективных методов решения
задач.
Дедукция— форма мышления, при которой утверждение логически выводится из уже известных ученику утверждений. Чтобы доказать неизвестную теорему, ее сводим к известной аксиоме, теореме или определению.
Аналогией называется рассуждение, которое имеет следующую схему:
А имеет свойства a, b, c,d
В имеет свойства a, b, c
Возможно, В обладает свойством d
В
творческой работе учащихся аналогия
имеет большое значение. Она может
подсказывать существование неизвестной
теоремы, способ ее доказательств, способ
решения задач. В обучении математике
она является основой одного из важнейших
методов обучения- обучения по образцам.
Учитель показывает образец изложения
доказательства теоремы, образец решения
задачи. А теперь рассмотрим, как, используя
всевозможные методы обучения (индукция,
дедукция, аналогия идр.) можно
совершенствовать методику работы
учителя математики.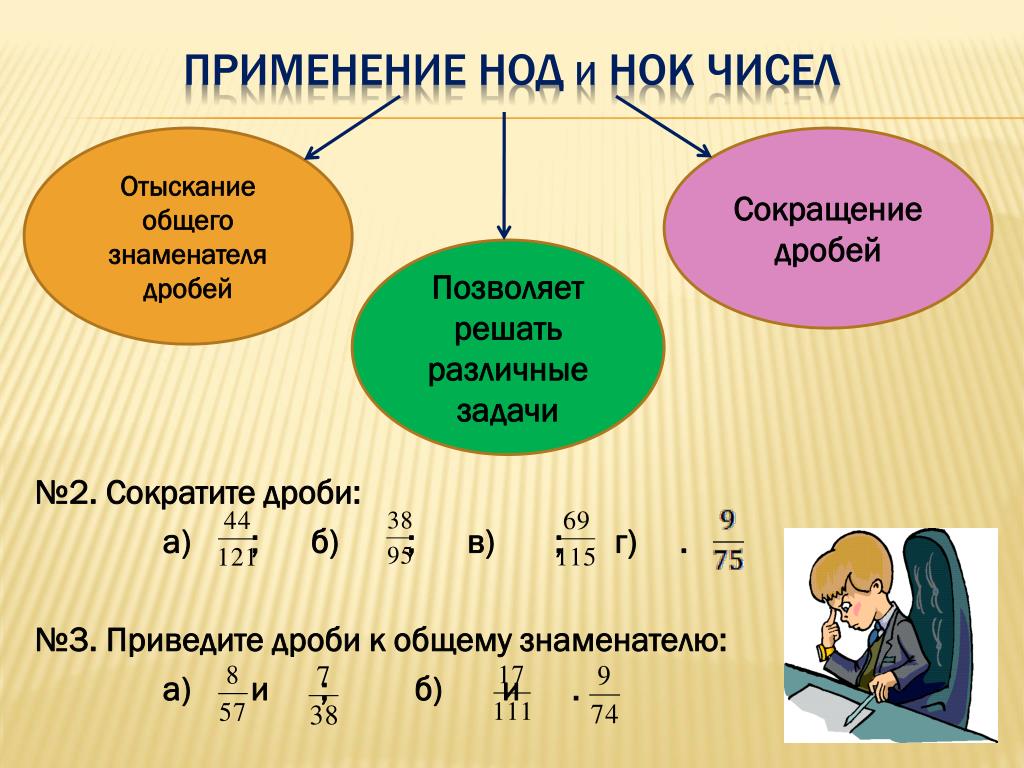
Неполная индукция является основой метода целесообразных задач. Метод целесообразных задач я применяю при изложении новой темы. При этом подбираю минимальное количество задач.
В восьмом классе при введении понятия параллелограмма предлагаю упражнение: «Проведите две параллельные прямые, пересеките их двумя другими параллельными прямыми. У вас получился четырехугольник, который называют параллелограммом. Попробуйте дать определение параллелограмма.» В моем классе учащиеся дали такую формулировку: «Параллелограмм- это такой четырехугольник, у которого противоположные стороны параллельны». Тогда даю контрпример. Черчу трапецию и подвожу под нее формулировку данного учащимися определения. Учащиеся догадываются включить в определение слово попарно. При изучении темы «Параллелограмм» целесообразно включить метод целесообразных задач.
При
введении понятия «ромб» предлагаю
учащимся упражнение. Постройте
параллелограмм, две смежные стороны
которого равны.
Такой параллелограмм
называют ромбом. Сформулируйте определение
ромба. Время, потраченное на выполнение
чертежа окупается с лихвой, так как он
тут же используется при доказательстве
теоремы о свойствах ромба.
Можно привести еще массу примеров, где используется метод целесообразных задач. Важно подчеркнуть, что этот метод фокусирует внимание учащихся на отдельных деталях новой темы, а значит, до осознания идеи нового материала затрудняет в общем его понимание. Поэтому, прежде чем применить этот метод, учителю надо подумать о его эффективности.
В выше приведенных примерах нетрудно заметить, что в основе целесообразных задач лежит метод неполной индукции. В свою очередь метод целесообразных задач является разновидностью более общего метода обучения- эвристического.
Эвристическим
называется метод, при котором учитель
вместо изложения материала в готовом
виде, подводит учащихся к «переоткрытию»
теорем, их доказательств, нахождению
алгоритма решения задач, к самостоятельному
формированию определений, к составлению
задач.
При изучении темы «Ромб» учителю лучше не в готовом виде формулировать свойство диагоналей ромба, а изучение материала строить в виде проблемного обучения. Можно дать следующие задания учащимся: «Наблюдением установите свойства диагоналей ромба». Некоторые учащиеся замечают эти свойства и формулируют приблизительно так: «Диагонали ромба пересекаются под прямым углом и делят его углы пополам.» Далее учителем задается вопрос: «А как доказать сформулированное утверждение?» если учащиеся затрудняются, а такое возможно, в зависимости от интеллектуального уровня учеников. Тогда учитель задает наводящие вопросы, такие как: «А каким уже известным свойством обладают диагонали ромба?» «Диагонали ромба точкой пересечения делятся пополам. То есть отрезки ВО и ОД равны. Чем является отрезок АО в △ ВАД и что за треугольник △ ВАД?»
Учащиеся
на эти вопросы обычно отвечают легко.
Они говорят: «АО- медиана треугольника
ВАД, треугольник ВАД- равнобедренный,
так как АВ=АД по определению ромба».
Далее учащиеся уже сами догадываются сформулировать свойство медианы равнобедренного треугольника.
При таком изучении материала срабатывает основная закономерность памяти, которая гласит: «если соблюдать два условия: учащийся выполняет над материалом активную мыслительную деятельность и эта деятельность способствует углубленному пониманию материала, то происходит успешное запоминание материала (произвольное или непроизвольное)».
Конечно, учитель должен дать установку учащимся: «Дети, дома надо обязательно повторить изученный материал».
Как и каждый метод, эвристический имеет свои достоинства и недостатки. Сначала расскажу о достоинствах этого метода.
Этот
метод позволяет активизировать
мыслительную деятельность учащихся.
Помогает хорошему усвоению материала,
развитию мышления, способностей учащихся,
но имеет и недостатки. Этот метод требует
большего времени, чем изложение готовых
знаний.
При этом методе сказываются
интеллектуальные способности учащихся,
которые быстро приходят к нужному
выводу, а некоторые пассивно наблюдают
за процессом обучения.
По мере возможности, можно исключить некоторые недостатки проблемного обучения. Например, на уроке можно решить нетрудоемкие проблемы, которые посильны основной массе с небольшой разницей по времени.
Приведу один пример применения эвристического метода обучения в пятом классе при изучении темы: «Делители».
Учитель: В повседневной жизни очень часто возникают задачи, с которыми вы сталкиваетесь. Одной из таких задач является следующая задача.
В 5 «а» классе несколькими учениками получено 12 пятерок, а в 5 «б» классе- 8 пятерок. Известно, что каждый учащийся обоих классов получил одинаковое количество пятерок, большего одного и меньшего восьми. Сколько пятерок мог получить каждый ученик? Какое наибольшее количество пятерок мог получить каждый ученик?
(на
доске схема задачи с пустыми клетками,
которые заполняют ученики).
D(12)= 2, 3, 4, 6
D(8)= 2, 4
Кол-во «5», полученных каждым учеником | |
5 «а» | 2; 3; 4; 6 |
5 «б» | 2, 4 |
Исходя из уровня подготовленности класса к мыслительным процессам. Задаю наводящие вопросы.
Учитель: как вы думаете, как можно ответить на первый вопрос задачи? Постарайтесь ответить на 1-ый вопрос задачи? Постарайтесь ответить на вопрос, разбив его на два подвопроса, то есть сколько «5» мог получить каждый ученик 5 «а» и 5 «б» классов в отдельности?
После
различных версий ответов, учащиеся
приходят к правильному варианту ответа.
Ученик: Так как каждый учащийся получил равное количество пятерок, то надо найти делители числа 12. Это будут 2, 3, 4, 6, а для 8- это 2 и 4. Заполняем клетки.
Учитель: итак, сколько «5» мог получить каждый ученик, если количество их в обоих классах одинаково? (Нетрудно теперь догадаться правильно ответить на поставленный вопрос)
Ученик: две или четыре пятерки. (Эти числа учитель подчеркивает в таблице).
Учитель: 2 и 4- делители 8 и 12. Как бы вы их назвали?
Ученики дают различные версии ответов: «Одинаковые, равные, общие».
Учитель: Их называют общими делителями. 2 и 4- общие делители 8 и 12. И пишут:
Д(8; 12)=2; 4
Учитель: какое наибольшее количество «5» мог получить каждый ученик? (вопрос не вызывает затруднений у учащихся)
Ученик:
так как каждый ученик мог получить две
или четыре «5», то выбирая наибольшее
из этих чисел, получаем 4.
Учитель: Значит, наибольший общий делитель чисел 8 и 12 равен 4. А это записывается так:
НОД (8; 12)= 4
Н-наибольший, О- общий, Д- делитель.
Далее систематизируем и обобщаем полученные знания.
Учитель: на практике очень часто приходится находить общие делители и НОД натуральных чисел. Попробуем обобщить полученные результаты, то есть составим правило (алгоритм) нахождения НОД для двух натуральных чисел. (С помощью коррекции учителя составляем правило нахождения НОД для двух натуральных чисел).
Правило нахождения НОД для натуральных чисел а и в.
Ученики: 1. Находим все делители чисел а и в.
2. Находим общие делители чисел а и в.
3. Среди общих делителей чисел а и в находим
НОД.
Нетрудно заметить, что в основе эвристического метода обучения лежит индуктивные метод.
В совей практике я пользуюсь еще одним методом обучения- это вопросно-ответный метод.
Вопросно-отчетный метод, которым я также пользуюсь, больше распространен в школьной практике. Сущность этого метода заключается в том, что новая тема излагается в виде беседы.
Этот метод имеет две разновидности: аналитико- синтетическую и синтетическую.
В первом случае вопросы учителя помогают ученику самому находить путь доказательства, решения. Во втором случае вопросы учителя соответствуют синтетическому ходу рассуждений, то есть дается доказательство в чистом виде и ученику не ясно, как самому найти путь доказательства. Приведу пример.
Изучая в восьмом классе свойство числовых неравенств по учебнику Мордковича, мы имеем следующее свойство 1.
Дано: ав, вс (1)
Доказать: ас (2)
Доказательство
этого свойства дается в учебнике
синтетическим способом.
Излагая
доказательство этим способом, учитель
фактически не помогает ученику разобраться
в доказательстве. Излагаю доказательство
теоремы синтетическим способом: «По
условию, ав,
то есть а-в
положительное число. Аналогично, так
как вс,
то в-с
положительное число».
Сложив положительные числа а-в и в-с, получим положительное число. Имеем: (а-в) + (в-с)= а-с. Значит, а-с положительное число, то есть ас. ч.т.д. ученику при таком способе доказательства непонятно, почему надо рассматривать разность а-в и в-с и устанавливать знак разности.
А теперь приведу пример аналитико-синтетического изложения доказательства свойства 1, когда ученики сами находят путь доказательства.
Дано: ав, вс (1)
Доказать: ас (2)
Учитель: Что нужно доказать?
Ученик: ас
Учитель: Для отыскания способа доказательства рекомендуется заменять понятия их определениями, поэтому вспомните, при каком условии ас?
Ученик: По определению, ас, если а-с0 (2)
Учитель: При доказательстве теорем, утверждений
пользуются или условием утверждений,
или ранее изученными определениями,
аксиомами.
В данном случае, так как мы
только приступили к изучению темы
«Неравенства», то воспользуемся условием
свойства: 1) ав
и вс.
как заменить эти понятия их определениями
вы, наверное, догадались.
Ученик: по определению ав и вс, если а-в0 и в-с0 (1)
Учитель: То есть а-в и в-с положительные числа.
а-в0
в-с0 (1)
Нам надо доказать, что а-с0 используя неравенства (1). Как это сделать? (если в ходе эвристической беседы ученики затрудняются, то после одного или двух ответов неверных лучше учителю самому ответить на поставленный вопрос).
Учитель: так как а-в и в-с положительные числа, то при их сложении мы получим положительное число, и, кроме того, переменная в входит в оба неравенства с противоположными знаками, поэтому при сложении уничтожается, то есть
а
+
+
(1)
– в 0в – с 0
(а-в) + (в-с) 0
а — в + в – с 0
а
– с 0, то есть ас,
ч.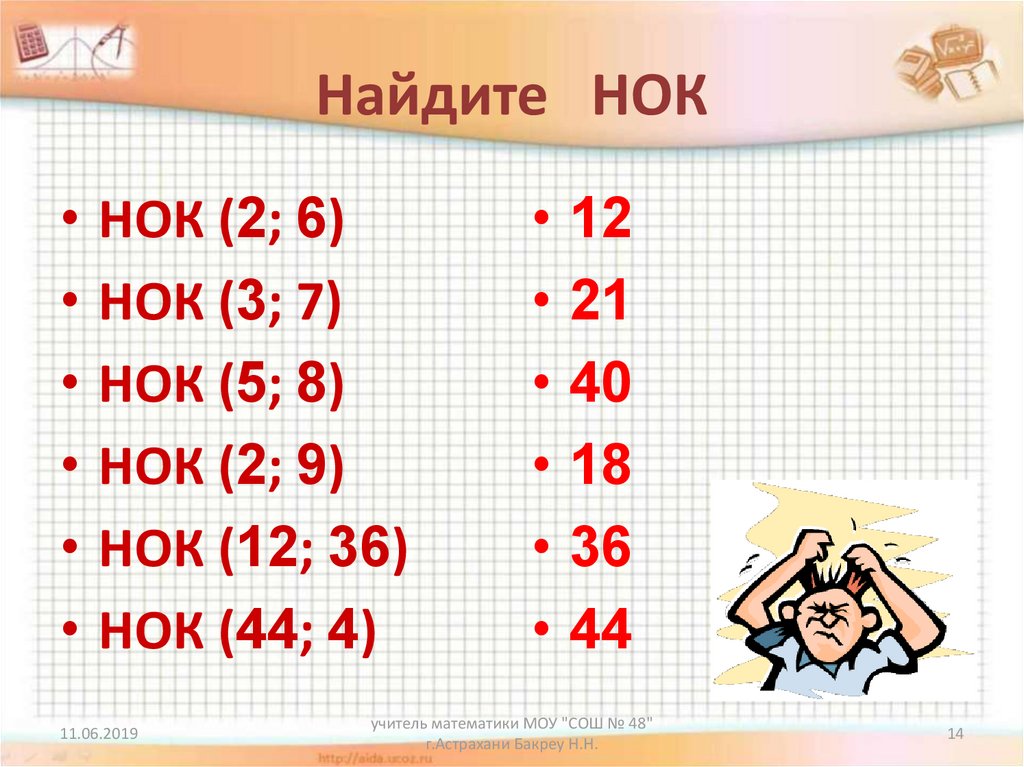
т.д.
Каковы достоинства и недостатки вопросно-ответного метода. Во-первых, вопросно-ответный метод при аналитико-синтетическом ходе рассуждений носит характер эвристической беседы, которая призвана активизировать мыслительную деятельность учащихся. С другой стороны, этот метод требует большей затраты времени, во время беседы нарушается целостность изложения материала, внимание рассеивается на второстепенные детали. Не вся масса учащихся осмысливает заданные вопросы, в результате чего сковывается инициатива учащихся.
Изучение нового материала можно провести вопросно-ответным методом, но можно провести и лекционным методом, то есть в виде рассказа учителя. Мы требуем от учащегося всегда логичного, красивого ответа, но и сами должны давать образцы таких ответов в виде связного рассказа. Так как любой лекционный метод обучения представляет собой образец ответа. То и методику лекционного обучения называем ОБРАЗЦОМ ОТВЕТА.
Лекционный метод будет протекать успешно, если учитель будет придерживаться некоторых требований:
1.
учителю надо подготовить учащихся к
пониманию материала;
2. изложить материал четко, ясно;
3. приступая к объяснению, учитель ставит классу конкретное задание, метод целесообразных задач, направленный на понимание нового материала.
В восьмом классе при изучении темы: «понятие квадратного корня» из неотрицательного числа предлагаем учащимся внимательно прочитать определение квадратного корня из неотрицательного числа и ответить на вопрос: « Нужно ли в определении указать, что число, стоящее под знаком корня неотрицательно?» При таком подходе учителя к изучаемому материалу класс значительно оживляется, повышается интерес учащихся к новому материалу, и это закономерно, согласно следующему условию активизации мыслительной деятельности учащихся.
Активность
мыслительной деятельности по ходу
ознакомления с материалом возрастает,
если соблюдаются следующие условия: 1)
учащийся, знакомясь с материалом,
одновременно выполняет конкретное
задание, помогающее глубже понять данный
материал; 2) это задание направляет
усилия учащегося на использование
определенного приема мыслительной
деятельности; 3) учащийся обладает
знаниями, необходимыми для выполнения
этого задания, и навыками применения
данного приема.
Приступая к объяснению теоремы, даю план доказательства в целом. План разбивает доказательство теоремы на элементарные задачи, которые учащиеся могут решить. План охватывает все доказательство в целом. Учащиеся чувствуют. Что с помощью плана им легче доказать и далее они могут самостоятельно составлять планы к доказательствам теорем. Приведу примеры.
К теореме: «Если в четырехугольнике противоположные стороны попарно равны, то он является параллелограммом»- предлагаю план: 1) провести диагонали; 2) доказать равенство полученных треугольников; 3) доказать параллельность противоположных сторон четырехугольника; 4) вывод.
К теореме: «Каждая точка биссектрисы неразвернутого угла равноудалена от его стороны»- предлагаю следующий план:
1. из произвольной точки, лежащей на биссектрисе угла, провести перпендикуляры к сторонам угла;
2. доказать равенство полученных треугольников;
3.
сделать вывод.
Конечно, по ходу объяснения мною доказательства теоремы, надо пользоваться и другими приемами. Например, где в доказательстве на какую аксиому, теорему, определение мы ссылаемся.
Выполняя подобные задания, учащиеся активно мыслят, повышают интерес к обучению математике.
Образец ответа, показанный учителем ученику трудно запомнить. И чтобы ученик мог выполнить задачу с нужными требованиями, совмещаю свой рассказ с другими методами обучения, такими, как алгоритмический.
В учебнике Мордковича эти алгоритмы уже даны, и поэтому их учителю составлять не надо, а надо внимательно контролировать и корректировать ответ учащихся по образцу.
Важное значение имеет следующая рекомендация учителя: «Читая и применяя алгоритм, старайтесь запоминать его». Подобная рекомендация вызывает у учащихся установку на прочное запоминание.
Выполняя
задание по алгоритму, учитель должен
требовать выделять каждый шаг алгоритма,
в результате чего у учащихся создается
обобщенная ассоциация, которая
способствует быстрому, верному изложению
решения.
Для успешного обучения математике очень важную роль играет метод элементарных и неэлементарных задач.
Задача называется элементарной, если она состоит из одного- двух умозаключений. Задача называется неэлементарной, если она состоит из более чем двух умозаключений. При решении неэлементарных задач у учеников формируются умения и навыки примене6ния отдельных теорем, определений и аксиом. При методе неэлементарных задач у учащихся формируются умения, навыки решения элементарных задач. А также навыки выполнения простых промежуточных действий.
Ученик,
не научившийся решать элементарные
задачи, никогда не научится решать
неэлементарные задачи. Учитель должен
постепенно переходить к неэлементарным.
Реализовать такой переход помогут
задачи по готовым чертежам. Наряду с их
успешным решением, надо и учить оформлять
письменно, чтобы у учащегося выработались
навыки грамотного оформления. При этом
желательно, чтобы учитель чаще проверял
тетради для обучения грамотного
оформления.
Приведу пример неэлементарной задачи, состоящей из нескольких умозаключений.
Задача № 377 (Атанасян)
В параллелограмме MNPA проведен перпендикуляр NH к прямой MA, причем точка Н лежит на стороне МА. Найдите стороны и углы параллелограмма, если известно, что МН= 3см. НА=5 см, MNH=30.Чтобы решить эту задачу, ученик должен решить ряд элементарных задач.
1.Найти гипотенузу в прямоугольном треугольнике, если катет лежит против угла в 30 градусов.
2.Найти длину всего отрезка, если точка делит отрезок на два отрезка.
3.Найти острый угол в прямоугольном треугольнике, если один из острых углов известен.
4.Две параллельные прямые пересечены секущей. Найти один из односторонних углов, если другой угол известен.
Поэтому,
задавая неэлементарные задачи, учитель
должен предусмотреть возможности
ученика, и, если есть необходимость,
начать неэлементарную задачу с
элементарной.
Я изложила ряд методов, которые я использую при обучении математике. Конечно, он неполон и требует постоянного совершенствования, ведь учитель обязан ежедневно, ежечасно искать, исследовать всевозможные методы и приемы для успешного обучения математике, используя многообразие мыслительной деятельности.
Каждый новый учебный год- это новое испытание для учителя быть достойным благородному призванию «УЧИТЕЛЬ».
План-конспект урока по теме «Наименьшее общее кратное» 6 класс
ПЛАН-КОНСПЕКТ УРОКА
__________________________________________
Тема урока «Наименьшее общее кратное»
Василихина Юлия Александровна | |
«Малостуденецкая СОШ» | |
Учитель математики и информатики | |
Математика | |
6 класс | |
«Наименьшее общее кратное» 3 урок | |
Н. |
Я. Виленкин, В.И. Жохов «Математика 6 класс» ФГОС, Издательство «Мнемозина», Москва, 2013годЦель урока: обобщение и закрепление знаний по теме «Делимость чисел».
Задачи:
— обучающие
отрабатывать умение решать задачи на использование НОК и НОД;
отрабатывать умение решать задачи алгебраическим способом;
подготовить учащихся к контрольной работе.
-развивающие
-воспитательные
Планируемые результаты
регулятивные: ученик научится самостоятельно ставить цели и планировать пути их достижения; самостоятельно контролировать своё время и управлять им; принимать решения в проблемной ситуации на основе переговоров;
коммуникативные: ученик научится учитывать разные мнения, осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь, организовывать и планировать учебное сотрудничество с учителем и сверстниками;
познавательные: ученик научится сравнивать и обобщать факты, строить логически обоснованное рассуждение, использовать доказательную математическую речь.
Тип урока: закрепление пройденного материала.
Формы работы учащихся:
Необходимое техническое оборудование:
Пояснительная записка.
Современный урок трудно представить без использования информационно-коммуникационных технологий. Использование электронных образовательных ресурсов (ЭОР) значительно облегчает и сокращает время подготовки учителя к уроку. ЭОРы развивают активно-деятельностные формы обучения; способствуют осознанию учащимися процесса обучения; развивают познавательную активность учащихся; способствуют достижению наивысшего возможного результата в общем развитии всех учеников, в том числе самых сильных и самых слабых; позволяют провести рефлексию знаний.
Более того, дают возможность «конструировать» школьные уроки и другие учебные занятия, определяя их оптимальное содержание, формы и методики обучения; способствует организации учебного процесса.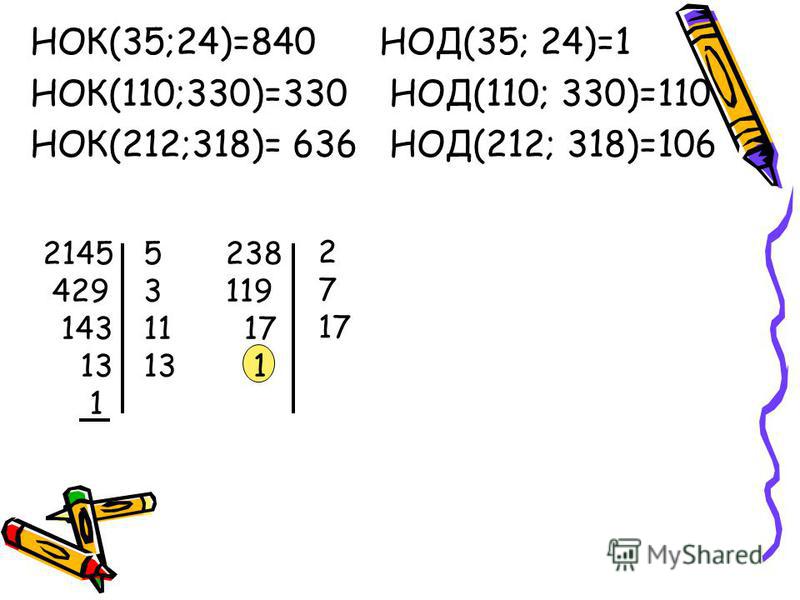
Задания, которые я использовала на уроке, дают возможность повторить и закрепить пройденный материал, подготовить учащихся к контрольной работе.
Структура и ход урока:
Этап урока | Задачи этапа | Деятельность учителя | Деятельность учеников | Время (в мин) | Формируемые УУД |
1. Организационный этап | Создать благоприятный психологический настрой на работу | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в деловой ритм урока. | 2 | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности. Личностные: мотивация учения |
2. Актуализация знаний | Актуализация опорных знаний и способов действий. | Организация устного счета, игры «АБВГДейка», решения задачи. | Участвуют в работе по повторению: решают устно примеры, вписывают пропущенные буквы в математические термины. | 11 | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание пройденного материала. Познавательные: структурирование собственных знаний. |
3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся. | Обеспечение мотивации учения детьми, принятие ими целей урока. | Мотивирует учащихся, вместе с ними определяет цель урока; акцентирует внимание учащихся на значимость темы. | Определяют цель и задачи урока. | 3 | Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. Регулятивные: целеполагание. Личностные: самоопределение. Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. |
4. Работа по теме урока | Дать качественную оценку работы класса и отдельных обучаемых. | Выявляет качество и уровень усвоения пройденного материала, а также устанавливает причины выявленных ошибок. | Работают у доски и в тетрадях, анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения примеров. | 9 | Коммуникативные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность. Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. Познавательные: способность к использованию выведенного алгоритма. Личностные: формирование позитивной самооценки. |
5.Физкультминутка | Смена деятельности. | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. | Учащиеся сменили вид деятельности и готовы продолжить работу. | 2 | |
6. Закрепление изученного материала | Выполнение практических заданий с использованием изученного материала. | Организует отработку навыков нахождения НОК и НОД, проверяет правильность выполнения заданий. | Выполняют задание, сравнивают с решением на доске, оценивают свое решение. | 11 | Коммуникативные: слушать собеседника, строить понятные для собеседника высказывания. Регулятивные: осуществляют самоконтроль процесса выполнения задания, оценивают предложенные варианты решений. Коррекция. Познавательные: сравнивать и обобщать факты, строить логически обоснованное рассуждение, использовать доказательную математическую речь. Личностные: уважительное отношение к ошибкам одноклассников, независимость и критичность мышления. |
7. Рефлексия (подведение итогов урока) | Дать количественную оценку работы учащихся. | Подводит итоги работы класса. | Учащиеся отвечают на вопросы учителя, оценивают свои ответы и ответы одноклассников. | 4 | Коммуникативные: выслушивают одноклассников, озвучивают своё мнение. Регулятивные: принимать и сохранять учебную цель и задачу, осуществлять итоговый и пошаговый контроль по результату, планировать будущую деятельность. Познавательные: анализировать степень усвоения нового материала. Личностные: независимость и критичность мышления. |
8. Информация о домашнем задании | Обеспечение понимания детьми содержания и способов выполнения домашнего задания | Объясняет домашнее задание. Предоставляет выбор разноуровневых заданий. | Учащиеся записывают в дневники задание. Планируют свои действия в соответствии с самооценкой. Самостоятельно выбирают уровень для выполнения домашнего задания. | 3 | Регулятивные: Адекватно осуществляют самооценку. Познавательные: Осуществляют актуализацию полученных знаний в соответствии с уровнем усвоения. Личностные: Принятие социальной роли обучающегося. |
Ход урока
Этапы урока | Деятельность | |||
учителя | учащихся | |||
Организационный этап | Здравствуйте, ребята. Я, как и всегда, рада вас видеть сегодня на уроке, рада вашим улыбкам и надеюсь, что время урока пролетит незаметно и будет для вас приятным и полезным. Откроем тетради, запишем число, классная работа. Я пока раздам вам ваши оценочные листы, не забывайте заносить в них баллы. | Учащиеся готовы к началу работы. | ||
Актуализации знаний | 1.Устный счёт.
№ 186. (Фронтальный опрос). 2. Игра «АБВГДейка».
— Я вам раздам листочки с правильными ответами, а вы обменяйтесь своими карточками с соседом по парте. Проверьте правильно ли вставлены буквы и поставьте количество ошибок. 3. Работа над задачей. — А теперь решим задачу № 200(1) | 1. 2. Вставляют буквы в математические термины. 3. Один ученик решает задачу у доски с комментарием, остальные в тетрадях. | ||
Постановка цели и задач урока | — Сегодня у нас последний урок по теме «Делимость чисел». Как вы думаете, какова цель нашего урока? — А какие мы поставим перед собой задачи, чтобы добиться этой цели? | Учащиеся ставят цель и задачи урока. | ||
Работа по теме урока |
| 1. 2.Один ученик выполняет задание у доски и проверяет правильность решения, остальные самостоятельно выполняют задание в тетрадях. После выполнения задания сверяют с доской. | ||
Физкультминутка | -А сейчас немного отдохнём. Я буду называть число и фамилию учащегося. Если это будет простое число, то этот ученик встаёт, а если составное – остаётся сидеть. Начинаем « 11, Закалюкина, 90, Журавлёв, и т.д.» | Выполняют упражнение | ||
Закрепление изученного материала | 1.ЭОР Наибольший общий делитель, наименьшее общее кратное и взаимно простые числа. К1 слайд 1. слайд 2 2.Разложите на простые множители число 2240. | 1. 2.Один ученик выполняет задание у доски и проверяет правильность решения, остальные выполняют задание в тетрадях. После выполнения задания сверяют с доской. 3. Один ученик раскладывает число на простые множители у доски, остальные в тетрадях самостоятельно. | ||
Рефлексия. Подведение итогов урока | — В течение всего урока вы заполняли лист самооценки, посчитайте количество баллов и выставьте себе оценку за урок и оцените пожалуйста своего одноклассника словесно. Послушаем вашу оценку товарища, а остальные сравнивают свою оценку с оценкой одноклассника. Постарайтесь объяснить свое оценивание. — Какую цель мы поставили в начале урока? Достигли ли вы цели? — Ребята, если вы хорошо усвоили тему урока, достигли цели урока, положите на край парты зеленый смайлик. Если остались непонятными какие-то моменты — желтый смайлик, вообще не усвоили тему, красный смайлик. | 1.Самооценка. Выступают с оценкой одноклассника. 2.Показывают с помощью смайлика степень усвоения материала. | ||
Домашнее задание | Учитель записывает на доске домашнее задание. Вы можете записать домашнее задание на выбор не менее двух номеров: Решить задачу № 200 (2), найти значение выражения № 210 (б), найти наибольший общий делитель № 190 (а-в), решить уравнение №206(г). Оцените выбор домашней работы (оценочный лист): 5 балла –выбрали все; 4 балла- выбрали 3 задания из 4, 2 балла – выбрали 2 номера. — Спасибо всем за активную работу. Наш урок окончен. | Ребята записывают домашнее задание в дневниках. | ||
Садитесь, пожалуйста.
.ное
Решают в уме, один из учеников проговаривает ответ.
Один ученик выполняет задание у доски и проверяет правильность решения, остальные выполняют задание в тетрадях
Один ученик вслух читает задание, все остальные слушают. Все обдумывают ответ, один отвечает. Если не правильно отвечает другой учащийся.
Приложение 1 Лист самооценки.
№ п/п | Деятельность учащегося | Критерии самооценки | Самооценка | Критерии оценки одноклассника | Оценка одноклассника (Ф. И.) |
1 | Формулировка темы урока, цели и задач урока | Я сам смог определить тему, цель и задачи урока-2 балла. Я смог определить только тему урока 1 балл. Я не смог определить тему, цель и задачи урока — 0 баллов. | Принимал участие в определении темы урока, цели урока, или задач урока — 1 балл. Не принимал участие в определении темы урока, цели урока, или задач урока — 0 баллов. | ||
2 | Устный счёт | Посчитал устно правильно – 1 балл. Посчитал устно неправильно – 0 баллов. | Посчитал устно правильно – 1 балл. Посчитал устно неправильно – 0 баллов. | ||
4 | Игра «АБВГДейка» | Вставил правильно все буквы – 1 балл. Вставил неправильно хотя бы одну букву – 0 баллов. | Не оценивается. | ||
5 | Выполнение № 200(1) | Сделал задачу сам- 2 балла. Сделал больше половины сам – 1 балл. Сделал меньше половины сам- 0 баллов. | Справился у доски с заданием — 1 балл. Не справился у доски с заданием 0 баллов. | ||
6 | Выполнение заданий (ЭОРы) | Правильно ответил на вопрос теста ЭОР Наибольший общий делитель, наименьшее общее кратное и взаимно простые числа. | Справился у доски с заданием – 1 балл Не справился у доски с заданием 0 баллов. | ||
7 | Разложения числа на простые множители | Разложил сам- 1 балла. Не справился – 0 баллов. | Разложил правильно число у доски – 1 балл. Не справился у доски с заданием — 0 баллов. | ||
8 | Выбор домашнего задания | 4 балла –выбрали все задания; 3 балла- выбрали 3 задания из 4, 2 балла – выбрали только 2 номера. | Не оценивается. |
К1 слайд 1. – 1 баллПоставьте себе оценку:
если вы набрали
10-12 баллов — «5»
7 – 9 баллов – «4»
4 – 6 баллов – «3».
Приложение 2 к плану-конспекту урока
Таблица 1.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
№ | Название ресурса | Тип, вид ресурса (И, П, К) | Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.) | Гиперссылка на ресурс, обеспечивающий доступ к ЭОР |
1 | Наименьшее общее кратное. П2 | П | иллюстрация | http://fcior.edu.ru/card/11122/naimenshee-obshee-kratnoe-p2.html |
2 | Наибольший общий делитель, наименьшее общее кратное и взаимно простые числа. | П | Тест, иллюстрация | http://fcior.edu.ru/card/3365/naibolshiy-obshiy-delitel-naimenshee-obshee-kratnoe-i-vzaimno-prostye-chisla-k1.html |
К1ЛИТЕРАТУРА:
Выговская В.В. Поурочные разработки по математике к учебному комплекту Н.Я. Виленкина. 6 класс Москва ВАКО 2011
http://festival.1september.ru/articles/532279/
Формула включений-исключений или принцип включений-исключений и примеры…
Привет, сегодня поговорим про формула включений-исключений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое формула включений-исключений, принцип включений-исключений, беспорядок, derangement , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
формула включений-исключений (или принцип включений-исключений ) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.
В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре .
Случай двух множеств
Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Формулировка
Формулу включений-исключений можно сформулировать в разных формах.
В терминах множеств
Пусть — конечные множества. Формула включений-исключений утверждает:
При получаем формулу для двух множеств, приведенную выше.
В терминах свойств
Принцип включений-исключений часто приводят в следующей альтернативной формулировке . Пусть дано конечное множество . Тогда имеет место формула:
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества ), и формулу включений-исключений можно переписать так:
Если теперь вместо «элемент », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
Доказательство
Существует несколько доказательств формулы включений-исключений.
Доказательство по индукции
Формулу включений-исключений можно доказать по индукции .
При формула включений-исключений тривиальна:
Пусть формула верна для .
Пусть каждый элемент множества :
Теперь применим формулу для свойств :
Наконец, применим формулу для одного свойства :
Комбинируя выписанные три формулы, получим формулу включений-исключений для .
Что и требовалось доказать. ■
Комбинаторное доказательство
Рассмотрим произвольный элемент .
Если элемент ).
Пусть элемент в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств . Что и требовалось доказать. ■
Доказательство через индикаторные функции
Пусть ).
Индикаторная функция их дополнений равна
а индикаторная функция пересечения дополнений:
Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получаем:
Это соотношение — одна из форм принципа включений-исключений.
Оно выражает собой логическое тождество и верно для произвольных множеств его мощность равна
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств). ■
Применение
Задача о беспорядках
Задача о беспорядках
Классический пример использования формулы включений-исключений — задача о беспорядках . Требуется найти число перестановок . Такие перестановки называются беспорядками.
Пусть беспорядков:
Это соотношение можно преобразовать к виду
Нетрудно видеть, что выражение в скобках является частичной суммой ряда перестановок:
Вычисление функции Эйлера
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера .
Пусть каноническое разложение числа на простые множители имеет вид
Число .
Количество .
По формуле включений-исключений находим
Эта формула преобразуется к виду:
Вариации и обобщения
Принцип включения-исключения для вероятностей
Пусть
Эта формула выражает принцип включений-исключений для вероятностей.
Ее можно получить из принципа включений-исключений в форме индикаторных функций:
Пусть , получим формулу включения-исключения для вероятностей.
Принцип включений-исключений в пространствах с мерой
Пусть имеет место формула включений-исключений:
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: .
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
Пусть , и получим формулу включений-исключений для меры.
Тождество максимумов и минимумов
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел , то получим соотношение для индикаторных функций множеств:
Обращение Мебиуса
Пусть следующим соотношением:
Тогда имеет место следующая формула обращения :
Это утверждение является частным случаем общей формулы обращения Мебиуса для алгебры инцидентности (англ.
) совокупности .
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств . Математически это можно записать так:
Тогда функция , определенная формулой
дает количество элементов, каждый из которых входит во все множества и, быть может, еще в другие. То есть
Заметим далее, что — количество элементов, не обладающих ни одним из свойств:
С учетом сделанных замечаний запишем формулу обращения Мебиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .
История
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (англ.) в 1854 году . Об этом говорит сайт https://intellect.icu . Но еще в 1713 году Николай Бернулли (англ.) использовал этот метод для решения задачи Монмора (англ.), известной как задача о встречах (фр.
Le problème des rencontres) , частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра[источник не указан 1933 дня] и английского математика Джозефа Сильвестра .
Принцип включений-исключений
Принцип включений-исключений — это важный комбинаторный прием, позволяющий подсчитывать размер каких-либо множеств, или вычислять вероятность сложных событий.
Формулировки принципа включений-исключений
Словесная формулировка
Принцип включений-исключений выглядит следующим образом:
Чтобы посчитать размер объединения нескольких множеств, надо просуммировать размеры этих множеств по отдельности, затем вычесть размеры всех попарных пересечений этих множеств, прибавить обратно размеры пересечений всевозможных троек множеств, вычесть размеры пересечений четверок, и так далее, вплоть до пересечения всех множеств.
Формулировка в терминах множеств
В математической форме приведенная выше словесная формулировка выглядит следующим образом:
Ее можно записать более компактно, через сумму по подмножествам. Обозначим через . Тогда принцип включений-исключений принимает вид:
Эту формулу приписывают Муавру (Abraham de Moivre).
Формулировка с помощью диаграмм Венна
Пусть на диаграмме отмечены три фигуры :
Тогда площадь объединения :
Аналогичным образом это обобщается и на объединение фигур.
Формулировка в терминах теории вероятностей
Если — их вероятности, то вероятность их объединения (т.е. того, что произойдет хотя бы одно из этих событий) равна:
Эту сумму также можно записать в виде суммы по подмножествам множества :
Доказательство принципа включений-исключений
Для доказательства удобно пользоваться математической формулировкой в терминах теории множеств:
где -ых.
Нам нужно доказать, что любой элемент, содержащийся хотя бы в одном из множеств , никак не могут быть учтены, поскольку отсутствуют в правой части формулы).
Рассмотрим произвольный элемент . Покажем, что он посчитается формулой ровно один раз.
Заметим, что:
- в тех слагаемых, у которых раз, со знаком плюс;
- в тех слагаемых, у которых ;
- в тех слагаемых, у которых раз, со знаком плюс;
- в тех слагаемых, у которых ;
- в тех слагаемых, у которых учтется ноль раз.
Таким образом, нам надо посчитать такую сумму биномиальных коэффициентов:
Проще всего посчитать эту сумму, сравнив ее с разложением в бином Ньютона выражения :
Видно, что при , что и требовалось доказать.
Применения при решении задач
Принцип включений-исключений сложно хорошо понять без изучения примеров его применений.
Сначала мы рассмотрим три простые задачи «на бумажке», иллюстрирующие применение принципа, затем рассмотрим более практические задачи, которые трудно решить без использования принципа включений-исключений.
Особо следует отметить задачу «поиск числа путей», поскольку в ней демонстрируется, что принцип включений-исключений может иногда приводить к полиномиальным решениям, а не обязательно экспоненциальным.
Простая задачка о перестановках
Сколько есть перестановок чисел от ?
Посчитаем число «плохих» перестановок, т.е. таких, у которых первый элемент .
Обозначим через
Проведя несложные комбинаторные вычисления, получаем, что это равно:
Отнимая это число от общего числа перестановок , мы получим ответ.
Простая задачка о (0,1,2)-последовательностях
Сколько существует последовательностей длины , причем каждое число встречается хотя бы раз?
Снова перейдем к обратной задаче, т.е. будем считать число последовательностей, в которых не присутствует хотя бы одно из чисел.
Обозначим через
Размеры каждого из (поскольку доступных цифр вообще не остается).
Вспоминая, что мы решали обратную задачу, получаем итоговый ответ:
Количество целочисленных решений уравнения
Дано уравнение:
где все ).
Требуется посчитать число решений этого уравнения.
Забудем сначала про ограничение местам:
Посчитаем теперь по формуле включений-исключений число «плохих» решений, т.е. таких решений уравнения, в которых один или более .
Обозначим через элементов исключены из рассмотрения и точно принадлежат первой группе. Таким образом:
Аналогично, мощность пересечения двух множеств равна числу:
Мощность каждого пересечения трех и более множеств равна нулю, поскольку .
Объединяя все это в формулу включений-исключений и учитывая, что мы решали обратную задачу, окончательно получаем ответ:
Количество взаимно простых чисел в заданном отрезке
Пусть даны числа .
Сразу перейдем к обратной задаче — посчитаем количество не взаимно простых чисел.
Рассмотрим все простые делители числа ).
Сколько чисел в отрезке ? Их количество равно:
Однако если мы просто просуммируем эти числа, то получим неправильный ответ — некоторые числа будут просуммированы несколько раз (те, которые делятся сразу на несколько ). Поэтому надо воспользоваться формулой включений-исключений.
Например, можно за -ых, посчитать их произведение, и прибавить или вычесть в формуле включений-исключений очередное слагаемое.
Итоговая реализация для подсчета количества взаимно простых чисел:
Асимптотика решения составляет .
Количество чисел в заданном отрезке, кратных хотя бы одному из заданных чисел
Даны .
Алгоритм решения практически совпадает с предыдущей задачей — делаем формулу включений-исключений над числами (иными словами, делящихся на их наименьшее общее кратное).
Таким образом, решение сводится к тому, чтобы за операций найти их наименьшее общее кратное, и прибавить или вычесть из ответа очередное значение.
Количество строк, удовлетворяющих заданному числу паттернов
Дано паттернам.
Заметим вначале, что мы можем легко посчитать число строк, удовлетворяющих сразу всем указанным паттернам. Для этого надо просто «пересечь» эти паттерны: посмотреть на первый символ (во всех ли паттернах на первой позиции стоит вопрос, или не во всех — тогда первый символ определен однозначно), на второй символ, и т.д.
Научимся теперь решать первый вариант задачи: когда искомые строки должны удовлетворять ровно паттернам.
Для этого переберем и зафксируем конкретное подмножество , и либо прибавляем к текущему ответу, либо отнимаем от него количество строк, подходящих под текущее множество:
где .
Если мы просуммируем , то получим ответ:
Однако тем самым мы получили решение за время порядка .
Решение можно ускорить, заметив, что в разных .
Перевернем формулу включений-исключений и будем вести суммирование по :
Решение получилось с асимптотикой .
Перейдем теперь ко второму варианту задачи: когда искомые строки должны удовлетворять как минимум паттернам.
Понятно, мы можем просто воспользоваться решением первого варианта задачи и просуммировать ответы от .
Таким образом, в итоговой формуле перед будет стоять другой коэффициент: не один биномиальный коэффициент с каким-то знаком, а их сумма:
Заглянув в Грэхема (Грэхем, Кнут, Паташник. «Конкретная математика» [1998] ), мы видим такую известную формулу для биномиальных коэффициентов:
Применяя ее здесь, получаем, что вся эта сумма биномиальных коэффициентов сворачивается в:
Таким образом, для этого варианта задачи мы также получили решение с асимптотикой :
Количество путей
Есть поле , избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать.
Предполагаем, что размеры ).
Для решения сразу в целях удобства отсортируем препятствия в том порядке, в каком мы можем их обойти: т.
е., например, по координате .
Также сразу научимся решать задачу без препятствий: т.е. научимся считать число способов дойти от одной клетки до другой. Если по одной координате нам надо пройти клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:
Теперь чтобы посчитать число способов дойти от одной клетки до другой, избежав всех препятствий, можно воспользоваться формулой включений-исключений: посчитаем число способов дойти, наступив хотя бы на одно препятствие.
Для этого можно, например, перебрать подмножество тех препятствий, на которые мы точно наступим, посчитать число способов сделать это (просто перемножив число способов дойти от стартовой клетки до первого из выбранных препятствий, от первого препятствия до второго, и так далее), и затем прибавить или отнять это число от ответа, в соответствии со стандартной формулой включений-исключений.
Однако это снова будет неполиномиальное решение — за асимптотику .
Покажем, как получить полиномиальное решение.
Решать будем динамическим программированием: научимся вычислять числа точки, поскольку к препятствиям добавляются стартовая и конечная клетки.
Если мы на секунду забудем про все препятствия и просто посчитаем число путей из клетки
Таким образом, значение .
Число взаимно простых четверок
Дано . Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.
Будем решать обратную задачу — посчитаем число «плохих» четверок, т.е. таких четверок, в которых все числа делятся на число .
Воспользуемся формулой включений-исключений, суммируя количество четверок, делящихся на делитель (но, возможно, делящихся и на больший делитель):
где .
Чтобы посчитать функцию , и биномиальным коэффициентом посчитать число способов выбрать из них четверку.
Таким образом, с помощью формулы включений-исключений мы суммируем количество четверок, делящихся на простые числа, затем отнимаем число четверок, делящихся на произведение двух простых, прибавляем четверки, делящиеся на три простых, и т.
д.
Число гармонических троек
Дано число , что они являются гармоническими тройками, т.е.:
либо ,
либо .
Во-первых, сразу перейдем к обратной задаче — т.е. посчитаем число негармонических троек.
Во-вторых, заметим, что в любой негармонической тройке ровно два ее числа находятся в такой ситуации, что это число взаимно просто с одним числом тройки и не взаимно просто с другим числом тройки.
Таким образом, количество негармонических троек равно сумме по всем числам от произведений количества взаимно простых с текущим числом чисел на количество не взаимно простых чисел.
Теперь все, что нам осталось для решения задачи — это научиться считать для каждого числа в отрезке , и затем перебора всевозможных произведений простых чисел из факторизации.
Поэтому нам понадобится более быстрое решение, которое подсчитывает ответы для всех чисел из отрезка сразу.
Для этого можно реализовать такую модификацию решета Эратосфена:
- Во-первых, нам надо найти все числа в отрезке , в факторизации которых никакое простое не входит дважды. Кроме того, для формулы включений-исключений нам потребуется знать, сколько простых содержит факторизация каждого такого числа.
Для этого нам надо завести массивы или нет.
После этого во время решета Эратосфена при обработке очередного простого числа мы пройдемся по всем числам, кратным текущему числу, и увеличим .
- Во-вторых, нам надо посчитать ответ для всех чисел от — количество чисел, не взаимно простых с данным.
Для этого вспомним, как работает формула включений-исключений — здесь фактически мы реализуем ее же, но с перевернутой логикой: мы словно перебираем слагаемое и смотрим, в какие формулы включений-исключений для каких чисел это слагаемое входит.
Итак, пусть у нас есть число нечетна, то надо прибавлять, иначе вычитать.
Кроме того, для формулы включений-исключений нам потребуется знать, сколько простых содержит факторизация каждого такого числа.
Реализация:
Асимптотика такого решения составляет итераций вложенного цикла.
Число перестановок без неподвижных точек
Докажем, что число перестановок длины без неподвижных точек равно следующему числу:
и приблизительно равно числу:
(более того, если округлить это выражение к ближайшему целому — то получится в точности число перестановок без неподвижных точек)
Обозначим через ).
Воспользуемся теперь формулой включений-исключений, чтобы посчитать число перестановок хотя бы с одной неподвижной точкой. Для этого нам надо научиться считать размеры множеств-пересечений , они выглядят следующим образом:
поскольку если мы знаем, что число неподвижных точек равно элементов могут стоять где угодно.
Подставляя это в формулу включений-исключений и учитывая, что число способов выбрать подмножество размера , получаем формулу для числа перестановок хотя бы с одной неподвижной точкой:
Тогда число перестановок без неподвижных точек равно:
Упрощая это выражение, получаем точное и приблизительное выражения для количества перестановок без неподвижных точек:
(поскольку сумма в скобках — это первые )
В заключение стоит отметить, что аналогичным образом решается задача, когда требуется, чтобы неподвижных точек не было среди m первых элементов перестановок (а не среди всех, как мы только что решали).
Формула получится такая, как приведенная выше точная формула, только в ней сумма будет идти до k, а не до n.
беспорядок
Беспорядок (Derangement) — это перестановка чисел от 1 , в которой ни один элемент не стоит на своем месте.
Теорема:
Количество беспорядков порядка n
Доказательство:
Воспользуемся принципом включения-исключения: обозначим за -ый элемент стоит на своем месте. Тогда по формуле включения-исключения имеем:
.
-ом месте.
Таким образом ,то есть количество искомых беспорядков.
Рассмотрим . Таким образом получаем, что:
Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем:
Раскрывая .
Примеры с подробным решением.
Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника.
Сколько школьников не знают ни одного языка?
Решение. I способ.
Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,
n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.
Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =
= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =
= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка:
100 – 80 = 20 школьников.
II способ.
Эту же задачу можно решить с помощью диаграммы Эйлера-Венна (рис. 1).
Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,
немецкий и французский — 8 – 3 = 5 школьников.
Только английский знают 42 –(2 + 3 + 7) = 30,
только немецкий — 30 – (2 + 3 + 5) = 20,
только французский — 28 – (3 + 5 + 7) = 13 школьников.
Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?
Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;
В — множество двузначных чисел, делящихся на 3;
С — множество двузначных чисел, делящихся на 5;
D — множество двузначных чисел, делящихся на 11.
n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.
n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –
– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –
– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +
+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).
n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,
n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,
n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,
n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.
Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1 = 68.
Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:
90 – 68 = 22.
Задача 3. Известно, что из n учеников спортом увлекаются a учеников, программированием b, математикой c, спортом и программированием d, спортом и математикой e, программированием и математикой f , спортом, математикой и программированием g учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
|
Вариант |
n |
a |
b |
c |
d |
e |
f |
g |
|
14 |
70 |
32 |
21 |
23 |
8 |
12 |
4 |
3 |
Решение.
Пусть A —множество учеников, которые увлекаются спортом,
B — программированием, С — математикой.
Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3
|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9
См. также
- Формула Грассмана
- операции над множествами
- множества
Напиши свое отношение про формула включений-исключений. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое формула включений-исключений, принцип включений-исключений, беспорядок, derangement
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов .
Комбинаторика.
Культура Нок — Энциклопедия всемирной истории
Культура Нок, названная в честь одноименного поселения, процветала на юге Западной Африки (современная Нигерия) в железном веке с 5 века до н.э. до 2 века н.э. Нок, известный своими характерными терракотовыми скульптурами человеческих голов и фигур, был первой известной культурой в Западной Африке, создавшей такое искусство, и, возможно, первой культурой к югу от Сахары, которая усовершенствовала технологию плавки железа.
Культура железного века
Культура Нок, расположенная к востоку от реки Нигер и к северу от реки Бенуэ на территории современной северной и центральной части Нигерии, названа в честь города, где были обнаружены первые артефакты. В основном это были фрагментарные скульптуры, засыпанные примерно 8 метрами (26 футов) песка и земли, которые были выброшены во время местных операций по добыче олова в первой половине 20 века нашей эры. Культура Нок процветала благодаря технологии выплавки железа, которая позволяла производить железные инструменты.
Культура Нок представляет собой самый ранний пример технологии выплавки железа в Африке к югу от Сахары, которая, возможно, пришла из Карфагена на север или, что более вероятно, учитывая грозный барьер пустыни Сахара, из Нубии на востоке. Возможно, это даже было местным изобретением, но, к сожалению, очень мало доказательств, подтверждающих любую из трех теорий, предшествующих двум другим. Откуда бы ни исходили идеи, это позволяло Ноку прыгать прямо из каменного века в железный век и пропускать стадию бронзового века, типичную для развития в других местах.
Удалить рекламу
Реклама
Раскопки в Таругах выявили старейшее известное поселение культуры Нок, заселенное между 4 и 2 веками до нашей эры.
Только в Таруга (55 км к юго-востоку от Абуджи) обнаружены остатки примерно 13 чугуноплавильных печей. Прочные железные инструменты, такие как мотыги, ручные топоры и тесаки, нашли хорошее применение для повышения эффективности сельского хозяйства.
Фермеры Нока могли выращивать злаки, такие как сорго, и такие овощи, как тыквы (которые были представлены в терракоте). Раскопки в Таруга обнаружили старейшее известное поселение культуры Нок, заселенное между 4 и 2 веками до нашей эры, согласно данным радиоуглеродного анализа древесного угля, обнаруженного в железных печах. Несмотря на появление железных технологий, каменные орудия все еще использовались, особенно более крупные инструменты, что говорит о том, что металл всегда был редким товаром. Жилье Нока состояло из плетеных и глинобитных хижин, которые плохо сохранились, но многие из них были построены на фундаменте, состоящем из кольца камней, и они сохранились на месте . Археология продолжается в 21 веке нашей эры в этом регионе и отодвигает временной период культуры Нок, возможно, уже к 900 году до нашей эры.
Карта территории культуры Нок
Локотус Борг (общественное достояние)
Культура Нок распространилась по центральной части Нигерии, возможно, занимая площадь до 78 000 квадратных километров (30 000 квадратных миль) или примерно площадь Португалии. Однако существуют региональные различия как в типах инструментов, так и в гончарных изделиях, изготовленных на разных стоянках Нока. Находки железных стрел и наконечников копий также предполагают, что жизнь среди Ноков и их соперничающих племен не всегда была мирной. Причина упадка культуры Нок около 200 г. н.э. неизвестна, но о ней свидетельствует резкое падение производства керамики. Обычными виновниками могли быть чрезмерная эксплуатация природных ресурсов, период неблагоприятного изменения климата, гражданские войны, приход соперничающих королевств или сочетание всех четырех факторов.
Удалить рекламу
Реклама
YouTube Следите за нами на Youtube!Нок Скульптура и керамика
Культура Нок производила скульптуры человеческих голов и фигуры людей и животных из терракоты, самые ранние подобные скульптуры, созданные в Африке к югу от Сахары. Терракотовые головы почти в натуральную величину часто были частью более полной фигуры, но эта часть обычно терялась. Действительно, большинство терракот были повреждены при обнаружении и перемещены под действием воды, поэтому их первоначальный контекст трудно определить.
Когда полая терракотовая фигурка обжигается в печи, газы и водяной пар, которые накапливаются и расширяются внутри нее, могут привести к тому, что фигурка треснет или даже полностью разрушится. Решение состоит в том, чтобы сделать вентиляционные отверстия в фигуре, и гончары Нока сделали это, но с художественной изюминкой. Глаза, рот, ноздри и ушные отверстия получили естественные отверстия, поэтому общий эстетический эффект фигуры не пострадал. В отличие от более крупных скульптур, статуэтки меньшего размера цельные.
Любите историю?
Подпишитесь на нашу бесплатную еженедельную рассылку по электронной почте!
Статуя кошки из культуры Нок
Усама Шукир Мухаммед Амин (Авторское право)
Фигуры были вырезаны для придания черт и линейного декора, по-видимому, когда глина частично затвердела, но до обжига. Многие полные фигуры сидят или стоят на основании, которое представляет собой перевернутый горшок. Обычная поза — сидящая фигура с одной рукой, опирающейся на одно поднятое колено (как в знаменитой скульптуре Огюста Родена «Мыслитель»). Некоторые фигуры носят оружие, но большинство, кажется, представляют участников ритуалов, поскольку они иногда носят особую одежду и почти всегда много бисерных украшений и подвесок, которые вряд ли носят каждый день. Мужские фигуры обычно имеют короткую квадратную бороду и любопытные усы, которые растут только в уголках рта. Есть также ряд фигур, которые не являются ни человеческими, ни чисто животными, а представляют собой воображаемую смесь того и другого. Например, есть люди с птичьим клювом, хвостом и ногами, а также голова слона с очень человеческими глазами и лбом.
включали неглубокие чаши с плоским дном, которые были украшены внутри глубокими насечками, хотя насечка могла быть предназначена для того, чтобы чаша могла функционировать как терка. Химический анализ глины из всех гончарных изделий Нока показывает, что она происходила из одного и того же источника (пока еще неизвестного), и поэтому предполагает, что промышленность могла быть централизованной и находиться под королевским контролем.
Удалить рекламу
Реклама
Наследие
Искусство Нок и культура в целом, возможно, оказали влияние на более поздние культуры в лесных районах реки Нигер, особенно на Игбо-Укву (расцвет которого пришелся на 9 в.н.э.) и Ифе (11-15 вв. н.э.). Конечно, открытие прекрасных произведений искусства, созданных культурой Нок, стало полезным прецедентом, который убедил всех сомневающихся в том, что произведения этих более поздних культур действительно были произведениями коренных чернокожих африканцев. По мере того как археология медленно и методично дополняет наши знания и расширяет временные периоды ключевых западноафриканских культур, тогда, возможно, нынешние предварительные связи между ними будут более прочными.
Редакционный обзор Перед публикацией эта статья прошла проверку на точность, надежность и соответствие академическим стандартам.
|
Получите ответы на свои вопросы о нокауте или снайпере на нашей странице часто задаваемых вопросов
Нок-аут или снайпер? Какой продукт мне подходит?
Ответ: Оба продукта имеют мощную формулу устранения запаха и полностью устраняют запах в источнике. Средство SNiPER® Disinfectant & Odor Eliminator зарегистрировано EPA и уничтожает бактерии (такие как грамотрицательные и грамположительные бактерии, а также внутрибольничные бактерии), вирусы (такие как собачий парвовирус и ВИЧ), убивает плесень и грибок, а также другие патогены. . Тем не менее, вы можете заказать любой продукт и получить такие же мощные результаты удаления запаха. Для простого удаления запахов и уборки в доме (подумайте, например, о проблемах с дымом/табаком, пожаре в микроволновой печи, вонючих спортивных сумках и одежде) Nok-Out идеально подходит для этой работы.
Если вашей организации/агентству необходима документация EPA, SNiPER® имеет регистрацию EPA. Если вам нужно предотвратить распространение плесени, предотвратить размножение бактерий и защитить окружающую среду от всего, что мы приносим домой из повседневной жизни на работе, дезинфицирующее средство SNiPER® является продуктом выбора.
Чем Нок-Аут отличается от дезинфицирующего средства СНиПЕР™?
Ответ: Nok-Out всегда обладал удивительной способностью устранять запахи и обладал мощными дезинфицирующими свойствами. Благодаря регистрации EPA (71700-2) дезинфицирующее средство SNiPER® теперь имеет обозначение «Больничное дезинфицирующее средство». SNiPER® может и действительно устраняет запахи, но он также работает для дезинфекции и дезодорации, если следовать указаниям. Обычный Нок-Аут всегда устраняет запахи, но к дезинфицирующим свойствам Нок-Аут претензий нет. Продукты тесно связаны между собой и должны выбираться в зависимости от проблемы, которую необходимо решить.
Почему я должен выбрать SNiPER™ в качестве дезинфицирующего средства/устранителя запаха?
Ответ: В качестве дезинфицирующего средства СНиПЕР® обладает наивысшей эффективностью и наименьшей токсичностью. Легко наносится и экологически безопасен. Его некоррозионная формула означает, что вы можете распылить, протереть, распылить и уйти. Нет необходимости приходить сзади и вытирать токсичные остатки, а SNIPER™ не будет выделять летучие органические соединения. Этот продукт достаточно мощный, чтобы убить собачий парвовирус, но достаточно мягкий, чтобы им можно было мыть руки. Он требует минимальной подготовки и не требует защитного снаряжения.
Как работает Нок-Аут?
Ответ: Нок-Аут — окислитель. Когда он вступает в непосредственный контакт с источником запаха, он «окисляет» (думаю, «меняет») этот вонючий материал во что-то, что больше не имеет запаха. Нок-Аут должен иметь прямой контакт с источником запаха, чтобы это могло произойти . (Поэтому, если вы входите в комнату в своем доме, и там плохо пахнет из-за мочи домашних животных на ковре, распыление воздуха не принесет вам особой пользы — вместо этого найдите источник запаха, очистите его, и распылите прямо на него.) Это химическое изменение, по-видимому, происходит во время процесса сушки, поэтому в большинстве случаев вам следует 9Распылите 0325, протрите, снова распылите и уходите , позволяя области высохнуть естественным путем.
Есть ли у Nok-Out запах?
Ответ: Нет, Nok-Out не имеет запаха и не маскирует запах, который вы устраняете. Если слабый запах «бассейна» сохраняется после обработки, продолжайте циркуляцию воздуха с помощью напольного вентилятора или системы циркуляции в автомобиле или дома.
Сможет ли Nok-Out вывести пятно мочи с ковра?
Ответ: Нок-Аут не предназначен для удаления пятен, однако клиенты сообщают нам, что во многих случаях Нок-Аут действительно удаляет пятна, а также обеспечивает полное устранение запаха. Чем новее пятно, тем больше вероятность, что Nok-Out успешно его удалит. Чем старее пятно, тем меньше вероятность, что ЧТО-НИБУДЬ его удалит.
Удаляет ли Nok-Out запахи с твердых или пористых поверхностей?
Ответ: Нок-Аут прекрасно работает на любой моющейся поверхности. Чтобы быть наиболее эффективным, он должен насыщать весь источник запаха, и это должно выполняться в щелочной или нейтральной среде pH.
Обесцветит ли Nok-Out ткань?
Ответ: Нок-Аут не оставляет пятен. Тем не менее, всегда целесообразно сначала нанести Nok-Out на небольшой уголок ткани, чтобы убедиться, что он не выцветает. Это больше, чтобы доказать вам, что не будет надвигающейся катастрофы! Осторожность! Если вы ранее использовали кислотное моющее средство, такое как уксус, рекомендуется сначала нейтрализовать эту кислоту раствором пищевой соды/воды. Приготовьте смесь из 1–2 чайных ложек пищевой соды на литр воды. Распылите этот раствор на участки, где вы ранее использовали уксус, и это позволит Nok-Out действовать наиболее эффективно и действенно.
Нужно ли разбавлять Нок-Аут?
Ответ: Для большинства применений Nok-Out можно разбавлять на 50% обычной водопроводной водой, при этом эффективность устранения запаха сохраняется. Напишите нам по электронной почте для конкретных коэффициентов разбавления для конкретных проблем.
Каков срок годности Нок-Аут и СНиПЕР®?
Ответ: Купленный вами Nok-Out будет эффективен долгие годы. Он очень медленно (не более 2 процентов в год) теряет прочность, но остается мощным нейтрализатором запаха.
Нок-Аут ДЕЙСТВИТЕЛЬНО работает?
Ответ: Еще бы! Пока вы можете добиться прямого контакта Nok-Out со ВСЕМИ источниками запаха, он будет эффективным и действенным, не причиняя вреда вам, вашей семье или вашим домашним животным. Сегодня на рынке нет другого продукта, который был бы столь же мощным и эффективным в борьбе с нежелательными запахами. Просто прочитайте нашу страницу с отзывами!
Являются ли эти продукты «зелеными»?
Ответ: Мы так думаем. Ни Нок-Аут, ни СНиПЕР® не оставляют токсичных соединений, которые могут способствовать загрязнению воздуха внутри помещений, и никогда не выделяют свободный хлор. Агентство по охране окружающей среды присвоило нам самый низкий рейтинг токсичности, который они присваивают, а активный ингредиент — диоксид хлора — используется на водоочистных сооружениях по всей планете.
Сравнение Duo Security и Nok Nok Labs 2022
- Home
- Duo Security и Nok Nok Labs
Duo Security
(22)
Fortinet FortiAuthenticator
(15)
Microsoft Authenticator
(7)
Fortinet FortiToken
(5)
Frontegg
(6)
PingID
(2)
UserLock
(2)
RSA SecurID Access
(1)
Entrust IdentityGuard
(2)
DigiCert PKI Platform
(1)
SafeNet Authentication Manager
3RSA Authentication Manager
(2)
Venafi
(1)
Symantec VIP Access Manager
(0)
Nok Nok Labs
(1)
OneSpan DIGIPASS
(1)
Secret Double Octopus
(1)
Symantec Advanced Authentication
(1)
PingFederate
(0)
RSA Adaptive Authentication
(0)
HID PIV
(0)
Jumio
(0)
Silverfort
(0)
Kaseya AuthAnvil
(0)
Thales Authenticators
(0)
i-Sprint AccessMatrix Universal Access Management
9(0)
One Identity Defender
(1)
In-Webo
(0)
Preempt
( 0)
CRYPTOCARD BlackShield
(0)
SecurEnvoy SecurAccess
(0)
Delinea Authentication Service
(0)
BIO-key
(0)
Swivel Secure PINsafe
(0)
DAON Identityx Платформа
(0)
Подтверждение ID
(0)
ESET Secure Authentication
(0)
Acuant AssureID
(0)
Securenvoy Securice
(0)
Authentify
(0)
101196666669 (0)10- 66666666669. МИД
(0)
NEVIS nevisAuth
(0)
SecureKey
(0)
Anakam.TFA
(0)
Старлинг-двухфакторная аутентификация
(0)
- цифровой цифровой0419 (0)
WiKID Systems
(0)
Socure
(0)
SMS PASSCODE
(0)
DetectID
(0)
KOBIL mIDLogin
(0)
Pindrop Passport
(0)
Datablink Mobile 200
(0)
Datablink Management Server
(0)
Thumbsignin
(0)
Datablink Device 200
(0)
919 (0)919 .Axiad Cloud
(5)
20419 (3)
1911 1 1 111111111111111111111111111111111111111111111111119Н
org/ListItem»>
1111111111111111111111111111
1
19ENTI0002 Acuant IDscan
(0)
0002 i-Sprint AccessMatrix Universal Authentication Server(0)
Cancel
You must select at least 2 products to compare !
Сравнение Руководство покупателя
Загрузить полный отчет
Руководство покупателя
Системы аутентификации
Сентябрь 2022 г.
Резюме
Мы провели сравнение между Duo Security и Nok Nok Labs на основе реальных отзывов пользователей PeerSpot.
Узнайте в этом отчете, как два решения Authentication Systems сравниваются с точки зрения функций, цен, обслуживания и поддержки, простоты развертывания и рентабельности инвестиций.
Чтобы узнать больше, ознакомьтесь с нашим подробным отчетом Duo Security и Nok Nok Labs (обновлено: сентябрь 2022 г.).
Скачать полный отчет
633 184 специалиста использовали наше исследование с 2012 года.
Избранный обзор
Анонимный пользователь
Менеджер по продажам в оптовом магазине/дистрибьюторе
Хорошо работает для всех уровней наших конечных пользователей, предоставляя им удобные варианты аутентификации
с точки зрения исправления, поскольку он просто утончен в предотвращении. Компания Duo проделала очень хорошую работу, чтобы убедиться, что проблема… Читать далее →
Использовать Nok Nok Labs?
Поделитесь своим мнением.
Цитаты участников
Мы попросили бизнес-профессионалов оценить решения, которые они используют.
Вот некоторые выдержки из того, что они сказали:
«Интеграция с Azure Active Directory и облаком AWS потрясающая, так как большинство продуктов в настоящее время требуют создания настраиваемой интеграции. С Duo Security это было больше похоже на нативную интеграцию, и мне потребовалось пять минут, чтобы зарегистрироваться».
«Он очень хорошо отвечает нашим требованиям безопасности. Он прост в использовании, к нему также доступна документация. Он также очень стабилен и масштабируем, и его поддержка также очень хороша. Нас устраивает это решение».
«Единая панель управления работает очень хорошо. Эта функция очень важна, потому что у нас много администраторов, которым приходится управлять Duo, и гораздо проще, когда это одна панель. Эта единственная панель также хороша тем, что регистрировать новые устройства легко».
«Двухфакторный вход в систему великолепен. Я получаю сообщение и просто должен нажать ОК.»
«Это был простой способ обеспечения двухфакторной аутентификации для удаленного доступа, когда мы столкнулись с пандемией COVID. Это было очень легко и быстро».
«Еще одна функция — это единая панель управления стеклом. Это важно для аналитики, а также для устранения неполадок. Это означает, что есть одно место, куда вы можете хотя бы начать процесс устранения неполадок».
«Duo позволил нам добавить дополнительный уровень безопасности в нашу организацию и установить доверие для каждого запроса на доступ, а также защитить нашу среду».
«Мы получаем меньше угроз для устранения благодаря двухфакторной аутентификации, которая не пропускает столько угроз.»
Другие специалисты по безопасности Duo →
«Техническая поддержка работает хорошо».
Другие специалисты Nok Nok Labs →
«Большая автоматизация и аналитика устройств были бы полезны для создания бесшовного единого окна. Наличие дополнительных возможностей для оптимизации процессов также улучшит ситуацию».
«Безопасность Duo может улучшиться за счет большей совместимости с другими поставщиками».
«Техническая поддержка может быть улучшена. Я не думаю, что вся поддержка должна проходить через соглашение.»
«Интеграция с таким продуктом, как Microsoft Sentinel, была бы отличной.
Поскольку продукт постоянно совершенствуется, я не уверен, доступна ли эта функция.» «Они могли бы просто продолжать добавлять больше интеграций.»
«Для серверной части могут быть применены дополнительные функции безопасности.»
«У нас есть 24-часовой таймер для файла cookie Duo, и мы хотели бы сократить его до более короткого времени при использовании Duo».
«У нас возникли проблемы с функцией сброса пароля.»
Другие минусы Duo Security →
«В решении, которое мы видим, нет ничего плохого. Однако, возможно, они могли бы немного улучшить, включив в свое решение децентрализованные модели блокчейна идентификации».
Еще Nok Nok Labs Минусы →
Советы по ценам и стоимости
» »Дополнительные советы по ценам и стоимости Duo Security →
Информация недоступна
Вопросы сообщества
Чем Duo Security отличается от Microsoft Authenticator?
Top Answer:Мы перешли на Duo Security для проверки личности. Мы использовали конкурента, но получили возможность оценить Duo в течение 30 дней, и мы не могли быть счастливее. Duo Security легко настроить… подробнее »
Что вам больше всего нравится в Duo Security?
Вернуться к началу Ответ:Процесс многофакторной аутентификации и функции геолокации великолепны.
Прочитать все 7 ответов →
Что вы думаете о ценах и затратах на Duo Security?
Top Answer:В настоящее время наша лицензионная плата взимается ежегодно. Мы рассматривали два уровня поддержки Duo. Первый уровень поддержки — это просто двухфакторная аутентификация — она не работает… подробнее »
Прочитать все 6 ответов →
Что вам больше всего нравится в Nok Nok Labs?
Наверх Ответ: Техническая поддержка очень хорошая.
Что вы думаете о ценах и стоимости Nok Nok Labs?
Наверх Ответ:Цены обсуждаются между компаниями. Я не могу говорить о точных расходах. Это может варьироваться.
Что нужно улучшить с Nok Nok Labs?
Top Ответ: Нет ничего плохого в том решении, которое мы видим. Однако, возможно, они могли бы немного улучшить, включив в свое решение децентрализованные модели блокчейна идентификации. Они делают… подробнее »
Ranking
1st
out of 58 in Authentication Systems
Views
12,053
Comparisons
10,421
Reviews
20
Average Words per Review
810
Rating
8.7
15-е место
из 58 систем аутентификации
просмотров
206
сравнений
77
отзывов
1
9000 слов в среднем на отзыв0003525
Рейтинг
8. 0
Сравнения
Microsoft Authenticator и Duo Security
Сравнение проводилось в 43% случаев.
Сравнение Fortinet FortiAuthenticator и Duo Security
в 11 % случаев.
Fortinet FortiToken и Duo Security
Сравнение проводилось в 11 % случаев.
Okta Workforce Identity и Duo Security
Сравнение проводилось в 8 % случаев.
UserLock и Duo Security
Сравнение проводилось в 6 % случаев.
больше конкурентов по безопасности дуэта →
+ добавить больше продуктов для сравнения
More Nok Nok Labs конкурентов →
+ добавить больше продуктов для сравнения
Узнайте больше
Nok Nok Labs
Operview
Cloud
Operview
Cloud Labs
Operview «/>
Cloud Labs
. поставщик аутентификации пользователей: аутентификация с помощью телефона, мобильного приложения Duo, стационарного телефона или токенов с подключением к Интернету или без него.
Nok Программные решения Nok Labs позволяют организациям развертывать простую, безопасную и масштабируемую аутентификацию на основе FIDO в своей внутренней и клиентской инфраструктуре, включая мобильные и веб-приложения. Решение Nok Nok позволяет организациям, развертывающим приложения для конечных пользователей, обеспечить превосходное взаимодействие с пользователями, лучшую безопасность и повышенную конфиденциальность при одновременном снижении затрат на разработку, развертывание и поддержку.
Узнайте больше о Duo Security
Учить больше
Узнайте больше о Nok Nok Labs
Узнайте больше
Пример клиентов
Treadp, Yelp, Etsy, Eventbrite
Fido Alliance
Topp, Etecy
Fido Alliance
Topp, Ete Event Brite
FIDO
Topp, Etsy, Event Brite
FIDO 9000 3
Topp, Etsy, Event Brite
FIDO 9000 2
. ОБОЗНАЧАЮЩИЕ
Аутсорсинговая компания13%
Производственная компания13%
Компания по разработке программного обеспечения13%
Фирма финансовых услуг13%
ПОСЕТИТЕЛИ, ЧИТАЮЩИЕ ОТЗЫВЫComputer Software Company18%
Comms Service Provider14%
Government9%
Manufacturing Company6%
No Data Available
Company Size
REVIEWERSSmall Business32%
Midsize Enterprise25%
Large Enterprise43%
ПОСЕТИТЕЛИ ЧИТАЮТ ОТЗЫВЫМалый бизнес28%
Средний бизнес18%
Крупный бизнес54%
Данные отсутствуют
Руководство покупателя
Системы аутентификации
Сентябрь 2022 г.
Скачать бесплатный отчет
Узнайте, что ваши коллеги говорят о Cisco, Fortinet, Microsoft и других в области систем аутентификации. Обновлено: сентябрь 2022 г.
ЗАГРУЗИТЬ СЕЙЧАС
633 184 специалиста воспользовались нашим исследованием с 2012 года. Duo Security имеет рейтинг 8,8, а Nok Nok Labs — 8,0. Главный обозреватель Duo Security пишет: «Интегрируется с множеством приложений, работает без сбоев и поставляется с отличной документацией». С другой стороны, главный обозреватель Nok Nok Labs пишет: «Прост в использовании, надежен и предлагает простую настройку». Duo Security больше всего сравнивают с Microsoft Authenticator, Fortinet FortiAuthenticator, Fortinet FortiToken, Okta Workforce Identity и UserLock, тогда как Nok Nok Labs больше всего сравнивают с .
См. наш список лучших поставщиков систем аутентификации.
Мы отслеживаем все отзывы о системах аутентификации, чтобы предотвратить мошеннические отзывы и поддерживать высокое качество отзывов. мы не публикуем
отзывы сотрудников компании или прямых конкурентов. Мы проверяем подлинность каждого отзыва с помощью перекрестных ссылок.
с LinkedIn и, при необходимости, личное общение с рецензентом.
Что означает Нок в медицинских терминах?
ближайших родственников человека (NOK) — это ближайший из ныне живущих кровных родственников этого человека.
Просмотр полный ответ на сайтеpatients-association.org.uk
Что означает NOK в больнице?
Ваш ближайший медицинский родственник — это человек, которого вы назначаете для получения информации о вашем медицинском обслуживании. Если вы не выбрали ближайших родственников, обычно предполагается, что это близкий кровный родственник, супруг или гражданский партнер. Они будут проинформированы о вашем уходе.
Просмотр полный ответ на сайтеpatients-association.org.uk
Что такое NOK в сестринском деле?
Ближайшие родственники, см. там.
Просмотр полный ответ на сайте medical-dictionary.thefreedictionary.com
Что означают инициалы NOK?
NOK. Норвежская крона (валюта Норвегии)
Просмотр полный ответ на acronyms.thefreedictionary.com
Как называется NOK?
Норвежская крона (NOK), начавшая обращение в 1875 году, является официальной валютой Норвегии. Регулирование и обращение кроны контролируются центральным банком страны, Norges Bank. Код валюты норвежской кроны — «NOK», а ее символ — «kr».
Просмотр полный ответ на investopedia.com
Общие сокращения, которые НУЖНО ЗНАТЬ в МЕДИЦИНСКОЙ ОБЛАСТИ!
Почему NOK падает?
Слабая норвежская крона, по-видимому, в значительной степени объясняется факторами, связанными с премией за риск, такими как снижение роли нефти в норвежской экономике, относительное сокращение ПИИ в Норвегии и падение цен на акции нефтяной отрасли.
Просмотр полный ответ на ssb.no
Что означает NOK в Snapchat?
МК в Snapchat — «Мм, ок». Этот сленг обычно используется для того, чтобы сказать «да», подтвердить утверждение или согласиться с человеком. Люди также используют МК, чтобы избежать текстовых сообщений от человека и закончить разговор еще до его начала.
Просмотр полный ответ на Republicworld.com
Что такое полная форма NOK в армии?
Планирование в армии. 7. Жертвы и выпуск сообщений с соболезнованиями от Ракша Мантри к следующему. родственников (NOK) военнослужащих, погибших в ходе различных операций.
Просмотр полный ответ на mod.gov.in
Что такое медицинский термин NFR?
Не для реанимации (NFR)
Неспецифический термин, обычно используемый для обозначения того, что в случае. коллапс пациента/резидента, никакие реанимационные мероприятия не будут начаты.
Просмотр полный ответ на peninsulahealth.org.au
Что делают медсестры, если пациент падает?
Включает в себя следующие восемь шагов:
- Оценка и мониторинг резидента в течение 72 часов после падения.
- Расследование обстоятельств падения.
- Запишите обстоятельства, резидентный результат и реакцию персонала.
- ФАКС Оповещение лечащему врачу.
- Немедленное вмешательство в течение первых 24 часов.
- Полная оценка падения.
Посмотреть полный ответ на ahrq.gov
Как врачи пишут один раз в день?
qd (qd или QD) один раз в день; qd расшифровывается как «quaque die» (что на латыни означает «один раз в день»).
Просмотр полный ответ на rxlist.com
Можно ли менять ближайших родственников в больнице?
Да. Если ваш ближайший родственник не хочет быть вашим ближайшим родственником, он может передать свои силы кому-то другому, если этот человек согласится. Для этого ближайший родственник может написать письмо, чтобы сообщить в больницу, что они выбирают кого-то другого на эту роль.
Просмотр полный ответ на сайте mind.org.uk
Могут ли ближайшие родственники дать согласие?
Термин «ближайшие родственники» широко используется, но ближайшие родственники не имеют юридических полномочий, прав или обязанностей. В частности, они не могут давать согласие на предоставление или отказ в каком-либо лечении или уходе.
Просмотр полный ответ на stchristophers.org.uk
Как мне получить карту ближайших родственников?
У Национальной службы здравоохранения есть бесплатная карта ближайших родственников, которую вы можете заполнить и носить с собой. Вы можете предоставить информацию о человеке, с которым вы хотели бы связаться, если вы были госпитализированы или умерли в больнице.
Просмотр полный ответ на сайте honorguide.co.uk
Что такое электронная почта NOK?
Резюме ключевых моментов. «Никто не знает» — наиболее распространенное определение NOK в Snapchat, WhatsApp, Facebook, Twitter, Instagram и TikTok. NOK.
Просмотр полный ответ на cyberdefinitions.com
Что такое кин в армии?
Первый уровень ближайших родственников — жена, если солдат состоит в браке, и мать, если он не женат. В армии также говорят, что в подобной поддержке нуждаются и ближайшие родственники отставных солдат, как живых, так и погибших.
Просмотр полный ответ на m.economictimes.com
Какой орган занимается назначением и продвижением по службе армейских офицеров?
Продвижение по службе и назначение офицеров выше бригадного и эквивалентных званий будет находиться в ведении недавно созданного Департамента по военным делам (DMA), возглавляемого начальником штаба обороны, для обеспечения большей тщательности и прозрачности процесса, источники, посвященные по делу сказали.
Просмотр
полный ответ на indiatoday. in
Что имеет в виду девушка, когда говорит МК?
Mk — это сленговый термин, то же самое, что сказать «ОК». Обычно его используют, когда говорят «да» на вопрос или соглашаются с кем-то. Этот термин обычно используется, когда кто-то не уверен, но все же отвечает утвердительно.
Просмотр полный ответ на slang.net
Что означает МК в тексте?
В общем текстовом чате МК обычно означает «Ммм ладно». Он используется для выражения согласия или принятия (но не всегда энтузиазма).
Просмотр полный ответ на сайте cyberdefinitions.com
Что означает KK в тексте?
(интернет-сленг) ладно, круто (сокращенный ответ, обычно используемый в конце разговора).
Просмотр полный ответ на en.wiktionary.org
NOK становится слабее?
Стоимость кроны по отношению к доллару сейчас самая низкая с мая 2020 года, когда покупка доллара стоила 11 норвежских крон или даже больше.
Просмотр полный ответ на newsinenglish.no
Будущее акций Nokia?
Nokia Oyj (NYSE:NOK)
23 аналитика, предлагающие 12-месячные прогнозы цен на Nokia Oyj, имеют средний целевой показатель 6,31, при этом верхний показатель составляет 8,15, а нижний — 4,89. Средняя оценка представляет собой увеличение на 29,27% по сравнению с последней ценой 4,88.
Просмотр полный ответ на money.cnn.com
← Предыдущий вопрос
Какое королевство самое сильное в Ведьмаке?
Следующий вопрос →
Как ВНЧС влияет на уши?
Основные характеристики NOK Culture — 1343 слова
Соглашение
- ВВЕДЕНИЕ
- Присутствие материала
- Влияние
- ВзМЕНТА
- Заключение
- СПИСОК СПИСОК 10
. само собой разумеющееся, но оно распространено в нашей повседневной жизни. Искусство — это использование воображения, индивидуальное восприятие и выражение чего-то особенного.
Это может быть изобразительное искусство, такое как картины и скульптуры, изобразительное искусство, такое как телевидение, реклама и логотипы, а также архитектура. Дизайн сочетает в себе простоту и эффективность; он пытается решить трудности, с которыми сталкивается человек в повседневной жизни.
Такие факторы, как экономическая эффективность, материалы, недостатки (окружающие окружающую среду) и функциональность, хорошо продуманы дизайнерами. Вместе дизайнеры и художники играют жизненно важную роль в обществе.
Благодаря своим новаторским занятиям они рисуют картину или отражение мира, в котором мы живем. Они помогают представить нашу культуру, сельское хозяйство, социальные обычаи, верования и религию.
Искусство и дизайн повсюду, от наших телефонов, ноутбуков, ручек, бутылок, одежды, дорог, автомобилей, поездов и самолетов (Davidson, 2000).
Одним из самых значительных произведений искусства является искусство Нок, свидетельство культуры Нок. Культура Нок появилась в районе Западной Африки в Нигерии. В нем описывается скульптура Нок в северной Нигерии, датируемая периодом с 500 г. до н.э. по 200 г. н.э.
Скульптуры Нок, терракотовые статуи, считаются самыми ранними следами замечательной традиции скульптуры к югу от Сахары. Открытие скульптур в 1943 указывают на использование железа, практику выплавки инструментов и подделок.
Скульптуры Нока различались по размеру от миниатюрных статуй до массивных скульптур коленопреклоненных, сидячих и стоячих фигур, в основном королей и священников. Самые популярные из скульптур Нока, изображающие людей и животных, — это терракотовые головы.
Основной характерной чертой терракот Нок является их полая структура. Они лепятся из глиняных валиков и высушиваются путем обжига в открытых и закрытых печах. Считается, что некоторые головы Ноков, раздробленные и разрушенные повреждениями и возрастом, являются частью целых тел.
Многие из этих скульптур были смоделированы индивидуально в аддитивной технике; другие были вылеплены в субтрактивной технике. Этот характерный субтрактивный метод предполагает аналогичную практику резьбы (Rupp & Breunig, 2005).
Из-за водной эрозии, прокатки и возраста большинство фрагментов терракоты претерпели незначительные реставрации, которые были очень необходимы, чтобы отразить суть искусства. Пропорционально головы относительно больше остальных частей тела, причины этого остаются неизвестными.
Перфорированные уши, рты, глаза треугольной формы с проколотыми зрачками — вот некоторые из типичных стилистических особенностей голов Нок. Отличительные прически, использование украшений и драгоценностей, разнообразие красоты в дизайне обеспечивают захватывающую историю украшения тела и украшений в культуре Нок.
Система здравоохранения культуры Нок также была представлена в некоторых статуэтках, а некоторые скульптуры изображали такие болезни, как слоновость и паралич. Примером терракоты Нок является ГОЛОВА РАФИНА КУРА, найденная в Рафин Кура в Нигерии.
Голова Рафина Кура имеет полый рот с разделенными губами, большие проколотые глаза и расширяющиеся ноздри. Провозглашенная основным доказательством доколониальной цивилизации, культура Нок остается загадкой.
Важность, функция и значение терракот Нока, как правило, до сих пор неизвестны (Kleiner, 2009).
Наличие материалов
Терракотовые фигурки также были найдены в Греции, Египте, Персии, Ассирии, Китае, Италии и Германии, а также в Северной и Западной Африке. Эти культуры использовали катушки из глины, которые были довольно грубыми и пористыми.
При обжиге в печах они приобретали цвет от тускло-охристого до красного. В северных районах Нигерии легко доступна глина: почва богата красно-оранжевой охрой. Почва содержит крупинки зерен, которые при смешивании с водой образуют кольца глины, из которых можно слепить скульптуры.
Разнообразие камешков в почве обеспечивает идеальную глазурь, придающую терракотам вид настоящей человеческой кожи. Для монументальных статуй, высотой более метра и весом более пятидесяти килограммов, стрельба производилась на открытом воздухе.
Из-за пустотелых конструкций мастера, работавшие в окрестностях Нока, старались поддерживать одинаковую толщину всей скульптуры. Перфорированные глаза, носы, уши и рты позволили уравнять тепло в процессе обжига.
Археология предполагает, что ремесленники того периода использовали стволы деревьев и ветки в качестве центрального ядра скульптур, чтобы предотвратить поломку или взрыв во время процесса обжига. Художники наносили глиняные валики на древесные сердцевины и лепили вручную.
В процессе горения древесное ядро будет гореть медленно, обеспечивая идеальное распределение тепла. Этот метод до настоящего времени также применяется в Нигерии; куски покрывают травой и ветками, а затем сжигают в течение нескольких часов.
Конечный продукт со сгоревшим дотла деревянным стержнем, отполированной, выглаженной и высушенной скульптурой получился блестящим с глянцевой поверхностью.
Это свидетельствует о степени компетентности народа Нок, талант и опыт ремесленников и мастеров того периода был огромен (Оньянс, 2004).
Влияние
Нок расположен в местном правительстве Джаба, штат Кадуна, на севере Нигерии. Искусство Нок было обнаружено в археологических памятниках Самун Дукия и Таруга.
Сходство между двумя археологическими памятниками, обнаруженными в этой области, предполагает связь между различными сельскохозяйственными культурами, в которых использовались железные орудия труда (Rupp & Breunig, 2005). Считается, что эта ассоциация могла оказать влияние на культуру Нок.
Например, использование техники вычитания; это похоже на резьбу по дереву. Маргарет Санчес, куратор Художественного музея Кливленда, излагает это убеждение.
Она отмечает сходство в манере моделирования керамики Нок и скульптуры, применяемой при резьбе по дереву. Среди археологов и ученых распространено мнение о существовании культуры, которая произошла от культуры Нок, это связано с сложностью художественного произведения Нок.
Искусство стрельбы, использование железа, а также техническая компетентность в их искусствах могут быть результатом прошлого влияния (Grunne, 1998).
Оценка
Имея более тридцати музеев, Нигерия находится на переднем крае сохранения культуры и истории. Большинство из этих музеев специализируются на искусстве, истории и археологии. В Национальном музее Лагоса, расположенном в центре Лагоса, хранится множество терракот Нок.
Другим музеем, в котором хранятся статуэтки, приписываемые народу Нок, является Национальный музей Джос. Сотни фигурок Нока сохранились и выставлены в музеях по всему миру. Имеются записи об искусстве Нок в США, Франции, Германии, Швейцарии, Бельгии и других частных коллекциях (Kleiner & Mamiya, 2008).
Очень интересны методы восстановления некоторых изношенных и фрагментированных деталей; им удалось передать выражение, эмоции и присутствие искусства. Искусство призвано отображать культуру общества, его образ жизни.
Искусство каким-то образом разговаривает со зрителем; насколько их функция или значение неизвестны, я считаю, что скульптура Нока очаровывает публику. В нем представлены сведения об образе жизни народа Нок того периода.
Как было показано ранее, их открытие предоставило доказательства использования железа, их системы лидерства, уровня ноу-хау и социальной активности. Признание и уважение к искусству широко распространены, отсюда и чувствительность.
Сохранение таких реликвий было серьезной проблемой для защитников природы; усугубляется незнанием природы керамики и опасностей различных методов очистки.
Лично мне нравится, насколько хорошо сохранились терракотовые головы. Посещение музея или даже поиск в Интернете будет очень полезен для любителей искусства.
В моем личном опыте посещения Национального музея Лагоса у меня была возможность хорошо рассмотреть великолепное произведение искусства. Вы увидите, насколько хороши люди Нока в создании терракот; вы чувствуете, что они смотрят прямо на вас.
Заключение
Туристы, исследователи и ученые продолжают наводнять музеи Нока и район Нока. Это свидетельствует о растущем интересе общества к искусству, что, в свою очередь, поощряет и способствует сохранению бесценных артефактов.
Ученые и исследователи сходятся во мнении, что культура Нок совершила переход от каменного века к железному веку (Hirst, 2009). Скульптуры Нока в настоящее время занимают значительное, но уединенное место в африканской истории искусства.
Ссылки
Дэвидсон, С. (2000). Изучение искусства и дизайна: вопросы и ответы Тематическое руководство .Crimson Publishing.
Грюн, Б. Люксембург, Б. (1998). Рождение искусства в Африке: скульптура Нок в Нигерии. Мичиганский университет.
Херст, К. (2009). Африканский железный век. Распространение железа – хронология и определение .
Клейнер, Ф. (2008). Искусство Гарднера сквозь века , том I. Cengage Learning EMEA.
Клейнер, Ф. и Мамия, К. (2009). Искусство Гарднера сквозь века: незападные взгляды . Издание 13, исправленное. Cengage Learning.
Онианс, Дж. (2004). Атлас мирового искусства . Издательство Лоуренса Кинга.
Рупп, А.