определения, формулы, примеры, угол поворота
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
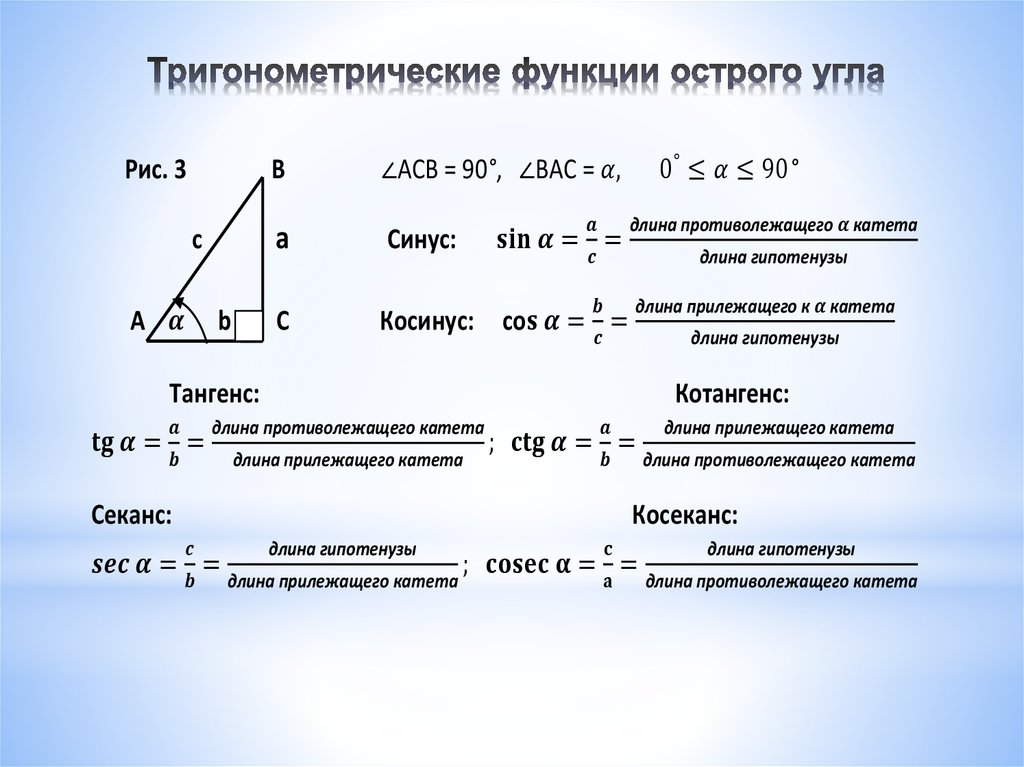
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функцийСинус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
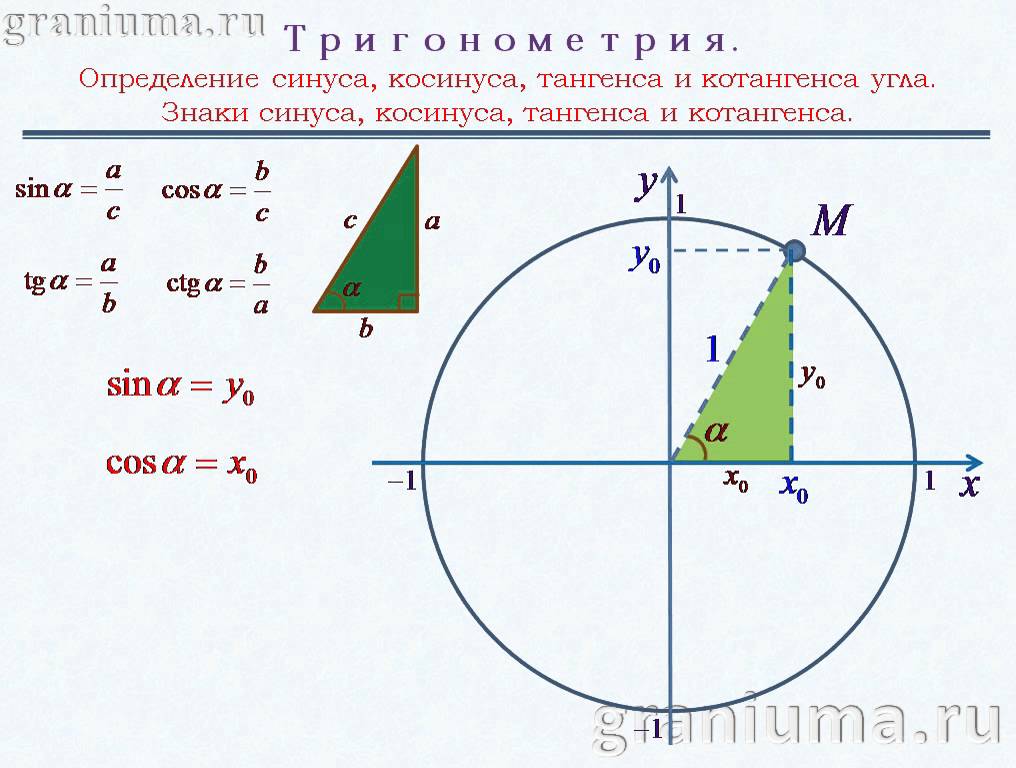
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус (sin) угла поворота Синус угла поворота α — это ордината точки A1(x , y). sin α=y Косинус (cos) угла поворотаКосинус угла поворота α — это абсцисса точки A1(x , y). cos α=х
Тангенс (tg) угла поворотаТангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котангенс (ctg) угла поворотаКотангенс угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числаСинусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.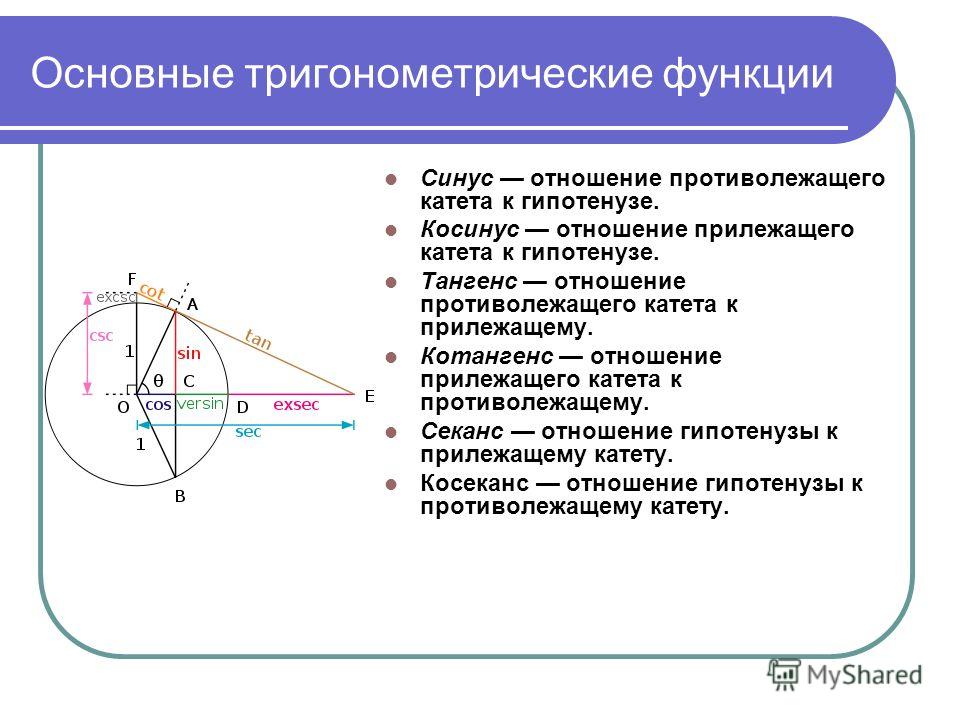
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа tСинус числа t — ордината точки единичной окружности, соответствующей числу  sin t=y
sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа tТангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрииСинус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
Определение синуса и косинуса произвольного угла с примерами решения
Содержание:
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
Построим точку
Рассмотрим прямоугольный треугольник в котором гипотенуза равна 1 (радиусу единичной окружности). По определению синуса и косинуса острого угла получим:
Таким образом, синус угла равен ординате точки а косинус угла равен абсциссе точки
Поскольку в тригонометрии рассматриваются углы то определим синус и косинус для любого угла
Определение синуса произвольного угла
Определение:
Синусом угла называется ордината точки полученной поворотом точки единичной окружности вокруг начала координат на угол
Определение косинуса произвольного угла
Определение:
Косинусом угла называется абсцисса точки полученной поворотом точки единичной окружности вокруг начала координат на угол
Для того чтобы найти синус и косинус произвольного угла нужно:
- Построить точку единичной окружности.

- Найти ординату точки
- Найти абсциссу точки
Найдите синус и косинус угла
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат Найдем Углу соответствует точка имеющая координаты По определению синус угла равен ординате точки значит, Косинус угла равен абсциссе точки т.е. (рис. 31).
Пользуясь определением синуса и косинуса угла получим, что:
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку
Например, выясним, может ли принимать значения, равные:
Значения синуса произвольного угла принадлежат отрезку значит, может принимать значения, равные и так как и Поскольку то не может принимать значения, равные
По определению синуса и косинуса угла синус угла равен ординате точки а косинус угла равен абсциссе этой точки.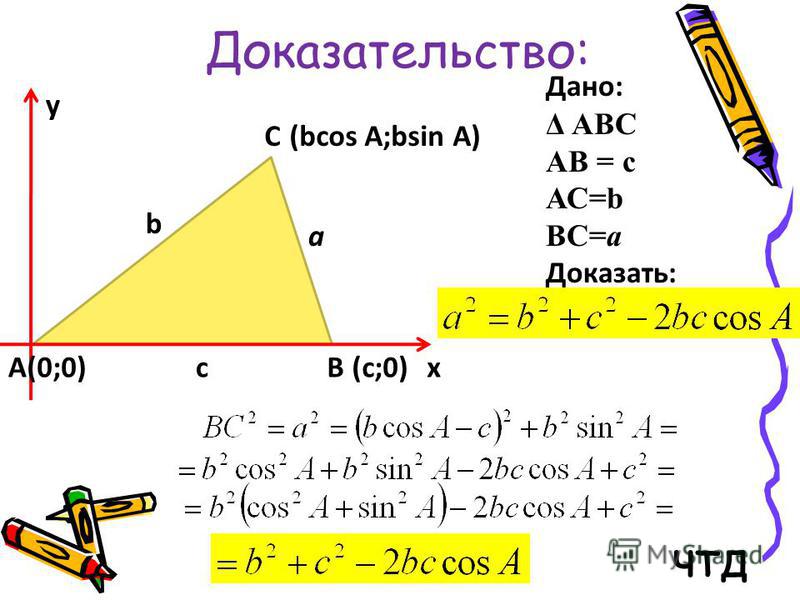
Определите знак выражения:
Решение:
а) Так как — угол второй четверти (рис. 32), а ординаты точек единичной окружности, находящихся во второй четверти, положительны, то
б) Так как — угол третьей четверти (см. рис. 32), а абсциссы точек единичной окружности, находящихся в третьей четверти, отрицательны, то
в) Так как — угол третьей четверти (см. рис. 32), а ординаты точек единичной окружности, находящихся в третьей четверти, отрицательны, то
г) Так как — угол первой четверти (см. рис. 32), а абсциссы точек единичной окружности, находящихся в первой четверти, положительны, то
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов
Пример №2Вычислите:
Решение:
а) Отметим на единичной окружности точку Поскольку известно, что а то ордината точки равна а абсцисса этой точки равна
Точки единичной окружности симметричны относительно оси абсцисс (рис. 33), значит, их ординаты (синусы углов противоположны, а абсциссы (косинусы углов и равны. Таким образом, а
33), значит, их ординаты (синусы углов противоположны, а абсциссы (косинусы углов и равны. Таким образом, а
б) Так как то точки единичной окружности симметричны относительно оси ординат (рис. 34). Тогда их ординаты (синусы углов равны, а абсциссы (косинусы углов и противоположны. Значит,
в) Точки единичной окружности симметричны относительно начала координат (рис. 35), поскольку Тогда и их ординаты противоположны, и их абсциссы противоположны, т. е.
г) Поскольку то точки и единичной окружности совпадают (рис. 36), а значит, их координаты равны. Тогда
Пример №3Вычислите:
Решение:
а) Так как то точка единичной окружности совпадает с точкой (рис. 37).
Поскольку
б) Точки единичной окружности симметричны относительно начала координат (см. рис. 37), а значит, их абсциссы (косинусы углов и отличаются только знаком. Так как
Пример №4Постройте один из углов, если:
Решение:
а) Так как то на оси ординат отметим Проведем прямую, параллельную оси абсцисс, и найдем на единичной окружности точки ордината каждой из которых равна Отметим один из углов, соответствующих точкам или (рис. 38, а).
38, а).
б) Так как то на оси абсцисс отметим 0,8. Проведем прямую, параллельную оси ординат, и найдем на единичной окружности точки и абсцисса каждой из которых равна 0,8. Отметим один из углов,соответствующих точкам или (рис. 38, б).
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5Точка единичной окружности имеет координаты Используя определение синуса и косинуса произвольного угла, найдите
Решение:
Синусом угла называется ордината точки полученной поворотом точки единичной окружности вокруг начала координат на угол По условию ордината точки равна значит,
Косинусом угла называется абсцисса точки полученной поворотом точки единичной окружности вокруг начала координат на угол По условию абсцисса точки равна значит,
Пример №6Если то угол может быть равен:
Выберите правильный ответ.
Решение:
Так как синусом угла называется ордината точки полученной поворотом точки единичной окружности вокруг начала координат на угол то нужно найти точку единичной окружности, ордината которой равна -1. Эта точка лежит на оси ординат, и из данных углов ей соответствует угол (рис. 39). Правильный ответ в).
Пример №7Если то угол может быть равен:
Выберите правильный ответ.
Решение:
Так как косинусом угла называется абсцисса точки полученной поворотом точки единичной окружности вокруг начала координат на угол то нужно найти точку единичной окружности, абсцисса которой равна 0. Эта точка лежит на оси ординат, и из данных углов ей соответствует угол (рис. 40). Правильный ответ в).
Пример №8Найдите значение выражения:
Решение:
а) Абсцисса точки соответствующей углу равна -1 (рис. 41), значит, Ордината точки соответствующей углу равна 1 (см.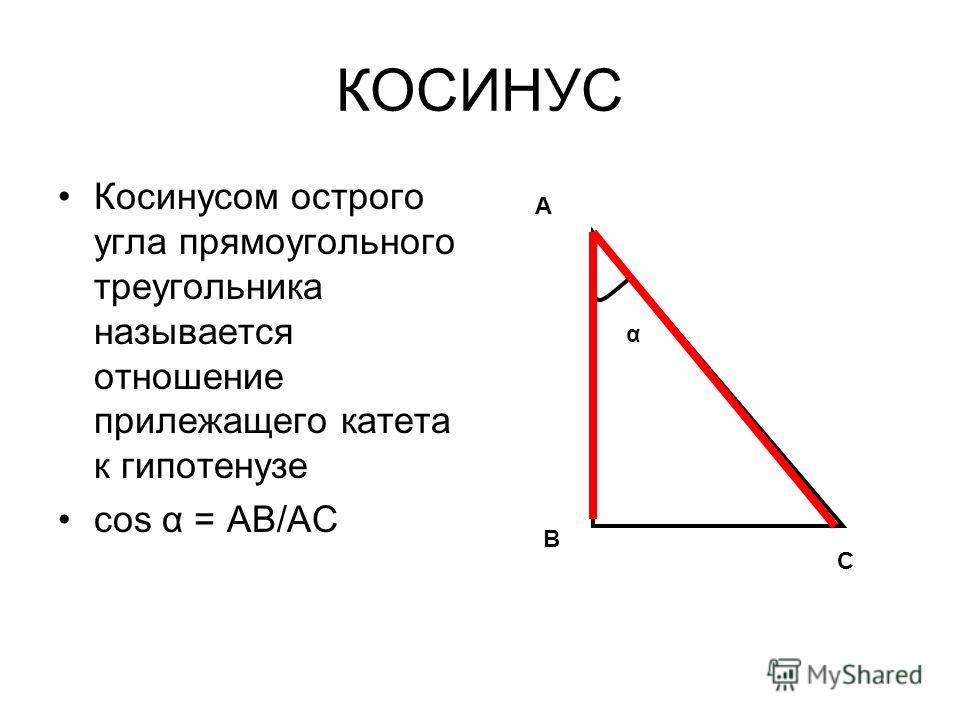 рис. 41), т. е. Значит,
рис. 41), т. е. Значит,
б) ( рис. 42) тогда
Может ли быть равным:
Решение:
Поскольку
а) не может быть равным 1,2, так как
б) может быть равным 0,89, так как
в) не может быть равным так как
г) может быть равным так как
Пример №9Определите знак выражения:
Решение:
а) так как — угол четвертой четверти, а косинус в четвертой четверти положителен;
б) так как — угол первой четверти, а косинус в первой четверти положителен;
в) так как угол второй четверти, а синус во второй четверти положителен;
г) так как 6 радиан — угол четвертой четверти, а синус в четвертой четверти отрицателен.
Пример №10Сравните:
Решение:
а) Отметим на единичной окружности точки, соответствующие углам и сравним ординаты этих точек. Ордината точки больше ординаты точки (рис. 43), значит,
б) Сравним абсциссы точек единичной окружности Так как абсцисса точки больше абсциссы точки (рис. 44), то
44), то
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки равна ординате точки (рис. 45), поэтому
б) Абсцисса точки противоположна абсциссе точки (см. рис. 45), поэтому
определения в тригонометрии, примеры, формулы
Для начала рассмотрим круг с радиусом 1 и с центром в (0;0). Для любого αЄR можно провести радиус 0A так, что радианная мера угла между 0A и осью 0x равна α. Направление против часовой стрелки считается положительным. Пусть конец радиуса А имеет координаты (a,b).
Определение синуса
Определение: Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается sinα и называется синусом угла α.
Пример: sin 3π cos3π/2 = 0 0 = 0
Определение косинуса
Определение: Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается cosα и называется косинусом угла α.
Пример: cos0 cos3π + cos3,5π = 1 (-1) + 0 = 2
Эти примеры используют определение синуса и косинуса угла через координаты конца единичного радиуса и единичной окружности. Для более наглядного представления необходимо нарисовать единичную окружность и отложить на ней соответствующие точки, а затем посчитать их абсциссы для вычисления косинуса и ординаты для вычисления синуса.
Определение тангенса
Определение: Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ.
Пример: tg0 tgπ = 0 0 = 0
Этот пример аналогичен предыдущему. Для вычисления тангенса угла нужно поделить ординату точки на её абсциссу.
Определение котангенса
Определение: Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ.
Рассмотрим пример на обычном прямоугольном треугольнике
Чтобы было понятнее, что же такое косинус, синус, тангенс и котангенс.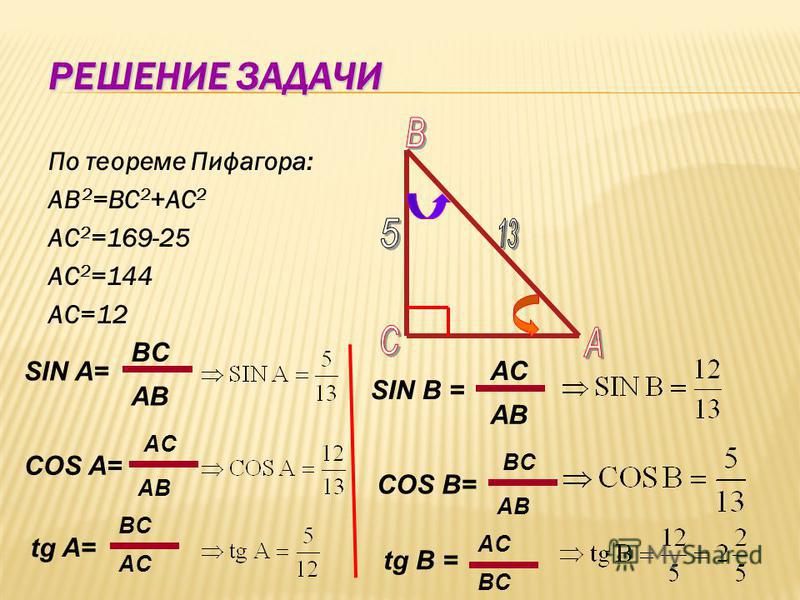
Определение: Синус угла y — это отношение противолежащего катета к гипотенузе: siny = а/с
Определение: Косинус угла y это отношение прилежащего катета к гипотенузе: сosy= в/с
Определение: Тангенс угла у — это отношение противолежащего катета к прилежащему: tgy = а/в
Определение: Котангенс угла y -это отношение прилежащего катета к противолежащему: ctgy= в/а
Cинус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями. У каждого угла есть свой синус и косинус. И практически у каждого есть свой тангенс и котангенс.
Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция соответственно, мы знаем угол. Созданы даже специальные таблицы, где расписаны тригонометрические функции для каждого угла.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники.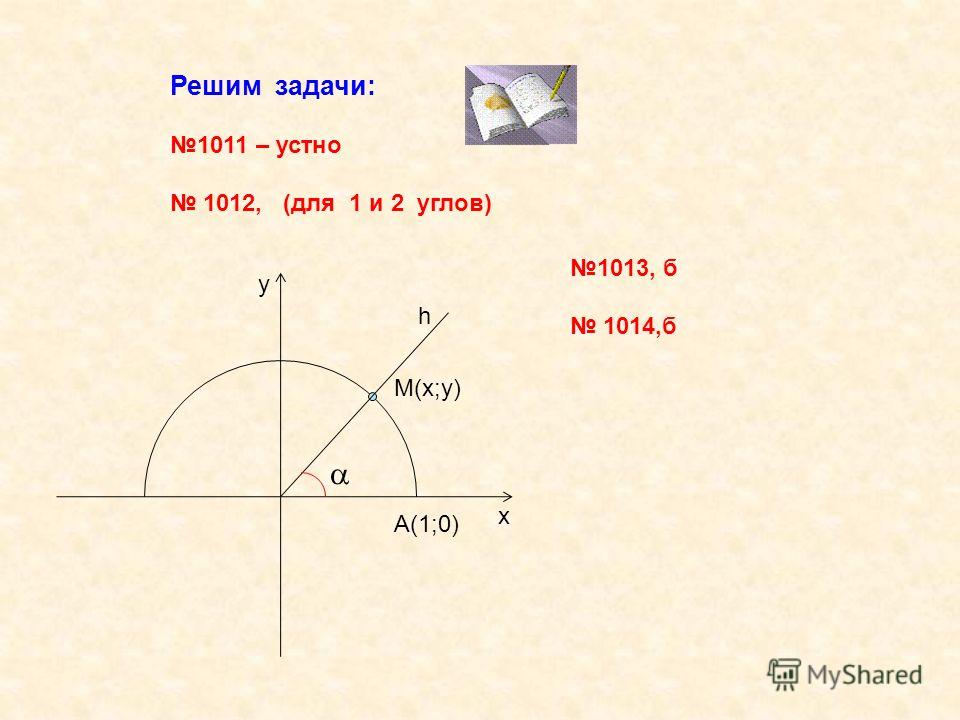 Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Как найти синус?
Изучение геометрии помогает развивать мышление. Этот предмет обязательно входит в школьную подготовку. В жизнедеятельности знание этого предмета может пригодиться — например, при планировке квартиры.
Этот предмет обязательно входит в школьную подготовку. В жизнедеятельности знание этого предмета может пригодиться — например, при планировке квартиры.
Из истории
В рамках курса геометрии изучается также тригонометрия, которая исследует тригонометрические функции. В тригонометрии мы изучаем синусы, косинусы, тангенсы и котангенсы угла.
Но на данный момент начнем с самого простого — синуса. Давайте рассмотрим более детально самое первое понятие — синус угла в геометрии. Что такое синус и как его найти?
Понятие «синус угла» и синусоиды
Синус угла — это соотношение значений противоположного катета и гипотенузы прямоугольного треугольника. Это прямая тригонометрическая функция, которая на письме обозначается как «sin (x)», где (х) — угол треугольника.
На графике синус угла обозначается синусоидой со своими особенностями. Синусоида выглядит как непрерывная волнообразная линия, которая лежит в определенных рамках на плоскости координат. Функция нечетная, поэтому симметрична относительно 0 на плоскости координат (выходит из начала отсчета координат).
Область определения этой функции лежит в диапазоне от -1 до +1 на декартовой системе координат. Период функции синус угла составляет 2 Пи. Это означает, что каждые 2 Пи рисунок повторяется, и синусоида проходит полный цикл.
Уравнение синусоиды
- sin х = a / c
- где а — противолежащий к углу треугольника катет
- с — гипотенуза прямоугольного треугольника
Свойства синуса угла
- sin (x) = — sin (x). Эта особенность демонстрирует, что функция симметрична, и если отложить на системе координат в обе стороны значения х и (-х), то ординаты этих точек будут противоположными. Они будут находиться на равном расстоянии друг от друга.
- Еще одной особенностью этой функции является то, что график функции возрастает на отрезке [- П/2 + 2 Пn]; [П/2 + 2Пn], где n — любое целое число. Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn].
- sin (x) > 0, когда х лежит в диапазоне (2Пn, П + 2Пn)
- (x)
Значения синусов угла определяются по специальным таблицам.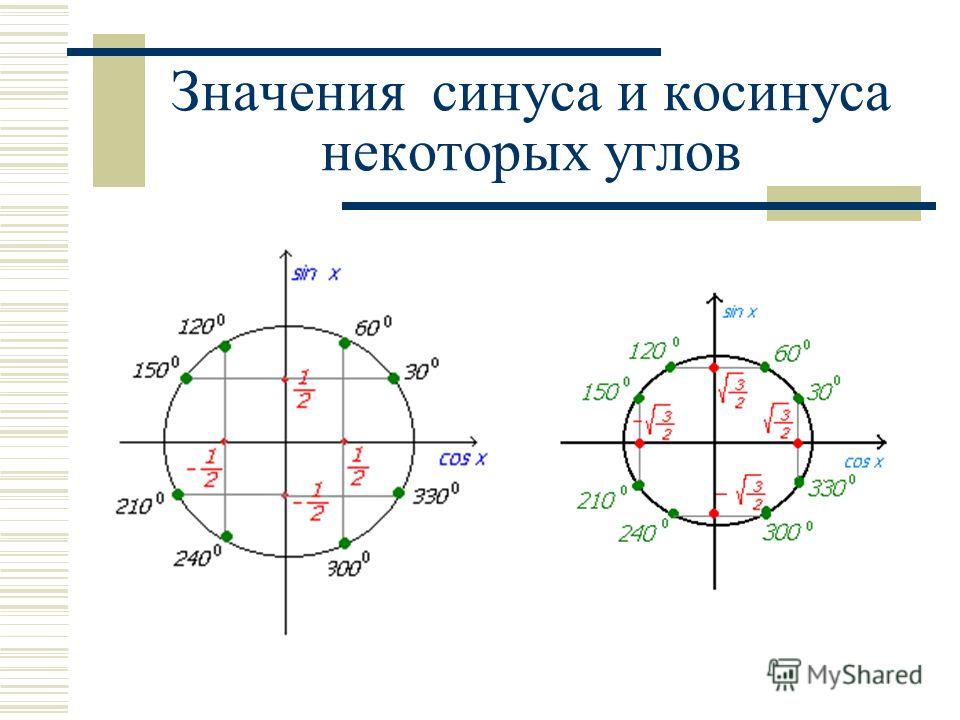 Созданы такие таблицы для облегчения процесса подсчета сложных формул и уравнений. Она легка в использовании и содержит значения не только функции sin (x), но также и значения других функций.
Созданы такие таблицы для облегчения процесса подсчета сложных формул и уравнений. Она легка в использовании и содержит значения не только функции sin (x), но также и значения других функций.
Более того, таблица стандартных значений этих функций включена к обязательному изучению на память, как таблица умножения. Особенно это актуально для классов с физико-математическим уклоном. В таблице можно увидеть значения основных используемых в тригонометрии углов: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 и 360 градусов.
Также существует таблица, определяющая значения тригонометрических функций нестандартных углов. Пользуясь разными таблицами, можно без труда вычислить синус, косинус, тангенс и котангенс некоторых углов.
С тригонометрическими функциями составляются уравнения. Решать эти уравнения легко, если знать простые тригонометрические тождества и приведения функций, например, такие, как sin (П/2 + х) = cos (x) и другие. Для таких приведений также составлена отдельная таблица.
Как найти синус угла
Когда стоит задача найти синус угла, а по условию у нас есть только косинус, тангенс, или котангенс угла, мы легко можем вычислить нужное с помощью тригонометрических тождеств.
- sin 2 x + cos 2 x = 1
Исходя из этого уравнения, мы можем найти как синус, так и косинус, в зависимости от того, какое значение неизвестно. У нас получится тригонометрическое уравнение с одним неизвестным:
- sin 2 x = 1 — cos 2 x
- sin x = ± √ 1 — cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
Из этого уравнения можно найти значение синуса, зная значение котангенса угла. Для упрощения замените sin 2 x = у, и тогда у вас получится простое уравнение. Например, значение котангенса равно 1, тогда:
- 1 + 1 = 1/у
- 2 = 1 / у
- 2у = 1
- у = 1/2
Теперь выполняем обратную замену игрека:
- sin 2 x = ½
- sin x = 1 / √2
Поскольку мы взяли значение котангенса для стандартного угла (45 0), полученные значения можно проверить по таблице .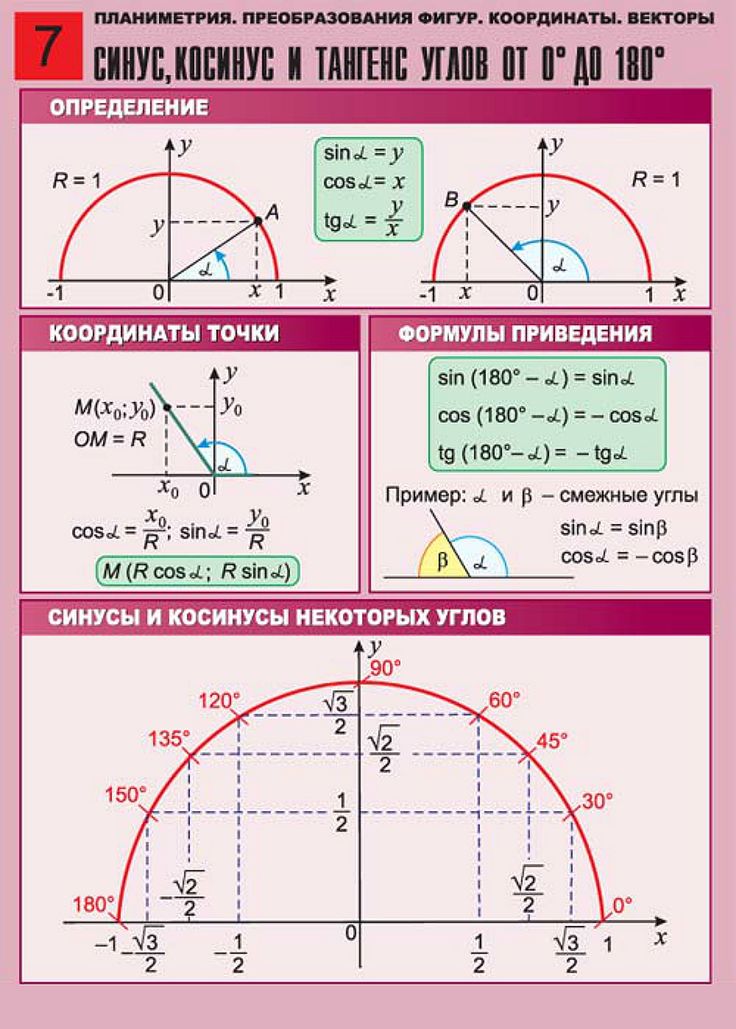
Если у вас дано значение тангенса, а нужно найти синус, поможет еще одно тригонометрическое тождество:
- tg x * ctg x = 1
Из этого следует, что:
- ctg x = 1 / tg x
Для того чтобы найти синус нестандартного угла, например, 240 0 , необходимо воспользоваться формулами приведения углов. Мы знаем, что π у нас соответствует 180 0 . Таким образом, мы выразим наше равенство с помощью стандартных углов путем разложения.
- 240 0 = 180 0 + 60 0
Нам необходимо найти следующее: sin (180 0 + 60 0). В тригонометрии есть формулы приведения, которые в данном случае пригодятся. Это формула:
- sin (π + х) = — sin (х)
Таким образом, синус угла 240 градусов равен:
- sin (180 0 + 60 0) = — sin (60 0) = — √3/2
В нашем случае, х = 60, а П, соответственно, 180 градусам. Значение (-√3/2) мы нашли по таблице значений функций стандартных углов.
Таким образом можно разложить нестандартные углы, например: 210 = 180 + 30.
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.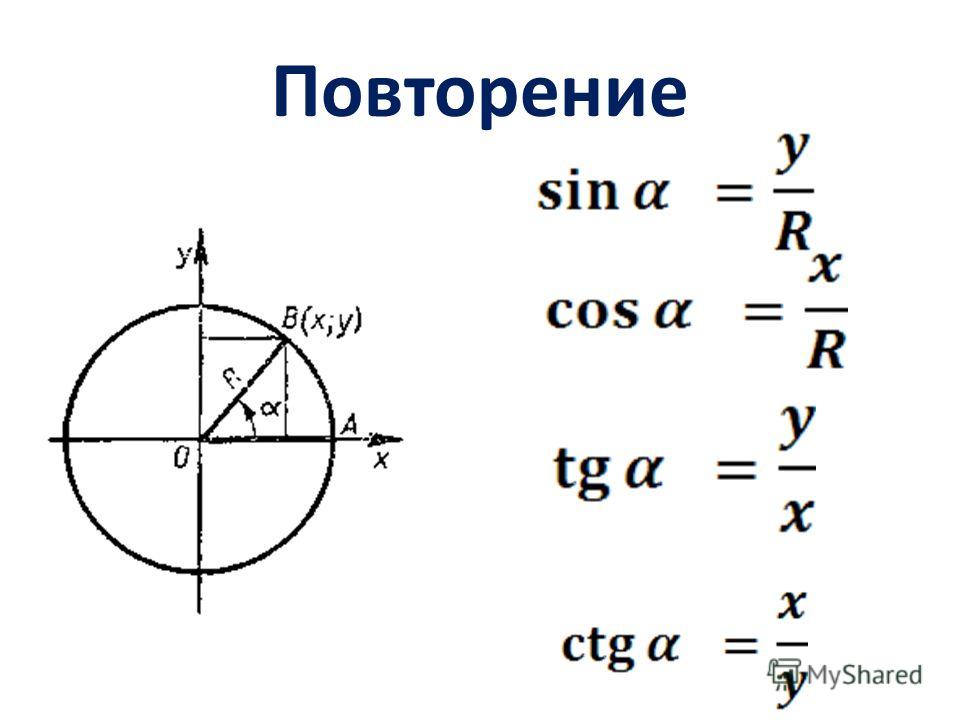
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины.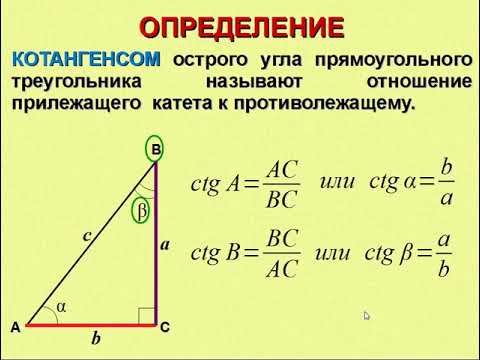 Представим единичную окружность с центром в начале декартовой системы координат.
Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.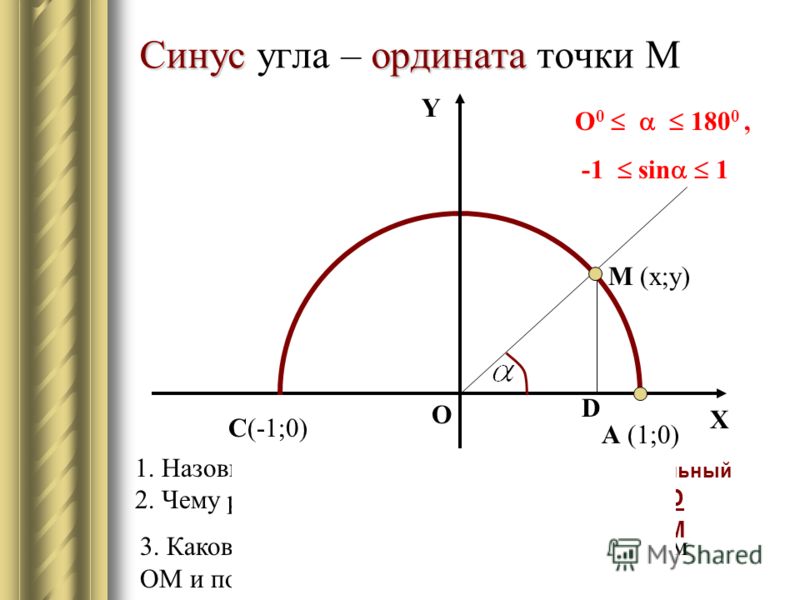
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления.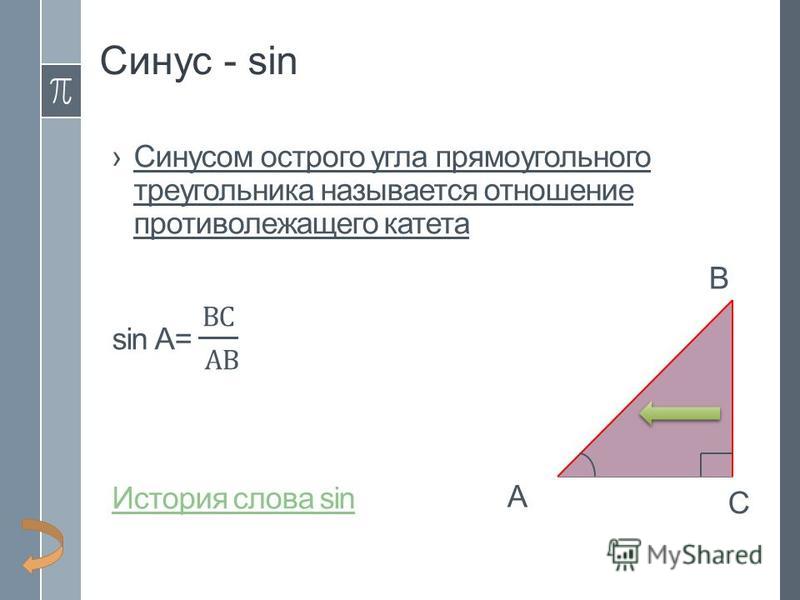 Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG.
Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов. Значения перечислены в таблице ниже.
Простейшие тригонометрические тождества
Уравнения, в которых под знаком тригонометрической функции присутствует неизвестное значение, называются тригонометрическими. Тождества со значением sin х = α, k — любое целое число:
- sin х = 0, х = πk.
- 2. sin х = 1, х = π/2 + 2πk.
 k * arcsin α + πk.
k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.

Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции.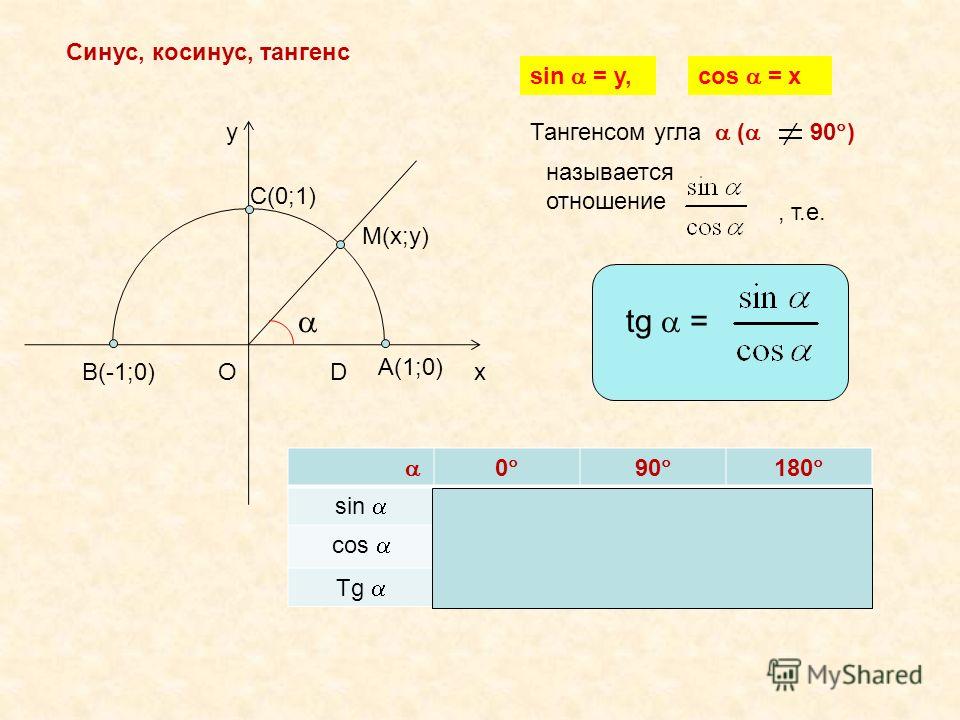 2 x/2) / (2tgx/2), при этом х = π + 2πn.
2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.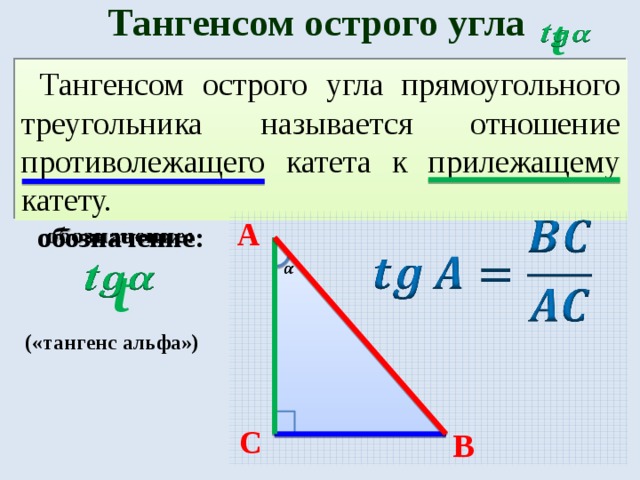 2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.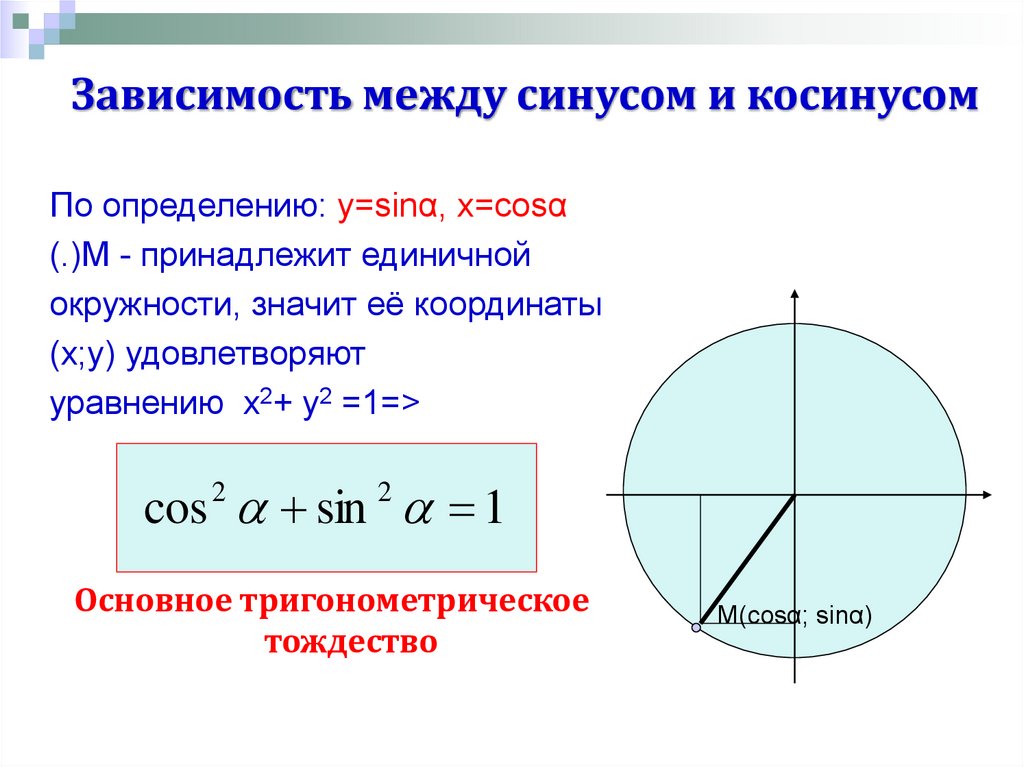
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
Определение синуса острого угла в прямоугольном треугольнике. Синус, косинус, тангенс и котангенс в тригонометрии: определения, примеры
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.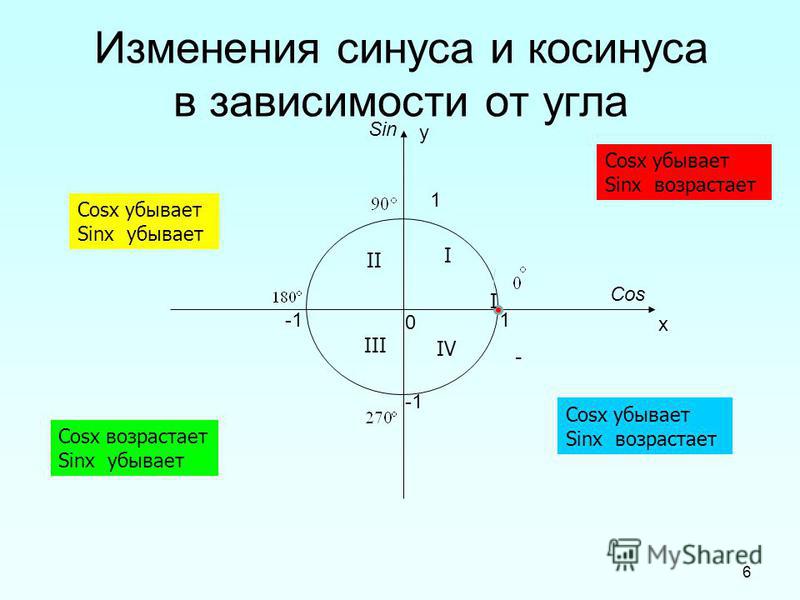
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы.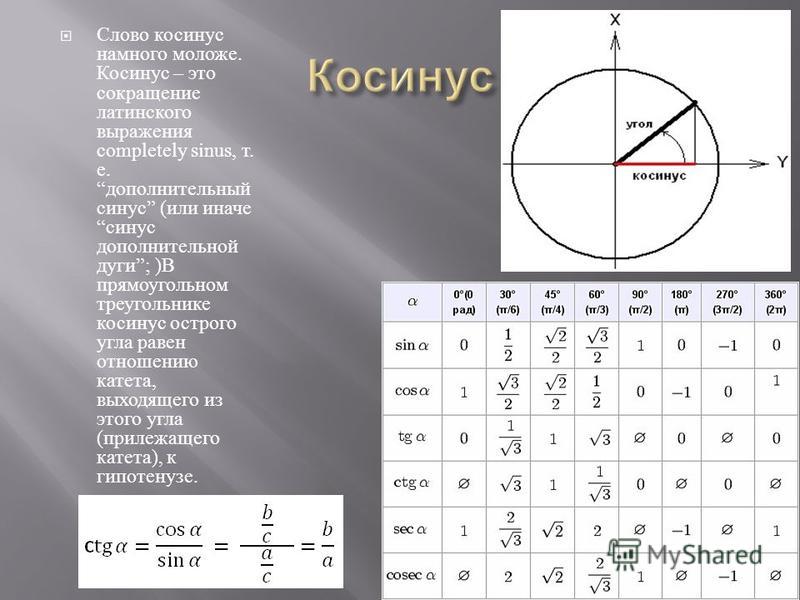 Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
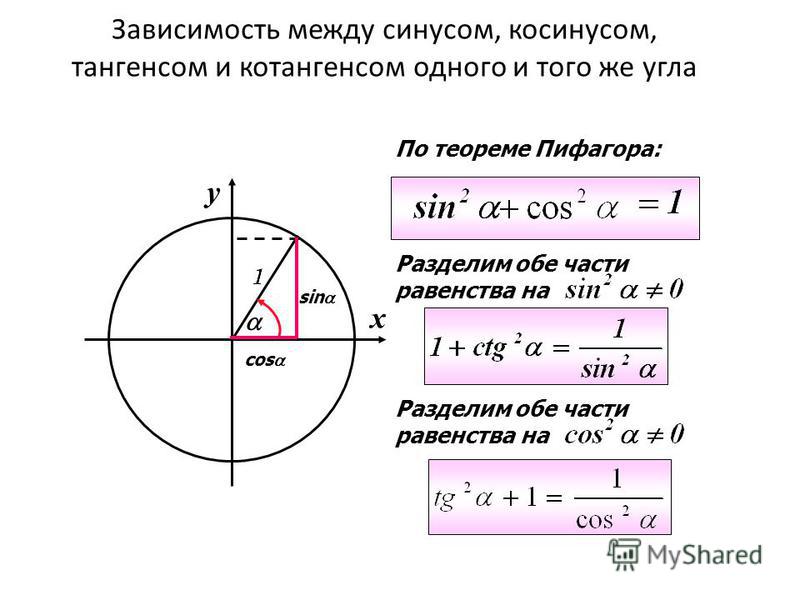
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол \alpha называют синусом произвольного угла поворота \alpha .
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha
называют косинусом произвольного угла поворота \alpha
.
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha .
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha .
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM , где M — точка единичной окружности, то
\sin \alpha=y_{M} , \cos \alpha=x_{M} , tg \alpha=\frac{y_{M}}{x_{M}} , ctg \alpha=\frac{x_{M}}{y_{M}} .
Например, если \angle AOM = -\frac{\pi}{4} , то: ордината точки M равна -\frac{\sqrt{2}}{2} , абсцисса равна \frac{\sqrt{2}}{2} и потому
\sin \left (-\frac{\pi}{4} \right)=-\frac{\sqrt{2}}{2} ;
\cos \left (\frac{\pi}{4} \right)=\frac{\sqrt{2}}{2} ;
tg ;
ctg
\left (-\frac{\pi}{4} \right)=-1
. {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.
Школьный предмет
Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.
Использование
Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?
Так что такое синус и косинус?
Определения
Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус — прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.
Что нужно запомнить
Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.
Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов.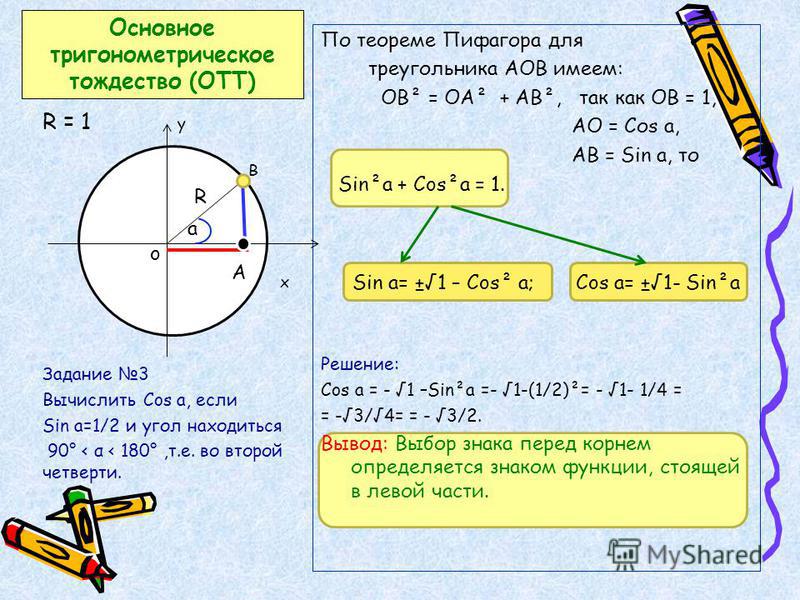 Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.
Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.
Теоремы
В базовой тригонометрии существует две основные теоремы: синусов и косинусов.
Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая — что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.
Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора.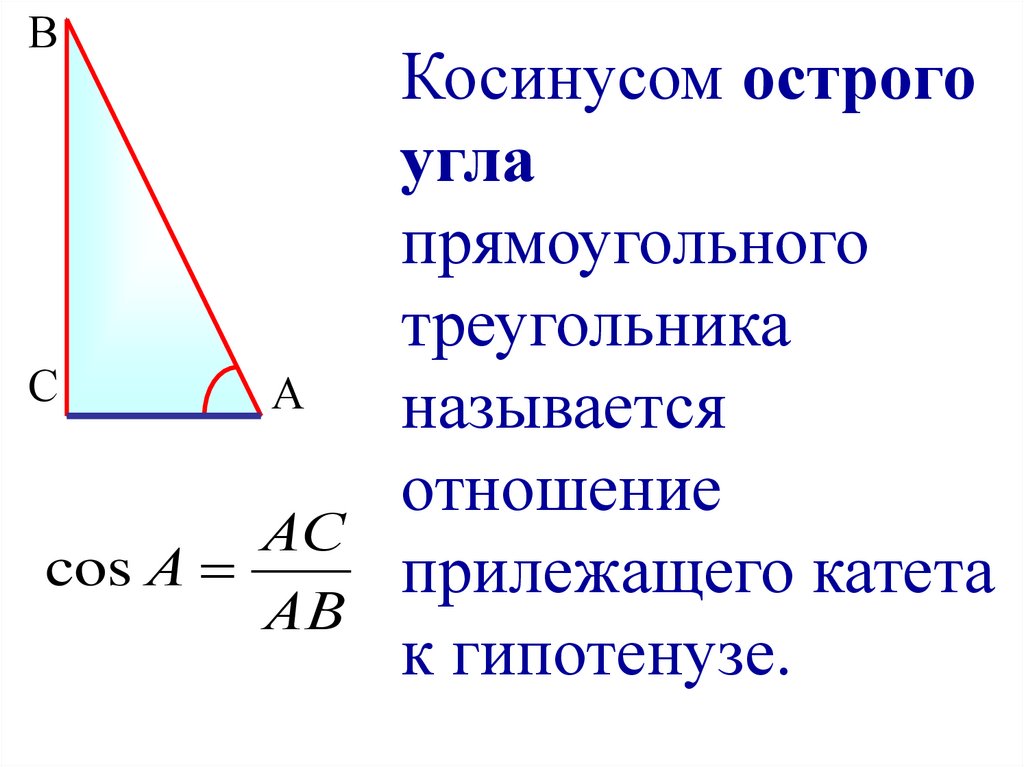 Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Цели и задачи
Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.
Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.
Нестыковки при изучении тригонометрии
Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?
Единицы измерения
Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга — 2 сантиметра, длина окружности составит 3,14*2, или 6,28.
Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.
Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева — «Пи». Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Заглянем в будущее
Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая — это прямая.
Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.
Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.
А ведь некоторые специалисты решают такие задачи ежедневно.
Тригонометрические функции в жизни
Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь — здесь приходится использовать более сложные формулы.
Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.
Заключение
Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться — стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия — это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.
Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.
В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс.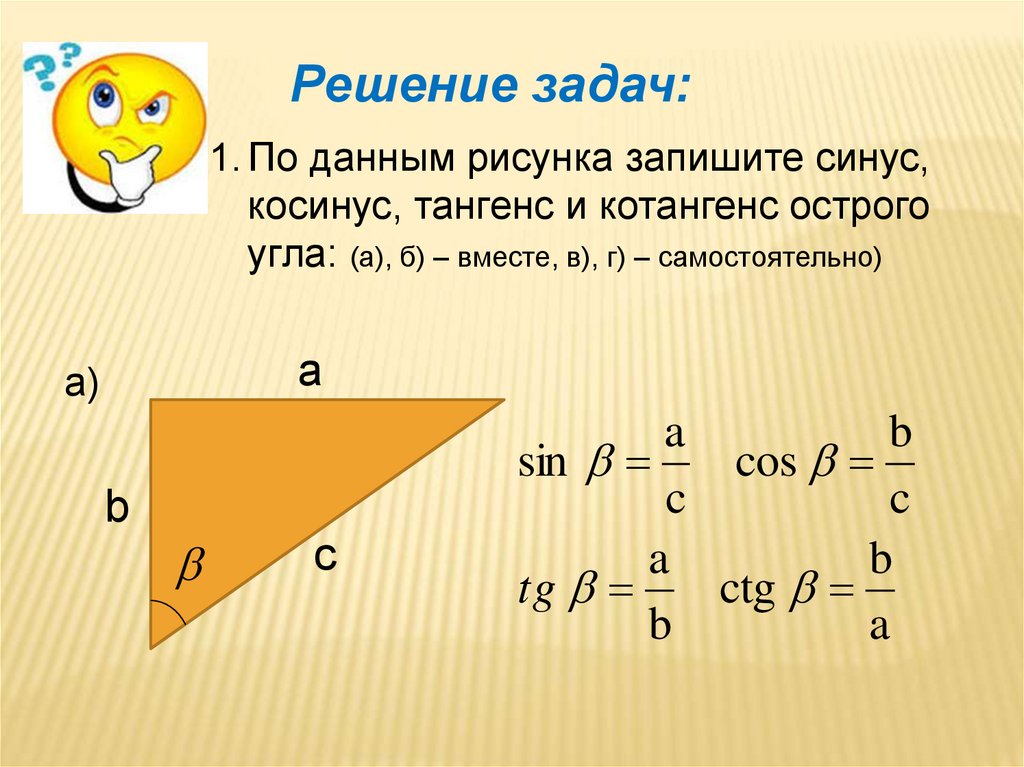 Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°.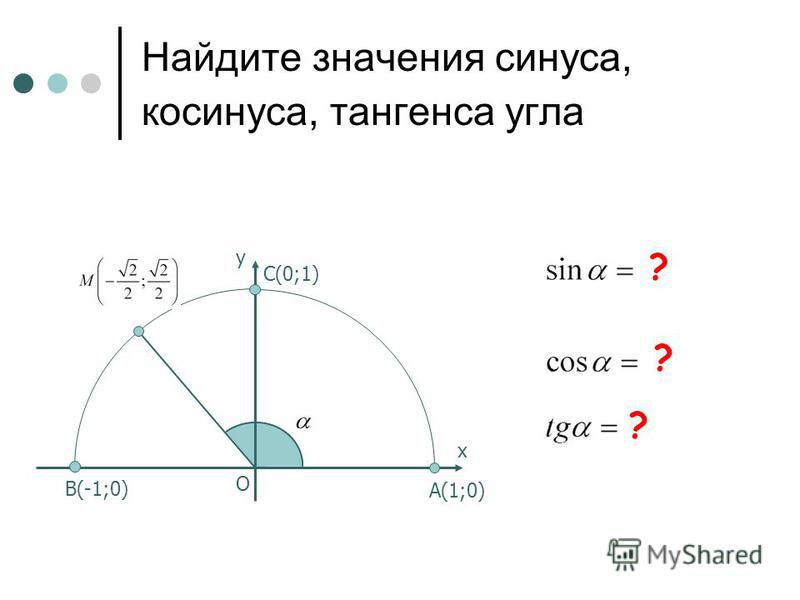 Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.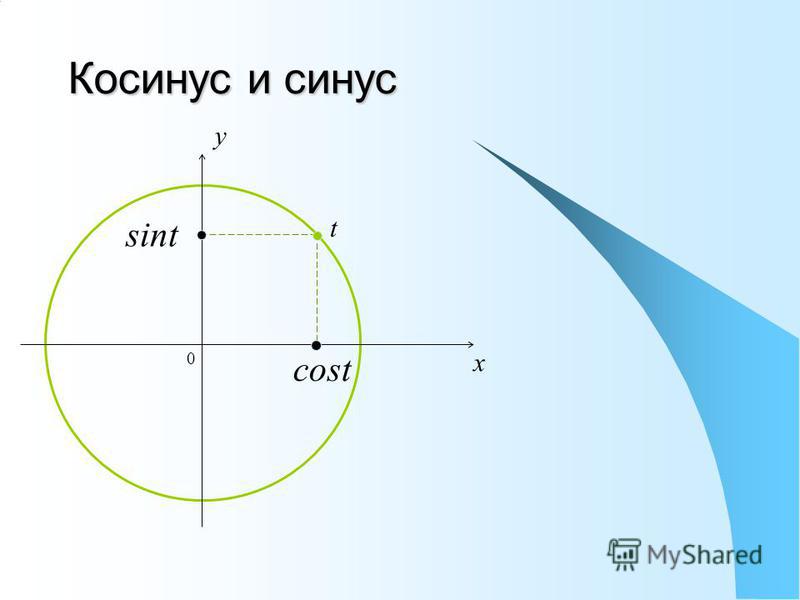
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто.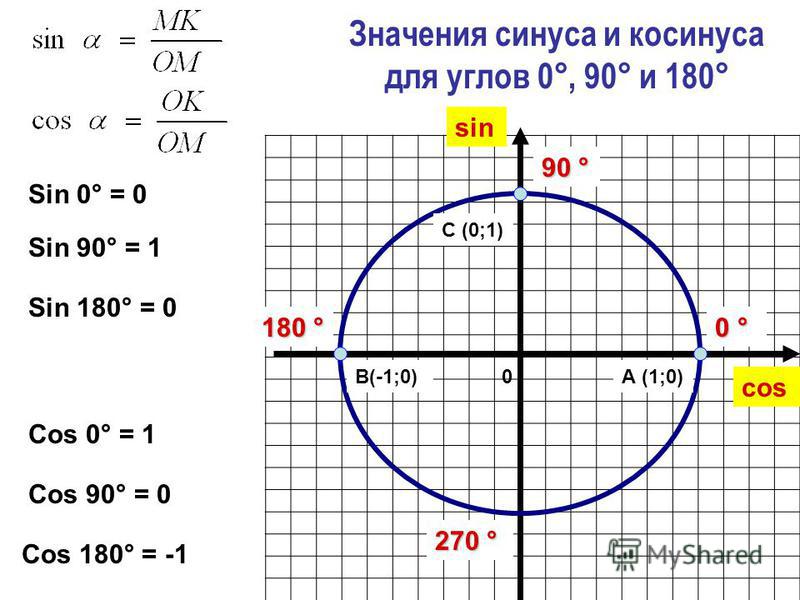 Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) .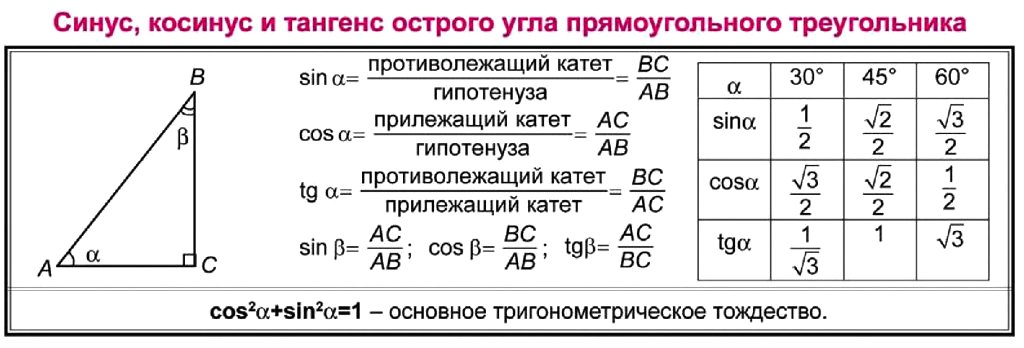 Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Решу огэ синус косинус тангенс котангенс
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции.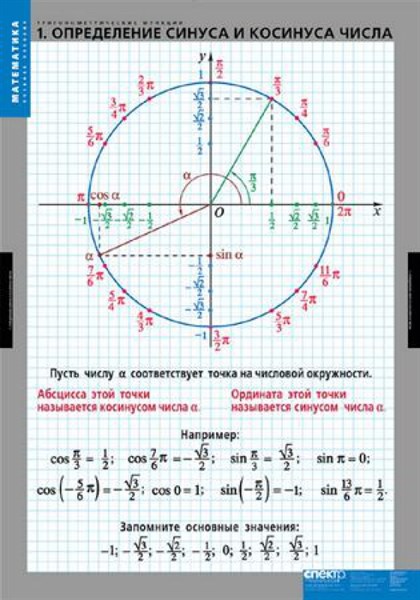 Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.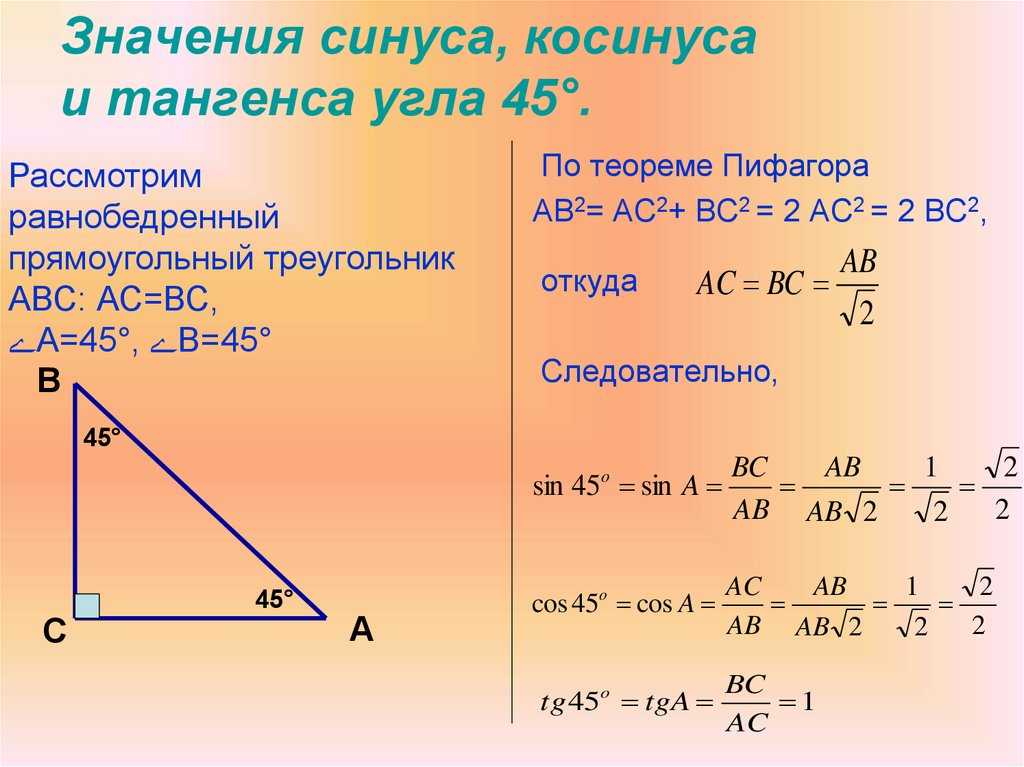
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x, y ).
Определение дается через координаты точки A 1 ( x, y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x, y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x, y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x, y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x, y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа T называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в T радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу T ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа T — ордината точки единичной окружности, соответствующей числу T. sin t = y
Косинус числа T — абсцисса точки единичной окружности, соответствующей числу T. cos t = x
Тангенс числа T — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу T. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу T, совпадает с точкой, в которую переходит начальная точка после поворота на угол T радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z ).
Можно сказать, что sin α, cos α, t g α, c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу T соответствует определенное значение синуса или косинуса числа T. Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x, y ) перпендикуляр к оси абсцисс.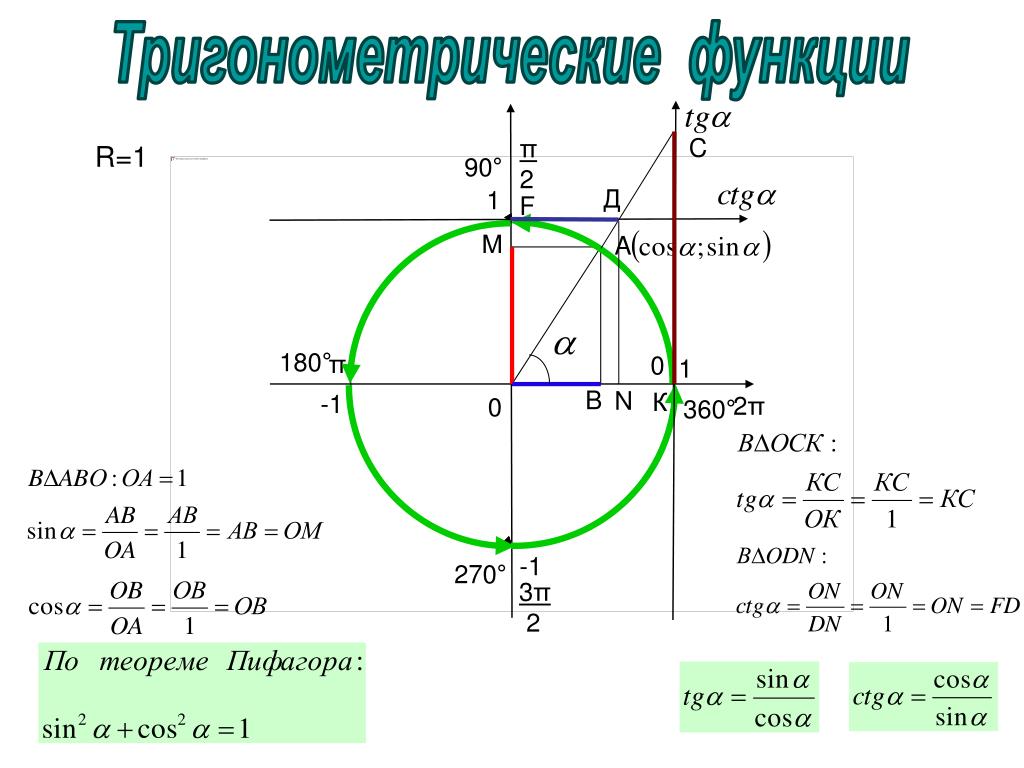 В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
Sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота.
Zaochnik. com
03.02.2019 0:48:09
2019-02-03 00:48:09
Источники:
Https://zaochnik. com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/
Синус косинус » /> » /> . keyword { color: red; }
keyword { color: red; }
Решу огэ синус косинус тангенс котангенс
Синус косинус, определение. Друзья! В прошлой статье, где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.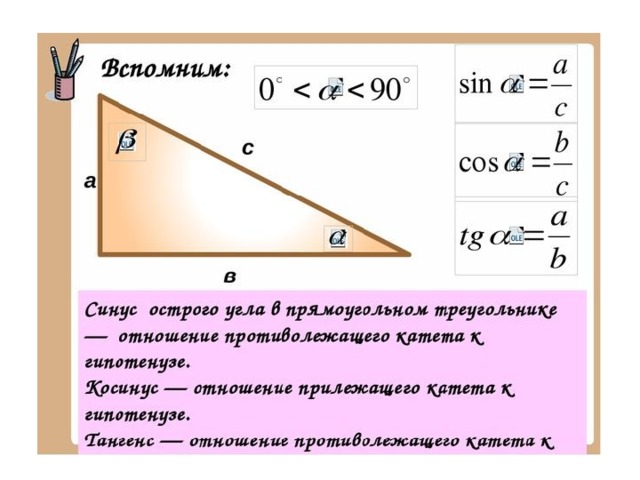
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… Отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.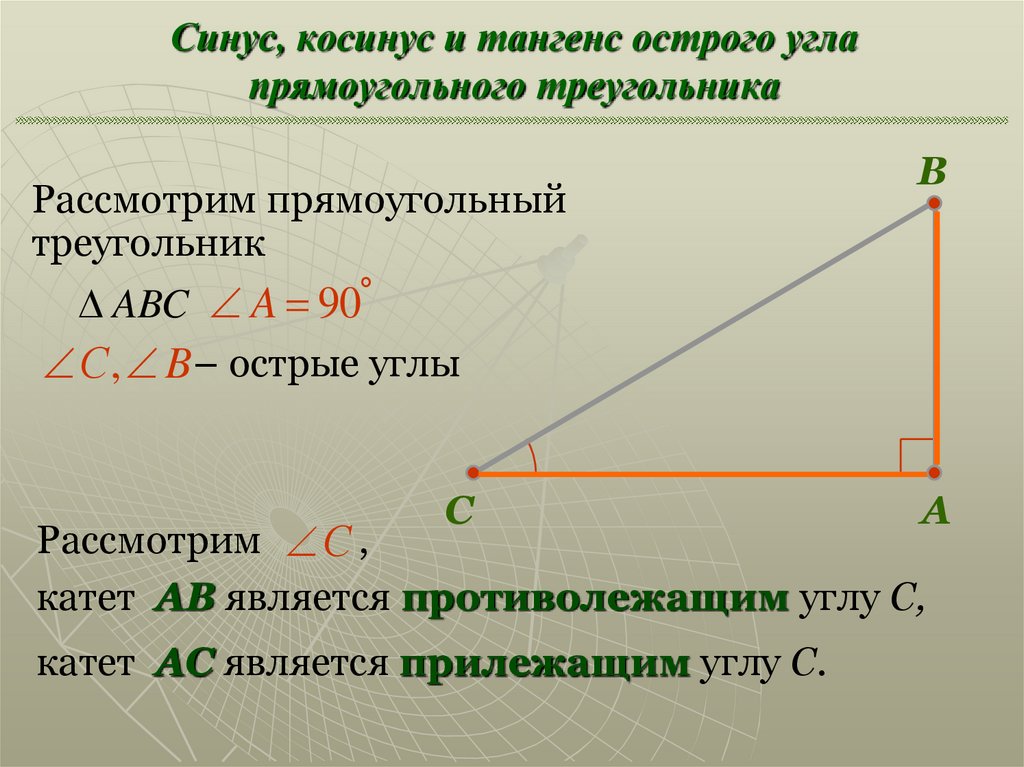
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте » Математический тандем « , посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Matematikalegko. ru
06.02.2018 8:14:02
2018-02-06 08:14:02
Источники:
Https://matematikalegko. ru/priyomy/sinus-i-kosinus-zapomnit-navsegda. html
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
Решу огэ синус косинус тангенс котангенс
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 3 № 52781
Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Сумма двух равных углов при основании треугольника равна 60°, поэтому каждый из них равен 30°. Тогда по теореме синусов
Задание 3 № 517192
В равнобедренном треугольнике ABC с основанием AB боковая сторона равна Найдите длину высоты AH.
Проведем из вершины C высоту CK, и заметим, что Выразим косинус через синус: откуда
Далее имеем: и тогда
Внимательный читатель заметит, что рисунок неверный! Действительно, синус угла при основании равен 0,25, значит, сам угол меньше 45°. Следовательно, угол при вершине больше 90° — треугольник тупоугольный. Тем не менее, решение верное: остроугольность треугольника в решении не использовалась, все рассуждения сохраняют свою силу.
Задание 3 № 517192
Задание 3 № 52781
Внимательный читатель заметит, что рисунок неверный.
Ege. sdamgia. ru
15.04.2020 4:42:42
2020-04-15 04:42:42
Источники:
Https://ege. sdamgia. ru/search? keywords=1&cb=1&search=1.2.1%20%D0%A1%D0%B8%D0%BD%D1%83%D1%81,%20%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81,%20%D1%82%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%81,%20%D0%BA%D0%BE%D1%82%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%81%20%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE%20%D1%83%D0%B3%D0%BB%D0%B0
что это? Отвечаем на вопрос.
 Как найти синус, косинус и тангенс?
Как найти синус, косинус и тангенс?Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза – это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул – как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.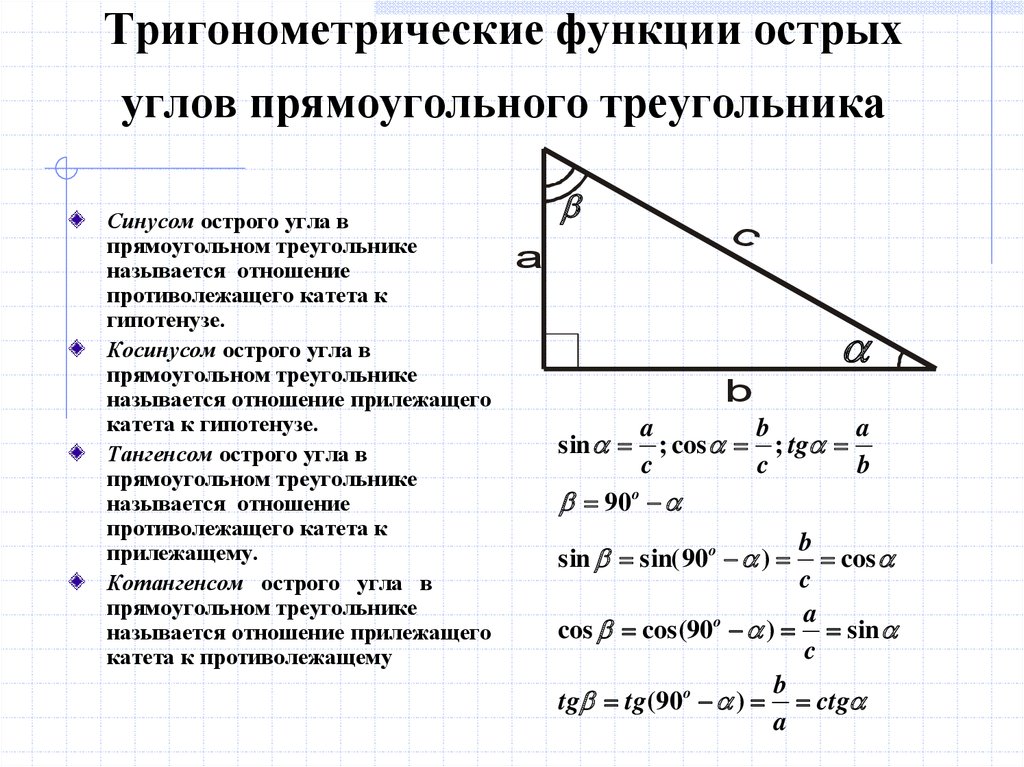
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих – в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Они полностью выводятся из предыдущих – в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны.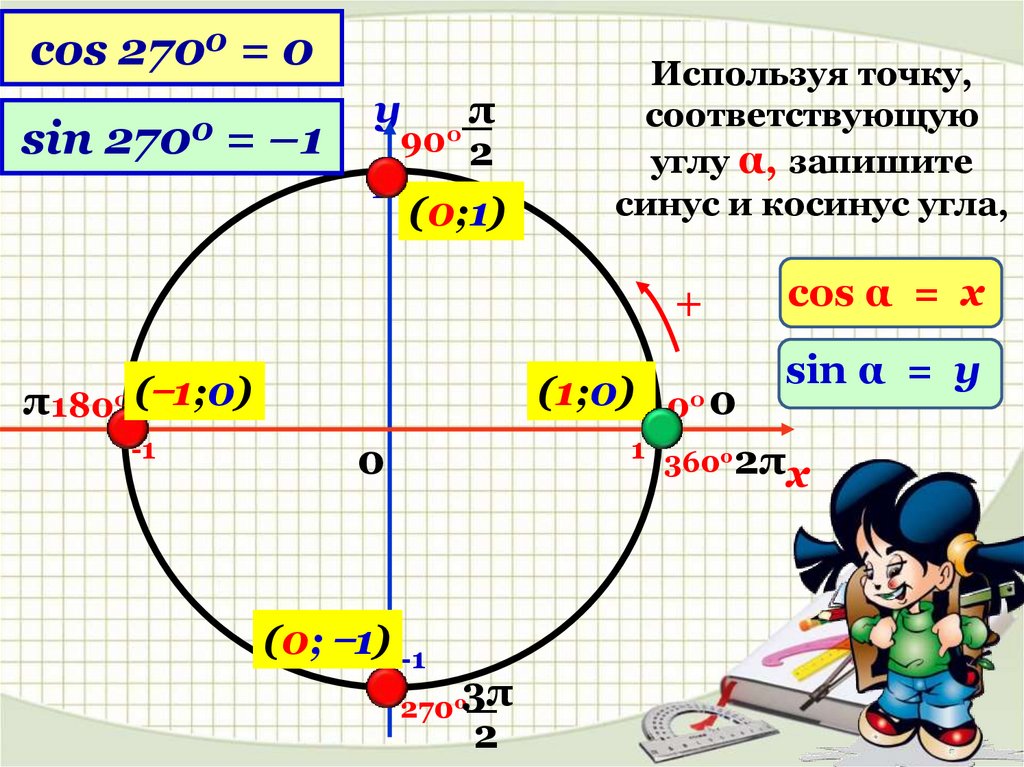 Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата – можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы знаете, что такое синус, косинус, тангенс.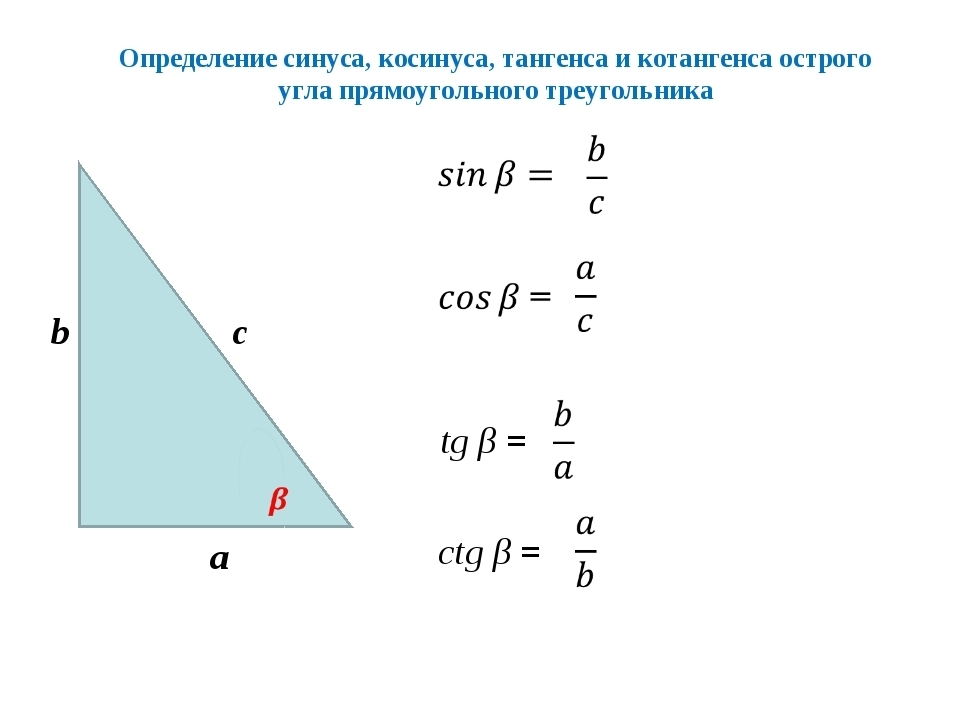 Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение – это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
косинусов
Как упоминалось ранее, мы обычно используем букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу B, и букву c для обозначения стороны. противоположный угол C. Так как сумма углов в треугольнике равна 180°, а угол C равен 90°, то углы A и B в сумме дают 90°, то есть являются дополнительными углами. Поэтому косинус B равно синусу A. Мы видели на прошлой странице, что sin A — это сторона, противоположная гипотенузе, то есть a/c. Следовательно, cos B равно a/c. Другими словами, косинус угла прямоугольного треугольника равен прилежащему катету, деленному на гипотенузу:
Поэтому косинус B равно синусу A. Мы видели на прошлой странице, что sin A — это сторона, противоположная гипотенузе, то есть a/c. Следовательно, cos B равно a/c. Другими словами, косинус угла прямоугольного треугольника равен прилежащему катету, деленному на гипотенузу:
Кроме того, cos A = sin B = b/c.
Тождество Пифагора для синусов и косинусов
Вспомним теорему Пифагора для прямоугольных треугольников. Он говорит, что
где c — гипотенуза. Это очень легко переводится в пифагорейское тождество синусов и косинусов. Разделите обе части на c 2 и вы получите
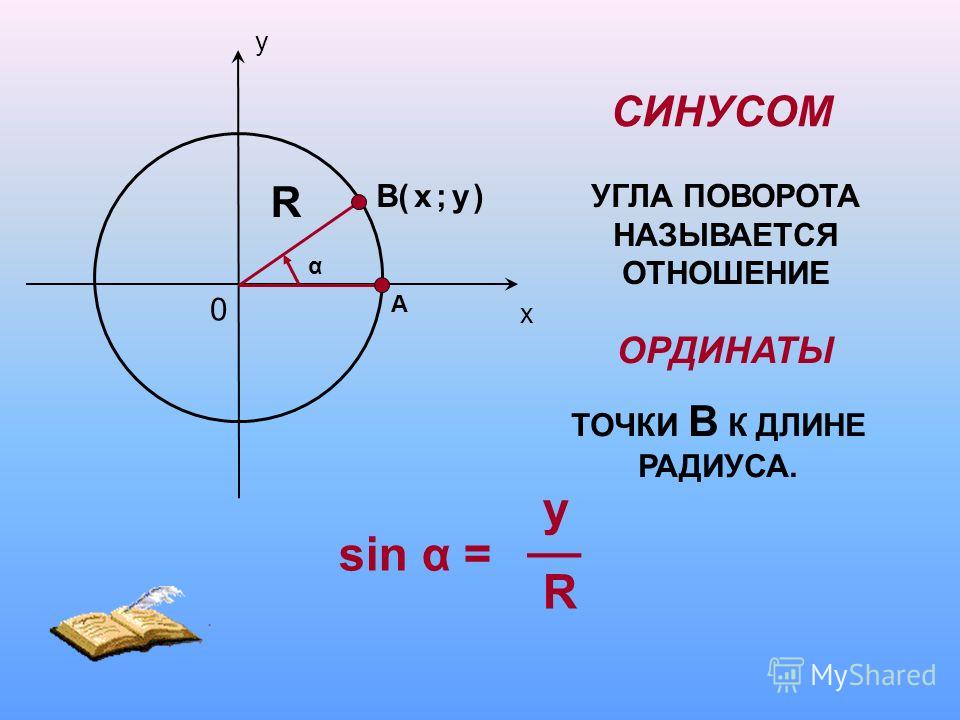
Но A 2 / C 2 = (SIN A ) 2 и B 2 / C 2 = (COS A ) 2 . Чтобы уменьшить количество круглых скобок, которые необходимо написать, принято соглашение, что обозначение sin 2 A является аббревиатурой для (sin A ) 2 , и аналогично для степеней другого триггера. функции. Таким образом, мы доказали, что
когда А острый угол. Мы еще не видели, какими должны быть синусы и косинусы других углов, но когда мы это увидим, мы получим для любого угла θ одно из важнейших тригонометрических тождеств, тождество Пифагора для синусов и косинусов:
Синусы и косинусы для особых общих углов
Мы можем легко вычислить синусы и косинусы для некоторых общих углов.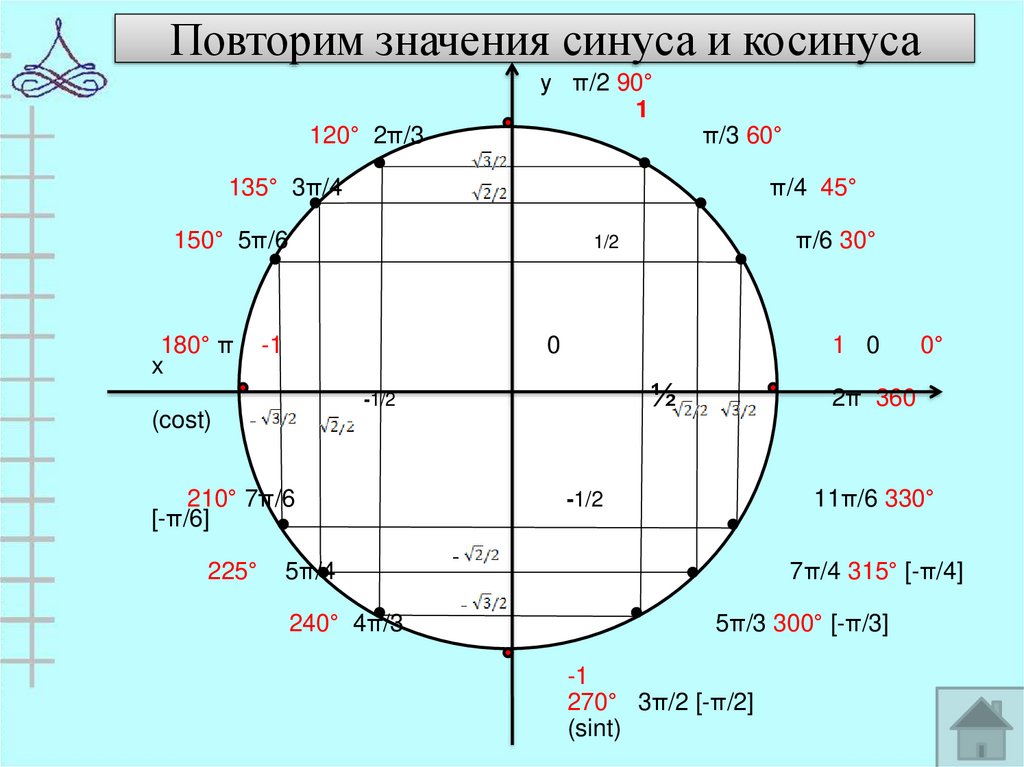 Рассмотрим сначала 45°
угол. Он находится в равнобедренном прямоугольном треугольнике, то есть 45°-45°-9треугольник 0°. В
любой прямоугольный треугольник c 2 = a 2 + b 2 , но в этом
один a = b, so c 2 = 2 a 2 . Следовательно c = a √2. Следовательно, и синус, и косинус
45° равно 1/√2, что также может быть записано как √2 / 2.
Рассмотрим сначала 45°
угол. Он находится в равнобедренном прямоугольном треугольнике, то есть 45°-45°-9треугольник 0°. В
любой прямоугольный треугольник c 2 = a 2 + b 2 , но в этом
один a = b, so c 2 = 2 a 2 . Следовательно c = a √2. Следовательно, и синус, и косинус
45° равно 1/√2, что также может быть записано как √2 / 2.
Далее рассмотрим углы 30° и 60°. В диапазоне 30°-60°-90° прямоугольный треугольник, отношения сторон равны 1 : √3 : 2. Отсюда следует, что sin 30° = cos 60° = 1/2 и sin 60° = cos 30° = √3 / 2.
Эти данные заносятся в эту таблицу.
| Angle | Degrees | Radians | cosine | sine |
|---|---|---|---|---|
| 90° | π /2 | 0 | 1 | |
| 60° | π /3 | 1/2 | √3 / 2 | |
| 45° | π /4 | √2 / 2 | √2 / 2 | |
| 30° | π /6 | √3 / 2 | 1/2 | |
| 0° | 0 | 1 | 0 |
Exercises
These exercises all относятся к прямоугольным треугольникам со стандартной маркировкой.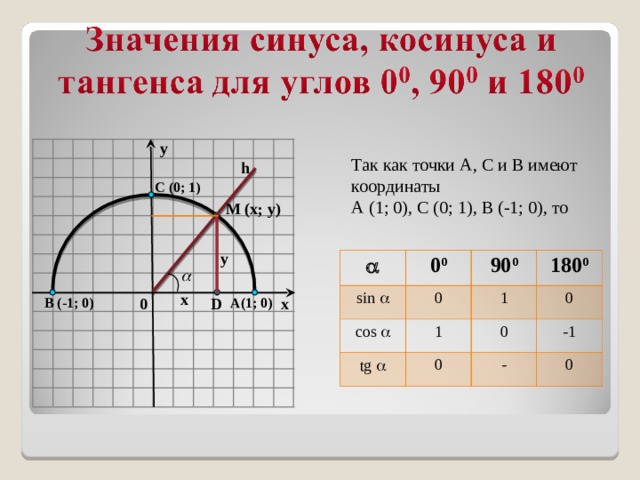
30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. б = 6,4, в = 7,8. Найдите А и А.
36. A = 23° 15′, c = 12,15. Найти а и б.
Подсказки
30. Косинус A связывает b с гипотенузой c, , так что вы можете сначала вычислить c. Зная b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух неизвестных вам сторон, а именно а/к. Тем не менее, это дает вам уравнение для работы: 1/3 = a/c. Тогда c = 3 a. Из теоремы Пифагора следует, что а 2 + 144 = 9 а 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b /cos A = 2,25/0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 дюйма, или 4’3′.
c = 3 и , что составляет 12,73 фута или 12 футов 9 дюймов.
35. cos A = b/c = 6,4/7,8 = 0,82. Следовательно, A = 34,86° = 34°52′, или около 35°.
a 2 = 7,8 2 – 6,4 2 = 19,9, поэтому a равно примерно 4,5.
36. a = c sin A = 12,15 sin 23°15′ = 4,796.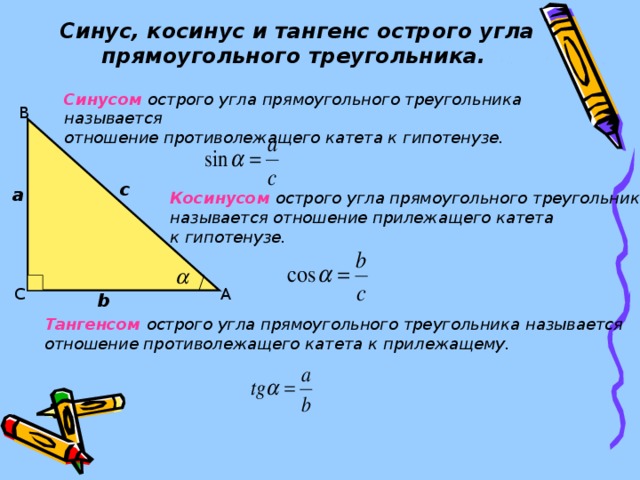
b = c cos A = 12,15 cos 23°15′ = 11,17.
Косинус Примеры и функции | Как использовать косинус
Математические курсы / Precalculus High School: помощь и обзор Курс / Понимание операций функций: справка и обзор Глава
Андерсон Гомеш Да Силва, Дженнифер Беддоу- Автор Андерсон Гомес да Силва
Андерсон имеет степени бакалавра и магистра (обе по математике) Федерального университета Флуминенсе и Папского католического университета Рио-де-Жанейро соответственно. Он был ассистентом преподавателя в Университете Делавэра (UD) в течение двух с половиной лет, ведя дискуссии и лабораторные занятия по исчислению I, II и III. Зимой 2021 года он был единственным инструктором одного из разделов исчисления I в UD.
Посмотреть биографию - Инструктор Дженнифер Беддоу
Дженнифер имеет степень магистра химии и степень бакалавра биологических наук.
Посмотреть биографию
Что такое определение косинуса? Изучите определение функции косинуса и значение cos. Кроме того, узнайте, как использовать косинус с помощью примеров косинуса. Обновлено: 04.11.2021
Содержание
- Определение косинуса
- Как использовать косинус
- Краткое содержание урока
Косинус Определение
С точки зрения прямоугольного треугольника косинус острого угла представляет собой тригонометрическое отношение, определяемое делением измерений прилежащей к нему стороны и гипотенузы треугольника. Рассмотрим рисунок 1, на котором изображен прямоугольный треугольник {eq}ABC {/eq} со сторонами, измеряющими {eq}a,~b {/eq} и {eq}c {/eq}, и внутренними углами {eq}A,~ B {/eq} и {eq}C {/eq}. 9{\ круг}. {/eq} Необходимость расширить эту концепцию на другие значения привела к появлению функции косинуса, которая определена для каждого действительного числа. Прямоугольные треугольники по-прежнему используются при определении функции косинуса, но они используются в сочетании с единичным кругом , то есть окружностью с центром в начале координат (точка {eq}(0,~0) {/eq} в декартовой плоскости) и радиусом {eq}1 {/eq}.
При работе с тригонометрическими функциями вообще принято указывать углы в радианах, а не в градусах. Другое соглашение состоит в том, чтобы считать, что положительные углы задаются вращением против часовой стрелки, тогда как отрицательные углы определяются вращением по часовой стрелке. 92~=~1 {/eq}, то есть единичный круг. Точка {eq}P(x,~y) {/eq} на окружности определяет с началом координат луч {eq}OP {/eq}. Лучи {eq}OX {/eq} и {eq}OP {/eq} образуют угол {eq}\alpha {/eq}, косинус которого является абсциссой (или значением x) {eq}P {/eq }. Другими словами, {eq}\cos~(\alpha)~=~x {/eq}. Это точное определение косинуса угла, и оно изображено на рисунке 2.
Поскольку абсцисса точек в первом и четвертом квадрантах положительна, функция косинуса положительна на {eq}[0,~\pi/2) {/eq} и {eq}(2\pi/3 ,~2\pi] {/eq}.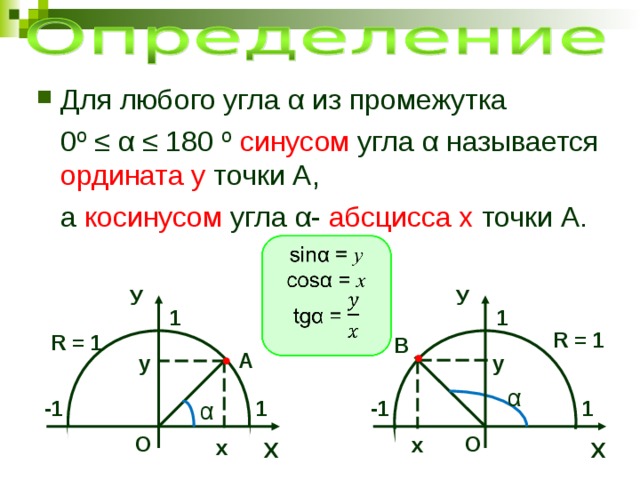 Аналогичным образом можно сделать вывод, что функция отрицательна на {eq}(\pi/2,~3\pi/2) {/eq}.
Аналогичным образом можно сделать вывод, что функция отрицательна на {eq}(\pi/2,~3\pi/2) {/eq}.
Период косинуса
Одним из интересных свойств функции косинуса (и тригонометрических функций вообще) является ее периодичность.Функция {eq}f {/eq} называется периодической, если существует действительное число, не равное нулю, скажем, {eq}p {/eq}, так что {eq}f(x~+~p)~=~f(x) {/eq} для каждого {eq}x {/eq} в домене { eq}f {/eq}. Наименьшее положительное {eq}p {/eq}, удовлетворяющее предыдущему свойству, называется период функции.
График функции косинуса показан на рисунке 3.
Фиолетовая часть, интервал {eq}[0, 2\pi] {/eq} имеет форму долины, и этот узор повторяется на {eq}[-2\pi,~0],~ [2\pi,~4\pi],~[4\pi,~6\pi] {/eq} и так далее. Таким образом, период функции косинуса равен {eq}2\pi {/eq}. Чтобы проверить это алгебраически, нужно убедиться, что {eq}\cos~(x)~=~\cos~(x~+~2\pi) {/eq}. Действительно, тригонометрическое тождество дает {eq}\cos~(x~+~2\pi)~=~\cos~(x)\cos~(2\pi)~-~\sin~(x)\sin~ (2\pi)~=~\cos~(x) {/eq}. Последнее равенство выполняется, поскольку {eq}\cos~(2\pi)~=~1 {/eq} и {eq}\sin~(2\pi)~=~0 {/eq}
Таким образом, период функции косинуса равен {eq}2\pi {/eq}. Чтобы проверить это алгебраически, нужно убедиться, что {eq}\cos~(x)~=~\cos~(x~+~2\pi) {/eq}. Действительно, тригонометрическое тождество дает {eq}\cos~(x~+~2\pi)~=~\cos~(x)\cos~(2\pi)~-~\sin~(x)\sin~ (2\pi)~=~\cos~(x) {/eq}. Последнее равенство выполняется, поскольку {eq}\cos~(2\pi)~=~1 {/eq} и {eq}\sin~(2\pi)~=~0 {/eq}
Тригонометрические функции
Существует шесть основных тригонометрических функций:
- Синус (sin)
- Косинус (cos)
- Тангенс (тангенс)
- Секанс (сек)
- Косеканс (csc)
- Котангенс (кроватка)
Эти функции используются для связи углов треугольника со сторонами этого треугольника. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, таких как волны, звук и свет.
Как использовать косинус
Теперь, когда дано определение косинуса и представлен его график, рассмотрим несколько примеров использования косинуса. Попробуйте решить проблемы, прежде чем смотреть на решения.
Попробуйте решить проблемы, прежде чем смотреть на решения.
- Пример 1
Используйте рисунок 4, чтобы найти косинус угла {eq}x {/eq}.
Один из способов запомнить это соотношение вместе с соотношениями для других наиболее распространенных тригонометрических функций — использовать мнемонику SOHCAHTOA:0033
CAH = C OSINE IS A DJACENT Более ч Ypotenus , или если вам нужно знать меру угла.
Пример:
Что такое cosΦ?
Косинус – это отношение стороны, примыкающей к углу, к гипотенузе.
cosΦ = 8/17
cosΦ = 0,4706
Функция косинуса как периодическая функция
Тригонометрические функции называются периодическими функциями , потому что они повторяются в течение заданного периода времени.
Посмотрите на график функции косинуса:
Как видите, график повторяется на расстоянии 2π. Следовательно, мы можем сказать, что функция косинуса имеет период 2π. Обычно, рассматривая функцию косинуса таким образом, вы используете не градусную меру, а радиан . Радиан — стандартная единица измерения угла, используемая в математике. Полный круг равен 2π радианам, что равно 360°.
Косинус и его отношение к единичной окружности
В тригонометрии единичная окружность — это окружность с центром в начале координат (0,0) координатной плоскости с радиусом 1.
Любая точка на окружности соответствует синусу и косинусу угла, образованного линией от центра окружности до этой точки и оси x. Если точка (x, y), отношение выглядит так —
sinθ = y
cosθ = x
Например:
Используя единичный круг, определите значение cos π/3?
Найдите точку на окружности, соответствующую π/3 (СОВЕТ: она находится в квадранте I в правом верхнем углу графика).
Какая точка находится на краю круга в этой точке?
Это (1/2, √(-3)/2) Поскольку 1/2 — это значение x, это значение cos π/3.
Итак, ответ на вопрос 1/2.
Таким образом, единичный круг можно использовать для нахождения синуса или косинуса любого угла, даже отрицательного или превышающего 360°
Заключение
Функция косинуса является одной из основных тригонометрических функций. Это важно для нахождения расстояний или высоты, а также может использоваться для нахождения угловых величин.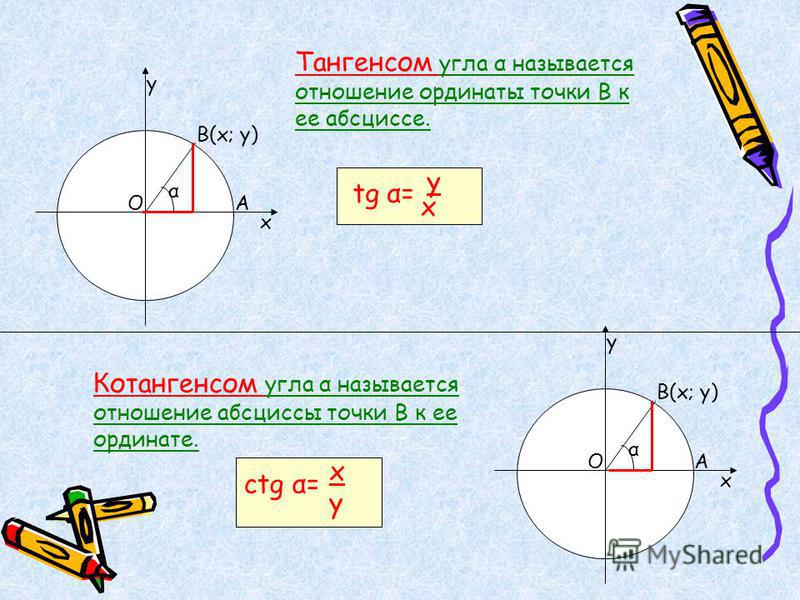 Единичный круг — это инструмент, который может быть полезен для нахождения значения косинуса для всех типов углов, особенно для тех, которые могут быть неочевидны.
Единичный круг — это инструмент, который может быть полезен для нахождения значения косинуса для всех типов углов, особенно для тех, которые могут быть неочевидны.
Результаты обучения
Знание приведенных выше сведений о косинусе может помочь вам:
- Назвать шесть основных тригонометрических функций
- Назовите функцию косинуса
- Вычисление косинуса угла с использованием единичной окружности
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Тригонометрические функции
Существует шесть основных тригонометрических функций:
- Синус (sin)
- Косинус (cos)
- Тангенс (тангенс)
- Секанс (сек)
- Косеканс (csc)
- Котангенс (кроватка)
Эти функции используются для связи углов треугольника со сторонами этого треугольника. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, таких как волны, звук и свет.
Функция косинуса
Функция косинуса определяется как отношение стороны треугольника, примыкающей к углу, деленному на гипотенузу.
Один из способов запомнить это соотношение вместе с соотношениями для других наиболее распространенных тригонометрических функций — использовать мнемонику SOHCAHTOA:
SOH = S ine равно O pposite over H ypotenuse
CAH9 =CAH9 =
CAH9 =
CAH9 осин равен A djacent над H ypotenuse
TOA = T angent равен O pposite над A djacent
Это соотношение можно использовать для решения задач, связанных с высотой или расстоянием угловая мера.
Пример:
Что такое cosΦ?
Косинус – это отношение стороны, примыкающей к углу, к гипотенузе.
cosΦ = 8/17
cosΦ = 0,4706
Функция косинуса как периодическая функция
Тригонометрические функции называются периодическими функциями , потому что они повторяются в течение заданного периода времени.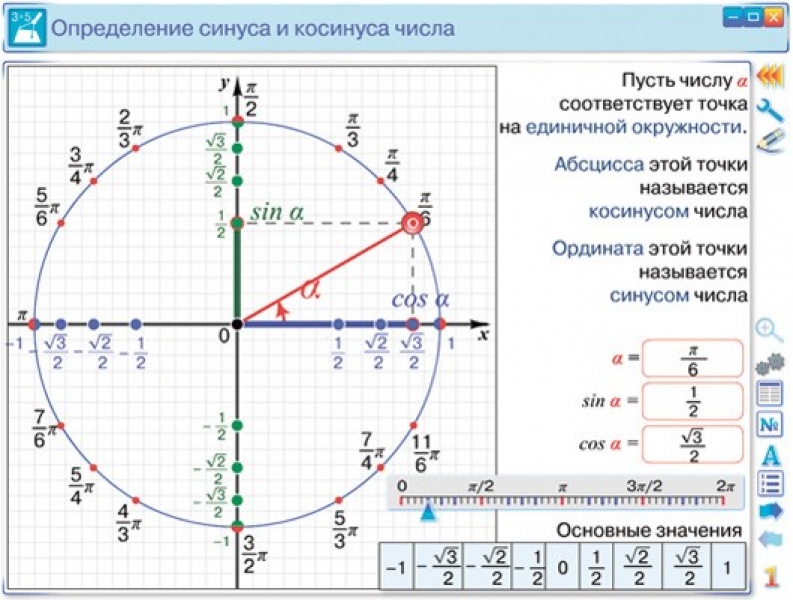
Посмотрите на график функции косинуса:
Как видите, график повторяется на расстоянии 2π. Следовательно, мы можем сказать, что функция косинуса имеет период 2π. Обычно, рассматривая функцию косинуса таким образом, вы используете не градусную меру, а радиан . Радиан — стандартная единица измерения угла, используемая в математике. Полный круг равен 2π радианам, что равно 360°.
Косинус и его отношение к единичной окружности
В тригонометрии число единичная окружность — это окружность с центром в начале координат (0,0) координатной плоскости с радиусом 1.
Любая точка на окружности соответствует синусу и косинусу угла, образованного линией от центра окружности до этой точки и оси x. Если точка (x, y), соотношение выглядит так:
sinθ = y
cosθ = x
Например:
Используя единичный круг, определите значение cos π/3?
Найдите точку на окружности, соответствующую π/3 (СОВЕТ: она находится в квадранте I в правом верхнем углу графика).
Какая точка находится на краю круга в этой точке?
Это (1/2, √(-3)/2) Поскольку 1/2 — это значение x, это значение cos π/3.
Итак, ответ на вопрос 1/2.
Таким образом, по единичной окружности можно найти синус или косинус любого угла, даже если он отрицательный или больше 360°
Вывод
Функция косинуса является одной из основных тригонометрических функций. Это важно для нахождения расстояний или высоты, а также может использоваться для нахождения угловых величин. Единичный круг — это инструмент, который может быть полезен для нахождения значения косинуса для всех типов углов, особенно для тех, которые могут быть неочевидны.
Результаты обучения
Знание приведенных выше сведений о косинусе может помочь вам:
- Назвать шесть основных тригонометрических функций
- Назовите функцию косинуса
- Вычисление косинуса угла с использованием единичной окружности
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
com.
Создайте свою учетную запись
Что такое косинус угла?
Рассмотрим круг с центром в начале координат и радиусом один. Отрезок от начала координат до точки P на единичной окружности образует угол x с положительной осью x. Абсцисса P — это косинус x.
Как найти косинус?
В прямоугольном треугольнике косинус угла находится путем деления длины прилежащей стороны на гипотенузу. Если угол не острый, используйте единичную окружность и подобие треугольников.
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже зарегистрирован? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков
и учебные ресурсы‐все
в одном месте.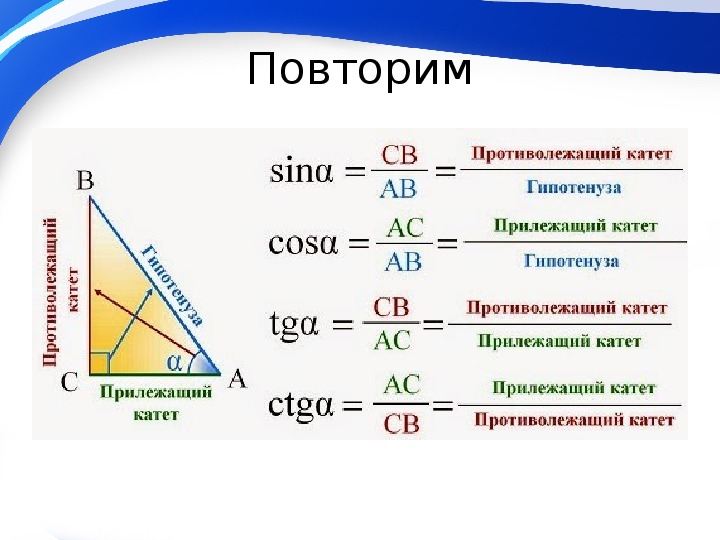
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. 909:49 Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
Функция синуса — определение математического слова
Функция синуса — определение математического слова — Math Open ReferenceОткрытый математический справочник
Главная Контакт О Тематический указатель
В
прямоугольный треугольник,
синус угла это отношение длины противолежащей стороны к длине стороны
гипотенуза.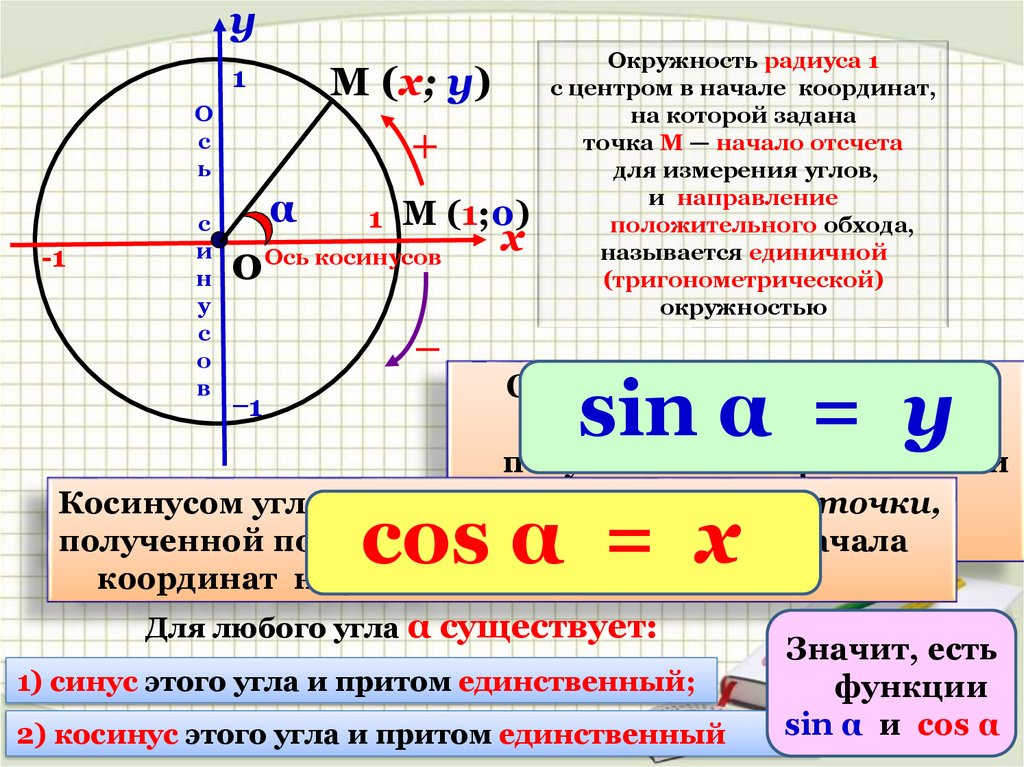
Попробуйте это Перетащите любой вершину треугольника и посмотреть, как вычисляются синусы A и C.
Функция синуса, наряду с косинусом и тангенсом, является одной из трех наиболее распространенных функций. тригонометрические функции. В любом прямоугольном треугольнике синус угла x — это длина противоположной стороны (O), разделенная на длину гипотенуза (Н). В формуле это записывается как «грех» без буквы «е»:
Часто вспоминается как «SOH» — что означает
Синус
Напротив
Гипотенуза.
См. SOH CAH TOA.
В качестве примера предположим, что мы хотим найти синус угла C на рисунке выше (сначала нажмите «сбросить»). Из приведенной выше формулы мы знаем, что синус угла равен противолежащему катету, деленному на гиупотенузу. Противоположная сторона AB и имеет длину 15. Гипотенуза AC с длиной 30. Таким образом, мы можем написать получается 0,5. Так что можно сказать « Синус 30° равен 0,5 «, или
С помощью калькулятора найдите синус 30°. Должно получиться 0,5, как указано выше.
Должно получиться 0,5, как указано выше.
(Если нет — убедитесь, что калькулятор настроен на работу в градусах, а не на
радианы).
Пример. Использование синуса для нахождения гипотенузы
Если мы посмотрим на общее определение — мы видим, что есть три переменных: мера угла x и длины двух сторон (противоположная и гипотенуза). Так что если у нас есть любые два из них, мы можем найти третий.
На рисунке выше нажмите «Сброс». Представьте, что мы не знали длину гипотенузы H. Мы знаем, что синус A (60°) — это противолежащая сторона (26), деленная на H. Из нашего калькулятора мы находим, что sin60 равно 0,866, поэтому мы можем написать Транспонирование: что выходит 30.02 *
* Примечание: Длины и углы на рисунке выше округлены для ясности. С помощью калькулятора они будут немного отличаться. Калькулятор правильный.
Функция обратного синуса — arcsin
Для каждой тригонометрической функции, такой как sin, существует обратная функция, которая работает в обратном порядке. Эти обратные функции имеют то же имя, но с «дугой» впереди.
(На некоторых калькуляторах кнопка арксинуса может быть помечена как in или иногда
грех -1 .)
Таким образом, обратным греху является арксинус и т. д. Когда мы видим «арксинус А», мы понимаем его как «угол, чей грех равен А».
Эти обратные функции имеют то же имя, но с «дугой» впереди.
(На некоторых калькуляторах кнопка арксинуса может быть помечена как in или иногда
грех -1 .)
Таким образом, обратным греху является арксинус и т. д. Когда мы видим «арксинус А», мы понимаем его как «угол, чей грех равен А».
| sin30 = 0,5 | Означает: синус 30 градусов равен 0,5 |
| угл 0,5 = 30 | Означает: угол, у которого sin равен 0,5, равен 30 градусам. |
См. также определение арксинуса и Обратные функции — тригонометрия
Большие и отрицательные углы
В прямоугольном треугольнике два переменных угла всегда меньше 90°.
(См. Внутренние углы треугольника).
Но мы можем найти синус любого угла, как бы он ни был велик, а также синус отрицательного угла.
Подробнее об этом см. Функции больших и отрицательных углов.
График функции синуса
Когда синус угла изображается в зависимости от угла, в результате получается форма, аналогичная приведенной выше, называется синусоидой.
Подробнее об этом см. в разделе График синусоидальной функции.
Производная sin(x)
В исчислении производная sin(x) равна cos(x) .
Это означает, что при любом значении x скорость изменения или наклон sin(x) составляет cos(x) . Подробнее об этом см. Производные тригонометрических функций вместе с производными других тригонометрических функций. См. также оглавление исчисления.
Другие темы по тригонометрии
Уголки
- Определение угла, свойства углов
- Стандартное положение на углу
- Начальная сторона угла
- Сторона конца угла
- Четырехугольники
- Котерминальные углы
- Базовый угол
Тригонометрические функции
- Знакомство с шестью триггерными функциями
- Функции больших и отрицательных углов
- Инверсные триггерные функции
- SOH CAH TOA Память
- Синусоидальная функция (sin) в прямоугольных треугольниках
- Функция обратного синуса (арксинус)
- График функции синуса
- Синусоидальные волны
- Функция косинуса (cos) в прямоугольных треугольниках
- Функция арккосинуса (arccos)
- График функции косинуса
- Касательная функция (тангенс) в прямоугольных треугольниках
- Функция арктангенса (арктангенс)
- График функции касательной
- Функция котангенса cot (в прямоугольных треугольниках)
- Функция секанса сек (в прямоугольных треугольниках)
- Функция косеканса csc (в прямоугольных треугольниках)
Решение задач по тригонометрии
- Общий подход
- Определение наклонного расстояния вдоль склона или пандуса
- Определение угла уклона или пандуса
Исчисление
- Производные тригонометрических функций
(C) 2011 Copyright Math Open Reference.
Все права защищены
Графики функций синуса и косинуса
Определения синуса и косинуса
Функции синуса и косинуса определяются через координаты точек, лежащих на единичной окружности с центром в начале координат.
Рассмотрим точку M ( x,y ) на единичной окружности. Предположим, что радиус r = OM составляет угол t с положительным направлением оси x .
Рис. 1.Вход функций \(\sin t\) и \(\cos t\) является мерой угла \(t.\) Выход синусоидальной функции \(\sin t\) равен вертикальная координата точки \(M.\) Соответственно, выходом функции косинуса \(\cos t\) является горизонтальная координата точки \(M.\)
Таким образом, координаты точки \(M\left( {x,y} \right)\) определяются функциями
\[x = \cos t,\;y = \sin t,\]
в зависимости от угла \(t.\)
График и свойства функции синуса
График функции синуса \(y = \sin t\)
Когда \(t = 0,\) точка \(M\) имеет координаты \(M\left( {1,0} \right),\), то есть
\[\sin\left( {t = 0} \right) = 0. \]
\]
При повороте точки \(M\) против часовой стрелки вокруг начала координат на \(90\) градусов от \(t = 0\) до \(t = \frac{\pi }{2},\) значение синуса увеличивается от \(0\) до \(1.\) При изменении угла от \(t = \frac{\pi }{2}\) до \(t = \pi ,\) значение \(\ sin t\) уменьшается от \(1\) до \(0.\). Затем, когда радиус \(r = OM\) входит в третий и четвертый квадранты, \(\sin t\) становится отрицательным и сначала уменьшается от \(0\) до \(-1\), а затем увеличивается с \(-1\) до \(0.\). Все эти изменения показаны на рисунке \(2\) ниже.
Рис. 2. Домени кодовый домен синусоидальной функции
Функция синуса определена для всех действительных чисел \(t\) и принимает все значения из замкнутого интервала \(\left[ { — 1,1} \right].\) Следовательно,
\[\text{dom}\left( {\sin t} \right) = \mathbb{R},\;\text{codom}(\sin t) = \left[ { — 1,1} \right ],\]
, где dom обозначает домен функции, а codom обозначает ее кодовый домен или диапазон.
Функция четности синуса
Функция синуса является нечетной функцией:
\[\sin \left( { — t} \right) = — \sin t.\]
Он симметричен относительно начала координат, как видно из графика выше.
Периодичность функции синуса
Функция синуса является периодической с наименьшим периодом \(2\pi:\)
\[\sin\left( {t + 2\pi n} \right) = \sin t,\]
, где \(n \in \mathbb{Z}.\)
Нули функции синуса
Решения уравнения \(\sin t = 0\) равны
\[t = \pi n,\;n \in \mathbb{Z}.\]
Экстремальные значения функции синуса
Функция синуса достигает своего максимального значения \(\sin t = 1\) в
\[{t_{\max}} = \frac{\pi }{2} + 2\pi n,\;n \in \mathbb{Z}.\]
Минимальное значение \(\sin t = -1\) достигается при
\[{t_{\min }} = \frac{3\pi }{2} + 2\pi n,\;n \in \mathbb{Z}.\]
График и свойства функции косинуса
График функции косинуса \(y = \cos t\)
Когда \(t = 0,\) точка \(M\) на единичной окружности имеет координаты \(M\left({1,0} \right),\), то
\[\cos \left( {t = 0} \right) = 1.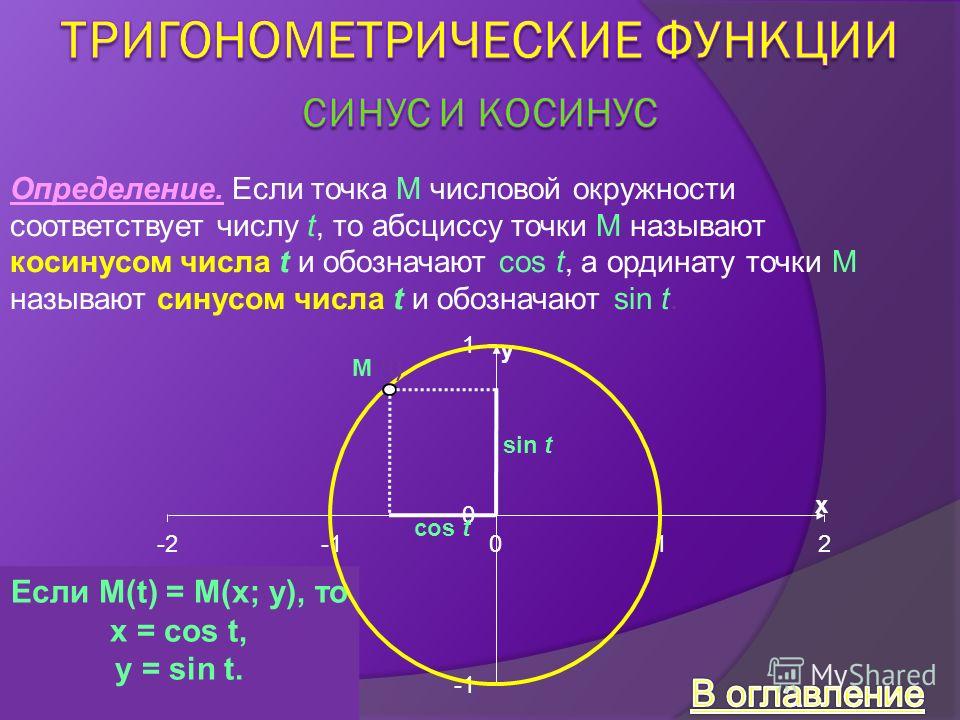 \]
\]
При вращении точки \(M\) против часовой стрелки вокруг начала координат от \(t = 0\) до \(t = \pi\) значение косинуса уменьшается от \(1\) до \(-1.\ ) Затем, когда угол увеличивается от \(t = \pi\) до \(t= 2\pi,\), значение \(\cos t\) увеличивается обратно от \(-1\) до \(1. \) По кофункциональному тождеству
\[\cos t = \sin \left( {t + \frac{\pi }{2}} \right).\]
Это означает, что мы можем получить график функции косинуса, сдвигая функцию синуса на \({\frac{\pi }{2}}\) влево.
Рисунок 3. Домени кодовый домен функции косинуса
Как и функция синуса, функция косинуса определена для всех действительных чисел \(t.\) Областью значений (или диапазоном) функции косинуса является интервал \(\left[ { — 1,1} \right].\) Итак, у нас есть
\[\text{dom}\left( {\cos t} \right) = \mathbb{R},\;\text{codom}(\cos t) = \left[ { — 1,1} \right ].\]
Функция четности косинуса
Функция косинуса является четной функцией:
\[\cos \left( { — t} \right) = \cos t. \]
\]
График функции косинуса симметричен относительно оси \(y-\).
Периодичность функции косинуса
Функция косинуса является периодической с наименьшим периодом \(2\pi:\)
\[\cos \left( {t + 2\pi n} \right) = \cos t,\;n \in \mathbb{Z}.\]
Нули функции косинуса
Решения уравнения \(\cos t = 0\) задаются как
\[t = \frac{\pi }{2} + \pi n,\;n \in \mathbb{Z}.\]
Экстремальные значения функции косинуса
Функция косинуса имеет максимальное значение \(\cos t = 1\) в
\[{t_{\max}} = 2\pi n,\;n \in \mathbb{Z}.\]
Минимальное значение \(\cos t = -1\) встречается в
\[{t_{\min}} = \pi + 2\pi n,\;n \in \mathbb{Z}.\]
См. решенные проблемы на стр. 2.
Триггерные термины — Словарь
Изучение слов с помощью карточек и другие занятия
Другие учебные занятия
Практика Ответьте на несколько вопросов по каждому слову. Используйте это, чтобы подготовиться к следующему тесту!
Vocabulary JamСоревнуйтесь с другими командами в режиме реального времени, чтобы увидеть, кто правильно ответит на большинство вопросов!
Проверка орфографии Проверьте свою орфографическую хватку.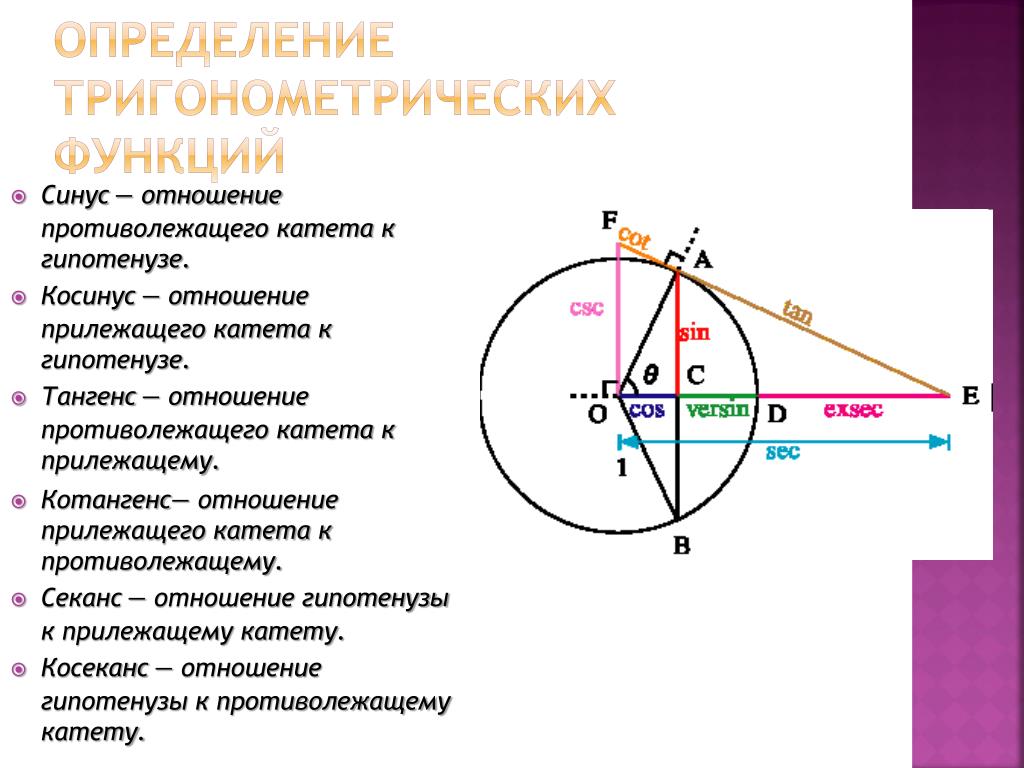 Прочитайте определение, послушайте слово и попробуйте написать его!
Прочитайте определение, послушайте слово и попробуйте написать его!
Инструменты для обучения
Викторина Создавайте и назначайте тесты своим ученикам, чтобы проверить их словарный запас. Назначайте занятия Назначайте учебные задания, включая практику, Vocabulary Jams и Spelling Bees, своим ученикам, и следите за их прогрессом в режиме реального времени.
- арккосинус
обратная функция косинуса
Обратные функции называются арксинусом, арккосинус и арктангенс соответственно.
- арктангенс
обратная функция тангенса
Обратные функции называются арксинусом, арккосинусом и арктангенс соответственно.
- котангенс
отношение прилежащей к противолежащей стороне прямоугольного треугольника
Обратные величины этих функций называются косекансом (csc или cosec), секансом (sec) и котангенс (котангенс) соответственно.

- арксинус
обратная функция синуса
Обратные функции называются арксинус , арккосинус и арктангенс соответственно.
- тригонометрическая функция
функция угла, выраженная как отношение длин сторон прямоугольного треугольника, содержащего угол
Эти соотношения определяются следующим образом тригонометрические функции известного угла A, где a, b и c относятся к длинам сторон на прилагаемом рисунке:
* Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
- тригонометрический
или относящийся к тригонометрии или в соответствии с принципами тригонометрии
Эти соотношения определяются следующим образом тригонометрические функции известного угла A, где a, b и c относятся к длинам сторон на прилагаемом рисунке:
* Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.

- радиан
единица измерения плоского угла, принятая Международной системой единиц; равен углу в центре окружности, опирающейся на дугу, длина которой равна радиусу (приблизительно 57,295 градуса)
Графический процесс y = csc(x) с использованием единичной окружности.
[править] Расширение определений
Графики функций sin(x) и cos(x), где угол x измеряется в радиан . - косеканс
отношение гипотенузы к противолежащему катету прямоугольного треугольника
Обратные величины этих функций называются косеканс (csc или cosec), секанс (sec) и котангенс (cot) соответственно.
- обратная функция
функция, полученная выражением зависимой переменной одной функции как независимой переменной другой; f и g являются обратными функциями, если f(x)=y и g(y)=x
обратные функции называются арксинусом, арккосинусом и арктангенсом соответственно.

- косинус
отношение прилежащего катета к гипотенузе прямоугольного треугольника
* Функция косинуса (cos), определяемая как отношение прилежащего катета к гипотенузе.
- секущая
прямая линия, пересекающая кривую в двух или более точках
Обратные величины этих функций называются косекансом (csc или cosec), секанс (сек) и котангенс (котангенс) соответственно.
- функция
что-то используется для
Эти отношения задаются следующими тригонометрическими функции известного угла A, где a, b и c относятся к длинам сторон на прилагаемом рисунке:
* Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
69″>
синус - касательная
линия, которая касается кривой только в одной точке
Многим легко запомнить, какие стороны прямоугольного треугольника равны синусу, косинусу или тангенс , запомнив слово SOH-CAH-TOA (см. ниже в разделе Мнемоника).
- угол
пространство между двумя пересекающимися линиями или плоскостями
Если один угол треугольника равен 90 градусов и один из других углов известен, тем самым фиксируется третий, потому что три угла любого треугольника в сумме составляют 180 градусов.

- соседний
имеющие общую границу или ребро
* Функция косинуса (cos), определяемая как отношение примыкает катет к гипотенузе.
отношение длины стороны, противолежащей данному углу, к длине гипотенузы прямоугольного треугольника
Эти отношения задаются следующими тригонометрическими функциями известного угла A, где a, b и c относятся к длинам сторон на прилагаемом рисунке:
* функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
Создано 9 июня 2010 г.
косинус — Англо-русский словарь на WordReference.com
- См. также:
- Косгрейв
- кош
- кошерный
- Кошоктон
- Веерная пачка Così
- сознак
- соподписант
- поручитель
- Козимо
- Козимо I
- косинус
- закон косинуса
- косм-
- косметика
- косметическая хирургия
- косметолог
- косметика
- косметика
- косметолог
- косметология
- космический
- Последние поиски:
- Посмотреть все
UK: * UK и, возможно, другие произношенияUK и, возможно, другие произношения/ˈkəʊˌsaɪn/US:USA произношение: respellingUSA произношение: respelling(kō ′ sin)
ⓘ Одна или несколько тем на форуме точно совпадают с искомым термином
на испанском | на французском | на итальянском | английские синонимы | Английский Использование | Конъюгатор | в контексте | картинки Приложения WR: Android и iPhone Слово дня
WordReference Random House Unabridged Dictionary of American English © 2022
co•sine (kō ′ sin), произношение США n.
- Математика[Тригоном.]
- (в прямоугольном треугольнике) отношение стороны, прилежащей к данному углу, к гипотенузе.
- синус дополнения данного угла или дуги. Сокращение: cos
- Математика (действительного или комплексного числа x ) функция cos x , определяемая бесконечным рядом 1 — ( x 2 /2!) + …, где ! обозначает факториал. Сокр.: cos Cf. синус (по умолчанию 3), факториал (по умолчанию 1).
- Неолатинский косинус. См. ко-, синус 1
- 1625–35
Collins Concise English Dictionary © HarperCollins Publishers::
косинус /ˈkəʊˌsaɪn/ n (угла)
- тригонометрическая функция, которая в прямоугольном треугольнике представляет собой отношение длины прилежащего треугольника к его стороне. гипотенуза; синус дополнения
Этимология: 17 век: от новой латыни cosinus; см. со-, синус 1
со-, синус 1
‘ косинус ‘ также встречается в этих статьях (примечание: многие из них не являются синонимами или переводами):
анализ Фурье — Закон Ламберта — закон Малюса — дуга cos — арккосинус — потому что — кош — закон косинусов — покрытый синус — угол направления — направленный косинус — функция — гармонический — гиперболическая функция — внутренний продукт — арккосинус — закон косинусов — сила — скалярное произведение — секанс — синус — касательная — тригонометрическая функция — сложенный косинус — слагаемый синус
Найдите слово «косинус» в Merriam-Webster
Найдите слово «косинус» в словаре.com
На других языках: Испанский | французский | итальянский | португальский | румынский | немецкий | голландский | Шведский | Русский | польский | чешский | Греческий | турецкий | китайский | японский | Корейский | Арабский
Ссылки:
⚙️Настройки |
Сокращения |
Прон.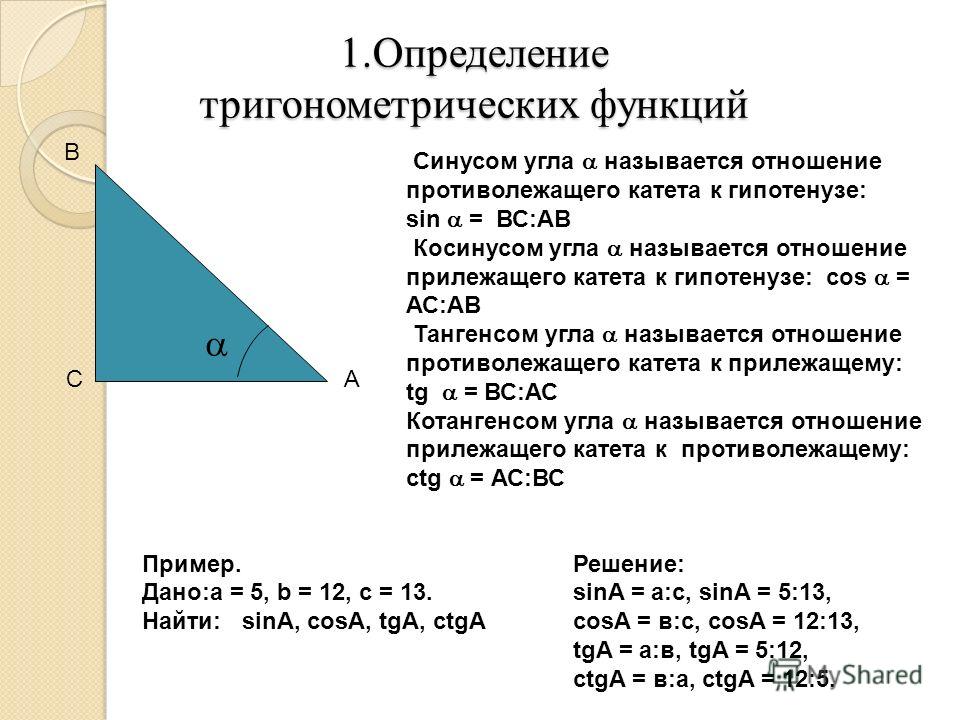


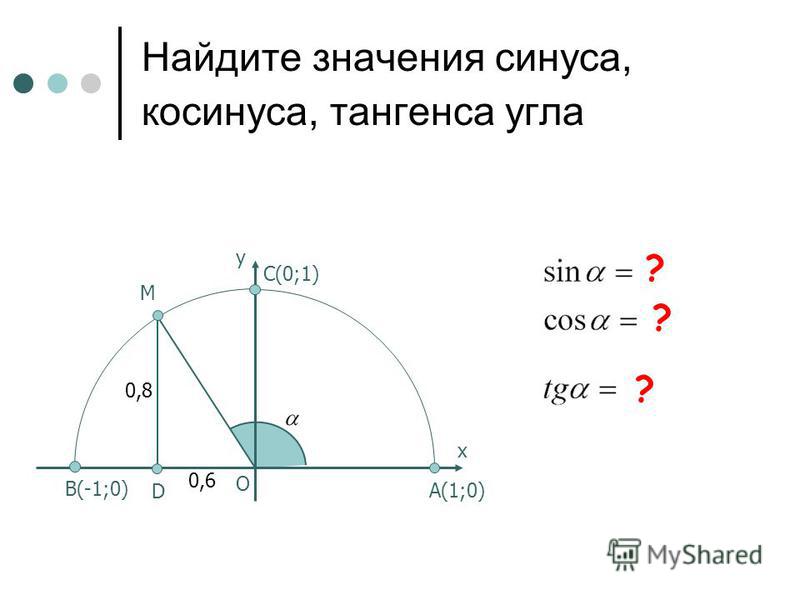 k * arcsin α + πk.
k * arcsin α + πk.


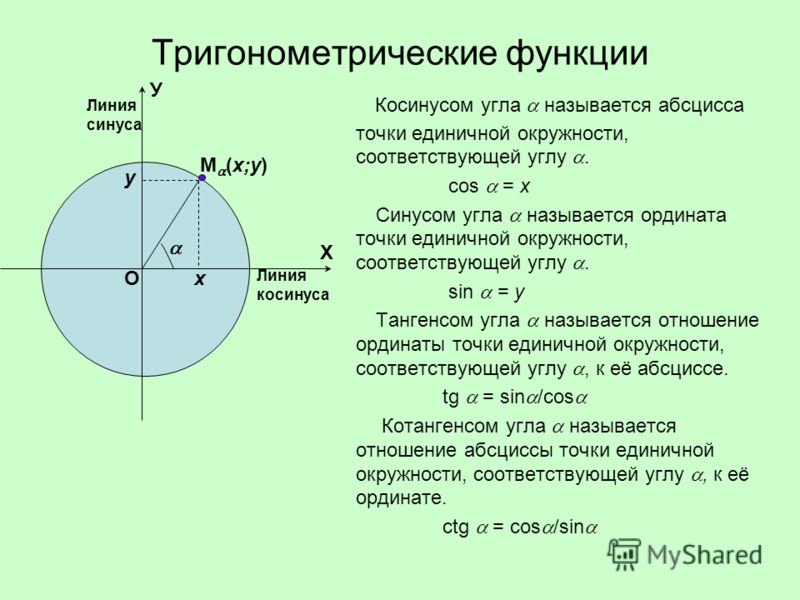 Чтобы расширить эту концепцию для углов, отличных от острых, необходимо включить единичную окружность и подобие треугольников.
Чтобы расширить эту концепцию для углов, отличных от острых, необходимо включить единичную окружность и подобие треугольников.