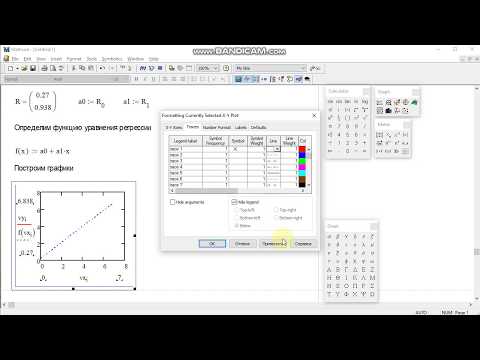
46. Аппроксимация функции,заданной таблично.Метод наименьших квадратов.Аппроксимировать экспериментальные данные гиперболической функцией в mathcad.
Пусть, изучая неизвестную функциональную зависимость между x и y в результате серии экспериментов, получена таблица значений.
Задача состоит в том, чтобы найти приближенную зависимость y=g(x), значение которой при х=хi (i=1,n) мало отличалось от табличных значений yi.
Приближенная зависимость y=g(x), полученная на основании экспериментальных данных называется эмпирической формулой.
Построение эмпирической формулы состоит из двух этапов:
1) Подбор общего вида формулы
2) Определение наилучших значений содержащихся в ней параметров.
Выбор эмпирической зависимости осуществляется из геометрических соображений:
-координаты
экспериментальных точек наносятся на
график – приблизительно угадывается
зависимость путем сравнения полученного
графика с графиками известных функций. Расчет параметров эмпирической
зависимости в большинстве случаев
осуществляется МНК (методом наименьших
квадратов).
Расчет параметров эмпирической
зависимости в большинстве случаев
осуществляется МНК (методом наименьших
квадратов).
В общем случае в МНК для аппроксимации используется многочлен g(x)=a0+a1*x+a2*x2+….amxm. При этом стараются подобрать степень полинома как можно меньше (2-3). Мерой отклонения многочлена g(x) от табличных точек является среднеквадратична разность, равная сумме квадратов разностей между значениями многочлена и табличной функции.
В этом функционале неизвестными являются a0….an. Задачей является поиск minS, т.е. минимума функции S, зависящей от многих переменных. Свободные коэффициенты необходимо найти из условия минимизации функции (равенства первых производных)
Таким образом получается система m линейных уравнений.
Аппроксимация полулогарифмической зависимостью:
Аппроксимация гиперболической зависимости:
Составление
программы для аппроксимации
полулогарифмической зависимости
осуществляется на основе программы
аппроксимации линейной зависимостью.
PRINT «tablichni0e y(«; i; «)»; y(i)
PRINT «raschetnie y(«; i; «)»; yr(i)
NEXT i
PRINT «summa kvadratov otklonenii»; s
END
13.2.1. Линейная регрессия MathCAD 12 руководство
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- CAD / CAM /
- MathCAD 12
- Интерполяция и регрессия
- 13.1. Интерполяция
- 13.1.1. Линейная интерполяция
- 13.1.2. Кубическая сплайн-интерполяция
- 13.1.3. Полиномиальная сплайн-интерполяция
- 13.1.4. Сплайн-экстраполяция
- 13.1.5. Экстраполяция функцией предсказания
- 13.1.6. Многомерная интерполяция
- 13.2. Регрессия
- 13.2.1. Линейная регрессия
- 13.2.2. Полиномиальная регрессия
- 13.2.3. Другие типы регрессии
- 13.2.4. Регрессия общего вида
- 13.3. Ввод/вывод данных
- 13.3.1. Ввод/вывод в текстовые файлы
- 13.3.2. Ввод/вывод в файлы других типов
- 13.
 3.3. Мастер импорта данных и функция READFILE
3.3. Мастер импорта данных и функция READFILE
Самый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi,yi) осуществляется линейной функцией у(х) = =b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 13.14). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и b вычисляются из условия минимизации суммы квадратов ошибок |b+axi-yi|.
ПРИМЕЧАНИЕ 1
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (xi,yi) другими зависимостями у(х). Исключение рассмотрено в листинге 13.9.
ПРИМЕЧАНИЕ 2
Различным расчетным аспектам реализации метода наименьших квадратов, в большинстве случаев сводящимся к решению систем алгебраических линейных уравнений, была посвящена значительная часть главы 8.
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа.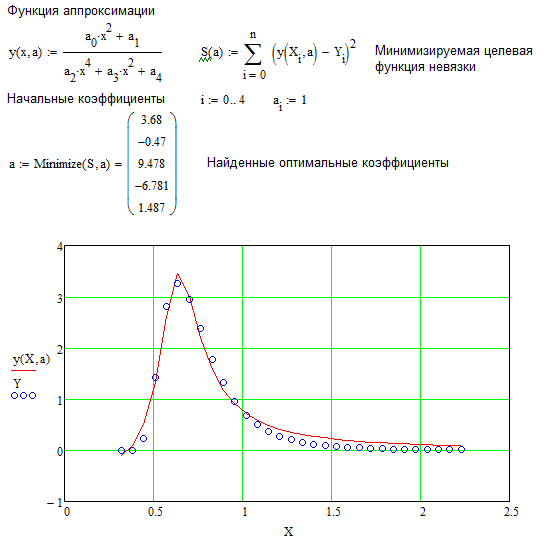 Правила их применения представлены в листингах 13.7 и 13.8. Результат обоих листингов получается одинаковым (рис. 13.14):
Правила их применения представлены в листингах 13.7 и 13.8. Результат обоих листингов получается одинаковым (рис. 13.14):
- line (х, у) — вектор из двух элементов (b,а) коэффициентов линейной регрессии b+ах;
- intercept (х, у) — коэффициент ь линейной регрессии;
- slope (x,y) — коэффициент а линейной регрессии:
Листинг 13.7. Линейная регрессия
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера.
Листинг 13.8. Другая форма записи линейной регрессии
Рис. 13.14. Линейная регрессия (продолжение листинга 13.7 или 13.8)
В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов
а и b (листинг 13.9):
- medfit(x,y) — вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной регрессии b-ах:
- х, у — векторы действительных данных одинакового размера.
Листинг 13.9. Построение линейной регрессии двумя разными методами (продолжение листинга 13.7)
Различие результатов среднеквадратичной и медиан-медианной регрессии иллюстрируется на рис. 13.15.
Рис. 13.15. Линейная регрессия по методу наименьших квадратов и методу медиан (продолжение листингов 13.7 и 13.9)
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9944 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6965 0
Глава 2 Работа с файлами Mathcad 11
12470 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2392 s
0.2392 s
— PTC Community
6 апреля 2002 г. 03:00
Сплайны методом наименьших квадратов
Несколько комментариев,
1. Mathcad действительно может предложить это (сплайны методом наименьших квадратов) в будущем. Я не уверен, но когда-то он был в их списке потенциальных обновлений, и я знаю, что они думают об этом. Я думаю, что есть готовые пакеты, которые предлагают множество оптимизаций, но я устал искать математику и просто написал это для своего приложения. Существуют всевозможные вариации на тему, которые можно адаптировать для конкретных задач. Я, вероятно, должен опубликовать рабочий лист наименьших квадратов в качестве компаньона к рабочему листу сплайна. Например, преобразование Фурье является примером линейного метода наименьших квадратов, подходящего для данных.
2. Что касается извлечения узлов, рабочий лист Mathcad, который показывает основную математику, позволяет вам размещать их где угодно. В dll используются только равноотстоящие узлы, что в большинстве случаев работает достаточно хорошо. Если вы укажете 2 ячейки, у вас будет 3 узла, расположенных в конечных точках данных и середине данных. Первоначально я думал о том, чтобы разрешить неравномерное расстояние между узлами, поэтому предпоследняя строка матрицы коэффициентов содержит значение x левого узла. Самая последняя строка содержит масштабное число, которое используется для обеспечения числовой стабильности математики методом наименьших квадратов. Остальные строки в матрице представляют собой полиномиальные коэффициенты, использующие масштабированные данные. Существует прямая связь между этими числами и числами, которые входят в сплайн mathcad, но я никогда не садился, чтобы понять это.
В dll используются только равноотстоящие узлы, что в большинстве случаев работает достаточно хорошо. Если вы укажете 2 ячейки, у вас будет 3 узла, расположенных в конечных точках данных и середине данных. Первоначально я думал о том, чтобы разрешить неравномерное расстояние между узлами, поэтому предпоследняя строка матрицы коэффициентов содержит значение x левого узла. Самая последняя строка содержит масштабное число, которое используется для обеспечения числовой стабильности математики методом наименьших квадратов. Остальные строки в матрице представляют собой полиномиальные коэффициенты, использующие масштабированные данные. Существует прямая связь между этими числами и числами, которые входят в сплайн mathcad, но я никогда не садился, чтобы понять это.
3. Я выполнил быструю подгонку к данным Spline2xV6 и заметил, что в конце списка данных есть посторонняя точка, которая вызывает ошибку с плавающей запятой в dll. Я, вероятно, должен был включить некоторую элементарную проверку ошибок, но не сделал этого.
4. Еще один комментарий по поводу данных Spline2xV6 заключается в том, что я обычно устанавливаю edge_order на единицу меньше, чем poly_order (параболические конечные условия), потому что подгонка очень плавная. Поэкспериментировав с подгонками, я заметил, что, как правило, данные с равномерными колебаниями по x хорошо подходят, если одна ячейка содержит одно отклонение, а полиномиальный порядок установлен достаточно высоко, чтобы следовать данным внутри ячейки. В этом случае я обычно устанавливаю edge_order=poly_order.
5. Что касается полной автоматизации подгонки, я делаю быстрый подсчет количества точек поворота, используя какую-то процедуру сглаживания, устанавливаю количество ячеек равным количеству точек поворота (у меня почти косинусные данные в моих задачах), а затем подогнать это количество ячеек к кубическому сплайну или, возможно, к параметрам poly_order=4 to 5, deriv_order=2. Он очень хорошо работал в полностью автоматизированных системах для меня.
Роберт
Ярлыки:
- Алгебра_Геометрия
19 ОТВЕТОВ 19
Функции регрессии » MathCadHelp.com » Номер 1 в назначениях MathCad
Mathcad включает ряд функций для выполнения регрессии. Как правило, эти функции создают кривую или поверхность определенного типа, которая в некотором смысле минимизирует ошибку между собой и данными, которые вы предоставляете.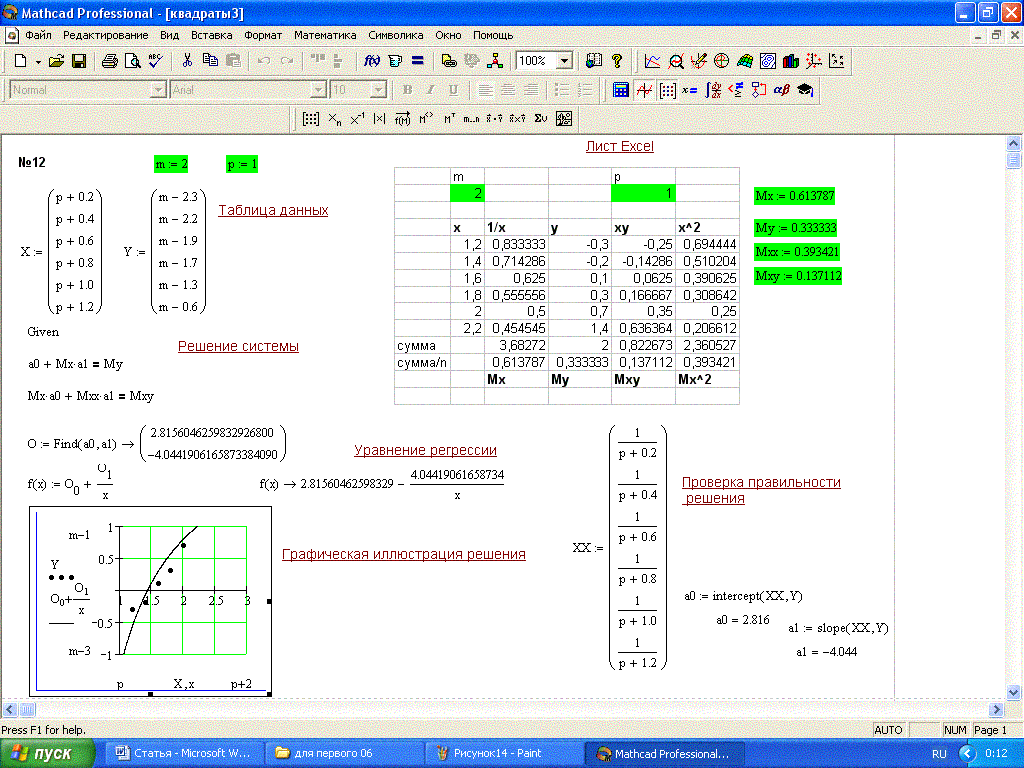 Функции различаются главным образом типом кривой или поверхности, которые они используют для сопоставления данных.
Функции различаются главным образом типом кривой или поверхности, которые они используют для сопоставления данных.
В отличие от функций интерполяции, описанных в предыдущем разделе, эти функции не требуют, чтобы аппроксимированная кривая или поверхность проходила через указанные вами точки данных. Поэтому функции регрессии в этом разделе гораздо менее чувствительны к ложным данным, чем функции интерполяции.
В отличие от функций сглаживания в следующем разделе, конечным результатом регрессии является фактическая функция, которую можно оценить в точках между указанными вами точками. Всякий раз, когда вы используете массивы в любой из функций, описанных в этом разделе, убедитесь, что каждый элемент в массиве содержит значение данных. Поскольку каждый элемент в массиве должен иметь значение, Mathcad присваивает 0 всем элементам, которые вы не назначили явно.
Линейная регрессия
Эти функции возвращают наклон и точку пересечения линии, которая лучше всего соответствует вашим данным в смысле наименьших квадратов.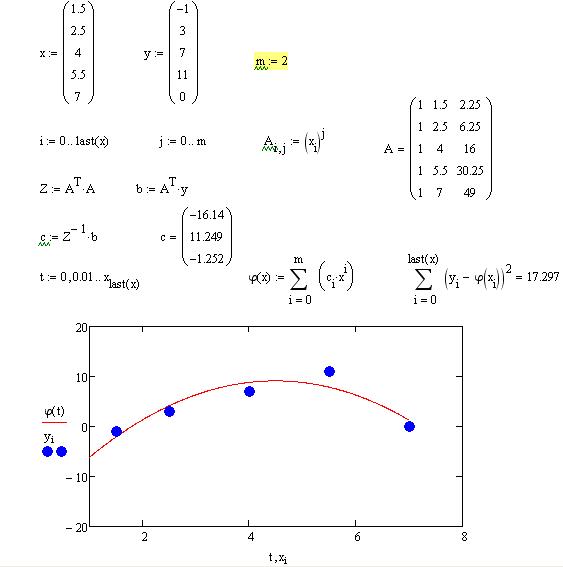 Если вы поместите значения x в вектор vx, а выбранные значения y в vy, эта линия будет иметь вид
Если вы поместите значения x в вектор vx, а выбранные значения y в vy, эта линия будет иметь вид
. Использование наклона и точки пересечения для линейной регрессии.
Полиномиальная регрессия
Эти функции полезны, когда у вас есть набор измеренных значений y, соответствующих значениям x, и вы хотите подобрать полином через эти значения y.
Используйте регрессию, если вы хотите использовать один полином, чтобы соответствовать всем вашим значениям данных. Функция регрессии позволяет подобрать полином любого порядка. Однако на практике редко требуется выходить за пределы n = 4.
Поскольку регрессия пытается учесть все ваши точки данных с помощью одного полинома, она не будет работать, если ваши данные не ведут себя как один полином. Например, предположим, что вы ожидаете, что ваш y i будет линейным от xl до x 10 и будет вести себя как кубическое уравнение от Xli до x20. Если вы используете регрессию с n = 3 (кубическое число), вы можете получить хорошее соответствие для второй половины, но ужасное соответствие для первой половины.
Функция лесса, доступная в Mathcad Professional, устраняет подобные проблемы, выполняя более локализованную регрессию. Вместо создания одного полинома, как это делает регресс, лёсс генерирует другой полином второго порядка, в зависимости от того, где вы находитесь на кривой. Он делает это путем изучения данных в небольшой окрестности интересующей вас точки. Размер этой окрестности контролирует аргумент span. По мере увеличения пролета лёсс становится эквивалентным регрессии с n = 2. Хорошее значение по умолчанию – размах = 0,75. .
На рис. 14-10 показано, как пролет влияет на аппроксимацию, созданную функцией лёсса. Обратите внимание, как меньшее значение диапазона делает подобранную кривую более эффективной для отслеживания колебаний данных. Чем больше значение Span, тем больше флуктуаций в данных не видно, и поэтому достигается более плавная подгонка.
Вектор, требуемый функцией interp для нахождения полинома n-го порядка, который лучше всего соответствует векторам данных vx и vy. vx – вектор элементов m, содержащий координаты x. vy — вектор элементов m, содержащий координаты y, соответствующие m точкам, указанным в vx.
vx – вектор элементов m, содержащий координаты x. vy — вектор элементов m, содержащий координаты y, соответствующие m точкам, указанным в vx.
Возвращает интерполированное значение y, соответствующее x. Вектор vs получается из оценки лесса или регрессии с использованием матриц данных vx и vy.
Влияние различных пролетов на функцию лёсса. Обратите внимание, что, поскольку
Многомерная полиномиальная регрессия
Функции лесса и регрессии, обсуждавшиеся в предыдущем разделе, также полезны, когда у вас есть набор измеренных значений z, соответствующих значениям x и y, и вы хотите подобрать полиномиальную поверхность через эти z ценности.
Свойства этих функций описаны в предыдущем разделе. При использовании этих функций для подбора значений z, соответствующих двум независимым переменным x и y, значения аргументов должны быть обобщены. А именно:
• Аргумент vx, который был вектором из m элементов значений x, становится массивом из m строк и 2 столбцов, Mxy.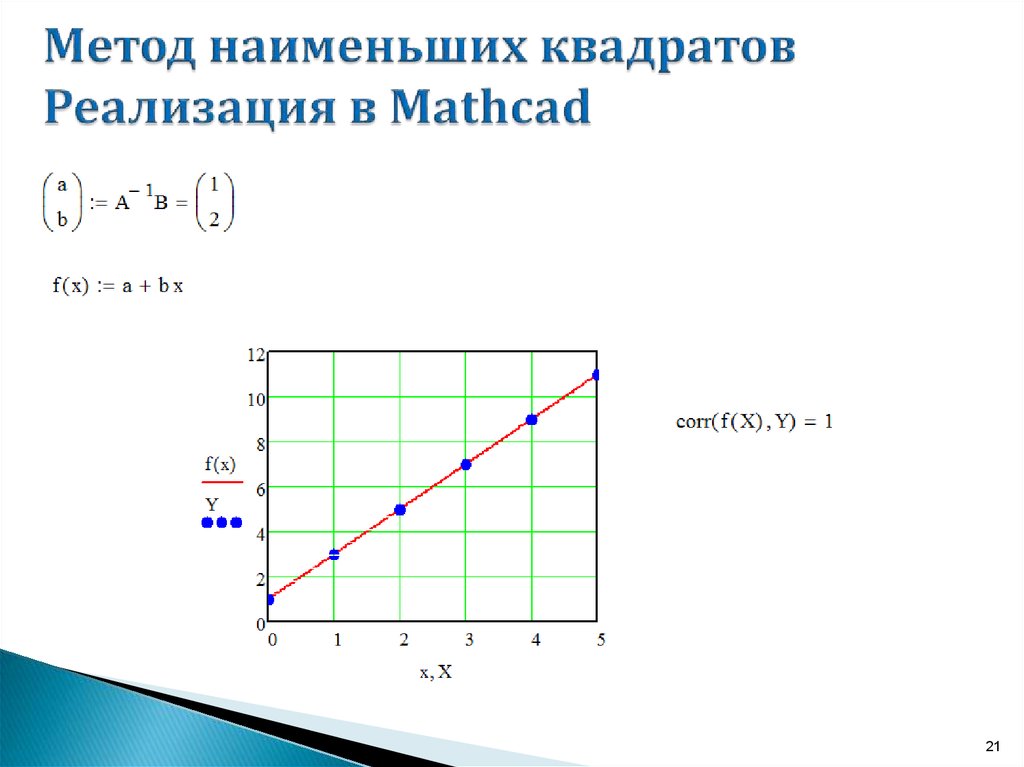 Каждая строка Mxy содержит x в первом столбце и соответствующее значение y во втором столбце.
Каждая строка Mxy содержит x в первом столбце и соответствующее значение y во втором столбце.
• Аргумент x для функции interp становится двухэлементным вектором v, элементами которого являются значения x и y, при которых вы хотите оценить полиномиальную поверхность, представляющую наилучшее соответствие точкам данных в Mxy и vz.
Вы можете добавлять независимые переменные, просто добавляя столбцы в массив Mxy. Затем вы должны добавить соответствующее количество строк к вектору v, который вы передаете функции interp. Функция регрессии может иметь любое количество независимых переменных. Однако регрессия будет выполняться медленнее и потребует больше памяти, если количество независимых переменных и степень больше четырех. Функция лёсса ограничена не более чем четырьмя независимыми переменными.
Имейте в виду, что для регрессии количество значений данных m должно удовлетворять
n, где
n – количество независимых переменных (отсюда количество столбцов в Mxy), k – степень требуемого многочлена, а m – количество значений данных (отсюда количество строк в vz). Например, если у вас есть пять независимых переменных и полином четвертой степени, вам потребуется более 126 наблюдений.
Например, если у вас есть пять независимых переменных и полином четвертой степени, вам потребуется более 126 наблюдений.
Обобщенная регрессия
К сожалению, не все наборы данных можно смоделировать с помощью линий или полиномов. Бывают случаи, когда вам нужно смоделировать данные с помощью линейной комбинации произвольных функций, ни одна из которых не представляет члены полинома. Например, в ряду Фурье вы пытаетесь аппроксимировать данные, используя линейную комбинацию сложных экспонент. Или вы можете полагать, что ваши данные можно смоделировать с помощью взвешенной комбинации полиномов Лежандра, но вы просто не знаете, какие веса присвоить.
Функция linfit предназначена для решения подобных проблем. Если вы считаете, что ваши данные могут быть смоделированы линейной комбинацией произвольных функций:
Все, что вы можете сделать с помощью linfit, вы также можете сделать, хотя и менее удобно, с помощью genfit. Разница между этими двумя функциями — это разница между решением системы линейных уравнений и решением системы нелинейных уравнений. Первое легко сделать с помощью методов линейной алгебры. Последнее гораздо сложнее и, как правило, должно решаться путем итерации. Это объясняет, почему genfit в качестве аргумента нужен вектор догадок, а linfit — нет.
Первое легко сделать с помощью методов линейной алгебры. Последнее гораздо сложнее и, как правило, должно решаться путем итерации. Это объясняет, почему genfit в качестве аргумента нужен вектор догадок, а linfit — нет.
На рис. 14-12 показан пример, в котором genfit используется для поиска показателя степени, который лучше всего соответствует набору данных.
Вектор, содержащий параметры, которые образуют функцию от параметров x и n uo, u1′ … , наилучшим образом аппроксимирующих данные в vx и vy. F – это функция, которая возвращает вектор из n + 1 элементов, содержащий f и его частные производные по n параметрам. vg – это n-элементный вектор предположительных значений для n параметров.
Использование linfit для нахождения коэффициентов для линейной комбинации
Использование genfit для нахождения параметров функции таким образом, чтобы она
наилучшим образом соответствовала данным.
Функции сглаживания
Значения y, более сглаженные, чем исходный набор.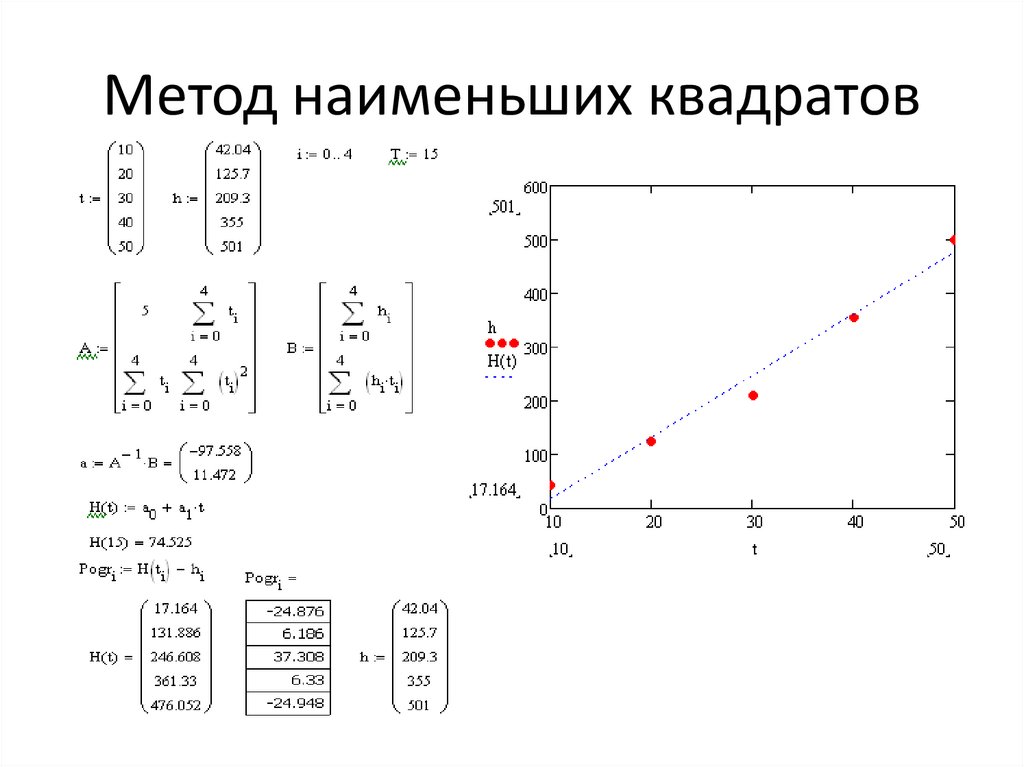 В отличие от функций регрессии и интерполяции, которые обсуждались ранее, сглаживание приводит к новому набору значений y, а не к функции, которую можно вычислить между указанными вами точками данных. Таким образом, если вас интересуют значения y между указанными вами значениями y, вам следует использовать функцию регрессии или интерполяции.
В отличие от функций регрессии и интерполяции, которые обсуждались ранее, сглаживание приводит к новому набору значений y, а не к функции, которую можно вычислить между указанными вами точками данных. Таким образом, если вас интересуют значения y между указанными вами значениями y, вам следует использовать функцию регрессии или интерполяции.
Всякий раз, когда вы используете векторы в любой из функций, описанных в этом разделе, убедитесь, что каждый элемент вектора содержит значение данных. Поскольку каждый элемент вектора должен иметь значение, Mathcad присваивает 0 всем элементам, которые вы не назначили явно. Функция medsmooth является наиболее надежной из трех, поскольку на нее меньше всего влияют ложные точки данных. Эта функция использует бегущее медианное сглаживание, вычисляет невязки, сглаживает невязки таким же образом и складывает вместе эти два сглаженных вектора. Подробности следующие:
• Оценка medsmooth(vy, n) начинается с бегущей медианы входного вектора vy. Мы назовем это «вы». i-й элемент определяется как:
Мы назовем это «вы». i-й элемент определяется как:
• Затем он оценивает остатки: vr = vy – vy’ .
• Вектор остатка vr сглаживается с использованием той же процедуры, которая описана в шаге 1. При этом создается сглаженный вектор остатка vr’ .
• Функция medsmooth возвращает сумму этих двух сглаженных векторов: medsmooth(vy, n) = vy’ + vr
Обратите внимание, что medsmooth оставит первую и последнюю (n – 1)/2 точки без изменений. На практике длина окна сглаживания n должна быть небольшой по сравнению с длиной набора данных.
Функция ksmooth в Mathcad Professional использует ядро Гаусса для вычисления локальных взвешенных средних значений входного вектора vy. Это сглаживание наиболее полезно, когда полоса данных имеет относительно постоянную ширину. Если ваши данные разбросаны по полосе, ширина которой значительно колеблется, вам следует использовать адаптивное сглаживание, такое как supsmooth, также доступное в Mathcad Professional.
и b — пропускная способность, которую вы указываете для функции ksmooth.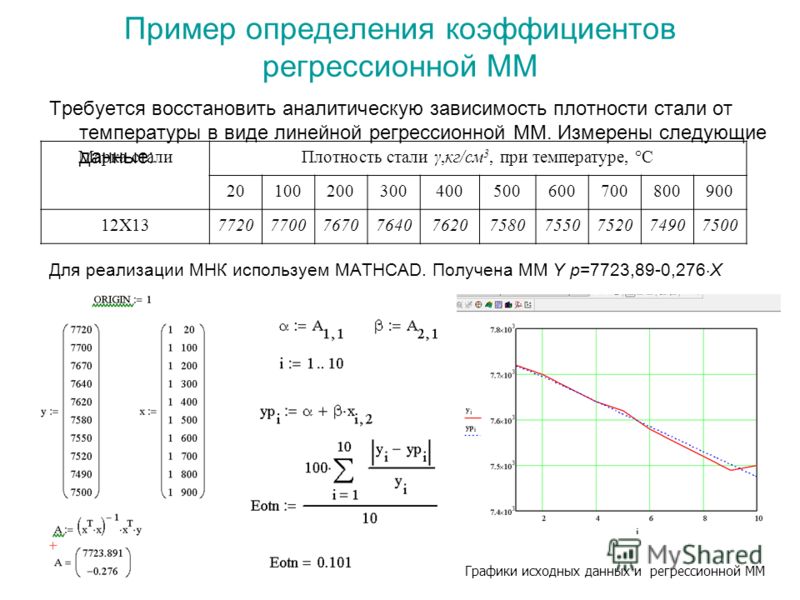

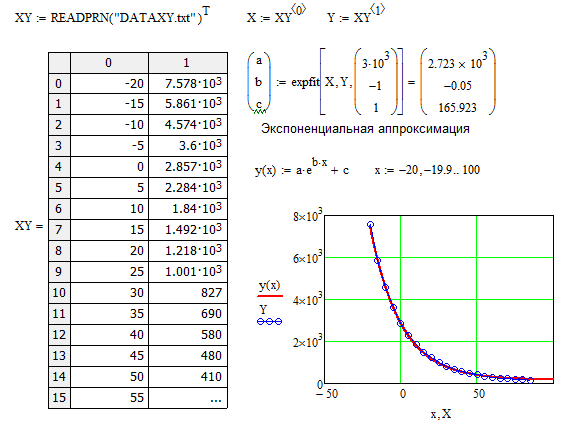 3.3. Мастер импорта данных и функция READFILE
3.3. Мастер импорта данных и функция READFILE