НОУ ИНТУИТ | Лекция | Задачи линейной алгебры
< Лекция 12 || Лекция 5: 123456789
Аннотация: Познакомимся с инструментами Octave, предназначенными для работы с векторами и матрицами, а также с возможностями, которые предоставляет пакет при непосредственном решении задач линейной алгебры.
5.1 Ввод и формирование векторов и матриц
Векторы и матрицы в Octave задаются путём ввода их элементов. Элементы вектора-строки отделяют пробелами или запятыми, а всю конструкцию заключают в квадратные скобки:
>>> a =[2 -3 5 6 -1 0 7 -9] a = 2 -3 5 6 -1 0 7 -9 >>> b =[ -1,0,1] b = -1 0 1
Вектор-столбец можно задать, если элементы отделять друг от друга точкой с запятой:
>>> c=[-pi; -pi / 2; 0; pi / 2; pi ] c = -3.14159 -1.57080 0.00000 1.57080 3.14159
Обратиться к элементу вектора можно указав имя вектора, а в круглых скобках — номер элемента, под которым он хранится в этом векторе:
>>> a( 1 ) ans = 2 >>> b( 3 ) ans = 1 >>> c( 5 ) ans = 3.1416
1416
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
>>> Matr=[0 1 2 3; 4 5 6 7 ] Matr = 0 1 2 3 4 5 6 7
Обратиться к элементу матрицы можно указав после имени матрицы, в круглых скобках, через запятую, номер строки и номер столбца, на пересечении которых элемент расположен:
>>> Matr ( 2, 3 ) ans = 6 >>> Matr ( 1, 1 ) ans = 0 >>> Matr ( 1, 1 )=pi; Matr ( 2, 4 )= _pi; >>> Matr Matr = 3.1416 1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 -3.1416
Матрицы и векторы можно формировать, составляя их из ранее заданных матриц и векторов:
>>> a=[-3 0 2 ]; b=[3 2 -1]; c =[5 -2 0 ]; >>> M=[a b c ] % Горизонтальная конкатенация векторов–строк M = -3 0 2 3 2 -1 5 -2 0 % результат — вектор–строка >>> N=[a; b; c ] % Вертикальная конкатенация векторов–строк, % результат — матрица N = -3 0 2 3 2 -1 5 -2 0 >>> Matrica =[N N N] % Горизонтальная конкатенация матриц Matrica = -3 0 2 -3 0 2 -3 0 2 3 2 -1 3 2 -1 3 2 -1 5 -2 0 5 -2 0 5 -2 0 >>> Tablica =[M;M;M] % Вертикальная конкатенация матриц Tablica = -3 0 2 3 2 -1 5 -2 0 -3 0 2 3 2 -1 5 -2 0 -3 0 2 3 2 -1 5 -2 0
intuit.ru/2010/edi»>Важную роль при работе с матрицами играет знак двоеточия «:». Примеры с подробными комментариями приведены в листинге 5.1.>>> Tabl =[ -1.2 3.4 0.8; 0.9 -0.1 1.1; 7.6 -4.5 5.6; 9.0 1.3 -8.5] Tabl = -1.20000 3.40000 0.80000 0.90000 -0.10000 1.10000 7.60000 -4.50000 5.60000 9.00000 1.30000 -8.50000 >>> Tabl( :, 3 ) % Выделить из матрицы 3-й столбец ans = 0.80000 1.10000 5.60000 -8.50000 >>> Tabl( 1, : ) % Выделить из матрицы 1-ю строку ans = -1.20000 3.40000 0.80000 >>> Matr=Tabl( 2 : 3, 1 : 2 ) % Выделить из матрицы подматрицу Matr = 0.90000 -0.10000 7.60000 -4.50000 % Вставить подматрицу в правый нижний угол исходной матрицы >>> Tabl( 3 : 4, 2 : 3 )=Matr Tabl = -1.20000 3.40000 0.80000 0.90000 -0.10000 1.10000 7.60000 0.90000 -0.10000 9.00000 7.60000 -4.50000 >>> Tabl( :, 2 ) = [ ] % Удалить из матрицы 2-й столбец Tabl = -1.20000 0.80000 0.90000 1.10000 7.60000 -0.10000 9.00000 -4.50000 >>> Tabl( 2, : ) = [ ] % Удалить из матрицы 2-ю строку Tabl = -1.20000 0.80000 7.60000 -0.10000 9.00000 -4.50000 >>> Matr % Представить матрицу в виде вектора–столбца Matr = 0.90000 -0.10000 7.60000 -4.50000 >>> Vector=Matr ( : ) Vector = 0.90000 7.60000 -0.10000 -4.50000 >>> V=Vector( 1 : 3 ) % Выделить из вектора элементы со 1-го по 3-й V = 0.90000 7.60000 -0.10000 >>> V( 2 ) = [ ] % Удалить из массива 2-й элемент V = 0.90000 -0.10000
Листинг 5.1. Пример использования знака двоеточия «:»
Дальше >>
< Лекция 12 || Лекция 5: 123456789
свойства векторов и линейные действия над векторами (сложение, вычитание, умножение)
О чем статья
Скалярные и векторные величины
Векторные величины – величины, для характеристики которых указывается как числовое значение, так и направление в пространстве.
Например, сила, скорость, ускорение, напряженность поля (магнитного, электромагнитного) и т. п.
Скалярные величины – это величины, для характеристики которых достаточно только числовое значение в соответствующих единицах измерения. Например, масса, температура, длина, площадь, объём, количества тепла и т. д.
Рис. 1
Вектор – это геометрическое изображение векторной величины в заданном масштабе.
На рис. 1 А – начальная точка вектора, В – конец вектора. Вектор обычно обозначается стрелочками, которые ставят вверху букв, но многие люди для удобства ставят обычные чёрточки. Иногда вектор обозначают одной буквой: . Расстояние от точки к точке называют длиной или модулем вектора, а обозначается так: или
Если начало и конец вектора совпадают, тогда такой вектор называется нулевым и обозначается Направление нулевого вектора может быть произвольным.
Два ненулевых вектора, которые лежат на параллельных прямых или на одной прямой называются коллинеарными, а обозначаются
Нулевой вектор считается коллинеарным производного вектора.
Векторы, которые параллельны одной и той же плоскости, или те, которые лежат в одной плоскости, называются компланарными.
Равными называются векторы, если они удовлетворяют такие условия:
1) они коллинеарны;
2) их модули равны;
3) они направлены в одну сторону, то есть:
= = ,
Например, на рис. 2, где ABCD – параллелограмм,
Рис. 2
где векторы = , = .
Если = , , тогда векторы и – противоположные.
Вектор противоположный вектору обозначают . Вектор противоположен вектору и записывается =
Из определения равенства векторов следует, что вектор можно переносить в пространстве параллельно самому себе, такие векторы называются свободными.
Вектор, модуль которого равен единице называется единичным, или ортом, и обозначается :
= ,
Линейные операции над векторами: сложение векторов, вычитание и умножение
Линейные операции над векторами или ещё говорят действия над векторами – это сложение векторов, вычитание и умножение вектора на число (скаляр).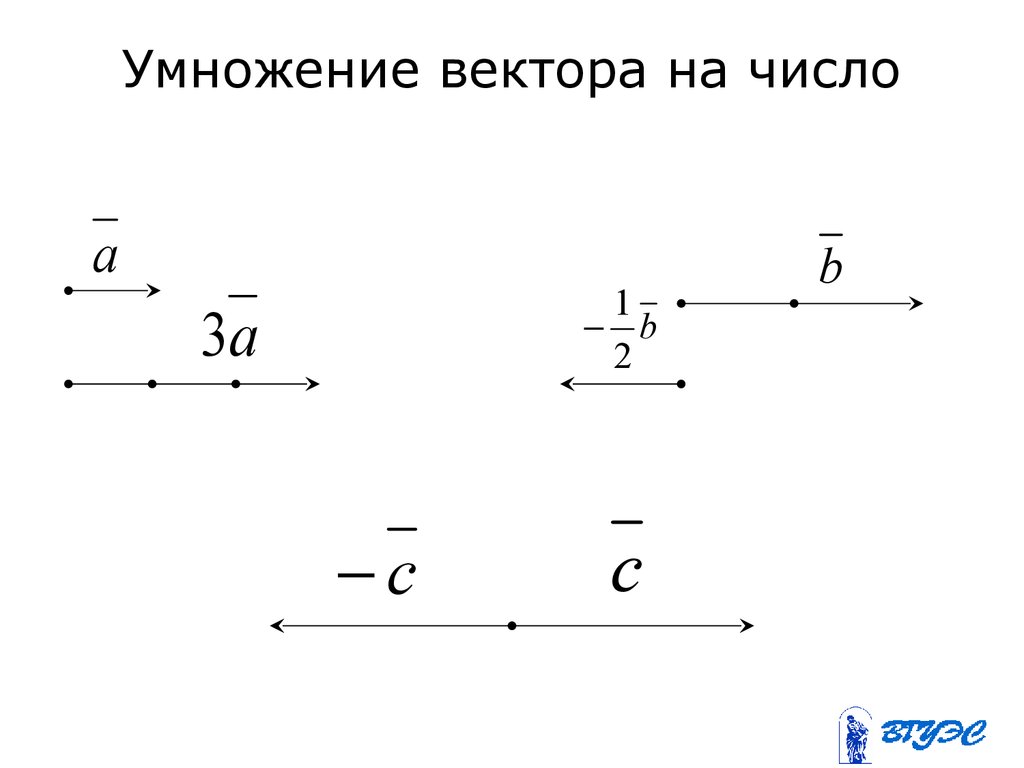
Сложение векторов
Пусть заданы два вектора и . Отложим с некоторой точки вектор = , а тогда из точки отложим вектор = и рассмотрим вектор = .
Рис. 3
Сумма двух векторов и называется вектор = , начало которого находится в начале вектора , а окончание в конце вектора при условии, что начало находится в конце .
Согласно рис. 3 вектор = и замыкает ломаную MNP, направление вектора берётся в конец последнего слагаемого .
По принципу замыкания находится сумма большего числа слагаемых.
Рис. 4
Вычитание векторов
Рис. 5
Посмотрите на рис. 5. Мы поместили начало векторов и в одну точку , и построили замыкающий вектор .
Разница двух векторов – это , которые выходят с одной точки, называются замыкающим вектором (обозначается ), направление которого выбирается в сторону уменьшаемого.
Умножение вектора на число
Произведением ненулевого вектора на число называется вектор и обозначается (), коллинеарный вектору , модуль которого .
Направление вектора совпадает с направлением вектора , если , и противоположному направлению вектора , если .
При , или считается, что – нулевой вектор.
Рис. 6
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Свойства векторов
Мы рассмотрели линейные операции над векторами и теперь можно рассмотреть свойства векторов, без которых невозможно решить многие задачи.
1).
Рис. 7
Свойство 1 называется переставным или коммутативным, понятно с рис. 7, что разрешается прибавлять векторы по правилу параллелограмма.
2). – ассоциативное или соединительное свойство (см. рис. 8).
Рис. 8
3). .
4). .
5). x .
6). = .
7). x .
8). .
Свойства 3 – 8 вы уже сможете проверить самостоятельно.
Примеры
Пример 1
За данными вектора и построить векторы:
а) ,
б) .
Решение покажем на рисунке:
Первый рисунок решения a:
Второй рисунок решения б:
Пример 2
В треугольнике проведена медиана (см. на рис. ниже). Выразить вектор через векторы и .
Решение:
Согласно определению о разнице векторов – , тогда = = – .
Согласно определению суммы векторов с у нас получается:
x = x .
Сложение векторов, вычитание и скалярное умножение
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Пример:
youtube.com/embed/jvdu7J3iLCE»>Графические методы – Колледж физики
Резюме
- Понимание правил сложения, вычитания и умножения векторов.
- Применять графические методы сложения и вычитания векторов для определения перемещения движущихся объектов.
На рис.
2 показано такое графическое представление вектора
ВЕКТОРОВ В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором [latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]{F},[/латекс], а направление переменной будет задано углом [латекс]{\тета}.[/латекс ]
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 o к северу от востока.
Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а заголовок (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2.
(a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, к началу вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, составляет 29,1 0 .Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5. Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 блоков на север). Поместите конец второго вектора в начало первого вектора .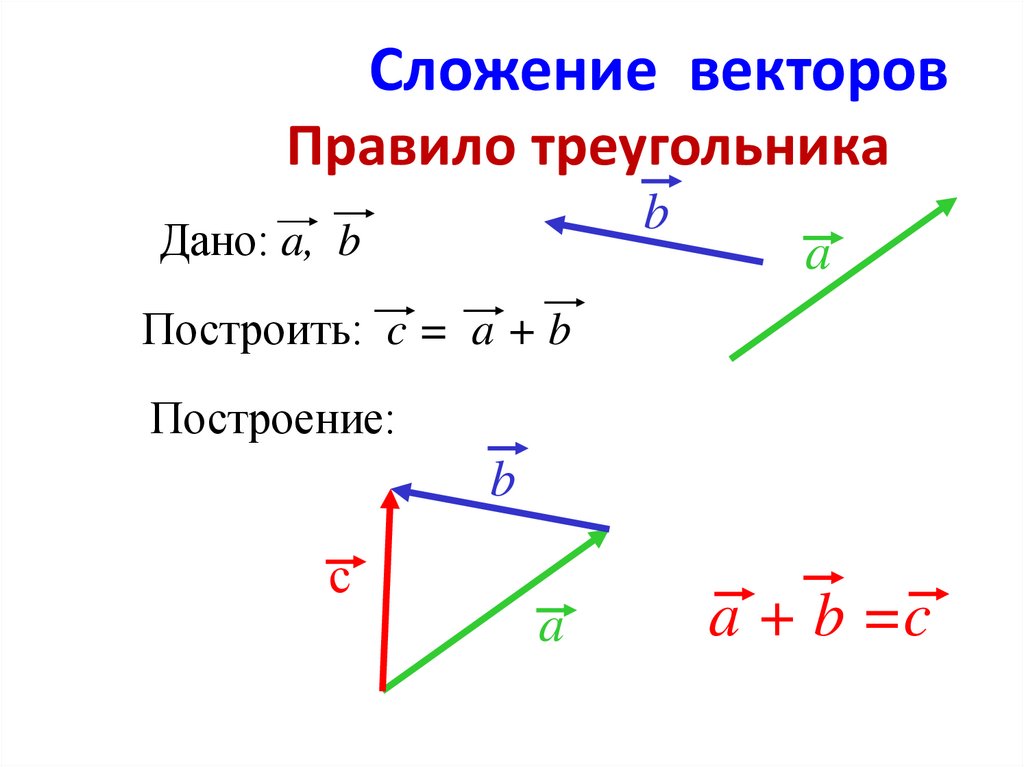
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7.Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.
)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9o}[/latex] к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически стрелкой, обозначив первый [latex]\textbf{A},[/latex], второй [latex]\textbf{B},[/latex] и третий [latex]\text{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого [latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 8.
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9.(3) Нарисуйте результирующий вектор, [latex]\textbf{R}.[/latex]
Рисунок 10.(4) Используйте линейку для измерения величины [latex]\ textbf{R},[/latex] и транспортир для измерения направления [latex]\textbf{R}.[/latex] Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9o}[/latex] к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис.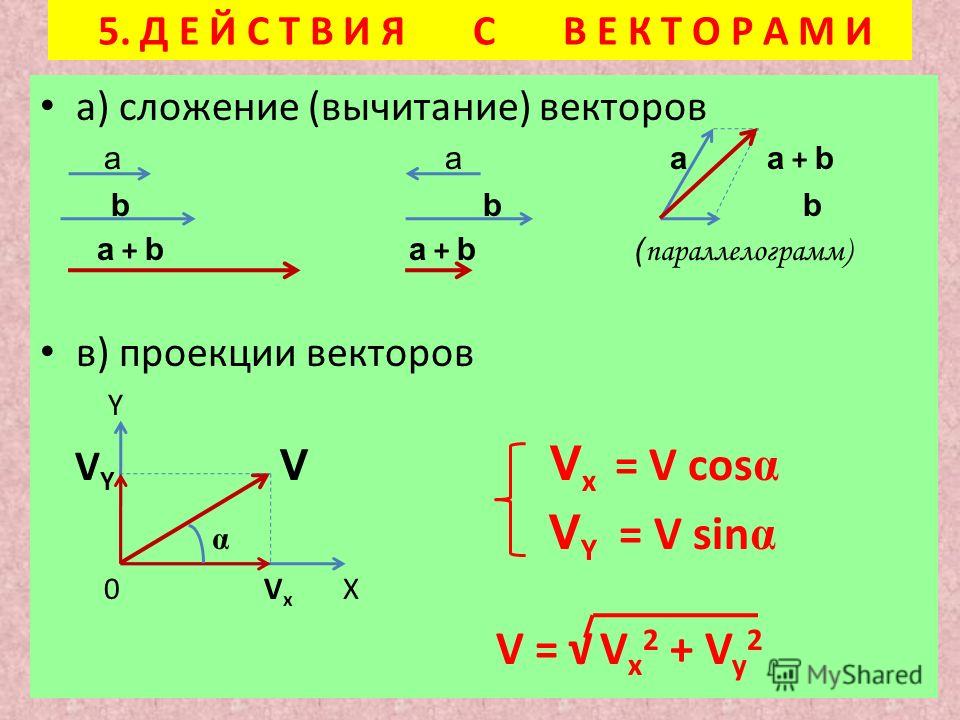
12, и все равно получим то же решение.
Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[latex]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это справедливо и для сложения обычных чисел— вы получите тот же результат, если вы добавите, например, [латекс]{2+3}[/латекс] или [латекс]{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс] из [латекс]\текстбф{А},[/латекс], записанного [латекс]{\текстбф{А}-\текстбф{В }}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0037 отрицательный вектора [latex]\textbf{B}[/latex] определяется как [latex]{-\textbf{B}};[/latex], то есть графически отрицательный элемент любого вектора имеет той же величины, но в противоположном направлении , как показано на рисунке 13.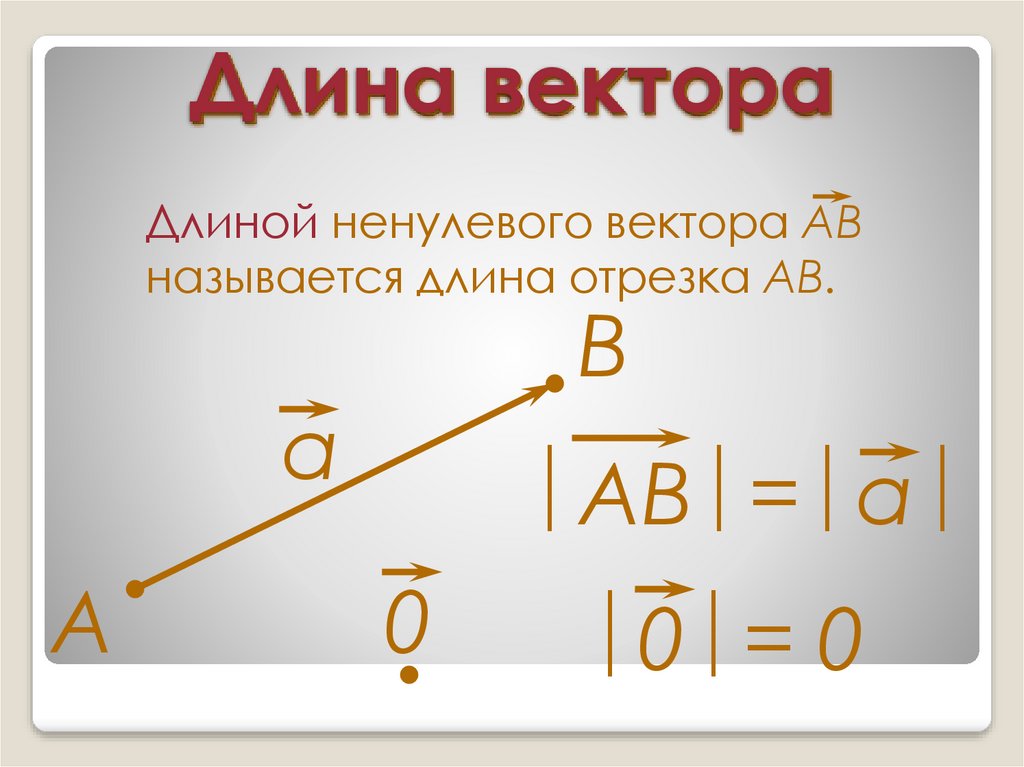
Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]{-\textbf{B}},[/latex ] но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора [latex]\textbf{B}[/latex] из вектора [latex]\textbf{A}[/latex] просто определяется как сложение [latex]{-\ textbf{B}}[/latex] в [latex]\textbf{A}.[/latex] Обратите внимание, что вычитание векторов — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
[латекс]{\textbf{A}-\textbf{B}=\textbf{A}+(-\textbf{B})}.[/latex]
Это аналогично вычитанию скаляров (где, например, [латекс]{5-2=5+(-2)}[/латекс] ).
o}[/латекс] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап пути с помощью вектора [latex]\textbf{A},[/latex] и второй этап пути с помощью вектора [latex] \textbf{B}.[/latex] Док находится в месте [latex]{\textbf{A}\:+\:\textbf{B}}.[/latex] Если женщина по ошибке путешествует в напротив 9o}[/latex] к югу от востока. Мы представляем это как [латекс]{-\textbf{B}},[/латекс], как показано ниже. Вектор [latex]{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [latex]{\textbf{A}+(-\textbf{B})},[/latex] или [latex]{\textbf{A}-\textbf{B}} .[/latex]
Рисунок 15. Мы выполним сложение векторов, чтобы сравнить местоположение дока, [latex]{\textbf{A}+\textbf{B}},[/latex] с местоположением в которую по ошибке прибывает женщина, [латекс]{\textbf{A}+(-\textbf{B})}.
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex]\textbf{A}[/latex] и [latex]{-\textbf{B}}.[ /latex]
(2) Разместите векторы «голова к хвосту».
(3) Нарисуйте результирующий вектор [latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.к югу от востока. 9o}[/latex] к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли [латекс]{3 \times 27,5\text{ м}},[/latex] или 82,5 м, в направлении [латекс]{66.
o}[/латекс] к северу от востока. Это пример умножения вектора на положительное число 9.0009 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение на него вектора изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор [latex]\textbf{A}[/latex] умножается на скаляр [latex]{c},[/latex]
- модуль вектора становится абсолютным значением [latex]{cA},[/latex]
- , если [latex]{c}[/latex] положительный, направление вектора не меняется,
- , если [latex]{c}[/latex] имеет отрицательное значение, направление меняется на противоположное.
В нашем случае [латекс]{с=3}[/латекс] и [латекс]{\текстбф{А}=27,5\текст{м}}.[/латекс] Во многих случаях векторы умножаются на скаляры. Обратите внимание, что деление является обратным умножению.
Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например, x – и y -компонентов, или компонентов север-юг и восток-запад. 9o}[/latex] к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора.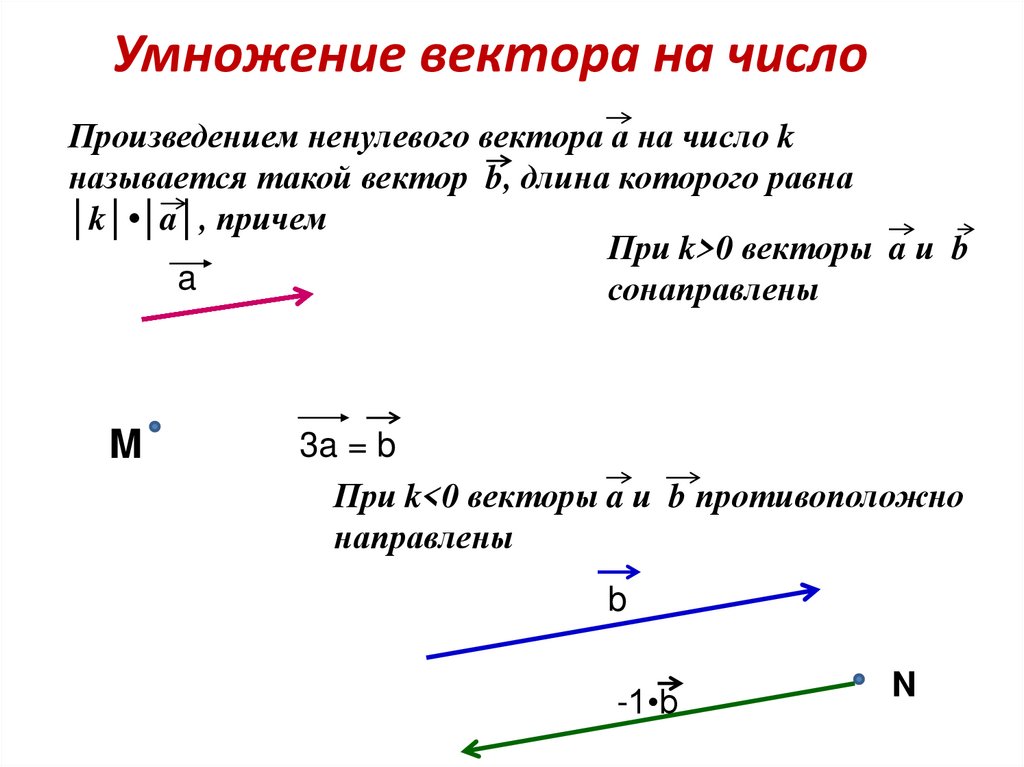
В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0009 заставляет в Главе 4 Динамика: Законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод сложения векторов [latex]\textbf{A}[/latex] и [latex]\textbf{B}[/latex] включает рисование векторов на графике и их сложение с использованием прямого метод хвоста. Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
- графический метод вычитания вектора [latex]\textbf{B}[/latex] из [latex]\textbf{A}[/latex] включает добавление противоположного вектора [latex]\textbf{B},[/latex] ] который определяется как [latex]{-\textbf{B}}.[/latex] В этом случае [latex]{\textbf{A}-\textbf{B}=\textbf{A}+(-\ textbf{B})=\textbf{R}}.[/latex] Затем обычным образом применяется метод сложения головы к хвосту для получения результирующего вектора [latex]\textbf{R}.[/ латекс]
- Сложение векторов коммутативно , такое что [латекс]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике и последующее размещение хвоста каждого последующего вектора в начале предыдущего вектора.
Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.