Тригонометрия начало 10 класс: Тригонометрия 10 класс. Первые уроки.

Первые уроки тригонометрии 10 класс (30 слайдов)

Слайд 1

Слайд 2

Что означает название предмета «Алгебра и начала анализа?» Алгебра – один из разделов математики, изучающий свойства величин, выраженных буквами, независимо от их конкретного числового значения. Математический анализ – это совокупность частей математики, в которых главным объектом исследования является функция, а оперативная часть опирается на выполнение операций дифференцирования и интегрирования. Основоположники математического анализа:

Слайд 3

Слайд 4

Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Слайд 5

Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Фалес
Жозеф Луи Лагранж

Слайд 6

Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека. С ее помощью можно определить расстояние до недоступных предметов и существенно упрощать процесс геодезической съемки местности для составления географических карт. Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функция сформировались в процессе долгого исторического развития. Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э. в работах великих математиков– Евклида, Архимеда, Апполония Пергского. Древнегреческие астрономы успешно решали вопросы из тригонометрии, связанные с астрономией.

Слайд 7

Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела, при измерении расстояний до недалёких звёзд в астрономии, между ориентирами в географии, при контроле системы навигации, в теории музыки, акустике, оптике, электронике, теории вероятностей, статистике, биологии, медицине (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтике, химии, сейсмологии, метеорологии, океанологии, картографии, архитектуре, экономике, электронной технике, машиностроении, компьютерной графике.

Слайд 8

Вспомним:
а
в
с
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе. Косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение противолежащего катета к прилежащему.

Слайд 9

В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось.

Слайд 10

Слайд 11

Слайд 12

Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
1
Р

Слайд 13

Слайд 14

х
у
1
1

Слайд 15

Синус угла определяется как ордината точки Косинус — абсцисса точки Тангенс – отношение ординаты к абсциссе точки Котангенс – отношение абсциссы к ординате точки

Слайд 16

Понятие синуса встречается уже в III в. до н. э. и имел название джива (тетева лука) , в IX в. заменено на арабское слово джайб (выпуклость) , XII в. заменено на латинское синус (изгиб, кривизна) . Косинус – это дополнительный синус. Тангенс переводится с латинского как «касающийся»

Слайд 17

1
1
-1
-1

Слайд 18

Запомним !
1
1

Слайд 19

(1; 0)
(0; 1)
(-1; 0)
(0;-1)

Слайд 20

Проверим:
—
0
1
0
-1
0
1
0
-1
0
1
0
0
0
0
0
—
—
—
—

Слайд 21

Знаки синуса, косинуса, тангенса, котангенса в координатных четвертях
+
+
+
+
+
+
+
+
—
—
—
—
—
—
—
—

Слайд 22

Четность, нечетность синуса, косинуса, тангенса, котангенса
Нечетные функции
Четная функция

Слайд 23

Периодичность тригонометрических функций
При изменении угла на целое число оборотов значения синуса, косинуса, тангенса, котангенса не изменяются

Слайд 24

х
у

Слайд 25

Слайд 26

Слайд 27

Радианная мера угла
R
С
центральный угол R – радиус С – длина дуги
Если R = C, то центральный угол равен одному радиану
Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности

Слайд 28

Слайд 29

Угол в градусах
Угол в радианах
Градусная и радианная меры углов

Слайд 30

Исследовательский проект по математике тригонометрия 10 класс

Муниципальное казенное общеобразовательное учреждение  Бондаревская средняя общеобразовательная школа

Кантемировского муниципального района Воронежской области

Исследовательская работа по математике на тему: «применение тригонометрии для решения задач планиметрии»

Выполнила

Ученица 10 класса

Журавлёва Алеся

Руководитель:

Учитель математики

Товменко Светлана Петровна

2020-2021гг.

Содержание………………………………………………………2

Введение…………………………………………………………………3

§1. Понятие тригонометрии и  тригонометрических функций………………………………………4

§1.1. Исторические сведения………………………………………….4

§2. Решение задач с использованием тригонометрических функций…………………………………………………5

§2.1. Решение практических задач……………….…6

§3.Заключение……………………………………………………………7

ВВЕДЕНИЕ

• Тригонометрия – достаточно серьезный раздел математики, и к его изучению надо подходить со всей ответственностью.
• Тригонометрические функции играют важную роль в математике и ее приложениях. Они удобны для описания связи между сторонами и углами треугольников. Использование тригонометрии способствует утверждению взгляда на понятие функции, как на важнейшее понятие математики, связывая тем самым курс алгебры и геометрии.
• Велико значение тригонометрических функций в формировании диалектического мировоззрения: они являются моделью многих процессов , и через их посредство, многие геометрический факты находят применение в непосредственно практической деятельности, в частности, при проведении различных измерительных работ на местности.
• Выбор темы «применение тригонометрии для решения задач планиметрии» не случаен: несмотря на то, что она начинает изучаться в курсе геометрии и  алгебры, подчас все вопросы приходится рассматривать «с нуля». А ведь тригонометрический материал весьма интересен и специфичен, так как находится на стыке геометрии и алгебры. В настоящее время эта тема актуальна как никогда, так как ЕГЭ вошел в систему оценки знаний учащихся, а в нем часто встречаются задачи с использованием тригонометрии.

Цель:

Научиться верно применять тригонометрические функции при решении практических измерительных задач; доказать, что знание основных тригонометрических функций позволяет решать вопросы во многих областях науки.

Задачи:

1) Дать определение тригонометрии, тригонометрическим функциям;

2) Решить некоторые задачи с использованием тригонометрических функций;

3) Сделать вывод о проведенной работе.

Актуальность моей работы заключается в том, что данная работа актуальна как для меня, так и для других учащихся, ведь по статистике именно тригонометрические задачи вызывают  наибольшую сложность на ОГЭ и ЕГЭ.

Гипотеза:

Есть такие задачи, решение и ответ которых можно найти только тригонометрическим способом.

§1. Понятие  тригонометрии, тригонометрических функций

Слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое τρίγωνον – треугольник, μετρεω – мера. Иными словами, тригонометрия – наука об измерении треугольников. Тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач в областях астрономии, мореплавания и в составлении географических карт.

§ 1.1. Исторические сведения

Тригонометрия зародилась в странах древнего Востока и, будучи тесно связанной с астрономией, сделала первые  шаги в своем развитии . Основы этой науки заложены в Древней Греции.

Гиппарх и Птолемей составили таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг.

Следующий шаг в развитии тригонометрии был сделан индийцами в период с V по XII в.

В отличие от греков  индийцы стали рассматривать и употреблять в вычислениях уже не целую хорду ММ′ соответствующего центрального угла, а только ее половину МР, т. е.  синуса α- половины центрального угла.

Наряду  с синусом индийцы ввели в тригонометрию косинус, точнее говоря, стали употреблять в своих вычислениях линию косинуса. Им были известны также соотношения cosα=sin(90°-α)  и sin2α+cos2α=r2, а также формулы для синуса суммы и разности двух углов.

Сам термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого «синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90°. «Синус дополнения» или ( по латыни) sinus complementi  стали сокращенно записывать как sinus co или co-sinus.

Развитие тригонометрии в странах Средней Азии , Ближнего Востока, Закавказья(VII-XV в.)

Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии.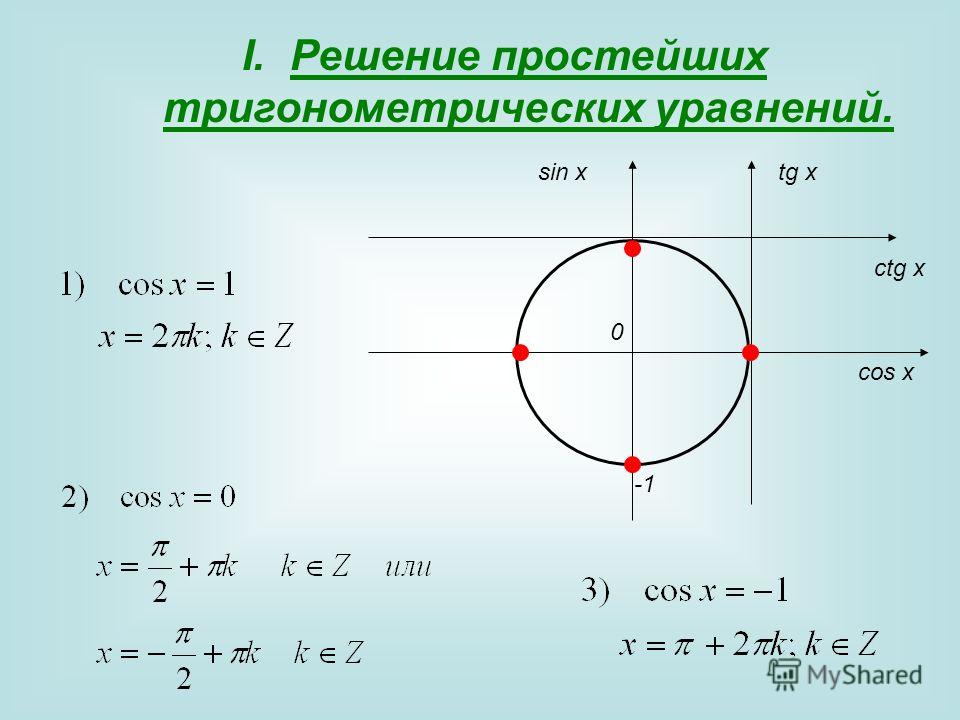 Из числа сделанных ими важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индийцам.

Тригонометрия отделяется от астрономии и становится самостоятельной наукой  (Х III в.)

В трудах среднеазиатских ученых тригонометрия превратилась из науки, обслуживающей астрономию, в особую математическую дисциплину, представляющую самостоятельный интерес.

Это отделение обычно связывают с именем азербайджанского математика Насирэддина Туси (1201-1274).

Позже тригонометрия начала широко изучаться в Европе.

Обширные таблицы синусов И. Региомонтана  через 10 с точностью до 7-ой цифры и его изложенный тригонометрический  труд     «Пять книг о треугольниках всех видов» имели большое значение для дальнейшего развития тригонометрии в XVI – XVII вв.

А Швейцарский математик  Иоганн Бернулли  (1642-1727)  уже применял символы тригонометрических функций.

В XVII – XIX вв. тригонометрия становится одной из глав математического анализа. Она находит большое применение в механике, физике и технике, особенно при изучении  колебательных движений и других периодических процессов.

О свойствах периодичности тригонометрических функций знал еще Виет, первые математические исследования которого относились к тригонометрии.

Жан Фурье доказал, что всякое периодическое движение может быть представлено ( с любой степенью точности) в виде суммы простых гармонических колебаний.

Леонард Эйлер является основоположником теории тригонометрических функций.

Во «Введении в анализ бесконечных» (1748 г) трактует синус, косинус и т.д. не как   тригонометрические линии, обязательно  связанные с окружностью, а как  тригонометрические функции, которые он рассматривал как отношения сторон  прямоугольного  треугольника, как числовые величины.

Разрабатывает учение о тригонометрических функциях любого аргумента.

В XIX веке продолжил развитие теории  тригонометрических функций Лобачевский.

« Геометрические рассмотрения ,- пишет Лобачевский,- необходимы до тех пор в начале тригонометрии, покуда они не послужат к открытию отличительного свойства тригонометрических функций… Отсюда делается тригонометрия совершенно независимой от геометрии и имеет все достоинства анализа».

В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть-учение о тригонометрических функциях -является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть- решение треугольников -рассматривается как глава геометрии.

§2. Решение задач с применением тригонометрии

Решить задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, правил, законов, формул), применяя которые к условиям задачи или к их следствиям, получаем то, что требуется в задаче, — ее ответ.

Весь процесс решения задачи можно разделить на восемь этапов:

1.         анализ задачи;

2.        схематическая запись задачи;

3.        поиск способа решения задачи;

4.        осуществление решения задачи;

5.        проверка решения задачи;

6.        исследование решения;

7.        формулирование ответа задачи;

8.        познавательный анализ решения задачи.

§ 2.1. Практические задачи

Какова должна быть высота горки, если ее длина  7м, а угол наклона не более 35°.

    Н=7*sin35°=7*0,5735=4,01(м)

    Значит, высота горки не должна превышать 4м, тогда угол будет меньше 35°, и кататься будет безопаснее.

 В равнобедренном треугольнике величина угла при вершине равна α, а площадь его равна S. Найти длину основания треугольника.

Дано:   ABC- равнобедренный, AB=BC,угол ABC=α

Найти: AC-?

Решение:

Интересный факт

Способ определения высоты дерева при помощи зеркала основан на законе отражения света: угол падения равен углу отражения.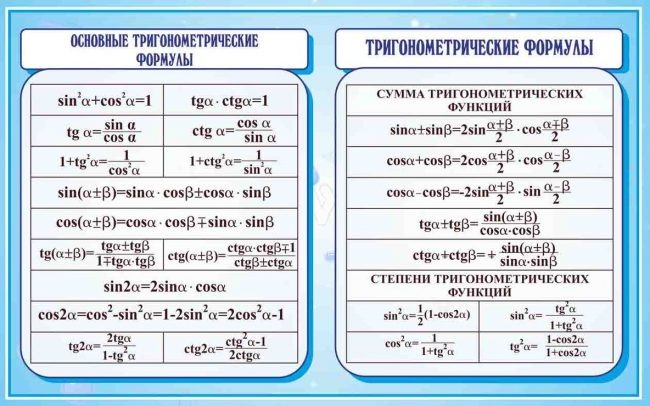 На некотором расстоянии от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ED), во сколько раз расстояние ВС от зеркала до дерева больше расстояния CD от зеркала до наблюдателя

Расстояние от человека до дерева – 6. 4 м. Необходимо найти высоту дерева и расстояние от верхушки до человека, если угол обзора
человека равен 42°.

Дано: ВС = 6. 4 м, угол C = 42°

Найти: АВ, АС

Решение:

1) tg α = AB/CB;

tg 42° = АВ/6. 4

AB = 6.4∙tg 42°

AB = 6.4 ∙ 0. 9004

AB ≈ 5. 76 м

2) cos α = BC/AC

cos 42° = 6.4/AC

AC = 6. 4/cos 42°

AC = 6.4/0. 7431

АС ≈ 8. 6

Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o — с другой. Найти длину скатов крыши.

Дано: AC=10м, угол ВАС=35градусов, угол ВСА=41градус

Найти: АВ-? ВС-? 

Решение:

Угол конька крыши АВС=180o — 35o- 41o=104o

По теореме синусов

,

Также по теореме синусов:

.

(используется таблица синусов)

Ответ: 6 м и 7 м

Насыпь шоссейной дороги имеет в верхней части ширину  60 м.  Найти ширину насыпи в нижней ее части, если угол наклона откосов равен 60°, а высота насыпи равна 12 м.

Дано:

ВС=60м, ВВ₁=12м, α=60°.

Найти: AD-?

 Решение:

 AD=AB1+B1C1+C1D, т.к. трапеция равнобедренная  АВ1=СD1.

AB1= ВВ1∙tg60°=12∙1,732=20,78(м)

AD=2∙20,76 + 60 =101,6 (м).

Ответ:101,6 м.

Пизанская известна тем, что она стоит не вертикально, а немного наклонена. Из-за этого наклона её ещё называют Падающей башней.

Высота Пизанской башни в самой высокой точке составляет 56,7м, отклонение вершины от вертикали-4,5м. Найдем угол наклона башни от вертикали.

Угол наклона башни от вертикали равен углу В

Дано: ВС=56,7м, АС=4,5м.

 Найти: угол В.

Решение:

tgB=AC:BC=4,5:56,7=0,080357,

Тогда угол В = 4°35´.

Самолет радирует капитану рыболовецкого судна, что он находится над косяком рыбы на высоте Z. C cудна определяют угол возвышения самолета, он равен  α. Вычислить расстояние судна от  косяка рыбы.

Дано: Z=3 км, α=43°

Найти: d-?

Решение: α=α₁

 (по свойству параллельные прямых: накрест лежащие углы равны).  

Тогда d=Z*ctgα = 3*1,072 = 3,22 км.

Ответ: 3,22км

§3. ВЫВОД

Тригонометрия — это не только раздел из школьного курса  математики, но и дисциплина, имеющая большое значение в различных областях науки и техники. В различных сферах деятельности человека.

 

Когда следует сдавать тригонометрию?

Автор: Вирджиния | 14 июля 2021 г., 10:35

Изучение школьной программы может показаться сложной задачей; давайте упростим вещи на математическом факультете! Если ваш ребенок решает, какие уроки математики выбрать в следующий раз, это удобное руководство поможет сделать идеальный выбор для расписания занятий на следующий семестр.

И хотя эти решения следует взвешивать с осторожностью, не нужно слишком беспокоиться о том, какой путь выбрать! Старшая школа закладывает основу для будущего каждого ученика — будущего, которое ни в коем случае не высечено на камне; есть много времени, чтобы усовершенствовать свое путешествие дальше по дороге.

Тем не менее, есть несколько полезных соображений, которые следует учитывать при подходе к математике в средней школе, и мы рассмотрим каждое из них здесь.

Когда нужно сдавать тригонометрию?

Как правило, тригонометрия изучается как часть математики на втором или младшем курсе. В дополнение к тому, что тригонометрия предлагается как отдельный курс, она часто включается в другие математические курсы как раздел или семестр.

Однако важно иметь в виду, что, хотя математика большую часть времени может происходить линейно, изучение математики не обязательно следует этому образцу. Как и при изучении любого другого предмета, , когда ваш ученик изучает то, что может варьироваться! Но сначала давайте взглянем на типичную последовательность математических предметов, прежде чем углубляться в более индивидуальный подход.

Предшествует ли тригонометрия исчислению?

В каком классе вы изучаете геометрию? Алгебра? Исчисление? Во-первых, давайте взглянем на типичный прогресс на уроках математики в старшей школе:

1.  Предварительная алгебра
2. Алгебра
3. Геометрия
4. Алгебра II/Тригонометрия
5. Предварительный расчет
6. Расчет/статистика

Как правило, дети изучают предметы, перечисленные вверху списка, на первом и втором курсе и продвигаются по другим темам в младших и старших классах.

Конечно, в этой последовательности есть много места для маневра. Многие средние школы объединяют некоторые из этих предметов в один учебный год по математике, предлагают факультативные курсы и/или предоставляют расширенные или коррекционные курсы по математике, которые будут немного отличаться от перечисленных здесь.

К тому же, как мы все знаем, обучение происходит не только в классе, даже когда дело касается математики.

Опытный репетитор по математике, увлекательные математические соревнования и интересные факты о математике — это лишь несколько дополнительных способов обогатить и поддержать обучение вашего ребенка.

Все дело в индивидуальной настройке — образе мышления, который работает далеко за пределами школьной программы по математике. Это также пригодится для постановки целей для детей, выбора курсов, факультативов и дополнительных занятий после школы!

Итак, когда следует сдавать статистику, предварительную алгебру и многое другое?

Короткий ответ на этот вопрос: когда ваш ученик будет готов!

А если серьезно, первым шагом в определении того, какая траектория является правильной для вашего ребенка, может быть просто отпустить «должен» и вместо этого спросить, каковы его индивидуальные потребности в обучении и цели. Это не только снизит нагрузку на ступеньку выше, но и позволит вам лучше работать со своим учеником, чтобы разработать наилучший путь обучения для его успеха.

Вот несколько соображений для начала. (Думайте об этом как о руководстве, чтобы начать уточнять выбор курсов математики для старшей школы.) 

Свяжитесь с учителями вашего ребенка и обсудите с ними наилучшие варианты . Поговорите с их школьным консультантом и учителями об их рекомендациях по поддержке и улучшению обучения вашего ребенка. Они могут предоставить идеи, примеры работ вашего ученика и другие ценные точки зрения.

Рассмотреть свои будущие цели . Если ваш ребенок заинтересован в карьере в области STEM, ему может понадобиться прочная база знаний по математике, и это стоит планировать заранее. Адаптируйте предметы и уровни к тому, чего надеется достичь ваш ученик, и у него будет больше мотивации усердно работать на пути к цели.

Построить сбалансированный график . Ничто не существует в вакууме, и выбор подходящего математического класса для вашего ученика — лишь одна из нескольких обязанностей, которыми он будет заниматься. С отличием биологию? Стоит подумать, какая поддержка может понадобиться, чтобы добавить в смесь продвинутый курс математики.

Исследуйте ресурсы за пределами школы . От веселых математических занятий до образовательных каналов на YouTube, учебных пособий по математике и множества повседневных способов сделать математику увлекательной — существует множество ценных ресурсов за пределами традиционной среды K-12. Ознакомьтесь с нашей страницей советов и ресурсов по математике, чтобы начать работу, и мыслите нестандартно!

Вирджиния

Вирджиния начала работать с iD Tech в Университете Денвера в 2015 году и с тех пор наслаждается каждой минутой! Бывший учитель по профессии, она имеет степень магистра в области образования и любит работать, чтобы вдохновлять следующее поколение с помощью STEM. Вне офиса вы обычно можете найти ее читающей хорошую книгу, борющейся на коврике для йоги или исследующей Скалистые горы.

Радиан и градусов тригонометрии — Прейрмира 10

Тема: Мат.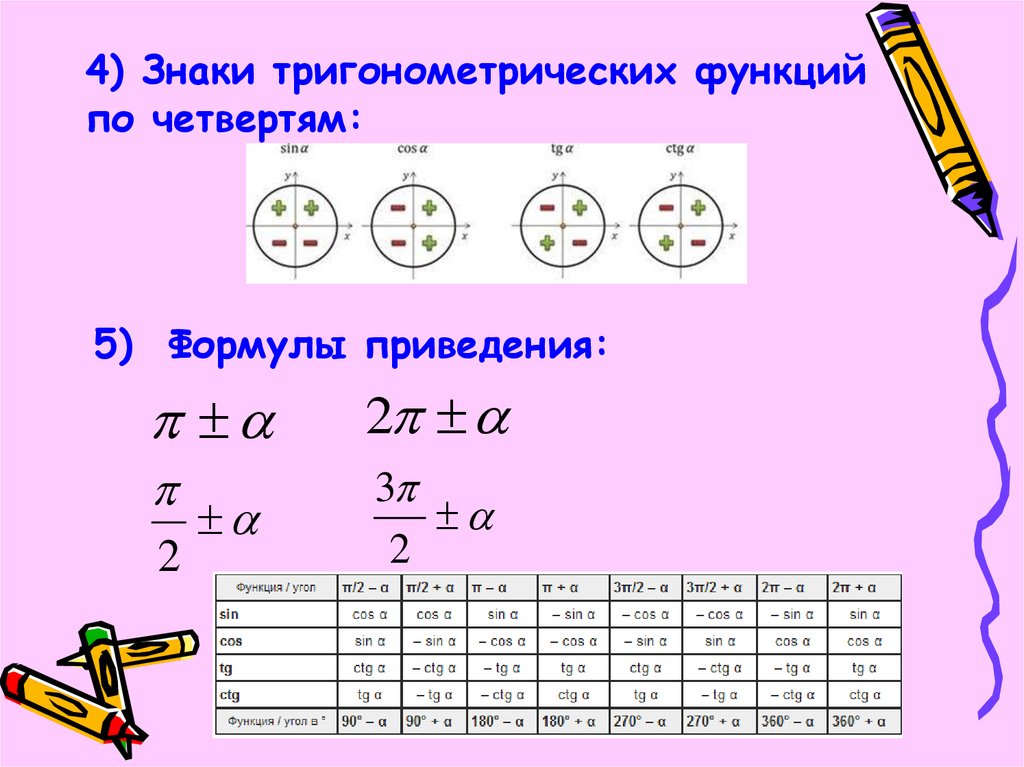 длина угла пропорциональна радиусу, а радиан определяется как постоянная пропорциональность.

Материалы:  

• Рабочий лист 1 – Радианы в круге
• Рабочий лист 2 – Градусы и радианы

Начальник:  

Произнести/ Сделать:

Задайте следующие вопросы (в зависимости от ответов) и позвольте учащимся ответить на них.

• Как мы измеряем углы?
• Какая единица измерения углов?
• Что такое острые, прямые и тупые углы?
• Сколько градусов имеет весь круг?
• Каков радиус окружности?
• Что такое дуга на окружности?

Убедитесь, что ваши учащиеся понимают основные понятия углов, радиуса и дуги окружности.

Главное: 

Произнести/ Сделать:

Произнести: Существует еще одна единица измерения помимо градусов, с помощью которых мы можем измерять углы. Эта единица называется радиан. Если радиус окружности отложить по краю окружности, чтобы получилась дуга, и провести линии от концов дуги к центру окружности, то образовавшийся угол равен одному радиану.

Нарисуйте круг, а затем выделите край круга длиной примерно в один радиус. Нарисуйте линии, чтобы создать угол, чтобы увидеть описание, которое вы только что дали.

Спросите: Сколько радианов может поместиться в целый круг? Сколько радиан может поместиться в полукруге?

Используйте рабочий лист 1 и позвольте учащимся поработать, чтобы выяснить, что в окружности примерно шесть радиан, а в полукруге три радиана.

Скажем: Половина круга чуть больше трех радиан. Это пи радианы, или примерно 3,1415 радиан. Четверть круга равна ½ пи радиана. (Или пи/2 радиана.)

Спросите: Сколько радиан составляет весь круг?

Убедитесь, что учащиеся знают, что весь круг равен 2 пи радианам. Спросите, есть ли у студентов какие-либо вопросы на данный момент, и ответьте на любые вопросы из уже пройденного материала.