Визначення методу найменших квадратів — Фінансова енциклопедія
Що таке метод найменших квадратів?
Метод ” найменших квадратів ” – це форма математичного регресійного аналізу, що використовується для визначення лінії, яка найкраще підходить для набору даних, забезпечуючи візуальну демонстрацію зв’язку між точками даних. Кожна точка даних представляє зв’язок між відомою незалежною змінною та невідомою залежною змінною.
Що говорить вам метод найменших квадратів?
Метод найменших квадратів забезпечує загальне обґрунтування розміщення лінії, що найкраще підходить серед досліджуваних точок даних. Найбільш поширене застосування цього методу, який іноді називають “лінійним” або “звичайним”, має на меті створити пряму лінію, яка мінімізує суму квадратів помилок, породжених результатами пов’язаних рівнянь, таких як як квадратичні залишки, що виникають внаслідок різниці у спостережуваному значенні, та очікуване значення на основі цієї моделі.
Цей метод регресійного аналізу починається з набору точок даних, які будуються на графіку осей x та y.
Аналітик, використовуючи метод найменших квадратів, сформує рядок, що найкраще підходить, що пояснює потенційний зв’язок між незалежними та залежними змінними.
При регресійному аналізі залежні змінні ілюструються на вертикальній осі y, тоді як незалежні змінні – на горизонтальній осі x. Ці позначення складатимуть рівняння для лінії, що найкраще підходить, що визначається методом найменших квадратів.
На відміну від лінійної задачі, нелінійна задача найменших квадратів не має замкненого рішення і, як правило, вирішується ітерацією.Відкриття методу найменших квадратів приписується Карлу Фрідріху Гаусу, який відкрив метод у 1795 р.
Ключові винос
- Метод найменших квадратів – це статистична процедура пошуку найкращого підходу для набору точок даних шляхом мінімізації суми зсувів або залишків точок від побудованої кривої.
- Регресія найменших квадратів використовується для прогнозування поведінки залежних змінних.
Приклад методу найменших квадратів
Прикладом методу найменших квадратів є аналітик, який хоче перевірити взаємозв’язок між прибутковістю акцій компанії та прибутковістю індексу, складовою якого є запас.
У цьому прикладі аналітик прагне перевірити залежність прибутковості акцій від прибутковості індексу. Для цього всі прибутки наносяться на діаграму. Потім прибутковість індексу позначається як незалежна змінна, а повернення запасів є залежною змінною. Лінія, що найкраще підходить, забезпечує аналітика коефіцієнтами, що пояснюють рівень залежності.
Рядок найкращого рівняння
Лінія, що найкраще підходить, визначена методом найменших квадратів, має рівняння, яке розповідає історію взаємозв’язку між точками даних. Рядок найкращих рівнянь може бути визначений за допомогою комп’ютерних програмних моделей, які включають зведення результатів для аналізу, де коефіцієнти та зведені результати пояснюють залежність змінних, що перевіряються.
Лінія регресії найменших квадратів
Якщо дані показують більш струнку залежність між двома змінними, лінія, яка найкраще відповідає цій лінійній залежності, відома як лінія регресії найменших квадратів, яка мінімізує вертикальну відстань від точок даних до лінії регресії.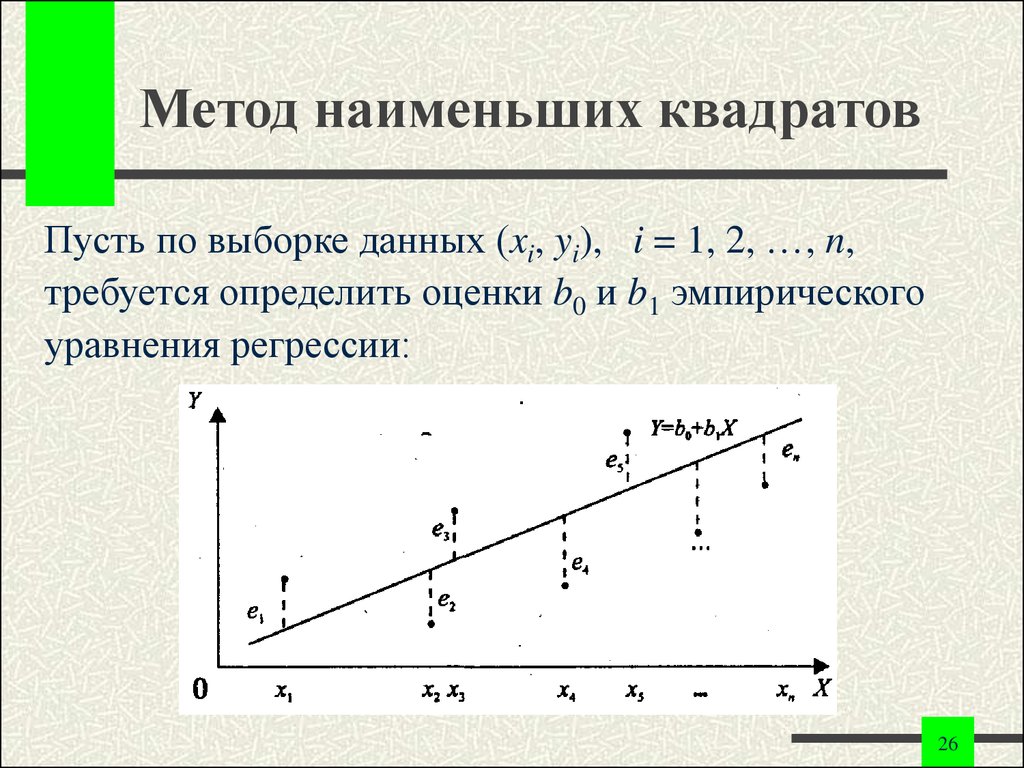
Термін “найменші квадрати” використовується, оскільки це найменша сума квадратів помилок, яку також називають “дисперсією”.
Питання що часто задаються
Що таке метод найменших квадратів?
Метод найменших квадратів – це математичний прийом, який дозволяє аналітикові визначити найкращий спосіб встановлення кривої поверх діаграми точок даних. Він широко використовується для полегшення інтерпретації розсіяних графіків і пов’язаний з регресійним аналізом. Вперше цю техніку розробив німецький математик Карл Фрідріх Гаус, який жив між 1777 і 1855 роками. У наші дні Метод найменших квадратів можна використовувати автоматично з використанням більшості статистичних програм.
Як використовується метод найменших квадратів у фінансах?
Метод найменших квадратів використовується у найрізноманітніших сферах, включаючи фінанси та інвестиції. Для фінансових аналітиків метод найменших квадратів може допомогти кількісно визначити взаємозв’язок між двома або більше змінними: наприклад, ціною акції акції та її прибутком на акцію (EPS).
Виконуючи такий тип аналізу, інвестори можуть спробувати спрогнозувати майбутню поведінку цін на акції або інших факторів.
Який приклад методу найменших квадратів?
Для ілюстрації розглянемо випадок інвестицій, які розглядають, чи варто інвестувати в золотодобувну компанію. Інвестор може побажати, наскільки чутлива ціна акцій компанії до змін ринкової ціни на золото. Для вивчення цього інвестор міг використовувати метод найменших квадратів, щоб простежити взаємозв’язок між цими двома змінними з часом на графіку розсіювання. Цей аналіз може допомогти інвестору передбачити ступінь, до якої ціна акцій, швидше за все, зростатиме або падатиме за будь-якого збільшення чи зниження ціни на золото.
10.2. Метод найменших квадратів
Суть методу найменших
квадратів полягає в
відшуканні параметрів моделі тренда,
яка краще всього описує тенденцію
розвитку якого-небудь випадкового явища
в часі або в просторі (тренд – це лінія,
яка й характеризує тенденцію цього
розвитку).
Завдання методу найменших
квадратів (МНК) зводиться до знаходження
не просто якоїсь моделі тренда, а до
знаходження кращої або оптимальної
моделі. Ця модель буде оптимальною, якщо
сума квадратичних відхилень між
спостережуваними фактичними величинами
й відповідними їм розрахунковими
величинами тренда буде мінімальною
(найменшою):
де — квадратичне відхилення між спостережуваною фактичною величиноюта відповідною їй розрахунковою величиною тренда;
— фактичне (спостережуване) значення явища, що вивчається;
— розрахункове значення моделі тренда;
— число спостережень за явищем, що вивчається .
МНК самостійно застосовується
досить рідко. Як правило, частіше за
всього його використовують лише як
необхідний технічний прийом при
кореляційних дослідженнях. Слід
пам’ятати, що інформаційною основою МНК
може бути тільки достовірний статистичний
ряд, причому число спостережень не
повинне бути менше 4-х, згладжуючі
процедури МНК можуть бути помилковими.
Інструментарій МНК зводиться до наступних процедур:
Перша процедура. З’ясовується, чи існує взагалі яка-небудь тенденція зміни результативної ознаки при зміні вибраного чинника-аргументу, або іншими словами, чи є зв’язок між « у» і «».
Друга процедура. Визначається, яка лінія (траєкторія) здатна краще всього описати або охарактеризувати цю тенденцію.
Третя процедура. Розраховуються параметри регресійного рівняння, що характеризує дану лінію, або іншими словами, визначається аналітична формула, що описує кращу модель тренда.
Приклад. Припустимо, ми маємо інформацію про середню врожайність соняшнику в досліджуваному господарстві (табл. 10.1).
Таблиця 10.1
Номер спостереження | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Роки | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
Урожайність, ц/га | 14,2 | 15,6 | 17,5 | 14,5 | 15,3 | 17,0 | 16,6 | 17,5 | 15,0 | 17,7 |
Оскільки рівень технології
при виробництві соняшнику в наший країні
за останні 10 років практично не змінився,
значить, коливання врожайності в
аналізований період дуже сильно залежали
від змін погодно-кліматичних умов.
Чи
дійсно це так?
Перша процедура МНК. Перевіряється гіпотеза про існування тенденції зміни врожайності соняшнику залежно від зміни погодно-кліматичних умов за аналізованих 10 років.
У даному прикладі за «y» доцільно прийняти врожайність соняшнику, а за «x» – номер спостережуваного року в аналізованому періоді. Перевірку гіпотези про існування якого-небудь взаємозв’язку між «» і «y» можна виконати двома способами: уручну й за допомогою комп’ютерних програм. Звичайно, за наявності комп’ютерної техніки дана проблема вирішується сама собою. Але, щоб краще зрозуміти інструментарій МНК доцільно виконати перевірку гіпотези про існування зв’язку між «» і «y» уручну, коли під рукою знаходяться тільки ручка та звичайний калькулятор. У таких випадках гіпотезу про існування тенденції краще за все перевірити візуальним способом за допомогою розташування графічного зображення аналізованого ряду динаміки — кореляційного поля:
Кореляційне поле в нашому
прикладі розташоване навколо повільно
зростаючої лінії.
Це вже само по собі
говорить про існування певної тенденції
в зміні врожайності соняшнику. Не можна
говорити про наявність якої-небудь
тенденції лише тоді, коли кореляційне
поле схоже на круг, коло, строго вертикальна
або строго горизонтальна хмара, або ж
складається з хаотично розкиданих
крапок. У решті всіх випадків слід
підтвердити гіпотезу про існування
взаємозв’язку між «»
і «y», і продовжити
дослідження.
Друга процедура МНК. Визначається, яка лінія (траєкторія) здатна краще всього описати або охарактеризувати тенденцію зміни врожайності соняшнику за аналізований період.
За наявності комп’ютерної техніки підбір оптимального тренда відбувається автоматично. При «ручній» обробці вибір оптимальної функції здійснюється, як правило, візуальним способом – по розташуванню кореляційного поля. Тобто, з вигляду графіка підбирається рівняння лінії, яка краще за все підходить до емпіричного тренду (до фактичної траєкторії).
Як відомо, у природі існує
величезна різноманітність функціональних
залежностей, тому візуальним способом
проаналізувати навіть незначну їх
частину — украй скрутно.
Пряма: | Гіпербола: | |
Парабола другого порядку: :
Неважко помітити, що в нашому прикладі краще всього тенденцію зміни врожайності соняшнику за аналізованих 10 років характеризує пряма лінія, тому рівнянням регресії буде рівняння прямої.
Третя процедура. Розраховуються параметри регресійного
рівняння, що характеризує дану лінію,
або іншими словами, визначається
аналітична формула, що описує кращу
модель тренда.
Знаходження значень параметрів рівняння регресії, у нашому випадку параметрів і , є серцевиною МНК. Даний процес зводиться до вирішення системи нормальних рівнянь.
(10.2)
Ця система рівнянь досить легко вирішується методом Гауса. Нагадаємо, що в результаті рішення, у нашому прикладі, знаходяться значення параметрів і. Таким чином, знайдене рівняння регресії матиме наступний вигляд:
У лінійному рівнянні параметр –коефіцієнт регресії указує, на скільки одиниць у середньому зміниться із зміноюна одиницю. Він має одиницю вимірювання результативної ознаки. У разі прямого зв’язку– величина позитивна, а при зворотному – негативна. Параметр– вільний член рівняння регресії, тобто це значенняпри. Якщоне набуває нульових значень, цей параметр має лише розрахункове призначення.
Приведемо також системи нормальних рівнянь для відшукування параметрів нелінійних рівнянь.
Таблиця 10.2
Форма зв’язку | Рівняння зв’язку | Система нормальних рівнянь |
параболічна | ||
гіперболічна |
Слід пам’ятати, що при зміні
хоч би одного значення вхідних даних
(пари значень
або одного з них) усі коефіцієнти змінять
у загальному випадку свої значення,
тому що вони повністю визначаються
вхідними даними.
страница не найдена — Колледж Уильямс
| ’62 Центр театра и танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий/помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр изучения карьеры, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Приемная, Уэстон Холл | 597-2211 | 597-4052 факс |
| Позитивные действия, Хопкинс Холл | 597-4376 | |
| Африканские исследования, Холландер | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архив и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art/Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Студия фотографии, Spencer Studio Art | 597-2030 | |
| Студия печати, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео/фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Голландия | 597-2391 | 597-3028 факс |
| Астрономия/астрофизика, Физика Томпсона | 597-2482 | 597-3200 факс |
| Отделение легкой атлетики, физического воспитания, отдыха, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочная пристань, озеро Онота | 443-9851 | |
| Вагоны | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Хоккейный каток Ice Line, Lansing Chapman | 597-2433 | |
| Очные, Спортивный центр Чендлера | 597-3321 | |
| Физкультура | 597-2141 | |
| Влажная линия бассейна, Спортивный центр Чандлера | 597-2419 | |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Корты для сквоша | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Биология Томпсона | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Биология Томпсона | 597-2126 | 597-3495 факс |
| Безопасность и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа/Системы сигнализации | 597-4970/4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Распределительный щит | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, выпуск 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория наук об окружающей среде, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литературы и культуры, Голландия | 597-2391 | 597-3028 факс |
| Арабистика, Голландия | 597-2391 | 597-3028 факс |
| Сравнительная литература, Hollander | 597-2391 | |
| Critical Languages, Hollander | 597-2391 | 597-3028 факс |
| Лингвистическая лаборатория | 597-3260 | |
| Русский, голландский | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Stetson Court 24 | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Томпсон Химия | 597-2323 | 597-4150 факс |
| Классика (греческая и латинская), голландская | 597-2242 | 597-4222 факс |
| Когнитивные науки, Бронфман | 597-4594 | |
| Колледж Маршал, Физика Томпсона | 597-2008 | |
| Отношения с колледжами | 597-4057 | |
| 25-я программа воссоединения, Фогт | 597-4208 | 597-4039 факс |
| 50-я программа воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Операции по развитию, Мирс Уэст | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Отношения с выпускниками, Мирс Уэст | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников и разработчиков, Mears West | 597-4369 | |
| Развитие, Фогт | 597-4256 | |
| Отношения с донорами, Фогт | 597-3234 | 597-4039 факс |
| Отдел планирования подарков, Фогт | 597-3538 | 597-4039 факс |
| Офис грантов, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Родительский фонд, фогт | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Mears | 597-4119 | 597-4178 факс |
| Начало и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Веб-группа, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Информатика, Химия Томпсона | 597-3218 | 597-4250 факс |
| Конференции и мероприятия, Парески | 597-2591 | 597-4748 факс |
| Справки о доме на дереве вяза, ферма Маунт-Хоуп | 597-2591 | |
| Офис диспетчера, Хопкинс-холл | 597-4412 | 597-4404 факс |
| Кредиторская задолженность и ввод данных, Hopkins Hall | 597-4453 | |
| Касса и кассовые чеки, Hopkins Hall | 597-4396 | |
| Финансовые информационные системы, Хопкинс-холл | 597-4023 | |
| Карточки для покупок, Хопкинс Холл | 597-4413 | |
| Студенческие кредиты, Hopkins Hall | 597-4683 | |
| Танец, ’62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Дом Дженнесс | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета, Хопкинс Холл | 597-4351 | 597-3553 факс |
| Обеденные услуги, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Пекарня, Парески | 597-4511 | |
| Питание, Факультет | 597-2452 | |
| Обеденный зал Дрисколла, Дрисколл | 597-2238 | |
| Эко-кафе, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Закусочная Lee, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Уитменс, Парески | 597-2889 | |
| Экономика, Шапиро | 597-2476 | 597-4045 факс |
| английский, голландский | 597-2114 | 597-4032 факс |
| Объекты, Сервисное здание объектов | 597-2301 | |
| Запрос автомобиля для колледжа | 597-2302 | |
| Вечерние/выходные чрезвычайные ситуации | 597-4444 | |
| Запросы на работу объектов | 597-4141 факс | |
| Особые события | 597-4020 | |
| Склад | 597-2143 | 597-4013 факс |
| Клуб факультета, Дом факультета/Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Офис стипендий, Хопкинс-холл | 597-3044 | 597-3507 факс |
| Финансовая помощь, Weston Hall | 597-4181 | 597-2999 факс |
| Геофизические науки, Кларк Холл | 597-2221 | 597-4116 факс |
| немецкий-русский, голландский | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Высшая программа по истории искусств, The Clark | 458-2317 факс | |
| Health and Wellness Services, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Санитарное просвещение | 597-3013 | |
| Услуги комплексного благополучия (консультации) | 597-2353 | |
| Экстренные ситуации, угрожающие жизни | Звоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Хопкинс Форест | 597-4353 | |
| Центр Розенбурга | 458-3080 | |
| Отдел кадров, здание B&L | 597-2681 | 597-3516 факс |
| Услуги няни, здание B&L | 597-4587 | |
| Преимущества | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Расчет заработной платы | 597-4162 | |
| Ресурсы для супругов/партнеров | 597-4587 | |
| Трудоустройство студентов | 597-4568 | |
| Weather Line (ICEY) | 597-4239 | |
| Гуманитарные науки, Шапиро | 597-2076 | |
| Информационные технологии, Джесуп | 597-2094 | 597-4103 факс |
| Пакеты для чтения курсов, почтовый ящик для офисных услуг | 597-4090 | |
| Центр кредитования оборудования, Додд, приложение | 597-4091 | |
| Служба поддержки преподавателей/персонала, [email protected] | 597-4090 | |
| Медиа-услуги и помощь в классе | 597-2112 | |
| Служба поддержки студентов, [электронная почта защищена] | 597-3088 | |
| Телекоммуникации/телефоны | 597-4090 | |
| Междисциплинарные исследования, Hollander | 597-2552 | |
| Международное образование и обучение вне дома, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс-холл | 597-4447 | |
| Офис в Бостоне | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Справедливость и право, Холландер | 597-2102 | |
| Latina/o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Биология Томпсона | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Hopkins Hall | 597-4376 | 597-4015 факс |
| Счетная палата студентов, Хопкинс Холл | 597-4396 | 597-4404 факс |
| Исследования производительности, ’62 Центр | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Физика Томпсона | 597-2482 | 597-4116 факс |
| Планетарий/Обсерватория Хопкинса | 597-3030 | |
| Старый театр обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати/почты для преподавателей/сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис проректора, Хопкинс-холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, здание B&L | 597-2195/4238 | 597-5031 факс |
| Ипотека преподавателей/сотрудников | 597-4238 | |
| Аренда жилья для преподавателей/сотрудников | 597-2195 | |
| Офис ЗАГСа, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, голландец | 597-2076 | 597-4222 факс |
| Романские языки, голландский | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 House | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Услуги доступа | 597-2501 | |
| Приобретение/Серийный номер | 597-2506 | |
| Услуги каталогизации/метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные услуги | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Научные и технологические исследования, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машиностроительный/модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Hardy | 597-3747 | 597-4530 факс |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Планирование студенческих мероприятий | 597-2546 | |
| Студенческое общежитие, Парески | 597-2555 | |
| Участие студентов | 597-4749 | |
| Жилищные программы высшего класса | 597-4625 | |
| Студенческая почта, Почта Парески | 597-2150 | |
| Устойчивое развитие/Zilkha Center, Harper | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямс | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Управление траста и недвижимости, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| ПО за Campus Life, Hopkins Hall | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжами, Mears | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрации, Хопкинс Холл | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр колледжа Уильямс, Детский центр Уильямс | 597-4008 | 597-4889 факс |
| Художественный музей колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Безопасность музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Аппаратная/стол для учащихся | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Уэст | 597-2192 | |
| Уильямс Рекорд, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Музей морского порта Mystic | 860-572-5359 | 860-572-5329 факс |
| Женские, гендерные и сексуальные исследования, Шапиро | 597-3143 | 597-4620 факс |
| Программы написания программ, Hopkins Hall | 597-4615 | |
| Центр экологических инициатив Зилха, Харпер | 597-4462 |
Метод наименьших квадратов | Реальная статистика с использованием Excel
В разделе «Корреляция» мы изучаем линейную корреляцию между двумя случайными величинами x и y.
Теперь посмотрим на линию на плоскости x y, которая лучше всего соответствует данным ( x 1 , y 1 ), …, ( x n , y 4 0 n ).
Напомним, что уравнение для прямой имеет вид y = bx + a , где
b = наклон прямой
a = y-пересечение, т.е. значение y в месте пересечения прямой с ось Y
Для наших целей мы запишем уравнение линии наилучшего соответствия как
и, таким образом, точка пересечения по оси y будет равна
. Для каждого i мы определяем x i на этой линии, и так
Наилучшей линией является линия, для которой сумма расстояний между каждой из n точек данных и линией является минимально возможной. Таким образом, математически полезный подход состоит в том, чтобы найти линию со свойством, что сумма следующих квадратов минимальна.
Theorem 1 : The best fit line for the points ( x 1 , y 1 ), …, ( x n , y n ) is given by
где
Щелкните здесь для доказательства теоремы 1.
Даны два доказательства, одно из которых не использует исчисление.
Определение 1 : Линия наилучшего соответствия называется линией регрессии .
Наблюдение : Теорема показывает, что линия регрессии проходит через точку ( x̄ , ȳ) и имеет уравнение
, где наклон равен
, а точка пересечения с осью Y равна . b = cov ( x ,y)/ var ( x ). Поскольку члены, включающие и , сокращаются, это можно рассматривать либо как ковариацию и дисперсию генеральной совокупности, либо как ковариацию и дисперсию выборки. Таким образом a и b можно вычислить в Excel следующим образом, где R1 = массив значений y и R2 = массив значений x : R2) / VARP(R2) a = INTERCEPT(R1, R2) = AVERAGE(R1) – b * AVERAGE(R2) Свойство 1 : Доказательство корреляции: по определению, 2 и, таким образом, согласно предыдущему наблюдению мы имеем Функции Excel : Excel предоставляет следующие функции для прогнозирования значения y для любого x на основе линии регрессии. НАКЛОН (R1, R2) = наклон линии регрессии, как описано выше ПЕРЕСЕЧЕНИЕ (R1, R2) = точка пересечения у линии регрессии, как описано выше.1833 х . Таким образом, ПРОГНОЗ (x, R1, R2) = a + b * x , где a = INTERCEPT (R1, R2) и b = НАКЛОН (R1, R2). TREND (R1, R2) = функция массива, которая создает массив предсказанных значений y, соответствующих x значениям, хранящимся в массиве R2, на основе линии регрессии, вычисленной из x значений, хранящихся в массиве R2, и значений y хранится в массиве R1. TREND (R1, R2, R3) = функция массива, которая предсказывает значения y, соответствующие 9Значения 1833 x в R3 на основе линии регрессии на основе значений x , хранящихся в массиве R2, и значений y, хранящихся в массиве R1. Чтобы использовать TREND(R1, R2), выделите диапазон, в котором вы хотите сохранить предсказанные значения y. Чтобы использовать TREND(R1, R2, R3), выделите диапазон, в котором вы хотите сохранить предсказанные значения y. Затем введите TREND и левую скобку. Затем выделите массив наблюдаемых значений для y (массив R1), введите запятую и выделите массив наблюдаемых значений для x (массив R2), затем еще одну запятую и выделите массив R3, содержащий значения для x , для которых вы хотите предсказать значения y на основе линии регрессии. Теперь введите правую скобку и нажмите Ctrl-Shft-Enter . Функция Excel 2016 : Excel 2016 представляет новую функцию ПРОГНОЗ.ЛИНЕЙНЫЙ , эквивалентную ПРОГНОЗУ. Пример 1 : Рассчитайте линию регрессии для данных в примере 1 проверки гипотезы одной выборки на предмет корреляции и нанесите результаты на график.
Здесь R1 = массив значений данных y, а R2 = массив значений данных x :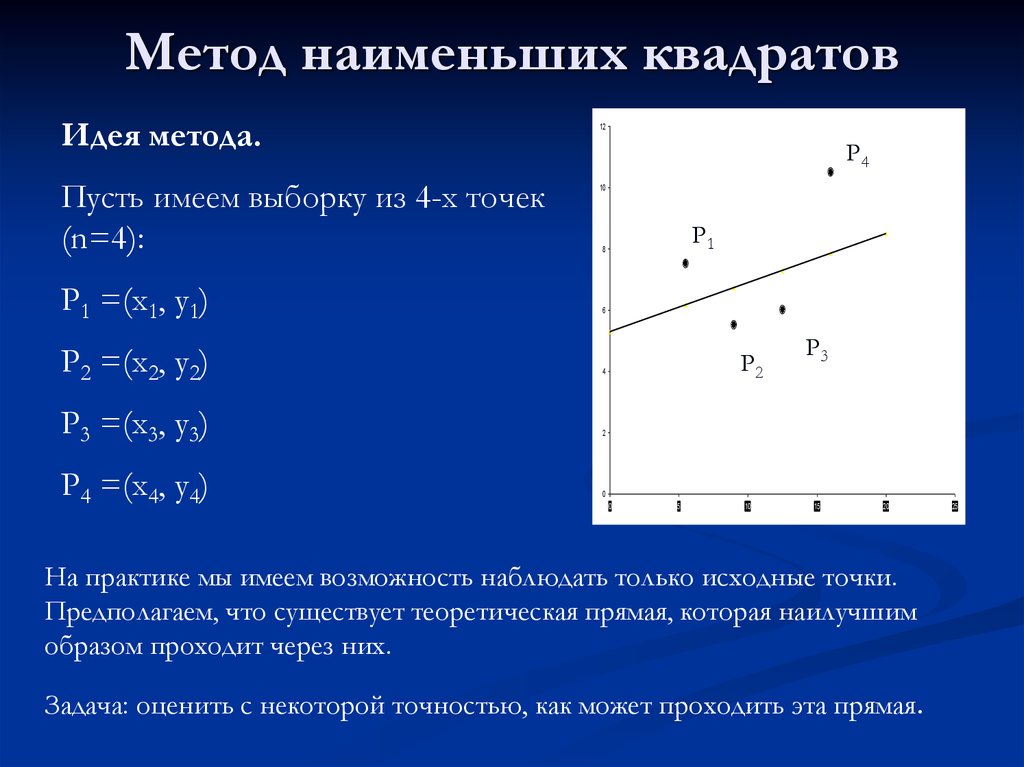
Затем введите TREND и левую скобку. Затем выделите массив наблюдаемых значений для y (массив R1), введите запятую и выделите массив наблюдаемых значений для x (массив R2), за которым следует правая скобка. Наконец нажмите Ctrl-Shft-Enter .