Метод ньютона онлайн: Метод Ньютона онлайн

Содержание

Метод Ньютона онлайн

Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.

Калькулятор метода Ньютона

Переменная уравнения: xyztupqsabc

Точность нахождения корня, ε = 1e-31e-41e-51e-61e-71e-81e-91e-101e-111e-121e-131e-141e-15

Макс. кол-во итераций: 3050100150200

Начальное приближение, x₀ =

Критерий останова вычислений: приращениеотличие функции от нуля

Методом Ньютона, найти корень (x — ?) уравнения:3x27x205с точностью ε1010,максимальное кол-во итераций: 100,критерий останова вычислений: xnxn1εначальное приближение: x00.

42.

Установить калькулятор на свой сайт

Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.

Пусть нам дано уравнение

Формула для поиска корня уравнения выглядит следующим образом:

и — приближённые значения корня уравнения на -ой и ()-ой итерациях соответственно, — значение функции в точке , — значение производной функции в точке .

Как видно, для того чтобы начать работу необходимо задать точку — начальное приближение для корня уравнения . От выбора точки зависит сойдётся ли алгоритм к решению или нет.

Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если и одновременно , где — кратный корень уравнения .

Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции к нулю в некоторой точке .

Критерий останова вычислений на основе приращения задаётся следующей формулой:

т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения ( и ) должны быть меньше, некоторой наперёд заданной величины .

Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:

т.е. отличие (по модулю) между функцией в некоторой точке и нулём меньше .

В тоже время, если последовательность к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.

На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения методом Ньютона.

В точке мы строим касательную к графику функции . Уравнение касательной в этой точке имеет вид:

Находим точку пересечения полученной касательной с осью абсцисс, т. е. рассматриваем точку с координатами . Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:

Из данного уравнения находим :

Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.

Другие полезные разделы:

Разложение на множители онлайн
Нули функции онлайн
Калькулятор тригонометрических уравнений

Оставить свой комментарий:

3.2.2. Метод Ньютона (касательных)

Постановка задачи.

Дано нелинейное уравнение (3.1) f(x)=0. Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.

Метод основан на стратегии постепенного уточнения корня. Формулу уточнения можно получить из геометрической иллюстрации идеи метода.

Рис. 3.12. Геометрическая иллюстрация метода Ньютона.

На отрезке существования корня выбирается начальное приближение x0. К кривой f(x) в точке А с координатами (x0, f(x0)) проводится касательная. Абсцисса x1 точки пересечения этой касательной с осью ОХ является новым приближением корня.

Из рисунка следует, что x1 = x0 − CB

Из ∆ABC: CD=. Но .

Следовательно,

Аналогично, для i-го приближения можно записать формулу итерационного процесса метода Ньютона:

, где x0 Î [a;b]. (3.13)

Условие окончания расчета: , (3.14)

Где −корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

(3.15)

Если на отрезке существования корня знаки и не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия

, x0Î[a;b].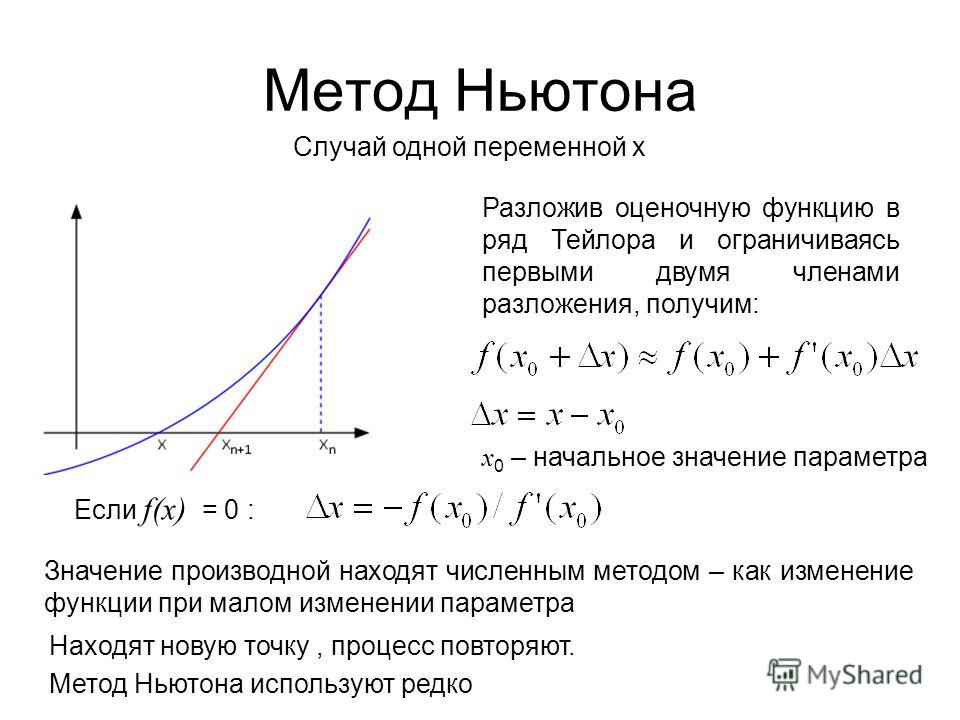 (3.16)

Т. е. в точке начального приближения знаки функций и ее второй производной должны совпадать.

Рис. 3.13. Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый, , тогда x0=b, т. к. f(b)>0.

Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).

●

Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0 , тогда x0 =a, т. к. f(a)<0.

Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.

Рис 3. 15. Схема алгоритма метода Ньютона:

Достоинства метода: высокая скорость сходимости; обобщается на системы уравнений.

Недостатки: сложный, т. к. требуется вычисление производных; сильная зависимость сходимости от вида функции и выбора начального приближения.

Пример 3.3.

Методом Ньютона уточнить корни уравнения x3 = 1− 2x с точностью ε=0,001. Корень отделён ранее (пример 3.1), x* Î [0,1].

Сначала нужно выбрать начальное приближение.

F(x) = x3+ 2 x−1

F ’(x) = 3 x2 +2

F ’’(x) = 6 x

Производные имеют постоянный знак на отрезке (0,1], поэтому для выбора начального приближения достаточно использовать условие (3.16).

Знак второй производной на отрезке положительный, следовательно

X0 = b = 1, т. к. f(b) = f(1) = 13+2·1−1 = 2 > 0

Вычислим несколько приближений:

X1 =

X2 =

X3 =0,464935−0,011468=0,453467

X3 =0,453463−0,0000695=0,453398

Решение получено за 4 итерации, так как поправка стала меньше заданной точности: 0,0000695 < ε.

< Предыдущая		Следующая >

Калькулятор метода Ньютона — поиск корней методом Ньютона

Онлайн-калькулятор метода Ньютона позволяет определить приближение корня реальной функции. Калькулятор использует формулу метода Ньютона для отображения итерации пошагового расчета. Здесь вы можете узнать больше о методе Ньютона, его формулах и примерах.

Что такое метод Ньютона?

В исчислении метод Ньютона (также известный как метод Ньютона-Рафсона) представляет собой алгоритм нахождения корня, который обеспечивает более точное приближение к корню (или нулю) функции с действительным знаком.

Метод Ньютона основан на касательных линиях. Основная идея состоит в том, что если x достаточно близко к корню f (x), касательная графика будет пересекать ось x в точке (x, f (x)) в точке, которая ближе к корню чем х.

(изображение)

Однако онлайн-калькулятор касательной позволяет определить касательную к неявной, параметрической, полярной и явной в конкретной точке.

Формула метода Ньютона:

Если x_n является оценочным решением функции f(x), которое равно нулю, и если f'(x_n) не равно нулю, то следующая оценка дается следующим образом: 92 = 1,5625

F'(x_2) = f'(1,25) = 2 (1,25) = 2,5

Теперь, используя формулу метода Ньютона:

X_3= x_2 – f(x_2) / f'(x_2)

X_3 = 1,25 – 1,5625/2,5

X_3 = 0,625

Следовательно, калькулятор метода Ньютона дает таблицу итераций для тех же значений:

Шаг	х	ф(х)	ф'(х)
1	2,5	25	10
2	1,25	6,25	5
3	0,625	1,5625	2,5

Однако онлайн-калькулятор производных позволяет определить производную функции по заданной переменной.

Как работает калькулятор метода Ньютона?

Калькулятор метода Ньютона реализует метод Ньютона, чтобы найти корень реальной функции и обеспечить итерации, следуя этим инструкциям:

Ввод:

Во-первых, подставьте функцию с действительным знаком и ее производную (необязательно).
Теперь подставьте начальное значение и максимальное число итераций в соответствии с требованиями.
Затем добавьте значащую цифру в соответствующее поле.
Нажмите кнопку расчета, чтобы найти количество итераций заданной функции.

Вывод:

Калькулятор метода Ньютона отображает заданную функцию и ее производную.
Калькулятор применяет правило степени к реальной функции и предоставляет таблицу итераций в соответствии с заданными значениями.
Он дает пошаговое решение для всех итераций за доли секунды.

Часто задаваемые вопросы:

Почему метод Ньютона не удался?

Если производная равна нулю, метод Ньютона не работает. Когда производная близка к нулю, касательная почти горизонтальна, поэтому она может превышать требуемый корень (численная сложность).

Всегда ли метод Ньютона сходится?

Метод Ньютона не всегда сходится. Его теория сходимости относится к «локальной» сходимости, что означает, что она должна начинаться вблизи корня, а «около» относится к функции, с которой вы хотите иметь дело.

Почему метод Ньютона быстрее, чем метод деления пополам?

Функция f должна иметь непрерывную производную. Если вы начнете слишком далеко от корня, метод Ньютона может не сойтись. Однако, когда он сходится, он быстрее, чем метод деления пополам, и обычно является квадратичным.

Будет ли метод Ньютона расходиться?

Если функция не может быть непрерывно дифференцирована вблизи корня, метод Ньютона всегда будет расходиться и давать сбой, если решение не будет угадано с первой попытки.

Какой самый быстрый метод сходимости?

Метод Ньютона — очень хороший метод. Когда условия выполняются, метод Ньютона сходится, и скорость сходимости выше, чем почти у любой другой альтернативной итерационной схемы, основанной на методе преобразования исходной f(x) в функцию с фиксированной точкой.

Вывод:

Воспользуйтесь онлайн-калькулятором метода Ньютона, чтобы найти действительные корни нелинейных функций. Потому что этот калькулятор предоставляет полную таблицу итераций с использованием формулы метода Ньютона. Поиск итераций вручную — длительный и трудоемкий метод. Чтобы вам было удобно, наш онлайн-калькулятор ньютонов бесплатно и быстро выполняет все расчеты, связанные с методом Ньютона.

Ссылка:

Из источника Википедии: Метод Ньютона, Трудность вычисления производной функции, Неспособность метода сходиться к корню, Выброс.

Из источника онлайн-примечаний Пола: Стационарная точка, Плохая начальная оценка, Смягчение неконвергенции, Анализ, Бассейны притяжения.

Из источника AMSI: Поиск решения с помощью геометрии, Ключевой расчет, Алгоритм, Использование метода Ньютона, Чувствительная зависимость от начальных условий.

Калькулятор метода Ньютона | Наилучшие шаги полного решения

f(x) =

Исходное предположение (x ₀ ):

Критерии сходимости (ε, δ):

(желаемая точность/прецизионность)

0.010.0010.00010.000010.000001

Решение:

Метод Ньютона Урок

7 9 Содержание урока

Что такое метод Ньютона?

В численном анализе мы используем алгоритм или уравнение для повторения вычислений для получения решения до тех пор, пока не будет достигнут желаемый уровень точности и прецизионности. Эти повторяющиеся вычисления называются итерациями.

Метод Ньютона, также известный как метод Ньютона-Рафсона, представляет собой численный алгоритм, который находит лучшее приближение корня функции с каждой итерацией.

Почему мы изучаем метод Ньютона?

Одним из многих реальных применений метода Ньютона является расчет того, столкнется ли астероид с Землей во время своего обращения вокруг Солнца.

Эллиптическая орбита Земли (белый цвет) и эллиптическая орбита астероида (синий цвет) вокруг Солнца 9{2}} = 1 $$

Поскольку эллипс представлен этой нелинейной формой уравнения, а путь Земли и астероида представлен собственным уникальным уравнением эллипса, пути двух объектов вокруг Солнца на самом деле представляют собой система нелинейных уравнений, которую можно решить, чтобы найти точки пересечения.

Обычно мы изучаем метод Ньютона в контексте поиска корней/нулей уравнения. Однако метод Ньютона настолько мощен, что его также можно использовать для решения системы уравнений, линейных и нелинейных.

Как только мы освоим метод Ньютона для одного уравнения, мы можем настроить модифицированную версию метода для решения нашей системы нелинейных уравнений эллипса Земля/астероид. Если точки пересечения найдены, мы можем использовать другие уравнения орбитальной механики, чтобы определить, когда каждый объект достигнет этих точек пересечения.

Если точек пересечения нет, астероид не столкнется с Землей. Если есть точки пересечения, но астероид и Земля достигают их в разное время, то астероид не столкнется с Землей. Если есть точки пересечения и астероид и Земля достигают их одновременно, астероид может столкнуться с Землей.

Как вычислить корни функции с помощью метода Ньютона

Общее уравнение для метода Ньютона имеет вид:

$$x_{i + 1} = x_{i} \; – \; \frac{f(x_{i})}{f'(x_{i})}; \; i=0, 1, 2…$$

Где x _{i + 1} — значение x , вычисляемое для новой итерации, x _i — значение x предыдущей итерации , f(x _i ) — значение функции в x _i и f ‘(x _i) — значение производной функции при x _i .

Для первой итерации i = 0 мы подставим 0 вместо i в общее уравнение. В результате получается:

$$x_{(0) + 1} = x_{(0)} \; – \; \frac{f(x_{(0)})}{f'(x_{(0)})} \; \Правая стрелка \; х_{1} = х_{0} \; – \; \frac{f(x_{0})}{f'(x_{0})}$$

Чтобы начать процесс вычислений, мы должны принять решение о первоначальном приближении корня, которое мы назовем х ₀ .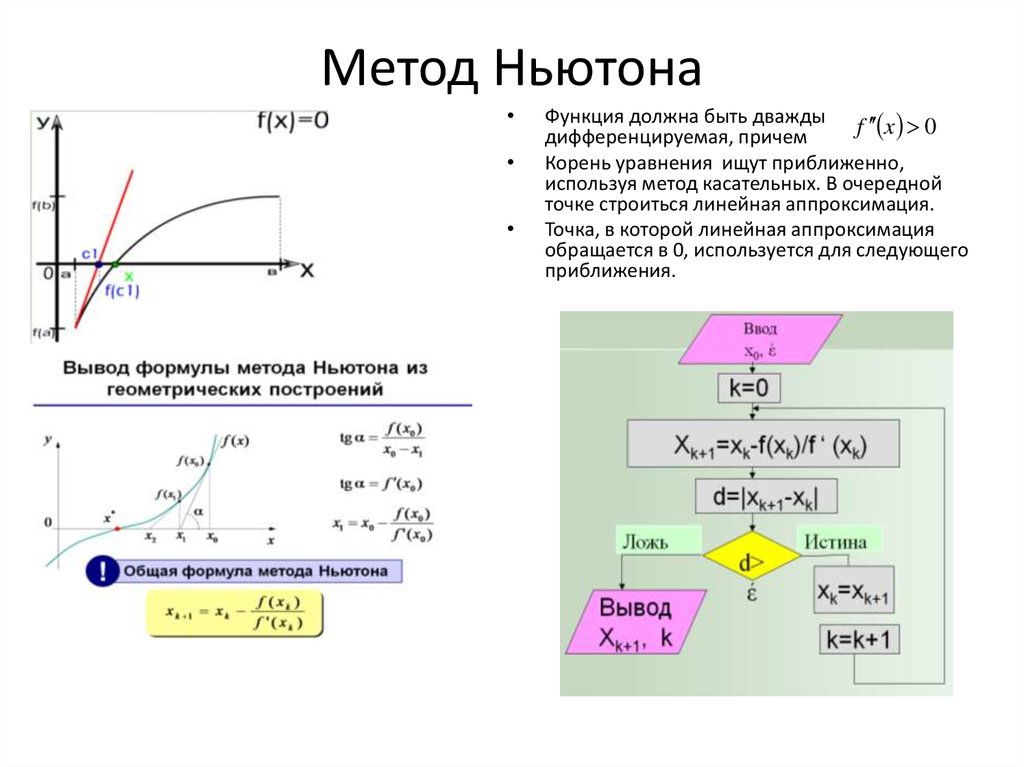 Начальное предположение может быть любым действительным числом, но имейте в виду, что чем ближе наше первоначальное предположение к фактическому корню функции, тем больше вероятность, что мы быстро найдем решение.

Затем оцените функцию и ее производную в x = x ₀ . Подставьте x ₀ , f(x ₀ ) и f ‘(x ₀ ) в уравнение, чтобы найти x _{1 _{0 . Мы завершили первую итерацию и должны определить, нужны ли еще итерации.}}

Чтобы определить, необходимы ли дополнительные итерации, мы используем следующие формулы критериев сходимости:

$$\lvert x_{i + 1} \; – \; x_{i} \rvert \leq \varepsilon \; \текст{ и } \; \lvert f(x_{i + 1}) \rvert \leq \delta $$

Где x _{i + 1} — это значение x , вычисляемое для новой итерации, x _i — это значение x предыдущей итерации, ε — желаемая точность (близость последовательных значений x), f(x _i+1 ) — значение функции при x _i+1 , а δ — желаемая точность (близость аппроксимированного корня к истинному корню).

Мы должны определиться со значениями ε и δ и оставить их постоянными на протяжении всего цикла итераций. Чем меньше эти значения, тем более точным и точным будет наше решение. Однако, если мы установим слишком малые значения, может потребоваться чрезмерное количество итераций, чтобы удовлетворить критерии сходимости.

Теперь мы проверяем, удовлетворяются ли критерии сходимости, подставляя значения соответствующих переменных в каждую из двух формул критериев сходимости. Для первой итерации i = 0 это будет выглядеть так:

$$ \begin{align} & \lvert x_{(0)+1} \; – \; x_{(0)} \rvert \leq \varepsilon \; \Правая стрелка \; \lvert x_{1} \; – \; x_{0}\rvert \leq \varepsilon \\ \\ & \lvert f(x_{(0) \; + \; 1}) \rvert \leq \delta \; \Правая стрелка \; \lvert f(x_{1}) \rvert \leq \delta \end{align}$$

Для выполнения критериев сходимости неравенства в каждой из формул должны выполняться. Если одно из неравенств верно, а другое нет, то сходимость не достигнута, и итерация должна продолжаться до тех пор, пока не будут удовлетворены критерии сходимости.

Если критерии сходимости были удовлетворены на данной итерации, расчеты останавливаются и в качестве решения берется значение x для этой итерации.

Иногда метод Ньютона отклоняется от решения, и критерии сходимости никогда не выполняются. Это может произойти за любое количество итераций. При использовании компьютера для решения с помощью метода Ньютона важно установить максимальное количество итераций, чтобы расчеты были остановлены до того, как произойдет потенциально бесконечное количество итераций.

Пример задачи

Вычислите корень из f(x) = x ² – 10 по методу Ньютона.

1.) Используя общее уравнение для метода Ньютона:

$$x_{i + 1} = x_{i} \; – \; \frac{f(x_{i})}{f'(x_{i})}$$

Схождение при:

$$\lvert x_{i + 1} \; – \; x_{i} \rvert \leq \varepsilon \: \text{ и } \: \lvert f(x_{i + 1}) \rvert \leq \delta$$

Использование ε = 0,0001 и Δ = 0,0001

2. 2-10}{2 \cdot (5)} \; \Правая стрелка \; х_{1} = 3,50000$$92-10\rvert = 0.00000\text{, }0.00000\leq0.0001$$

Критерий сходимости выполнен.

Как работает калькулятор

Этот калькулятор написан с использованием технологий веб-программирования HTML, CSS и JavaScript (JS). HTML строит структуру калькулятора, CSS стилизует структуру, а JS обеспечивает взаимодействие с пользователем и выполнение вычислений.

JS запускается в интернет-браузере так же, как программа запускается в операционной системе компьютера. Поскольку этот калькулятор использует только JS для выполнения вычислений, он может предоставить пользователю мгновенные решения.

Внутри JS-кода, на котором работает этот калькулятор, находится та же подпрограмма, которая описана в этом уроке. Введенное пользователем начальное предположение подставляется в формулу метода Ньютона, и вычисляется новое значение 90 297 x 90 300. Формулы критериев сходимости оцениваются и сравниваются с введенным пользователем значением критериев сходимости.