Проект «Решение систем линейных уравнений различными методами» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Проект «Решение систем линейных уравнений различными методами»
Автор: Пономарева Софья Сергеевна
Место работы/учебы (аффилиация): МАОУ «Лицей №15 им. Н.Н. Макаренко», г.Кызыл, Республика Тыва, 10 класс
Научный руководитель: Яговдик Надежда Васильевна
В работе рассмотрены различные математические методы решения систем линейных уравнений, показаны алгоритмы и примеры решения линейных алгебраических уравнений различными методами. Дается краткая историческая справка о жизни ученых, занимавшихся данной проблемой. Приводятся примеры использования СЛАУ. Данная тема способствует формированию математической интуиции, которая поможет ориентироваться в способах решения систем.
Целью работы является оценка различных методов решения систем линейных уравнений с точки зрения вычислительной сложности.
Задачи:
- обобщение методов решения СЛАУ, знакомых с 7 класса;
- знакомство с новыми методами решения СЛАУ;
- изучение истории вопроса (развития теории, имена ученых, их достижения).
При работе над данным проектом прослежено развитие алгебры на протяжении 2,5 тысяч лет, накоплен банк задач, решенных разными методами. Исследованы методы решения систем уравнений. Например, графический метод решения более удобен для системы из двух линейных уравнений (наглядно и быстро), а метод Гаусса для этой цели менее пригоден. Он проигрывает с точки зрения наглядности. Однако, именно метод Гаусса и метод Крамера являются наиболее универсальными для решения систем уравнений с большим количеством уравнений и переменных.
Работа на выбранную тему является актуальной в связи с тем, что она систематизирует знания и позволяет учащимся лучше понять данную тему, т.к. способы решения систем линейных уравнений собраны в единое пособие.
Загрузка. ..
..
Проектная работа «Нестандартные способы умножения»
Тема очень актуальна, поскольку простое умножение — это долгое и скучное занятие, а вот с нестандартными способами это занятие становиться весёлым и быстрым. Цель: подробно рассмотреть несколько нестандартных способов умножения и выявить самый удобны…
Посмотреть работу
Исследовательская работа «Многоугольники на целочисленной решетке»
Мы часто предпочитаем рисовать и чертить на клетчатой бумаге. И даже не задумываемся о том, что она (а точнее – узлы клетчатой бумаги) являются одним из важнейших примеров точечной решетки на плоскости. Решетки на плоскости позволяют переводить на ге…
Посмотреть работу
Исследовательский проект «Уравнения высших степеней»
Решение алгебраических уравнений высших степеней с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Интерес к ним велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школ…
Интерес к ним велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школ…
Посмотреть работу
Исследовательский проект «Золотое сечение — красота и гармония окружающего нас мира»
Актуальность: окружающий нас мир многообразен. Все, наверное, обращали внимание, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность, несоразмерность воспринимаются нами как безобразное и п…
Посмотреть работу
Исследовательский проект «Множества на диаграмме Эйлера-Венна и ее практическое применение»
Множества встречаются в различных областях знаний: математике, физике, биологии, химии, лингвистике и т.д. Множества состоят из различных элементов, например, страны, дома, птицы, числа, фигуры, точки и т.д. В математике множество рассматривается в к…
Посмотреть работу
4″>Исследовательская работа «Прогрессии вокруг нас»Доступна к просмотру полнотекстовая версия работы
В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материала с жизнью. В 9 классе мы сталкиваемся с темой «Прогрессии», даем определение термину, также используем основные формулы прогрессии…
Посмотреть работу
Мероприятие завершено
Решение системы линейных уравнений методом Гаусса онлайн
Система линейных уравнений
Для решения любой системы линейных уравнений метод Гаусса или метод последовательного исключения неизвестных является наиболее универсальным и достаточно простым при небольшом количестве переменных. Этот метод универсален, его применяют, когда система уравнений имеет:
- единственное решение;
- бесконечное множество решений;
- вовсе не имеет решений.
Суть метода состоит в переходе от заданной системы линейных уравнений к более простой с помощью таких эквивалентных преобразований в системе, как:
- перемена двух уравнений местами;
- умножение обеих частей уравнения на любое действительное число, не равное 0;
- прибавление к одному уравнению соответствующих частей другого, умноженных на произвольное число.

С помощью преобразований последовательно исключаем одну переменную за другой пока в одной из строк не будет определена переменная xi.
Метод Гаусса позволяет решать СЛАУ при небольшом числе вычислительных операций.
Алгоритм решения:
- записываем систему в виде расширенной матрицы;
- прямой ход — приводим матрицу к ступенчатому виду;
- обратный ход — приводим матрицу к специальному ступенчатому виду.
Пусть дана система из n уравнений с n неизвестными переменными:
Определитель основной матрицы не равен 0.
Исключим из всех уравнений системы переменную х1, начиная со 2-го, для чего:
- ко 2-му уравнению прибавим 1-е, умноженное на — а21/а11;
- к 3-му уравнению прибавим 1-е, умноженное на — а31/а11, и т.д.;
- к n-му уравнению прибавим 1-е, умноженное на — аn1/а11.
В результате преобразований система приняла вид:
Далее таким же путем исключаем неизвестную переменную х2 из всех уравнений, начиная с 3-го.
Для этого к 3-му уравнению прибавляем 2-е, умноженное на — а32/а22 и т.д. К n-му уравнению прибавим 2-е, умноженное на — аn2/а22.
Таким же способом исключаем неизвестную х3 из всех уравнений системы, начиная с 4-го.
Прямой ход продолжается, пока в последнем уравнении не останется единственная неизвестная. Система будет иметь вид:
аnn(n-1) хn = bn(n-1)
После окончания прямого хода метода Гаусса — последовательного исключения неизвестных, вычисляем неизвестную в последнем уравнении:
- из последнего уравнения системы находим хn по формуле:
- из предпоследнего уравнения находим х n-1 и т.д.
- из первого уравнения находим х1.
Последовательное нахождение неизвестных, начиная с последнего уравнения к первому, называется обратным ходом.
Заметим, если в матрице есть хоть одна нулевая строка, у которой правая часть (свободный член) не равна 0, система несовместима, решения отсутствуют.
Для быстрого и правильного решения СЛАУ методом Гаусса можно воспользоваться калькулятором онлайн.
Решение системы линейных уравнений методом Гаусса
| 123456 — количество неизвестных |
Предыдущая Метод хорд решения нелинейных уравнений
Следующая Линейная интерполяция
detector
гауссовых решений | Стохастический анализ и диффузионные процессы
Фильтр поиска панели навигации Oxford AcademicСтохастический анализ и диффузионные процессыПрикладная математикаВероятность и статистикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicСтохастический анализ и диффузионные процессыПрикладная математикаВероятность и статистикаКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Cite
Kallianpur, Gopinath, and P. Sundar,
Sundar,
‘Gaussian Solutions’
,
Stochastic Analysis and Diffusion Processes
(
Oxford,
2014;
online edn,
Oxford Academic
, 16 апреля 2014 г.
), https://doi.org/10.1093/acprof:oso/9780199657063.003.0009,
, по состоянию на 12 ноября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicСтохастический анализ и диффузионные процессыПрикладная математикаВероятность и статистикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicСтохастический анализ и диффузионные процессыПрикладная математикаВероятность и статистикаКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
Гауссовы решения стохастических дифференциальных уравнений играют особую роль в задачах линейной фильтрации. После обсуждения специальной факторизации Гохберга-Крейна исследуется ее связь с гауссовыми процессами. Установлено неупреждающее представление гауссовского процесса, эквивалентного винеровскому процессу. Изучаются гауссовы решения функциональных стохастических дифференциальных уравнений и их представления.
После обсуждения специальной факторизации Гохберга-Крейна исследуется ее связь с гауссовыми процессами. Установлено неупреждающее представление гауссовского процесса, эквивалентного винеровскому процессу. Изучаются гауссовы решения функциональных стохастических дифференциальных уравнений и их представления.
Ключевые слова: Специальная факторизация Гохберга-Крейна, эквивалентность гауссовских мер, гауссовские процессы, неупреждающие представления, функциональные стохастические дифференциальные уравнения
Предмет
Прикладная математика Вероятность и статистика
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти с помощью личного кабинета
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Обзор последних достижений в методах регрессии гауссовых процессов
Лю, К. , Лю, X. и Михайлова, Л. orcid.org/0000-0001-5856-2223
(Принято: 2022 г.) Обзор последних достижений в методах регрессии гауссовых процессов. В:
Материалы британского семинара по вычислительному интеллекту 2022 года. UKCI’2022 — Семинар Великобритании по вычислительному интеллекту, 07–09 сентября 2022 г., Шеффилд, Великобритания.
Достижения в области интеллектуальных систем и вычислений
.
Спрингер Природа
.
(Под давлением)
, Лю, X. и Михайлова, Л. orcid.org/0000-0001-5856-2223
(Принято: 2022 г.) Обзор последних достижений в методах регрессии гауссовых процессов. В:
Материалы британского семинара по вычислительному интеллекту 2022 года. UKCI’2022 — Семинар Великобритании по вычислительному интеллекту, 07–09 сентября 2022 г., Шеффилд, Великобритания.
Достижения в области интеллектуальных систем и вычислений
.
Спрингер Природа
.
(Под давлением)
Abstract
Методы гауссовского процесса (ГП) в последнее время широко изучаются, особенно для крупномасштабных систем с большими данными и даже в более экстремальных случаях, когда данных мало. Ключевые преимущества этих методов заключаются в следующем: 1) способность обеспечить встроенные способы оценки влияния неопределенностей (особенно в данных и окружающей среде) на решения, 2) иметь эффективные реализации на основе факторизации и 3) может быть легко реализована в распределенными способами и, следовательно, обеспечивают масштабируемые решения.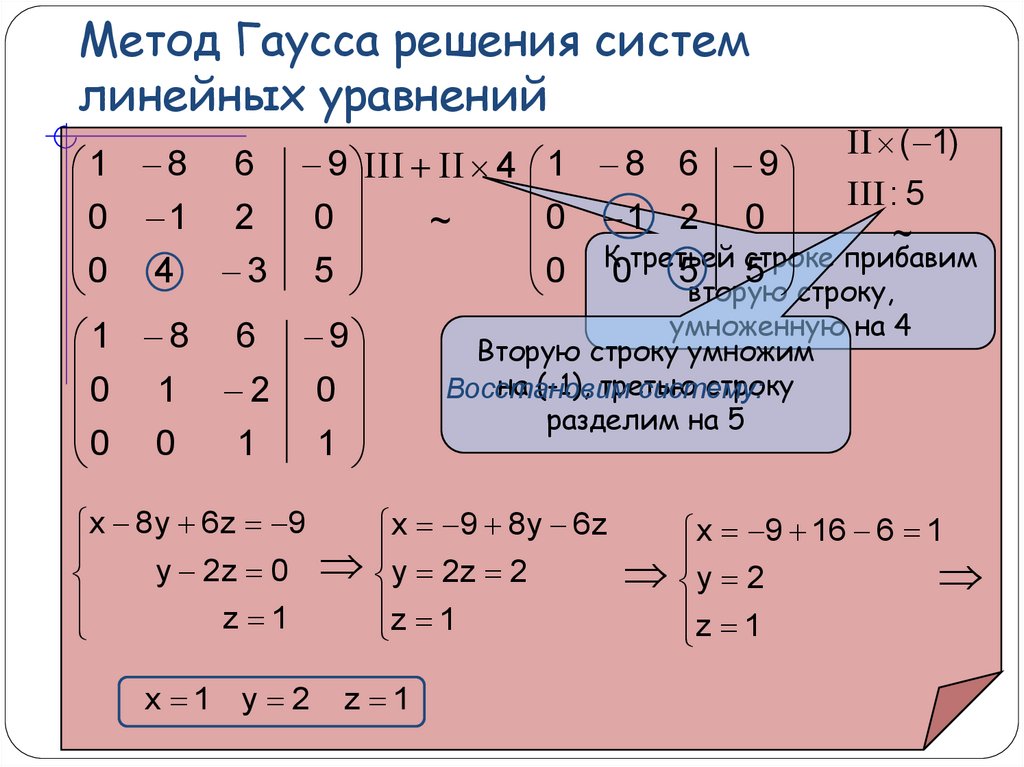 В этой статье рассматриваются недавно разработанные ключевые факторизованные методы ГП, такие как иерархические недиагональные методы аппроксимации низкого ранга и ГП со структурами Кронекера. Пример иллюстрирует производительность этих методов в отношении точности и вычислительной сложности.
В этой статье рассматриваются недавно разработанные ключевые факторизованные методы ГП, такие как иерархические недиагональные методы аппроксимации низкого ранга и ГП со структурами Кронекера. Пример иллюстрирует производительность этих методов в отношении точности и вычислительной сложности.
Метаданные
| Авторы/создатели: |
| ||||
|---|---|---|---|---|---|
| Авторские права, издатель и дополнительная информация: | © 2022 Авторы. | ||||
| Ключевые слова: | Гауссовский процесс; факторизация; ковариационная матрица; иерархический недиагональная матрица; низкоранговое приближение | ||||
| Даты: |
| ||||
| Учреждение: | Университет Шеффилда | ||||
| Академические единицы: | Университет Шеффилда > Инженерный факультет (Шеффилд) > Факультет автоматического управления и системотехники (Шеффилд) | ||||
| Информация о финансировании: |
| ||||
| Вносящий пользователь: | Симплектический Шеффилд | ||||
| Дата депонирования: | 09 авг 2022 10:38 | ||||
| Последнее изменение: | 09 авг 2022 10:38 | ||||
| Статус: | В прессе | ||||
| Издатель: | Спрингер Природа | ||||
| Название серии: | Достижения в области интеллектуальных систем и вычислений | ||||
| Рефери: | Да | ||||
| Связанные URL: |
|
Скачать
Принятая версия
Под временным эмбарго
Имя файла: UKCI20229890_GPM.


 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.
