Метод подстановки система уравнений: Решение систем уравнений — метод как решить систему линейных уравнений

Урок по теме: «Решение систем уравнений способом подстановки» | План-конспект урока по алгебре (7 класс):

Урок  по теме: «Решение систем уравнений способом подстановки»

Дата: 10.04.2015 г.                                                                 Алгебра 7 класс

Цель: обеспечить осознанное усвоение обучающимися алгоритма решения систем линейных уравнений способом подстановки.

Задачи урока:

— расширить знания обучающихся о системах линейных уравнений, совместно с обучающимися составить алгоритм решения систем уравнений способом подстановки,

 — способствовать развитию аналитического мышления, формированию культуры речи, обеспечить усвоение обучающимися способа подстановки при решении систем линейных уравнений,

— работать над формированием у каждого школьника навыков самообучения и самоконтроля, включить каждого обучающегося в осознанную учебную деятельность, предоставить возможность продвигаться в изучении материала в оптимальном для себя темпе.

ХОД УРОКА

                                                         Математику уже затем учить надо,  

                                                         что она ум в порядок приводит.

                                                                                            М.В. Ломоносов

1.Организационный момент. Мотивация.

Здравствуйте, присаживайтесь.  У меня к вам будет просьба: попробуйте сейчас достать левой рукой правое ухо… Вы видите, что сделать это можно по-разному. Да, кто-то испытал сейчас определенные неудобства, но главное — цель достигнута. Сегодня на уроке мы также будем искать способы решения различных заданий.

Перед вами знакомая аббревиатура — ЕГЭ. Как вы думаете, наш урок, какое к ней имеет отношение? ….. Конечно, мы коснемся тем, которые есть в заданиях ЕГЭ, а вы готовы при этом экспериментировать? …. Предлагаю превратить нашу тему в девиз: Если Готов – Экспериментируй!

2. Актуализация знаний

У каждого из вас на парте лежит лист, который называется рабочим полем. Тетради вам сегодня не понадобятся, все необходимые вычисления вы будете выполнять в рабочем поле.

— выполните действие:

 

— выразите одну переменную через другую:

-найдите два каких-либо решения данного уравнения, выразив «y» через «x»:

— выполните решение уравнения:

Какие теоретические знания вы использовали при выполнении этих заданий?

(Составление кластера)

Умножение                     Выражение из уравнения                  Нахождение

одночлена на                  одной переменной через                    значения

многочлен        другую                                              выражения

Линейное         Система двух                  Линейное уравнение

уравнение           линейных                       с двумя переменными

                                                       уравнений

                                  Нахождение

                            решения линейного

                                  уравнения

Работа с обучающимися после составления кластера:

— Линейное уравнение с двумя переменными – что это?

-Что называют решением линейного уравнения с двумя переменными?

— Что получится, если объединить 2 уравнения с двумя переменными?

-Что называют решением системы уравнений?

3. Объяснение нового материала

На прошлом уроке мы с вами решали вот такую задачу:

Сумма двух чисел равна 12, а их разность  — 2. Найдите эти числа.

Методом подбора мы с вами определили значения: 5 и 7. Дома вам было предложено самостоятельно разобрать способ решения этой системы уравнений.

(Один ученик у доски объясняет способ решения, затем сформулировать этапы алгоритма, пропустив 2 этап «подстановку»)

Алгоритм решения системы двух уравнений

1.Выразить из одного уравнения системы одну переменную через другую.

2.Подставить в другое уравнение системы вместо этой переменной полученное уравнение.

3. Решить получившееся уравнение с одной переменной.

4. Найти соответствующее значение второй переменной.

Какое название дали бы вы этому способу?

Запишите тему урока в рабочем поле: «Решение систем двух уравнений способом подстановки»

4. Физкультминутка

Мы сидели и писали,

Мышцы тела все устали.

Потянулись и зевнули,

Спинки дружно все прогнули.

Повернулись вправо, влево –

Стало гибким наше тело.

Головой все повращаем

И урок наш продолжаем!

5. Практическая часть

 Решение систем уравнений:

             2.        3*.

6. Первичный контроль

Обучающимся предлагается выбрать и решить 1 из 3 систем линейных уравнений различного уровня сложности (с последующей самопроверкой).

1 уровень                                  Ответ: (1;3)

 2 уровень                                          Ответ: (-20;-2)

 

3 уровень                       Ответ: (28;7)

7.  Домашнее задание

обязательный уровень – №1070 (б,г)

повышенный уровень — № 1100  

 В мастерской «Автосервис» всего отремонтировали 22 легковых и грузовых автомобиля. Среди них легковых было на 8 меньше, чем грузовых. Сколько грузовых автомобилей отремонтировали в мастерской?

(совместно с обучающимися рассмотреть составление системы по условию задачи)

8. Итог урока

Продолжи фразу:

«Сегодня на уроке я повторил…»

«Сегодня на уроке я узнал. »

«Сегодня на уроке я закрепил.»

«Сегодня на уроке мне понравилось…»

«Сегодня на уроке мне понравилось…»

Выставление оценок:

  — за работу  у доски;

  — за активную работу на уроке;

  — за самостоятельную работу (после проверки).

Обучение общему приёму решения систем уравнений

В настоящее время образовательные стандарты стали все больше обращаться к компетенциям как к ведущему критерию подготовленности учащихся к эффективной деятельности в определенной сфере. Одна из компетенций – умение ориентироваться в информации, умение ее получать, анализировать и т.д., т.е. учащиеся должны владеть определенными общими приемами деятельности. На материале темы “Системы рациональных уравнений” (8-ой класс) мы рассмотрим один из таких приемов, касающийся анализа данной системы и построения (выбора) способа ее решения в зависимости от ее вида. При этом закладывается такое важное качество знаний, которое называется обобщенностью.

Основные общие методы решения систем уравнений отрабатываются в средней школе при изучении темы “Системы линейных уравнений” в 7-ом классе. Это метод подстановки, метод сложения, уравнивания коэффициентов. На материале темы “Системы рациональных уравнений” (8-ой класс по учебнику С.М. Никольского и др.) обычно предполагается тренировка тех же методов на системах другого вида и иногда введение дополнительных общих методов решения систем. В реальной практике, когда ученик сталкивается с системой уравнений, ему необходимо самому сориентироваться и выбрать способ ее решения, но анализ учебных пособий показал, что в них процесс анализа системы и выбора способа решения не делается предметом специального усвоения, а лишь тренируется умение применять изученный метод к данной системе. В итоге учащиеся не всегда владеют полной системой знаний и умений, ориентируясь на которые можно выбрать (построить) адекватный, наиболее эффективный способ решения заданной системы.

Нами была сделана попытка формирования такой системы знаний и умений. Ведь решение систем уравнений важно не только в плане содержания курса математики; они используются в физике, химии, при решении технических, инженерных задач, при работе с моделями экономических, социальных, биологических и пр. явлений и процессов.

Покажем на примере нескольких уроков для 8-го класса, каким образом мы планируем организовать совместную деятельность учащихся и учителя по выделению содержания названного умения на первом этапе. Так как одним из компонентов является анализ заданной системы на наличие решений, то один из первых уроков посвятим именно этому вопросу. Затем попытаемся выделить общий прием решения систем уравнений и связать с известными школьникам методами. Для этого нами разработаны рекомендации и специальная система заданий.

Принципы построения системы заданий для первого этапа обучения следующие:

– порядок заданий фиксирован, он выполняет направляющую функцию, позволяя школьникам вместе с учителем выстроить ориентировочную основу деятельности по решению произвольной системы рациональных уравнений и создать в итоге схему ее решения,

– каждая следующая система связана с предыдущими заданиями и рассуждениями, но содержит в себе одну или несколько новых важных идей, логично развивающих тему,

– переменные в системах варьируются: не всегда привычные x и y (ведь при моделировании системами уравнений реальных задач из самых разных областей не всегда удобно вводить обозначения x и y),

– помимо заданий, где система уравнений задана, предлагаются и творческие задания, связанные с придумыванием тех или иных систем.

Материалы к урокам

1. Системы, не имеющие решений.

а) Случай, когда в системе имеется противоречивое уравнение (не имеющее решений):

№ 1. Ответ: .

Один из самых очевидных случаев: сразу можно заметить, что первое уравнение не имеет решений. Если же в правой части первого уравнения стояло бы неотрицательное число, то такая система имела бы решение. Немного усложнив данную систему, вместе со школьниками можно “придумать”, например, следующие не имеющие решений системы:

и т.д. Ответ: .

Обращаем внимание школьников на то, что каким бы в данном случае ни было второе уравнение системы, решений она иметь не будет (вспомним определение решения системы уравнений).

№ 2.

Ответ: .

Первое уравнение системы имеет решения. В левой части второго уравнения сумма двух неотрицательных чисел, а в правой – отрицательное число. Противоречие. Отметим, что достаточно хотя бы одного противоречивого уравнения, чтобы дать ответ.

№ 3. Ответ: .

Несколько более замаскировано противоречивое уравнение. Здесь, чтобы его распознать, нужно увидеть во втором уравнении формулу квадрата разности. Далее аналогично номеру 1.

Задание школьникам: составьте еще системы, не имеющие решений.

№ 4. Ответ: .

Если сразу заметить или вспомнить, что дробь с ненулевым числителем не может быть равна нулю, то ответ очевиден. Если же заменить в условии ноль на ненулевое число, то решения системы могут появиться.

№ 5. Ответ: .

Результат деления отрицательного числа на отрицательное не может быть отрицательным, поэтому первое уравнение (а значит и система) не имеет решений.

б) Случай, когда в системе имеются неопределенные выражения (ОДЗ пусто):

№ 6. Ответ: .

В первом уравнении под знаком корня (радикала) стоит отрицательное выражение, значит, такого арифметического квадратного корня не существует ни при каких значениях x. Вспоминаем определение решения системы уравнений и делаем вывод о том, что система несовместна, т.е. не имеет решений. Таким образом, решение этой системы (и ряда других) нужно начинать с ОДЗ. Ведь если становится ясно, что ОДЗ пусто (как в данной системе), то и множество решений будет пусто.

Эта система не является системой рациональных уравнений, т.е. не входит в рассматриваемую тему, но она содержит принципиально важную идею, поэтому ее полезно дать и на данном этапе. К тому же это позволит повторить и закрепить определение системы рациональных уравнений.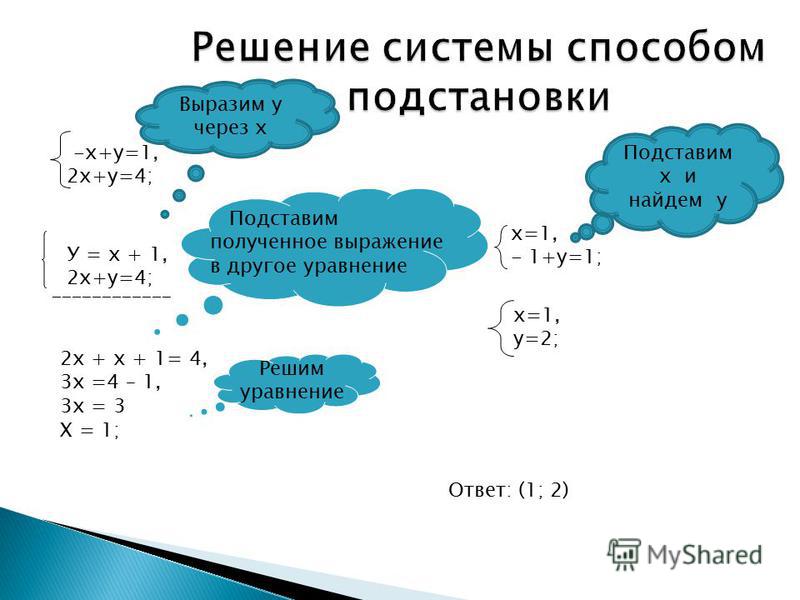 Определение и свойства арифметического квадратного корня восьмиклассникам уже известны.

Обсуждение: Как еще можно “построить” противоречивое уравнение? Какие ограничения на значения выражений могут быть? Из этой части урока делам вывод о том, что уравнение (а значит и соответствующая система уравнений) не имеет решений, когда:

а) не может выполняться равенство из-за тех или иных свойств:

ограничения по знаку: , , ,

дробь при ,

комбинации: , , при и и т.п.

б) какое-то входящее в него выражение не определено (т.е. не существует, не имеет смысла) (см. задание №  4):

не существует при ,

не существует при .

Здесь стоит провести параллель с заданиями, опирающимися на те же идеи. Это задания найти ОДЗ переменных в выражении, область определения функции (ООФ), множество значений функции (выражения).

в) Случай, когда в системе одно уравнение противоречит другому:

№ 7. Ответ: .

Один из самых явных случаев: видим, что левые части обоих уравнений совпадают, а правые – нет. Противоречие.

№ 8. Ответ: .

Если разделить второе уравнение на 4 и перенести все члены каждого уравнения в одну сторону, то станет видно, что уравнения противоречат друг другу.

Здесь логично возникает вопрос: а что делать, если не заметили сразу, что система несовместна? Ответ: решать ее известными методами. Ответ получится сам собой, если все делать верно и понимать про вырожденные уравнения (0=0, 4=0 и т.п.), при встрече с которыми многие школьники теряются, как показывает школьная практика. Поэтому для преодоления возможных затруднений здесь важно обратить внимание учащихся на то, что при решении любых уравнений или систем вопрос ставится всегда один и тот же: “При каких значениях неизвестной верно равенство?” или соответственно “При каких парах (тройках, четверках, …) переменных верны одновременно все равенства системы?”.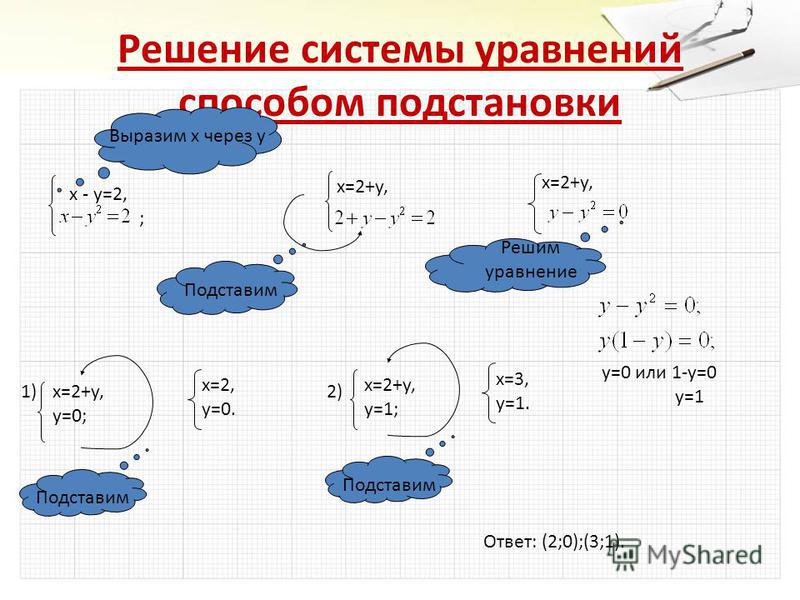

Помня это, нетрудно понять, что если в ходе решения получилось что-то вроде 0=4, то решений у этого “уравнения” и у исходной системы нет; а если же получилось, например, 0=0 и нет других противоречий, то решений у системы бесконечно много.

Задание школьникам: придумайте еще несколько систем, не имеющих решений, таких чтобы при замене в ней одного числа или знака на другое решения у нее появлялись. Придуманные системы по парам занесите в таблицу:

Система, не имеющая решений	Система, имеющая решения

Таким образом, результатом первичного анализа системы может быть один из трех

важных выводов:

1) (–) система не имеет решений дальнейшее решение не нужно,

2) (+) система имеет решение (решения) нужно решать,

3) (?) система может иметь решения (а может и не иметь) нужно решать и помнить про сказанное выше.

После этой части урока вместе со школьниками делается вывод о том, что начинать решение системы нужно с ее анализа, т.к. если сразу удастся понять, что она не имеет решений, то не надо будет тратить время на решение, а сразу можно будет дать верный ответ. В этом присутствует и воспитательный эффект, касающийся важности предварительного анализа ситуации, объекта, явления.

На данном материале идет отработка важного навыка “всматривания” в систему и ее составные части – уравнения. Заметим, что тот же навык может отрабатываться и при решении уравнений (например, методом замены неизвестной). Он же пригодится и при решении систем, имеющих решение.

Стоит обратить внимание школьников на различные термины, употребляющиеся по отношению к уравнениям и системам, не имеющим решений (несовместным, противоречивым). Это важно для понимания математических задач и текстов, взятых из различных источников.

Для закрепления материала, в том числе терминологии, и проверки результатов этой части урока ученикам предлагается небольшое задание: заполнить следующую таблицу (в каждой ячейке проставьте знаки +, – или ? в зависимости от того, характеризует ли указанное в заголовке столбца данную систему). Столбцы таблицы: система | имеет решения | ответ: ? | не определено какое-то выражение | противоречива | несовместна | совместна.

2. Случай, когда одно из уравнений содержит лишь одну неизвестную.

№ 9. Ответ: и .

Очевидных противоречий в данной системе нет (в отличие от предыдущих). Можно заметить, что в первом уравнении системы присутствует только одна переменная (d), поэтому первое уравнение мы можем сразу решить. Его корни: -1 и 2. Подставляем эти значения по очереди во второе уравнение и находим другую неизвестную – z. Здесь вспоминаем, что решением системы двух уравнений с двумя неизвестными являются пары чисел.

При решении данной системы у школьников возникает разумный вопрос: “В каком порядке записывать в ответе числа, ведь здесь не x и y?”. Ответ: в алфавитном (как и в случае с x и y).

3. Случай, когда в явном виде имеется общее выражение в нескольких уравнениях, т.е. обобщенная подстановка, приводящая к ответу, уже подготовлена.

Вспоминаем стандартный метод подстановки, известный школьникам с 7-го класса. Отмечаем, что он работает в любых системах уравнений, не только в системах линейных уравнений.

Рассматриваем идею о том, что подставлять в другое уравнение можно не только переменную, но и некое выражение. Для этого должны иметься одинаковые выражения в нескольких уравнениях системы.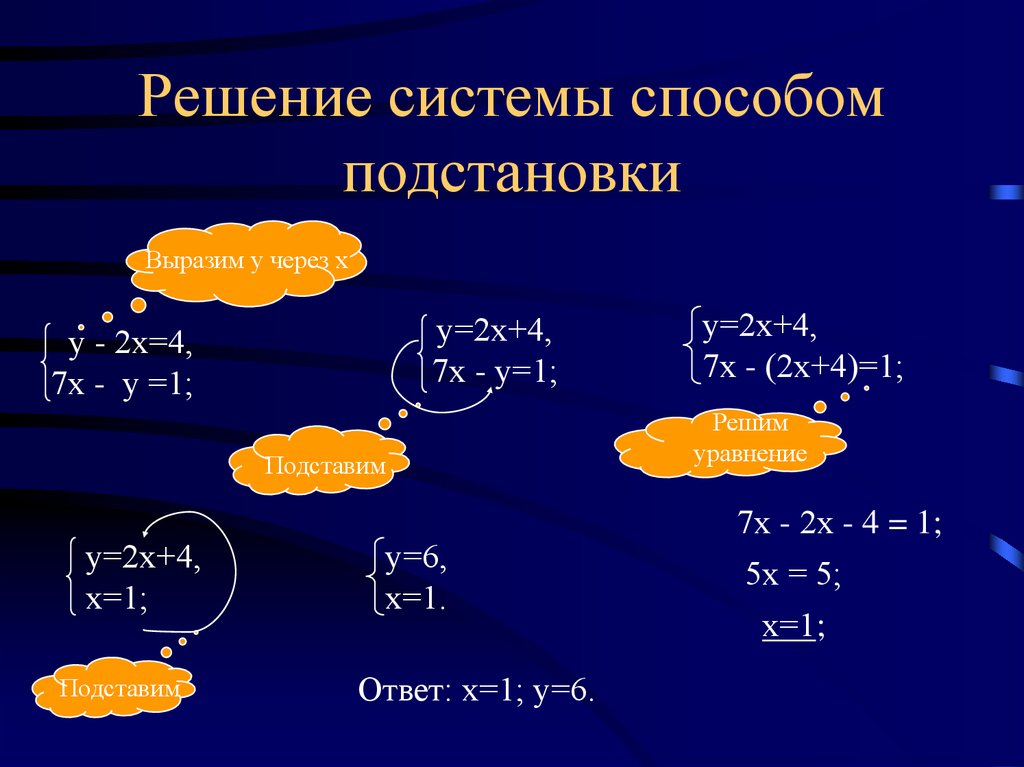 В данном случае это так. Здесь же может возникнуть разумный вопрос: “Что делать, если одинаковых выражений в уравнениях нет?”

Таким образом, переходим к обобщенному методу подстановки и затрагиваем идею о выражении как обобщенной переменной (отсюда берет начало метод замены неизвестной, используемый при решении уравнений и систем.). В данной системе можно заменить на новую переменную z. Тогда система примет вид элементарной системы линейных уравнений. Анализ учебных пособий и методов решения систем уравнений показал, что очень широкий класс систем, предлагаемых в школьном курсе математики, решается с помощью обобщенного метода подстановки, который можно назвать центральным, главным методом. Попробуем этим методом решать все предлагаемые далее системы.

Тут два варианта проведения обобщенной подстановки: b² и b² + u². Второй в данном случае удобнее, хотя чтобы его применить, исходную систему надо “подготовить”: разложить левую часть второго уравнения на множители. Первый требует больше алгебраических преобразований, следовательно, вероятность ошибок при решении возрастает. Таким образом, иногда подстановку придется подготовить (прежде чем выполнять).

Здесь начнем выявлять и фиксировать приемы, позволяющие выделять общие выражения в двух уравнениях. В данном примере – прием разложения на множители. Какие еще могут быть приемы? Их может быть очень много. Эту область можно назвать “творческой”, т.к. здесь нужно “изобрести” способ сделать так, чтобы появились одинаковые выражения, причем удобные для дальнейшего решения системы. “Творческая” область весьма обширна.

Здесь тоже два варианта выполнения подстановки. В указанном выше варианте используется другой прием – домножение обеих частей одного из уравнений системы на неизвестную. Тонкий момент: домножать на ноль нельзя . Но именно такова здесь ОДЗ!

4. Случай, когда в уравнениях нет подходящих общих выражений для подстановки, но они легко могут быть выделены.

На примере этой системы можно “изобрести” новый для 8-классников метод – метод почленного деления. Эта система решается методом деления и решается методом обобщенной подстановки, который в данном случае фактически дублирует в неявном виде метод деления.

№ 17.

Здесь сталкиваемся с тем, что решений у системы не конечное, а бесконечное количество. Как записать ответ в этом случае? У школьников часто возникают сложности в таких случаях.

5. Переход к методу сложения.

№ 18. . Ответ: .

Можно выполнить обобщенную подстановку (2 варианта подстановки), а можно сложить уравнения. Вспоминаем метод сложения (метод вычитания). Отметим, что метод сложения в данном случае фактически дублирует метод обобщенной подстановки, лишь немного упрощая выкладки.

Кстати, в данном случае на уровне обыкновенной логики можно было сразу сделать вывод, что решений у системы нет.

6. Случай, когда есть несколько вариантов подстановки.

№ 19.

Есть выбор: иметь дело с целыми числами (если подставлять r²) или с дробными (если подставлять j²). Удобнее и надежнее работать с целыми числами, поэтому лучше выбрать первый вариант, хотя к ответу приведут оба. Можно здесь сделать замену, но необходимости нет.

Можно ли к данной системе применить метод сложения? Сразу к исходной системе бессмысленно, т.к. обе неизвестные останутся. Но если домножить уравнения на подходящие числа, то сложение полученных уравнений может избавить от одной из неизвестных, что поможет решить систему. Получаем обобщенный метод сложения или метод уравнивания коэффициентов (в литературе называется по-разному).

7. Случай, когда удобна замена неизвестной

№ 20.

Нетрудно заметить одинаковые выражения в уравнениях, их замена на новые неизвестные позволит упростить систему. Приходим к методу замены неизвестной.

8. Система трех уравнений с тремя неизвестными.

№ 21. Ответ: и .

Обобщенный метод подстановки здесь по-прежнему работает, однако подстановку нужно будет выполнить несколько раз. А что если попробовать сложить все уравнения? Получится a = 1. Т.е. в данном случае метод сложения весьма удачен.

Из очередной части урока делаем вывод:

Обобщенный метод подстановки позволяет решить широкий спектр систем уравнений. Для решения этим методом нужно выделить подходящие общие выражения в нескольких уравнениях, выразить из какого-то уравнения одно из выражений через остальные переменные и подставить в другие равенства системы для того, чтобы свести систему к уравнению с одной неизвестной. При этом стандартный метод подстановки является частным случаем обобщенного, а методы сложения (вычитания), уравнивания коэффициентов, почленного деления, замены неизвестной являются “помощниками” обобщенного метода подстановки, позволяющими несколько упростить выкладки.

9. Дополнительные задания.

Рассуждаем далее: метод сложения, вычитания, деления был. А как же с методом умножения? Есть ли он? Полезен ли он? Да. Пример:

№ 22. подставляем.

Обобщенный метод подстановки здесь “напрашивается”, т.к. имеются общие выражения (x²y), но не помогает. Зато хорошо работает метод умножения одного уравнения системы на другое.

№ 23.

Из первого уравнения системы можно найти и x и y, однако это не пара, которая войдет в ответ.

Домашнее задание:

Придумайте и нарисуйте схему, отражающую предлагаемый вами алгоритм решения произвольной системы уравнений с учетом всего рассмотренного и сказанного на уроках. Так чтобы если дается система уравнений и ваша схема, то, пользуясь последней как подсказкой, человек решил бы данную систему.

На следующих уроках – проверка этого задания, обсуждение предлагаемых схем и создание одной общей для класса схемы, отражающей всю полноту ориентировочной основы деятельности по анализу и решению данной системы уравнений. Дальнейшая работа будет направлена на организацию усвоения выявленной и зафиксированной совместно со школьниками схемы решения систем уравнений.

рабочих листов | TPT

by

Обучаемый учитель

25,00 $

20,00 $

Bundle

Универсальные отрывки для чтения дают вашим учащимся возможность практиковать фонетику и беглость речи с помощью этих отрывков на понимание прочитанного. Лучшая часть? С вашей стороны не требуется никакой подготовки! Теперь включает в себя оригинальный PDF + НОВЫЕ цифровые версии каждого отрывка для чтения по фонетике для дистанционного обучения! Каждый отрывок для чтения дает вашим ученикам возможность практиковать целевой навык фонетики в контексте чтения. Каждый фонический отрывок также развивает беглость речи и понимание. это комплект

Субъекты:

ELA Test Prep, Фоника, чтение

Оценки:

1 -й — 2 -й

Типы:

Английский (Великобритания), Книги с руководством, печатные изделия

по

My Nerdy By Alina V

100,00 $

19,00 $

⭐⭐⭐ ФЛЭШ-РАСПРОДАЖА ⭐⭐⭐Купите Mega Bundle The Decodable Readers Passages всего за 19 долларов! Спешите, время истекает! Ваши ученики могут практиковаться в чтении весело и увлекательно, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 2-й

Виды:

Занятия, Центры, Печатные формы

CCSS, RF.K.3.K. .K.3c, RF.1.2c, RF.1.2d…

by

Учитель по соседству

18,00 $

14,25 $

Bundle

Ищете способ сделать обучение написанию параграфов намного проще? Хотите помочь своим ученикам писать хорошо продуманные абзацы? Этот полный набор для написания абзацев как в печатном, так и в цифровом виде поможет вам научить каждую часть абзаца напрямую! Он сочетает в себе четыре из моих очень популярных наборов стратегий письма: цветовое кодирование и выделение абзацев, тематические предложения, переходы в письме и заключительные предложения. Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать

Предметы:

Английская словесность, информационный текст, письменное разъяснение

Классы:

3-8

Типы:

Графические органайзеры, плакаты

CCSS:

4, W.3.3004, W.30003 .5.2, W.5.2a, W.5.2b…

by

На втором месте с Aris

Скоропись — важная часть писательского пути учащегося! Эти практические занятия по рукописному письму не только помогут вашим ученикам улучшить свои навыки письма, но и научатся творческому самовыражению и получат массу удовольствия. ✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет

Тема:

Вернуться в школу, почерк, написание

Оценки:

2 -е — 5 -е

Типы:

, печатные изготовления, рабочие листы

на

Games 4. игры, которые повторяют умножение до 12 x 12. Это интересный способ помочь учащимся развить беглость фактов. Это игры PRINT and PLAY. Они НЕ требуют ПОДГОТОВКИ. Просто распечатайте и раздайте. Каждая игра требует определенного навыка умножения. Они разработаны, чтобы заставить студентов применять свои факты, а также заставить их думать. ПРАКТИКУЙТЕСЬ, А ТОГДА ИГРАЙТЕ: Каждая игра в этом наборе теперь имеет соответствующее задание в БЕЗ ПОДГОТОВКИ Упражнения на умножение.0003

Субъекты:

Основные операции, математика, ментальная математика

Оценки:

2 -е — 4 -е

Типы:

Центры, игры

CCSS:

3.OA.C.7

Также включены в::

3.OA.C. Набор рабочих листов, игр и занятий по умножению Факты умножения Беглость

на

Dana’s Wonderland

Этот продукт содержит 21 отрывок на понимание прочитанного с вопросами, нацеленными на беглость речи и понимание. 21 отрывок для чтения представлен дважды в 2 версиях для облегчения различения. Отрывки также можно использовать в цифровом виде в качестве упражнения на мольберте. В версии 1 детей просят ответить на каждый вопрос полным предложением и раскрасить доказательства в тексте. Версия 2 учит детей смотреть в текст и находить текстовые доказательства без написания предложения. Учащиеся должны будут: * прочитать

Субъекты:

Закрытие чтения, английское языковое искусство, чтение

Оценки:

1 -й — 2 -й

Типы:

Графические организаторы, книги с руководством чтения, печатные изделия

CCSS:

Rl.1.1, RL.1.10:

Rl.1.1, RL.1.10 , Rl.2.1, rl.2.10, ri.1.1…

Также включены в: Отрывки по пониманию чтения и вопросы, комплект

по

My Teaching Pal

$ 22.00

$ 15,00

. тетради по математике для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D

Субъекты:

Основные операции, математика, номера

Оценки:

Типы:

печатные изделия, рабочие тетради, рабочие листы

на

просто Kinder

$ 972.00

$ 25.00

. книги, игры, раскрашивание по коду и многое другое для более чем 200 высокочастотных слов! ЛУЧШИЙ ПРОДАВЕЦ на TpT с более чем 7000 отзывов учителей! Оцените эту невероятную стоимость всего, что вам нужно для практики словесного зрения! Ваша практика словесного зрения стала намного лучше благодаря этому огромному файлу печатных форм, занятий, центров и многого другого. Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса

Предметы:

Английский язык, чтение

Классы:

PreK — 1st

Типы:

Занятия, распечатки, рабочие листы

CCSS, RF. 3.K.9002 .K.3c

by

Lucky Little Learners

34,00 $

23,00 $

Bundle

Отрывки для чтения фонетики, или Phonics Mats, — это идеальный изолированный ресурс, который помогает учащимся без подготовки, распечатайте и приступайте к работе. читаем текст! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью

Предметы:

Акустика, чтение, письмо

Классы:

Типы:

Печатные формы, рабочие листы

CCSS:

RF.2.3, RF.2.3c, RF.2.3b, RF.2.2.2 .2.3d…

by

Patricia Pat Resources

Трудно ли вашим ученикам писать полные предложения или структуру предложений? Если это так, вам понравится, как эти рабочие листы для построения предложений помогут вам научить писать полные предложения. ✏️ Многочисленные изображения в рабочем листе помогут вашим ученикам ПОНЯТЬ и ЗАПОМНИТЬ правильную структуру предложения. ✏️ Это ресурс без подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с помощью ТРЕХ дифференциаций и строительных лесов, сделанных за вас. ✏️ Эти практические рабочие листы будут

Предметы:

EFL — ESL — ELD, английский язык, специальное образование

Классы:

K — 2nd

Типы:

Центры, Домашнее обучение, Домашнее задание

9.1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b

Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Маленькие группы

by

My Nerdy Teacher by Alina V

$100,00

$19,00

! (СТОИМОСТЬ 100 долл. США) Вы ищете веселые и увлекательные занятия по программе Reading Intervention, связанные с наукой о чтении? Получите МЕГАНАБОР Ultimate Phonics Reading Intervention всего за 19 долларов США! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти задания помогут вашим ученикам практиковать фонетические модели, которые вы преподаете

Предметы:

Акустика, чтение, письмо

Классы:

ПреК — 1-й

Типы:

Деятельность, Центры, Печатные формы

CCSS:

РФ.К.1, РФ.К.1а, РФ.К.1б, РФ.К.1с, РФ.К. 1d…

по

Crystal McGinnis

Это задание по поиску и выделению алфавита делает его идеальным центром изучения алфавита! Этот 26-страничный пакет заданий по алфавиту дает учащимся возможность распознавать прописные и строчные буквы алфавита. Учащиеся находят и выделяют прописные и строчные буквы каждой буквы алфавита. Это могло бы стать отличной станцией для обучения грамоте или утренним рабочим занятием. Я также добавил версию этих печатных форм для TPT Easel. (ноябрь 2021 г.) Ваши учащиеся могут просматривать и выделять печатные формы в цифровом виде

Субъекты:

Сбалансированная грамотность

Оценки:

Prek — 1st

Типы:

ПЕЧАТНЫЕ ДЛЯ

CCSS:

RF. K.1D

Также включены в: Dollar Deal Complet Bundle!!! (ВСЕ МОИ ДОЛЛАРОВЫЕ СДЕЛКИ)

by

ThatKinderMama

10,00 $

Это четырехнедельный блок иллюстраций, который поможет писателям детского сада/первоклассника стать уверенными в своих навыках рисования и раскрашивания. Учащиеся начальных классов научатся рисовать фигуры и людей с разными выражениями лица, прическами и оттенками кожи. Это иллюстративное исследование настраивает учащихся детского сада на успех до конца года во время писательского семинара. Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили

Предметы:

Искусство и музыка, Снова в школу, Письмо

Классы:

PreK — 1st

Типы:

Уроки, Печатные формы

Также включены в: LEGROWND Writing Units | Мастерская писателей

by

Susan Jones

Эти занятия и игры, связанные с чувством чисел, идеально подходят для того, чтобы помочь первоклассникам и первоклассникам освоить числа от 0 до 20. Учащиеся практикуются в упорядочивании чисел, сравнении чисел, построении чисел и выявлении различных способов составления чисел от 0 до 20. Что такое чувство числа? Чувство числа — это способность идентифицировать числа и осмысливать их. Мы хотим, чтобы наши ученики с раннего возраста могли определять различные величины и понимать, что означают эти цифры. В этом блоке студенты f

Предметы:

Математика, Цифры

Классы:

PreK — 1st

Типы:

Занятия, игры, распечатки

CCSS:

, KCCB.5.C.A.5.5.A.3 K. , K.NBT.A.1, 1.NBT.A.1

by

Rachel Lynette

Префиксы, суффиксы и корни необходимы для расширения словарного запаса, и эти рабочие листы идеально подходят для того, чтобы учащиеся практиковали приставки, суффиксы, и корневые проблемы.ЧТО ВКЛЮЧЕНО:✍️ ПЕЧАТЬ:40 рабочих листовКлючи ответовЦИФРОВОЙ:120 Google Slides»Worksheet Style» Google SlidesСамооценка префикса и суффикса Быстрые викторины (Google Forms)Easel ActivityВАРИАНТЫ РАЗЛИЧИЯ:Цифровой или печатныйСамопроверка или краткий ответМного разных уровней рабочих листовВеликолепно для 3, 4, 5 или 6 класса! ПОСМОТРЕТЬ ПРЕДВАРИТЕЛЬНУЮ

Субъекты:

EFL — ESL — ELD, ELA TEST PREP, Словарь

Оценки:

3 -е — 6th

Типы:

Независимый рабочий пакет, рабочие листы

CCSS:

L. 3.4B, L. 4.4b, L.5.4b, CCRA.L.4

Также включено в: ELA Review No Prep Bundle, Grammar and Vocabulary Printed and Digital Versions

by

Kim Miller

Вам трудно учить своих учеников как найти основную идею и вспомогательные детали отрывка? Многие студенты борются с этим навыком. Они склонны путаться и зацикливаться на всех мелочах. Эти отрывки для чтения с графическими органайзерами идеально подходят для использования учащимися, когда они тренируются в поиске основной идеи и вспомогательных деталей. После многих лет проб и ошибок я обнаружил, что это решение работает снова и снова.0003

Субъекты:

Английский язык, информационный текст, стратегии чтения

Оценки:

3 -е — 5 -е

Типы:

ПЕЧАТНЫ

Также включено в: Основная идея и вспомогательные детали Мероприятия Графические организаторы Центральный пакет идей

by

Fishyrobb

Ваши ученики любят знать, что происходит в их день? Они постоянно спрашивают вас, что будет дальше? Когда перерыв? Уже пора обедать? Эти ежедневные карточки с расписанием занятий дают учащимся простой способ самостоятельно находить информацию, не спрашивая вас в течение всего дня. Этот ресурс поможет вам легко создать привлекательное визуальное расписание, которое позволит учащимся узнать, что и когда происходит в течение учебного дня. карты сочетаются с любым декором в классе, а также

Предметы:

Снова в школу, Управление классом

Классы:

K — 3-й

Типы:

Идеи для доски объявлений, формы для занятий, плакаты Плакаты для специальных областей

на

Miss Kindergarten Love

18,00 $

15,00 $

Интересный способ помочь вашим ученикам научиться распознавать числа! Эти печатные формы для практики с числами — интересный способ помочь вашим маленьким ученикам попрактиковаться в формировании чисел, чувстве чисел и распознавании чисел. Помогите своим учащимся дошкольного, детского сада и первого класса с помощью веселых и увлекательных способов попрактиковаться в развитии чувства числа, определяя, записывая и считая числа до 50. ⭐️СОЕДИНЯЙТЕ И СОХРАНЯЙТЕ⭐️Возьмите эти не требующие предварительной подготовки печатные формы ПЛЮС еще больше заданий на чувство числа с числовыми центрами и числом

Субъекты:

Математика, номера

Оценки:

Prek — 1 -е

Типы:

Центры, печатные изделия, рабочие листы

также включены в: детские знания по математике и центры.

Sight Word Poems Упражнение Sight Word — Вы ищете упражнение на понимание прочитанного и беглость чтения, которое включает в себя слова с вида для ваших начинающих читателей? Я создал этот набор из 40 стихотворений со словами для зрения, чтобы использовать их во время совместного чтения в классе моего детского сада. Используйте этот набор из 40 стихотворений для тренировки слов. Этот набор предоставит вам по одному стихотворению на каждую неделю в школе. Эти предсказуемые стихи наполнены словами для зрения, чтобы ваши дети могли выучить слова для зрения в «те 9».0003

Предметы:

Сбалансированная грамотность, Поэзия

Классы:

К — 1-й

Виды:

Занятия, Печатные издания

СССС:

, РФК.К.К.а,РФ.К.К.а,РФ.К.1004. 1b, RF.K.1c, RF.K.2a…

Также включено в: ПОЛНЫЙ НАБОР Стихотворных слов для совместного чтения (поэзия для начинающих)

by

Обучаемый учитель

Редактируемые рабочие листы со словами для детского сада, Первоклассники и второклассники с эффективной и увлекательной практикой чтения слов. Волшебная часть этих действий со словами-визуалами заключается в том, что они эффективны и для вас! Были ли у вас рабочие листы со словами для зрения, но затем вы изменили классы или ваша школа изменила свой список слов для зрения,

Объекты:

EFL — ESL — ELD, орфография, словарь

Оценки:

K — 2 -й

Типы:

Мероприятия, печатные изделия, рабочие листы

от

Rees

. за предоставление практического опыта учащимся. Этот интерактивный блокнот «Карты, континенты и формы рельефа» не является исключением! Пакет удобен в использовании как для ученика, так и для учителя. ✅ Нажмите ЗДЕСЬ, чтобы СЭКОНОМИТЬ 20% на этом ресурсе с блоком «Карты, континенты и формы рельефа» и комплектом плакатов! ✅ Нажмите ЗДЕСЬ, чтобы ЭКОНОМИТЬ еще больше, купив ВСЕ 15 интерактивных тетрадей по общественным наукам и мини-блоков в одном годовом комплекте. Нажмите на кнопку ПРЕДПРОСМОТР выше, чтобы увидеть все t

Предметы:

География, Другое (Обществоведение — История), Обществознание — История

Классы:

3-5

Типы:

Самостоятельные рабочие пакеты, печатные формы, рабочие листы

Также включены в классы Занятия по обществознанию и набор интерактивных тетрадей для 4-го класса

на

Мой учитель-ботаник, автор Алина В.

Вы ищете веселые и увлекательные рабочие листы по алфавиту от А до Я для своих учеников? Этот пакет идеально подходит для тех, кто рано заканчивает работу, утренней работы, выполнения домашних заданий и многого другого. Каждый рабочий лист включает 5 различных заданий, которые ваши ученики могут использовать, чтобы узнать все о прописных и строчных буквах. — — — — — — — — — > Проверьте наш БЕСКОНЕЧНЫЙ НАБОР АЛФАВИТА и получите этот ресурс с огромной скидкой!! <- - - - - - - - -ВКЛЮЧЕННЫЕ МЕРОПРИЯТИЯ: • Произнеси по буквам! Напишите буквы в коробках • Раскрасьте! Цвет

Предметы:

Акустика, Изобразительное искусство

Классы:

PreK — K

Виды:

Задания, Печатные формы, Рабочие листы

CCSS,

.К.К.а, РФ. K.1b, RF.K.1c, RF.K.1d…

Также включено в: Рабочий лист «Начальные звуки». Буквенная практика. Бесплатные карточки с алфавитом. Карточки с заданиями для проверки навыков понимания Привлекайте своих читателей интересными отрывками для понимания прочитанного и соответствующими вопросами! Этот ресурс включает в себя 32 карточки с информационными текстовыми заданиями на полстраницы с 4 вопросами на понимание и заданиями на КАЖДОЙ карточке, всего 128 информационных текстовых вопросов! Вовлеките своих учащихся в осмысленную практику внимательного чтения и просмотрите ключевые навыки чтения, связанные с информационным и научно-популярным текстом

Субъекты:

ELA PREP TEST PREP, АНГЛИЙСКОЕ ЯЗЫКИ, Информационный текст

Оценки:

3 -е — 5 -е

Типы:

Центры, целевые карты

CCSS:

RI. 3.1, RI.3.2, RI RI:

RI.3.1, RI.3.2, RI RI .3.3, RI.3.4, RI.3.5…

Также включено в: Комплект карточек с заданиями на понимание прочитанного | Цифровые и печатные версии

by

Карен Джонс

10,00 $

Один из самых продаваемых фонических ресурсов TPT! Этот пакет содержит более 100 страниц готовых к использованию листов для печати по фонетике! Никаких подготовительных работ не требуется, просто распечатайте и скопируйте! Каждая страница представляет собой отдельное задание, над которым ваши ученики могут работать самостоятельно. Они отлично подходят для практики работы со словами, утренней работы, центров грамотности или домашних заданий. Каждая страница включает в себя какой-либо интерактивный элемент вырезания и склейки, раскрашивания или сортировки. Версия PowerPoint и файлы изображений также включены для загрузкиi

Предметы:

Английский язык, Акустика

Классы:

K — 1st

Типы:

Мероприятия, Центры, Печатные формы

CCSS:

, RF. K.2a

CCSS:

, RF.K.2a

.K.2c, RF.K.2d, RF.K.3…

Решение систем уравнений методом подстановки

Решение систем уравнений методом подстановки

В этом методе сначала находим значение единицы переменная (y) через другую переменную (x) из одного уравнения. Подставьте это значение y во второе уравнение. Второе уравнение становится линейным уравнением только относительно x и может быть решено относительно x.
Подставляя значение x в первое уравнение, мы можем найти значение y.
Этот метод решения системы линейных уравнений известен как метод исключения путем замены.
«Исключение», потому что мы избавляемся от y или «исключаем» y из второго уравнения. «Подстановка», потому что мы «подставляем» значение y во второе уравнение. (1)
a ₂ x + b ₂ y + c ₂ = 0                      ….(2)
Шаг I: Найдите значение одной переменной, скажем, y, через другую, т. е. уравнение, скажем (1).
Шаг II: Подставьте значение y, полученное на шаге 1, в другое уравнение, т. е. уравнение (2). Это уравнение становится уравнением только с одной переменной x.
Шаг III: Решите уравнение, полученное на шаге II, чтобы получить значение x.
Шаг IV: Подставляем значение x из шага II в уравнение, полученное на шаге I. Из этого уравнения получаем значение y. Таким образом, мы получаем решение, то есть значения x и y.
Примечание: Проверка является обязательной для проверки ответа.

Примеры метода подстановки

Пример 1:    Решите каждую из следующих систем уравнений, исключив x (подстановкой):
(i) x + y = 7              2х – 7у = 1
2x — 3y = 11 12x + 5y = 7 4x + 3y = 15
(iv) 3x — 5y = 1 (v) 5x + 8y = 9
5x + 2y = 19 2x + 3y = 4
Sol.     (i) Имеем,
x + y = 7           …. (1)
2x – 3y = 11    ….(2)
Исключим x, подставив его значение из одного уравнения в другое. из уравнения (1) получаем
x + y = 7           ⇒   x = 7 – y
Подставляя значение x в уравнение (2), получаем
2 × (7 – y) – 3y = 11
⇒  14 – 2y – 3y      = 11
⇒  –5y = – 3          или,        y = 3/5
Теперь, подставляя значение y в уравнение (1), получаем
x + 3/5 = 7     ⇒     x = 32/5.
Следовательно, x = 32/5 и y = 3/5

(ii) Имеем
x + y = 7         ….(1)
12x + 5y = 7   ….(2)
Из уравнения ( 1) имеем
x + y = 7    ⇒   x = 7 – y
Подставляя значение y в уравнение (2), получаем
⇒ 12(7 – y) + 5y = 7
⇒ 84 ​​– 12y + 5y = 7
⇒ –7г = – 77
⇒ y = 11
Теперь, подставляя значение y в уравнение (1), получаем
x + 11 = 7    ⇒   x = – 4
Следовательно, x = – 4, y = 11.

(iii) Имеем,
2x – 7y = 1 ….(1)
4x + 3y = 15 ….(2)
Из уравнения (1) получаем
2x – 7y = 1    ⇒  x = \(\frac{7y +1}{2}\)
Подставляя значение x в уравнение (2), получаем ;
\(\Стрелка вправо 4\times \frac{7y+1}{2}+3y=15\)
\(\Стрелка вправо \frac{28y+4}{2}+3y=15\)
⇒ 28y + 4 + 6y = 30
⇒ 34y = 26     ⇒  y = \(\frac{13}{17}\)
Теперь, подставляя значение y в уравнение (1), мы получаем
2x – 7 × \(\frac{13}{17}\) = 1
⇒ 2x = 1 + \(\frac{91}{17 }\) =  \(\frac{108}{17}\)      ⇒    x = \(\frac{108}{34}\) = \(\frac{54}{17}\)
Следовательно,  x = \ (\frac{54}{17}\) , y = \(\frac{13}{17}\)

(iv)  Имеем,
3x – 5y = 1     …. (1)
5x + 2y = 19  …. (2)
Из уравнения (1) получаем;
3x – 5y = 1     ⇒    x = \(\frac{5y+1}{3}\)
Подставляя значение x в уравнение (2), получаем
⇒ 5 × \(\frac{5y+1}{3}\) + 2y = 19
⇒ 25y + 5 + 6y = 57     ⇒    31y = 52
Таким образом, y = \(\frac{52}{31} \)
Теперь, подставляя значение y в уравнение (1), мы получаем
3x – 5 × \(\frac{52}{31}\) = 1
⇒  3x – \(\frac{260}{31 }\) = 1    ⇒  3x = \(\frac{291}{31}\)
⇒  x = \(\frac{97}{31}\)
Следовательно, x = \(\frac{97}{31 }\) , y =  \(\frac{52}{31}\)

(v)  Имеем,
5x + 8y = 9 ….(1)
2x + 3y = 4 ….(2)
Из уравнения (1) получаем
5x + 8y = 9⇒   x =  \(\frac{9-8y}{5}\)
Подставляя значение x в уравнение (2), получаем
⇒  2 × \(\frac{9-8y}{5}\) + 3y = 4
⇒  18 – 16y + 15y = 20
⇒  –y = 2 или y = – 2
Теперь, подставляя значение y в уравнение (1), получаем
5x + 8 (–2) = 9
5x = 25     ⇒   x = 5
Следовательно, x = 5, y = – 2.

Пример 2:    Решите следующие системы уравнений, исключив ‘y’ (подстановкой):
(i) 3x – y = 3          (ii) 7x + 11y – 3 = 0           (iii) 2x + y – 17 = 0
7x + 2y = 20         8x + y – 15 = 0                    17x – 11y – 8 = 0
Sol.     (i) Имеем,
3x – y = 3      ….(1)
7x + 2y = 20 ….(2)
Из уравнения (1) получаем ;
3x – y = 3     ⇒   y = 3x – 3
Подставляя значение y в уравнение (2), получаем
⇒ 7x + 2 × (3x – 3) = 20
⇒ 7x + 6x – 6 = 20
⇒  13x = 26 ⇒   x = 2
Теперь, подставив x = 2 в уравнение (1), мы получим;
3 × 2 – y = 3
⇒  y = 3
Следовательно, x = 2, y = 3,

(ii) Имеем,
7x + 11y – 3 = 0 ….(1)
8x + y – 15 = 0 …..(2)
Из уравнения (1) получаем;
7x + 11y = 3
⇒  y = \(\frac{3-7x}{11}\)
Подставляя значение ‘y’ в уравнение (2), мы получаем
⇒  8x + \(\frac{3 -7x}{11}\) = 15 
⇒  88x + 3 – 7x = 165 
⇒  81x = 162 
⇒  x = 2 
Теперь, подставляя x = 2 в уравнение (2), получаем
8 × 2 + y = 15
⇒  y = – 1
Следовательно, x = 2, y = – 1.

(iii) Имеем,
2x + y = 17 ….(1)
17x – 11y = 8 ….(2)
Из уравнения (1) получаем;
2x + y = 17   ⇒   y = 17 – 2x
Подставляя значение y в уравнение (2), получаем
⇒ 17x – 11 (17 – 2x) = 8
⇒ 17x – 187 + 22x = 8
⇒  39x = 195
⇒  x = 5
Теперь, подставляя значение ‘x’ в уравнение (1), получаем
2 × 5 + y = 17
⇒  y = 7
Следовательно, x = 5, y = 7

Пример 3:     Решите следующие системы уравнений:
(i) \(\frac{15}{u}\) + \(\frac{2}{v}\) = 17           (ii)\ (\frac{11}{v}\) – \(\frac{7}{u}\) = 1
\(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{36}{5}\)                   \(\frac{9}{v}\ ) + \(\frac{4}{u}\) = 6
Сол.     (i) Данная система уравнений имеет вид
\(\frac{15}{u}\) + \(\frac{2}{v}\) = 17   ….(1)
\(\frac {1}{u}\) + \(\frac{1}{v}\) = \(\frac{36}{5}\)    ….(2)
Учитывая, что 1/u = x, 1/v = y, приведенная выше система линейных уравнений может быть записана как
15x + 2y = 17          …. (3)
x + y = \(\frac{36}{5}\)       ….(4)
Умножение (4) ) на 15 и (iii) на 1, получаем
15x + 2y = 17                           ….(5)
15x + 15y = \(\frac{36}{5}\) × 15 = 108        ….(6)
Вычитая (6) из (5), получаем
–13y = – 91      ⇒     y = 7
Подставляя y = 7 в (4), получаем
x + 7 = \(\frac{36}{5}\)      ⇒  x = \(\frac{36}{5 }\) – 7 = \(\frac{1}{5}\)
Но, y = \(\frac{1}{v}\) = 7        ⇒   v = \(\frac{1}{7} \)
и,       x = \(\frac{1}{u}\)  = \(\frac{1}{5}\) ⇒  u = 5

Следовательно, искомое решение данной системы есть u = 5, v = 1/7.

(ii) Данная система уравнений имеет вид
\(\frac{11}{v}\) – \(\frac{7}{u}\) = 1; \(\frac{9}{v}\) + \(\frac{4}{u}\) = 6
Приняв 1/n = x и 1/u = y, приведенную выше систему уравнений можно записать в виде
11x – 7y = 1            ….(1)
9x – 4y = 6              ….(2)
Умножая (1) на 4 и (2) на 7, получаем
44x – 28y = 4         ….(3)
63x – 28y = 42        ….