Симулятор машины тьюринга онлайн: Эмулятор машины Тьюринга | cmc@msu

Машина Тьюринга Детерминированная и недетерминированная машина Тьюринга…

Привет, Вы узнаете про машина тьюринга детерминированная, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое машина тьюринга детерминированная, недетерминированная машина тьюринга, машина тьюринга , настоятельно рекомендую прочитать все из категории Теория автоматов.

• 1 Устройство машины Тьюринга
• 2 Описание машины Тьюринга
• 3 Пример машины Тьюринга
• 4 Полнота по Тьюрингу
• 5 Варианты машины Тьюринга
  • 5.1 машина тьюринга , работающая на полубесконечной ленте
  • 5.2 Двумерные машины Тьюринга
• 6 Недетерминированной машины Тьюринга
• 7 Устройство недетерминированной машины Тьюринга
• 8 Определение недетерминированной машины Тьюринга
• 9 Эквивалентность с детерминированной машиной Тьюринга
• 10 Пример недетерминированной машины Тьюринга
• 11 Другие абстрактные исполнители и формальные системы вычислений

Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Черча — Тьюринга, способна имитировать все исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

Художественное представление машины Тьюринга

​

Устройство машины Тьюринга

В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделенная на ячейки, и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особыйпустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.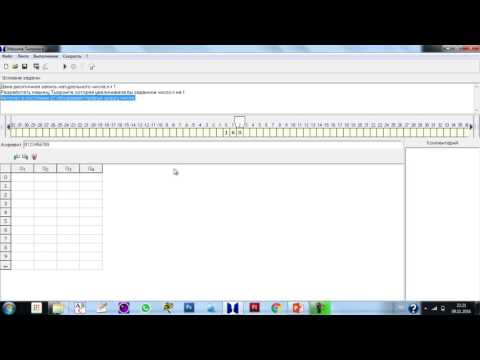

Описание машины Тьюринга

Конкретная машина Тьюринга задается перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации i, aj> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

Пример машины Тьюринга

Приведем пример МТ для умножения чисел в унарной системе счисления. Запись правила «qiaj→qi1aj1R/L/N» следует понимать так: qi — состояние при котором выполняется это правило, aj — данные в ячейке, в которой находится головка, qi1 — состояние в которое нужно перейти, aj1 — что нужно записать в ячейку, R/L/N — команда на перемещение.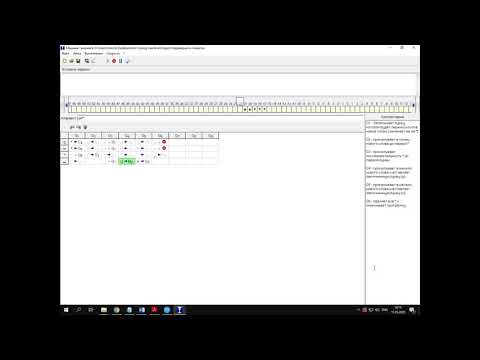

Машина работает по следующему набору правил:

	q0	q1	q2	q3	q4	q5	q6	q7	q8
1	q01→q01R	q11→q2aR	q21→q21L	q31 → q4aR	q41→q41R			q71→q2aR
×	q0×→q1×R		q2×→q3×L		q4×→q4×R		q6×→q7×R		q8×→q9×N
=			q2=→q2=L		q4=→q4=R			q7=→q8=L
a			q2a→q2aL	q3a→q3aL	q4a→q4aR		q6a→q61R	q7a→q7aR	q8a→q81L
*	q0*→q0*R			q3*→q6*R	q4*→q51R
						q5 →q2*L

Описание состояний:

Начало
q0	начальное состояние.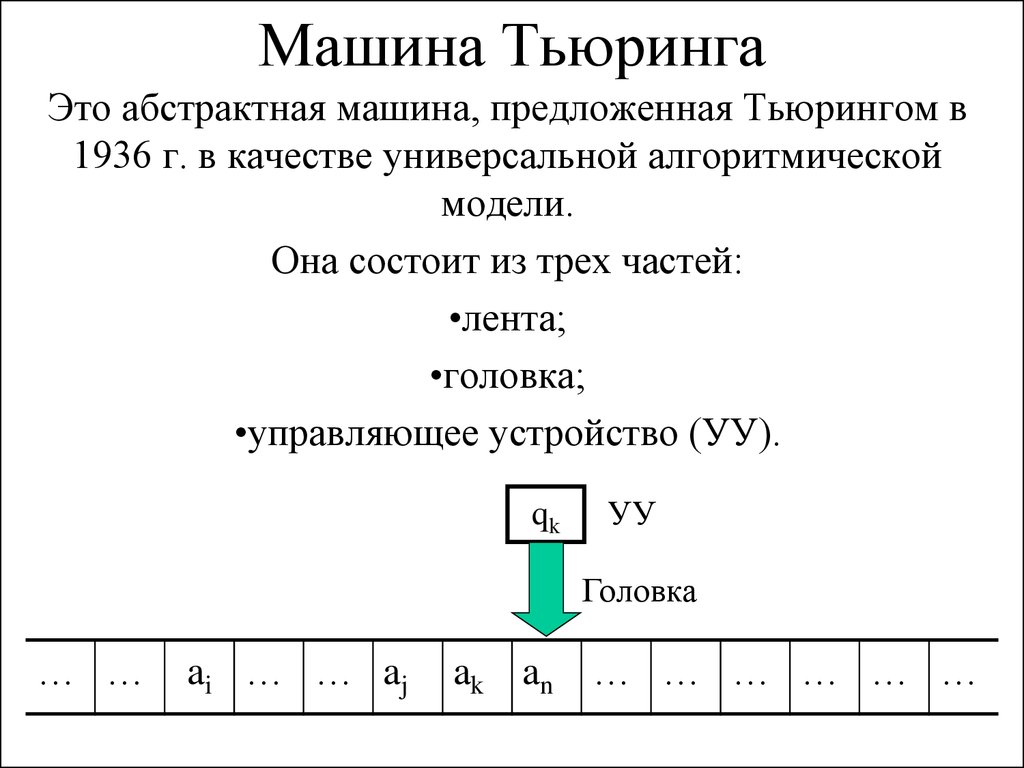 Ищем «x» справа. При нахождении переходим в состояние q1
q1	заменяем «1» на «а» и переходим в состояние q2
Переносим все «1» из первого числа в результат
q2	ищем «х» слева. При нахождении переходим в состояние q3
q3	ищем «1» слева, заменяем ее на «а» и переходим в состояние q4. В случае если «1» закончились, находим «*» и переходим в состояние q6
q4	переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5
q5	добавляем «*» в конец и переходим в состояние q2
Обрабатываем каждый разряд второго числа
q6	ищем «х» справа и переходим в состояние q7 . Об этом говорит сайт https://intellect.icu . Пока ищем заменяем «а» на «1»
q7	ищем «1» или «=» справа при нахождении «1» заменяем его на «а» и переходим в состояние q2 при нахождении «=» переходим в состояние q8
Конец
q8	ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем заменяем «а» на «1»
q9	терминальное состояние (остановка алгоритма)

Умножим с помощью МТ 3 на 2 в единичной системе. В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчеркнутый символ).

Начало. Находимся в состоянии q0, ввели в машину данные: *111×11=*, головка машины располагается на первом символе *.

1-й шаг. Смотрим по таблице правил что будет делать машина, находясь в состоянии q0 и над символом «*». Это правило из 1-го столбца 5-й строки — q0*→q0*R. Это значит, что мы переходим в состояние q0 (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введенному нами тексту «*111×11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q01 (1-й столбец 1-я строка) обрабатывается правилом q01→q01R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берем состояние (индекс при q), берем символ, на котором стоим (подчеркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.

Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя ее на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путем поочередной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц — значит умножение завершено.

Полнота по Тьюрингу

Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий.

Элементарность действий заключается в том, что действие меняет лишь небольшой кусочек данных в памяти (в случае машины Тьюринга — лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить все, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.

Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.

Имитация заключается в следующем. На вход второй машине подается описание программы (правил работы) первой машины и входные данные , которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные .

Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, за исключением конкурентных, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

На машине Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).

Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью (суммарная память компьютера — оперативная память, жесткие диски, различные внешние носители данных, регистры и кэш процессора и др. — может быть очень большой, но, тем не менее, всегда конечна).

Примеры реализации машин Тьюринга

Сложение десятичных чисел

Вычитание десятичных чисел

Варианты машины Тьюринга

Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.

Машина Тьюринга, работающая на полубесконечной ленте

В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.

Рассмотрим доказательство, приведенное Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:

Затем перенумеруем ячейки, причем будем считать, что символ «*» не содержится в словаре МТ:

Наконец, изменим машину Тьюринга, удвоив число ее состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна ее работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:

Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.

Тут, следует отметить, что термин «полубесконечность» едва ли имеет какой-либо внятный смысл, поскольку бесконечность деленная надвое также является бесконечностью, которая, в свою очередь, не имеет никаких «концов» по-определению. Тут, видимо, произошла терминологическая неточность из-за того, что в определении машины Тьюринга часто используется неформальное слово «бесконечная в обе стороны».

недетерминированная машина тьюринга

Недетерминированная машина Тьюринга — машина Тьюринга, функция перехода которой представляет собой недетерминированный конечный автомат.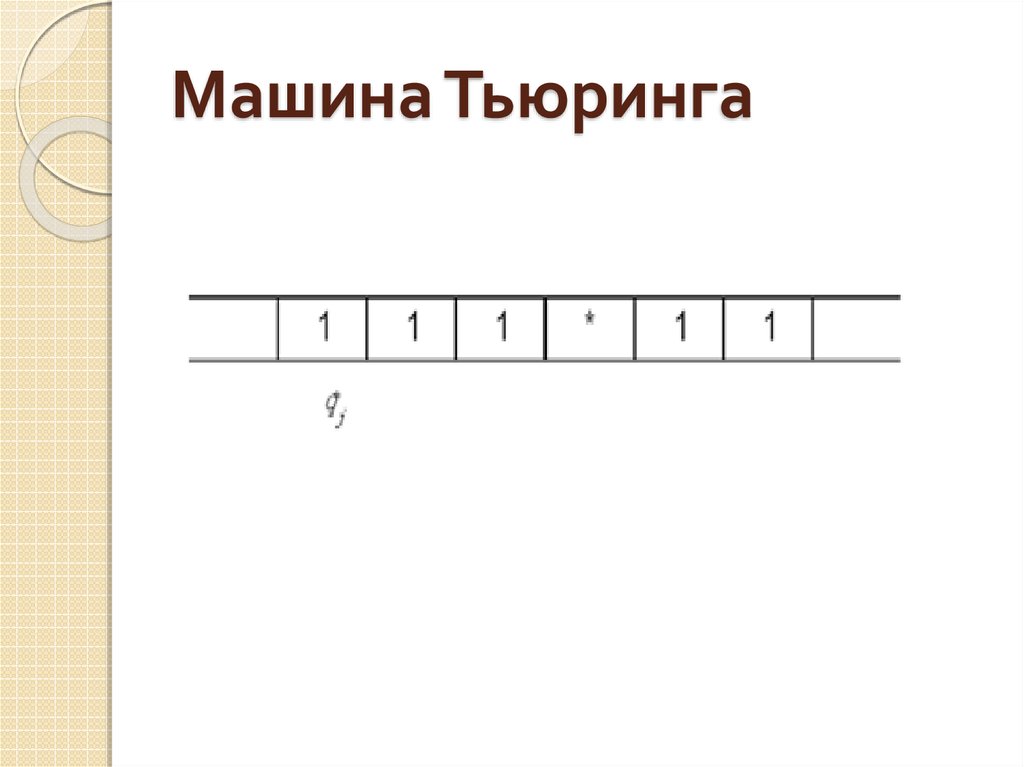

Устройство недетерминированной машины Тьюринга

Детерминированная (обычная, классическая) машина Тьюринга имеет функцию перехода, которая по комбинации текущего состояния и символа на ленте определяет три элемента: символ, который будет записан на ленте, направление смещения головки по ленте и новое состояние конечного автомата. Например, X на ленте в состоянии 3 однозначно определяет переход в состояние 4, запись на ленту символа Y и перемещение головки на одну позицию влево.

В случае недетерминированной машины Тьюринга, комбинация текущего состояния автомата и символа на ленте может допускать несколько переходов. Например, X на ленте и состоянии 3 допускает как состояние 4 с записью на ленту символа Y и смещением головки вправо, так и состояние 5 с записью на ленту символа Z и смещением головки влево.

В отличие от детерминированной машины Тьюринга, которая имеет единственный «путь вычислений», недетерминированный вариант имеет «дерево вычислений» (в общем случае — экспоненциальное число путей). Говорят, что недетерминированная машина Тьюринга допускает входные данные, если какая-нибудь ветвь этого дерева останавливается в допускающем состоянии, иначе НМТ входные данные не допускает. (Таким образом, ответы «да» и «нет» в случае недетерминированных вычислений несимметричны.)

Определение недетерминированной машины Тьюринга

Формально, недетерминированная машина Тьюринга — это шестерка объектов , где:

• Q — конечное множество состояний
• — конечное множество символов (алфавит ленты)
• — начальное состояние
• — символ пробела
• — конечное множество допускающих состояний
• — многозначное отображение из пары состояние-символ, называемое функцией перехода.

Эквивалентность с детерминированной машиной Тьюринга

Несмотря на кажущуюся большую мощность недетерминированных машин в связи с тем, что они выполняют несколько возможных вычислений сразу (требуя только, чтобы хоть одно из них заканчивалось в допускающем состоянии), любой язык, допускающийся недетерминированной машиной Тьюринга, также допускается и обычной детерминированной машиной Тьюринга, поскольку она может моделировать любой недетерминированный переход, делая многократные копии состояния, если встречается неоднозначность.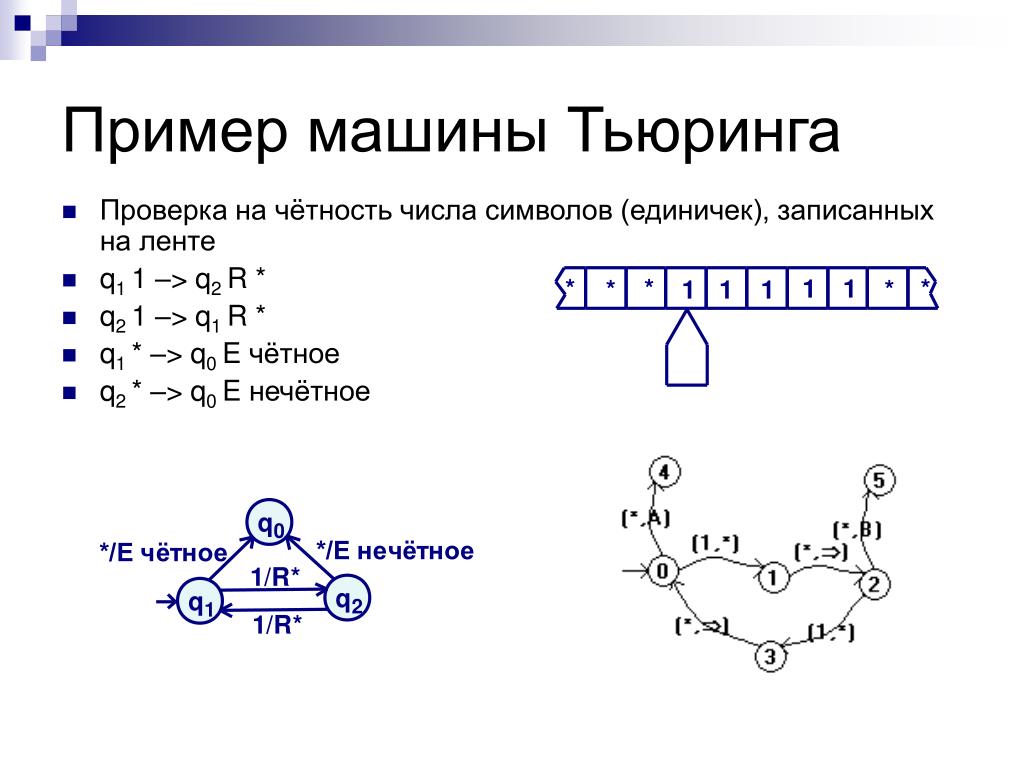

Моделирование недетерминизма требует значительно больше времени, вопрос об оценке разницы затрат открыт: в частном случае ограничения по времени в виде полинома от длины входа этот вопрос представляет собой классическую задачу «P = NP».

Класс алгоритмов, выполняемых за полиномиальное время на недетерминированных машинах Тьюринга, называется классом NP.

Пример недетрминированной машины Тьюринга

Рассмотрим задачу проверки того, что данное b-разрядное целое число является составным. Тогда b — длина входных данных, по отношению к которой рассматривается время вычисления. Ответ «ДА» — число составное и «НЕТ» — простое. Эта задача является комплементарной к тесту на простоту.

Недетерминированный алгоритм для этой задачи может быть, например, следующий:

• Выбрать недетерминированно целое число m такое что 1.
• Разделить нацело N на m, остаток обозначим через a.
• Если a=0 выдать ответ «ДА» (m тогда — делитель N), иначе выдать ответ «НЕТ».

(Алгоритм написан не непосредственно в виде определения машины Тьюринга.)

Во времени вычисления этого алгоритма определяющей частью является время выполнения деления, которое может быть выполнено за шагов, что представляет собой полиномиальное время. Таким образом, задача находится в классе NP.

Для реализации такого времени вычисления требуется удачно выбирать число m или выполнять вычисления по всем возможным путям (для всех возможных m) одновременно на множестве копий машины.

Если моделировать этот алгоритм на детерминированной машине Тьюринга, пробуя по очереди все возможные варианты, требуется проверить N- ветвей. Таким образом, общее время вычислений будет шагов, что представляет собой уже экспоненциальное время, которое существенно больше, чем полиномиальное время. Таким образом, этот алгоритм не попадает в класс P. (Однако, могут быть применены другие, более быстрые алгоритмы для этой задачи, которые работают за полиномиальное время и, таким образом, задача попадает в класс P. )

Двумерные машины Тьюринга

• Муравей Лэнгтона

См. также

• JFLAP кроссплатформенная программа симулятор автоматов, машины Тьюринга , грамматик, рисует граф автомата
• Универсальная машина Тьюринга
• Недетерминированная машина Тьюринга
• Вероятностная машина Тьюринга
• Квантовая машина Тьюринга
• Теория алгоритмов
• Тьюринговская трясина

Другие абстрактные исполнители и формальные системы вычислений

• Нормальный алгоритм Маркова (продукционное программирование)
• Машина Поста ( автоматное программирование )
• Рекурсивная функция ( теория вычислимости)
• Лямбда-исчисление ( функциональное программирование )
• Brainfuck (императивное программирование )

К сожалению, в одной статье не просто дать все знания про машина тьюринга детерминированная. Но я — старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое машина тьюринга детерминированная, недетерминированная машина тьюринга, машина тьюринга и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов

Квантовые вычисления: основные принципы 10 класс онлайн-подготовка на Ростелеком Лицей

Традиционные компьютеры, основанные на использовании полупроводниковых логических элементов, уже приблизились к пределу своего развития — дальнейшая миниатюризация транзисторов и «упаковка» ещё большего числа вычислительных компонентов в тот же объём скоро станет невозможной. Поэтому инженеры и учёные пытаются создавать вычислительные устройства на новых принципах. 

В их числе — квантовые вычислительные машины, которые основаны на использовании ряда квантовых эффектов, таких как квантовая запутанность и квантовая суперпозиция. Благодаря этому они способны решать задачи, на которые «обычные» классические компьютеры потратили бы миллиарды лет (это, например, расчёт поведения сложных молекул, моделирование нейронных связей в мозге или решение сложных логистических задач).

Квантовые компьютеры обещают решить эту проблему, однако пока в реальности созданы только экспериментальные квантовые установки, которые ещё не показали «квантового превосходства» — значимой прибавки в скорости вычислений по сравнению с обычными компьютерами.

В этом модуле вы узнаете:

• как возникла идея квантового компьютера;
• из чего строят квантовые машины, что такое кубит;
• почему квантовые компьютеры могут превзойти обычные;
• какие существуют квантовые алгоритмы.

История идеи квантового компьютера

Идею квантовых вычислительных устройств впервые высказал в 1980 году советский математик Юрий Манин. В книге «Вычислимое и невычислимое», говоря о сложности процесса считывания и записи биологической информации с молекул ДНК, он замечает, что для моделирования этого процесса могли бы подойти квантовые устройства.

Годом позже, в мае 1981 года, идею квантового компьютера сформулировал физик и нобелевский лауреат Ричард Фейнман в докладе, посвящённом возможности моделирования физических процессов. Физик подчёркивает, что все явления подчиняются квантовым законам (а классическая физика — только приближение). Если поведение одиночного квантового объекта достаточно легко поддаётся моделированию с помощью компьютера, то нарастание количества элементов ведёт к экспоненциальному росту сложности вычислений. Из этого следовало два варианта, говорил Фейнман: первый — признать, что квантовые системы не поддаются моделированию с помощью компьютеров, и второй — построить вычислительную машину из квантовых элементов, которые будут подчиняться тем же квантовым законам, что и моделируемая система.

В своем докладе Фейнман впервые сформулировал понятие квантового симулятора — квантовой системы, которая воспроизводит поведение какой-то другой квантовой системы, а также универсального квантового компьютера — такой квантовой системы, которую можно перенастроить (перепрограммировать) так, чтобы она была способна моделировать поведение многих других систем. Он также впервые описал пример работы системы из кубитов, созданных из фотонов с определённой поляризацией.

Работа одного из элементов квантового компьютера в представлении Фейнмана

В 1985 году Дэвид Дойч из Оксфордского университета разрабатывает теорию универсального квантового компьютера как квантовой машины Тьюринга.

Однако первый в мире квантовый компьютер мог появиться намного раньше, ещё до статей Манина и Фейнмана, в 1950-е годы. Тогда японский учёный Гото Эйичи экспериментировал с низкотемпературной электроникой для разработки миниатюрного магнитно-управляемого бита, то есть системы, которая может находиться в двух состояниях и служить, как и обычный полупроводниковый транзистор, основным элементом компьютера.

Эйичи назвал свой бит параметроном, и его первый прототип был создан в 1958 году в Токийском университете.

Гото Эйичи и его команда добивались, чтобы энергетический барьер между двумя состояниями битов был достаточно высоким, чтобы их гарантированно можно было различить. Иначе говоря, японские учёные добивались, чтобы устройство ни в коем случае не оказывалось в бистабильном состоянии, то есть в состоянии квантовой суперпозиции. Такое состояние рассматривалось как нечто, вызывающее неуправляемый и нежелательный шум, в то время как квантовые эффекты могли дать им принципиально новый метод вычислений. Если бы не их стремление к избавлению от ошибок, возможно, квантовые симуляторы появились бы на полвека раньше.

Пределы роста для классических компьютеров

Современные компьютеры, включая самые мощные, основаны на использовании множества полупроводниковых «переключателей» — транзисторов, их вычислительная мощность в конечном счёте зависит от количества этих транзисторов и скорости их срабатывания. 31 битов, что примерно на 40 порядков выше возможностей современных вычислительных машин. Это означает, что закон Мура должен действовать ещё примерно 250 лет, чтобы добраться до этого окончательного предела.

Однако большинство экспертов считают, что рост возможностей современной электроники упрётся в потолок намного раньше, и закон Мура перестанет работать. Пределы роста связывают с ограничениями на миниатюризацию самих транзисторов — уже сейчас слои диэлектрика в них могут иметь лишь несколько атомов в толщину, на работе их начинают сказываться квантовые эффекты, например, туннелирование. Сложности создаёт и пропускная способность межсоединений между транзисторами. Еще в 2013 году некоторые учёные объявили о конце закона Мура (пока лишь в области твёрдотельных накопителей).

Поэтому большинство крупных ИТ-компаний ищет варианты, которые позволят продолжить рост. В качестве перспективных рассматривается возможности создания оптических компьютеров (где информация кодируется и обрабатывается в световых импульсах), спинтронных компьютеров (где данные кодируются не в колебаниях электрического тока, а в спинах электронов).  

Одной из альтернатив современной электронике некоторые считают квантовые вычислительные устройства, которые способны обеспечить резкий рост вычислительной мощности при решении некоторых типов задач. Попробуем разобраться, как устроен квантовый компьютер.

Устройство квантового компьютера: биты и кубиты

Классические компьютеры оперируют битами — объектами, у которых есть только два возможных состояния, например, 1 или 0. В качестве такого максимально простого классического объекта можно рассматривать, например, монету, у которой виден либо аверс, либо реверс, то есть орёл или решка.

Все обычные компьютеры работают именно с классическими битами, то есть с наборами двоичных значений, нулей или единиц. Эквивалентом бита в квантовом мире будет кубит — квантовый бит. Фундаментальным отличием кубита является тот факт, что он, в отличие от бита, может находиться в состоянии квантовой суперпозиции. 

Состояние кубитов описывает волновая функция Ψ, которую можно представить как точку на единичной сфере — сфере Блоха. Положение этой точки задаётся двумя комплексными числами (ɑ и ꞵ). Это означает, что при каждом измерении кубита может получиться одно из двух значений |0> или |1>, с вероятностями, заданными ɑ и ꞵ.

Следует отметить, что никакого промежуточного положения волновой функции зафиксировать не получится в силу квантовых законов, любые измерения будут выдавать только 0 или 1, а соотношение комплексных коэффициентов можно будет определить только путем многих повторений и подсчёта вероятностей.

Квантовые компьютеры состоят из множества таких кубитов, приготовленных определённым образом, — так, чтобы соотношения вероятностей соответствовали тому процессу, который нужно моделировать (или задаче, которую надо решить). Кроме того, кубиты могут взаимодействовать друг с другом, что и обеспечивает возможности для вычислений. Каким же образом квантовые компьютеры могут стать первыми?

Квантовое преимущество

Чтобы показать, как квантовые компьютеры могут превзойти классические, обратимся снова к монетной аналогии. 42 точках, на что потребуется энергия всех электростанций Земли примерно за 100 лет.

Для того чтобы описать механику работы квантового вычислительного устройства, можно использовать многомировую интерпретацию квантовой механики (известную также как интерпретация Эверетта). Аспирант из Принстона Хью Эверетт в своей диссертации пытался справиться с проблемой квантовой неопределённости путём умножения вселенных. Каждый раз, когда происходит некоторое вероятностное событие, возникает две Вселенных, в одной из которых кот Шрёдингера погиб, а во второй выжил.

В соответствии с этим представлением квантовый компьютер можно представить как множество одновременно работающих во множестве вселенных классических компьютеров — и все они одновременно ищут решения множества задач, например, однотипных задач с отличающимися условиями, то есть квантовый компьютер может заменить огромное количество «обычных» вычислительных устройств, и в этом и заключается его «квантовое превосходство».

Следует отметить, что квантовый компьютер по определению выдаёт вероятностные решения, и в момент измерения кубитов мы получаем только одно из множества этих решений, но наиболее вероятное. Существующие квантовые вычислительные устройства сегодня используют не для поиска одного лучшего решения задачи, но для поиска нескольких хороших решений.

Квантовые алгоритмы

Универсальный и пригодный для практического применения квантовый компьютер ещё не создан — пока в лабораториях и исследовательских центрах тестируют квантовые симуляторы или устройства с небольшим количеством кубитов. Однако учёные уже разработали ряд алгоритмов, которые могут быть запущены на квантовых компьютерах и которые способны показать существенный выигрыш по сравнению с классическими вычислительными машинами. Расскажем о самых известных среди них.

Алгоритм Дойча — Йожи 

Был предложен в 1992 году Давидом Дойчем и Ричардом Йожей. Это было первое описание вычислительной процедуры, в которой использовалось квантовое преимущество, то есть квантовые эффекты запутанности и суперпозиции давали значительный прирост скорости расчёта по сравнению с классическими алгоритмами.

Суть этой задачи Дойча — Йожи состоит в процедуре поиска бракованной монеты, описанной выше. Математически она формулируется так:

Дано: «чёрный ящик», который вычисляет функцию

f: {0,1}ⁿⁿ→ {0,1}.

Заранее известно: выполняется одно из двух:

(к) функция f — константа;

(б) функция f сбалансирована, т. е. число нулей и единиц у неё одинаково.

Выяснить: какой из случаев имеет место.

Другими словами, есть «чёрный ящик», который может быть устроен двумя способами, и нужно определить, каким именно. Этот алгоритм был специально разработан так, чтобы квантовое вычислительное устройство показало при его решении серьёзное преимущество.

Алгоритм Шора

Самый известный квантовый алгоритм, который описывает квантовую процедуру факторизации — разложения числа на множители.

Дело в том, что умножение и противоположная ему процедура разложения на множители асимметричны — «трудозатраты» на факторизацию растут гораздо быстрее, чем сложность умножения соответствующих чисел. Скажем, компьютер может без особенных усилий перемножить два двухсотзначных числа. А вот для того, чтобы разложить на множители 400-значное число, самому мощному современному суперкомпьютеру потребуется примерно 10 миллиардов лет.

Алгоритм, придуманный Питером Шором в 1994 году, позволяет решить эту задачу на квантовом компьютере всего лишь за три года.

Именно алгоритм Шора заставил многих говорить о квантовом компьютере как об информационной атомной бомбе. Дело в том, что на асимметрии умножения и факторизации основано большинство современных алгоритмов шифрования с открытым ключом, и если окажется, что разложить числа на множители так же просто, как перемножить, они все станут бесполезными.

RSA — один из распространённых алгоритмов шифрования, который станет уязвимым из-за алгоритма Шора.

 

Проверка четности с помощью машины Тьюринга (Python и онлайн-симулятор)

Машина Тьюринга:

Машина Тьюринга — это вычислительная модель, такая как конечные автоматы (FA) и автоматы Pushdown (PDA), которые работают с неограниченной грамматикой. Машина Тьюринга — самая мощная вычислительная модель по сравнению с ФА и КПК. разделен на ячейки. В этих ячейках присутствуют символы ленты.​

Присутствует конечный элемент управления, который управляет работой машин Тьюринга на основе заданных входных данных.

Конечный элемент управления имеет головку чтения/записи, которая указывает на ячейку на ленте. слева и справа от одной ячейки к другой.

Машина Тьюринга может быть определена с помощью 7-кортежа:

Проверка четности :

Проверка четности, которая была создана для устранения ошибок передачи данных, представляет собой простой метод проверки сетевых данных и имеет простой и понятный рабочий механизм.

Проверка четности — это процесс, обеспечивающий точную передачу данных между узлами во время связи.​

Бит четности добавляется к исходным битам данных для создания четного или нечетного числа бит; количество битов со значением один.​

Затем источник передает эти данные по ссылке, а биты проверяются и подтверждаются в пункте назначения. ​

Данные считаются точными, если количество битов (четных или нечетных) совпадает с числом, переданным из источника.​

Машина Тьюринга:

Онлайн-симулятор:

Сайт: https://turingmachine.io/

Код:

 ввод: '1011001'
пустой: ' '
начальное состояние: q0
стол:
  д0:
    1: {запись: 1, R: q1}
    0: {запись: 0, R: q0}
  q1:
    1 : {запись: 1, R: q2}
    ' ' : {написать: 1, R: q3}
    0: {запись: 0, R: q1}
  д2:
    1 : {запись: 1, R: q1}
    0: {запись: 0, R: q2}
    ' ' : {запись: 0,R: q3}
  q3: 

Диаграмма состояний:

Реализация Python:

Машинный код Тьюринга:

источник: https://python-course.eu/applications-python/turing-machine.php

Лента класса (объект):
    
    пустой_символ = " "
    
    def __init__(я,
                 лента_строка = ""):
        self.__tape = dict((перечислить(tape_string)))
        # последняя строка эквивалентна следующим трем строкам:
        #self. __tape = {}
        # для i в диапазоне (len (tape_string)):
        # self.__tape[i] = input[i]
        
    защита __str__(я):
        с = ""
        min_used_index = min(self.__tape.keys())
        max_used_index = max(self.__tape.keys())
        для i в диапазоне (min_used_index, max_used_index):
            s += self.__tape[i]
        вернуть с
   
    защита __getitem__ (я, индекс):
        если индекс в self.__tape:
            вернуть себя.__лента[индекс]
        еще:
            вернуть Tape.blank_symbol
    def __setitem__(я, позиция, символ):
        self.__tape[pos] = символ
        
класс TuringMachine (объект):
    
    def __init__(я,
                 лента = "",
                 пустой_символ = " ",
                 начальное_состояние = "",
                 final_states = нет,
                 функция_перехода = Нет):
        self.__tape = Лента(лента)
        self.__head_position = 0
        self.__blank_symbol = пустой_символ
        self.__current_state = начальное_состояние
        если функция_перехода == Нет:
            self. __transition_function = {}
        еще:
            self.__transition_function = функция_перехода
        если final_states == Нет:
            self.__final_states = set()
        еще:
            self.__final_states = набор (final_states)
        
    защита get_tape (я):
        вернуть ул (я.__лента)
    
    шаг определения (сам):
        char_under_head = self.__tape[self.__head_position]
        x = (self.__current_state, char_under_head)
        если x в self.__transition_function:
            y = self.__transition_function[x]
            #print(self.__tape,self.__head_position)
            self.__tape[self.__head_position] = y[1]
            если у[2] == "R":
                self.__head_position += 1
            Элиф у[2] == "L":
                self.__head_position -= 1
            self.__current_state = у [0]
    окончательная защита (я):
        если self.__current_state в self.__final_states:
            вернуть Истина
        еще:
            вернуть ложь
 

Проверка четности с помощью машины Тьюринга:

начальное_состояние = "q0",
accepting_states = ["q1","q2","q3"],
transition_function = {("q0","0"):("q0", "0", "R"),
                       («q0», «1»): («q1», «1», «R»),
                       («q1», «0»): («q1», «0», «R»),
                       («q1», «1»): («q2», «1», «R»),
                       ("q1", "_"): ("q3", "1", "R"),
                       («q2», «0»): («q2», «0», «R»),
                       («q2», «1»): («q1», «1», «R»),
                       ("q2", "_"): ("q3", "0", "R")
                       }
final_states = {"q3"}
строка = "1011001__"
t = TuringMachine (строка,
                  начальное_состояние = "q0",
                  пустой_символ="_",
                  конечные_состояния = конечные_состояния,
                  функция_перехода=функция_перехода)
print("Ввод на ленту:\n" + t. get_tape())
пока не t.final():
    t.шаг()
print("Результат расчета на машине Тьюринга:")
печать (t.get_tape())
 

Вывод:

Надеюсь, что этот блог будет полезен, и не стесняйтесь присылать отзывы, а также комментировать мои блоги для моих дальнейших улучшений.

Получите содержимое, доставленное на ваш почтовый идентификатор, введя свой почтовый идентификатор на ГЛАВНОЙ странице.

Нравится:

Нравится Загрузка…

27 ноября 2021 г. Prasanth S N

Глава 1

Вставка 1.3: Машины Тьюринга

Существует небольшой интерактивный симулятор JavaScipt Turing Machine, доступный онлайн по адресу http://www.turing.org.uk/turing/ записки/tmjava.html

1.2 Обсуждения

C. Мимика, моделирование и поведение

A.L.I.C.E. бот доступен для онлайн-чата по адресу: http://alice.pandorabots.com

Или попробуйте Cleverbot «учится у пользователей» по адресу: http://www. cleverbot.com

Или хорошо названный Jabberwacky по адресу: http://www.jabberwacky.com

А.Л.И.С.Е. расшифровывается как Artificial Linguistic Internet Computer Entity, и программа (которая теперь является частью более крупного проекта с открытым исходным кодом под названием AIML) использует многие из тех же «быстрых и грязных» разговорных трюков, которые использовались PARRY, ELIZA и другими подобными ранними программами. «чат-боты». Очень интересную стенограмму разговора между двумя такими ботами, Алисой и Джабберваки, см. по адресу: http://discovermagazine.com/2007/brain/i-chat-therefore-i-am#.UMc_ExxlhCY.

При определенных обстоятельствах у Алисы все получится. Несколько раз (в 2000, 2001, 2004) он удостаивался премии Лебнера как «самый человекоподобный болтун». Но требования для этого довольно тонкие, сводятся только к тому, чтобы произвести впечатление на неспециалистов в течение короткого (5-минутного) периода времени. Есть более крупные призы Лебнера, которые еще предстоит присудить, в том числе 100 000 долларов в качестве награды для первого (но окончательного: соревнование прекращается навсегда) победителя «мультимодального этапа», который требует обработки мультимодального ввода (например, музыки, речи, изображений). , видео) таким образом, чтобы судьи не могли отличить программу от человека-участника; см.: http://www.loebner.net/Prizef/loebner-prize.html.

IBM «Watson» — программа, способная решать задачи, поставленные на естественном языке, которая, как известно, получила приз в миллион долларов (победив двух предыдущих звездных участников) в викторине Jeopardy в 2011 году. как Watson удалось это сделать из информационного бюллетеня IBM по адресу: http://www.research.ibm.com/deepqa/faq.shtml.

Вставка 1.6: Конкурс Botprize

Целью конкурса является программирование или развитие автоматизированных ботов, поведение которых другим (людям) кажется более вероятным, чем поведение человека, а не бота: http://botprize .орг

Классная штука. Но действительно ли результаты оправдывают заголовок Science Daily http://www.sciencedaily.com, который 26 сентября 2012 года гласил: «Искусственно интеллектуальные игровые боты проходят тест Тьюринга к столетию Тьюринга»?

1.