Определители и их применения — презентация онлайн
Похожие презентации:
Матрицы, определители, Формулы Крамера
Понятие и виды матриц
Определители, системы
Определитель и метод Крамера
Определители и их свойства. Лекции 9,10
Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства
Матрицы и определители
Матрицы и определители
Элементы линейной алгебры
Определители. Свойства определителей
«ОПРЕДЕЛИТЕЛИ
И ИХ ПРИМЕНЕНИЯ»
2. ПЛАН
1. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙМАТРИЦЫ
2. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ
ДОПОЛНЕНИЯ
3. СПОСОБЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛИТЕЛЕЙ
4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
2
3. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
34. ОБОЗНАЧЕНИЯ
КВАДРАТНАЯ МАТРИЦА n-го ПОРЯДКАa11
A
a
n1
a1n
ann
ОБОЗНАЧЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
a11
a1n
an1
ann
A det A
4
5.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1-го ПОРЯДКАa11 a11
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2-го ПОРЯДКА
a11
a12
a21
a 22
a11 a22 a21 a12
5
6. МНЕМОНИЧЕСКОЕ ПРАВИЛО
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ2-го ПОРЯДКА РАВЕН
ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ
ГЛАВНОЙ ДИАГОНАЛИ
МИНУС
ПРОИЗВЕДЕНИЕ ЭЛЕМЕНТОВ
ПОБОЧНОЙ ДИАГОНАЛИ
6
7. Вычислить:
1-3
2
6
3
-9
-7
6
1
2
3
4
2
3
4
5
3
4
5
6
1
3
2
4
1
-3
2
6
7
8. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
89. МИНОР ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯ
МИНОРОМ ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯНАЗЫВАЕТСЯ ОПРЕДЕЛИТЕЛЬ,
ПОЛУЧЕННЫЙ ИЗ ИСХОДНОГО
ОПРЕДЕЛИТЕЛЯ ПРИ ПОМОЩИ
ВЫЧЕРКИВАНИЯ СТРОКИ И
СТОЛБЦА, В КОТОРЫХ
СТОИТ ЭТОТ ЭЛЕМЕНТ.
9
10. ПРИМЕР ВЫЧИСЛЕНИЯ МИНОРА
МИНОР M 21 ЭЛЕМЕНТА a21 ОПРЕДЕЛИТЕЛЯ3
4
7
1 2
2
0
9 1
10
11.
АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕАЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ AijЭЛЕМЕНТА aij ОПРЕДЕЛИТЕЛЯ
НАЗЫВАЕТСЯ ЧИСЛО
Aij ( 1)
i j
M ij ,
ГДЕ M ij МИНОР ЭЛЕМЕНТА aij
11
M
12
13. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
1314. РАЗЛОЖЕНИЕ ПО ЛЮБОЙ СТРОКЕ (ЛЮБОМУ СТОЛБЦУ)
ОПРЕДЕЛИТЕЛЬРАВЕН СУММЕ ПРОИЗВЕДЕНИЙ
ЭЛЕМЕНТОВ ЛЮБОЙ СТРОКИ
(ЛЮБОГО СТОЛБЦА) НА ИХ
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
14
15. ПРИМЕР ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ
РАЗЛОЖИМ ОПРЕДЕЛИТЕЛЬ ПО 2-й СТРОКЕ3
1
4
2
7
9 1
2
4* 2 1
0 ( 1)
1
3
2
( 1) 2 2
0
9 1
1
2
2*
7
1 (3 14) 19 11 8
=4* ( 1) ( 1 18) 2∙
=4∙19-2∙11=
15
Определитель N-го порядка находится по формуле:
где
aij – элемент матрицы;
Мij – минор элемента aij. Минором элемента aij
матрицы А называется определитель матрицы,
которая была получена путем удаления из
матрицы А строк и столбцов, которые содержат
элемент aij
16
17.
МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКАМЕТОД ТРЕУГОЛЬНИКОВ ДЛЯВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА
a12
a33 a31
a22
a
31
a13
a21
a12
a11
a22
a23 a21
a11
a33
a32
a32
a13
a23
17
18
19. Вычислить:
1-3
2
6
3
-9
-7
6
1
2
3
4
2
3
4
5
3
4
5
6
1
3
2
4
1
-3
2
6
19
20. ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДА ТРЕУГОЛЬНИКОВ
23
5
1 3
3
2
4
1
2 1 1 3 ( 3) ( 3) 5 ( 2) 4
4 1 ( 3) 5 3 1 ( 2) ( 3) 2
2 27 40 12 15 12 26
20
21. ОПРЕДЕЛИТЕЛЬ ТРЕУГОЛЬНОЙ МАТРИЦЫ РАВЕН ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ ГЛАВНОЙ ДИАГОНАЛИ
30
0
1 2
2
0 3 2 1 6
0 1
21
1
-3
2
2
6
-1
3
-7
3
1
2
3
2
2
1
3
1
3
Вычислите
определители
третьего порядка
1
2
1
2
2
3
3
1
1
2
1
1
2
2
3
1
3
1
3
1
2
1
2
2
3
3
1
22
23.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА2324. ОБЩИЙ ВИД СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ
a11 x1 a12 x2a x a x
21 1
22 2
an1 x1 aт 2 x2
a1n xn b1 ,
a2 n xn b2 ,
ann xn bn
24
25. МАТРИЧНЫЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
a11a
21
…
a
n1
a12
…
a22
…
…
…
an 2
…
a1n x1 b1
a2 n
x2
b2
… … …
ann xn bn
25
26. ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
a11a12
…
a1n
a21
a22
…
a2 n
…
…
…
…
an1
an 2
…
ann
26
27. ПРИМЕНЕНИЕ МЕТОДА КРАМЕРА НА ПРИМЕРЕ СИСТЕМЫ ИЗ 3-х УРАВНЕНИЙ
a11a
21
a
31
a12
a22
a32
a13 x1 b1
a23 x2 b2
a33 x3 b3
27
28. НЕОБХОДИМОЕ УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛ КРАМЕРА
a11a12
a13
a21
a22
a23 0
a31
a32
a33
28
29.
ВЫЧИСЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙb1 a12 a13a11
1 b2 a22 a23 ; 2 a21
b3 a32 a33
a31
a11
a12
b1
3 a21
a22
b2
a31
a32
b3
b1
a13
b2
a23
b3
a33
29
30. ФОРМУЛЫ КРАМЕРА ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
1x1
,
2
x2
,
3
x3
30
31. ПРИМЕР РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
2 x y 3z 13,4 x 3 y z 7,
x 2 y 5 z 15
31
32. ВЫЧИСЛЕНИЕ ГЛАВНОГО И ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ
21
4
3
1
2
3
1 30 24 1 9 4 20 14 0,
5
13 1
1 7
3
15 2
3
1 195 42 15 135 26 35 42,
5
32
33. ПРОДОЛЖЕНИЕ ВЫЧИСЛЕНИЙ ОПРЕДЕЛИТЕЛЕЙ
2 132 4
1 70 130 13 21 30 260 14,
7
1 15
2
3 4
1
3
5
1 13
3
7 90 140 7 39 28 60 28.
2 15
33
34. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ
1 42x
3,
14
2 14
y
1,
14
3 28
z
2.
14
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
English Русский Правила
Определитель третьего порядка
Определитель третьего порядка:
, – элементы определителя .
Следует запомнить, что элементы образуют главную диагональ определителя, элементы составляют его побочную диагональ.
Вычисление определителя третьего порядка.
Вычисление определителя третьего порядка по правилу треугольников
Рис. 1 Рис. 2
Данное правило
заключается в том, что первые три
слагаемые в правой части равенства
вычисляются так, как это показано на
Рис.
1, они представляют собой произведения
элементов, стоящих на главной диагонали
и вершинах двух треугольников, у которых
одна из сторон параллельна главной
диагонали. Остальные три слагаемых
правой части равенства вычисляются
аналогично (Рис. 2), только за основу
взята побочная диагональ. Причем эти
слагаемые берутся с обратным знаком.
Определение: Минором данного элемента определителя третьего порядка называется определитель второго порядка, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
— минор данного элемента определителя третьего порядка.
Определение: Алгебраическое дополнение данного элемента – это минор, взятый со знаком «плюс», если сумма — четное число, и со знаком «минус», если эта сумма нечетная. — алгебраическое дополнение данного элемента определителя третьего порядка. .
Замечание.
Здесь означает номер строки, а — номер столбца, на пересечении которых находится данный элемент.
Пример 2. Дана матрица . Найти .
Решение
Минор , соответствующий элементу , есть определитель . Он получается, если вычеркнуть из данного определителя третьего порядка третью строку и первый столбец.
По формуле (14) находим алгебраическое дополнение для элемента .
Разложение определителя по элементам строки (или столбца).
— разложение определителя по элементам первой строки.
Определитель равен сумме произведений элементов какой – либо строки (или столбца) на их алгебраические дополнения.
Замечание.
Все свойства определителей второго порядка остаются справедливыми для определителей третьего и более высокого порядка.
Определители высших порядков
Определитель n – го порядка. .
— разложение определителя n – го порядка по элементам первой строки.
Замечание.
Для определителей любых порядков остаются в силе определения минора и алгебраического дополнения данного элемента.
Пример 3. Вычислить определитель третьего порядка .
по правилу треугольников
используя разложение по элементам строки (или столбца)
используя разложение по элементам строки (или столбца), с предварительным образованием нулей.
Решение
Вычисляем определитель по правилу треугольников, используя формулу (2).
Разложим определитель по элементам первой строки, используя формулу (3)
Используя свойство (8), можно значительно упростить вычисление определителя, получая нули в некотором столбце или строке.
Умножая третью строку на (- 4) и складывая ее со второй, а умножая третью строку на (- 2) и складывая ее с первой, получим
. Вычислим этот определитель, разлагая его по элементам второго столбца (т. к. из трех элементов – два нуля): . Согласно свойству (3) , из первого столбца выносим (-1), а из второго (-5), получаем .
линейная алгебра — определитель треугольной матрицы
спросил
Изменено 4 года, 11 месяцев назад
Просмотрено 1к раз
$\begingroup$
Насколько я понимаю, определитель матрицы можно найти по ее диагонали, если она имеет треугольную форму.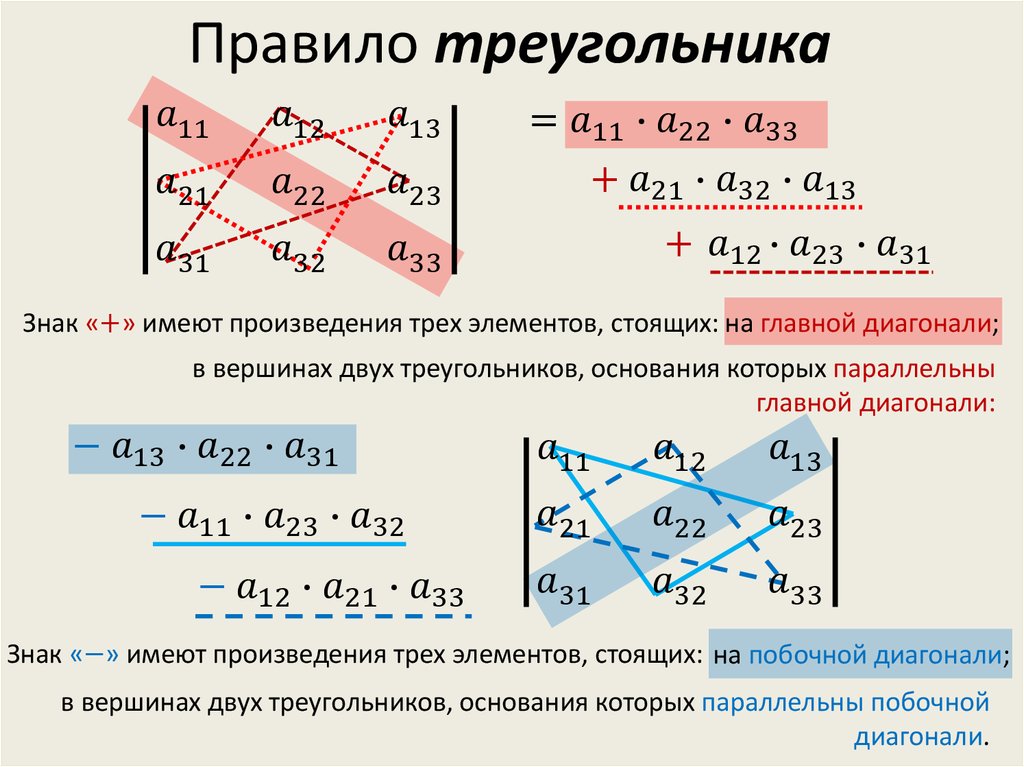
Для такой матрицы:
$$
\begin{pmatrix}
1 и 5 и 0\\
2 и 4 и -1\\
0 &-2 & 0
\end{pматрица}
$$
При переводе в треугольную форму я получаю:
$$
\begin{pmatrix}
1 и 5 и 0\\
0 и 1 и 1/6\\
0 и 0 и 1/3
\end{pматрица}
$$
Поскольку я умножил вторую строку на -1/6 во время сокращения строки, я ожидаю, что определитель будет
$$
1\cdot 1\cdot 1/3\cdot (-1/6),$$
но ответ для определителя исходной матрицы равен -2. Где именно я ошибаюсь?
- линейная алгебра
- матрицы
$\endgroup$
6
$\begingroup$
Вы можете добавить кратное число любой строки к другой строке без изменения определителя. Итак, я проделаю такие операции, чтобы получить треугольную форму.
Начните с
$$\begin{matrix} 1 & 5 & 0 \\ 2 & 4 & -1 \\ 0 &-2 &0 \end{matrix}$$
Вычесть дважды первую строку из второй:
$$\begin{matrix} 1 & 5 & 0 \\ 0 & -6 & -1 \\ 0 &-2 &0 \end{matrix}$$
Вычтите одну треть новой второй строки из третьей:
$$\begin{matrix} 1 & 5 & 0 \\ 0 & -6 & -1 \\ 0 & 0 & \frac{1}{3} \ end{matrix}$$
Произведение по диагонали равно $-2$.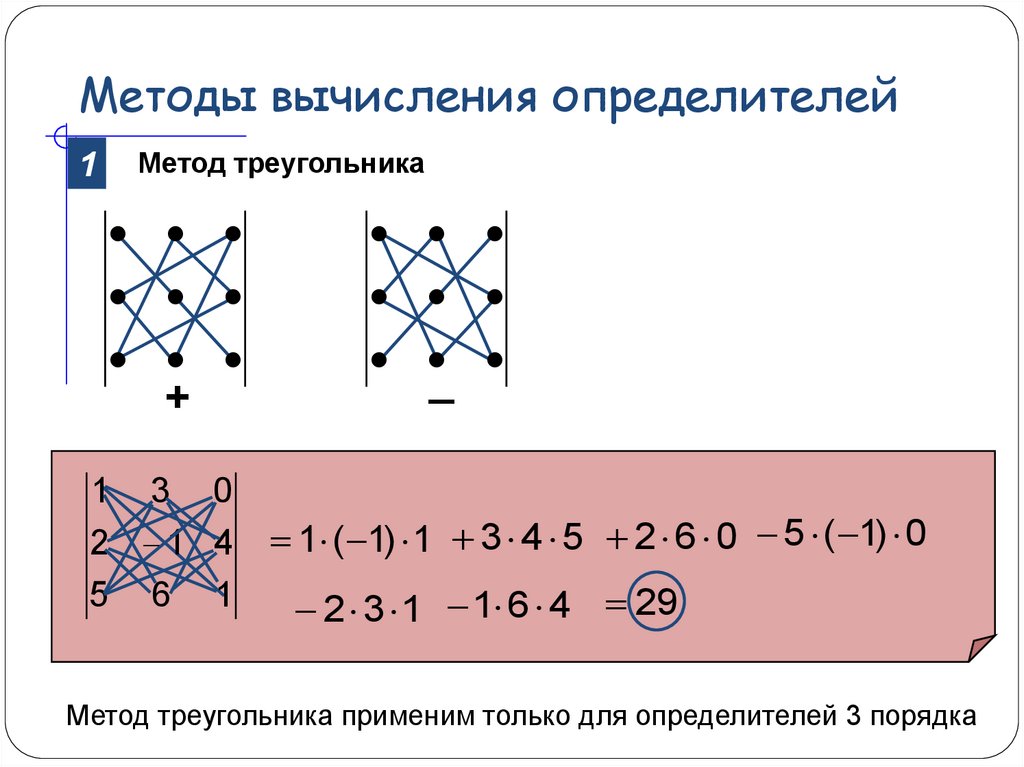
Однако удаление множителя из одной из строк изменяет определитель на этот множитель. Вы вытащили $-1/6$ из второй строки, поэтому вычисленный определитель от диагонали в вашем вопросе был занижен на этот коэффициент.
$\endgroup$
8
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
линейная алгебра — Нахождение определителя матрицы 5×5, но не может представить его в нижнем треугольном виде
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 18 тысяч раз
$\begingroup$Как найти определитель этой матрицы 5×5? Я не могу представить его в форме нижнего или верхнего треугольника, поэтому я запутался. Я действительно не знаю, как использовать расширение Лапласа
$\begin{bmatrix}3&0&0&3&0\\-3&0&-2&0&0\\0&-1&0&0&-3\\0&0&0&3&3\\0&-1&2&0&0\end{bmatrix}$
Я попытался получить все нули по диагонали, а затем удалил строку 1, столбец 1, так что теперь у меня есть матрица 4×4, поэтому я сделал
$R_2 = R_1 + R_2$, затем я сделал $R_4 = R_2 — R_4$, затем я получил $3 \begin{bmatrix}0&-2&3&0\\- 1&0&0&-3\\0&-2&0&-3\\-1&2&0&0\end{bmatrix}$ = $3(-1)(-2)(2)(-1) + 3(-2)(3)(-3) (-3) = -498 $, но я сделал $R_2 — R_4$, поэтому я разделил на коэффициент -1 и получил $\det(A) = -498/-1 = 498$, что все еще было неверным
- линейная алгебра
- определитель
$\endgroup$
14
$\begingroup$
Метод ERO:
$$\begin{align}\begin{vmatrix}3&0&0&3&0\\-3&0&-2&0&0\\0&-1&0&0&-3\\0&0&0&3&3\\0&-1&2&0&0\end{vmatrix} &= \begin{vmatrix}3&0&0&3&0\\0&0&-2&3&0\\0&-1&0&0&-3\\0&0&0&3&3\\0&-1&2&0&0\end{vmatrix} \tag{$R_2\to R_2+R_1$}\\ &=\color{ red}{-}\begin{vmatrix}3&0&0&3&0\\0&-1&0&0&-3\\0&0&-2&3&0\\0&0&0&3&3\\0&-1&2&0&0\end{vmatrix} \tag{$R_3\leftrightarrow R_2$} \\ &= -\begin{vmatrix}3&0&0&3&0\\0&-1&0&0&-3\\0&0&-2&3&0\\0&0&0&3&3\\0&0&2&0&3\end{vmatrix} \tag{$R_5\to R_5-R_2$} \\ &=-\begin{ vmatrix}3&0&0&3&0\\0&-1&0&0&-3\\0&0&-2&3&0\\0&0&0&3&3\\0&0&0&3&3\end{vmatrix} \tag{$R_5\to R_5+R_3$} \\ &=-\begin{vmatrix}3&0&0&3&0\ \0&-1&0&0&-3\\0&0&-2&3&0\\0&0&0&3&3\\0&0&0&0&0\end{vmatrix} \tag{$R_5\to R_5-R_4$} \\ &=0\end{align}$$
Метод расширения Лапласа:
В каждой строке и столбце есть записи по $2$, поэтому я не вижу никакого стратегического способа выбрать, где это расширить.
Итак, сначала я пройдусь по первой строке:
$$\begin{align}\begin{vmatrix}3&0&0&3&0\\-3&0&-2&0&0\\0&-1&0&0&-3\\0&0&0&3&3\\0&-1&2&0&0\end{vmatrix} &= 3\begin{vmatrix}0&-2&0&0 \\-1&0&0&-3\\0&0&3&3\\-1&2&0&0\end{vmatrix} + -3\begin{vmatrix}-3&0&-2&0\\0&-1&0&-3\\0&0&0&3\\0&-1&2&0\end{vmatrix} \end{выравнивание}$$
Теперь расширю по первой строке первого и первому столбцу второго:
$$=3\left[-(-2)\begin{vmatrix}-1 & 0 & -3 \\ 0 & 3 & 3 \\ -1 & 0 & 0\end{vmatrix}\right]+-3\left[-3\begin{vmatrix}-1 & 0 & -3 \\ 0 & 0 & 3 \\ — 1 & 2 & 0\end{vmatrix}\right]$$
Отсюда расширяем третью и вторую строки и вычисляем определитель $2\times 2$ обычным способом, чтобы получить $$=6[-(0- -9)]+9[-3(-2-0)] = 0$$
Внешний метод продукта:
$$\begin{align}&(3e_1-3e_2)\клин (-e_3-e_5)\клин (-2e_2+2e_5)\клин (3e_1+3e_4)\клин (-3e_3 +3e_4) \\ &= \big[3e_1\клин(-e_3-e_5)\клин(-2e_2+2e_5)\клин(3e_1+3e_4)\клин (-3e_3+3e_4)\big] \\ &\quad -\big[3e_2\клин(-e_3-e_5)\клин(-2e_2+2e_5)\клин(3e_1+3e_4)\клин (-3e_3+3e_4)\большой] \\ &= \big[3e_1\клин( -e_3-e_5)\клин(-2e_2+2e_5)\клин(3e_4)\клин (-3e_3+3e_4)\большой] \\&\quad -\big[3e_2\клин (-e_3-e_5)\клин( 2e_5)\клин(3e_1+3e_4)\клин (-3e_3+3e_4)\большой] \\ &= -9\big[e_1\клин e_3\клин (-2e_2+2e_5)\клин e_4\клин (-3e_3+3e_4)\big] \\ &\quad -9\big[e_1\клин e_5\клин (-2e_2+2e_5) )\клин e_4\клин (-3e_3+3e_4)\большой] \\ &\quad +6\big[e_2\клин e_3\клин e_5\клин (3e_1+3e_4)\клин (-3e_3+3e_4)\большой] \\ &\quad +6\big[e_1\wedge e_5\wedge e_5\wedge(3e_1+3e_4)\wedge (-3e_3+3e_4)\big] \\ &= -9\big[0\big]-9 \big[e_1\клин e_5\клин(-2e_2)\клин e_4\клин (-3e_3)\big] +6\big[e_2\клин e_3\клин e_5\клин(3e_1+3e_4)\клин (3e_4)\ большой]+6\большой[0\большой] \\ &= (-9\cdot 6)I+(6\cdot9)I \\ &=0I\end{align}$$
Метод линейной зависимости от случайного уведомления:
Обратите внимание, что $R_1 = -R_2+R_3 +R_4-R_5$.