Решение уравнений матрица: Обратная матрица онлайн

Содержание

Публикация не была найдена — Студопедия

Поделись

Продолжительность: 180 мин.

Дисциплина: Информатика

Предназначено: для студентов по направлениям: менеджмент, экономика, международная экономика, налоги и налогообложение, юриспруденция.

Цель:научиться использовать программу Excel для решения задач линейной алгебры (вычисление определителей матрицы, умножение матриц, вычисление обратной матрицы, решение систем линейных уравнений), а также находить корни нелинейных уравнений.

Результат обучения:пользовательсможет с помощью программы Excel находить корни уравнений и решать системы линейных уравнений, вычислять определители матрицы и использовать матричное исчисление для решения экономических задач.

План занятий:

I).Вычислить определители матриц А и В;

II).Найти матрицу, обратную к матрице А и выполнить проверку

III). Вычислить произведение матриц А и В;

IV).Решении практических задач матричным способом

V).Решение систем линейных уравнений

VI). Решение алгебраического уравнения

Для решения задач, связанных с необходимостью умножения матриц, вычисления обратных матриц, вычисления определителей матрицы, используемых для решения систем линейных алгебраических уравнений в программе Excel предусмотрены соответствующие функции, расположенные в Мастере функций. Любая матрица представляет собой массив данных, представляемый в виде таблицы размера mx n с числовыми данными. Познакомимся с предоставляемыми возможностями программы Excelна примере решения следующих задач:

I).Загрузите программу Exсel.Переименуйте лист 1 (новое название листа —

Матрицы). Даны две матрицы A и В вычислить определители матриц
Для решения первой задачи в окне электронной таблицы введем элементы матриц А и В. В ячейке В1 введем заголовок — Матрица А, сами элементы матрицы расположим в ячейках А2:D5, каждое число — элемент матрицы вводится в отдельную ячейку. Соответственно в ячейке F1 введем заголовок — Матрица В, расположив ниже в ячейках F2:I5 элементы этой матрицы.
В ячейках А7 и F7 наберите заголовки: Определитель А=и Определитель В=.
Функция, используемая для вычисления определителя, имеет имя МОПРЕД, в качестве ее аргумента используется блок ячеек с элементами матрицы. В ячейку А8 введите формулу: МОПРЕД(А2:D5)и нажмите клавишу ввода Enter. В результате вы получите вычисленное значение определителя матрицы
А. Аналогично в ячейке F8 вычисляется определитель матрицы В. Для ввода формулы можно использовать клавиатуру или Мастер функций.
Сохранить документ в папке Excel в файле lab-4.xls.
II. )Для вычисления матрицы А^-1, обратной к матрице А, используется функция МОБР, аргументом которой является массив данных исходной «матрицы А». Обратная матрица будет существовать, если определитель матрицы А # 0. В ячейку А10 введите заголовок: Обратная матрица. Поставьте курсор на ячейку А11 и выделите блок ячеек А11:D14. Войдите в Мастер функций
и найдите функцию МОБР,в окне функции введите ее аргумент — А2:D5, завершите ввод, нажавклавиши Shift+Ctrl+Enter. В результате в ячейках А11:D14 вы получите элементы обратной матрицы.
Проверьте правильность вычисления обратной матрицы А^-1умножением на нее исходной матрицы А, в результате должна получиться единичная матрица Е.
В ячейках A17:D20, где представлены результаты проверки, задайте числовой формат — два десятичных знака после запятой.
Сохранить документ под тем же именем lab-4.xls. При повторном сохранении под тем же именем достаточно нажать кнопку «Сохранить» .
III.)Для умножения матриц А и В используется функция МУМНОЖ,
аргументами которой являются элементы этих матриц. При умножении двух матриц необходимо помнить, что число колонок 1-й матрицы должно равняться числу строк второй, т.е. если 1-я матрица имеет размер mxn, а 2-я матрица nxk, то в результате получится матрица размера mxk.
Введите в ячейку А22 заголовок — Результирующая матрица.Так как у нас матрицы А и В имеют размер 4х4, то в результате также будет матрица размера 4х4. Поставьте курсор в ячейку А23 и мышью выделите блок ячеек A23:D26. Вызовите Мастер функций и выберите функцию МУМНОЖ. В окне функции введите ее аргументы — блоки ячеек А2:D5и F2:I5.В ячейке А23 вы увидите вводимую функцию. Для завершения ее ввода в блок ячеек
нажмите клавиши Shift+Ctrl+Enter.В результате в ячейках вы получите элементы результирующей матрицы- произведения матриц А и В.
IV.) Решении практических задач матричным способом
Умножение матриц часто используется при решении практических задач, где данные представлены в табличной форме.
Решим одну из таких задач:Продовольственная база снабжает сеть из 11 магазинов. В течение квартала в магазины осуществляется завоз набора основных продуктов. График завоза продуктов приведен в таблице 4.1. Набор основных требуемых продуктов по магазинам приведен в таблице 4.2. Необходимо определить общее количество продуктов, требуемое ежемесячно и в течение квартала. Результат поместить в таблицу 3.
Откройте новый рабочий лист.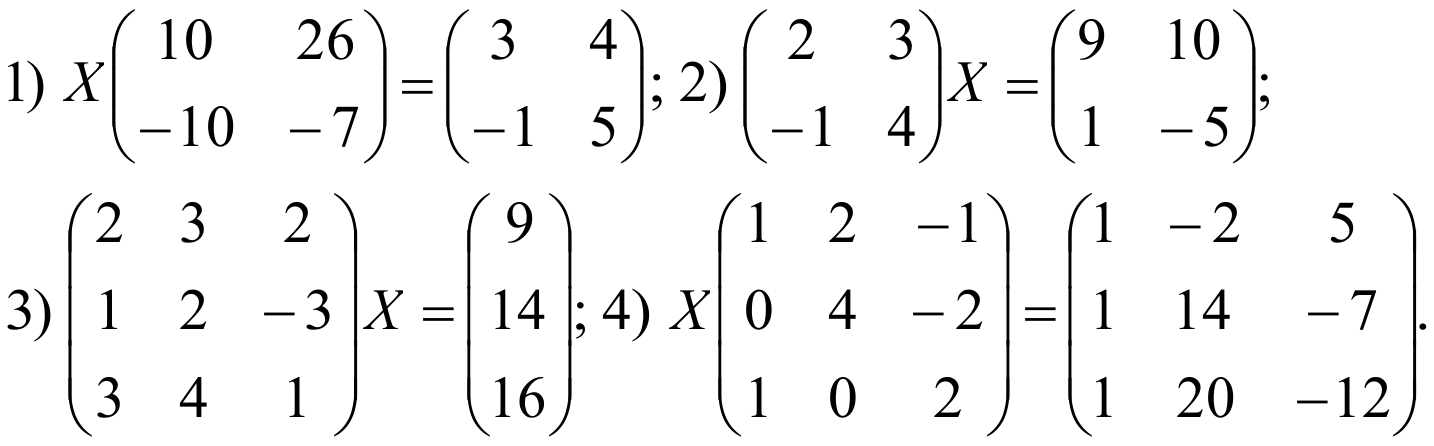 Присвойте листу новое имя — Задача. Наберите и оформите на этом листе представленные таблицы 4.1 и 4.2.

Таблица 4.1. План завоза продуктов по магазинам.
Номера магазинов
Месяцы N10 N12 N15 N18 N19 N20 N22 N25 N30 N32 N34
Январь
Февраль
Март

Итого
В строке Итого необходимо просуммировать значения в соответствующих столбцах с помощью кнопки «Автосумма» . Для этого выделите ячейки от N10 до цифры 9 в последнем столбце и пустую строку итого затем нажмите . В результате в пустой строке появятся значения суммы.
Данные, представленные в этих таблицах, образуют две матрицы размера 4х11 и 11х6. Решение задачи получается умножением соответствующих элементов 1-й и 2 таблиц, т.е. обычным умножением матриц. Результирующая матрица, образующая Таблицу 4.3, будет иметь размер 4х6.

Таблица 4.2. Объем поступлений продуктов при каждом завозе по магазинам.
N магазина Консервы рыб., шт. Мясо, т. Колбасн. изд, кг Сахар, ц. Крупы, ц. Макарон. издел., ц.
N10
N12
N15
N18
N19
N20
N22
N25
N30
N32
N34
Подготовьте форму таблицы 4.
3. Ее верхняя строка заголовков получается копированием верхней строки с заголовками Таблицы 4.2, а левые заголовки получаются копированием левой колонки с заголовками Таблицы 4.1.
Таблица 4.3. Требуемое количество продуктов на 1-й квартал.
Месяцы Консервы рыб., шт. Мясо, т. Колбасн.изд, кг Сахар, ц. Крупы, ц. Макарон. издел., ц.
Январь
Февраль
Март
Итого
Результаты внутри Таблицы 4. 3 получаются как результат умножения данных Таблицы 4.1 (матрица А) на данные Таблицы 4.2 (матрица В) аналогично выполненному ранее умножению матриц.
V).Решить систему линейных уравнений
Задание:Для решения системы линейных уравнений откройте новый рабочий лист, присвойте ему имя Система уравнений.
Система линейных уравнений в матричной форме имеет вид: АХ=В, где А — матрица, составленная из коэффициентов при неизвестных в уравнениях, Х — вектор из неизвестных,В — вектор, составленный из правых частей уравнений. Решение системы линейных уравнений в матричной форме имеет вид: Х=А^-1•В, т.е. для нахождения решения системы Х необходимо:
а) найти матрицу, обратную к исходной матрице А;
б) умножить получившуюся обратную матрицу на вектор свободных членов уравнений В.
Подготовьте на листе необходимые заголовки для решения системы уравнений для этого введите текст в ячейки: А1 —Исходная матрица, F1- Правая часть системы уравнений, A7- Обратная матрица, F7- Решение, H7- Проверка.
Для редактирования текста выделите ячейки А1-D1 и нажмите кнопку на панели инструментов «Объединить и поместить в центре» , аналогично проделайте с ячейками A7:D7.
Рис. 4.1.
Введите в соответствующие ячейки ниже заголовков матрицу из коэффициентов при неизвестных в уравнениях и правые части системы уравнений как показано на рисунке 4.1.
С помощью функции МОБР вычислите обратную матрицу для этого выделите ячейки А9:D12 нажмите = откройте мастер функций , категории математические, функцию МОБР. В появившемся диалоговом окне в строке массив выделите мышью матрицу А, в результате появятся ячейки (A2:D5).
Решение системы линейных уравнений, т.е. Х=А^-1•В С помощью функции умножения матриц умножьте обратную матрицу на вектор свободных членов и результат поместите в соответствующей части рабочего листа (выделить F9:F12 нажать = и выполнить умножение матриц как показано на рис.4. 2.)
Рис. 4.2.
Проверьте полученное решение системы линейных уравнений. Для этого надо умножить исходную матрицу на полученное решение. В результате должен получиться вектор свободных членов (см. Рис.4.3.).
Рис.4.3.
VI). Решение уравнений.Для решения алгебраических уравнений до 3 степени включительно существуют формульные выражения, позволяющие через коэффициенты при неизвестных в уравнении находит корни уравнения (например формула Виетта). Уравнения, начиная с 4-й степени и выше, а также трансцендентные уравнения обычно в радикалах не решаются. Для нахождения корней таких уравнений обычно используются приближенные методы решения, позволяющие по начальному приближению вычислять корни уравнения с задаваемой точностью. Наиболее часто используются метод касательных и метод хорд. Для применения этих методов необходимо выделить интервал, на котором корень уравнения будет единственным. На концах интервала функция должна принимать противоположные по знаку значения. На этом интервале функция должна быть непрерывной, монотонно возрастающей или убывающей (знак производной постоянен) и не иметь точек перегиба. Тогда решение уравнения может быть найдено приближенными методами. Эти методы реализованы в программе Excel в виде команды меню Сервис/Поиск решения. С помощью этой команды можно также находить точки экстремума и вычислять экстремальные значения функции (минимум/максимум).
Задание:Найти корни уравнения: 3x⁵— 5x²+ 2x -7 = 0 и найти минимум функции на интервале (-2; 3).
Алгоритм выполнения задания:
1)Вставить новый лист (Вставка ®Лист) и переименовать (Формат ®Лист®Переименовать) в «Поиск решения».
2)в ячейке А1 введите заголовок Решение уравнения, в ячейке В1 введите заголовок Функция, в ячейке С1 — Точка экстремума,в ячейке D1 — заголовок Минимум функции;
3) в ячейках А2 и С2 наберите начальное приближение — 0;
4) в ячейке В2 с помощью Мастера функций введите функцию, находящуюся в левой части уравнения (в качествех будет ячейка А2): =3*A2^5-5*A2^2+2*A2-7;
5) в ячейке D2 также наберите нашу функцию, только вместо А2 необходимо набрать С2;
6) вызовите команду меню Сервис/Поиск решения. В открывшемся окне команды необходимоустановить целевую ячейку В2 равной значению0. В опции команды Изменяя ячейкиуказать ячейку, в которой мы ищем решение (А2). Так как найти корни уравнения и минимум функции надо на интервале (-2; 3), то введем ограничение (нажмите опцию ): A2>=-2; еще раз А2<=3. После ввода всех необходимых для поиска решения данных нажмите кнопку .В результате в ячейке А2 вы получите решение уравнения см. рис. 4.4. Значение функции в ячейке В2 будет приблизительно (с заданной вами точностью) равно -5,83Е-07 в экспоненциальной форме записи, или является числом -0,000000583 в числовой форме записи.
Рис. 4.4.
Выполним форматирование ячейки В2, для этого курсор установим в В2 откроем пункт меню Формат®Ячейки откроется диалоговое окно см рис.4.5. Далее выполняются действия по порядку обозначенные на рисунке 1. «Число» ®2.«Числовой»®3. «Число десятичных знаков:» 9 ®4. ОК.
Рис.4.5.
В результате проделанных операций в В2 значение -0,000000583 округлим это значение с помощью панели инструментов кнопки «Уменьшить разрядность» до сотых (0,00).
Примечание: Если в результате поиска решение не может быть найдено (об этом на экране будет выведено соответствующее сообщение), это означает, что заданный вами интервал поиска или начальное приближение подобраны неудачно и вам необходимо изменить интервал поиска, задаваемый ограничением;
7) для нахождения минимального значения функции необходимо вызвать команду Сервис/Поиск решения и в ее окне указать целевую ячейку D2 равной минимальному значению, изменяемая ячейка — С2, а ограничения поиска минимума (интервал (-2;3)), задается ограничениями C2>-2 и C2<3. В результате выполнения поиска решения в ячейке С2 вы получите точку экстремума, а в ячейке D2 — минимальное значение функции на интервале.
5. Сохранить полученные результаты с помощью кнопки «Сохранить» при этом книга Excel с ее страницами сохраняется под именем lab-4.xlsприсвоенном в начале лабораторной работы.

НОУ ИНТУИТ | Лекция | Сравнения и матрицы
< Лекция 15 || Лекция 3: 1234
Аннотация: В данной лекции рассматриваются матрицы и операции с матрицами вычетов, которые широко используются в криптографии. Используя матрицы вычетов решается набор уравнений сравнения.
Ключевые слова: прямоугольный массив, скалярное умножение, детерминант, рекурсивное определение, инверсия, Единичная матрица, криптография, множества, линейное уравнение, коэффициентами системы, бинарная операция, делимое, алгоритм Евклида, центили
3.1. Матрицы
ru/2010/edi»>В криптографии мы должны обрабатывать матрицы. Хотя эта тема принадлежит специальному разделу алгебры, который называется линейной алгеброй, необходим краткий обзор матриц для подготовки к изучению криптографии. Читатели, знакомые с этими вопросами, могут пропустить часть или весь этот раздел. Раздел начинается с некоторых определений и примеров использования матрицы в модульной арифметике.
Определения
Матрица — прямоугольный массив, содержащий l x m элементов, в которых l — число строк, m — число столбцов. Матрица обычно обозначается заглавной буквой, такой, как A. Элемент a_ij расположен в i -той строке и j -том столбце. Хотя элементы матрицы могут быть любым множеством чисел, мы обсуждаем только матрицы с элементами в Z. Пример матрицы с m столбцами и l строками
Если матрица имеет только одну строку ( l = 1 ), она называется матрицей-строкой ; если она имеет только один столбец ( m = 1 ), то называется матрицей-столбцом. Матрица называется квадратной, если число строк равно числу столбцов ( l = m ) и содержит элементы a₁₁, a₂₂, ……, a_mm. Матрица обозначается 0, если все строки и все столбцы содержат нули. Единичная матрица обозначается I, если она квадратная и содержит все единицы на главной диагонали и все нули на других местах. Рисунок 3.2 показывает некоторые примеры матриц с элементами из Z.
Рис. 3.2. Примеры матриц
Операции и уравнения
В линейной алгебре для матриц определены одно уравнение (равенство) и четыре операции (сложение, вычитание, умножение и скалярное умножение).
Равенство
Две матрицы равны, если они имеют одинаковое число строк и столбцов и соответствующие элементы равны. Другими словами, A = B, если мы имеем a_ij = b_ij для всех i и j.
Сложение и вычитание
Операция сложения двух матриц может применяться, если матрицы имеют одинаковое число столбцов и строк. Сложение записывают как C =A + B. В этом случае полученная в результате матрица C имеет тот же самый номер строк и столбцов, как A или B. Каждый элемент C — сумма двух соответствующих элементов A и B: a_ij + b_ij.
Операция вычитания производится аналогично сложению, за исключением того, что каждый элемент B вычитается из соответствующего элемента A: d_ij= a_ij – b_ij.
Пример 3.1
Ниже показан пример сложения и вычитания.
Умножение
Две матрицы различного размера могут быть перемножены, если число столбцов первой матрицы совпадает с числом строк второй матрицы.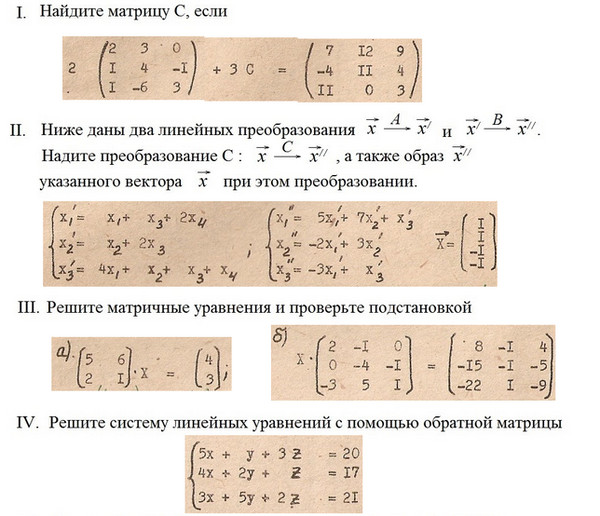 Если A — матрица размера l x m, а матрица B размера m x p, то произведением будет матрица C размером l x p. Если элемент матрицы A обозначить a_ij, а каждый элемент матрицы B обозначить b_jk, то элемент матрицы C — c_ik — вычисляется следующим образом:
Пример 3.2
Рисунок 3.3 показывает произведение матрицы-строки ( ) на матрицу-столбец ( ). В результате получаем матрицу размером .
Рис. 3.3. Умножение матрицы-строки на матрицу-столбец
Пример 3.3
Рисунок 3.4 показывает произведение матрицы на матрицу . В результате получаем матрицу
Рис. 3.4. Умножение матрицы 2 x 3 на матрицу 3 x 4.
Скалярное умножение
Мы можем также умножить матрицу на число (называемое скаляр ). Если A — матрица и x — скаляр, то C = xA — матрица , в которой .
Рис. 3.5. Скалярное умножение
Пример 3.4
Рисунок 3.5 показывает пример скалярного умножения.
Дальше >>
< Лекция 15 || Лекция 3: 1234
Решение систем линейных уравнений с матрицами
Правовые операции с матрицами
Рис. 1
На Рис. решение системы уравнений черным шрифтом слева. Этот система была решена путем сложения двух уравнений. Это дополнение вызвало переменная y отбрасывается, и получается уравнение с одной переменной. Этот позволили нам решить для x . Как только мы узнали x , мы могли легко найти и .
Справа на рис. 1 выше, в синяя надпись , вы можете видеть аналогичную работу, выполняемую над строками матрицы. Строка матрицы 1,1,8 просто представляет уравнение: 1 x + 1 y = 8. Таким образом, строка матрицы — это просто коэффициенты уравнения. Матрица ряд 1,-1,4 представляет уравнение:
1 х — 1 у = 4,
Точно так же, как мы можем сложить два уравнения слева, мы можем добавлять к строкам справа. Вы можете видеть это в строке a + b —> a , где вы видите новый ряд 2,0,12. Это просто сумма строк a и b . Следующая строка помечена a — b —> b показывает результат вычитания строки b из строки a , а именно, 0,2,4.
Последний раздел справа показывает, что только как законно умножать уравнение на число или делить уравнение на число число, допустимо также умножать или делить строку матрицы на число (скаляр).
В левом нижнем углу приведена сводка юридических операции внутри матриц. Вы можете на законных основаниях выполнить любую из этих трех процедур. Вы также можете выполнять любую комбинацию этих трех операций. Действительно, эти юридические операции — это те же допустимые операции, которым вы научились ранее использовать в алгебре.
Решение системы уравнений с помощью Алгебра
Рисунок 2
На рисунке 2 выше мы берем решение система сначала использует методы алгебры, которые вы должны знать из своей алгебры фон. Система трех уравнений показана в левом верхнем углу. Сначала я напомнить вам о том, что если вы решаете систему с тремя переменными, вы нужно 3 уравнения. Если вы решаете систему с 9 переменными, вам нужно 9уравнения. В общей ситуации, если вы решаете систему с n переменных, вам нужно n уравнений. Итак, вы видите, что для этой системы с 3 переменных, у нас есть 3 уравнения.
В процессе решения такой системы мы нужно исключить переменные, пока мы не дойдем до уравнения с 1 переменной. Поэтому нам нужно найти какие-то способы легально избавиться от некоторых переменных.
Вы можете заметить, что если добавить уравнения и и b , вы можете удалить переменную y . Вы также можете получить y отбросить, если добавить уравнения b и c .
Теперь у нас осталось 2 уравнения с 2 переменные. Выше эти уравнения помечены как уравнения d и e . Нам еще нужно избавиться от еще одной переменной. Мы видим, что если умножить уравнение d на 2 и добавить его к уравнению e , мы действительно можем решить для одной из наших переменных. Мы находим, что x = 1. Это не займет много времени. дольше, чтобы увидеть из уравнения b, что y должен быть равен -2. И наконец, подставляя x = 1 и y = -2 в уравнение a , мы можем найдите, что z должно равняться -1. Мы не закончим, пока не проверим все три приводит к каждому из трех уравнений, с которых мы начали.
Красная стрелка на рисунке 2 указывает на матрицу форме тех же трех уравнений, с которых мы начали. Эта матрица 3 x 4 имеет квадрат матрица слева и дополнительный столбец справа. Поскольку эта матрица имеет был добавлен, его иногда называют расширенная матрица . В настоящее время мы будем работать над решением этой же системы, просто используя матрицу.
Рисунок 3
На рисунке 3 выше показаны два важных элемента. для нашей процедуры решения матрицы. В верхней части рисунка 3 вы видите «Желаемая цель». Это форма, которую мы хотим, чтобы наша матрица была по образцу. Обратите внимание, что мы хотим, чтобы левая часть матрицы стала тождеством . матрица . Также будет дополнительная колонка с тремя величинами в них. Эти количества a , b и c , причем решения системы. Верхняя строка гласит: «1 x + 0 y + 0 z = a «, что фактически говорит: « x = a «. вторая строка говорит: « y = b ». Третья строка фактически говорит: « z = c .» И так, матрица в таком виде полностью решается.
Вторая часть рисунка 3 выше — это рекомендуемый стратегический порядок получения левой части матрицы преобразуется в единичную матрицу . Причина предоставления вам этот рекомендуемый стратегический порядок состоит в том, чтобы свести к минимуму или устранить впустую усилие. По мере того, как мы будем работать над проблемой ниже, вы в конце концов увидите, что это заказ поможет устранить любую напрасную работу.
Рисунок 4
На рисунке 4 выше мы видим, что 1 в второй ряд обведен. Это потому, что в нашем плане стратегического заказа мы в первую очередь преобразование этой первой ячейки во вторую строку. Что мы хотим этого первой ячейкой во втором ряду стать? Беглый взгляд на рисунок 3 должен сказать нам, что мы хотим, чтобы это был ноль. Как мы можем заставить это стать нулем? Что ж, мы, конечно, должны следовать только допустимым операциям, показанным на рис. 1. Один план, который позволит достичь этого, состоит в том, чтобы умножить строку b на -2 и добавить результат в строке a . Затем мы поместим результат в строку b . Этот обозначен выше с помощью обозначения -2 b + a —> b . Конечно, мы должны выполнить эту операцию для каждого числа в строке b . (все 4) Во второй матрице виден результат после переноса вне этой операции.
Рисунок 5
Следующее число, которое нам нужно изменить, это нижний левый элемент, который обведен кружком на рис. 5 выше. Нам снова нужно это число, которое нужно преобразовать в ноль. Мы видим, что строка b не делает хороший. Ноль плюс что угодно ничего не меняет. Итак, теперь мы знаем, что у нас есть использовать строку a . Мы могли бы взять 3 раза строку и и -2 раза строку c . Сложение этих двух вместе даст ноль в первой позиции. Рисунок 5 показывает, что произойдет, если вы выполните этот план на весь ряд.
Рисунок 6
Следующее число, которое нам нужно изменить, это второй элемент в строке c . Нам нужно, чтобы этот элемент был нулем. Это очень важно на данном этапе задачи помнить, что пока мы хотим изменить второй элемент в строке c , нам нужно защитить ноль, который мы ранее было изменено на ноль. Для защиты нуля в первом позицию, нам нужно работать со строкой, которая также имеет ноль в первой должность. Это говорит нам о том, что нам нужно выполнить операцию, которая включает строку 9. 0072 б . Наш план состоит в том, чтобы умножить -3 на строку c , добавить к b и подставить c . Выполните эту операцию и посмотрите, получится ли у вас такая же нижняя строка, как показано на рисунке 6. выше.
Рисунок 7
Следующее число, которое нам нужно изменить, это второй элемент в строке b . Это первый элемент, который мы хотим превратиться в 1. Вам понравятся эти преобразования. Чтобы преобразовать element в 1, требуется только операция с одной строкой. Все, что вам нужно сделать, это разделить каждый элемент строки б по -3. Результаты вернутся в ряд б . См. результаты на рис. 7 выше.
Рисунок 8
Следующий элемент, который необходимо преобразовать является третьим элементом в строке c . Его нужно преобразовать в 1. Преобразования элемента в единицу являются самыми простыми из всех. Опять же, все мы нужно умножить каждый элемент в строке c на -1/20.
Рисунок 9
Наше следующее преобразование — третий элемент в ряд б . Этот элемент должен быть нулем. Здесь забота состоит в том, чтобы «защитить» первые два элемента этого ряда, над которыми мы работали трудно получить в их нынешнем виде. Два начальных нуля в строке c равны идеальная защита для этих двух элементов. Поэтому мы хотим сделать b,c операция. Наш план состоит в том, чтобы умножить строку c на 1/3, и прибавить результат к б .
Рисунок 10
Готово два ряда! Обратите внимание, что теперь строки b и c полностью сделаны. Сейчас мы работаем над преобразованием третьего элемент в строке a до нуля. В ряду и нет ничего, что нуждается в защите. Мы просто вычтем строку из минус строку c , и поместите результат обратно в строку a .
Рисунок 11
Теперь нам нужно преобразовать второй элемент в строку в в ноль. У нас есть один элемент для защиты в строке и , поэтому мы замечаем, что строка b является идеальной защитой, потому что в ней стоит ноль. третья позиция. Здесь мы можем просто добавить строку a к строке b и поставить назад в строке и .
Рисунок 12
Последний элемент для трансформации. Потому что это элемент должен быть единицей, мы можем просто разделить строку a на 2. Готово! Теперь, поскольку матрица имеет единичную матрицу слева, наши ответы таковы: сидит в третьей колонне. Система решена.

Особые ситуации
Некоторые системы уравнений не имеют решений. Если вы представляете система уравнений выше как система трех линий в трехмерном пространство. то вы вполне можете себе представить, что 3 таких линии не обязательно должны пересекаться в 1 общая точка. На самом деле, было бы довольно редко, чтобы они пересекались в одном месте. общая точка.
При решении матриц мы изо всех сил пытаемся сделать левую часть матрицы в единичную матрицу. Если матрица не имеет решение, то вы увидите матрицы, которые в конечном итоге будут выглядеть так:

Обратите внимание, что нижняя строка фактически говорит нам, что 0*X + 0*Y + 0*Z = 1, что невозможно. Это наша реплика, что это невозможно Матрица, из которой нужно найти единственное решение.
В результате наших усилий по достижению единичная матрица в левой части матрицы. Ниже находится этот тип:

Здесь у нас есть уникальная нижняя строка из всех нулей. Алгебраический уравнение, которое это представляет, а именно, 0*X + 0*Y + 0*Z = 0 верно. это правда, но это точно ничего не говорит нам о системе уравнения. Эта система имеет бесконечно много решений.
Вы должны уметь распознавать эти два специальных типа результатов матрицы и что они означают.
Решение линейных уравнений с использованием матриц и Python
В предыдущей статье мы рассмотрели решение задачи ЛП, то есть системы линейных уравнений с ограничениями-неравенствами. Если наш набор линейных уравнений имеет детерминированные ограничения, мы можем представить задачу в виде матриц и применить матричную алгебру. Матричные методы компактно представляют несколько линейных уравнений с использованием функций существующей библиотеки матриц.
Мы будем использовать NumPy (здесь хороший учебник) и SciPy (здесь справочное руководство). Для установки этих удивительных пакетов в Интернете есть множество ресурсов, мы просто указываем на Установка стека SciPy.
Пример
В качестве практики мы продолжим с примером, сначала написав матричную модель, а затем используя Numpy для решения.

Теперь мы можем формализовать задачу с помощью матриц:

Тогда линейные уравнения можно записать следующим образом: уравнение записывается следующим образом:

Использование numpy для решения системы
импортировать numpy как np # определить матрицу A, используя массивы Numpy A = np.массив([[2, 1, 1], [1, 3, 2], [1, 0, 0]]) # определить матрицу B B = np.массив ([4, 5, 6]) # linalg.solve — это функция NumPy для решения системы линейных скалярных уравнений. напечатать "Решения:\n",np.linalg.solve(A, B) Решения: [ 6. 15. -23.]
Итак, решения:
Когда матрицы растут
По мере увеличения числа переменных размер матрицы A также увеличивается и становится равным
требует значительных вычислительных ресурсов для получения матричной инверсии A. Среди различных методов мы рассмотрим 3 процедуры для того, чтобы разложить матрицу A на более простые матрицы: LU-разложение, QR-разложение и итерационный метод Якоби.
LU-разложение
LU-разложение, также известное как факторизация сверху вниз, является одним из методов решения квадратных систем линейных уравнений. Как следует из названия, LU-факторизация разлагает матрицу A на произведение A двух матриц: нижней треугольной матрицы L и верхней треугольной матрицы U. Разложение можно представить следующим образом:0005

Разложение LU с помощью SciPy

#import linalg пакет модуля SciPy для разложения LU импортировать scipy.linalg как linalg #импорт NumPy импортировать numpy как np #define То же, что и раньше A = np.массив([[2., 1., 1.], [1., 3., 2.], [1., 0., 0.]]) #определить Б B = np.массив ([4., 5., 6.]) #вызов функции lu_factor LU = linalg.lu_factor(A) #решить заданные LU и B x = linalg.lu_solve(LU, B) напечатать "Решения:\n",x # получаем то же решение, что и раньше Решения: [ 6. 15. -23.] #теперь мы хотим посмотреть, как была факторизована A, P - это так называемая матрица перестановок P, L, U = scipy.
No related posts.