Ранг матрицы
Пусть задана некоторая матрица :
.
Выделим в этой матрице произвольных строк ипроизвольных столбцов. Тогда определитель-го порядка, составленный из элементов матрицы, расположенных на пересечении выделенных строк и столбцов, называется минором-го порядка матрицы.
Определение 1.13.Рангом матрицыназывается наибольший порядок минора этой матрицы, отличного от нуля.
Для вычисления ранга матрицы следует рассматривать все ее миноры наименьшего порядка и, если хоть один из них отличный от нуля, переходить к рассмотрению миноров старшего порядка. Такой подход к определению ранга матрицы называется методом окаймления (или методом окаймляющих миноров).
Задача 1.4.Методом окаймляющих миноров определить ранг матрицы.
.
Рассмотрим окаймление первого порядка, например, . Затем перейдем к рассмотрению некоторого окаймления второго порядка.
Например, .
Наконец, проанализируем окаймление
третьего порядка.
.
Таким образом, наивысший порядок минора, отличного от нуля, равен 2, следовательно, .
При решении задачи 1.4 можно заметить, что ряд окаймляющих миноров второго порядка отличны от нуля. В этой связи имеет место следующее понятие.
Определение 1.14.Базисным минором матрицы называется всякий, отличный от нуля минор, порядок которого равен рангу матрицы.
Теорема 1.2.(Теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы.
Заметим, что строки (столбцы) матрицы линейно зависимы тогда и только тогда, когда хотя бы одну из них можно представить как линейную комбинацию остальных.
Теорема 1.3.Число линейно независимых строк матрицы равно числу линейно независимых столбцов матрицы и равно рангу матрицы.
Теорема 1.4.(Необходимое и достаточное
условие равенства нулю определителя).
Для того, чтобы определитель-го
порядкабыл равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
Вычисление ранга матрицы, основанное на использовании его определения, является слишком громоздкой операцией. Особенно это становится существенным для матриц высоких порядков. В этой связи на практике ранг матрицы вычисляют на основании применения теорем 10.2 — 10.4, а также использования понятий эквивалентности матриц и элементарных преобразований.
Определение 1.15.Две матрицыиназываются эквивалентными, если их ранги равны, т.е..
Если матрицы иэквивалентны, то отмечают.
Теорема 1.5.Ранг матрицы не меняется от элементарных преобразований.
Будем называть элементарными преобразованиями матрицы любые из следующих действий над матрицей:
— замену строк столбцами, а столбцов соответствующими строками;
— перестановку строк матрицы;
— вычеркивание строки, все элементы которой равны нулю;
— умножение какой-либо строки на число, отличное от нуля;
— прибавление к элементам одной строки
соответствующих элементов другой строки
умноженных на одно и то же число
.
Следствие теоремы 1.5.Если матрицаполучена из матрицыпри помощи конечного числа элементарных преобразований, то матрицыиэквивалентны.
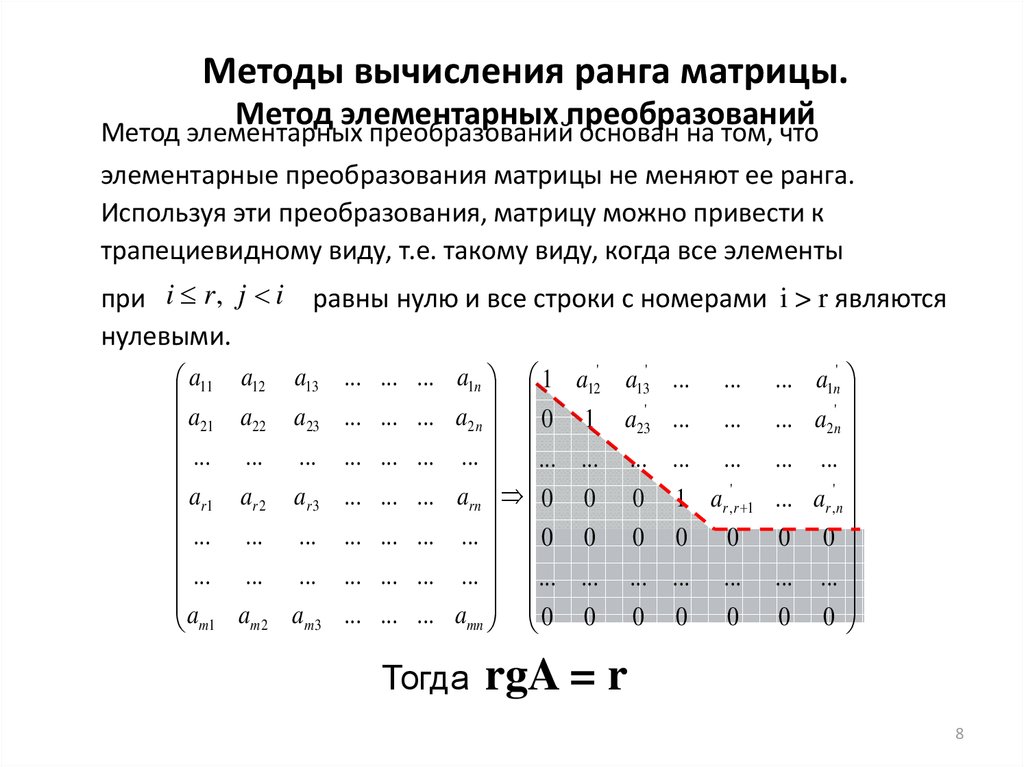
При вычислении ранга матрицы ее следует привести при помощи конечного числа элементарных преобразований к трапециевидной форме.
Определение 1.16.Трапециевидной будем называть такую форму представления матрицы, когда в окаймляющем миноре наибольшего порядка отличного от нуля все элементы, стоящие ниже диагональных, обращаются в нуль. Например:
.
Здесь , элементы матрицыобращаются в нуль. Тогда форма представления такой матрицы будет трапециевидной.
Как правило, матрицы к трапециевидной
форме приводят при помощи алгоритма
Гаусса. Идея алгоритма Гаусса состоит
в том, что, умножая элементы первой
строки матрицы на соответствующие
множители, добиваются, чтобы все элементы
первого столбца, расположенные ниже
элемента
,
превращались бы в нуль. Затем, умножая
элементы второго столбца на соответствующие
множители, добиваются, чтобы все элементы
второго столбца, расположенные ниже
элемента,
превращались бы в нуль.
Задача 1.5.Определить ранг матрицы путем сведения ее к трапециевидной форме.
.
Для удобства применения алгоритма Гаусса можно поменять местами первую и третью строки.
.
Очевидно, что здесь . Однако, для приведения результата к более изящному виду можно далее продолжить преобразования над столбцами.
.
24
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда. Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Рангом r(A) матрицы A называется наивысший порядок отличного от нуля минора этой матрицы (наибольший из порядков тех определителей, отличных от 0, которые можно составить из рядов матрицы, наибольшее число линейно независимых строк или столбцов таблицы). 1 метод нахождения: нахождение наибольшего из порядковых определителей, не равных 0, составленных из рядов данной матрицы 2 метод: приведение матрицы к ступенчатому виду путем элементарных преобразований, ранг будет равен числу не нулевых строк. Ранг диагональной матрицы порядка n равен числу ее ненулевых элементов При элементарных преобразованиях матрицы ее ранг не изменяется Теорема Кронекера-Капелли. Система Совместна (имеет хотя бы одно решение) тогда и только тогда, когда Ранг матрицы системы равен рангу расширенной матрицы. Система линейных уравнений имеет решение, если ранг матрицы системы равен рангу расширенной матрицы, причем, если он равен и числу неизвестных, то решение – единственное. Если ранг расширенной матрицы больше ранга матрицы системы, то система решения не имеет Запись и решение системы линейных алгебраических уравнений в матричном виде. алгебраических уравнений вида , которые в матричной форме записываются как , где — основная матрица системы, — матрица-столбец неизвестных переменных, — матрица свободных членов. Решение системы линейных алгебраических уравнений методом Гаусса. 1. Записываем матрицу в расширенном виде: 2. С помощью элементарных преобразований приводим ее к ступенчатому виду 3. Переходим назад к переменным и находим их Понятие действительной функции действительной переменной. График функции. Основные свойства функций. Если каждому значению х множества Х ставится в соответствие вполне определенное значение y множества Y, то говорят, что на множестве Х задана функцияy=f(x) График функции —представление о геометрическом образе функции. Графический способ задания функции состоит в изображении графика функции — множества точек плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие у. Свойства: · Четностьf(-x)=f(x), нечетность f(-x)=-f(x), общего вида · Монотонность (возрастающие, убывающие функции — монотонны) · Ограниченность (если сущеествует такое м>0 что функция меньше м для любого х) · Периодичность (f(x+T)=f(x)) Предел числовой последовательности. Число А называется пределом последовательности {an}, если для любого ε> 0 существует такой номер N, что все члены последовательности с большими номерами отличаются от А менее, чем на ε. Предел функции в бесконечности и в точке. ⇐ Предыдущая1234Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
Использование элементарных операций над строками для определения A−1
Говорят, что линейная система представляет собой в квадрате , если количество уравнений соответствует количеству неизвестных. Если система A x = b является квадратной, то матрица коэффициентов A является квадратной. Если A имеет обратную, то решение системы A x = b можно найти, умножив обе части на A −1 :
Этот расчет дает следующий результат:
Теорема D . Если A является обратимой матрицей n на n , то система A x = b имеет единственное решение для для каждого n -вектор 05 A b 90 и 905 A b 90 −1 б .
Поскольку для определения A −1 обычно требуется больше вычислений, чем для исключения Гаусса и обратной замены, этот метод не обязательно является улучшенным методом решения A x = b (И, конечно, если A не квадратное, то оно не имеет обратного, поэтому этот метод даже не вариант для неквадратных систем.) Однако, если матрица коэффициентов Число является квадратным, и если известно A −1 или требуется решение A x = b для нескольких различных b , то этот метод действительно полезен, как из теоретической и практической точки зрения. Цель этого раздела — показать, как элементарные операции со строками, которые характеризуют исключение Гаусса-Жордана, могут применяться для вычисления обратной квадратной матрицы.
Во-первых, определение: если к единичной матрице применяется элементарная операция со строками (перестановка двух строк, умножение строки на ненулевую константу или прибавление кратного одной строки к другой) I , результат называется элементарной матрицей . Для иллюстрации рассмотрим единичную матрицу 3 на 3. Если поменять местами первую и третью строки,
Для иллюстрации рассмотрим единичную матрицу 3 на 3. Если поменять местами первую и третью строки,
или если вторая строка I умножается на -2,
или если -2 раза первая строка добавляется ко второй строке,
все эти результирующие матрицы являются примерами элементарных матриц. Первый факт, который потребуется для вычисления A −1 , звучит так: получится, если ту же элементарную операцию со строками применить к A . Другими словами, элементарная операция над строкой матрицы × может быть выполнена путем умножения × слева на соответствующую элементарную матрицу. Например, рассмотрим матрицу
Добавление -2 раз первой строки ко второй строке дает
Если ту же операцию элементарной строки применить к I ,
, то приведенный выше результат гарантирует, что EA должно равняться A ′. Вы можете убедиться, что
действительно верно.
Если A является обратимой матрицей, то некоторая последовательность операций с элементарными строками преобразует A в единичную матрицу I . Так как каждая из этих операций эквивалентна умножению слева на элементарную матрицу, первый шаг при сокращении A к I будет дан произведением E 1 A , второй шаг будет дано E 2 E 1 A и так далее. Таким образом, существуют элементарные матрицы E 1 , E 2 ,…, E k такие, что
Но из этого уравнения ясно, что E k … E 2 E 1 = A −1 5 : 4 Начиная с E k … E 2 E 1 = E K … E 2 E 1 I , где правая сторона. Пример 1 : Определить обратную матрицу Поскольку элементарные операции со строками, которые будут применяться к A , будут применяться и к I , здесь удобно дополнить матрицу A единичной матрицей I : Затем, когда A преобразуется в I, I будет преобразовано в A −1 : Теперь последовательность элементарных операций со строками, которые будут выполнять это преобразование: С момента трансформации [ A | I ] → [ I | A −1 ] читается как обратная данная матрица A равно Пример 2 : В каком состоянии должны быть элементы общей матрицы 2 на 2 , чтобы A было обратимым? Что в этом случае является обратным к ? Цель состоит в том, чтобы осуществить трансформацию [ A | I ] → [ I | А -1 ]. Теперь, если a = 0, поменяйте местами строки. Если c также равно 0, то процесс сокращения A до I не могу даже начать. Таким образом, одно необходимое условие для того, чтобы A было обратимым, состоит в том, что записи a и c не равны 0. Предположим, что a ≠ 0. Тогда Далее, при условии, что ad − до н.э. ≠ 0, Следовательно, если ad − bc ≠ 0, то матрица A обратима, а обратная ей равна (требование о том, что a и c не оба 0 автоматически включается в условие записи вне диагонали, а затем деление на количество ad − bc . Эту формулу для обратной матрицы 2 x 2 следует запомнить . Для иллюстрации рассмотрим матрицу Поскольку ad − bc = (−2)(5) − (−3)(4) = 2 ≠ 0, матрица обратима, и ее обратная матрица равна Вы можете убедиться, что и что А -1 А = I также. Пример 3 : Пусть A будет матрицей Является ли A обратимым? № Сокращение строки A производит матрицу Строка нулей означает, что A нельзя преобразовать в единичную матрицу последовательностью операций с элементарными строками; A необратим. Другой аргумент в пользу необратимости A следует из теоремы D. Если бы A было обратимым, то теорема D гарантировала бы существование решения для A x = b для каждые вектор-столбцов б = ( б 1 , б 2 , б 3 ) Т . Но A x = B согласуется только для векторов B , для которых B 1 + 3 B 2 + B 3 = 0. Пример 4 : Что можно сказать о решениях однородной системы A x = 0 , если матрица A обратима? Теорема D гарантирует, что для обратимой матрицы A система A x = b непротиворечива для любого возможного выбора вектора-столбца b и что единственное решение дается формулой A −1 б . В случае однородной системы вектор b равен 0 , поэтому система имеет только тривиальное решение: x = A −1 0 = 0 . Пример 5 : Решите матричное уравнение AX = B , где Решение 1 . Следовательно, значит Раствор 2 . Пусть b 1 и b 2 обозначают соответственно столбец 1 и столбец 2 матрицы B . Если решение до A x = B 1 — x 1 , а решение A x = B 2 — x 40149 2 — x 9 40149 2 — x 9999 4 2 — x 999 4 2 . одновременно: Исключение Гаусса-Жордана завершает оценку компонентов x 1 и x 2 : Из этой окончательной расширенной матрицы сразу следует, что как раньше. Легко проверить, что матрица X действительно удовлетворяет уравнению AX = B : Обратите внимание, что преобразование в Решении 1 было [ A | I ] → [ I | А −1 ], из которых А −1 В было вычислено, чтобы получить X . Теперь обратим внимание на специальный тип матрицы, называемый элементарной матрицей . Элементарная матрица всегда является квадратной матрицей. Напомним операции со строками, данные в определении 1.3.2. Любая элементарная матрица, которую мы часто обозначаем через \(Е\), получается применением одна строковая операция для единичной матрицы того же размера. Например, матрица \[E = \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right]\nonumber \] является элементарной матрицей, полученной путем переключения двух ряды. Матрица \[E = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber \] является элементарная матрица, полученная умножением второй строки единичной матрицы \(3\times 3\) на \(3\). Матрица \[E = \left[ \begin{array}{rr} 1 & 0 \\ -3 & 1 \end{array} \right]\nonumber \] представляет собой элементарную матрицу, полученную сложением \(-3\ ) умножает первую строку на третью строку. Вы можете построить элементарную матрицу из любой операции со строками, но помните, что вы можете применить только одну операцию. Рассмотрим следующее определение. Пусть \(E\) — матрица \(n \times n\). Тогда \(E\) является элементарной матрицей , если она является результатом применения одной операции строки к \(n \times n\) единичной матрице \(I_n\). Те, которые включают переключение строк единичной матрицы, называются матрицами перестановок. Таким образом, \(E\), построенная выше путем замены двух строк \(I_2\), называется матрицей перестановок. Элементарные матрицы можно использовать вместо операций со строками, поэтому они очень полезны. Оказывается, умножение (в левой части) на элементарную матрицу \(E\) будет иметь тот же эффект, что и выполнение операции со строками, используемой для получения \(E\). Следующая теорема является важным результатом, который мы будем использовать на протяжении всего текста. Для выполнения любой из трех операций со строками над матрицей \(A\) достаточно взять произведение \(EA\), где \(E\) — элементарная матрица, полученная с помощью требуемой операции над единицей матрица. Таким образом, вместо выполнения операций со строками над матрицей \(A\), мы можем уменьшить строку путем умножения матрицы на соответствующую элементарную матрицу. Мы подробно рассмотрим эту теорему для каждой из трех операций со строками, данных в определении 1.3.2. Сначала рассмотрим следующую лемму. 9{th}\) строка \(A\) на \(k\). Мы рассмотрим эту лемму дальше в следующем примере. Пусть \[E \left(5, 2\right) = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 1 \end{array} \right], A = \left[ \begin{array}{cc} a & b \\ c & d \ \ e & f \end{array} \right] \nonumber\] Найдите матрицу \(B\), где \(B = E \left(5, 2\right)A\) Как видите, \(E \left(5, 2\right)\) получается умножением второй строки единичной матрицы на \(5\). Используя нашу обычную процедуру умножения матриц, мы можем вычислить произведение \(E \left(5, 2\right)A\). Результирующая матрица имеет вид \[B =\left[ \begin{array}{cc} a & b \\ 5c & 5d \\ e & f \end{array} \right] \nonumber\] Обратите внимание, что \(B\) получается путем умножения второй строки \(A\) на скаляр \(5\). 9{th}\) строка \(A.\) Рассмотрим следующий пример. Let \[E\left( 2 \times 1+3\right) = \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 0 & 1 \end{array} \right], A = \left[ \begin{array}{cc} a & b \\ c & d \\ e & f \end{массив} \right] \nonumber\] Найдите \(B\), где \(B = E\left( 2 \times 1+3\right)A\). Вы можете видеть, что матрица \(E\left( 2 \times 1+3\right)\) была получена добавлением \(2\) раз первой строки \(I\) к третьей строке \ (Я\). Используя нашу обычную процедуру, мы можем вычислить произведение \(E\left( 2 \times 1+3\right)A\). Вы можете видеть, что \(B\) — это матрица, полученная путем прибавления \(2\) первой строки \(A\) к третьей строке. Предположим, мы применили операцию строки к матрице \(A\). Рассмотрим операцию со строкой, необходимую для возврата \(A\) к исходной форме, чтобы отменить операцию со строкой. Оказывается, этим действием мы находим обратную элементарную матрицу \(Е\). Рассмотрим следующую теорему. Каждая элементарная матрица обратима, и ее обратная матрица также является элементарной матрицей. На самом деле, обратная элементарная матрица строится, выполняя 9{-1}\) правильно. Предположим, что \(m \times n\) матрица \(A\) приведена по строкам к приведенной ступенчато-строковой форме. Отслеживая каждую завершенную операцию строки, это сокращение строки может быть завершено путем умножения на элементарные матрицы. Рассмотрим следующее определение. Пусть \(A\) будет матрицей \(m \times n\), а \(B\) будет уменьшенной строчно-ступенчатая форма \(A\). Тогда мы можем написать \(B = UA\), где \(U\) — произведение всех элементарных матриц, представляющих операции со строками, выполненные с \(A\) для получения \(B\). Рассмотрим следующий пример. Пусть \(A = \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ 2 & 0 \end{массив} \right]\). Найдите \(B\), редуцированную построчно-ступенчатую форму \(A\) и запишите ее в виде \(B=UA\). Чтобы найти \(B\), сократите строку \(A\). Для каждого шага мы будем записывать соответствующую элементарную матрицу. Сначала поменяйте местами строки \(1\) и \(2\). \[\left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ 2 & 0 \end{array} \right] \rightarrow \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ 2 & 0 \end{массив} \right]\nonumber \] 9{12} =\left[ \begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right]\) и \(A\) . Затем добавьте \((-2)\) умноженное на строку \(1\) к строке \(3\). \[\left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ 2 & 0 \end{array} \right] \rightarrow \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{массив} \right]\nonumber \] Это эквивалентно умножению на матрицу \(E(-2 \times 1 + 3) = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{array} \right]\). Обратите внимание, что результирующая матрица представляет собой \(B\), искомую уменьшенную ступенчатую форму строки \(A\). 9{12} \\ &= \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{array} \right] \left[ \ begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right] \\ &= \left[ \begin{array}{rrr} 0 & 1 & 0\\ 1 & 0 & 0 \\ 0 & -2 & 1 \end{array} \right]\end{aligned}\] Мы можем проверить, что \(B = UA\) выполняется для этого матрица \(U\): \[\begin{align} UA &= \left[ \begin{array}{rrr} 0 & 1 & 0\\ 1 & 0 & 0 \\ 0 & -2 & 1 \end {массив} \right] \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \\ 2 & 0 \end{массив} \right] \\ &= \left[ \begin{массив} {rr} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{массив} \right] \\ &= B \end{aligned}\] Хотя процесс, используемый в приведенном выше примере, надежен и прост, когда используется только несколько операций со строками, он становится громоздким в случае, когда требуется много операций со строками для переноса \(A\) в \(B\). Пусть \(A\) — матрица \(m \times n\), а \(B\) — ее редуцированная строка -эшелонная форма. Тогда \(B = UA\), где \(U\) — обратимая \(m \times m\) матрица, найденная путем формирования матрицы \(\left[ A | I_m \right]\) и сокращения строки до \( \влево[ B |U \вправо]\). Давайте вернемся к приведенному выше примеру, используя процесс, описанный в теореме \(\PageIndex{3}\). Пусть \(A = \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \ \ 2 & 0 \end{массив}\right]\). Используя процесс, описанный в теореме \(\PageIndex{3}\), найдите \(U\) такое, что \(B=UA\). Сначала настройте матрицу \(\left[ A | I_m \right]\). \[\left[ \begin{array}{rr|rrr} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ 2 & 0 & 0 & 0 & 1 \end{array }\right]\nonumber \] Теперь уменьшите эту матрицу по строкам до тех пор, пока левая часть не станет равной уменьшенной ступенчатой форме строки \(A\). \[\begin{align} \left[ \begin{array}{rr|rrr} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ 2 & 0 & 0 & 0 & 1 \end{массив}\right] &\стрелка вправо \left[ \begin{array}{rr|rrr} 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 2 & 0 & 0 & 0 & 1 \end{массив}\right] \\ &\стрелка вправо \left[ \begin{массив}{rr|rrr} 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & -2 & 1 \end{массив}\right]\end{выровнено}\] Левая часть этой матрицы равна \(B\), а правая часть — \(U\). Сравнивая это с матрицей \(U\), найденной выше в примере \(\PageIndex{5}\), вы можете видеть, что одна и та же матрица получается независимо от того, какой процесс используется. Напомним из алгоритма 2.7.1, что \(n \times n\) матрица \(A\) обратима тогда и только тогда, когда \(A\) можно преобразовать в \(n \times n\) единичную матрицу используя обычные операции со строками. Это приводит к важному следствию, связанному с приведенным выше обсуждением. 9{-1} E_1{-1}\end{выровнено}\] и \(A\) можно записать в виде произведения элементарных матриц. Пусть \(A\) — матрица \(n \times n\). Тогда \(А\) обратим тогда и только тогда, когда его можно записать в виде произведения элементарных матриц. Рассмотрим следующий пример. Пусть \(A = \left[ \begin{array}{rrr} 0 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & -2 & 1 \end{массив} \right]\). Запишите \(A\) как произведение элементарных матриц. Мы воспользуемся процессом, описанным в теореме \(\PageIndex{3}\), чтобы записать \(A\) как произведение элементарных матриц. Мы настроим матрицу \(\left[ A | I \right]\) и уменьшим строку, записывая каждую операцию строки как элементарную матрицу. Первый: \[\left[ \begin{array}{rrr|rrr} 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & — 2 & 1 & 0 & 0 & 1 \end{массив} \right] \rightarrow \left[ \begin{array}{rrr|rrr} 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & -2 & 1 & 0 & 0 & 1 \end{массив} \right] \nonumber\] представлено элементарной матрицей \(E_1= \left[ \begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right]\ ). Во-вторых: \[\left[ \begin{array}{rrr|rrr} 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & — 2 & 1 & 0 & 0 & 1 \end{array} \right] \rightarrow \left[ \begin{array}{rrr|rrr} 1 & 0 & 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & -2 & 1 & 0 & 0 & 1 \end{массив} \right] \nonumber\] представлено элементарной матрицей \(E_2 = \left[ \begin{array}{rrr} 1 & -1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \). Наконец: \[\left[ \begin{array}{rrr|rrr} 1 & 0& 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & — 2 & 1 & 0 & 0 & 1 \end{массив} \right] \rightarrow \left[ \begin{array}{rrr|rrr} 1 & 0 & 0 &-1 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 2 & 0 & 1 \end{массив} \right] \nonumber\] 9{-1} \\ &= \left[ \begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \ begin{array}{rrr} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array} \right] \\ &= A\end{aligned}\] Это дает \(A\), записанное как произведение элементарных матрицы. единичная матрица I , те же элементарные операции со строками, которые преобразуют A в I, преобразуют I в A −1 . Для n по n матриц A с n > 3 это описывает наиболее эффективный метод определения А -1 .
единичная матрица I , те же элементарные операции со строками, которые преобразуют A в I, преобразуют I в A −1 . Для n по n матриц A с n > 3 это описывает наиболее эффективный метод определения А -1 . Во-первых, дополните A единичной матрицей 2 на 2:
Во-первых, дополните A единичной матрицей 2 на 2:
 Ясно, тогда, тогда, тогда, тогда, тогда, тогда, тогда, тогда существует (бесконечно много) векторов b , для которых A x = b несовместно; таким образом, A не может быть обратимым.
Ясно, тогда, тогда, тогда, тогда, тогда, тогда, тогда, тогда существует (бесконечно много) векторов b , для которых A x = b несовместно; таким образом, A не может быть обратимым. Поскольку A равно 3 x 3, а B равно 3 x 2, если существует матрица X такая, что AX = B , тогда X должно быть 3 x 2. Если A обратимо, один из способов найти X состоит в том, чтобы определить A −1 , а затем вычислить X = . −1 В . Алгоритм [ A | I ] → [ I | A −1 ], чтобы найти A −1 , получается
Поскольку A равно 3 x 3, а B равно 3 x 2, если существует матрица X такая, что AX = B , тогда X должно быть 3 x 2. Если A обратимо, один из способов найти X состоит в том, чтобы определить A −1 , а затем вычислить X = . −1 В . Алгоритм [ A | I ] → [ I | A −1 ], чтобы найти A −1 , получается решение AX = B = [ b 1 b 2 ] равно X = [ x 1 x 2 ]. То есть процедура исключения может быть выполнена на двух системах ( A x = b 1 и A x = b 2 ) )
решение AX = B = [ b 1 b 2 ] равно X = [ x 1 x 2 ]. То есть процедура исключения может быть выполнена на двух системах ( A x = b 1 и A x = b 2 ) ) Однако преобразование в Решении 2, [ A | B ] → [ I | X ], дал X напрямую.
Однако преобразование в Решении 2, [ A | B ] → [ I | X ], дал X напрямую. 2.8: Элементарные матрицы — Mathematics LibreTexts

Определение \(\PageIndex{1}\): элементарные матрицы и операции со строками

Теорема \(\PageIndex{1}\): умножение на элементарную матрицу и операции со строками
Пример \(\PageIndex{2}\): умножение строки на 5 с использованием элементарной матрицы
Решение

Пример \(\PageIndex{3}\): прибавление первой строки к последней
Решение
 Результирующая матрица \(B\) имеет вид \[B = \left[ \begin{array}{cc} a & b \\ c & d \\ 2a+e & 2b+f \end{array} \right ] \nonumber\]
Результирующая матрица \(B\) имеет вид \[B = \left[ \begin{array}{cc} a & b \\ c & d \\ 2a+e & 2b+f \end{array} \right ] \nonumber\] Теорема \(\PageIndex{2}\): элементарные матрицы и обратные

Определение \(\PageIndex{2}\): форма \(B=UA\)
Пример \(\PageIndex{5}\): форма \(B=UA\)
Решение

 Следующая теорема дает альтернативный способ найти матрицу \(U\).
Следующая теорема дает альтернативный способ найти матрицу \(U\). Теорема \(\PageIndex{3}\): нахождение матрицы \(U\)
Пример \(\PageIndex{6}\): пересмотренная форма \(B=UA\)
Решение


Теорема \(\PageIndex{4}\): Произведение элементарных матриц
Пример \(\PageIndex{7}\): произведение элементарных матриц
Решение


 ..
.. Не превосходит меньшего из ее размеров.
Не превосходит меньшего из ее размеров.
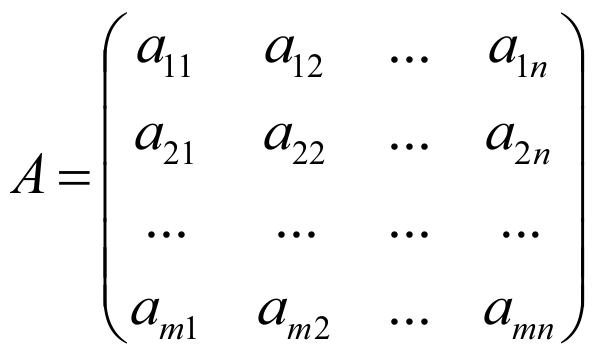 Признаки существования предела последовательности. Основные свойства сходящихся последовательностей.
Признаки существования предела последовательности. Основные свойства сходящихся последовательностей. ..
..