Метод Крамера: что это такое, пример решения и как вычислить определитель
Метод Крамера — это метод решения систем линейных алгебраических уравнений (СЛАУ) с одинаковым количеством уравнений и переменных.
Метод Крамера нельзя использовать, когда определитель основной матрицы равен 0 (в этом случае применяется метод Гаусса).
Как решить систему линейных уравнений методом Крамера
Пример
Нужно решить систему линейных уравнений:
2x + 1y + 1z = 3
1x – 1y – 1z = 0
1x + 2y + 1z = 0
1. Нужно найти главный определитель
2. Теперь заменяем по очереди каждый из столбцов на столбец ответов:
В первую колонку, для x и вычисляем определитель:
Во вторую колонку, для y и вычисляем определитель:
В третью колонку, для z и вычисляем определитель:
Последний шаг: нужно разделить каждый на главный определитель.
То есть:
x = Δx ÷ Δ = 3 ÷ 3 = 1
y = Δy ÷ Δ = (-6) ÷ 3 = -2
z = Δz ÷ Δ = 9 ÷ 3 = 3
Как вычислить определитель?
Матрицы 2 × 2
Матрицы 3 × 3
Существует несколько способов вычисления определителя матрицы 3 × 3.
Этот способ, под названием правило Саррюса, выглядит наиболее простым.
Нужно найти определитель матрицы 3 × 3
1. Дополнить матрицу первыми двумя столбцами (т. е. скопировать первые 2 столбца и дополнить её):
2. Умножить и сложить по диагоналям вниз:
3. Умножить и сложить по диагоналям вверх:
4. Из первой суммы (зелёной, по диагонали вниз) вычесть вторую (красную, по диагонали вверх): 8 — 2 = 6, т. е. det (A) = 6.
Узнайте про Интегралы, Логические операции и Корреляции.
Другие значения и понятия, которые могут вас заинтересовать
- Метод наименьших квадратов
- Схема Горнера
- Диалектика
- Герменевтика
- Эмпирическое познание
- Корреляция
- Стандартное отклонение
- Экспонента
- Парадокс
- Плюрализм
Узнай Что Такое: узнайте значения, понятия и определения.
ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас
2018 — 2023 © 7Graus
Метод Крамера — 📙 Математика
1. Общие понятия
2. Способы расчета определителей матриц
3. Использование метода Крамера
Методом Крамера, или как его еще называют, правилом Крамера, является такой способ нахождения неизвестных для заданной системы уравнений. Такой метод используется лишь тогда, когда количество неизвестных равняется числу уравнений системы, иными словами, матрица, образованная из заданной системы уравнений, должна быть квадратной без нулевых строк и ее главный определитель не должен равняться нулю. Рассмотрим теорему Крамера:
При условии, что главный детерминант матрицы \(D\), состоящей их коэффициентов системы уравнений, не равняется нулю, эта система уравнений считается совместной, с существующим для нее единственным решением. Неизвестные этих систем линейных уравнений рассчитывают по формуле Крамера: \(x_i={D_i\over D}\).
Порядок определения неизвестных по методу Крамера включает такие действия:
- Сперва рассчитывают главный детерминант матрицы \(D\). Если найденный детерминант равняется нулю, то для данной системы уравнений не существует решений или их существует бесконечное множество. В таком варианте рекомендуют воспользоваться методом Гаусса для определения базисного решения.
- Если же главный детерминант не равняется нулю, то эту систему уравнений рассчитывают методом Крамера. Левый столбик главной матрицы заменяют на столбик свободных членов и рассчитывают детерминант \(D_1\).
- Проделывают те же действия для всех следующих столбиков по порядку и определяют детерминанты \(D_1, D_2, …, D_n\), где \(n\) – число столбиков.
- Теперь, имея все детерминанты, рассчитывают все переменные от \(x_1\) до \(x_n\).
Для расчета определителей матриц, размером более 2х2, применяют различные способы, рассмотрим их подробнее:
1. Метод Гаусса, второе его название – метод понижения порядка определителя.
При данном методе матрицу преобразуют к форме треугольника, после этого перемножают составляющие главной диагонали. Стоит отметить, что при применении этого метода запрещено множить или делить строки, или столбцы на числа, не вынося их как множители или делители.
При данном методе можно лишь плюсовать или минусовать строки, или столбцы друг с другом, перед этим перемножив минусуемую строку на нуль. Необходимо также помнить, что во время перестановки столбиков или строк местами, нужно изменять знак матрицы.
2. Правило треугольников или правило Саррюса, которые очень похожи между собой. Для применения правила Саррюса, вначале записывают матрицу, а потом справа от нее снова записывают ее первый и второй столбики.
Числа матрицы и этих столбиков соединяют диагоналями, числа, что лежат на главной и параллельных диагоналях, записывают с плюсом, а числа, что лежат на побочной и параллельных ей диагоналях – с минусом.
Правило треугольников заключается в том, что для расчета детерминанта произведения всех чисел, что соединены на рисунке красной линией слева, записывают с плюсом, а те, что соединены так же справа – с минусом.
Оба способа применимы для матриц величиной 3х3.
3. Для расчета систем линейных арифметических уравнений с четырьмя неизвестными, стоит отметить, что более применимым для расчета определителей является метод Гаусса, либо также применяют метод миноров.
Метод Крамера применяют для определения неизвестных в системах линейных арифметических уравнений.
Разберем применение метода Крамера для расчета системы уравнений с двумя неизвестными:
\( \begin{cases} a_1 x_1+a_2 x_2=b_1 \\ a_3 x_1+a_4 x_2=b_2 \end{cases}\)
Преобразуем ее в такую форму:
Рассчитаем главный определитель системы, его так же именуют детерминантом основной матрицы:
\(D= \begin{vmatrix} {a_1 a_2\\a_3 a_4 } \end{vmatrix} =a_1∙a_4-a_3∙a_2\)
Далее, если главный детерминант не равняется нулю, рассчитываем систему линейных уравнений методом Крамера. Для этого рассчитываем все детерминанты, заменяя поочередно столбики основной матрицы столбиками свободных членов:
\(D_1=\begin{vmatrix}{b_1 a_2\\b_2 a_4}\end{vmatrix}=b_1∙a_4-b_2∙a_2\)
\(D_2=\begin{vmatrix}{a_1 b_1\\a_3 b_2 }\end{vmatrix}=a_1∙b_2-a_3∙b_1\)
Затем по формуле Крамера рассчитаем все переменные:
\(x_1={D_1\over D} \\ x_2={D_2\over D}\)
Рассмотрим задачу с конкретными уравнениями.
Рассчитаем данную систему уравнений методом Крамера:
\(\begin{cases}3x_1-2x_2+4x_3=21\\3x_1+4x_2+2x_3=9\\2x_1-x_2-x_3=10\end{cases}\)
Порядок решения:
1. Определим главный детерминант по вышеизложенному принципу:
\(D=\begin{vmatrix}3&-2&4\\3&4&-2\\2& -1&1\end{vmatrix}=\) \(3∙4∙(-1)+2∙(-2)∙2+4∙3∙(-1)-4∙4∙2-3∙(-2)∙(-1)-(-1)∙2∙3=\)
\(=-12-8-12-32-6+6=-64. \)
2. Далее рассчитаем остальные детерминанты:
\(D_1=\begin{vmatrix}21& -2&4\\9&4&-2\\10& -1&1\end{vmatrix}=\)\(21∙4∙(-1)+2∙(-2)∙10+4∙9∙(-1)-4∙4∙10-9∙(-2)∙(-1)-(-1)∙2∙21=\)
\(=-84-40-36-160-18+42=-296.\)
\(D_2=\begin{vmatrix}3&21&4\\3& 9& -2\\2&10&1\end{vmatrix}=\)\(=3∙9∙(-1)+2∙21∙2+4∙3∙10-4∙9∙2-3∙21∙(-1)-10∙2∙3=\)
\(D_3=\begin{vmatrix}3 &-2&21\\3&4& 9\\2& -1&10\end{vmatrix} =\)\(=3∙4∙10+9∙(-2)∙2+21∙3∙(-1)-21∙4∙2-3∙(-2)∙10-(-1)∙9∙3=\)
\(120-63-36-198+60+27=-60.
\)
3. Затем рассчитаем наши неизвестные, применяя формулы Крамера:
\(x_1={D_1\over D}={-296\over-64}=4,625\)
\(x_2={D_2\over D}={108\over-64}=-1,6875\)
\(x_2={D_3\over D}={-60\over-64}=0,9375\)
Правило Габриэля Крамера
Применение закона напряжения Кирхгофа к каждой петле в схеме гитарного усилителя приводит к одному уравнению на петлю. Эти уравнения необходимо решать одновременно, чтобы определить искомый ответ, которым обычно является выходное напряжение как функция входного напряжения. Давайте рассмотрим пример и решим его, используя грубый, но работающий метод, известный как простая замена. Позже мы продемонстрируем, как концепция, называемая правилом Крамера, может облегчить жизнь и сделать ее менее подверженной математическим ошибкам.
Проблема
Рассмотрим звуковой стек Sovtek MIG 50 Master Volume, который такой же, как у Fender Bassman 5F6-A, за исключением номиналов партий. На низких частотах конденсатор с отводом высоких частот действует как разомкнутая цепь.
Если мы установим регуляторы высоких и средних частот на минимум, а регулятор низких частот на максимум, то эффективная схема показана ниже. Какова связь между выходным напряжением и входным напряжением в этих условиях?
Новый! Электроника гитарного усилителя: Fender Deluxe — от передней панели телевизора до узкой панели, от коричневой до черной реверберации |
Раствор
Для MIG 50 значения деталей: R 1 = 51 кОм, C 1 = 0,022 мкФ и C 2 = 0,047 мкФ. С регулятором низких частот 1M на максимуме и регулятором средних частот 25k на минимуме они включены последовательно и, таким образом, образуют эквивалентное сопротивление R 9.0025 БМ = 1,025М. Формируем две петли, одну для текущего i 1 и другую для i 2
Сопротивления конденсаторов чисто мнимые.
(Верно, но какое странное заявление, вырванное из контекста!) Для частоты 100Гц, например, они
В первом контуре происходит одно повышение напряжения: входное напряжение. Есть два падения напряжения из-за R 1 и Z 2 , которые по закону Ома представляют собой полное сопротивление, умноженное на ток. Обратите внимание, что Z 2
Обратите внимание, что на втором шаге мы объединили токи вместе. Обычно это самая удобная форма.
Во втором контуре скачков напряжения нет, а падение напряжения на Z 2 обусловлено током i 2 минус ток i 1 :
Нас интересует выходное напряжение, которое по закону Ома равно R BM умножить на i 2 .
Итак, мы используем уравнение для второго цикла, чтобы получить
а затем подставить этот результат в уравнение для первого контура, тем самым исключив неизвестный ток i 1 , знать который нам не нужно. Теперь у нас есть входное напряжение как функция только тока i 2 .
что упрощает до
Мы переформулируем уравнение, чтобы вычислить ток как функцию входного напряжения:
По закону Ома выходное напряжение равно R BM i 2 .
Мы добились своего результата. Теперь у нас есть выходное напряжение как функция входного напряжения и импеданса. Неуклюжая процедура, которую мы использовали, устраняя один из неизвестных токов путем замены, была так же привлекательна, как холодная пайка на револьверной плате.
Электроника гитарного усилителя: основная теория
— освоить основы проектирования предусилителя, усилителя мощности и блока питания. |
Помимо низкой эстетической ценности, подобная процедура делает вас склонными к ошибкам. Что нам нужно, так это более элегантный подход, который с меньшей вероятностью приведет к ошибкам. Полномасштабная матричная математика является окончательным методом в этом отношении, но для ламповых усилителей вполне достаточно метода, известного как правило Крамера.
Правило Крамера
Правило Габриэля Крамера обрабатывает 90 процентов уравнений, которые мы видели в нашей задаче Sovtek MIG 50. Мы используем закон Кирхгофа о напряжении для обоих контуров, как и раньше. Тогда правило Крамера дает нам ток i 2 во втором контуре как функцию входного напряжения. В этот момент все, что мы делаем, это применяем закон Ома, чтобы получить результат.
Вот как это работает.
Нам все еще нужно применить закон Кирхгофа о напряжении к двум петлям. Каждое из двух результирующих уравнений имеет одно или несколько повышений напряжения, вызванных источниками напряжения, и падения напряжения, вызванные импедансами и токами.
Любое из напряжений может быть равно нулю. Каждое из импедансов Z 11 , Z 12 , Z 21 и Z 22 может быть единичным значением, суммой импедансов или нулем.
Основы проектирования систем гитарных усилителей — спроектируйте свой усилитель, используя структурированную профессиональную методологию. |
Мы складываем эти два уравнения в матрицу, подобную этой
Математикам эта матрица говорит ровно то же самое. Это просто выражает наши два отдельных уравнения как одно большое уравнение только с одним знаком равенства. В матрице импеданса есть две диагонали, одна идет от верхнего левого угла Z 11 к нижнему правому углу Z 22 . Вторая диагональ идет от левого нижнего угла Z 21 до правого верхнего угла Z 9.
0025 12 . Определитель матрицы равен произведению первой диагонали на произведение второй:
Обычно нас интересует только один из неизвестных токов, поэтому нужен только один дополнительный определитель. Чтобы вычислить i 1 , мы заменяем столбец напряжений первым столбцом матрицы:
Чтобы получить i 2 , подставляем напряжения во второй столбец:
Тогда неизвестные токи
Электроника гитарного усилителя: моделирование цепей — узнайте, работает ли ваша конструкция, измеряя производительность в каждой точке усилителя. |
Проблема
Снова решите проблему со стеком Sovtek MIG 50, но на этот раз с помощью правила Крамера.
Решение
Мы использовали закон Кирхгофа о напряжении, чтобы получить следующие формулы для первого и второго контуров:
Таким образом, матрица импеданса
Определитель
что упрощает до
Чтобы получить i 2 , подставляем столбец напряжений во второй столбец матрицы и вычисляем определитель.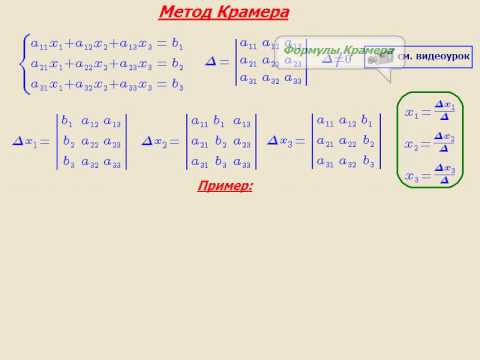
Таким образом, неизвестный ток
По закону Ома выходное напряжение R БМ и 2 .
Правило Крамера требует меньше шагов, чем метод подстановки. Что еще более важно, он намного надежнее на практике, потому что присущая ему элегантность снижает вероятность ошибки.
Удовлетворены ли мы небрежной проводкой, которой просто достаточно, чтобы заставить усилитель работать, или мы хотим качественного исполнения, которое гарантирует будущие характеристики? То же самое можно сказать о простой замене по сравнению с правилом Крамера.
СЛЕДУЩАЯ СТРАНИЦА
Крамер, Кэтрин Дж. – Департамент политологии – Университет Вашингтона – Мэдисон
Связан с Центром исследования выборов, Школа журналистики и массовых коммуникаций, Школа общественных дел Лафоллет, IRP, Центр интегрированных сельскохозяйственных систем, Центр развития штата Висконсин послесреднего образования, Центр общественных и некоммерческих исследований
Образование:
Кандидат наук.
Кандидат политических наук, Мичиганский университет, 2000 г.
B.A. Кандидат политических наук и журналистики, Университет Висконсин-Мэдисон, 19 лет.94
Научные интересы:
Гражданская активность, гражданское и гуманитарное образование, гражданское общество, консерватизм, обсуждение, вопросы культуры, география, политическая коммуникация, политическая культура, политическое участие, популизм, общественное мнение, раса, социальный класс, университетская политика, Поведение при голосовании
Биография:
Кэтрин Крамер (бакалавр гуманитарных наук, Университет Висконсин-Мэдисон, 1994 г., доктор философии, Мичиганский университет, 2000 г.) — профессор политологии и заведующая кафедрой литературы и науки Натали С. Холтон. В течение 2018-2019 гг.В течение учебного года она является приглашенным профессором в Лаборатории социальных машин Медиа-лаборатории Массачусетского технологического института. Она является аффилированным преподавателем Центра исследования выборов Университета Вашингтона в Мэдисоне, Школы журналистики и массовых коммуникаций, Школы по связям с общественностью Лафоллета, Института исследований бедности, Центра общественных и некоммерческих исследований, Висконсинского центра развития послесреднего образования, и Центр интегрированных сельскохозяйственных систем.
Ее работа сосредоточена на том, как люди в Соединенных Штатах понимают политику и свое место в ней. Она известна своим новаторским подходом к изучению общественного мнения, в котором она использует такие методы, как приглашение в разговоры с группами людей, чтобы узнать, как они понимают общественные дела. Ее отмеченная наградами книга «Политика обиды: сознание сельских жителей в Висконсине и восхождение Скотта Уокера», пролила свет на недовольство сельских жителей городами и его значение для современной политики, а также стала важным источником для понимания голосов на президентских выборах 2016 г. (Университет Чикаго Пресс, 2016). Она также публиковалась под именем Кэтрин Крамер Уолш и является автором книг Talking about Race: Community Dialogues and the Politics of Difference (University of Chicago Press, 2007) и Говоря о политике: неформальные группы и социальная идентичность в американской жизни (University of Chicago Press, 2004). Она была названа Висконсинской академией наук, искусств и литературы в 2018 году и является лауреатом премии APSA Heinz Eulau Award 2018 за лучшую статью, опубликованную в Perspectives on Politics (с Бенджамином Тоффом), в разделе качественных и мультиметодных исследований APSA 2017 года.
Премия Джованни Сартори за лучшую книгу по разработке или использованию качественных методов, опубликованную в 2016 году; финалист премии Фонда Вудро Вильсона APSA 2017 года за лучшую книгу о правительстве, политике или международных отношениях; награда Секции качественных и мультиметодных исследований APSA 2012 г. за лучшую качественную или мультиметодическую работу, представленную в Американском обзоре политических наук; Премия канцлера UW-Madison за выдающиеся заслуги перед преподаванием в 2006 году; Премия UW-Madison Vilas Associate Award 2012–2014; стипендия факультета Леона Эпштейна на 2015–2017 годы; и Премия UW-Мэдисон Келлетт для преподавателей среднего звена в 2017–2022 гг. В 2019 годуона была избрана в Американскую академию искусств и наук.
Курсы:
PS 410 СИТИФИТАНИЕ, Демократия и разница осенью 2019-20202020 гг. и Difference Fall 2015-2016
Награды:
2018
Выбран в качестве члена Висконсинской академии искусств и наук.