Тесты Графики тригонометрических функций по теме алгебры
Последний раз тест пройден 11 часов назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
График какой функции изображен на рисунке?
y=ctg(x)
y=tg(x)
y=sin(x)
y=cos(x)
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Какими свойствами обладает функция у = 2 – sin 3x ?
нечетная, периодическая
ни четная ни нечетная, непериодическая
четная, периодическая
ни четная ни нечетная, периодическая
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
График какой функции изображен на рисунке?
y=cos(x)
y=tg(x)
y=sin(x)
y=ctg(x)
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Найдите наименьший положительный период функции у = 2sin 3x
π
3π
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Какие функции имеют период T=π?
y=cos(x),y=ctg(x)
y=sin(x),y=cos(x)
y=sin(x),y=tg(x)
y=tg(x),y=ctg(x)
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
График какой функции изображен на рисунке?
у = tg x/2
y=ctg x/2
y=2tg x
y=2ctg x
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Какие функции имеют период T=2π?
y=cos(x),y=ctg(x)
y=sin(x),y=cos(x)
y=sin(x),y=tg(x)
y=tg(x),y=ctg(x)
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Какими свойствами обладает функция у = 3x + cos x
нечетная, периодическая
ни четная ни нечетная, непериодическая
четная, периодическая
ни четная ни нечетная периодическая
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
График какой функции изображен на рисунке?
y=tg 2x
y=tg x
y=ctg 2x
y=ctg x
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Найдите наименьший положительный период функции у = 2sin
6π
3π
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ульяна Кравецкая
8/10
Вова Редькин
10/10
Инна Лиманская
10/10
Иван Ткаченко
10/10
Надежда Козловцева
10/10
Рейтинг теста
3.2
Средняя оценка: 3.2
Всего получено оценок: 951.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Онлайн-консультации с лучшими специалистами федеральных центров – уже сегодня
Россияне могут бесплатно получить онлайн-консультации врачей ведущих федеральных медицинских центров. По информации Благотворительного фонда Лиги здоровья нации, в рамках всероссийского проекта «Облако здоровья» удаленные приемы сложных пациентов проводят лучшие специалисты Центра сердечно-сосудистой хирургии имени Бакулева, Центра кардиологии имени академика Чазова, Центра оториноларингологии ФМБА России, МНТК «Микрохирургия глаза» имени академика Федорова и Центра акушерства, гинекологии и перинатологии имени Кулакова.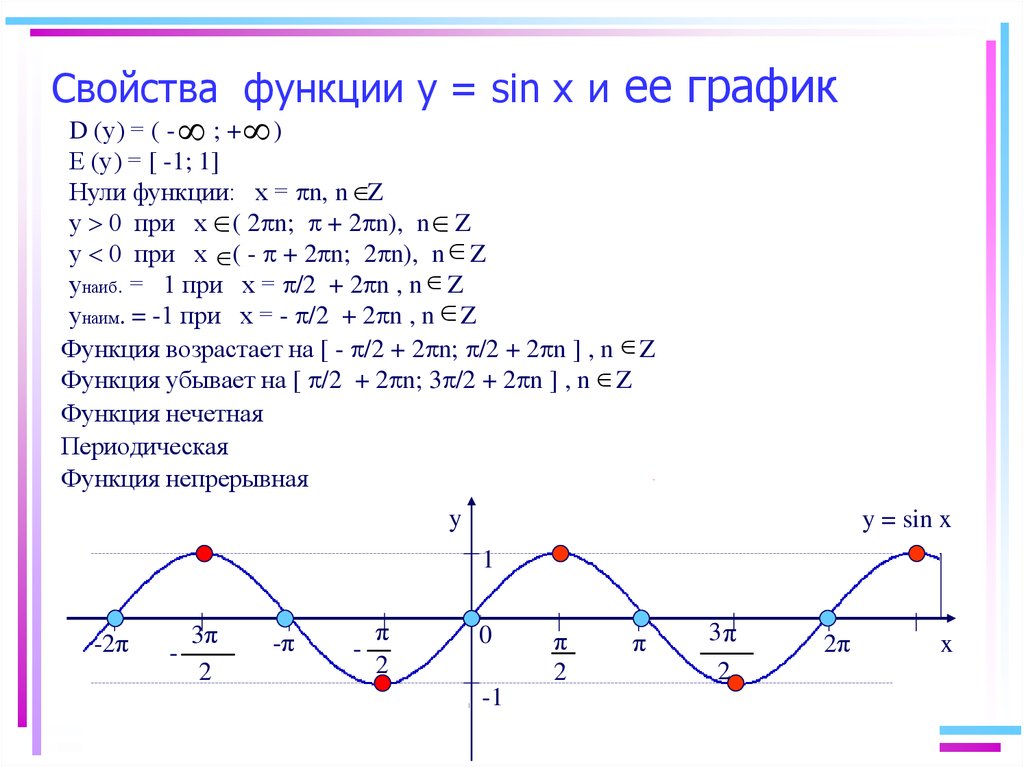 Проект реализуется при поддержке Фонда президентских грантов.
Проект реализуется при поддержке Фонда президентских грантов.
Всероссийский проект «Облако здоровья» стартовал во время пандемии коронавирусной инфекции, когда из-за постоянных карантинов стало сложно получить плановую медицинскую помощь. Тогда больных сердечно-сосудистыми заболеваниями консультировали врачи двух ведущих российскихкардиоцентров – «Бакулевского» и «Кулаковского».
Сейчас к «Облаку здоровья» присоединились еще нескольких федеральных центров: врачи, имеющие огромный опыт лечения самых сложных пациентов, дают столь важное, особенно в сложных случаях, «второе мнение».
«Облако здоровья» сегодня — это современный комплексный проект, целью которого является содействие в оказании своевременной медицинской помощи людям, по разным причинам оставшимся без необходимого профессионального внимания, или ищущим «второе мнение». Сейчас количество пациентов, нуждающихся уже в постковидной реабилитации и помощи специалистов, значительно выросло.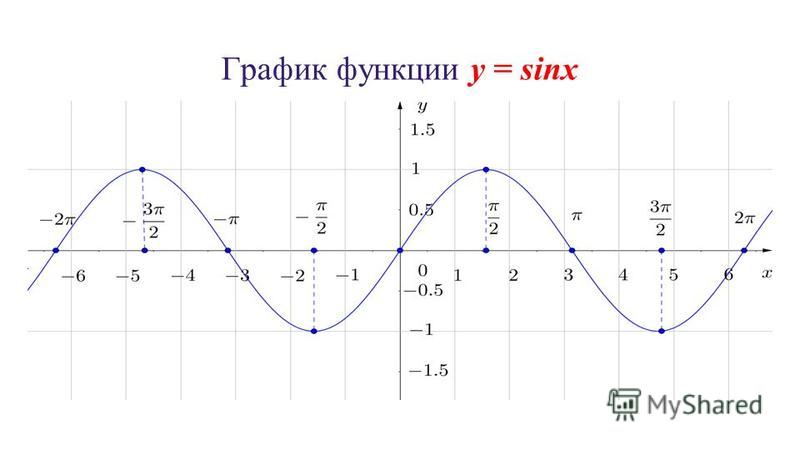 Последствия пандемии страна будет испытывать еще длительное время. Известно, что ковид стал причиной роста сердечно-сосудистых заболеваний, вызвал серьезные осложнения со зрением и слухом у россиян, повлиял на женское здоровье, — поясняют в Лиге здоровья нации.
Последствия пандемии страна будет испытывать еще длительное время. Известно, что ковид стал причиной роста сердечно-сосудистых заболеваний, вызвал серьезные осложнения со зрением и слухом у россиян, повлиял на женское здоровье, — поясняют в Лиге здоровья нации.
Перечень диагнозов, по которым проводятся дистанционные консультации, очень обширен: это ишемическая болезнь сердца, врожденные и приобретенные пороки сердца, аритмия, терминальная хроническая сердечная недостаточность; миопия (близорукость), астигматизм, кератоконус, заболевания роговицы, катаракта, заболевания хрусталика, глаукома, заболевания зрительного нерва, макулярные дегенерации и другие заболевания глаз; болезни носа и носовых синусов, полипы носа, кисты носового синуса, хронический синусит, хронический и аллергический ринит, адгезивная болезнь среднего уха, болезни миндалин, аденоиды (хирургическое лечение), доброкачественные новообразования ЛОР-органов (хирургическое вмешательство) и многое другое; гинекологические заболевания у женщин и девочек, бесплодие, онкологические заболевания во время беременности, онкологические заболевания женских половых органов, доброкачественные образовании матки и придатков и многое другое.
Чтобы получить помощь пациентам нужно зарегистрироваться или авторизоваться в телемедицинском сервисе «Облако здоровья» https://oblakozdorovia.ru/ и отравить заявку на получение бесплатной онлайн-консультации.
Для этого необходимо выбрать заявку в нужный медицинский центр и нажать кнопку «Получить услугу». Далее следовать инструкциям в заявке. Конечно, придется подготовить и отправить федеральным экспертам сканы результатов проведенных ранее исследований и другой медицинской документации (конкретный перечень в каждом случае свой, уточнить его можно в соответствующем федеральном центре). После обработки данных пациент получит приглашение на онлайн-консультацию к врачу на конкретный день и время.
«Консультации возможны в трех форматах (по решению специалистов и в соответствии с заявленным форматом специализированного медицинского центра): дистанционное заочное консультирование по представленным документам, дистанционная онлайн-консультация по подаче заявки, дистанционная дежурная онлайн-консультация (по расписанию дежурных врачей)», — пояснили организаторы программы.
Для проведения консультаций пациентам необходимо наличие компьютера с микрофоном и веб-камерой или мобильного телефона с установленным браузером Chrome. Для каждого устройства обязательно подключение к Сети (скорость не менее: для видео 2 Мб/с, для аудио 512 Кб/с). Также нужно иметь под рукой все медицинские документы в отсканированном или сфотографированном виде.
графическое представление функции sin(x)
Программное обеспечение 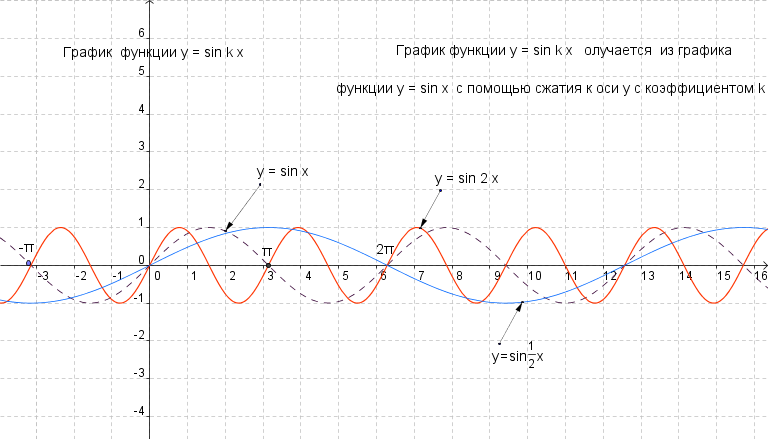
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.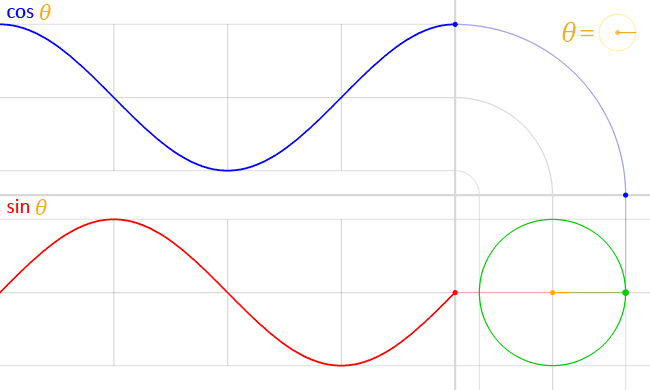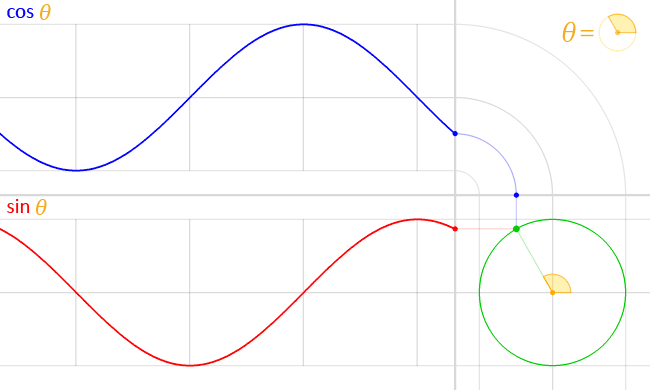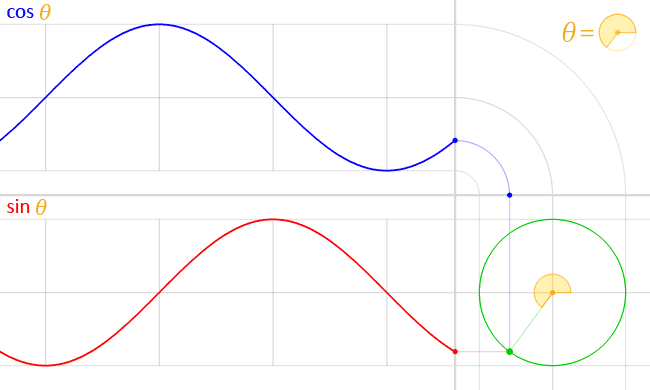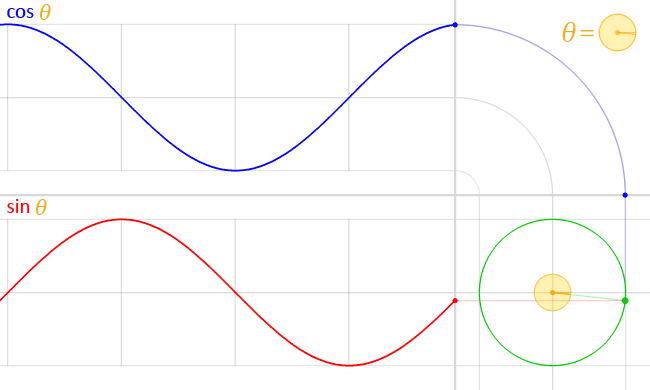
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.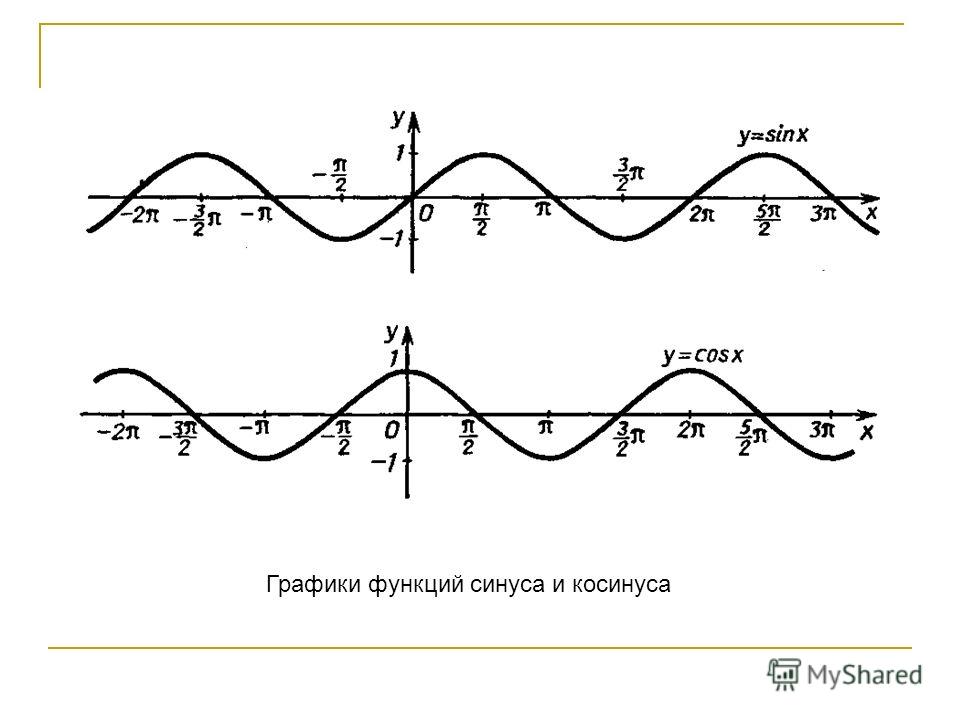
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.
Графики синуса и косинуса
Откуда берутся эти графики?
Функция синуса дает $y$-значения точек на единичной окружности.
Функция косинуса дает $x$-значения точек на единичной окружности.
Так как единичный круг имеет радиус $\,1\,$, все его точек имеют координаты между $\,-1\,$ и $\,1\,$.
Вот почему оба графика (синус и косинус) застревают между $\,y = -1\,$ и $\,y = 1\,$.
| Вот как можно визуализировать график функции синуса: Поместите палец в точку $\,(1,0)\,$ на единичной окружности. |
Синусоидальная функция отслеживает движения пальца вверх/вниз:
Более высокий уровень понимания функции синуса:
В Radian Measure мы «оборачиваем» линию вещественного числа вокруг единичного круга.
Таким образом, каждое действительное число связано с точкой (называемой конечной точкой ) и соответствующим углом на единичной окружности.
Тогда реальное число является мерой этого угла в радианах!
| Оберните числовую прямую вокруг единичного круга! | … связан с точкой на единичной окружности … | … и соответствующий угол. 9\круг\,$) | |
| При переходе $\,x\,$ от $\,\frac{\pi}{2}\,$ к $\,\pi\,$, $\,\sin x\,$ переходит из $\,1\,$ обратно в $\,0\,$. 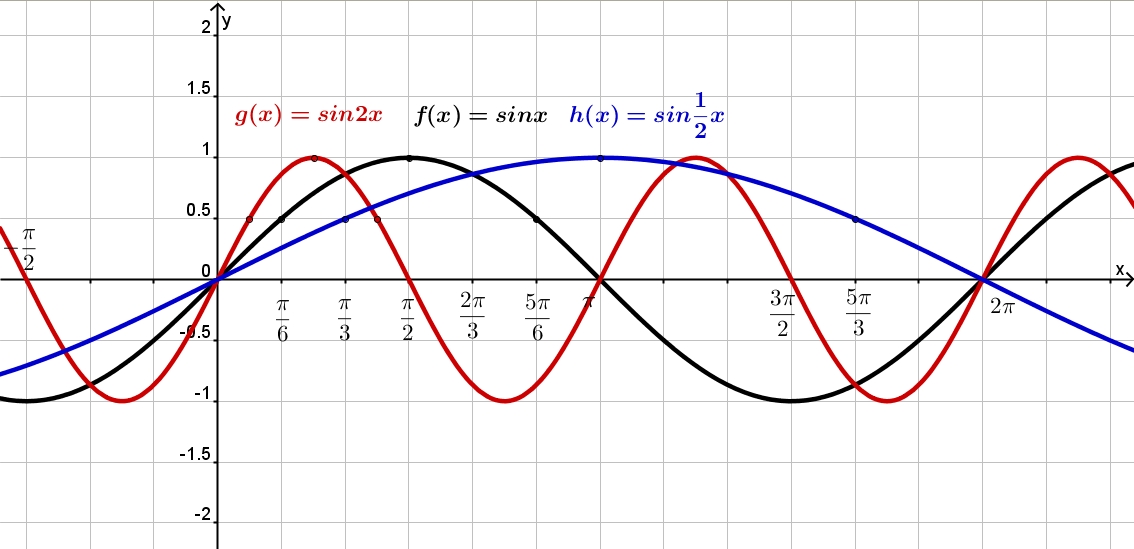 |

 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения