Теорема об односторонних углах / Параллельные прямые / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема об односторонних углах
Теорема
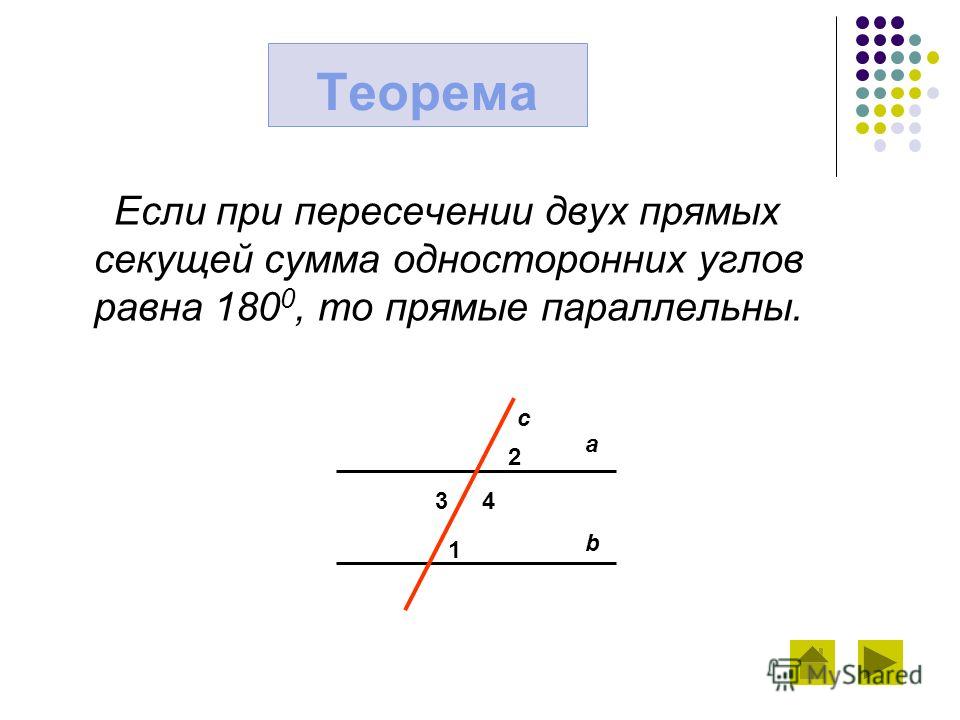
| Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800. |
Дано: , — секущая, 1 и 2 односторонние (Рис.1).
Доказать: 1 + 2 = 1800.
Доказательство:
По условию , значит соответственные углы 2 и 3 равны, т. е. 2 =
е. 2 =
Из равенств 2 =3 и 1 +3 = 1800 следует, что 1 +2 = 1800. Что и требовалось доказать.
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 298, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 377, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 391, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 428, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 891, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1043, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1072, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1233, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Признак параллельности прямых по сумме градусных мер односторонних углов
Урок 15.
 Геометрия 7 класс
Геометрия 7 классНа данном уроке мы изучаем признак параллельности прямых по сумме градусных мер односторонних углов. А также рассматриваем задачи, для решения которых нам нужно применить не только данный признак, но признаки параллельности прямых по равенству накрест лежащих углов и по равенству соответственных углов.
Конспект урока «Признак параллельности прямых по сумме градусных мер односторонних углов»
Первый признак параллельности прямых:
Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
Второй признак параллельности прямых:
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
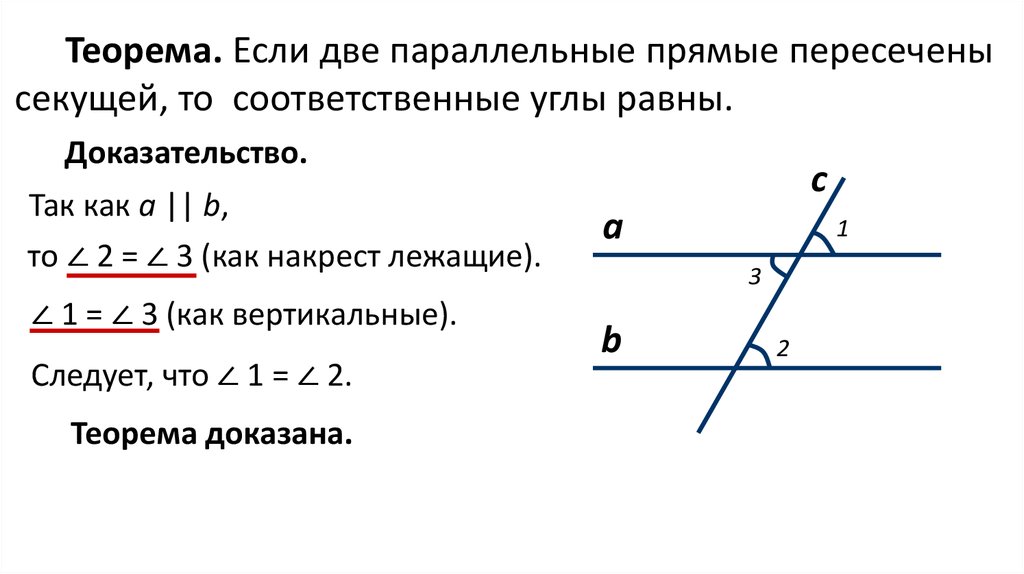
Теорема:
Если
при пересечении двух прямых секущей сумма градусных мер односторонних углов
равна 180 градусам, то прямые параллельны.
Доказательство:
Пусть при пересечении прямых а и b секущей c сумма односторонних углов 1 и 2 равна 180 градусам.
Так как углы 2 и 3 являются смежными, то ∠2+∠3=180 градусов.
Из равенств ∠1+∠2=180 градусов и ∠2+∠3=180 градусов следует, что ∠1=∠3. А поскольку ∠1 и ∠3 являются накрест лежащими, то прямые а и b параллельны. Теорема доказана.
Пример.
При пресечении двух параллельных прямых
Так как прямая а параллельна прямой b, то ∠7=∠1=130 градусов как внешние накрест лежащие углы.
∠5=∠1=130 градусов как соответственные углы.
∠3=∠1=130 градусов как вертикальные.
По свойству смежных углов ∠2=180-∠1=50 градусов.
∠8=∠2=50 градусов как внешние накрест лежащие углы.
∠6=∠2=50
градусов
как соответственные углы.
∠4=∠2=50 градусов как вертикальные углы.
Пример.
В треугольнике АВС стороны АВ и ВС равны. А ∠ВАС=60 градусов. Луч СD - биссектриса угла ВСЕ смежного с углом АСВ. Доказать, что прямая АВ параллельна прямой СD.
Так как АВ=ВС, то треугольник АВС является равнобедренным. Углы ВАС и АСВ равны как углы при основании равнобедренного треугольника и равны 60 градусов.
Углы ВСЕ и АСВ являются смежными, поэтому ∠ВСЕ=180-∠АСВ=120 градусов.
∠BCD=60 градусов, так как по условию задачи СD - биссектриса угла ВСЕ.
Тогда ∠ВАС + ∠DСА=180 градусов.
Следовательно, прямые АВ и СD параллельны. Что и требовалось доказать.
Пример.
В треугольнике АВС, ∠А=40 градусов, а ∠В=70 градусов. Через вершину В проведена прямая ВD так, что луч ВС является биссектрисой угла АВD. Доказать, что прямые ВD и АС параллельны.
Рассмотрим
прямые АС, ВD
и секущую прямую АВ. Углы ВАС и АВD -
внутренние односторонние.
Углы ВАС и АВD -
внутренние односторонние.
По условию задачи ВС — биссектриса угла АВD, а значит ∠АВС=∠СВD=70 градусов. Тогда угол ∠АВD=140 градусов.
Угол ∠ВАС+∠АВD=40+40=80 градусов. А так как эти углы являются внутренними односторонними, то получаем, что прямая АС параллельна прямой BD. Что и требовалось доказать.
Предыдущий урок 14 Признак параллельности прямых по равенству соответственных углов
Следующий урок 16 Аксиома параллельных прямых
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 7 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Сумма углов в многоугольнике — Значение | Формула
LearnPracticeDownload
Сумма углов многоугольника зависит от количества ребер и вершин.
| 1. | Типы полигонов |
| 2. | Типы углов правильного многоугольника |
| 3. | Сумма внутренних углов многоугольника |
| 4. | Сумма внешних углов многоугольника |
| 5. | Решенные примеры |
| 6. | Практические вопросы |
| 7. | Часто задаваемые вопросы о сумме углов в многоугольнике |
Типы многоугольников
Многоугольники подразделяются на различные категории в зависимости от их свойств, количества сторон и величины их углов. По количеству сторон многоугольники можно разделить на следующие категории:
- Треугольник (3 стороны)
- Четырехугольник (4 стороны)
- Пентагон (5 сторон)
- Шестигранник (6 сторон)
- Семиугольник (7 сторон)
- Октагон (8 сторон)
- Нонагон (9 сторон)
- Decagon (10 сторон) и так далее
На основании других свойств многоугольники можно разделить на следующие категории:
- Правильные многоугольники и неправильные многоугольники
- Вогнутые многоугольники и выпуклые многоугольники
- Равносторонние многоугольники и равноугольные многоугольники
Типы углов правильного многоугольника
Правильный многоугольник — это многоугольник, у которого все углы и стороны равны. В правильном многоугольнике есть 2 типа углов:
В правильном многоугольнике есть 2 типа углов:
- Внутренние углы. Углы, лежащие внутри фигуры, обычно многоугольника, называются ее внутренними углами.
- Внешние углы. Внешний угол многоугольника — это угол между стороной и прилегающей к ней расширенной стороной.
Сумма внутренних углов многоугольника
Внутренние углы многоугольника — это те углы, которые лежат внутри многоугольника. Обратите внимание на внутренние углы A, B и C в следующем треугольнике. Внутренние углы правильного многоугольника всегда равны друг другу. Поэтому, чтобы найти сумму внутренних углов многоугольника, мы используем формулу: Сумма внутренних углов = (n − 2) × 180 °, где n = количество сторон многоугольника.
Другой способ вычислить сумму внутренних углов — проверить количество треугольников, образованных внутри многоугольника, с помощью диагоналей. Поскольку сумма внутренних углов треугольника равна 180°, сумму внутренних углов любого многоугольника можно рассчитать, умножив 180° на количество треугольников, образованных внутри многоугольника. Например, четырехугольник можно разделить на два треугольника с помощью диагоналей, поэтому сумма внутренних углов четырехугольника равна 2 × 180° = 360°. Точно так же пятиугольник можно разделить на 3 треугольника, поэтому сумма внутренних углов пятиугольника составит 3 × 180 ° = 540 °
Например, четырехугольник можно разделить на два треугольника с помощью диагоналей, поэтому сумма внутренних углов четырехугольника равна 2 × 180° = 360°. Точно так же пятиугольник можно разделить на 3 треугольника, поэтому сумма внутренних углов пятиугольника составит 3 × 180 ° = 540 °
Пример:
Какова сумма внутренних углов шестиугольника?
Решение:
Шестиугольник имеет 6 сторон, следовательно, n = 6
Сумма внутренних углов правильного многоугольника, S = (n − 2) × 180
S = (6-2) × 180° 90 121
⇒ S = 4 × 180
⇒ S=720°
Следовательно, сумма внутренних углов шестиугольника равна 720°.
Сумма внешних углов многоугольника
Внешний угол (внешний угол) любой формы или правильного многоугольника представляет собой угол, образованный одной стороной и продолжением смежной стороны этого многоугольника. Обратите внимание на внешние углы , показанные в следующем многоугольнике.
Сумма внешних углов многоугольника равна 360°. Это можно доказать, выполнив следующие шаги:
- Мы знаем, что сумма внутренних углов правильного многоугольника с n сторонами = 180 (n-2).
- Внутренний и внешний углы в каждой вершине образуют линейную пару. Следовательно, в многоугольнике будет n линейных пар. Теперь, поскольку сумма каждой линейной пары составляет 180°, сумма всех линейных пар будет равна: 180n°.
- Итак, сумма внешних углов = Сумма всех линейных пар — Сумма внутренних углов
- Это означает: Сумма внешних углов = 180n – 180(n-2) = 180n – 180n + 360. Следовательно, сумма внешних углов пятиугольника равна 360°.
Статьи по теме:
Ознакомьтесь с этими интересными статьями, посвященными сумме углов многоугольника. Нажмите, чтобы узнать больше!
- Формула суммы углов
- Внутренний уголок Формула
- Полигоны
Пример 1 .
 Если три внутренних угла четырехугольника равны 96°, 114° и 41°, то какова мера четвертого внутреннего угла?
Если три внутренних угла четырехугольника равны 96°, 114° и 41°, то какова мера четвертого внутреннего угла?Решение:
Мы знаем, что сумма внутренних углов правильного многоугольника = (n-2) × 180°, где n — количество сторон
Поскольку это четырехугольник, n = 4.
Следовательно, сумма внутренних углов четырехугольника = (4-2) × 180°= 360°
Пусть четвертый внутренний угол равен x.
Следовательно, 96° + 114° + 41° + x = 360°
⇒ 251° + x = 360°
⇒ х = 360° — 251°
⇒ x = 109°Четвертый внутренний угол равен 109°.
Пример 2. Внешние углы правильного пятиугольника равны y, 2y, 3y, 4y и 8y.
Какова величина наименьшего внутреннего угла этого пятиугольника?Решение:
Сумма внешних углов правильного многоугольника равна 360°.
Следовательно, у + 2у + 3у + 4у + 8у = 360°
⇒ 18у = 360°
⇒ у = 360°/18
⇒ y = 20°Размер наибольшего внешнего угла = 8 × y = 8 × 20° = 160°
Мы знаем, что сумма внешнего угла и прилежащего к нему внутреннего угла = 180°.

Следовательно, размер наименьшего внутреннего угла = 180° − 160° = 20°
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о сумме углов в многоугольнике
Чему равна сумма всех внутренних углов правильного многоугольника?
Сумма всех внутренних углов правильного многоугольника рассчитывается по формуле S=(n-2) × 180°, где n — количество сторон многоугольника. Например, чтобы найти сумму внутренних углов пятиугольника, мы подставим значение n в формулу: S=(n-2) × 180°; в этом случае n = 5. Итак, (5-2) × 180° = 3 × 180° = 540°.
Чему равна сумма всех внешних углов правильного многоугольника?
Сумма всех внешних углов правильного многоугольника равна 360°.
Чему равна сумма внутреннего и внешнего углов при одной и той же вершине?
Сумма внутреннего и внешнего углов одной и той же вершины всегда равна 180 ° , поскольку они образуют линейную пару.
Чему равна сумма всех внутренних углов четырехугольника?
Формула, используемая для нахождения суммы внутренних углов многоугольника: S=(n-2) × 180°. В этом случае n = 4. Следовательно, сумма внутренних углов четырехугольника равна (4-2) × 180° = 360°.
Как найти внутренний угол правильного многоугольника?
Величина внутреннего угла правильного многоугольника рассчитывается по формуле: 180° × (n-2)/n, где n — количество сторон многоугольника.
Как найти величину внешнего угла правильного многоугольника?
Мера внешнего угла правильного многоугольника рассчитывается по формуле: 360°/n, где n — количество сторон многоугольника.
Скачать бесплатные материалы для исследования
Рабочий лист на многоугольниках
Математические листы и
Визуальная учебная программа
Сумма внутренних и внешних углов (видео) Полигоны, Pentagon & More
.
Факт проверен
Полом Маццола
Нахождение суммы внутренних и внешних углов
Многоугольники подобны домикам в мире двухмерной геометрии. Они создают внутреннее, называемое внутренним, и внешнее, называемое внешним. Вы можете измерить внутренние углы и внешние углы. Вы также можете сложить суммы всех внутренних углов и суммы всех внешних углов правильных многоугольников.
Наша формула работает с треугольниками, квадратами, пятиугольниками, шестиугольниками, четырехугольниками, восьмиугольниками и другими объектами.
Что такое правильный многоугольник?
Чтобы многоугольник был правильным многоугольником, он должен удовлетворять этим четырем требованиям:
Быть двумерным
Заключать пространство, создавая внутреннюю и внешнюю части
Использовать только отрезки для трех сторон
2
Имеют все стороны, равные по длине друг другу, и все внутренние углы, равные друг другу по размеру
Сумма внутренних углов многоугольника
Правильные многоугольники существуют без ограничений (теоретически), но по мере того, как вы получаете все больше и больше сторон, многоугольник все больше и больше становится похожим на круг. Правильный многоугольник с наименьшим количеством сторон – тремя – это равносторонний треугольник.
Правильный многоугольник с наименьшим количеством сторон – тремя – это равносторонний треугольник.
Правильный многоугольник с наибольшим количеством сторон, обычно используемый на уроках геометрии, вероятно, представляет собой двенадцатиугольник, или 12-угольник, с 12 сторонами и 12 внутренними углами:
Сумма внутренних углов многоугольникаЗаманчиво, не правда ли? Но только потому, что у него есть все эти стороны и внутренние углы, не думайте, что вы не можете многое понять о нашем двенадцатиугольнике. Предположим, например, что вы хотите знать, сколько в сумме составляют все эти внутренние углы в градусах?
Сумма внутренних углов
Треугольники просты. Их 90 318 внутренних углов 90 319 добавляют к 90 318 180° 90 319. Точно так же квадрат (правильный четырехугольник) добавляется к 360° , потому что квадрат можно разделить на два треугольника.
Слово «многоугольник» означает «множество углов», хотя большинство людей, кажется, больше замечают стороны, чем углы, поэтому они создали такие слова, как «четырехугольник», что означает «четыре стороны».
Правильные многоугольники имеют столько внутренних углов, сколько у них сторон, поэтому треугольник имеет три стороны и три внутренних угла. Квадрат? Четыре каждого. Пентагон? Пять и так далее.
Наш двенадцатиугольник имеет 12 сторон и 12 внутренних углов .
Формула суммы внутренних углов
Формула для суммы внутренних углов этого многоугольника очень проста. Пусть n равно количеству сторон любого правильного многоугольника, который вы изучаете. Вот формула:
Сумма внутренних углов ФормулаСумма углов в треугольнике
Вы можете сделать это. Попробуйте сначала с нашим равносторонним треугольником:
Сумма углов треугольникаСумма углов квадрата
И снова попробуйте для квадрата:
Сумма углов квадратаКак найти один внутренний угол? .
Новая формула очень похожа на старую:
Формула для нахождения величины одного внутреннего углаСнова проверьте ее для равностороннего треугольника:
И для квадрата:
Эй! Оно работает! И это работает каждый раз . Давайте займемся этим двенадцатиугольником сейчас.
Давайте займемся этим двенадцатиугольником сейчас.
Примеры внутренних углов
Помните, как выглядит 12-угольник? Найдем сумму внутренних углов, а также один внутренний угол:
Примеры внутренних угловНайдем сумму внутренних углов двенадцатиугольника
Теперь найдем один внутренний угол
Сумма внешних углов
Каждый правильный многоугольник имеет внешних углов . Это , а не угол рефлекса (более 180° ), созданный вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение.
Например, в равностороннем треугольнике внешний угол равен , а не 360° — 60° = 300° , как если бы мы вращались от одной стороны вокруг вершины до другой стороны.
Сумма внешних угловВнешние углы создаются путем продолжения одной стороны правильного многоугольника за фигуру и последующего измерения в градусах от этой продолженной линии до следующей стороны многоугольника.
Поскольку вы расширяете сторону многоугольника, этот внешний угол обязательно должен быть дополнительным к внутреннему углу многоугольника.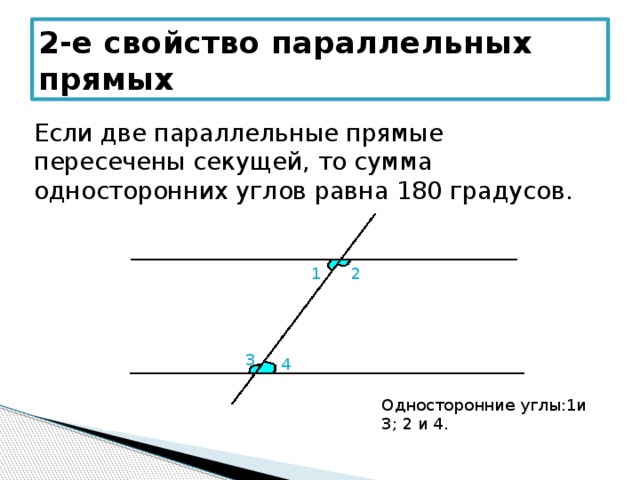 Вместе смежные внутренние и внешние углы составят 180° .
Вместе смежные внутренние и внешние углы составят 180° .
Внешний угол любой вершины нашего равностороннего треугольника равен 120° . Для квадрата внешний угол равен 90° .
Формула внешнего угла
Если вы предпочитаете формулу, вычтите внутренний угол из 180° :
Примеры внешних углов
Что осталось в нашей коллекции правильных многоугольников? Этот двенадцатиугольник! Мы знаем, что любой внутренний угол равен 150° , поэтому внешний угол равен:
Формула суммы внешних углов и примерыПроверка вашей работы
Внимательно посмотрите на три внешних угла, которые мы использовали в наших примерах:
Приготовьтесь удивиться . Умножьте каждое из этих измерений на количество сторон правильного многоугольника:
Это выглядит как волшебство, но геометрическая причина этого на самом деле проста: чтобы перемещаться по этим фигурам, вы делаете один полный оборот или поворот на 360° .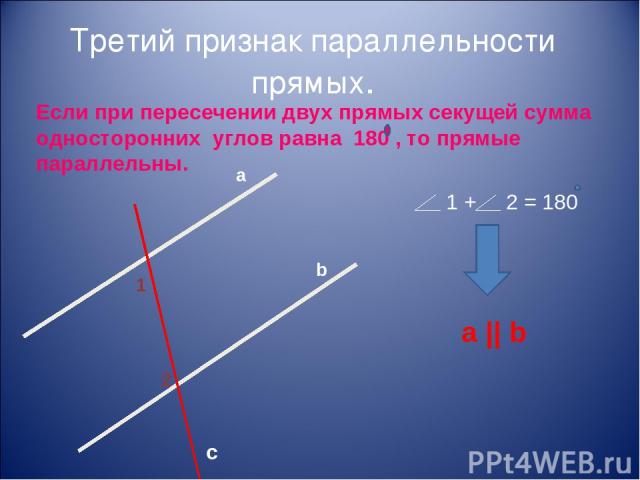

 Если три внутренних угла четырехугольника равны 96°, 114° и 41°, то какова мера четвертого внутреннего угла?
Если три внутренних угла четырехугольника равны 96°, 114° и 41°, то какова мера четвертого внутреннего угла?