Обзор основных методов математической оптимизации для задач с ограничениями / Хабр
Я долго готовился и собирал материал, надеюсь в этот раз получилось лучше. Эту статью посвящаю основным методам решения задач математической оптимизации с ограничениями, так что если вы слышали, что симплекс-метод — это какой-то очень важный метод, но до сих пор не знаете, что он делает, то возможно эта статья вам поможет.
P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.
Преамбула
Задача математической оптимизации — это задача вида «Найти в множестве элемент такой, что для всех из выполняется », что в научной литературе скорее будет записано как-то так
Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например ).
Задачи минимизации над пространством вида таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).
Технически, совершенно любое множество можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как
однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т.
п.). Тем не менее, часто можно представить в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай
где — выпуклые (но не обязательно дифференцируемые) функции, — матрица. Для демонстрации работы методов я буду использовать два примера:
- Задача линейного программирования
По сути эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решение задачи — точка (4.7, 3.5) — самая «правая» в многоугольнике). А вот собственно и сам многоугольник - Минимизация квадратичной функции с одним квадратичным ограничением
Симплекс-метод
Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно).
Идея симплекс-метода состоит из двух частей:
- Системы линейных неравенств и равенств задают многомерные выпуклые многогранники (политопы). В одномерном случае это точка, луч или отрезок, в двумерном — выпуклый многоугольник, в трехмерном — выпуклый многогранник. Минимизация линейной функции — это по сути нахождение самой «дальней» точки в определенном направлении. Думаю, интуиция должна подсказывать, что этой самой дальней точкой должна быть некая вершина, и это действительно так. В общем случае, для системы из неравенств в -мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно из этих неравенств обращаются в равенства (при условии, что среди неравенств нет эквивалентных). Таких точек всегда конечное число, хоть их и может быть очень много.
- Теперь у нас есть конечный набор точек, вообще говоря можно их просто взять и перебрать, то есть сделать что-то такое: для каждого подмножества из неравенств решить систему линейных уравнений, составленных на выбранных неравенствах, проверить, что решение подходит в исходную систему неравенств и сравнить с другими такими точками.
Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи
Если для решения этой задачи такое, что , то выполняется , иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять с произвольным . Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.
Траектория двухфазового симплекс-метода
Траектория была сгенерирована с помощью scipy.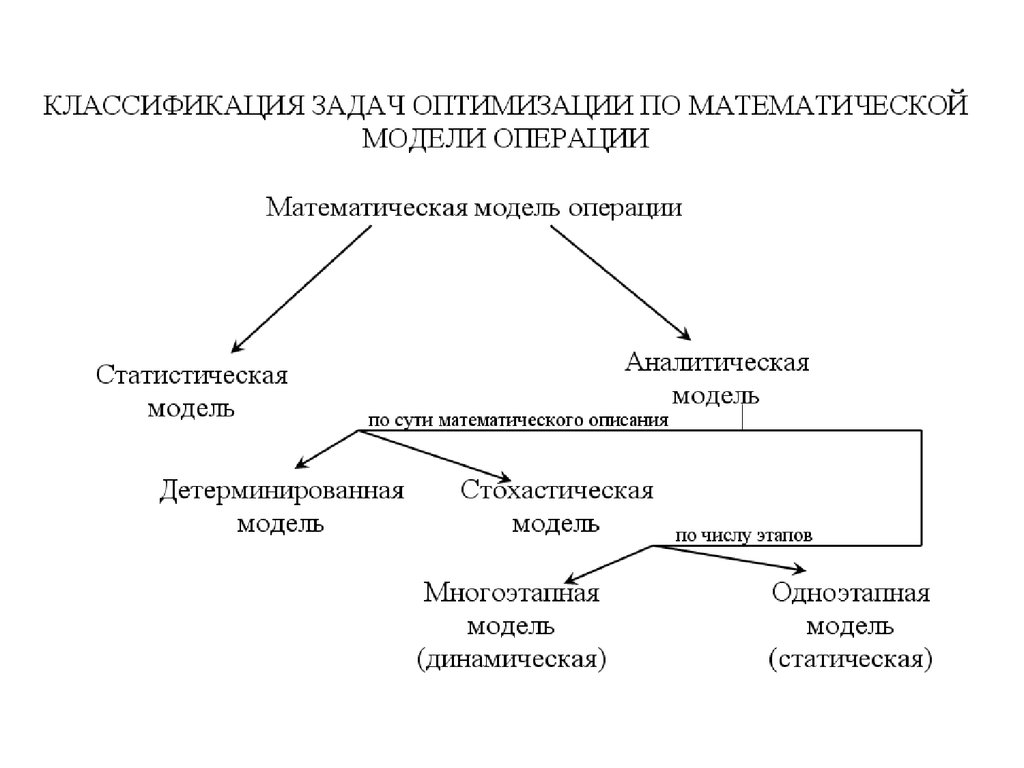
optimize.linprog.
Проективный градиентный спуск
Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции , то при правильном выборе параметров получаем глобальный минимум . Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество , то в результате мы получим минимум функции на . Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
где
Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке вычисляет ближайшую к ней точку множества .
Роль расстояния здесь играет , стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!
На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид
Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то так
Траектория проективного градиентного спуска для задачи линейного программирования
А вот как выглядит траектория проективного градиентного спуска для второй задачи, если
выбирать большой размер шага
и если
выбирать небольшой размер шага
Метод эллипсоидов
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции.
- На каждом шаге метода есть некоторое множество, которое содержит решение задачи.
- На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону выбранной гиперплоскости, и, возможно, к этому множеству добавятся какие-то новые точки
Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций
Если зафиксировать , то для выпуклой функции полупространство содержит только точки со значением не меньше, чем в точке , а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.
Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек.
В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.
Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом
Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.
А вот собственно как он работает для
линейного программирования
и для
квадратичного программирования
Метод внутренней точки
Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод.
Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция называется барьерной функцией для множества , если
Здесь — внутренность , — граница . Вместо исходной задачи предлагается решать задачу
и заданы только на внутренности (по сути отсюда и название), свойство барьера гарантирует, что у минимум по существует. Более того, чем больше , тем больше влияние . При достаточно разумных условиях можно добиться того, что если устремить к бесконечности, то минимум будет сходиться к решению исходной задачи.
Если множество задано в виде набора неравенств , то стандартным выбором барьерной функции является логарифмический барьер
Точки минимума функции для разных образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для
Примера с линейным программированием
Аналитический центр — это просто
Наконец сам метод внутренней точки имеет следующий вид
- Выбрать начальное приближение ,
- Выбрать новое приближение методом Ньютона
- Увеличить
Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку,
, поэкспериментировали, в таком виде не всегда выдает.
Ну и наконец, так выглядит траектория метода внутренней точки
Задача линейного программирования
Прыгающая черная точка — это , т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.
Задача квадратичного программирования
Методы оптимизации | LETIteach
Кафедра САПР
Enrollment in this course is by invitation only
О курсеНаша цель — дать теоретические и практические знания и навыки для решения задач оптимизации. Акцент сделан на классических детерминированных алгоритмах нелинейного программирования. К особенностям данного курса относится широкое использование демонстрационного материала: каждый раздел сопровождается пояснением в виде рисунка, видеоряда или кода.
Цели и задачи дисциплины- Изучение методов и алгоритмов оптимизации одномерных и многомерных задач.
- Формирование навыков разработки оптимизационных программ, учитывающих вычислительные аспекты алгоритмов поиска оптимальных решений.
- Освоение умений формализации оптимизационных задач и средств разработки, закрепление знаний об области применения программ оптимального поиска.
- Тематические видеолекции
- Тестовые задания
- Лабораторные работы
Результаты тестирований оцениваются по рейтинговой системе.
Структура курса- Модуль 1. Базовые понятия функционального анализа
- Множество и функция
- Поле и пространство
- Экстремумы. Критические и стационарные точки. Задача оптимизации
- Ряд Тейлора
- Квадратичные формы
- Окончание поиска и численное дифференцирование
- Модуль 2. Одномерная оптимизация
- Двухточечное и трехточечное деление
- Метод золотого сечения, Фибоначчи
- Метод Ньютона. Метод секущих
- Методы на основе аппроксимации параболами. Метод Брента-Деккера
- Модуль 3. Многомерная оптимизация
- Градиентные методы
- Метод наискорейшего спуска. Овражные задачи
- Метод Ньютона. Демпфированный метод Ньютона
- Методы Нестерова-Немировского и Левенберга-Марквардта
- Методы Барзилая-Борвейна
- Условия Вульфа
- Методы сопряженных градиентов
- Квазиньютоновские методы
- Метод БФГШ с ограниченной памятью
- Метод доверительных областей
- Метод ускоренного градиента Нестерова
- Метод Хука-Дживса
Одномерная оптимизацияИнформатика и вычислительная техника
Целевая аудиторияКурс рассчитан на магистров первого года обучения
Автор курсаКаримов Артур Искандарович
кандидат технических наук, доцент кафедры систем автоматизированного проектирования
Optimization Toolbox
Решение задач линейной, квадратичной, конической, целочисленной и нелинейной оптимизации
Получить бесплатную пробную версию
Посмотреть цены
Optimization Toolbox™ предоставляет функции для поиска параметров, которые минимизируют или максимизируют цели при соблюдении ограничений.
Набор инструментов включает решатели для линейного программирования (LP), смешанно-целочисленного линейного программирования (MILP), квадратичного программирования (QP), конусного программирования второго порядка (SOCP), нелинейного программирования (NLP), ограниченного линейного метода наименьших квадратов, нелинейного метода наименьших квадратов, и нелинейные уравнения.
Вы можете определить задачу оптимизации с помощью функций и матриц или задав переменные выражения, отражающие лежащую в основе математику. Вы можете использовать автоматическое дифференцирование целевых функций и функций ограничений для более быстрого и точного решения.
Решатели набора инструментов можно использовать для поиска оптимальных решений непрерывных и дискретных задач, выполнения анализа компромиссов и включения методов оптимизации в алгоритмы и приложения. Набор инструментов позволяет выполнять задачи по оптимизации конструкции, включая оценку параметров, выбор компонентов и настройку параметров.
Он позволяет находить оптимальные решения в таких приложениях, как оптимизация портфеля, управление энергопотреблением и торговля, а также планирование производства.
Начало работы:
- Определение проблем оптимизации
- Решение проблем оптимизации
- Нелинейное программирование
- Линейное, квадратичное и коническое программирование
- Смешанно-целочисленное линейное программирование
- Многоцелевая оптимизация
- Метод наименьших квадратов и решение уравнений
- Развертывание
2:46 Продолжительность видео 2:46.
Что такое инструментарий оптимизации?
БЕСПЛАТНЫЕ Шпаргалки
9 шпаргалок MATLAB по науке о данных и машинному обучению
Получить шпаргалки
Определение задач оптимизации
Моделирование проблемы проектирования или решения как проблемы оптимизации.
Установите проектные параметры и решения в качестве переменных оптимизации. Используйте их при определении целевой функции для оптимизации и использования ограничений для ограничения возможных значений переменных.
Моделирование
Преобразование описания проблемы в математическую форму путем определения переменных, целей и ограничений, чтобы ее можно было решить с помощью методов оптимизации.
Обзор теории оптимизации
Проблемы, решаемые решателями Optimization Toolbox
Различия между подходами, основанными на проблеме, и подходами, основанными на решении
Математическое моделирование с оптимизацией, часть 1: от описания задачи к математической программе.8:51 Продолжительность видео 8:51.
Математическое моделирование с оптимизацией, часть 1: от описания задачи к математической программе
Проблемно-ориентированная оптимизация
Запишите цели и ограничения с выражениями переменных оптимизации.
Решайте быстрее и надежнее благодаря автоматическому дифференцированию нелинейных выражений. Примените автоматически выбранный решатель. Создайте и решите проблему в интерактивном режиме с помощью задачи «Оптимизация Live Editor», а затем сгенерируйте код для совместного использования или использования в своем приложении.
Настройка оптимизации на основе проблем
Нелинейное программирование
Линейное программирование
Смешанно-целочисленное линейное программирование
Математическое моделирование с оптимизацией, часть 2а: проблемно-ориентированное линейное программирование.6:04 Продолжительность видео 6:04.
Математическое моделирование с оптимизацией, часть 2а: линейное программирование на основе задач
Оптимизация на основе решателя
Запись нелинейных целей и ограничений с использованием функций; запишите линейные цели и ограничения, используя матрицы коэффициентов. Создайте и решите проблему в интерактивном режиме с помощью задачи «Оптимизация Live Editor», а затем сгенерируйте код для совместного использования или использования в своем приложении.
Настройка задачи оптимизации на основе решателя
Нелинейное программирование
Линейное программирование
Смешанно-целочисленное линейное программирование
Математическое моделирование с оптимизацией, часть 2b: линейное программирование на основе решателя.10:46 Продолжительность видео 10:46.
Математическое моделирование с оптимизацией, часть 2b: линейное программирование на основе решателя
Решение задач оптимизации
Примените решатель к задаче оптимизации, чтобы найти оптимальное решение: набор значений переменных оптимизации, которые дают оптимальное значение целевой функции, если таковые имеются, и удовлетворяют ограничениям, если таковые имеются.
Выбор решателя
Используйте задачу Оптимизировать Live Editor с подходом, основанным на проблеме или на основе решателя, чтобы помочь выбрать решатель, подходящий для типа проблемы.
Решатели инструментов оптимизации
Местная и глобальная Оптима
Таблица решений по оптимизации
Оптимизация задачи Live Editor
Как использовать задачу оптимизации Live Editor на основе проблем.
3:04 Продолжительность видео 3:04.
Как использовать задачу «Оптимизация на основе проблем в реальном времени»
Настройка параметров
Установите параметры оптимизации для настройки процесса оптимизации, например, для выбора алгоритма оптимизации, используемого решателем, или для установки условий завершения. Задайте параметры для отслеживания и отображения прогресса решателя оптимизации.
Установка и изменение параметров
Опции № по каталогу
Выбор алгоритма
График и сохранение истории итераций
Настройка параметров оптимизации.4:48 Продолжительность видео 4:48.
Настройка параметров оптимизации
Просмотр и улучшение результатов
Просмотрите сообщения о выходе, показатели оптимальности и итеративное отображение для оценки решения. Повысьте производительность при решении нелинейных задач, используя автоматическое дифференцирование, предоставление градиентов или использование параллельных вычислений для оценки градиентов.
Выходные данные решателя и итеративное отображение
Улучшить результаты
Автоматическое дифференцирование
Ускорение с помощью параллельных вычислений
Мониторинг выполнения решателя с помощью итеративного отображения.
Нелинейное программирование
Решение задач оптимизации с нелинейной целью или с нелинейными ограничениями.
Решатели
Применение квазиньютоновских алгоритмов, алгоритмов доверительной области или симплексных алгоритмов Нелдера-Мида для решения задач без ограничений. Применяйте алгоритмы внутренней точки, последовательного квадратичного программирования (SQP) или алгоритмы рефлексии доверительной области для решения задач с ограничениями.
Решение задач нелинейной оптимизации
Неограниченные нелинейные алгоритмы
Ограниченные нелинейные алгоритмы
Учебник по нелинейной оптимизации
Математическое моделирование с оптимизацией, часть 4: проблемно-ориентированное нелинейное программирование.
5:15 Продолжительность видео 5:15.
Математическое моделирование с оптимизацией, часть 4: проблемно-ориентированное нелинейное программирование
Приложения
Используйте нелинейную оптимизацию для оценки и настройки параметров, поиска оптимальных планов, расчета оптимальных траекторий, построения надежных портфелей и других приложений, где существует нелинейная связь между переменными.
Минимизация потенциальной электростатической энергии
Оптимизация моделирования или обыкновенного дифференциального уравнения
Параметры гидравлического клапана, расход (8:02)
Параметры гидравлического клапана, частотная характеристика (6:51)
Поиск оптимального пути с помощью Optimization Toolbox.7:28 Продолжительность видео 7:28.
Поиск оптимального пути с помощью Optimization Toolbox
Линейное, квадратичное и коническое программирование
Решите задачи выпуклой оптимизации, которые имеют линейные или квадратичные цели и подчиняются линейным или конусным ограничениям второго порядка.
Решатели линейного программирования
Применение алгоритмов двойного симплекса или внутренних точек для решения линейных программ.
Решение задач линейной оптимизации
Алгоритмы линейного программирования
Выявление конфликтующих линейных зависимостей
Допустимая область и оптимальное решение линейной программы.
Решатели для квадратичного и конусного программирования второго порядка
Применение алгоритмов внутренней точки, активного набора или доверительной области для решения квадратичных программ. Применение методов внутренних точек для решения конусных программ второго порядка.
Минимизация квадратичных функций с учетом ограничений
Алгоритмы квадратичного программирования
Алгоритм программирования конуса второго порядка
Допустимая область и оптимальное решение квадратичной программы.
Приложения
Используйте линейное программирование для решения таких задач, как распределение ресурсов, планирование производства, смешивание и планирование инвестиций.
Используйте квадратичное и конусное программирование второго порядка для решения таких задач, как оптимизация конструкции, оптимизация портфеля и управление плотинами гидроэлектростанций.
Многопериодное производственное планирование
Увеличение долгосрочных инвестиций
Оптимизация портфеля
Равновесие линейной системы масса-пружина
Оптимальная стратегия управления найдена с помощью квадратичного программирования.
Линейное программирование со смешанными целыми числами
Решение задач оптимизации, имеющих линейные цели с линейными ограничениями, с дополнительным ограничением, заключающимся в том, что некоторые или все переменные должны быть целочисленными.
Решатели
Решение задач линейного программирования со смешанными целыми числами с использованием алгоритма ветвей и границ, который включает в себя предварительную обработку, эвристику для создания допустимых точек и плоскостей сечения.
Решите задачи линейной оптимизации с целочисленными ограничениями
Смешанно-целочисленные алгоритмы линейного программирования
Настройка алгоритмов целочисленного программирования
Математическое моделирование с оптимизацией, часть 3: проблемно-ориентированное смешанно-целочисленное линейное программирование (4:31)
Применение алгоритма ветвей и границ.
Алгоритмы линейного программирования со смешанными целыми числами
Используйте решатель смешанного целочисленного линейного программирования для создания специальных алгоритмов.
Задача коммивояжера
Проблема с резкой заготовки
Смешанно-целочисленная квадратичная оптимизация портфеля
Самый короткий тур с посещением каждого города только один раз.
Приложения
Модель с целыми переменными, когда есть решения включения/выключения или логические ограничения, а также когда значения переменных должны быть целыми.
Типичными приложениями являются задачи маршрутизации, составления графиков, планирования, назначения и составления бюджета капиталовложений.
Оптимальная диспетчеризация генераторов
Фабрика, склад и модель распределения продаж
Решайте головоломки судоку с помощью целочисленного программирования
Офисные задания
Оптимизация планирования и операций смешивания в обрабатывающей промышленности (32:00)
График работы двух генераторов при разных ценах на электроэнергию.
Многокритериальная оптимизация
Решение задач оптимизации с несколькими целевыми функциями с учетом набора ограничений.
Решатели
Формулировать задачи либо как достижение цели, либо как минимакс. Используйте достижение цели, когда для каждой из целей есть необязательные взвешенные целевые значения. Используйте минимакс, чтобы минимизировать наихудшее значение набора целевых функций.
Минимизация нескольких целевых функций с учетом ограничений
Алгоритмы многокритериальной оптимизации
Сгенерируйте и постройте фронт Парето
Фронт Парето, вычисленный с использованием функции fgoalattain .
Приложения
Используйте многоцелевую оптимизацию, когда требуются компромиссы для противоречивых целей. Примерами являются вес и прочность в структурном дизайне, а также риск и доходность в оптимизации портфеля.
Проектирование нелинейного фильтра конечной точности
Проектирование КИХ-фильтра
Решение задачи о размещении полюса
Оптимизируйте параметры управления в Simulink Model
Величина отклика для начальных и оптимизированных коэффициентов фильтра.
Метод наименьших квадратов и решение уравнений
Решение нелинейных задач наименьших квадратов и нелинейных систем уравнений с учетом граничных ограничений. Решите линейные задачи наименьших квадратов с учетом связанных и линейных ограничений.
Решатели
Применение алгоритмов Левенберга-Марквардта, доверительной области, активного множества или внутренних точек.
Подгонка данных с использованием кривых, поверхностей и непараметрических методов
Алгоритмы наименьших квадратов
Алгоритмы решения уравнений
Нелинейные системы уравнений с ограничениями
Сравнение локального и глобального подходов.
Линейные приложения наименьших квадратов
Используйте линейные решатели наименьших квадратов, чтобы подогнать линейную модель к полученным данным или решить систему линейных уравнений, в том числе, когда параметры подчиняются связанным и линейным ограничениям.
Кратчайшее расстояние до самолета
Решение проблемы оптического устранения размытия
Восстановление размытого изображения путем решения линейной задачи наименьших квадратов.
Приложения нелинейного метода наименьших квадратов
Используйте нелинейные решатели метода наименьших квадратов для подгонки нелинейной модели к полученным данным или для решения системы нелинейных уравнений, в том числе, когда параметры подчиняются граничным ограничениям.
Подгонка нелинейных данных
Подходящие параметры управления в модели Simulink
Подбирайте модель к комплексным данным
Подходящие параметры обыкновенного дифференциального уравнения
Подгонка кругового пути к системе обыкновенных дифференциальных уравнений Лоренца.
Развертывание
Создание средств поддержки принятия решений и проектирования на основе оптимизации, интеграция с корпоративными системами и развертывание алгоритмов оптимизации во встроенных системах.
Поддержка компилятора MATLAB
Используйте MATLAB Compiler™ и MATLAB Compiler SDK™ для развертывания моделей оптимизации MATLAB ® в виде автономных исполняемых файлов, веб-приложений, совместно используемых библиотек C/C++, сборок Microsoft ® .NET, классов Java
3® 4® . и пакеты Python ® .
Приложение, которое рассчитывает оптимальный график выработки электроэнергии.
Генерация кода
Создавайте переносимый и читаемый код C или C++ для решения задач оптимизации с помощью MATLAB Coder™. Скомпилируйте сгенерированный код для любого оборудования, включая встроенные системы.
Генерация кода для основ оптимизации
Генерация кода оптимизации для приложений реального времени
Поиск оптимального пути с помощью генерации кода
Отчет MATLAB Coder для функции оптимизации траектории.
Ресурсы продукта:
Документация Функции Технические статьи Истории пользователей Требования к продукту Примечания к выпуску Видео и вебинары Примеры
Что дальше?
БЕСПЛАТНЫЕ Шпаргалки
9 шпаргалок MATLAB по науке о данных и машинному обучению
Особенности выпуска
Что нового в последней версии MATLAB и Simulink
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
Методы оптимизации для распределения задач и планирования в распределенных многоагентных операциях
- Идентификатор корпуса: 56577983
title={Методы оптимизации распределения и планирования задач в распределенных многоагентных операциях},
автор = {Марк Ф. Томпкинс},
год = {2003}
} 
Томпкинс},
год = {2003}
} - Марк Ф. Томпкинс
- Опубликовано в 2003 г.
- Информатика
В этой диссертации рассматриваются сценарии, в которых несколько автономных агентов сотрудничают для достижения глобальной цели. [] Ключевой метод Подход смешанного целочисленно-линейного программирования (MILP) представлен в контексте многоагентной структуры решения проблем, которая позволяет вычислять оптимальные сроки выполнения для сложных классификаций задач планирования, учитывающих множество различных параметров. В то время как представленный алгоритм требует экспоненциального времени для решения, и поэтому его можно использовать только для ограниченного…
dspace.mit.edu
Чередующийся подход к распределению и планированию задач на основе признаков
В этом документе представлен подход, основанный на поиске для расширенного по времени распределения задач на основе характеристик под названием Incremental Task Allocation Graph Search (ITAGS) и представляет собой новую структуру, которая чередует распределение задач, планирование и планирование движения.
Автоматизированный инструмент планирования (APT): средство решения задач нелинейного программирования смешанного целочисленного типа для планирования заказов на работу
- A. Purwar
Информатика, бизнес
- 2022
Основные детали модели оптимизации, инфраструктура облачных вычислений, используемая для решения этой сложной задачи NP, основные моменты формулировки модели MINLP и запуск достигается время в диапазоне 5-20 минут.
Двухэтапная стратегия планирования заданий в грид-среде на основе метода динамического программирования
- Казимыр В., Прила О.
Информатика
- 2014
В статье предложено применение метода динамического программирования к задаче планирования рабочего процесса и приведены результаты экспериментальной оценки эффективности предлагаемого решения.
Стратегия декомпозиции для оптимального охвата интересующей области с использованием разнородной группы БПЛА
- Мохсен Мехдизаде
Информатика
- 2012
Команда «определяет оптимальное покрытие и выполнение» миссии рабочая нагрузка для каждого агента, участвующего в миссии, определяется с помощью процедуры многокритериальной оптимизации.
Оптимизационный подход к процессу планирования профилактического обслуживания
- Манар Мохаммед Альтемази, С. Сулиман, Ясер Аль-Алави
Информатика
- 2017
сформулированы для задачи планирования капитального ремонта и предложен алгоритмический подход к оптимизации, который объединяет планирование и распределение рабочей силы в одной фазе.
Назначение и планирование иерархических графов задач разнородным ресурсам
- P. Alefragis, Christos G Gogos, Christos Valouxis, G. Goulas, N. Voros, E. Housos
Информатика
- 2014
В этой статье представлен метод решения задачи HTG. Идея постепенного решения проблемы путем замены подграфов виртуальными узлами является результатом решения проблемы подграфа с использованием целочисленного программирования.
Распределение задач и планирование параллельных приложений для многопроцессорных систем
- К. Койцер, К. Равиндран
Информатика, бизнес
- 2008
Койцер, К. РавиндранЭта диссертация является попыткой развить понимание эффективных и гибких методов распределения и планирования параллельных приложений для многопроцессорных архитектур. практических методов планирования, которые обеспечивают различные компромиссы в отношении вычислительной эффективности, качества результатов и гибкости.
Методы целочисленного программирования для статического планирования систем жесткого реального времени
- Ana Guasque, H. Tohidi, P. Balbastre, José María Aceituno, J. Simó, A. Crespo
Computer Science
IEEE Access
- 2020
- Н. Сатиш, К. Равиндран, К. Койцер
Информатика
2007 Дизайн, автоматизация и тестирование в Европе Конференция и выставка
- 2007
- C. Chekuri, M. A. Burender,
Информатика
J. Алгоритмы
- 1998
- Д. Энгельс, Дж. Фельдман, Дэвид Р. Каргер, М. Рул
Информатика
SODA ’01
- 2001
- J. Baxter, R. Hepplewhite
Информатика
- 2000
- Гуонин Ляо, Э. Альтман, В. Агарвал, Г. Гао
Бизнес, информатика
1994 Труды двадцать седьмой Гавайской международной конференции по системным наукам
- 19924 900 исследование Используя случайные, но программно-подобные входные графы, были обнаружены различия в производительности различных эвристик, связанные с степенью параллелизма во входном графе, и обнаружено, что ни одна эвристика последовательно не дает наилучших расписаний при вызовах программных структур и многопроцессорных конфигурациях.
Последние разработки в области детерминированной последовательности и планирования: обзор: (препринт)
- Э. Лоулер, Дж. Ленстра, А. Кан
Бизнес
- 1981
- О.
7 90 и алгоритмы аппроксимации и интерпретировать их с точки зрения теории сложности вычислений.
Замкнутый иерархический контроль военно-воздушных операций
7 70 % времени, необходимого для получения оптимального решения по сравнению с базовыми подходами, и позволяет достичь лучших результатов, чем эвристика, при попытке уменьшить временные параметры, такие как время отклика, переключение контекста и дрожание.
Подход к оптимизации ограничений на основе декомпозиции для статического планирования графов задач с задержками связи с мультипроцессорами
Стратегия оптимизации для ускорения декомпозиции представлена многопроцессорная задача планирования и итеративно изучается ограничения для сокращения пространства решений в порядке декомпозиции Бендерса.
Представления назначений задач в распределенных системах с использованием таблиц Юнга и симметричных групп
Табло задач, агентов и назначений предлагается для представления назначения задач для секционированных агентов (соответственно задач) в распределенной системе и позволяет повысить выразительность агентов секционирования и их назначения задач.
ПОКАЗАНЫ 1-10 ИЗ 23 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
Эффективный алгоритм аппроксимации для минимизации времени изготовления на однотипно связанных машинах
Chekuri, M. A. Burender,Новый эффективный алгоритм аппроксимации для планирования заданий с ограничением приоритета на машинах с различными скоростями, основанный на новой нижней границе, которая представляет независимый интерес и может быть расширена до получить коэффициент приближения O(logm), даже если задания имеют даты выпуска.
Планирование параллельного процессора с ограничением задержки
В этой работе рассматривается проблема планирования заданий единичной длины на идентичных параллельных машинах таким образом, чтобы время выполнения результирующего расписания было минимальным, и представлялось первое известное полиномиальное время. алгоритм для случая, когда граф ограничения предшествования представляет собой лес внутренних деревьев, число машин m фиксировано, а задержки ограничены константой D.
Динамическое планирование критического пути: эффективный метод распределения графов задач к мультипроцессорам
Алгоритм статического планирования для распределения графов задач по полносвязным мультипроцессорам, который имеет допустимую временную сложность, экономичен по количеству используемых процессоров и подходит для широкого спектра структур графов.
Предварительная оценка метода критического пути для планирования задач в многопроцессорных системах
Показано, что расписания, созданные с помощью простого метода приоритета критического пути, близки к оптимальным для случайно сгенерированных графов вычислений.
Иерархическая распределенная структура планирования для смоделированных объектов поля боя
Описана иерархия различных систем планирования, которая включает в себя более реактивное поведение агентов на более низком уровне иерархии должно руководствоваться более обдуманным планированием со стороны агентов, находящихся над ними в иерархии.
