Методы систем решений уравнений: Решение систем линейных уравнений — как решать СЛАУ методами Гаусса, Крамера, подстановки и почленного сложения

Содержание

9. Методы решения систем уравнений

Задачи инженерной практики зачастую сводятся к необходимости решения не одного уравнения, а систем связанных уравнений. Эти системы уравнений могут быть линейными и нелинейными, с постоянными или с переменными коэффициентами. Решение их возможно точными (аналитическими, символьными) и приближенными (численными) методами. Первые – дают решение в общем виде, что, в силу общности и удобства анализа полученного результата, всегда более предпочтительно. Однако, набор систем уравнений, который может быть решен аналитическими методами, крайне ограничен. Эти методы пригодны лишь для решения систем линейных алгебраических уравнений и, в редких случаях, для решения систем нелинейных уравнений невысокого порядка.

Численные методы позволяют, в принципе, получить решение любых систем уравнений (как линейных, так и нелинейных) с заданной точностью путем организации сходящихся итерационных процессов.

Рассмотрим систему n

линейных алгебраических уравнений относительно неизвестных х₁, х₂, …, х_n:

(9. 1)

Здесь, a_i_,_j – коэффициенты в i—ом уравнении при j—ом неизвестном, b_i –свободные члены.

Система уравнений называется совместной, если она имеет, хотя бы одно решение, при этом совместная система может иметь единственное решение или бесконечное множество решений. В последнем случае систему называют неопределенной.

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме в виде

Ах = b, (9.2)

где введены следующие обозначения:

. (9.3)

Матрица А называется матрицей системы, матрица-столбец b – матрицей (вектором) правой части, а матрица-столбец х, – вектором решения системы.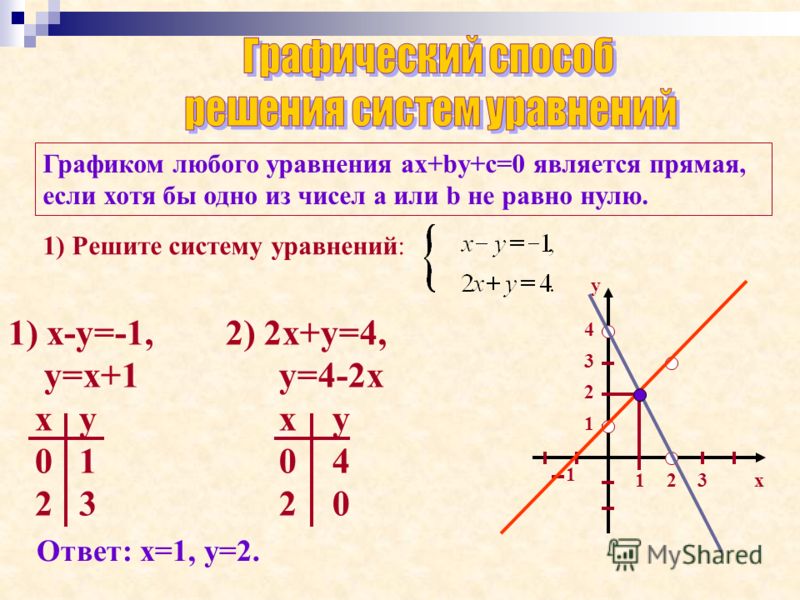 Очевидно, что число строк квадратной матрицы A и вектора b должно совпадать.

Если матрица А является невырожденной (т.е. ее определитель det A  0), то существует обратная матрица А^—¹ и, умножая обе части уравнения (3.3) на неё, получим выражение для решения системы, которое является единственным:

(9.4)

Пакет MathCADпозволяет сформировать обратную матрицу и получить решение (4.4) непосредственно, а также, используя для этой цели встроенную функциюlsolve(A,b).

Альтернативным способом решения системы уравнений является метод исключений Гаусса. Он состоит в том, что систему (9.1) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей:

(4.5)

решение которой может быть найдено по рекуррентным формулам:

(4.6)

В матричной записи метод Гаусса сводится к преобразованию расширенной матрицы эквивалентной системы, которая получена объединением матриц системы и вектора правой части к такому виду, чтобы в первых n столбцах получилась единичная матрица, тогда последний, (n + 1) столбец этой матрицы и будет содержать решение системы (9. 1).

Напомним, что в пакете MathCAD формирование расширенной матрицы С производится с помощью встроенной функции augment (A,b) (число строк у A и b должно совпадать), а процедуру ее преобразования (т.н. прямой и обратный ходы метода Гаусса) выполняет встроенная функция

rref(С). Затем вектор решения можно выделить как последний столбец преобразованной матрицы. Ниже приведен фрагмент документа MathCAD, в котором проиллюстрировано применение различных точных методов решения систем уравнений:

Рис. 9.1. Реализация точных методов решения систем уравнений в пакете MathCAD

Рис. 9.2. Реализация точных методов решения систем уравнений в пакете MathCAD

Как уже отмечалось выше, аналитическая форма решения уравнений представляется более удобной для анализа результатов, поскольку может выразить корни через параметры, входящие в уравнения системы. Поэтому, вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном решении.

Решение в аналитической форме (symbolic) удобно производить внутри блока решений, который, как и ранее, открывается ключевым словом Given. Ниже его в любом порядке печатаются уравнения, причем для ввода знака = используется знак «жирного» равенства [Ctrl]=. Завершает блок функция Find, аргументами которой являются искомые переменные, входящие в состав системы. Для того, чтобы эта функция возвратила аналитическое решение системы уравнений необходимо поместить за ней символьный знак равенства ..

Внутри блока решения выражения недопустимыми является следующие выражения:

ограничения со знаком ;
дискретный аргумент или выражения, содержащие дискретный (ранжированный) аргумент в любой форме;
сложные неравенства вида a < b < c.

Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.

Вместе с тем решение системы уравнений в аналитической форме может быть получено и с помощью рассмотренного ранее матричного метода, в котором следует считать матрицу системы и вектор правой части зависящими от параметров системы уранений.

Пример символьного решения системы уравнений представлен в нижеследующем фрагменте документа MathCAD.

Рис. 9.3. Аналитическое решение системы линейных уравнений

Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными

Главная
Справочники
Справочник по математике 5-9 класс
Алгебра
Системы линейных уравнений с двумя переменными

Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными

Рассмотрим задачу:

Разность двух чисел равна 4, а их произведение 12. Найдите эти числа.

Решение:

Обозначим первое число буквой , а второе буквой . По условию задачи разность чисел равна 4, т.е. — = 4.

Так как произведение чисел равно 12, то = 12.

Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений — = 4 и = 12, т.е. найти общие решения этих уравнений. В таких случаях говорят, что требуется решить систему уравнений.

Систему уравнений записывают с помощью фигурной скобки. Поэтому, составленную нами систему уравнений, можно записать так:

Пара значений переменных = 6, = 2 является решением каждого уравнения системы, т.к. оба равенства 6 — 2 = 4 и 62 = 12 являются верными. Такую пару называют решением системы.

Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение в верное равенство.

Решить систему уравнений — это значит найти все ее решения или убедиться, что их нет.

Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать использовать графики уравнений.

Решим систему уравнений:

Выразив из уравнения переменную через переменную , получим линейную функцию . Построим в координатной плоскости график этой функции.

Для этого составим таблицу значений функции для некоторых значений аргумента .

Отметим на координатной плоскости точки с координатами (1; 0) и (3; 2) и проведем через них прямую, которая является графиком линейной функции .

Выразив из уравнения переменную через переменную (для этого перенесем переменную из левой части уравнения в правую, изменив ее знак, и разделим обе части уравнения на 2), получим линейную функцию . Построим в той же координатной плоскости график этой функции.

Для этого составим таблицу значений функции для некоторых значений аргумента .

Отметим на имеющейся координатной плоскости точки с координатами (1; 3) и (5; 1) и проведем через них прямую, которая является графиком линейной функции .

Мы получили, что прямые, которые соответствуют уравнениям и , пересекаются в точке Р(3; 2), координаты этой точки удовлетворяют как первому уравнению системы, так и второму, т.е. являются

решением системы. Значит, рассматриваемая система имеет единственное решение: = 3, = 2.

Описанный выше метод решения системы уравнений называют графическим.

Суть графического метода решения системы уравнений с двумя переменными:

1) построить на одной координатной плоскости графики уравнений, входящих в систему;

2) найти координаты всех точек пересечения построенных графиков;

3) полученные пары чисел и будут искомыми решениями.

Заметим, что графический способ обычно позволяет находить решения лишь приближенно. Поэтому графический метод эффективен в тех случаях, когда требуется определить количество решений системы.

Определим, сколько решений может иметь система двух линейных уравнений с двумя переменными.

1) Если одно из уравнений системы не имеет решения, то и вся система решений не имеет.

2) Если графиком одного из уравнений системы является вся плоскость, то система имеет бесконечно много решений.

3) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

если прямые пересекаются, то система имеет единственное решение.

Рассмотренная нами выше система

имеет единственное решение = 3, = 2.

если прямые совпадают, то система имеет бесконечно много решений.

Рассмотрим систему

Если умножить обе части первого уравнения этой системы на 3, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:

В полученной системе первое и второе уравнения одинаковые, значит, решения этой системы совпадают с решениями уравнения . Но это уравнение имеет бесконечно много решений, а следовательно, и рассматриваемая система имеет бесконечно много решений.

если прямые параллельны, то система решений не имеет.

Рассмотрим систему

Если умножить обе части первого уравнения этой системы на 5, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:

Очевидно, что не существует такой пары значений и , при которых выражение одновременно принимает значения и 45, и 11. Следовательно, рассматриваемая система не имеет решений.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Уравнения с двумя переменными

Линейное уравнение с двумя переменными и его график

Решение систем линейных уравнений методом подстановки

Решение систем линейных уравнений методом сложения

Решение задач с помощью систем линейных уравнений

Введение в алгебру

Линейное уравнение с одной переменной

Решение задач с помощью уравнений

Тождественно равные выражения. Тождества

Степень с натуральным показателем

Свойства степени с натуральным показателем

Одночлены

Многочлены

Сложение и вычитание многочленов

Умножение одночлена на многочлен

Умножение многочлена на многочлен

Разложение многочленов на множители

Формулы сокращенного умножения

Функции

Системы линейных уравнений с двумя переменными

Алгебра

Правило встречается в следующих упражнениях:

7 класс

Номер 1, Мерзляк, Полонский, Якир, Учебник

Номер 5, Мерзляк, Полонский, Якир, Учебник

Номер 6, Мерзляк, Полонский, Якир, Учебник

Номер 1009, Мерзляк, Полонский, Якир, Учебник

Номер 1010, Мерзляк, Полонский, Якир, Учебник

Номер 1047, Мерзляк, Полонский, Якир, Учебник

Номер 1062, Мерзляк, Полонский, Якир, Учебник

Номер 1080, Мерзляк, Полонский, Якир, Учебник

Номер 1100, Мерзляк, Полонский, Якир, Учебник

Номер 1225, Мерзляк, Полонский, Якир, Учебник

Алгебра — Системы уравнений

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Это довольно короткая глава, посвященная решению систем уравнений. Система уравнений — это набор уравнений, каждое из которых содержит одну или несколько переменных.

Мы сосредоточимся исключительно на системах двух уравнений с двумя неизвестными и трех уравнений с тремя неизвестными, хотя рассмотренные здесь методы можно легко распространить на другие уравнения. Также, за исключением последнего раздела, мы будем иметь дело только с системами линейных уравнений.

Вот список тем в этом разделе.

Линейные системы с двумя переменными. В этом разделе мы будем решать системы с двумя уравнениями и двумя переменными. Мы будем использовать метод подстановки и метод исключения для решения систем в этом разделе. Введем также понятия несовместных систем уравнений и зависимых систем уравнений.

Линейные системы с тремя переменными. В этом разделе мы рассмотрим несколько быстрых примеров, иллюстрирующих, как использовать метод подстановки и метод исключения, представленные в предыдущем разделе, применительно к системам из трех уравнений.

Расширенные матрицы. В этом разделе мы рассмотрим еще один метод решения систем. Введем понятие расширенной матрицы. Это позволит использовать метод исключения Гаусса-Жордана для решения систем уравнений. Мы будем использовать метод с системами двух уравнений и системами трех уравнений.

Подробнее о расширенной матрице. В этом разделе мы еще раз вернемся к случаям противоречивых и зависимых решений систем и к тому, как их идентифицировать с помощью метода расширенной матрицы.

Нелинейные системы. В этом разделе мы кратко рассмотрим решение нелинейных систем уравнений. Нелинейная система уравнений – это система, в которой хотя бы одно из уравнений не является линейным, т.е. имеет степень два и более. Также обратите внимание, что обсуждение здесь не охватывает все возможные методы решения нелинейных систем. Решение нелинейных систем часто является гораздо более сложным процессом, чем решение линейных систем.

Метод исключения (системы линейных уравнений)

Основная концепция метода исключения заключается в создании терминов с противоположными коэффициентами , потому что они компенсируют друг друга при добавлении. В конце концов, мы должны решить простое линейное уравнение, подобное одношаговому уравнению относительно x или y.

Я могу обобщить «большие» идеи о методе исключения при решении систем линейных уравнений, используя иллюстрации ниже. Здесь я представляю два идеальных случая, которых я хочу достичь в процессе решения. Взгляните на них, и, надеюсь, это имеет смысл. В противном случае перейдите непосредственно к шести (6) проработанным примерам, чтобы увидеть, как решаются реальные проблемы.

Случай 1 : При сложении двух уравнений переменная «x» исключается

Коэффициенты переменной x противоположны.

Случай 2 : Путем сложения двух уравнений переменная «y» исключается

Коэффициенты переменной y противоположны.

Примеры решения систем линейных уравнений методом исключения

Пример 1: Решить систему линейных уравнений методом исключения.

Я заметил, что добавление столбца x не удалит переменную x. Однако, если я добавлю столбец y, переменная y исчезнет. Это происходит потому, что коэффициенты при y противоположны друг другу по знаку. Теперь я продолжу второй вариант.

После этого я прихожу к простому уравнению.

Я делю обе части на коэффициент при x, что дает ответ x = 4.

Следующим шагом является нахождение соответствующего значения y. Это легко найти, так как я уже знаю, что такое x. Я выберу любое из двух исходных уравнений, в данном случае я выбрал верхнее уравнение. Затем я подставлю значение x = 4, чтобы получить y. Процесс или процедура решения для y должны быть аналогичны ниже.

Здесь я получаю y = — \,4. Окончательный ответ в точечной нотации показан ниже.

Графически решение выглядит так.

Пример 2: Решить систему линейных уравнений методом исключения.

Это очень интересно, потому что никакие переменные не отменяются при добавлении. Я хочу ввести множитель в одно из уравнений или в оба, а затем посмотреть, получу ли я некоторые коэффициенты, которые отличаются только знаками.

Есть несколько способов сделать это. Однако, глядя на столбец x, я могу легко превратить -3 в -12, умножив первое уравнение на +4. Теперь я могу продолжить добавление столбца x.

Умножение всего уравнения на любое ненулевое число не меняет его исходного значения. Что изменится, так это только его форма. Я называю этот процесс, уравнение «пересмотром» или «модификацией».

Это одношаговое уравнение, поэтому я решаю y, разделив обе части на коэффициент.

Отлично! Я получил значение y = 2. Далее я решу x с помощью обратной подстановки, используя любое из исходных уравнений. Для этого я буду использовать первое уравнение, потому что оно менее сложное.

Я получил значение x = — 1. Теперь я могу записать окончательный ответ в виде приведенной ниже упорядоченной пары.

График ниже подтверждает правильность нашего решения.

Пример 3: Для решения используйте метод исключения или линейной комбинации.

В этой задаче есть некоторая хитрость, потому что коэффициенты переменных x абсолютно одинаковы, и — 2. Единственное, что мне нужно здесь исправить, это сделать один из них положительным. Теперь я решил умножить верхнее уравнение на −1. Оно также должно работать, если я умножу нижнее уравнение на −1,9.0003

Вы должны увидеть, что план работает, так как добавление результатов столбца x к отмене x.

Я вычислил значение y, разделив обе части на −17, в результате чего y = 3. На этот раз я решу значение x с помощью нижнего уравнения, потому что знаю, что такое y.

После нескольких шагов решения приведенного выше уравнения я прихожу к x = 2. Окончательный ответ в виде упорядоченной пары показан ниже.

Действительно, две линии пересекаются в точке, которую мы нашли в наших расчетах.

Пример 4: Для решения используйте метод исключения или линейной комбинации.

Этот пример повторяет пример 3, где у нас точно такие же коэффициенты. Я вижу, что обе переменные y имеют коэффициенты, равные 8. Поэтому мне нужно будет немного изменить их, чтобы сделать их знаки противоположными. Теперь у меня есть два варианта дальнейших действий. Я могу умножить верхнее уравнение на -1 или нижнее уравнение на -1. Для этого упражнения я выбираю последнее.

Применение множителя − 1 к нижнему уравнению и сложение их вместе приводит к исчезновению y.

Решите полученное из него простое уравнение.

Я получил x = 4, разделив обе части на −9. Следующий очевидный шаг — найти другую переменную y с помощью обратной подстановки. Выберите любое из исходных уравнений, подставьте x = 4, и вы мгновенно получите y.

Ответ: y = — \,1. Окончательный ответ в виде упорядоченной пары показан ниже.

Графическое решение выглядит следующим образом.

Пример 5: Для решения используйте метод исключения или линейной комбинации.

В задаче такого типа требуется одновременное умножение верхнего и нижнего уравнения на некоторое число, чтобы получить коэффициенты с противоположными знаками.

Если я решу исключить x, я могу умножить верхнее уравнение на — 2, а нижнее на 9. Таким образом, я должен получить x членов, 18x и -18x соответственно, которые сокращаются при сложении.

В этом упражнении я хочу исключить y. Поэтому я умножу верхнюю часть на 5, а нижнюю на 3.

Как и было предсказано, я смог избавиться от y, что оставляет нам простое уравнение.

Вы должны получить x = 1.