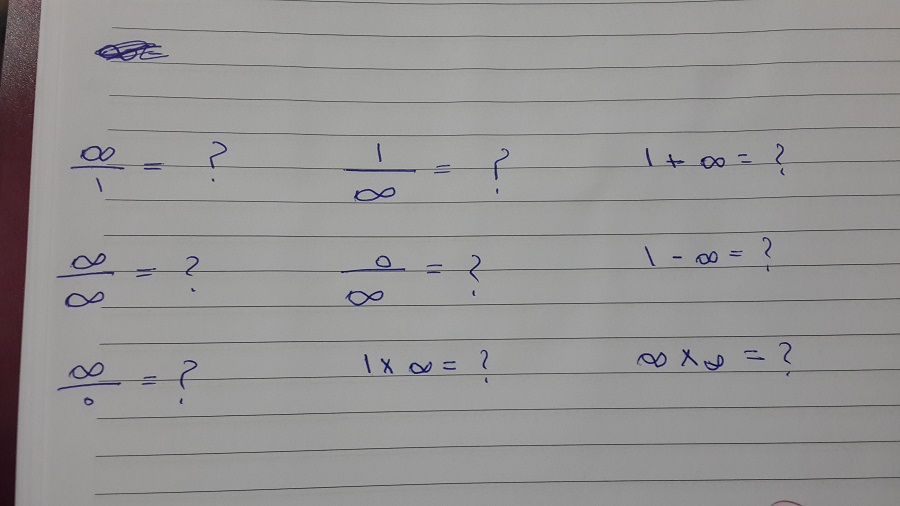0 бесконечность
Вы искали 0 бесконечность? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 0 в степени 0 неопределенность, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «0 бесконечность».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 0 бесконечность,0 в степени 0 неопределенность,0 в степени бесконечность,0 в степени бесконечность неопределенность,0 делить на 0 предел,0 делить на бесконечность,0 делить на бесконечность равно,0 на 0 бесконечность на бесконечность,0 на 0 предел,0 на 0 равно бесконечность,0 на бесконечность делить,0 на бесконечность делить на,0 на бесконечность умножить на бесконечность,0 разделить на бесконечность,0 умножить на бесконечность,1 умножить на бесконечность,бесконечность 0,бесконечность в 0 степени,бесконечность в нулевой степени,бесконечность в степени,бесконечность в степени 0,бесконечность в степени бесконечность пределы,бесконечность в степени бесконечность раскрытие неопределенности,бесконечность в степени минус бесконечность равно,бесконечность в степени ноль,бесконечность деленная на бесконечность равно,бесконечность делить на 0,бесконечность делить на 0 равно,бесконечность делить на бесконечность минус бесконечность,бесконечность делить на бесконечность предел,бесконечность делить на бесконечность равно,бесконечность делить на бесконечность равно бесконечность,бесконечность делить на минус бесконечность равно,бесконечность делить на ноль,бесконечность делить на ноль равно бесконечность,бесконечность минус бесконечность делить на бесконечность,бесконечность минус бесконечность неопределенность,бесконечность на бесконечность неопределенность,бесконечность на бесконечность предел,бесконечность на бесконечность равно,бесконечность на ноль,бесконечность на ноль неопределенность,бесконечность на ноль предел,бесконечность на ноль равно бесконечность,бесконечность равно 0,бесконечность разделить на 0,бесконечность разделить на бесконечность равно,бесконечность разделить на ноль,бесконечность умножить на 0,бесконечность умножить на 1,бесконечность умножить на бесконечность равно,бесконечность умножить на ноль,деление бесконечность на бесконечность,делить на 0 бесконечность,делить на 0 равно бесконечность,как раскрыть неопределенность бесконечность в степени бесконечность,минус бесконечность делить на бесконечность,минус бесконечность делить на бесконечность равно,неопределенность 0 в степени 0,неопределенность 0 в степени бесконечность,неопределенность 0 на 0,неопределенность 0 на бесконечность,неопределенность 1 в степени бесконечность как раскрыть,неопределенность бесконечность в степени 0,неопределенность бесконечность в степени бесконечность,неопределенность бесконечность на 0,неопределенность бесконечность на бесконечность,неопределенность бесконечность на ноль,неопределенность бесконечность умножить на бесконечность,неопределенность бесконечность умножить на ноль,неопределенность вида,неопределенность вида бесконечность в степени бесконечность,неопределенность вида бесконечность минус бесконечность,неопределенность вида бесконечность на бесконечность,неопределенность вида бесконечность умножить на бесконечность,неопределенность ноль на бесконечность,неопределенность ноль на ноль,неопределенность ноль умножить на бесконечность,неопределенность ноль умножить на ноль,ноль в степени бесконечность,ноль делить на бесконечность равно,ноль делить на ноль предел,ноль на бесконечность,ноль на бесконечность неопределенность,ноль на бесконечность предел,ноль на бесконечность умножить на бесконечность,ноль на ноль предел,ноль на ноль пределы,ноль на ноль равно бесконечность,ноль разделить на бесконечность,предел 0 делить на 0,предел 0 на 0,предел бесконечность в степени бесконечность,предел бесконечность делить на бесконечность,предел бесконечность на бесконечность,предел бесконечность на ноль,предел неопределенность бесконечность на бесконечность,предел ноль делить на ноль,предел ноль на бесконечность,предел ноль на ноль,пределы бесконечность в степени бесконечность,пределы бесконечность на бесконечность,пределы ноль на ноль,разделить бесконечность на ноль,раскрытие неопределенностей вида бесконечность на бесконечность,раскрытие неопределенности 1 в степени бесконечность,раскрытие неопределенности бесконечность в степени бесконечность,раскрытие неопределенности бесконечность на бесконечность,таблица неопределенностей,число в степени бесконечность равно,что будет если бесконечность разделить на бесконечность.
Решить задачу 0 бесконечность вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Раскрытие неопределенностей при вычислении пределов
С данной статьи начинаем цепочку публикаций, которые научат Вас находить особенности в границах, классифицировать неопределенности и применять правильную методику раскрытия. Дело заключается в том, что разработано много правил и приемов, которые позволяют по виду заданной функции или последовательности быстро сориентироваться как находить предел.
Однако при изучении теоретического материала или на практических занятиях Вам или на этом не отмечают, или Ваши мысли гуляют за пределами аудитории.
Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.
Пример 1. Вычислить предел последовательности:
Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее. В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности
Все числа, что останутся и укажут куда стремится предел.
Пример 2. Вычислить предел последовательности:
Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.
Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись
Пример 3. Найти предел функции:
Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение .
В результате получим множитель (x-3), на который упрощаем дробь.
Далее предел вычисляется методом подстановки переменной
Пример 4. Найти предел функции:
Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.
Внимательно разберите приведенный пример, он Вас многому научит.
На практике довольно трудно найти условие, которое бы объединяла несколько формул, поэтому учитесь на сложных примерах.
Тогда точно не будет сложностей в исчислении простых примеров.
Пример 5. Вычислить предел функции:
Решение: Подстановка 3 в функцию дает особенность вида единица в степени бесконечность (1^∞).
Для ее раскрытия и в функции в скобках, и в дроби, что является показателем выделяем часть, что вносит особенность (х-3).
Далее, для упрощения манипуляций с выражениями делаем замену переменных x-3=t, новая переменная при этом стремится к нулю.
После этого выделяем второй замечательный предел и ищем лимит показателя, что остался.
На этом разбор распространенных примеров, которые распространены в учебной практике не завершается.
В соседней публикации будут проанализированы новые алгоритмы вычислений, и примеры пределов функций та последовательностей, которые помогут Вам быстрее освоить теоретический материал и подготовиться к контрольной, модулю, экзамене.
Исчисление I — Типы бесконечности
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Приложение A.7: Типы бесконечности
Большинство учащихся сталкивались с бесконечностью в какой-то момент времени перед уроком математического анализа. Однако, когда они имели дело с этим, это был просто символ, используемый для представления очень, очень большого положительного или очень, очень большого отрицательного числа, и это было его пределом. Как только они попадают в класс исчисления, студентов просят выполнить базовую алгебру с бесконечностью, и здесь у них возникают проблемы. Бесконечность НЕ является числом и по большей части не ведет себя как число. Однако, несмотря на это, в этом разделе мы будем думать о бесконечности как о очень, очень, очень большом числе, которое настолько велико, что нет другого числа, большего, чем оно.
Итак, начнем думать о сложении с бесконечностью. Когда вы добавляете два ненулевых числа, вы получаете новое число. Например, \(4 + 7 = 11\). С бесконечностью это не так. С бесконечностью у вас есть следующее.
\[\begin{align*}\infty + a & = \infty \hspace{0,25 дюйма}{\mbox{где }}a \ne — \infty \\ \infty + \infty & = \infty \end{align *}\]
Другими словами, очень-очень большое положительное число (\(\infty \)) плюс любое положительное число, независимо от размера, все равно будет очень-очень большим положительным числом. Точно так же вы можете добавить отрицательное число ( , т. е. \(a < 0\)) в очень, очень большое положительное число и останется очень, очень большим и положительным.
Таким образом, сложением, включающим бесконечность, можно заниматься интуитивно, если вы будете осторожны. Также обратите внимание, что \(a\) НЕ должно быть отрицательной бесконечностью. Если это так, есть некоторые серьезные проблемы, с которыми нам нужно разобраться, как мы вскоре увидим.
Вычитание с отрицательной бесконечностью в большинстве случаев также может быть реализовано интуитивно. Очень, очень большое отрицательное число за вычетом любого положительного числа, независимо от его размера, все равно будет очень, очень большим отрицательным числом. Вычитание отрицательного числа ( , т. е. \(a < 0\)) из действительно очень большого отрицательного числа все равно будет очень, очень большим отрицательным числом. Или
\[\begin{align*} — \infty — a & = — \infty \hspace{0.25in}{\mbox{где}}a \ne — \infty \\ — \infty — \infty & = — \infty \конец{выравнивание*}\]
Опять же, \(a\) не должно быть отрицательной бесконечностью, чтобы избежать некоторых потенциально серьезных трудностей.
С умножением также можно справиться довольно интуитивно. Очень, очень большое число (положительное или отрицательное), умноженное на любое число, независимо от размера, все равно будет очень, очень большим числом, нам просто нужно быть осторожным со знаками. В случае умножения имеем
\[\begin{array}{c}\left( a \right)\left( \infty \right) = \infty \hspace{0,25 дюйма}{\mbox{if}}a > 0\hspace{0,75 дюйма} \left( a \right)\left( \infty \right) = — \infty \hspace{0.25in}{\mbox{if}}a < 0\\ \\ \left( \infty \right)\left( \infty \right) = \infty \hspace{0.5in}\left( { - \infty } \right)\left( { - \infty } \right) = \infty \hspace{0.75in}\left( { - \infty } \right)\left( \infty \right) = - \infty \end{массив}\]
То, что вы знаете о произведениях положительных и отрицательных чисел, верно и здесь.
С некоторыми формами деления можно работать и интуитивно. Действительно, очень большое число, деленное на не слишком большое число, все равно остается очень, очень большим числом.
\[\begin{align*}\frac{\infty}{a} & = \infty & \hspace{0,25in} & {\mbox{if}}a > 0,a \ne \infty & \hspace{0,75 in}\frac{\infty} {a} & = — \infty & \hspace{0,25in}{\mbox{if}}a < 0,a \ne - \infty \\ \frac{{ - \infty} }{a} & = - \infty & \hspace{0,25in} & {\mbox{ if }}a > 0,a \ne \infty & \hspace{0,75in}\frac{{ — \infty}}{ a} & = \infty & \hspace{0,25in}{\mbox{, если }}a < 0,a \ne - \infty \end{align*}\]
Деление числа на бесконечность несколько интуитивно понятно, но есть пара тонкостей, о которых нужно знать. Когда мы говорим о делении на бесконечность, мы на самом деле говорим об ограничивающем процессе, в котором знаменатель стремится к бесконечности. Таким образом, число, которое не слишком велико, деленное на все большее число, является все более малым числом. Другими словами, в нашем пределе
\[\frac{a}{\infty} = 0\hspace{0,5 дюйма}\hspace{0,5 дюйма}\hspace{0,25 дюйма}\frac{a}{{ — \infty}} = 0\]
Итак, мы рассмотрели почти все основные алгебраические операции с бесконечностью.
Есть два случая, которые мы еще не рассмотрели. Это
\[\infty — \infty = {\mbox{?}}\hspace{0,5 дюйма}\hspace{0,5 дюйма}\frac{{ \pm \,\infty}}{{ \pm \,\infty}} = ?\]
Проблема этих двух случаев в том, что интуиция здесь не особо помогает. Очень, очень большое число минус очень, очень большое число может быть чем угодно (\( — \infty \), константой или \(\infty \)). Точно так же очень, очень большое число, деленное на очень, очень большое число, также может быть чем угодно (\( \pm \infty \) — это зависит от проблем со знаком, 0 или ненулевой константы).
Здесь мы должны помнить, что есть очень, очень большие числа и есть очень, очень, очень большие числа. Другими словами, одни бесконечности больше других бесконечностей. Со сложением, умножением и первым набором деления, с которым мы работали, это не было проблемой. Общий размер бесконечности просто не влияет на ответ в этих случаях. Однако в случаях вычитания и деления, перечисленных выше, это имеет значение, как мы увидим.
Вот один из способов понять идею о том, что одни бесконечности больше других. Это довольно сухой и технический способ думать об этом, и ваши задачи по исчислению, вероятно, никогда не будут использовать этот материал, но это хороший способ взглянуть на это. Кроме того, обратите внимание, что я не пытаюсь дать здесь точное доказательство чего-либо. Я просто пытаюсь дать вам небольшое представление о проблемах с бесконечностью и о том, как некоторые бесконечности можно считать большими, чем другие. Более подробное (и определенно более точное) обсуждение см. в 9.0003
http://www.math.vanderbilt.edu/~schectex/courses/infinity.pdf
Начнем с того, сколько существует целых чисел. Ясно, надеюсь, что их бесконечное множество, но давайте попробуем лучше понять «размер» этой бесконечности. Итак, выберите любые два целых числа совершенно случайным образом. Начните с меньшего из двух и перечислите в порядке возрастания все целые числа, которые следуют за ним. В конце концов мы достигнем большего из двух целых чисел, которые вы выбрали.
В зависимости от относительного размера двух целых чисел перечисление всех целых чисел между ними может занять очень и очень много времени, и в действительности это не имеет смысла. Но это можно было бы сделать, если бы мы захотели, и это важная часть.
Поскольку мы могли бы перечислить все эти целые числа между двумя случайно выбранными целыми числами, мы говорим, что целые числа счетно бесконечны . Опять же, нет никакой реальной причины делать это, это просто то, что можно сделать, если мы захотим это сделать.
В общем случае набор чисел называется счетно бесконечным, если мы можем найти способ перечислить их все. В более точной математической постановке это обычно делается с помощью функции особого типа, называемой биекцией, которая связывает каждое число в наборе ровно с одним из положительных целых чисел. Чтобы увидеть более подробную информацию об этом, см. PDF-файл, приведенный выше.
Можно также показать, что множество всех дробей также счетно бесконечно, хотя это немного сложнее показать, и это не является целью данного обсуждения.
Чтобы увидеть доказательство этого, см. pdf, приведенный выше. У него есть очень хорошее доказательство этого факта.
Давайте сравним это, попытавшись выяснить, сколько чисел содержится в интервале \( \left(0,1\right) \). Под числами я подразумеваю все возможные дроби, которые лежат между нулем и единицей, а также все возможные десятичные дроби (которые не являются дробями), которые лежат между нулем и единицей. Следующее похоже на доказательство, приведенное в pdf выше, но оно было достаточно хорошим и достаточно простым (надеюсь), поэтому я хотел включить его сюда.
Для начала предположим, что все числа в интервале \( \left(0,1\right) \) счетно бесконечны. Это означает, что должен быть способ перечислить их все. У нас может быть что-то вроде следующего:
\[\begin{align*}{x_1} & = 0,692096 \cdots \\ {x_2} & = 0,171034 \cdots \\ {x_3} & = 0,993671 \cdots \\ {x_4} & = 0,045908 \cdots \\ \vdots \,\, & \hspace{0,6 дюйма} \vdots \end{align*}\]
Теперь выберите \(i\) -й десятичный из \({x_i}\), как показано ниже
\[\begin{align*}{x_1} & = 0.
\underline 6 92096 \cdots \\ {x_2} & = 0.1\underline 7 1034 \cdots \\ {x_3} & = 0.99\underline 3 671 \cdots \ \ {x_4} & = 0.045\underline 9 08 \cdots \\ \vdots \,\, & \hspace{0.6in} \vdots \end{align*}\]
и сформируйте из этих цифр новый номер. Итак, для нашего примера у нас будет число
. \[х = 0,6739\cdots\]
В этом новом десятичном числе замените все тройки на 1 и замените все остальные числа на 3. В нашем примере это даст новое число
\[\overline x = 0,3313 \cdots \]
Обратите внимание, что это число находится в интервале \( \left(0,1\right) \), а также обратите внимание, что, учитывая то, как мы выбираем цифры числа, это число не будет равно первому числу в нашем списке, \({x_1}\), потому что первая цифра каждого из них гарантированно не будет одинаковой. Точно так же это новое число не будет совпадать со вторым в нашем списке, \({x_2}\), потому что вторая цифра каждого из них гарантированно не будет одинаковой.
Продолжая в том же духе, мы можем видеть, что это новое число, которое мы построили, \(\overline x \), гарантированно не будет в нашем списке. Но это противоречит первоначальному предположению, что мы можем перечислить все числа в интервале \( \left(0,1\right) \). Следовательно, не должно быть возможности перечислить все
числа в интервале \( \left(0,1\right) \).
Наборы чисел, такие как все числа в \( \left(0,1\right) \), которые мы не можем записать в список, называются неисчислимо бесконечными.
Причина перехода в следующем. Бесконечность, неисчислимо бесконечная, значительно больше, чем бесконечность, которая только счетно бесконечна. Итак, если мы возьмем разницу в две бесконечности, у нас будет пара возможностей.
\[\begin{align*}\infty \left( {{\mbox{uncountable}}} \right) — \infty \left( {{\mbox{countable}}} \right) & = \infty \\ & \\ \infty \left( {{\mbox{countable}}} \right) — \infty \left( {{\mbox{uncountable}}} \right) & = — \infty \end{align*}\]
Обратите внимание, что мы не записали разность двух бесконечностей одного типа.
В зависимости от контекста все еще может быть некоторая двусмысленность в отношении того, каким будет ответ в этом случае, но это совершенно другая тема.
Мы могли бы сделать что-то подобное и для частных бесконечностей.
\[\ begin{align*}\frac{{\infty \left({{\mbox{countable}}} \right)}}{{\infty \left({{\mbox{uncountable}}} \right) }} & = 0\\ & \\ \frac{{\infty \left( {\mbox{uncountable}}} \right)}}{{\infty \left({{\mbox{countable}}} \ справа)}} & = \infty \end{align*}\]
Опять же, мы избегали отношения двух бесконечностей одного и того же типа, поскольку, опять же, в зависимости от контекста, его значение может быть неоднозначным.
Итак, это все, надеюсь, вы узнали что-то новое из этого обсуждения. Бесконечность просто не является числом, и, поскольку существуют разные виды бесконечности, обычно она ведет себя не так, как число. Будьте осторожны, имея дело с бесконечностью.
Как считать до бесконечности
Нет самого большого, последнего числа… кроме бесконечности.
Только бесконечность не число. Но некоторые бесконечности буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Эй, Всоус! Майкл здесь.
Какое самое большое число вы можете придумать? Гугол? Гуголплекс? Миллион-миллион-оплекс? Ну, на самом деле, самое большое число — 40.
Покрывая более 12 000 квадратных метров земли, эти 40, сделанные из стратегически посаженных деревьев в России, больше, чем маркеры батальонов на Сигнальном холме в Калгари, 6, найденные на значки Фованта в Англии — даже миля числа пи, которую Брейди развернул на Numberphile. 40 — это самое большое число … на Земле с точки зрения площади поверхности.
Но с точки зрения количества вещей, которое мы обычно подразумеваем под «большим» числом, 40, вероятно, не самое большое число. Например, есть 41. О, а еще есть 42, и 43 … миллиард, триллион; знаете, какое бы большое число вы ни придумали, вы всегда можете подняться выше.
Значит, нет самого большого, последнего числа… кроме бесконечности? Нет.
Бесконечность — это не число. Вместо этого это своего рода число. Вам нужны бесконечные числа, чтобы говорить о бесконечных количествах и сравнивать их, но некоторые бесконечные количества — некоторые бесконечности — буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Обо всем по порядку. Когда число указывает на количество вещей, оно называется «кардинальным числом». Например, 4 банана. 12 флагов. 20 точек. 20 — это «мощность» этого набора точек. Теперь два набора имеют одинаковую мощность, когда они содержат одинаковое количество вещей. Мы можем продемонстрировать это равенство, сопоставив каждый член одного набора один к одному с каждым членом другого. Та же кардинальность, довольно просто.
Мы используем натуральные числа — то есть 0, 1, 2, 3, 4, 5 и т. д. — как количественные значения всякий раз, когда говорим о том, сколько существует вещей, но сколько существует натуральных чисел? Это не может быть какое-то число в натуральных числах, потому что после него всегда будет 1 плюс это число.
Вместо этого у этой суммы есть уникальное название: «алеф-нуль» (ℵ 0 ). Алеф — первая буква еврейского алфавита, а алеф-нуль — первая наименьшая бесконечность. Это количество натуральных чисел. Это также сколько четных чисел, сколько нечетных чисел; это также то, сколько существует рациональных чисел, то есть дробей. Это может показаться удивительным, поскольку на числовой прямой дроби кажутся более многочисленными, но, как показал Кантор, существует способ упорядочить каждое возможное рациональное число так, чтобы натуральные числа можно было поставить в соответствие с ними один к одному. Они имеют одинаковую мощность.
Дело в том, что алеф-нуль — это большое количество; больше любой конечной суммы. Гугол, гуголплекс, гуголплекс факториал в степени гуголплекса в гуголплекс, умноженный на число Грэма в квадрате? Алеф-нуль больше. Но мы можем считать мимо него. Как? Что ж, давайте воспользуемся нашим старым другом — сверхзадачей. Если мы нарисуем кучу линий и сделаем каждую следующую линию частью размера и части расстояния от каждой последней линии, то мы сможем уместить бесконечное количество линий в конечное пространство.
Количество строк здесь равно количеству имеющихся натуральных чисел. Эти два могут быть сопоставлены один к одному. Всегда есть следующий естественный, но всегда есть и следующая строка. Оба набора имеют кардинальность алеф-нуль.
Но что произойдет, если я это сделаю? Теперь, сколько линий есть? Алеф-нулевой плюс один? Нет. Бесконечные суммы не похожи на конечные суммы. Здесь по-прежнему только строки с нулевыми алефами, потому что я могу сопоставлять натуральные числа один к одному, как и раньше. Я просто начинаю здесь, а затем продолжаю с самого начала. Понятно, что количество строк не изменилось. Я даже могу добавить еще две строки, еще три, еще четыре — всегда получаю только нулевые алефы. Я могу даже добавить еще один бесконечный алеф-нуль строк и все равно не изменить количество. Каждое четное число может сочетаться с этими и каждое нечетное число с этими. На каждого натурала еще очередь.
Еще один классный способ увидеть, что эти линии не складываются в общую сумму, — показать, что вы можете составить ту же самую последовательность, вообще не рисуя новые линии.
Просто возьмите каждую вторую строку и переместите их все вместе в конец. Это то же самое.
Но подождите секунду. В этом и в этом может быть одинаковое количество вещей, но в них явно есть что-то другое, верно? Я имею в виду, если не из скольких вещей они сделаны, то из чего? Что ж, давайте вернемся к тому, чтобы иметь только одну строку после коллекции размером с нулевой алеф. Что, если вместо того, чтобы сопоставлять натуральные числа один к одному, мы настаиваем на нумерации каждой строки в соответствии с порядком, в котором она была нарисована? Итак, мы должны начать здесь и нумеровать слева направо. Теперь, какой номер получает эта строка? В царстве бесконечности маркировка вещей по порядку — это совсем другое, чем их подсчет. Видите ли, эта строка не участвует в сумме, но для того, чтобы пометить ее в соответствии с порядком, в котором она появилась, нам нужен набор меток чисел, выходящий за пределы натуральных чисел. Нам нужны порядковые номера.
Первый трансфинитный порядковый номер — это омега (ω), строчная греческая буква омега.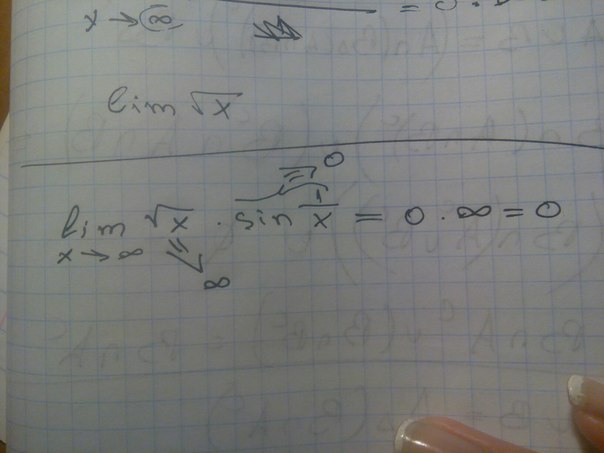
Это не шутка и не уловка, это буквально просто следующая метка, которая вам понадобится после того, как вы сначала израсходуете бесконечную коллекцию каждого отдельного числа. Если бы вы заняли ω-е место в гонке, это означало бы, что гонку финишировало бесконечное количество людей, и тогда это сделали вы. После ω следует ω+1, которое на самом деле не похоже на число, но так оно и есть, точно так же, как 2, 12 или 800. Затем идут ω+2, ω+3… порядковые номера обозначают вещи по порядку. Порядковые числа — это не количество вещей, а то, как они устроены — тип их порядка.
Тип порядка набора — это просто первый порядковый номер, который не требуется для маркировки всего набора по порядку. Таким образом, для конечных чисел мощность и тип порядка одинаковы. Тип порядка всех натуральных чисел — ω. Тип порядка этой последовательности — ω+1, а теперь — ω+2. Какой бы длинной ни была аранжировка, пока она хорошо упорядочена, пока каждая ее часть содержит начальный элемент, все это описывает новый порядковый номер.
Всегда. Это будет очень важно в дальнейшем.
Здесь следует отметить, что если вы когда-либо играли в игру, в которой вы можете назвать наибольшее число, и вы думаете о том, чтобы сказать «омега плюс один», вам следует быть осторожным. Ваши оппоненты могут потребовать, чтобы число, которое вы называете, было кардиналом, обозначающим сумму. Эти числа относятся к одному и тому же количеству вещей, просто расположенных по-разному. ω+1 не больше, чем ω, оно просто идет после ω.
Но алеф-нуль — это не конец. Почему? Ну, потому что можно показать, что существуют бесконечности больше алеф-нуль, которые буквально содержат больше вещей. Один из лучших способов сделать это — использовать диагональный аргумент Кантора. В моем эпизоде о парадоксе Банаха-Тарского я использовал его, чтобы показать, что количество действительных чисел больше, чем количество натуральных чисел. Но для целей этого видео давайте сосредоточимся на другом, более важном, чем алеф-нуль: наборе мощности алеф-нуль.
Силовой набор набора — это набор всех различных подмножеств, которые вы можете из него составить. Например, из набора 1 и 2 я могу составить набор из ничего, или 1, или 2, или 1 и 2. Степенной набор 1,2,3: пустой набор, 1 и 2, и 3, и 1 и 2, и 1 и 3, и 2 и 3, и 1,2,3. Как видите, набор мощности содержит гораздо больше элементов, чем исходный набор. Если быть точным, два в той степени, в какой сколько членов было в исходном наборе. Итак, какова мощность всего природного?
Что ж, посмотрим. Представьте себе список всех натуральных чисел. Прохладный. Теперь подмножество всех, скажем, четных чисел будет выглядеть так: да, нет, да, нет, да, нет и так далее. Подмножество всех нечетных чисел будет выглядеть так. Вот подмножество только 3, 7 и 12. А как насчет всех чисел, кроме 5. Или ни одного числа, кроме 5. Очевидно, что этот список подмножеств будет, ну, бесконечным. Но представьте, что все они сопоставляются один к одному с натуральным. Если даже в этом случае есть способ продолжать создавать новые подмножества, которые явно нигде здесь не перечислены, мы будем знать, что у нас есть множество, в котором членов больше, чем натуральных чисел — бесконечность больше, чем алеф-нуль.
Чтобы сделать это, нужно начать здесь, в первом подмножестве, и просто сделать противоположное тому, что мы видим. 0 является членом этого, поэтому наш новый набор не будет содержать 0. Затем двигайтесь по диагонали вниз к членству 1 во втором подмножестве. 1 является его членом, поэтому его не будет в нашем новом. 2 не находится в третьем подмножестве, поэтому оно будет в нашем, и так далее. Как видите, мы описываем подмножество, которое по определению будет отличаться по крайней мере одним способом от любого другого подмножества в этом нулевом списке. Даже если мы вернем это новое подмножество, диагонализация все еще может быть выполнена.
Силовой набор натуралов всегда будет сопротивляться прямому соответствию с натуралами. Это бесконечно больше, чем алеф-нуль. Многократное применение набора мощности приведет к созданию наборов, которые нельзя привести во взаимно-однозначное соответствие с последними, так что это отличный способ быстро создавать все большие и большие бесконечности.
Дело в том, что кардиналов больше после нулевого алеф. Попробуем добраться до них.
Теперь вспомните, что после ω ординалы разделяются, и эти числа больше не являются количественными. Они не относятся к большему количеству, чем последний кардинал, которого мы достигли, но, возможно, они могут привести нас к одному из них. Подождите … что мы делаем? Алеф-нулевой? Омега? Да ладно, мы использовали эти числа, как будто в этом нет никакой проблемы, но если в любой момент здесь внизу вы всегда можете добавить один — всегда — можем ли мы действительно говорить об этом, об этом бесконечном процессе, как о совокупности, а затем проследить за ним с помощью что-нибудь?
Конечно можем. Это математика, а не наука! Вещи, которые мы считаем истинными в математике, называются аксиомами, и вероятность того, что аксиома, которую мы придумываем, верна, не выше, если она лучше объясняет или предсказывает то, что мы наблюдаем. Наоборот, это правда, потому что мы так говорим. Его последствия просто становятся тем, что мы наблюдаем.
Мы не приспосабливаем наши теории к какой-то физической вселенной, чье поведение и основные законы были бы одинаковыми, были бы мы здесь или нет; мы сами создаем эту вселенную. Если аксиомы, которые мы провозглашаем истинными, приводят нас к противоречиям или парадоксам, мы можем вернуться и изменить их или просто отказаться от них, или мы можем просто отказаться позволять себе делать то, что вызывает парадоксы. Вот и все. Удивительно, однако, что, следя за тем, чтобы принимаемые нами аксиомы не приводили к проблемам, мы превратили математику в нечто, что, как говорится, «необоснованно эффективно в естественных науках». Так что в какой степени мы все это изобретаем или открываем — трудно сказать. Все, что нам нужно сделать, чтобы получить ω, это сказать «да будет омега», и все будет хорошо.
Это то, что сделал Эрнест Цермело в 1908 году, когда он включил аксиому бесконечности в свой список аксиом для работы в математике. Аксиома бесконечности — это просто заявление о том, что существует одно бесконечное множество — множество всех натуральных чисел.
Если вы отказываетесь принять это, ничего страшного — это делает вас финитистом, тем, кто верит, что существуют только конечные вещи. Но если вы примете это, как это делает большинство математиков, вы сможете продвинуться довольно далеко — мимо этого и через это… в конце концов мы придем к ω+ω, за исключением того, что мы достигли еще одного потолка. Пройти весь путь до ω + ω означало бы создать еще одно бесконечное множество, а аксиома бесконечности гарантирует только то, что это существует.
Придется ли нам добавлять новую аксиому каждый раз, когда мы описываем алеф-нуль-больше чисел? Нет. Здесь нам может помочь Аксиома Замещения. Это предположение гласит, что если вы возьмете набор — например, набор всех натуральных чисел — и замените каждый элемент чем-то другим — например, бананами, — то, что у вас останется, тоже будет набором. Звучит просто, но невероятно полезно. Попробуйте так: возьмите каждый порядковый номер до ω, а затем вместо бананов поставьте перед каждым «ω+». Теперь мы достигли ω+ω, или ω×2.
Используя замену, мы можем делать прыжки любого размера, какого захотим, если мы используем только те числа, которые уже достигли. Мы можем заменить каждый порядковый номер вплоть до ω на омега-кратное число, чтобы получить ω×ω , ω 2 . Мы сейчас готовим! Аксиома замены позволяет бесконечно конструировать новые ординалы. В конце концов мы добираемся до ω до ω до ω до ω до ω… и у нас заканчиваются стандартные математические обозначения. Без проблем! Это просто называется «эпсилон-ноль» (ε 0 ), и мы продолжим отсюда.
А теперь подумайте обо всех этих ординалах. Все разные способы упорядочить алеф-нулевые вещи. Ну, они хорошо упорядочены, поэтому у них есть тип порядка — некоторый порядковый номер, который идет после всех них. В данном случае этот порядковый номер называется «омега-один» (ω1). Теперь, поскольку по определению ω 1 следует после каждого отдельного типа заказа или вещей с нулевым алефом, он должен описывать расположение буквально большего количества вещей, чем последний алеф.
Я имею в виду, что если бы это было не так, то оно было бы где-то здесь, но это не так. Кардинальное число, описывающее количество вещей, использованных для размещения с типом заказа ω 1 , равно «алеф-один» (ℵ 1 ).
Неизвестно, где на этой прямой находится набор мощности натуралов. Этого не может быть между этими кардиналами, потому что между ними нет кардиналов. Оно может быть равно алеф-один — это убеждение называется гипотезой континуума. Но он также может быть больше; мы просто не знаем. Гипотеза континуума, между прочим, пожалуй, самый большой вопрос без ответа во всей этой теме, и сегодня, в этом видео, я не буду его решать, а буду подниматься все выше и выше, во все большие и большие бесконечности.
Теперь, используя аксиому замены, мы можем взять любой уже достигнутый порядковый номер, например, ω, и перейти от алеф к алеф до алеф-омега. Или, черт возьми, почему бы не использовать больший порядковый номер, например ω 2 , для построения алеф-омега-квадрат? Алеф-омега-омега-омега-омега-омега-омега-о… Наша система обозначений позволяет мне добавлять сюда только счетное число омег, но замена не заботится о том, есть ли у меня способ записать числа, которых она достигает.
Где бы я ни приземлился, там будет еще больше чисел, что позволит мне совершать еще большие и многочисленные прыжки, чем раньше. Все это представляет собой дико ускоряющуюся петлю обратной связи эмбиггенинга. Мы можем продолжать в том же духе, достигая все больших и больших бесконечностей снизу.
Замена и повторяющиеся наборы мощности, которые могут совпадать или не совпадать с алефами, могут продолжать наше восхождение вечно. Так что ясно, что за ними ничего нет, верно? Не так быстро. Это то, что мы говорили о переходе от конечного к омеге. Почему бы не принять как аксиому, что существует какое-то следующее число, настолько большое, что никакие замены или настройки чего-то меньшего никогда не смогут вас туда привести. Такое число называется «недоступным кардиналом», потому что до него невозможно добраться снизу.
Теперь интересно, что среди чисел, которых мы уже достигли, можно найти тень такого числа: алеф-нуль. Вы также не можете добраться до этого числа снизу. Все числа, меньшие этого числа, конечны, и конечное число конечных чисел нельзя сложить, умножить, возвести в степень, заменить конечными скачками конечное число раз или даже установить мощность конечное число раз, чтобы получить что-либо, кроме другого конечного числа.
количество. Несомненно, набор мощности от миллиона к гуголплексу, к гуголплексу к гуголплексу действительно велик, но он все же конечен. Даже близко не алеф-нуль, первая наименьшая бесконечность. По этой причине алеф-нуль часто считается недоступным числом. Однако некоторые авторы этого не делают, говоря, что недоступное также должно быть неисчисляемым, что, ладно, имеет смысл — я имею в виду, что мы уже получили доступ к алеф-нулю, но помните, что единственный способ, которым мы могли бы это сделать, — это прямо объявить его существование аксиоматически. Нам придется сделать то же самое для недоступных кардиналов.
Очень трудно понять, насколько непостижимы размеры недоступного кардинала. Я просто оставлю это на этом: концептуальный прыжок из ничего в первую бесконечность подобен прыжку из первой бесконечности в недоступное. Теоретики множеств описали числа больше, чем недоступные, каждое из которых требует новой аксиомы большого кардинального числа, утверждающей его существование, расширяющей высоту нашей вселенной чисел.
Настанет ли когда-нибудь момент, когда мы придумаем аксиому, подразумевающую существование стольких вещей, что она подразумевает противоречащие друг другу вещи? Ответим ли мы когда-нибудь на гипотезу континуума? Может быть, и нет, но есть многообещающие направления, а до тех пор остается удивительным факт, что многие из этих бесконечностей — возможно, все они — настолько велики, что не совсем ясно, существуют ли они на самом деле или могут ли быть показаны в реальности. физическая вселенная. Если они есть, если однажды физика найдет им применение, это прекрасно, но если нет, то это тоже прекрасно. Это означало бы, что с этим мозгом, крошечной штукой, в септиллион раз меньшей, чем крошечная планета, на которой она живет, мы открыли что-то истинное за пределами физического мира. Что-то, что применимо к реальному миру, но в то же время достаточно сильное, чтобы идти дальше, за пределы того, что даже сама Вселенная может вместить, или показать нам, или чем быть.
И, как всегда, спасибо за просмотр.