Список степеней двойки | Гугология Вики
в: Числа, степени двойки, списки,
и еще 5
Посмотреть источникЭта страница содержит неназванные степени числа 2, о которых раньше были статьи на Googology Wiki. Прежнее содержание этих статей также включено сюда.
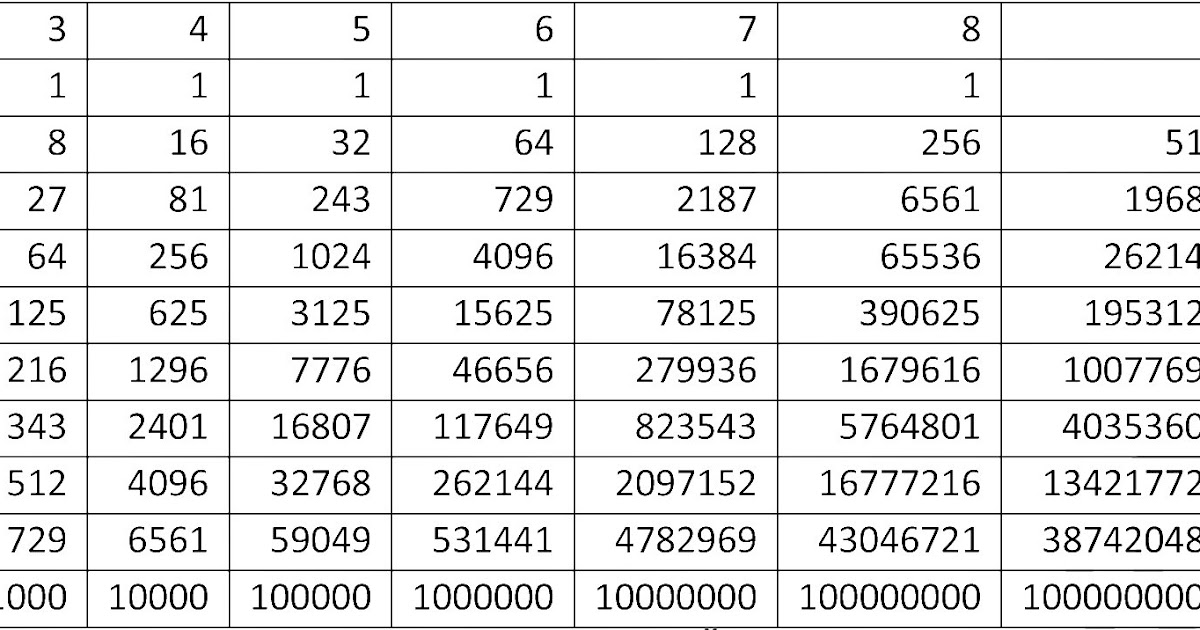
Список мощностей 2
512 равен 2 9 . 512 — число Дьюдени, то есть оно равно кубу суммы своих цифр. Это наименьшее число Дьюдени с основанием 10 (остальные 4,9).13, 5832, 17576 и 19683).
В конкурсе Bignum Bakeoff количество участников ограничено 512 символами (без учета пробелов).
2 10 = 1024
2 048 — положительное целое число, расположенное между числами 2 047 и 2 049. Это 11-я степень числа 2, равная f 2 (8) и f 3 (2) в быстрорастущей иерархии.
Это также наибольшая известная степень числа 2, в которой все цифры четные.
2048 — это также название веб-игры, в которой вы перемещаете плитки, представляющие степени двойки, по доске и пытаетесь комбинировать их, чтобы получить все более и более высокие степени двойки. Самая большая плитка, которую вы можете достать, это 131072.
131 072 — это 17-я степень числа 2.
В игре 2048 это самая большая плитка, до которой вы можете дотянуться.
262 144 — четвертое экспофакториальное число, равное 4 3 2 95 — 1}\). В компьютерных науках он известен тем, что является абсолютным значением максимального отрицательного значения 32-битного целого числа со знаком или пределом 32-битного целого числа; которые имеют диапазон [-2147483648, 2147483647].
Его полное название на английском языке: «два миллиарда/миллиард сто сорок семь миллионов четыреста восемьдесят три тысячи шестьсот сорок восемь», где в короткой шкале используется «миллиард», а в длинной — «миллиард».
2 63 = 9 223 372 036 854 775 808 Это абсолютное значение максимального отрицательного значения 64-битного целого числа со знаком в диапазоне [-9 223 372 036 854 775 808, 9 223 372 036 854 775 807].
2 86 = 77 371 252 455 336 267 181 195 264 — наибольшая известная степень двойки, не содержащая нуля.
2 168 = 374,144,419,156,711,147,060,143,317,175,368,453,031,918,731,001,856 [3]
2 219 = 842,498 333,348 457 493,583,344,221,469,363,458 551,160,763,204,392877777877877878787787787878787878787878787878787878787878787878787878787878787878787878787878787878787878787er8.
2 1.024 = 2 2 10 = 1797693134862315907729305190783361797697894230657273430081157732675805500963132708477322407536021120113879871393357658789768814416622492847430639474124377767893424865485276302219601246094119453082952085005768838150682342462881473913110540827237163350510684586298239947245938479716304835356329624224137216
 Во многих видеоиграх, использующих сценарии, превышение этого числа будет читаться как «Бесконечность».
Во многих видеоиграх, использующих сценарии, превышение этого числа будет читаться как «Бесконечность».2 1 000 000 ≈ 9,623 × 10 301 029
Аппроксимация этих чисел
Для 131 072:
| Обозначение | Нижняя граница | Верхняя граница | 95\) (точно)
|---|---|---|
| Стрелочное обозначение | \(2↑17\) (точно) | |
| Обозначение Штайнхауса-Мозера | 6[3] | 7[3] |
| Копировать обозначение | 1[6] | 2[6] |
| Многомерная функция Аккермана Таро | А(3,14) | А(3,15) |
| Обозначение фунт-звезда | #*(36)*3 | #*(37)*3 |
| ГОЛОВКА 95\) | ||
| Стрелочное обозначение | \(2\стрелка вверх18\), \(4\стрелка вверх9\) | |
| Обозначение Штайнхауса-Мозера | 6[3] | 7[3] |
| Копировать обозначение | 2[6] | 3[6] |
| Обозначение со стрелкой в виде цепочки | \(2\стрелка вправо18\), \(4\стрелка вправо9\) | |
| Многомерная функция Аккермана Таро | А(3,14) | А(3,15) |
| Обозначение фунт-звезда | #*(16)*4 | |
| Дебютная запись PlantStar | [3] | [4] |
| ГОЛОВКА | \(\{2,18\}, \{4,9\}\) | |
| Обозначение Hyper-E | Э[2]18, Э[4]9 | |
| Матричная система Башику | (0)[512] | |
| Обозначение гиперфакториального массива | 4!1 | |
| Обозначение массива Берда | 98\) (точно)||
| Стрелочное обозначение | \(2↑29\) (точно) | |
| Обозначение Штайнхауса-Мозера | 9[3] | 10[3] |
| Копировать обозначение | 4[9] | 5[9] |
| Многомерная функция Аккермана Таро | А(3,25) | А(3,26) |
| Обозначение фунт-звезда | #*(99)*4 | #*(38)*5 |
| ГОЛОВКА 99\) (точно) | ||
| Стрелочное обозначение | \(2 \стрелка вверх 31\) (точно) | |
| Обозначение Штайнхауса-Мозера | 9[3] | 10[3] |
| Копировать обозначение | 21[5] | 2[10] |
| Многомерная функция Аккермана Таро | А(3,28) | А(3,29) |
| Обозначение фунт-звезда | #*(2,2,3)*3 | #*(24)*6 |
Источники
- ↑ Бессмысленный гигантский список чисел — Часть 1 (0 ~ 1 000 000) — Бессмысленные большие числа
- ↑ Prime Curios!: 536870912
- ↑ OEIS A137214
Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.
Начальные цифры степени двойки
Первая цифра степени двойки является единицей чаще, чем любая другая цифра. Степени двойки начинаются с 1 примерно в 30% случаев. Это потому, что степени числа 2 подчиняются закону Бенфорда. Мы докажем это ниже.
Когда первая цифра числа 2 n равна k ? Когда 2 n находится между k × 10 p и ( k +1) × 10 p 79 p 90 90 для некоторого положительного целого числа 90. Логарифмируя по основанию 10, мы находим, что это эквивалентно дробной части n log 10 2, находящейся между log 10 k и log 10 ( k +1).
Карта
x ↦ ( x + log 10 2 ) mod 1
эргодична. Я писал об иррациональных поворотах несколько недель назад, и это, по сути, то же самое. Вы можете масштабировать x на 2π и думать об этом как о вращении по кругу вместо арифметического мода 1 на интервале.
Многократное умножение на 2 соответствует добавлению log 10 2 на логарифмической шкале. Таким образом, степени двойки соответствуют итерациям приведенной выше карты, начиная с 9.0579 x = 0. Эргодическая теорема Биркгофа говорит нам, что количество итераций этой карты, попадающих в интервал [ a , b ], равно b – a . Таким образом, для k = 1, 2, 3, … 9 отношение степеней числа 2, начинающихся с k , равно log 10 ( k + 1) – log 10 ( k ). = log 10 (( k + 1) / k ).
Это закон Бенфорда. В частности, доля степеней числа 2, начинающихся с 1, равна log 9.0033 10 (2) = 0,301.
Обратите внимание, что единственная особенность числа 2 заключается в том, что log  Для каких значений b степени b не подчиняются закону Бенфорда? Те, у которых log 10 b рациональны, то есть степени 10. Очевидно, что степени 10 не следуют закону Бенфорда, потому что их первая цифра всегда равна 1!
Для каких значений b степени b не подчиняются закону Бенфорда? Те, у которых log 10 b рациональны, то есть степени 10. Очевидно, что степени 10 не следуют закону Бенфорда, потому что их первая цифра всегда равна 1!
[Интерпретация «!» выше как факториал или восклицательный знак, как вам угодно.]
Давайте рассмотрим степени двойки эмпирически, чтобы увидеть закон Бенфорда на практике. Вот простая программа на Python для просмотра первых цифр степени 2.
count = [0]*10
N = 10000
определение первая_цифра (n):
вернуть целое (строка (n) [0])
для я в диапазоне (N):
n = первая_цифра ( 2 ** я )
количество[n] += 1
распечатать (количество)
К сожалению, это работает только для умеренных значений N . Он пробежал менее чем за секунду с N .установлено значение 10 000, но для больших значений N это быстро становится непрактичным.
Вот гораздо более эффективная версия, которая работала примерно за 2 секунды с N = 1 000 000.
из математического журнала импорта 10
N = 1000000
количество = [0] * 10
определение first_digit_2_exp_e(e):
г = (log10(2.0)*е) % 1
для я в диапазоне (2, 11):
если r < log10(i):
вернуть я-1
для я в диапазоне (N):
n = первая_цифра_2_exp_e( я )
количество[n] += 1
распечатать (количество)
Можно повысить эффективность, кэшируя значения log10 , а не пересчитывая их. Это сократило время выполнения примерно до 1,4 секунды. Это хорошее улучшение, но оно не сравнится с улучшением на порядки величины от изменения алгоритмов.
Вот результаты сравнения фактических значений с предсказаниями закона Бенфорда (с округлением до ближайшего целого числа).
|---------------+--------+-----------| | Начальная цифра | Фактический | Прогноз | |---------------+--------+-----------| | 1 | 301030 | 301030 | | 2 | 176093 | 176091 | | 3 | 124937 | 124939 | | 4 | 96911 | 96910 | | 5 | 79182 | 79181 | | 6 | 66947 | 66948 | | 7 | 57990 | 57992 | | 8 | 51154 | 51153 | | 9 | 45756 | 45757 | |---------------+--------+-----------|
Согласие почти слишком хорошее, чтобы поверить, никогда не отличается более чем на 2.