Минус косинус икс: синус икс минус косинус икс и равно нулю. как решать дальше?

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значение
cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87 Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94
Найти точное значение		arcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы
88 град.

Решение уравнения sin x — cos x = 1. Урок-семинар

Цели урока:

Главная дидактическая цель: рассмотреть все возможные способы решения данного уравнения.

Обучающие: изучение новых приемов решения тригонометрических уравнений на примере данного в творческой ситуации урока-семинара.

Развивающие: формирование общих приемов решения тригонометрических уравнений; совершенствование мыслительных операций учащихся; развитие умений и навыков устной монологической математической речи при изложении решения тригонометрического уравнения.

Воспитывающие: развивать самостоятельность и творчество; способствовать выработке у школьников желания и потребности обобщения изучаемых фактов.

Вопросы для подготовки и дальнейшего обсуждения на семинаре.

  1. Приведение уравнения к однородному относительно синуса и косинуса.
  2. Разложение левой части уравнения на множители.
  3. Введение вспомогательного угла.
  4. Преобразование разности (или суммы) тригонометрических функций в произведение.
  5. Приведение к квадратному уравнению относительно одной из функций.
  6. Возведение обеих частей уравнения в квадрат.
  7. Выражение всех функций через tg x (универсальная подстановка).
  8. Графическое решения уравнения.

Все учащиеся разбиваются на группы (по 2-4 человека) в зависимости от общего количества учащихся и их индивидуальных способностей и желания. Самостоятельно определяют для себя тему для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.

Организационный момент.

Учащимся сообщаются:

Тема урока:

“Различные способы решения тригонометрического уравнения sin x — cos x = 1

Форма проведения: урок – семинар.

Эпиграф к уроку:

“Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия. Задача, которую вы решаете, может быть скромной, но если она бросает вызов вашей любознательности и заставляет вас быть изобретательными и если вы решаете ее собственными силами, то вы сможете испытать ведущее к открытию напряжение ума и насладиться радостью победы”

(Д. Пойа)

Задачи урока:

а) рассмотреть возможность решения одного и того же уравнения различными способами;
б) познакомиться с различными общими приемами решения тригонометрических уравнений;
в) изучение нового материала (введение вспомогательного угла, универсальная подстановка).

План семинара

  1. Приведение уравнения к однородному относительно синуса и косинуса.
  2. Разложение левой части уравнения на множители.
  3. Введение вспомогательного угла.
  4. Преобразование разности (или суммы) тригонометрических функций в произведение.
  5. Приведение к квадратному уравнению относительно одной из функций.
  6. Возведение обеих частей уравнения в квадрат.
  7. Выражение всех функций через tg x (универсальная подстановка).
  8. Графическое решения уравнения.

Содержание.

1. Слово предоставляется первому участнику.

Приведение уравнения sin x — cos x = 1 к однородному относительно синуса и косинуса.
Разложим левую часть по формулам двойного аргумента, а правую часть заменим тригонометрической единицей, используя основное тригонометрическое тождество:

2 sin cos — cos + sin = sin + cos ;

2 sin cos — cos =0 ;
cos = 0;
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом не теряют смысла, поэтому следует

cos =0 ; =

= 0 - однородное уравнение первой степени.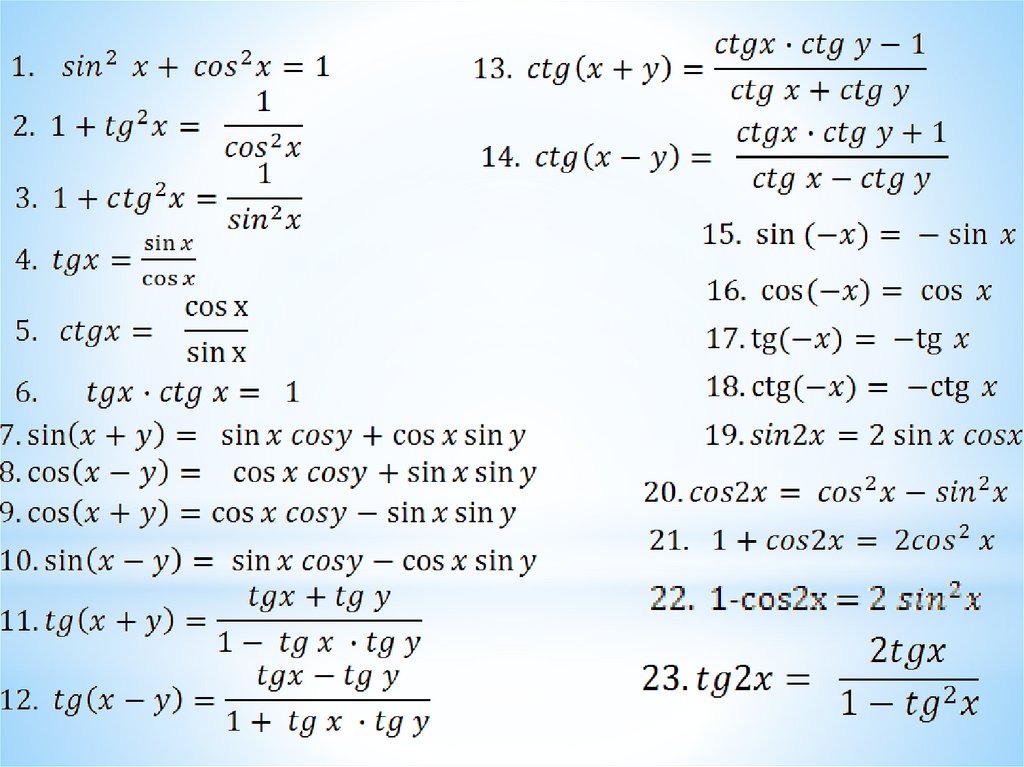 Делим обе части уравнения на cos . (cos 0, так как если cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит тригонометрическому тождеству sin + cos = 1).

Получим tg -1 = 0 ; tg = 1 ; =
Ответ:
2. Слово предоставляется второму участнику.

Разложение левой части уравнения sin x — cos x = 1 на множители.

sin x – (1+ cos x ) = 1; используем формулы 1+ cos x = 2 , получим ;
далее аналогично:

произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом не теряют смысла, поэтому следует

cos =0 ; =
= 0 - однородное уравнение первой степени. Делим обе части уравнения на cos . (cos 0, так как если cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит тригонометрическому тождеству sin + cos = 1)

Получим tg -1 = 0 ; tg = 1 ; =
Ответ:

3. Слово предоставляется третьему участнику.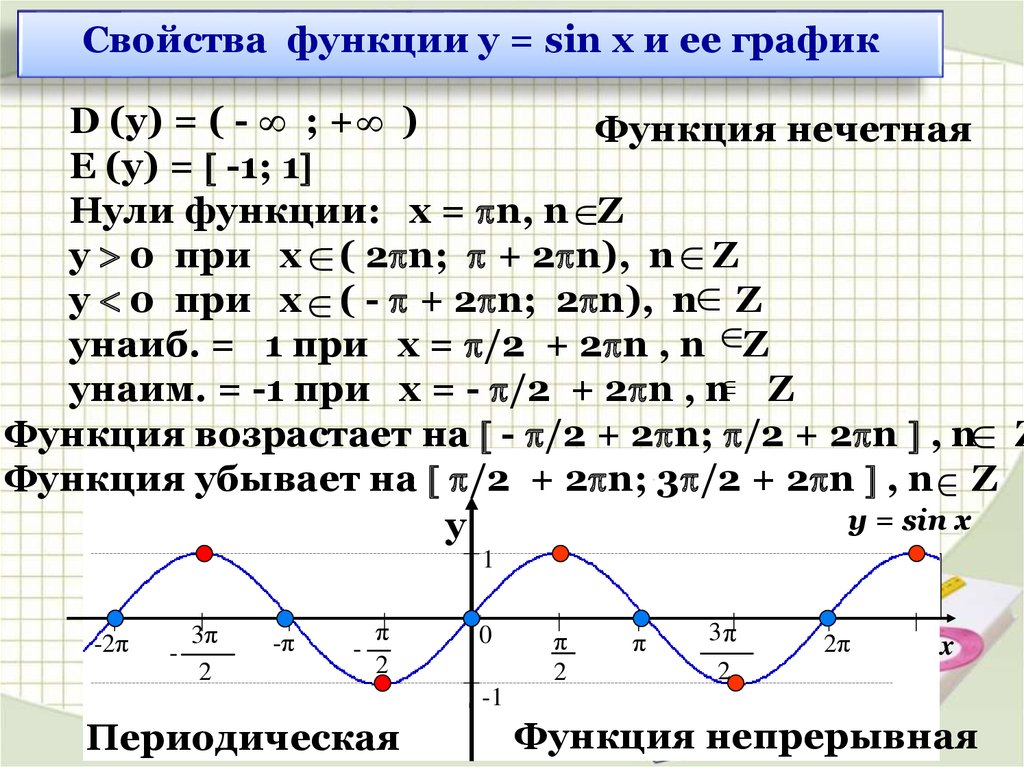

Решение уравнения sin x — cos x = 1 введением вспомогательного угла.

Рассмотрим уравнение sin x — cos x = 1. Умножим и разделим каждое слагаемое левой части
уравнения на . Получим и вынесем в левой части уравнения за скобку. Получим ; Разделим обе части уравнения на и используем табличные значения тригонометрических функций. Получим ; Применим формулу синус разности.
;

Легко установить(с помощью тригонометрического круга), что полученное решение распадается на два случая:

;

Ответ:

4. Слово предоставляется четвертому участнику.

Решение уравнения sin x — cos x = 1 способом преобразования разности (или суммы) тригонометрических функций в произведение.

Запишем уравнение в виде , используя формулу приведения . Применяя формулу разности двух синусов, получим

;

и так далее, аналогично предыдущему способу.

Ответ:

5. Слово предоставляется пятому участнику.

Решение уравнения sin x — cos x = 1 способом приведения к квадратному уравнению относительно одной из функций.

Рассмотрим основное тригонометрическое тождество , откуда следует
подставим полученное выражение в данное уравнение.
sin x — cos x = 1 ,

Возведем обе части полученного уравнения в квадрат:

В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка. Выполним ее.

Полученные решения эквивалентны объединению трех решений:

Первое и второе решения совпадают с ранее полученными, поэтому не являются посторонними. Остается проверить третье решение Подставим.
Левая часть:

Правая часть: 1.

Получили: , следовательно, – постороннее решение.

Ответ:

6. Слово предоставляется шестому участнику.

Возведение обеих частей уравнения sin x — cos x = 1 в квадрат.

Рассмотрим уравнение sin x — cos x = 1. Возведем обе части данного уравнения в квадрат.

;

;

Используя основное тригонометрическое тождество и формулу синуса двойного угла, получим ; sin 2x = 0 ; .

Полученное решение эквивалентно объединению четырех решений:

(эти решения можно нанести на единичную окружность). Проверка показывает, что первое и четвертое решения — посторонние.

Ответ:

7. Слово предоставляется седьмому участнику.

Использование универсальной подстановки в решении уравнения sin x — cos x = 1. Выражение всех функций через tg x по формулам:


Запишем данное уравнение с учетом приведенных формул в виде .
,

получим

ОДЗ данного уравнения – все множество R. При переходе к из рассмотрения выпали значения, при которых не имеет смысла, т. е. или .

Следует проверить, не являются ли решениями данного уравнения. Подставим в левую и правую часть уравнения эти решения.

Левая часть: .

Правая часть: 1.

Получили 1=1. Значит, — решение данного уравнения.

Ответ:

8. Слово предоставляется восьмому участнику.

Рассмотрим графическое решение уравнения sin x — cos x = 1.

Запишем рассматриваемое уравнение в виде sin x = 1 + cos x.

Построим в системе координат Оxy графики функций, соответствующих левой и правой частям уравнения. Абсциссы точек пересечения графиков являются решениями данного уравнения.

y = sin x – график: синусоида.
y = cos x +1 – график: косинусоида y = cos x, смещенная на 1 вверх по оси Oy. Абсциссы точек пересечения являются решениями данного уравнения.

Ответ:

Итог урока.

  • Учащиеся научились решать тригонометрические уравнения вида , освоили новый материал.
  • На примере одного уравнения рассмотрели несколько способов решения.
  • Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.
  • Учащиеся получили навыки самостоятельной работы с дополнительной литратурой.

Список использованной литературы:

  1. Татарченкова С.С. Урок как педагогический феномен – Санкт-Петербург: Каро, 2005
  2. Выгодский Н.В. Справочник по элементарной математике.-М.: Наука, 1975.
  3. Виленкин Н.Я. и др. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 класса – М.: Просвещение, 1996.
  4. Гнеденко Б.В. Очерки по истории математики в России – М.: ОГИЗ, 1946.
  5. Депман И.Я. и др. За страницами учебника математики – М.: Просвещение, 1999.
  6. Дорофеев Г. В. и др. Математика: для поступающих в вузы – М.: Дрофа, 2000.
  7. Математика: Большой энциклопедический словарь. – М.: БСЭ, 1998.
  8. Мордкович А.Г. и др. Справочник школьника по математике. 10-11кл. Алгебра и начала анализа. – М.: Аквариум, 1997.
  9. 300 конкурсных задач по математике. – М.: Рольф, 2000.
  10. 3600 задач по алгебре и началам анализа. – М.: Дрофа, 1999.
  11. Школьная программа в таблицах и формулах. Большой универсальный справочник. – М.: Дрофа, 1999.
  12. Торосян В.Г. История образования и педагогической мысли: учеб. для студентов вузов. - М.: Изд-во ВЛАДОС-ПРЕСС, 2006.- 351 с.
  13. Крылова Н.Б. Педагогическая, психологическая и нравственная поддержка как пространство личностных изменений ребёнка и взрослого.// Классный руководитель.- 2000.- №3. –С.92-103.

Как найти отрицательный косинус

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Тригонометрия » косинус » Как найти отрицательный косинус

Если и , каково значение ?

Возможные ответы:

Правильный ответ:

Объяснение:

На основе этих данных мы можем составить небольшой треугольник, который выглядит так:

Это потому, что .

Теперь это означает, что должно быть равно. (Напомним, что функция косинуса во втором квадранте отрицательна.) Теперь ищем:

 или . Это косинус опорного угла:

Глядя на наш маленький треугольник выше, мы видим, что косинус   равен .

Сообщить об ошибке

Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла. (Поэтому он называется «угол отсчета».)  

Теперь проще всего представить это так, будто вы рисуете маленький треугольник в третьем квадранте декартовой плоскости.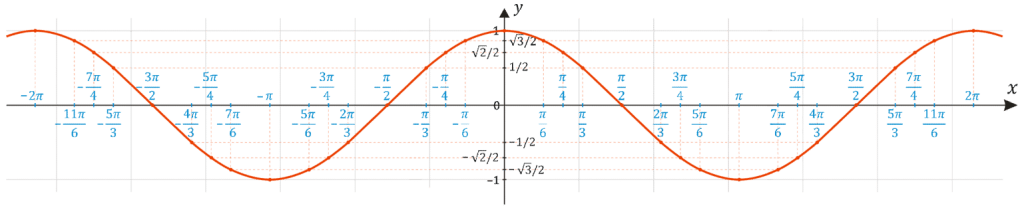 Это будет выглядеть так:

Итак, сначала нужно вычислить гипотенузу. Это можно сделать с помощью теоремы Пифагора, , где и  – длины катетов треугольника и  длина гипотенузы. Преобразовав уравнение для решения, вы получите:

Подставив полученные значения:

Итак, косинус угла равен:

 или, для ваших данных, .

Это примерно . Округление, это . Однако, поскольку  находится в третьем квадранте, ваше значение должно быть отрицательным: .

Сообщить об ошибке

Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла.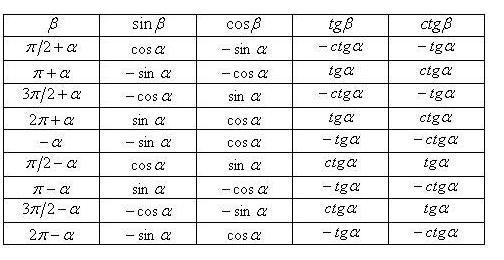 (Поэтому он называется «угол отсчета».) Теперь проще всего думать об этом, как будто вы рисуете маленький треугольник во втором квадранте декартовой плоскости. Это будет выглядеть так:

Итак, сначала нужно вычислить гипотенузу:

Итак, косинус угла равен:

 или, для ваших данных, .

Это примерно . Округление, это . Однако, поскольку  находится во втором квадранте, ваше значение должно быть отрицательным: .

Сообщить об ошибке

Чему равен косинус угла между началом и точкой с точностью до ? Допустим вращение против часовой стрелки.

Возможные ответы:

Правильный ответ:

Объяснение:

Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами  и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:

Таким образом,

Теперь SOHCAHTOA говорит нам об этом, поэтому мы знаем, что:

Таким образом, наш косинус приблизительно равен .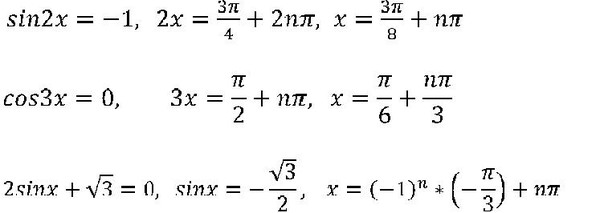 Однако, поскольку мы находимся в третьем квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .

Сообщить об ошибке

Чему равен косинус угла, образованного на сетке между линией от начала координат до  и осью x?

Возможные ответы:

Правильный ответ:

Объяснение:

Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами  и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:

Таким образом, .

Теперь SOHCATOA  говорит нам об этом, поэтому мы знаем, что:

Таким образом, наш косинус приблизительно равен . Однако, поскольку мы находимся во втором квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .

Сообщить об ошибке

Уведомление об авторских правах

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

Тригонометрия

— Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса — отрицательные?

$\begingroup$

Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса отрицательные?

Я имею в виду

$\cos(-\theta) = +\cos(\theta)$

$\sin(-\theta) = -\sin(\theta)$

$\tan(-\ theta) = -\tan(\theta)$

и, пожалуйста, объясните общие углы в простых мирах?

  • тригонометрия

$\endgroup$

11

$\begingroup$

Изменение знака $\theta$ соответствует обходу в другом направлении. Поскольку $\theta$ отсчитывается от положительной оси $x$, все, что нужно сделать, это перевернуть конечную точку по оси $x$, как показано ниже.

Поскольку косинус — это $x$-компонента $P$, а синус — это $y$-компонента, переворот по оси $x$ сведет на нет $\sin\theta$, но не $\cos\ тета$. Надеюсь, это проясняет, почему синус и косинус ведут себя именно так. 95/5!\pm…$

Обратите внимание, что изменение знака для cos не имеет значения (поскольку у нас есть все четные степени x), но изменение знака для sin имеет значение (поскольку у нас есть все нечетные степени x ).

Также $\tan (-\theta)=\frac {sin (-\theta)}{cos (-\theta)}\frac {-sin (\theta)}{cos (\theta)}=-tan (\тета)$.

$\endgroup$

$\begingroup$

Функция $f(x)$ называется четной, если $f(-x) = f(x)$. С другой стороны, функция $g(x)$ называется нечетной, если $g(-x) = -g(x)$. Таким образом, мы хотим знать, почему $cos(x)$ — четная функция, а $sin(y)$ — нечетная. Теперь мы можем представить, как синус и косинус зависят от угла тета ($θ$), используя единичный круг в декартовых координатах. Нарисуйте любой радиус единичной окружности, образуя угол $θ$ с положительной половиной оси x. Точка на окружности, где пересекается этот радиус, будет иметь координаты x и y как $\cos(θ)$ и $\sin(θ)$ соответственно. Это естественное следствие того, что гипотенуза соответствующего прямоугольного треугольника равна 1 (любой радиус единичного круга по определению будет равен 1). Радиус единичной окружности как гипотенуза прямоугольного треугольника Теперь при изменении угла $\theta$ мы получаем различные значения $sinθ$ и $cosθ$. Они были нанесены на следующий график: Графики $\cos(x)$ и $\sin(y)$

Как видите, график косинуса симметричен относительно оси y, что означает, что для каждого $x$ $\cos(x) = \cos(-x)$. Сделать косинус четной функцией. С другой стороны, если вы посмотрите на график синуса, вы заметите, что $|\sin(x)|$ = $|\sin(-x)|$, но знак противоположный. То есть абсолютное значение совпадает с пересечением оси $y$, но с обратным направлением. Сделать синус нечетной функцией.

$\endgroup$

$\begingroup$

Ну косинус принимает значения от 1 до -1 в интервале $[0,\pi]$, а синус принимает значения от 0 до 1. Я не знаю, что вы имеете в виду под общими углами простыми словами. 92-2bc\cos\альфа. $$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.

Синусы и косинусы позже были определены для любого угла; расширение можно обосновать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\alpha $$ просто глядя на тригонометрический круг.

$\endgroup$ 92-2bc\cos\альфа. $$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.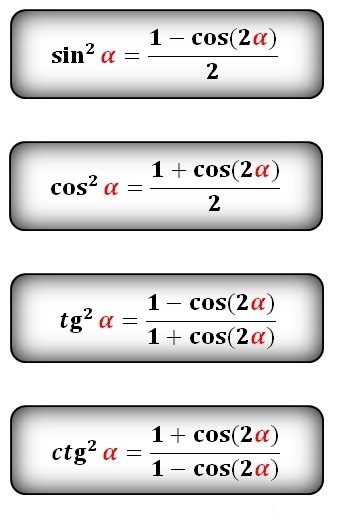

Синусы и косинусы позже были определены для любого угла; расширение можно оправдать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\ alpha $$ просто взглянув на тригонометрический круг.

$\endgroup$

$\begingroup$

$\cos(-\theta)=\cos(0-\theta)=\cos0\cos\theta+\sin0\sin\theta=\cos(\theta)$.

$\sin(-\theta)=\sin(0-\theta)=\sin0\cos\theta-\cos0\sin\theta=-\sin(\theta)$.

$\tan(-\theta)=\frac {\sin(-\theta)}{\cos(-\theta)}=-\tan(\theta)$. (Используя два приведенных выше равенства.)

$\endgroup$

$\begingroup$

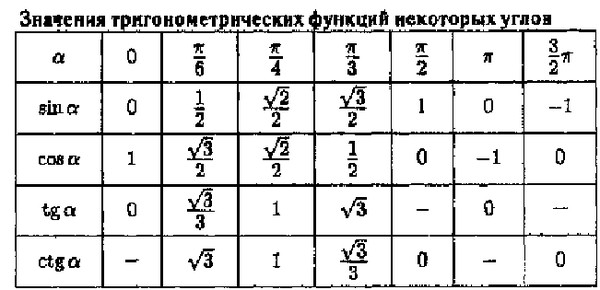
Помните, что углы отсчитываются от положительной оси $x$. Нарисуйте линию, образующую угол $\theta$ с положительной осью $x$. Эта прямая пересекает единичную окружность в точке $(\cos\theta,\sin\theta)$ и имеет уравнение $y=x\tan\theta$.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *