Минус на минус равно: «Почему минус на минус даёт плюс ?» — Яндекс Кью

Содержание

Знаки плюс, минус, равно

Главная → Публикации → Математика → Уроки → 1 класс → Знаки плюс, минус, равно

Цель: познакомить с названиями и значением знаков +, -, =.

Содержимое публикации

Цель:

познакомить с названиями и значением знаков +, -, =.

Планируемые результаты:

— предметные: уметь понимать значение знаков +, -, =; читать полученные равенства;

метапредметные

— регулятивные: уметь организовывать своё рабочее место под руководством учителя; определять цель выполнения заданий на уроке;

— коммуникативные: уметь обмениваться мнениями, слушать другого ученика, учителя, обсуждать, делать умозаключения;

— познавательные: уметь самостоятельно выделять и формулировать познавательную цель, сравнивать, группировать;

— личностные: уметь оценивать себя, границы своего знания и незнания, работать в паре, оценивать товарища, стремиться к повышению культуры речевого общения.

Материально-техническое обеспечение:

Проектор, экран, компьютер, слайды, учебник, тетрадь на печатной основе, карточки со знаками и цифрами, знаки дорожного движения – картинки, ободки для выступления, раздаточный материал – геометрические фигуры, тренажёр Базарного.

Ход урока

Организационный момент.

Проверить готовность принадлежностей, приветствие учителя стоя.

Парта – это не кровать

И на ней нельзя лежать.

Прозвенел звонок и смолк.

Начинается урок.

Тихо девочки за парты сели,

Тихо мальчики за парты сели,

На меня все посмотрели.

Повторение изученного материала.

— Прежде, чем мы приступим к изучению новой темы, предлагаю вам математическую разминку.

а) логическая разминка:

— Сколько хвостов у трех китов? (3 хвоста)

— Сколько ушей и двух мышей? (4 уха)

— У кого больше лап, у утки или у утенка? (одинаково, по 2 лапы)

б) устный счет:

— Посчитайте:

От 1 до 10 и обратно хором;

На доске корзина с грибами

— Составьте вопросы со словом «сколько» и ответьте на них.

(сколько грибов в корзине, сколько грибов на поляне, сколько грибов всего в корзине и на поляне)

Работа по теме урока.

Целеполагание.

На доске знаки (+, -, =, 1, 2, 3 и знаки дорожного движения «Автобусная остановка», «Пешеходный переход», «Пункт первой медицинской помощи», «Осторожно, дети!»)

— Что изображено на первом рисунке?(Автобусная остановка)
— Как вы понимаете значение слова «знак»?
— Представьте, что вы оказались в незнакомом районе города, спросить не у кого, но вы знаете, что в ваш район идет автобус № 410. Что вы будете делать?
(Предлагают найти автобусную остановку с помощью знака.)
— Верно. Знак молчит, но и сообщает нам о чем- то. Указывает на место, где останавливается автобус.

— А какие еще дорожные знаки вы знаете и что они сообщают?
— Теперь вы можете мне сказать, что такое знак?

Рефлексия: Знак — это указание или сообщение о каком-либо объекте.

— Нас окружает множество знаков. Посмотрите на карточки (на доске знаки плюс, минус, равно, цифры) и скажите, что это?
(Версии разные: цифры, числа, знаки. )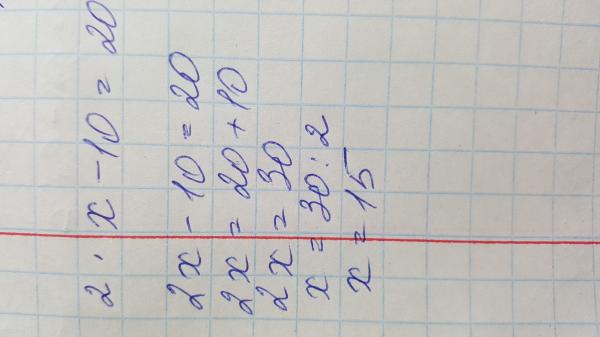

— Эти записи являются тоже знаками, номатематическими. Цифра это тоже математический знак, который используют для записи чисел.
— Какие из этих знаков вам знакомы?

— Какие новые? Кто знает, что это за знаки? (Гипотеза, предположение)

— Догадались, какая тема сегодняшнего урока? (Знаки плюс, минус, равно)

— Чему вы хотели бы научиться сегодня?(пользоваться знаками: плюс, минус, равно).

Знакомство со знаками «плюс» (+), «минус» (–), равно (=).

Практическая работа.

— Положите два оранжевых треугольника.

Какой цифрой мы это обозначим? ( один ученик к доске находит и крепит цифру 2)

— Рядом положитесиний квадрат.

Какой цифрой обозначим?( 1).

— Фигур стало больше или меньше? Сколько фигур получилось?

— Какими словами можно заменить слово положили? (прибавили, добавили)

— Чтобы записать это выражение в математике используются цифры и математический знак «+». А действие при этом называется сложение.

запись: 2+1

— Плюс – знак добрый, он всем дает, прибавляет и всего становится больше.

Ученик (Сизяков Рома) рассказывает стихотворение:

Я – плюс,

И этим я горжусь.

Я для сложения гожусь

Я – добрый знак соединенья

И в том мое предназначение.

— Какую работу он выполняет? (Он всем дает, прибавляет, всего становится больше.)

— Сколько у вас т фигур на столе? (3 фигуры)

Уберите синий квадрат. Фигур стало больше или меньше? Сколько фигур осталось? (2 фигуры)

— Слово уберите, тоже можно заменить знаком. Этот математический знак называется – минус.

Запись: 3-1

— Этот знак у всех отбирает, отнимает и всего становится меньше. Действие при этом называется вычитание.

Ученик (Спиридонов Никита) рассказывает стихотворение:

Я – минус.

Тоже добрый знак.

Ведь не со зла я отнимаю

Я свою роль лишь выполняю.

— Как называется математический знак, который у всех отнимает и при этом всего становится меньше? (Знак минус)

— Посмотрите на записи, которые у насполучились. Кто сможет их прочитать? (читают записанные на доске выражения)

Запись: 2+1 3

3 – 1 2

—Какого знака не хватает?

— Чтобы записать слово получится, используют знак равно (=) .

Запись: 2+1=3

3 – 1=2

Такие записи называют выражения.

— Давайте вместе прочитаем выражения, используя новые термины.

— Итак, какие же знаки используют математики, для записи выражений?

Работа в тетради на печатной основе.

— Откройте тетрадь на стр.10.

«Я тетрадь свою открою

И наклонно положу.

А ручку я вот так держу.

Сяду прямо, не согнусь,

За работу я возьмусь.»

— Посмотрите на клеточки, какие знаки написаны?

— Посмотрите внимательно, а по какому правилу расположены здесь знаки? (через клетку)

(Показ, как правильно пишутся знаки «+», «–».

Затем учащиеся обводят их по точечным контурам и пишут с а м о с т о я т е л ь н о.)

— Поменяйтесь тетрадями со своим соседом. Оцените работу. Посмотрите внимательно, получилось ли прописать красиво, аккуратно? Сохранили ли вы закономерность, все ли знаки у вас прописаны через клетку? Если всё верно – зелёный светофорик, если ошибка – жёлтый, если совсем неверно – красный.

Закрепление.

Работа по учебнику.

— Откройте учебник на стр.28.

— Посмотрите, о ком мы сейчас будем говорить? (О ежах.)

— Сколько было ежиков сначала? (1 ёжик)

— Что изменилось потом? (подбежал еще 1)

— Сколько их стало? (2)

(Чтение под картинкой рассказа) – Правильно вы ответили на вопросы?

— Какое слово заменили знаком «плюс» (подбежал). Прочитайте полученное выражение в учебнике.

2) Работа в парах:

— Посмотрите на картинку ниже и составьте рассказ. О ком вы будете составлять рассказ? Аналогично разбирается рисунок с зайцами.

– Данную запись можно прочитать так: «Три минус два равно одному». (Чтение детьми вслух.) Или по-другому: «Из трёх вычесть два, получится один».(Чтение детьми вслух.)

V.Подведение итогов.

– Давайте вспомним, что мы хотели узнать в начале урока? (Хотели узнать, как пользоваться знаками плюс, минус, равно)

— Вы достигли результата?

– Каким знаком будем пользоваться, если услышим слова: «убежали, убрали»? (Знаком минус)

— Каким знаком будет пользоваться, если услышите слова: «добавили, пришли»? (Знаком плюс)

— А какие это знаки + и – и =? (дорожные или математические)

VI. Рефлексия.

—оцените себя с помощью светофора: если вы всё поняли, всё удалось выполнить – зелёный свет;

если что-то осталось непонятно и были допущены ошибки – жёлтый. И после урока подойдёте ко мне – я ещё раз вам объясню;

если всё было непонятно – красный, и тогда нужно подробно ещё раз разобрать тему.

Спасибо вам большое за урок, завтра мы продолжим учиться пользоваться нашими новыми знаками и познакомимся с новой цифрой. Урок окончен.

Приложение.

В течении урока, проводится 2-3 физминутки. Время проведения первой через 7-10 минут после начала урока, следующие по усмотрению учителя и временной промежуток зависит от работоспособности класса.

Физминутка

Раз – подняться, потянуться,

Два – согнуться, разогнуться,

Три – в ладоши три хлопка,

Головою три кивка.

На четыре руки шире,

Пять – руками помахать,

Шесть за парту тихо сесть.

Пальчиковая физминутка

Этот пальчик бабушка, (большие)

Этот пальчик дедушка, (указательные)

Этот пальчик мамочка, (средние)

Этот пальчик папочка. (безымянные)

Этот пальчик я. (мизинцы)

Это вся моя семья! (хлопки и встряхивание кистями рук)

Физминутка для глаз

Тренажёр Базарного на доске

Вам также может понравиться:

-192

Всероссийский конкурс детско-юношеского творчества к Дню китов «ПУТЕШЕСТВИЕ В МОРСКИЕ ГЛУБИНЫ »

30 Ноября – 30 Ноября

Олимпиады 8 работ

Всероссийская образовательная олимпиада для дошкольников «БЕЗОПАСНАЯ ЗИМА »

05 Декабря – 05 Марта

Конкурсы 91 работа

Всероссийский творческий конкурс для педагогов «НОВОГОДНЕЕ ВДОХНОВЕНИЕ »

01 Декабря – 28 Февраля

Свидетельство участника экспертной комиссии Оставляйте комментарии к работам коллег
и получите документ БЕСПЛАТНО! Подробнее

Предыдущая работа
Следующая работа

Также вас может заинтересовать

Разное по математике для «Математика-царица наук» ^{Математика}
Разное по математике для «Контрольные работы по математике за 2 класс» ^{Математика}
Планирование по математике для дошкольников «Перспективное планирование по познавательному развитию (ФЭМП) во 2 младшей группе)» ^{Математика}
Уроки по математике для 4 класса «Технологическая карта урока математики в 4 классе по теме «Нумерация. Счёт предметов. Разряды»» ^{Математика}
Разное по математике для «Тематический комплект по математике «Числа от 1 до 10″» ^{Математика}

Тема » Знаки +(плюс), — (минус). =(равно)»

КОНСПЕКТ УРОКА МАТЕМАТИКИ1 КЛАСС УМК ПЕРСПЕКТИВА: ТЕМА: ЗНАКИ + ( ПЛЮС), — (МИНУС), = (РАВНО). Автор: Стельмах Наталья Николаевна Цели: 1)Познакомить учеников с математическими знаками (+,-,=),узнать их место в математике. Познакомить с новым термином-выражение, научить правильно его читать. 2)Закрепить ведение количественного и порядкового счета предметов, развивать логическое мышление. Оборудование: Корзинка, три яблока, веера цифр, электронное приложение к учебнику Г.В. Дорофеева Математика 1 класс 1.ОРГАНИЗАЦИОННЫЙ МОМЕНТ. Мы начинаем новый день. Прогоняй скорее лень! Почаще улыбайся. Прилежным быть старайся!

2. АКТУАЛИЗАЦИЯ ЗНАНИЙ. 1) Счет прямой и обратный от 1 до 10, от 6 до 10, от 7 до 3.Какое число находится между 2 и 4,стоит перед число7, 5,2, следует за числом 3,8.

2) Задание на логику. — В корзине сидят котята. У всех котят 3 пары ушек. Сколько котят в корзине? — У Толи 2 пары варежек. Сколько варежек на левую руку? -По двору ходят куры. У всех кур Петя насчитал 6 ног. Сколько кур? -Бабушка связала Нине две пары носков. Сколько носков связала бабушка Нине?

3.ФИЗМИНУТКА: Мы считали и устали,
Дружно все мы тихо встали.
Ручками похлопали: раз, два, три.
Ножками потопали: раз, два, три.
Сели, встали, встали, сели.
И друг друга не задели.
Мы немножко отдохнем,
И опять считать начнем.

4. МОТИВАЦИОННО- ЦЕЛЕВОЙ ЭТАП. ПОСТАНОВКА ПРОБЛЕМЫ. РАБОТА ПО ТЕМЕ УРОКА.

-Я положу в корзинку 2 яблока. Какой цифрой мы их обозначим? (Ученики работают на местах с веерами цифр, а учитель пишет на доске цифру 2). Добавлю еще одно яблоко. Какой цифрой мы его обозначим?(1). Ребята, яблок стало больше или меньше? Сколько яблок получилось? -Какими словом можно заменить слово добавить? ( Сложить). А кто знает каким математическим знаком можно заменить слова добавить, сложить? (знаком +) — Правильно, чтобы записать это выражение в математике используются цифры и математический знак «+».( Учитель на доске записывает 2+1.Просмотр электронного приложения к учебнику). — Ребята, послушайте стихотворение о знаке плюс:

Я – плюс, И этим я горжусь. Я для сложения гожусь. Я – добрый знак соединения. И в том мое предназначение.

— Посмотрите на этот знак. Как его имя в математике? (плюс). Какую работу он выполняет? (Он прибавляет, всего становится больше.)

— Сколько у нас теперь яблок в корзинке? (3.Учитель пишет на доске цифру 3) А если я от трех наших яблок уберу одно, сколько их станет: больше или меньше? ( Меньше) Сколько яблок осталось? (2. Учитель пишет на доске).- Как вы думаете слово уберу, убрать, можно заменить знаком?( знаком -) —Правильно. Этот математический знак называется – минус.(Учитель на доске записывает 3-1.Просмотр электронного приложения к учебнику). —Послушайте стихотворение о знаке минус.

Я – минус. Тоже добрый знак. Ведь не со зла я отнимаю. Я свою роль лишь выполняю. — Какое имя у математического знака, который все убавляет, и всего становится меньше? 5.ФИЗМИНУТКА. Ветер дует нам в лицо,
Закачалось деревцо.
Ветер тише, тише, тише —
Деревцо все выше, выше.

6.РАБОТА ПО ТЕМЕ УРОКА. — Посмотрите на записи, которые у нас получились. Кто сможет их прочитать? (Ученики читают записанные на доске выражения) -Вы произносите слово получится, а как это записать, может кто-нибудь знает? (Ответы детей) -Все верно. Чтобы записать слово получится используют математический знак равно (=) и такие записи ( показ на доску) называют выражения ( Просмотр электронного приложения). — Давайте вместе прочитаем выражения у нас на доске, используя новые термины. (Хоровое чтение) –Так какие же знаки мы будем использовать для записи выражений?(+,-,=)? А какую работу выполняют знаки + и -?( Ответы учеников)

Работа по учебнику стр.54-55

7.ФИЗМИНУТКА. Можешь пальцы посчитать? Один, два, три, четыре, пять.
На другой руке опять:
Один, два, три, четыре, пять.
Десять пальцев, пара рук —
Вот твое богатство, друг. 8.РАБОТА ПО ТЕМЕ УРОКА. Работа в тетради стр. 42(задание1-2), стр.43 (задание4-5).

9. ПОДВЕДЕНИЕ ИТОГА УРОКА. РЕФЛЕКСИЯ.

-Что нового вы узнали на уроке? — С какими новыми математическими знаками познакомились? — Для чего нужен знак «-»,а знак «+»? — Какие умения вы приобрели? – Кто на уроке был самым активным? — Оцените свою работу на уроке? -Хорошо ребята, всем спасибо за урок!

Передача сигналов белка

G в растениях: минус умножить на минус равно плюс

Обзор

. 2016 Декабрь; 34: 127-135.

doi: 10.1016/j.pbi.2016.11.001. Epub 2016 19 ноября.

Дэйв Статечны ¹ , Джара Оппенгеймер ¹ , Питер Боммерт ²

Принадлежности

¹ Гамбургский университет, биоцентр Klein Flottbek, кафедра биологии развития, Ohnhorststr. 18, D-22609 Гамбург, Германия.
² Гамбургский университет, биоцентр Klein Flottbek, кафедра биологии развития, Ohnhorststr. 18, D-22609 Гамбург, Германия. Электронный адрес: [email protected].

PMID: 27875794
DOI: 10. 1016/j.pbi.2016.11.001

Обзор

Dave Stateczny et al. Curr Opin Plant Biol. 2016 Декабрь

. 2016 Декабрь; 34: 127-135.

doi: 10.1016/j.pbi.2016.11.001. Epub 2016 19 ноября.

Авторы

Дэйв Статечны ¹ , Джара Оппенгеймер ¹ , Питер Боммерт ²

Принадлежности

¹ Гамбургский университет, биоцентр Klein Flottbek, кафедра биологии развития, Ohnhorststr. 18, D-22609 Гамбург, Германия.
² Гамбургский университет, биоцентр Klein Flottbek, кафедра биологии развития, Ohnhorststr. 18, D-22609 Гамбург, Германия. Электронный адрес: [email protected].

PMID: 27875794
DOI: 10.1016/j.pbi.2016.11.001

Абстрактный

Гетеротримерные G-белки являются ключевыми регуляторами передачи внеклеточных сигналов как у животных, так и у растений. У растений передача сигналов гетеротримерного G-белка играет важную роль в развитии и в ответ на биотический и абиотический стресс. Однако за последнее десятилетие стало ясно, что растения обладают уникальными механизмами передачи сигналов G-белка. Хотя растения имеют общие основные компоненты гетеротримерных G-белков, некоторые из них проявляют необычные свойства по сравнению с их аналогами животных. Кроме того, у растений нет общих функциональных GPCR. Следовательно, хорошо зарекомендовавшая себя парадигма цикла передачи сигналов животного G-белка неприменима к растениям. В этом обзоре мы обобщаем последние данные об этих уникальных механизмах передачи сигналов G-белка у растений, уделяя особое внимание очевидному потенциалу передачи сигналов G-белка в качестве мишени для изменения параметров развития и физиологических параметров, важных для повышения урожайности.

Цитируется

Исследование экзогенного применения тидиазурона при размере семян Brassica napus L.
Чжай Л., Се Л., Сюй Дж., Сюй Б., Донг Дж., Чжан С. Чжай Л. и др. Фронт завод науч. 2022 6 сент.; 13:998698. doi: 10.3389/fpls.2022.998698. Электронная коллекция 2022. Фронт завод науч. 2022. PMID: 36147221 Бесплатная статья ЧВК.
GCR1 положительно регулирует закрытие устьиц, вызванное УФ-В и этиленом, посредством активации зависимых от GPA1 АФК и продукции NO.
Li X, Fu Q, Zhao FX, Wu YQ, Zhang TY, Li ZQ, He JM. Ли Х и др. Int J Mol Sci. 2022 15 мая; 23 (10): 5512. дои: 10.3390/ijms23105512. Int J Mol Sci. 2022. PMID: 35628324 Бесплатная статья ЧВК.
Гетеротримерные G-белки растений: канонические и атипичные Gα-субъединицы.
Марута Н., Трусов Ю., Джонс А.М., Ботелла М.Р. Марута Н. и др. Int J Mol Sci. 2021 31 октября; 22 (21): 11841. дои: 10. 3390/ijms222111841. Int J Mol Sci. 2021. PMID: 34769272 Бесплатная статья ЧВК. Рассмотрение.
Успехи в исследованиях гетеротримерных α-субъединиц G-белка и неканонических рецепторов, связанных с G-белком, в растениях.
Лю И, Ван С, Донг Д, Го Л, Донг С, Лэн Дж, Чжао Б, Го Ю Д, Чжан Н. Лю Ю и др. Int J Mol Sci. 2021 12 августа; 22 (16): 8678. дои: 10.3390/ijms22168678. Int J Mol Sci. 2021. PMID: 34445383 Бесплатная статья ЧВК. Рассмотрение.
Конвергенция и дивергенция передачи сигналов сахара и цитокинина в развитии растений.
Ван М., Ле Гуррирек Дж., Цзяо Ф., Демотес-Майнар С., Перес-Гарсия М.Д., Оге Л., Хамама Л., Креспел Л., Бертелут Дж., Чен Дж., Граппин П., Сакр С. Ван М и др. Int J Mol Sci. 2021 28 января; 22 (3): 1282. дои: 10.3390/ijms22031282. Int J Mol Sci. 2021. PMID: 33525430 Бесплатная статья ЧВК. Рассмотрение.

Просмотреть все статьи «Цитируется по»

Типы публикаций

термины MeSH

вещества

Отрицательное значение, умноженное на отрицательное

Минус, умноженный на минус, дает плюс,
Причину этого нам не нужно обсуждать.
— Огден Нэш Бассейн
Вот аналогия наполнения или слива воды в бассейне: Если вы наполняете бассейн со скоростью 3 литра в секунду (+3) через 4 секунды (+4) количество воды увеличится на 12 литров (+3 * +4 = +12). Если вы сливаете бассейн со скоростью 3 литра в секунду (-3) через 4 секунды (+4) количество воды уменьшится на 12 литров (-3 * +4 = -12).

Если вы наполняете бассейн со скоростью 3 литра в секунду (+3) 4 секунды назад (-4) воды было на 12 литров меньше (+3 * -4 = -12). Если вы сливаете бассейн со скоростью 3 литра в секунду (-3) 4 секунды назад (-4) количество воды было на 12 литров больше, чем есть сейчас (-3 * -4 = +12). Эта аналогия может дать учащимся интуитивный Основы правил умножения положительных и отрицательных чисел.
Этот пример может не сработать для вас, и вы можете прочитать другие ниже.

Номер строки
Представьте числовую линию, по которой вы идете. Умножение x * y требует x шагов, каждый из которых имеет размер y. Отрицательные шаги требуют, чтобы вы смотрели на отрицательный конец линии, прежде чем начать ходьбу, а отрицательные размеры шагов — это шаги назад (т. е. сначала пяткой). Итак, -x*-y означает стоять на нуле, смотреть в отрицательном направлении, а затем делать x шагов назад, каждый размером y.

Шаблоны
Давайте посмотрим, как математик может понять, что происходит, когда отрицательное число умножается на отрицательное число.

Вот аргумент правдоподобия, взятый из шаблонов умножения:

          3 х -3 = -9
          2 х -3 = -6
          1 х -3 = -3
          0 х -3 = 0
         -1 х -3 = ?

Математическое объяснение
Если мы можем согласиться с тем, что отрицательное число — это просто положительное число, умноженное на -1, то мы всегда можем записать произведение двух отрицательных чисел следующим образом:

   (-a)(-b) = (-1)(a)(-1)(b) = (-1)(-1)ab

Например,

    -2 * -3 = (-1)(2)(-1)(3)
 
            = (-1)(-1)(2)(3)

            = (-1)(-1) * 6

Итак, настоящий вопрос,

   (-1)(-1) = ?

, и ответ заключается в следующем соглашении. принят:

   (-1)(-1) = +1

Эта конвенция принята по простой причине что любое другое соглашение может привести к поломке.

Например, если мы приняли соглашение о том, что (-1)(-1) = -1, распределительное свойство умножения не будет работать для отрицательные числа:

   (-1)(1 + -1) = (-1)(1) + (-1)(-1)

        (-1)(0) = -1 + -1

              0 = -2

Как заметил Шерлок Холмс, «Когда вы исключили невозможное, все, что остается, каким бы невероятным оно ни было, должно быть правдой».

Поскольку все, кроме +1, можно исключить как невозможное, отсюда следует что, каким бы невероятным это ни казалось, (-1)(-1) = +1.

Более подробное математическое объяснение
Может показаться, что кто-то просто придумал правило из воздуха, не придавая ему особого значения. причина, по которой ответ должен быть положительным. Но есть цепочка рассуждений — математический «аргумент» — который показывает, почему правило *должно* быть таким отрицательное умноженное на отрицательное равно положительному. Вот как рассуждают:

(1) Нуль, умноженный на что-либо, равен нулю. (2) Каждое число имеет ровно одно аддитивное обратное. Это означает, что если Н является положительным числом, то -N является его аддитивным обратным числом, так что N + (-N) = 0. Точно так же аддитивным обратным к -N является N. (3) Мы хотим, чтобы отрицательные числа подчинялись дистрибутивному закону. Этот Говорит, что а*(б+с) = а*б + а*с (4) Теперь мы вынуждены принять новый закон, что отрицательные времена положительное равно отрицательному.

Это потому, что мы можем использовать дистрибутивный закон для выражения типа 2*(3 + (-3)). Это равно 2*(0), что равно нулю. Но по дистрибутивному закону это также равно 2*3 + 2*(-3). Таким образом, 2 * (-3) выполняет работу аддитивной, обратной 2 * 3, и поэтому 2 * (-3) является аддитивной инверсией 2 * 3. Но аддитивное число, обратное 6, равно -6. Итак, 2 умножить на -3 равно -6. (5) Затем мы вынуждены принять еще один новый закон, отрицательный умноженное на отрицательное равно положительному. Очень похоже на пример в (4). Воспользуемся дистрибутивным законом, скажем, -3*(5 + (-5)). Это снова равно нулю. Но по дистрибутивному закону также равно -3*5 + (-3)*(-5). Мы знаем первое, (-3*5) равно -15 по закону в (4). Итак, (-3)*(-5) выполняет работу аддитивного обратного из -15. Мы знаем, что -15 имеет ровно одну аддитивную обратную, а именно 15.

Минус на минус равно: «Почему минус на минус даёт плюс ?» — Яндекс Кью

Знаки плюс, минус, равно

Содержимое публикации

Всероссийский конкурс детско-юношеского творчества к Дню китов «ПУТЕШЕСТВИЕ В МОРСКИЕ ГЛУБИНЫ »

Всероссийская образовательная олимпиада для дошкольников «БЕЗОПАСНАЯ ЗИМА »

Всероссийский творческий конкурс для педагогов «НОВОГОДНЕЕ ВДОХНОВЕНИЕ »

Также вас может заинтересовать

Тема » Знаки +(плюс), — (минус). =(равно)»

G в растениях: минус умножить на минус равно плюс

Принадлежности

Авторы

Принадлежности

Абстрактный

Похожие статьи

Цитируется

Типы публикаций

термины MeSH

вещества

Отрицательное значение, умноженное на отрицательное

Добавить комментарий Отменить ответ