Калькулятор дробей с тремя дробями онлайн: Калькулятор рациональных выражений

Содержание

Калькулятор добавления нескольких дробей

Сложение нескольких дробей

Арифметический оператор :

+ (Сложение) x (Умножение) Среднее

Дроби и смешанные числа:

введите входные значения, разделенные пробелами

ОранжевыйСинийРозовыйЗеленый

Примечания

Вставьте этот код виджета в любое место внутри тега body
Используйте код как есть для правильной работы.

Обратная связь

Калькулятор

Информация

ИСТОРИЯ

Дом
Математические функции
Добавление FRCACES Calculator

getCalC.com. Сомесльные номера. Сомесльные номера FRACED SACLATUTUTURE и ISLACER CALCATUTE онлайн-инструмент базовой математической функции для поиска эквивалентной дроби для сложения двух или более дробных чисел с одинаковыми или разными (равными или разными) знаменателями, смешанными и целыми числами.

Пользователи могут использовать этот калькулятор для создания полной тренировки для заданных входных значений, чтобы проверить или попрактиковаться в решении задач сложения дробей и смешанных чисел с пошаговыми вычислениями. Чтобы узнать или проверить сложение между расчетом нескольких дробей, введите входные значения для создания полной тренировки с пошаговым расчетом, чтобы помочь учащимся начальной или начальной школы эффективно решать рабочие листы или домашние задания. Чтобы использовать смешанные числа в этом калькуляторе сложения дробей, пользователям не требуется отдельно преобразовывать смешанные числа в их эквивалентные дроби, вместо этого пользователи могут использовать смешанные числа непосредственно в формате X(Y/Z) ; где X — целое число, Y и Z — числитель и знаменатель дроби. Например, смешанное число 3 1/2 должно быть представлено в калькуляторе как 3(1/2).

Другие калькуляторы дробей

Умножение кратных дробей и смешанных чисел
Калькулятор вычитания дробей
Калькулятор деления дробей
Калькулятор среднего значения дробей

Множественные дроби и смешанные средние числа
Калькулятор сложения дробей
Калькулятор умножения дробей

Сложение двух или более дробей и формула

Сложение нескольких дробей — это основная арифметическая операция, которая объединяет две или более дроби вместе. Приведенная ниже формула представляет собой математическое представление для сложения любого количества дробей с одинаковыми или разными знаменателями, положительных и отрицательных дробей или дробей с целыми или смешанными числами. Используйте этот калькулятор дробей и смешанных чисел, чтобы проверить результаты сложения двух или более дробей, смешанных чисел и целых чисел.

Формула сложения дробей, смешанных и целых чисел

Как найти сумму кратных дробей

Для дробей с одинаковыми или равными знаменателями сумма дробей равна сумме числителей, деленной на общие знаменатели, а для дроби с разными, неравными или разными знаменателями, сумма дробей рассчитывается с использованием метода НОК (наименьшее общее кратное). Пользователи могут обратиться к приведенным ниже решенным примерам с пошаговым расчетом, чтобы узнать, как найти эквивалентную дробь путем добавления двух, трех или более чисел дроби с одинаковыми или разными знаменателями.

Как найти сумму двух, трех и более дробей
Как найти сумму нескольких дробей и целых чисел
Как найти сумму нескольких положительных и отрицательных дробных чисел.

Сложение трех дробей с разными знаменателями

Приведенный ниже пример решения с пошаговым расчетом или тренировкой может помочь пользователям узнать, как найти эквивалентную дробь путем сложения трех дробей (с разными или разными знаменателями) 1/2, 2/ 3 и 4/5.
Задача
Найдите сумму трех дробей с разными или разными знаменателями, например 1/2, 2/3 и 4/5.

Пошаговая тренировка
шаг 1 Адрес формула , вводимые значения.
Ввод значений:
1/2,2/3,4/5
1/2+2/3+4/5= ?

шаг 2 Для дробей с разными знаменателями найдите НОК (наименьшее общее кратное) для всех знаменателей . 30 — НОК для 2, 3 и 5.

шаг 3 Умножьте НОК 30 на каждый числитель и знаменатель

=(1 x 30)/(2 x 30)+(2 x 30)/(3 x 30)+(4 x 30)/(5 x 30)

шаг 4 Просто приведенное выше выражение имеет те же знаменатели для все дроби.
=15/30+20/30+24/30
=(15 + 20 + 24)/30

шаг 5 Сложите все числители и перепишите в единой форме.
= 59/30
1/2+2/3+4/5=59/30

59/30 равнозначная дробь, полученная путем сложения трех дробей 1/2, 2/3 и 4/5.

Сложение трех дробей с одинаковыми знаменателями

Приведенный ниже пример решения с пошаговым вычислением или упражнением может помочь пользователям узнать, как найти эквивалентную дробь путем сложения трех дробей (с одинаковыми или равными знаменателями) 5/9, 7/9 и 4/9.
Задача
Найдите сумму трех дробей с одинаковыми или равными знаменателями, например 5/9, 7/9 и 4/9.

Пошаговая тренировка
шаг 1 Формула адреса и входные значения.
Входные значения:
Заданные дроби:
5/9,7/9,4/9
5/9+7/9+4/9= ?

шаг 2 Для одинаковых знаменателей сложите все числители напрямую и перепишите дробь, как показано ниже
=5/9+7/9+4/9
=(5 + 7 + 4)/9
5/9+7/9+4/9= 16/9

16/9 эквивалентная дробь для сложения трех дробей с одинаковыми знаменателями 5/9, 7/9 и 4/9.

Сложение нескольких дробей и целых чисел

Приведенный ниже пример решения с пошаговым вычислением может помочь пользователям узнать, как найти эквивалентную дробь путем сложения нескольких дробей (с разными или разными знаменателями) и целых чисел.
Задача
Найдите эквивалентную дробь для сложения 1/2, 1, 5/3, 2, 1/4, 2/5 и 3.

Пошаговая тренировка
шаг 1 Адресная формула и вводимые значения.
Входные значения:
1/2, 1,5/3, 2 ,1/4,2/5 , 3
1/2 + 1 +5/3 + 2 + 1/4 + 2/5 + 3 = ?

шаг 2 Преобразуйте целые числа в дроби и перепишите, как показано ниже
Любое целое или целое число является рациональным числом (частное от 1), следовательно, знаменатель для всех целых чисел равен 1 и может быть записан как
1 = 1/1
2 = 2/1
3 = 3/1

шаг 3 Разложите все числа в виде дробей.
1/2+1/1 + 5/3 + 2/1+ 1/4+2/5+3/1

шаг 4 Найдите НОК (наименьшее общее кратное) для всех знаменателей, если все знаменатели не совпадают друг другу.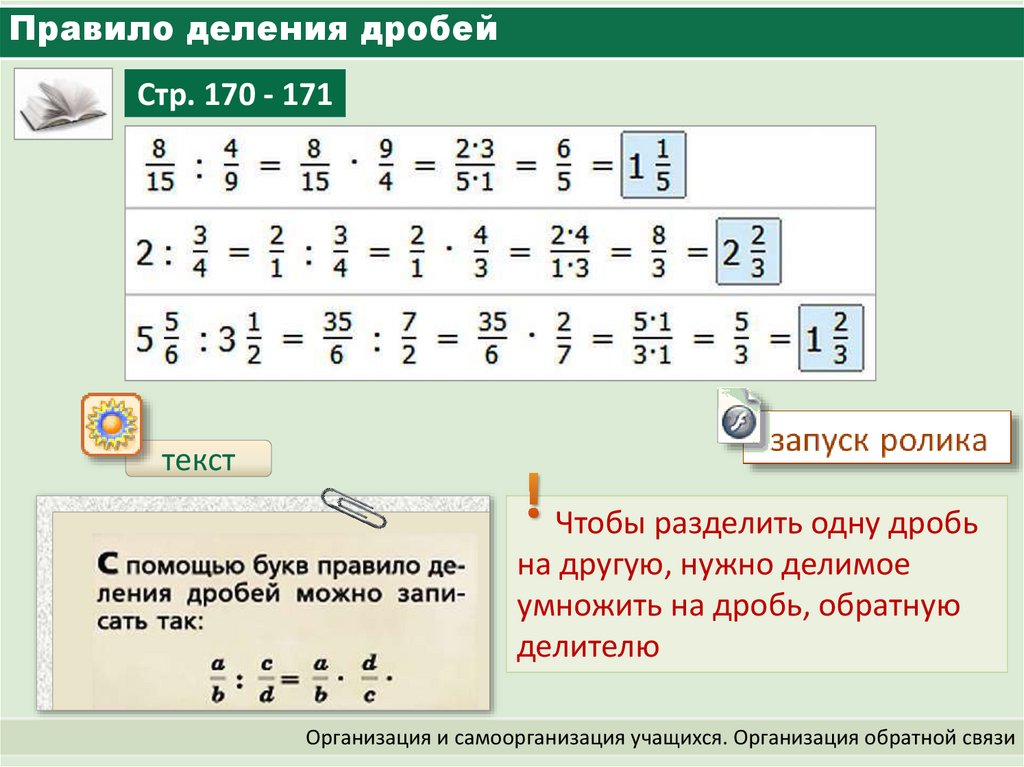
60 — НОК для знаменателей 2, 1, 3, 1, 4, 5 и 1.

шаг 5 Умножьте НОК 60 на все числители и знаменатели каждой дроби
(1 x 60)/(2 x 60) + (1 х 60)/(1 х 60) + (5 х 60)/(3 х 60)+(2 х 60)/(1 х 60)+(1 х 60)/(4 х 60)+(2 x 60)/(5 x 60) +(3 x 60)/(1 x 60)

шаг 6 Упростите и перепишите приведенное выше выражение, чтобы оно имело общие знаменатели
30/60+60/60+100/60+ 120/60+25/60+24/60+180/60

шаг 7 Сложите все числители и упростите
=(30 + 60 + 100 + 120 + 25 + 24 + 180)/60
=539/60
1/2+ 1 +5/3 + 2 + 1/4 + 2/5 + 3 =539/60

539/60 — эквивалентная дробь для сложение нескольких дробей и целых чисел, таких как 1/2, 1, 5/3, 2, 1/4, 2/5 и 3.

Добавление нескольких положительных и отрицательных дробей

Решенный ниже пример с пошаговым вычислением может помочь пользователям узнать, как найти эквивалентную дробь, складывая несколько положительных и отрицательных дробей (с разными или разными знаменателями).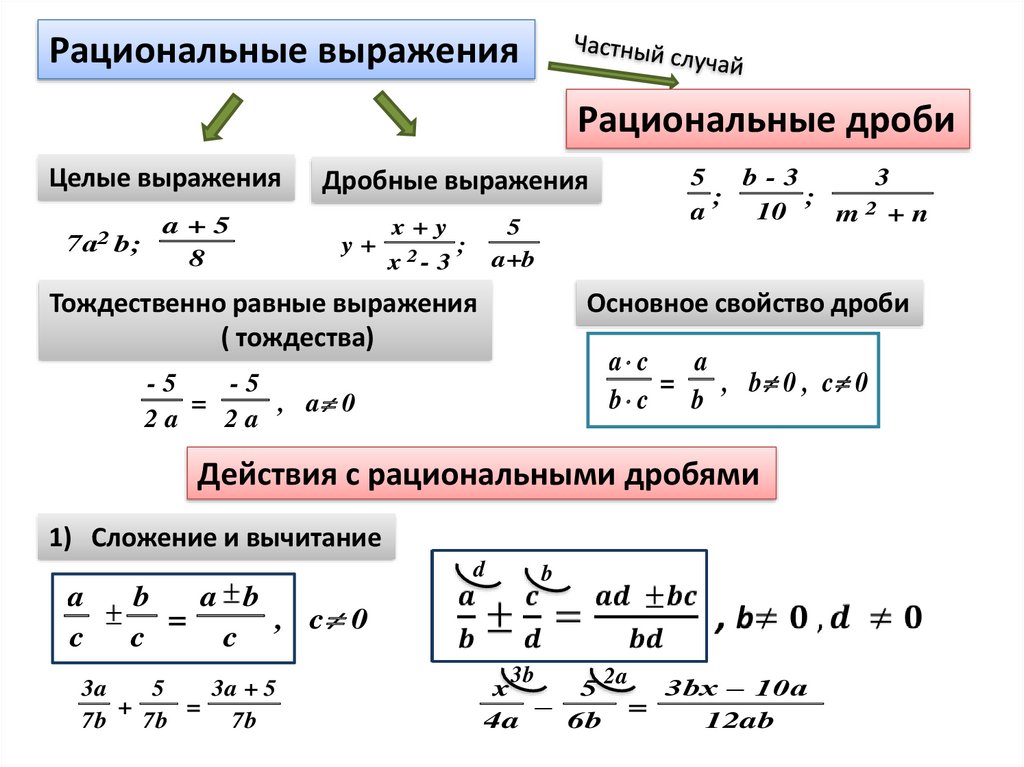

Задача
Найдите эквивалентную дробь для сложения положительных и отрицательных дробей 5/6, 1/3, -2/7, 1/6, -4/7 и 4/5.

шаг 1 Формула адреса и входные значения.
Входные значения:
5/6,1/3,-2/7,1/6,-4/7,4/5
5/6+1/3+-2/7+1/6+-4 /7+4/5= ?

Шаг 2 Найдите НОК (наименьшее общее кратное) для всех знаменателей, если все знаменатели не идентичны друг другу.
210 — НОК для знаменателей 6, 3, 7, 6, 7 и 5.

шаг 3 Умножьте НОК 210 на все числители и знаменатели каждой дроби
(5 х 210)/(6 х 210)+(1 х 210)/(3 х 210)+-(2 х 210)/(7 х 210)+(1 х 210)/(6 х 210)+ -(4 x 210)/(4 x 210)+(4 x 210)/(5 x 210)

шаг 4 Упростите и перепишите приведенное выше выражение, чтобы получить общие знаменатели
175/210+70/210-60/210 +35/210-210/210+24/210+168/210

шаг 5 Складываем все числители и упрощаем
=(175 + 70 — 60 + 35 — 210 + 24 + 168)/210
=202/210
=101/105
5/6+1/3+-2/7+1/6+-4/7+4/5=202/210

202/210 эквивалентная дробь для сложения нескольких положительных и отрицательные дроби 5/6 + 1/3 + (-2/7) + 1/6 + (-4/7) + 4/5.

Сложение двух или более дробей и смешанных чисел

Приведенный ниже пример решения для сложения двух или более дробей, смешанных чисел и целых чисел. Номера дробей включают правильные, неправильные, отрицательные или положительные дроби с одинаковыми или разными знаменателями. Ниже приведены пошаговые инструкции, как найти эквивалентную дробь для сложения нескольких дробей, смешанных и целых чисел 1/2, 1/3, 1/4, 6, 7 (1/5), 8 (1/6) и 1. /7. Задача
Найдите эквивалентную дробь для сложения нескольких дробей, смешанных и целых чисел 1/2, 1/3, 1/4, 6, 7(1/5), 8(1/6) и 1/7 .
Пошаговая тренировка

шаг 1 Адресная формула и вводимые значения.
Входные значения:
1/2,1/3,1/4, 6 ,71/5, 8 1/6,1/7
1/2+1/3+1/4 + 6 + 71/5+ 8 1/6 +1/7 = ?

шаг 2 Преобразуйте целые числа в дроби и перепишите, как показано ниже
6 = 6/1

шаг 3 Преобразуйте смешанные дроби в дроби и перепишите, как показано ниже
7 1/5= ((7 x 5) + 1)/5= 36/5
8 1/6= ((8 x 6) + 1)/6= 49/6

шаг 4 Расставьте все числа в виде дробей.
1/2+1/3 + 1/4 + 6/1+ 36/5+49/6+1/7

шаг 5 Для дробей с разными знаменателями найти НОК (наименьшее общее кратное) для всех знаменателей . 420 — НОК для 2, 3, 4, 1, 5, 6 и 7.

шаг 6 Умножьте НОК 420 на все числители и знаменатели каждой дроби
=(1 x 420)/(2 x 420)+( 1 x 420)/(3 x 420)+(1 x 420)/(4 x 420)+(6 x 420)/(1 x 420)+(36 x 420)/(5 x 420)+(49 x 420)/(6 x 420)+(1 x 420)/(7 x 420)

шаг 7 Упростите и перепишите приведенное выше выражение, чтобы получить общие знаменатели
=(1 х 210)/420 +(1 х 140)/420+(1 х 105)/420+(6 х 420)/420+(36 х 84)/420+(49 х 70)/420+ (1 x 60)/420
=210/420 +140/420+105/420+2520/420+3024/420+3430/420+60/420

шаг 5 Сложите все числители и упростите
=(210 + 140 + 105 + 2520 + 3024 + 3430 + 60)/420
=9489/420
=3163/140
1/2+1/3+1/4 + 6 + 71/5+ 8 1/6 +1 /7 = 3163/140

3163/140 эквивалентная дробь для сложения нескольких дробей, смешанных и целых чисел 1/2 + 1/3 + 1/4 + 6 + 7(1/5) + 8(1 /6) + 1/7.

Калькулятор умножения дробей — Онлайн калькуляторы

Калькулятор умножения дробей — Онлайн калькуляторы | Веб-расчет

Этот калькулятор умножения дробей позволяет умножать дроби, чтобы найти произведение. Вы вводите числитель и знаменатель каждой дроби, а калькулятор вычисляет произведение дробей.

Процесс умножения дробей заключается в перемножении числителей дробей, чтобы найти числитель произведения, а затем перемножении знаменателей дробей, чтобы найти знаменатель произведения. Полученную дробь затем упрощают, если это возможно.

Вы также можете добавить целые числа.

Целое число 1 (необязательно):
Числитель 1:
Знаменатель 1:
Целое число 2 (необязательно):
Числитель 2:
Знаменатель 2:

Калькулятор преобразования дробей в десятичную дробь
Калькулятор доли в проценты
Добавление калькулятора дробей
Калькулятор вычитания дробей

Как умножать дроби

Чтобы умножить дроби, выполните следующие действия:

1. Перемножьте числители (верхние числа) двух дробей.
Например, если вы хотите перемножить дроби 1/2 и 3/4, вы должны умножить 1 * 3 = 3.

2. Перемножьте знаменатели (нижние числа) двух дробей вместе.
Например, если вы хотите перемножить дроби 1/2 и 3/4, вы должны умножить 2 * 4 = 8.

3. Результатом шагов 1 и 2 является числитель и знаменатель дроби продукта.
Таким образом, в примере доля продукта составляет 3/8.

4. Если возможно, упростите результат.
Например, дробь 3/8 можно упростить до 3/8 = 3/8 * 1/1 = 3/8.

Вот еще один пример:

Чтобы умножить дроби 3/5 и 4/7, выполните следующие действия:

Умножьте числители: 3 * 4 = 12.
Умножьте знаменатели: 5 * 7 = 35,
Фракция продукта 12/35.
Если возможно, упростите результат: 12/35 = 12/35 * 1/1 = 4/15.

Таким образом, результат умножения дробей 3/5 и 4/7 равен 4/15.

Умножение смешанных дробей

Смешанная дробь представляет собой целое число, объединенное с дробью, например 3 1/2.