Мнк метод: Метод наименьших квадратов (Least-Squares method) · Loginom Wiki

Содержание

Метод наименьших квадратов (МНК)—Справка | ArcGIS Desktop

Краткая информация
Иллюстрация
Использование
Синтаксис
Пример кода
Параметры среды
Информация о лицензиях

Краткая информация

Выполняет глобальный Метод наименьших квадратов (МНК) для линейной регрессии, чтобы создать прогнозы или смоделировать зависимую переменную в терминах её взаимосвязей с описанными переменными.

Доступ к результатам этого инструмента (в том числе дополнительному PDF-файлу отчета) можно получить в окне Результаты (Results). Если отключить фоновую обработку, результаты также будут показаны в диалоговом окне Ход процесса (Progress).

Подробнее о том, как работает Метод наименьших квадратов (МНК)

Иллюстрация

Регрессия по Методу наименьших квадратов: предсказанные значения по отношению к наблюдаемым значениям

Использование

Основным результатом работы этого инструмента является файл отчета, который записывается в окне Результаты (Results). Если щелкнуть правой кнопкой мыши запись Сообщения (Messages) в окне Результаты (Results) и выбрать Вид (View), итоговый отчет инструмента Исследовательская регрессия можно будет просмотреть в диалоговом окне Сообщение (Message).
Примечание:

Если данный инструмент является частью пользовательского инструмента моделирования, дополнительные таблицы будут отображаться в окне Результаты только в том случае, если перед запуском инструмента они были заданы в качестве параметров модели.
Инструмент МНК также создает выходной класс объектов и дополнительные таблицы с информацией о коэффициентах и диагностике. Все это доступно в окне Результаты. Выходной класс объектов автоматически добавляется в таблицу содержания со схемой отображения горячих/холодных точек, применяемой к невязкам моделей. Полное пояснение по каждому результату см. в разделе Интерпретация результатов по МНК.
Результаты регрессии МНК являются заслуживающими доверия только в том случае, если ваши данные и регрессионная модель удовлетворяет всем допущениям, неотъемлемо требуемым этим методом. Проанализируйте таблицу Распространенные проблемы, последствия и решения регрессии в Основах анализа регрессии, чтобы гарантировать, что ваша модель должным образом определена.
Зависимые и независимые переменные должны храниться в числовых полях, содержащих разнообразие значений. МНК не может работать, когда все переменные имеют одинаковые значения (например, все значения для поля равны 9.0). Линейные методы регрессии, такие, как МНК, не являются подходящими для предсказания бинарных результатов (например, все значения для зависимой переменной равны или 1 или 0).
Поле Уникальный ID (Unique ID) связывает интерполяции модели с каждым объектом. Следовательно, значения поля Уникальный ID (Unique ID) должны быть уникальными для каждого объекта и, как правило, это поле должно быть постоянным полем, принадлежащим классу объектов. Если у вас нет поля Уникальный ID (Unique ID), вы можете легко создать его путем добавления нового целого поля в вашу таблицу класса объектов и введения значений поля, аналогичных полю FID/OID. Вы не можете непосредственно использовать поле FID/OID для параметра Уникальный ID (Unique ID).
Всякий раз, когда есть статистически значимая пространственная автокорреляция остатков регрессии, модель МНК будут считаться неопределенной и, следовательно, результаты регрессии по МНК будут ненадежными. Примените инструмент Пространственная автокорреляция к невязкам вашей регрессии, чтобы оценить потенциальные проблемы. Статистически значимая пространственная автокорреляция невязок регрессии почти всегда указывает на один или несколько недостающих ключевых независимых переменных модели.
Вы должны визуально оценить все очевидные отклонения прогнозов в большую и меньшую сторону в невязках вашей регрессии, чтобы увидеть, дают ли они представления о потенциальных недостающих переменных в вашей регрессионной модели. Иногда проведение Анализа горячих точек по невязкам помогает визуализировать пространственную кластеризацию отклонений прогнозов в большую и меньшую сторону.
Если неопределенность является результатом попытки моделировать нестационарные переменные, используя глобальную модель (МНК – это глобальная модель), то может быть использована Географически взвешенная регрессия для улучшения прогнозов и лучшего понимания нестационарности (региональных вариаций) в ваших независимых переменных.
Если результатом вычисления является бесконечность или неопределенность, результат для файлов, которые не являются шейп-файлами, будет Null; для шейп-файлов результат будет – DBL_MAX (например, -1.7976931348623158e+308).
Итоговые результаты диагностики модели записываются в итоговый отчет по МНК и в дополнительную выходную таблицу результатов диагностики. Обе записи включают результаты диагностики исправленного Информационного критерия Akaike (AICc), коэффициент определения, соединенную F-статистику, статистику Вальда, стьюдентизированную Кенкером статистику Бреуша-Пагана и статистику Жарке-Бера.
Диагностическая таблица также включает неисправленные значения AIC и квадратов Sigma.
Дополнительный коэффициент и/или диагностические выходные таблицы, если они уже существуют, будут переписаны, если отмечена опция перезаписи результатов операций геообработки.
Этот инструмент при необходимости создает PDF-файл отчета со сводным представлением результатов. PDF-файл не отображается автоматически в окне Каталога. Если вы хотите, чтобы PDF-файлы отображались в окне Каталога, откройте приложение ArcCatalog, выберите опцию меню Настройка (Customize), щелкните Опции ArcCatalog (ArcCatalog Options) и выберите закладку Типы файлов (File Types). Нажмите кнопку Новый тип (New Type) и укажите PDF, как показано ниже, для параметра Расширение файла (File Extension).
На компьютерах с языковыми пакетами ArcGIS для китайского или японского языков в Выходном файле отчета (Output Report File) формата PDF может отсутствовать текст или элементы форматирования. Эти проблемы можно исправить, изменив настройки шрифта.
Слои карты можно использовать для определения Входного класса объектов (Input Feature Class). Если в слое есть выборка, только выбранные объекты будут включены в анализ.

Внимание:

При использовании шейп-файлов, помните, что в них нельзя хранить нулевые (null) значения. Инструменты или другие процедуры, создающие шейп-файлы из прочих входных данных, могут хранить значения NULL в виде 0 или оперировать ими как нулем. В некоторых случаях нули в шейп-файлах хранятся как очень маленькие отрицательные числа. Это может привести к неожиданным результатам. Дополнительные сведения см. в разделе Рекомендации по геообработке выходных данных шейп-файла.

Синтаксис

OrdinaryLeastSquares_stats (Input_Feature_Class, Unique_ID_Field, Output_Feature_Class, Dependent_Variable, Explanatory_Variables, {Coefficient_Output_Table}, {Diagnostic_Output_Table}, {Output_Report_File})

Параметр	Объяснение	Тип данных
Input_Feature_Class	Класс пространственных объектов, содержащий зависимые и независимые переменные для анализа.	Feature Layer
Unique_ID_Field	Целое поле, содержащее разное значение для каждого объекта в Входном классе объектов.	Field
Output_Feature_Class	Выходной класс объектов с оценками зависимых переменных и невязками.	Feature Class
Dependent_Variable	Числовое поле, содержащее значения, для которых вы пытаетесь моделировать.	Field
Explanatory_Variables [Explanatory_Variables,…]	Перечень полей, представляющих независимые переменные в вашей регрессионной модели.	Field
Coefficient_Output_Table (Дополнительный)	Полный путь к дополнительной таблице, в которую будут записаны коэффициенты модели, стандартизированные коэффициенты, стандартные ошибки и вероятности для каждой независимой переменной.	Table
Diagnostic_Output_Table (Дополнительный)	Полный путь к дополнительной таблице, в которую будут записаны суммарные диагностические параметры модели.	Table
Output_Report_File (Дополнительный)	Полный путь к дополнительному PDF-файлу, создаваемому инструментом по вашему требованию. Этот файл отчета включает данные диагностики модели, графические данные и примечания, которые помогают интерпретировать результаты регрессии по МНК.	File

Пример кода

Пример OrdinaryLeastSquares 1 (Метод наименьших квадратов) (окно Python)

Следующий скрипт в окне Python демонстрирует, как использовать инструмент OrdinaryLeastSquares.

import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID","olsResults.shp", 
                                 "GROWTH","LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                                 "olsCoefTab.dbf","olsDiagTab.dbf")

Пример OrdinaryLeastSquares 2 (Метод наименьших квадратов) (автономный скрипт Python)

Следующий автономный скрипт Python демонстрирует, как использовать инструмент OrdinaryLeastSquares.

# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables. ..
workspace = r"C:\Data"
try:
    # Set the current workspace (to avoid having to specify the full path to the feature classes each time)
    arcpy.workspace = workspace
    # Growth as a function of {log of starting income, dummy for South
    # counties, interaction term for South counties, population density}
    # Process: Ordinary Least Squares... 
    ols = arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID", 
                        "olsResults.shp", "GROWTH",
                        "LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                        "olsCoefTab.dbf",
                        "olsDiagTab.dbf")
    # Create Spatial Weights Matrix (Can be based off input or output FC)
    # Process: Generate Spatial Weights Matrix... 
    swm = arcpy.GenerateSpatialWeightsMatrix_stats("USCounties.shp", "MYID",
                        "euclidean6Neighs.swm",
                        "K_NEAREST_NEIGHBORS",
                        "#", "#", "#", 6) 
                        
    # Calculate Moran's Index of Spatial Autocorrelation for 
    # OLS Residuals using a SWM File.
   
    # Process: Spatial Autocorrelation (Morans I)...      
    moransI = arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual",
                        "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE", 
                        "EUCLIDEAN_DISTANCE", "NONE", "#", 
                        "euclidean6Neighs.swm")
except:
    # If an error occurred when running the tool, print out the error message.
    print(arcpy.GetMessages())

Параметры среды

Выходная система координат (Output Coordinate System)
Географические преобразования (Geographic Transformations)
Текущая рабочая область (Current Workspace)
Временная рабочая область (Scratch Workspace)
Стандартизированные имена полей (Qualified Field Names)
Выходные данные содержат значения M (Output has M values)
Разрешение M (M Resolution)
Допуск M (M Tolerance)
Выходные данные содержат Z значения (Output has Z values)
Выходное значение Z по умолчанию (Default Output Z Value)
Разрешение Z (Z Resolution)
Допуск Z (Z Tolerance)
Разрешение XY (XY Resolution)
Допуск XY (XY Tolerance)

Информация о лицензиях

ArcGIS Desktop Basic: Да
ArcGIS Desktop Standard: Да
ArcGIS Desktop Advanced: Да

Связанные разделы

Метод наименьших квадратов

Метод наименьших квадратов (МНК) — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Данный метод применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

При применении МНК используется подстановка в начальные уравнения неизвестных величин. При этом в правых частях уравнений получаются если не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.

Система одновременных уравнений — это система уравнений, содержащая взаимозависимые переменные, которые включены в одно из уравнений модели в качестве результативного признака, а в другие уравнения — в качестве факторного признака. Коэффициенты системы одновременных уравнений нельзя определить обычным МНК, так как правая часть системы одновременных уравнений содержит эндогенные переменные. Наиболее распространенным методом для расчета является двухшаговый метод наименьших квадратов (ДМНК).

ДМНК состоит в следующем:

составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют ДМНК, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели;
обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.

ДМНК производит оценку коэффициентов заданного регрессионного уравнения: y = Y·a + X·b + u.

Где:

y. Зависимая переменная уравнения;
Y. Матрица n*g наблюдений над другими значениями эндогенных переменных, входящих в уравнение;
X. Матрица n*k наблюдений над предопределёнными переменными, входящими в уравнение;
a. Вектор g*1 структурных коэффициентов, относящихся к переменным из матрицы Y;
b. Вектор k*1 коэффициентов, относящихся к переменным из матрицы X;
u. Вектор n*1 случайных возмущений.

Метод применяется для оценивания коэффициентов модели y = Xβ + e, минимизирующей сумму квадратов отклонений e’e. Оценивание выполняется по формуле β = (X’X)-1X’Y.

При этом особо рассматривается случай мультиколлинеарности, когда матрица X’X близка к вырожденной (абсолютная величина определителя мала). В этих случаях оценка коэффициентов неоднозначна вследствие линейной зависимости столбцов матрицы X. Для получения однозначной оценки исключаем столбцы из матрицы X до тех пор, пока она не станет иметь максимальный ранг.

Взвешивание применяется для оценивания коэффициентов модели Y =Xβ + ε в предположении гетероскедастичности остатков .

Случай сводится к стандартной модели множественной линейной регрессии с гомоскедастичными остатками несложным преобразованием:

Оценивание полученной модели выполняется стандартным МНК.

В случае линейной регрессионной модели Y =Xβ + ε в предположении распределения остатков ε по закону N(0, σ2Ω) с заданной матрицей ковариаций Ω, оценка доступного обобщенного метода наименьших квадратов реализуется формулой:

При наличии в модели константы, подлежащей автоматическому оцениванию, следует дополнить матрицу X единичным столбцом.

См. также:

Линейная регрессия | Контейнер моделирования: модель «Линейная регрессия (оценка МНК)» | Анализ временных рядов: Линейная регрессия | IModelling.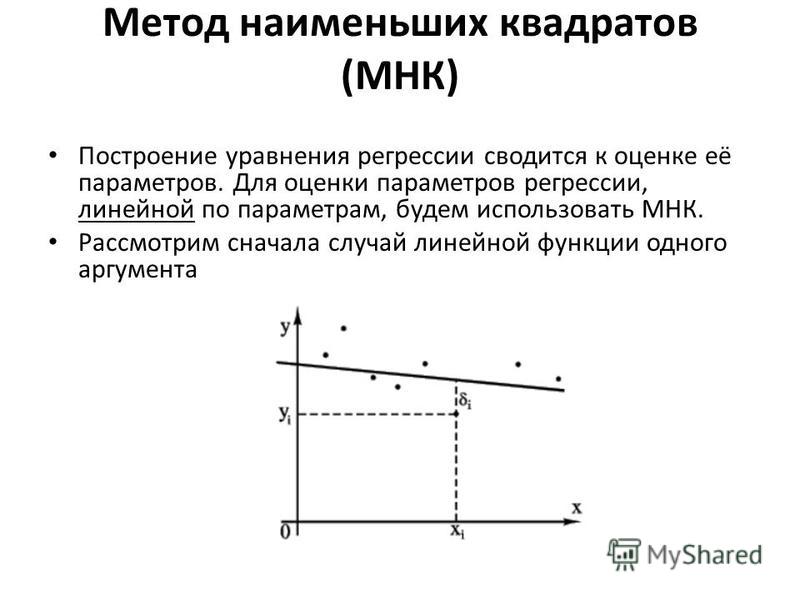 Ols | ISmSimultaneousSystem

Метод наименьших квадратов – формула, определение, примеры

Метод наименьших квадратов – это процесс нахождения линии регрессии или наиболее подходящей линии для любого набора данных, описываемого уравнением. Этот метод требует уменьшения суммы квадратов остаточных частей точек от кривой или линии, а тенденция исходов находится количественно. Метод подгонки кривой виден, в то время как регрессионный анализ и уравнения подгонки для получения кривой представляют собой метод наименьших квадратов.

Давайте рассмотрим простой пример. Мисс Долма сказала в классе: «Ученики, которые тратят больше времени на свои задания, получают более высокие оценки». Учащийся хочет оценить свою оценку за то, что потратил на задание 2,3 часа. С помощью магии метода наименьших квадратов можно определить прогностическую модель, которая поможет ему гораздо точнее оценивать оценки. Этот метод намного проще, потому что он не требует ничего, кроме некоторых данных и, возможно, калькулятора.

В этом разделе мы изучим метод наименьших квадратов, поймем, что он означает, изучим общую формулу, шаги для ее построения на графике, узнаем, каковы ее ограничения, и посмотрим, какие приемы мы можем использовать с методом наименьших квадратов.

1.	Определение метода наименьших квадратов
2.	Ограничения для метода наименьших квадратов
3.	График метода наименьших квадратов
4.	Формула метода наименьших квадратов
5.	Часто задаваемые вопросы о методе наименьших квадратов

Определение метода наименьших квадратов

Метод наименьших квадратов — это статистический метод, используемый для нахождения линии наилучшего соответствия формы уравнения, такого как y = mx + b, заданным данным. Кривая уравнения называется линией регрессии. Наша главная цель в этом методе — максимально уменьшить сумму квадратов ошибок. Именно поэтому этот метод называется методом наименьших квадратов. Этот метод часто используется при подборе данных, когда предполагается, что результат наилучшего подбора уменьшает сумму квадратов ошибок, которая считается разницей между наблюдаемыми значениями и соответствующим подобранным значением. Сумма квадратов ошибок помогает найти изменение в наблюдаемых данных. Например, у нас есть 4 точки данных, и с помощью этого метода мы получаем следующий график.

Две основные категории задач наименьших квадратов — это обычные или линейные задачи наименьших квадратов и нелинейные задачи наименьших квадратов.

Ограничения для метода наименьших квадратов

Несмотря на то, что метод наименьших квадратов считается лучшим методом поиска линии наилучшего соответствия, он имеет несколько ограничений. Вот они:

Этот метод демонстрирует только взаимосвязь между двумя переменными. Все остальные причины и следствия во внимание не принимаются.
Этот метод ненадежен, если данные распределены неравномерно.
Этот метод очень чувствителен к выбросам. Фактически, это может исказить результаты анализа методом наименьших квадратов.

График метода наименьших квадратов

Посмотрите на график ниже, прямая линия показывает потенциальную связь между независимой переменной и зависимой переменной. Конечная цель этого метода состоит в том, чтобы уменьшить эту разницу между наблюдаемым откликом и откликом, предсказанным линией регрессии. Меньший остаток означает, что модель подходит лучше. Точки данных необходимо минимизировать методом уменьшения остатков каждой точки от линии. Различают вертикальные невязки и перпендикулярные невязки. Вертикаль в основном используется в задачах с полиномами и гиперплоскостями, тогда как перпендикулярность используется в целом, как показано на изображении ниже.

Формула метода наименьших квадратов

Метод наименьших квадратов — это кривая, которая лучше всего соответствует набору наблюдений с минимальной суммой квадратов невязок или ошибок.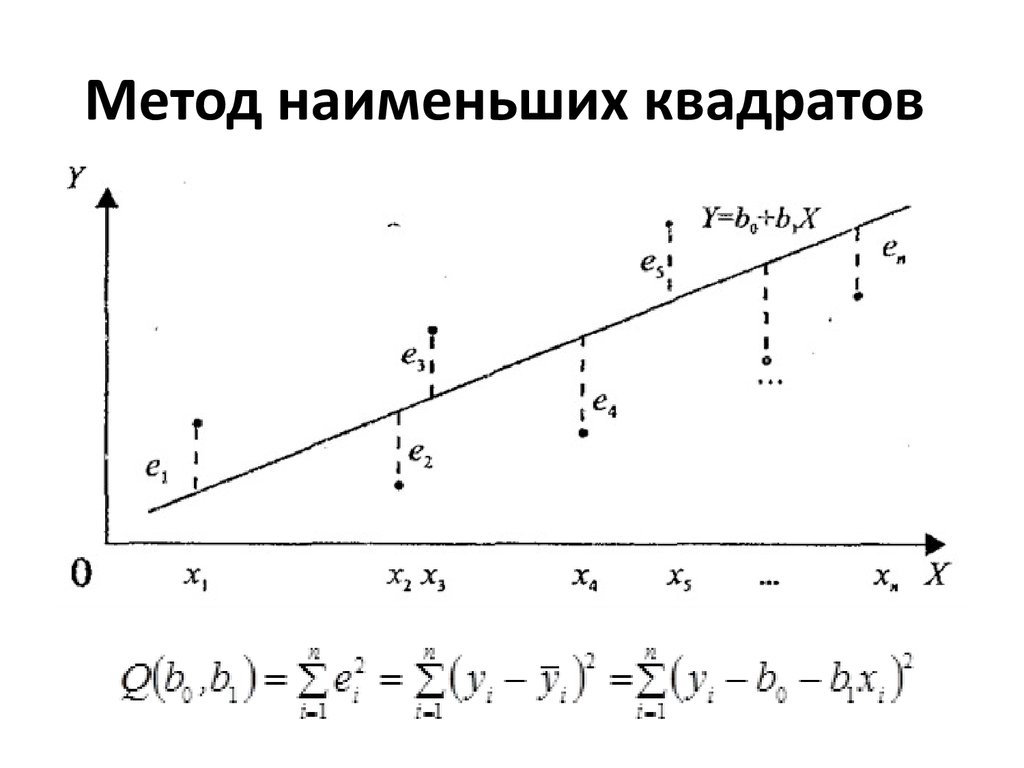 Предположим, что заданы точки данных (x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ ), …, (x _n , y _n ), в котором все x являются независимыми переменными, а все y являются зависимыми. Этот метод используется для нахождения линейной линии вида y = mx + b, где y и x — переменные, m — наклон, а b — точка пересечения с осью y. Формула для расчета уклона m и значения b:

m = (n∑xy — ∑y∑x)/n∑x ² — (∑x) ²

b = (∑y — m∑x)/n

Здесь n – количество точек данных.

Ниже приведены шаги для вычисления метода наименьших квадратов с использованием приведенных выше формул.

Шаг 1: Нарисуйте таблицу с 4 столбцами, где первые два столбца соответствуют точкам x и y.
Шаг 2: В следующих двух столбцах найдите xy и (x) ² .
Шаг 3: Найдите ∑x, ∑y, ∑xy и ∑(x) ² .
Шаг 4: Найдите значение уклона m, используя приведенную выше формулу.
Шаг 5: Рассчитайте значение b по приведенной выше формуле.
Шаг 6: Подставьте значения m и b в уравнение y = mx + b

Давайте рассмотрим пример, чтобы лучше понять это.

Пример: Допустим, у нас есть данные, как показано ниже.

х	1	2	3	4	5
у	2	5	3	8	7

Решение: Мы будем следовать шагам, чтобы найти линейную линию.

х	и	ху	х ²
1	2	2	1
2	5	10	4
3	3	9	9
4	8	32	16
5	7	35	25
∑x =15	∑у = 25	∑ху = 88	∑x ² = 55

Найдите значение m по формуле ×88) – (15×25)]/(5×55) – (15) ²

м = (440 – 375)/(275 – 225)

m = 65/50 = 13/10

Найдите значение b по формуле

b = (25 — 19,5)/5

b = 5,5/5

Итак, требуемое уравнение наименьших квадратов: y = mx + b = 13/10x + 5,5/5.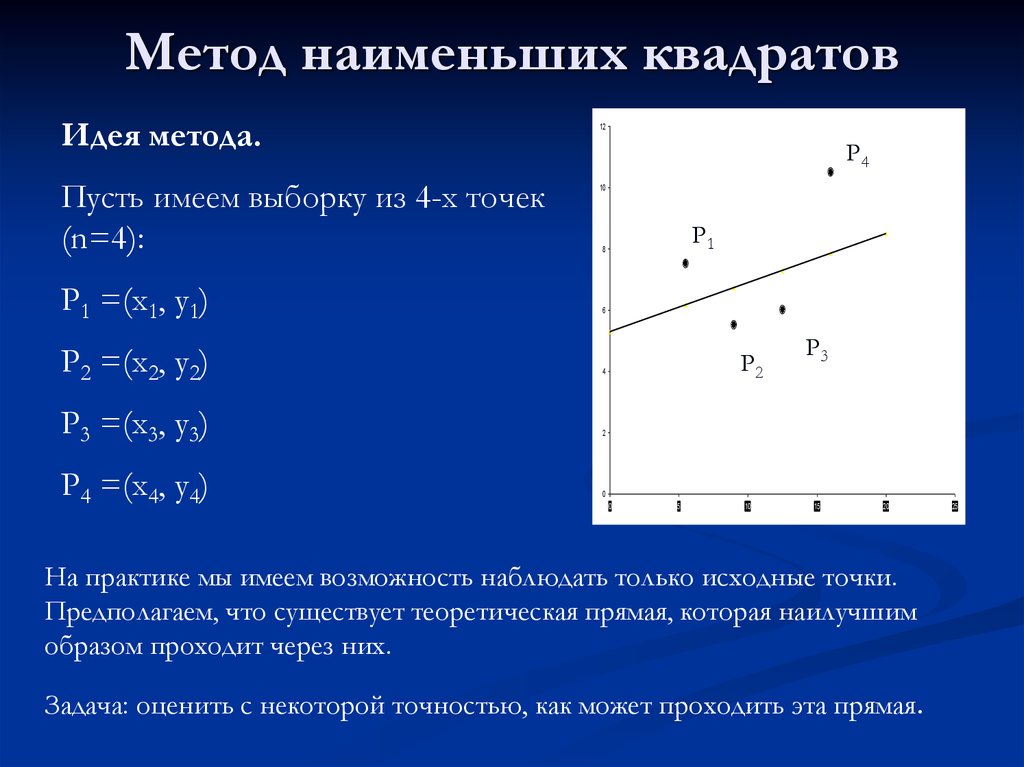

Важные примечания

Метод наименьших квадратов используется для прогнозирования поведения зависимой переменной по отношению к независимой переменной.
Сумма квадратов ошибок называется дисперсией.
Основной целью метода наименьших квадратов является минимизация суммы квадратов ошибок.

Связанные темы

Ниже перечислены некоторые темы, связанные с методом наименьших квадратов.

Парабола
Гипербола
график x и y
Склон

Часто задаваемые вопросы о методе наименьших квадратов

Для чего используются обычные методы наименьших квадратов?

Обычный метод наименьших квадратов используется для поиска прогностической модели, которая лучше всего соответствует нашим точкам данных.

Метод наименьших квадратов — это то же самое, что и линейная регрессия?

Нет, линейная регрессия и метод наименьших квадратов — это не одно и то же. Линейная регрессия — это анализ статистических данных для прогнозирования значения количественной переменной. Метод наименьших квадратов — это один из методов, используемых в линейной регрессии для поиска прогностической модели.

Как выбросы влияют на линию регрессии методом наименьших квадратов?

Наличие необычных точек данных может исказить результаты линейной регрессии. Это делает достоверность модели очень важной для получения обоснованных ответов на вопросы, мотивирующие формирование прогностической модели.

Что такое формула метода наименьших квадратов?

Для определения уравнения прямой для любых данных нам нужно использовать уравнение y = mx + b. Формула метода наименьших квадратов заключается в нахождении значения m и b по формулам:

m = (n∑xy — ∑y∑x)/n∑x ² — (∑x) ²

b = (∑y — m∑x)/n

Здесь n — количество точек данных.

Что такое метод наименьших квадратов в регрессии?

Регрессия по методу наименьших квадратов помогает вычислить линию наилучшего соответствия набора данных как по уровням активности, так и по соответствующим общим затратам.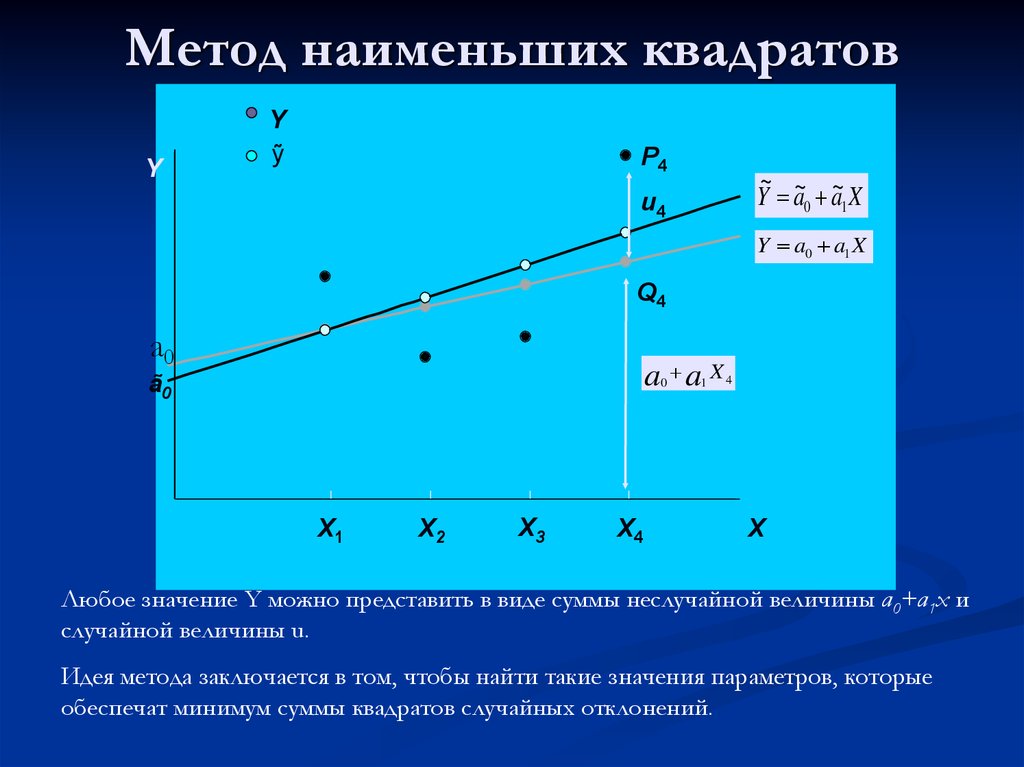 Идея вычисления состоит в том, чтобы минимизировать сумму квадратов вертикальных ошибок между точками данных и функцией стоимости.

Почему используется метод наименьших квадратов?

Метод наименьших квадратов используется как эквивалент максимального правдоподобия, когда остатки модели нормально распределены со средним значением 0.

Что такое Аппроксимация кривой методом наименьших квадратов?

Метод наименьших квадратов — это процесс подбора кривой по заданным данным. Это один из методов, используемых для определения линии тренда для заданных данных.

Используйте НАИМЕНЬШИЙ способ решения проблем для рассмотрения жалоб клиентов

Поиск:

Наши блоги > Статьи круглосуточного магазина > Сообщение в блоге

Менеджмент, обучение

Проблемы с обслуживанием клиентов неизбежны в бизнесе круглосуточного магазина. Иногда у клиентов есть законная жалоба, которая требует вашего немедленного внимания. В других случаях проблема может быть незначительной или полностью вне вашего контроля.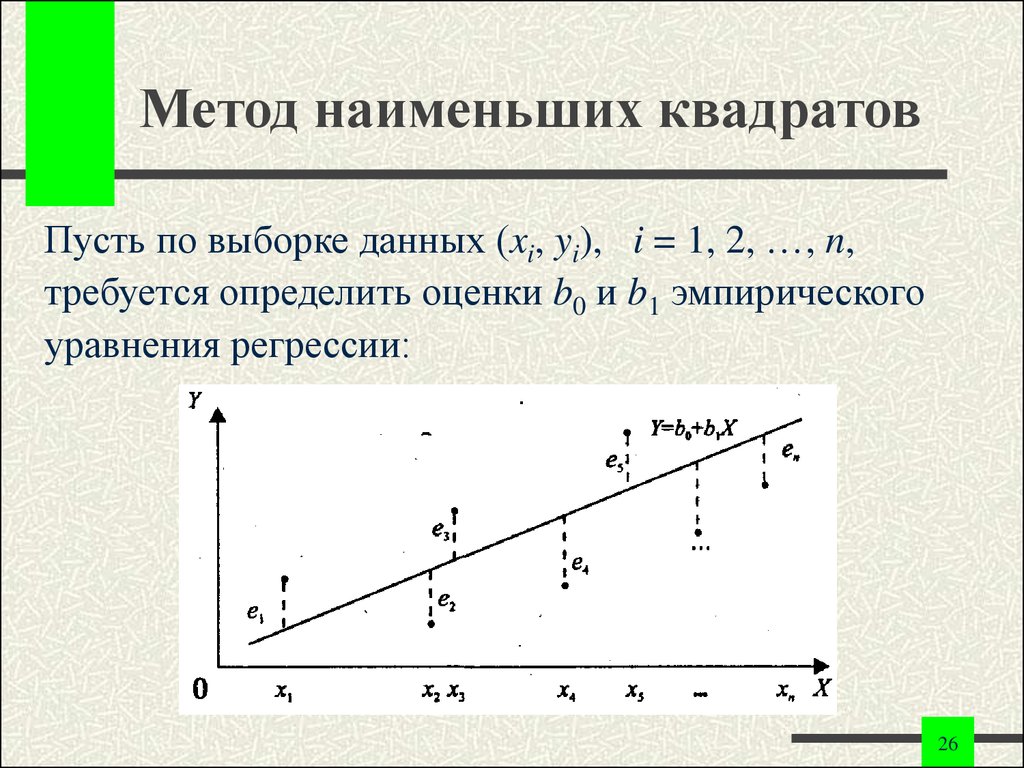 Независимо от того, в чем проблема, каждый недовольный клиент заслуживает вашего внимания. НАИМЕНЬШАЯ техника решения проблем гарантирует, что клиенты будут услышаны и, что более важно, оценены.

Следуйте LEAST, чтобы решить жалобы клиентов

Аббревиатура L-E-A-S-T может помочь вам и вашим сотрудникам решить большинство проблем, с которыми сталкиваются клиенты. Вот шаги:

L означает слушать: Когда у клиента возникает проблема, самое первое, что вам нужно сделать, это выслушать его беспокойство. Будьте внимательны и не перебивайте. Будьте терпеливы и убедитесь, что вы полностью понимаете беспокойство клиента.

E для Empathize: Поставьте себя на место клиента. Если вы не можете связать точную проблему, вспомните время, когда вы были разочарованы. Оставайтесь на связи с клиентом. Если вы покажетесь скучающим или незаинтересованным, клиент будет чувствовать себя проигнорированным.

A означает извиниться: Искреннее «извините» имеет большое значение для решения проблемы. Всегда говорите клиенту, что вы сожалеете о его негативном опыте, даже если вы не сделали ничего плохого.

S означает Решить: Этот шаг является наиболее важным: предложить решение. Используйте здравый смысл, чтобы найти решение, приемлемое для клиента. Если вы не можете решить проблему немедленно, сообщите им, что вы поговорите со своим менеджером. Не перекладывайте ответственность и не давайте обещаний, которые вы не можете выполнить.

T is for Благодарность: Всегда благодарите покупателя за то, что он обратил ваше внимание на проблему, и за то, что он в первую очередь выбрал ваш магазин. Покупатель, который чувствует, что его ценят, с большей вероятностью даст вам и вашему магазину второй шанс.

Найдите силу в профилактике и подготовке

Проактивность поможет вам предотвратить многие распространенные жалобы клиентов. Например, когда вы превосходите потребности в персонале, вы можете предотвратить проблемы, связанные с нехваткой персонала. Если вы будете следовать передовым методам заказа и получения, вы сможете избежать проблем, связанных с отсутствующими товарами. Когда вы должным образом обучаете персонал своего магазина, вы можете превзойти ожидания клиентов благодаря отличному обслуживанию. Даже если вы делаете все возможное, чтобы избежать проблем с обслуживанием клиентов, они все равно будут время от времени возникать. Подготовка является ключевым моментом. Сотрудники, которые обучены использовать НАИМЕНЬШИЙ метод решения проблем, имеют возможность создать более положительное впечатление о вашем магазине, чем если бы у покупателя никогда не было проблем.

Тренинг по наименьшему количеству проблем

Наш пакет обучения для интернет-магазинов включает в себя курс, специально посвященный реализации стратегии решения наименьших проблем в условиях магазина. Нажмите здесь для предварительного просмотра и узнать больше.

Подпишитесь на наши блоги

Не пропустите ни одной статьи.

Статьи по теме

Менеджмент

Альберт Эйнштейн однажды сказал: «Если вы хотите прожить счастливую жизнь, привяжите ее к цели, а не к людям или предметам».