Многоугольник распределения дискретной случайной величины: Многоугольник распределения — примеры

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).

Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. 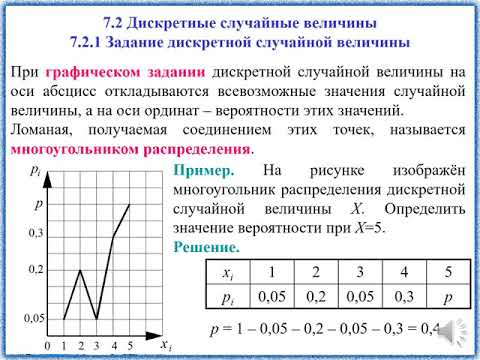Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

Закон распределения дискретной случайной величины. Многоугольник распределения — Мегаобучалка

Введение

 

Настоящее учебно-методическое пособие написано авторами на основе многолетнего опыта преподавания теории вероятностей в общем курсе “Высшая математика” на химическом факультете ННГУ.

Учебно-методическое пособие содержит краткие теоретические сведения, такие как понятие случайной величины, законы распределения случайных величин, функция распределения, числовые характеристики случайных величин, а также важнейшие законы распределения случайных величин.

Пособие включает в себя подробно решенные типовые задачи и достаточно большое количество разнообразных задач с ответами для самостоятельной работы.

Данное учебно-методическое пособие носит учебный характер. Его цель – помочь студентам лучше усвоить общие теоретические положения и развить навыки в их применении при решении конкретных задач.

 

Понятие случайной величины. Закон распределения случайной величины

Одним из важнейших понятий теории вероятностей (наряду со случайным событием и вероятностью) является понятие случайной величины.

Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, причем заранее, до опыта, неизвестно, какое именно.

Случайные величины обозначаются заглавными буквами латинского алфавита – , , , …, а принимаемые ими значения — соответствующими малыми буквами .

Случайная величина, принимающая конечное или счетное множество значений: называется дискретной или прерывной случайной величиной.

Непрерывной случайной величиной называется случайная величина, бесконечное несчетное множество возможных значений которой есть некоторый промежуток (конечный или бесконечный) числовой оси. (Строгое определение непрерывной случайной величины будет дано ниже).

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

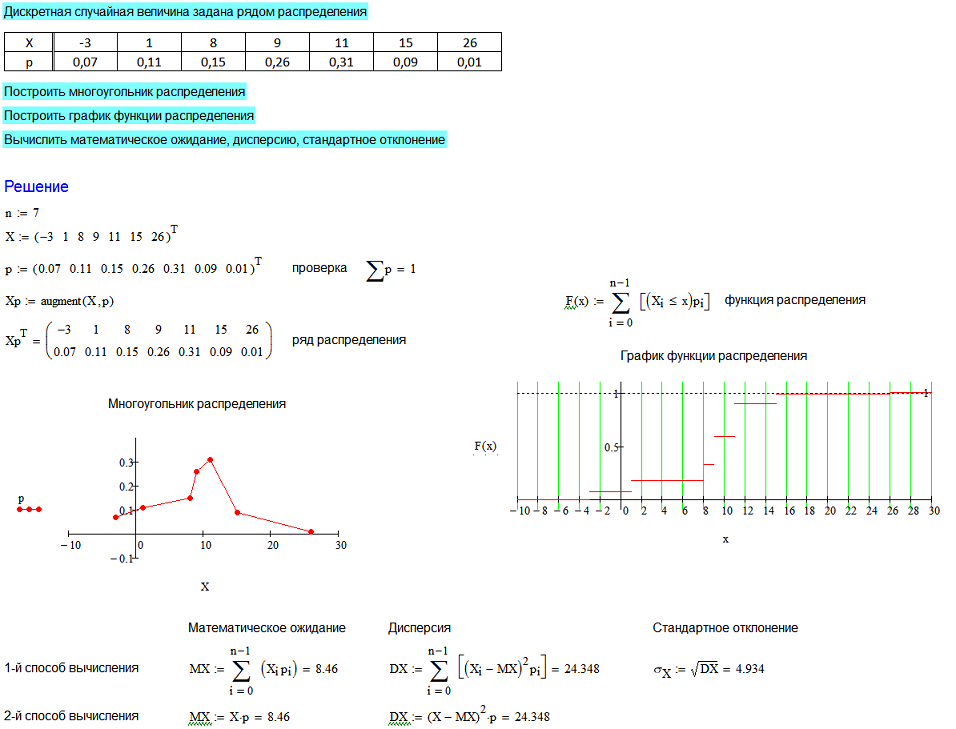
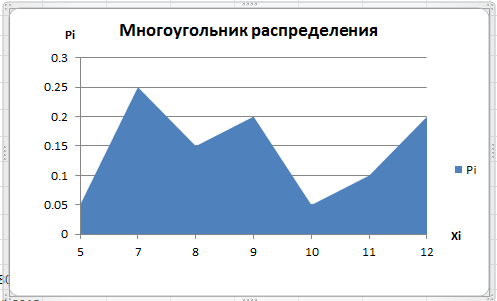
Закон распределения дискретной случайной величины. Многоугольник распределения

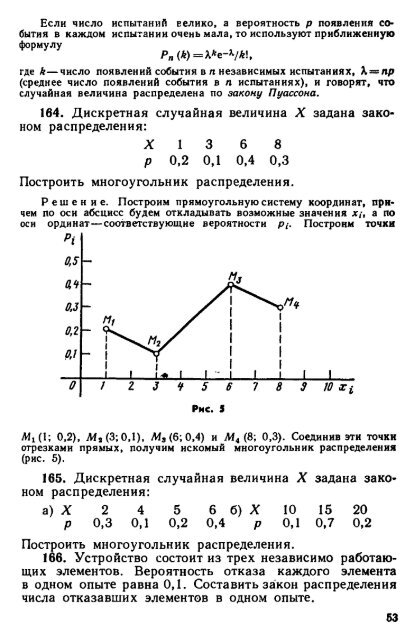
Закон распределения может иметь разные формы. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискретной случайной величины X является таблица (матрица), в которой в порядке возрастания перечислены все возможные значения случайной величины и соответствующие их вероятности, т.е.

или , где ; .

Такая таблица называется рядом распределениядискретной случайной величины X.

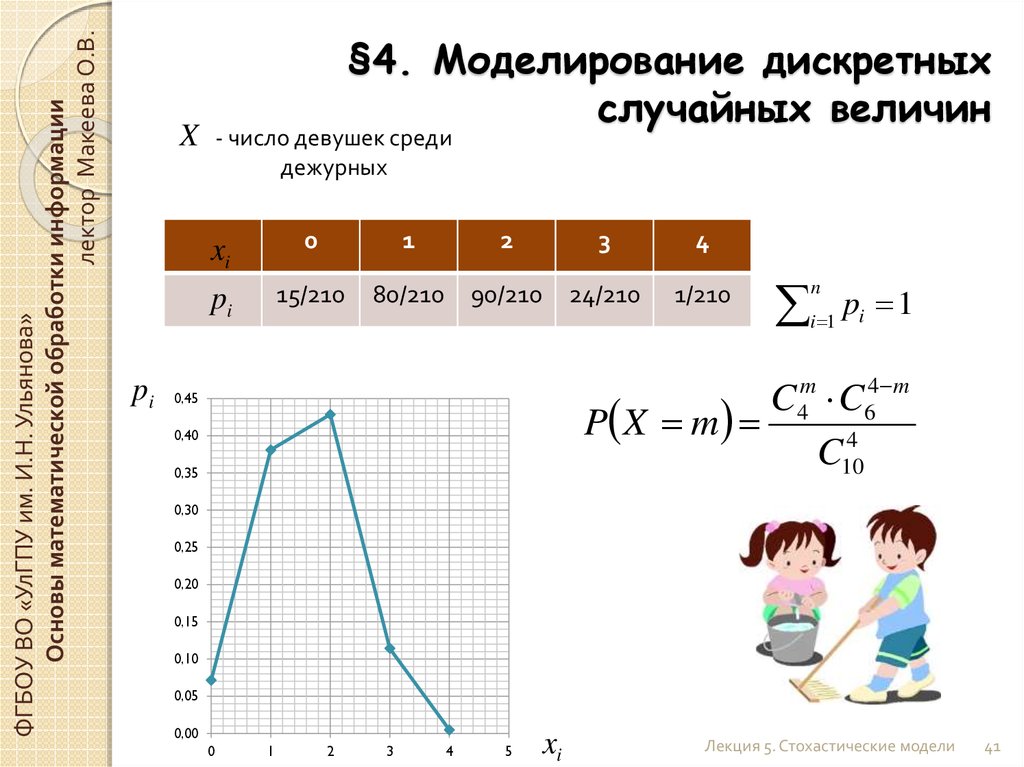
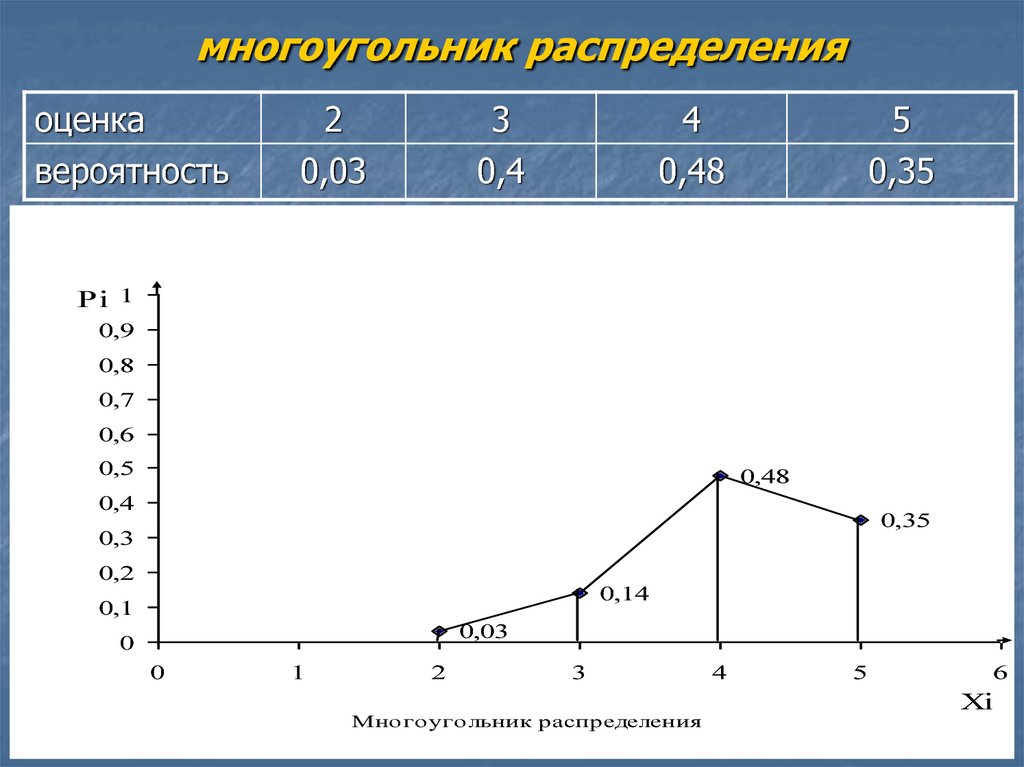
Графическое изображение ряда распределения (см. рис.1) называется многоугольником (или полигоном) распределения.

Рис. 1

4.2 Вероятностное распределение дискретной случайной величины – Введение в статистику

• Распознавать, понимать и строить дискретные распределения вероятностей.

Случайная величина описывает результаты статистического эксперимента словами. Значения случайной величины могут меняться при каждом повторении эксперимента.

---

_{Посмотрите это видео: Случайные величины и распределения вероятностей от Dr Nic’s Maths and Stats [4:38]}

---

Распределение вероятностей n для случайной величины содержит список всех возможных значений случайной величины и вероятности, которую случайная величина принимает при каждом значении. Распределение вероятностей для случайной величины описывает, как вероятности распределяются по значениям случайной величины. Распределение вероятностей может быть таблицей со столбцом для значений случайной величины и другим столбцом для соответствующей вероятности или графиком, например гистограммой со значениями случайной величины на горизонтальной оси и вероятностями на вертикальной оси. ось.

В распределении вероятностей каждая вероятность находится в диапазоне от 0 до 1 включительно. Поскольку все возможные значения случайной величины включены в распределение вероятностей, сумма вероятностей равна 1,

.

Детский психолог интересуется, сколько раз плач новорожденного ребенка будит его мать после полуночи. Для случайной выборки из 50 матерей была получена следующая информация. Пусть [latex]X[/latex] будет количеством раз в неделю, когда плач новорожденного ребенка будит его мать после полуночи. В этом примере значения случайной величины равны [латекс]х = 0, 1, 2, 3, 4, 5[/латекс].

В таблице левый столбец содержит все возможные значения случайной величины, а правый столбец [latex]P(x)[/latex] представляет собой вероятность того, что [latex]X[/latex] примет соответствующее значение [латекс]х[/латекс]. Например, в первой строке значение случайной величины равно 0, а вероятность того, что случайная величина равна 0, равна [латекс]\displaystyle{\frac{2}{50}}[/latex]. В контексте данного примера это означает, что вероятность того, что плач новорожденного ребенка разбудит его мать 0 раз в неделю, равна [латекс]\displaystyle{\frac{2}{50}}[/latex].

«>

[латекс]x[/латекс]	[латекс]P(x)[/латекс]
0	[латекс]\фракция{2}{50}[/латекс]
1	[латекс]\фракция{11}{50}[/латекс]
2	[латекс]\фракция{23}{50}[/латекс]
3	[латекс]\frac{9}{50}[/латекс]
4	[латекс]\frac{4}{50}[/латекс]
5	[латекс]\фракция{1}{50}[/латекс]

Поскольку [латекс]X[/латекс] может принимать только значения 0, 1, 2, 3, 4 и 5, [латекс]Х[/латекс] является дискретной случайной величиной. Обратите внимание, что каждая вероятность находится в диапазоне от 0 до 1, а сумма вероятностей равна 1:

 

[латекс]\displaystyle{\frac{2}{50}+\frac{11}{50}+\frac{23 {50}+\frac{9}{50}+\frac{4}{50}+\frac{1}{50}=1}[/latex]

Предположим, Нэнси занимается три дня в неделю.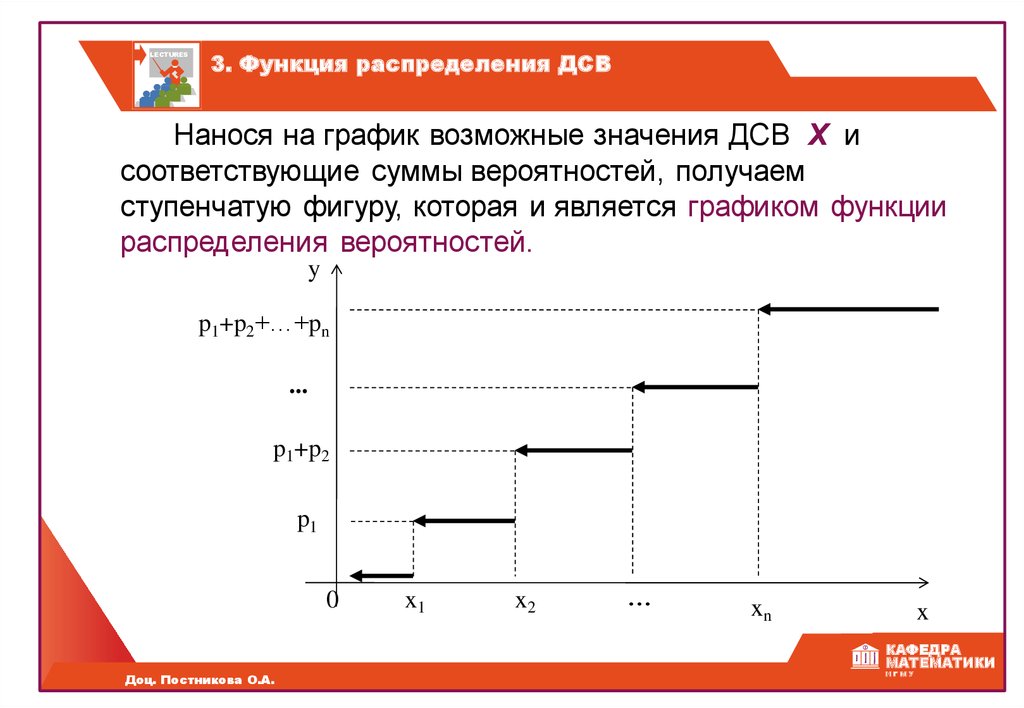 Она посещает занятия три дня в неделю 80 % времени, два дня в неделю 15 % времени, один день в неделю 4 % времени и ни дня 1 %   времени. Предположим, что одна неделя выбрана случайным образом.

1. Пусть [латекс]Х[/латекс] будет количеством дней Нэнси ____________________.
2. [латекс]Х[/латекс] принимает какие значения?
3. Предположим, что одна неделя выбрана случайным образом. Постройте таблицу распределения вероятностей, как в примере выше. В таблице должно быть два столбца с пометками [latex]x[/latex] и [latex]P(x)[/latex]. Чему равна сумма столбца [latex]P(x)[/latex]?

Нажмите, чтобы увидеть Решение

1. Пусть [latex]X[/latex] будет количеством дней, в течение которых Нэнси посещает занятия в неделю.
2. 0, 1, 2 и 3.

3. [латекс]x[/латекс]	[латекс]P(x)[/латекс]
   0	0,01
   1	0,04
   2	0,15
   3	0,80

   Сумма столбца [latex]P(x)[/latex] равна 1,

Джеремайя занимается баскетболом два дня в неделю. Девяносто процентов времени он посещает обе тренировки. Восемь процентов времени он посещает одну тренировку. В двух процентах случаев он не посещает ни одну из тренировок. Что такое [latex]X[/latex] и какие значения он принимает?

Решение:

[латекс]X[/латекс] — это количество дней, в течение которых Иеремия посещает баскетбольные тренировки в неделю. [latex]X[/latex] принимает значения 0, 1 и 2.

---

_{Посмотрите это видео: Построение распределения вероятностей для случайной величины от Khan Academy [6:47]}

---

Обзор концепции

4.1 Функция распределения вероятностей (PDF) для дискретной случайной величины — статистика

Существует два типа случайных величин: дискретные случайные величины и непрерывные случайные величины.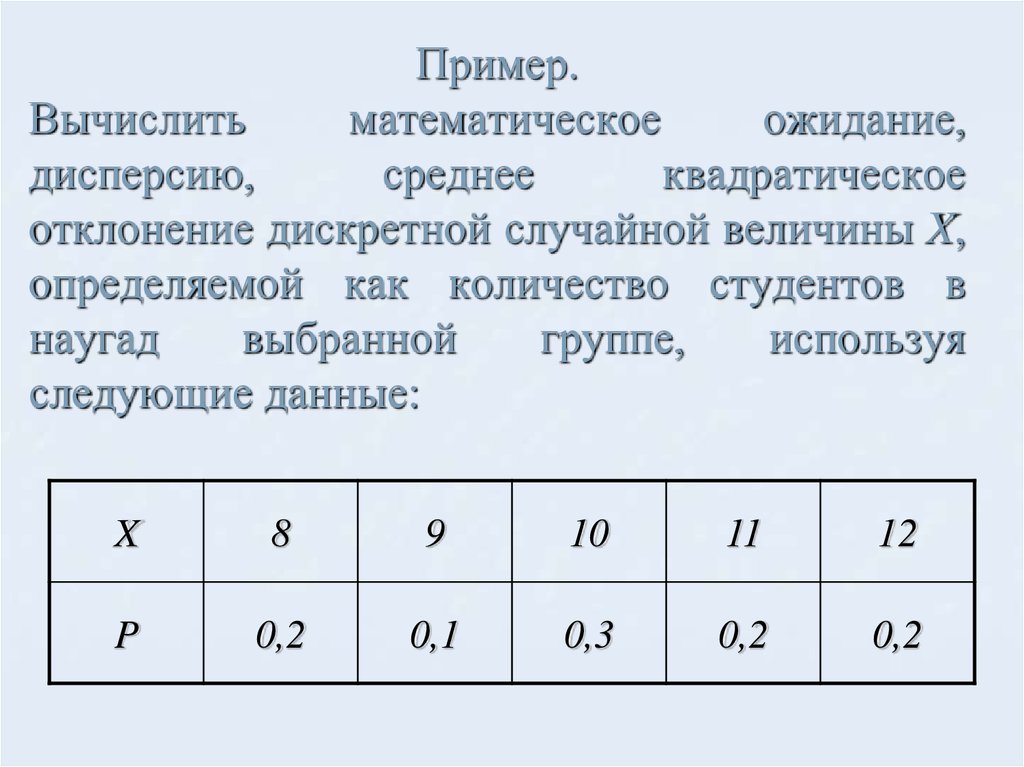 Значения дискретной случайной величины являются счетными, что означает, что значения получены путем подсчета. Все случайные величины, которые мы обсуждали в предыдущих примерах, являются дискретными случайными величинами. Мы подсчитали количество красных шаров, количество голов или количество девочек, чтобы получить соответствующие значения случайной величины. Ценности непрерывная случайная величина являются несчетными, что означает, что значения не получены путем подсчета. Вместо этого они получаются путем измерения. Например, пусть X = температура случайно выбранного дня в июне в городе. Значение X может быть 68°, 71,5°, 80,6° или 90,32°. Эти значения получают путем измерения термометром. Другим примером непрерывной случайной величины является рост случайно выбранного старшеклассника. Значение этой случайной величины может быть 5 футов 2 дюйма, 6 футов 1 дюйм или 5 футов 8 дюймов. Эти значения получаются путем измерения линейкой.

Дискретная функция распределения вероятностей имеет две характеристики:

1. Каждая вероятность находится в диапазоне от нуля до единицы включительно.
2. Сумма вероятностей равна единице.

Пример 4.1

Детский психолог интересуется, сколько раз плач новорожденного ребенка будит его мать после полуночи. Для случайной выборки из 50 матерей была получена следующая информация. Пусть X = количество раз в неделю, когда плач новорожденного ребенка будит его мать после полуночи. Для этого примера x = 0, 1, 2, 3, 4, 5.

P ( x ) = вероятность того, что x примет значение x .

х	Р ( х )
0	Р ( х = 0) = 250250
1	Р ( х = 1) = 11501150
2	Р ( х = 2) = 23502350
3	Р ( х = 3) = 950950
4	Р ( х = 4) = 450450
5	P ( х = 5) = 150150

Стол 4. 2

X принимает значения 0, 1, 2, 3, 4, 5. Это дискретный PDF, потому что мы можем подсчитать количество значений x , а также по следующим двум причинам:

1. Каждый P ( x ) находится в диапазоне от нуля до единицы, поэтому включительно
2. Сумма вероятностей равна единице, то есть

250+1150+2350+950+450+150=1250+1150+2350+950+450+150=1

Пример 4.2

Предположим, у Нэнси занятия три дня в неделю. Она посещает занятия три дня в неделю 80 процентов времени, два дня 15 процентов раз, один день 4 процента времени и без дней 1 процент времени. Предположим, что одна неделя выбрана случайным образом.

Проблема

Опишите случайную величину словами. Пусть X = количество дней Нэнси ________.