минус | это… Что такое минус?
ТолкованиеПеревод
- минус
- ми́нус
сущ., м., употр. сравн. часто
Морфология: (нет) чего? ми́нуса, чему? ми́нусу, (вижу) что? ми́нус, чем? ми́нусом, о чём? о ми́нусе; мн. что? ми́нусы, (нет) чего? ми́нусов, чему? ми́нусам, (вижу) что? ми́нусы, чем? ми́нусами, о чём? о ми́нусах
1. В математике минус — это знак -, который обозначает действие вычитания или указывает на отрицательную величину.
Поставить минус. | Минус пять в третьей степени.
2. Слово минус обозначает само действие вычитания или саму отрицательную величину.
Десять минус шесть равно четыре.
3. Слово минус используется для обозначения отрицательного значения температуры (ниже 0 градусов по шкале Цельсия).
Сегодня обещали до минус пятнадцати.
4. Если ученик получил оценку пять, четыре и т. п. с минусом, значит, его знания немного ниже, чем оценка пять, четыре и т. п.
За диктант мне поставили четыре с минусом.
5. Минусом называют недостаток, отрицательную сторону чего-либо или кого-либо.
Данная технология имеет свои минусы. | В каждом человеке есть плюсы и минусы. | Его главный минус — лень.
6.
Если вы остались в минусе, значит, вы понесли убытки, вложили денег больше, чем получили; разговорное выражение. Предприниматель может легко остаться в минусе. | Баланс не сходится, вы в минусе.
• ми́нусовый прил.
• вариант: минусо́вый
Минусовая величина. | Минусовая температура.
Если вы остались в минусе, значит, вы понесли убытки, вложили денег больше, чем получили; разговорное выражение. Толковый словарь русского языка Дмитриева. Д. В. Дмитриев. 2003.
.
Игры ⚽ Нужно сделать НИР?
Синонимы:
апатия, ахиллесова пята, вычтя, дефект, знак, изъян, кризис, недоработка, недостаток, недочет, несовершенство, отрицательный момент, пассив, порок, пробел, слабая сторона, слабина, слабое звено, слабое место, слабость, теневая сторона, тире, уязвимое место, червоточина, червоточинка, шероховатость
Антонимы:
плюс
- минувший
- минута
Полезное
Ответ на вопрос, почему минус на минус даёт плюс?
Со школьных времён все знакомы с таким правилом арифметики: умножение чисел с разными знаками даёт отрицательный результат, а с одинаковыми — положительный.
И многих интересовало: почему же минус на минус даёт плюс? Во многих школах этот факт оставляли без объяснения и ученики воспринимали это как данность. Сегодня мы разберёмся, почему же минус на минус даёт плюс.
Давайте пройдём по всей логической цепочке от начала до конца. В древности, когда арифметика только формировалась, отрицательных чисел не существовало, а все арифметические операции появлялись для упрощения с развитием торговых отношений. Давайте представим себе такую ситуацию: вы работали 5 дней, зарабатывая по 10 долларов в день, очевидно, что если просуммировать все доходы у вас выйдет: 10+10+10+10+10=50 или 10*5=50 долларов, таким образом, операция умножения появилась как сокращённая запись суммы.
Допустим, позже вы решили сходить в магазин и так вышло, что продуктов вы набрали на 60 долларов, вы с продавцом договариваетесь о том, что должны будете потом отдать ему недостающую десятку и он вам даёт записку, где указан ваш долг. Итого, на балансе у вас 50-60=-10 долларов.
Таким образом, и появились отрицательные числа обозначающие нечто, что мы отдаём или должны. Если такая же ситуация повторится и на следующей неделе, то наш долг будет составлять 2*(-10)=-20 долларов и отсюда уже понятно, что умножение положительного числа на отрицательное даёт минус, ведь фактически суммируются несколько долгов.
Пускай через неделю, когда вы поработали ещё пять дней и имеете на счету -10+5*10=40 долларов, вы встретили этого продавца, и он попросит вас о некой услуге, а вместо того, чтобы платить за неё, он предлагает простить долг, эту ситуацию описывает следующие выражение: 40-1*(-10) ведь мы отдаём (поэтому минус) одну бумажку с -10 долларами. Логично, что после этого у вас на балансе будет 50 долларов, тогда и результатом вышеупомянутого выражения должно быть 50, а, значит, -1*(-10) должно равняться +10. Именно на таком обыденном опыте люди когда-то пришли к выводу, что произведение двух отрицательных чисел должно равняться положительному.
Давайте ещё взглянем на этот вопрос с точки зрения чистой математики: когда в неё ввели отрицательные числа, учёным хотелось, чтобы для них были справедливы такие же математические операции, что и для натуральных чисел.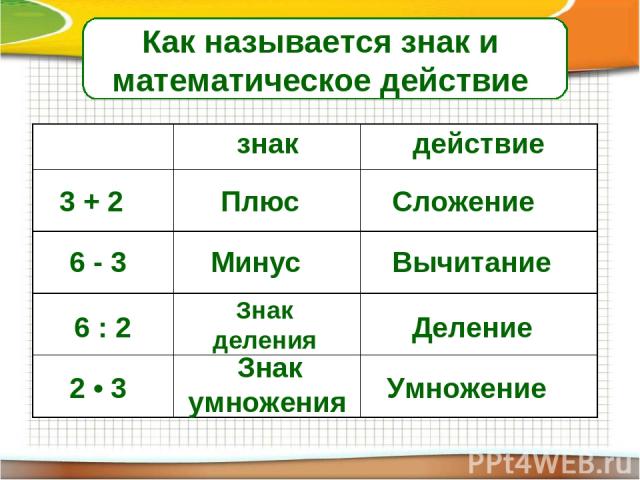
Таким образом, утверждение, что минус на минус даёт плюс не является просто договорённостью между математиками, а имеет под собой логические основания.
Автор: Владислав Кигим. Редакция: Фёдор Карасенко.
Понравилась публикация? Поделись ей с друзьями!
Понравился сайт? Подпишьсь на нас в соцсетях!
Базовая математика | Все о вычитании
Поиск на моем сайте:
Вычитание — математическая операция; это процесс или действие, которое вы выполняете с числами.
Это процесс нахождения разницы двух чисел.
Используемый символ: — (минус). В этом процессе мы берем число и уменьшаем его до меньшего числа. То есть отнимаем одно число от другого.
Щелкните здесь, чтобы просмотреть некоторые задачи на сложение и вычитание.
Разница между 7 и 5 равна 2. |
Вот несколько способов помочь вашему ребенку понять, как вычитать.
(Нажмите здесь, чтобы просмотреть несколько шаблонов для использования с ребенком.)
- Использование реальных объектов
- Числовые связи
- Рисование моделей
- Понимание оператора вычитания
- Использование числовой линии
- Вопросы о вычитании
- Более или менее
- Научитесь вычитать большие числа
Использование реальных предметов
Дайте ребенку несколько фишек (пуговицы, монеты, скрепки или другие мелкие предметы).
Попросите ее посчитать предметы.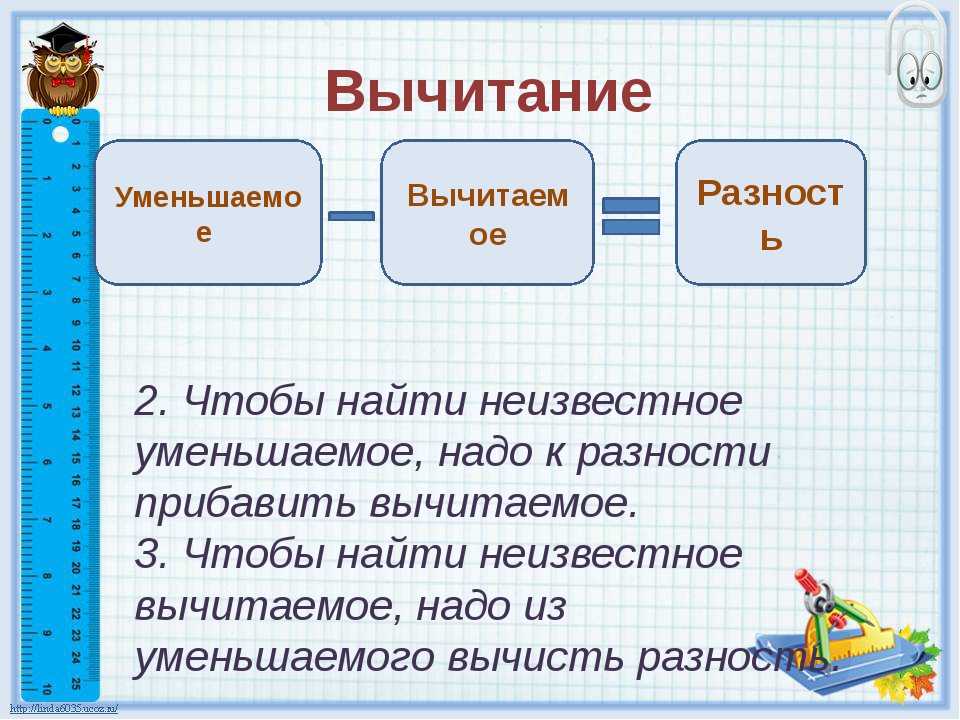
Обратитесь к таблице с числами, если ваш ребенок забывает свои числа.
Сосчитай и убери часть предметов.
Попросите ее сосчитать оставшиеся предметы.
Не забывайте использовать математические термины, такие как вычитание, разница, остаток, остаток и т. д.
Примеры: «Вычтем 2 из 9» или «Сколько у нас осталось?»
Проделайте это несколько раз с разным количеством предметов.
Теперь превратите это в игру.
- Сначала подсчитайте количество предметов вместе.
- Дайте ей подсчитать оставшиеся предметы, а затем спросите: «Сколько… я удалил?»
- После того, как она даст ответ, дайте ей подсчитать, какие предметы вы убрали, чтобы проверить, правильно ли она ответила.
- Не забудьте позволить ребенку проверить и вас.Дети чувствуют себя более уверенными в своем обучении, если вы позволяете им исследовать предмет, задавая вопросы.
Содержание
Числовые связи
Числовые связи — это основная математическая концепция, которая может помочь вашему ребенку понять вычитание и сложение.
Связка чисел показывает, что два числа соединяются в большее число (как если бы число состояло из разных частей).
Верно и обратное. Число можно разбить на более мелкие.
Эта связь чисел показывает, что из двух меньших чисел (3, 4) можно получить большее число (7). | Эта связь чисел показывает, что большее число (7) может быть «разделено» на два меньших числа (5, 2). |
Используйте физические объекты, такие как пуговицы, игрушки и т. д., чтобы продемонстрировать идею числовых связей.
Нарисуйте несколько цифр на карточках, чтобы помочь вашему ребенку понять эту концепцию:
- Дайте ребенку несколько предметов.
- Пусть ваш ребенок посчитает и напишет число в кружке слева.
- Разделите предметы на 2 группы, затем сосчитайте и запишите числа в кружках справа.
Теперь давайте объединим идеи.
Модели для рисования
Вы также можете рисовать картинки или модели, чтобы помочь вашему ребенку понять вычитание. Это очень полезный метод, так как его можно использовать, чтобы помочь вашему ребенку понять очень сложные вопросы позже.
Вот 2 модели, которые можно использовать для понимания этих двух вопросов:
a) 4 + ___ = 7
b) 7 — 4 = ___
Узнайте больше о методе рисования моделей.
4 + ____ = 7 | 7 — 4 = _____ |
При рисовании моделей мы рисуем прямоугольники вместо кругов для представления чисел. Основная идея остается той же — числа могут объединяться в большие числа или разбиваться на меньшие числа.
Этот метод может быть более точным, потому что мы можем рисовать квадраты большего размера для представления больших чисел. Это будет очень полезно позже при работе с большими числами.
Они помогут вашему ребенку понять, что сложение — это объединение чисел, а вычитание — это разбивание чисел.
Содержание
Понимание оператора вычитания
Как только ваш ребенок понял принцип нахождения разницы, пора научиться писать оператор или уравнение.
Вычитание — это идея «отнять».
7 — 5 означает вычитание 5 из 7.
Число, от которого отнимается число, называется уменьшаемым. Это самое большое число в уравнении.
Попрактикуйтесь с наборами из 3 чисел, которые можно использовать для составления оператора вычитания, и пусть он сам напишет оператор.
Попросите его проверить свой ответ, используя настоящие счетчики. Вы можете распечатать несколько шаблонов здесь.
Щелкните здесь, чтобы просмотреть некоторые задачи на сложение и вычитание.
Использование числовой строки
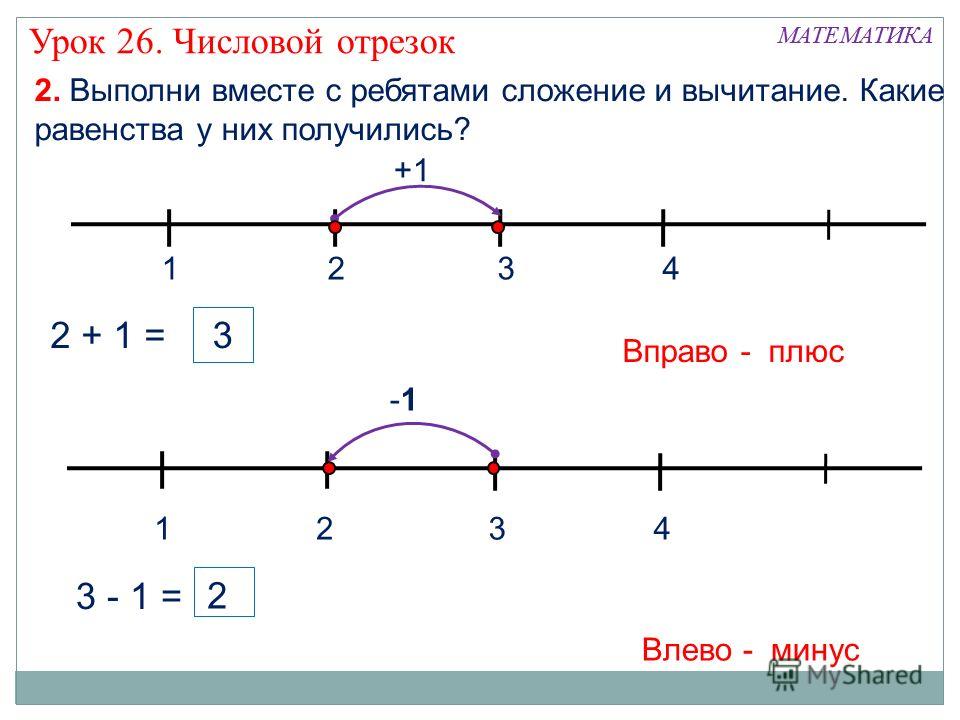
Процесс вычитания аналогичен обратному счету. Вы можете показать это на числовой прямой.
- Нарисуйте числовую линию.
- Запишите первое число (уменьшаемое) в операторе вычитания в строке.
- Подсчитайте количество шагов назад, соответствующих второму числу (вычитаемому), записывая числа в строке по мере счета.
- Число, на которое вы попали, и есть ответ (разница).
Содержание
Вычитание и сложение
Вычитание тесно связано со сложением. Иногда не так просто сказать, какую операцию использовать. См. эти примеры:
- 3 + 5 = ___ (это типичный вопрос на сложение)
- 8 — 3 = ___ (это типичный вопрос на вычитание)
- 3 + ___ = 8 (это похоже на вопрос на сложение, но он решается используя вычитание: 8 — 3)
- ___ — 5 = 3 (это похоже на вопрос на вычитание, но решается с помощью сложения: 5 + 3)
Нажмите здесь, чтобы использовать шаблон, который я создал для изучения различных способы сложения и вычитания.
Щелкните здесь, чтобы просмотреть некоторые задачи на сложение и вычитание.
Вопросы о больше или меньше
Некоторые дети ассоциируют сложение и вычитание с терминами «больше чем» и «меньше чем». Это может быть не всегда так.
Щелкните здесь, чтобы открыть рабочий лист «больше чем» и «меньше чем». Используйте шаблон, чтобы создать больше вопросов для вашего ребенка.
Попытайтесь выяснить, какую операцию следует использовать для получения правильного ответа: сложение или вычитание. Попробуйте применить стратегии, которым вы научились, например, рисование моделей или использование числовой прямой.
Не забудьте разрешить ребенку задавать вопросы, чтобы проверить вас. Сделайте это семейной задачей по математике.
Считаете ли вы эту страницу полезной? Поделись!
Научитесь вычитать большие числа
(Щелкните здесь, чтобы увидеть несколько плиток с числами единиц, десятков и сотен, которые можно использовать с ребенком.)
Чтобы вычитать большие числа, подумайте о них следующим образом: + 7
15 = 10 + 5
Или, используя разрядность:
37 = 3 десятка и 7 единиц
15 = 1 десяток и 5 единиц
Давайте решим этот вопрос:
37 — 15
1.
Начните с 3 десятков и 7 единиц, чтобы получилось 37.
3. У нас осталось 2 десятка и 2 единицы, чтобы составить число 22.
4. 37 — 15 = 22
Давайте попробуем один с переносом или перегруппировкой:
Q: 42 — 25
94
3. Измените один из десятков на 10 единиц. Теперь у нас есть 3 десятка и 12 единиц.
4. Отнимите 2 десятка и 5 единиц.
5. Остались 1 десяток и 7 единиц или число 17.
Оглавление
Больше Math Fun
Fun Math
Карточки с округлением
Поделитесь этой информацией со своими родными и друзьями, которые хотят помочь своим детям построить прочный фундамент в области математики.
Mathwords: Установить вычитание
Mathwords: Установить вычитание
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
