Калькулятор расчета подмножеств в множестве онлайн
Множество — это набор элементов, которые обладают общим свойством. В каждом неупорядоченном множестве существует определенное количество подмножеств, которые можно рассчитать при помощи онлайн-калькулятора.
Множество
Множество представляет собой набор элементов, сгруппированных по определенному признаку. В математике это может быть множество натуральных, целых или рациональных чисел. В природе это множества яблок на дереве, песчинок в пустыне или звезд в космосе. На практике множество может представлять собой набор данных, массивы результатов измерений или входных воздействий. Множество — это простейший математический объект, поэтому с ним можно осуществлять простые арифметические действия, то есть складывать, вычитать или разбивать на составляющие — подмножества.
Несобственные подмножества
Каждое множественный объект имеет два несобственных подмножества: само множество и пустое. Согласно канторовской теории, любое множество считается подмножеством самого себя. Пустое множество — это своеобразный нуль теории множеств, и такой набор не содержит ни одного элемента. Потребность в пустом множестве обусловлена аксиомой, что любой результат операции между множествами также должен быть множеством. Пустой набор элементов также считается подмножеством для любого набора чисел.
Пустое множество — это своеобразный нуль теории множеств, и такой набор не содержит ни одного элемента. Потребность в пустом множестве обусловлена аксиомой, что любой результат операции между множествами также должен быть множеством. Пустой набор элементов также считается подмножеством для любого набора чисел.
Собственные подмножества
Помимо самого себя и пустого множества, набор чисел может иметь определенное количество собственных подмножеств. Их численность определяется мощностью множества, то есть количеством его элементов. Для объекта A, которое состоит из n-ного числа элементов, существует количество собственных подмножеств, которое определяется по формуле:
N = 2n — 2.
Из этого следует, что для набора из 3 элементов существует 23 — 2 = 6 собственных подмножеств, из 4 членов — 24 — 2 = 14 собственных подмножеств и так далее. К примеру, для множества {X, Y, Z} существуют следующие подмножества:
- {X};
- {Y};
- {Z};
- {XY};
- {XZ};
- {ZY}.

Если не разделять подмножества на собственные и несобственные, то для каждого множества существует подмножества, количеством:
N = 2n,
где n — количество элементов.
Это означает, что для того же набора {X, Y, Z} добавятся также пустое множество и оно само.
Подмножества и парадоксы
Канторовская теория множеств зашла в тупик, когда ее постулаты породили парадоксы. Наиболее известной проблемой наивной теории множеств считается парадокс Рассела. Известный британский философ и ученый Бертран Рассел рассмотрел бесконечные множества как абстрактные объекты. Если любое множество считается подмножеством самого себя, то верно выражение A Î A. Допустим, существует глобальное множество S, содержащее в себе все наборы объектов, которые не включают самих себя.
Далее возникает вопрос, верно ли, что S Î S? Если верно, то выходит, что S не содержит самого себя, так как изначально набор S содержит все множества, не содержащие себя, следовательно, S Î S. Если неверно, значит, набор S не соответствует первичному определению, следовательно, S Î S.
Если неверно, значит, набор S не соответствует первичному определению, следовательно, S Î S.
Данный парадокс так же известен как проблема цирюльника. Некий брадобрей заявляет, что будет брить только тех, кто не бреет сам себя. Тех, кто сами справляются с бритвой, цирюльник брить отказывается. Возникает парадокс: кто побреет цирюльника? Если он бреется сам, то он не должен себя брить, а если не бреется, то брить себя обязан. Для решения подобных парадоксов в теорию множеств была внесен раздел о типах объектов. Согласно теории типов, подмножества всегда должны быть низшего порядка по отношению к своему надмножеству.
Наша программа позволяет сгенерировать все возможные подмножества для любого заданного набора чисел. Для этого вам достаточно ввести числа через запятую в форму онлайн-калькулятора, после чего программа рассчитает все подмножества для выбранного набора, включая собственные и несобственные. Рассмотрим пример генерации подмножеств.
Пример работы калькулятора
Допустим, у нас есть множество последовательных натуральных чисел мощностью 4.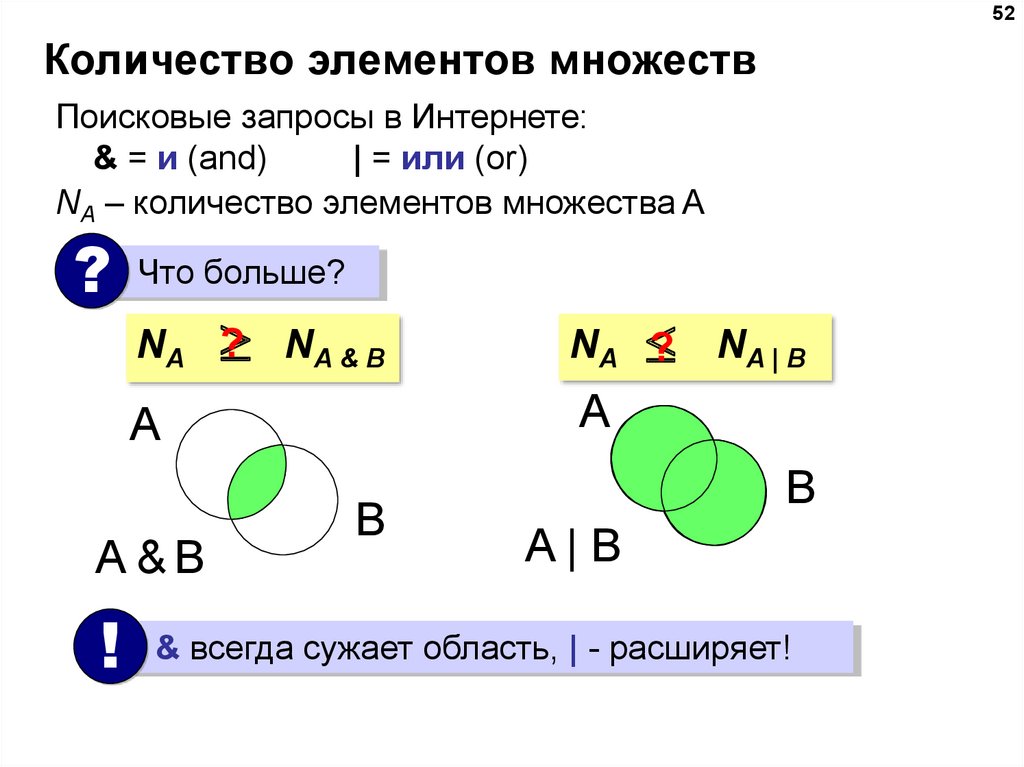 Это означает, что наш объект выглядит как А = {1, 2, 3, 4,}. Согласно формуле, для A существует 24 = 16 подмножества: 14 собственных и 2 несобственных. При помощи калькулятора рассчитаем эти составляющие. Мы получим:
Это означает, что наш объект выглядит как А = {1, 2, 3, 4,}. Согласно формуле, для A существует 24 = 16 подмножества: 14 собственных и 2 несобственных. При помощи калькулятора рассчитаем эти составляющие. Мы получим:
- пустое множество — {};
- одноэлементные наборы — {1}, {2}, {3}, {4};
- двухэлементные — {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4};
- трехэлементные — {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4};
- само множество — {1, 2, 3, 4}.
Точно также вы можете рассчитать количество подмножеств для множества произвольной мощности.
Заключение
Множество — это элементарный математический объект, с которым можно осуществлять разные арифметические операции. Используйте наши онлайн-калькуляторы для работы с множественными объектами.
Калькулятор определения подмножества из множества онлайн
Подмножество множества A — это такой набор B, все члены которого принадлежат A. Существует знакомое всем с детства множество натуральных чисел N, а наборы четных E и нечетных O элементов являются подмножествами N.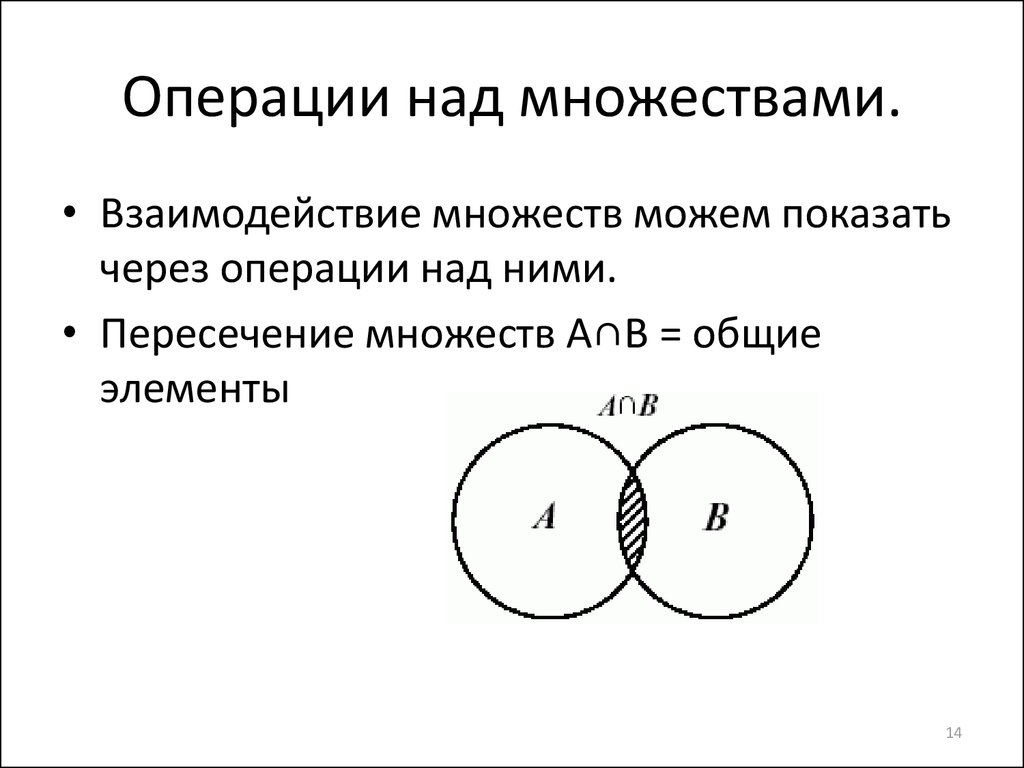
Теория множеств
Проблема отображения бесконечности действительных чисел волновала математиков с самой древности. Натуральные числа люди использовали при счете, рациональные, то есть дроби – при операциях с частями целого, а действительные числа нашли свое применение в измерениях. Первым действительным и иррациональным числом, о котором узнали древние математики, было число, отображающее длину диагонали квадрата. Затем появилось Пи (отношение диаметра круга к его окружности), позднее и другие числа.
При измерении длины стороны фигуры или ее диагонали мы можем постоянно повышать точность измерений и получать все новые и новые числа. Например, диагональ единичного квадрата равна корню из двух. Мы можем выразить ее длину как 1,4 или 1,41 или 1,4142 или 1,41421356237. И это все разные действительные числа. Можно ли создать список всех действительных чисел от 0 до 1? Нет, так как каждый раз будет находиться еще одно число, отличное от всех, представленных в этом списке.
Именно с этой проблемой работал Георг Кантор, который создал наивную теорию множеств. Наивной его теория стала в результате образования нескольких логических парадоксов, которые были успешно решены при трансформации канторовской теории в аксиоматическую теорию множеств.
Наивной его теория стала в результате образования нескольких логических парадоксов, которые были успешно решены при трансформации канторовской теории в аксиоматическую теорию множеств.
Подмножество
Давайте начнем с самого простого – множество натуральных чисел. Это бесконечная последовательность целых положительных чисел, которые мы используем при счете предметов. В отличие от измерений, мы не можем повышать точность счета. Если мы видим 5 яблок, то точнее мы выразить их количество никак не сможем. Кроме того, мы без проблем можем перечислить все натуральные числа в диапазоне от 1 до 10. Все натуральные числа могут быть как четными, так и нечетными, следовательно, натуральное множество содержит в себе четное и нечетное подмножества.
Целые числа – это продолжение натуральной последовательности в отрицательную область. К целым относится ноль, все натуральные числа, а также противоположные натуральным, то есть со знаком минус. Очевидно, что натуральное множество является подмножеством целых чисел.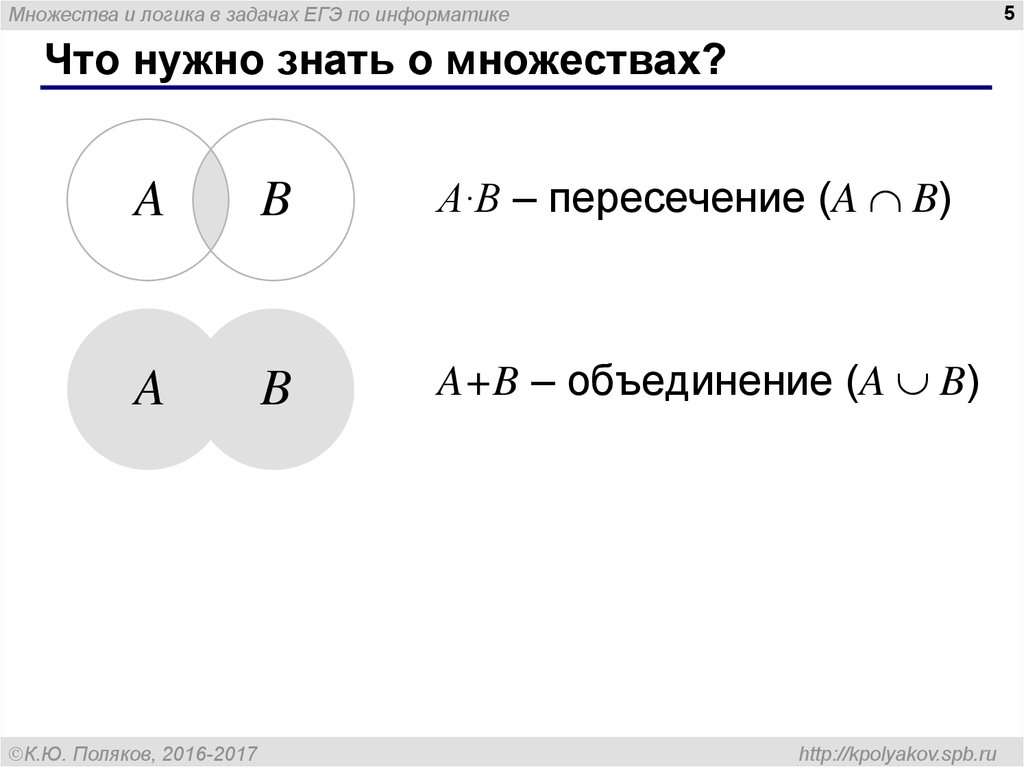
Рациональное множество – это набор всех дробных чисел, которые возможно представить в виде обыкновенной дроби. В виде дроби мы можем выразить 0,25 – 1/4, 0,5 – 1/2, 1 – 1/1. В качестве дроби легко записать любое целое или натуральное число, например: 5/5 или 50/50. Таким образом, рациональное множество содержит два подмножества – наборы целых и натуральных чисел.
Действительное множество – это все числа на числовой оси. К ним относятся натуральные, целые, рациональные и иррациональные числа, которые формируют соответствующие подмножества во множестве действительных чисел. Множество действительных чисел – это самое мощное множество, которое стремится в бесконечность. Кроме того, пустое множество, которое не содержит ни одного элемента, является подмножеством любого выбранного набора чисел. Но и это еще не все. Каждое множество является подмножеством самого себя.
Мы перечислили глобальные примеры подмножеств, однако на практике нам может потребовать определить является ли один набор чисел подмножеством другого набора? К примеру, если у нас есть пара значений {3, 11}, то является ли она подмножеством набора {1, 3, 5, 7, 11, 13}? Очевидно, что ответ положительный, так как и 3, и 11 встречаются во множестве {1, 3, 5, 7, 11, 13}. Однако это верно только для множеств с неразличимыми элементами, то есть для обычного набора чисел. Если же важен порядковый номер элементов множества, то результат противоположный и {3, 11} не является подмножеством {1, 3, 5, 7, 11, 13}.
Однако это верно только для множеств с неразличимыми элементами, то есть для обычного набора чисел. Если же важен порядковый номер элементов множества, то результат противоположный и {3, 11} не является подмножеством {1, 3, 5, 7, 11, 13}.
Наш калькулятор определения подмножеств позволяет выяснить, является набор чисел B подмножеством набора A. Программа использует алгоритм для надежно различимых элементов множества, для которых важен порядок расположения членов.
Пример определения подмножества
Выше мы выяснили, что четное множество – это подмножество натурального ряда. Для неразличимых элементов объект B = {2, 4, 6} является подмножеством набора A = {1, 2, 3, 4, 5, 6}. Однако представим, что это база данных, и n-ному элементу множества соответствует свое значение. Выходит, что первый член объекта B имеет значение 2, а первый элемент набора A равен 1. Второй элемент множества B равен 4, а второй элемент объекта A = 2. По такой логике это совершенно разные объекты, следовательно, множество B не является подмножеством набора A.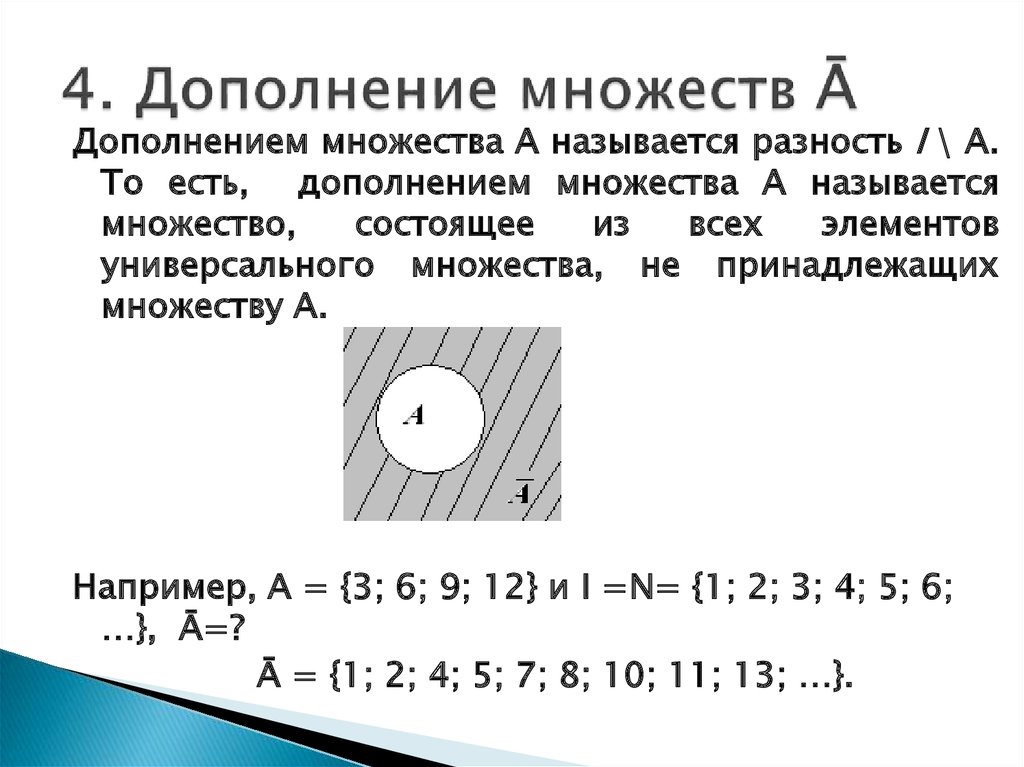
Заключение
Множество – это набор математических объектов, каждый из которых обладает определенным свойством. Каждое множество имеет минимум два подмножества: пустое и свое собственное. Для поиска других подмножеств используйте наш калькулятор, который позволяет определить принадлежность одного набора чисел к другому.
Set Калькулятор обозначений
Set Калькулятор обозначенийКак работает калькулятор набора обозначений?
Учитывая два набора чисел A и B, это определяет следующее:
* Союз A и B, обозначенный A U B
* Пересечение A и B, обозначенное A ∩ B
* Элементы в A не в B, обозначенные A — B
* Элементы в B не в A, обозначаются B — A
* Симметричная разница A Δ B
* Конкатенация A · B
* Декартово произведение A x B
* Мощность A = |A|
* Мощность B = |B|
* Индекс Жаккара J(A,B)
* Расстояние Жаккара J σ (A,B)
* Коэффициент кости
* Если A является подмножеством B
* Если B является подмножеством A
Этот калькулятор имеет 2 входа.
Какие 7 формул используются для калькулятора набора обозначений?
- А Δ В = (А — В) U (В — А)
- А С = U — А
- A ∩ B = A + B — A U B
- J(A,B) = |A ∩ B|/|A U B|
- J σ (A,B) = 1 — J(A,B)
Дополнительные математические формулы см. в нашем досье формул
Какие 11 понятий используются в калькуляторе обозначений?
- мощность
- мера количества элементов множества
- коэффициент
- числовая или постоянная величина, стоящая перед переменной и умножающая ее в алгебраическом выражении
- разность
- результат одной из важных математических операций, которая получается путем вычитания двух чисел
- элемент
- элемент (или член) множества – это любой из отдельных объектов, принадлежащих этому множеству.
 В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов.
В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов. - индекс
- индикатор, знак или мера чего-либо
- пересечение
- множество, содержащее все элементы A, которые также принадлежат B, или, что то же самое, все элементы B, которые также принадлежат A.
A ∩ B - продукт
- Ответ при перемножении двух или более значений
- набор
- набор разных вещей; множество содержит элементы или члены, которые могут быть математическими объектами любого вида
- обозначение множества
- Способы записи множеств, их элементов и свойств
- подмножество
- A является подмножеством B, если все элементы множества A являются элементами комплекта B
- соединение
- Сочетайте элементы двух и более наборов
Установить калькулятор видео
- Электронная почта: donsevcik@gmail.
 com
com - Тел.: 800-234-2933
- Математическая тревога
- судоку
- Раздор
- Информационный бюллетень о недобросовестном преимуществе
- Биографии математиков
- Подкаст цены за клик
- Математические Мемы
- Глоссарий по математике
- Предметы
- бейсбольная математика
- Друзья
- Спонсоры
- Связаться с нами
- Вакансии учителя математики
- Политика в отношении файлов cookie
- политика конфиденциальности
- Политика возврата
- СМИ
Калькулятор подмножеств — Найдите количество подмножеств в наборе
Онлайн-калькулятор подмножеств позволяет определить общее количество правильных и неправильных подмножеств в наборах. Также этот калькулятор сообщает о подмножествах с определенным количеством элементов. Здесь мы объясним разницу между подмножеством и правильным подмножеством и как найти подмножества данного набора.
Также этот калькулятор сообщает о подмножествах с определенным количеством элементов. Здесь мы объясним разницу между подмножеством и правильным подмножеством и как найти подмножества данного набора.
Согласно определению подмножества, если все элементы множества A также существуют в множестве B, то множество A называется подмножеством множества B. Другими словами, множество A включено в множество.
В математике подмножество обозначается символом ⊆ и произносится как «обозначение подмножества».
Обозначение подмножества может быть выражено как P⊆Q
Это означает, что множество P является подмножеством множества Q.
Однако онлайн-калькулятор набора мощностей будет использоваться для создания наборов мощностей данного набора.
Подмножества Пример:
Если в множестве P есть {A, B}, а в множестве Q есть {A, B, C}, то P является подмножеством Q, поскольку в множестве » В».
Существует два разных типа подмножеств:
- Надлежащее подмножество
- Неверное подмножество
Правильное подмножество содержит несколько элементов исходного набора, а неправильное подмножество содержит каждый элемент Исходного набора, а также калькулятор пустого набора и подмножества, который дает количество правильных и неправильных подмножеств в наборе. Для подмножества не было найдено конкретной формулы. Вместо этого нам нужно перечислить все подмножества, чтобы отличить правильные от неправильных.
Пример:
Если набор P = {10, 14, 16}, то
Количество подмножеств:
$${10}, {14}, {16}, {10, 14}, {14, 16}, {10, 16}, {10, 14, 16}, {}$$
Правильные подмножества:
$${}, {10}, {14}, {16}, {10 , 14}, {14, 16}, {10, 16}$$
Неправильное подмножество:
$${10, 14, 16}$$
Что такое правильное подмножество? Если множество Q содержит хотя бы один элемент, не входящий в множество P, то множество P считается правильным подмножеством множества Q.
Правильное подмножество — это специальное подмножество. Есть два требования, чтобы множество P стало правильным подмножеством множества Q.
- P является подмножеством Q, а именно PQ, и P не равно Q, то есть P≠Q.
- Обозначение подмножества: P⊂Q: это означает, что множество P является правильным подмножеством множества Q.
Пример:
Если вы устанавливаете P с элементами {5, 10}, а Q имеет значение {5, 10, 15}, множество P является допустимым подмножеством Q, поскольку 15 не существует в множестве P.
Обозначение правильного подмножества:Обозначение подмножества для правильного подмножества обозначается как ⊂ и читается как «является правильным подмножеством». С помощью этого символа мы можем представить множество P и множество Q как правильное подмножество:
$$P ⊂ Q$$
Однако онлайн-калькулятор записи интервалов поможет вам найти значения интервалов из заданной записи интервалов.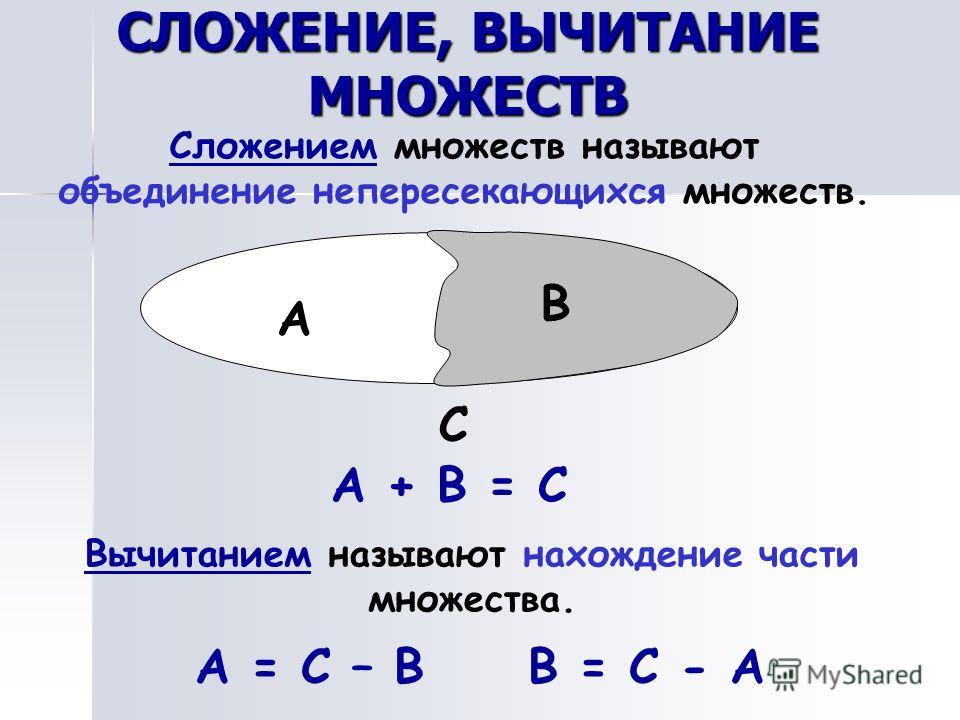 n\) 93 – 1$$
n\) 93 – 1$$
$$= 8 – 1 = 7$$
Количество правильных подмножеств равно 7.
Что такое неправильное подмножество?Содержит подмножество всех элементов исходного набора. Это называется неправильным подмножеством.
Дарится как ⊆.
Пример
Если набор Q = {10, 14, 16}, то
Количество подмножеств:
$${10}, {14}, {16}, {10, 14}, { 14, 16}, {10, 16}, {10, 14, 16}, {}$$
Неверное подмножество:
$${10, 14, 16}$$
Некоторые важные атрибуты подмножеств:- Каждый набор считается подмножеством самого указанного набора. Это означает, что P⊂P или Q⊂Q, а пустое множество считается подмножеством всех множеств.
- P является подмножеством Q. Это означает, что множество P находится в Q.
- Если множество P является подмножеством множества Q, мы можем сказать, что Q является надмножеством P.
Используйте этот онлайн-калькулятор подмножеств, который поможет вам найти подмножества заданного набора, следуя этим инструкциям:
Ввод:- Сначала выберите параметр, тип которого вы хотите вычислить, например, набор элементов или кардинальность.

- Теперь введите заданные значения и убедитесь, что все значения разделены запятой.
- Нажмите кнопку «Рассчитать» для получения результатов.
Калькулятор подмножеств дает:
- Он отображает значения подмножеств и правильных подмножеств.
- Калькулятор подскажет, сколько подмножеств в элементах.
- Создает список подмножеств, если вы выберете опцию набора элементов.
Мощность пустого множества равна количеству элементов. Мощность пустого множества равна 0, поскольку пустое множество не содержит элементов. В устоявшихся символах пишем |Ø| = 0.
Является ли число пи правильным подмножеством? Пустое множество, число пи — это правильное подмножество любого заданного множества, которое содержит хотя бы один элемент и неподходящее подмножество числа пи.


 В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов.
В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов. com
com