Геометрия. Урок 6. Анализ геометрических высказываний
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Верные утверждения
Аксиомы
Углы
Треугольники
Четырехугольники
Окружности
Симметрия
- Неверные утверждения
Для того, чтобы найти нужное утверждение, воспользуйтесь поиском по сайту (вверху страницы) или сочетанием клавиш Ctrl+F.
В данном уроке мы вспомним различные определения, теоремы и свойства из курса геометрии. Очень многие девятиклассники допускают ошибки именно в 13 задании ОГЭ “Анализ геометрических высказываний”. Здесь мы рассмотрим различные утверждения, которые встречаются в ОГЭ и разберём, какие из них являются верными, а какие нет и почему.
Для удобства, утверждения расклассифицированы по темам: Аксиомы, Углы, Треугольники, Четырехугольники, Окружности, Симметрия.
Объем утверждений достаточно большой, но есть хорошая новость: если с первого раза вы с утверждением согласны, если для вас оно очевидно, то зубрить его не надо. Стоит серьёзно отнестись к утверждениям, которые с первого раза очевидными не кажутся. Но и их зазубривать тоже не нужно, их надо осмыслить, понять. Сделайте картинку к такому утверждению, подумайте, почему оно верно (или неверно).
Зубрёжка – бесполезное занятие. Любое утверждение можно сформулировать по-разному, поэтому самое главное – это понимание. В любой непонятной ситуации делайте рисунок и размышляйте. Удачи!
Аксиомы
- Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
- Через любую точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной, и притом только одну.
- Если две прямые параллельны третьей прямой, то эти две прямые параллельны.
- Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

- Любые три прямые имеют не более одной общей точки.
- Через любую точку проходит более одной прямой.
- Через любую точку проходит не менее одной прямой.
- Через любые две точки можно провести прямую.
- Через любые три точки проходит не более одной прямой.
- Через любые три точки проходит не более одной прямой.
Углы
- Вертикальные углы равны.
- Если угол равен 45°, то вертикальный с ним угол равен 45°.
- Если угол равен 108°, то вертикальный с ним равен 108°.
- Сумма смежных углов равна 180°.
- Если угол равен 60°, то смежный с ним равен 120°.
- Если при пересечении двух прямых третьей прямой соответственные углы равны, то эти прямые параллельны.
- Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
- Если при пересечении двух прямых третьей прямой внешние накрест лежащие углы равны, то эти прямые параллельны.
- Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180°, то эти прямые параллельны.

- Если при пересечении двух прямых третьей прямой сумма внешних односторонних углов равна 180°, то эти прямые параллельны.
- Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
- Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
- Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
Треугольники
- Сумма углов любого треугольника равна 180° .
- Сторона треугольника меньше суммы двух других сторон данного треугольника. (неравенство треугольника)
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (1 признак равенства треугольников)
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
 (2 признак равенства треугольников)
(2 признак равенства треугольников) - Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (3 признак равенства треугольников)
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. (1 признак подобия треугольников)
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. (2 признак подобия треугольников)
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. (3 признак подобия треугольников)
- Напротив равных углов лежат равные стороны.
- Если два угла треугольника равны, то равны и противолежащие им стороны.
- Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне.
- Площадь треугольника равна полупроизведению двух сторон треугольника на синус угла между ними.

- Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, является медианой (то есть делит основание на две равные части) и высотой (перпендикулярна основанию).
- Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
- В прямоугольном треугольнике катет, лежащий напротив угла 30° равен половине гипотенузы.
- В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине этой гипотенузы.
- Площадь прямоугольного треугольника меньше произведения его катетов.
- Площадь прямоугольного треугольника равна половине произведения его катетов.
- Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
 (теорема косинусов).
(теорема косинусов). - Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
- Стороны треугольника пропорциональны синусам противолежащих углов. (теорема синусов)
- Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
- Один из углов треугольника всегда не превышает 60°.
- Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
- Биссектрисы треугольника пересекаются в центре его вписанной окружности.
Четырехугольники
- Сумма углов четырехугольника равна 360°.
- Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
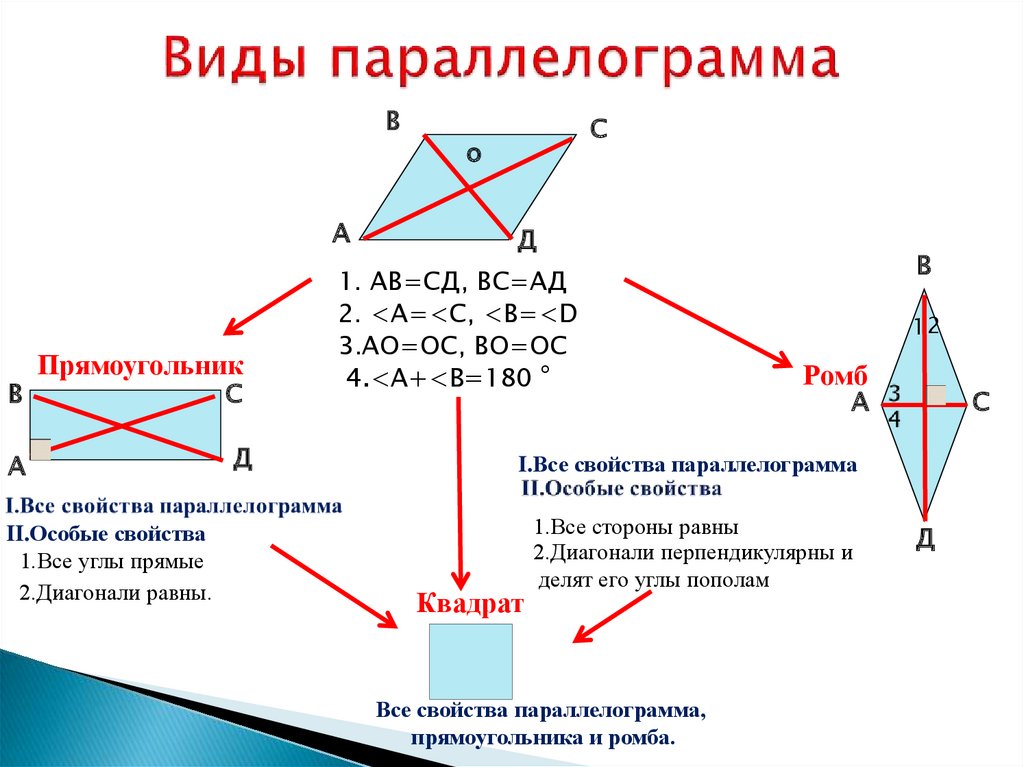
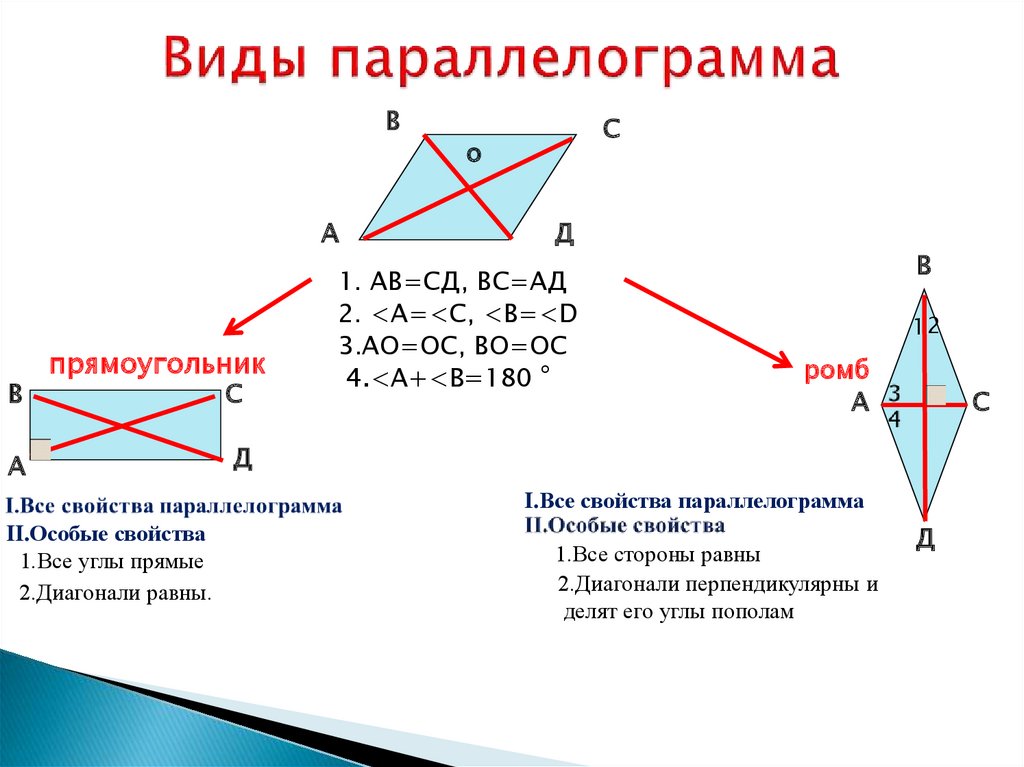
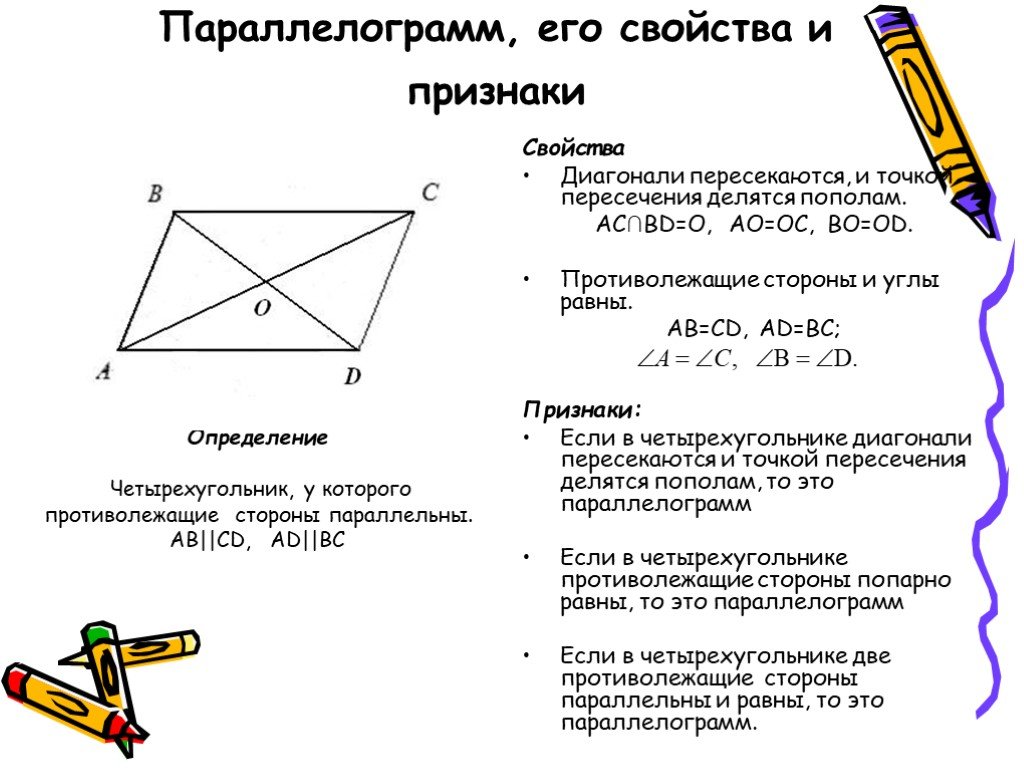
- Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
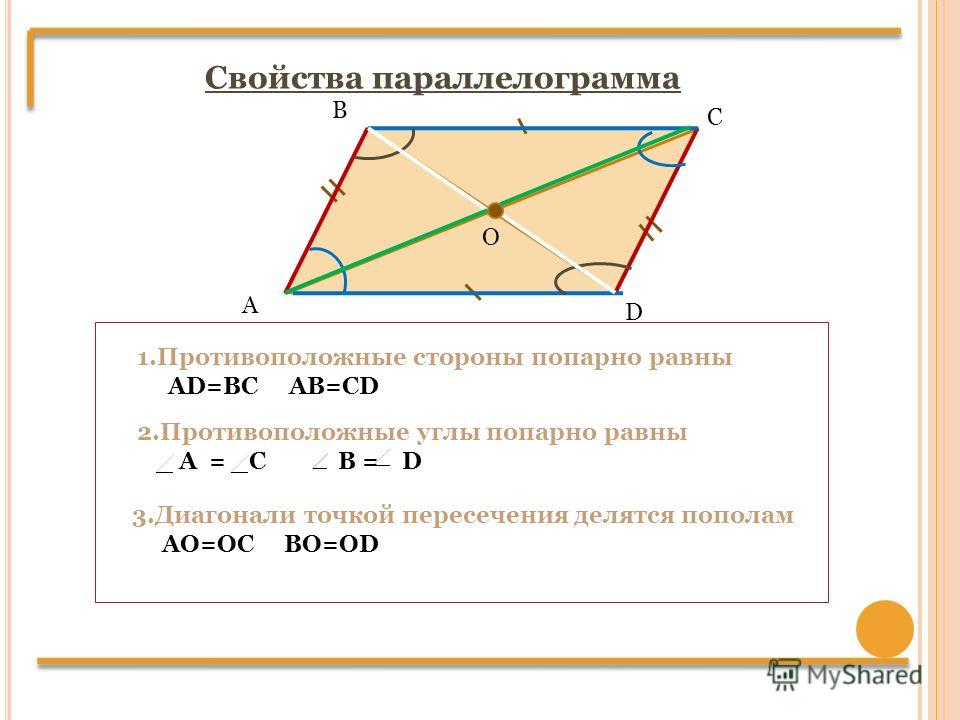
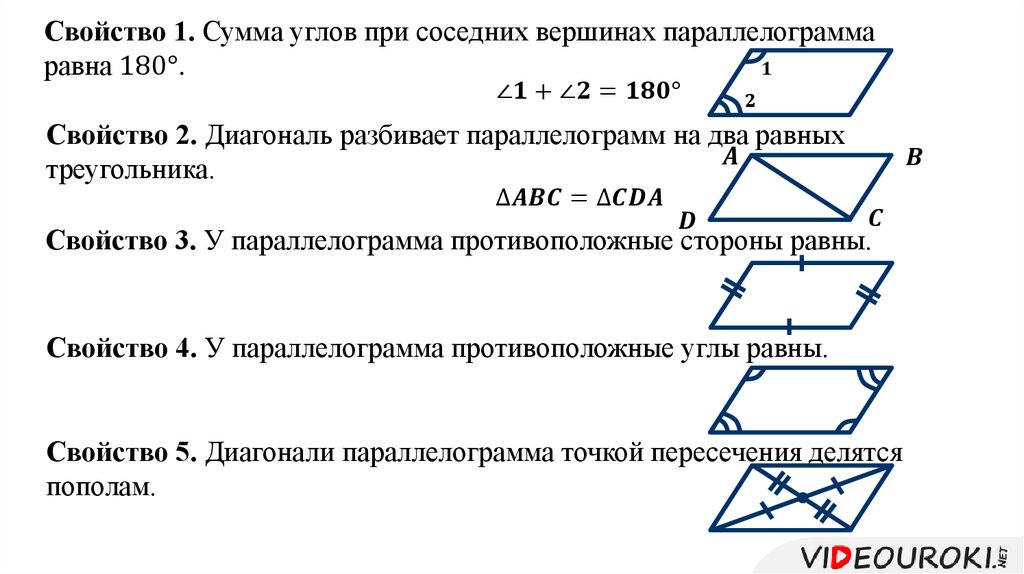
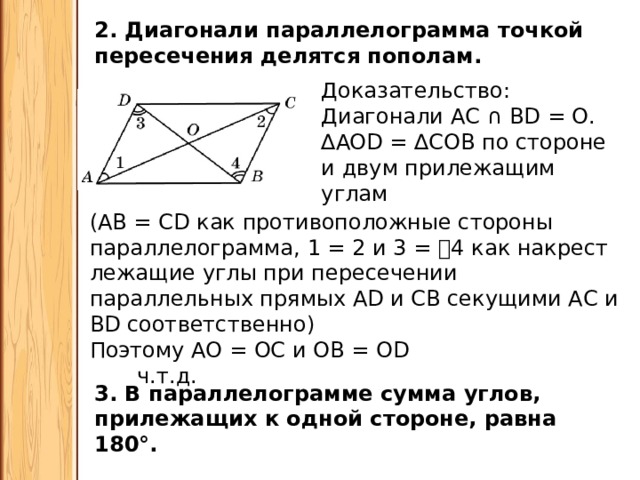
- В параллелограмме противолежащие углы равны.
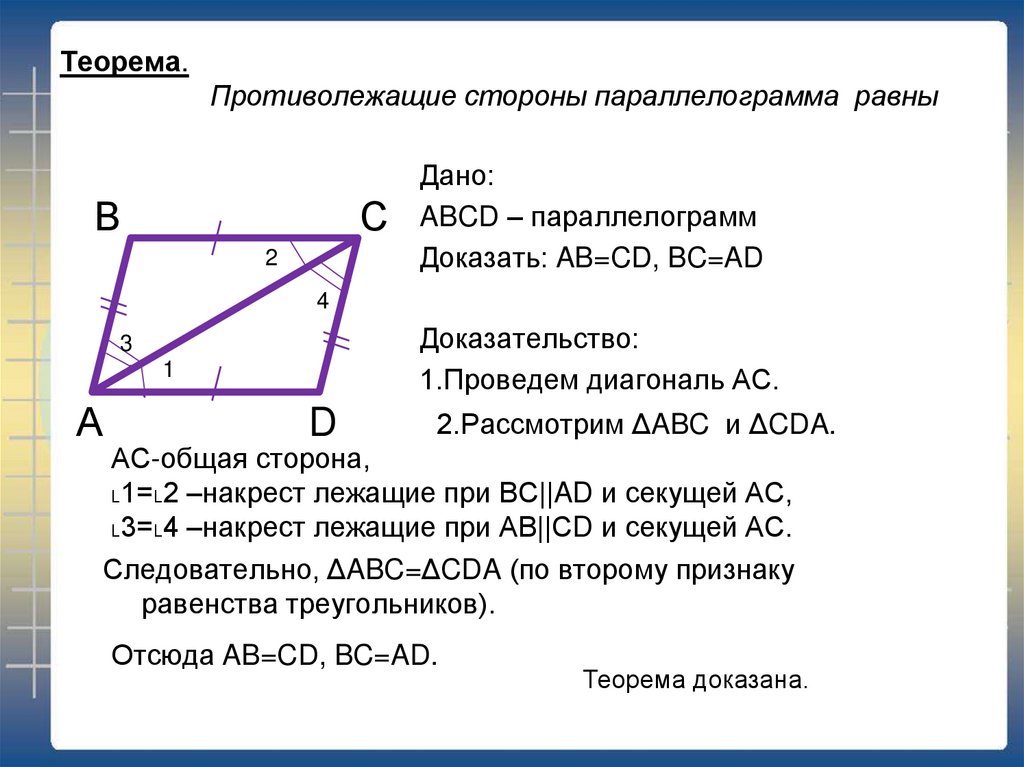
- В параллелограмме противолежащие стороны равны.
- В параллелограмме сумма смежных углов равна 180°.
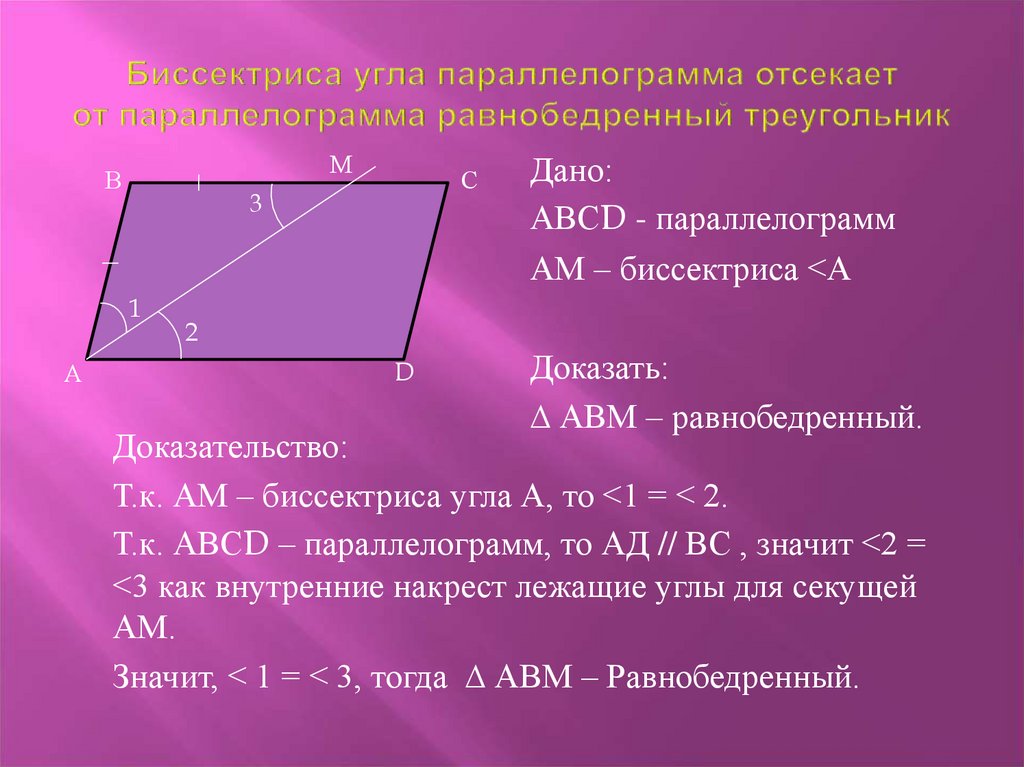
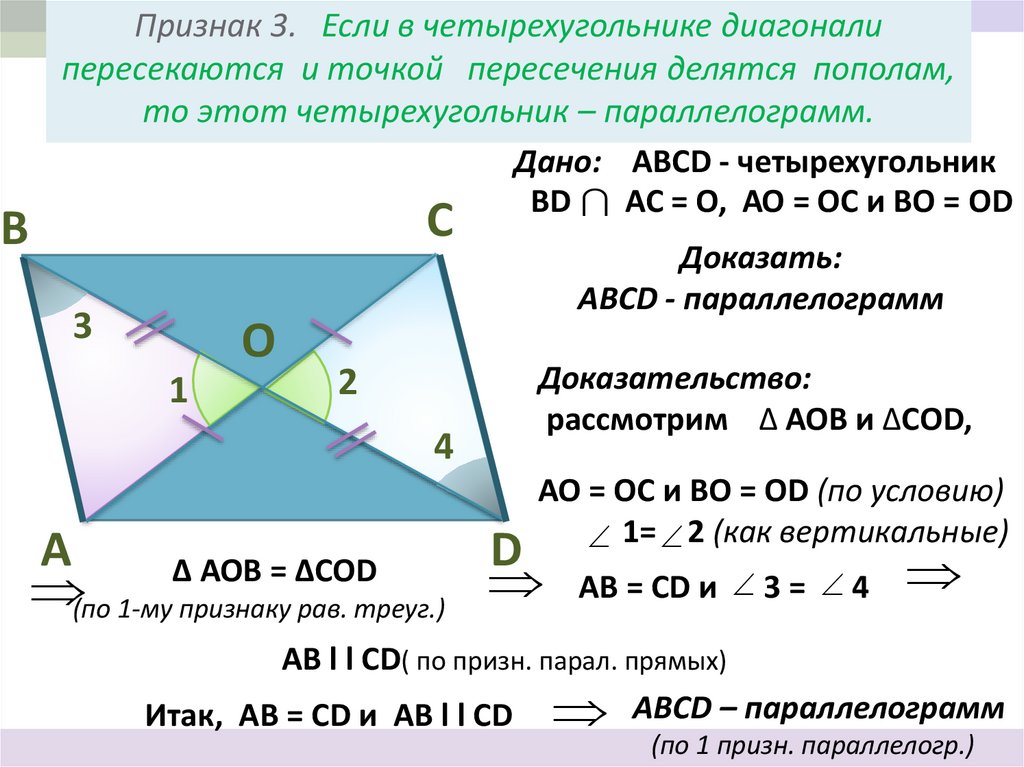
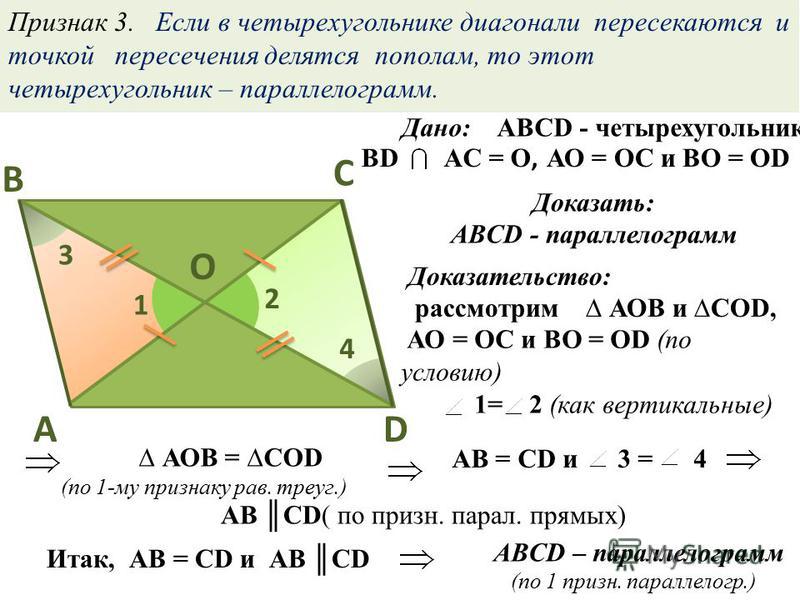
- Если диагонали параллелограмма являются биссектрисами углов, из которых они выходят, этот параллелограмм является ромбом.

- Если в параллелограмме диагонали равны, этот параллелограмм является прямоугольником.
- Если в прямоугольнике диагонали перпендикулярны, этот прямоугольник является квадратом.
- Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
- Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
- Диагонали ромба перпендикулярны.
- Диагонали квадрата взаимно перпендикулярны.
- Диагонали квадрата делят его углы пополам.
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
- Площадь параллелограмма равна произведению смежных сторон на синус угла между ними.
- Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
- Площадь ромба равна половине произведения диагоналей.
- Площадь квадрата равна произведению двух его смежных сторон.
- Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
- Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.

- Если диагонали ромба равна 3 и 4, то его площадь равна 6.
- Трапеция – четырехугольник две стороны которого параллельны, а две другие нет.
- У равнобедренной трапеции диагонали равны.
- У равнобедренной трапеции углы при основании равны.
- Средняя линия трапеции параллельна основаниям.
- Средняя линия трапеции равна полусумме оснований.
- Площадь трапеции равна произведению полусуммы оснований на высоту.
- Площадь трапеции равна произведению средней линии на высоту.
- Площадь трапеции меньше произведения суммы оснований на высоту.
Окружности
- В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
- Все диаметры окружности равны между собой.
- Все радиусы окружности равны между собой.
- Вокруг любого треугольника можно описать окружность.
- Около всякого треугольника можно описать не более одной окружности.
- В любой треугольник можно вписать не менее одной окружности.

- Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис.
- Центр описанной вокруг треугольника окружности лежит в точке пересечения серединных перпендикуляров.
- Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы.
- Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
- Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
- Центр описанной окружности может находиться внутри треугольника (если он остроугольный), на стороне (если он прямоугольный) и вне треугольника (если он тупоугольный).
- В равностороннем треугольнике центры вписанной и описанной окружностей совпадают.
- Около любого правильного многоугольника можно описать не более одной окружности.
- Любой прямоугольник можно вписать в окружность.
- Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

- Если расстояние между центрами окружностей равно сумме радиусов, то окружности касаются в одной точке.
- Если расстояние между центрами окружностей больше суммы радиусов, то окружности не имеют общих точек.
- Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
- Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
- Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.
- Центральный угол равен градусной мере дуги, на которую он опирается.
- Вписанный угол равен половине градусной меры дуги, на которую он опирается.
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
- Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

- Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
- Через любые три точки проходит не более одной окружности.
- Если четырехугольник вписан в окружность, сумма противолежащих углов равна 180°.
- Если в четырехугольник вписана окружность, суммы длин его противолежащих сторон равны.
Симметрия
- Правильный n-угольник имеет n осей симметрии.
- Правильный пятиугольник имеет пять осей симметрии.
- Правильный шестиугольник имеет шесть осей симметрии.
- Центром симметрии ромба является точка пересечения его диагоналей.
- Центром симметрии прямоугольника является точка пересечения диагоналей.
- Существует квадрат, который не является прямоугольником.
(Любой квадрат является частным случаем прямоугольника, потому что прямоугольник – это четырехугольник, у которого все углы по 90°). - В любом прямоугольнике диагонали взаимно перпендикулярны.
(В любом прямоугольнике диагонали равны. Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат).
Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат). - Существует квадрат, который не является ромбом.
(Любой квадрат – частный случай ромба, ромб – четырехугольник, у которого все стороны равны. У квадрата все стороны равны). - Если угол острый, то смежный с ним угол также является острым.
(Если угол острый, то смежный с ним угол будет тупым). - Через любые три точки проходит ровно одна прямая.
(Не всегда можно провести через три точки одну прямую, они могут «не попасть» на эту прямую). - Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1
(Расстояние от точки до прямой – минимальная длина отрезка, который соединяет заданную точку с произвольной точкой на прямой. Если расстояние меньше единицы, то любой другой отрезок, соединяющий зааднную точку с произвольной точкой на прямой будет больше или равен единицы). - Любые две прямые имеют не менее одной общей точки.

(Только параллельные прямые не имеют общих точек. Две пересекающиеся прямые имеют одну общую точку). - Любые три прямые имеют не менее одной общей точки.
(Эти три прямые могут быть параллельны друг другу и не иметь общих точек вообще). - Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
(Если две параллельные прямые пересечены третьей, то внутренние накрест лежащие углы равны. Сумма этих углов не поможет определить, являеются ли прямые параллельными или нет). - Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
(Вписанные углы должны опираться на одну и ту же дугу, чтобы они были равны. Хорда стягивает две дуги. При такой формулировке один из углов может опираться на хорду с одной стороны (опираться на меньшую дугу), а второй угол – с другой стороны (опираться на большую дугу). Тогда равенство этих углов не будет выполняться). - Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

(Из рисунка видно, что это не так). - Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.
(Из рисунка видно, что это не так). - Сумма углов выпуклого четырехугольника равна 180°.
(Сумма углов выпуклого четырехугольника равна 360°). - Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
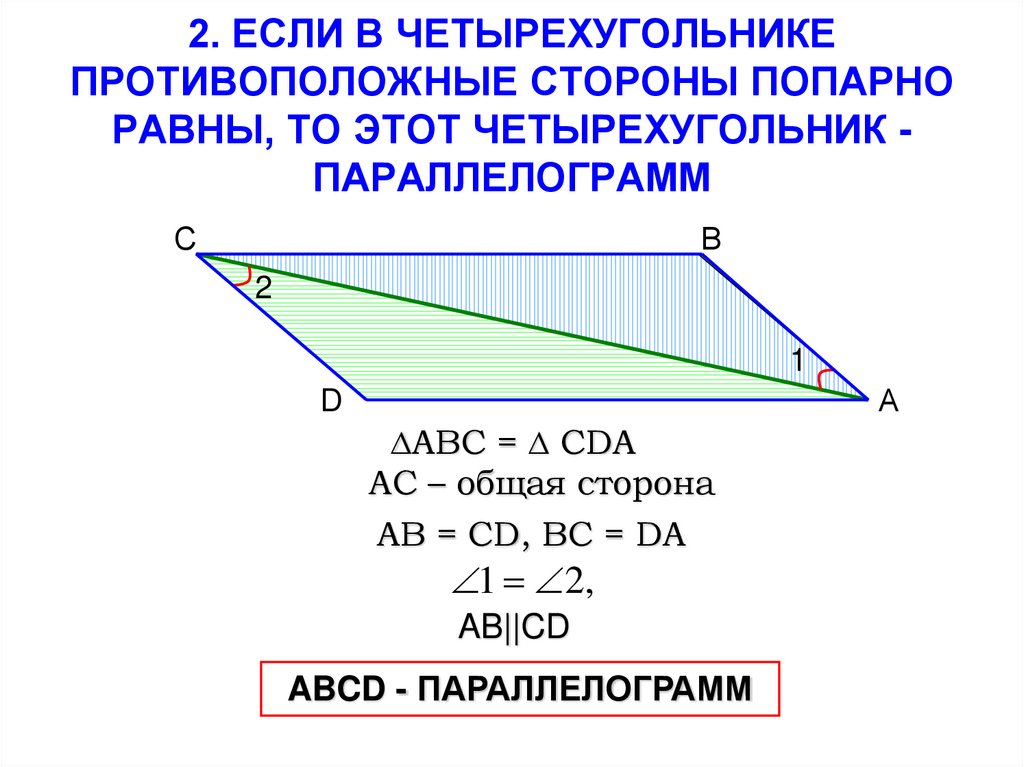
(Противолежащие углы в параллелограмме равны. Так что противолежащий угол должен быть равен тоже 60°). - Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
(Признак параллелограмма: если в четырехугольнике две стороны равны и параллельны, то такой четырехугольник параллелограмм). - Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
(Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°). - Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

(Центром окружности, вписанной в треугольник, является точка пересечения биссектрис). - Около любого ромба можно описать окружность.
(Только если этот ромб – квадрат). - Окружность имеет бесконечно много центров симметрии.
(Окружность имеет лишь один центр симметрии – центр окружности). - Прямая не имеет осей симметрии.
(Прямая имеет бесконечное множество осей симметрии – любая перпендикулярная ей прямая будет являться осью её симметрии). - Квадрат не имеет центра симметрии.
(Центр симметрии квадрата – точка пересечения его диагоналей). - Равнобедренный треугольник имеет три оси симметрии.
(Равнобедренный треугольник имеет одну ось симметрии – высоту, проведенную к основанию). - Центром симметрии равнобедренной трапеции является точка пересечения ее диагоналей.
(У равнобедренной трапеции нет центра симметрии). - Любые два равнобедренных треугольника подобны.
(У подобных треугольников должны быть равны углы. Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого).
Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого). - Любые два прямоугольных треугольника подобны.
(У подобных треугольников должны быть равны углы. Если взять два произвольных прямоугольных треугольника, то не обязательно два острых угла одного треугольника будут соответственно равны двум острым углам другого). - Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
(Данный треугольник прямоугольный, так как в нем работает теорема Пифагора:
9 + 16 = 25). - Стороны треугольника пропорциональны косинусам противолежащих углов.
(Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.) - Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
(Если бы в формулировке вместо синуса стоял косинус, было бы верным данное утверждение).
- Если площади фигур равны, то равны и сами фигуры.
(Не обязательно. Для примера возьмем квадрат со стороной 2 и прямоугольный треугольник со сторонами 1 и 4. Тогда площади этих фигур будут равны, но сами фигуры, разумеется, равными друг другу не будут. Еще пример: возьмем прямоугольник со сторонами 2 и 6 и другой прямоугольник со сторонами 1 и 12. Их площади тоже будут равны, но сами фигуры равными друг другу не будут). - Площадь трапеции равна произведению суммы оснований на высоту.
(Площадь трапеции равна произведению полусуммы оснований на высоту). - Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
(Площадь должна равняться 5). - Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
(Площадь многоугольника, описанного около окружности, равна произведению его полупериметра на радиус вписанной окружности).
- Треугольник со сторонами 1, 2, 4 существует.
(Не выполняется неравенство треугольника: одна из сторон должна быть меньше, чем сумма двух других. 4 > 1+2 – неверно). - Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
(Если треугольник тупоугольный, то центр описанной вокруг него окружности лежит за его пределами). - Площадь трапеции равна половине высоты, умноженной на разность оснований.
(Площадь трапеции равно половине высоты, умноженной на сумму оснований). - В любую равнобедренную трапецию можно вписать окружность.
(Вокруг любой равнобедренной трапеции можно описать окружность). - Диагональ параллелограмма делит его углы пополам.
(Если диагональ параллелограмма делит его углы пополам, то этот параллелограмм является ромбом). - Каждая из биссектрис равнобедренного треугольника является его медианой.
(Только биссектриса, проведенная к основанию. Биссектриса, проведенная к боковой стороне не будет являться медианой).
- У любой трапеции боковые стороны равны.
(Только у равнобокой трапеции боковые стороны равны). - Диагональ трапеции делит её на два равных треугольника.
(Диагональ параллелограмма делит его на два равных треугольника. Для трапеции такое утверждение неверно). - Смежные углы равны.
(Сумма смежных углов равна 180°. Если смежные углы равны, то каждый из них равен 90°, но это частный случай). - Любые две прямые имеют ровно одну общую точку.
(Параллельные прямые не имеют общих точек). - Если угол равен 47°, то смежный с ним равен 153°.
(Смежных с ним угол должен быть равен 180°-47°=133°). - Через любую точку проходит ровно одна прямая.
(Через любую точку можно провести бесконечное множество прямых). - Если угол равен 120°, то смежный с ним равен 120°.
(Сумма смежных углов равна 180°. Если один из смежных углов равен 120°, то второй должен быть равен 60°). - При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

(Накрест лежащие углы должны быть равны). - Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
(Центром окружности, описанной около треугольника является точка пересечения его серединных перпендикуляров). - Диагонали параллелограмма равны.
(Диагонали прямоугольника и квадрата равны, а у параллелограмма они разной длины). - Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
(Угол должен находиться между этими сторонами, в данной формулировке об этом ни слова). - В тупоугольном треугольнике все углы тупые.
(В тупоугольном треугольнике один из углов тупой. Все углы не могут быть тупыми, так как их сумма станет больше 180°). - Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
(Первый признак равенства треугольников: Если две стороны одного треугольника и угол между ними соответственно равны стороне и угла между ними другого треугольника, то такие треугольники равны).
- Точка пересечения двух окружностей равноудалена от центров этих окружностей.
(Равноудалена – находится на одном и расстоянии от обоих центров. Если окружности будут разного радиуса, то точка пересечения окружностей будет ближе к центру окружности меньшего радиуса). - Площадь прямоугольного треугольника равна произведению длин его катетов.
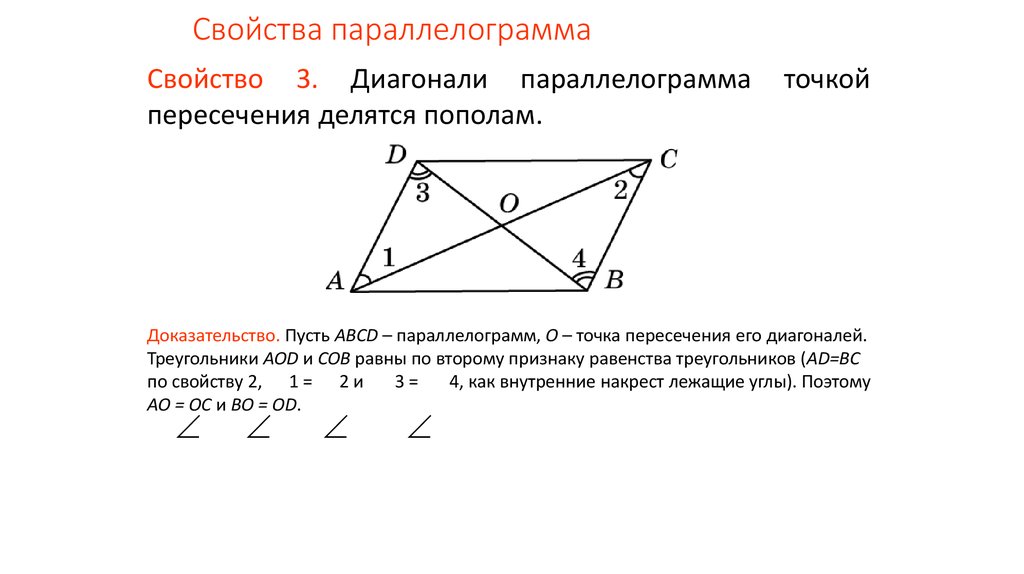
(Площадь прямоугольного треугольника равна половине произведения длин его катетов). - Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
(Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам). - Все радиусы равны между собой.
(Все радиусы в одной окружности равны между собой. А радиусы в разных окружностях между собой не равны). - Все диаметры равны между собой.
(Диаметры в одной окружности равные между собой. А диаметры в разных окружностях между собой не равны). - Сумма углов любого треугольника равна 360°.
(Сумма углов в треугольнике равна 180°).
- Сумма вертикальных углов равна 180°.
(Вертикальные углы равны. Сумма смежных углов равна 180°). - Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
(Важно, чтобы были равны углы. Простой пример: квадрат со стороной 1 не равен ромбу со стороной 1, хотя стороны этих четырехугольников равны). - Все углы ромба равны.
(Противолежащие углы ромба равны). - Все углы параллелограмма равны.
(Противолежащие углы параллелограмма равны). - Все хорды одной окружности равны между собой.
(Все диаметры одной окружности равны между собой. Хорда же соединяет две точки окружности). - Всегда один из двух смежных углов острый, а другой тупой.
(Возможен случай, когда оба смежных угла равны 90°).
Задача 19 ОГЭ математика
MATHM >> ОГЭ >>
Задача 19
Сложность у всех задач примерно одинаковая
-
Какое из следующих утверждений верно?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.
2) Сумма углов прямоугольного треугольника равна 180°.
3) Любая медиана равнобедренного треугольника является его высотой.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Дана окружность. Через любую точку плоскости можно провести к ней касательную прямую.
2) Если в параллелограмме некоторый угол равен 90°, то это квадрат.
3) В любом ромбе найдется угол меньше 120°.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Внутренние односторонние углы при пересечении параллельных прямых секущей равны.
2) Площадь трапеции равна произведению высоты на сумму оснований.
3) В любом квадрате все углы равны.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Сумма катетов длиннее гипотенузы.
2) Длина суммы векторов длиннее суммы длин самих векторов.
3) В любом треугольнике найдется острый угол.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Сумма длин трех сторон четырехугольника всегда длиннее четвертой стороны.
2) В любой выпуклый четырехугольник можно вписать окружность.
3) Диагонали ромба равны.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Площадь треугольника равна произведению стороны на высоту, проведенную к этой стороне.
2) Треугольники равны, если их соответствующие стороны равны.
3) У подобных треугольников площади равны.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Сумма вертикальных углов равна 180°.
2) Корень квадратный из площади квадрата равен длине его стороны.
3) Периметр прямоугольника всегда больше его площади.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) У подобных треугольников соответствующие углы равны.
2) В правильном пятиугольнике все углы равны.
3) Площадь прямоугольника равна квадрату любой его стороны.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) В правильном шестиугольнике все углы по 160°.
2) Не существует треугольника со сторонами 10,12 и 16.
3) Диагонали прямоугольника равны.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) В любой прямоугольник можно вписать окружность.
3) Если угол между векторами равен 90°, то их скалярное произведение равно нулю.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

-
Какое из следующих утверждений верно?
1) Косинус угла в прямоугольном треугольнике это отношение прилежащего катета к противолежащему катету.
2) Катет лежащий против угла в 60° в два раза короче гипотенузы.
3) Диагонали ромба перпендикулярны.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Центр окружности вписанной в треугольник находится на пересечении биссектрис.
2) В правильном шестиугольнике все стороны равны.
3) Сумма двух соседних углов параллелограмма равна 180°.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Дана прямая. Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
2) Высоты треугольника пересекаются в одной точке.
3) Высота треугольника всегда лежит внутри треугольника.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Диагонали ромба пересекаются и точкой пересечения делятся пополам.
2) Площадь прямоугольника равна произведению двух противоположных сторон.
3) Длина вектора равна сумме квадратов его координат.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Сумма смежных углов равна 180°.
2) Если скалярное произведение векторов равно нулю, то векторы параллельны.
3) В любой трапеции есть, по крайней мере, два острых угла.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Площадь любого треугольника равна половине произведения сторон на синус угла между ними.
2) Все точки лежащие на биссектрисе некоторого угла равноудалены от сторон этого угла.
3) Площадь ромба равна половине произведения сторон.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Если две окружности касаются, то у них радиусы равны.
2) Периметр прямоугольника равен произведению двух соседних сторон.
3) Сумма углов пятиугольника равна 540°.
В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Вокруг любого четырехугольника можно описать окружность.
2) Если некоторая окружность касается прямой, то расстояние от центра окружности до этой прямой равно радиусу окружности.
3) Если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Через точку, лежащую на окружности, всегда можно провести касательную к этой окружности.
2) Длина окружности всегда больше ее радиуса.
3) Если в треугольнике одна сторона равна половине второй, то в треугольнике есть угол в 30°.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Если в параллелограмме все углы равны, то это квадрат.
2) Длина самой длинной стороны в треугольнике меньше суммы длин двух других сторон.
3) Вокруг любого четырехугольника можно описать окружность.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Диагональ параллелограмма делит его на два равных треугольника.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
-
Какие из следующих утверждений верны?
1) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Любой квадрат является прямоугольником.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Каждая из биссектрис равнобедренного треугольника является его медианой.
3) В любой ромб можно вписать окружность.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

-
Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Стороны треугольника пропорциональны синусам противолежащих углов.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Треугольник со сторонами, длины которых равны 3,4 и 5, является тупоугольным.
2) Прямоугольник обладает центром симметрии.
3) Любой прямоугольный треугольник не обладает центром симметрии.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) У квадрата ровно две оси симметрии.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Площадь прямоугольного треугольника меньше произведения его катетов.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) В правильный шестиугольник всегда можно вписать окружность.
2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
3) Сумма вертикальных углов равна 180°.В ответ запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Через любые две точки на плоскости можно провести окружность, причем только одну.
2) У прямоугольного треугольника не может быть оси симметрии.
3) Диагонали трапеции всегда пересекаются.В ответ запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
2) В параллелограмме есть два равных угла.
3) Площадь параллелограмма меньше или равна произведению двух его соседних сторон.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Косинус острого угла прямоугольного треугольника равен отношению катета, прилежащего к этому углу, к гипотенузе.
2) Если в параллелограмме все углы равны, то это прямоугольник.
3) Все высоты равнобедренного треугольника лежать внутри этого треугольника.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) К двум окружностям всегда можно провести две общие касательные.
2) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник – параллелограмм.
3) Точка пересечения биссектрис любого треугольника всегда лежит внутри этого треугольника.В ответ запишите номер выбранного утверждения.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Какие из следующих утверждений верны, а какие нет? а) Диагонали параллелограмма равны. б) Диагонали прямоугольника перпендикулярны друг другу. в) Диагонали ромба равны. 8 видео 15 (б) Ложь
(в) Ложь
Ответьте
Пошаговое решение, разработанное экспертами, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Какие из следующих утверждений верны для
Прямоугольник?
У него две пары равных сторон.
У него все стороны одинаковой длины.
Его диагонали равны.
Его диагонали делят друг друга пополам.
Его диагонали перпендикулярны.
Его диагонали перпендикулярны и делят каждую пополам.
другой.
Его диагонали равны и делят друг друга пополам.
Его диагонали равны и перпендикулярны, и
делят друг друга пополам.
Все прямоугольники являются квадратами.
Все ромбы являются параллелограммами.
Все квадраты являются ромбами, а также прямоугольниками.
Все квадраты не являются параллелограммами.
Прямоугольник – это параллелограмм, у которого один из углов равен прямому.
1536752
कर्ण परस्पर समद्विभाजित करते हैं?
руб. समलम्ब ख. समांतर चतुर्भुज ग. समचतुर्भुज घ. आयत।
इनमें से किन-किन के विकर्ण परस्पर लम्ब होंगे?
इनमें से किन-किन के विकर्ण परस्पर बराबर होंगगे
109837032
Текстовое решение
सत्य/असत्य बताइए —
र चतुर्भुज के विकर्ण एक-दूसरे पर लम्ब और बराब। हहह आयत होता है।
226124695
Диагонали ромба равны (Верно/Неверно)
277383552
Какие из следующих утверждений верны, а какие нет?
Диагонали прямоугольника перпендикулярны друг другу.
283265373
Какие из следующих утверждений верны, а какие нет?
Диагонали ромба равны.
283265375
Диагонали параллелограмма равны. (Верно или неверно)
318516152
Какие из следующих утверждений верны для Прямоугольник? У него две пары равных сторон. У него все стороны одинаковой длины. Его диагонали равны. Его диагонали делят друг друга пополам. Его диагонали перпендикулярны. Его диагонали перпендикулярны и делят каждую пополам. другой. Его диагонали равны и делят друг друга пополам. Его диагонали равны и перпендикулярны, и делят друг друга пополам. Все прямоугольники являются квадратами. Все ромбы являются параллелограммами. Все квадраты являются ромбами, а также прямоугольниками. Все квадраты не являются параллелограммами.
642590357
Утверждение A: В прямоугольнике противоположные стороны равны и диагонали равны. Утверждение Б: В параллелограмме противоположные стороны равны и диагонали равны. Утверждение C: В ромбе все стороны равны, а диагонали не равны.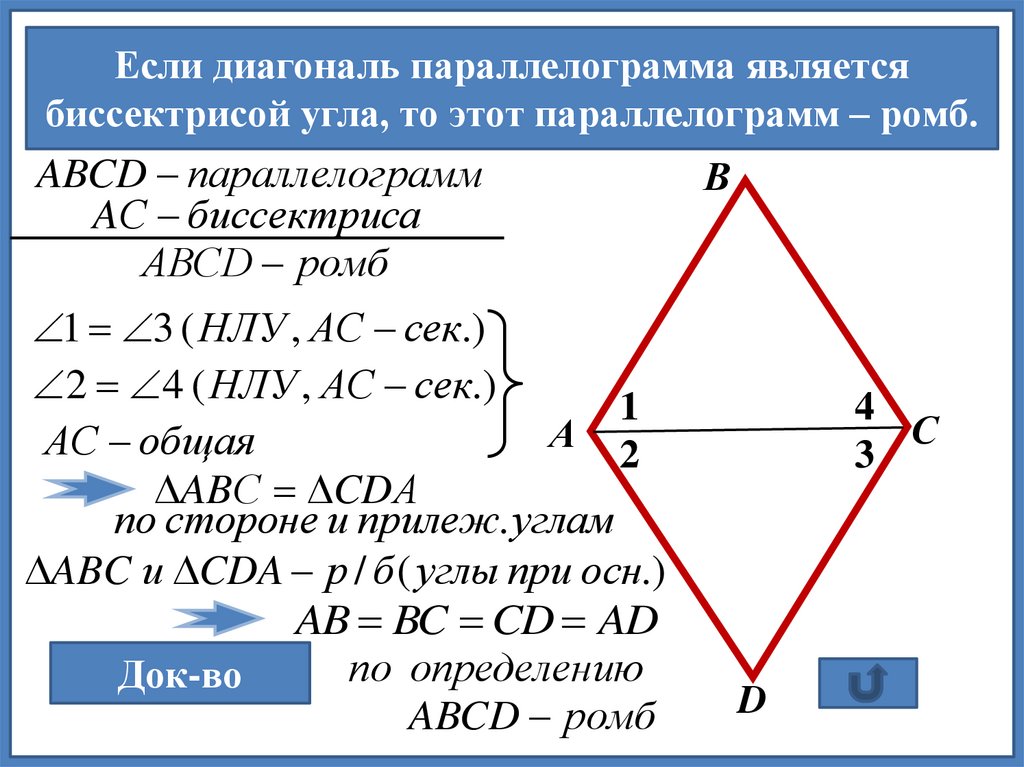 Какие из следующих утверждений верно?
Какие из следующих утверждений верно?
643831144
Какое из следующих свойств неверно?
Диагонали параллелограмма делят друг друга пополам.
Диагонали прямоугольника равны
Диагонали ромба перпендикулярны друг другу.
Диагонали воздушного змея являются биссектрисами, перпендикулярными друг другу.
644262346
त्य हैं।
समांतर चतुर्भुज के विकर्ण एक-दूसरे क। समद्वति रते हैं।
644940787
यदि समांतर चतुर्भुज के विकर्ण बराबर हों, तोययो यो ता है।
644940790
Диагонали ромба равны и перпендикулярны друг другу.
645477266
Укажите, верны ли утверждения (T) или (F) ложны.
Диагонали ромба равны и перпендикулярны друг другу.
645588297
Какое из следующих утверждений верно или неверно :
Диагонали параллелограмма делят друг друга пополам.
645659313
Какие из следующих утверждений верны (T), а какие нет (F)? В параллелограмме диагонали равны. В параллелограмме диагонали делят друг друга пополам.
 В параллелограмме диагонали пересекаются под прямым углом.
В любом четырехугольнике, если пара противоположных сторон равны, он является параллелограммом.
Если все углы четырехугольника равны, то это параллелограмм.
Если три стороны четырехугольника равны, то это параллелограмм.
Если три угла четырехугольника равны, то это параллелограмм.
Если все стороны четырехугольника равны, то это параллелограмм
В параллелограмме диагонали пересекаются под прямым углом.
В любом четырехугольнике, если пара противоположных сторон равны, он является параллелограммом.
Если все углы четырехугольника равны, то это параллелограмм.
Если три стороны четырехугольника равны, то это параллелограмм.
Если три угла четырехугольника равны, то это параллелограмм.
Если все стороны четырехугольника равны, то это параллелограммВопрос
Обновлено:26/05/2018
RD SHARMA-QUADRILATERALS-Все вопросы
20 видеоРЕКЛАМА
Текст Решение
Решение
(i)ложное. Диагонали параллелограмма не обязательно равны. (ii) Верно. Это известное свойство параллелограмма. (iii) Ложь. Диагонали параллелограмма могут пересекаться под любым углом. (iv) Ложь. Четырёхугольник можно назвать параллелограммом только в том случае, если обе пары его противоположных сторон равны. (v) Верно. Если все углы равны, то это означает, что его противоположные углы также равны, что является условием для того, чтобы четырехугольник назывался параллелограммом. (vi) Ложь. Основным условием параллелограмма является параллельность сторон.
(vii) Ложь. Обе пары противоположных углов должны быть равны, чтобы четырехугольник можно было назвать параллелограммом.
(viii) Верно. Если все стороны равны, то равны и противоположные стороны.
(vi) Ложь. Основным условием параллелограмма является параллельность сторон.
(vii) Ложь. Обе пары противоположных углов должны быть равны, чтобы четырехугольник можно было назвать параллелограммом.
(viii) Верно. Если все стороны равны, то равны и противоположные стороны.Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Видео по теме
Если диагонали четырехугольника делят друг друга пополам, то четырехугольник — параллелограмм.
Если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом.
1340596
Теорема в параллелограмме доказывает, что (i) противоположные стороны равны; (ii) противоположные углы равны; (iii) диагонали делят друг друга пополам.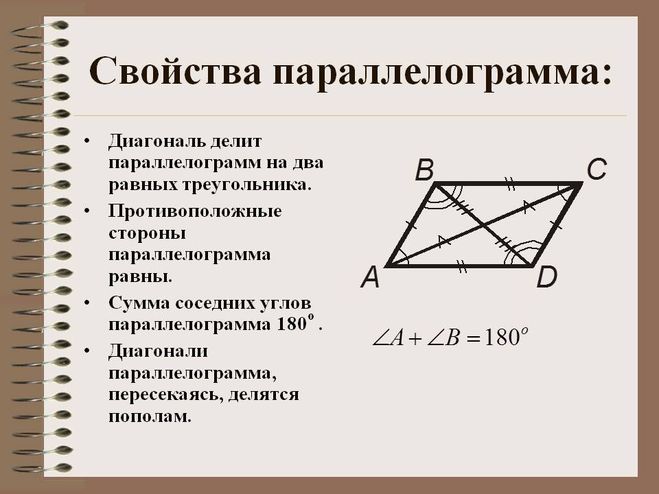
1528522
Обратное из приведенных выше свойств также верно, т. е. (i) Четырехугольник является параллелограммом, если его противоположные стороны равны. (ii) Четырехугольник является параллелограммом, если его противоположные углы равны. (iii) Четырехугольник является параллелограммом, если у него одна пара противоположных сторон параллельна и равна. (iv) Четырехугольник является параллелограммом, если его диагонали делят друг друга пополам.
1528523
Закрыть Закрыть ह समान्तर चतुर्भुज है
127118427
नीचे (a)औऍ (b) मरम म र थनो में से प्रत्येक के लिए (i) और (ii) में दिए गए कथनो में से कौन प्रतिधनात्मरहर हर ोम है पहचानिए :
(b) यदि एक चतुर्भुज के विकर्ण थक — सक समद्विभाजित नहीं करते है , तो चतुर्भुज चक समांतर ुज नहीं है ।
(i) यदि किसी चतुर्भुज विकर्ण एक — दूसरे को समतद्विि नहीं करते है , तो चतुर्भुज एक समांतर चतुर्भुज ।हु नह। 90 015 है तो वह समांतर चतुर्भुज है । (a) और (b) रत्येक के लिए संगत प्रतिधनात्मक और विलोम कथन नहन नहन पहि कथि नहन पहि नहम कथि नहि नहि 15 (б) क-दूसरे को Количество номеров:
(1) दूसरे को समद्विभाजित करते हैं, तो चतुर्भुज सरम सर तुर्भुज है।
(2). नहीं करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुह तो
नहीं करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुह तो
226120391
ण एक-दूसरे को समद्विभाजित करें तो वह समानान्।र र ज होगा।
226124737
निम्नलिखित कथनों में से कौन-सह सते सते और कौन असत्य (F) हैं ?
(i) समांतर चतुर्भुज में, विकर्ण बराबर होते हं।
(ii) Закрыть ते हैं।
(iii) करते हैं।
(iv) राबर है, तो वह समांतर चतुर्भुज है।
(в) ्भुज है।
(vi) यदि चतुर्भुज की सभी भुजाएँ बराबर हैं, तो वम तर तुर्भुज है।
(vii). चतुर्भुज है।
(viii) र्भुज है।
408033914
Текст Решение
Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам , и наоборот, если диагонали четырехугольника делят друг друга пополам, то это параллелограмм.
412653385
При следующих утверждениях:
A: Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом.
B: Если диагонали четырехугольника не делят друг друга пополам, то этот четырехугольник не является параллелограммом.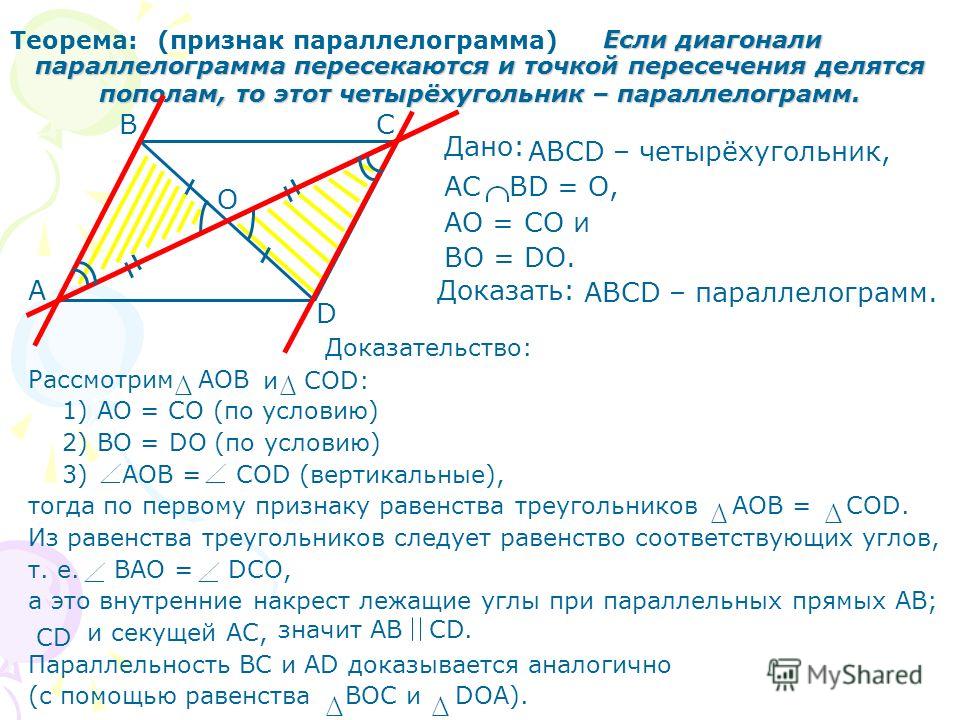
Идентифицируйте их как противоположные или противоположные друг другу.
452583662
Данные заявления в a и b. Определите приведенные ниже утверждения как противоположные или противоположные друг другу.
Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам.
(i) Если диагонали четырехугольника не делят друг друга пополам, то этот четырехугольник не является параллелограммом
(ii) Если диагонали четырехугольника делят друг друга пополам, то он является параллелограммом.
560945816
Если диагонали четырехугольника делят друг друга пополам, то четырехугольник — параллелограмм.
642565052
Что из следующего
утверждения истинны (T), а какие ложны (F)?
(i) В параллелограмме
диагонали равны.
(ii) В параллелограмме
диагонали делят друг друга пополам.
(iii) В параллелограмме
диагонали пересекаются под прямым углом.
(iv) В любом четырехугольнике
если пара противоположных сторон равна, то это параллелограмм.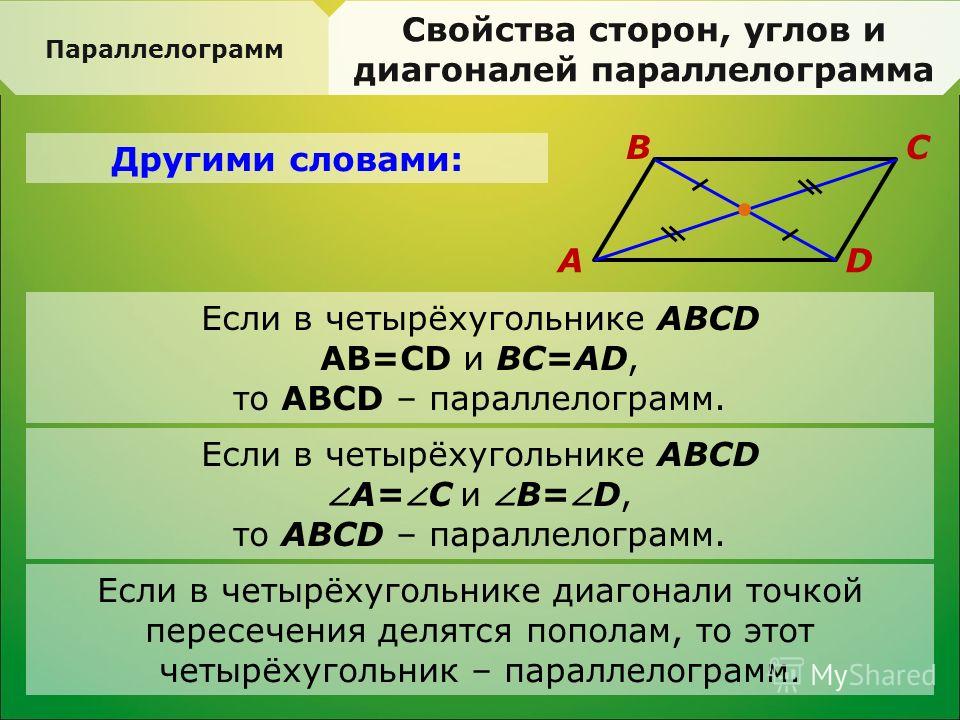


 (2 признак равенства треугольников)
(2 признак равенства треугольников)
 (теорема косинусов).
(теорема косинусов).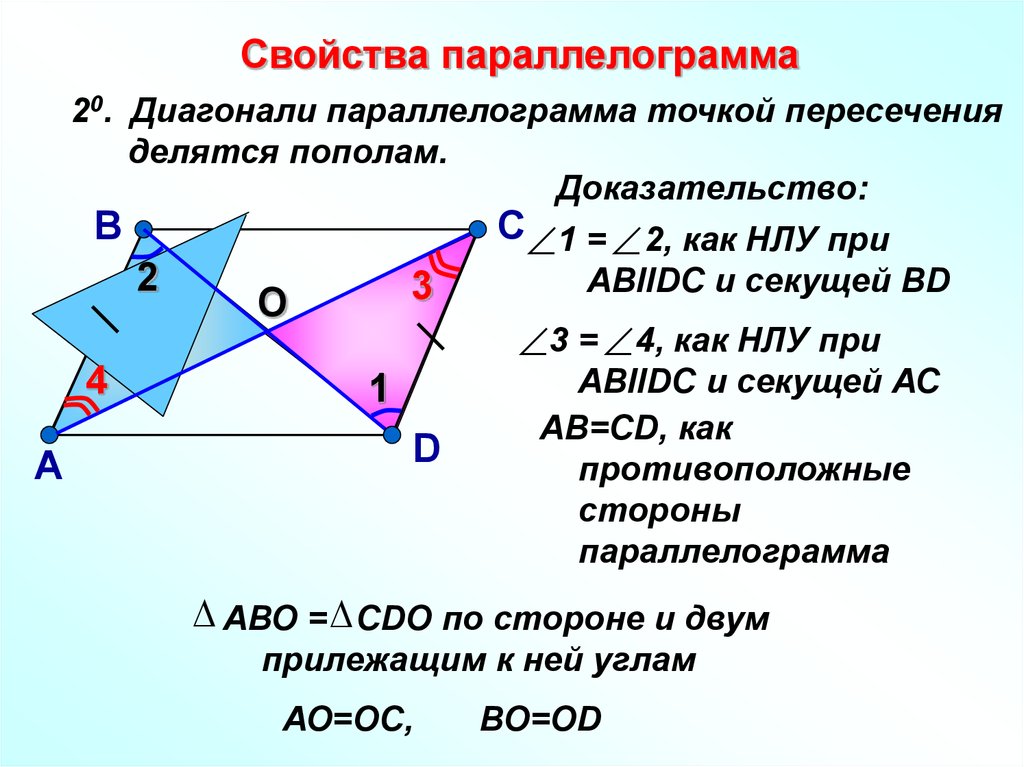




 Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат).
Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат).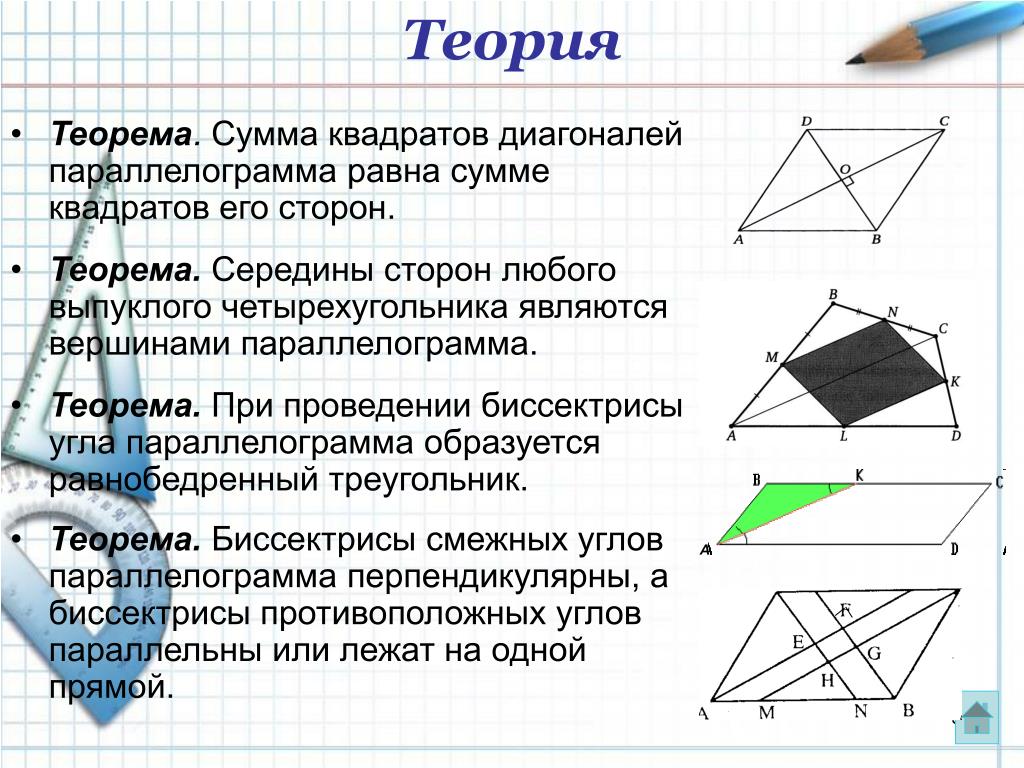


 Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого).
Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого).




 Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.