| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
е. температура меньше 0 градусов;Простейшие понятия теории множеств
§1.
Множества. Операции над множествами.Множество– совокупность объектов той или иной природы, обладающих некоторым заданным свойством, понятие первоначальное, неопределяемое. Всякое множество определяется некоторым свойством
обозначение | что означает |
А, В, С,… а, b, с,…
| множество элемент множества элементы аиbсовпадают элементы аиbразличныэлемент апринадлежит множествуА элемент ане принадлежит множествуА |
Способы задания множеств:
1.
перечисление
его элементов.
Если множество Асостоит из элементовx,y,z, то записывают
.
2. указание характеристического свойства.
Если множество Асостоит из элементов принадлежащих универсальному множествуЕи обладающих свойствомР, то записывают
.
Схематичное изображение множеств в виде фигур на плоскости (кругов, эллипсов) даёт наглядное представление о простейших свойствах множеств и об операциях над ними. Такие схемы носят название диаграмм Эйлера-Венна. Универсальное множество принято изображать прямоугольни-ком.
Включение множеств. Равные множества.
Рассмотрим два множества АиВизЕ.
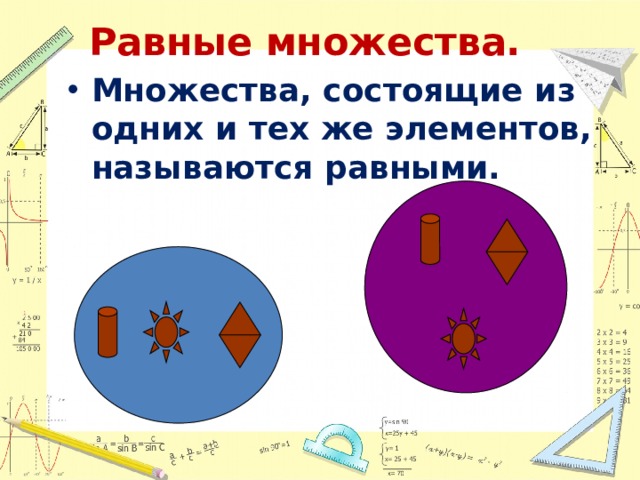
Определение 1.МножествоВназываетсяподмножеством множества А (множество В содержится во множестве А),если каждый элемент множества Вявляется одновременно элементом множестваА:
.
Обозначается .
Определение 2.МножествоВне содержитсяво множествеА, если существует хотя бы один элемент, такой что:
.
Обозначается .
Определение 3.МножестваАиВназываютсяравными, если они состоят из одних и тех же элементов.
Обозначается .
Отношение включения двух множеств обладает следующими свойствами:
1. ;
2. если и, то;
3. если и, то.
Упражнение. Доказать самостоятельно свойства 1-3.
Свойство 2 выражает собой так называемый метод встречных включений,применяемый для доказательства равенства множеств
.
Понятие пустого множества
Рассмотрим
множество элементов aиз Е, для которых.
Такое множество не содержит ни одного
элемента, оно называетсяпустым
множествоми обозначается:
.
Если множество Ане является пустым, то оно содержит хотя бы один элемент. Множество, состоящее из одного элемента, называетсяодноэлементным множеством.
Определение 4.Собственным подмножеством множества А называется любое подмножество этого множества, отличное отАи от пустого множества. Само множествоА и пустое множество называютсянесобственными подмножествами множества А.
Справедливы следующие свойства:
4. Пустое множество является подмножеством любого множества: .
5. .
Упражнение. Доказать самостоятельно свойства 4-5.
Операции над множествами
Пусть А и В – два множества изЕ.
Определение 5. Объединением или суммой множеств А и Вназывается множествоС, состоящее из всех элементов, принадлежащих хотя бы одному из множеств АилиВ.
Обозначается . Аналогично под записьюпонимается объединение любого числа множеств, где индекспринадлежит некоторому множеству. В частности,
— объединение конечного числа множеств;
-объединение последовательности множеств.
Определение 6.Пересечением или произведением множеств А и Вназывается множествоС, состоящие из элементов, принадлежащих одновременно множествамАи В.
Обозначается . Записьобозначает пересечение любого числа множеств. В частности,
— пересечение конечного числа множеств;
— пересечение последовательности
множеств.
Теория множеств
Набор представляет собой группу объектов, чисел и т.д. {1,2,3} — это множество, состоящее из чисел 1,2 и 3. Условно «3 — это элемент множества {1,2,3}». Чтобы показать это символически, используйте символ ∈, который читается как «является элементом» или «является членом». Следовательно, вы могли бы написать:
3 ∈ {1,2,3}
Специальные множества
Подмножество — это множество, содержащееся в другом множестве, или оно может быть всем множеством. Множество {1,2} является подмножеством множества {1,2,3}, а множество {1,2,3} является подмножеством множества {1,2,3}. Когда в подмножестве отсутствуют некоторые элементы из множества, с которым оно сравнивается, это правильное подмножество. Когда подмножество является самим набором, это неправильное подмножество. Символ, используемый для обозначения «является правильным подмножеством» — ⊂. Когда существует возможность использования неправильного подмножества, используется символ ⊆.
Следовательно, {1,2} ⊂ {1,2,3} и {1,2,3} ⊆ {1,2,3}. Универсальный набор является набором общей категории или набором всех рассматриваемых элементов. Пустой набор , нулевой набор или , — это набор без элементов или членов . Пустой набор или нулевой набор представлен символом ⊘ или { }. Однако он никогда не представлен {⊘}.
И универсальный набор, и пустой набор являются подмножествами каждого набора.
Описание наборов
Правило — это метод именования множества путем описания его элементов.
{ x : x > 3, x — целое число} описывает множество с элементами 4, 5, 6,…. Следовательно, { х : х > 3, х — целое число} — это то же самое, что и {4,5,6,…}. { x : x > 3} описывает все числа больше 3. Этот набор чисел не может быть представлен в виде списка и представлен с помощью числовой линейной диаграммы.
Реестр — это метод именования набора путем перечисления его членов.
{1,2,3} — это набор, состоящий только из элементов 1,2 и 3. Существует много способов представить этот набор с помощью правила. Вот два правильных метода:
{ x : x < 4, x — натуральное число}
{ x :0 < x < 4, x — целое число} {9000 x :0 < x < 4}, поскольку это правило включает ВСЕ числа от 0 до 4, а не только числа 1, 2 и 3.
Типы наборов
Конечные множества состоят из счетного числа элементов. Например, { a,b,c,d,e } — это набор из пяти элементов, поэтому он является конечным набором. Бесконечные множества содержат несчетное количество элементов. Например, {1,2,3,…} — это множество с бесконечным числом элементов, поэтому это бесконечное множество.
Сравнение наборов
Равные множества — это те, которые имеют одинаковые элементы — {1, 2, 3} = {3, 2, 1}.
Эквивалентные наборы — это наборы с одинаковым количеством элементов — {1, 2, 3} | { а, б, в }.
Диаграммы Венна (и Окружности Эйлера ) — это способы графического описания множеств, как показано на рис. 1.
Рисунок 1. Диаграмма Венна
A представляет все элементы в меньшем овале; B представляет все элементы большего овала; а C представляет собой все элементы, находящиеся в обоих овалах одновременно.
Операции с множествами
Объединение двух множеств представляет собой множество, содержащее все числа в этих множествах, но любые дубликаты записываются только один раз. Символ для нахождения объединения двух множеств — ∪.
Пример 1
Найдите союз {1,2,3} ∪ {3,4,5}.
{1,2,3} ∪ {3,4,5} = {1,2,3,4,5}
Объединение набора с элементами 1, 2, 3 вместе с набором с элементами 3 , 4, 5 — набор с элементами 1, 2, 3, 4, 5.
Пересечение двух наборов — это набор, содержащий только те элементы, которые находятся в каждом наборе одновременно. Символ для нахождения пересечения двух множеств — ∩.
Пример 2
Найдите пересечение {1,2,3} ∩ {3,4,5}.
{1,2,3} ∩ {3,4,5} = {3}
Пересечением множества с элементами 1, 2, 3 вместе с множеством с элементами 3, 4, 5 называется множество, имеет только 3.
Если бы вы позволили набору с {1,2,3} установить A , а набору с {3,4,5} установить B , тогда вы могли бы использовать Venn диаграммы, иллюстрирующие ситуацию (см. рис. 2).
Рисунок 2. Пересечение множества A и множества B
Объединением будут все числа, представленные на диаграмме, {1,2,3,4,5}. Пересечение будет там, где два овала перекрываются в диаграмма, {3}.
Пример 3
Найдите {1,2,3} ∩ {4,5}.
Так как нет элементов, которые находятся одновременно в обоих множествах, то {1,2,3} ∩ {4,5} = ⊘.
Пересечение набора с элементами 1, 2, 3 вместе с набором с элементами 4, 5 является пустым набором или нулевым набором. В обоих множествах одновременно нет элементов.
Пролог: списки, состоящие из одного элемента
Я считаю, что проблема у меня очень глупая, но не смог найти ответ в Интернете. Я хочу, чтобы функция всегда возвращала список элементов, даже если список состоит только из одного элемента. Я не знаю, всегда ли так в прологе (т. е. списки из одного элемента преобразуются в простую константу), но здесь я вдаюсь в подробности.
Во-первых, у меня есть набор предикатов (например, composeBase(<,<,[<]). ), на основе которых функция, о которой я говорил, compose/3 , выполняет свои вычисления:
compose (Х, Y, Z): -
композицияBase(X,Y,Z).
Так, например, compose/3 делает это:
compose(<, <, L). Л = (<) . составить(<, =, L). Л = (<) . составить (=, =, L). Л = (=) .
Итак, почему в первом примере не возвращается [<] , если предикат говорит composeBase(<,<,[<]). ? Есть ли способ заставить его вернуть список 
[<] вместо этого?
Если нет или мой вопрос не имеет никакого смысла, вот в чем проблема с невозможностью сделать это (если есть, конечно, даже не утруждайте себя чтением! :) Если только вы хочется дать мне предложения для моего наивного кода, которые я был бы очень признателен как новичок).
Мне нужно написать функцию composeList/3 , который, учитывая два списка элементов, должен вычислить список, содержащий все возможные композиции элементов в двух наборах.
Поэтому, например, composeList/3 должен делать так:
composeList([<], [<, =], L). L = [<, =] . составить список([<,=], [<, =], L). L = [<, =] .
А вот код:
composeList(_,[],[]). составить список([],_,[]). composeList([X|Xs], [Y|Ys], L):- составить (X, Y, L1), составить список(Xs, [Y| Ys], L2), составить список([X| Xs], Ys, L3), объединение (L1, L2, L4), объединение(L3,L4,L).
