Пожалуйста, откройте решение!
Задача 2
Какое из следующих утверждений верно?
A) $Q\subseteq I$
B) $N\subseteq Q$
C) $Z\nsubseteqq R$
D) Верные A, B, C
Задача 3
Верно ли, что $3\in Z$?
Задача 4
Верно ли, что $-3\in N$?
Задача 5
Верно ли, что $\sqrt{2}\in Q$
Задача 6
$\frac{3}{4}$ рациональное число и $2$ натуральное число. Каким числом является $\frac{3}{4}+2$?
Задача 7
Верно ли следующее утверждение?
Каждое натуральное число также является целым числом.
Задача 8
Верно ли следующее утверждение?
Каждое натуральное число также является рациональным числом.
Задача 9
Верно ли следующее утверждение?
Каждое иррациональное число можно записать в виде дроби.
Задача 10
Верно ли, что $-2\in Q$?
Задача 11
Верно ли, что
$\pi \in I$?
Задача 12
Сколько из следующих чисел являются целыми числами?
$0,$ $\frac{-4}{2},2^{3},\frac{5}{2},e,\sqrt{2},-\sqrt{9}$
Задача 13
Пусть число $n=\frac{3}{5}-2$
Какое из следующих утверждений является ложным?
$n$ иррациональное число
$n=-\frac{7}{5}$
$n$ действительное число
$n$ рациональное число
Задача 14
Если $m,n$ рациональные числа, то какое из следующих утверждений верно?
$m-n$ целое число
$m-n=0$
$m-n$ рациональное
Ни одно из них.
Задача 15
Число $3,25$ является рациональным или иррациональным?
Рациональное
Иррациональное
Задача 16
Число $n=2,151515151515…….$ имеет бесконечные количество десятичных знаков и 15 повторяется бесконечное количество раз.
Является ли оно рациональным или иррациональным?
Рациональное
Иррациональное
Задача 17
Является ли число $\frac{\sqrt{5}}{2}$ рациональным или иррациональным?
Рациональное
Иррациональное
Задача 18
Является ли произведение двух рациональных чисел рациональным числом?
Задача 19
Является ли произведение двух иррациональных чисел иррациональным числом?
Да
Нет
Это зависит
Прислать задачу
Правильный:
Неверный:
Неразрешенные задачи:
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
05.18
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Поиск наборов номеров/Проверка ℕ,ℤ,ℚ,ℝ,ℂ — N Z Q R C
Калькулятор наборов номеров
Номер для проверкиПрограмма проверки наборов номеров
| Набор | Протестировать все наборы N: натуральные целые числа Z: относительные целые числа D: десятичные числа Q: рациональные числа R: действительные числа I: чисто мнимые числа C: комплексные числа |
См.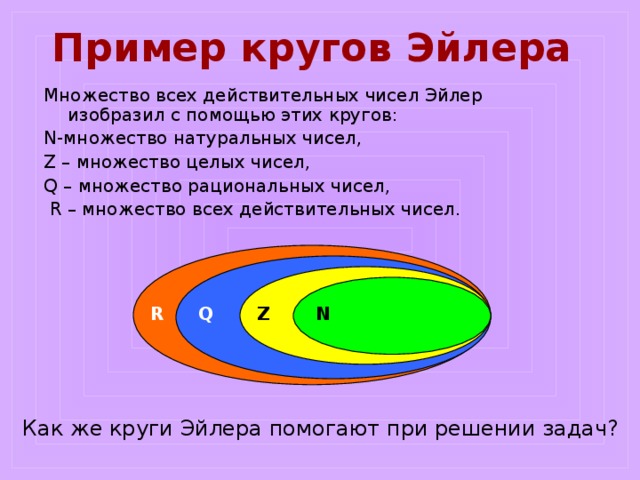
также: Решатель уравнений — Калькулятор
Ответы на вопросы (FAQ)
Что такое набор чисел? (Определение)
Набор чисел — это математическое понятие, позволяющее помещать различные типы чисел в различные категории, иногда включаемые между ними.
Классическим представлением обычных множеств является $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $$
Что такое общие числовые наборы?
В математике существует несколько наборов : натуральные числа N (или ℕ), набор целых чисел Z (или ℤ), все десятичные числа D или $ \mathbb{D} $, набор рациональных чисел Q (или ℚ), набор действительных чисел R (или ℝ) и набор комплексных чисел C (или ℂ). Эти 5 наборов иногда обозначаются аббревиатурой NZQRC .
Другие наборы, такие как набор десятичных чисел D или $ \mathbb{D} $, или набор чисто мнимых чисел I или $ \mathbb{I} $.
Существуют также наборы трансцендентных чисел, кватернионов или гиперкомплексных чисел, но они зарезервированы для продвинутых математических теорий, NZQRC являются наиболее распространенными наборами.
Что означает символ ∈?
Знак ∈ (Unicode 2208) означает, что элемент или принадлежит .
Пример: $ 2 \in \mathbb{N} $ читается 2 является элементом множества N
Также имеется знак ∊ (Unicode 220A), который такой же, но меньшего размера.
Знак ∉ (Unicode 2209) означает, что не является элементом или не принадлежит .
9{+} $
NB: В некоторых (старых) учебниках указана буква W вместо N для этого набора, W означает Целые числа
Набор N входит в наборы Z, D, Q, R и C.
Что такое набор номеров Z?
Z — множество целых чисел, т.е. положительное, отрицательное или ноль.
Пример: …, -100, …, -12, -11, -10, …, -5, -4, -3, -2, — 1, 0, 1, 2, 3, 4, 5 , … 10, 11, 12, …, 100, … $ \in \mathbb{Z} $
9{p}} , a \in \mathbb{Z}, p \in \mathbb {N} \right\} $$Все десятичные дроби в D — это числа, которые можно записать конечным числом цифр (числа, содержащие точка и конечная десятичная часть).
Пример: -123,45, -2,1, -1, 0, 5, 6,7, 8,987654 $ \in \mathbb{D} $
Таким образом, числа, использующие точки подвеса … для их десятичной записи, имеют бесконечное число десятичных знаков и поэтому не принадлежат множеству D.
Множество D входит в состав множеств Q, R и C.
Наборы N и Z включены в набор D (поскольку все целые числа являются десятичными числами без десятичных разрядов). Любое число в N или Z также находится в D.
Что такое число Q?
Q есть набор рациональных чисел , т.е. представлена дробью a/b, где a принадлежит Z, а b принадлежит Z * (исключая деление на 0).
Пример: 1/3, -4/1, 17/34, 1/123456789 $ \in \mathbb{Q} $
Множество Q входит в множества R и C.
Наборы N, Z и D включены в набор Q (поскольку все эти числа можно записать дробью). Любое число в N, Z или D также содержится в Q.
Какой набор чисел R?
R — это набор действительных чисел , т.е. все числа, которые могут реально существовать, содержит кроме рациональных чисел, нерациональные или иррациональные числа в виде $\pi$ или $\sqrt{2}$.
Иррациональные числа имеют бесконечную непериодическую десятичную часть.
Набор R входит в набор C.
Наборы N, Z, D и Q входят в набор R. Любое число из N или Z или D или Q также входит в R.
Что такое I номер установлен?
I — это набор (чистых) мнимых чисел, то есть комплексных чисел без действительных частей, квадратные корни отрицательных действительных чисел являются чисто мнимыми.
2=-1 $
Набор I входит в набор C.
Что такое набор C?
C — это набор комплексных чисел , набор, созданный математиками как расширение набора действительных чисел , к которому добавляются числа, содержащие мнимую часть.
Пример: $ a + i b \in \mathbb{C} $
Наборы N, Z, D, Q, R и I включены в набор C. Любое число из N или Z или D или Q или R или I тоже в C.
Что такое пустой набор Ø?
Пустой набор отмечен Ø , как следует из его названия, он пуст и не содержит ни одного номера.
Что такое конструируемое число?
Составные числа — это все числа, которые можно геометрически изобразить с помощью линейки и циркуля.
Пример: $ \sqrt{2} $ — конструируемое число, а $ \pi $ — нет.
Что такое алгебраическое число?
Алгебраические числа — это набор чисел, которые можно вычислить как корень многочлена с рациональными коэффициентами.
Что такое трансцендентное число?
Трансцендентные числа — это набор чисел, которые нельзя вычислить как корень многочлена с рациональными коэффициентами (то есть не алгебраическими).
Среди действительных или комплексных чисел большинство — трансцендентные числа.
Что такое иррациональные числа?
Иррациональные числа — это наборы чисел, которые нельзя записать в виде дроби (т. е. все числа, не входящие в $\mathbb{Q} $)
Что такое наборы чисел E и O?
Некоторые книги определяют наборы E для четных чисел и O для нечетных чисел. Это не стандартное обозначение.
Что входит в наборы?
Связи между различными множествами представлены включениями: $$ N \подмножество Z \подмножество D \подмножество Q \подмножество R \подмножество C $$
Символ подмножества ⊆ является символом включения (в широком смысле), A ⊆ B, если каждый элемент A является элементом B.
Символ подмножества 93$.
Как записать числовой набор в LaTeX?
Набор чисел записывается с тегом mathbb : \mathbb{Z} for $ \mathbb{Z} $
Исходный код
dCode сохраняет право собственности на исходный код «Наборы чисел». За исключением явной лицензии с открытым исходным кодом (указана Creative Commons / бесплатная), алгоритма «Наборы чисел», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Наборы чисел» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или API-доступ для «Наборов номеров» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Наборы чисел» или любых ее результатов разрешено, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .txt осуществляется нажатием значка export . , https://www.dcode.fr/number-sets
Наборы номеров Finder/Checker ℕ,ℤ,ℚ,ℝ,ℂ — N Z Q R C
Калькулятор наборов чисел
Номер для проверкиПрограмма проверки наборов номеров
| Набор | Протестировать все наборы N: натуральные целые числа Z: относительные целые числа D: десятичные числа Q: рациональные числа R: действительные числа I: чисто мнимые числа C: комплексные числа |
См. также: Решатель уравнений — Калькулятор
Ответы на вопросы (FAQ)
Что такое набор чисел? (Определение)
Набор чисел — это математическое понятие, позволяющее помещать различные типы чисел в различные категории, иногда помещая их между собой.
Классическим представлением обычных множеств является $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $$
Что такое общие числовые наборы?
В математике существует несколько наборов : натуральные числа N (или ℕ), набор целых чисел Z (или ℤ), все десятичные числа D или $ \mathbb{D} $, набор рациональных чисел Q (или ℚ), набор действительных чисел R (или ℝ) и набор комплексных чисел C (или ℂ). Эти 5 наборов иногда обозначаются аббревиатурой NZQRC .
Другие наборы, такие как набор десятичных чисел D или $ \mathbb{D} $, или набор чисто мнимых чисел I или $ \mathbb{I} $. Существуют также наборы трансцендентных чисел, кватернионов или гиперкомплексных чисел, но они зарезервированы для продвинутых математических теорий, NZQRC являются наиболее распространенными наборами.
Что означает символ ∈?
Знак ∈ (Unicode 2208) означает, что элемент или принадлежит .
Пример: $ 2 \in \mathbb{N} $ читается 2 является элементом множества N
Также имеется знак ∊ (Unicode 220A), который такой же, но меньшего размера.
Знак ∉ (Unicode 2209) означает, что не является элементом или не принадлежит .
9{+} $
NB: В некоторых (старых) учебниках указана буква W вместо N для этого набора, W означает Целые числа
Набор N входит в наборы Z, D, Q, R и C.
Что такое набор номеров Z?
Z — множество целых чисел, т.е. положительное, отрицательное или ноль.
Пример: …, -100, …, -12, -11, -10, …, -5, -4, -3, -2, — 1, 0, 1, 2, 3, 4, 5 , … 10, 11, 12, …, 100, … $ \in \mathbb{Z} $
9{p}} , a \in \mathbb{Z}, p \in \mathbb {N} \right\} $$ Все десятичные дроби в D — это числа, которые можно записать конечным числом цифр (числа, содержащие точка и конечная десятичная часть).
Пример: -123,45, -2,1, -1, 0, 5, 6,7, 8,987654 $ \in \mathbb{D} $
Таким образом, числа, использующие точки подвеса … для их десятичной записи, имеют бесконечное число десятичных знаков и поэтому не принадлежат множеству D.
Множество D входит в состав множеств Q, R и C.
Наборы N и Z включены в набор D (поскольку все целые числа являются десятичными числами без десятичных разрядов). Любое число в N или Z также находится в D.
Что такое число Q?
Q есть набор рациональных чисел , т.е. представлена дробью a/b, где a принадлежит Z, а b принадлежит Z * (исключая деление на 0).
Пример: 1/3, -4/1, 17/34, 1/123456789 $ \in \mathbb{Q} $
Множество Q входит в множества R и C.
Наборы N, Z и D включены в набор Q (поскольку все эти числа можно записать дробью). Любое число в N, Z или D также содержится в Q.
Какой набор чисел R?
R — это набор действительных чисел , т.
2=-1 $
Набор I входит в набор C.
Что такое набор C?
C — это набор комплексных чисел , набор, созданный математиками как расширение набора действительных чисел , к которому добавляются числа, содержащие мнимую часть.
Пример: $ a + i b \in \mathbb{C} $
Наборы N, Z, D, Q, R и I включены в набор C. Любое число из N или Z или D или Q или R или I тоже в C.
Что такое пустой набор Ø?
Пустой набор отмечен Ø , как следует из его названия, он пуст и не содержит ни одного номера.
Что такое конструируемое число?
Составные числа — это все числа, которые можно геометрически изобразить с помощью линейки и циркуля.
Пример: $ \sqrt{2} $ — конструируемое число, а $ \pi $ — нет.
Что такое алгебраическое число?
Алгебраические числа — это набор чисел, которые можно вычислить как корень многочлена с рациональными коэффициентами.
Что такое трансцендентное число?
Трансцендентные числа — это набор чисел, которые нельзя вычислить как корень многочлена с рациональными коэффициентами (то есть не алгебраическими).
Среди действительных или комплексных чисел большинство — трансцендентные числа.
Что такое иррациональные числа?
Иррациональные числа — это наборы чисел, которые нельзя записать в виде дроби (т. е. все числа, не входящие в $\mathbb{Q} $)
Что такое наборы чисел E и O?
Некоторые книги определяют наборы E для четных чисел и O для нечетных чисел. Это не стандартное обозначение.
Что входит в наборы?
Связи между различными множествами представлены включениями: $$ N \подмножество Z \подмножество D \подмножество Q \подмножество R \подмножество C $$
Символ подмножества ⊆ является символом включения (в широком смысле), A ⊆ B, если каждый элемент A является элементом B.