Понятие множества / Множества / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Множества
- Понятие множества
| Словом «множество» в математическом языке обозначают любую совокупность объектов или предметов, объединенных каким-либо общим признаком. |
Примеры множеств:
множество месяцев в году, множество материков на планете Земля, множество игроков в футбольной команде, множество коров в стаде и т.д.
Множества как правило обозначают большими буквами латинского алфавита: А, В, С, D, М, N и т.д.
| Элемент множества — каждый объект (предмет), входящий в это множество. |
Например, январь элемент, входящий в множество месяцев в году.
Для записи множества используют фигурные скобки.
Например, множество дней в неделе записывают так:
{понедельник, вторник, среда, четверг, пятница, суббота воскресенье}.
| Числовое множество — это множество, элементами которого являются числа. |
Например, {1, 3, 5, 7, 9} — множество однозначных нечетных чисел.
Обратите внимание, множество {3, 5, 7} и множество {7, 3, 5} — это одно и то же множество, состоящее из чисел 3, 5 и 7.
Для того, чтобы на математическом языке записать предложение » — элемент множества А» (или, то же самое, «принадлежит множеству А«), используют знак . Соответствующая запись выглядит так: . Также, можно догадаться, что запись «» означает «не является элементом множества А«.
Множества бывают конечные и бесконечные.
Конечные множества — это множества, которые содержат конечное число элементов (например, количество учеников одного класса — конечное множество).
Бесконечные множества — это множества, которые содержат бесконечное число элементов (например, множество натуральных чисел).
Также множество может состоять из одного элемента. Например, множество натуральных чисел, расположенных межу числами 99 и 101: {100}.
Бывает такое, что описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Например, множество А — множество чисел, которые делятся на 9, но не делятся на 3. Таких чисел не существует. Получается, мы описали множество, которое не содержит ни одного элемента — пустое множество
Рассмотрим множества {2, 4, 6, 8} и {4; 8}. Каждый элемент второго множества принадлежит также и второму. Тогда говорят, что второе множество является подмножеством первого.
Тогда говорят, что второе множество является подмножеством первого.
| Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В. Пустое множество считают подмножеством любого другого множества. |
Если множество А является подмножеством множества В, то в символическом виде это записывают: .
Изобразить то, что можно следующим образом:
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Объединение и пересечение множеств
Множества
Правило встречается в следующих упражнениях:
5 класс
Задание 866, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 870, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 872, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 875, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 879, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 896, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 897, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 910, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 919, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Задание 6, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 35, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 60, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 66, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 114, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 190, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 873, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 55, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 579, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 586, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
2
ГЛАВА 1
Сегодня
мы знаем, что, логически говоря, возможно вывести почти всю современную
математику из единого источника – теории множеств.
ОСНОВЫ ТЕОРИИ МНОЖЕСТВ
1.1. Множество. Задание множеств
Оказывается, что понятие «множество» нельзя строго определить. Для того чтобы определить какое-либо понятие, нужно прежде всего указать, частным случаем какого более общего понятия оно является, расшифровать его через более простые. Но эти более простые понятия сами нуждаются в определении через еще более простые и еще более общие, для которых в свою очередь мы должны найти еще более простые и т.д. Таким образом, в конце концов, мы должны будем прийти к некоторым простейшим, первоначальным, наиобщим понятиям, упростить смысл которых, а значит, и точно определить, мы не в состоянии. И все, что можно сделать для их «определения» — разъяснить эти первоначальные понятия на ряде примеров, договориться, что под ними мы будем понимать.
Понятие
«множества» в математике и есть одно из самых простых, первоначальных и
общих.
Часто приходится говорить о нескольких вещах, объединенных некоторым
общим признаком. Так, можно говорить о множестве предметов, находящихся на
столе, множестве студентов, присутствующих в данный момент в аудитории,
множестве звезд, наблюдаемых на небе, множестве всех точек, равноудаленных от
данной, множестве всех клеток человеческого организма и т.д. Человеческому
мышлению свойственно трактовать то или иное собрание предметов, родственных по
какому-либо признаку, как самостоятельный объект. Совокупность кофейника,
молочника, сахарницы, шести чашек и блюдец мы называем сервизом.
Основное и самое существенное в понятии множества – это акт объединения различных объектов в одно целое.
Основатель
теории множеств немецкий математик и философ Георг Кантор писал: «Под
многообразием или множеством я понимаю вообще всякое многое, которое можно
мыслить как единое, т.е. всякую совокупность определенных элементов, которая
может быть связана в одно целое с помощью некоторого закона»[1].
Перефразируя Кантора, можно сказать, что множество — любая совокупность
определенных и различимых между собой объектов, рассматриваемых как единое
целое. Природа таких объектов может быть совершенно любой. Это могут быть
числа, функции, книги, молекулы, высказывания, сами множества. Соединенные
Штаты Америки – множество из 50 элементов – штатов, каждый из которых, в свою
очередь, есть множество округов.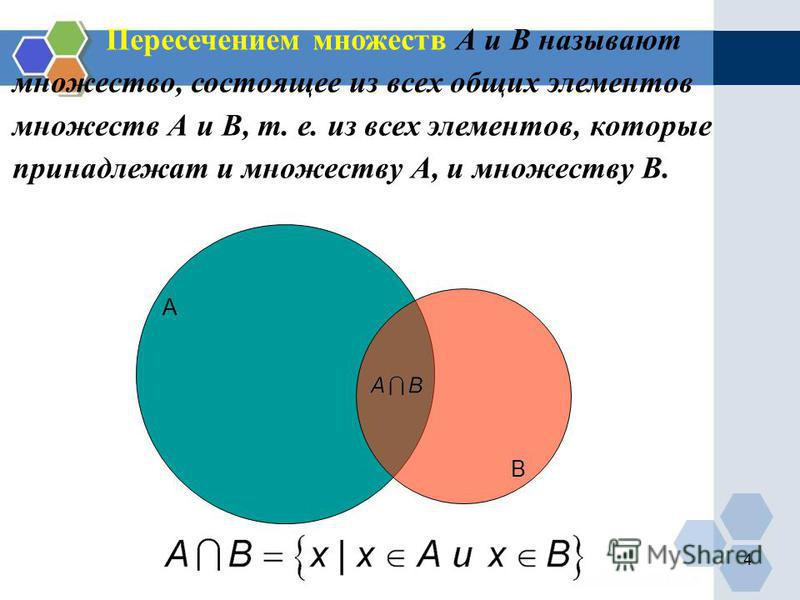
Трактовка слова «множество» в обыденном языке отличается от математической, ибо подразумевает некоторое изобилие. В математике этот термин такого оттенка совсем не имеет. Множество может состоять из двух элементов (например, множество естественных спутников Марса – Фобос и Деймос), может состоять из одного элемента (множество естественных спутников Земли – Луна), может вообще не иметь элементов (об этом речь пойдет далее).
Существенными в понятии множества являются следующие признаки:
1. Объекты, входящие во множество, определенные. Это означает, что для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет.
2.
Объекты, входящие во множество, различимы между
собой. Следовательно, во множестве не может быть двух или более одинаковых
объектов.
3. Все объекты, входящие во множество, мыслятся как единое целое. Этим подчеркивается, что все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются.
Слова «совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона» позволяют сказать, что множество определяется либо своими элементами, либо законом (характеристическим признаком), согласно которому происходит объединение различных объектов в одно целое. Поэтому можно сказать, что основным понятием теории множеств будет являться отношение принадлежности отдельных объектов к совокупности.
Множества обычно обозначают прописными курсивными
буквами латинского алфавита: A, B, C и т.д. Для наиболее важных числовых множеств
приняты постоянные обозначения. Множество натуральных чисел стандартно
обозначается буквой N, множество целых чисел – С, множество действительных чисел – буквой R. Эти множества широко используются в школьном курсе
математики.
Эти множества широко используются в школьном курсе
математики.
Объекты, составляющие данное множество, называют его элементами и обозначают строчными курсивными буквами латинского алфавита: а, x, y. Для того, чтобы указать, что x – элемент множества А, записывают xÎA (читается: «x принадлежит А»). Например, если А – множество дней недели, а x – понедельник, то xÎA. Чтобы указать, что x не является элементом множества А, записывают xÏА («x не принадлежит А»). В нашем примере, если x – ноябрь, то xÏА.
Из канторовского понятия множества следует, что
задать множество можно двумя способами. Первый способ – явный или перечислительный
– состоит в простом перечислении всех элементов, в совокупности составляющих
данное множество. Элементы множества заключаются в фигурные скобки { }, которые показывают, что элементы объединены в
одно целое, в совокупность. Если А –
множество дней недели, то записывают А={понедельник,
вторник, среда, четверг, пятница, суббота, воскресенье}; множество
арифметических действий B
задают так: B={сложение,
вычитание, умножение, деление}; множество корней квадратного уравнения X: X={2, 3}.
Элементы множества заключаются в фигурные скобки { }, которые показывают, что элементы объединены в
одно целое, в совокупность. Если А –
множество дней недели, то записывают А={понедельник,
вторник, среда, четверг, пятница, суббота, воскресенье}; множество
арифметических действий B
задают так: B={сложение,
вычитание, умножение, деление}; множество корней квадратного уравнения X: X={2, 3}.
Согласно определению, во множестве не бывает одинаковых элементов. Поэтому запись {2, 2, 3} считается некорректной. Ее необходимо заменить на следующую {2, 3}. Порядок следования элементов во множестве роли не играет. Поскольку {2, 3, 4} и {4, 3, 2} состоят из одних и тех же элементов, они задают одно и то же множество.
В
тех случаях, когда множество содержит много элементов, такой способ оказывается
неудобным. Кроме того, при таком задании множества остается замаскированным сам
принцип его образования.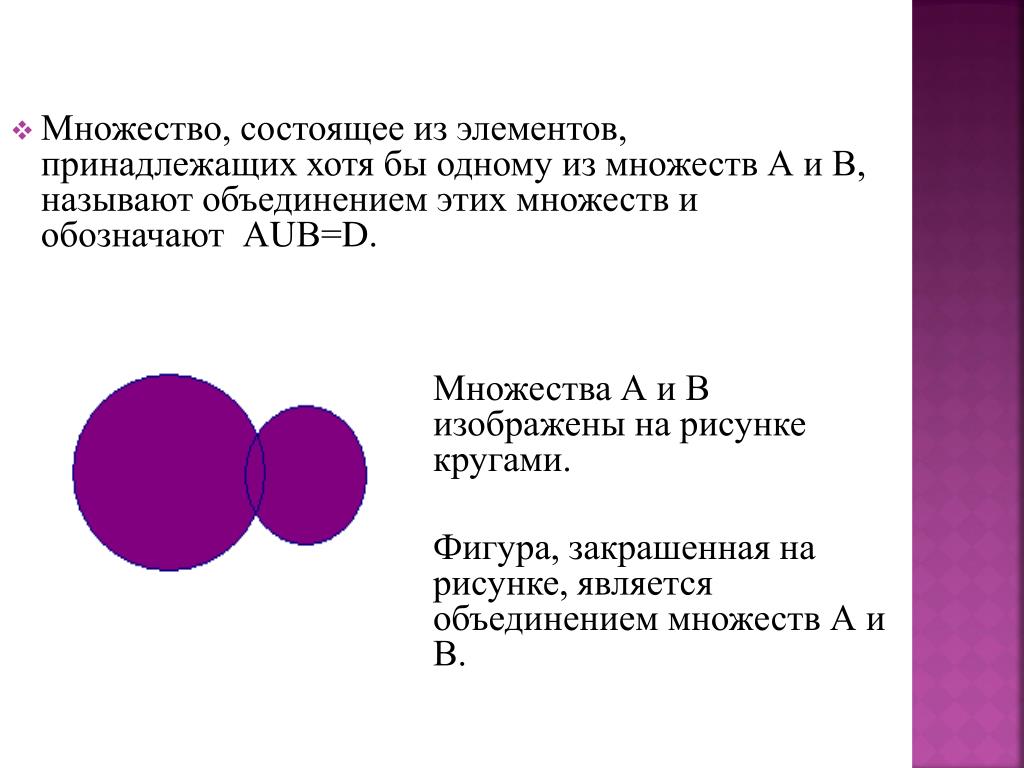
Второй способ задания состоит в том, что мы указываем условие, по которому выбираем эти и только эти элементы в множество, признак, характеризующий все элементы множества. Такой способ называется описательным. В этом случае для задания множества X c элементами x применяется следующая запись: X={x | признак}. Например, X={x | }, А={a | a – день недели}, В={b | b – арифметическое действие}. Описательный способ задания множества напрямую связан с алгеброй высказываний, так как записываемый признак и есть высказывание, касающееся элементов рассматриваемого множества.
Задание множества описательным способом иногда
приводит к некоторым осложнениям. Может получиться, что два различных способа
задания задают одно и то же множество. Большие трудности при задании множеств
возникают из-за недостаточной точности описания характеризующего признака
вследствие неоднозначности человеческой речи. Например, задавая множество всех
деревьев на земном шаре, нужно сказать, идет ли речь о деревьях, которые
существовали и будут существовать на Земле или о деревьях, существующих с
некоторой определенной даты. Кроме того, существует ряд промежуточных форм
между деревьями и кустарниками и нужно четко определить, какие из них относятся
к рассматриваемому множеству.
Например, задавая множество всех
деревьев на земном шаре, нужно сказать, идет ли речь о деревьях, которые
существовали и будут существовать на Земле или о деревьях, существующих с
некоторой определенной даты. Кроме того, существует ряд промежуточных форм
между деревьями и кустарниками и нужно четко определить, какие из них относятся
к рассматриваемому множеству.
Даже множество планет Солнечной системы определено не вполне однозначно. Наряду с большими планетами существуют также около 1600 малых (астероидов), поперечник которых доходит всего до 1 км. По мере улучшения методов наблюдений открываются все более и более мелкие. И возникает вопрос, где заканчиваются планеты, а начинаются метеориты.
Существуют
случаи, когда задание множества обладает внутренними противоречиями (парадокс
брадобрея и др.). Изучение вопроса, при каких случаях это может произойти,
привело к глубоким исследованиям в области логики, полностью изменившим эту
науку. Неразумно рассматривать множество идей, множество капель воды в стакане
и т. п. Так как само понятие множества не является достаточно четким, нельзя
рассматривать также и множество всех множеств (это приводит к противоречию).
Неразумно рассматривать множество идей, множество капель воды в стакане
и т. п. Так как само понятие множества не является достаточно четким, нельзя
рассматривать также и множество всех множеств (это приводит к противоречию).
В дальнейшем мы будем рассматривать только такие множества, которые определены точно, без противоречий, состав которых не вызывает сомнений.
элементарная теория множеств. Почему набор из одного элемента не равен элементу?
Я думаю, вы сбиваетесь с толку, потому что пытаетесь использовать понятия из «теории множеств» 1 непосредственно на реальных вещах. Математика не работает в реальном мире — она работает в мире аксиом, утверждений и доказательств.
Отступление в формальную логику
Теория есть не что иное, как:
- набор символов: операторы, функциональные символы, переменные и т. д., и
- аксиомы: утверждения, сделанные с использованием этих операторов, функциональных символов и переменных в сочетании с символами, определяемыми используемой логикой, часто логикой первого порядка, также известной как логика предикатов (как в случае с теорией множеств).

Это все чисто теоретических и символических объектов. Они не имеют смысла (по крайней мере, внутреннего смысла). Итак, для теории множеств у нас есть оператор $\in$, постоянный символ $\emptyset$ и бесконечное множество 2 переменных. 3
Аксиомы — это утверждения, подобные аксиоме экстенсиональности в теории множеств: $$\forall x \forall y [ \forall z ( z \in x \iff z \in y) \подразумевает x = y].$$ Символы $\forall$, $\iff$, $\implies$ и $=$ определяются логикой первого порядка. Мы можем построить другие операторы чисто символически из грамматики операторов, функциональных символов и переменных. Эти утверждения также не имеют внутреннего смысла.
Из утверждения мы можем попытаться доказать или опровергнуть утверждение, строя различные доказательства, используя логическую систему в сочетании с аксиомами. Само доказательство (опять же) чисто символическое. Если мы можем доказать утверждение, мы говорим, что оно «истинно», а если мы можем опровергнуть его, мы говорим, что оно «ложно».
Я постоянно упоминаю, что все эти объекты являются чисто символическими, потому что важно понимать, что теория сама по себе бесполезна, по крайней мере, для целей описания множеств. Во вселенной теории множеств нет даже ничего , называемого множеством — только операторы, утверждения, аксиомы и значения истинности. Она называется «теорией множеств» только потому, что мы имеем в виду ее конкретное применение.
Назад к реальности
Итак, если теории чисто символичны и бессмысленны, что хорошего в теории множеств или даже в формальной математике? Ответ заключается в том, что мы выбираем другие системы, называемые моделями, и сопоставляем теорию с моделью. Мы обеспечиваем отображение символических объектов на объекты в модели и показываем, что аксиомы «истинны» 4 для модели. Мы говорим, что модель является интерпретацией теории, и тогда мы знаем, что для любого формального утверждения в нашей теории есть соответствующее утверждение о модели с тем же значением истинности. (Здесь я машу рукой.)
(Здесь я машу рукой.)
Так почему же $x \neq \{x\}$?
Потому что, в конце концов, если мы хотим применить теорию теории множеств к нашей модели множеств, нам нужно выбрать модель множеств, которая интерпретирует теорию теории множеств — а в теории множеств утверждение $\exists x \exists y (x = y \land x \in y)$ может быть опровергнуто, следовательно, ложно, и, следовательно, соответствующее утверждение должно быть ложным в нашей модели. Итак, мы знаем, что ваша модель, в которой армия одного солдата равна самому солдату, — это , а не модель теории множеств.
Так почему же создатели теории множеств решили, что их теория работает именно так? Как я уже сказал, у теории нет внутреннего смысла, поэтому ее создатели имели возможность выбирать из бесчисленной бесконечной вселенной теорий — так что это был реальный выбор. Я думаю, вероятно, потому, что они сочли свою теорию хорошим компромиссом:
- интуитивно понятный: наличие моделей, понятных большинству математиков,
- полезно: иметь модели, которые понадобятся математикам в их работе,
- мощный: наличие аксиом, которые могут фиксировать истинностное значение самых разных утверждений, и
- сговорчивый: наличие аксиом, которые фактически позволяют доказать большинство полезных утверждений.
 5
5
Как уже говорили другие, можно определить других теорий, которые охватывают свойство, которое вы упомянули, но, по-видимому, у них есть компромиссы в этих областях. Мы решили построить большую часть нашей математики на основе современной формулировки теории множеств, так что это было Достаточно хорошо™ .
1 Я взял эту фразу в устрашающие кавычки, потому что на протяжении веков существовало множество формулировок теорий множеств. Наиболее популярной сегодня является теория множеств Цермело-Френкеля, и именно ее имеет в виду большинство людей, говоря «теория множеств».
2 Это, конечно, , немного , вызывающий вопрос, потому что мы определяем теорию множеств , используя множеств, но есть различие. Набор переменных не часть вселенной множеств, описываемых теорией. Это чисто часть формализации теории.
3 Обратите внимание, что оператор скобок $\{\cdot\}$, также известный как нотация построения множеств, не является частью этой теории. Он определяется исключительно с точки зрения $\in$ и $=$.
Он определяется исключительно с точки зрения $\in$ и $=$.
4 Больше пугающих кавычек, потому что, как видите, это рекурсивное определение. Нам потребуется использовать некоторую формальную логическую систему, чтобы доказать это соответствие. Есть причина, по которой Уайтхед и Рассел Principia Mathematica только завершает доказательство того, что $1 + 1 = 2$ во втором томе .
5 Теорема Гёделя о неполноте показывает, что любая «достаточно мощная» теория в логике первого порядка либо неполна (имеет утверждения, которые нельзя доказать или опровергнуть), либо непоследовательна (имеет утверждения, которые могут быть и доказаны и опровергнуты ). Таким образом, цель теории состоит в том, чтобы сделать многие полезные утверждения доказуемыми и избежать противоречий. Это часть «ремесла» формальной логики.
логика — Можно ли считать набор из одного элемента равным своему элементу?
Да! ZFC — Регулярность согласуется с тем количеством атомов Куайна, которое вы можете добавить. Однако, чтобы ответить на ваш вопрос, многое зависит от того, что вы имеете в виду, говоря «$\{x\}=x$ для каждого $x$»
Однако, чтобы ответить на ваш вопрос, многое зависит от того, что вы имеете в виду, говоря «$\{x\}=x$ для каждого $x$»
Если вы имеете в виду:
$\forall x \exists y (y= \{x\} \land y=x)$
Тогда моделью этой теории было бы непустое множество атомов Куайна, теперь мы можем иметь это множество бесконечным, существование такого множества можно доказать в версии ZFC-Регулярность. Выполнимой в такой модели была бы теория с аксиомами экстенсиональности. Каждое множество является атомом Куайна, и для любых объектов $x_1,..,x_n$ существует объект, отличный от них всех.
Такая теория слаба, но она удовлетворяет этой сильной интерпретации вашего утверждения, и она интересна согласно квалификации, которую вы ей дали.
Если под «$\{x\}=x$ для каждого $x$» подразумевается:
$\forall x \forall y (y=\{x\} \to y=x)$
Тогда дело обстоит иначе, так как из этого не следует, что для каждого множества должно существовать множество, содержащее его как единственный элемент, так что вы можете работать с теорией, в которой только 9*(P(U)))$ будет служить моделью для теории при второй интерпретации вашего утверждения, и здесь эта теория будет иметь силу арифметики второго порядка, которая имеет достаточную силу, чтобы формализовать БОЛЬШУЮ часть традиционной математики!
Теория, выводимая в этой модели, будет иметь следующие аксиомы:
Экстенсиональность: $\forall z (z \in x \leftrightarrow z \in y) \to x=y$
Атомы: $\forall x \forall y (x=\{y\} \to x=y)$
Кратность: $\forall x_1,. .,x_n \exists y (singleton(y) \land y \neq x_1 \land ..\land y \neq x_n)$
.,x_n \exists y (singleton(y) \land y \neq x_1 \land ..\land y \neq x_n)$
Определить : $elm( x) \equiv_{df} \exists y (x \in y)$
Понимание: $\not \exists ! x (elm(x) \phi) \to \exists s \forall x (x \in s \leftrightarrow elm(x) \phi)$
Членство: $x \text { множество множеств одиночек } \to elm(x)$
Теперь определим количественные числа как классы эквивалентности множеств одиночек при отношении эквивалентности «непересекающаяся биекция»
мы говорим, что «$x$ имеет непересекающуюся биекцию с $y$» тогда и только тогда, когда существует множество $z$ такое, что $z$ не пересекается как с $x$, так и с $y$, и $x$ биективен* (используя неупорядоченные пары) с $z$, а $z$ биективен* с $y$. Если это происходит, мы обозначаем это как $|x|=|y|$. Если $x$ имеет непересекающуюся биекцию с подмножеством $y$, то мы помечаем это как $|x| \leq |y|$
Обоснованность: $\forall y \in x (y \text { кардинальное число}) \land x \neq 0 \to \\\exists m \in x \forall y \in x (|m| \leq |y|)$
Конечно, натуральных чисел могут быть определены как количественные числа, у которых каждое кардинальное число меньше или равно им, имеющему непосредственно предшествующее кардинальное число или иным образом являющееся первым количественным числом.


 5
5