Степени числа 3 и 2: Степени 3. Степени числа 3. Таблица степеней 3. 3 в степени

как возвести число в степень, таблица степеней, число в нулевой степени в 2022 году

Что такое степень числа? Показатель степени и основание. Возведение в степень

На предыдущих уроках мы рассматривали умножение как сумму равных слагаемых. Например,

О числовом равенстве слева можно сказать, что сумму равных слагаемых свернули в произведение. Справа числовое равенство читается как произведение 7 × 10 развернутых в сумму равных слагаемых.

Теперь рассмотрим запись произведения одинаковых множителей: 7 × 7 × 7 × 7 × 7 × 7 × 7 × 7 × 7 × 7. Для свернутой записи произведения нескольких одинаковых множителей используют специальное выражение: 7^10. Такое выражение называют степенью. И читают так: семь в десятой степени или десятая степень числа семь.

В этом выражении число 7 принято называть основой степени. Основа степени показывает, какое число умножаем самое на себя. Основа степени – число, которое преподносят к степени.

Выполните возведение в степень: решаем примеры

Пример 1. Возведите число 3 в 6 степень

Возвести число 3 в 6 степень – это значит умножить число 3 шесть раз.

3⁶ = 3 × 3 × 3 × 3 × 3 × 3 = 729

3 – основание степеня, 6 – показатель степеня, 729 или 3⁶ – шестая степень числа 3.

Особенности степеней

1. Если поменять местами основание степени и ее показатель, то значение степени изменится.

Значение степени не изменится только в том случае, когда основание степени равно ее показателю. Например, 4⁴, 55⁵⁵ – в этом случае, если поменять местами основание и показатель степени, значение степени не изменится.

2. Если основание степени – число 1, то при любом натуральном показателе степени n, значение степени будет равно 1.

То есть 1ⁿ=1, 1⁵¹=1, 1³⁰⁰=1

3. Если показатель степени равен 1, то значение степени при любом натуральном а равно а:

a¹= a, 5¹=5, 653¹=653

Число в нулевой степени равно 1

Если показатель степени равен нулю, то при возведении любого натурального числа к нулевой степени, получим в результате число 1.

Или простыми словами: любое натуральное число в нулевой степени равно 1.

a⁰ = 1, 2⁰ = 1 (два в нулевой степени равно 1), 5⁰ = 1 (5 в нулевой степени равно 1)

Вторая и третья степень числа: возведение чисел в квадрат, куб

Особое внимание следует уделить возведению чисел в 2 и 3 степени. Вторую степень принято называть квадратом числа, а третью – кубом. Например, 5² – читается как пять в квадрате, 5³ – пять в кубе.

Выполним возведение в квадрат, куб:

5² = 25, 5³ = 125

6² = 36, 6³ = 216

7²

 = 49, 7³ = 343

Возведение в квадрат чисел, которые оканчиваются на цифру 5

Для возведения в квадрат числа, оканчивающегося на цифру 5, необходимо число его десятков умножить на число увеличенное на единицу, и до произведения справа дописать 25.

Пример. Выполните возведение в степень: 45²

Умножим число десятков 4 на число десятков, увеличенное на 1, т.е. на 5: 4×5=20

Допишем справа число 25, получим 2025. Проверяем, 45² = 45 × 45 = 2025

Возведение в квадрат двузначных чисел, начинающихся на цифру 5

Для того чтобы возвести в квадрат двузначное число, имеющее 5 десятков, необходимо к 25 добавить цифру единиц числа и к результату дописать справа квадрат числа единиц так, чтобы в результате получилось четырехзначное число.

Пример. Выполните возведение в степень: 57²

К 25 прибавляем 7 (число единиц): 25 + 7 = 32

Дописываем квадрат числа единиц: 7² = 49. Получим результат 3249.

Пример. Выполните возведение в степень: 51²

25 + 1 = 26

1²=1, справа дописываем 01, чтобы в результате получилось четырехзначное число: 2601

Порядок выполнения арифметических действий в выражениях со степенями

Возведение в степень – это пятое арифметическое действие, а также действие третьей степени, поэтому его выполняют первым перед умножением и делением, сложением и вычитанием. То есть в выражении со степенями порядок выполнения действий будет следующим:

1. Возведение в степень
2. Умножение и деление
3. Сложение и вычитание

Пример. 3 × 4³ + 18 : 3 =

4³ = 64, 3 × 64 = 192, 18 : 3 = 6, 192 + 6 = 198

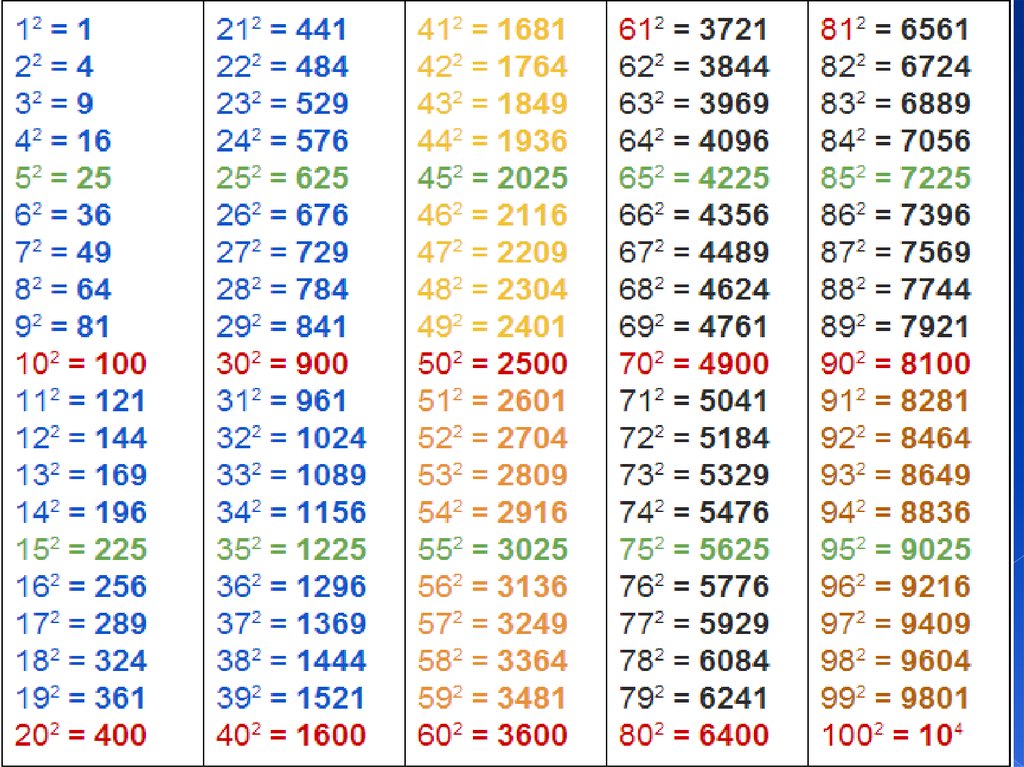
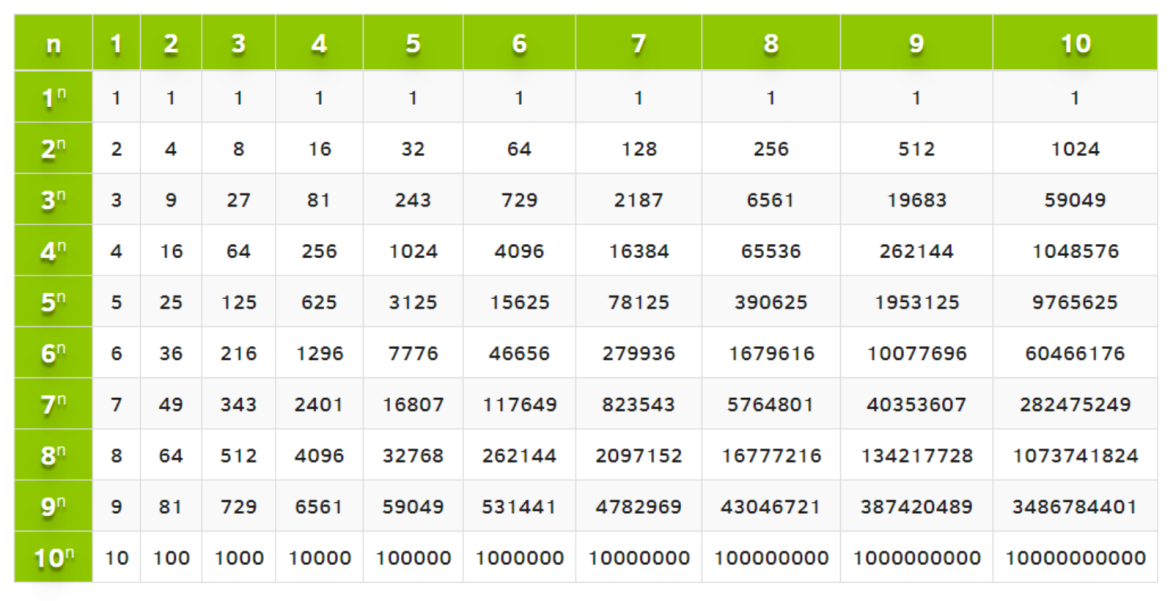
Таблица степеней натуральных чисел от 1 до 10

Предлагаем вашему вниманию таблицу степеней для натуральных чисел от 1 до 10, с помощью которой вы сможете быстро производить расчеты. Напоминаем, в данной таблице основание и показатель степени ограничивается числами 1-10.

Калькулятор возведения в степень

Степень числа. Квадрат и куб числа | Математика | 5 класс

На данном уроке Вы познакомитесь с определением степени числа, квадрата и куба числа, а также научитесь решать задачи по данной теме.

Определение степени

Мы с вами знаем, что если дана сумма одинаковых слагаемых, например,

 ,

то её можно записать как , или, например,

Мы видим, что первое число в правых частях равенств показывает, сколько элементов мы складывали, а второе – какие элементы мы складывали.

Было бы неплохо, если бы для умножения тоже существовала более компактная запись. Например, для того чтобы упростить запись такого выражения

Такая запись есть. Она называется четвертой степенью числа 3. Почему четвертой? Потому что троек у нас 4 штуки.

Так выглядит данная запись:

Читается как «три в четвертой степени» или «три в четвертой».

Такая запись читается как «икс в пятой степени» или «икс в пятой».

Квадрат и куб

У второй и третьей степеней есть свои названия.

Когда мы n умножим на n, получим n во второй степени. Но также мы можем сказать, что получили n в квадрате. Если у нас есть квадрат со стороной, равной n, то его площадь равна .

Если а умножим на себя два раза, то получим a в третьей степени:

Обычно про такую запись говорят не a в третьей степени, а a в кубе. Ведь объем кубика со стороной a равен .

Пример 1. 

Пример 2. 

Пример 3. 

Есть ли первая степень? Да, есть. Если степень равна 1, значит, у нас есть один сомножитель. Например,

 

---

Нулевая степень

Нулевая степень означает, что мы рассматриваем 0 сомножителей.

Принято считать, что нулевая степень любого числа равна 1.

---

 

Решение примеров со степенями

Пример 4. Представьте произведение в виде степени.

1)       

У элементов степени есть специальные названия. То, что мы возводим в степень, называется основанием степени. В нашем примере это 1. Число, обозначающее степень, называется показателем. В нашем примере это 4.

2)             

3)           

Пример 5. Представьте степень в виде произведения.

1) 

2) 

3) 

Пример 6. Вычислите сумму квадратов чисел 5 и 4.

Что такое сумма квадратов? Данная запись выглядит так:

То есть сначала мы возводим каждое число в степень, а затем складываем.

Стоит отличать данную запись от следующей:

В таком случае мы сначала складываем, а потом возводим в степень.

Пример 7. Вычислите куб разности чисел 2 и 1.

Сначала нам необходимо найти разность, а потом полученное число возвести в третью степень:

Совершенно другой результат мы получим при вычислении разности кубов, то есть если мы сначала возведем числа в третью степень, а затем выполним вычитание.

 

---

Возведение в квадрат чисел, оканчивающихся на 5

Возведем число 35 в квадрат:

Возьмем первую цифру нашего числа – 3 – и умножим ее на следующую, то есть ту, которая идет после нее в натуральном ряду – 4. Получим 12. Теперь просто припишем к 12 число 25:

Мы получили число тысяча двести двадцать пять.

1) 

2) 

Почти то же самое работает и для трехзначных чисел. Только теперь мы берем не цифру, которая стояла перед цифрой 5, а число.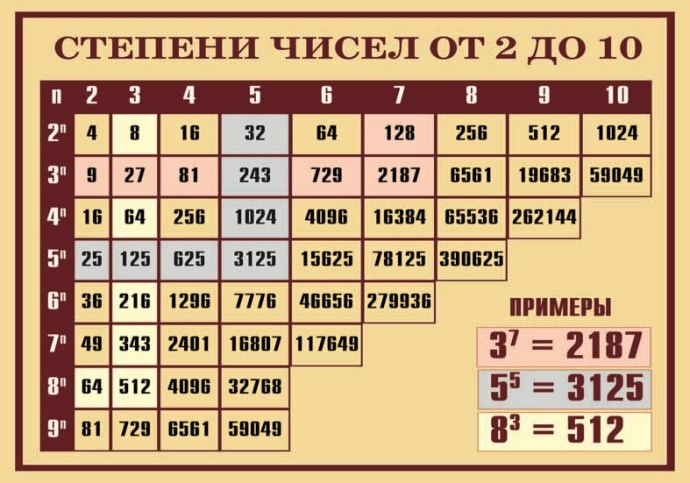 Например,

Получили одиннадцать тысяч двадцать пять.

---

 

Заключение

Мы познакомились с такими понятиями, как квадрат и куб числа, кроме того, дали чуть более сложное определение степени; узнали, что такое показатель степень, основание степени; научились преобразовывать произведение одинаковых чисел в степень и наоборот.

 

Список рекомендованной литературы

1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика, 5 класс (в 2 частях). ООО «ИОЦ МНЕМОЗИНА».
2. Мерзляк А. Г., Полонский В. Б., Якир М. С. Математика. 5 класс – М.: Вентана-Граф.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Теоретический материал (Источник)
2. Учебник Н. Я. Виленкина. Математика 5 класс (Источник)
3. Презентация (Источник)

 

Домашнее задание

1. Представьте в виде степени произведение:

а) 

б) 

в) 

г) 

2. Запишите выражение в виде степени и вычислите значение:

а) 2 в квадрате

б) 3 в пятой степени

в) 7 в кубе

3. Представьте степень в виде произведения:

а) 

б) 

в) 

г) 

n$ не может быть кратным 10:

9n$ быть кратным 10?

Как видно из следующей таблицы, цифры единиц степени числа

два повторяются в повторяющемся порядке 2, 4, 8, 6, 2, 4, 8, 6”¦

Все числа, кратные 10, имеют единичная цифра 0. Однако, как видно из шаблона
, ни одна из степеней 2 не имеет единичной цифры, оканчивающейся на 0.
Следовательно, никакая степень 2 не кратна 10.

Александр из школы университетского колледжа заметил следующее по вопросам расширения:

9n$ равно 0, 0, 0, 0”¦

Таким образом, единичные разряды степеней любого числа повторяются в цикле длиной четыре знака, так как все числа заканчиваются одной из указанных выше 10 цифр. цифры степеней x равны a, b, c, d… и пусть Образец единичных цифр степеней другого числа y равен e, f, g, h”¦

В результате сумма / разность единичных цифр степеней x и y находится в повторяющемся шаблоне: a + e, b + f, c + g и d + h, или a — e, b — f, c — g и д — ч.

В результате, независимо от комбинации степеней, сложения или вычитания, единичные разряды всегда представляют собой шаблон из 4 повторяющихся чисел.

Молодцы все!

Использование шаблонов целочисленных экспонент

В этом разделе мы увидим, как использовать шаблоны целочисленных экспонент для нахождения следующих членов в последовательности чисел.

 В таблице ниже показаны степени чисел 5, 4 и 3.

Вопрос 1 : 

Какую закономерность вы видите в степенях числа 5?

Ответ:

При уменьшении степени на 1 значение степени делится на 5.

Вопрос 2:

Какую закономерность вы видите в степенях 4?

Ответ:

При уменьшении степени на 1 значение степени делится на 4.

Ответ:

При уменьшении степени на 1 значение степени делится на 3.

Вопрос 4:

Чему равны 5 ^-2  и 5 ^-3  ?

Ответ :

Из таблицы мы узнаем тот факт, что при уменьшении показателя степени на 1 значение степени делится на 5. 

А также из таблицы имеем 5 ¹  =  5,

Поскольку 5 ¹   =  5, получаем 5 ⁰   =  5 ÷ 5  =  1.

Поскольку 5 ⁰  =  1, получаем 5 ⁰    

Так как 5 ^-1   =  1/5, мы получаем   5 ^-2  = (1/5) ÷ 5  =  1/25.

Так как 5 ^-2   =  1/25, мы получаем 5 ^-3   =  (1/25) ÷ 5  =  1/125.

Вопрос 5 :

Каковы значения 4 ⁰ , 4 ^-1 , 4 ^-2 и 4 ^-3  ?

Ответ :

Из таблицы мы узнаем тот факт, что при уменьшении степени на 1 значение степени делится на 4. 

А также из таблицы имеем 4 ¹ = 5.

С 4 ¹ = 4, мы получаем 4 ⁰ = 4 ÷ 4 = 1.

С 4 ⁰ = 1, мы получаем 4 ^-1 = 1 ÷ 4 = 1. /4.

Поскольку 4 ^-1   =  1/4, мы получаем 4 ^-2   =  (1/4) ÷ 4  =  1/16.

Так как 4 ^-2   =  1/16, мы получаем 4 ^-3   =  (1/16) ÷ 4  =  1/64.

Вопрос 6 :

Каковы значения 3 ⁰ , 3 ^-1 , 3⁻² и 3⁻³ ?

Ответ :

Из таблицы мы узнаем тот факт, что при уменьшении степени на 1 значение степени делится на 3.

Степень двойки	Ответить	Единицы Число
1	2	2
2	4	4
3	8	8
4	16	6
5	32	2
6	64	4