Множество. Подмножество — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
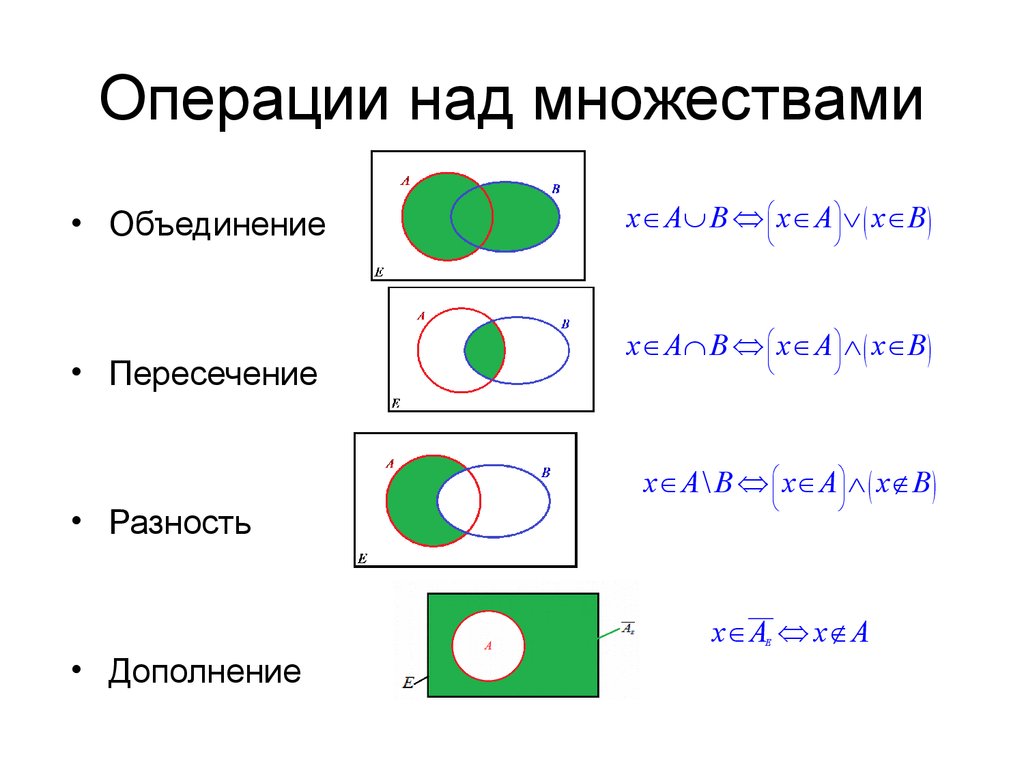
1. Множество
Совокупность элементов,объединённых каким-либо
характеристическим
свойством (признаком)
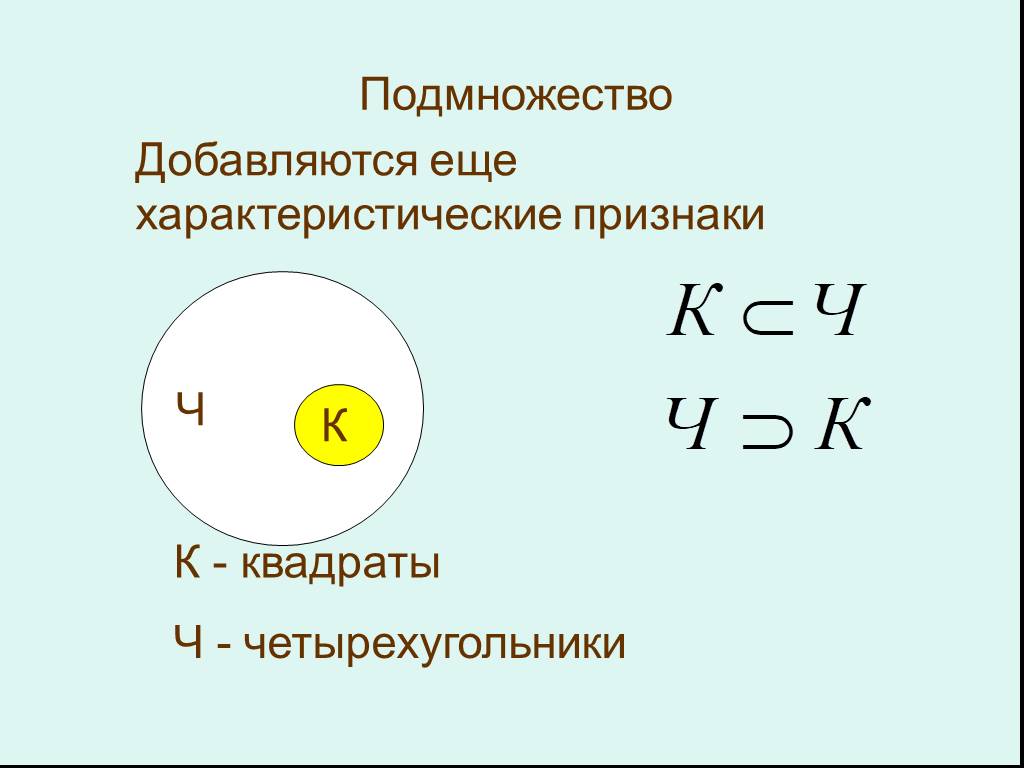
2. Подмножество
Множество К называетсяподмножеством множества А, если
любой элемент множества К
принадлежит множеству А
K A
К
А
x
3. Подмножество
Множество К называетсяподмножеством множества А, если
любой элемент множества К
принадлежит множеству А
х К х А
4.
 КванторыСпециальные математические
КванторыСпециальные математическиесимволы, облегчающие запись
математических выражений
Георг Кантор
Кантор придумал кванторы
5. Кванторы
кванторвсеобщности
«для любого»
All (англ)
6. Кванторы
кванторсуществования
«существует»
Exist (англ)
7. Универсальное множество
Множество , которому принадлежат всеэлементы, обладающие данным
характеристическим свойством
Универсальное множество своё для
каждой задачи
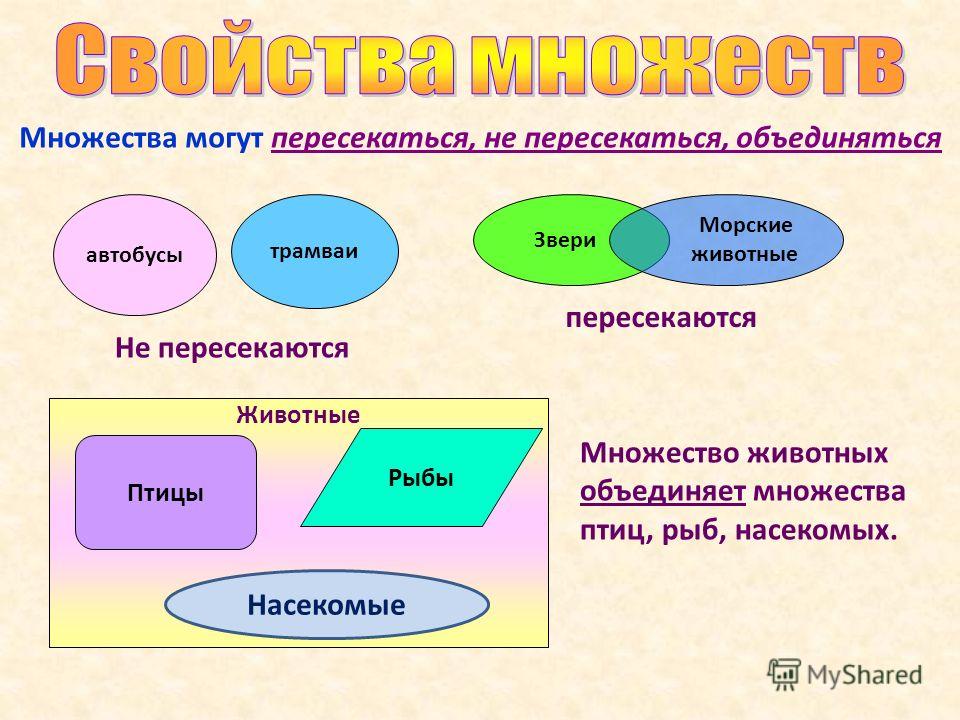
8. Равные множества
Множества, состоящие из одинаковыхэлементов
А = {1, 2, 4, 8, 16}
B = {20, 21, 22, 23, 24}
C = {x : x= 2n, n = 0, 1, 2, 3, 4}
A=B=C
9. Равные множества
Если A = B , тоA B и B A
10. Задача
На множестве U всех букв русскогоалфавита заданы множества
А = {ё, к, л, м,н}
В ={к, о, з, ё, л}
С = {б, ы, ч, о, к}
Найдите следующие множества и
изобразите их кругами Эйлера
1) AUB 2) A∩B 3) (A∩B)UC
4) (AUC)∩B 5) U\(AUB UС)
11.
 ЗадачаДаны числовые промежутки
ЗадачаДаны числовые промежуткиА= [-4; 5], В =(2; 6), С = (5, 10]
Найдите следующие множества и
изобразите их на числовой прямой и
кругами Эйлера
1) AUB 2) A∩B 3) (СUB)\(A∩B)
4) (A∩B)UC 5) (AUB)\ (A∩B)
12. Формула мощности объединения множеств
13. Задача 1
В Асбестовском филиале Уральскогопромышленно-экономического
техникума 2 группы юристов.
В группе азПСОу-108 учится 11
человек.
В группе азПСОу-304 – 9 человек.
Сколько всего студентов-юристов в
Асбестовском филиале?
14. Обозначения
А – множество студентов группыазПСОу-108
А =11
В – множество студентов группы
азПСОу-304
В =9
15. Диаграммы Венна
АВ
АUВ = А + В =11+9=20
16. Задача 2
Все студенты группы азПСОу-108 очень любятзаниматься рукоделием. При этом они
предпочитают только 2 вида рукоделия:
плетение из бисера и вышивку крестиком.
1. 7 человек плетут фенечки из бисера.
2.
 6 студентов занимаются вышивкой крестиком.
6 студентов занимаются вышивкой крестиком.3. 2 человека занимаются обоими видами
рукоделия.
Сколько студентов в группе азПСОу-108?
17. Обозначения
А – множество студентов группыазПСОу-108, увлекающихся
бисероплетением
А =7
В – множество студентов группы
азПСОу-108, вышивающих
крестиком
В =6
18. Обозначения
А∩В – множество студентовгруппы азПСОу-108,
увлекающихся бисероплетением
и вышивкой одновременно
А∩В =2
19. Диаграммы Венна
АВ
АUВ = А + В =13
20. Диаграммы Венна
АВ
АUВ = А + В — А∩В =13-2=11
21. Формула мощности объединения двух множеств
АUВ = А + В — А∩В22. Формула мощности объединения трёх множеств
ФОРМУЛАМОЩНОСТИ
ОБЪЕДИНЕНИЯ
ТРЁХ МНОЖЕСТВ
23. Задача 3
Все студенты группы азПСОу-108очень любят заниматься спортом.
При этом они предпочитают только 3
вида спорта: синхронное плавание,
кёрлинг и спортивное перетягивание
каната.

Сколько студентов в этой
талантливой группе, если:
24. Задача 3
1. 6 человек плавают синхронно.2. 6 студентов занимаются кёрлингом.
3. 7 человек перетягивают канат.
4. Двое кёрлингистов также занимаются синхронным
плаванием.
5. Перетягивать канат любят четыре человека из
команды кёрлингистов.
6. Синхронным плаванием и перетягиванием каната
одновременно увлекаются 3 человека.
7. Всеми тремя видами спорта занимается только 1
студент
25. Обозначения
А – множество студентов азПСОу-108,занимающихся в секции синхронного плавания
А =6
В – множество студентов-кёрлингистов группы
азПСОу-108
В =6
С – множество студентов группы азПСОу-108,
любящих перетягивать канат
С =7
26. Обозначения
А∩B – множество студентов азПСОу108, занимающихся синхроннымплаванием и кёрлингом одновременно
А∩B =2
В∩C – множество студентовкёрлингистов группы азПСОу-108,
любящих перетягивать канат
В∩С =4
27.
 ОбозначенияА∩С – множество студентов группы
ОбозначенияА∩С – множество студентов группыазПСОу-108, занимающихся перетягиванием
каната и синхронным плаванием
А∩С =3
А∩В∩С – множество студентов группы
азПСОу-108, занимающихся всеми тремя
видами спорта
А∩В∩С =1
28. Диаграммы Венна
АВ
С
А = 6
В =6
С = 7
29. Диаграммы Венна
АВ
С
А∩В = 2
30. Диаграммы Венна
АВ
С
В∩С = 4
31. Диаграммы Венна
АВ
С
А∩С = 3
32. Формула мощности объединения трёх множеств
АUВUС == А + В + С — А∩В — А∩С — С∩В
33. Формула мощности объединения трёх множеств
АUВUС ==6+6+7-2-4-3=10
34. Диаграммы Венна
АВ
С
35. Диаграммы Венна
АВ
С
А∩В∩ С = 1
36. Формула мощности объединения трёх множеств
АUВUС == А + В + С — А∩В — А∩С — С∩В +
+ А∩В ∩С
37. Формула мощности объединения трёх множеств
АUВUС ==6+6+7-2-4-3+1=11
38.
 Задача 1VИз 35 студентов, побывавших на каникулах в
Задача 1VИз 35 студентов, побывавших на каникулах вМоскве, все, кроме двоих, делились
впечатлениями.
О посещении Большого театра с восторгом
вспоминали 12 чел., Кремля – 14, а 16 – о
концерте. По три студента запомнили
посещение театра и Кремля, а также театра и
концерта, четверо – концерта и пребывания в
Кремле.
Сколько студентов сохранили воспоминания
одновременно о театре, концерте и Кремле?
А
В
С
U
40. Обозначения
U – множество студентов, посетившихМоскву – универсальное множество
U =35
А – множество запомнивших Большой театр
А =12
В – множество студентов, рассказывавших о
Кремле
В =14
41. Обозначения
С – множество студентов, вспоминавших оконцерте
С =16
А∩В – множество тех, кто рассказывал о
Большом театре и Кремле
А∩В =3
А∩С – множество тех, кто делился
впечатлениями о Большом театре и концерте
А∩С =3
42. Обозначения
B∩С – множество тех, кто делился впечатлениямио Кремле и концерте
B∩С =4
D = U /(АUВUС) – множество тех, кто не стал
делиться воспоминаниями
D =2
А∩В∩С – множество тех, кто сохранил
воспоминания о Большом театре, Кремле и
концерте.

А∩В∩С =?
А∩В∩С =
АUВUС — А — В — С +
+ А∩В + А∩С + С∩В
А∩В∩С =
АUВUС — А — В — С +
+ А∩В + А∩С + С∩В
АUВUС = U — D
АUВUС =35 -2=33
А∩В∩С = 33 -12 -14-16 +3+3+ 4 = 1
English Русский Правила
Страница не найдена — ПриМат
По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.
Искать:© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2),
Как определить, является ли набор подмножеством другого набора в Python
Сара Танвир
Наборы — это неупорядоченные структуры данных, не содержащие дубликатов.
Что такое подмножество?
Если все значения набора A также содержатся в большем наборе B, то A является подмножеством B.
Набор A является подмножеством B
1. Как использовать
issubset( ) Встроенная функция issubset() может использоваться для определения того, является ли набор подмножеством другого набора.
setA.issubset(setB)
Функция issubset() принимает один аргумент: больший набор. Здесь мы проверяем, является ли setA подмножеством setB .
Функция вернет True , если setA является подмножеством setB , и False , если это не так.
setA = {1, 2, 3, 4, 5}
setB = {1, 2, 3}
setC = {1, 2, 3, 6, 7}
print("setA: " , setA)
print("setB: ", setB)
print("setC: ", setC)
print("Является ли setB подмножеством setA?: ", setB.
issubset(setA))print ("Является ли setA подмножеством setB?:", setA.issubset(setB))
print("Является ли setC подмножеством setA?: ", setC.issubset(setA))
2. Как использовать
пересечение() Встроенная функция пересечения() возвращает набор, содержащий элементы, общие для двух наборов.
набор.пересечение(набор1)
Если набор, возвращаемый пересечением и , равен меньшему набору, то меньший набор является подмножеством большего набора.
setA = {1, 2, 3, 4, 5}
setB = {1, 2, 3}
setC = {1, 2, 3, 6, 7}
print("setA: " , setA)
print("setB: ", setB)
print("setC: ", setC)
print("Является ли setB подмножеством setA?: ", setA.intersection(setB) == setB)
print("Является ли setA подмножеством setB?: " , setA.intersection(setB) == setA)
print("Является ли setC подмножеством setA?: ", setA.
intersection(setC) == setC)
3. Как использовать цикл
для Мы можем использовать простой цикл for для обхода потенциального подмножества, скажем, setB .
Если любой элемент из setB не входит в другой набор, setA , тогда setB является , а не подмножеством setA . В противном случае setB является подмножеством setA .
setA = {1, 2, 3, 4, 5}
setB = {1, 2, 3}
print("setA: ", setA)
print("setB: ", setB)
subSet = True
для i в наборе B:
, если i не в наборе A:
subSet = False
, если subSet == False:
print("SetB не является подмножеством SetA")
else:
print("SetB является подмножеством SetA")
для i в setA:
если i не в setB:
subSet = False
if subSet == False:
print("SetA не является подмножеством SetB")
else:
print("SetA является подмножеством SetB")
СВЯЗАННЫЕ ТЭГИ
python CONRITBU
Сара Танвир
Лицензия: Creative Commons-Attribution-ShareAlike 4. 0 (CC-BY-SA 4.0)
0 (CC-BY-SA 4.0)
2.1: Подмножества и равенство — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4867
- Pamini Thangarajah
- Mount Royal University
Для этого раздела пусть A и B будут множествами.
Подмножества
Определение: Подмножество
A является подмножеством B (обозначается \(A \subseteq B\)), если каждый элемент A также является элементом B.
ШАБЛОН Чтобы доказать \(A \subseteq B\):
Нам НУЖНО показать Если \(x \in A\), то \(x \in B.\)
Пример \(\PageIndex{1}\):
Пусть \(A\) быть набором. Тогда \(\emptyset\) и \(A\) являются подмножествами \(A\).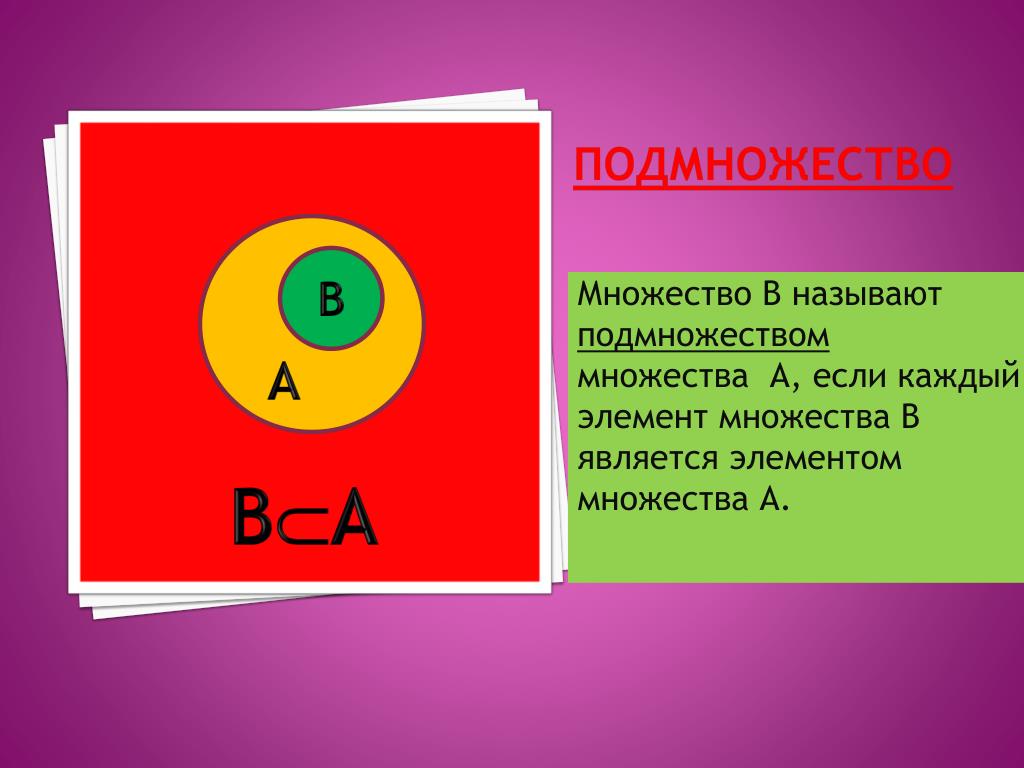
Итак, \(A, \, \emptyset \subseteq A\).
Мы можем использовать набор обозначений, чтобы указать и помочь описать наши стандартные системы счисления. Следующие первые четыре стандартных набора даны от меньшего к большему:
- \(\mathbb{N}\) представляет набор всех натуральных чисел : \(\mathbb{N} = \{1, 2, 3 , 4…\}\)
- \(\mathbb{W}\) представляет собой набор всех целых чисел : \( \mathbb{W} = \{0, 1, 2, 3…\} \)
- \(\mathbb{Z}\) представляет набор всех целых чисел : \(\mathbb{Z} = \{ …-2, -1, 0, 1, 2…\}\) . \(i\) не используется, потому что он используется для комплексных чисел.
- \(\mathbb{Q}\) представляет собой набор всех рациональных чисел : \(\mathbb{Q} = \{0, \pm1, \pm\frac{1}{2}, \pm\frac {1}{3}…\}\)
- \(\mathbb{Q}\) c представляет набор всех иррациональных чисел
- \(\mathbb{R}\) представляет набор всех действительных чисел
- \(\mathbb{U}\) представляет универсальный набор , набор, подмножеством которого являются все остальные.

Одинаковые наборы
Определение: равное множество
A равно B, обозначаемому \(A = B\), если \(A \subseteq B\) и \(B \subseteq A\).
Правильные подмножества
Определение: Подмножество
A является правильным подмножеством B (обозначается \(A \subset B\)) при \(A \subseteq B\) и \(A \neq B\).
Пример \(\PageIndex{2}\):
Пусть \(A = \{1, 3, 5\}, \, B = \{1, 5\}, \, C = \{1, 3, 5\}, \, D = \{1, 4\}\)
- \(В \подмножество А\). так как \(3 \notin B, B \ne A.\)
- \(D \nsubseteq A\), потому что \(4 \notin A\).
Пример \(\PageIndex{3}\):
Рассмотрим \( \mathbb{N} \) и \( \mathbb{W} \) наборы натуральных и целых чисел.
\(\mathbb{N} \subset \mathbb{W}\), поскольку все элементы \( \mathbb{N} \) присутствуют в \( \mathbb{W} \).
Однако, поскольку \(0 \notin \mathbb{N}\), \(\mathbb{N} \nsubseteq \mathbb{W}\).
Power Sets
Определение: Power Set
Пусть \(A\) — множество. Тогда множество всех подмножеств \(A\) называется степенным множеством \(A\) и обозначается \(P(A)\).
Тогда множество всех подмножеств \(A\) называется степенным множеством \(A\) и обозначается \(P(A)\).
Пример \(\PageIndex{4}\):
Пусть установлено \(A = \{Алекс, Билли, Кейси\}\)
\(P(A)\):
| {Алекс} | {Алекс, Билли} | {Алекс, Билли, Кейси} |
| {Билли} | {Алекс, Кейси} | \(\пустой набор\) |
| {Кейси} | {Билли, Кейси} |
Мощность
Определение: Мощность
Пусть \(A\) — множество. тогда количество элементов в множестве \(A\) называется мощностью множества \(A\) и обозначается через \(|A|\) или \(n(A)\). Если \(n(A)\) конечно, то \(A\) называется конечным множеством, в противном случае оно называется бесконечным множеством.
9n.\)
Новые обозначения и определения
\(\subseteq\): обозначает, что набор является подмножеством другого набора.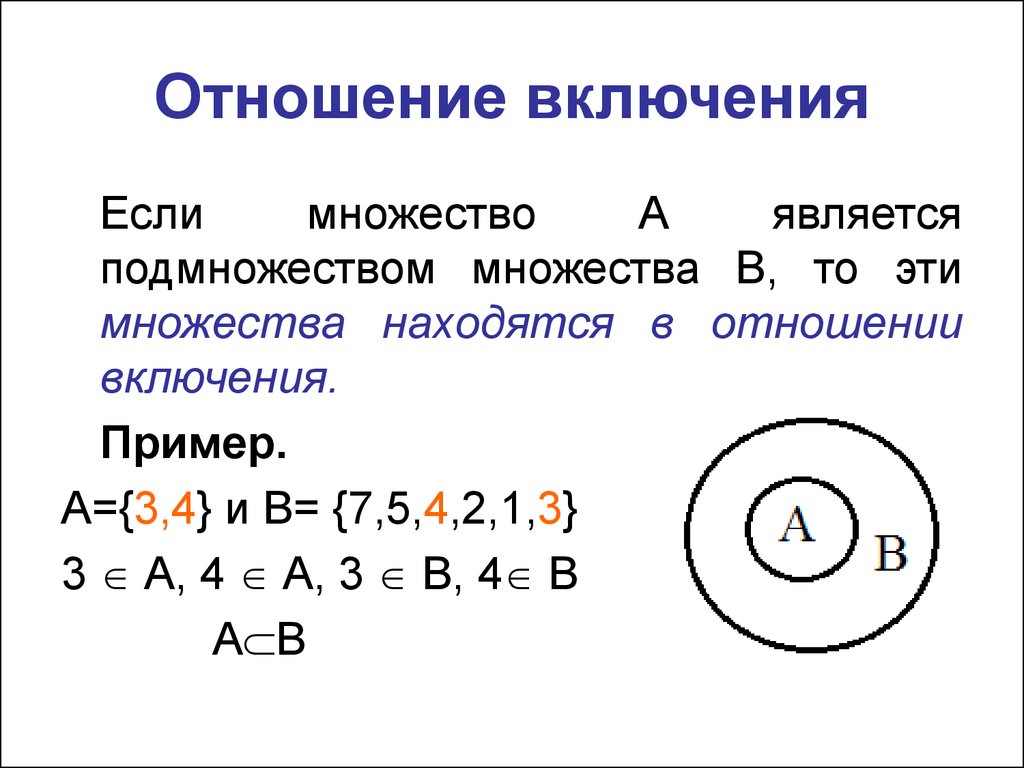


 intersection(setC) == setC)
intersection(setC) == setC) 