Что такое модуль примеры. Калькулятор онлайн.Решение уравнений и неравенств с модулями
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа , и как правильно раскрывать выражения, содержащие знак модуля , то наличие в уравнении выражения, стоящего под знаком модуля , перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x)
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3
Чтобы решить уравнение, содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля .
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x 2 +4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3
2. Мы получили два числовых промежутка: х≥3 и х
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
и решим это уравнение.
Это уравнение имеет корни:
х 1 =0, х 2 =3
Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 2 =3.
Б) При x
Внимание! Это уравнение существует только на промежутке х
Раскроем скобки, приведем подобные члены. Получим уравнение:
х 1 =2, х 2 =3
Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
МБОУ СОШ №17 г. Иванова
«Уравнения с модулем»
Методическая разработка
Составлена
учителем математики
Лебедевой Н.В.
20010 г.
Пояснительная записка
Глава 1. Введение
Раздел 2. Основные свойства Раздел 3. Геометрическая интерпретация понятия модуля числа Раздел 4. График функции у = |х| Раздел 5. Условные обозначения
График функции у = |х| Раздел 5. Условные обозначения
Глава 2. Решение уравнений, содержащих модуль
Раздел 1.Уравнения вида |F(х)| = m (простейшие) Раздел 2. Уравнения вида F(|х|) = m Раздел 3. Уравнения вида |F(х)| = G(х) Раздел 4. Уравнения вида |F(х)| = ± F(х) (красивейшие) Раздел 5. Уравнения вида |F(х)| = |G(х)| Раздел 6. Примеры решения нестандартных уравнений Раздел 7. Уравнения вида |F(х)| + |G(х)| = 0 Раздел 8. Уравнения вида |а 1 х ± в 1 | ± |а 2 х ± в 2 | ± …|а n х ± в n | = m
Раздел 9. Уравнения, содержащие несколько модулейГлава 3. Примеры решения различных уравнений с модулем.
Раздел 1. Тригонометрические уравнения Раздел 2. Показательные уравнения Раздел 3. Логарифмические уравнения Раздел 4. Иррациональные уравнения Раздел 5. Задания повышенной сложности Ответы к упражнениям Список литературы
Понятие абсолютной величины (модуля) действительного числа является одной из существенных его характеристик. Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень
Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень
 Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются).
Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются).
: Абсолютной величиной (модулем) действительного числа а называется неотрицательное число: а или –а.
Обозначение: │ а │ Запись читается следующим образом: «модуль числа а» или «абсолютная величина числа а»│ а, если а > 0
│а│ = │ 0, если а = 0 (1)
│ — а, если а
Примеры: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 — √2│ = √2 – 1 Раскрыть модуль выражения:
а) │х — 8│, если х > 12 б) │2х + 3│, если х ≤ -2 │х – 8│= х – 8 │ 2х + 3│= — 2х – 3Раздел 2.
 Основные свойства. Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │— а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│
Основные свойства. Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │— а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│
При рассмотрении следующих свойств ограничимся их формулировкой, так как их доказательство приводится в Свойство №2: Абсолютная величина суммы конечного числа действительных чисел не превосходит суммы абсолютных величин слагаемых: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │
Раздел 3.
 Геометрическая интерпретация понятия модуля числа.
Геометрическая интерпретация понятия модуля числа. Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа
Представленная геометрическая иллюстрация наглядно подтверждает свойство №1, т.е. модули противоположных чисел равны. Отсюда легко понимается справедливость равенства: │х – а│= │а — х│. Также более очевидным становиться решение уравнения │х│= m, где m ≥ 0, а именно х 1,2 = ± m.Примеры:
1) │х│= 4 х 1,2 = ± 4 2) │х — 3│= 1
х 1,2 = 2; 4
Раздел 4.
 График функции у = │х│
График функции у = │х│Область определения данной функции все действительные числа.
Раздел 5. Условные обозначения.
В дальнейшем при рассмотрении примеров решения уравнений будут использованы следующие условные обозначения: { — знак системы [ — знак совокупности При решение системы уравнений (неравенств) находится пересечение решений входящих в систему уравнений (неравенств). При решении совокупности уравнений (неравенств) находится объединение решений входящих в совокупность уравнений (неравенств).
Раздел 1. Уравнения вида │F (х)│= m
Уравнение данного вида называется простейшим. Оно имеет решение тогда и только тогда, когда m ≥ 0. По определению модуля, исходное уравнение равносильно совокупности двух уравнений: │F (х)│= m
Примеры:№1.

Решите уравнение: │7х — 2│= 9
Ответ: х 1 = — 1; х 2 = 1 4 / 7
│х 2 + 3х + 1│= 1
х 2 + 3х + 2 = 0 х 2 +3х = 0 х 1 = -1; х 2 = -2 х · (х + 3) = 0 х 1 = 0; х 2 = -3 Ответ: сумма корней равна — 2 .
│х 4 -5х 2 + 2│= 2 х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0 х 2 · (х 2 – 5) = 0 обозначим х 2 = m, m ≥ 0 х = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – оба значения удовлетворяют условию m ≥ 0 х 2 = 1 х 2 = 4 х = ± 1 х = ± 2 Ответ: количество корней уравнения 7. Упражнения:
№1.Решите уравнение и укажите сумму корней: │х — 5│= 3
№2. Решите уравнение и укажите меньший корень: │х 2 + х│= 0
№3.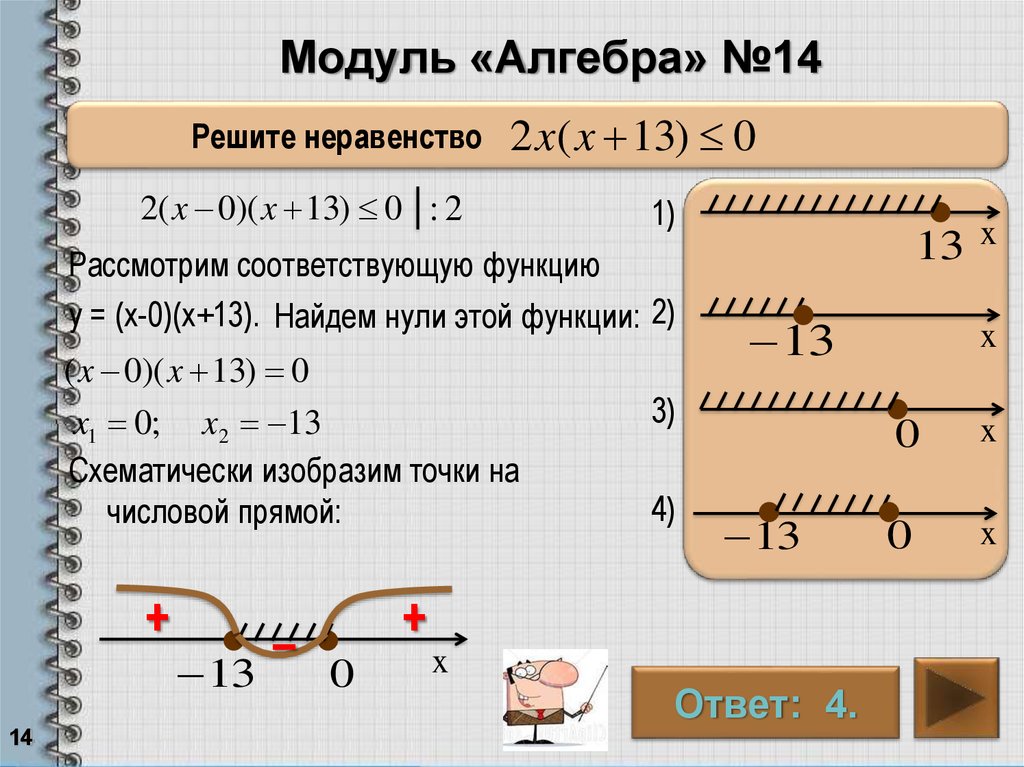 Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4
Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4
.Решите уравнение и укажите целый корень: │2х 2 – 7х + 6│= 1
№5.Решите уравнение и укажите количество корней: │х 4 – 13х 2 + 50│= 14
Раздел 2. Уравнения вида F(│х│) = m
Аргумент функции в левой части находится под знаком модуля, а правая часть не зависит от переменной. Рассмотрим два способа решения уравнений данного вида.
1 способ: По определению абсолютной величины исходное уравнение равносильно совокупности двух систем. В каждой из которых накладывается условие на подмодульное выражение. F (│х│) = m
Так как функция F(│х│) – чётная на всей области определения, то корни уравнений F(х) = m и F(- х) = m – это пары противоположных чисел. Поэтому достаточно решить одну из систем (при рассмотрении примеров указанным способом будет приводиться решение одной системы).
Применение метода введения новой переменной. При этом вводиться обозначение │х│= а, где а ≥ 0. Данный способ менее объёмный по оформлению.
Примеры: №1. Решите уравнение: 3х 2 – 4│х│= — 1 Воспользуемся введением новой переменной. Обозначим │х│= а, где а ≥ 0. Получим уравнение 3а 2 — 4а + 1 = 0 Д = 16 – 12 = 4 а 1 = 1 а 2 = 1 / 3 Возвращаемся к исходной переменной: │х│=1 и │х│= 1 / 3 . Каждое уравнение имеет два корня. Ответ: х 1 = 1; х 2 = — 1; х 3 = 1 / 3 ; х 4 = — 1 / 3 .
№2.Решите уравнение: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2
Найдём решение первой системы совокупности: 4х 2 + 5х – 2 =0 Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8 Заметим, что х 2 не удовлетворяет условию х ≥ 0. Решением второй системы будет число, противоположное значению х 1 . Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .
Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .
Решите уравнение: х 4 – │х│= 0 Обозначим │х│= а, где а ≥ 0. Получим уравнение а 4 – а = 0 а · (а 3 – 1) = 0 а 1 = 0 а 2 = 1 Возвращаемся к исходной переменной: │х│=0 и │х│= 1 х = 0; ± 1 Ответ: х 1 = 0; х 2 = 1; х 3 = — 1.
Упражнения:
Решите уравнение: 2│х│ — 4,5 = 5 – 3 / 8 │х│
№7. Решите уравнение, в ответе укажите количество корней: 3х 2 — 7│х│ + 2 = 0
№8. Решите уравнение, в ответе укажите целые решения: х 4 + │х│ — 2 = 0
Раздел 3. Уравнения вида │F(х)│ = G(х)
Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G(х) ≥ 0. Исходное уравнение можно решить двумя способами:
Исходное уравнение можно решить двумя способами:
Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем. │F (х)│ = G (х)
Данный способ рационально использовать в случае сложного выражения для функции G(x) и мене сложного – для функции F(х), так как предполагается решение неравенств с функцией F(х).
Состоит в переходе к равносильной системе, в которой накладывается условие на правую часть. │F (x )│= G (x )
Данный способ удобнее применять, если выражение для функции G(х) мене сложное, чем для функции F(х), так как предполагается решение неравенства G(х) ≥ 0. Кроме того, в случае нескольких модулей этот способ рекомендуется применять второй вариант.
Решите уравнение: │х + 2│= 6 -2х
(1 способ) Ответ: х = 1 1 / 3

│х 2 – 2х — 1│= 2·(х + 1)
(2 способ) Ответ: Произведение корней – 3.
Решите уравнение,в ответе укажите сумму корней:
│х — 6│= х 2 — 5х + 9
Ответ: сумма корней равна 4.
Упражнения:
│х + 4│= — 3х
№10.Решите уравнение, в ответе укажите число решений:│х 2 + х — 1│= 2х – 1
№11. Решите уравнение, в ответе укажите произведение корней:│х + 3│= х 2 + х – 6
Раздел 4. Уравнения вида │F(x)│= F(x) и │F(x)│= — F(x)
Уравнения данного вида иногда называют «красивейшими». Так как правая часть уравнений зависит от переменной, решения существуют тогда и только тогда, когда правая часть неотрицательна. Поэтому исходные уравнения равносильны неравенствам:
│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= — F(x) F(x)
. Решите уравнение, в ответе укажите меньший целый корень: │5х — 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1
Решите уравнение, в ответе укажите меньший целый корень: │5х — 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1
Решите уравнение, в ответе укажите длину промежутка: │х 2 — 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Ответ: длина промежутка равна 6.
№3. Решите уравнение, в ответе укажите число целых решений: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Ответ: 4 целых решения.
№4. Решите уравнение, в ответе укажите наибольший корень:
│4 – х —
│= 4 – х –
х 2 – 5х + 5 = 0 Д = 5 х 1,2 =
≈ 1,4
Ответ: х = 3.
Упражнения: №12. Решите уравнение, в ответе укажите целый корень: │х 2 + 6х + 8│= х 2 + 6х + 8№13. Решите уравнение, в ответе укажите число целых решений: │13х – х 2 — 36│+ х 2 – 13х + 36 = 0№14. Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:
Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:
Раздел 5. Уравнения вида │F(x)│= │G(x)│
Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений: │F (x )│= │ G (x )│
Примеры:
Решите уравнение, в ответе укажите целый корень: │х + 3│=│2х — 1│
Ответ: целый корень х = 4.
Решите уравнение: │ х – х 2 — 1│=│2х – 3 – х 2 │
Ответ: х = 2.
. Решите уравнение, в ответе укажите произведение корней:
Корниуравнения 4х 2 + 2х – 1 = 0 х 1,2 = — 1±√5 / 4 Ответ: произведение корней равно – 0,25. Упражнения: №15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х — 1│ №16. Решите уравнение, в ответе укажите меньший корень:│5х — 3│=│7 — х│ №17 . Решите уравнение, в ответе укажите сумму корней:
Упражнения: №15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х — 1│ №16. Решите уравнение, в ответе укажите меньший корень:│5х — 3│=│7 — х│ №17 . Решите уравнение, в ответе укажите сумму корней:
Раздел 6. Примеры решения нестандартных уравнений
В данном разделе мы рассмотрим примеры нестандартных уравнений, при решении которых абсолютная величина выражения раскрывается по определению.
Примеры:№1. Решите уравнение, в ответе укажите сумму корней: х · │х│- 5х – 6 = 0
Ответ: сумма корней равна 1 №2. . Решите уравнение, в ответе укажите меньший корень: х 2 — 4х ·
— 5 = 0
Ответ: меньший корень х = — 5. №3. Решите уравнение:
Ответ: х = -1. Упражнения: №18. Решите уравнение и укажите сумму корней: х · │3х + 5│= 3х 2 + 4х + 3
№19. Решите уравнение: х 2 – 3х =
Решите уравнение: х 2 – 3х =
№20. Решите уравнение:
Раздел 7. Уравнения вида │F(x)│+│G(x)│=0
Нетрудно заметить, что в левой части уравнения данного вида сумма неотрицательных величин. Следовательно, исходное уравнение имеет решение тогда и только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно системе уравнений: │F (x )│+│ G (x )│=0
. Решите уравнение:
Ответ: х = 2.
Решите уравнение: Ответ: х = 1.
Упражнения: №21.Решите уравнение:
№22. Решите уравнение, в ответе укажите сумму корней:
№23.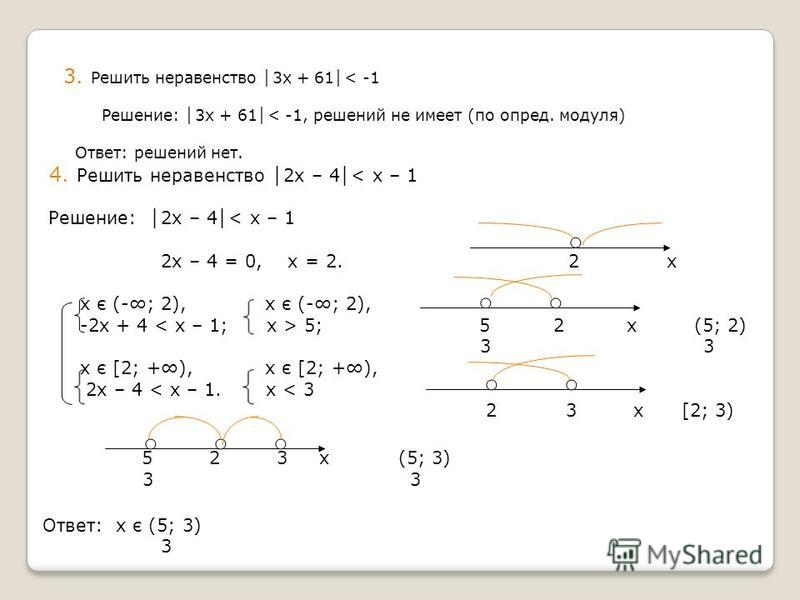 Решите уравнение, в ответе укажите количество решений:
Решите уравнение, в ответе укажите количество решений:
Раздел 8. Уравнения вида │а 1 х + в 1 │±│а 2 х + в 2 │± … │а n х +в n │= m
Для решения уравнений данного вида применяется метод интервалов. Если его решать последовательным раскрытием модулей, то получим n совокупностей систем, что очень громоздко и неудобно. Рассмотрим алгоритм метода интервалов: 1). Найти значения переменной х , при которых каждый модуль равен нулю (нули подмодульных выражений):
2). Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 ) 3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки) 4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов.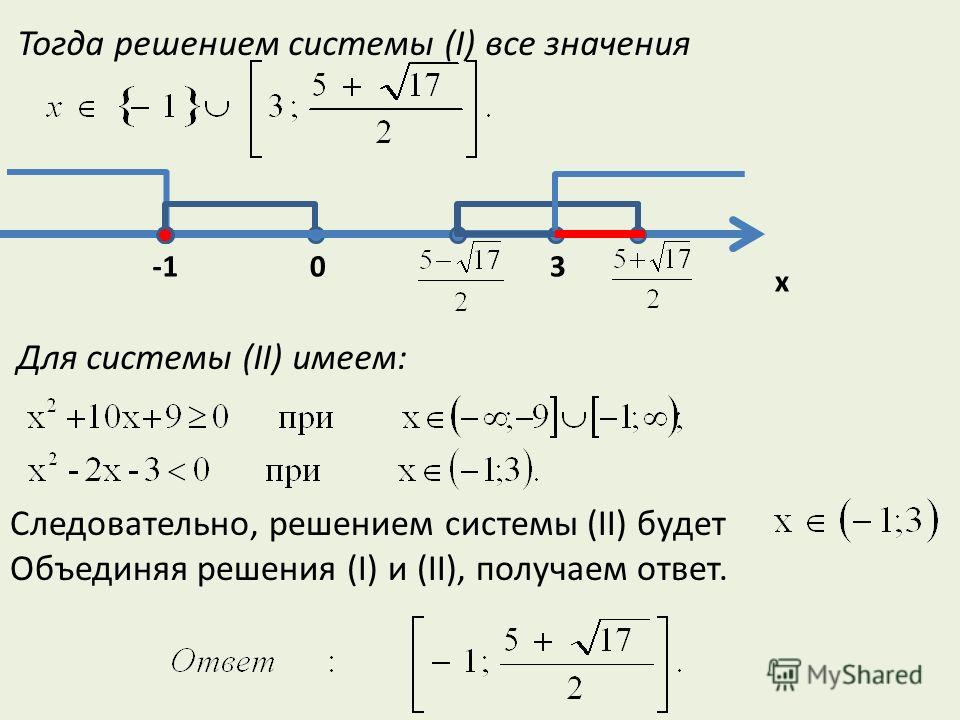 Примеры:
Примеры:
. Решите уравнение, в ответе укажите наибольший корень:
1). Найдём нули подмодульных выражений: х = 2; х = -3 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:
х – 2 х – 2 х – 2 — — + — 3 2 х 2х + 6 2х + 6 2х + 6 — + + 3)
— нет решений Уравнение имеет два корня. Ответ: наибольший корень х = 2.
Решите уравнение, в ответе укажите целый корень:
1). Найдём нули подмодульных выражений: х = 1,5; х = — 1 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х + 1 х + 1 х + 1 — + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 — — +
3).
Последняя система не имеет решений, следовательно, уравнение имеет два корня. В ходе решения уравнения следует обратить внимание на знак « — » перед вторым модулем. Ответ: целый корень х = 7.
Ответ: целый корень х = 7.
Решите уравнение, в ответе укажите сумму корней: 1). Найдём нули подмодульных выражений: х = 5; х = 1; х = — 2 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х – 5 х – 5 х – 5 х – 5 — — — +
-2 1 5 х х – 1 х – 1 х – 1 х – 1 — — + + х + 2 х + 2 х + 2 х + 2 — + + +
3).
Уравнение имеет два корня х = 0 и 2. Ответ: сумма корней равна 2.
. Решите уравнение: 1). Найдём нули подмодульных выражений: х = 1; х = 2; х = 3. 2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах. 3).
Объединим решения первых трёх систем. Ответ: ; х = 5.
Упражнения:
Решите уравнение:
№25.Решите уравнение, в ответе укажите сумму корней:
№26.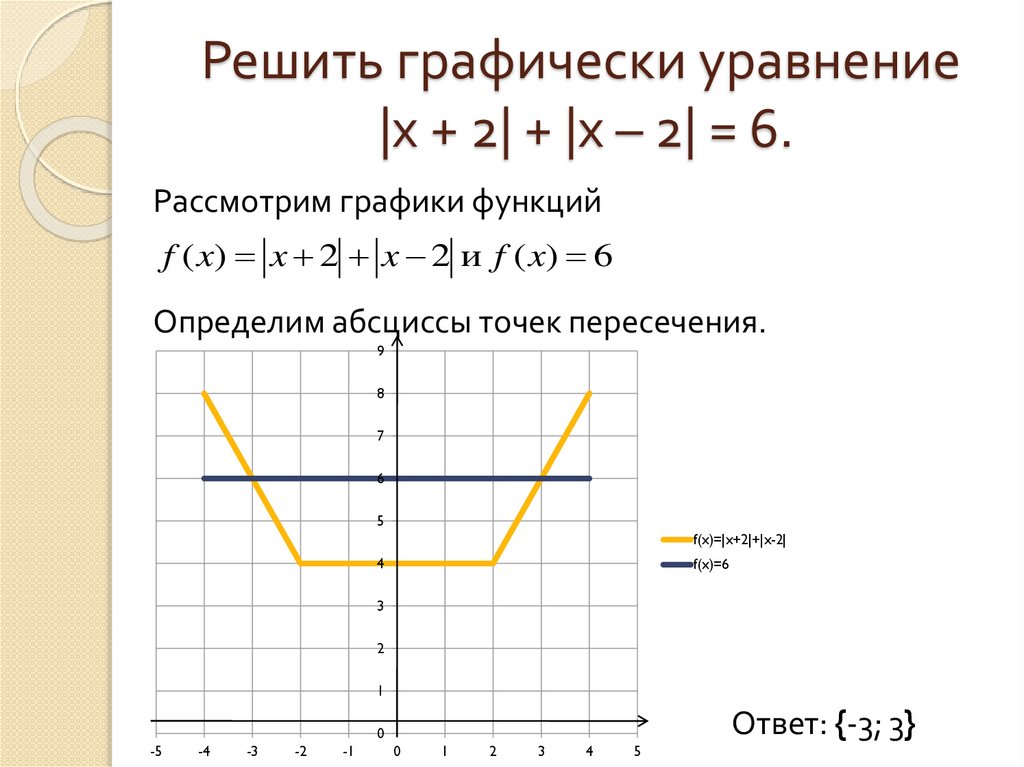
Решите уравнение, в ответе укажите меньший корень:
№27.Решите уравнение, в ответе укажите больший корень:
Раздел 9. Уравнения, содержащие несколько модулей
Уравнения, содержащие несколько модулей, предполагают наличие абсолютных величин в подмодульных выражениях. Основной принцип решения уравнений данного вида – это последовательное раскрытие модулей, начиная с «внешнего». В ходе решения используются приёмы, рассмотренные в разделах №1, №3.
Примеры: №1. Решите уравнение:
Ответ: х = 1; — 11. №2. Решите уравнение:
Ответ: х = 0; 4; — 4. №3. Решите уравнение, в ответе укажите произведение корней:
Ответ: произведение корней равно – 8. №4. Решите уравнение:
Обозначим уравнения совокупности (1) и (2) и рассмотрим решение каждого из них отдельно для удобства оформления. Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.(1)
Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.(1)
(2)
Ответ:
Упражнения: №36. Решите уравнение, в ответе укажите сумму корней: 5 │3х-5│ = 25 х №37. Решите уравнение, если корней более одного, в ответе укажите сумму корней: │х + 2│ х – 3х – 10 = 1 №38. Решите уравнение: 3 │2х -4│ = 9 │х│ №39. Решите уравнение, в ответе укажите количество корней на : 2 │ sin х│ = √2 №40 . Решите уравнение, в ответе укажите количество корней:
Раздел 3. Логарифмические уравнения.
Перед решением следующих уравнений необходимо повторить свойства логарифмов и логарифмической функции.
Примеры: №1. Решите уравнение, в ответе укажите произведение корней: log 2 (х+1) 2 + log 2 │x+1│ = 6 О. Д.З. х+1≠0 х≠ — 1
Д.З. х+1≠0 х≠ — 1
1 случай: если х ≥ — 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворяет условию х ≥ — 1 2 случай: если х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = — 5 – удовлетворяет условию х — 1
Ответ: произведение корней равно – 15.
№2. Решите уравнение, в ответе укажите сумму корней: lg
О.Д.З.
Ответ: сумма корней равна 0,5.
№3. Решите уравнение: log 5
О.Д.З.
Ответ: х = 9. №4. Решите уравнение: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Воспользуемся формулой перехода к другому основанию. │2 — log 5 x│+ 3 = │1 + log 5 x│
│2 — log 5 x│- │1 + log 5 x│= — 3 Найдём нули подмодульных выражений: х = 25; х = Эти числа делят область допустимых значений на три интервала, поэтому уравнение равносильно совокупности трёх систем.
Ответ: }
Решение модульных уравнений
Автор: Валентина Галиневская
●
14.08.2015
●
Раздел: Математика
Для того, чтобы научиться решать уравнения с модулем, надо вспомнить и выучить определение модуля.
Из определения видно, что модуль любого числа неотрицателен. Кроме того, определение показывает как можно избавляться от знака модуля в уравнении.
На практике это делается так:
1) Находят значения переменной, при которых выражения стоящие под знаком модуля обращаются в нуль.
2) Отмечают все нули на числовой прямой. Они разобьют эту прямую на лучи и промежутки, на которых все подмодульные выражения имеют постоянный знак.
Они разобьют эту прямую на лучи и промежутки, на которых все подмодульные выражения имеют постоянный знак.
3) Определяем знаки подмодульных выражений на каждом промежутке и раскрываем все модули (заменяя их подмодульными выражениями со знаком плюс или со знаком минус в зависимости от знака подмодульного выражения).
4) Решаем получившиеся уравнения на каждом промежутке (сколько промежутков, столько и уравнений).Обратите внимание, что обязательно выбираем только те решения, которые находятся в данном промежуток (полученные решения могут и не принадлежать промежутку).
Хватит уже теории, пора на примерах посмотреть как решаются уравнения с модулем. Начнем с более простого.
Решение уравнений с модулями
Пример 1. Решить уравнение .
Решение. Так как , то . Если , то , и уравнение принимает вид .
Отсюда получаем .
Ответ: .
Пример 2. Решить уравнение .
Решить уравнение .
Решение. Из уравнения следует, что .
Поэтому , , , и уравнение принимает вид или .
Так как , то исходное уравнение корней не имеет.
Ответ: корней нет.
Пример 3. Решить уравнение .
Решение. Перепишем уравнение в равносильном виде .
Полученное уравнение относится к уравнениям типа .
Известно, что уравнение такого типа равносильно неравенству . Следовательно, здесь имеем или .
Ответ: .
Думаю, как решать такого вида уравнения с модулем вы уже разобрались. Попробуем разобраться с более сложным уравнением.
Пример 4. Решить уравнение: |x2 + 2x| – |2 – x| = |x2 – x|
Находим нули подмодульных выражений:
х2 + 2х = 0, х(х + 2) = 0, х = 0 или х = ‒ 2. При этом парабола у = х2 + 2х положительна на промежутках (–∞; –2 ) и (0; +∞), а на промежутке (–2; 0 ) она отрицательна (см. рисунок).
При этом парабола у = х2 + 2х положительна на промежутках (–∞; –2 ) и (0; +∞), а на промежутке (–2; 0 ) она отрицательна (см. рисунок).
х2 ‒ х = 0, х(х – 1) =0, х = 0 или х = 1. Эта парабола у = х2 ‒ х положительна на промежутках (–∞; 0 ) и (1; +∞), а на промежутке (0; 1) она отрицательна (см. рисунок).
2 – х = 0, х = 2, модуль положителен на промежутке (–∞; 0) и принимает отрицательные значения на промежутке (2; +∞) (см. рисунок).
Теперь решаем уравнения на промежутках:
1) х ≤ ‒2: х2 + 2х – (2 – х) = х2 ‒ х, х2 + 2х – 2 + х = х2 ‒ х, 4х = 2, х = 1/2 (не входит в рассматриваемый промежуток)
2) –2 ≤ x <0: ‒(х2 + 2х) – (2 – х) = х2 ‒ х, ‒х2 ‒ 2х – 2 + х = х2 ‒ х, ‒2 х2 = 2, х2 = ‒1, решений нет.
3) 0 ≤ x <1: х2 + 2х ‒ (2 – х) = ‒ (х2 ‒ х), х2 + 2х ‒ 2 + х = ‒х2 + х, 2х2 + 2х – 2 = 0, х2 + х – 1 = 0, √D = √5,
х1 = (‒1 ‒ √5)/2 и х2 = (‒1 + √5)/2.
Так как первый корень отрицательный, то он не принадлежит нашему промежутку, а второй корень больше нуля и меньше единицы это и есть наше решение на данном промежутке.
4) 1 ≤ x <2: х2 + 2х – (2 – х) = х2 ‒ х, х2 + 2х – 2 + х = х2 ‒ х, 4х = 2, х= 1/2 (не входит в рассматриваемый промежуток)
5) х ≥ 2: х2 + 2х –(‒(2 – х)) = х2 ‒ х, х2 + 2х + 2 ‒ х = х2 ‒ х, 2х = ‒ 2, х = ‒1 (не входит в рассматриваемый промежуток).
Ответ: (‒1 + √5)/2.
Вы заметили, что решается это уравнение также как и предыдущие, отличие в количестве промежутков. Так как под модулем стоят квадратные выражения то корней получилось больше, а соответственно и больше промежутков.
А как же решать уравнение в котором модуль стоит под модулем? Давайте посмотрим на примере.
Пример 5. Решите уравнение |3 – |x – 2|| = 1
Решите уравнение |3 – |x – 2|| = 1
Подмодульное выражение может принимать значение либо 1 либо – 1. Получаем два уравнения:
3 ‒ |х ‒ 2|= ‒1 или 3 ‒ |х ‒ 2|= 1
Решаем каждое уравнение отдельно.
1) 3 ‒ |х ‒ 2|= ‒1, ‒|х ‒ 2|= ‒1 – 3, ‒|х ‒ 2|= ‒4, |х ‒ 2|= 4,
х ‒ 2= 4 или х ‒ 2= ‒ 4, откуда получаем х1 = 6, х2 = ‒2.
2) 3 ‒ |х ‒ 2|= 1, ‒|х ‒ 2|= 1 ‒ 3, ‒|х – 2|= ‒2, |х – 2|= 2,
х – 2 = 2 или х – 2 = ‒2,
х3 = 4 , х4 = 0.
Надеюсь, после изучения данной статьи вы будете успешно решать уравнения с модулем. Если остались вопросы, записывайтесь ко мне на уроки. Репетитор Валентина Галиневская.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос
Методы решения уравнений, содержащих модуль
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Методы решения уравнений, содержащих модуль
Тема урока:Методы решения
уравнений,
содержащих
модуль
Цели урока:
познакомить с методами решения
уравнений, содержащих под знаком
модуля выражение с переменной;
сформировать умение решать данные
уравнения;
научить выбирать наиболее
рациональный метод решения
уравнений;
закрепить изученный материал.

«Я всегда старался,
насколько позволяли
мои силы и способности,
отделаться от трудности и скуки
вычислений,
докучность которых обыкновенно
отпугивает многих от изучения
математики»
Джон Непер
4. I. Фронтальная работа
Сформулируйте определение модуля.Сформулируйте геометрическое
истолкование модуля.
Может ли быть отрицательным значение
суммы 2 +∣х∣?
Может ли равняться нулю значение
разности 2 -∣х∣?
Как сравниваются два отрицательных
числа?
5. II. Устная работа
Раскройте модуль:1.
6.
2.
7.
3.
8.
при
4.
9.
при
5.
10.
при
6. Методы решения уравнений, содержащих модуль
1. Метод интервалов.2. Метод возведения в квадрат обеих
частей уравнения.
3. Метод введения новой переменной.
4. Метод замены уравнения совокупностью
систем.
5. Графический метод.
6. Решение уравнений, содержащих
модуль под знаком модуля.

1. Метод интервалов
Для того, чтобы решить уравнение,
содержащее неизвестную под
знаком модуля, необходимо
освободиться от знака модуля,
используя его определение.
Для этого следует:
1. найти значения переменной, при
которых выражения, стоящие под
знаком модуля, обращаются в нуль;
2. разбить область допустимых
значений уравнения на
промежутки, на каждом из которых,
выражения, стоящие под знаком
модуля сохраняют знак ;
3. на каждом из этих промежутков
уравнение записать без знака
модуля, а затем решить его.
Объединение решений, найденных на
всех промежутках, и составляет
решение исходного уравнения.
10. Решите уравнения:
1)Ответ:
2)
Ответ:
3)
+
+
—
—
+
+
любое число
Ответ:
13. 2. Возведение в квадрат обеих частей уравнения
Решите уравнение:1)
Возведем в квадрат обе части уравнения:
Найдём ОДЗ:
Ответ:
2)
Возведем в квадрат обе части уравнения:
Найдём ОДЗ:
Ответ:
3.
 Метод введения новой
Метод введения новойпеременной
Иногда уравнение, содержащее
переменную под знаком модуля,
можно решить довольно просто,
используя метод введения новой
переменной.
Продемонстрируем данный метод на
конкретных примерах:
Решите уравнение:
1)
Пусть
тогда
Уравнение принимает вид:
Ответ:
Решите уравнение:
2)
Пусть
тогда
уравнение принимает вид:
Ответ:
4. Метод замены уравнения
совокупностью систем
Методом замены уравнения
совокупностью систем можно
решать уравнения вида:
Причем данное уравнение можно
заменять совокупностью систем
двумя способами:
I способ:
II способ:
Если в уравнении
функция
имеет более простой вид, нежели функция
то имеет смысл исходное уравнение заменять
первой совокупностью систем, а если более
простой вид имеет функция
тогда
исходное уравнение следует заменять второй
совокупностью систем.
В частности уравнение
при C>0 равносильно совокупности уравнений
и
т.
 е.
е.при
при
решений не имеет.
Воспользуемся данным методом при решении
следующих уравнений:
1)
совокупности двух уравнений:
Ответ:
2)
Уравнение
совокупности двух уравнений:
Первое уравнение совокупности равносильно
совокупности двух уравнений:
Второе уравнение совокупности решений не имеет, т.к.
Ответ:
5. Графический метод
Метод основан на геометрической интерпретации
понятия абсолютной величины числа, а именно
модуль х равен расстоянию от точки С(х) до
точки с координатой О на числовой прямой Ох.
Используя геометрическую интерпретацию,
легко решаются уравнения вида:
где
a, b, c
— числа
Решить уравнение вида
|x — a|= c
– это значит найти все точки на числовой оси
Ох, которые отстоят от точки С(а) на
расстояние с.
При C < 0, уравнение решений не имеет;
При C = 0, уравнение имеет один корень;
При C > 0, уравнение имеет два корня
25. Решить уравнение вида |x — a| + |x — b| = c
— это значит найти все точки на числовойоси Ох, для каждой из которых сумма
расстояний от неё до точки с
координатами а и b равна с.

Аналогично интерпретируется решение
уравнения вида |x — a|-|x — b|= c.
Решите уравнение:
1)
На числовой оси Ох найдем все точки, для каждой
из которых разность расстояния от нее до точки
с координатой 1 и расстояния от неё до точки с
координатой 3 равна 2. Так как длина отрезка
[1;3] равна 2,то ясно, что любая точка с
координатой
удовлетворяет данному
уравнению, а любая точка с координатой х<3 не
удовлетворяет ему. Таким образом, решением
исходного уравнения является множество чисел
промежутка
.
Ответ:
Рассмотренный метод можно отнести к
графическим методом решения
уравнения. Все необходимые построения
здесь производились на числовой оси.
Рассмотрим теперь метод решения
уравнения, в котором будем использовать
построения на координатной плоскости.
Этим методом, теоретически, можно
решать уравнения с модулем любого
вида, однако практическая реализация
метода иногда бывает довольно сложной.

Суть метода состоит в следующем. Решить
уравнение f(х)=q(x) это значит найти все
значения х, для которых значение функций
y=f(x) и y=q(x) равны, т.е. найти абсциссы
всех точек пересечения графиков этих
функций. Если же графики не имеют общих
точек, то уравнение не имеет корней.
Следует, однако, иметь в виду, что точное
построение графиков функций практически
невозможно, поэтому решение, найденное
графическим способом требует проверки
подстановкой.
Решите уравнение: 2)
Построим графики двух функций
и
Из чертежа видно, что графики имеют 2 общие точки.
Координаты этой точки: (8; 3), другой: (-4; 3).
Следовательно, исходное уравнение имеет
два решения:
,
.
Как уже говорилось, при каждом методе
значения корней уравнения определяются
приблизительно, и только проверка
позволит доказать, что найденные
значения действительно являются
корнями исходного уравнения.
При подстановке
,
в уравнение
получаем, соответственно два верных
числовых равенства: |-3|=3 и |3|=3.

Ответ:
Так как при графическом методе
решения зачастую не удается найти
точное значение корня, но
применение данного метода бывает
обосновано, если требуется найти
не сами корни, а всего лишь
определить их количество.
6. Решение уравнений, содержащих
модуль под знаком модуля
При решении уравнения, в котором
под знаком модуля содержится
выражение, также содержащее
модуль следует:
1. освободиться от внутренних
модулей;
2. в полученных уравнениях раскрыть
оставшиеся модули.
Решите уравнение:
Уравнение
совокупности двух систем:
— система решения не имеет
ЛОЖНО!
Ответ:
Решите уравнение:
Левая часть уравнения неотрицательна для всех х,
следовательно правая часть его должна быть такой же.
Значит
т.е.
Ответ: корней нет.
V. Закрепление
изученного материала
Решите самостоятельно двумя способами:
36. Проверь себя:
1 способ:1.Найдем значения переменной, при
которых выражения, стоящие под
знаком модуля, обращаются в
нуль:
2.
 Разобьем область допустимых
Разобьем область допустимыхзначений уравнения на промежутки,
на каждом из которых, выражения,
стоящие под знаком модуля
сохраняют знак :
+
—
+
+
—
—
—
+
любое число
Ответ:
2 способ:
Сумма двух неотрицательных выражений
неотрицательна, значит левая часть
уравнения неотрицательна для всех х,
следовательно и правая часть его должна
быть такой же,
совокупности
двух систем:
— система решения не имеет
ВЕРНО!
Ответ:
VI. Домашнее задание
1. Проработать теоретический материал.
2. Практикум «Уравнения с модулем».
Решите уравнения с модулем рациональным способом.
English Русский Правила
Решение уравнений с модулем. Решить квадратное уравнение онлайн
Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , вначале приведите уравнение к общему виду:
ax 2 + bx + c = 0
Заполните соответственно поля формы:
| Как решить квадратное уравнение: | Виды корней: |
1.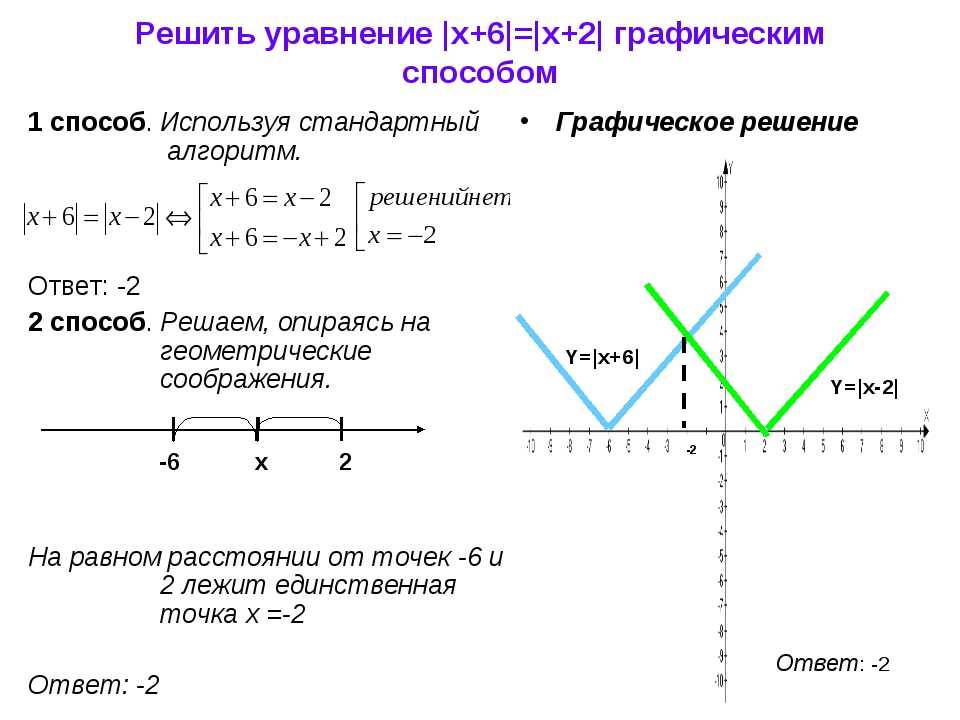 Привести квадратное уравнение к общему виду: Привести квадратное уравнение к общему виду: Общий вид Аx 2 +Bx+C=0 Пример: 3х — 2х 2 +1=-1 Приводим к -2х 2 +3х+2=0 2. Находим дискриминант D. 3. Находим корни уравнения. | 1. Действительные корни. Причем. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Действительные корни совпадают. x1 равно x2 3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2 5. Уравнение имеет бесчисленное множество решений. 6. Уравнение решений не имеет. |
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений .
Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x 2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число 1/2 !
x1=(-В+D 1/2)/2А = (-3+7)/2 = 2
x2=(-В-D 1/2)/2А = (-3-7)/2 = -5
Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10
Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х 2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k 2 – AC = 16 – 16 = 0
X = -k/A = 4
Подставим
(x-4)*(x-4) = (x-4)2 = X 2 – 8x + 16
Пример 3. Решение квадратного уравнения с комплексными корнями.
Решение квадратного уравнения с комплексными корнями.
13х 2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b 2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.
X1=(-В+D 1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D 1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1
Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа , и как правильно раскрывать выражения, содержащие знак модуля , то наличие в уравнении выражения, стоящего под знаком модуля , перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x)
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3
Чтобы решить уравнение, содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля .
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x 2 +4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3
2. Мы получили два числовых промежутка: х≥3 и х
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
и решим это уравнение.
Это уравнение имеет корни:
х 1 =0, х 2 =3
Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 2 =3.
Б) При x
Внимание! Это уравнение существует только на промежутке х
Раскроем скобки, приведем подобные члены.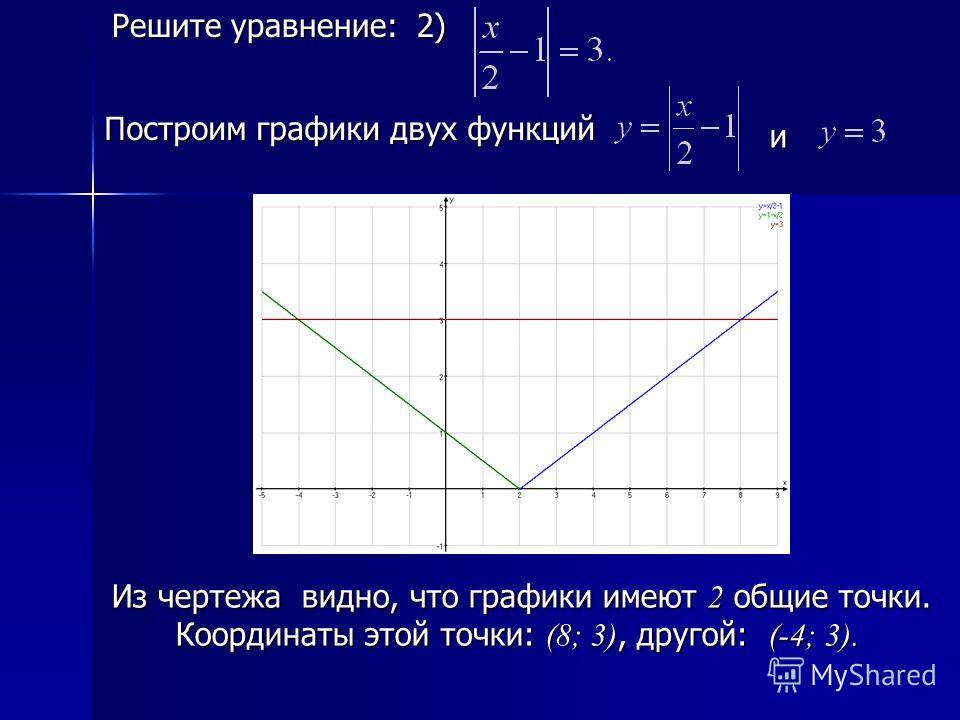 Получим уравнение:
Получим уравнение:
х 1 =2, х 2 =3
Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
Состоит в том, что бетон, армируемый прочными стальными каркасами, является высокопрочным строительным материалом и не подвержен многочисленным воздействиям окружающей среды, благодаря чему конструкция фундамента опоры ВЛ способна удерживать стальные и железобетонные опоры ЛЭП без угрозы их опрокидывания в течение не одного десятка лет. Долговечность, стойкость к нагрузкам и прочность — основные преимущества применения изделий железобетонные фундаменты МФ2х2-0 малозаглубленные в энергетическом строительстве.
Железобетонные фундаменты МФ2х2-0 малозаглубленные изготавливаются из тяжелого бетона классом по прочности на сжатие не ниже В30, марка — от М300. Марка бетона по морозостойкости — не ниже F150, по водонепроницаемости — W4 — W6. Цемент и инертные, применяемые для изготовления бетона, должны удовлетворять требованиям СНиП I-В. 3-62 и ТП4-68. Наибольший размер зерен в структуре бетона не должен превышать 20-40 мм. Контроль прочности бетона фундаментов опор в соответствии с ГОСТ 10180-67 «Бетон тяжелый. Методы определения прочности» и ГОСТ 10181-62 «Бетон тяжелый. Методы определения подвижности и жесткости бетонной смеси».
3-62 и ТП4-68. Наибольший размер зерен в структуре бетона не должен превышать 20-40 мм. Контроль прочности бетона фундаментов опор в соответствии с ГОСТ 10180-67 «Бетон тяжелый. Методы определения прочности» и ГОСТ 10181-62 «Бетон тяжелый. Методы определения подвижности и жесткости бетонной смеси».
В качестве арматуры фундаменты МФ2х2-0 малозаглубленные применяются: стрежневая горячекатаная арматурная сталь класса А-I, стержневая горячекатаная арматурная сталь периодического профиля класса А-III, стержневая арматурная сталь периодического профиля класса А-IV и обыкновенная арматурная проволока класса В1. Для монтажных петель применяется только стержневая горячекатаная арматура класса А-I из углеродистой спокойной стали.
Перед фундаментами опор ЛЭП для энергетического строительства стоит ответственная задача — много лет сохранять устойчивость и прочность опор ЛЭП в разных климатических условиях, в любое время года и в любую погоду. Поэтому к фундаментам опор предъявляются очень высокие требования. Перед отправкой заказчику, фундаменты опор МФ2х2-0 малозаглубленные проходят проверку по различным параметрам, например, таких как степень устойчивости, прочность, долговечность и износостойкость, сопротивляемость отрицательным температурам и атмосферным воздействиям. Перед сваркой детали стыков должны быть очищены от ржавчины. Железобетонные фундаменты с толщиной защитного споя бетона менее 30 мм, а также фундаменты, устанавливаемые в агрессивных грунтах, должны быть защищены гидроизоляцией.
Перед отправкой заказчику, фундаменты опор МФ2х2-0 малозаглубленные проходят проверку по различным параметрам, например, таких как степень устойчивости, прочность, долговечность и износостойкость, сопротивляемость отрицательным температурам и атмосферным воздействиям. Перед сваркой детали стыков должны быть очищены от ржавчины. Железобетонные фундаменты с толщиной защитного споя бетона менее 30 мм, а также фундаменты, устанавливаемые в агрессивных грунтах, должны быть защищены гидроизоляцией.
Во время эксплуатации за фундаменты МФ2х2-0 малозаглубленные подлежат тщательному надзору, особенно в первые годы работы ВЛ. Одним из самых серьезных дефектов сооружения фундаментов, трудноустранимых в условиях эксплуатации, является нарушение технологических норм при их изготовлении: применение некачественного или плохо промытого гравия, нарушение пропорций при составлении бетонной смеси и т.д. Не менее серьезным дефектом является послойное бетонирование фундаментов, когда отдельные элементы одного и того же фундамента бетонируются в разное время без предварительной подготовки поверхности. При этом не происходит схватывания бетона одного элемента фундамента с другим и может произойти разрушение фундамента при внешних нагрузках, которые значительно меньше расчетных.
При этом не происходит схватывания бетона одного элемента фундамента с другим и может произойти разрушение фундамента при внешних нагрузках, которые значительно меньше расчетных.
При изготовлении железобетонных фундаментов опор также иногда нарушаются нормы: используется недоброкачественный бетон, закладывается арматура не тех размеров, которые предусмотрены проектом. В процессе сооружения линий электропередач на сборных или свайных железобетонных фундаментах возможно появление серьезных дефектов, которые не допускает энергетическое строительство. К таким дефектам относятся установка сломанных железобетонных фундаментов, недостаточное их заглубление в грунте (особенно при установке опор на склонах холмов и оврагов), нетщательная трамбовка при засыпке, установка сборных фундаментов меньших размеров и др. К дефектам установки относится неправильный монтаж железобетонных фундаментов, при котором отдельные сборные фундаменты, предназначенные в качестве основания металлической опоры, имеют различные вертикальные отметки или сдвиг отдельных фундаментов в плане. При неправильной разгрузке фундаменты МФ2х2-0 малозаглубленные могут быть испорчены, может произойти скол бетона и обнажение арматуры. В процессе приемки особое внимание следует обращать на соответствие анкерных болтов и их гаек проектным размерам.
При неправильной разгрузке фундаменты МФ2х2-0 малозаглубленные могут быть испорчены, может произойти скол бетона и обнажение арматуры. В процессе приемки особое внимание следует обращать на соответствие анкерных болтов и их гаек проектным размерам.
В условиях эксплуатации железобетонные фундаменты МФ2х2-0 малозаглубленные повреждаются как от воздействий внешней среды, так и от больших внешних нагрузок. Арматура фундаментов, имеющих пористую структуру бетона, повреждается от агрессивного воздействия грунтовых вод. Трещины, образующиеся на поверхности фундаментов, при воздействии эксплуатационных знакопеременных нагрузок, а также ветра, влаги и низкой температуры, расширяются, что в конечном итоге приводит к разрушению бетона и обнажению арматуры. На территориях, расположенных вблизи химических заводов, быстро разрушаются анкерные болты и верхняя часть металлических подножников.
Поломка фундамента опор также может произойти в результате несоосности его со стойками, что служит причиной появления больших изгибающих моментов. Подобная поломка может произойти и при размыве основания фундамента грунтовыми водами и отклонении его от вертикального положения.
Подобная поломка может произойти и при размыве основания фундамента грунтовыми водами и отклонении его от вертикального положения.
В процессе приемки фундаменты МФ2х2-0 малозаглубленные проверяются их соответствие проекту, глубина заложения, качество бетона, качество сварки рабочей арматуры и анкерных болтов, наличие и качество защиты от действия агрессивных вод. Производятся замер вертикальных отметок фундаментов и проверка расположения анкерных болтов по шаблону. При обнаружении каких-либо несоответствий нормам все дефекты устраняются до засыпки котлованов. Фундаменты, имеющие в верхней части сколы бетона и обнаженную арматуру, ремонтируются. Для этого устраивается бетонное обрамление толщиной 10-20 см, заглубленное ниже уровня земли на 20 — 30 см. Следует иметь в виду, что энергетическое строительство не допускает обрамление из шлакобетона, так как в шлаке имеется примесь серы, которая вызывает интенсивную коррозию арматуры и анкерных болтов. При более значительных повреждениях фундаментов (в том числе и монолитных) поврежденная часть накрывается арматурой, сваренной с арматурой основного фундамента, и после установки опалубки бетонируется.
Модуль бронирования MaxiBooking для сайта и социальных сетей
Поставьте модуль бронирования без комиссии
- Увеличивает прямые продажи вашего отеля
- Подходит для любого сайта
- Работает без комиссии
Зачем использовать систему онлайн-бронирования отелей MaxiBooking?
Модуль онлайн бронирования позволяет клиентам в считаные секунды выбрать желаемые номера и услуги и получить подтверждение бронирования в удобной для них форме.
Отображает актуальную информацию о свободных номерах, тарифах, акциях и спецпредложениях. Мгновенно информирует клиента о стоимости номеров и услуг.
Возможность выбора предложений на точно заданные даты и диапазон дат. Формирование предложений различной продолжительности дней/ночей.
При отсутствии свободных номеров на заданный период, модуль автоматически сформирует предложения на ближайшие даты.
Система бронирования отелей — самый простой способ для онлайн-продаж
Чтобы увеличить продажи и привлечь новых клиентов, необходимо иметь кнопку онлайн-бронирования прямо на сайте. Требуется решение, которое легко использовать? Мы здесь ради вас!
Отличный дизайн
Кнопка онлайн бронирования отлично смотрится на любом сайте отеля. Цвета, поля и шрифты могут быть легко настроены для веб-сайта на основе предпочтений. Форма бронирования предоставляет всю необходимую информацию с возможностью выбора макета и критериев ввода в соответствии с ожиданиями клиентов.
Автоматическая синхронизация
Полезность кнопки бронирования как канала прямых продаж веб-сайта невозможно переоценить, особенно когда она работает с несколькими платформами продаж и бронирования. Система бронирования отелей MaxiBooking с помощью MaxiBooking Channel Manager связана с несколькими платформами бронирования и обновляет данные о бронировании по всем активированным каналам продаж, автоматически помогая предотвратить перебронирование.
Легкодоступная информация
Благодаря системе определения цен и дат интернет-бронирования MaxiBooking клиенты могут легко получить информацию, необходимую для бронирования. Доступные тарифы и даты в режиме реального времени позволяют клиентам мгновенно принимать решения о бронировании и обеспечивают владельцам отеля комфорт при бронировании на основе самой последней актуальной информации.
Легкое кредитное плечо
Готовый механизм онлайн-бронирования экономит время и бюджет отельеров и подходит для веб-сайтов на любой платформе. Система бронирования легко устанавливается и безупречно вписывается в инфраструктуру сети отелей. Простая и интуитивно понятная кнопка бронирования отлично сочетается с любым макетом, благодаря чему веб-страницы выглядят более грамотно.
Планируете использовать бесплатный механизм бронирования отелей? Не спешите устанавливать софт, пока не попробуете нашу кнопку онлайн-бронирования, которую мы предлагаем! MaxiBooking предлагает программное обеспечение, которое хорошо подходит для любого типа веб-сайтов и упрощает использование как для онлайн-клиентов, так и для отельеров.
Мы предлагаем больше возможностей, чем другие и то, что лучше всего подходит именно для вашего отеля
Выбор отеля
Солнечный берег
Дата заезда
22.08.19
Дата выезда
22.08.19
Тип номера
Полулюкс
Взрослые
3
Возраст детей
1
5
7
Вы можете включить в модуль бронирования те поля, которые считаете важными.
Выбор отеля (для сети)
Тип номера
Количество гостей
Возраст детей
МаксиБукинг превращает посетителей сайта в ваших клиентов
В настоящее время Интернет повсеместно вошел в нашу жизнь. Он помогает пользователям расширить границы возможностей оказания услуг, внедряя новые технологии, тем самым совершенствуя работу вашего бизнеса. Теперь клиенты могут зарезервировать номер в отеле за считанные минуты, воспользовавшись формой онлайн-бронирования. Предлагаемая нами система подходит для любых гостиниц, отелей, баз отдыха, санаториев, пансионатов, хостелов и прочих заведений, в которых останавливаются туристы.
Предлагаемая нами система подходит для любых гостиниц, отелей, баз отдыха, санаториев, пансионатов, хостелов и прочих заведений, в которых останавливаются туристы.
Модуль онлайн бронирования гостиниц полностью встраивается в сайт отеля, легко адаптируясь под его параметры. Вы контролируете все права доступа в систему и динамику заполняемости отеля, постоянно получая информацию о комнатах и ценах на них, количестве свободных номеров и действующих тарифах.
После установки модуля бронирования гостиниц на сайте программа не просто будет отражать достоверные сведения о вашем отеле, выступая «визитной карточкой», но и будет играть роль активного участника вашего бизнеса, улучшая отдельные его составляющие.
Форма бронирования отелей на сайте комфортна как для самих гостиниц, так и их клиентов.
Возможности модуля онлайн бронирования для сайта гостиниц:
- широкодоступный поиск всех предложений.
- регистрация контактных данных клиента.
Что позволит вашим клиентам:
- ознакомиться с перечнем текущих актуальных предложений и цен на проживание в вашей гостинице.

- самостоятельно выбрать, заказать и оплатить номер.
Это дает вам следующие преимущества:
- онлайн бронирование доступно круглосуточно, сокращая расходы на персонал.
- система исключает двойное бронирование, позволяя избежать ошибок, допускаемых обычным менеджером.
Система очень эффективно выполняет возложенную на неё работу, привлекая реальных клиентов, способствуя увеличению клиентской базы и, соответственно, вашего дохода.
Система бронирования отелей для сайта — увеличьте ваши продажи
Почему важна система онлайн-бронирования? Это не только экономит время гостей — наличие инструмента онлайн-бронирования прямо на главной странице означает более высокую активность пользователей и конверсию посетителей в клиентов. В то время как сторонние платформы бронирования взимают плату за свои услуги, наличие кнопки прямого бронирования позволяет владельцам отелей получать больший доход от тех же тарифов.
MaxiBooking — корпоративная система бронирования для вашего гостиничного бизнеса
«Подходит ли это для моего бизнеса по аренде?» — спросили бы. Независимо от типа размещения — отдельные апартаменты, B & B, хостел, пансионат, гостиница — система онлайн бронирования MaxiBooking поможет вам в этом!
MaxiBooking онлайн бронирование кнопки предоставляет корпоративные решения для онлайн-продаж для аренды на время отпуска независимо от размера бизнеса. С настраиваемыми правами доступа нет ограничений на количество пользователей и отдельных свойств, которыми можно управлять из одной учетной записи!
MaxiBooking мобильная система бронирования отелей
MaxiBooking онлайн бронирование Кнопка представляет собой гибкий инструмент бронирования для веб-сайта, который отлично работает как на настольных, так и на мобильных экранах. Механизм бронирования адаптируется для платформ и гаджетов. Мобильная система бронирования отелей в мобильной версии сайта предоставляет пользователям ту же функциональность и удобную навигацию, что и бронирование на рабочем столе.
Модуль бронирования поддерживает все популярные способы оплаты
С МаксиБукинг Вы сможете предложить своим клиентам любой удобный для вас
способ платежей и % предоплаты
Сайт для отеля
PMS для отеля
Менеджеров каналов
Оптимизация бронирования
Читайте также
Все статьи
Коллекции кухонь от Модуль-онлайн
Коллекции кухонь от Модуль-онлайнСмотреть проект
Шкаф Вуд / Урбан
Смотреть проект
Шкаф Вуд
Смотреть проект
Смотреть проект
Смотреть проект
Модуль
Смотреть проект
Смотреть проект
Смотреть проект
Смотреть проект
Шкаф Урбан
Смотреть проект
Шкаф Урбан
Смотреть проект
Модуль
Смотреть проект
Винчестер
Смотреть проект
Вуд / Модуль
Смотреть проект
Стоун / Глосс
Смотреть проект
Вуд / Глосс
Смотреть проект
Смотреть проект
Вуд / Глосс
Смотреть проект
Смотреть проект
Глосс / Вуд
Дизайн
—
Разработан европейским дизайнерским бюро, мы учитываем современные тенденции в производстве мебели
Доступная цена
—
Мы скажем точную цену Вашего проекта, и эта цена не изменится в момент заказа
Материалы
—
Мы работаем только с лучшими концернами Европы, такими как EGGER, HETTICH, RENOLIT, BLUM и др. , потому можем предложить лучшее качество по доступной цене
, потому можем предложить лучшее качество по доступной цене
Срок доставки
—
Вам не нужно ждать 2 месяца, свою новую кухню вы сможете получить через 15-25 дней
Гарантия 24 мес
—
Мы уверены в качестве своей мебели и даем гарантию, которую предложит не каждый производитель
- Хит продаж
- Новинка
-
Хит продаж
Быстрый просмотр
Хит продаж
Быстрый просмотр
Хит продаж
Быстрый просмотр
Популярные категории
Весь каталогВся мебель
Коллекции
Хиты продаж
Вы можете комбинировать различные модули кухонной мебели в режиме on- line. Все проекты, отображаются в 3D формате и сохраняются в Вашем личном кабинете. Вы просто выбираете понравившиеся модули, расставляете их в виртуальном помещении, и конструктор автоматически просчитывает точную стоимость Вашей кухни. Создавайте любое количество проектов с разной планировкой и ценой и выбирайте те, которые Вам больше всего понравится.
Все проекты, отображаются в 3D формате и сохраняются в Вашем личном кабинете. Вы просто выбираете понравившиеся модули, расставляете их в виртуальном помещении, и конструктор автоматически просчитывает точную стоимость Вашей кухни. Создавайте любое количество проектов с разной планировкой и ценой и выбирайте те, которые Вам больше всего понравится.
Начать
Акции
Все акцииМы в Instagram
Все записи
Модуль выравнивания
Введение
Модуль выравнивания Ekos обеспечивает высокоточные переходы с точностью до доли секунды дуги, а также может измерять и исправлять ошибки полярного выравнивания. Это возможно благодаря решателю astrometry.net. Ekos начинает с захвата изображения звездного поля, передачи этого изображения в решатель astrometry.net и получения центральных координат (RA, DEC) изображения. Решатель, по сути, выполняет распознавание образов в каталоге из миллионов звезд. Как только координаты определены, становится известно истинное наведение телескопа. Часто возникает несоответствие между тем, куда, по мнению телескопа, он смотрит, и тем, куда он указывает на самом деле. Величина этого несоответствия может варьироваться от нескольких угловых минут до пары градусов. Затем Ekos может исправить несоответствие, либо синхронизировавшись с новыми координатами, либо повернув монтировку к желаемой изначально запрошенной цели.
Как только координаты определены, становится известно истинное наведение телескопа. Часто возникает несоответствие между тем, куда, по мнению телескопа, он смотрит, и тем, куда он указывает на самом деле. Величина этого несоответствия может варьироваться от нескольких угловых минут до пары градусов. Затем Ekos может исправить несоответствие, либо синхронизировавшись с новыми координатами, либо повернув монтировку к желаемой изначально запрошенной цели.
Кроме того, Ekos может измерить смещение полярной оси, сделав пару снимков вблизи меридиана и к востоку/западу от меридиана. Это позволит пользователю регулировать крепление до тех пор, пока несоосность не будет сведена к минимуму.
Как минимум вам потребуется ПЗС/веб-камера и телескоп, который поддерживает команды Slew & Sync. Большинство популярных коммерческих телескопов в настоящее время поддерживают такие команды.
Для работы модуля Ekos Alignment Module у вас есть возможность использовать онлайн-решатель astrometry. net или автономный решатель. Онлайн-решатель не требует настройки, и в зависимости от пропускной способности вашего Интернета загрузка и решение изображения может занять некоторое время. Автономный решатель может быть быстрее и не требует подключения к Интернету. Чтобы использовать автономный решатель, вы должны установить astrometry.net в дополнение к необходимым индексным файлам. Если вы используете Ubuntu, вы можете установить его, выполнив следующую команду:
net или автономный решатель. Онлайн-решатель не требует настройки, и в зависимости от пропускной способности вашего Интернета загрузка и решение изображения может занять некоторое время. Автономный решатель может быть быстрее и не требует подключения к Интернету. Чтобы использовать автономный решатель, вы должны установить astrometry.net в дополнение к необходимым индексным файлам. Если вы используете Ubuntu, вы можете установить его, выполнив следующую команду:
sudo apt-get install astrometry.net
После установки astrometry.net необходимо загрузить и установить необходимые индексные файлы, подходящие для поля зрения вашего телескопа+ПЗС (FOV). Вам необходимо установить индексные файлы, охватывающие от 100% до 10% вашего FOV. Например, если ваше поле зрения составляет 60 угловых минут, вам необходимо установить индексные файлы, охватывающие метки неба от 6 угловых минут (10 %) до 60 угловых минут (100 %). Существует множество онлайн-инструментов для расчета FOV, например, калькулятор поля зрения Starizona.
| Имя файла индекса | FOV (угловые минуты) | Пакет Debian |
|---|---|---|
| индекс-4219.подходит для | 1400 — 2000 | астрометрические данные-4208-4219 |
| индекс-4218.подходит для | 1000 — 1400 | |
| индекс-4217.подходит для | 680 — 1000 | |
| индекс-4216.подходит для | 480 — 680 | |
| индекс-4215.подходит для | 340 — 480 | |
| индекс-4214.подходит для | 240 — 340 | |
| индекс-4213.подходит для | 170 — 240 | |
| индекс-4212.подходит для | 120 — 170 | |
| индекс-4211.подходит для | 85 — 120 | |
| индекс-4210.подходит к | 60 — 85 | |
| индекс-4209.подходит к | 42 — 60 | |
индекс-4208. подходит для подходит для | 30 — 42 | |
| индекс-4207-*.подходит для | 22 — 30 | астрометрические данные-4207 |
| индекс-4206-*.подходит для | 16 — 22 | астрометрические данные-4206 |
| индекс-4205-*.подходит для | 11 — 16 | астрометрические данные-4205 |
| индекс-4204-*.подходит для | 8 — 11 | астрометрические данные-4204 |
| индекс-4203-*.подходит для | 5,6–8,0 | астрометрические данные-4203 |
| индекс-4202-*.подходит для | 4,0–5,6 | астрометрические данные-4202 |
| индекс-4201-*.подходит для | 2,8–4,0 | астрометрические данные-4201-1 астрометрические данные-4201-2 астрометрические данные-4201-3 астрометрические данные-4201-4 |
| индекс-4200-*.подходит для | 2,0–2,8 | астрометрические данные-4200-1 астрометрические данные-4200-2 астрометрические данные-4200-3 астрометрические данные-4200-4 |
Пакеты Debian подходят для любого дистрибутива на основе Debian (Ubuntu, Mint и т. д.). Если вы загрузили указанные выше пакеты Debian для своего диапазона FOV, вы можете установить их из своего любимого менеджера пакетов или с помощью следующей команды:
д.). Если вы загрузили указанные выше пакеты Debian для своего диапазона FOV, вы можете установить их из своего любимого менеджера пакетов или с помощью следующей команды:
sudo dpkg -i astrometry-data-*.deb
С другой стороны, если вы загрузили индексные файлы FITS напрямую, скопируйте их в каталог /usr/share/astrometry .
Рекомендуется использовать менеджер загрузок как таковой DownThemAll! для Firefox для загрузки пакетов Debian, так как встроенный менеджер загрузки браузера может иметь проблемы с загрузкой больших пакетов.
Параметры выравнивания
Параметры выравнивания передаются решателю astrometry.net и Ekos каждый раз при захвате изображения:
- CCD : Выберите CCD для захвата с
- Воздействие : Продолжительность воздействия в секундах
- Bin X : Установка горизонтального бинирования ПЗС
- Bin Y : Установка вертикального бинирования ПЗС
- RA : Координаты RA шаблона поиска
- DEC : Координаты DEC шаблона поиска
- Радиус : Радиус в градусах шаблона поиска
- Параметры : Параметры, которые передаются решателю astrometry.
 net. Дополнительные сведения о параметрах см. на сайте astrometry.net .
net. Дополнительные сведения о параметрах см. на сайте astrometry.net . - Обновить координаты после поворота : Если этот флажок установлен, он будет автоматически обновлять значения RA и DEC для шаблона поиска решателя всякий раз, когда телескоп завершает успешный поворот/отслеживание.
- Предварительный просмотр : Если флажок установлен, отображать захваченное изображение FITS в инструменте FITSViewer.
- Verbose : Если флажок установлен, отображать подробную информацию в окне регистрации.
По умолчанию решатель будет искать по всему небу, чтобы определить координаты захваченного изображения. Это может занять много времени ; поэтому, чтобы ускорить решатель, вы можете ограничить его поиском только в пределах указанной области неба, обозначенной параметрами RA, DEC и Radius выше. Координаты RA и DEC Солвера могут обновляться автоматически всякий раз, когда монтировка успешно полностью поворачивается, если Обновление координат после проверки поворота . Кроме того, вы можете использовать значок копирования, чтобы скопировать координаты телескопа в параметры решателя. Хотя координаты телескопа, безусловно, будут отличаться от фактических координат цели (если вы уже не идеально выровнены!), они достаточно близки, чтобы решатель мог правильно их использовать.
Кроме того, вы можете использовать значок копирования, чтобы скопировать координаты телескопа в параметры решателя. Хотя координаты телескопа, безусловно, будут отличаться от фактических координат цели (если вы уже не идеально выровнены!), они достаточно близки, чтобы решатель мог правильно их использовать.
Режимы выравнивания
Ekos предоставляет два режима выравнивания:
GOTO
Используя режим GOTO, Ekos захватывает и решает изображение, и если решатель успешен, он может выполнять следующие действия:
- Синхронизация : Синхронизирует координаты телескопа с координатами решения.
- Поворот к цели : Синхронизирует координаты телескопа с координатами решения, а затем поворачивает к цели.
- Ничего : Просто решите изображение и отобразите координаты решения.
Полярное выравнивание
Используя режим полярного выравнивания, Ekos может измерять и исправлять ошибки полярного выравнивания. Чтобы измерить ошибку азимута, наведите монтировку на звезду, расположенную близко к меридиану. Если вы живете в северном полушарии, вы укажете гору на южный меридиан. Нажмите на Измерьте ошибку Az , чтобы начать процесс. Ekos попытается измерить дрейф между двумя изображениями и соответствующим образом рассчитает ошибку. Вы можете попросить Ekos исправить ошибку азимута, нажав кнопку Correct Az Error . Экос повернется в новое место и попросит вас отрегулировать ручки азимута монтировки, пока звезда не окажется в центре поля зрения. Вы можете использовать функцию «Кадрирование» модуля «Фокус», чтобы смотреть на изображение во время внесения корректировок.
Чтобы измерить ошибку азимута, наведите монтировку на звезду, расположенную близко к меридиану. Если вы живете в северном полушарии, вы укажете гору на южный меридиан. Нажмите на Измерьте ошибку Az , чтобы начать процесс. Ekos попытается измерить дрейф между двумя изображениями и соответствующим образом рассчитает ошибку. Вы можете попросить Ekos исправить ошибку азимута, нажав кнопку Correct Az Error . Экос повернется в новое место и попросит вас отрегулировать ручки азимута монтировки, пока звезда не окажется в центре поля зрения. Вы можете использовать функцию «Кадрирование» модуля «Фокус», чтобы смотреть на изображение во время внесения корректировок.
Аналогично, чтобы измерить ошибку высоты, нажмите кнопку Measure Alt Error . Вам нужно направить монтировку на восток или запад и установить соответствующее поле со списком Altitude Direction . Ekos сделает два изображения и рассчитает ошибку. Вы можете попросить Ekos исправить ошибку Altitude, нажав на кнопку Correct Alt Error . Как и в случае с азимутальной коррекцией, Ekos повернется в новое место и попросит вас отрегулировать ручки высоты монтировки, пока звезда не окажется в центре поля зрения.
Вы можете попросить Ekos исправить ошибку Altitude, нажав на кнопку Correct Alt Error . Как и в случае с азимутальной коррекцией, Ekos повернется в новое место и попросит вас отрегулировать ручки высоты монтировки, пока звезда не окажется в центре поля зрения.
После исправления рекомендуется снова измерить ошибки азимута и высоты и измерить разницу. Возможно, вам придется выполнить коррекцию более одного раза, чтобы получить оптимальные результаты.
Перейти к рабочему процессу
Используя модуль Ekos Alignment, выравнивание монтировки с помощью выравнивания контроллера по 1, 2 или 3 звездам не является строго обязательным, хотя для некоторых креплений рекомендуется выполнить приблизительное выравнивание по 1 или 2 звездам перед использованием выравнивания Ekos модуль. Если вы используете EQMod, вы можете сразу начать использовать модуль выравнивания Ekos. Типичный рабочий процесс для выравнивания GOTO включает следующие шаги:
- Установите монтировку в исходное положение (обычно NCP для экваториальной монтировки)
- Выберите Поворот к цели в опциях GOTO.

- Проверьте Обновить координаты после поворота в параметрах Plate Solver.
- Направление к ближайшей яркой звезде
- После завершения поворота нажмите Захват и решение
Если решатель будет успешным, Экос синхронизируется, а затем направится к звезде. Вы можете убедиться в этом, сделав снимок в модуле CCD. Вы можете повторить этот процесс по мере необходимости. Для таких драйверов, как EQMod, чем больше точек синхронизации вы добавляете в модель, тем лучше становится модель выравнивания.
Рабочий процесс полярного выравнивания
Прежде чем запускать инструмент Polar Alignment, вы должны выполнить описанный выше рабочий процесс GOTO хотя бы для одной точки на небе. После того, как ваше крепление выровнено, выполните следующее (при условии, что вы живете в северном полушарии):
- Направлен на яркую звезду (4-й величины или меньше) вблизи южного меридиана (азимут 180).
 Убедитесь, что выбран параметр Slew to Target . Захват и решить. Звезда должна быть точно по центру поля зрения вашей ПЗС.
Убедитесь, что выбран параметр Slew to Target . Захват и решить. Звезда должна быть точно по центру поля зрения вашей ПЗС. - Переключить режим на Выравнивание полюсов . Щелкните Измерить ошибку Az . Он попросит вас направиться к звезде на южном меридиане, что мы уже сделали, нажмите «Продолжить». Теперь Ekos выполнит расчет ошибки.
- Если все в порядке, ошибка отображается в полях вывода. Чтобы исправить ошибку, нажмите Исправить ошибку Az . Экос теперь повернется в другую точку неба, и вам потребуется ТОЛЬКО отрегулировать ручки азимута монтировки, чтобы центрировать звезду в поле зрения. Самый удобный способ наблюдения за звездным полем — перейти на 9-е место.0376 Модуль Focus и нажав Start Framing . Если ошибка по азимуту велика, звезда может быть не видна в поле зрения ПЗС, и поэтому приходится делать слепых подстроек (или просто смотреть в искатель) до тех пор, пока звезда не войдет в поле зрения ПЗС.

- Начинайте настройку азимута, пока яркая звезда, к которой вы изначально повернулись, не окажется настолько близко к центру, насколько это возможно
- Останов кадрирования в модуле Фокус.
- Повторите Measure Az Error , чтобы убедиться, что мы действительно исправили ошибку. Возможно, вам придется запустить его более одного раза, чтобы убедиться, что результаты действительны.
- Переключить режим на ПЕРЕЙТИ К .
- Теперь направьте на яркую звезду либо на восточном, либо на западном горизонте, предпочтительно выше 20 градусов над уровнем моря. Он должен быть как можно ближе к восточной (90° азимут) или западной (270°) сторонам света.
- После завершения уничтожения захватите и решите. Теперь звезда должна быть в мертвой точке поля зрения ПЗС.
- Переключить режим на Полярное выравнивание
- Щелкните Измерить альтернативную ошибку . Он попросит вас направиться к звезде либо на восток (азимут 90), либо на запад (азимут 270), что мы уже сделали, нажмите «Продолжить».
 Теперь Ekos выполнит расчет ошибки.
Теперь Ekos выполнит расчет ошибки. - Чтобы исправить ошибку, нажмите Исправить альтернативную ошибку . Экос теперь направится в другую точку неба, и вам потребуется ТОЛЬКО отрегулировать ручки высоты монтировки, чтобы центрировать звезду в поле зрения. Начните кадрировать, как это делалось ранее, в модуле фокусировки, чтобы помочь вам с центрированием.
- После завершения центрирования остановите кадрирование.
- Повторите Measure Alt Error , чтобы убедиться, что мы действительно исправили ошибку. Возможно, вам придется запустить его более одного раза, чтобы убедиться, что результаты действительны.
- Выравнивание полюсов завершено!
Крепление может повернуться в опасное положение, и вы рискуете задеть штатив и/или другое оборудование. Внимательно следите за движением крепления. Используйте на свой риск.
Новый способ обучения для повышения уровня преподавания
Знакомство с модулями ePyramid Представляем модель ePyramid, нашу программу онлайн-обучения для детей младшего возраста. Узнайте, как улучшить социально-эмоциональное развитие детей младшего возраста, не выходя из класса. Мы создали эти онлайн-курсы, которые облегчают найм и повторное обучение вашего персонала. Как и вся наша работа, курсы основаны на фактических данных и способствуют развитию отношений между персоналом и детьми. Каждый из наших курсов предоставляется по запросу, поэтому ваши сотрудники учатся в своем темпе.
Узнайте, как улучшить социально-эмоциональное развитие детей младшего возраста, не выходя из класса. Мы создали эти онлайн-курсы, которые облегчают найм и повторное обучение вашего персонала. Как и вся наша работа, курсы основаны на фактических данных и способствуют развитию отношений между персоналом и детьми. Каждый из наших курсов предоставляется по запросу, поэтому ваши сотрудники учатся в своем темпе.
Для получения дополнительной информации о содержании каждого модуля, [электронная почта защищена] или позвоните по телефону 406-698-5231.
Когортная помощь доступна для всех пакетов!
Мы рады предложить отдельным лицам или группам возможность присоединиться к когорте для получения виртуальных сеансов облегчения. Эти когорты предназначены для поддержки применения и внедрения практик ePyramid. За 329 долларов США на человека участники получат пакет обучения по вашему выбору с подключенным групповым коучингом. Мы отвечаем на часто задаваемые вопросы (FAQ) по ePyramid и Cohort Coaching здесь .
Эти когорты предназначены для поддержки применения и внедрения практик ePyramid. За 329 долларов США на человека участники получат пакет обучения по вашему выбору с подключенным групповым коучингом. Мы отвечаем на часто задаваемые вопросы (FAQ) по ePyramid и Cohort Coaching здесь .
Чтобы получить дополнительную информацию или записаться на когорту, свяжитесь с Эрин Каланик, [адрес электронной почты защищен] или позвоните по телефону 406-698-5231 .
Руководство лидера эпирамидыРуководство по лидерам дошкольного возраста PDF
Руководство по лидеру младенцев/лидера. Руководство PDF
Доступны несколько курсов модуля ePyramid:
Этот курс рассчитан на 18 контактных часов.
Модуль 1: Социально-эмоциональное развитие в контексте отношений
Содержание Включает:
- Понимание важности социально-эмоционального развития и того, как оно проявляется в младенчестве и раннем возрасте.

- Что такое социально-эмоциональное развитие?
- Принимая во внимание основополагающий характер раннего опыта отношений.
- Формирование и поддержание отношений с маленькими детьми, семьями и коллегами.
- Определение стратегий чуткого ухода, которые взрослые могут использовать для поддержки младенцев и детей ясельного возраста.
Модуль 2: Реагирующие процедуры, среда и целевые стратегии
Содержание включает:
- Определение того, как высококачественная поддерживающая среда может способствовать социально-эмоциональному развитию младенцев и детей ясельного возраста.
- Изучение того, как окружающая среда может помочь оказать поддержку и предотвратить нежелательное поведение.
- Целевые стратегии для улучшения социально-эмоционального благополучия младенцев и детей ясельного возраста.
- Понимание положительного воздействия чуткого режима ухода и хорошо продуманной среды обучения.

Модуль 3: Индивидуальное вмешательство: определение значения поведения и выработка соответствующих ответов
Содержание включает:
- Обзор поддержки позитивного поведения
- Обзор аспектов общения: форма и функция
- Рассмотрение поведения, в том числе проблемного поведения, как коммуникации
- Введение в функциональную оценку
- Понимание развития планирования поддержки поведения
Этот курс рассчитан на 18 контактных часов.
Модуль 1: Построение отношений и создание благоприятной среды
Содержание включает:
- Понимание взаимосвязи между вызывающим поведением и социально-эмоциональным развитием
- Изучение наше отношение к сложному поведению
- Построение положительных отношений
- Проектирование физической среды
- Графики, процедуры и переходы
- Планирование, которые способствуют участию
- .

Модуль 2: Стратегии социально-эмоционального обучения
Содержание включает:
- Определение важности преподавания социальных эмоциональных навыков
- Разработка дружбы
- Улучшение эмоциональной грамотности
- КОНТРОЛЬНЫЙ ГНЕЙ И ИМПУЛИСА
- Развивая навыки решения проблем
- Индивидуализация Индивидуализации
- , партнеры
- Индивидуализация.
Модуль 3: Индивидуальное вмешательство; Определение смысла поведения и выработка соответствующих ответов
Содержание включает:
- Обзор поддержки позитивного поведения
- Анализ аспектов общения: форма и функция
- Рассмотрение поведения, включая вызывающее поведение, как общение
- Введение в функциональную оценку
- Понимание развития планирования поддержки поведения
Этот курс рассчитан на 18 контактных часов.
Модуль 1: Построение отношений и создание благоприятной среды
Содержание включает:
- Понимание взаимосвязи между сложным поведением и социально-эмоциональным развитием
- Что такое социально-эмоциональное развитие?
- Принимая во внимание фундаментальный характер раннего опыта отношений.

- Формирование и поддержание отношений с маленькими детьми, семьями и коллегами.
- Определение стратегий чуткого ухода, которые взрослые могут использовать для поддержки младенцев и детей ясельного возраста.
- Изучение нашего отношения к проблемному поведению
- Планирование физической среды
- Расписания, рутины и переходы
- Планирование деятельности, способствующей вовлеченности
- Указание указаний и обучение правилам в классе 902 Позитивное внимание
- Постоянное наблюдение и внимание
Модуль 2: Стратегии обучения социально-эмоциональным навыкам
Содержание включает:
- Определение важности обучения социально-эмоциональным навыкам
- Определение того, как высококачественная поддерживающая среда может способствовать социально-эмоциональному развитию младенцев и детей ясельного возраста.
- Целевые стратегии для улучшения социально-эмоционального благополучия младенцев и детей ясельного возраста.

- Понимание положительного воздействия чуткого ухода за больными
- Развитие навыков дружбы
- Повышение эмоциональной грамотности
- Контроль гнева и импульсивности
- Развитие навыков решения проблем
- Индивидуальные инструкции0197
- Партнерство с семьями
Модуль 3: Индивидуальное вмешательство: определение значения поведения и выработка соответствующих ответов
Содержание включает:
- Обзор поддержки позитивного поведения
- Обзор аспектов общения: форма и функция, включая проблемное поведение,
- в качестве сообщения
- Введение в функциональную оценку
- Понимание разработки планирования поддержки поведения
Este curso es de 18 horas presenciales.
Módulo 1: Construción de Relaciones y Creación de Ambientes de Apoyo Favorabals
El Contenido Incluye:
- Комборство eReciOn eRemiOLOLOLOLOLESLOLOLOLESOLOLESOLOLESOLOLES
- Комградер LAE RECION ENTRE
- SOCION1.

- Учтите, что основные принципы отношений между временными отраслями
- Formar y mantener relaciones con sus niños y niñas pequeños, familias y compañeros de trabajo
- Identificar estrategias que brindan atención receptiva que los Adultos pueden usar para apoyar a los bebes, niaspeños y nios.
- Examinar nuestras actitudes sobre los comportamientos dificiles.
- Diseñar el entorno físico
- Rutinas, Horarios y Transiciones
- Planificar actividades que promuevan la participación
- Dar instrucciones y enseñar las reglas de la clase
- Monitoreo continuo y atención positiva
Módulo 2: Estrategias de enseñanza socioemocionales
CEl contenido incluye:
- Identificar la importancia de la enseñanza de habilidades socioemocionales
- Identificar formas de apoyo de los entornos de alta calidad para el desarrollo de los bebés, niños y niñas pequeños
- Estrategias dirigidas a mejorar el bienestar socie-emocional de bebes, niños y niñas pequeños.

- Comprender el impacto positivo de relaciones responsivas positivas
- Desarrollo de habilidades de amistad
- Mejorar la alfabetización emocional de los niños y niñas pequeños
- Regular la ira y los impulsos
- Desarrollar habilidades para resolver problemas
- Individualizar la instrucción
- Сотрудничество с семьями
Модули 3: Индивидуальное вмешательство: определение важности соответствия и выяснения надлежащих ответов
El contenido incluye:
- Descripción general de apoyos para un comportamiento positivo
- Revisar las dimensiones de la comunicación: Forma y Función
- Consideración del comportamiento como medio de comunicación
- Proporcionar una introducción a la evaluación funcional
- Comprender el Desarrollo de la Conducta para una planificación de apoyo
Этот курс рассчитан на 8 контактных часов.

Эти модули помогут пользователю пройти обучение по модели пирамиды раннего вмешательства. Они помогут вам определить и понять практики Модели пирамиды в контексте раннего вмешательства/Часть C. Знания, которые вы приобретете из этих модулей, помогут вам понять, что представляют собой практики Модели пирамиды в раннем вмешательстве и как их использовать. с большим намерением на протяжении всей вашей работы с семьями. Модули предназначены для всех, кто работает и тренирует семьи с младенцами и детьми младшего возраста. Практики, указанные в этом тренинге, согласуются с Инструментом верности практик раннего вмешательства, также известным как EIPPFI, который является инструментом, который может использоваться специалистами раннего вмешательства и коучами при наращивании потенциала персонала в использовании практик Модели пирамиды с точностью.
Этот курс рассчитан на 8 контактных часов.
Коучинг, основанный на практике (PBC) — это основанная на исследованиях система коучинга для поддержки практикующих специалистов в области раннего детства в использовании основанных на фактических данных методов обучения.
Этот курс будет: В этих модулях мы рассмотрим, почему коучинг стал популярным средством поддержки профессионального развития, что такое коучинг, основанный на практике, и как PBC может быть реализован для поддержки внедрения эффективных практик.
В этих модулях мы рассмотрим, почему коучинг стал популярным средством поддержки профессионального развития, что такое коучинг, основанный на практике, и как PBC может быть реализован для поддержки внедрения эффективных практик.- Познакомить с моделью коучинга, основанного на практике
- Описать характеристики партнерских отношений
- Определить практики, на которых фокусируется коучинг, основанный на практике и практиковать целенаправленное наблюдение
- Выявлять ключевые особенности и практиковать поддерживающие размышления и обеспечивать обратную связь
Этот курс рассчитан на 5 контактных часов.
Онлайн-уроки «Уход с учетом травм и модель пирамиды» — это то, что вам нужно, чтобы учителя понимали влияние травмы на маленьких детей и их семьи.Добавление линзы «Уход с учетом травм» к вашим существующим практикам «Пирамида» поможет внедрить практики, способствующие социально-эмоциональному развитию, исцелению и устойчивости детей.
Преимущества лечения с учетом травм и модели пирамиды Онлайн-уроки:
- Помогает учителям понять влияние травмы на маленьких детей и их семьи, а также распознать признаки и симптомы травмы у маленьких детей.
- Обеспечивает понимание учителями предпосылок и принципов информированного ухода при травмах.
- Создает основу для поддержки устойчивости и восстановления детей.
- Поддерживает внедрение конкретных практик для учителей и семей для реализации практик Модели информированной помощи при травмах в раннем детстве.
Этот курс рассчитан на 2 контактных часа.
Оздоровление: Забота о себе Онлайн-уроки помогут персоналу:- Понять влияние благополучия взрослых на социально-эмоциональное развитие детей.
- Определите симптомы стресса, усталости от сострадания, вторичной травмы и заместительной травмы.
- Изучите стратегии снижения стресса и улучшения самочувствия.

- Узнайте, как внимательность может уменьшить стресс и улучшить самочувствие.
- Практикуйте осознанность.
- Разработайте план самообслуживания.
Это единственный инструмент, который вам нужен, чтобы помочь учителям понять связь между их собственным благополучием и поведением детей. Используйте эти уроки, чтобы предпринять шаги по улучшению самочувствия сотрудников вашей программы, что приведет к более качественному уходу за детьми. Онлайн-уроки «Здоровье: забота о себе» являются отличным дополнением к онлайн-урокам «Информационная помощь при травмах» и «Модель пирамиды».
Этот курс рассчитан на 2 контактных часа.
В этом модуле основное внимание уделяется важности практики, учитывающей культурные особенности, для улучшения результатов для всех детей, особенно детей из разных слоев общества. Роль неявного смещения будет обсуждаться. Участникам будут предложены различные виды деятельности для реализации 7 принципов культурно-чувствительных практик, которые помогают нам распознавать и выявлять скрытую предвзятость.
 Кроме того, участникам будут предложены идеи о том, как использовать ценности семьи и сообщества для обучения и обучения через призму модели пирамиды. Разработка этого модуля (2 часа) частично поддерживалась проектом Pyramid Equity Project в сотрудничестве с Университетом Южной Флориды, Университетом Колорадо в Денвере и Центром PBIS при финансировании национальной деятельности в рамках гранта на развитие дошкольных учреждений.
Кроме того, участникам будут предложены идеи о том, как использовать ценности семьи и сообщества для обучения и обучения через призму модели пирамиды. Разработка этого модуля (2 часа) частично поддерживалась проектом Pyramid Equity Project в сотрудничестве с Университетом Южной Флориды, Университетом Колорадо в Денвере и Центром PBIS при финансировании национальной деятельности в рамках гранта на развитие дошкольных учреждений.*Данный курс соответствует правилам штата Колорадо. Никакая информация в этом курсе не заменяет какие-либо правила или законы в вашем штате. Правила для всех штатов доступны на веб-сайте Национального ресурсного центра по охране здоровья и безопасности в сфере ухода за детьми и раннего образования (NRC). Нажмите на ссылку, предоставленную для просмотра правил в вашем штате.
Давайте учиться.
Купить курс
Как создать учебный модуль: пошаговое руководство
Хотите представить свою компанию как отличное место для трудоустройства? Откажитесь от чрезмерных удобств, таких как игровые комнаты и капсулы для сна, в пользу того, что действительно нужно сотрудникам.

Опрос молодых специалистов, проведенный компанией Deloitte, показал, что «возможность учиться» является одним из самых желанных преимуществ, которые может предложить работодатель. Чтобы сделать корпоративное обучение эффективным, крайне важно предоставить учащимся соответствующий контент.
В этой статье мы покажем вам, как создать учебный модуль, который будет поддерживать мотивацию и вовлеченность ваших сотрудников.
Содержание 1. Что такое учебный модуль? 2. Типы учебных модулей 3. Как разработать лучший учебный модуль, шаг за шагом 4. Шаг 1. Определите проблему 6. Шаг 3. Создайте учебный модуль правильного типа 7. Шаг 4. Соберите отзывы и пересмотрите 8. Шаг 5. Запустите пилотный учебный модуль с тестовой аудиторией 9.  Шаг 6. Создайте окончательную версию, загрузите и запустите
Шаг 6. Создайте окончательную версию, загрузите и запуститеЧто такое учебный модуль?
Учебный модуль — это компонент онлайн-курса , посвященный определенной цели и предназначенный для обучения по определенной теме. Каждый модуль подобен главе книги, ведущей к следующей. В целом учебные модули составляют целый пласт знаний и рассказывают законченную историю.
Так же, как сложный курс может состоять из нескольких модулей, каждый модуль может включать несколько уроков или учебных объектов, которые являются еще меньшими элементами образовательного контента.
Типы учебных модулей
Разнообразие типов контента позволяет создать более насыщенный и надежный учебный процесс для всех учащихся. Давайте более подробно рассмотрим различные типы модулей электронного обучения, чтобы понять, какие форматы лучше всего подходят для ваших конкретных потребностей.
1. Информационный электронный курс
Информационный курс — популярный формат обучения, обычно представляющий собой набор слайдов с текстом, картинками и кнопками «Далее».
 Это дает учащимся информацию по конкретной теме.
Это дает учащимся информацию по конкретной теме.Лучше всего подходит для
- Предоставление стандартизированных знаний или навыков широкой аудитории учащихся.
- Обучение сотрудников основным навыкам и знаниям.
- Срочное обучение, такое как адаптация, безопасность, осведомленность о безопасности или обучение соответствию требованиям.
- Предоставление информации о новом продукте, технологии или обновлении политики.
2. Интерактивное оценивание
Интерактивное оценивание — это тип онлайн-викторины, который включает различные типы вопросов, настраиваемые ответвления и сценарии.
Лучше всего подходит для
- Измерение уровня знаний учащихся в отношении их работы и/или способности применять знания.
- Создание тестов со встроенным обучением, чтобы помочь учащимся не сбиться с пути.
- Сложные задачи, требующие сертификации или сертификации.

- Подтверждение завершения обучения.
- Выявление учащихся, которым может потребоваться дополнительная поддержка.
- Выявление высокоэффективных сотрудников, которые могут быть кандидатами на повышение.
3. Взаимодействие с часто задаваемыми вопросами
Взаимодействие с часто задаваемыми вопросами — это обучающий модуль, который дает пользователям доступ одним щелчком мыши к справочной информации и часто задаваемым вопросам.
Лучше всего подходит для
- Создание стандартного формата для организации и представления основной информации.
- Глоссарии, определения или другие факты базового уровня знаний.
- Просмотр сведений о предмете в формате вопросов и ответов.
- Предоставление информации, являющейся дополнительной к основному содержанию курса.
4. Видеолекция и скринкаст
- Видеолекция — это обучающее видео, которое было записано и сохранено для просмотра в будущем.

Лучше всего подходит для
- Предоставление большой аудитории учащихся доступа к конкретному уроку или выступлению.
- Стандартизация процесса обучения для определенной темы или события.
- Скринкаст — это видеозапись действий, происходящих на экране.
Лучше всего подходит для
Учебники для демонстрации основных бизнес-задач, таких как доступ к программам, навигация по онлайн-системе или заполнение форм.
5. Симуляция диалога
Симуляция диалога помогает вашим учащимся развивать коммуникативные навыки, применяя свои знания в реальных беседах с коллегами и клиентами.
Лучше всего подходит для
- Обучение обслуживанию клиентов и продажам, позволяющее учащимся отрабатывать сценарии развития отношений с клиентами и заключения сделок.
- Обучение руководителей, сотрудников отдела кадров и других лиц, которым необходимо предоставлять конфиденциальную информацию подчиненным или членам команды.

- Обучение коучей и инструкторов, которые должны систематически передавать информацию отдельным лицам или аудитории.
6. Модуль микрообучения
Модуль микрообучения — это небольшой урок, который дает целенаправленный ответ на одну проблему или вопрос. Такой учебный модуль обычно можно пройти примерно за пять минут в момент необходимости. Если он слишком длинный, лучше разбить его на более мелкие части.
Лучше всего подходит для
- Онлайн-обучение в свободное время и немедленное применение новых знаний на практике
- Прохождение курсов на ходу на смартфоне или планшете
- Очень быстрое предоставление информации о новых продуктах или услугах, обновленной политике или новых условиях
- Предоставление основ темы до очных учебных занятий или во время Тематические обсуждения с участием одного человека
7. Цифровая инструкция по работе
Цифровая инструкция по работе — это документ или презентация, которые доступны виртуально и могут быть воспроизведены, загружены, сохранены или распечатаны учащимся.

Лучше всего подходит для
- Любой учащийся, желающий сохранить документ в цифровом формате на своем компьютере, мобильном устройстве или на внутреннем диске.
- Руководства, руководства, инструкции, статьи с практическими рекомендациями, процессы, процедуры и другие ресурсы, которые могут понадобиться людям для выполнения их работы.
Читайте также : → 5 видов обучения сотрудников
Как разработать лучший учебный модуль, шаг за шагом
Давайте рассмотрим, как можно поэтапно построить учебный модуль. Имейте в виду, что начальные шаги больше касаются подготовительной работы, а не процесса создания фактических учебных модулей. Однако они закладывают основу для успешной реализации проекта. Так что не пропускайте их.
Посмотрите это видео или прочитайте статью о передовых методах создания учебного модуля.
ispringsolutions.com» data-lf-yt-playback-inspected-3p1w24dxzbj4my5n=»true» data-lf-yt-playback-inspected-3p1w24dxpbg4my5n=»true» data-gtm-yt-inspected-11=»true»>Шаг 1: Определите проблему
Первое правило успешного обучения: Решите правильную бизнес-задачу!
Отправной точкой качественного обучения является общение. Чтобы решить бизнес-проблему, вам нужно понять проблему и то, как она влияет на производительность на рабочем месте. Одним из первых шагов в создании учебного модуля является задавание подробных и наводящих открытых вопросов, чтобы выяснить:
- Какова природа решаемой проблемы?
- Какие знания или навыки необходимы для преодоления этого разрыва?
- Каков фактический уровень знаний или производительности ваших сотрудников?
- Каков ожидаемый уровень знаний или производительности ваших сотрудников по этой теме?
Ответы, которые вы получите, обеспечат четкое понимание бизнес-проблемы и помогут вам установить цели обучения для вашего учебного курса и модулей.

Шаг 2: Напишите цель SMART
Цель или задача обучения подтверждают причину обучения и сообщают о направленности учебного модуля. В цели должны быть указаны навыки, знания или преимущества, которые учащийся получит в результате прохождения этого модуля. Для достижения наилучших результатов мыслите SMART и поставьте цель, которая будет:
- Конкретная – учащийся знает, что он узнает или сможет сделать после окончания учебного модуля;
- Измеримый – учащиеся будут последовательно использовать эти знания для каждого отчета;
- Достижимый – учащийся сможет выполнять задачи, перечисленные в учебном модуле;
- Релевантный – учебный модуль будет сосредоточен на основных знаниях и навыках работы;
- Своевременно – учащийся сможет завершить учебный модуль своевременно.

SMART-цель будет мотивировать сотрудника, показывая ему, «что в этом для меня» в этом учебном модуле.
Шаг 3: Создайте правильный тип учебного модуля
После того, как вы изучите проблему и определите свою цель, вы готовы создать учебный модуль!
Секрет успешного обучения заключается в том, чтобы правильно подобрать модуль к поставленной учебной задаче. На приведенной ниже диаграмме различные типы модулей онлайн-обучения приведены в соответствие с потребностями в обучении.
Типы контента электронного обучения для конкретных учебных потребностей Учебные/организационные навыки или потребность Recommended eLearning Solutions - Job knowledge
- Compliance and safety
- Onboarding
- E-course
- Interactive assessment
- Townhall meetings
- Видеолекция
- Процессы или процедуры
- Ресурсы «Как сделать»
- FAQ interaction
- Screencast
- E-Book
- Hands-on interaction
- Product knowledge training
- E-course
- Video lecture
- Webinar
- Обучение программному обеспечению и системам
- Скринкасты
- Практическое взаимодействие
- Видеоруководство
- Sales and customer service training
- Soft skills
- Leadership development
- Video lecture
- Dialogue simulation
- Podcast
- Proof of competency or skills achievement
- Сертификация
- Интерактивная оценка
В начале этой статьи мы предоставили подробное описание различных типов учебных модулей.
 Теперь мы покажем примеры учебных модулей и объясним, как их легко создавать с помощью iSpring Suite Max.
Теперь мы покажем примеры учебных модулей и объясним, как их легко создавать с помощью iSpring Suite Max.iSpring — это простой в использовании инструментарий для разработки электронного обучения, который включает в себя целый ряд надежных инструментов и мощных функций. Это помогает преподавателям создавать интерактивный учебный контент и повышать вовлеченность и производительность учащихся.
Пример информационного электронного курса
Как создать такой учебный модуль
iSpring Suite Max можно использовать для:
- создания курсов с нуля или
- превращения презентаций PowerPoint в полнофункциональные модули электронного обучения.
iSpring также предоставляет возможность создавать тесты, видеоролики, взаимодействия и симуляции разговоров, которые можно рассматривать как единый учебный модуль.
Пример интерактивного оценивания
Как создать такой учебный модуль
С помощью iSpring Suite вы можете:
- Создавать надежные оцениваемые оценивания с различными типами вопросов, включая множественный выбор, верно или неверно, заполнение пробелов, перетаскивание, сопоставление и упорядочивание.

- Добавьте к своим вопросам видео и мультимедийные материалы.
- Создавайте обратную связь на уровне вопросов или ответов и разветвления, чтобы предоставить каждому учащемуся индивидуальное обучение.
- Автоматически оценивайте результаты учащихся и отправляйте их на адреса электронной почты инструктора и учащихся или на сервер.
Пример взаимодействия с часто задаваемыми вопросами
Как создать такой учебный модуль
iSpring Suite Max включает шаблон часто задаваемых вопросов, который можно настроить в соответствии с вашими потребностями. Вы можете представить взаимодействие часто задаваемых вопросов в виде серии вопросов и ответов или списка тем и деталей. Добавьте ключевые слова в свои темы, чтобы улучшить функциональность поиска в учебном модуле.
В дополнение к шаблону часто задаваемых вопросов iSpring Suite предлагает еще 11 готовых шаблонов для создания взаимодействий, включая временные рамки, справочники, глоссарии и каталоги, которые отлично отображаются на всех устройствах.

Пример видеолекции
Как создать такой обучающий модуль
Видеостудия iSpring позволяет делать видео профессионального качества, записывая экран, веб-камеру или оба потока вместе. Вы можете дополнить свою видеолекцию и скринкаст изображениями, инфографикой и подписями. Студия также позволяет легко микшировать видео и сопровождать их музыкой или голосом за кадром.
Пример имитации диалога
Как создать такой учебный модуль
С помощью iSpring Suite вы можете:
- Создавать диалоговые сцены с разветвленными сценариями.
- Добавьте фоны и персонажей из библиотеки содержимого iSpring, чтобы создать реалистичную среду.
- Добавьте голос за кадром к речи персонажа, чтобы полностью имитировать реальный диалог.
- Измерение результатов моделирования.
Пример модуля микрообучения
Посмотреть полный модуль обучения →
Как создать такой модуль обучения
С помощью iSpring Suite вы можете:
- Создавать адаптивные микрокурсы онлайн почти так же, как вы пишете пост в социальных сетях
- Добавить проверку знаний с помощью трех типов вопросов к учебному модулю: множественный выбор, множественный ответ и краткий ответ
- Совместная работа над учебными модулями онлайн с вашей командой
- Хранение всего учебного контента в едином онлайн-пространстве
Пример цифрового пособия по работе
Как создать такой учебный модуль
С помощью iSpring Suite Max вы можете быстро превратить любые документы Word, презентации PPT или PDF-файлы в электронные книги с эффектом перелистывания страниц .
 Такие электронные книги обеспечивают приятное чтение на iPad и других мобильных устройствах.
Такие электронные книги обеспечивают приятное чтение на iPad и других мобильных устройствах.Шаг 4: обратная связь и пересмотр
После небольшой работы с вашей стороны первая версия учебного модуля готова! Теперь пришло время направить ваш первый проект экспертам в предметной области (SME) и заинтересованным сторонам для отзывов и одобрения. Не удивляйтесь, если ваши партнеры оставят много отзывов о ваших первоначальных усилиях! Даже если вы усердно выполняли все рекомендации ваших малых и средних предприятий и заинтересованных сторон, вы можете обнаружить, что у них все еще есть дополнительная информация, которой они могут поделиться с вами после просмотра первого проекта вашего учебного модуля.
Чтобы не попасть в бесконечную петлю обратной связи, большинство команд L&D будут следовать трехэтапному протоколу проектирования, известному как альфа/бета/золото:
- Первый вариант учебного модуля известен как альфа-проект. Опытный педагог-дизайнер должен быть в состоянии создать альфа-версию, которая на 75-80% правильна.
 Как правило, именно здесь вы получите наибольшее количество отзывов от своих МСП.
Как правило, именно здесь вы получите наибольшее количество отзывов от своих МСП. - Пересмотренная вторая версия учебного модуля известна как бета-версия. Если вы получили качественную обратную связь от вашего эксперта во время первого раунда, ваша бета-версия учебного модуля должна быть около 9Точность 5-98%. Таким образом, у вас должно быть гораздо меньше ревизий на этом этапе.
- Окончательный вариант называется золотой версией. Если ваши малые и средние предприятия не упустили важную информацию в предыдущих раундах проверки, золотая версия должна быть правильной на 99–100%. Обзор золотого проекта со стороны МСП и заинтересованных сторон должен произойти быстро. Когда ваши партнеры подпишут золотую версию вашего учебного модуля, у вас будет отличный учебный контент, готовый для учащихся.
Шаг 5. Запустите пилотный проект с тестовой аудиторией
Рекомендуется запускать пилотную версию любого нового обучения, прежде чем запускать его в своей организации.
 Основная функция пилотного тестирования состоит в том, чтобы обеспечить дополнительный уровень проверки и показать, способны ли учащиеся достичь поставленных целей.
Основная функция пилотного тестирования состоит в том, чтобы обеспечить дополнительный уровень проверки и показать, способны ли учащиеся достичь поставленных целей.Для начала выберите тестовую аудиторию, состоящую из небольшой группы сотрудников вашей компании. Для достижения наилучших результатов ваша аудитория не должна обладать высоким уровнем знаний по вашей теме и может пройти обучение, не имея заранее представлений о том, на что оно должно быть похоже.
Соберите отзывы от тестовой аудитории. Узнайте, что, по их мнению, лучше всего работает в обучении, а что можно улучшить. Если тестовая аудитория не может достичь намеченных целей после завершения учебного модуля, просмотрите результаты оценки, чтобы увидеть, какие пробелы могут существовать. Работайте с вашими малыми и средними предприятиями и заинтересованными сторонами, чтобы найти способы заполнить пробелы и улучшить общий опыт обучения и ваш учебный модуль как таковой.
Шаг 6. Создайте окончательную версию, загрузите и запустите
На этом этапе вы готовы создать «окончательную финальную» версию своего учебного модуля и загрузить ее в систему управления обучением (LMS).
 Возможно, вы захотите поработать со своими деловыми партнерами, менеджерами по изменениям или руководителями проектов, чтобы координировать официальное развертывание нового обучения.
Возможно, вы захотите поработать со своими деловыми партнерами, менеджерами по изменениям или руководителями проектов, чтобы координировать официальное развертывание нового обучения.Вы также можете предоставить подробные отчетные данные о потреблении и результатах обучения через 30, 60 и 90 дней после запуска вашей программы. Отслеживание данных по показателям производительности на рабочем месте — отличный способ показать влияние обучения на развитие сотрудников и реальную производительность труда.
Выводы по созданию учебного модуля
- Первое общее правило успешного обучения, которому вы должны строго следовать: Решите правильную бизнес-задачу!
- Цели обучения SMART являются конкретными, измеримыми, достижимыми, актуальными и привязанными ко времени.
- Секрет успешного обучения заключается в том, чтобы правильно подобрать модуль для учебной задачи. Избегайте стремления сделать так, чтобы все ваши модули онлайн-обучения выглядели, звучали или ощущались одинаково.
 Попробуйте разные стили.
Попробуйте разные стили. - Используйте средства обучения: авторский инструмент, такой как iSpring Suite, для создания увлекательных учебных материалов и LMS для управления обучением.
- Участие МСП, обратная связь и пересмотр являются важными частями процесса создания учебного модуля.
- Настройте пилотную программу, чтобы «опробовать» новый тренинг для выбранной аудитории, прежде чем сделать его доступным для всей организации.
Обучение никогда не бывает одноразовым. Организации всегда жаждут улучшений, поэтому срок годности даже самого лучшего электронного обучения может составлять от нескольких месяцев до чуть более года. Проверяйте правильность всех своих учебных модулей не реже двух раз в год; ожидайте, что вам придется либо обновлять, либо полностью пересматривать свои учебные модули на ежегодной основе.
У вас все еще нет iSpring Suite Max? Загрузите это программное обеспечение для создания курсов бесплатно прямо сейчас и начните создавать увлекательные учебные модули прямо сейчас!
Если вам нужна надежная и простая в использовании LMS, получите пробную версию iSpring Learn или запросите демонстрацию!
Алгебра ясно объясняется в бесплатных онлайн-уроках
Перейти к основному содержанию
- Демо MathHelp.
 com
com - Регистрация MathHelp.com
- Логин
Purplemath
Нужна помощь по алгебре?
Попробуйте уроки Purplemath ниже!MathHelp.com
Индивидуальные курсы алгебры с учителем!
Уроки Purplemath составлены таким образом, чтобы их можно было изучать любым способом, который учащийся считает наиболее полезным. Разные учебники охватывают разные темы в разном порядке. Уроки Purplemath стараются не предполагать какой-либо фиксированный порядок тем, чтобы любой ученик, независимо от учебника, мог извлечь из этого пользу.
Ниже уроки Purplemath перечислены в группах в соответствии с общими значениями алгебры «начальный», «средний» и «продвинутый». Если вы не знаете, где найти нужную тему, воспользуйтесь полем «Поиск» выше.
Перейти к списку уроков «в порядке изучения»
Предварительные темы
- Абсолютное значение
- Факторинговые номера
- Дроби
- Геометрические формулы
- LCM и GCF
- Метрические преобразования
- Отрицательные числа
- Основы счисления
(двоичный, восьмеричный и т. д.)
д.) - Свойства номера
(дистрибутивная, ассоциативная, коммутативная и т. д.) - Типы номеров
(натуральное, целое, действительное и т. д.)
- Преобразование десятичных дробей, дробей и процентов
- Место Значение
- Римские цифры
- Округление (и значащие цифры)
- Установить обозначение
MathHelp.com
Индивидуальные курсы алгебры с учителем!
Начальные темы по алгебре
- Отмена единиц
- Формула расстояния
- Технические обозначения
- Оценка
- Экспоненты:
- Основные правила
- Отрицательные показатели
- Дробные показатели степени
- Обзор графика
- График абсолютного значения
- Графики линейных уравнений
- График радикальных уравнений
- Графики линейных неравенств
(вида «y < 2x + 3") - Обзор неравенств
(три метода решения) - Перехваты
- Формула средней точки
- Порядок действий
- Многочлены
(определения и «подобные термины») - Полиномы: сложение и вычитание
- Многочлены: умножение
- Многочлены: деление
- Радикалы
(квадратный корень, кубический корень, рационализирующие знаменатели и т. д.)
д.) - Соотношение и пропорция
- Диаграммы рассеяния и регрессии
- Научное обозначение
- Простой факторинг
например «2x + 6 = 2(x + 3)» - Упрощение с экспонентами
- Упрощение в скобках
- Наклон прямой
- Наклон и построение графика
- Наклон и точка пересечения с осью Y
(их значение в контексте текстовых задач) - Решение абсолютных значений
- Решение линейных неравенств
(например, «2x < 4") - Уравнения
- Решение линейных уравнений
- Решение буквенных уравнений
- Решение радикальных уравнений
- Уравнения прямых
(у = мх + б) - Переменные
- x, y-Плоскость
(точки построения и т. д.)
д.)
Темы алгебры среднего уровня
- Заполнение квадрата:
- круги
- эллипсы
- решение квадратичных уравнений
- найти вершину
- Правило знаков Декарта
- Домен и диапазон
- Четные и нечетные функции
- Фактор Теорема
- Факторные полиномы
- Факторинг Квадратика
- Нахождение полиномов по их нулям
- Обозначение функций
- Функции
- Преобразование функций
- Квадратичный график
- Уравнения
- Получение формулы вершины
- Графики систем линейных неравенств
- Неравенства: абсолютное значение
- Неравенства: квадратное
- Линейное программирование
- Численное приближение нулей
- Операции над функциями
- Кусочные функции:
- определение
- графическое изображение
- Полиномиальные графики
- Тест рациональных корней
- Теорема об остатках
- Квадратичная формула
- Получение квадроцикла.
 Формула
Формула
- Получение квадроцикла.
- Последовательности и серии
- Решение многочленов
- Решение квадратных уравнений
- Решение систем нелинейных уравнений
- Специальные формулы факторинга (разность квадратов, суммы и разности кубов и т. д.)
- Симметрия
- Синтетический отдел
- Вариация (прямой, обратный и совместный)
- Тест вертикальной линии
Дополнительные темы по алгебре
- Асимптоты
- Биномиальная теорема
- Сложные дроби
- Комплексные числа
- Состав функций
- Коники: Обзор
- Параболы
- Круги
- Эллипсы
- Гипербола
- Правило Крамера
- Детерминанты
- Экспоненты
- Графики экспоненциальных уравнений
- Графики логарифмических уравнений
- Графики рациональных уравнений
- Индукционные доказательства
- Неравенства: многочлен
- Неравенства: рациональные выражения
- Обратные функции
- Логарифмы
- Правила журнала
- Определения матриц
- Матричное сложение и вычитание
- Умножение матриц
- Операции со строками матрицы
- Инверсия матрицы
- Миноры и кофакторы
- Следующий номер в последовательности
- Разложение на неполные доли
- Рациональные выражения: упрощение
- Рациональные выражения: добавление
- Рациональные выражения: умножение
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- Решение рациональных уравнений
- Решающие системы
- Линейные уравнения
Решение словесных задач
Перевод: Как перевести текстовые задачи с английского языка в математические уравнения
- «возрастные» текстовые задачи
- «площадь/объем/периметр»
задачи по геометрии - «монета» (деньги) проблемы
- «расстояние»
d = rt словесные задачи - «инвестиции»
простые проценты I = Prt - проблемы со «смесью»
- «число» (целое число) задач
- «рабочие» проблемы
- Решающие задачи со словами
- Экспоненциальные и логарифмические задачи
- «Процент» словесных задач
(включая проблемы с увеличением/уменьшением) - Квадратичные задачи со словами
(включая движение снаряда) - Текстовые задачи на системы уравнений
Приложение
- «Действительно ли Библия
- сказать «π = 3»
- Диаграммы прямоугольной формы
- Факториалы
- Как 0,999.
 .. = 1?
.. = 1?
Форматирование математики как текста
(как вводить математику при отправке сообщений по электронной почте или размещении вопросов на форумах по обучению)- Как рассчитать мою оценку?
- Среднее значение, медиана и мода
- Вступительные тесты
- Участки со стеблями и листьями
- Диаграммы Венна
- Почему я должен сдавать алгебру?
…и начало триггера
- Расширенные графики триггеров
- Углы возвышения/отклон.
- Основные тригонометрические соотношения
- Конвенции
- Оценка с использованием идентификаторов
- Греческие буквы и их названия
- Обратные коэффициенты триггера
- Подтверждение личности триггера
- Теорема Пифагора
- Квадранты и углы
- радианы и градусы
- Пробы слов прямоугольного треугольника
- Секторы, области и дуги
- Решение триггерных уравнений
- Специальные значения углов
- Триггерные функции и графики
- Тригонометрические тождества
- Единичный круг
URL: https://www.
 purplemath.com/modules/index.htm
purplemath.com/modules/index.htmмодулей STEP Support Foundation | Программа поддержки STEP
перейти к содержанию- Учеба в Кембридже
- Бакалавриат
- Курсы
- Применение
- Мероприятия и дни открытых дверей
- Сборы и финансы
- Студенческие блоги и видео
- Выпускник
- Почему Кембридж
- Квалификация каталог
- Как подать заявку
- Сборы и финансирование
- Часто задаваемые вопросы вопросы
- Международный ученики
- Непрерывное образование
- Исполнительное и профессиональное образование
- Курсы по образованию
- Об университете
- Как Университеты и колледжи работают
- История
- Посещение университета
- Даты семестра и календари
- карта
- Для СМИ
- Видео и аудио
- Найти эксперта
- Публикации
- Международный Кембридж
- Новости
- События
- Взаимодействие с общественностью
- Работа
- Отдача в Кембридж
- Исследования в Кембридже
- Для персонала
- Для текущих студентов
- Для выпускников
- Для бизнеса
- Колледжи и факультеты
- Библиотеки и удобства
- Музеи и коллекции
- Электронная почта и поиск по телефону
Поддержка STEP — Назначение 1
Этот модуль включает в себя некоторые алгебраические манипуляции и некоторую работу над квадратными уравнениями.
 Есть также вопрос по геометрии с неожиданным результатом.
Есть также вопрос по геометрии с неожиданным результатом.Подробнее
Поддержка STEP — Задание 2
Этот модуль включает в себя еще немного алгебры, рисование графиков и нахождение максимальных и минимальных значений некоторых функций.
Читать дальше
Поддержка STEP — Задание 3
Этот модуль включает в себя некоторую работу с сериями, введение в функцию «пола» и линейное диофантово уравнение.
Подробнее
Поддержка STEP — Задание 4
Этот модуль включает в себя доказательство теоремы о круге, наброски неравенств с двумя переменными и пару логических головоломок. Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Подробнее
Поддержка STEP — Задание 5
Этот модуль включает в себя некоторую тригонометрию и вопрос о тетраэдре (и вопрос о носках!).
 Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.Подробнее
Поддержка STEP — Задание 6
Этот модуль охватывает механизмы и некоторые проблемы с вероятностью. Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Подробнее
Поддержка STEP — Задание 7
Этот модуль включает в себя наброски графиков и работу над корнями уравнений. Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Подробнее
Поддержка STEP — Задание 8
Этот модуль знакомит с неравенством AM-GM и пересечениями окружностей и эллипсов. Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Подробнее
Поддержка STEP — Задание 9
Этот модуль включает в себя некоторые доказательства с использованием треугольников и рисунков кубов.
 Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.Читать дальше
Поддержка STEP — Назначение 10
Этот модуль выводит некоторые сложные формулы тригонометрии ($\sin(\alpha + \beta)$ и т.д.) и вводит новую функцию. Предыдущие задания можно найти здесь, но вы можете выполнить это, не выполняя сначала другие.
Подробнее
Загрузить надстройку Solver в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel для iPhone Excel для планшетов с Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов с Android Excel Mobile Дополнительно…Меньше
Надстройка «Поиск решения» — это надстройка Microsoft Office Excel, доступная при установке Microsoft Office или Excel.
Однако, чтобы использовать надстройку Solver, ее сначала необходимо загрузить в Excel.

В Excel 2010 и более поздних версиях выберите Файл > Параметры
Примечание. Для Excel 2007 нажмите кнопку Microsoft Office , а затем выберите Параметры Excel .
Щелкните Надстройки , а затем в поле Управление выберите Надстройки Excel .
Нажмите Перейти .
В поле Доступные надстройки установите флажок Надстройка Solver и нажмите OK .

Примечания:
Если надстройка Solver не указана в списке Доступные надстройки , нажмите Обзор , чтобы найти надстройку.
Если появится сообщение о том, что надстройка Solver в настоящее время не установлена на вашем компьютере, нажмите Да , чтобы установить ее.
После загрузки надстройки Solver команда Solver доступна в Analysis на вкладке Данные .
- SOCION1.
В меню Инструменты выберите Надстройки Excel .
В поле Доступные надстройки установите флажок Надстройка Solver и нажмите OK .
Если надстройка Solver не указана в списке Доступные надстройки , щелкните Обзор , чтобы найти надстройку.
Если появится сообщение о том, что надстройка Solver в настоящее время не установлена на вашем компьютере, нажмите Да в диалоговом окне, чтобы установить ее.

После загрузки надстройки Solver 9Кнопка 0360 Solver доступна на вкладке Data .
Надстройка Solver от Frontline Systems в настоящее время недоступна для Excel на мобильных устройствах.
Solver — это бесплатная надстройка для Excel 2013 с пакетом обновления 1 (SP1) и более поздних версий. Для получения дополнительных сведений выполните поиск Solver в Магазине Office.
Надстройка Solver от Frontline Systems в настоящее время недоступна для Excel на мобильных устройствах.
Solver — это бесплатная надстройка для Excel 2013 с пакетом обновления 1 (SP1) и более поздних версий. Для получения дополнительных сведений выполните поиск Solver в Магазине Office.
Надстройка Solver от Frontline Systems в настоящее время недоступна для Excel на мобильных устройствах.
Solver — это бесплатная надстройка для Excel 2013 с пакетом обновления 1 (SP1) и более поздних версий.


 Уравнение становиться линейным.
Уравнение становиться линейным.
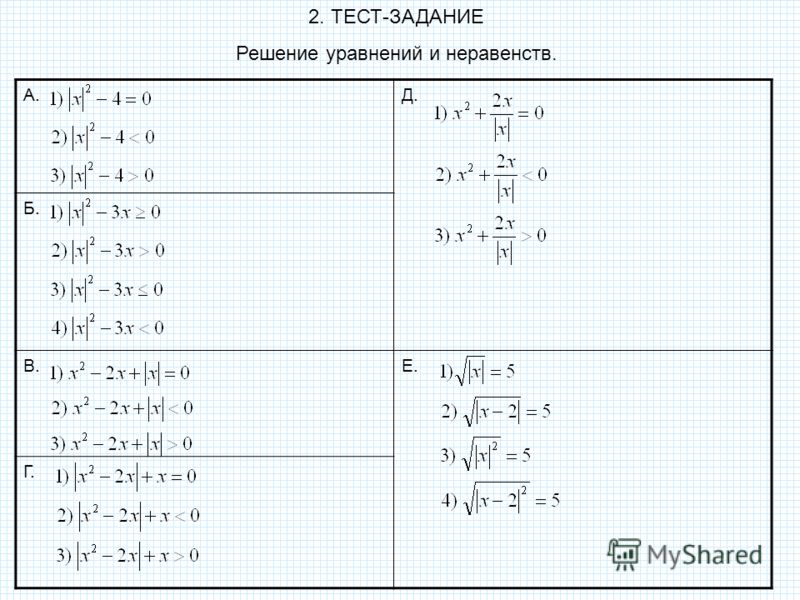 net. Дополнительные сведения о параметрах см. на сайте astrometry.net
net. Дополнительные сведения о параметрах см. на сайте astrometry.net
 Убедитесь, что выбран параметр Slew to Target . Захват и решить. Звезда должна быть точно по центру поля зрения вашей ПЗС.
Убедитесь, что выбран параметр Slew to Target . Захват и решить. Звезда должна быть точно по центру поля зрения вашей ПЗС.
 Теперь Ekos выполнит расчет ошибки.
Теперь Ekos выполнит расчет ошибки.







 В этих модулях мы рассмотрим, почему коучинг стал популярным средством поддержки профессионального развития, что такое коучинг, основанный на практике, и как PBC может быть реализован для поддержки внедрения эффективных практик.
В этих модулях мы рассмотрим, почему коучинг стал популярным средством поддержки профессионального развития, что такое коучинг, основанный на практике, и как PBC может быть реализован для поддержки внедрения эффективных практик.

 Кроме того, участникам будут предложены идеи о том, как использовать ценности семьи и сообщества для обучения и обучения через призму модели пирамиды. Разработка этого модуля (2 часа) частично поддерживалась проектом Pyramid Equity Project в сотрудничестве с Университетом Южной Флориды, Университетом Колорадо в Денвере и Центром PBIS при финансировании национальной деятельности в рамках гранта на развитие дошкольных учреждений.
Кроме того, участникам будут предложены идеи о том, как использовать ценности семьи и сообщества для обучения и обучения через призму модели пирамиды. Разработка этого модуля (2 часа) частично поддерживалась проектом Pyramid Equity Project в сотрудничестве с Университетом Южной Флориды, Университетом Колорадо в Денвере и Центром PBIS при финансировании национальной деятельности в рамках гранта на развитие дошкольных учреждений.
 Шаг 6. Создайте окончательную версию, загрузите и запустите
Шаг 6. Создайте окончательную версию, загрузите и запустите Это дает учащимся информацию по конкретной теме.
Это дает учащимся информацию по конкретной теме.





 Теперь мы покажем примеры учебных модулей и объясним, как их легко создавать с помощью iSpring Suite Max.
Теперь мы покажем примеры учебных модулей и объясним, как их легко создавать с помощью iSpring Suite Max.

 Такие электронные книги обеспечивают приятное чтение на iPad и других мобильных устройствах.
Такие электронные книги обеспечивают приятное чтение на iPad и других мобильных устройствах. Как правило, именно здесь вы получите наибольшее количество отзывов от своих МСП.
Как правило, именно здесь вы получите наибольшее количество отзывов от своих МСП. Основная функция пилотного тестирования состоит в том, чтобы обеспечить дополнительный уровень проверки и показать, способны ли учащиеся достичь поставленных целей.
Основная функция пилотного тестирования состоит в том, чтобы обеспечить дополнительный уровень проверки и показать, способны ли учащиеся достичь поставленных целей. Возможно, вы захотите поработать со своими деловыми партнерами, менеджерами по изменениям или руководителями проектов, чтобы координировать официальное развертывание нового обучения.
Возможно, вы захотите поработать со своими деловыми партнерами, менеджерами по изменениям или руководителями проектов, чтобы координировать официальное развертывание нового обучения. Попробуйте разные стили.
Попробуйте разные стили. com
com  д.)
д.) д.)
д.) д.)
д.) Формула
Формула .. = 1?
.. = 1? purplemath.com/modules/index.htm
purplemath.com/modules/index.htm Есть также вопрос по геометрии с неожиданным результатом.
Есть также вопрос по геометрии с неожиданным результатом.