Скалярное и векторное произведения векторов
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Математика. Лекция 3.
Скалярное и векторноепроизведения векторов.
•В отличие от умножения двух чисел
операция умножения вектора на вектор
может
быть
определена
двумя
различными способами, каждый из
которых имеет своё математическое и
прикладное значение.
3. Скалярным произведением векторов называют число, равное произведению модулей перемножаемых векторов на косинус угла между ними:
Часто для обозначения скалярного произведенияупотребляют и запись:
F
A
M
Рассмотрим пример из механики,
приводящий к понятию скалярного произведения.

Пусть материальная точка М движется по прямой
из положения А в положение В, проходя при
этом расстояние s , а на точку действует
F . Работа, совершаемая при
этом перемещении силой F , будет равна:
постоянная сила
А F s cos . Если ввести вектор
перемещения
AB , то получим:
А F AB
5. Свойства скалярного произведения.
• Скалярное произведение двух векторовобладает переместительным свойством :
6. Свойства скалярного произведения.
• Скалярное произведение двух векторов равнопроизведению модуля одного из векторов и
проекции другого вектора на направление первого:
7. Свойства скалярного произведения.
• Проекция вектора на некоторое направление равнаскалярному произведению единичного вектора
рассматриваемого направления и данного вектора.
8. Свойства скалярного произведения.
• Скалярное произведение обладает сочетательным свойствомотносительно скалярного множителя.
• Скалярное произведение обладает распределительным свойством
9.
 Свойства скалярного произведения.• Скалярное произведение равно нулю, если равен нулю
Свойства скалярного произведения.• Скалярное произведение равно нулю, если равен нулюодин из перемножаемых векторов или косинус угла
между ними (т.е. векторы ортогональны).
• Это утверждение непосредственно следует из
определения.
• Верно и обратное : если векторы ортогональны, то их
скалярное произведение равно нулю.
• Для того, чтобы два ненулевых вектора были
ортогональны, необходимо и достаточно равенство
нулю их скалярного произведения.
10. Свойства скалярного произведения.
• Скалярное произведение вектора самого на себяравно квадрату его модуля.
• Модуль вектора равен корню квадратному из
скалярного квадрата этого вектора.
11. Скалярное произведение в координатной форме
• Пусть векторы заданы в координатной форме• Выразим скалярное произведение векторов через их
координаты, для чего воспользуемся разложением
векторов по координатным осям и полученными
свойствами скалярного произведения
12.
 Скалярное произведение в координатной формеУчитывая, что в силу ортогональности ортов осей их скалярные
Скалярное произведение в координатной формеУчитывая, что в силу ортогональности ортов осей их скалярныепроизведения равны нулю, а их скалярные произведения на
себя равны единице, получаем:
13. Скалярное произведение в координатной форме
скалярное произведение двух векторов равносумме произведений одноименных координат.
14. Правые и левые тройки векторов.
• Назовём тройку векторовправой, если кратчайший
поворот от первого вектора
ко второму будет виден с
конца третьего вектора
происходящим против хода
часовой стрелки.
15. Векторное произведение двух векторов.
• Векторным произведениемвектора
на вектор
назовём
вектор , направленный
перпендикулярно к обоим
векторам, образующим с этими
векторами в порядке a , b , c
правую тройку и по модулю
равный площади
параллелограмма, построенного
на векторах
и
как на
сторонах.
16. Векторное произведение двух векторов.
 • Для векторного произведения будем использовать
• Для векторного произведения будем использоватьобозначения
или
.
• С векторным произведением связаны многие физические
величины: момент силы относительно центра; скорость точки
при вращательном движении твёрдого тела; сила, действующая
на движущийся в магнитном поле заряд.
Пусть к твёрдому телу в точке А приложена сила F . В физике и теоретической механике
вводится понятие момента силы относительно центра, например, точки О, как вектора
M o F , модуль которого равен произведению модуля силы на длину плеча d
силы F
относительно центра О и который направлен перпендикулярно плоскости, проходящей
через точку О и линию действия силы F , в ту сторону, откуда поворот тела,
совершаемый силой, будет виден против хода часовой стрелки. Рассмотрим теперь
r F . Этот вектор направлен перпендикулярно к векторам r
F , то есть к плоскости ОАВ, в сторону, откуда кратчайший поворот от r к F виден
векторное произведение
и
против хода часовой стрелки, и равен по модулю
18.
 Свойства векторного произведения• При перестановке сомножителей векторное
Свойства векторного произведения• При перестановке сомножителей векторноепроизведение меняет знак, сохраняя модуль.
• Векторное произведение обладает
распределительным свойством:
19. Свойства векторного произведения
• Векторное произведение обладает сочетательнымсвойством относительно скалярного множителя.
• Если векторное произведение равно нуль-вектору, то
либо один из сомножителей равен нуль-вектору, либо
синус угла между векторами равен нулю, то есть векторы
коллинеарны.
20. Векторное произведение в координатных ортов.
21. Векторное произведение в координатной форме
22. Смешанное произведение трех векторов
• Рассмотрим три вектора a , b , cи первые два вектора
умножим векторно, а затем полученный вектор умножим
скалярно на третий вектор , в итоге получим число.
Такое произведение называют смешанным
произведением трёх векторов:
• Для записи смешанного произведения используют также
еще одну форму записи:
23.
 Смешанное произведение трех векторов• Пусть векторы заданы в координатной форме. Тогда смешанное
Смешанное произведение трех векторов• Пусть векторы заданы в координатной форме. Тогда смешанноепроизведение через координаты сомножителей выражается как
определитель 3-го порядка:
24. Смешанное произведение трех векторов
• Объём параллелепипеда,построенного на трех
некомпланарных векторах, как
на сторонах, равен модулю их
смешанного произведения.
• Для компланарности трёх
векторов необходимо и
достаточно, чтобы их
смешанное произведение
равнялось нулю.
25. Лекция окончена.
Спасибо за внимание.English Русский Правила
Векторное произведение векторов — онлайн справочник для студентов
Определение
Векторное произведение ненулевых векторов
\(\
\overline{a}
\) и \(\
\overline{b}
\) называется вектором \(\
\overline{c}
\), обозначаемым символом \(\
[\overline{a}, \overline{b}]
\) или \(\
\overline{a} \times \overline{b}
\) , длина которого \(\
|\overline{c}|=|\overline{a}||\overline{b}| \sin (\overline{a}, \overline{b})
\) (рис.
1. \(\ [\overline{a}, \overline{b}]=\overline{0} \) если и только если \(\ \overline{a}\|\overline{b} \)
2. \(\ [\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}] \)
3. Модуль векторного произведения \(\ |[\overline{a}, \overline{b}]| \) равен площади параллелограмма, построенного на указанных векторах \(\ \overline{a} \) и \(\ \overline{b} \) (рис. 2), т.е.
\(\ S=|[\overline{a}, \overline{b}]|=|\overline{a}| \overline{b}|\sin (\overline{a}, \overline{b}) \)
4.\(\ [\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}] \)
5.\(\ \left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right] \)
Если векторы задаются своими координатами \(\ \overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right), \overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right) \) то векторное произведение находится по формуле:
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{lll}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}}\end{array}\right| \)
Пример

Найти векторное произведение векторов \(\ \overline{a}=(6 ; 7 ; 10) \) и \(\ \overline{b}=(8 ; 5 ; 9) \)
Составляем определитель и вычисляем его:
\(\ \overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+k \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|= \)
\(\ =\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)= \)
\(\ =13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Скалярное произведение векторов Угол между векторами Длина (модуль) вектора Координаты вектора.
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Как найти векторное произведение векторов
Угол между векторами
Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами. \circ$.
\circ$.
Обозначение: $∠(\overline{α},\overline{β})$
Понятие векторного произведения векторов и формула нахождения
Определение 1
Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Математически это выглядит следующим образом:
- $|\overline{α}х\overline{β}|=|\overline{α}||\overline{β}|sin∠(\overline{α},\overline{β})$
- $\overline{α}х\overline{β}⊥\overline{α}$, $\overline{α}х\overline{β}⊥\overline{β}$
- $(\overline{α}х\overline{β},\overline{α},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 2)
Рисунок 2. Произведение векторов. Автор24 — интернет-биржа студенческих работ
Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:
- Если длина одного или обоих векторов равняется нулю.
 \circ=4\cdot 3\cdot 1=12$
\circ=4\cdot 3\cdot 1=12$Ответ: $12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Иначе, раскрывая определитель, получим следующие координаты
$\overline{α}х\overline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Пример 2
Найти вектор векторного произведения коллинеарных векторов $\overline{α}$ и $\overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.

Решение.
Воспользуемся формулой, приведенной выше. Получим
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\0&3&3\\-1&2&6\end{vmatrix}=(18-6)\overline{i}-(0+3)\overline{j}+(0+3)\overline{k}=12\overline{i}-3\overline{j}+3\overline{k}=(12,-3,3)$
Ответ: $(12,-3,3)$.
Свойства векторного произведения векторов
Для произвольных смешанных трех векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$, а также $r∈R$ справедливы следующие свойства:
$\overline{α}х\overline{β}=-(\overline{β}х\overline{α})$
Верность этого свойства будет следовать из третьего пункта определения 1.
$(r\overline{α})х\overline{β}=r(\overline{α}х\overline{β})$ и $\overline{α}х(r\overline{β})=r(\overline{α}х\overline{β})$
Из формулы для нахождения векторного произведения будем получать:
$(r\overline{α})\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\rα_1&rα_2&rα_3\\β_1&β_2&β_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=r(\overline{α}х\overline{β})$
$\overline{α}х(r\overline{β})=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\rβ_1&rβ_2&rβ_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=r(\overline{α}х\overline{β})$
$\overline{α}х(\overline{β}+\overline{γ})=\overline{α}\overline{β}+\overline{α}\overline{γ}$ и $(\overline{α}+\overline{β})\overline{γ}=\overline{α}\overline{γ}+\overline{β}\overline{γ}$.

Данное свойство векторного произведения векторов также можно проверить с помощью формулы.
Следующее свойство называют геометрическим смыслом векторного произведения:
Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)
Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ
Пример 3
Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.
Решение.
Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):
Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $\overline{α}=(3,0,0)$ и $\overline{β}=(0,8,0)$. Используя четвертое свойство, получим:
$S=|\overline{α}х\overline{β}|$
Найдем вектор $\overline{α}х\overline{β}$:
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\3&0&0\\0&8&0\end{vmatrix}=0\overline{i}-0\overline{j}+24\overline{k}=(0,0,24)$
Следовательно
$S=|\overline{α}х\overline{β}|=\sqrt{0+0+24^2}=24$
Ответ: $24$.

3.2.4. Примеры решения задач по теме «Векторное и смешанное произведения»
Задача 1.
Найти модуль вектора [A – 3B, 2A + B], если |A| = 6, |B| = 7, а угол между векторами А и B равен 30о.
Указание
Векторное произведение коллинеарных векторов равно нулю, поэтому
[A, а] = 0.
Операция векторного умножения некоммутативна,
[B, А] = — [A, B]
Решение
Используя свойства векторного произведения, получим:
[A – 3B, 2A + b] = 2[A, A] – 6[B, A] + [A, b] – 3[B, b] = 2·0 + 6[A, b] + [A, b] – 3·0 =
= 7[A, b].

Следовательно, |[A – 3B, 2A + b]| = 7|[A, b]| = 7 |A| |B| sin φ = 7·6·7·0,5 =147.
Ответ: |[A – 3B, 2A + b]| = 147.
Задача 2.
Известно, что |A| = 2, |B| = 10 и |[A, B]| = 12. Найти скалярное произведение Ab.
Указание
Поскольку |[A, B]| = |A| |B| sin J, можно найти sin J, а затем с помощью основного тригонометрического тождества вычислить cos J.
Решение
Поскольку |[A, B]| = |A| |B| sin J, где J – угол между векторами A И B, получаем:
12 = 2·10·sin J, откуда sin J = 0,6.
 Тогда cos2J = 1 – sin2J = 0,64.
Тогда cos2J = 1 – sin2J = 0,64.Если угол между векторами A И B острый, то cos J = 0,8, и Ab = 2·10·0,8 = 16; если же этот угол тупой, то cos J = -0,8, и Ab = -16.
Ответ: Ab = +16.
Задача 3.
Найти координаты векторного произведения векторов A = {3; 2; 1} и
B = {-1; 1; -2}.
Указание
Воспользуйтесь формулами для координатной записи векторного произведения:
Решение
Ответ: [A,B] = {-5; 5; 5}.
Задача 4.
Даны точки А(1; -1; 2), В(5; -6; 2), С(1; 3; -1). Найти площадь треугольника АВС.
Указание
Рассмотрите векторы
Модуль векторного произведения [AB, AC] равен площади параллелограмма АВМС, построенного на них как на смежных сторонах, а площадь треугольника АВС равна половине площади АВМС.

Решение
Рассмотрим векторы
Модуль векторного произведения [AB, AC] равен площади параллелограмма АВМС, построенного на них как на смежных сторонах, а площадь треугольника АВС равна половине площади АВМС.
Рис. 7
Ответ: 12,5.
Задача 5.
Даны векторы A = {4; -1; 2} и B = {1; 1; -3}. Найти координаты векторного произведения [A – 4B, B].
Указание
Воспользуйтесь тем, что
Решение
Ответ: {1; 14; 5}.
Задача 6.
Даны векторы A = {2; -1; 1}, B = {3; 3; 4} и С = {2; 0; 2}. Найти координаты вектора D, если известно, что он перпендикулярен векторам A и B, а скалярное произведение Dc = -8.
Указание
Векторное произведение [A, B] перпендикулярно обоим сомножителям,
То есть [A, B] перпендикулярен А и B.

Решение
Векторное произведение [A, B] перпендикулярно обоим сомножителям,
То есть [A, B] перпендикулярен А и B.
Следовательно, вектор D || [A,B], поэтому координаты вектора D Пропорциональны координатам [A,B].
Пусть D = {-7K; -5K; 9K}, тогда Dc = -7K ·2 + 9K ·2 = 4K = -8.
Следовательно, K = -2, и D = {14; 10; -18}.
Ответ: D = {14; 10; -18}.
Задача 7.
Вычислить объем тетраэдра, вершины которого находятся в точках
А(2; 2; 2), В(3; 1; 5), С(0; 4; 3), D(5; 0; 7).
Указание
Модуль смешанного произведения векторов AB, AC, AD равен объему параллелепипеда, построенного на этих векторах как на смежных ребрах.

Решение
Модуль смешанного произведения векторов AB, AC, AD равен объему параллелепипеда, построенного на этих векторах как на смежных ребрах. У треугольной пирамиды ABCD высота равна высот параллелепипеда, а площадь основания вдвое меньше площади основания параллелепипеда. Поэтому
Рис. 8
Ответ: .
< Предыдущая Следующая > Найти векторное произведение. Векторное произведение двух векторов. Он-лайн калькулятор. Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника мы находим выражение векторного произведения векторов
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.
Отложим для начала векторы a → , b → , c → от одной точки.
 Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .
Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой , если по часовой стрелке – левой .
Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения.
 Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.Определение 1
Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a → и b → коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
- его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
- тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) называют вектор c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , где i → , j → , k → являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k →
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a → × b → = — b → × a → ;
- дистрибутивность a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- ассоциативность λ · a → × b → = λ · a → × b → или a → × (λ · b →) = λ · a → × b → , где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативности
По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = — i → j → k → b x b y b z a x a y a z = — b → × a → , что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .
Пример 1
Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

Решение
С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Ответ: 15 2 2 .
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) .
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2
В прямоугольной системе координат заданы два вектора a → = (2 ; 1 ; — 3) , b → = (0 ; — 1 ; 1) .
 Найдите их векторное произведение.
Найдите их векторное произведение.Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → = = (1 · 1 — (- 3) · (- 1)) · i → + ((- 3) · 0 — 2 · 1) · j → + (2 · (- 1) — 1 · 0) · k → = = — 2 i → — 2 j → — 2 k → .
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k → .
Ответ: a → × b → = — 2 i → — 2 j → — 2 k → .
Пример 3
Найдите длину векторного произведения векторов i → — j → и i → + j → + k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i → — j → × i → + j → + k → в данной прямоугольной системе координат.

Известно, что векторы i → — j → и i → + j → + k → имеют координаты (1 ; — 1 ; 0) и (1 ; 1 ; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → .
Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты (- 1 ; — 1 ; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6 .
Ответ: i → — j → × i → + j → + k → = 6 . .
Пример 4
В прямоугольной декартовой системе координат заданы координаты трех точек A (1 , 0 , 1) , B (0 , 2 , 3) , C (1 , 4 , 2) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.
Решение
Векторы A B → и A C → имеют следующие координаты (- 1 ; 2 ; 2) и (0 ; 4 ; 1) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи.
 Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .
Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .Ответ: — 6 i → + j → — 4 k → . — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Пример 5
Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → .
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b →
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b →
Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b → = — 6 · a → × b → — b → × a → .
 .
.Из антикоммутативности векторного произведения следует — 6 · a → × b → — b → × a → = — 6 · a → × b → — (- 1) · a → × b → = — 5 · a → × b → . .
Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → — b → × a → — 2 · b → = = — 5 · a → × b → .
По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → — b → × a → — 2 · b → = — 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Ответ: 3 · a → — b → × a → — 2 · b → = 60 .
Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .

Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Определение 3
Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).

Векторное произведение обладает распределительным свойством , то есть
Выражение векторного произведения через координаты векторов.
Пусть даны два вектора
(как найти координаты вектора по координатам его начала и конца — см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Зачем нужно векторное произведение?
Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.
Также огромное количество применений существует в электричестве и магнетизме.

Он-лайн калькулятор векторного произведения.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Угол между векторами
Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.
Пусть нам даны два вектора $\overline{α}$ и $\overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $\overline{α}=\overline{OA}$ и $\overline{β}=\overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).
Обозначение: $∠(\overline{α},\overline{β})$
Понятие векторного произведения векторов и формула нахождения
Определение 1
Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
 \circ=4\cdot 3\cdot 1=12$
\circ=4\cdot 3\cdot 1=12$Ответ: $12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Иначе, раскрывая определитель, получим следующие координаты
$\overline{α}х\overline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Пример 2
Найти вектор векторного произведения коллинеарных векторов $\overline{α}$ и $\overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.

Решение .
Воспользуемся формулой, приведенной выше. Получим
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\0&3&3\\-1&2&6\end{vmatrix}=(18-6)\overline{i}-(0+3)\overline{j}+(0+3)\overline{k}=12\overline{i}-3\overline{j}+3\overline{k}=(12,-3,3)$
Ответ: $(12,-3,3)$.
Свойства векторного произведения векторов
Для произвольных смешанных трех векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$, а также $r∈R$ справедливы следующие свойства:
Пример 3
Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.
Решение .
Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):
Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $\overline{α}=(3,0,0)$ и $\overline{β}=(0,8,0)$.
 j
;
j
;2) |k |=1, но | i x j | = |i | |J | sin(90°)=1;
3) векторы i , j и k образуют правую тройку (см. рис. 16).
7.2. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).
Векторы а хb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , b x a противоположной ориентации). Стало быть a xb = -(b xa ).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l (а хb ) = (l а ) х b = а х (l b ).
Пусть l >0. Вектор l (а хb ) перпендикулярен векторам а и b . Вектор ( l а )хb также перпендикулярен векторам а и b (векторы а , l а лежат в одной плоскости). Значит, векторы l (а хb ) и ( l а )хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
Поэтому l (a хb )= l а хb .
 Аналогично доказывается при
l
Аналогично доказывается при
l3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а ||b а хb =0 .
В частности, i *i =j *j =k *k =0 .
4. Векторное произведение обладает распределительным свойством:
(a +b ) хс = а хс +b хс .
Примем без доказательства.
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов i , j и k :
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а =а х i +a y j +a z k и b =b x i +b y j +b z k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
Полученную формулу можно записать еще короче:
так как правая часть равенства (7.
 1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.7.4. Некоторые приложения векторного произведения
Установление коллинеарности векторов
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а | * |b |sin g , т. е. S пар = |а х b |. И, значит, D S =1/2|а х b |.
Определение момента силы относительно точки
Пусть в точке А приложена сила F =АВ и пусть О — некоторая точка пространства (см. рис. 20).
Из физики известно, что моментом си лы F относительно точки О называется вектор М , который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо
3) образует правую тройку с векторами ОА и A В .

Стало быть, М =ОА х F .
Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ , где О-некоторая неподвижная точка оси (см. рис. 21).
Использование векторного произведения ВЕКТОРОВ
для вычисления площади
некоторых геометрических фигур
Исследовательская работа по математике
Ученика 10 Б класса
МОУ СОШ №73
Перевозникова Михаила
Руководители:
Ассистент каф. математического анализа механико-математического факультета СГУ им. Н.Г. Чернышевского Бердников Глеб Сергеевич
Саратов, 2015
Введение.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трёхмерном Евклидовом пространстве: определение понятия.

1.5. Координаты векторного произведения векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма. Выведение формулы и геометрический смысл векторного произведения векторов.
2.2. Зная только координаты точек, найти площадь треугольника. Доказательство теоремы
2.3. Проверка на примерах правильности формулы.
2.4. Практическое использование векторной алгебры и произведения векторов.
Заключение
Введение
Как известно, многие геометрические задачи имеют два ключевых способа решения – графический и аналитический. Графический метод связан с построением графиков и чертежей, а аналитический предполагает решение задач преимущественно с помощью алгебраических действий. В последнем случае алгоритм решений задач связан с аналитической геометрией. Аналитическая геометрия – это область математики, а точнее линейной алгебры, которая рассматривает решение геометрических задач средствами алгебры на основе метода координат на плоскости и в пространстве.
 Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо иногда применяется векторное произведение векторов.
Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо иногда применяется векторное произведение векторов.В связи с широким распространением трехмерных пространственных технологий, изучение свойств некоторых геометрических фигур с использованием векторного произведения представляется актуальным.
В связи с этим была обозначена цель данного проекта – использование векторного произведения векторов для вычисления площади некоторых геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и дать определение векторному произведению векторов в системе координат;
2. Проанализировать наличие связи векторного произведения с площадью треугольника и параллелограмма;
3. Вывести формулу площади треугольника и параллелограмма в координатах;
4.
 Проверить на конкретных примерах верность выведенной формулы.
Проверить на конкретных примерах верность выведенной формулы.1. Теоретический обзор.
Векторы и вычисления с векторами
Векторомназывается направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка А , концом отрезка – точка В . Сам вектор обозначен через
или . Чтобы найти координаты вектора
, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:= { B x — A x ; B y — A y }
Коллинеарными называются векторы, лежащие на параллельных прямых или на одной прямой. При этом вектор отрезок, характеризующийся длиной и направлением.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
Длина вектора || в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

С векторами можно совершать различные действия.
Например, сложение. Чтобы их сложить, нужно провести сначала второй вектор из конца первого, а потом соединить начало первого с концом второго (рис. 1). Суммой векторов является другой вектор с новыми координатами.
Сумму векторов = {a x ; a y } и = {b x ; b y } можно найти воспользовавшись следующей формулой:
+ = {a x + b x ; a y + b y }
Рис. 1. Действия с векторами
Вычитая векторы, нужно сначала провести их из одной точки, а потом соединить конец второго с концом первого.
Разность векторов = {a x ; a y } и = {b x ; b y } можно найти по формуле:
— = { a x — b x ; a y — b y }
Также, векторы можно умножать на число.
 Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.Произведение вектора = {a x ; a y } и числа k можно найти воспользовавшись следующей формулой:
k · = {k · a x ; k · a y }
А можно ли умножать вектор на вектор? Конечно, и даже двумя вариантами!
Первый вариант – скалярное произведение.
Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов можно использовать угол между данными векторами, показанный на рисунке 3.
Из формулы следует, что скалярное произведение равно произведению длин данных векторов на косинус угла между ними, его результатом является число. Важно, что если векторы перпендикулярны, то их скалярное произведение равно нулю, т.к. косинус прямого угла между ними равен нулю.

В координатной плоскости вектор также имеет координаты. Вектора, их координаты и скалярное произведение являются одними из самых удобных методов вычисления угла между прямыми (или их отрезками), если введена система координат. И если координаты
, то их скалярное произведение равно:В трехмерном пространстве существует 3 оси и, соответственно, у точек и векторов в такой системе будет по 3 координаты, а скалярное произведение векторов вычисляется по формуле:
1.2. Векторное произведение векторов в трехмерном пространстве.
Вторым вариантом вычисления произведения векторов является векторное произведение. Но, чтобы его определить требуется уже не плоскость, а трехмерное пространство, в котором начало и конец вектора имеют по 3 координаты.
В отличие от скалярного произведения векторов в трёхмерном пространстве операция «векторное умножение» над векторами приводит к иному результату. Если в предыдущем случае скалярного умножения двух векторов результатом было число, то в случае векторного умножения векторов результатом будет другой вектор, перпендикулярный обоим вступившим в произведение векторам.
 Поэтому это произведение векторов называется векторным.
Поэтому это произведение векторов называется векторным.Очевидно, что при построении результирующего вектора , перпендикулярного двум, вступившим в произведение — и , может быть выбрано два противоположных направления. При этом направление результирующего вектора определяется по правилу правой руки, или правилу буравчика.Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
Рис. 7. Правило правой руки
1.3. Свойства векторного произведения векторов.
Длина результирующего вектора определяется по формуле
.
При этом
векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен
, а его направление определяется по правилу правой руки.Векторное произведение зависит от порядка сомножителей, именно:
Векторное произведение ненулевых векторов равно 0, если они коллинеарны, тогда синус угла между ними будет равен 0.

Координаты векторов в трехмерном пространстве выражаются следующим образом: . Тогда координаты результирующего вектора находим по формуле
Длина результирующего вектора находится по формуле:
.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма в плоскости. Геометрический смысл векторного произведения векторов.
Пусть нам дан треугольник ABC (рис. 8). Известно, что .
Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника мы находим выражение векторного произведения векторов:
Из выше сказанного можно определить геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки.
Другими словами, длина векторного произведения векторов и равна площади параллелограмма, построенного на векторах и , со сторонами и и углом между ними, равным .

Рис. 9. Геометрический смысл векторного произведения векторов
В связи с этим, можно привести еще одно определение векторного произведения векторов:
Векторным произведением вектора на вектор называется вектор , длина которого численно равна площади параллелограмма построенного на векторах и , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от к вокруг вектора осуществлялось против часовой стрелки, если смотреть с конца вектора (рис. 10).
Рис. 10. Определение векторного произведения векторов
с использованием параллелограмма
2.2. Вывод формулы для нахождения площади треугольника в координатах.
Итак, нам дан треугольник АВС в плоскости и координаты его вершин. Найдем площадь этого треугольника (рис. 11).
Рис. 11. Пример решения задачи на нахождение площади треугольника по координатам его вершин
Решение.
Для начала, рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и АС.

По данной прежде формуле подсчитаем координаты их векторного произведения. Длина этого вектора равна 2 площадям треугольника АВС. Площадь треугольника равна 10.
Более того, если мы рассмотрим треугольник на плоскости, то первые 2 координаты векторного произведения всегда будут равны нулю, поэтому мы можем сформулировать следующую теорему.
Теорема: Пусть дан треугольник АВС и координаты его вершин (рис. 12).
Тогда .
Рис. 12. Доказательство теоремы
Доказательство.
Рассмотрим точки в пространстве и вычислим координаты векторов ВС и ВА. . По приведенной раньше формуле вычислим координаты векторного произведения этих векторов. Обратим внимание, что все члены, содержащие z 1 или z 2, равны 0, т.к. z 1и z 2 = 0. УБРАТЬ!!!
Итак, следовательно,
2.3. Проверка правильности формулы на примерах
Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
a × b=
I(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
I(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5 j — 5 k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
| a × b| =
√ 02 + 52 + 52 =
√ 25 + 25 =
√ 50 =
5√ 2
Ответ: SΔ = 2.
 5√2.
5√2.Заключение
2.4. Приложения векторной алгебры
и скалярного и векторного произведения векторов.
Где же нужны векторы? Векторное пространство и векторы носят не только теоретический характер, но и имеют вполне реальное практическое применение в современном мире.
В механике и физике многие величины имеют не только численное значение, но и направление. Такие величины называются векторными. Вместе с использованием элементарных механических понятий, опираясь на их физический смысл, многие величины рассматриваются как скользящие векторы, а их свойства описываются как аксиомами, как это принято в теоретической механике, так и при помощи математических свойств векторов. Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, момент импульса и сила Лоренца математически записываются с помощью векторов.
В физике важны не только сами вектора, но в большой степени важны и их произведения, которые помогают вычислять некоторые величины.
 Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.Еще один пример: скалярное произведение используется для вычисления работы по приведенной ниже формуле, где F – вектор силы, а s – вектор перемещения.
Одним из примеров использования произведения векторов является момент силы, равный произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое из того, что вычисляется в физике по правилу правой руки является векторным произведением. Найти подтверждения, привести примеры.
Стоит еще заметить, что двухмерным и трехмерным пространством не исчерпываются возможные варианты векторных пространств. Высшая математика рассматривает пространства большей размерности, в которых также определяются аналоги формул для скалярного и векторного произведения.
 Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.В то же время результатом векторного произведения векторов в трёхмерном Евклидовом пространстве является не число, а результирующий вектор со своими координатами, направлением и длиной.
Направление результирующего вектора определяется по правилу правой руки, что является одним из самых удивительных положений аналитической геометрии.
Векторное произведение векторов может быть использовано в нахождении площади треугольника или параллелограмма по заданным координатам вершин, что было подтверждено выведением формулы, доказательством теоремы и решением практических задач.
Векторы широко используются в физике, где такие показатели как скорость, импульс и сила могут быть представлены в виде векторных величин и вычисляются геометрически.
Список использованных источников
Атанасян Л.
 С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с.
С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с.Атанасян Л.С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10-11 классы: учебник для общеобразовательных организаций: базовый и профильный уровни. М.: , 2013. 255 с.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
Математика. Клевер.
Изучение математики онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm
Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5
Решение параллелограмма онлайн. Векторное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) .
 Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками.
 Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор.
Определение векторного произведения Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а».
 Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе .
 Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони.
 В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны.
 Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулеваяТаким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми.
 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания.
 Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане.
 Поэтому пусть будет.
Поэтому пусть будет.2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле .
 Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения.
 Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .

а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.

3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a (x1;y1;z1), а вектора b (x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними.
 Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.
Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7).
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). - Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
- Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.
 5.
5. - В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
| Формула, определение, использование
Создано Bogna Szyk и Álvaro Díez
Отредактировано Steven Wooding и Jack Bowater
Последнее обновление: 06 апреля 2022 г. Как вычислить векторное произведение двух векторов
- Как использовать калькулятор векторного векторного произведения
- Скалярное произведение против векторного произведения
- Перекрестное произведение и физика: Лучшие друзья навсегда
- Правило правой руки в физике: чем оно так полезно?
-
c— Новый вектор, полученный в результате перекрестного произведения; -
a— Один из начальных векторов; -
b— Второй из начальных векторов; -
θ— Угол между обоими векторами; и -
n— Единичный вектор, перпендикулярный кaиbодновременно. - Первым шагом является введение компонентов вектора
a. То есть:х = 2,у = 3иz = 7. - Далее следует ввести компоненты вектора
b. То есть:
То есть: x = 1,y = 2иz = 4. - Теперь калькулятор обрабатывает информацию, применяет формулу, которую мы видели раньше, и…
- Вуаля! Вы только что вычислили:
c = a × b = (-2, -1, 1). - Повторяйте, пока не рассчитаете все необходимые перекрестные произведения.
- Поделитесь с друзьями революционным опытом расчета векторных перекрестных произведений. 😉
- Что такое векторное произведение?
- Как сделать векторное произведение двух векторов
- Модуль векторного произведения
- Векторное произведение двух векторов в R2
- Тройное векторное произведение
- Свойства векторного произведения
- Применение векторного произведения
- Перпендикулярное направление к двум векторам
- Направление по правилу штопора или правой руке.

- Антиконмутативность: a x b = — (b x a)
- а — (а х б) = 0
- Если a x b = 0, т.е. a≠0 и b≠0, это означает, что векторы параллельны и их векторное произведение равно нулю.
- (а + б) х с = а х с + б х с
- a x (b x c) + c x (a x b) + b x (c x a) = 0 согласно тождеству Якоби
- Degrees to radians
- Apothem
- Antilogarithm calculator
- Division calculator
- Exponent calculator
- Exponential Function Calculator
- Logarithm Calculator
- Neperian logarithm calculator
- Prime Number Calculator
- Odd or even calculator
- Exponent calculator
- Калькулятор кубического корня
- Калькулятор n-го корня числа
- Калькулятор квадратных уравнений
- Онлайн-калькулятор факториала
- Калькулятор гипотенузы
- Калькулятор наибольшего общего делителя
- Калькулятор наименьшего общего кратного
- Калькулятор умножения
- Онлайн-калькулятор
- Добавление матрицы
- Вычитание матрицы
- Умножение матриц
- Скалярное произведение
- Перекрестное произведение
- и множество других операций над матрицами
- +
- —
- *
- /
- % К элементам применяются
- Помощь при входе
- Сертифицировано и протестировано для использования в медицинских учреждениях
- Обеспечивает постоянное оптимальное заземление и выдерживает экстремальные изгибы
- Защита от вытягивания для предотвращения спотыкания и отключения машин от сети
- Некоторые модели обеспечивают дополнительную защиту от бактерий
- 2* 5G/4G MIMO кросс-поляризованная всенаправленная дипольная антенна
- Охватывает все мировые диапазоны сотовой связи ниже 6 ГГц от 400 МГц до 6000 МГц
- Степень защиты IP65 и различные варианты монтажа
- 3 м кабеля с низкими потерями
- Акселерометры
- Беспроводная связь
- Управление питанием
- Брызгозащищенный центробежный вентилятор SANYO DENKI 100×25 мм, тип 9W2TM
- Защита от воды и пыли со степенью защиты IP68
- Высокий расход воздуха и высокое статическое давление
- Подходит для цифровых вывесок, зарядных станций для электромобилей и телекоммуникационного оборудования
- Высокоэффективный и экономичный
- Небольшая площадь основания 1 x 1 дюйм или 1 x 2 дюйма
- Широкий диапазон входного напряжения, включая некоторые модели до 480 В переменного тока
- Оптимизированный режим ожидания и совместимость с ЭМС
- Схемы от 2 до 12
- Подходит для контактов размера 16 (13A)
- Совместимость с существующими отраслевыми решениями
- Защита от воздействия окружающей среды — IP67, IP68 и IP69K (при сопряжении)
- Для общего коммерческого использования
- Работа на частоте 18 ГГц
- Конструкция из позолоченной латуни
- Компактная ширина 45 мм
- 1 дополнительный замыкающий контакт в комплекте
- Сканируемый QR-код для быстрого доступа к документации
- Клеммное соединение с винтовым зажимом
Без калькулятора векторного векторного произведения трудно понять, как вычислить векторное произведение. К счастью для вас, мы создали инструмент, который поможет вам понять формулу векторного произведения двух векторов. Мы также сравним определения скалярного произведения и перекрестного произведения и объясним, почему они не являются одной и той же операцией. И в качестве бонуса у нас также есть список из практических приемов , таких как правило правой руки, чтобы вы могли стать мастером в том, как делать векторное произведение двух векторов.
Мы также сравним определения скалярного произведения и перекрестного произведения и объясним, почему они не являются одной и той же операцией. И в качестве бонуса у нас также есть список из практических приемов , таких как правило правой руки, чтобы вы могли стать мастером в том, как делать векторное произведение двух векторов.
Определение векторного векторного произведения
Вектор — это математический инструмент , широко используемый в физике . Он позволяет очень эффективно работать с наборами чисел (каждый из которых представляет измерение). Набор операций, правил и свойств для работы с векторами называется векторной алгеброй и, подобно алгебре чисел, включает умножение.
Однако векторы более сложны, чем числа , так как они несут в себе гораздо больше информации, которой нужно более тщательно манипулировать. Это одна из причин, почему в векторной алгебре есть два разных типа операций умножения или произведения: векторное произведение и скалярное произведение.
Определение, принятое в математике, очень техническое. Тем не менее, мы объясним, что это значит, с точки зрения непрофессионала (и менее точного), так что, даже если у вас нет сильного математического образования, вам все будет понятно .
Одно из определений перекрестного произведения, также называемого векторным произведением :
Бинарная операция над двумя векторами в трехмерном пространстве, обозначаемая символом ×. Учитывая два линейно независимых вектора, a и b векторное произведение a × b представляет собой вектор, перпендикулярный обоим a и b и, следовательно, перпендикулярный плоскости, содержащей их.
Это действительно многословно, но мы можем перевести это с математического жаргона на простое объяснение. Во-первых, определение говорит о трехмерном пространстве , подобном тому, в котором мы живем. Это потому, что это наиболее распространенное использование векторного произведения, но мы можем расширить его до большего количества измерений; однако это выходит за рамки этого текста и большинство математических степеней.
Это потому, что это наиболее распространенное использование векторного произведения, но мы можем расширить его до большего количества измерений; однако это выходит за рамки этого текста и большинство математических степеней.
Определение говорит нам, что векторное произведение любых двух векторов является третьим вектором , который перпендикулярен обоим из них (и плоскости, которая их содержит). Это возможно в трехмерном пространстве, потому что в нем есть три независимых направления. Вы можете думать об этих трех направлениях как о высоте , ширине и глубине .
Чтобы узнать, как этот новый третий вектор будет выглядеть с точки зрения величины и математического описания, мы можем использовать формула векторного произведения двух векторов . В следующем разделе вам будет представлена формальная математическая формула, которая говорит вам, как сделать перекрестное произведение любых двух векторов. Мы также объясним, что означает это уравнение и как его использовать простым, но точным способом.
Формула перекрестного произведения
Прежде чем представить формулу векторного произведения, нам понадобятся два вектора, которые мы назовем a и b . Эти два вектора не должны лежать на одной прямой (он же не должен быть параллельным) по причинам, которые мы объясним позже.
Итак, без лишних слов, давайте посмотрим на формулу:
c = a × b = |a| * |б| * sin θ * n
Эта формула состоит из:
Фактор перпендикулярности вместе с функцией синуса, представленной в формуле, являются хорошими индикаторами геометрической интерпретации векторного векторного произведения. Подробнее об этом мы поговорим в следующих разделах.
Подробнее об этом мы поговорим в следующих разделах.
Вы также можете понять, почему два вектора a и b не должны быть параллельны. Если бы они были параллельны, это привело бы к нулевому углу между ними ( θ = 0 ). Следовательно, и sin θ , и c будут равны нулю, что является очень неинтересным результатом . Также интересно отметить тот факт, что простая перестановка на и на b на изменит только направление на , поскольку -sin(θ) = sin(-θ) .
Как выполнить векторное произведение двух векторов
Мы видели математическую формулу для векторного векторного произведения, но вы все еще думаете, «Это все хорошо, но как на самом деле рассчитать новый вектор?» И это отличный вопрос! Самое быстрое и простое решение — воспользоваться нашим калькулятором векторного векторного произведения, но если вы дочитали до этого места, вероятно, вы ищете не только результаты, но и знания .
Процесс можно разделить на три этапа: вычисление модуля вектора, вычисление угла между двумя векторами и вычисление перпендикулярного унитарного вектора. Ставим все эти три промежуточных результата вместе с помощью простого умножения дадут желаемый вектор.
Вычисление углов между векторами может оказаться слишком сложным в трехмерном пространстве ; и, если все, что мы хотим сделать, это знать, как вычислить векторное произведение между двумя векторами, это может не стоить хлопот. Вместо этого давайте изучим более простой и практичный способ вычисления векторного перекрестного произведения с использованием другой формулы перекрестного произведения.
В этой новой формуле используется разложение трехмерного вектора на три его компонента. Этот метод является очень распространенным способом описания и работы с векторами, в которых каждый компонент представляет направление в пространстве , а число, сопровождающее его, представляет длину вектора в определенном направлении. Канонически три измерения трехмерного пространства, с которым мы работаем, называются
Канонически три измерения трехмерного пространства, с которым мы работаем, называются x , y и z и представлены унитарными векторами 9.0025 i , j и k соответственно.
Следуя этой номенклатуре, мы можем представить каждый вектор как сумму этих трех унитарных векторов . Векторы обычно опускаются для краткости, но все же подразумеваются и имеют большое значение для результата векторного произведения. Таким образом, вектор v может быть выражен как: v = (3i + 4j + 1k) или, короче: v = (3, 4, 1) , где положение чисел имеет значение. Используя это обозначение, мы теперь можем понять, как вычислить векторное произведение двух векторов.
Назовем наши два вектора: v = (v₁, v₂, v₃) и w = (w₁, w₂, w₃) . Для этих двух векторов формула выглядит так:
v × w = (v₂w₃ - v₃w₂, v₃w₁ - v₁w3, v₁w₂ - v₂w₁)
Этот результат может выглядеть как случайный набор операций между компонентами каждого вектора, но нет ничего более далекого от реальности. Для тех из вас, кто задается вопросом, откуда все это взялось, мы предлагаем вам открыть это самостоятельно. Все, что вам нужно сделать, это начать с обоих векторов, выраженных как:
Для тех из вас, кто задается вопросом, откуда все это взялось, мы предлагаем вам открыть это самостоятельно. Все, что вам нужно сделать, это начать с обоих векторов, выраженных как: v = v₁i + v₂j + v₃k и w = w₁i + w₂j + w₃k и умножить каждый компонент вектора на все компоненты другого.
В качестве небольшой подсказки мы можем сказать вам, что при выполнении векторного произведения векторов, умноженных на числа, результатом будет » обычное » произведение чисел, умноженное на векторное произведение между векторами . Также будет полезно помнить, что векторное произведение параллельных векторов (и, следовательно, вектора с самим собой) всегда равно 0 .
Как использовать калькулятор векторного векторного произведения
После всего того, о чем мы говорили, пришло время узнать, как использовать наш калькулятор векторного произведения, чтобы сэкономить время и получить результаты для любых двух векторов в трехмерном пространстве. пространство. Как видите, переменные разделены на три секции, по одной для каждого вектора, участвующего в вычислении перекрестного произведения. Из этих трех векторов
пространство. Как видите, переменные разделены на три секции, по одной для каждого вектора, участвующего в вычислении перекрестного произведения. Из этих трех векторов c , вероятно, должен вас больше всего волновать, так как он является результатом перекрестного произведения. Каждый вектор имеет три компонента, как упоминалось ранее: x , y и z , относящиеся к каждому из трех измерений: глубине, ширине и высоте.
Как только мы поймем, что делает каждое из полей, давайте кратко рассмотрим типичный вариант использования этого калькулятора. Чтобы включить пример для вычисления перекрестного произведения двух векторов, мы будем использовать векторы a = (2, 3, 7) и b = (1, 2, 4) .
Вы можете вычислить векторное произведение любых векторов, даже не задумываясь об этом. Тем не менее, мы настоятельно рекомендуем вам использовать упомянутые выше свойства для сложных операций, чтобы сэкономить ваше время и хлопот. Например, если один из векторов просто кратен другому, вам даже не нужно использовать наш калькулятор; вы можете предсказать, что результат будет нулевым, поскольку эти два вектора коллинеарны.
Скалярное произведение против векторного произведения
Мы рассмотрели наиболее важные математические аспекты векторного произведения двух векторов в трехмерном пространстве, поэтому пришло время поговорить о некоторых интересных фактах и использовании этой векторной операции . Для начала мы поговорим о двоюродном брате перекрестного произведения: скалярном произведении.
Для начала мы поговорим о двоюродном брате перекрестного произведения: скалярном произведении.
Эти две операции имеют обманчиво похожие названия, но на самом деле представляют разные понятия в геометрии. Кроме того, вычисление скалярного произведения, возможно, проще, чем вычисление перекрестного произведения; тем не менее, мы также сделали калькулятор, который поможет вам рассчитать скалярное произведение 2 векторов, тоже называется скалярным произведением .
Следуя тенденции очевидного сходства между скалярным произведением и перекрестным произведением, мы можем внимательно рассмотреть формулу скалярного произведения:
v = a · b = |a| * |б| * cos θ
Единственным различием между перекрестным произведением и скалярным произведением является тригонометрическая функция, используемая в формуле, и тот факт, что здесь результатом является число (скаляр, отсюда и название), а не вектор.
Эти незначительные различия могут заставить вас поверить в то, что обе операции очень похожи, но они очень различны по своей природе .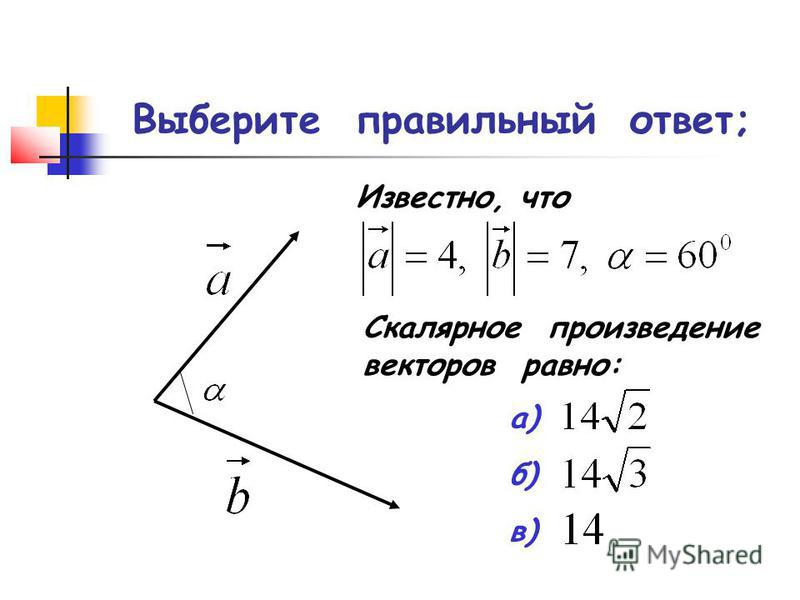 Во-первых, перекрестное произведение — это операция, которая берет два вектора и возвращает другой вектор, перпендикулярный обоим, в то время как скалярное произведение дает число без направления. Скалярный продукт более легко обобщается на более высокие или более низкие измерения, в то время как векторный продукт даже не существует в двумерном . Их интерпретация в геометрических терминах также сильно отличается, поскольку вы можете думать о скалярном произведении как о 9.0025 длина проекции одного из векторов на другой .
Во-первых, перекрестное произведение — это операция, которая берет два вектора и возвращает другой вектор, перпендикулярный обоим, в то время как скалярное произведение дает число без направления. Скалярный продукт более легко обобщается на более высокие или более низкие измерения, в то время как векторный продукт даже не существует в двумерном . Их интерпретация в геометрических терминах также сильно отличается, поскольку вы можете думать о скалярном произведении как о 9.0025 длина проекции одного из векторов на другой .
Все эти различия делают их концептуально очень разными операциями. Следовательно, эти две операции не являются взаимозаменяемыми или переводимыми. Как мы увидим в следующих разделах, обе операции полезны как в математике, так и в физике.
Взаимное произведение и физика: лучшие друзья навсегда
Большинство из нас интересуются не только чисто математическими свойствами и использованием векторного произведения, но и практическое применение в реальном мире . И есть ли лучший способ получить полезное применение математических понятий, чем через физику? Перекрестное произведение не является исключением; это очень полезная операция в физике. Мы могли бы углубиться в квантовую теорию поля, где широко используются как скалярное произведение, так и перекрестное произведение.
И есть ли лучший способ получить полезное применение математических понятий, чем через физику? Перекрестное произведение не является исключением; это очень полезная операция в физике. Мы могли бы углубиться в квантовую теорию поля, где широко используются как скалярное произведение, так и перекрестное произведение.
Тем не менее, мы останемся в сфере осязаемых и математически совершенных теорий и рассмотрим примеры в местах и событиях, к которым мы все можем иметь отношение.
Электромагнетизм — это первая область, которую мы обсудим, в которой свойства векторного произведения широко используются . В природе электрические и магнитные поля, как правило, перпендикулярны друг другу, что идеально связано с тем, как выражается перекрестное произведение двух векторов. Такие вещи, как расчет магнитных сил на проводе с током или расчеты магнитного момента системы, требуют использования операции векторного произведения.
Другим примером, который нельзя не упомянуть, является так называемый эффект Холла, очень важный в физике твердого тела.
Наиболее распространенные приложения векторного произведения включают исследование момента инерции и вращающихся объектов. Мы могли бы бесконечно говорить о том, насколько умопомрачительна эта часть физики. Вместо этого лучше посмотреть видео, где Уолтер Левин (один из лучших преподавателей физики) объясняет и демонстрирует все об этом явлении.
Правило правой руки в физике: чем оно так полезно?
Векторы широко распространены в физике, от скорости до веса или даже площади, кажется, что у всего есть вектор, связанный с ним. И именно поэтому векторное векторное произведение очень важно в физическом мире.
Одной из самых страшных частей физики является осмысление всей математической работы , которую нужно проделать, чтобы рассчитать почти что угодно. Поскольку мы включаем векторы и несколько измерений, это может быстро превратиться в неконтролируемый беспорядок, который, кажется, не имеет ничего общего с реальностью. Чтобы решить эти проблемы, физики разработали некоторые приемы, которые помогут вам ориентироваться в этих мутных водах .
Вероятно, самым известным из них является «Правило правой руки» , которое помогает в вычислении кросс-векторного произведения. Это правило позволяет вам предсказать, куда будет направлен результирующий вектор векторного произведения, используя только вашу руку.
Есть две версии правила правой руки в физике : одна с растопыренными пальцами и неподвижной рукой, а другая включает переход от открытой ладони к сжатому кулаку.
Первый вариант (более распространенный) состоит из расставления среднего и указательного пальцев, как показано на картинке выше. Вытянув большой палец, вы должны стремиться совместить указательный палец с первым вектором, а средний палец со вторым. В этом положении вытянутый большой палец покажет направление результирующего вектора из вычисления векторного векторного произведения.
Второй способ, на наш взгляд, проще в использовании . Открытой ладонью вы выравниваете пальцы с первым вектором. Затем вы сжимаете руку в кулак по направлению ко второму вектору. После выполнения этих действий вы получите руку с поднятым или опущенным большим пальцем. Как и в предыдущем случае, направление большого пальца укажет направление вектора, полученного в результате операции перекрестного произведения.
Затем вы сжимаете руку в кулак по направлению ко второму вектору. После выполнения этих действий вы получите руку с поднятым или опущенным большим пальцем. Как и в предыдущем случае, направление большого пальца укажет направление вектора, полученного в результате операции перекрестного произведения.
Все эти может показаться детскими играми , но это мощные уловки. С помощью простого жеста рукой вы можете получить четкое представление о том, как будет выглядеть векторное перекрестное произведение. Вас может даже удивить, что эти уловки постоянно используются исследователями всякий раз, когда их работа связана с вычислением векторного произведения, например, при расчете магнитных сил между проводами.
Богна Шик и Альваро Диес
Вектор a
Вектор b
Вектор c = a × b
Посмотреть 38 похожих калькуляторов координатной геометрии 📈
Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35 из двух векторов ? Воспользуйтесь нашим онлайн-калькулятором и узнайте результат автоматически, без выполнения каких-либо операций.
Просто введите компоненты i, j и k двух векторов и нажмите кнопку расчета, чтобы получить их векторное произведение. Например, если вам дан вектор
= (1, 2, 3) y = (4, 5, 6), значения каждого из его компонентов — это те, которые вы должны записать в инструмент. Если вы не знаете , как вычислить векторное произведение , читайте дальше, и мы объясним вам это.
Разделы статей
Что такое векторное произведение?
Векторное произведение двух векторов дает другой вектор с:
Что говорит правило правой руки? Правило правой руки или штопор говорит нам направление, которое будет иметь вектор. según el movimiento de un sacacorchos (o destornillador, tornillo… и т. д.).
En el caso de la figura que tenéis encima de estas líneas podéis ver que si hacemos girar el sacacorchos hacia la izquierda (sentido antihorario), el sacacorchos sube hacia arriba y, por lo tanto, esa será la dirección del vector «c» результат.
Очень важно не путать вектор со скалярным произведением.
Как сделать векторное произведение двух векторов
Чтобы решить векторное произведение двух векторов
= (a 1 , a 2 , a 3 ) y = (b 1 , b 2 , b 3 ), компоненты вектора «c»:
В принципе, необходимо escribir en un determinante de 3×3 y descomponerlo en tres determinantes 2×2 для каждого компонента i, j, k.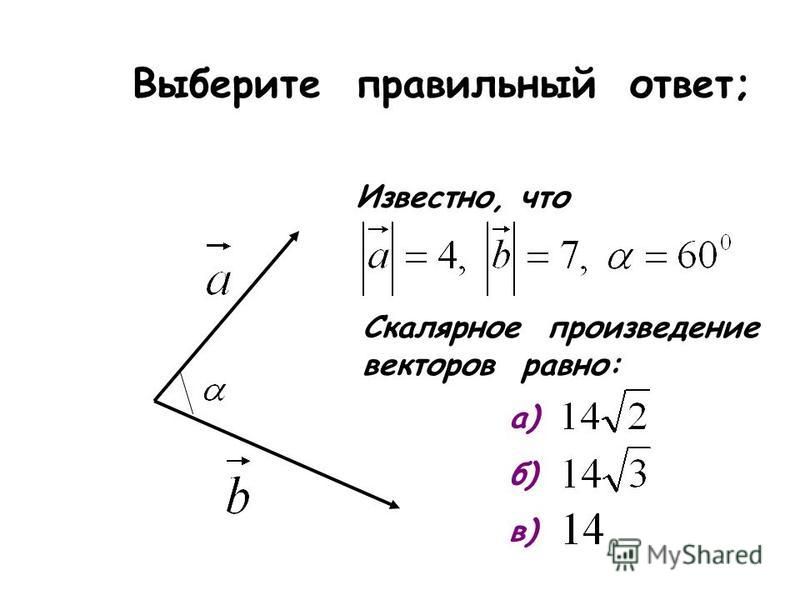
Вам не нужно запоминать элементы определителя, связанные с каждым элементом, поскольку их можно легко вывести. Просто вы должны вычислить прилагаемый определитель , es decir, tienes que eliminar la fila y columna en la que se encuentra cada elemento i, j, k de tal forma que con los elementos restantes formas un determinante 2×2. Aqui te enseñamos cómo разрешитель ип determinante де уна матриз 2×2.
Например, мы увидим решенное упражнение, в котором нас просят вычислить векторное произведение векторов
= (2, 0, -1) y = (1, 1, -2):
В результате векторного произведения имеем такой вектор:
Существует второй метод вычисления векторного произведения двух векторов по следующей математической формуле:
Метод состоит в умножении их модулей на синус угла, который они образуют, и унитарный вектор » n» , который ортогонален векторам и смысл и направление которого определяются правилом правой руки.
Если вы не знаете, как это сделать, вот как это сделать вычислить модуль вектора.
Модуль векторного произведения
Для вычислите модуль векторного произведения двух векторов , вы должны использовать эту формулу:
В этом случае результатом будет скалярное число, представляющее длину, которую сегмент результирующего вектора будет иметь.
Векторное произведение двух векторов в R2
Если нас попросят вычислить векторное произведение двух векторов в R2 Дальнейший процесс точно такой же, как и в R3. Нам просто нужно дополнить 0 недостающую компоненту вектора.
Например, вычислим векторное произведение векторов в R2
= (3, 2) y = (2, -1).
Как видите, no tenemos componente «k», así que los elementos a 3 y b 3 будет равно нулю . Принимая во внимание эту деталь, мы решаем упражнение, и у нас остается следующее:
Тройное векторное произведение
Тройное векторное произведение (также известное как двойное векторное произведение) состоит из векторного умножения двух векторов на полученный результат сделать еще одно векторное произведение с отсутствующим вектором. Например:
Например:
A × (B × C) = B (A — C) — C (A — B)
Путем умножения векторов B x C мы получаем вектор, который мы затем должны векторно умножить на A. результатом будет вектор , лежащий в плоскости, определяемой B и C.
Поскольку двойное векторное произведение обладает антикоммутативным свойством , мы также можем выразить его следующим образом:
A × (B × C) = — C x (A x B)
Наконец, следует отметить, что тройное произведение не имеет ассоциативного свойства .
Свойства векторного произведения
Вот еще не упомянутые свойства векторного произведения:
У нас есть много приложений для векторного произведения в мире математики, физики или астрономии.
Некоторые из тех, которые всегда используются в качестве примеров и которые позволяют нам вычислить площадь и объем некоторых фигур геометрических фигур, таких как треугольник или параллелограмм.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
10.
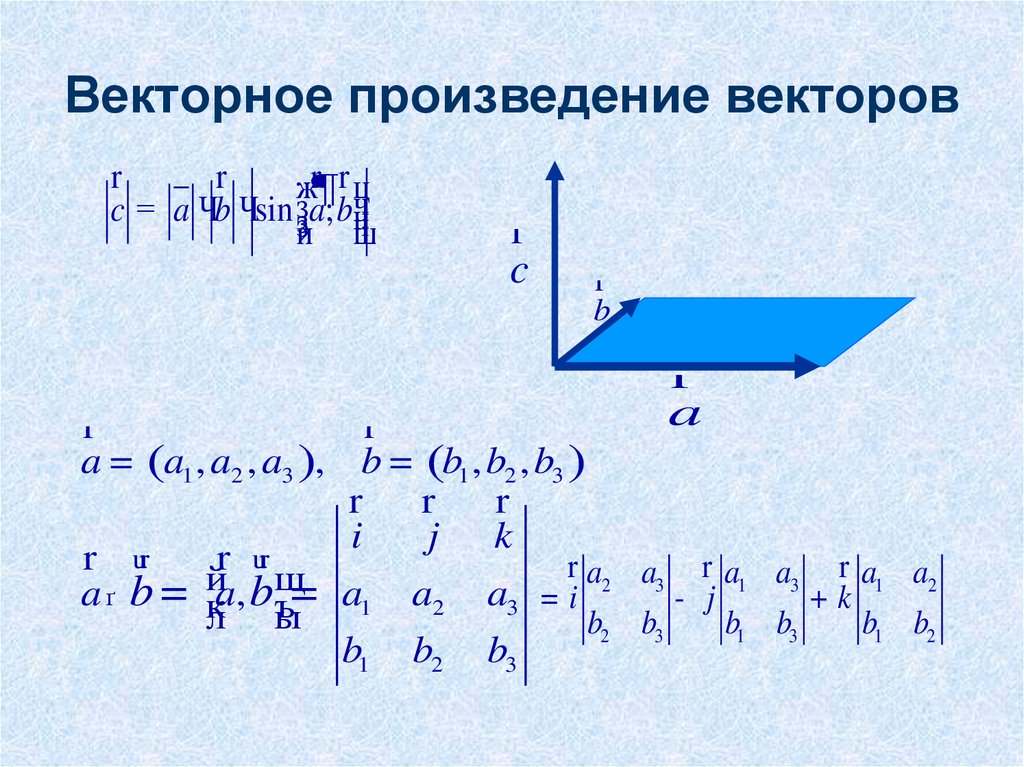 Матричная арифметика в NumPy и Python
Матричная арифметика в NumPy и PythonАвтор Бернд Кляйн . Последнее изменение: 24 марта 2022 г.
На этой странице ➤
В предыдущей главе нашего введения в NumPy мы продемонстрировали, как создавать и изменять массивы. В этой главе мы хотим показать, как мы можем выполнять в Python с модулем NumPy все основные матричные арифметики, такие как
Стандартные арифметические операторы
, это означает, что массивы должны иметь одинаковый размер.
импортировать numpy как np х = np.массив ([1, 5, 2]) у = np.массив ([7, 4, 1]) х + у
ВЫВОД:
массив ([8, 9, 3])
ВЫВОД: массив
([ 7, 20, 2])
ВЫВОД:
массив ([-6, 1, 1])
ВЫВОД: массив
([0,14285714, 1,25, 2.])
ВЫВОД:
массив ([1, 1, 0])
Сложение и вычитание векторов
Многие знают сложение и вычитание векторов из физики, а точнее из параллелограмм сил. Это метод решения (или визуализации) результатов приложение двух сил к объекту.
Сложение двух векторов, в нашем примере (см. рисунок) x и y, может быть представлено графически, поместив начало стрелки y на кончик стрелки x, а затем рисование стрелки от начала (хвоста) x до кончика (головки) y. Нарисованная новая стрелка представляет собой вектор x + y
.х = np.массив ([3, 2]) у = np.массив ([5, 1]) г = х + у г
ВЫВОД:
массив ([8, 3])
Вычитание вектора равносильно добавлению его отрицательного значения. Итак, разность векторов x и y равна сумме x и -y:
х — у = х + (-у)
Вычитание двух векторов можно геометрически определить следующим образом: чтобы вычесть y из x, мы помещаем конечные точки x и y в одну и ту же точку, а затем рисуем стрелку от вершины y к вершине x. Эта стрелка представляет собой вектор x — y, см. рисунок справа.
Эта стрелка представляет собой вектор x — y, см. рисунок справа.
Математически мы вычитаем соответствующие компоненты вектора y из вектора x.
Живое обучение Python
Нравится эта страница? Мы предлагаем живых обучающих курсов Python , охватывающих содержание этого сайта.
См.: Обзор курсов Live Python
Зарегистрироваться здесь
Скалярное произведение / скалярное произведение
В математике скалярное произведение — это алгебраическая операция, которая принимает два координатных вектора одинакового размера и возвращает одно число. Результат вычисляется путем умножения соответствующих записи и добавление этих продуктов. Название «точечный продукт» происходит от того факта, что центрированная точка «·» часто используется для обозначения эта операция. Название «скалярное произведение» акцентирует внимание на скалярной природе результата. результата.
Определение скалярного произведения:
Из определения скалярного произведения видно, что его можно использовать для вычисления косинуса
угла между двумя векторами.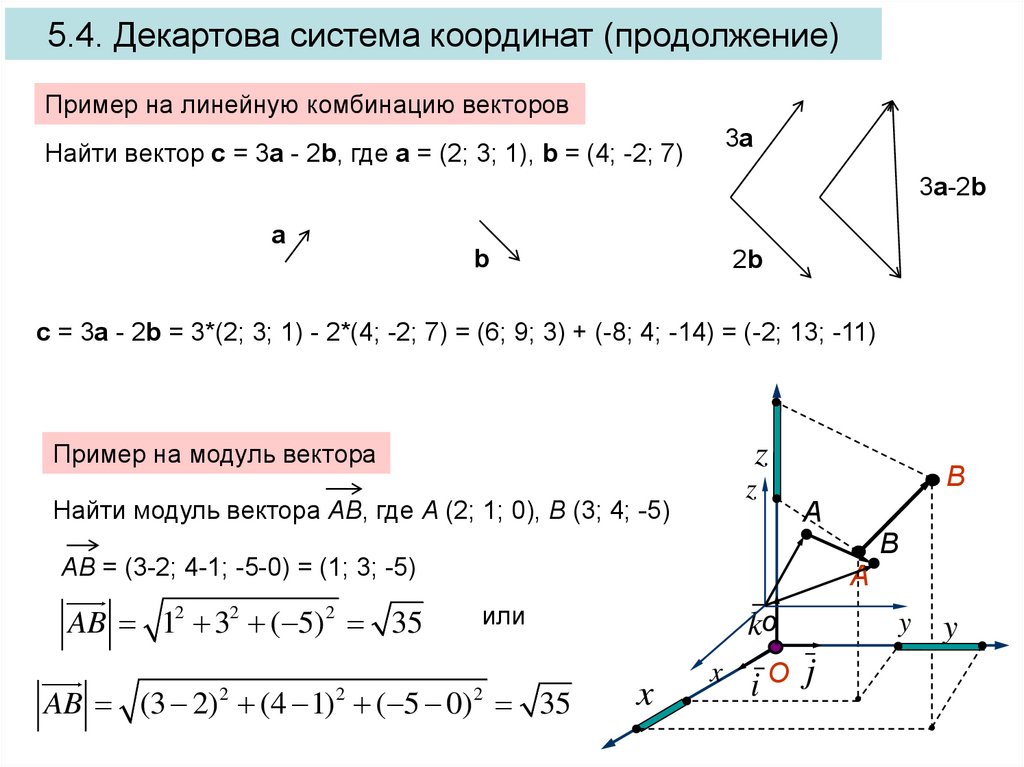
Расчет скалярного произведения:
Наконец, мы хотим продемонстрировать, как вычислить скалярное произведение в Python:
х = np.массив ([1, 2, 3]) у = np.массив ([-7, 8, 9]) np.dot (х, у)
ВЫХОД:
точка = np.dot (х, у) x_modulus = np.sqrt((x*x).sum()) y_modulus = np.sqrt((y*y).sum()) cos_angle = dot / x_modulus / y_modulus # косинус угла между x и y угол = np.arccos(cos_angle) угол
ВЫХОД:
0,8082337825
угол * 360/2/np.pi # угол в градусах
ВЫХОД:
46.308384970187326
36 >>> точка = np.dot(x,y) >>> x_modulus = np.sqrt((x*x).sum()) >>> y_modulus = np.sqrt((y*y).sum()) >>> cos_angle = dot / x_modulus / y_modulus # косинус угла между x и y >>> угол = np.arccos(cos_angle) >>> угол 0,808233782499 >>> angle * 360/2/np.pi # угол в градусах
ВЫХОД:
46.308384970187326
Матричный продукт
Произведение двух матриц можно вычислить, если количество столбцов левого
матрица равна количеству строк второй или правой матрицы.
Произведение (l x m)-матрицы A = (a ij ) i=1…l, j= 1..m и (m x n)-матрица B = (b ij ) i=1…m, j= 1..n является матрицей C = (c ij ) i=1…l, j= 1..n , что вычисляется следующим образом:
Следующий рисунок иллюстрирует это дополнительно:
Если мы хотим выполнить умножение матриц с двумя массивами numpy (ndarray), мы должны использовать скалярный продукт:
х = np.массив (((2,3), (3, 5)) y = np.matrix(((1,2), (5,-1)) печать (np.dot (х, у))
ВЫВОД:
[[17 1] [28 1]]
Живое обучение Python
Нравится эта страница? Мы предлагаем живых обучающих курсов Python , охватывающих содержание этого сайта.
См.: Обзор онлайн-курсов Python
Предстоящие онлайн-курсы
Python для инженеров и ученых
с 17 октября 2022 г. по 21 октября 2022 г.
Анализ данных с помощью Python
с 19 октября 2022 г.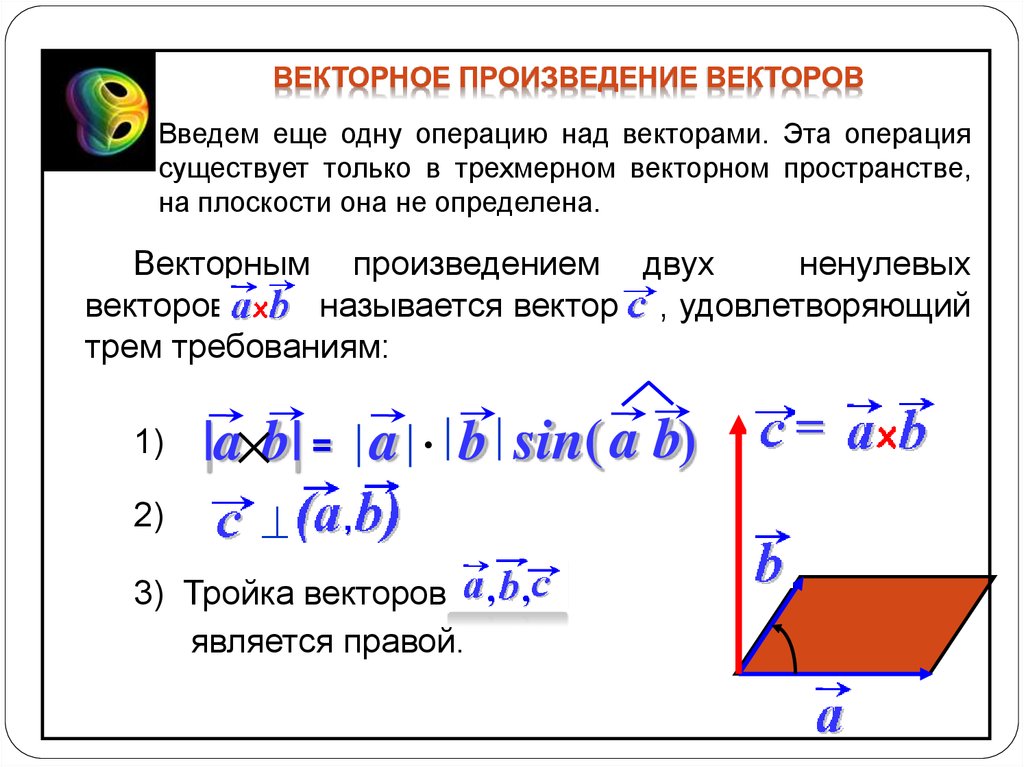 по 21 октября 2022 г.
по 21 октября 2022 г.
Зарегистрироваться здесь
Простое практическое приложение для умножения матриц
В следующем практическом примере мы подошли к разговору о радостях жизни.
Предположим, есть четыре человека, и мы назовем их Лукас, Миа, Леон и Ханна. Каждый из они купили шоколадные конфеты на выбор из трех. Марка А, В и С, не очень рыночный, мы должны признать. Лукас купил 100 г марки А, 175 г марки В и 210 г марки С. Миа выбирает 90 г А, 160 г В и 150 г С. Леон купил 200 г А, 50 г В и 100 г C. Ханне, видимо, не понравился бренд B, потому что она не покупала ни одного из них. Но она она, кажется, настоящая поклонница марки С, потому что купила их 310 г. Кроме того, она купил 120 г А.
Итак, какова цена в евро этих конфет: А стоит 2,98 за 100 г, В стоит 3,90 и только С 1,99 евро.
Если нам нужно подсчитать, сколько каждый из них должен был заплатить, мы можем использовать Python, NumPy и Matrix. умножение:
импортировать numpy как np NumPersons = np.массив([[100, 175, 210], [90, 160, 150], [200, 50, 100], [120, 0, 310]]) Price_per_100_g = np.array([2,98, 3,90, 1,99]) Price_in_Cent = np.dot (NumPersons, Price_per_100_g) Цена_в_евро = Цена_в_центах / 100 Цена_в_евро
ВЫВОД: массив
([13,984, 11,907, 9,9, 9,745])
Перекрестное произведение
Давайте перестанем есть вкусный шоколад и вернемся к более математическим и менее калорийная тема, т.е. перекрестное произведение.
Перекрестное произведение или векторное произведение — это бинарная операция над двумя векторами в трехмерном пространстве. пространство. Результатом является вектор, который перпендикулярен перемножаемым векторам и нормали к плоскости, содержащей их.
Перекрестное произведение двух векторов a и b обозначается как a × b.
Определяется как:
, где n — единичный вектор, перпендикулярный плоскости, содержащей a и b, в направлении
задается правилом правой руки.
Если любой из перемножаемых векторов равен нулю или векторы параллельны, то их перекрестное произведение равно нулю. В более общем случае величина произведения равна площади параллелограмм с векторами в качестве сторон. Если векторы перпендикулярны, то параллелограмм представляет собой прямоугольник, а величина произведения равна произведению их длин.
х = np.массив ([0, 0, 1]) у = np.массив ([0, 1, 0]) нп.кросс(х, у)
ВЫВОД:
массив ([-1, 0, 0])
нп.крест(у, х)
ВЫВОД:
массив ([1, 0, 0])
Живое обучение Python
Нравится эта страница? Мы предлагаем живых обучающих курсов Python , охватывающих содержание этого сайта.
См.: Обзор онлайн-курсов Python
Предстоящие онлайн-курсы
Python для инженеров и ученых
с 17 октября 2022 г. по 21 октября 2022 г.
Анализ данных с помощью Python
с 19 октября 2022 г. по 21 октября 2022 г.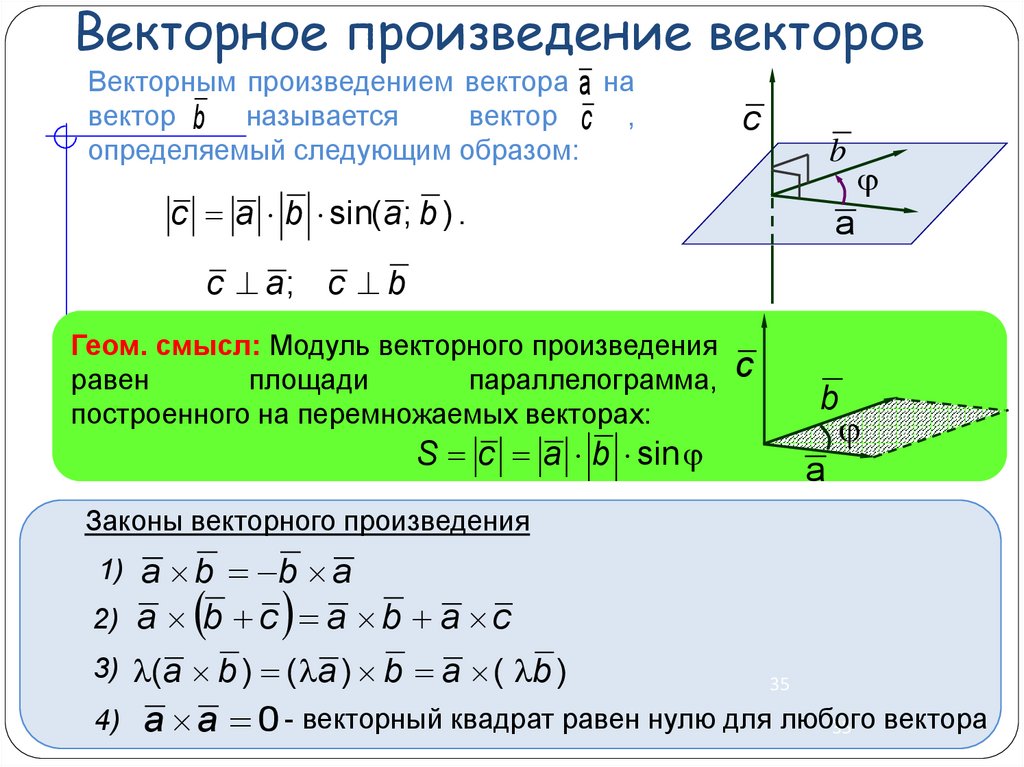
Зарегистрируйтесь здесь
HealthStream — Healthcare Workforce Solutions
HealthStream — Решения для кадров здравоохраненияНаши решения
Клиническая разработка
Получите душевное спокойствие, чтобы принимать обоснованные решения, обеспечивать компетентное оказание помощи и расширять возможности своих врачей в рамках или в рамках бюджета.
Реанимация
Комплексное решение для реанимации, позволяющее предотвратить то, что можно предотвратить, реанимировать то, что можно реанимировать, и улучшить результаты лечения
Удостоверение
Предоставляет все необходимое для запроса, сбора и проверки информации о поставщике, чтобы создать единый источник достоверной информации для последующих процессов.
Планирование и управление мощностями
Решения по оптимизации рабочей силы, повышающие производительность, удовлетворенность работой и пропускную способность.
Обучение и производительность
Инструменты для обучения и повышения квалификации, позволяющие вашим сотрудникам оказывать наилучшую медицинскую помощь
Качество и соответствие
Будьте уверены, что ваши программы обеспечения качества и соответствия требованиям соответствуют всем требованиям и улучшают результаты лечения пациентов.
Возмещение
Оптимизация возмещения расходов с помощью инновационного увлекательного обучения
Client Spotlight
Программа Красного Креста позволяет проводить количественную оценку производительности в соответствии со стандартом, который может быть воспроизведен во всей организации. Теперь у нас есть точный и измеримый способ оценки производительности для повышения эффективности СЛР.
Рассел Смит
Менеджер по обучению симов
Медицинский центр Cedars-Sinai
Этот продукт выполняет обещание предоставить медсестре необходимую информацию о подготовке, процедурах, осознании рисков, наилучших доказательствах — и все это таким образом, чтобы эффективно уважать время медсестры и ее потребность в концентрации внимания
Гей Ландстром
Главный медсестра
Система здравоохранения Сент-Джонс-Провиденс
Нам нужен был сложный и всеобъемлющий инструмент для оптимизации процессов COI, который был бы прост в освоении и использовании. Поэтому для нас было важно сотрудничать с поставщиком, который предлагал проверенное решение и послужной список 9.0003
Поэтому для нас было важно сотрудничать с поставщиком, который предлагал проверенное решение и послужной список 9.0003
Рон Джордж
Ушедший в отставку главный исполнительный директор
Система здравоохранения Генри Форда
Менее чем за 18 месяцев использования CE Unlimited в качестве варианта онлайн-обучения для медсестер PHSSC более 4500 курсов прошли более 1200 отдельных медсестер! Это показатель успеха и желание пользователей использовать этот тип обучения! Я взволнован!
Кэти Харрен, MSN, MHA, NEA-BC
Региональный директор Института сестринского дела
Providence & Health Services Южная Калифорния
Выберите партнеров
Мы гордимся тем, что сотрудничаем с лучшими в своем деле.
Узнайте, как стать партнером.
Актуальные темы
Восстановить трудовые ресурсы
Акцент на быструю адаптацию без ущерба для качества/компетентности, информацию для обоснованных решений, которые максимизируют результаты, и создание культуры автономии и вовлеченности, демонстрирующей приверженность работодателя.
Безопасность, качественное обслуживание
Компания HealthStream стремится помогать организациям уделять первоочередное внимание культуре качества и безопасности с помощью проверенных решений, нацеленных на изменение поведения медицинского персонала.
HealthStream: большой прорыв в сфере здравоохранения
От прорыва к оптимизму. Почему понадобилась пандемия, чтобы добиться значимых изменений, и куда, по мнению топ-менеджеров, движется отрасль.
РЕКОМЕНДУЕМЫЙ ПРОДУКТ
Jane®
Познакомьтесь с Jane®, запатентованным интеллектом, который ускоряет и индивидуализирует развитие компетенций.
Узнать больше
Дополнительные продукты
BLS, ALS & PALS
Более разумный и гибкий выбор для реанимации, наше адаптивное решение ориентировано на высокоэффективную СЛР.
[Подробнее]
Управление качеством
Комплексная система управления качеством, которая позволяет вам быть уверенным в качестве обслуживания, предоставляемого вашим учреждением
[Подробнее]
Резидентура медсестры
Расширьте свою программу резидентуры медсестер с помощью проверенных инструментов для поддержки лидеров, наставников и резидентов-медсестер.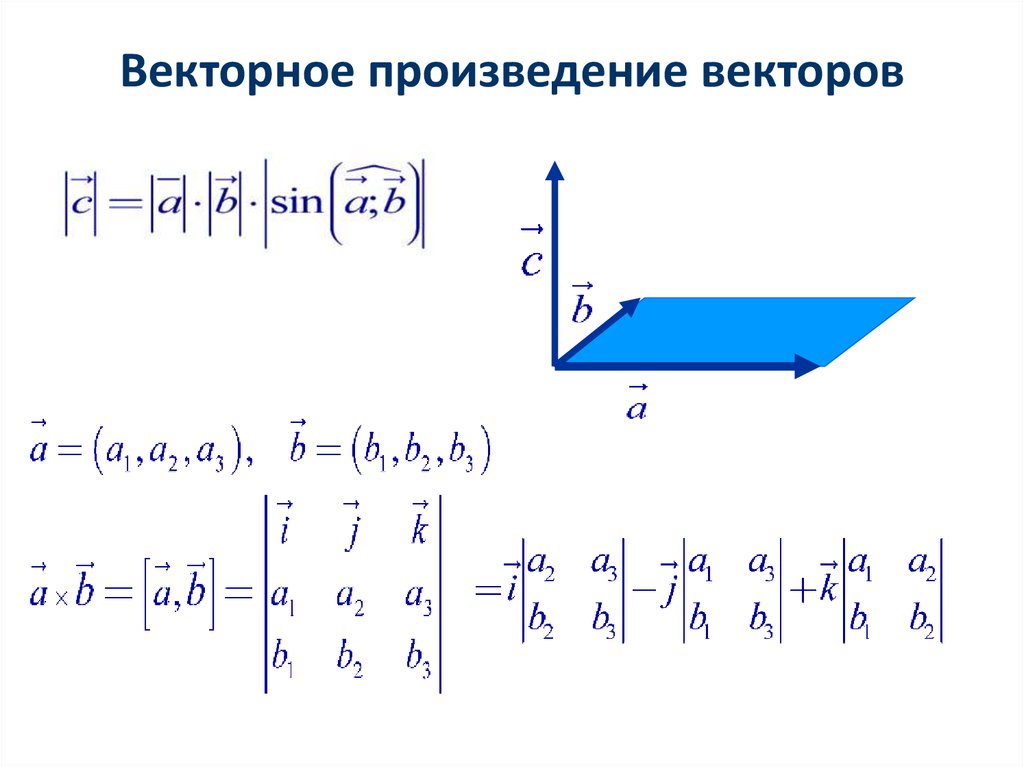
[Подробнее]
Compliance Education
Выявление пробелов в корпоративном соответствии и назначение персонализированного обучения на основе результатов оценки
[Подробнее]
Решения на базе
Свяжитесь с нами сегодня
Мы понимаем вашу потребность в максимальном использовании ресурсов при решении все более сложных потребностей в уходе, привлечении и удержании персонала, а также в постоянно меняющейся среде здравоохранения.
Запросить демонстрацию
DigiKey Electronics — Дистрибьютор электронных компонентов
Беспроводной модуль типа ABR
Модуль Murata Type ABR Wi-Fi® 11b/g/n+MCU со встроенной антенной на печатной плате основан на беспроводном микроконтроллере NXP 88MW320. Этот модуль поддерживает Wi-Fi 802.11b/g/n со скоростью передачи данных PHY до 72,2 Мбит/с со встроенным микроконтроллером Arm® Cortex®-M4F 200 МГц для приложений на стороне хоста.
Этот модуль поддерживает Wi-Fi 802.11b/g/n со скоростью передачи данных PHY до 72,2 Мбит/с со встроенным микроконтроллером Arm® Cortex®-M4F 200 МГц для приложений на стороне хоста.
Узнать больше
Разъем питания USB Type-C®
Автономная система розеток QKRC-10-05 не требует внешнего источника питания. QKRC-10-05 содержит блок питания, который преобразует входной переменный ток в выходную мощность 5 В 2 А постоянного тока. Для установки требуется только вставить розетку в панель или систему и подключить прилагаемые 24-дюймовые провода.
Узнать больше
ЦП DA1470x Arm® Cortex®-M33TM
Многоядерные беспроводные микроконтроллеры Renesas сочетают в себе процессор приложений и блок вычислений с плавающей запятой. DA1470x основан на процессоре Arm Cortex-M33 с восьмисегментным MPU, расширениями DSP и FPU одинарной точности, предлагающими до 240 dMIPS.
Узнать больше
Кабели питания для больниц Tripp Lite от Eaton
Узнать больше
Ручной инструмент для установки кабельных стяжек
Эргономичная серия инструментов Panduit с ручным управлением, натяжением и обрезанием кабельных стяжек с ручным управлением является наиболее предпочтительным ручным инструментом в отрасли. Эти универсальные инструменты можно использовать для производства, обслуживания или строительства.
Узнать больше
Двойной осевой PCI Express® Gen 4.0
Удлинители PCIeкомпании 3M обеспечивают расширение с низкими потерями от материнской платы до периферийного устройства. Позволяет пользователям перемещать слот для карты PCIe или соединять слоты на двух разных печатных платах и совместима с электромеханическими разъемами карты (CEM).
Узнать больше
Мощные датчики для крошечных пространств — Q2X
Миниатюрный датчик серии Q2X имеет компактный корпус, идеально подходящий для промышленных помещений и оборудования с ограниченным пространством, а также обеспечивает превосходную надежность обнаружения и стабильный отклик. Q2X имеет множество применений, включая электронику, прецизионную сборку и полупроводники.
Узнать больше
Всенаправленная сотовая антенна TGX.45
Узнать больше
СИРИУС Модульный
Наличие машин и установок является предпосылкой для максимальной производительности. Длительные простои могут быть не только дорогостоящими, но и означать, что клиенты начинают терять доверие. SIRIUS Modular предлагает вам уникальный и всеобъемлющий портфель промышленных систем управления.
Узнать больше
SiC-диод Шоттки 6-го поколения, 650 В, 10 А
Благодаря преимуществам производительности диодов с барьером Шоттки из карбида кремния (SiC) от Wolfspeed системы силовой электроники могут рассчитывать на соответствие более высоким стандартам эффективности, чем решения на основе кремния, а также достигать более высоких частот и удельной мощности.
Узнать больше
Управление питанием
Соединители полюса батареи и шины батареи Phoenix Contact обеспечивают съемное, надежное и безопасное подключение к системам накопления энергии (ESS). Разъемы, разработанные для этих стандартизированных систем хранения постоянного тока, рассчитаны на напряжение до 1500 В постоянного тока и до 350 А.
Узнать больше
Решения для Интернета вещей
ROHM предлагает широкий ассортимент продуктов, специально предназначенных для удовлетворения сложных требований приложений IIoT, в том числе:
Узнать больше
Стабильная работа в суровых условиях
Узнать больше
Датчики Eaton
Ассортимент Eaton состоит из термисторов NTC и PTC, включая сборки от SMD до NTC для высокоточного измерения температуры. Он также включает в себя широкий спектр резисторов из металлической фольги и пластин, а также мощных шунтов с низкими допусками TCR и DCR для высокоточного измерения тока.
Он также включает в себя широкий спектр резисторов из металлической фольги и пластин, а также мощных шунтов с низкими допусками TCR и DCR для высокоточного измерения тока.
Узнать больше
ODU AMC® Series T Новое решение «3 в 1»
На один разъем можно установить три варианта блокировки: двухтактный, отрывной или резьбовой. Эти высокопрочные разъемы можно быстро и легко очищать даже в экстремальных условиях и под нагрузкой. Они водонепроницаемы в соответствии со стандартом MIL 810 (до 20 м) и имеют диапазон температур от -65°C до +175°C.
Подробнее
Серия RACxx-K: модули переменного/постоянного тока в наличии
Узнать больше
Соединители Cannon серии IT
Узнать больше
Адаптеры SMA коммерческого класса
Узнать больше
Контакторы Schneider Electric Easy TeSys
Узнать больше
Online CRM Software Systeme & Lösungen
Überspringen, direct zum Inhalt
NEU: Salesforce Genie, Echtzeit-Plattform, mit der Sie Zeit und Geld span und den Umsatz steigern.
Мехр эрфарен
Демо-видео
Новое в Salesforce
Мастер-классы
Inspirierende Einblicke in Themen rund um Technologien und Entscheidungen.
Кабинет
Lesen Sie jetzt unsere neue KMU-Trendstudie.

Состояние маркетинга
Был ли beschäftig führende Marketingexperten?
Так что канн Ihr Unternehmen von Salesforce Produkten Produkten Produkten
Finden Sie die perfect Lösung für Ihre Branche
Jetzt энддекен
Erfahren Sie mehr darüber, wie Sie das Wachstum Ihres Unternehmens fördern können
Студиен
«Состояние продаж» — Bericht
Die neue Studie zeigt, wie Unternemen trotz einer weltweiten Krise erfolgreich verkaufen.
Видеосериал
Как сделать серию видео
Lernen Sie wie ein CRM alle Unternehmensbereiche unterstützt
Virtuelle Salesforce Events – ганц, созданный в домашних условиях
Erweitern Sie Ihre Kenntnisse – kostenlos mit der Online-Lernplattform Trailhead
Nutzen Sie Salesforce mit hilfreichen Apps und fundierter Expertise noch beser.
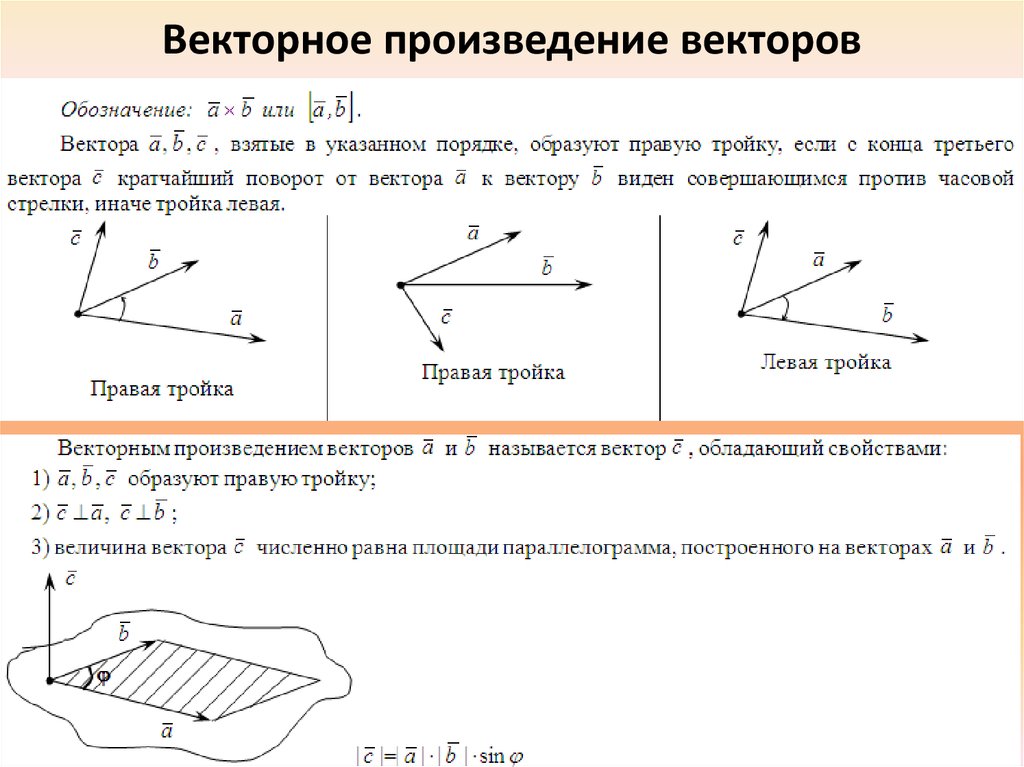

 \circ=4\cdot 3\cdot 1=12$
\circ=4\cdot 3\cdot 1=12$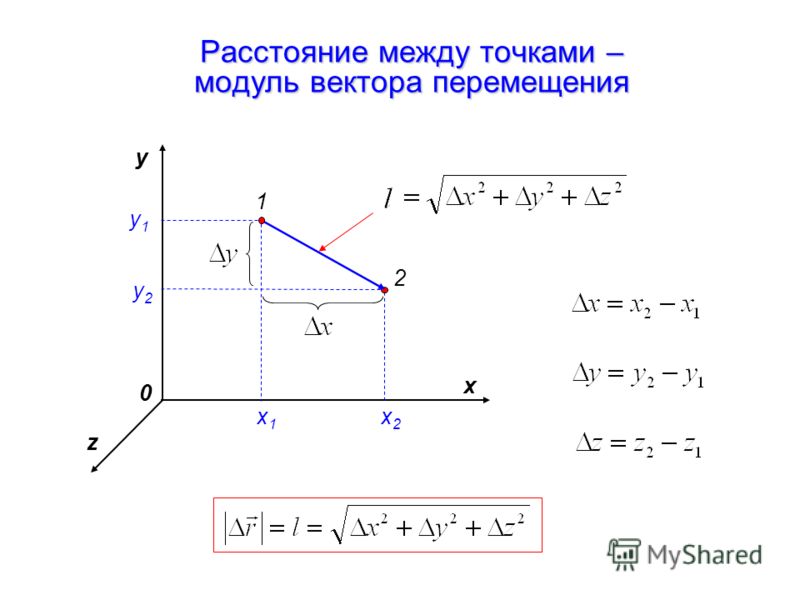



 Тогда cos2J = 1 – sin2J = 0,64.
Тогда cos2J = 1 – sin2J = 0,64.


 Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .
Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → . Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.


 Найдите их векторное произведение.
Найдите их векторное произведение.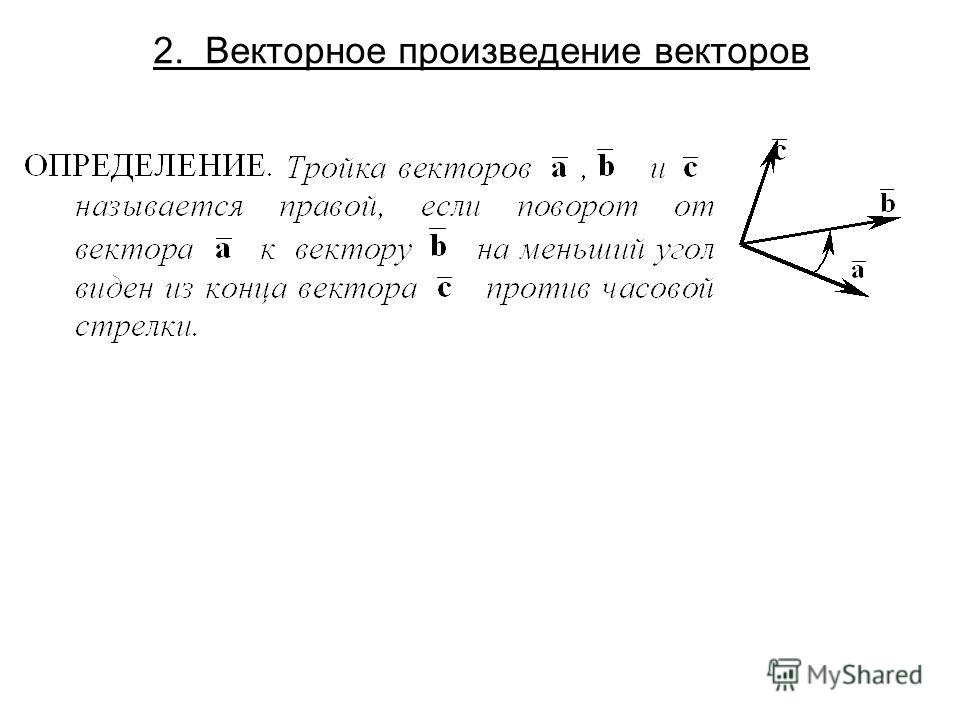
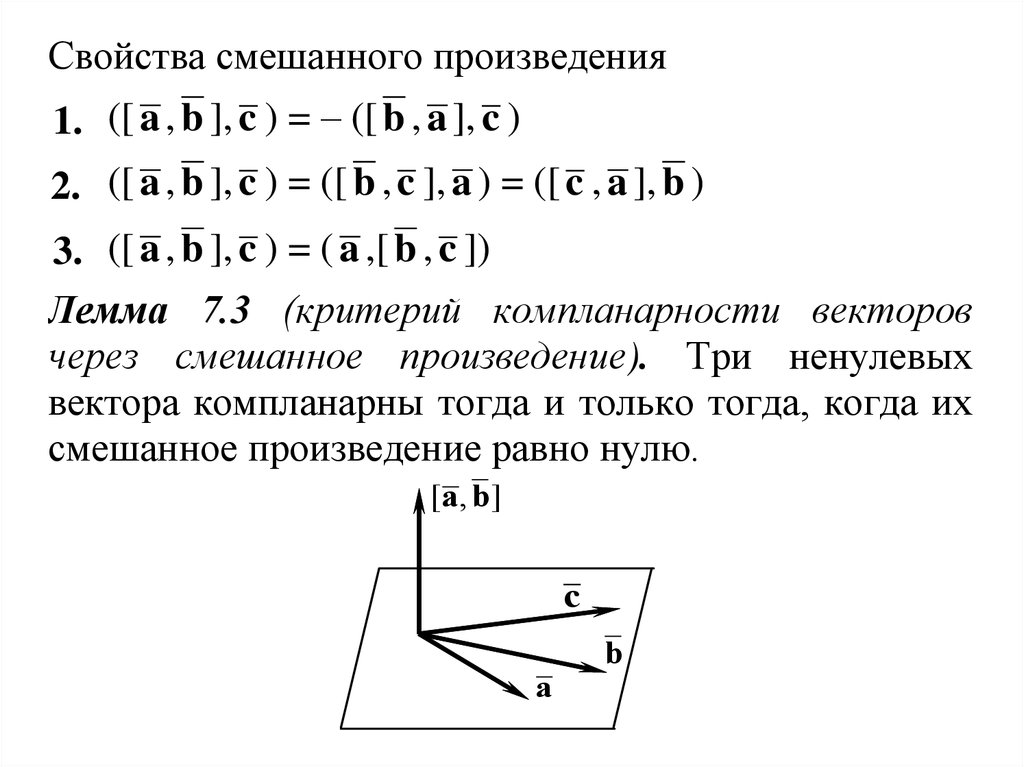 Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .
Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → . .
.


 \circ=4\cdot 3\cdot 1=12$
\circ=4\cdot 3\cdot 1=12$
 j
;
j
; Аналогично доказывается при
l
Аналогично доказывается при
l 1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.

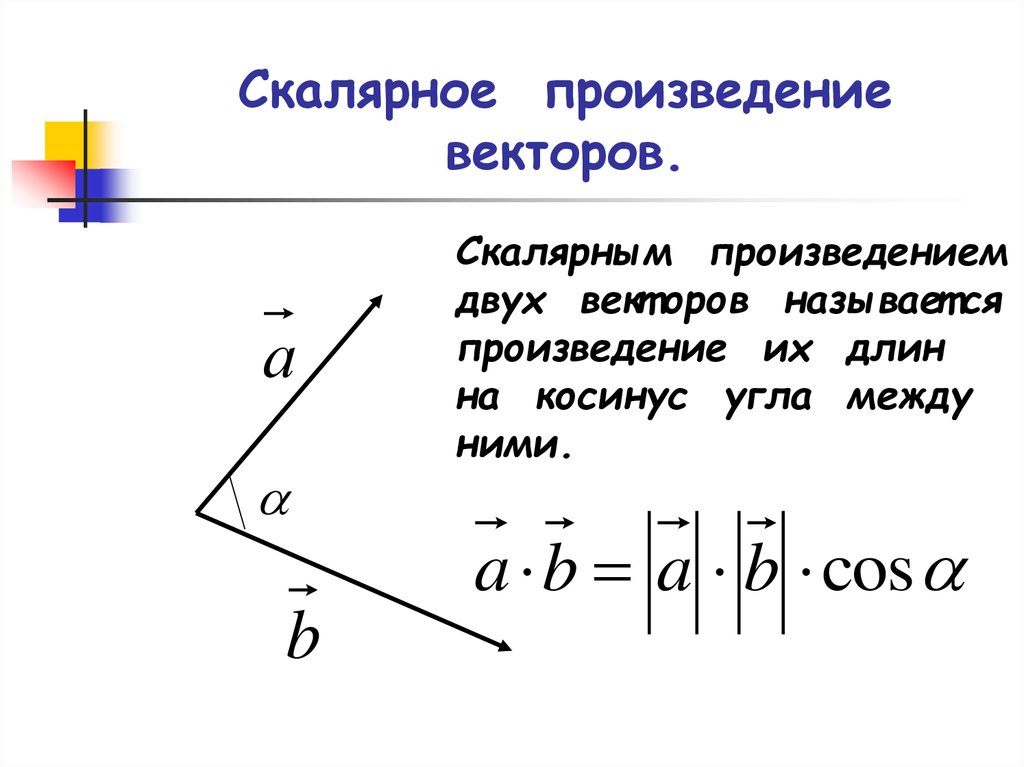 Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо иногда применяется векторное произведение векторов.
Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо иногда применяется векторное произведение векторов. Проверить на конкретных примерах верность выведенной формулы.
Проверить на конкретных примерах верность выведенной формулы.
 Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
 Поэтому это произведение векторов называется векторным.
Поэтому это произведение векторов называется векторным.


 5√2.
5√2. Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны. Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с.
С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =) Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще! Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву . Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения: В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)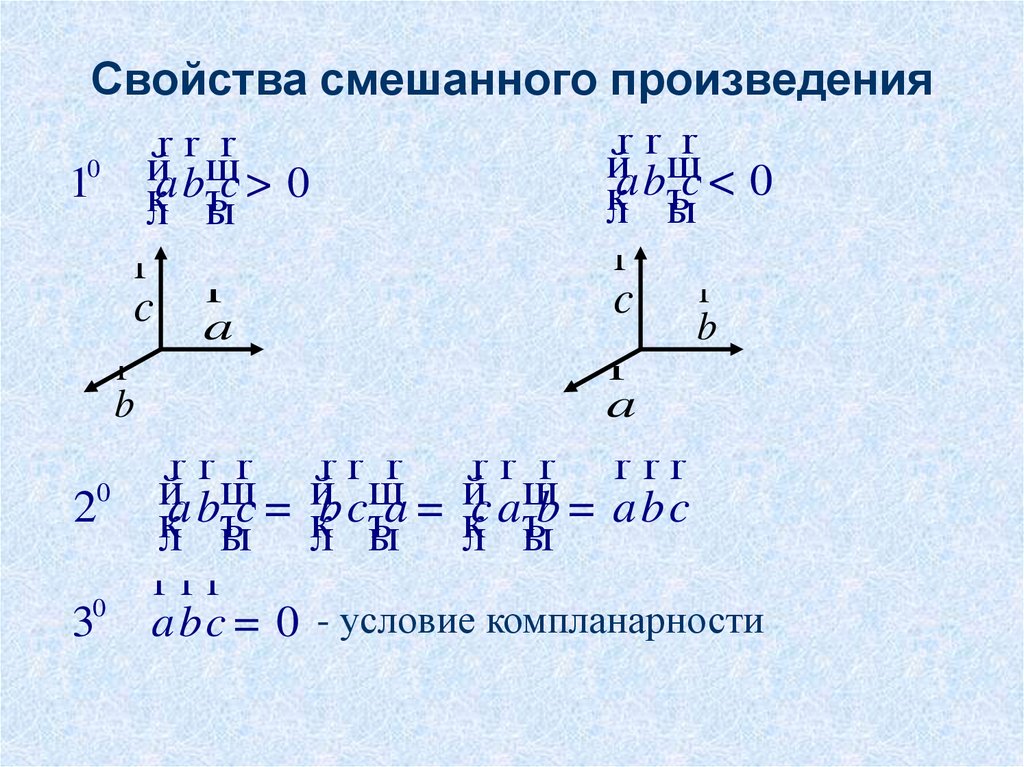 Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться! Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.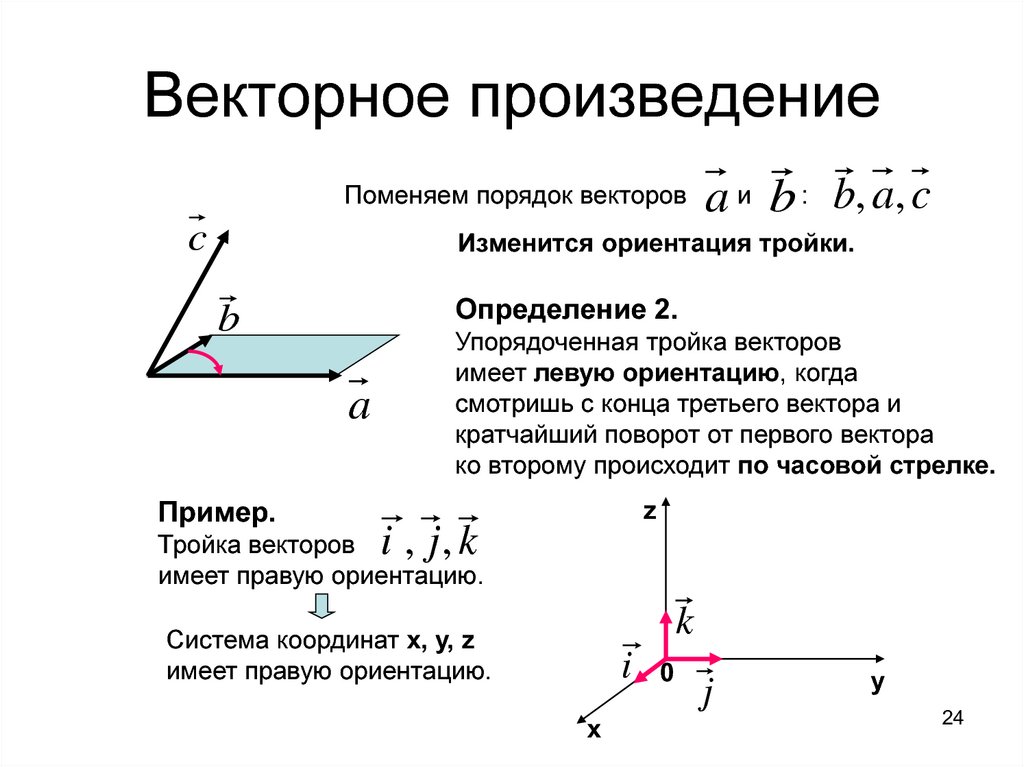 Поэтому пусть будет.
Поэтому пусть будет.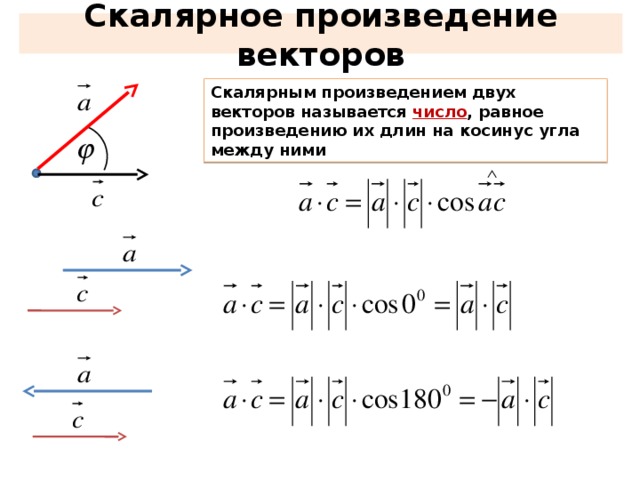 Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа: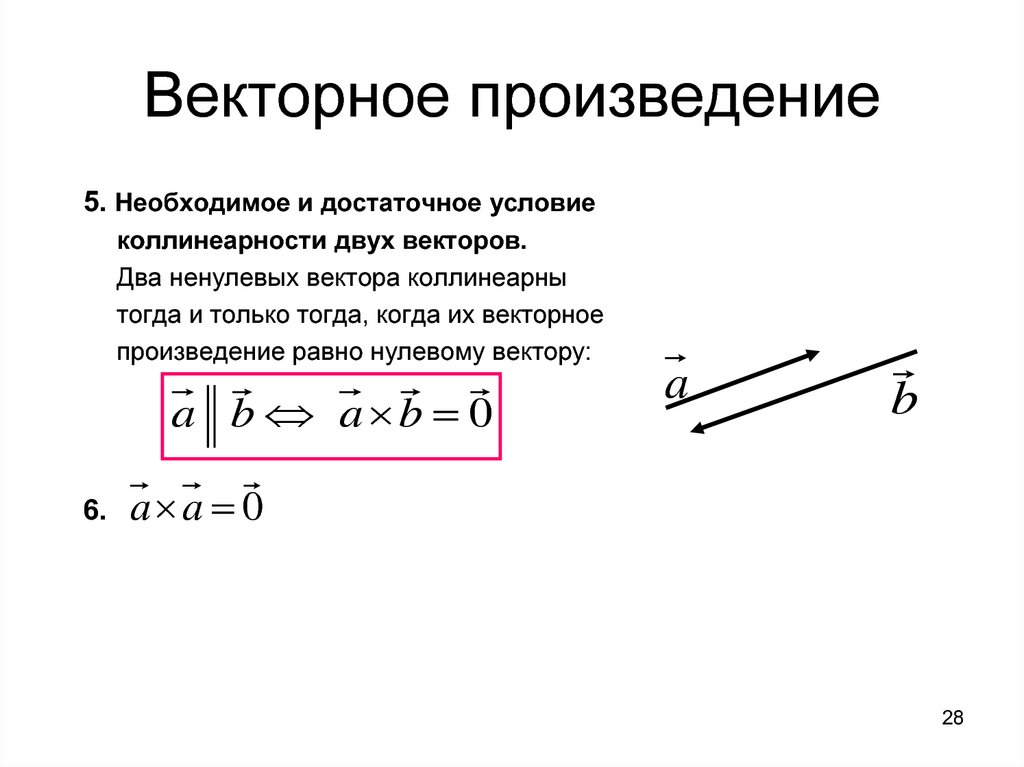 Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:



 Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами. Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). 5.
5.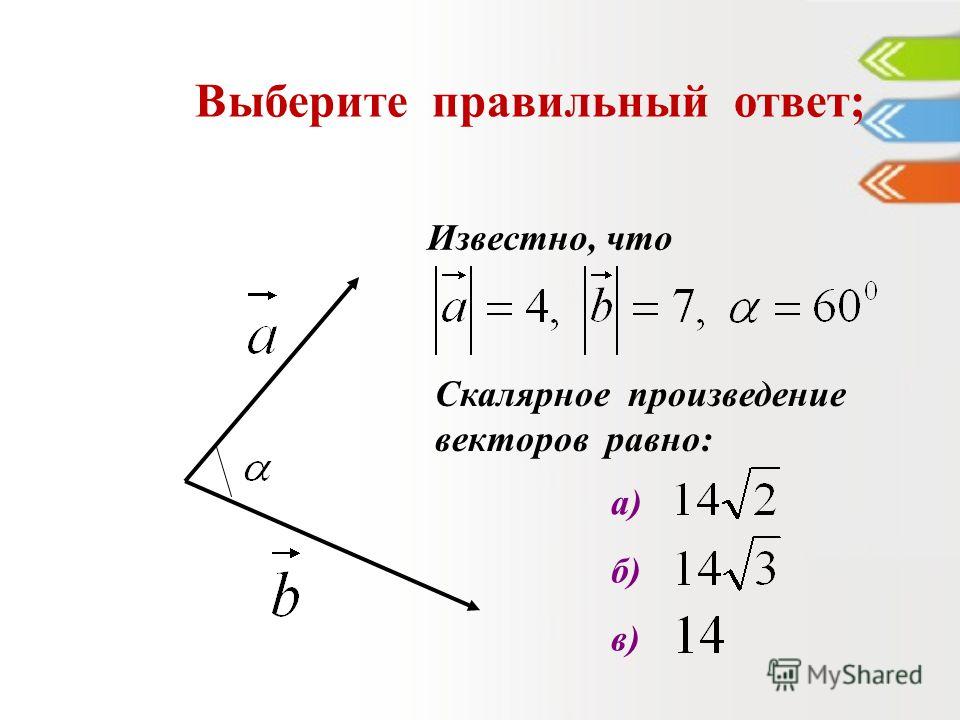 То есть:
То есть: 
 ])
])
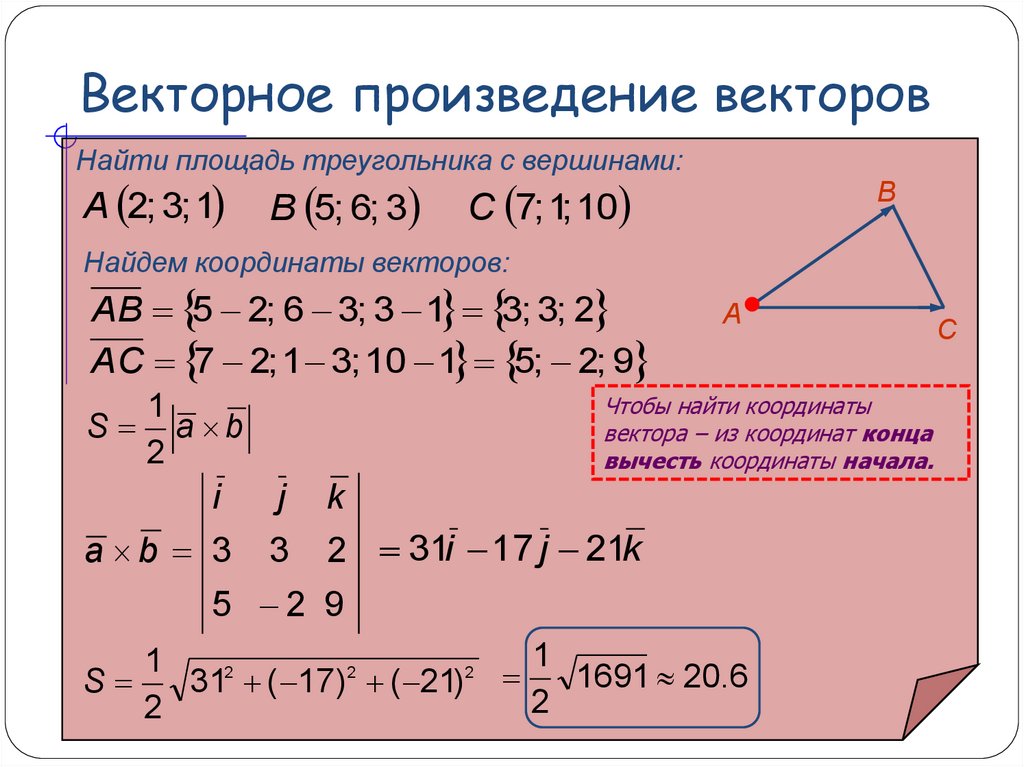 массив([[100, 175, 210],
[90, 160, 150],
[200, 50, 100],
[120, 0, 310]])
Price_per_100_g = np.array([2,98, 3,90, 1,99])
Price_in_Cent = np.dot (NumPersons, Price_per_100_g)
Цена_в_евро = Цена_в_центах / 100
Цена_в_евро
массив([[100, 175, 210],
[90, 160, 150],
[200, 50, 100],
[120, 0, 310]])
Price_per_100_g = np.array([2,98, 3,90, 1,99])
Price_in_Cent = np.dot (NumPersons, Price_per_100_g)
Цена_в_евро = Цена_в_центах / 100
Цена_в_евро