Что такое синус и косинус? Что такое тангенс и котангенс?
Откуда появилась тригонометрия?
Знакомство наше начнём с глубокой древности. С древнего Египта, Вавилона и Китая. Не переживайте, все 20 веков тригонометрии мы с вами освоим всего за 20 минут. Можете засекать время.)
Итак, откуда же и как появилась тригонометрия?
Первоначально, на заре своего становления, тригонометрия не являлась самостоятельным разделом математики. Она, скорее, была частью астрономии. Дело всё в том, что древним астрономам, которые интересовались нашими главными небесными телами (Луной и Солнцем) и вовсю изучали их поведение, постоянно приходилось просчитывать и расстояния до них. С достаточной точностью для того далёкого времени, между прочим.) Скажем, чтобы предсказывать затмения. Или приливы/отливы. Просчитывать эти самые расстояния древним людям приходилось с помощью обыкновенного… треугольника. ) Да-да! Просчитывать — значит, искать какие-то неизвестные элементы треугольника по известным другим. Это могут быть стороны (т.е. расстояния), а могут быть и какие-то углы. Всё зависело от того, какую именно задачу решали древние люди. И тот факт, что между сторонами и углами треугольника существует взаимосвязь, уже тогда у древних людей не вызывал сомнений.
) Да-да! Просчитывать — значит, искать какие-то неизвестные элементы треугольника по известным другим. Это могут быть стороны (т.е. расстояния), а могут быть и какие-то углы. Всё зависело от того, какую именно задачу решали древние люди. И тот факт, что между сторонами и углами треугольника существует взаимосвязь, уже тогда у древних людей не вызывал сомнений.
Чуть позже, по мере развития цивилизации, большинство учёных стало осознавать чрезвычайную важность тригонометрии не только в астрономии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика, навигация в дальних морских походах, геодезия и картография… Слово «триангуляция» (разбиение местности на треугольники) вам знакомо? Нет? А тригонометрическая вышка или тригонометрический знак? Тоже нет? Что ж, если попутешествуете по нашей необъятной Родине, то на открытых местах (на вершинах холмов, в полях и т.п.) вы можете заметить небольшие пирамидки или башенки. Эти пирамидки — и есть тригонометрические знаки. Или геодезические пункты. Они служили верой и правдой геодезистам и картографам тех далёких времён для составления карт местности.) Этих знаков сохранилось по России очень много.)
Эти пирамидки — и есть тригонометрические знаки. Или геодезические пункты. Они служили верой и правдой геодезистам и картографам тех далёких времён для составления карт местности.) Этих знаков сохранилось по России очень много.)
Короче, в любых областях, где приходилось сталкиваться с обычным треугольником и вычислением его элементов (сторон и углов) через другие его элементы, людям неизбежно приходилось сталкиваться с тригонометрией.
А дальше — теория колебаний, электричество, акустика, радиосвязь… И в основе всего этого богатства — тоже тригонометрия, да…)
И не было бы у нас сегодня ни мобильников, ни телевизоров, ни микроволновок, ни спутниковых навигаторов, ни многих других современных атрибутов комфортной жизни, кажущихся нам обыденностью…
Итак, в основе всей тригонометрии лежит обыкновенный треугольник! Да-да! Именно так.
Почему именно треугольник и откуда собственно взялось это красивое слово «тригонометрия» — об этом далее. )
)
Синус, косинус, тангенс и котангенс… Что за звери?
Для начала нарисуем в тетрадке самый обычный прямоугольный треугольник. Стороны его обозначим как a, b и c, а один из острых углов обозначим буквой α. Это греческая буква «альфа», при написании очень похожая на «двойку без головы». Самая распространённая буква в тригонометрии для обозначения углов. Привыкаем.)
Вот такая картинка у нас получится:
На всякий случай, напомню, что стороны, образующие прямой угол, называются катетами (a и b — катеты), а третья сторона, лежащая напротив прямого угла, называется гипотенузой (c — гипотенуза).
Казалось бы, треугольник и треугольник, эка невидаль! Что с ним делать-то? Спокойствие. Сейчас всё узнаете.)
Сейчас, как и древние люди, мы будем наш треугольник измерять. Да-да! Кстати, страшное слово «тригонометрия» с древнегреческого языка на русский так и переводится — измерение треугольников.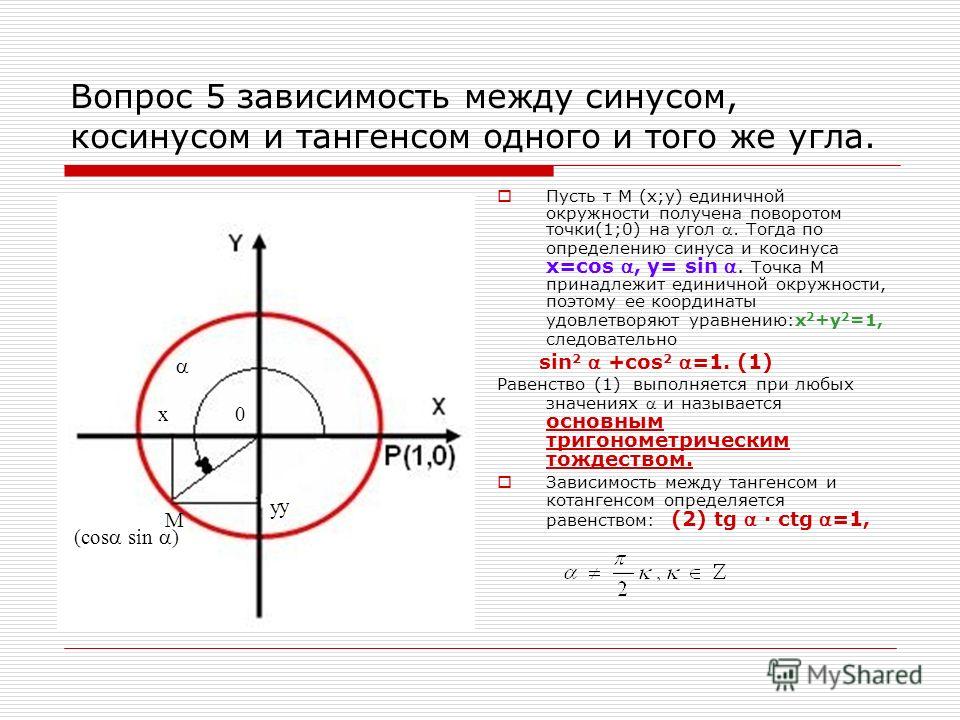 Намёк понятен?)
Намёк понятен?)
Вот и измеряем. На рисунке специально клеточки нарисованы, как и в заданиях ЕГЭ или ОГЭ бывает. Чему равен катет a? Трём клеточкам (a = 3). А катет b? Не вопрос! Четырём клеточкам он равен (b = 4). А гипотенуза? Гипотенузу, конечно, по клеточкам не посчитаешь, но, воспользовавшись великой и могучей теоремой Пифагора, легко можно получить, что гипотенуза равна пяти (c = 5).
Кстати сказать, прямоугольный треугольник со сторонами 3, 4, 5 — весьма интересная фигура! Он известен ещё с античных времён и называется египетским треугольником. Ибо активно применялся для построения прямых углов египетскими землемерами и архитекторами. В том числе и при построении пирамид, между прочим.)
А вообще, целые числа a, b, c, которые могут быть длинами сторон прямоугольного треугольника, т.е. для которых выполняется теорема Пифагора
a2 + b2 = c2,
в математике так и называются — пифагоровыми тройками.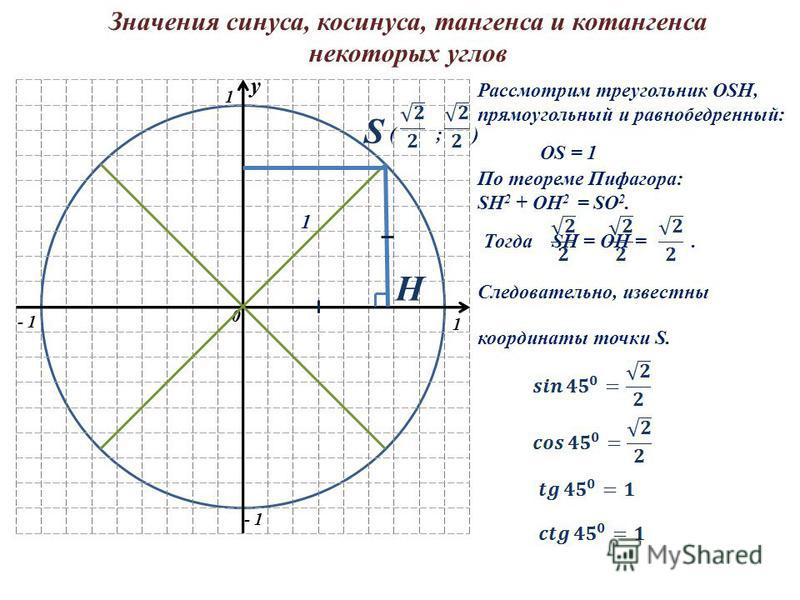 Тройка (3; 4; 5) — самая известная. Ещё распространена тройка чисел (5; 12; 13). Или (8; 15; 17). Таких троек известно очень и очень много. Кому интересно, прогуляйтесь по ссылке и почитайте. Для самообразования.)
Тройка (3; 4; 5) — самая известная. Ещё распространена тройка чисел (5; 12; 13). Или (8; 15; 17). Таких троек известно очень и очень много. Кому интересно, прогуляйтесь по ссылке и почитайте. Для самообразования.)
А мы продолжим. Теперь сделаем следующее. Поделим длину катета a на длину катета b. Или, как принято говорить в математике, возьмём отношение a к b.
Получим:
a/b = 3/4
Можно наоборот, поделить b на a. Получим 4/3. Или, скажем, поделить a на c. Получим 3/5. Иными словами, можно брать любые стороны прямоугольного треугольника, делить их длины друг на друга и получать какие-то числа. Безразмерные.
И что из этого? Согласен, пока ничего особенного. Бессмысленное занятие, одним словом.)
А теперь я поступлю следующим образом. Увеличу треугольник, продлив стороны b и c, но не как попало, а так, чтобы наш треугольник остался прямоугольным. Это важно. На картинке я для удобства увеличил все стороны треугольника в два раза.
Это важно. На картинке я для удобства увеличил все стороны треугольника в два раза.
Вот так:
Угол α, как видно, остался прежним. Старые стороны a, b и с превратились в новые стороны x, y, z. Их длины, естественно, изменились, увеличившись вдвое:
x = 6
y = 8
z = 10
А вот отношения новых длин сторон — не изменились!
Смотрите сами.
Было: a/b = 3/4.
Стало: x/y = 6/8 = 3/4.
И для других соответствующих сторон их отношения также не изменятся. Можно что угодно делать с треугольником — увеличивать, уменьшать, сохраняя при этом угол α, а отношения соответствующих сторон всё равно останутся прежними. Кому интересно, можете попробовать и проверить. Это полезно.)
А вот это уже крайне важно! Соотношения сторон в прямоугольном треугольнике никак не зависят от длин этих самых сторон при одном и том же угле α. Этот факт настолько важен, что указанные отношения сторон даже заслужили свои специальные названия. Ну что, знакомимся? 🙂
Этот факт настолько важен, что указанные отношения сторон даже заслужили свои специальные названия. Ну что, знакомимся? 🙂
Синус угла α — это отношение противолежащего катета к гипотенузе:
sin α = a/c
Косинус угла α — это отношение прилежащего катета к гипотенузе:
cos α = b/c
Тангенс угла α — это отношение противолежащего катета к прилежащему:
tg α = a/b
Котангенс угла α — это отношение прилежащего катета к противолежащему:
ctg α = b/a
Вот такая вот весёлая семейка. Возможно, особо внимательные и любознательные ученики заметили, что я ничего не сказал здесь про отношения гипотенузы к катетам c/a и с/b. Они имеют какие-то свои специальные названия? Конечно! Секанс и косеканс.)
Возможно, особо внимательные и любознательные ученики заметили, что я ничего не сказал здесь про отношения гипотенузы к катетам c/a и с/b. Они имеют какие-то свои специальные названия? Конечно! Секанс и косеканс.)
sec α = c/b
cosec α = c/a
Но эти соотношения никакого практического смысла не имеют и в школе не рассматриваются. И мы тоже не будем.)
Вся эта великолепная четвёрка (синус, косинус, тангенс и котангенс) называется тригонометрическими функциями.
Зачем я всё это так занудно повторяю и некоторые слова выделяю жирным шрифтом? Да затем, что это надо запомнить! Причём запомнить железно. Улавливаете?
Процесс запоминания можно существенно облегчить, если для начала запомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе гипотенуза появляется.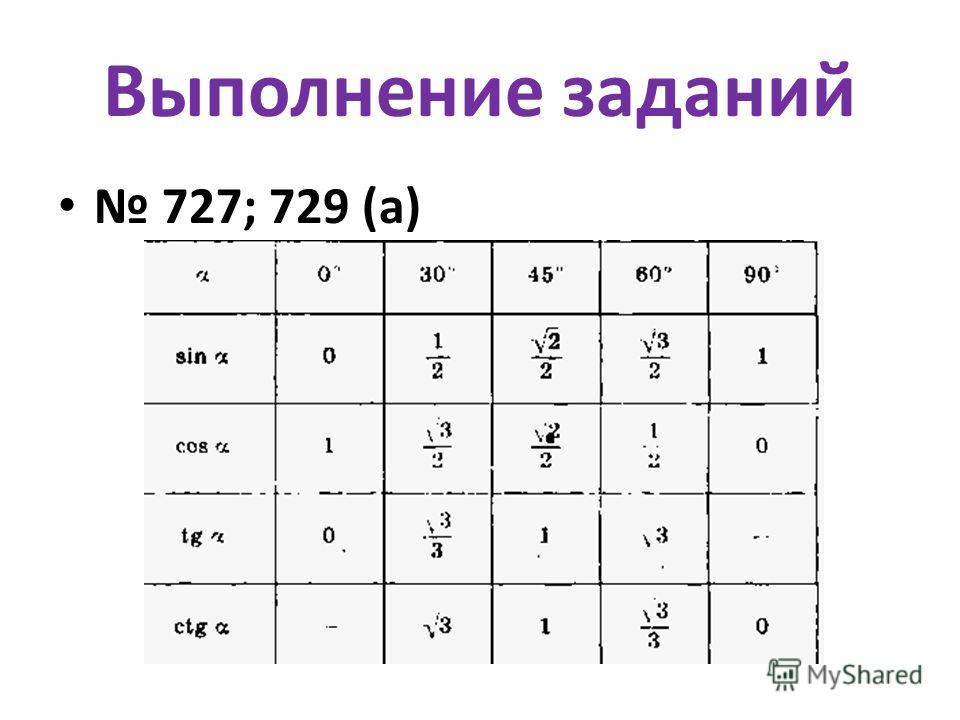 Кроме того, ещё могут нахлынуть сомнения, какой из катетов, противолежащий или прилежащий, сидит соответственно у синуса/косинуса. Да и у тангенса/котангенса тоже. Здесь работает принцип под условным названием «дальше/ближе».
Кроме того, ещё могут нахлынуть сомнения, какой из катетов, противолежащий или прилежащий, сидит соответственно у синуса/косинуса. Да и у тангенса/котангенса тоже. Здесь работает принцип под условным названием «дальше/ближе».
Например: синус угла — это отношения дальнего от угла (т.е. противолежащего) катета к гипотенузе, а косинус — отношение ближнего (т.е. прилежащего) катета к гипотенузе.
Тангенс — отношение дальнего от угла катета к ближнему. А котангенс — наоборот.
Подведём предварительный итог. Как вы видите, всё просто. Синус, косинус, тангенс и котангенс — это просто какие-то числа. Безразмерные. Ни больше ни меньше. Для каждого конкретного угла — свои персональные.
А теперь давайте поразмышляем вот над чем. Как вы думаете, почему мы всегда говорим синус, косинус, тангенс и котангенс угла? Вроде бы мы отношения сторон считаем.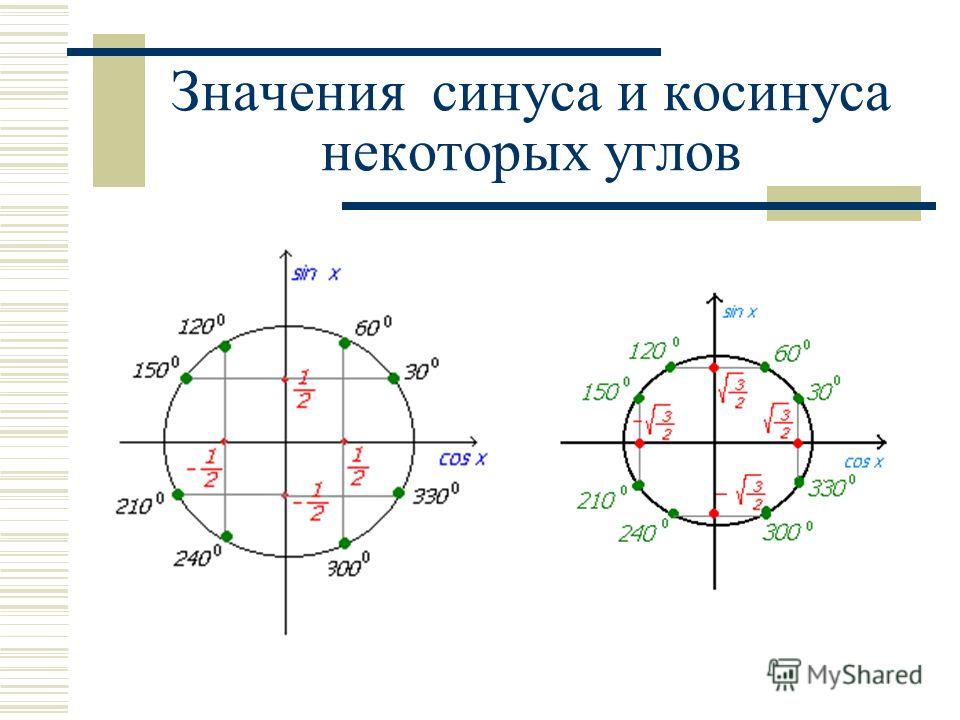 Угол-то тут при чём? Догадались? Если нет, то тогда смотрим на следующую картинку:
Угол-то тут при чём? Догадались? Если нет, то тогда смотрим на следующую картинку:
Что здесь нового? Я изменил (увеличил) угол с α до β («бета»). При этом все отношения сторон стали другими!
Скажем, было a/b = 3/4, а стало m/b = 5/4. И все остальные отношения сторон также поменялись. Какой вывод можно сделать? Да! При одном и том же угле α отношения длин сторон никак не зависят от их длин. Но при этом колоссально зависят от этого самого угла! И только от него. Именно поэтому тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к углу. И говорить, скажем, о тангенсе, без конкретного угла — бессмысленно. Угол — ключевая действующая фигура в тригонометрии.
Отсюда можно сделать важный вывод: если нам известен некий угол, то мы автоматически знаем и все его тригонометрические функции. Это неразрывная связь, которую надо уяснить железно.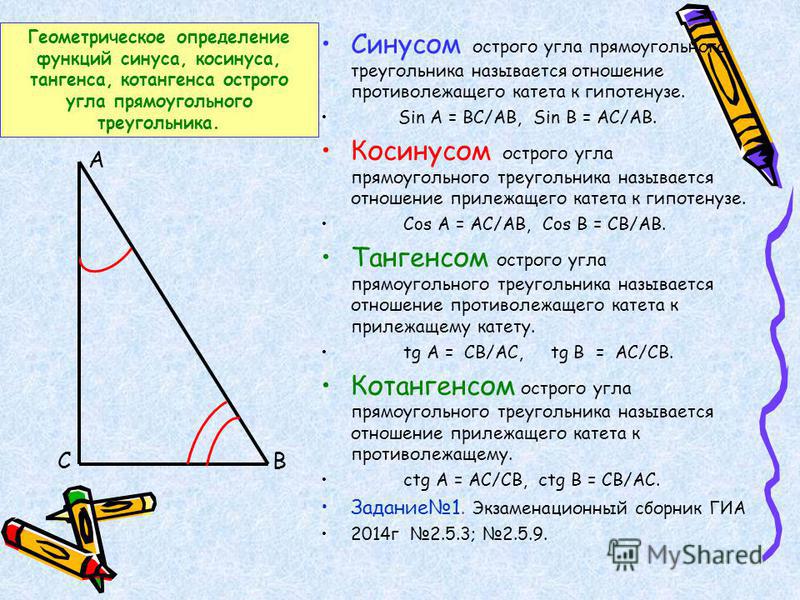
Стало быть, если нам дан угол, то считается, что все его тригонометрические функции нам тоже известны. Полностью весь комплект, от синуса до котангенса. И наоборот, если нам дана какая-то из тригонометрических функций угла (скажем, косинус), то автоматически нам известен и сам угол.
Запоминаем: если нам известен угол, то нам автоматически известны и ВСЕ его тригонометрические функции. И наоборот — известна какая-то из тригонометрических функций (хотя бы одна), то известен и сам угол.
У каждого угла есть свои персональные синус и косинус. И почти у каждого — свои тангенс и котангенс.
Слово «почти» для тангенса и котангенса стоит не случайно. Об этом узнаете дальше.)
Сейчас, в век калькуляторов и компьютеров, найти тригонометрическую функцию какого-либо угла — не проблема. И наоборот, по функции найти угол. Нажал нужную кнопочку и — ответ готов.) А вот раньше, во времена отсутствия вычислительной техники, для тригонометрических функций углов существовали свои специальные таблицы. Таблицы Брадиса назывались. Они, конечно же, существуют и поныне, но, благодаря техническому прогрессу, давно отошли на задний план и пылятся на полках. Но знать об их существовании и уметь ими пользоваться — очень и очень полезно.
Таблицы Брадиса назывались. Они, конечно же, существуют и поныне, но, благодаря техническому прогрессу, давно отошли на задний план и пылятся на полках. Но знать об их существовании и уметь ими пользоваться — очень и очень полезно.
Конечно же, запомнить все-все значения тригонометрических функций всех-всех углов нереально. И не нужно.) Но среди всего многообразия углов есть некоторые углы, про которые вы обязаны знать всё. Об этом в следующих уроках будет. Но общий принцип «знаю угол — знаю его тригонометрические функции» срабатывает всегда! Безотказно.)
А зачем нам вообще нужны все эти синусы, косинусы, тангенсы и котангенсы — спросите вы? Вопрос резонный.
Пожалуйста! Вот вам типичная задачка из ЕГЭ:
Всё. Никаких данных, кроме тех, что на картинке, больше нет. Нужно найти длину катета AB.
Что делать будем? Клеточки не спасают: треугольник как-то неправильно ориентирован. Специально, похоже. ) Известна длина гипотенузы (6 клеток). Зачем-то дан ещё и угол…
) Известна длина гипотенузы (6 клеток). Зачем-то дан ещё и угол…
Вот тут самое время вспомнить про тригонометрию. Раз нам дан угол, то вспоминаем заклинание: «знаю угол — знаю и его тригонометрические функции!» И какую же из функций в дело пускать? А что нам дано в задачке? Нам дана гипотенуза AB, дан угол А, а найти просят прилежащий к этому углу катет.
Понятное дело, что надо косинус в дело пускать. Вот и действуем. Прямо по определению косинуса (отношение прилежащего катета к гипотенузе) пишем:
cos A = AB/AC
Гипотенуза AC равна 6 клеток, угол А у нас 60 градусов. Про этот угол известно, что его косинус равен 1/2. Это одно из тех значений, которое ученик знать обязан. Безо всяких таблиц и безо всяких калькуляторов!
Подставляем наши данные и получаем:
1/2 = АВ/6
Простенькое линейное уравнение с величиной АВ в качестве неизвестного. Решаем и получаем:
Решаем и получаем:
АВ = 3
Что и является верным ответом.
В этой задачке нам, конечно, пришлось вспомнить, чему равен косинус угла в 60 градусов. Для знающих учеников никаких проблем. А вот у новичков, ещё не знакомых с тригонометрическими функциями популярных углов, пока остаются вопросы… Откуда и почему именно 1/2? А не 1? Или, может быть, 2/3…
Ответы на эти вопросы будут позже. В соответствующем уроке.)
Ещё из той же оперы, ближе к нашей теме. Уже чисто на определение и понимание смысла тригонометрических функций. Никаких конкретных табличных значений знать не требуется.
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.
Внушает? Вспоминаем определение тангенса — отношение противолежащего катета к прилежащему. Но… где здесь катеты? Дан просто угол, а для тангенса нам позарез нужен прямоугольный треугольник.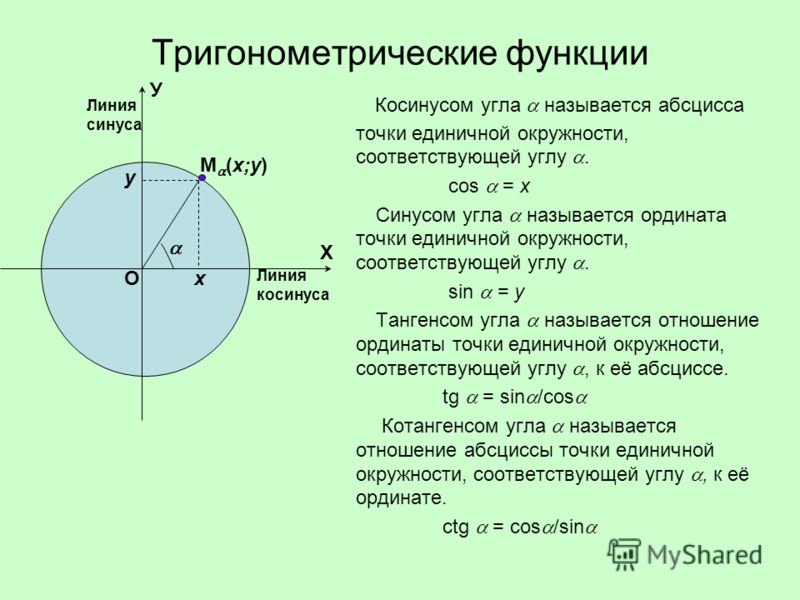 Где его взять?!
Где его взять?!
Не беда! Раз надо, значит… сделаем!) Привяжем наш угол к некоторому прямоугольному треугольнику, про который мы точно знаем всё что нам нужно. А именно — катеты. Первое что напрашивается — опустить перпендикуляр из точки А на сторону ОВ.
Вот так:
Ну и как? Осеняет? Вот вам и прямоугольный треугольник и катеты! Противолежащий катет AH = 2, а прилежащий OH = 4.
Прямо по определению тангенса записываем и считаем:
И все дела.) Это правильный ответ.
А теперь задачка для самостоятельного решения.
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите все тригонометрические функции этого угла.
Что, круто, да? Да-да, надо найти полный набор функций — от синуса до котангенса включительно. Тренироваться так тренироваться.)
Но где здесь прямоугольный треугольник? Нету его! Да и угол как-то совсем уж скверно расположен. Ни одну из сторон напрямую по клеточкам не посчитать, да…
Ни одну из сторон напрямую по клеточкам не посчитать, да…
Что ж, подскажу немного, что именно надо дополнительно построить, чтобы не надорваться. Снова, как и в предыдущей задаче, опускаем перпендикуляр из точки А на сторону OB. Получим прямоугольный треугольник AHO.
Смотрим картинку:
А теперь внимание! Клеточки, конечно, дело хорошее, удобное и красивое. Но… Кто гарантировал, что основание перпендикуляра (точка Н) уляжется ровно на середину отрезка OB (т.е. строго в один из узлов сетки)? Интуиция? Интуиция в математике — штука опасная. Особенно при рисовании картинок, да…
Поэтому, прежде чем что-то решать, что-то считать, делаем задание по элементарной геометрии. На доказательство. А именно — докажите, что отрезок AH, проведённый так, как показано на картинке, действительно будет перпендикулярен отрезку OB. Или, что то же самое, треугольник AHO — действительно прямоугольный. И да помогут вам вспомогательные синие пунктирные линии и теорема Пифагора (это подсказка)! Ну и клеточки спасут, само собой.:)
И да помогут вам вспомогательные синие пунктирные линии и теорема Пифагора (это подсказка)! Ну и клеточки спасут, само собой.:)
Без доказательства этого важного факта и без прямоугольного треугольника говорить о каких-либо тригонометрических функциях бессмысленно. Пока что… Придёт время — и мы с вами научимся считать любые тригонометрические функции любых углов без прямоугольного треугольника. Вообще. Как? Совсем скоро узнаете. Всему своё время.)
А пока — доказываем перпендикулярность отрезков, а затем считаем синус, косинус, тангенс и котангенс угла. После доказательства все необходимые данные для расчёта тригонометрических функций у вас уже будут. Обязательно.)
Ответы (в беспорядке):
А где какая функция — это уж вы сами как-нибудь.)
Итак, вот мы с вами и освоили синус, косинус, тангенс и котангенс на самом примитивном уровне. С помощью обычного прямоугольного треугольника. Но это пока только первый шаг.
Но это пока только первый шаг.
Когда древние люди поняли, что у каждого угла имеется свой набор тригонометрических функций, они озадачились вполне логичным вопросом — а не связаны ли как-нибудь синус, косинус, тангенс и котангенс между собой? Чтобы, зная какую-то одну из функций, можно было бы отыскать и все остальные? Не вычисляя сам угол.
Обо всём об этом — в следующем уроке.)
Тригонометрия — синус, косинус, тангенс, котангенс
Математика синус косинус тангенс котангенс
Возьмём x-axis и y-axis (orthonormal) и пусть O будет началом. Окружность с центром в точке O и с радиусом = 1 известна как Тригонометрическая окружность или Единичная окружность.
- x — координата P называется косинусом t. Записывается как cos(t) ; y — координата P называется синусом t. Записывается как sin(t) ; Число sin(t)/cos(t) называется тангенсом t. Записывается как tg(t) ; число cos(t)/sin(t) называется котангенсом t.
 Записывается как ctg(t) .
Записывается как ctg(t) .Функция синуса
Sin : R -> R
Все тригонометрические функции являются периодическими. Период синуса равен 2π.
Диапазон функции: [-1,1].
Функция косинуса
Cos : R -> R
Период косисинуса равен 2π.
Диапазон функции: [-1,1].
Функция тангенса
Tg : R -> R
Диапазон функции равен R. В этом случае период равен π и функия не может быть определена для
X = (π/2) + kπ, k=0,1,2.
График функции тангенса в интервале 0 — π
Анимираная графика тангенса(открыть в новом окне):
График функции тангенса в интервале 0 — 2 π
Функция котангенса
Ctg : R -> R
Диапазон функции равен R. В этом случае период равен π и функция не может быть определена для
X = kπ, k=0,1,2.
Значения sin, cos, tan, cot при значениях углов 0°, 30°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°
| $\alpha rad$ | $0$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\pi$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $\frac$ | $2\pi$ |
| $sin\alpha$ | $0$ | $\frac$ | $\frac$ | $\frac$ | $1$ | $\frac$ | $\frac$ | $\frac$ | $0$ | $-\frac$ | $-\frac$ | $-\frac$ | $-1$ | $-\frac$ | $-\frac$ | $-\frac$ | $0$ |
| $cos\alpha$ | $1$ | $\frac$ | $\frac$ | $\frac$ | $0$ | $-\frac$ | $-\frac$ | $-\frac$ | $-1$ | $-\frac$ | $-\frac$ | $-\frac$ | $0$ | $\frac$ | $\frac$ | $\frac$ | $1$ |
| $tan\alpha$ | $0$ | $\frac$ | $1$ | $-$ | $-\sqrt$ | $-1$ | $-\frac$ | $0$ | $\frac$ | $1$ | $\sqrt$ | $-$ | $-\sqrt$ | $-1$ | $-\frac$ | $0$ | |
| $cot\alpha$ | $-$ | $\sqrt$ | $1$ | $\frac$ | $0$ | $-\frac$ | $-1$ | $-\sqrt$ | $-$ | $\sqrt$ | $1$ | $\frac$ | $0$ | $-\frac$ | $-1$ | $-\sqrt$ | $-$ |
Самый простой способ, чтобы запомнить основные значения sin и cos углов 0°, 30°, 60°, 90°:
Sin([0, 30, 45, 60, 90]) = cos([90, 60, 45, 30, 0]) = $\sqrt>$
Тригонометрические тождества
Для t радиан одна точка соответствует с координатами P(cos(t),sin(t)) на единичной окружности.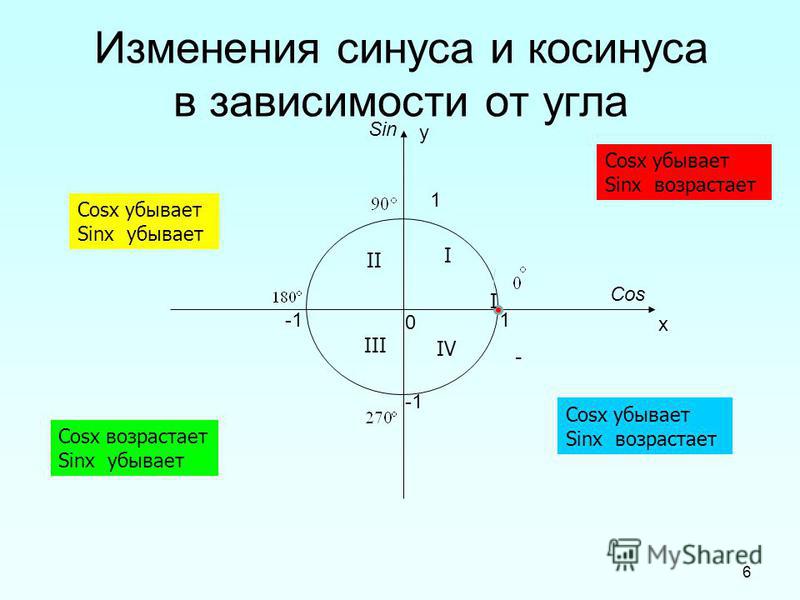 4\alpha$
4\alpha$
Формулы понижения степени
Формулы сложения
$\sin(\alpha + \beta) = \sin(\alpha)\cdot \cos(\beta) + \cos(\alpha)\cdot \sin(\beta)$
$\sin(\alpha — \beta) = \sin(\alpha)\cdot \cos(\beta) — \cos(\alpha)\cdot \sin(\beta)$
$\cos(\alpha + \beta) = \cos(\alpha)\cdot \cos(\beta) — \sin(\alpha)\cdot \sin(\beta)$
$\cos(\alpha — \beta) = \cos(\alpha)\cdot \cos(\beta) + \sin(\alpha)\cdot \sin(\beta)$
$\sin(\alpha + \beta + \gamma) = \sin\alpha \cos\beta \cos\gamma + \cos\alpha \sin\beta \cos\gamma + \cos\alpha \cos\beta \sin\gamma — \sin\alpha \sin\beta \sin\gamma$
$\cos(\alpha + \beta + \gamma) = \cos\alpha \cos\beta \cos\gamma — \sin\alpha \sin\beta \cos\gamma — \sin\alpha \cos\beta \sin\gamma $
$- \sin\alpha \cos\beta \sin\gamma — \cos\alpha \sin\beta \sin\gamma$
$\textrm(\alpha + \beta + \gamma) = \frac\alpha + \textrm\beta + \textrm\gamma — \textrm\alpha\cdot \textrm\beta \cdot \textrm\gamma>\alpha\cdot\textrm\beta — \textrm\beta\cdot\textrm\gamma — \textrm\alpha\cdot\textrm\gamma>$
Функция синуса
Sin : R -> R
Все тригонометрические функции являются периодическими. Период синуса равен 2π.
Период синуса равен 2π.
Диапазон функции: [-1,1].
Cos : R -> R
Период косисинуса равен 2π.
Диапазон функции: [-1,1].
Sin R — R Все тригонометрические функции являются периодическими.
Www. math20.com
25.12.2017 9:51:11
2017-12-25 09:51:11
Источники:
Https://www. math20.com/ru/algebra/trigonometriya. html
Синус, косинус, тангенс и котангенс в тригонометрии: определения, формулы, примеры, угол поворота » /> » /> .keyword { color: red; }
Математика синус косинус тангенс котангенс
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x, y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x, y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x, y ). cos α = х
cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x, y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x, y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа T называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу T ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа T — ордината точки единичной окружности, соответствующей числу T. sin t = y
Косинус числа T — абсцисса точки единичной окружности, соответствующей числу T. cos t = x
Тангенс числа T — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу T. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу T, совпадает с точкой, в которую переходит начальная точка после поворота на угол T радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z ).
Можно сказать, что sin α, cos α, t g α, c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу T соответствует определенное значение синуса или косинуса числа T. Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x, y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
Sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Zaochnik. com
14.07.2018 15:11:28
2018-07-14 15:11:28
Источники:
Https://zaochnik. com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/
Синус, косинус, тангенс и котангенс: формулы, таблица » /> » /> .keyword { color: red; }
Математика синус косинус тангенс котангенс
Тригонометрия — один из видов науки о математике, изучающий функции по тригонометрии с применением их в геометрии.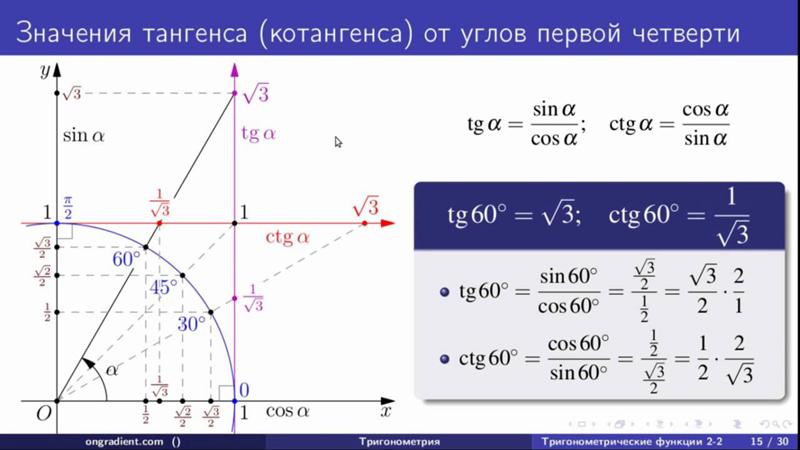
Начало своего изучения данный научный раздел берет где-то в античной Греции, считается что первыми стали применять такие функции астрономы, а после в землемерии и строительстве. В средние века, большое внимание тригонометрии уделяли учёные Индии и Востока.
В этой статье будут рассмотрены понятия и различные определения тригонометрической науки. А также основные функции которыми являются: синус, косинус, тангенс, котангенс.
В начале стоит поговорить об определениях:
- Угол определяется в двух величинах: градусы и радианы. Так как окружность определяется 360 единицами, то 1∘равен 1\360 части окружности. Гипотенуза — напротив лежащая сторона относительно прямого угла; Катеты — две стороны, отходящие от прямого угла.
Определения основных функций
По началу понятие функций тригонометрии, значением которого был угол, вычислялось через отношение сторон треугольника, который обладает прямым углом.
Определения для острого угла прямоугольника.
- Функция Sin a — Синус угла — отношение напротив лежащего катета к гипотенузе Cos a — Косинус угла — отношение стороны треугольника (катета), который прилегает к данному углу и гипотенузы; Tg a — Тангенс угла — отношение стороны треугольника который называется катетом и лежит напротив угла к прилежащему углу катету ; Ctg a — Котангенс угла — прилежащего катета к противолежащему.
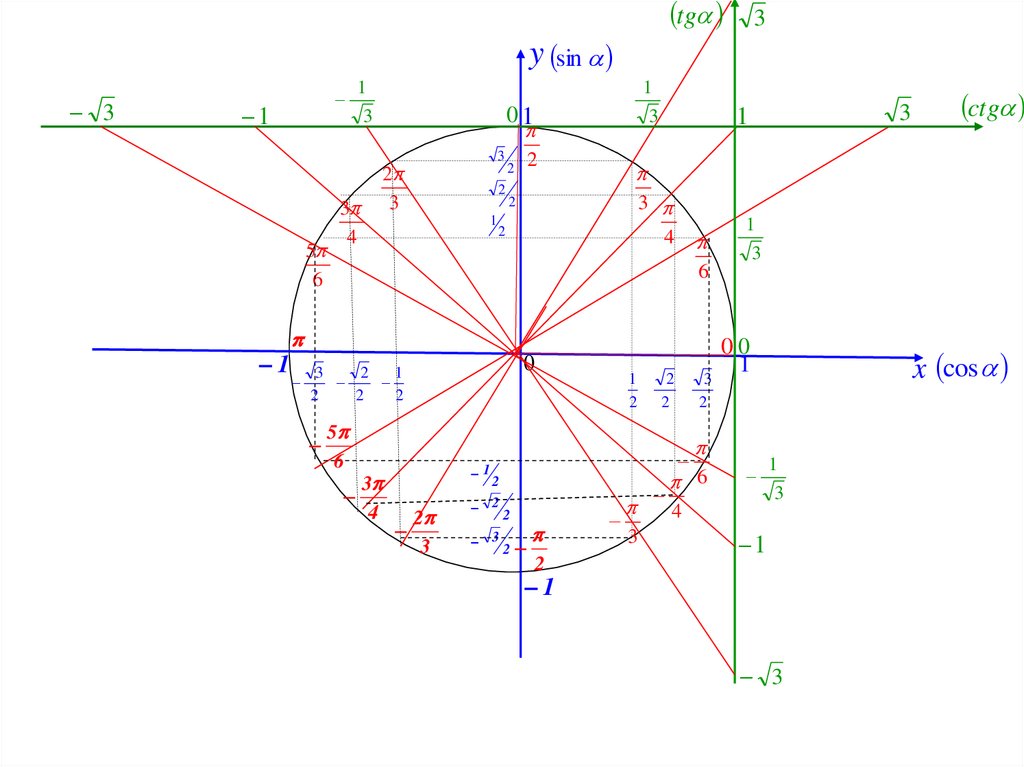
Теорема синусов в формуле:
Угол поворота.
Как уже говорилось выше определения, которые мы рассмотрели относятся к острым углам треугольника. Но существует и понятие угол поворота, в котором исчисляемый угол не будет равен значению от 0 градусов до 90. При этом угол поворота может быть любым числом, от +бесконечности и до — бесконечности.
В данной связи можно выдвинуть определение синуса, косинуса, тангенса и котангенса угла любой величины. Для этого представим окружность в системе координат с двумя взаимно перпендикулярными осями.
Заданная точка А, имеющая координатные значения 1,0, делает поворот вокруг центра оси на угол α, переходя в точку А1. рассматривая определение через координаты А1(х, у).
Sin угла поворота α, это ордината точки А1(х, у), то есть sinα=у
Косинус α — абсцисса точки А1 (cosα=х)
Tg данного угла — ‘это деление (отношение) ординаты А1 к абсциссе. tgα=у\х
Котангенс поворотного угла α — отношение её абсциссы к ординате, ctgα=х\у
Заметим, что синус и косинус можно выделить для любого угла, а вот тангенс и котангенс нет.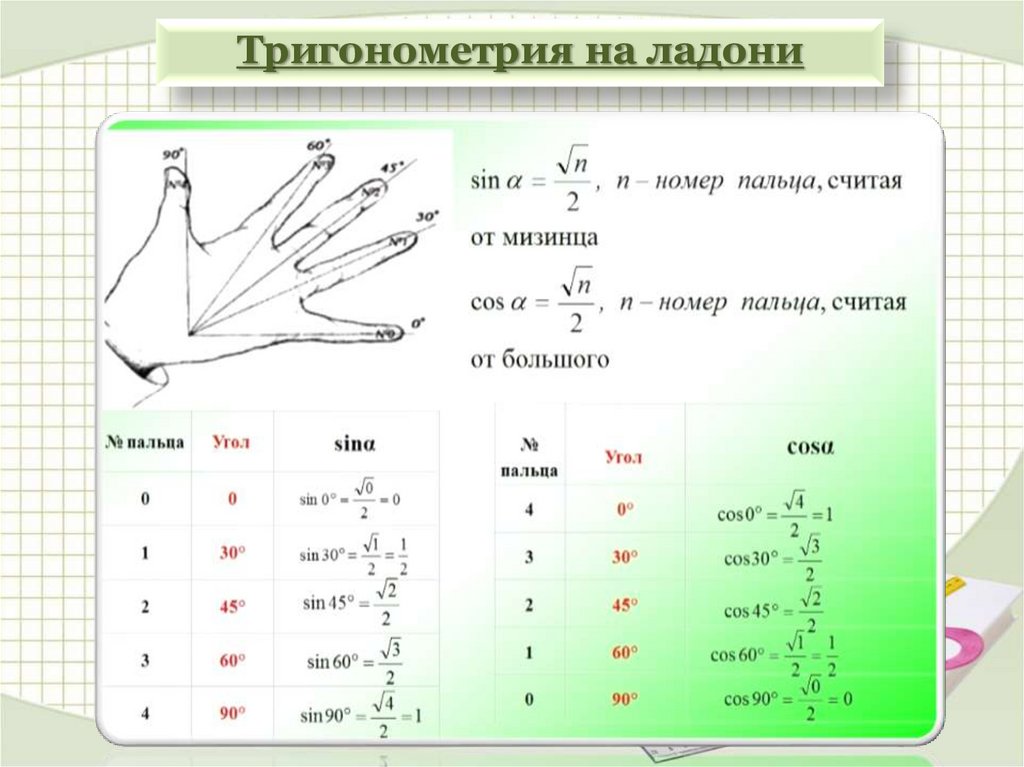 И это абсолютно логично, так как при переходе точки в значение ноля для абсциссы, тангенс посчитать невозможно, так как невозможно деление на 0. Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
И это абсолютно логично, так как при переходе точки в значение ноля для абсциссы, тангенс посчитать невозможно, так как невозможно деление на 0. Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
Sin и cos можно вычислить для любых углов α. тогда как tg всех кроме α = 90°+180°* k, k ∈ Z ( α = π 2 + π * k, k ∈ Z ) α=90°+180°*k, k∈Z (α=π2+π*k, k∈Z)
Котангенс так же можно вычислить не для всех углов, например для α = 180 ° * k, k ∈ Z ( α = π * k, k ∈ Z, это сделать нельзя.
Отметим, что на практике при решении примеров словосочетание угол поворота опускается из речевого оборота.
Для удобства существуют таблицы значений часто используемых углов, которые вычисляются в тригонометрических функциях, к примеру, для первой четверти круга:
| 0° | 30° | 45° | 60° | 90° | |
| Sin | 0 | 1 2 | √2 2 | √3 2 | 1 |
| Cos | 1 | √3 2 | √2 2 | 1 2 | 0 |
| Tg | 0 | 1 √3 | 1 | √3 | – |
| Ctg | – | √3 | 1 | 1 √3 | 0 |
Здесь можно посмотреть таблицу синусов, косинусов и других функций.
Вычисление тригонометрических функций числа
В данном пункте рассмотрим случай, когда определение рассматриваемых нами функций тригонометрии, происходит из числового значения, а не угла. Таких подходов два:
Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону. На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки. Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.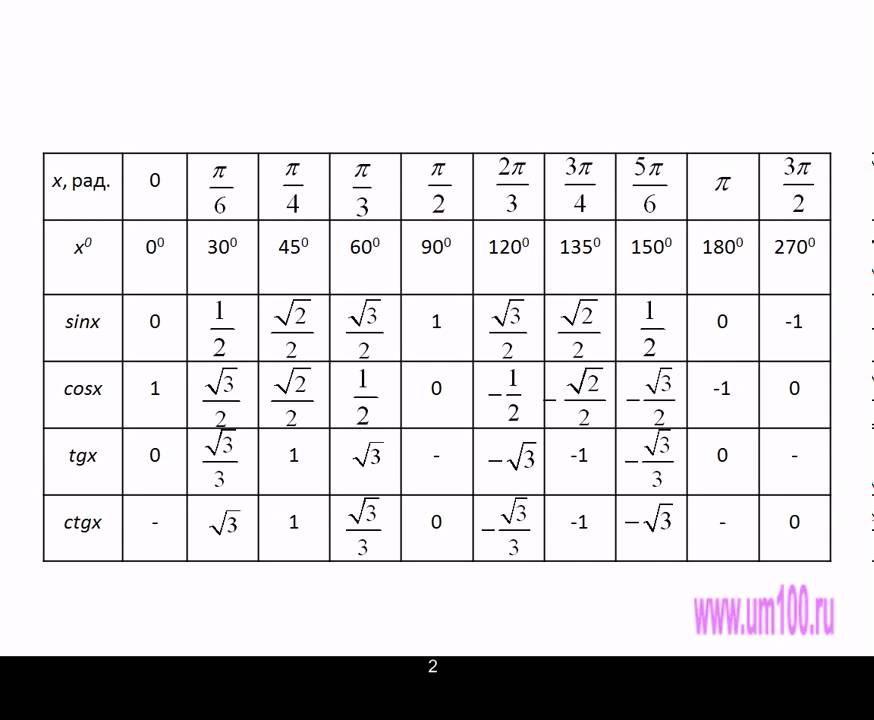
В связи с этим выделяют следующие функции:
- (sin f = y) Синус числа f — определяется ординатой точки единичной окружности, которая равна числу f; (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f; (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
Функции аргумента угла и числа
Каждому значению угла а, существует своё значение sin, сos, данного угла, которое ему соответствует. А также углам α, кроме от α = 90 ° + 180 ° * k, k ∈ Z ( α = π 2 + π * k, k ∈ Z ) будет соответствовать определенное значение тангенса. Так же котангенс α, кроме α = 180 ° * k, k ∈ Z ( α = π * k, k ∈ Z ).
Из чего следует что синус а, косинус а, тангенс а, котангенс а — это и есть функции углового аргумента.
Точно также определяются функции числового аргумента. Выбранное любое действительное число, имеет своё соответственное значение функций тригонометрии, все кроме перечисленных исключений.
Теорема синусов в формуле:
Как уже говорилось выше определения, которые мы рассмотрели относятся к острым углам треугольника. Но существует и понятие угол поворота, в котором исчисляемый угол не будет равен значению от 0 градусов до 90. При этом угол поворота может быть любым числом, от +бесконечности и до — бесконечности.
Но существует и понятие угол поворота, в котором исчисляемый угол не будет равен значению от 0 градусов до 90. При этом угол поворота может быть любым числом, от +бесконечности и до — бесконечности.
В данной связи можно выдвинуть определение синуса, косинуса, тангенса и котангенса угла любой величины. Для этого представим окружность в системе координат с двумя взаимно перпендикулярными осями.
Заданная точка А, имеющая координатные значения 1,0, делает поворот вокруг центра оси на угол α, переходя в точку А1. рассматривая определение через координаты А1(х, у).
Sin угла поворота α, это ордината точки А1(х, у), то есть sinα=у
Косинус α — абсцисса точки А1 (cosα=х)
Tg данного угла — ‘это деление (отношение) ординаты А1 к абсциссе. tgα=у\х
Котангенс поворотного угла α — отношение её абсциссы к ординате, ctgα=х\у
Заметим, что синус и косинус можно выделить для любого угла, а вот тангенс и котангенс нет. И это абсолютно логично, так как при переходе точки в значение ноля для абсциссы, тангенс посчитать невозможно, так как невозможно деление на 0. Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
Sin и cos можно вычислить для любых углов α. тогда как tg всех кроме α = 90°+180°* k, k ∈ Z ( α = π 2 + π * k, k ∈ Z ) α=90°+180°*k, k∈Z (α=π2+π*k, k∈Z)
Котангенс так же можно вычислить не для всех углов, например для α = 180 ° * k, k ∈ Z ( α = π * k, k ∈ Z, это сделать нельзя.
Отметим, что на практике при решении примеров словосочетание угол поворота опускается из речевого оборота.
Для удобства существуют таблицы значений часто используемых углов, которые вычисляются в тригонометрических функциях, к примеру, для первой четверти круга:
| 0° | 30° | 45° | 60° | 90° | |
| Sin | 0 | 1 2 | √2 2 | √3 2 | 1 |
| Cos | 1 | √3 2 | √2 2 | 1 2 | 0 |
| Tg | 0 | 1 √3 | 1 | √3 | – |
| Ctg | – | √3 | 1 | 1 √3 | 0 |
Здесь можно посмотреть таблицу синусов, косинусов и других функций.
При этом угол поворота может быть любым числом, от бесконечности и до бесконечности.
Www. napishem. ru
24.09.2019 19:06:02
2017-03-14 04:37:29
Источники:
Https://www. napishem. ru/spravochnik/matematika/opredeleniya-v-trigonometrii-sinus-kosinus-tangens-kotanges. html
Применение тригонометрических функций
История тригонометрических функций
Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
В1770 г. появилось и удерживается до наших дней название Тригонометрические функции. Его ввел Г. С. Клюгель в работе “Аналитическая тригонометрия”.
Определение и графики тригонометрических функций
|
Величины углов (аргументы функций): α, x |
Радиус круга: r |
- Тригонометрические функциипредставляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике.
 Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. - К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанси косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
- Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OMи положительным направлением оси Ox равен α.
Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/rТангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой.
 Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1 -
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
синуса, косинуса, тангенса и котангенса
Синус острого угла α прямоугольного треугольника – это отношение противолежащего
катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего
катета к гипотенузе.
Обозначается так: cos α.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a . Сторона с – гипотенуза. β – второй острый угол).
b | sin 2 α + cos 2 α = 1 | |
a | 1 | |
b | 1 | |
a | 1 1 | |
sin α |
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение :
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.
Решение .
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = — = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Открытый урок по теме «Синус, косинус, тангенс и котангенс»
Цели урока:
- Образовательные: ввести понятие тригонометрических функций синуса, косинуса, тангенса и котангенса, как координат точки единичной окружности; определить множество значении этих функций; рассмотреть перевод градусной меры измерения улов в радианную меру и наоборот; сформировать умение определять знаки тригонометрических функций; рассмотреть зависимости между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента; научить находить значения тригонометрических функций по тригонометрической окружности выполнять действия с тригонометрическими функциями.

- Развивающие: развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки.
- Воспитательные: воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.
Тип урока: комбинированный.
Форма работы: фронтальная и индивидуальная.
Методы обучения: диалогическое изложение материала с использованием ИКТ.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал, презентация к уроку.
I. Организационный момент. (2 мин.)Проверить готовность группы и кабинета к уроку. Настроить учащихся на тему урока.
Открываем тетради. Записываем сегодняшнее число и тему нашего урока: «Синус, косинус, тангенс, котангенс».
Все новое и необычное всегда привлекает к себе и люди, пусть даже неосознанно, стремятся это узнать. Таджикский поэт Рудаки так говорил об этом:
Таджикский поэт Рудаки так говорил об этом:
С тех пор как существует мирозданье,
Такого нет, кто б ни нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек!
Сегодня мы начинаем изучать тригонометрию. Тригонометрия – это греческое слово и в переводе означает измерение треугольников. Возникновение тригонометрии было связано сземле измерением, астрономией, строительным делом. Выходит, что знание и понимание этой темы важно не только для будущей сдачи экзамена по математике, но для освоения и выбранной вами профессией.
II. Активизация знаний. (3 мин.)С этим разделом математики вас познакомили учителя на уроках геометрии при изучении отношений между сторонами и углами в прямоугольном треугольнике.
Давайте вспомним: какие понятий связывают стороны и острые углы прямоугольного треугольника?
Итак, синус, косинус, тангенс и котангенс – это некоторые числа. Причем для каждого угла свои и их значение зависит только от величины угла.
Причем для каждого угла свои и их значение зависит только от величины угла.
Также вам уже известно, что синус, косинус, тангенс и котангенс называют тригонометрическими функциями, и мы можем их найти по величине угла или наоборот найти величину угла, если нам известно значение одной из этих функций. Для этого существуют специальные таблицы Брадиса. Правда, в настоящее время мы обращаемся к ним редко, а скажите почему?
III. Историческая справка. (2 мин.)Понятие синуса угла, как отношение отрезков треугольника появилось уже 3 веке до нашей эры в работах математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В 1 веке нашей эры оно исследовалось Минелаем, но еще не получило своего сегодняшнего названия. В 4-5 веках индийский ученый Ариабхаты ввел специальный термин джива – «тетива», который при переводе арабских текстов на латынь был заменен синусом, что означает изгиб, кривизна.
Слово косинус намного моложе. Косинус – это сокращение латинского выражения, которое означает «дополнительный синус».
Абу-Абдалах, арабский астроном и математик 10 века, наблюдая за солнечными часами, создал первые таблицы таких тригонометрических функций, как тангенс и котангенс, не вводя эти понятия. Сам термин, в переводе с латинского означающий «отрезок касательной» был введен только в 1583 году датским математиком Томасом Финком.
IV. Изложение нового материала. (25 мин.)Сегодня на уроке мы продолжим изучать эти тригонометрические функции, а также познакомимся с тригонометрической окружностью, рассмотрим понятие этих функций с помощью окружности, научимся находить по ней значения функций, их знаки, вспомним основные тригонометрические тождества и разберем, как их применять для решения задач.
Рассмотрим окружность единичного радиуса центр, которой совпадает с началом прямоугольной системы координат. Это означает, что у нас есть знакомые нам ось абсцисс (ось х) и ось ординат (ось у). Центр окружности мы совместили с началом координат. Наша окружность единичная, то есть радиус у нее равен 1. Значит, координаты точек пересечения с окружностью будут равны 1 и -1 на каждой оси. Возьмем точку с координатами (1;0), которая будет двигаться по нашей окружности, обозначим ее . За положительное направление выбирают движение против часовой стрелки, за отрицательное движение по часовой стрелке. Начальное положение, которое занимает наша точка, примем за начало отсчета пути, пройденного точкой по окружности. Пусть точка двигается против часовой стрелки, то есть в положительном направлении. При движении по окружности она займет положение точки М, которая будет иметь координаты (х; у), так как точка расположена в координатной плоскости. Проведем к этой точке радиус и угол между этой точкой М и радиусом обозначим . Значит, положение точки М мы можем задать двумя способами: с одной стороны координатами (х; у), так как точка лежит в координатной плоскости и с другой стороны с помощью угла поворота этой точки вокруг начала координат. И если мы можем положение точки задать двумя способами, значит между ними, должна быть какая-то связь.
Значит, координаты точек пересечения с окружностью будут равны 1 и -1 на каждой оси. Возьмем точку с координатами (1;0), которая будет двигаться по нашей окружности, обозначим ее . За положительное направление выбирают движение против часовой стрелки, за отрицательное движение по часовой стрелке. Начальное положение, которое занимает наша точка, примем за начало отсчета пути, пройденного точкой по окружности. Пусть точка двигается против часовой стрелки, то есть в положительном направлении. При движении по окружности она займет положение точки М, которая будет иметь координаты (х; у), так как точка расположена в координатной плоскости. Проведем к этой точке радиус и угол между этой точкой М и радиусом обозначим . Значит, положение точки М мы можем задать двумя способами: с одной стороны координатами (х; у), так как точка лежит в координатной плоскости и с другой стороны с помощью угла поворота этой точки вокруг начала координат. И если мы можем положение точки задать двумя способами, значит между ними, должна быть какая-то связь. То есть координаты точки (х; у) и величина угла должны быть связаны некоторой функцией. Таким образом, у нас появляются тригонометрические функции, которые выражают зависимость между координатами точки единичной окружности в системе координат и углом поворота, при помощи которого мы попадаем из нашей начальной точки при движении, в точку М. Выразим эту зависимость, определяя, координаты точки М. Опускаем перпендикуляры на координатные оси. Получаем прямоугольный треугольник.
То есть координаты точки (х; у) и величина угла должны быть связаны некоторой функцией. Таким образом, у нас появляются тригонометрические функции, которые выражают зависимость между координатами точки единичной окружности в системе координат и углом поворота, при помощи которого мы попадаем из нашей начальной точки при движении, в точку М. Выразим эту зависимость, определяя, координаты точки М. Опускаем перпендикуляры на координатные оси. Получаем прямоугольный треугольник.
Применим уже известные нам отношения между сторонами и углами прямоугольного треугольника и получим, что координата х (абсцисса) точки М будет равна:
, . Так как у нас единичная окружность, то ОМ=1. Ордината у точки М находится аналогично и будет равна: , у=
Для функций тангенс и котангенс получаем следующие равенства из того же прямоугольного треугольника:
Итак, косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующей данному углу α.
Получаем, что ось х – это ось косинуса, ось у – это ось тангенса. Функции тангенс и котангенс также имеют свои оси. Осью тангенсов является касательная к единичной окружности в точке с координатой (1; 0), а осью котангенсов — касательная к окружности в точке с координатой (0; 1) и значит значения этих функций находят по данным осям.
Так как синус и косину это по сути координаты точки на единичной окружности и из ее рассмотрения видно, что они лежат в пределах от -1 до 1, то можем сделать вывод, о том какие значения могут принимать наши функции:
Зная это мы, можем ответить на вопрос: может ли .
Значение угла может быть любым: отминус бесконечности до плюс бесконечности.
Обратимся к нашему треугольнику и вспомним теорему Пифагора. Радиус единичной окружности — это гипотенуза треугольника, а ее катеты равны соответственно и . Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством:
Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством:
А сейчас давайте разберемся, как нам определять знаки тригонометрических функций. Это не сложно. Знаки тригонометрических функций соответствуют знакам координат точки единичной окружности. Координатные оси разбивают всю координатную плоскость и окружность на четыре координатные четверти. Нумерация четвертей совпадает с началом движения точки по окружности в положительном направлении, то есть против часовой стрелки. (далее указываем по рисунку номера четвертей). Границы наших четвертей: от точки – это до , от до , от до , от до .
Определим знаки тригонометрических функций в каждой четверти, для этого заполним таблицу:
| I | II | III | IV | |
| + | + | — | — | |
| + | — | — | + | |
| + | — | + | — | |
| + | — | + | — |
Вы уже знаете, что величины углов могут измеряться в радианной мере и градусной мере. А. А это означает, что вы должны уметь переходить от радианной меры измерения угла к градусной.
А. А это означает, что вы должны уметь переходить от радианной меры измерения угла к градусной.
Углом в 1 радиан это центральный угол, который опирается на дугу, равную радиусу. Длина окружности равна: . То есть в нашей окружности помещается ровно два пи дуг длина которых равна радиусу и значит, во всей нашей окружности помещается два пи углов в один радиан. Вся окружность равна . Значит, соответствует радианам, а соответствует радиан.
При переходе от радианной меры к градусной и наоборот проще всего использовать это соотношение:.
Выразить радианы в градусы несложно, достаточно вместо подставить и вычислить. Например:
.
В случае, когда надо перейти от градусной меры в радианную можно применять формулу: Но формулы имеют свойство забываться, поэтому я предлагаю вам при необходимости составлять пропорцию.. Например, выразим 30 в радианах:
Наиболее часто употребляемыми углами являются углы в . Давайте переведем их в радианы и запишем на нашей окружности. Углы в находятся в первой четверти и составляют от него третью часть, половину и две третьих.
Давайте переведем их в радианы и запишем на нашей окружности. Углы в находятся в первой четверти и составляют от него третью часть, половину и две третьих.
Так как значение , значит , значит , следовательно, на окружности точка 1 расположена выше . Значение , , , .
Значит, если мы хотим найти угол в 2 радиана, то видим, что он лежит между значениями 1,57 и 3,14, то есть во II четверти. Не забывайте, что угол мы отмечаем от положительного направления оси ОХ. Соответственно угол в -1 радиан лежит в IV четверти. Также мы определяем, где лежит угол в , -. Для определения четверти для углов, равных или мы должны определить, какая из них правильная дробь, а какая неправильная дробь. Правильную дробь сравнить со значением и если она больше ее, то угол лежит во второй четверти (или наоборот), а неправильную дробь со значением и если она меньше его, то угол лежит в третьей четверти. В итоге получаем, что .
Мы, с вами рассматривая, новый материал при помощи единичной окружности выяснили, что ее еще называют тригонометрической, так как координатами точки на окружности являются функции синус, косинус, тангенс и котангенс. Определили, что синус и косинус могут принимать значения только от -1 до 1, а тангенс и котангенс от – бесконечности до + бесконечности. Рассмотрели координатные четверти, их границы, как найти в какой четверти лежит угол, разобрали, как связаны между собой радианы и градусы. При этом наша тригонометрическая окружность изменялась, обрастала все новыми значениями. Если бы мы продолжили работу по нахождению значений координат точки и углов, соответствующих координатам по нашей окружности, то она бы приняла вот такой вид. (Идет демонстрация слайда с единичной окружностью и говорится, что такие же окружности есть у вас на столах, для удобства в работе).
Определили, что синус и косинус могут принимать значения только от -1 до 1, а тангенс и котангенс от – бесконечности до + бесконечности. Рассмотрели координатные четверти, их границы, как найти в какой четверти лежит угол, разобрали, как связаны между собой радианы и градусы. При этом наша тригонометрическая окружность изменялась, обрастала все новыми значениями. Если бы мы продолжили работу по нахождению значений координат точки и углов, соответствующих координатам по нашей окружности, то она бы приняла вот такой вид. (Идет демонстрация слайда с единичной окружностью и говорится, что такие же окружности есть у вас на столах, для удобства в работе).
Разберем, как работать с этой окружностью. Нахождение значений угла или функции напоминает нахождение координаты точки по графику или определение положения точки по заданным координатам.
Например, найдем, чему будут равны:
При помощи круга мы можем находить значения углов не только до 360, но и больших, так движение по кругу напоминает движение по спирали: один оборот, второй оборот и так далее. Например, найдем, чему равны значения функций:
Например, найдем, чему равны значения функций:
Вы должны находить значение тригонометрических функций по известному значению одной из них. Например, найти чему будет равен косинус, тангенс или котангенс какого-то угла, если синус этого же угла принимает такое-то значение. Для этого надо знать формулы, которые связывают известную и неизвестную величины. В тригонометрии их называют тригонометрические тождества.
Вот основные из них: это основное тригонометрическое тождество, мы его с вами вывели ранее вместе с вот этим формулами: . А вот эти три тождества вытекают из предыдущих:
V.
Первичное закрепление материала. (10 мин.)Мы рассмотрели тригонометрические функции, но еще Жан Жак Руссо говорил, что час работы научит больше, чем день объяснения. Значит, пора переходить к решению упражнений. Но перед этим давайте еще раз коротко обговорим, какие новые знания мы сегодня получили и должны запомнить. Проведем блиц опрос по рассмотренному материалу.
Проведем блиц опрос по рассмотренному материалу.
Устная работа (повторение теории). Вопросы для учащихся.
- Какие тригонометрические функции мы рассматривали?
- Как определяют функцию синус, косинус, тангенс, котангенс?
- На какой оси находятся значения синуса, косинуса, тангенса котангенса?
- В каких пределах может изменяться значение синуса, косинуса, тангенса и котангенса?
- В какой четверти косинус больше 0, синус отрицателен, тангенс положителен, а котангенс меньше нуля?
- Что необходимо знать, чтобы определить знак функции?
- Какое направление считается положительным, а какое отрицательным?
- В каких единицах может выражаться угол?
- Как выполнить переход от радианной меры к градусной и наоборот?
Устная работа (решение упражнений). Задания для устной работы.
- Верно ли равенство: ?
- Определите знак функции: ?
- Переведите радианную меру угла в градусную: .

- Найдите при помощи круга значение функций, объясните ответ: .
- Найдите при помощи круга значение синуса, косинуса, тангенса, если величина угла равна:
После окончания устной работы, отметить активных учащихся, поставить оценки за первый урок.
VI. Решение упражнений, работа по учебнику. (25 мин.)Работа по решению упражнений идет у доски с вызовом учащихся и на местах. Каждое задание при наличии времени желательно разобрать перед решением.
1 задание: №3 ( а и в) из учебника «Алгебра 10-11» Колмогорова.
а)
б) .
2 задание: текст задания дан на слайде презентации: найдите знак произведения:
а)
б)
в)
г)
3 задание: № 7 (а) по учебнику.
Найдите: , , .
Решение.
Так угол лежит в 3 четверти, то
Ответ: 0,6 ;; .
VII. Самостоятельная работа. (15 мин.)Выполняется на листах через копирку. После решения работа первый раз проверяется учащимися в виде взаимопроверки, выставляются следующие оценки: за 3 задания –«3», за 4 задания – «4», за все 5 заданий оценка 5.
Задания для самостоятельной работы.
I вариант.
- Выразите в градусной мере величину угла: .
- Выразите величину угла в радианах: .
- Найдите знак произведения, используя правило знаков по четвертям: .
- Вычислите значение выражения:.
- Найдите значение функции , если и .
II вариант.
- Выразите в градусной мере величину угла: .

- Выразите величину угла в радианах: .
- Найдите знак произведения, используя правило знаков по четвертям: .
- Вычислите значение выражения: .
- Найдите значение функции , если и .
Задание на дом вывести на слайд презентации: по учебнику № 31 (а и в), № 15 (г), № 3 (в и г).
IX. Рефлексия. (3 мин.)Подвести итоги урока, проведя беседу с учащимися по вопросам: что узнали, что решали?
Приложение
Тригонометрические функции и их графики: кофункции
Синус и косинустангенс
Purplemath
Как мы видели на двух предыдущих страницах, определения отношений синуса, косинуса и тангенса можно расширить, создав синус, косинус, и касательные функции. Мы можем сделать то же самое с другими отношениями; а именно, секанс, косеканс и котангенс.
(Примечание: легко сказать, что котангенс соответствует тангенсу, но что насчет других? Я держу их прямыми, помня, что косеканс есть величина, обратная отношению к синусу, а секанс есть обратная величина косинуса. Другими словами, я держу их прямыми, помня, что их соответствие не имеет для меня смысла. Я имею в виду, не должно ли ко- идти с ко-? Но нет.)
Другими словами, я держу их прямыми, помня, что их соответствие не имеет для меня смысла. Я имею в виду, не должно ли ко- идти с ко-? Но нет.)
Содержание продолжается ниже
MathHelp.com
График функции косеканса
Коэффициент косеканса является величиной, обратной отношению синуса. Мы создаем функцию косеканса , взяв обратное значение функции синуса (кроме случаев, когда синус равен нулю). И это дает нам полезную информацию для понимания и построения графика функции косеканса.
Поскольку косеканс является обратной величиной синуса, тогда, когда синус равен нулю, косеканс будет неопределенным, потому что мы не можем делить на ноль. Функция синуса имеет нулевое значение при каждом кратном π, поэтому функция косеканса будет иметь вертикальную асимптоту при каждом кратном π. Синусоида колеблется между y — значения −1 и +1. Обратное значение каждого из этих значений равно самому себе, поэтому косеканс будет принимать те же значения при тех же значениях угла.
Если функция синуса положительна, она находится в диапазоне от 0 до +1; обратные значения этих значений находятся между +1 и всегда вверх, поднимаясь по вертикальной асимптоте «до» бесконечности. (Бесконечность на самом деле не является числом, поэтому график косеканса никогда не «достигнет» бесконечности; его значения и будут становиться все больше и больше.) И наоборот, когда функция синуса отрицательна, она находится между 0 и −1; обратные величины этих значений находятся в диапазоне от -1 до бесконечности, уменьшая вертикальную асимптоту «до» -бесконечности. (И нет, −бесконечность тоже не число.)
Подводя итог, мы видим, что всякий раз, когда синус достигает своего максимального значения 1, косеканс достигает своего минимального значения 1; всякий раз, когда синус достигает своего минимального значения -1, косеканс достигает своего максимального значения -1. Везде, где синус положительный, но меньше 1, косеканс будет положительным, но больше 1, поднимаясь по асимптотам; везде, где синус отрицателен, но больше -1, косеканс будет отрицательным, но меньше -1, уменьшая асимптоты.
Итак, чтобы построить график моей функции косеканса, я сначала слегка нарисую синусоиду:
← пролистните , чтобы просмотреть полное изображение →
Везде, где синус пересекает ось x , я нарисую вертикальные асимптоты для косеканс. И я нарисую точки в максимальных/минимальных точках синусоиды, так как это будут минимальные/максимальные точки графика косеканса:
← пролистните , чтобы просмотреть полное изображение →
Везде, где синус положителен, так же и его обратный, косеканс; везде, где синус отрицателен, также и косеканс. Я могу использовать эту информацию, чтобы заполнить остальную часть графика косеканса:
← пролистните для просмотра полного изображения →
Образец косеканса повторяется на той же длине, что и синус, поэтому период косеканса совпадает с периодом синуса 2π. Но, как и в случае с тангенсом (и его вертикальными асимптотами), понятие «амплитуда» не применяется к косекансу.
Примечание. Не бойтесь слегка рисовать карандашом график синуса (как я сделал выше) перед рисованием графика косеканса. Вы нарисуете «официальную» диаграмму темнее, а затем, возможно, сотрете синусоидальную диаграмму, прежде чем сдать свою работу. Просто убедитесь, что вы хорошо понимаете синусоидальные волны!
Не бойтесь слегка рисовать карандашом график синуса (как я сделал выше) перед рисованием графика косеканса. Вы нарисуете «официальную» диаграмму темнее, а затем, возможно, сотрете синусоидальную диаграмму, прежде чем сдать свою работу. Просто убедитесь, что вы хорошо понимаете синусоидальные волны!
График секущих
Отношение секущих является обратной величиной отношения косинусов. Мы создаем функцию секанса , взяв обратные величины значений функции косинуса (за исключением случаев, когда косинус равен нулю). Звучит знакомо? Да, мы можем понять и построить график функции секущей, используя ту же логику, что и для функции косеканса.
Везде, где косинус равен нулю, график секущей будет иметь вертикальную асимптоту. Везде, где косинус имеет значение -1 или +1, секанс будет иметь такое же значение. На каких бы интервалах ни был положителен косинус, таким же будет и секанс; на промежутках, где косинус отрицателен, секанс будет таким же.
Итак, используя те же рассуждения и методы, которые мы использовали с синусоидой и графиком косинуса, я начинаю свой график секущих, слегка нарисовав волну косинуса. Везде, где косинус пересекает ось x , я рисую вертикальную асимптоту; везде, где косинус находится в точке максимума/минимума, я рисую соответствующую точку минимума/массы секанса. Затем я рисую то, что выглядит как U-образные кривые множества-объединения и множества-пересечения между парами асимптот. Это позволяет мне построить график секущих:
Везде, где косинус пересекает ось x , я рисую вертикальную асимптоту; везде, где косинус находится в точке максимума/минимума, я рисую соответствующую точку минимума/массы секанса. Затем я рисую то, что выглядит как U-образные кривые множества-объединения и множества-пересечения между парами асимптот. Это позволяет мне построить график секущих:
← проведите пальцем по экрану для просмотра полного изображения →
Как косинус, так и секанс: они оба имеют период длиной 2π. Как и в случае с косекансом и тангенсом, с их вертикальными асимптотами, понятие амплитуды не применяется к секансу.
(И повторяю: не стесняйтесь использовать свои знания о косинусах, чтобы облегчить себе жизнь, когда дело доходит до секущих. на графике секущих сотрите все косинусные элементы, которые, по вашему мнению, ваш инструктор может не захотеть видеть.)
График котангенса
Котангенс является обратной величиной тангенса. Везде, где тангенс равен нулю, котангенс будет иметь вертикальную асимптоту; везде, где тангенс имеет вертикальную асимптоту, котангенс будет иметь ноль. Но переворачивание дроби (то есть нахождение ее обратной величины) не меняет знак дроби. Поэтому знаки на каждом интервале (между нулем и асимптотой) будут для котангенса такими же, как и для тангенса.
Но переворачивание дроби (то есть нахождение ее обратной величины) не меняет знак дроби. Поэтому знаки на каждом интервале (между нулем и асимптотой) будут для котангенса такими же, как и для тангенса.
Чтобы построить график котангенса, я сначала делаю легкий набросок графика касательной. (Да, я все еще делаю это.) Я преобразовываю нули тангенса в вертикальные асимптоты котангенса и асимптоты тангенса в нули котангенса. Везде, где тангенс выше x -ось, котангенс тоже будет, но загибается в другую сторону; везде, где касательная находится ниже оси x , котангенс тоже будет, но изгибается вниз в другом направлении.
Собрав все вместе, мой график котангенса выглядит так:
← проведите пальцем по экрану , чтобы просмотреть полное изображение →
Котангенс имеет период π, и понятие амплитуды не применяется, как и в случае с тангенсом.
Когда вам нужно построить графики кофункций, у вас может возникнуть соблазн попытаться вычислить множество точек графика. Но все, что вам действительно нужно знать, это функции синуса, косинуса и тангенса. Возьмите то, что вы знаете, и переверните это для любой совместной функции, которую вы хотите изобразить на графике. Из этого вы можете узнать, где ваш график будет равен нулю, где он будет равен ± 1 и где у него будут вертикальные асимптоты. Зная поведение функции в нескольких точках (скажем, в x = 0, π/2, π, 3π/2 и 2π, тогда вы можете заполнить остальные. Это действительно все, что вам нужно.
Но все, что вам действительно нужно знать, это функции синуса, косинуса и тангенса. Возьмите то, что вы знаете, и переверните это для любой совместной функции, которую вы хотите изобразить на графике. Из этого вы можете узнать, где ваш график будет равен нулю, где он будет равен ± 1 и где у него будут вертикальные асимптоты. Зная поведение функции в нескольких точках (скажем, в x = 0, π/2, π, 3π/2 и 2π, тогда вы можете заполнить остальные. Это действительно все, что вам нужно.
URL: https://www.purplemath.com/modules/triggrph4.htm
Page 1Page 2
Csc Sec Cot — Formula, Table, Domain, Graph, Examples форма записи тригонометрических функций функции косеканса, секанса и котангенса. У нас есть в основном шесть тригонометрических функций — синус, косинус, тангенс, косеканс, секанс и котангенс. Csc sec cot основаны на трех других тригонометрических функциях sin, cos и tan соответственно. Поскольку csc sec cot являются величинами, обратными sin, cos, tan соответственно, их также называют обратными тригонометрическими функциями.

В этой статье мы рассмотрим концепцию csc sec cot и обсудим их домен и диапазон, формулы и построим графики. Мы также поймем тригонометрические формулы, включающие csc sec cot и их значения, и решим несколько примеров, основанных на использовании функций косеканса, секанса и котангенса для лучшего понимания.
| 1. | Что такое детская кроватка Csc Sec? |
| 2. | Детская кроватка Csc Sec Формула |
| 3. | Домен и диапазон функций косеканса, секанса и котангенса |
| 4. | Csc Sec Детская кроватка График |
| 5. | Csc Sec Детская кроватка Диаграмма |
| 6. | Идентификаторы детской кроватки Csc Sec |
| 7. | Часто задаваемые вопросы о Csc Sec Cot |
Что такое Csc Sec Cot?
Csc sec cot — три тригонометрические функции, косеканс, секанс и котангенс соответственно. Эти функции также называются обратными тригонометрическими функциями, поскольку они являются обратными функциями синуса, косинуса и тангенса соответственно. Давайте рассмотрим три функции csc sec cot по отдельности:
Эти функции также называются обратными тригонометрическими функциями, поскольку они являются обратными функциями синуса, косинуса и тангенса соответственно. Давайте рассмотрим три функции csc sec cot по отдельности:
Функция косеканса
Функция косеканса является обратной функцией синуса и наоборот. Он определяется как отношение гипотенузы к противолежащему углу прямоугольного треугольника. Косеканс — одна из шести основных тригонометрических функций, сокращенно обозначаемая как csc x или cosec x, где x — угол.
Функция секущей
Функция секущей определяется как отношение гипотенузы к прилежащей стороне угла в прямоугольном треугольнике. Это функция, обратная косинусу. Математически это записывается как sec x, где x — угол. Поскольку это величина, обратная cos, она записывается как sec x = 1 / cos x.
Функция котангенса
Функция котангенса является обратной функцией тангенса. Итак, он определяется как отношение основания и перпендикуляра прямоугольного треугольника. Обозначим функцию котангенса как ctg x, где x — угол в градусах или радианах. Поскольку кроватка является обратной величиной тангенса, мы можем записать ее как кроватка х = 1 / тангенс х.
Обозначим функцию котангенса как ctg x, где x — угол в градусах или радианах. Поскольку кроватка является обратной величиной тангенса, мы можем записать ее как кроватка х = 1 / тангенс х.
Детская кроватка Csc Sec Формула
Теперь, когда мы знаем определение функций csc sec cot, давайте пройдемся по их формулам. Мы используем эти формулы для решения различных тригонометрических задач. Формулы для csc sec cot приведены ниже:
- csc x = Гипотенуза / Перпендикуляр (ИЛИ) Гипотенуза / Противоположная сторона
- сек x = гипотенуза / основание (или) гипотенуза / смежная сторона
- кроватка x = Перпендикулярно / Основание (ИЛИ) Противоположная сторона / Смежная сторона
Мы также можем записать формулы csc sec cot через sin cos tan, как показано ниже:
- csc x = 1/sin x
- сек х = 1/cos х
- детская кроватка х = 1/тан х
Домен и диапазон функций косеканса, секанса и котангенса
Csc x определяется для всех действительных чисел, за исключением значений, где sin x равен нулю, то есть nπ, где n — целое число. Диапазоном функции косеканса являются все действительные числа, кроме (-1, 1). Областью определения sec x являются все действительные числа, кроме точек, где косинус не определен, то есть (2n + 1)π/2, где n — целое число. Диапазон функции секущей — это набор всех действительных чисел с величиной, большей или равной 1. С другой стороны, котангенс не определен для действительных чисел, где тангенс равен нулю. Функция тангенса равна нулю, где синус равен нулю. Итак, функция кроватки определена для всех действительных чисел, кроме nπ. Диапазон котангенса — все действительные числа.
Диапазоном функции косеканса являются все действительные числа, кроме (-1, 1). Областью определения sec x являются все действительные числа, кроме точек, где косинус не определен, то есть (2n + 1)π/2, где n — целое число. Диапазон функции секущей — это набор всех действительных чисел с величиной, большей или равной 1. С другой стороны, котангенс не определен для действительных чисел, где тангенс равен нулю. Функция тангенса равна нулю, где синус равен нулю. Итак, функция кроватки определена для всех действительных чисел, кроме nπ. Диапазон котангенса — все действительные числа.
В приведенной ниже таблице указаны домен и диапазон csc sec cot:
| Функция | Домен | Ассортимент |
|---|---|---|
| КСК | Р — № | (-∞, -1] U [+1, +∞) |
| сек | Р — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Детская кроватка | Р — № | (-∞, +∞) |
Csc Sec Детская кроватка График
Теперь мы знаем домен и диапазон функций csc cot sec. Давайте теперь построим их графики, нанеся точки и соединив их. Графики csc sec cot имеют вертикальные асимптоты, так как в некоторых точках они не определены.
Давайте теперь построим их графики, нанеся точки и соединив их. Графики csc sec cot имеют вертикальные асимптоты, так как в некоторых точках они не определены.
Csc Sec Детская кроватка Диаграмма
Для решения различных тригонометрических задач мы используем таблицу тригонометрии. Мы запоминаем некоторые часто используемые значения тригонометрических функций для облегчения вычислений. В приведенной ниже таблице показаны значения csc sec cot для конкретных углов, которые обычно используются для быстрых расчетов различных тригонометрических вопросов.
| Угол (в радианах) | Csc | сек | Детская кроватка |
|---|---|---|---|
| 0 | Не определено | 1 | Не определено |
| №/6 | 2 | 2/√3 | √3 |
| №/4 | √2 | √2 | 1 |
| №/3 | 2/√3 | 2 | 1/√3 |
| №/2 | 1 | Не определено | 0 |
| № | Не определено | -1 | Не определено |
| 3π/2 | -1 | Не определено | — |
| 2π | Не определено | 1 | Не определено |
| -π/2 | -1 | Не определено | 0 |
| -π | Не определено | -1 | Не определено |
Идентификаторы детской кроватки Csc Sec
До сих пор мы понимали концепцию функций косеканса, секанса и котангенса. Давайте теперь исследуем тригонометрические формулы и тождества, включающие csc sec cot. Эти тождества упрощают тригонометрические задачи и облегчают вычисления. Ниже приведен список идентификаторов csc sec cot:
Давайте теперь исследуем тригонометрические формулы и тождества, включающие csc sec cot. Эти тождества упрощают тригонометрические задачи и облегчают вычисления. Ниже приведен список идентификаторов csc sec cot:
- 1 + детская кроватка 2 x = csc 2 x
- 1 + тангенс 2 x = сек 2 x
- раскладушка x = csc x / сек x
- раскладушка x = cos x / sin x
- csc (π/2 — x) = сек x
- сек (π/2 — x) = csc x
- детская кроватка (π/2 — x) = загар x
- загар (π/2 — x) = детская кроватка x
- детская кроватка (π — x) = — детская кроватка x
- csc (π — x) = csc x
- сек (π — х) = — сек х
Приведенные выше тождества помогают нам решать тригонометрические задачи с помощью простых вычислений.
Важные примечания по Csc Sec Cot
- Csc sec cot — это сокращенные формы тригонометрических функций косеканс, секанс и котангенс соответственно.

- Csc sec cot являются обратными значениями sin cos tan соответственно.
- Произведение csc sec cot равно 1/sin 2 .
☛ Похожие темы:
- Тригонометрические тождества
- Тригонометрические уравнения
- Тригонометрические соотношения
Часто задаваемые вопросы о Csc Sec Cot
Что такое Csc Sec Cot в тригонометрии?
Csc sec cot — это тригонометрические функции, называемые косекансом, секансом и котангенсом соответственно. Csc sec cot являются обратными функциями sin cos tan соответственно.
Что такое Csc Sec Cot Formulas?
Формулы csc sec cot следующие:
- csc x = Гипотенуза / Перпендикуляр (OR) Гипотенуза / Противоположная сторона
- сек x = гипотенуза / основание (или) гипотенуза / смежная сторона
- детская кроватка x = Перпендикулярно / Основание (ИЛИ) Противоположная сторона / Смежная сторона
Что такое область определения и диапазон функций косеканса, секанса и котангенса?
Домен и диапазон csc sec cot приведены в таблице ниже:
| Функция | Домен | Диапазон |
|---|---|---|
| КСК | Р — № | (-∞, -1] U [+1, +∞) |
| сек | Р — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Детская кроватка | Р — № | (-∞, +∞) |
Как пользоваться детской кроваткой Csc Sec?
Мы можем использовать csc sec cot, подставив их формулы в задачу и тем самым упростив ее. Формулы:
Формулы:
- csc x = Гипотенуза / Перпендикуляр (OR) Гипотенуза / Противоположная сторона
- сек x = гипотенуза / основание (или) гипотенуза / смежная сторона
- детская кроватка x = Перпендикулярно / Основание (ИЛИ) Противоположная сторона / Смежная сторона
Мы также можем использовать их идентификаторы, чтобы упростить вычисления.
Что означает детская кроватка Csc Sec?
Csc sec cot обозначает функции косеканса, секанса и котангенса в тригонометрии.
Что такое Csc Sec Cot Formulas с точки зрения Sin Cos Tan?
Мы можем записать формулы csc sec cot через sin cos tan, как показано ниже:
- csc x = 1/sin x
- сек х = 1/cos х
- детская кроватка х = 1/тан х
Тригонометрические функции. Обратные тригонометрические функции
Предыдущий Следующий
Мы рассмотрели синус, косинус и тангенс. Мы эксперты по одному маленькому кусочку тригонометрической недвижимости. (Сады Марвина? Парк Плейс? Дощатый настил? Вытащите свои деньги из Монополии.) Слава вам, но это еще не все.
Мы эксперты по одному маленькому кусочку тригонометрической недвижимости. (Сады Марвина? Парк Плейс? Дощатый настил? Вытащите свои деньги из Монополии.) Слава вам, но это еще не все.
Синус, косинус и тангенс имеют обратную функцию. Взаимность, взаимность — подумайте о том, чтобы переворачивать вещи, например, гамбургеры на гриле, блины на сковородке, яйца. (Когда мы едим?) Мы уже знаем, что у правильных чисел есть обратные числа (2 и 1 / 2 являются обратными, например), но мы также можем перевернуть наши триггерные функции с ног на голову.
Косеканс является обратной величиной синуса. Его аббревиатура — csc. Чтобы определить csc, просто переверните sin.
Секанс является обратной величиной косинуса. Его аббревиатура — сек. Чтобы определить sec, просто переверните cos.
Котангенс является обратной величиной тангенса. Его аббревиатура — детская кроватка. Чтобы определить кроватку, просто переверните загар. (Попробуйте вспомнить все это, думая: «После вечера греха Джо растянулся на раскладушке на заднем дворе, а затем перевернулся, чтобы лучше загореть». Странно, но это работает.)
Чтобы определить кроватку, просто переверните загар. (Попробуйте вспомнить все это, думая: «После вечера греха Джо растянулся на раскладушке на заднем дворе, а затем перевернулся, чтобы лучше загореть». Странно, но это работает.)
И нет, они не шипят, когда их переворачивают.
Пример задачи
Если a = 8 и b = 15, найдите шесть тригональных отношений угла A .
Нам понадобится недостающая гипотенуза, поэтому сначала используйте a 2 + b 2 = c 2 , чтобы найти 900.
8 2 + 15 2 = с 2
64 + 225 = C 2
289 = C 2
C = 17
Теперь подключите эти стороны в наши отношения для SIN, COS и TAN. Помните СОХКАТОА. Мы смотрим на угол A , поэтому противоположная сторона равна 8, прилежащая сторона равна 15, а гипотенуза равна 17. Готово, вперед.
Готово, вперед.
Теперь возьмем обратные величины или перевернем каждую функцию.
Пример задачи
Каковы шесть коэффициентов триггера угла B ?
Еще раз, нам нужно отследить эту гипотенузу, прежде чем мы сможем отправиться в Тригвиль. Позвони своему приятелю Пифагору.
A 2 + B 2 = C 2
Мы знаем две ножки треугольника, так что плагин — для A и B .
3 2 + 4 2 = C 2
9 + 16 = C 2
25 = C 2
C 2 C 29000. C 2
18 2. , и тангенс угла B .
Чтобы найти обратные числа, просто переверните дроби.
Пример задачи
У равнобедренного прямоугольного треугольника две стороны длины 1. Если угол A является одним из непрямых углов, каковы синус, косинус, тангенс, косеканс, секанс и котангенс угла А ?
Если угол A является одним из непрямых углов, каковы синус, косинус, тангенс, косеканс, секанс и котангенс угла А ?
«Равнобедренный» выглядит довольно странно, но на самом деле это просто означает, что обе ноги имеют одинаковую длину. У нас нет картинки, чтобы помочь нам, но кому нужны картинки? Мы здесь математических детективов .
Итак, мы знаем обе стороны, что означает a = 1 и b = 1 в нашей теореме Пифагора. Найдем c .
1 2 + 1 2 = с 2
1 + 1 = с 2
c 2 = 2
Вот наша гипотенуза. Теперь мы знаем угол . А — это , а не , прямой угол треугольника. Это один из других парней, что означает, что его противоположная сторона и соседняя сторона равны 1. Примените триггерные коэффициенты и не забудьте рационализировать свои знаменатели.
Переворачивая дроби, чтобы найти обратные, используйте исходную дробь (с предварительно рационализированным знаменателем). Это сэкономит ваше время и душевную боль.
Это сэкономит ваше время и душевную боль.
Кофункции
Нет, вы не споткнетесь о кофункции, если окажетесь в Узле Дисфункции. Они глубоко встроены в тригонометрические функции. Вы заметили «со» в косинусе, косекансе и котангенсе?«Co» — сокращение от «дополнительный».
Co + функция = co дополнительные функции.
Вам знакомо слово «дополнительный»? Из геометрии мы узнали, что дополнительные углы в сумме образуют 9угол 0°.
Мы также знаем, что сумма углов треугольника должна быть 180°. Таким образом, если угол C является прямым углом (90°), сумма двух других углов должна составлять остальные 90°.
Поскольку A + B = 90°, A и B являются дополнительными углами.

Немного поменяв местами, мы увидим, что:
B = 90° – A
и
A = 90° – B
Теперь давайте применим наше «со» к триггерным функциям.
Косинус является co дополнительной функцией синуса.
Косеканс является co дополнительной функцией секанса.
Котангенс — это co дополнительная функция тангенса.
О чем все это? Вот сделка. Взгляните еще раз на наш треугольник:
В этом треугольнике косинус угла A равен синусу угла 9.0017 Б
cos A = sin B
Давай, позвольте этому усвоиться на секунду. Косинус — это сторона, прилежащая к гипотенузе (CAH), а синус — сторона, противоположная гипотенузе (SOH). Но сторона, примыкающая к углу A , есть то же самое , что и сторона, противолежащая углу B . Вот почему cos A = sin B . Они дают нам точно такое же соотношение.
Вот тут-то и вступают в дело совместные функции. Подстановка в B = 90° – A дает нам:
cos A = sin(90° – A )
Видите, что мы там сделали? Косинус A совпадает с синусом дополнительного угла A .
Аналогично:
CSC A = SEC B
CSC A = SEC (90 ° — A )
и:
Cot A = TAN B3
A = TAN B339393939397779. A
= TAN B3 A = TAN B3A = TAN B9001 и:
COT A = TAN B 3
A . = тангенс(90° – A )
Это работает и в обратную сторону:
sin A = cos B = cos(90° – A )
сек A = csc B – csc )
tan A = кроватка B = кроватка(90° – A )
Пример задачи
Запишите sin(30°) в терминах его кофункции.
Это намного холоднее, чем может показаться. Кофункция синуса — это просто косинус. Используя sin A = cos(90° – A ), получаем:
sin(30°) = cos(90° – 30°)
sin(30°) = cos(60°)
Да, это так. Синус 30° — это то же самое, что и косинус 60°. Вбейте их в калькулятор, если не верите нам.
Пример задачи
Запишите csc(70°) в терминах ее кофункции.
Косеканс идет рука об руку с секансом, поэтому мы снова будем использовать дополнительные углы. На этот раз формула csc A = sec(90° – A ).
csc(70°) = sec(90° – 70°)
csc(70°) = sec(20°)
Пример задачи
Запишите tan(10°) в терминах его кофункции.
Мы хотим превратить этот тангенс в котангенс, поэтому воспользуемся формулой tan A = cot(90°– A ).
tan(10°) = cot(90° – 10°)
tan(10°) = cot(80°)
Особые треугольники
углы снова и снова, до бесконечности , до тошноты . Эти углы составляют два специальных треугольника. Мы рассмотрим специальные треугольники в следующем разделе.
Эти углы составляют два специальных треугольника. Мы рассмотрим специальные треугольники в следующем разделе.
Специальные треугольники
Треугольники 45°-45°-90°
Если мы работаем с углом 45° в триггере, мы должны иметь возможность нарисовать этот эталонный треугольник.
Хитрость? Сначала нарисуйте равнобедренный прямоугольный треугольник. У равнобедренных треугольников две катеты одинаковой длины.
Обозначьте каждый катет цифрой 1. Вот так:
Тогда, благодаря теореме Пифагора, мы можем найти гипотенузу:
1 2 + 1 2 = C 2
1 + 1 = C 2
C 2
C 2 = 2
C 2 = 2
C 2 = 2
C 9038 2 = 2
C = 2 = 2
C и WAL угол и один угол 90°, мы знаем, что третий угол должен быть 180° — 90° — 45° = 45°.
Мы знаем намного больше, чем когда начинали. Мы знаем не только о триггерных функциях, но и об их дополнительных функциях. Иди к нам. Теперь, вот как мы применяем это в триангулированном мире.
При переходе от гипотенузы к катету → разделить на .
При переходе от катета к гипотенузе → умножить на .
Эти приемы работают для любого треугольника 45°-45°-90°, независимо от длины его сторон. Треугольник с двумя углами по 45° и одним по 90° всегда будет равнобедренным, а это значит, что у него всегда будут две равные стороны.
Пример задачи
Найти x.
Сначала поверните эталонный треугольник, чтобы он совпал с проблемным треугольником.
У нас есть нога. Теперь нам нужна гипотенуза. Умножить на . Ответ . Обратите внимание, что мы также могли бы использовать теорему Пифагора, если бы захотели, но этот способ был быстрее.
Пример задачи
Найти x.
Нарисуйте контрольный треугольник рядом с проблемой.
У нас есть гипотенуза. Теперь нам нужна нога. Разделить на .
Теперь нам просто нужно рационализировать знаменатель. Вы же знаете, как учителя математики ненавидят радикальную табличку в подвале.
Пример задачи
Найти x .
Это подпруга. Поскольку у нас есть угол 45° и угол 90°, это должно означать, что у нас есть равнобедренный треугольник (ноги равной длины, помните?). Ответ: 5.
Треугольники 30°-60°-90°
Если мы работаем с углом 30° или 60°, нам нужно уметь рисовать этот эталонный треугольник.
Чтобы нарисовать этого плохого мальчика, сначала нарисуйте равносторонний треугольник и обозначьте каждую сторону цифрой 2. Вот так:
Теперь разделите треугольник пополам, разделив угол при вершине пополам. Пометьте каждую половину основания цифрой 1. Вот так:
Теперь найдите высоту h . Это красная линия. Это также катет прямоугольного треугольника, так что мы можем использовать нашего главного пифагора.
1 2 + h 2 = 2 2
h 2 = 2 2 – 1 2
h 2 = 4 – 1
ч 2 = 3
Победа. У вас есть эталонный треугольник 30°-60°-90°.
Вот как все это применяется в мире триггеров.
Короткий катет равен длине гипотенузы. Или, если вы оптимист, гипотенуза в два раза длиннее короткого катета. Кстати, короткая нога всегда является стороной, противоположной углу 30°.
Чтобы перейти от короткого катета к гипотенузе → умножьте на 2.
Чтобы перейти от гипотенузы к короткому катету → разделите на 2.
Чтобы перейти от короткого участка к длинному → умножить на .
Чтобы перейти от длинного участка к короткому → разделите на .
Если у нас длинная ветвь и нам нужна гипотенуза, нам придется пройти длинный путь в обход. Сначала найдите короткий катет, а затем найдите гипотенузу.
Если у вас есть гипотенуза и вам нужен длинный катет, сначала найдите короткий катет, а затем длинный катет.
Чувак, это звучит как марафон LEGO или папино длинноногая конвенция — с цифрами. Повесить там.
Пример задачи
Найти x.
Сначала поверните опорный треугольник и нарисуйте его рядом. Как это.
У нас короткий катет и нужна гипотенуза. Умножьте короткую ногу на 2. Ответ равен 10.
Пример задачи
Найдите x.
Поверните опорный треугольник.
У нас есть короткая нога, нам нужна длинная. Умножить на . Ответ 4. Мы могли бы делать это весь день.
Пример задачи
Найти x.
У нас есть гипотенуза и нам нужен короткий катет, поэтому мы должны разделить на 2. Предыдущий Следующий
Тригонометрия
Что такое тригонометрия?
Тригонометрия, или сокращенно «Тригонометрия», — это изучение соотношений между углами
и стороны треугольников. В основном мы будем иметь дело с прямоугольными треугольниками, но все треугольники
можно анализировать с помощью триггера. Тригонометрия — жизненно важный раздел математики, потому что в нем много
реальные приложения в технике, архитектуре, оптике и многих других областях.
В основном мы будем иметь дело с прямоугольными треугольниками, но все треугольники
можно анализировать с помощью триггера. Тригонометрия — жизненно важный раздел математики, потому что в нем много
реальные приложения в технике, архитектуре, оптике и многих других областях.
Тригонометрические функции
Тригонометрические функции являются основными функциями, которые используются для описания отношений между углами и сторонами фигур.
Треугольник ниже — хороший способ визуализировать опорный угол $(\theta)$ есть, и каковы разные стороны.
Синус, косинус и тангенс
Тремя основными триггерными функциями являются функции синуса, косинуса и тангенса. Давайте
начните с рассмотрения функции синуса.
Давайте
начните с рассмотрения функции синуса.
В контексте прямого угла функция синуса, записанная как $\sin{\theta}$, равна делению противоположной стороны опорного угла $(\theta)$ на гипотенузу, или длинная сторона треугольника.
$$\sin{\theta} = \frac{\text{напротив}}{\text{гипотенуза}}$$
Аналогично функция косинуса, обозначаемая как $\cos{\theta}$, определяется как отдел прилежащей стороны к опорному углу, деленному на гипотенузу.
$$\cos{\theta} = \frac{\text{adjacent}}{\text{гипотенуза}}$$
Касательная функция, обозначаемая как $\tan{\theta}$, определяется как подразделение
противоположную сторону опорного угла соседней стороной.
$$\tan{\theta} = \frac{\text{opposite}}{\text{adjacent}}$$
Косеканс, секанс и котангенс
Поскольку ранее описанные тригонометрические функции описываются как дроби, мы можем взять обратные функции и получить 3 новые функции. Косеканс функция является обратной функцией синуса, секанс является обратной функцией Косинус и котангенс обратны тангенсу.
\begin{array}{c}
\csc{\theta} = \frac{1}{\sin\theta} = \frac{\text{гипотенуза}}{\text{adjacent}}\\
\ sec{\theta} = \frac{1}{\cos\theta} = \frac{\text{гипотенуза}}{\text{напротив}}\\
\cot{\theta} = \frac{1}{ \tan\theta} = \frac{\text{смежный}}{\text{напротив}}\\
\end{массив}
Тригонометрические тождества
Все тригонометрические функции связаны с единичным кругом, поэтому естественно
следовать, что есть способы написать их в терминах друг друга. Способ письма
тригонометрическая функция через другие тригонометрические функции называется тригонометрической
личность. Ниже приведены некоторые из наиболее распространенных тригонометрических тождеств, которые вы будете использовать.
встреча в триггерном курсе.
92\тета\\
Способ письма
тригонометрическая функция через другие тригонометрические функции называется тригонометрической
личность. Ниже приведены некоторые из наиболее распространенных тригонометрических тождеств, которые вы будете использовать.
встреча в триггерном курсе.
92\тета\\
\конец{массив}
Частные тождества
\begin{array}{c c}
\tan\theta = \frac{\sin\theta}{\cos\theta} & \cot\theta = \frac{\cos\theta}{\ sin\theta}\\
\end{массив}
Тождества кофункций
\begin{array}{c c}
\sin\theta=\cos\left(\frac{\pi}{2}-\theta\right), & \cos\theta=\sin\ влево (\ frac {\ pi} {2} — \ тета \ вправо) \\
\sec\theta=\csc\left(\frac{\pi}{2}-\theta\right), & \csc\theta=\sec\left(\frac{\pi}{2}-\theta \right)\\
\tan\theta=\cot\left(\frac{\pi}{2}-\theta\right), & \cot\theta=\tan\left(\frac{\pi}{ 2}-\theta\right)\\
\end{массив}
Полуугольные тождества
\begin{array}{c}
\sin\frac{\theta}{2}=\pm\sqrt{\frac{1-\cos\theta}{2}}\\
\cos\frac{\theta}{2}=\pm\sqrt{\frac{1+\cos\theta}{2}}\\
\tan\frac{\theta}{2}=\frac{\ sin\theta}{1+\cos\theta}=\frac{1-\cos\theta}{\sin\theta}\\
\конец{массив}
Тождества суммы/разности
\begin{array}{c}
\sin(\theta\pm\phi) = \sin\theta\cdot\cos\phi \pm \cos\theta\cdot\sin\phi \\
\cos(\theta\pm\phi) = \cos\theta\cdot\cos\phi \mp \sin\theta\cdot\sin\phi\\
\tan(\theta\pm\phi) = \frac{\tan\theta\pm\tan\phi}{1\mp\theta\theta\cdot\tan\phi}\\
\end{массив}
Как построить график синуса, косинуса и тангенса вручную ✍ | Бретт Берри | Математические лайфхаки
В нашем современном мире может показаться, что графическое отображение функций вручную — это… ну… немного архаично. Когда вы можете легко ввести любую функцию, которую вы хотите, в Desmos или Wolfram Alpha , не выходя из вашего телефона, зачем вам учиться строить графики функций от руки? Особенно более сложные функции, подобные тем, с которыми мы сталкиваемся в тригонометрии?
Когда вы можете легко ввести любую функцию, которую вы хотите, в Desmos или Wolfram Alpha , не выходя из вашего телефона, зачем вам учиться строить графики функций от руки? Особенно более сложные функции, подобные тем, с которыми мы сталкиваемся в тригонометрии?
Что ж, помимо очевидной вероятности того, что вы читаете это, потому что в каком-то курсе тригонометрии, предварительного исчисления или исчисления ваш преподаватель требует, чтобы вы рисовали графики без технологий, я хотел бы представить аргумент, что истинное понимание может быть достигнуто только через *делает*. Факт остается фактом: вы не можете выучить математику, стоя в стороне. Математика – это активный вид спорта. Вы можете читать о математике, слушать лекции, смотреть, как другие занимаются математикой, но если вы на самом деле не возьмете карандаш и бумагу и не будете бороться с задачами, вы никогда не выучите математику.
В наше время, когда мы так легко неверно истолковываем разговоры о том, что делаем, как реальное действие, математика остается одной из тех дисциплин, которые невозможно подделать. Если вы изо всех сил пытаетесь продвинуться в математике, спросите себя, действительно ли вы ПРАКТИКУЕТЕ математику или вы думаете — или говорите — о том, чтобы заниматься математикой вместо этого?
Если вы изо всех сил пытаетесь продвинуться в математике, спросите себя, действительно ли вы ПРАКТИКУЕТЕ математику или вы думаете — или говорите — о том, чтобы заниматься математикой вместо этого?
Обратите внимание, что здесь мы говорим «заниматься математикой». Точно так же, как вы занимаетесь игрой на инструменте или спортом, вы новичок, стремящийся к совершенствованию, независимо от того, на каком уровне математики вы сейчас находитесь. Да, вы неправильно понимаете проблемы. Да, вы запутаетесь. Да, у вас будут вопросы и вам понадобится помощь. Это только часть практики. 🙂
Ладно, хватит разговоров. Давайте приступим к рисованию некоторых тригонометрических графиков!
📸 insta 📸 Вы, наверное, слышали термин Родительская функция применительно к построению графиков. Родительские функции — это OG функций. Это неизменные формы ваших уравнений. Архетипы. Например, уравнение y=x является исходной линейной функцией; уравнение y=2x+1 по-прежнему является линейной функцией, но не является родительской функцией. Это измененная форма родителя, в которой мы изменили наклон и точку пересечения по оси Y.
Это измененная форма родителя, в которой мы изменили наклон и точку пересечения по оси Y.
Эта идея родительских функций применима ко всем типам функций. В тригонометрии нашими основными родительскими функциями являются: y=sin x, y=cos x, y=tan x, y=csc x, y=sec x и y=cot x.
Это функции, с которыми вы будете в основном работать в тригонометрии (хотя по мере продвижения вы можете узнать о других интересных функциях, таких как обратные или гиперболические триггерные функции). Итак, вот функции, которые мы будем сегодня изучать!
Эти три функции определенно являются звездами триггера. Вы, вероятно, помните эти функции из геометрии, когда впервые познакомились с тригонометрией прямоугольного треугольника. Хотя графики синуса, косинуса и тангенса могут показаться совершенно отличными от того, что вы изучали в геометрии, на самом деле мы просто наблюдаем новую картину той же самой геометрической концепции.
СОХ КАХ ТОА | Прямоугольный треугольник Trig Синус, косинус и тангенс по-прежнему представляют SOH CAH TOA, но в тригонметрии мы узнаем о некоторых новых и творческих способах представления этой информации.
По сути, то, что мы здесь сделали, это масштабирование наших специальных прямоугольных треугольников так, чтобы их гипотенуза была равна 1 единице длины, организация их вокруг начала координатной плоскости xy и обмен понятиями градусов на радианы (то есть просто углы измеряется относительно кругового вращения).
Когда мы разложим все эти треугольники вокруг начала координат, мы сможем соединить крайние точки, чтобы сформировать круг с радиусом в 1 единицу. Этот круг — Единичный Круг и одна из самых важных тем в тригонометрии!
Теперь точки, лежащие на окружности окружности, можно перевести в графики, которые мы будем изучать сегодня.
- Согласно SOH CAH TOA мы видим, что координата x относится к значению косинуса (выход) при заданном угле поворота (вход).
- Координата Y относится к значению синуса (выход) при заданном угле поворота (вход).
- И, наконец, тангенс можно определить как косинус, деленный на синус, поэтому частное y/x представляет собой значение тангенса (выход) при данном повороте (вход).

Теперь мы можем графически отобразить эту информацию, которую мы почерпнули из единичного круга, создав график, где ось x представляет вращение в радианах, а ось y представляет значение нашего синуса, косинуса или касательной функции при заданном угле.
Когда я пишу это, я понимаю, что это сложный набор взаимосвязей для понимания, поэтому я собираюсь составить отдельный учебник, чтобы объяснить, как все эти понятия соотносятся, но пока терпите меня !
В следующем видеоруководстве я показываю, как графически отображать функции синуса, косинуса и тангенса, используя простой шаблон и их периодический характер (т.е. повторяющийся), а затем я соотношу его с единичным кругом, чтобы вы могли видеть, эти очки приходят от 🙂
🎥 Youtube 🎥 Другие три функции, с которыми вы столкнетесь в базовой тригонометрии, — это косеканс, секанс и котангенс. Эти функции часто называют обратными значениями синуса, косинуса и тангенса , поскольку они определяются обратными (т. е. перевернутыми вверх ногами) отношениями SOH CAH TOA.
е. перевернутыми вверх ногами) отношениями SOH CAH TOA.
Мы можем использовать эти взаимные тождества, чтобы упростить построение графиков Csc, Sec и Cot на основе наших знаний о Sin, Cos и Tan. Смотри ⬇
🎥 Youtube 🎥Итак, теперь, когда мы узнали о шести стандартных родительских функциях тригонометрии, мы готовы взглянуть на то, как мы можем манипулировать родительскими функциями для создания и рисования интересных графиков вручную — что является одним из основных Причины, по которым нам нужно знать, как построить график родительских функций вручную!
Как только у вас появится четкое представление о том, как строить графики ваших родительских функций, вы можете применить некоторые основные математические принципы, чтобы получить графики для любого варианта ваших родительских функций 🙌
В следующем уроке я объясню, как мы можем изменить родительскую функцию для создания отражений по осям X и Y, горизонтального и вертикального растяжения, сжатия и смещения. Перейдите на 14 минут, чтобы увидеть три примера графических преобразований графиков тангенса, косинуса и синуса.
Перейдите на 14 минут, чтобы увидеть три примера графических преобразований графиков тангенса, косинуса и синуса.
- Ознакомьтесь с разделом Math Hacks на YouTube, чтобы найти больше практических руководств по математике , охватывающих популярные темы из алгебры, тригонометрии, предварительного исчисления и комбинаторики, новые видео добавляются еженедельно.
- Вы можете найти ряд интересных математических тем и задач прямо здесь, на Medium, просто нажмите кнопку «Подписаться»!
Спасибо, что присоединились ко мне!
❤ Бретт
Функции запуска Math.com
Функции запуска Math.com| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
Триггерные функции: Функции
Функции обычно обозначаются аббревиатурой: синус (sin), косинус (cos), тангенс (tan) косеканс (csc), секанс (sec) и котангенс (cot). Часто бывает проще запомнить триггерные функции с точки зрения только синус и косинус:
Функции обычно обозначаются аббревиатурой: арксинус (арксинус) Согласно стандартным обозначениям обратных функций (f -1 ), вы также часто будете видеть их записанными как sin -1 , cos-1 , tan -1 arccsc -1 , arcsec -1 и arccot -1 . Остерегайтесь , хотя есть и другое общепринятое обозначение, которое записывает квадрат триггерных функций, таких как (sin(x)) 2 как грех 2 (х). Это может сбивать с толку, для вас тогда может быть тогда можно подумать, что sin -1 (x) = (sin(x)) -1 , что , а не правда. Отрицательный верхний индекс здесь является специальным обозначение, обозначающее обратные функции (не мультипликативные обратные). См. также: обзор. | |||||||||||||||||||||||||||||||||
© 2000-2005 Math. |

 Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 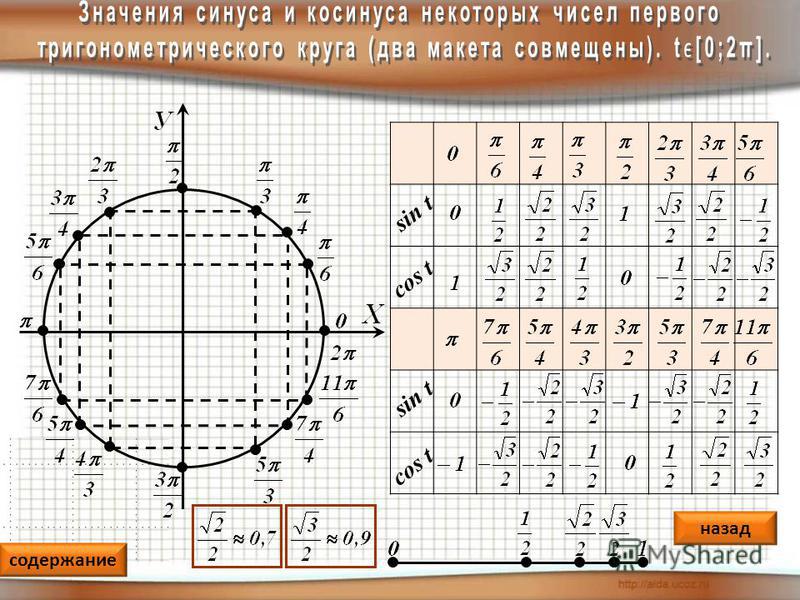

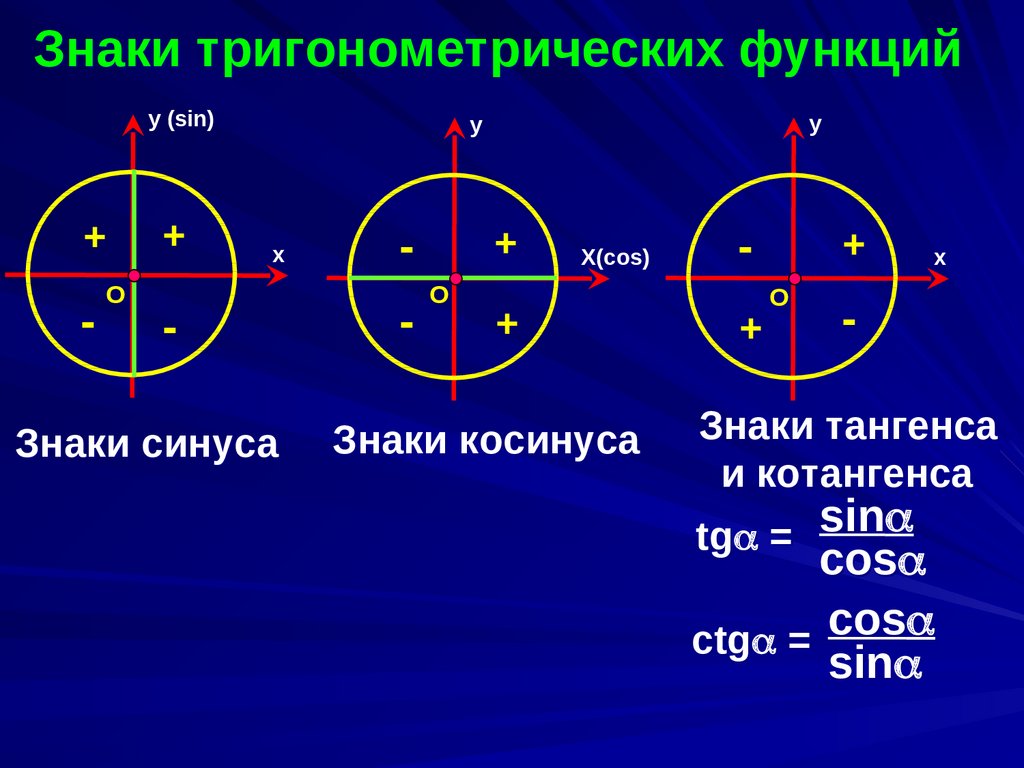 {2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
{2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
 Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
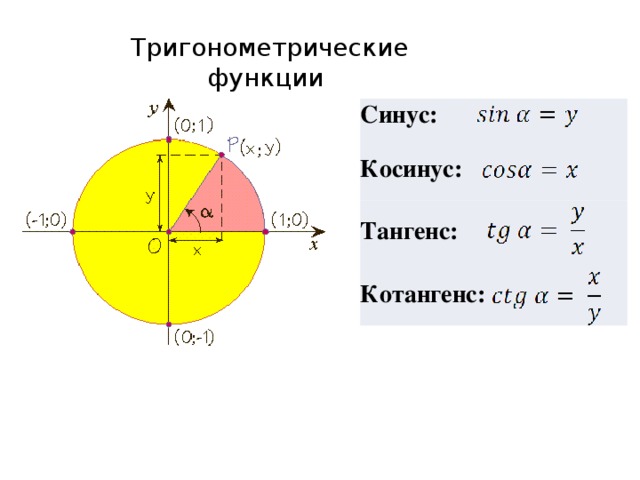 Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.
Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны. Как всё это связано между собой?
Как всё это связано между собой?
 Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
 Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.